High spatial overlap but diverging age‐related trajectories of cortical magnetic resonance imaging markers aiming to represent intracortical myelin and microstructure

Abstract

Statistical effects of cortical metrics derived from standard T1‐ and T2‐weighted magnetic resonance imaging (MRI) images, such as gray–white matter contrast (GWC), boundary sharpness coefficient (BSC), T1‐weighted/T2‐weighted ratio (T1w/T2w), and cortical thickness (CT), are often interpreted as representing or being influenced by intracortical myelin content with little empirical evidence to justify these interpretations. We first examined spatial correspondence with more biologically specific microstructural measures, and second compared between‐marker age‐related trends with the underlying hypothesis that different measures primarily driven by similar changes in myelo‐ and microstructural underpinnings should be highly related. Cortical MRI markers were derived from MRI images of 127 healthy subjects, aged 18–81, using cortical surfaces that were generated with the CIVET 2.1.0 pipeline. Their gross spatial distributions were compared with gene expression‐derived cell‐type densities, histology‐derived cytoarchitecture, and quantitative R1 maps acquired on a subset of participants. We then compared between‐marker age‐related trends in their shape, direction, and spatial distribution of the linear age effect. The gross anatomical distributions of cortical MRI markers were, in general, more related to myelin and glial cells than neuronal indicators. Comparing MRI markers, our results revealed generally high overlap in spatial distribution (i.e., group means), but mostly divergent age trajectories in the shape, direction, and spatial distribution of the linear age effect. We conclude that the microstructural properties at the source of spatial distributions of MRI cortical markers can be different from microstructural changes that affect these markers in aging.

Cortical MRI markers and their statistical effects are often thought to be driven by intracortical myelin. We report higher spatial relations of these markers with indicators of myelin and glial cells compared to neuronal cells. Comparing markers between themselves, we show generally high spatial overlap but divergent age trajectories, highlighting that the microstructural properties at the source of spatial distributions of MRI cortical markers can be different from microstructural changes that affect these markers in aging.

1. INTRODUCTION

The varying microstructural organization of the human brain is defined, in aggregate, by numerous cellular‐level compositions including the cytoarchitecture (neuronal cell bodies), myeloarchitecture (organization of myelin sheaths), iron distribution, neuronal processes, vasculature, and glial cells (Bock et al., 2009; Eickhoff et al., 2005; Fukunaga et al., 2010; Tardif et al., 2016). The observable T1‐weighted (T1w) and T2‐weighted (T2w) magnetic resonance imaging (MRI) intensities are thought to result from the underlying distributions of combinations of these microstructural properties. However, the relationship between intensity values and these biological sources is not yet completely understood (Tardif et al., 2016). The neurobiological specificity attributable to different intensities in T1w and T2w images is further confounded by experimental design choices such as MRI hardware and sequence acquisition parameters. Nonetheless, there are still some clues that allow us to better understand the underlying neurobiological basis of these signals. For instance, histological studies have demonstrated that cortical T1w signal is influenced by both myelo‐ and cyto‐architectural properties, although myelin was shown to be the main contributor to the contrast (Bock et al., 2009; Eickhoff et al., 2005). Other studies observed that myelin was the largest contributor to quantitative T1 contrast, while iron was the largest contributor to quantitative T2* contrast (Stüber et al., 2014). However, iron in cortical gray matter is mostly localized in oligodendrocytes, which are the cell bodies of myelin sheaths (Fukunaga et al., 2010). Taken together, these findings relate the cortical MRI signal mainly to myeloarchitecture in the healthy cortex.

In spite of these biophysical contrast mechanisms, several studies use metrics derived from the signal intensity as a representation of cortical “microstructure,” a non‐specific term that does not have an agreed‐upon biologically meaningful definition. Furthermore, metrics derived from T1w and T2w images are often interpreted as being influenced by myeloarchitecture, and more specifically the density or concentration of gray matter (GM) myelin (Glasser & Van Essen, 2011; Olafson et al., 2021; Salat et al., 2009). The most frequently derived cortical MRI markers of microstructure are, first, the ratio of gray‐to‐white matter T1w signal intensities (gray–white matter contrast [GWC]), as originally proposed in Salat et al. (2009), which is often used as a putative marker for myelination of deeper cortical layers (Chwa et al., 2020; Drakulich et al., 2021; Jørgensen et al., 2016; Vidal‐Piñeiro et al., 2016). Second, the ratio of T1w to T2w signal (T1w/T2w ratio), has been proposed to be more sensitive to myelin than either image alone (Glasser & Van Essen, 2011; Grydeland et al., 2013, 2019) due to the general inverse dependence of T1w and T2w signals on myelin.

In addition to these, our group developed the boundary sharpness coefficient (BSC), which examines the sharpness of the change in T1w signal intensity from superficial white matter (SWM) to cortical gray matter (Olafson et al., 2021). The BSC was inspired by methods used in cytoarchitectonic histological examinations in Avino and Hutsler (2010) and is less sensitive to confounds related to cortical curvature that can be observed in GWC. Lastly, cortical thickness (CT) measurements rely on the placement of the gray‐white matter boundary on T1w images, which is typically established by algorithms as the location where the greatest change in contrast occurs (Salat et al., 2009), thus potentially influenced by intracortical myelin density. Indeed, Natu et al. (2019) found that CT reductions in the visual cortex observed during development were driven by myelination of deep cortical layers.

These cortical measures have also been reported as being sensitive to maturation and aging (Drakulich et al., 2021; Fjell et al., 2009; Grydeland et al., 2019; Olafson et al., 2021; Salat et al., 2009, 2011; Vidal‐Piñeiro et al., 2016). Such statistical effects of GWC, T1w/T2w ratio, BSC, and to a lesser extent CT measures, are generally interpreted similarly (i.e., effects of intracortical myelin) despite an overall lack of validation with post‐mortem measures of microstructure from different modalities. As previously mentioned, other neuroanatomical properties such as cortical iron and overall cell density have been shown to affect MRI signal (Eickhoff et al., 2005; Fukunaga et al., 2010), thus potentially also impacting the statistical effects of cortical measures. Furthermore, SWM myelin could also have an impact, especially for the BSC and GWC markers, which sample intensities partly in the SWM. These other potential microstructural sources are rarely mentioned.

In humans, whole‐brain ex vivo assessments of microstructure are extremely difficult and time‐consuming to acquire. Consequently, such measurements are typically done on a single or very few subjects, resulting in inadequate sample sizes to assess the microstructural sources of subtle MRI statistical effects (Amunts et al., 2013; Hawrylycz et al., 2012). Because of this limitation, it may be more feasible to assess the similarity of statistical effects between these MRI cortical markers that have similar microstructural interpretations in the same sample with uniform MRI acquisitions and processing, with the rationale that effects driven by the same microstructural tissue property (i.e., density of intracortical myelin) should, as a minimal condition, result in similar statistical effects between the measures.

In sum, there is a need to assess the biological specificity of MRI cortical markers (i.e., GWC, T1w/T2w ratio, BSC, CT) to help validate these biological interpretations. In the first part of the manuscript, we assessed gross anatomical distribution relationships of the cortical MRI markers between themselves and with microstructural measurements derived from other modalities. More specifically, we compared the average spatial distributions of these measures with (1) the density of seven canonical cell types derived from gene expression data (Seidlitz et al., 2020), (2) overall cell density in GM and SWM from the histology‐derived BigBrain dataset (Amunts et al., 2013), and (3) quantitative R1 maps, an MRI contrast less biased by experimental choices and more specific to biophysical properties of the tissue (Marques et al., 2010; Tardif et al., 2016). In the second part of the manuscript, to better quantify the similarity between the microstructural sources of subtle MRI statistical effects across the whole cortex and to demonstrate the impact of their differential sensitivity, we compared the age effect of MRI cortical markers between themselves in a healthy population spanning the adult lifespan. More specifically, we assessed similarities and differences in age‐related trends with respect to the shape, direction, and spatial distribution of the linear age effect between the measures.

2. MATERIALS AND METHODS

2.1. Participants

A total of 174 healthy individuals were recruited across two studies, the Alzheimer's Disease Biomarkers (ADB) and Healthy Aging (HA) studies. Signed informed consent from all participants was obtained and the research protocol was approved by the Research Ethics Board of the Douglas Mental Health University Institute, Montreal, Canada. Exclusion criteria for both cohorts included a history of neurological and psychiatric illness, physical injuries such as head trauma and concussion, alcohol/substance abuse or dependence, and current drug use. Data from these two cohorts were published in previous papers from our group (Bussy, Plitman, et al., 2021; Bussy, Patel, et al., 2021; Tullo et al., 2019). The original data can be obtained through collaborative agreement and reasonable request but is not publicly available due to the lack of informed consent by these human participants. Complete demographic information of both samples is detailed in Table 1, and associated histograms for each variable are available in Figure S1.

• Alzheimer's disease biomarkers (ADB). In this cohort, subjects were recruited across the Alzheimer's disease spectrum, but only the healthy controls were included in this study. The cognition of the participants was evaluated with the Mini‐Mental State Exam (MMSE; Arevalo‐Rodriguez et al., 2015), Montreal Cognitive Assessment (MoCA; Nasreddine et al., 2005), and Repeatable Battery for the Assessment of Neuropsychological Status (RBANS; Randolph et al., 1998). Subjects with an MMSE ≥24/30 and a MoCA ≥26/30 were categorized in the control group.

• Healthy aging (HA). In this cohort, participants throughout the healthy adult lifespan were recruited. The cognitive abilities of the subjects were also evaluated with the MMSE and RBANS (but not the MoCA), and their IQ was assessed with the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 2007).

TABLE 1.

Subject demographics.

	Pre‐QC			Post‐QC			R1 subsample
	Total	ADB	HA	Total	ADB	HA	Total	ADB	HA
N	174	68	106	127	45	82	35	26	9
Mean age (years ± SD)	55.3 ± 17.6	69.9 ± 5.6	45.8 ± 16.1	53.4 ± 18.0	69.6 ± 5.7	44.5 ± 16.1	62.7 ± 13.3	70.0 ± 5.2	41.8 ± 4.9
Sex (female:male)	95:79	41:27	54:52	76:51	29:16	47:35	21:14	16:10	5:4
WASI (±SD)	104.3 ± 18.8	–	104.3 ± 18.8	105.5 ± 18.8	–	105.5 ± 18.8	102.1 ± 21.1	–	102.1 ± 21.1
MMSE (±SD)	28.6 ± 1.5	28.3 ± 1.7	28.8 ± 1.3	28.7 ± 1.5	28.2 ± 1.8	29.0 ± 1.3	28.5 ± 1.6	28.3 ± 1.8	29.0 ± 0.8
MOCA (±SD)	25.5 ± 2.7	25.5 ± 2.7	–	25.2 ± 2.8	25.2 ± 2.8	–	25.2 ± 3.0	25.2 ± 3.0	–
RBANS (±SD)	99.9 ± 13.8	97.1 ± 12.9	101.6 ± 14.0	101.3 ± 13.0	98.2 ± 13.6	102.9 ± 12.4	98.0 ± 13.0	94.5 ± 12.8	106.6 ± 9.1

Note: Demographic information by dataset before quality control (QC), after QC, and in the R1 subsample (see Section 2.2).

Abbreviations: ADB, Alzheimer's Disease Biomarkers cohort (controls only); HA, Healthy Aging cohort; MMSE, Mini‐Mental State Exam; MOCA, Montreal Cognitive Assessment; RBANS, Repeatable Battery for the Assessment of Neuropsychological Status; SD, standard deviation; WASI, Wechsler Abbreviated Scale of Intelligence.

2.2. MRI acquisition

MRI images were acquired at the Cerebral Imaging Center, associated with the Douglas Research Center in Montréal, Canada. All scans were conducted on the same Siemens Trio 3T MRI scanner using a 32‐channel head coil.

• T1‐weighted. T1w images were derived from the magnetization‐prepared rapid acquisition gradient echo (MPRAGE) sequence acquired with parameters established by the Alzheimer's Disease Neuroimaging Initiative (Jack et al., 2008); repetition time [TR] = 2300 ms; echo time [TE] = 2.98 ms; inversion time [TI] = 900 ms; flip angle [α] = 9°; GRAPPA = 2; slice thickness = 1 mm for 1 mm isotropic voxels.

• T2‐weighted. T2w images derived from the SPACE sequence with the following parameters (TR = 2500 ms; TE = 198 ms; FOV = 206 mm; slice thickness = 0.64 mm for 0.64 mm isotropic voxel dimensions). The slice partial Fourier was set to 6/8 for the T2w scan of the ADB cohort, as a means to shorten the scan time and reduce the likelihood of motion artifacts. While this technique slightly decreases the signal‐to‐noise ratio, the image contrast should not be affected (Feinberg et al., 1986), and the two T2w sequences should be directly comparable. These images were originally acquired to facilitate examination of the hippocampal subfields (Bussy, Patel, et al., 2021; Bussy, Plitman, et al., 2021).

• MP2RAGE. R1 maps were derived from the MP2RAGE sequence (Marques et al., 2010) acquired for a subset of the participants (N = 52) with the following parameters (TI1 = 700 ms; TI2 = 2000 ms, TE = 2.01 ms; TR = 5000 ms; α1 = 4°; α1 = 5°; FOV = 256 × 240 mm²; slice thickness = 0.8 mm for 0.8 mm isotropic voxels).

2.3. Image processing

2.3.1. Preprocessing

T1w images were preprocessed using the minc‐bpipe‐library (https://github.com/CobraLab/minc-bpipe-library). The procedure consists of an N4 bias field correction (Tustison et al., 2010), cropping of the neck region, and brain extraction using the BEaST algorithm (Eskildsen et al., 2012). An example of the preprocessed T1w volume for one subject is available in Figure S2. The preprocessed T1w volumes were used for the extraction of CT, GWC, and BSC measures.

2.3.2. Generation of cortical surfaces

From these outputs, the gray–white matter boundary and pial surfaces were generated with the CIVET 2.1.0 processing pipeline (https://www.bic.mni.mcgill.ca/ServicesSoftware/CIVET-2-1-0-References) (Kim et al., 2005), and were then transformed into standard MNI space using BestLinReg (Collins et al., 1994; Dadar et al., 2018).

2.3.3. Quality control

Quality control procedures for all raw scans and cortical segmentations are detailed in supplementary methods. After these procedures, a total of 127 participants (51 males and 76 females, mean age = 53.35 ± 18.04, age range 18–81) were included in the main analyses. The R1 subsample consisted of 35 participants (9 from the Healthy Aging cohort and 24 from the Alzheimer's disease Biomarkers cohort, 14 males and 21 females, mean age = 62.71 ± 13.52, age range 36–79). Other demographic variables are available in Table 1 and histograms are available in Figure S1.

2.4. Cortical marker generation

In order to extract the cortical markers, surfaces generated by CIVET were used. Figure 1 illustrates how each marker is calculated. All markers were surface smoothed with a 20 mm full‐width half‐maximum (FWHM) heat kernel and were projected onto a common cortical surface mesh (the ICBM 152‐2009b sym model) to enable cross‐subject comparisons. Additionally, analyses are rerun on markers smoothed with a 5‐mm FWHM heat kernel applied after regressing out curvature in order to assess if our results are robust to those parameter variations (see Figures S9–S13).

FIGURE 1.

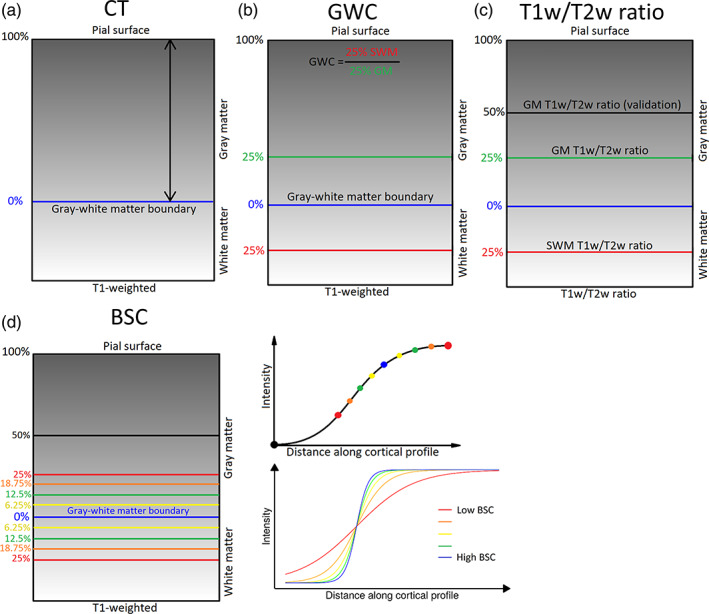
Methods for generating markers. (a) Cortical Thickness (CT) estimates were calculated as the Laplacian distance between the pial surface and the gray–white matter boundary surface at each vertex on the T1‐weighted volume in native space. (b) Gray‐white matter contrast (GWC) was calculated by dividing the intensity at 25% of CT translated into superficial white matter (SWM) by the intensity at 25% of CT into gray matter (GM) at each vertex on the T1‐weighted volume in MNI space. (c) The T1w/T2w ratio measures were generated by sampling the T1w/T2w ratio volume in native space at various distances. GM T1w/T2w ratio was sampled at 25% of CT. SWM T1w/T2w ratio was sampled at 25% of CT translated into SWM. Additionally, a second GM T1w/T2w ratio measure was sampled at 50% of CT in GM (referred to as GM T1w/T2w ratio at 50% of CT). (d) The boundary sharpness coefficient (BSC) was calculated by first sampling 10 T1‐weighted intensities in MNI space around the gray‐white matter boundary (between 50% of CT in GM and 25% of CT in SWM), then fitting a sigmoid curve to the resulting intensity profile at each vertex. The BSC represents the growth parameter of the sigmoid curve, with a higher BSC indicating a sharper gray–white matter transition and a lower BSC representing a more gradual transition.

2.4.1. Cortical thickness

CT estimates were generated with the CIVET 2.1.0 processing pipeline which calculated the Laplace distance between the gray–white matter boundary surface and the pial surface at each vertex (Figure 1a). These surfaces were subsequently used for the processing of the other markers, by providing a base from which other surfaces were generated in order to sample the intensities at various fractions of CT.

2.4.2. Gray–white matter contrast

GWC measures are calculated on the T1w volume linearly transformed in MNI space by dividing the white matter intensity sampled at a distance equivalent to 25% of the CT in the direction of white matter by the gray matter intensity sampled at 25% of the CT along the normal of the surface at each vertex (Figure 1b). The GM sampling distance was chosen because previous studies show higher rates of myelination changes in childhood at around ¼ of the cortical depth (Whitaker et al., 2016), potentially indicating a higher sensitivity to aging, while the WM sampling distance was chosen in order to minimize partial volume effects.

2.4.3. T1w/T2w ratio

The T1w/T2w ratio was developed by Glasser and Van Essen (2011) following the rationale that the T1w and T2w sequences are both sensitive to myelin, but in opposite directions (T1w signal being proportional to the quantity of myelin, while T2w signal being inversely proportional to the quantity of myelin). Hence, the ratio of those two images enhances the contrast‐to‐noise ratio of myelin (Glasser & Van Essen, 2011). To enable voxel‐by‐voxel correspondence between the two images, T2w images were rigidly registered to T1w images using BestLinReg (Collins et al., 1994; Dadar et al., 2018). The two volumes were then mathematically divided to obtain T1w/T2w ratio images. An example of the resulting volume for one subject is available in Figure S2. Subsequently, the T1w/T2w ratio values were sampled at both 25% and 50% of CT in GM at each vertex (Figure 1c). This was in order to make sure that our results were not dependent on the specific cortical depth at which the T1w/T2w ratio was sampled. However, we chose the T1w/T2w ratio at 25% of CT to be the primary GM T1w/T2w ratio analysis, as this sampling distance is the same as the GM sampling distance of the GWC, and given the higher concentration of myelin at more superficial layers previously described (Whitaker et al., 2016). Furthermore, to obtain SWM T1w/T2w ratio values, the T1w/T2w ratio was sampled at 25% of CT translated in the direction of white matter.

2.4.4. Boundary sharpness coefficient

The BSC measures the T1w intensity transition between cortical GM and SWM. Compared to the GWC, the BSC is less affected by the gray–white matter boundary placement as it quantifies the transition zone continuously, and has been shown to correlate only in limited regions to cortical curvature (Olafson et al., 2021). The computation of the BSC is explained in detail by Olafson et al. (2021). The BSC is defined as the growth parameter of a sigmoid function fit to a depth profile of 10 T1w intensity values (from 25% of CT in WM to 50% of CT in GM) along a path perpendicular to the gray‐white matter boundary surface (Figure 1d). High BSC values represent a sharper transition between gray and white matter, while low BSC values represent a more gradual transition. Values were log‐transformed in order to ensure that the assumption of a normal distribution of the general linear model was respected.

2.4.5. Mean curvature

Since cortical markers previously described have been shown to correlate with the curvature of the cortical surfaces (Olafson et al., 2021; Shafee et al., 2015), we acquired curvature estimates of the gray–white matter surface with the CIVET 2.1.0 pipeline to residualize the markers against mean curvature and limit its influence on downstream age‐related trends. This process is done after the smoothing procedure for analyses in the main text, and before the smoothing procedure in supplementary analyses (see Figures S9–S13).

2.5. Gross anatomical distribution relationships

We assessed the spatial correspondence of cortical MRI markers with cell‐specific microstructural measurements derived from other modalities in order to examine the putative biological correlates of the gross anatomical distribution of these measures. All spatial correlations between surface maps were assessed and hypothesis‐tested following the “spin test” procedure detailed in Section 2.7.

First, the average spatial distribution of each MRI cortical marker was generated by calculating the vertex‐wise mean value across subjects. Resulting surface maps were then correlated between themselves (Figure 2). Considering the wide age range of our sample (18–81 years old), we compared the spatial distribution of cortical MRI markers of younger and older participants (based on a median split, which was defined as younger or older than 57 years old) as a preliminary analysis. Since spatial distributions of cortical markers in younger and older participants are virtually identical (r > 0.97; see Figure S3), we did not perform additional analyses separating these two age groups.

FIGURE 2.

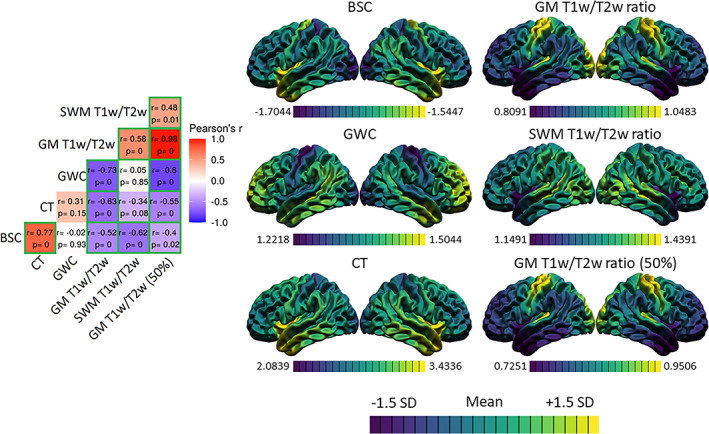
Spatial distributions of the markers and correlations. For each marker, the mean and standard deviation of the surface were calculated and used to threshold the colors. Purple areas indicate lower values relative to the mean of that marker, while yellow areas indicate higher values. The correlation matrix includes Pearson's correlation coefficients (r) and FDR‐corrected p‐values. The color of each correlation block is linked to the correlation coefficient: positive coefficients are red and negative coefficients are blue, high coefficients are more saturated and low coefficients tend toward white. Significant correlations at the FDR 0.05 level are highlighted with a green outline.

Second, we correlated cortical MRI markers with density maps of seven canonical cell types derived from gene expression data (Seidlitz et al., 2020). This open‐access cell‐type atlas is derived by examining transcription factors related to single‐cell RNA sequencing experiments. It was retrieved from https://github.com/jms290/PolySyn_MSNs/blob/master/Data/AHBA/cell_classes_AHBA_lh152parc.txt on April 4, 2022. In brief, the authors used data from five single‐cell gene expression studies (Darmanis et al., 2015; Habib et al., 2017; Lake et al., 2018; Li et al., 2018; Zhang et al., 2016) to categorize each gene into 58 different cell classes. The median expression for each cell class gene set of the aligned and averaged microarray gene expression data from the six adult donors of the Allen Human Brain Atlas (AHBA; Hawrylycz et al., 2012; Romero‐Garcia et al., 2019) was computed. The 58 cell classes were then clustered into seven categories with hierarchical clustering (based on spatial overlap) and t‐distributed stochastic neighborhood embedding. This process resulted in cell density maps for each of the seven cell types (astrocytes [astro], endothelial [endo], microglia [micro], excitatory neurons [neuro‐ex], inhibitory neurons [neuro‐in], oligodendrocytes [oligo], oligodendrocyte precursor cells [OPC]), which are parcellated in a 152‐region subparcellation of the Desikan‐Killany atlas spanning the left hemisphere only (the right hemisphere was omitted because it was under‐sampled in the AHBA). To make the MRI cortical marker maps comparable to the cell‐type maps, we parcellated the left hemisphere of the MRI cortical markers' average spatial distribution maps into the same 152‐region Desikan–Killany subparcellation of the cell‐type atlas. The resulting correlations with cortical MRI markers are available in Figure 4. Of note, these analyses are not repeated with a 5‐mm smoothing kernel because the data is parcellated.

FIGURE 4.

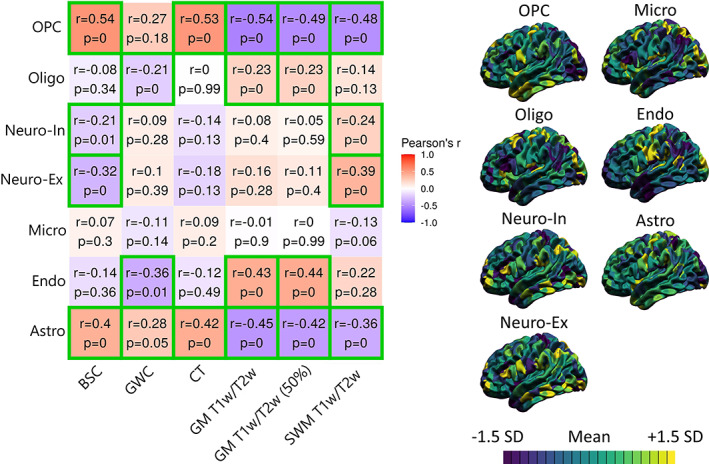
Correlations between MRI markers and gene‐expression‐derived densities of seven canonical cell types. For each marker, the mean and standard deviation were calculated and used to threshold the colors. More specifically, purple areas indicate lower values relative to the mean of that marker, while yellow areas indicate higher values. The correlation matrix includes Pearson's correlation coefficient (r) and FDR‐corrected p‐values. The color of each correlation block is linked to the correlation coefficient: positive coefficients are red and negative coefficients are blue, high coefficients are more saturated and low coefficients tend toward white. Significant correlations at the FDR 0.05 level are highlighted with a green outline.

Third, we related cortical MRI markers with overall cell density maps derived from histology. The “BigBrain” is an ultrahigh resolution (up to 20 μm isotropic voxel dimension) digital reconstruction of a complete brain that was sliced and stained for cell bodies (Amunts et al., 2013) using the Merker staining method (Merker, 1983), where areas with high cell‐body density (e.g., gray matter) have low intensities and areas with low cell‐body density (e.g., white matter) have high intensities (i.e., intensity is inversely related to the density of cells), as can be seen in Figure S2. The brain was donated by a 65‐year‐old male. The digital reconstruction was then non‐linearly registered to the standard MRI template ICBM152 (Fonov et al., 2009). High‐resolution gray–white matter boundary and pial surfaces were then generated on the BigBrain volume downsampled to 400 μum isotropic voxels in MNI space (Lewis et al., 2014). In this study, we used the 8‐bit 400 um resolution BigBrain volume in MNI ICBM 152 space, which is the same space as our MRI surface results. BigBrain surfaces were downsampled from 163,842 vertices per hemisphere to 40,962 vertices per hemisphere (i.e. the same number of vertices as MRI CIVET surfaces), thus allowing for direct comparison between BigBrain and MRI findings. BigBrain intensities were sampled at the same depths as the T1w/T2w ratio measures (i.e., 25% of CT in GM, 50% of CT in GM, and 25% of CT in SWM). These values were inverted to simplify the interpretation of results since raw BigBrain intensities are inversely related to cell‐body density. The resulting correlations with cortical MRI markers are available in Figure 5.

FIGURE 5.

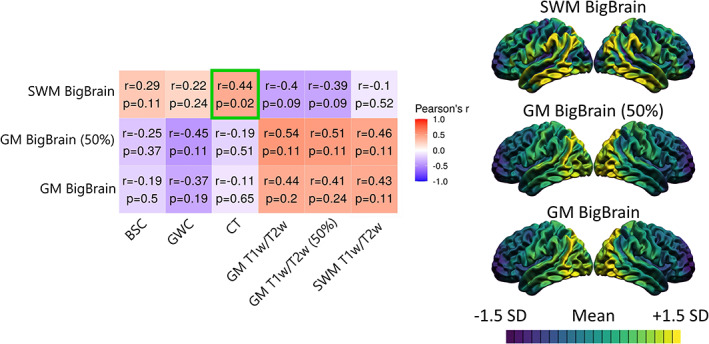
Correlations between MRI markers and histologically derived overall cell density from the BigBrain dataset. For each marker, the mean and standard deviation were calculated and used to threshold the colors. More specifically, purple areas indicate lower values relative to the mean of that marker, while yellow areas indicate higher values. The correlation matrix includes Pearson's correlation coefficient (r) and FDR‐corrected p‐values. The color of each correlation block is linked to the correlation coefficient: positive coefficients are red and negative coefficients are blue, high coefficients are more saturated and low coefficients tend toward white. Significant correlations at the FDR 0.05 level are highlighted with a green outline.

Fourth, we related the cortical MRI markers, which are derived from weighted MRI sequences, to R1 maps derived from quantitative MRI. Quantitative MRI sequences differ from conventional (i.e., weighted) MRI sequences in that they directly measure the absolute relaxation times of the observable protons. As a result, they are a more interpretable measure of the physical properties of the tissue, and to some degree of the biology (Weiskopf et al., 2021). The rate of longitudinal relaxation time R1 (1/T1) has been shown to be highly positively correlated with myelin content (Stüber et al., 2014). The R1 images calculated from the MP2RAGE sequence (Marques et al., 2010) in native space were used to extract GM and SWM R1 values. The CIVET surfaces of each subject generated on T1w images were registered and transformed to the subject‐specific R1 volume. The R1 values were sampled at both 25% and 50% of CT in GM, and at 25% of CT in the direction of white matter at each vertex. An example of the R1 volume for one subject is available in Figure S2. Resulting correlations with other cortical MRI markers are available in Figure 6.

FIGURE 6.

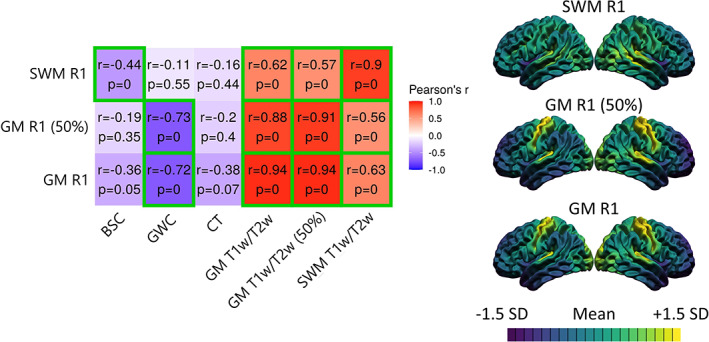
Correlations between the spatial distributions of MRI markers and quantitative R1 maps. For each marker, the mean and standard deviation were calculated and used to threshold the colors. More specifically, purple areas indicate lower values relative to the mean of that marker, while yellow areas indicate higher values. The correlation matrix includes Pearson's correlation coefficient (r) and FDR‐corrected p‐values. The color of each correlation block is linked to the correlation coefficient: positive coefficients are red and negative coefficients are blue, high coefficients are more saturated and low coefficients tend toward white. Significant correlations at the FDR 0.05 level are highlighted with a green outline.

2.6. Comparing age‐related trends between MRI markers

To better quantify the similarity between the microstructural sources of subtle MRI statistical effects across the whole cortex, we compared age‐related trends of MRI cortical markers between themselves in a healthy population spanning the adult lifespan with the rationale that effects driven by the same microstructural tissue property (i.e., density of intracortical myelin) should, as a minimal condition, result in similar statistical effects between the measures.

As a preliminary step, and since we observed widespread vertex‐wise correlations between curvature and the BSC, GWC, and CT metrics (see Figure S6), curvature was regressed out of all markers at the vertex‐wise level to limit its influence on our downstream analyses for age‐related trajectories.

First, for each cortical MRI marker, we calculated the shape of age‐related trends that best fit the data. Age trajectories were modeled using linear models in R version 3.5.1 (https://www.r-project.org), more specifically with the vertexLm function of the RMINC package version 1.5.2.3 (Lerch et al., 2017). We compared linear, quadratic, and cubic models of age, with sex as a covariate, at each vertex using the Akaike information criterion (AIC) as in our previous work (Bedford et al., 2019; Bussy, Plitman, et al., 2021; Tullo et al., 2019):

 

1: Marker ~ age + sex.

2: Marker ~ age + age² + sex.

3: Marker ~ age + age² + age³ + sex.

 

The AIC respects the principle of parsimony by penalizing every additional predictor variable added to the statistical model (Mazerolle, 2006). Hence, the model with the lowest AIC at each vertex was considered the model which best fit the data. The number of vertices that were best fit by each model was computed for each marker in order to compare the shape of the age trajectories between the markers (see Figure 7a).

FIGURE 7.

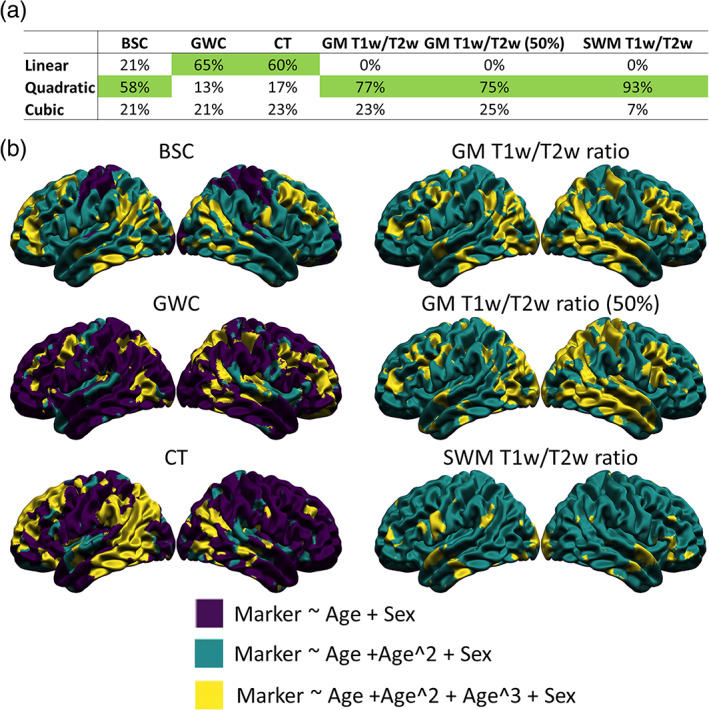
Vertex‐wise best age trajectory shape between linear, quadratic, and cubic for each marker. (a) Table illustrating the proportion of vertices best fitted by each age model for each marker according to the Akaike Information Criterion (AIC), with the age model best fitting the highest proportion of vertices highlighted in green. (b) Spatial distribution of the AIC results. Purple areas indicate a better fit of the linear age trajectory, green areas indicate a better fit of the quadratic age trajectory, and yellow areas indicate a better fit of the cubic age trajectory.

Second, to further quantitatively compare the age trajectories between the markers, we compared the spatial distribution of the age effect. To do so, using a unified and simple age model for all markers was necessary. A linear age model with sex as a covariate (model 1 above) was fit at each vertex of each marker. Purely for visualization purposes, the resulting p‐values were corrected for multiple comparisons using the false discovery rate (FDR) correction, which controls the proportion of null hypotheses that are falsely rejected (Genovese et al., 2002). We then quantitatively compared the un‐thresholded beta coefficients of the age component by performing correlations between the surface maps (Figure 8a). We further visualized linear trajectories for each marker at a single vertex in the precentral gyrus, where the linear age effect of all markers was significant (see Figure 8b).

FIGURE 8.

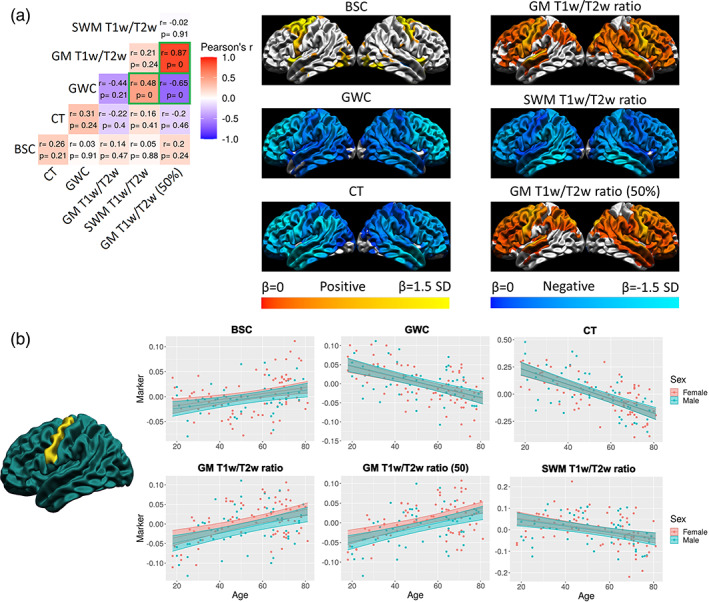
Spatial distribution of the linear age effect of the markers and correlations. (a) For each marker, the mean and standard deviation of the age betas were calculated and used to threshold the colors. Cortical maps are thresholded for significance at the FDR 0.05 level. Cold colors indicate negative age betas and warm colors indicate positive age betas. Light colors indicate higher age betas and dark colors indicate lower age betas. The correlation matrix includes Pearson's correlation coefficient (r) and FDR‐corrected p‐values. The color of each correlation block is linked to the correlation coefficient: positive coefficients are red and negative coefficients are blue, high coefficients are more saturated and low coefficients tend toward white. Significant correlations at the FDR 0.05 level are highlighted with a green outline. (b) Example of the age trajectory of each marker at one vertex in the precentral gyrus where the age beta of each marker was significant at the FDR 0.05 level. Blue observations represent male participants and red observations represent female participants. The x‐axis is age and the y‐axis is the marker value residualized for mean curvature.

2.7. Spatial correspondence between surface maps

The spatial correspondence between bilateral surface maps (i.e., left and right hemispheres bundled together) generated with the previous steps was assessed with Pearson's correlation coefficients. Each correlation was then hypothesis‐tested using a bilateral “spin test” (Alexander‐Bloch et al., 2018). This novel statistical technique generates a null distribution of the spatial overlap across a set of random rotations to spherical projections of the surfaces around each axis. Critically, this approach maintains the spatial relationship between vertices, in contrast with conventional parametric approaches that falsely assume independence of each vertex which leads to excessively high rates of false positives (Alexander‐Bloch et al., 2018). In our analyses, we chose to do 1000 permutations, because results have been shown to converge between 500 and 1000 permutations (Markello & Misic, 2021). This technique outputs a p‐value for each correlation. The p‐values were then corrected for multiple comparisons using the FDR within each analysis (i.e. each correlation matrix) and considered significant below the 0.05 threshold. Of note, the medial wall was excluded from all analyses since the cortical markers are not valid in those regions. Furthermore, the correlation coefficient has to be interpreted in a spatial context. For example, if the correlation coefficient is positive, it means that where the values of the first surface are higher, the values on the second surface also tend to be higher, and vice versa.

In addition to the correlations, linear regressions on the Z‐scored cortical maps were calculated. By definition, the beta of that regression, which is standardized, is exactly the same value as the Pearson's correlation coefficient. This allows us to (1) graphically examine the relationship between cortical maps, and (2) map the residuals to the common cortical surface. It is then possible to assess which areas exhibit the relationship more (i.e., areas with lower residuals) and which areas exhibit the relationship less (i.e., areas with higher residuals).

3. RESULTS

3.1. Comparing the spatial distributions between MRI markers

We assessed the spatial correspondence between average distributions of MRI cortical markers (see Figure 2). The values of the BSC were higher, indicating a sharper gray‐white matter transition, in the temporal pole, the precentral gyrus, and the insula, while the values were lower in the occipital pole and postcentral regions, indicating a more gradual gray‐white matter transition. For the GWC, the values were higher in lateral temporal, prefrontal lobe, and temporo‐parietal regions, while the values were lower in sensorimotor areas, occipital pole, and insula. For CT, the values were higher in the temporal pole and insula, while the values were lower in the occipital lobe and postcentral gyrus. For the GM T1w/T2w ratio at both cortical depths (i.e., 25% of CT and 50% of CT), the values were higher in the occipital lobe and sensorimotor regions, while the values were lower in the frontal lobe, the lateral temporal and temporo‐parietal regions. Lastly, for the SWM T1w/T2w ratio, the values were higher in the lateral occipital and superior temporal lobe while the values were lower in the insula and temporal pole.

The spatial correspondence between these surface maps was assessed with correlations, which were then hypothesis‐tested via spin tests, and the resulting p‐values were corrected for multiple comparisons using the FDR (see Figure 2). There was a positive spatial correspondence between BSC and CT maps (r = 0.77, p < .001). Moreover, this relationship was exhibited across the vast majority of the cortex, as only a few regions in the medial temporal inferior cortex displayed high residuals (see Figure 3).

FIGURE 3.

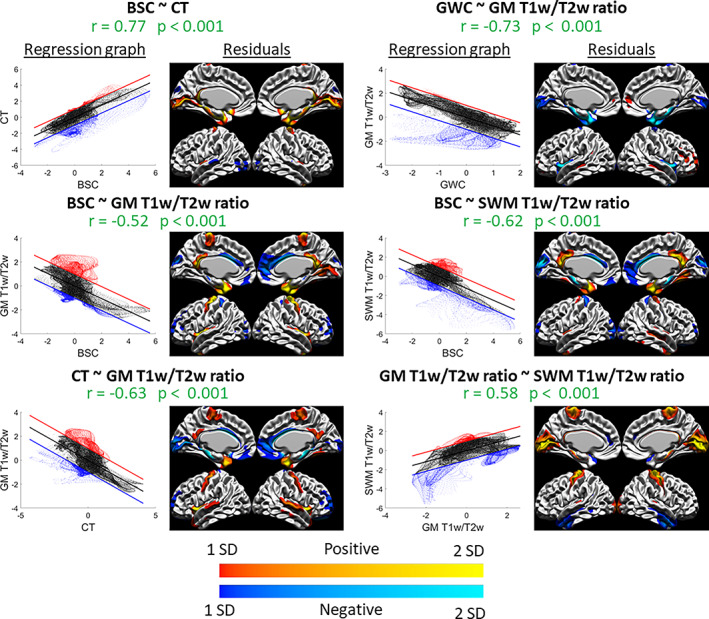
Spatial distribution relationships: graphs and residuals. For each significant correlation, the left figure is the spatial regression in graph form, where the x‐axis is the Z‐scored values of the first marker, the y‐axis is the Z‐scored values of the second marker, the regression line is shown in black, and the +1 SD and −1 SD lines are shown in red and blue, respectively (representing the thresholds set for values that are far from the regression line and exhibit less the observed relationship). The right figure is the vertex‐wise residuals from the regression thresholded at ±1 SD (cold colors indicate vertices below the regression line in blue in the left graph and warm colors indicate vertices above the regression line in red in the left graph, and lighter colors indicate higher residual values and darker colors indicate lower residual values). For example, the relationship between GWC and GM T1w/T2w ratio (top right) is linear in most areas, as seen in the graph on the left, except for a group of vertices below the regression line which we can locate in the residual figure on the right (in this case, in the insula and medial temporal pole).

The spatial distribution of GM T1w/T2w ratio sampled at 25% of CT correlated negatively and significantly with all other markers, and the correlation was highest with the GWC (r = −0.73, p < .001), followed by the correlation with CT (r = −0.63, p < .001) and the correlation with the BSC (r = −0.52, p < .001). In general, these relationships showed higher residuals in the precentral gyrus, the insula, and the lateral temporal pole, indicating a poorer fit of the correlation in those regions (see Figure 3). Also, a significant positive correlation was found between GM T1w/T2w ratio and SWM T1w/T2w ratio (r = 0.58, p < .001). This relationship showed higher residuals in sensorimotor regions, the medial occipital lobe, and the inferior lateral temporal lobe (see Figure 3). The correlations assessed with the GM T1w/T2w ratio at 50% of CT were not meaningfully different (see Figure 2).

Lastly, a significant and negative spatial correspondence was found between SWM T1w/T2w ratio and the BSC (r = −0.62, p < .001), which showed higher residuals mostly in medial cortical regions (see Figure 3). All other correlations of the spatial distribution between the markers were not significant at the FDR 0.05 level.

Using a 5‐mm smoothing kernel (instead of 20 mm), we found generally lower correlation coefficients, but a significant spatial correlation between SWM T1w/T2w ratio and CT which was not found in the main analysis (Figure S9). We conclude that there is a generally high spatial correspondence of the gross anatomical distribution of the cortical MRI markers between themselves.

3.2. Correlations between MRI markers and gene‐expression‐derived densities of seven canonical cell types

We then assessed the spatial correspondence of cortical MRI markers with cell‐specific microstructural measurements derived from other modalities in order to examine the putative biological correlates of the gross anatomical distribution of these measures.

We analyzed the spatial correspondence between average distributions of MRI markers and densities from seven canonical cell types derived from gene expression data (Seidlitz et al., 2020) (see Figure 4). Astrocyte density correlated positively with BSC (r = 0.40, p < .001), GWC (r = 0.28, p = .025), and CT (r = 0.42, p < .001) measures, and negatively with GM T1w/T2w ratio (r = −0.45, p < .001) and SWM T1w/T2w ratio (r = −0.36, p < .001) measures. Endothelial cell density correlated negatively with the GWC (r = −0.36, p = .007), and positively with GM T1w/T2w ratio (r = 0.43, p = .002). Microglial density did not correlate significantly with any MRI markers. Both inhibitory and excitatory neuronal densities correlated negatively with the BSC (r = −0.21, p = .004; r = −0.32, p < .001), and positively with SWM T1w/T2w ratio (r = 0.24, p < .001; r = 0.38, p < .001). Oligodendrocyte density correlated negatively with the GWC (r = −0.21, p = .001), and positively with GM T1w/T2w ratio (r = 0.23, p < .001) measures. Oligodendrocyte precursor cell (OPC) density correlated positively with BSC (r = 0.54, p < .001) and CT (r = 0.53, p < .001) measures, and negatively with GM T1w/T2w ratio (r = −0.54, p < .001) and SWM T1w/T2w ratio (r = −0.48, p < .001) measures. In sum, the spatial distribution of cortical MRI markers was in general more related to glial cell topography, particularly with OPCs and astrocytes, compared to neuronal densities.

3.3. Correlations between MRI markers and histologically derived overall cell density

In order to assess the overlap between MRI markers and overall cell density, we correlated the spatial distribution of the MRI markers to GM and SWM cell densities from the BigBrain (Amunts et al., 2013) (see Figure 5). In GM at both cortical depths, BigBrain cell densities were higher in posterior regions and lower in anterior regions. In SWM, cell densities were higher in temporo‐parietal regions and lower in frontal and occipital regions. In general, T1w/T2w ratio measures correlated positively with GM BigBrain cell densities and negatively with SWM BigBrain cell densities, while the inverse pattern was observed for CT, BSC, and GWC measures. However, despite correlation coefficients being moderately high for some relationships (r between 0.4 and 0.6), the only significant correlation at the FDR <0.05 level is between the SWM BigBrain cell density and CT (r = 0.44, p = .018). Residuals from that relationship were higher in temporo‐parietal and frontal regions (see Figure S4). Using a 5‐mm smoothing kernel (instead of 20 mm), spatial distribution maps of BigBrain densities were visually noisier and we found additional significant relationships of SWM BigBrain cell density with BSC, GM T1w/T2w, and SWM T1w/T2w ratio, despite generally lower correlation coefficients. Hence, while some relationships between cortical MRI markers and overall cell density were observed, most of these were not significantly different from chance, thus preventing us from concluding that cortical MRI markers and GM cytoarchitecture are related, although some methodology‐dependent relationships between SWM cytoarchitecture and cortical MRI markers were uncovered.

3.4. Correlations between MRI markers and quantitative R1

We then related cortical MRI markers with quantitative R1, a measure also derived from MRI but less influenced by nonbiological sources and more sensitive to intracortical myelin (see Figure 6). SWM R1 correlated negatively with the BSC (r = −0.44, p = .002), while the GWC correlated negatively with GM R1 at both cortical depths (r = −0.72, p < .001; r = −0.73, p < .001). R1 and T1w/T2w ratio sampled at the same cortical depths showed very high positive spatial correspondence (25% of CT in GM: r = 0.94, p < .001; 50% of CT in GM: r = 0.91, p < .001; 25% of CT in SWM: r = 0.90, p < .001). Again, residuals of those relationships were mostly located in medial regions and the insula (Figure S5). Using a 5‐mm smoothing kernel, we additionally detected relationships for GM R1 with BSC and CT, and for SWM R1 with CT. We conclude that the GWC and T1w/T2w ratio measures are spatially similar to myelin‐related physical properties of the tissue, while the BSC was more related to these properties in SWM.

3.5. Comparing the shape of age trajectories

To better quantify the similarity between the microstructural sources of subtle MRI statistical effects across the whole cortex, we compared age‐related trends of MRI cortical markers between themselves in a healthy population spanning the adult lifespan with the rationale that effects driven by the same microstructural tissue property (i.e., density of intracortical myelin) should, as a minimal condition, result in similar statistical effects between the measures.

In order to determine which age trajectory shape was more appropriate for each marker, linear models with linear, quadratic, and cubic age variables at each vertex (with sex as a covariate) were compared using the AIC. For each marker, the number of vertices for which each age model was the best fit was counted (see Figure 7a). For CT and GWC measures, a linear model was the best fit for most vertices, followed by a cubic model and a quadratic model. For the BSC, a quadratic model was the best fit for most vertices, followed by a linear model and a cubic model. For all T1w/T2w ratio measures, a quadratic model was the best fit for most vertices, followed by a cubic model and a linear model. The spatial distribution of age trajectory shapes is available in Figure 7b.

Using a 5‐mm smoothing kernel after regressing out curvature, spatial maps of age trajectory shapes appeared visually noisier, and the BSC showed mostly linear age‐related trends compared to quadratic in the main analysis (Figure S12). In sum, there is significant heterogeneity regarding the shape of age‐related trends between the markers.

3.6. Comparing the spatial distribution of the age trajectories

To compare the spatial distribution of the age trajectories of the different markers, linear models with a linear age term and sex as a covariate were fit at each vertex. Since the goal of this study is not to best describe the age trajectories of the different markers, but to compare the age effect between markers, using a uniform and simpler linear age model across the markers is a preferred approach (Figure 8a).

A significant linear increase of the BSC with age was found primarily in anterior superior frontal regions and in parts of the insula and lateral occipital lobe. For the GWC, a significant linear decrease with age was observed across most of the cortex, and this decrease was steeper in frontal regions. For CT, a similar widespread significant linear decrease with age was observed, which was steeper in frontal and temporal regions. For GM T1w/T2w ratio, a significant linear increase with age was found across most of the frontal lobe and in temporo‐parietal regions, with the latter mostly in the right hemisphere, and no areas showed drastically steeper change with age. For SWM T1w/T2w ratio, a significant linear decrease was observed across most of the cortex and was steeper in the inferior temporal lobe. Graphs of the linear age trajectories of each marker at one vertex in the precentral gyrus (where the linear age betas of all markers were significant) are available in Figure 8b.

The spatial correspondence between these surface maps was assessed with correlations, which were then hypothesis‐tested via spin tests and the resulting p‐values were corrected for multiple comparisons using the FDR (see Figure 8a). While the vertex‐wise age betas shown in the figure are thresholded for significance at the FDR 0.05 level, the cortical maps that were correlated were not thresholded. There was a significant positive relationship between the spatial distribution of the age betas of the GWC and the SWM T1w/T2w ratio (r = 0.48, p < .001), meaning that where the GWC decreases more rapidly with age, the SWM T1w/T2w ratio also tends to decrease more rapidly. There was a significant negative relationship between the GWC and the GM T1w/T2w ratio only at mid cortical depth (r = −0.65, p < .001), meaning that where the GWC decreases more rapidly with age, the GM T1w/T2w ratio at mid cortical depth tends to increase more rapidly. Higher residuals of both relationships were mostly found in superior frontal and medial temporal regions (see Figure S7). Using a 5‐mm smoothing kernel after regressing out curvature, we observed that significant linear changes with age are less spatially extensive and visually noisier in the supplementary analysis, but spatial correlations between markers are more significant (i.e., lower p‐values), although correlation coefficients remain generally low and similar to ones in the main analysis (Figure S13). In sum, few spatial relationships of linear age effect between markers above what is expected by chance were detected, highlighting that it is highly unlikely that all measures are equally sensitive to the same microstructural property (i.e., intracortical myelin density) in aging.

Even if it is not the main goal of this article, the quadratic age trajectories of each marker were described, in order to compare our results with previous findings of quadratic age trajectories for some markers (Drakulich et al., 2021; Grydeland et al., 2013, 2019) and to accurately describe for the first time the quadratic age trajectory of the BSC. To do so, linear regressions with age linear, age quadratic and sex as predictors were fit at each vertex for each marker. The betas of the quadratic age term were then thresholded at the FDR 0.05 level and mapped to the common cortical surface (see Figure 9a). For the BSC, the quadratic age term was significant and positive, indicating a u‐shaped trajectory, across most of the cortex, except for sensorimotor regions and in the occipital pole. CT and GWC measures did not show significant quadratic age betas across the cortex. The T1w/T2w ratio, both in GM and in SWM, showed significant and negative quadratic age terms across the cortex, indicating inverted U‐shaped age trajectories. Graphs of the quadratic age trajectories of each marker at one vertex in the precentral gyrus are available in Figure 9b.

FIGURE 9.

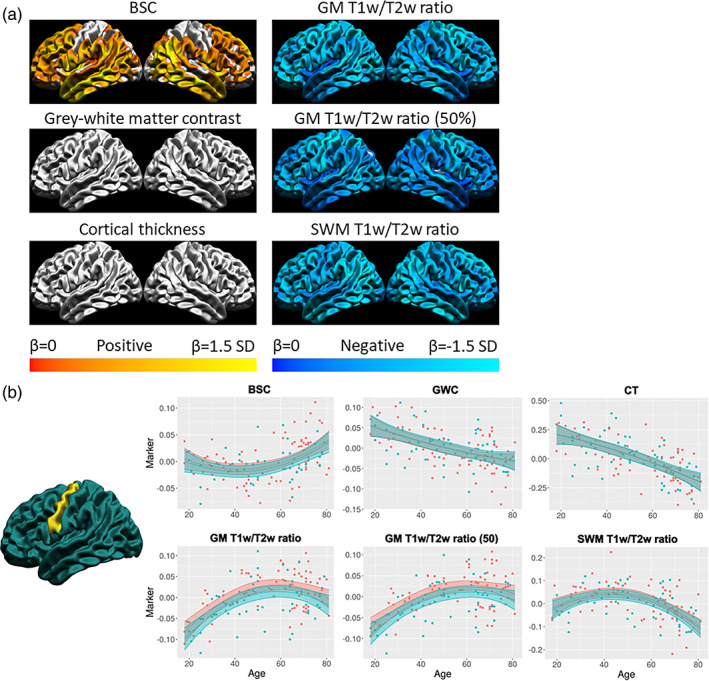
Quadratic age trajectories. (a) For each marker, the mean and standard deviation of the age betas were calculated and used to threshold the colors. Cortical maps are thresholded for significance at the FDR 0.05 level. Cold colors indicate negative age betas and warm colors indicate positive age betas. Light colors indicate higher age betas relative to the marker mean, and dark colors indicate lower age betas. (b) Example of the age trajectory of each marker at one vertex in the precentral gyrus. Blue observations represent male participants and red observations represent female participants. The x‐axis is age and the y‐axis is the marker value residualized for mean curvature.

4. DISCUSSION

Commonly used MRI markers of microstructure, namely CT, GWC, BSC, and T1w/T2w ratio measures, and their associated statistical effects are often interpreted as being representative of intracortical myelin density. Indeed, a higher gray–white matter boundary sharpness on T1w images (indicated by a lower BSC), higher contrast between cortical gray matter and SWM on T1w images (indicated by a lower GWC), lower gray matter T1w/T2w ratio, and to a lesser extent lower CT, could all be interpreted as being driven by decreases in the overall density of intracortical myelin. Although these measures are sometimes used interchangeably, there is significant relevance to compare these measures against one another and to assess their sensitivity to more biologically specific microstructural assessments. In this study, to investigate microstructural sources of cortical MRI markers, we assessed gross anatomical distribution relationships between these markers and putative biological measurements derived from more specific modalities. We then assessed the similarity of age‐related trends between cortical MRI markers to investigate if similar microstructural properties were at the source of these trends.

Our results generally showed high correlations between the spatial distributions of these markers, as well as higher spatial correlations between MRI markers and myelin and glial cell indicators compared to other cell types and cytoarchitecture. However, the age trajectories of these markers diverge to a large extent, both in the shape, direction, and spatial distribution of the age effect, indicating that different microstructural properties are likely at the source of more subtle age‐related trends.

4.1. High spatial correspondence of cortical MRI markers with myelin‐related indicators from other modalities

We investigated spatial correspondence of cortical MRI markers with more biologically‐specific microstructural measures derived from gene expression, histology, and quantitative MRI. At the level of individual metrics, our observed average spatial distributions are highly consistent with the literature. Indeed, we found spatial distributions of CT (Fjell et al., 2009), GWC (Salat et al., 2009), BSC (Olafson et al., 2021), T1w/T2w ratio (Glasser & Van Essen, 2011), and R1 measures (Sereno et al., 2013) that correspond with previously reported spatial patterns. This provides confidence in our methodology and the generalizability of our findings outside our sample.

For cell‐specific spatial densities derived from the AHBA and single‐cell RNA sequencing studies, we reported generally higher spatial relationships with cortical MRI markers and glial cells than neuronal cells. This is with the exception of the BSC, which also showed significant negative relationships with inhibitory and excitatory neuronal densities, possibly demonstrating a higher sensitivity to neuronal topography than other markers. Interestingly, the GM T1w/T2w ratio measures showed inverted spatial relationships with OPCs and oligodendrocyte density (i.e., positive correlation to oligodendrocytes and negative correlation to OPCs). This finding could be explained by observations that myelination continues well into adulthood with different ages of peak myelination between regions (Grydeland et al., 2019), thus resulting in late‐myelinating regions that would have a lower oligodendrocyte density but higher OPC density, and inversely for early myelinating regions. For example, Grydeland et al. (2019) report late‐myelination (between 40 and 50 years old) of most of the temporal lobe, which is a region with low oligodendrocyte density and high OPC density in the cell‐density atlas (Seidlitz et al., 2020). Hence, we believe that our findings still support higher spatial overlap between some cortical MRI markers and myelin indicators. However, this was mostly the case for GM T1w/T2w ratio, since oligodendrocyte density did not correlate significantly with BSC, CT, and SWM T1w/T2w ratio measures and OPC density did not correlate significantly with the GWC. Furthermore, all markers correlated significantly with astrocyte density, and some markers (GWC and GM T1w/T2w ratio) correlated with endothelial cell density. This is possibly explained by the high concentration of iron in glial cells. Indeed, while oligodendrocytes are the cell type with the highest iron concentration, it is estimated that astrocytes contain on average more than twice the intra‐cellular iron of neuronal cells (Reinert et al., 2019). Endothelial cells are also critically involved in iron homeostasis and can store iron (Chiou et al., 2019). This shows that the spatial overlap with MRI markers is not limited to myelin‐related cells, but to iron‐rich glial cells in general (with the exception of microglial cells), which is consistent with the known impact of iron on MRI signal (Fukunaga et al., 2010). It is important to note that we cannot infer a causal link between the densities of these different cell types and cortical MRI markers from our reported spatial correlations.

Investigating the spatial correspondence of cortical MRI markers and overall cell density derived from the BigBrain histological dataset, our results are somewhat inconclusive. While some correlations were moderately high (r > 0.4), the only relationship that attained significance was the correlation between SWM cell density and CT. Using a smoothing kernel of 5 mm instead of 20 mm (see Figure S10), relationships were more significant, but only with SWM cell density. We speculate that the added noise stemming from the single‐subject nature of the BigBrain dataset resulted in low statistical power, which prevented us from detecting meaningful spatial associations with cortical MRI markers. We thus cannot confidently conclude that there is a spatial correspondence between GM cytoarchitecture and cortical MRI markers above what is expected by chance, but there are some methodology‐dependent spatial correspondences between SWM cell density and BSC, CT, and GM T1w/T2w ratio. Interestingly, this supports our previously observed higher sensitivity of the BSC to cytoarchitecture.

Lastly, our results with the R1 maps derived from quantitative MRI showed very high spatial correspondence with the T1w/T2w ratio in the same regions (e.g., GM T1w/T2w ratio with GM R1), similar to previous reports (Shams et al., 2019). The GM R1 also correlated significantly with the GWC, and SWM R1 correlated significantly with the BSC. These results are to be interpreted cautiously since both the cortical MRI markers and R1 measures are derived from MRI and influenced by similar physical properties of the tissue. Large correlations could thus stem from similar physical rather than biological underpinnings. Still, quantitative MRI has a large advantage over metrics derived from qualitative MRI sequences in measuring microstructure in vivo since it is less influenced by non‐biological variations and is better interpretable with minimal processing. From that analysis, we conclude that the T1w/T2w ratio and GWC measures are more related to physical tissue properties related to myelin in GM, while BSC is more related to these properties in SWM.

Taken together, our results point to a higher spatial correspondence of cortical MRI markers with myelin and glial markers than with cytoarchitectural and neuronal markers. This was particularly the case for the GM T1w/T2w ratio as it was related to the gene‐expression‐derived density of oligodendrocytes, OPCs, astrocytes, and endothelial cells, as well as showing very high correlations with quantitative MRI‐derived GM R1 measures but no significant correlation with histology‐derived overall cell density. This sensitivity (but not specificity) to myelin of the T1w/T2w ratio corresponds well with findings by Ritchie et al. (2018) who reported that the T1w/T2w ratio was related to gene‐expression‐derived indicators of myelin, but also molecule size, mitochondria, and PH. Comparatively, the spatial distribution of the BSC was related additionally to neuronal densities, SWM cell density (methodology‐dependent), and SWM R1, thus being more sensitive to cytoarchitecture and SWM microstructure than other markers. This is an important finding, as SWM microstructure is often ignored despite the BSC sampling MRI signal in SWM. The GWC was related to OPC, endothelial cell, and astrocyte density (but not oligodendrocyte density), as well as with GM R1. As such, it was still mostly related to myelin and glial indicators, but to a lesser extent than the T1w/T2w ratio. Lastly, there were fewer correlations between the spatial distribution of CT and microstructural measures derived from other modalities, as we only observed significant relationships with OPC and astrocyte density, as well as an intriguing relationship with SWM cell density. This was to be expected since CT is thought to be influenced by intracortical myelin in certain contexts and regions (Natu et al., 2019), but does not aim to represent myelin as it is a morphological measure and not a microstructural measure. Still, we did not replicate the previously reported spatial correspondence between CT and GM R1 (Patel, Shin, et al., 2020).

4.2. Diverging age‐related trends between cortical MRI markers

To investigate if cortical MRI markers are sensitive to similar microstructural changes in aging, we assessed the similarity of age‐related trends between these MRI cortical markers that have similar microstructural interpretations in the same sample with uniform MRI acquisitions and processing, with the rationale that effects driven by the same microstructural tissue property (i.e., density of intracortical myelin) should, as a minimal condition, result in similar statistical effects between the measures. Again, our observed age‐related trends across the adult lifespan were highly similar to those reported in the literature. Indeed, a widespread linear decrease of CT in healthy aging was observed both in Fjell et al. (2009) and in our sample, with a steeper age‐related decline in frontal regions. For the GWC, our observation of a linear decline with aging higher in the frontal lobe was consistent with previous findings (Vidal‐Piñeiro et al., 2016). For the GM T1w/T2w ratio, we reproduce the well‐known inverted‐U‐shaped age trajectory (Grydeland et al., 2013, 2019). To our knowledge, this is the first time the age trajectory of SWM T1w/T2w ratio was characterized, showing an inverted‐U‐shaped aging pattern similar to GM T1w/T2w ratio, but with a steeper decline in the elderly. This is somewhat similar to previously described age trajectories of fractional anisotropy (FA) in SWM (Nazeri et al., 2015), but we observed a more pronounced increase in SWM T1w/T2w ratio in early adulthood and a delayed decline compared to SWM FA. Compared to one study reporting a mixture of inverted U‐shaped and linear age trajectories of the magnetization transfer ratio (MTR) in SWM, another measure sensitive to myelin, our SWM T1w/T2w ratio quadratic age trajectories are more widespread (Wu et al., 2016). Lastly, we have described the age effect of the BSC in the adult lifespan for the first time. Paired with the developmental trajectories described in Olafson et al. (2021), we can describe for the first time the general age trajectory of the BSC across the whole lifespan: the boundary between GM and SWM becomes more gradual during childhood and adolescence, plateaus in adulthood, and becomes sharper in the elderly, showing a U‐shaped age trend across the whole lifespan.

Next, we compared how between‐marker gross anatomical spatial distribution correlations differ from between‐marker age‐related trends since this directly shows how spatial correlations compare to subtle statistical effects. An important contribution of this paper is the observed discrepancy between spatial distribution relationships and aging relationships. Most of the correlations between the spatial distributions of the markers are significant and are of moderate to high effect sizes (r > 0.4). As an example, GM T1w/T2w ratio, which we interpret as the cortical MRI marker that is most likely sensitive to intracortical myelin based on our previously‐described findings, correlated significantly and negatively with the BSC, GWC, and CT, which could be interpreted as a myelin‐specific dependency for these markers. On the other hand, the spatial correlations of the linear age effect between the markers are mostly non‐significant and have much smaller effect sizes. For example, the spatial distribution of the BSC correlated negatively with the GM T1w/T2w ratio. Meanwhile, the spatial distribution of the linear age effect of the BSC does not correlate significantly with the GM T1w/T2w ratio. Furthermore, the shape and direction of the age trajectories differed to a large extent, with the BSC showing quadratic U‐shaped trajectories increasing in the elderly, T1w/T2w ratio measures showing quadratic inverted U‐shaped trajectories, and CT and GWC showing linear decline trajectories. While the general direction of BSC and T1w/T2w ratio age trajectories would point to a decrease of intracortical myelin density under the common interpretation and thus follow the known myelin decline in the elderly (Wang et al., 2020), the GWC (and to a lesser extent CT) age trajectories would point to intracortical myelin increases in the elderly under the common interpretation. This discrepancy highlights an important point: it is highly unlikely that change in overall intracortical myelin density is the primary microstructural driver in aging of all the cortical MRI markers, and our findings indicate that while some measures tend to spatially overlap at the cortex‐wide level, age trajectories are likely influenced by different interactions of microstructural changes. This also shows that microstructural properties driving spatial distributions of MRI markers can be different from microstructural properties at the source of statistical effects. As such, while most markers were spatially correspondent with myelin and glial cell indicators, this does not necessarily translate to these same microstructural properties being the primary drivers of age‐related effects. This rationale can also potentially extend to other pathology‐related effects. Our findings warrant caution in the interpretation of age‐ and pathology‐related MRI effects as being driven by the same microstructural properties as the spatial distribution.

For example, the GWC spatial distribution correlated significantly, and in the expected direction, with oligodendrocyte density, GM R1, and GM T1w/T2w ratio but not SWM T1w/T2w ratio, while its age trajectory, which is not in the expected direction of intracortical myelin decreases in the elderly, was also related to SWM T1w/T2w ratio. This supports findings of a change in SWM microstructure and T1w signal driving age‐related effects of GWC (Westlye et al., 2009) and further demonstrates that a microstructural property with little spatial overlap on average could still be a source of variation of more subtle statistical effects of cortical MRI markers.

While these findings highlight an important limitation in the biological interpretations of these commonly acquired cortical MRI markers, it also indicates that markers are likely sensitive to different microstructural cortical changes and could thus provide complementary predictive power on cognition, behavior, and other clinical variables. For example, one study has implemented the GWC together with CT measures to better predict cognitive changes in Alzheimer's disease (Li et al., 2020). Hence, a more complete characterization of cortical changes with all cortical MRI markers included in this study could leverage the additional microstructural information available in commonly acquired T1w and T2w images and increase prediction accuracy (e.g., for a particular diagnosis), but would be limited in biological inference without further histological validation studies.

Interestingly, some between‐marker spatial relationships visually appeared non‐linear (e.g., between GM T1w/T2w ratio and SWM T1w/T2w ratio). While our goal was to assess the amplitude of spatial relationships, which is done adequately with linear correlations, analyzes aiming to provide a more detailed description of spatial overlap should not assume a linear relationship.

4.3. High residuals of spatial correlations in the medial cortex

One incidental finding in our analyses was the high residuals from most spatial correlations in medial regions, most prominently in the medial temporal lobe. While this area may have a different relationship between biological microstructure and MRI signal than the rest of the cortex, a more probable explanation is the unreliability of the measures caused by very low cortical thickness (<2 mm), which could induce partial volume effects. Indeed, the GWC, BSC, and T1w/T2w ratio measures are calculated by sampling the signal at different fractions of CT. Hence, very low CT could lead to the multiple sampling points being very close to each other, thus leading to unreliable measures. In order to test this hypothesis, we spatially correlated CT with the residuals from the six significant spatial distribution correlations (see Figure S8B). Supporting this hypothesis, 4 out of 6 of those correlations were significant. Furthermore, we calculated the sum of squared residuals from the sigmoid curve used to generate the BSC at each vertex, then averaged the values across subjects, and found high residuals in the same areas, meaning a worse fit of the sigmoid curve to the cortical profile in those areas (Figure S8A). Following those observations, we advise caution in interpreting the results of these cortical markers in medial areas of very low CT.

4.4. Influence of smoothing kernel and curvature regression order

The main analyses done on markers smoothed with a 20 mm FWHM heat kernel applied before regressing out curvature (Figures 2, 5, 6, 7, 8) are compared with supplementary analyses done on markers smoothed with a 5‐mm FWHM heat kernel applied after regressing out curvature (Figures S9–S13). In general, results from the supplementary analyses are similar and lead to similar conclusions compared to results from the main analyses, with the possible exception of a mostly linear age trajectory of the BSC in the supplementary analysis as opposed to a mostly quadratic age trajectory in the main analysis. Since cortical maps at a lower smoothing kernel appear visually noisier, and since higher smoothing kernels have been shown to increase precision (Lerch & Evans, 2005), we conclude that the higher smoothing kernel used in the main analyses was the most appropriate for our data. Interestingly, correlation coefficients are in general lower in the supplementary analyses, but p‐values derived from spin tests (Alexander‐Bloch et al., 2018) are generally lower (more significant). One possible explanation is that correlation coefficients from spun surfaces (i.e., correlations forming the null distribution for the spin test) are disproportionately lower than the correlation of the non‐spun surfaces at lower smoothing kernel values, thus leading to a bigger difference between the original correlation and the null distribution resulting in a lower p‐value. This interaction between p‐values derived from spin tests and smoothing kernels should be further investigated in the future.

4.5. Limitations

As a first limitation, it is important to note that our analyses are at the cortex‐wide level. Hence, some interactions in local areas between markers and intracortical myelin could still be present. For instance, Natu et al. (2019) reported that the increased myelination of the cortex during development directly leads to reductions in CT specifically in the ventral temporal cortex, and this finding was validated histologically.

Second, our analyses cannot exclude that different characteristics of the myeloarchitecture could cause the age‐related trends of the markers. In other words, the overall density of myelin in GM can be uncorrelated with some markers, but specific changes in laminar patterns of myelin could still differentially affect each of the markers, leading to dissimilar age trajectories that are caused by changes in different aspects of myelination. However, we argue that such interpretations would need to be precisely characterized and empirically justified. It is also possible that the gross anatomical distribution of the markers, and the T1w signal, represents myelin to a large extent, but that more subtle age‐ or disease‐related changes could stem from changes in other microstructural properties also contributing to the signal, such as iron (Callaghan et al., 2014).

Third, the linear age effects we used to compare the spatial distribution of the age trajectories between the markers are not optimal models in all cases, since the BSC and T1w/T2w ratio measures display mostly quadratic trajectories. However, those markers still display a significant linear component of those age trajectories, with the possible exception of the BSC showing somewhat spatially constrained significant linear age effects in anterior frontal areas. We argue that the different age trajectory shapes between the markers, rendering the quantitative comparison of the spatial distribution of the age effect more difficult, supports our interpretation that the age trajectories are different and driven by different microstructural properties.

4.6. Future work

Our results advise against attributing a specific microstructural property to the source of age‐ or pathology‐related changes of cortical MRI markers without further validation. While our findings highlight a discrepancy in the microstructural interpretation of the cortical markers, our conclusions do not aim to discourage the use of these MRI‐derived markers, as they have been reported to be sensitive to various pathologies (Olafson et al., 2021; Salat et al., 2011), and could be useful for such purposes. Future work aiming to assess specific cortical microstructural properties and infer biologically relevant information should consider the use of multimodal quantitative MRI. Indeed, the advent of quantitative MRI allows for the unprecedented assessment of brain microstructural properties in vivo, sometimes referred to as in‐vivo histology (Weiskopf et al., 2021). However, the same rationale displayed here could also apply to quantitative MRI, meaning that the microstructural properties contributing the most to the contrast could be different from microstructural properties at the source of statistical effects. Hence, we advise for the use of combined quantitative MRI modalities in order to increase the confidence of biological interpretations, as we have demonstrated in recent work from our group (Patel, Steele, et al., 2020; Robert et al., 2022). However, as the adoption of quantitative MRI is lagging, our findings illustrate that many largely independent markers can be derived from the growing number of publicly available standard T1w and T2w scans, although specific biological underpinnings of these markers would need to be further investigated.

5. CONCLUSION

In this study, with the goal of better understanding the biological underpinnings of commonly‐acquired MRI markers claiming to represent intracortical myelin, we first investigated the gross anatomical distribution relationships of the BSC, GWC, CT, and T1w/T2w ratio with more biologically specific microstructural assessments derived from gene expression, histology, and quantitative MRI. We observed higher spatial correlations of cortical MRI markers with indicators of myelin and glial cells than cytoarchitecture, with the T1w/T2w ratio showing the most consistent relationships with intracortical myelin indicators.

In the second part of the manuscript, we examined and compared the spatial distributions and age trajectories of cortical MRI markers between themselves in order to assess if microstructural properties at the source of age‐related trends were similar. Our results showed similar spatial distributions between the markers, but few relationships in aging. We conclude that the microstructural properties at the source of spatial distributions of MRI cortical markers (e.g., GM myelin) can be different from microstructural changes that affect these markers in aging. This warrants care in interpreting the age‐ or disease‐related effects of these MRI markers when aiming to show changes in a specific property of the cortical microstructure.

AUTHOR CONTRIBUTIONS

Olivier Parent: conceptualization, formal analysis, funding acquisition, investigation, methodology, software, visualization, writing original draft, writing review and editing. Emily Olafson: methodology, visualization, writing review and editing. Aurélie Bussy: formal analysis, methodology, writing review and editing. Stephanie Tullo: resources, writing review and editing. Nadia Blostein: methodology, software, writing review and editing. Alyssa Dai: methodology, software, writing review and editing. Alyssa Salaciak: resources, writing review and editing. Saashi A. Bedford: resources, writing review and editing. Sarah Farzin: resources, writing review and editing. Marie‐Lise Béland: resources, writing review and editing. Vanessa Valiquette: data curation, resources, writing review and editing. Christine L. Tardif: conceptualization, supervision, writing review & editing. Gabriel A. Devenyi: formal analysis, methodology, software, visualization, writing review and editing. M. Mallar Chakravarty: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, supervision, writing original draft, writing review and editing.

CONFLICT OF INTEREST STATEMENT

The authors have no actual or potential conflicts of interest.

Supporting information

Data S1: Supplementary Information

Parent, O. , Olafson, E. , Bussy, A. , Tullo, S. , Blostein, N. , Dai, A. , Salaciak, A. , Bedford, S. A. , Farzin, S. , Béland, M.‐L. , Valiquette, V. , Tardif, C. L. , Devenyi, G. A. , & Chakravarty, M. M. (2023). High spatial overlap but diverging age‐related trajectories of cortical magnetic resonance imaging markers aiming to represent intracortical myelin and microstructure. Human Brain Mapping, 44(8), 3023–3044. 10.1002/hbm.26259

DATA AVAILABILITY STATEMENT

Original scans from participants can be obtained through collaborative agreement and reasonable request but are not publicly available due to the lack of informed consent by these human participants. All pipelines used for processing the MRI data are publicly available tools, referenced throughout the manuscript. All processed data used to run all primary analyses is available on the Canadian Open Neuroscience Platform. Furthermore, the code to run all primary analyses, as well as our obtained results in raw form, are available on GitHub (https://github.com/CoBrALab/cortical_markers_paper).