Abstract
Clinical measurement of corneal biomechanics can aid in the early diagnosis, progression tracking, and treatment evaluation of ocular diseases. Over the past two decades, interdisciplinary collaborations between investigators in optical engineering, analytical biomechanical modeling, and clinical research has expanded our knowledge of corneal biomechanics. These advances have led to innovations in testing methods (ex vivo, and recently, in vivo) across multiple spatial and strain scales. However, in vivo measurement of corneal biomechanics remains a long-standing challenge and is currently an active area of research. Here, we review the existing and emerging approaches for in vivo corneal biomechanics evaluation, which include corneal applanation methods, such as ocular response analyzer (ORA) and corneal visualization Scheimpflug technology (Corvis ST), Brillouin microscopy, and elastography methods, and the emerging field of optical coherence elastography (OCE). We describe the fundamental concepts, analytical methods, and current clinical status for each of these methods. Finally, we discuss open questions for the current state of in vivo biomechanics assessment techniques and requirements for wider use that will further broaden our understanding of corneal biomechanics for the detection and management of ocular diseases, and improve the safety and efficacy of future clinical practice.
Keywords: Corneal biomechanics, Young’s modulus, Elastography, Optical coherence elastography, Brillouin microscopy, Ocular response analyzer, Corneal visualization scheimpflug technology
Graphical Abstract
1. Introduction
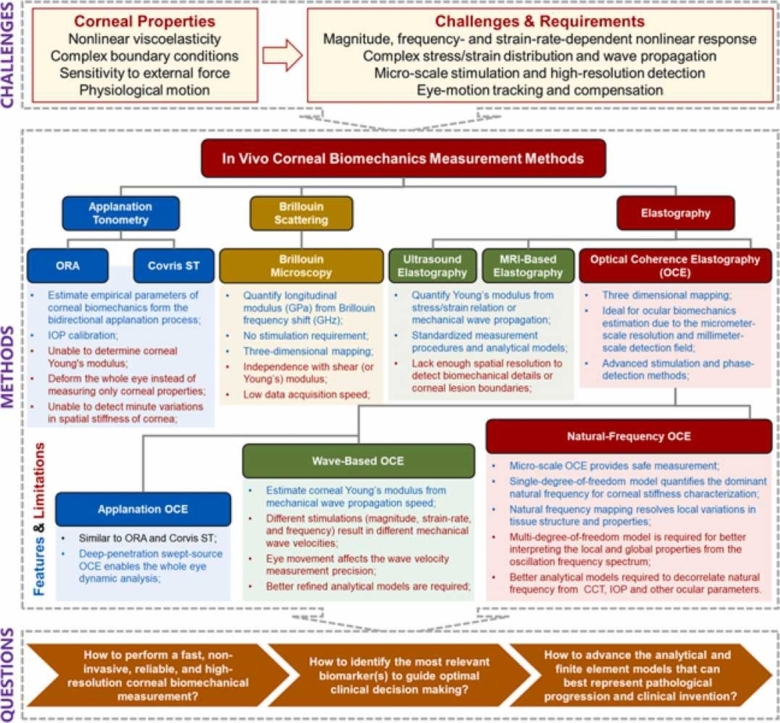
The human cornea is a transparent, avascular, and highly innervated tissue located at the outermost surface of the eye. It is the principal refracting surface for the eye (40–44 diopters, ∼65–75% of the total optical power) and serves as an important structural barrier protecting the delicate intraocular components [1], [2]. Corneal tissue exhibits distinctive nonlinear, viscoelastic, and spatially heterogeneous biomechanical properties, which can influence the structural stability and therefore the visual function of the human eye. Because these structural attributes are influenced by normal physiological function and pathological conditions, it is important to study and understand the interplay between corneal biomechanical properties and visual performance [3]. Aging and ocular diseases, such as keratoconus [4], [5], glaucoma [6], [7], and myopia [8], [9], [10], can alter corneal biomechanical properties, resulting in a biomechanical change that often precedes any clinical symptoms or morphological alterations of the eye [11]. Corneal biomechanical properties can also be altered by clinical treatments such as refractive surgery [12], [13], [14], [15] and corneal collagen cross-linking [16]. Methods enabling clinicians to accurately assess corneal biomechanics in a clinical setting would be useful to identify degenerative corneal conditions such as keratoconus and track its progression [17], [18], to screen refractive-surgery candidates preoperatively to avoid post-surgical complications such as ectasia [19], [20], and to evaluate the outcomes of medical or surgical treatments [21].
The ability to perform in vivo measurements of corneal biomechanical properties is a long-standing challenge, and remains an active area of current investigation [22]. One reason this is so challenging is because corneal tissue is highly nonlinearly viscoelastic, i.e., the stress–strain response is both nonlinear and strain-rate-dependent. Each measuring instrument and method is applicable for respective stress-strain range. As a results, estimates for the Young’s modulus of corneal tissue range widely, from ∼kPa [23] to tens of MPa [24], using existing devices and methods. Unfortunately, there is no standardized stress–strain region for each method for Young’s modulus estimation nor any other well accepted metric yet to better describe corneal biomechanics to guide clinical diagnosis and evaluation. The layered architecture and complicated boundary conditions of the cornea further complicate interpretation of the stress–strain distribution and elastic wave propagations for dynamic biomechanical property reconstructions. Because the cornea is also one of the most innerved tissues in the human body, with an innervation density that is 300–600 times that of the skin and 20–40 times that of the tooth pulp, it is highly sensitive to any external force applied, further limiting options for mechanical testing in vivo [25], [26]. Eye motion (particularly lateral movements) present another challenge for clinical imaging, which not only causes incorrect measurement position but also affects wave-based elastography methods because eye motion speed is very close to the shear wave propagation speed (several millimeters per millisecond).
For a long time, ex vivo measurement (e.g., using uniaxial or biaxial strip extension, compression, and inflation tests) has been the primary source of our knowledge and is still widely considered the standard for quantifying corneal biomechanics [24], [27], [28], [29], [30], [31], [32], [33], [34], [35]. Advances in speed and spatial resolution for microscopic imaging technologies, such as atomic force microscopy, have enabled cellular-level biomechanical property assessments with sub-nanometer spatial resolution and pico-newton force sensitivity [36]. However, this ex vivo measurement cannot faithfully represent the in vivo measurement environment or be used as the basis for clinical diagnosis due to its destructive nature, and loss of normal physiological and anatomical structure, including hydration control [37], [38]. In vivo measurements for human corneal biomechanical properties advanced in 2005 after Luce and colleagues introduced the ocular response analyzer [39]. Since then, several other methods have been developed for in vivo corneal biomechanics assessment, including the corneal visualization Scheimpflug technology (Corvis ST) [40], Brillion microscopy [41], [42], [43], and multiple elasticity imaging techniques: ultrasound elastography [44], [45], magnetic resonance elastography[46], and optical coherence elastography [22], [47], [48], [49], [50], [51]. Despite significant progress in recent decades, developing these techniques and instruments for in vivo corneal biomechanical assessment is still in early stages [52].
In this review, we first describe important features of corneal structure and anatomy that determine the complex corneal biomechanical properties (Section 2). In particular, we provide a comprehensive summary of previous ex vivo and in vivo studies that have measured the Young's modulus of human corneas. In Section 3, we investigate the correlations between corneal biomechanics and the progression of various ocular diseases, as well as their treatment interventions. In Section 4, we introduce the fundamental concepts, applications, and limitations for existing in vivo methods to estimate corneal biomechanics, including corneal applanation methods (e.g., ORA and Corvis ST), Brillouin microscopy, and elastography methods. In Section 5, we describe recent advances for in vivo optical coherence elastography (OCE) methods, focusing on the advantages and limitations of applanation OCE, wave-based OCE, and natural frequency OCE strategies. In Section 6, we provide a summary of the clinical application requirements for corneal biomechanics and the current technical status of modern approaches. Additionally, we discuss the major progress that has been achieved in this field, as well as the open questions that remain. As this is a lengthy and comprehensive review, each section is independent and self-contained, allowing readers to select a specific focus based on their individual needs.
2. Corneal anatomy and biomechanics
Corneal biomechanics (e.g., nonlinear elasticity, viscosity, anisotropy) are highly associated with corneal anatomical structure [53]. At the tissue scale, corneal shape determines the eye’s refractive power and is itself determined by its biomechanical properties [3]. The cornea has to be both soft enough to form an aspheric transparent shell, and hard enough to maintain its shape while simultaneously resisting the chronic stress induced by air pressure and intraocular pressure (IOP) [3]. On a microscopic scale, the cornea is a five-layered structure that includes cellular components (epithelial cells, keratocytes, and endothelial cells) and acellular components (collagen and glycosaminoglycans). Collagen provides the major structural component of the cornea. Collagen fibrils in the cornea are highly ordered to maintain optical transparency. In the anterior third, these fibrils form interwoven lamellar ribbons that provides resistance to lateral extension, compression, and shear forces. These lamellar sheets become wider, thicker, and more regularly oriented in the posterior 2/3 of the cornea with less interweaving and less resistance to lateral shearing. While the collagen fibrils provide elasticity and strength, the ground substance, composed of proteoglycans, is responsible for viscosity. The spatially heterogeneous biomechanical profile is largely the result of depth and lateral positionally-dependent variations in collagen fibril orientation and branching [54]. Complex interactions between extracellular matrix (ECM) components are required to meet biomechanical demands and maintain corneal transparency. These interactions include the attachment of proteoglycans and glycosaminoglycans to collagen fibers, the organization of collagen structure, the corneal swelling pressure, and the production/degradation of ECM components by keratocytes.
2.1. Corneal anatomy
The cornea is horizontally oval with greater white-to-white (or limbus-to-limbus) diameters in the horizontal direction (11.71 ± 0.42 mm) than in the vertical direction (10.63 ± 0.63 mm) [1], [55], [56]. The cornea has a convex aspherical shape, with a gradually increasing thickness from the center to the periphery. The anterior surface has a average radius of 7.77 ± 0.25 mm and an asphericity of 0.28 ± 0.11, whereas the posterior surface has a average radius of 6.35 ± 0.23 mm and an asphericity of 0.31 ± 0.12 mm [57]. The central corneal thickness is 0.54 ± 0.03 mm [57], and the peripheral corneal thickness can be 26% (140 µm) greater than the central point values [58]. The average refractive index and Abbe-number of the healthy cornea relative to the green light (wavelength: 588 nm) can be assumed as 1.3770 and 56.28 [57].
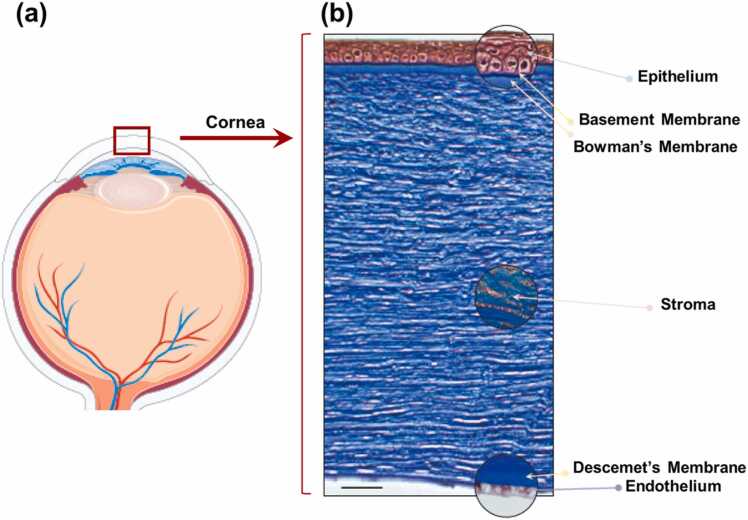
The cornea is a highly structured, membrane-bound, transparent collagenous tissue that connects to the more disordered and opaque sclera at the limbus. The cornea is comprised of a stratified non-keratinized squamous epithelium (50 µm), an acellular anterior limiting layer (Bowman’s layer: 15 µm), stroma (450 µm), the acellular posterior limiting layer (Descemet’s membrane: 5 µm), and the endothelial layer (5 µm) (Fig. 1). Each layer contributes, to the overall structural properties of the cornea, however, the stromal collagen, comprising nearly 90% of the total thickness largely determines its overall properties, making it the primary focus of current corneal biomechanics modeling and measurement studies. Most previous studies have treated the cornea as a simplified single-layered material, whereas the property of the stroma typically represents the cornea as a whole [3].
-
(1)
The corneal epithelium is a ∼50-μm-thickness nonkeratinized stratified squamous epithelium comprised of 5–7 uniform layers of cells including superficial cells, wing cells, and basal cells. Basal cells are mitotically active and can produce the wing and superficial cells. Cornea epithelial cells undergo involution, apoptosis, and desquamation every 7–10 days. The corneal epithelium functions as a barrier to microbes, chemicals, and water. The overlying tear film interacts closely with the glycocalyx of the corneal epithelial cells to allow hydrophilic spreading of the tear film with each eyelid blink and to provide a smooth ocular surface for ocular refraction. Elsheikh et al. showed that the epithelium contributes far less stiffness to the total corneal biomechanics than the stroma in their measurement of human donor eyes [60].
-
(2)
The anterior limiting layer (Bowman’s layer) is an 8–14-µm thick acellular structure of randomly distributed high-density collagen fibrils. The fibrils are linked to the fibrils in the underlying stroma, which is believed to help in maintaining the corneal shape [61] and is of major importance for corneal stability after laser ablative surgery [62]. This layer has no regenerative ability and may result in scar formation following injury. Although many studies suggest that the anterior limiting layer does not contribute significantly to the overall mechanical stability of the cornea [63], [64], disruption in this layer is known to be related to corneal ectasia [65].
-
(3)
The corneal stroma is a specialized connective tissue layer that accounts for 90% (∼450 µm) of the total corneal thickness in humans and is known to contribute the majority of the cornea’s mechanical behavior. The corneal stroma is mainly comprised of extracellular matrix (ECM) and keratocytes, the stromal fibroblast cells that are embedded within it. Keratocytes, have a flat dendritic morphology, occupy ∼3–10% of the stromal volume, and decrease in density from anterior to posterior stroma [1]. The functional activities of keratocytes include ECM synthesis, stromal repair, and remodeling. These cells synthesize collagen and proteoglycans such as keratocan, decorin, lumican, and mimecan [66]. The ECM is composed of collagens and glycosaminoglycans. Corneal collagen is a heterotypic dimer of Type I/Type V pro-collagen subunits with Type I collagen making up the majority of the corneal collagen (68% of the dry weight). Other forms of collagen are also present in smaller proportions: types VI, III, IV, and XII) which contribute in various ways to fibril spacing, connections, and tissue transparency [67]. The collagen fibrils are remarkably uniform in diameter (∼32 nm [68]) and regularly spaced, packed in 300 stacked arrays (lamellae). Most collagen fibrils in the central cornea adopt a preferred orientation in the inferior-superior and nasal–temple directions [69]. Collagen fibrils near the corneal center appear to be more densely packed than those in the peripheral cornea. This appears to confer additional tissue strength and, consequently, curvature stability in the pupillary region where corneal thickness is least [2]. Corneal lamellae have a thin-belt shape with a width of ∼0.2 mm and a thickness of ∼1–2 µm that is wider, and thicker in the posterior stroma [70]. These posterior lamellae are predominantly oriented parallel to the tissue surface with collagen fibrils that lie orthogonal to one another in successive layers in the posterior 2/3 of the cornea [71]. The spacing of individual collagen fibrils significantly increases from the central cornea (∼57 nm) to the margin of the limbus (∼62 nm), followed by an even greater increase at the limbus [70]. In the anterior third of the stroma, collagen fibrils are highly interwoven, branching laterally and in depth (anterior/posterior) [72], [73]. The posterior portion of the central cornea contains a greater proportion of keratan sulfate binding proteoglycans that can more easily swell, whereas the more interlaced lamellar architecture and lower concentration of keratan sulfate in the anterior and middle stroma cannot [2]. The orientation and depth-arranged pattern of the collagen fibers/lamellae have a significant impact on the transparency and tensile strength of the cornea [74]. Previous reports suggest that as much as 50% of the tensile strength of the normal cornea is associated with the anterior 30% of the cornea [75]. The amorphous ground substance (primarily, dermatan and keratan sulfate proteoglycans) surrounding the collagen fibrils regulates the interfibrillar distance and may serve as an interfibrillar or interlamellar “glue,” which plays a pivotal role in the organization of the collagen fibers and the maintenance of the cohesive force between the lamellae [1], [76]. The anisotropic, heterogeneous, and viscoelastic stromal tissue results in complex corneal biomechanical properties. Collagen provides elasticity and strength, and the ground substance is responsible for viscosity, while the depth-dependent organization of collagen fibers/lamellae results in the spatially heterogeneous biomechanical profile (specifically, that the anterior stroma is stiffer than the posterior stroma) [54].
-
(4)
Descemet’s membrane is the acellular posterior limiting layer formed by the endothelium of the cornea, with a thickness that accumulates over time, ranging from ∼3 µm at birth to> 10 µm in the elderly [77]. Descemet’s membrane consists of collagen types IV, VIII, and XII, perlecan, nidogen, netrin, fibronectin, and laminin, among other proteins [78]. This layer consists of an anterior banded layer that develops in the fetus and a posterior non-banded layer that is constantly synthesized by endothelial cells throughout adulthood [79]. The posterior limiting layer attaches strongly to the back surface of the corneal stroma and can reflect morphological changes in the stroma, even though the collagen fibers in the stroma are discontinuous with those in Descemet’s membrane [80].
-
(5)
The endothelium is a 5 µm-thick single layer structure of hexagonal cells that form a honeycomb-like mosaic on the posterior surface of the cornea. The active endothelial pump mechanism plays an essential role regulating stromal hydration to maintain corneal transparency. This is achieved through active transport of metabolites and ions with secondary movement of fluids exchanged between the stroma and the aqueous humor in the anterior chamber [81]. The endothelial cell density is ∼3500–4000 cells/mm2 at birth, and typically ∼2500 cells/mm2 in adult human eyes. Endothelial cells are thought to have little to no regenerative capacity in adults. The number of endothelial cells decreases, with an average loss of 0.3–0.6% annually, while the remaining endothelial cells expand and migrate to maintain normal corneal hydration and transparency [82].
Fig. 1.
Schematic of the human corneal structure. (a) Human eye. (b) A section of the human corneal tissue using Masson’s trichrome stain.
Reproduced from [59].
2.2. Corneal biomechanics
The human cornea is viscoelastic with both elastic and viscous responses to the loading force. Young’s modulus (E) represents the elasticity of a material and is defined as the ratio of stress (σ) to strain (ɛ), according to Hook's law. Young’s modulus was originally introduced for rigid body elastic materials, and has become the primary standard in material comparisons due to its ability to represent only the material’s elasticity in a simple and straightforward manner, without incorporating other properties such as mass, volume, and geometry. This concept was readily applied to organ and tissue biomechanics (including the cornea), even though most human tissues, excluding bone, are soft and nonlinearly viscoelastic. Early-stage tissue biomechanical testing relied on ex vivo mechanical testing methods, such as extension or compression, to determine the nonlinear stress-strain curves of biotissues. Later, elastography methods, such as ultrasound elastography, were developed and can now measure the mechanical wave propagation speed and convert the group or frequency-dependent phase speeds to Young’s modulus using specific analytical models, e.g. shear wave models.
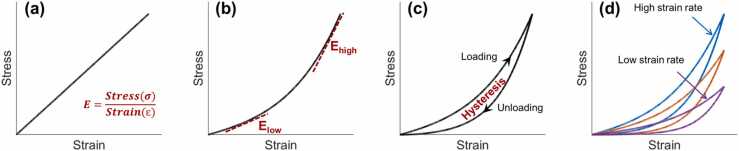
Fig. 2 shows the stress-strain curves that materials typically exhibit during mechanical testing, such as extension or compression. Fig. 2a demonstrates a linear stress–strain relation of an ideal elastic material, in which Young’s modulus is equal to the slope of the curve (σ/ɛ). However, most biological tissues are viscoelastic [83], and their mechanical responses are difficult to describe using a simple elastic expression [84]. Fig. 2b shows a nonlinearly elastic response curve. In this case, the estimated elastic moduli can vary widely over different stress–strain regions. The analytical methods can either estimate the mechanical property by fitting the stress–strain curve as an exponential function, such as , where A and B are fitting coefficients [30], or estimate Young’s modulus using both low- and high-strain values (Elow and Ehigh in Fig. 2b). For example, Xue et al. demonstrated a significant difference between the low-strain tangent modulus (1.32 ± 0.50 MPa and 1.17 ± 0.43 MPa, in horizontal and vertical directions, strain<0.03) and the high-strain tangent modulus (51.26 ± 8.23 MPa and 43.59 ± 7.96 MPa, strain range: 0.32–0.53) [24]. Viscoelastic materials such as the cornea dissipate energy during the deformation process, as observed through hysteresis in the stress–strain curve in Fig. 2c. Hysteresis represents the energy loss value during the loading and unloading periods and is defined as the difference between the strain energy required to generate given stress in the sample and the elastic energy at that stress [85]. As viscoelastic behavior is time-dependent, the loading-unloading stress–strain behavior (hysteresis) also depends on the strain rate, as shown in Fig. 2d. A faster strain rate typically produces a stiffer response [53]. Therefore, the experimental setting significantly impacts the measurement results of Young’s modulus and hysteresis.
Fig. 2.
Demonstration of the stress–strain curves. (a) An ideal case of linear elastic material. (b) Nonlinear stress–strain relationship for a typical elastic material. (c) Hysteresis represents the difference between the strain energy required to generate given stress in the sample and the elastic energy at that stress. (d) The stress–strain curves and hysteresis loops are typically strain-rate-dependent in a viscoelastic material such as the cornea.
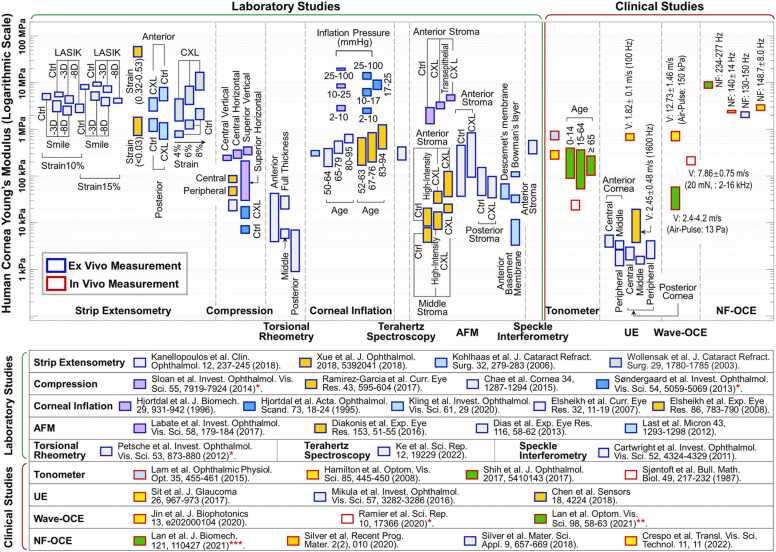
Because of the nonlinear stress–strain behavior of the cornea, the estimated Young’s modulus has a wide range from ∼kPa to ∼several tens of MPa. The wide estimation range is due to the different techniques and conditions under which it is measured (ex vivo vs in vivo; non-destructive versus destructive; dehydration states; the difference in amplitude or rate of the applied force). Fig. 3 illustrates the literature report results of the measured Young’s modulus (in logarithmic scale) of the human cornea across various testing methods. We roughly sorted the measurement methods into two categories: the laboratory group includes the ex vivo assessment of corneal mechanical properties; whereas the clinical group (including both ex vivo and in vivo measurement results) encompasses techniques and methodologies that are intended for clinical applications. The laboratory group includes strip extensometry [24], [28], [86], [87], compression [88], [89], [90], [91], torsional rheometry [23], corneal inflation [92], [93], [94], [95], [96], speckle interferometry [97], Terahertz spectroscopy [98], atomic force microscopy (AFM) [99], [100], [101], [102]; while the clinical group includes tonometer [103], [104], [105], [106], ultrasound elastography (UE) [44], [45], [107], wave-based OCE [22], [47], [48], natural frequency (NF) OCE [49], [50], [51], [108]. In studies marked with an asterisk (*), the shear modulus was originally reported, and a simple estimation was made by assuming Young’s modulus to be three times the shear modulus (Eq. (7), Section 5.2.1). Likewise, in the research marked with double asterisks (**), the shear wave speed was converted to Young’s modulus using a surface wave equation (Section 5.2.3). In the study marked with triple asterisks (***), the empirical natural frequency equation (Eq. (18) from Reference [51]) was used to convert the natural frequency values, which may not be entirely accurate* ** , owing to the variations in the stimulation techniques and stress-strain range, as discussed in Section 5.2.3. Fig. 3 compares different parameters that affect Young’s modulus, including strain values [24], [28], [86], inflation pressures [92], [93], corneal regional variations [23], [89], [90], [91], [102], [107], aging [94], [95], [103], corneal collagen crosslinking (CXL, Section 3.1) [28], [86], [87], [90], [99], [100], [101], and refractive surgeries [28], such as laser-assisted in situ keratomileusis (LASIK) and small incision lenticule extraction (SMILE). The in vivo measurement methods of human corneal biomechanics are discussed in detail in 4, 5.
Fig. 3.
Young’s modulus estimation for the human cornea using various testing methods, both ex vivo and in vivo. Ctrl: Control group, LASIK: Laser-assisted in situ keratomileusis, SMILE: Small incision lenticule extraction, V: Mechanical wave velocity, NF: Natural frequency. In work* , the shear modulus was originally reported, and a simple estimation (Young’s modulus = 3 ×shear modulus, Eq. (7)) was made for a comparison purpose. Similarly, the shear wave speeds (**) and natural frequency values (***) were converted to Young’s moduli using a surface wave equation and a natural frequency equation (5.3.2, 5.3.3, respectively). For more information, see the following studies: strip extensometry [24], [28], [86], [87], compression [88], [89], [90], [91], torsional rheometry [23], corneal inflation [92], [93], [94], [95], [96], speckle interferometry [97], Terahertz spectroscopy [98], atomic force microscopy (AFM) [99], [100], [101], [102], tonometer [103], [104], [105], [106], ultrasound elastography [44], [45], [107], wave-based OCE [22], [47], [48], and natural frequency (NF) OCE [49], [50], [51], [108]. Further details on the in vivo measurement methods and results are shown in 4, 5.
Although there is significant variation in corneal Young’s modulus measurements, earlier studies have greatly improved our understanding of corneal biomechanics, both in normal corneas and in those affected by disease or treatments. It is important to note that the measurement of Young’s modulus is highly stress-strain range dependent, as evident in studies using extension [24], [28], [86] and inflation methods [92], [93]. This could be the main reason for wide ranges in reported estimates of corneal Young’s modulus. Therefore, investigators reporting Young’s modulus of the cornea should also report the conditions under which it was measured. It is also worth noting that corneal stiffness varies in different regions and directions. The anterior portion of the cornea has the most strength, followed by the middle part, while the posterior part is the softest [23]. The central cornea is also generally more elastic than the peripheral cornea [89], especially in the anterior portion [107]. The regional dependent corneal stiffness and elasticity are correlated to corneal anatomy, specifically the interwoven collagen fibrils (shown in Section 2). Furthermore, corneal stiffness has been found to increase with age [94], [95]. Although tonometer measurements show conflicting results between Young’s modulus and aging [103], this study may be suspect as tonometer measurement is heavily affected by IOP. Compared to untreated corneas, CXL treatments greatly enhance the total corneal strength [28], [86], [87], [90], [99], [100], [101], particularly in the anterior and middle stroma, but is not intended to modify the posterior stroma [87], [100]. A more detailed description of the correlation between corneal biomechanics, disease progression and treatment is provided in Section 3.
3. Corneal biomechanics associated with disease and treatment
Aging, keratoconus, iatrogenic ectasia from refractive surgery, and treatment such as collagen cross-linking are all known to alter the morphological features of the cornea, and hence the corneal biomechanical properties [109]. Here, we discuss the mutual relationship between cornel biomechanics and disease progression and treatment.
3.1. Keratoconus and corneal collagen cross-linking
Keratoconus is a structurally degenerative disease that results in progressive thinning, scarring, and protrusion of the cornea and leads to decreased visual acuity and irregular astigmatism [110]. Keratoconus scarring is produced by activated keratocytes in subepithelial or anterior stromal regions. In contrast, thinning and protrusion (with a conical shape) are associated with the loss of normal lamellae architecture in the stromal tissue [111], leading to a significant reduction in mechanical stability [17], [112]. The annual incidence of keratoconus in patients aged 10–40 years is 0.013%, while its estimated prevalence in the general population is 0.267%, with a mean age at diagnosis of 28.3 years [113]. The most typically reported histopathological features include progressive stromal thinning, rupture of the anterior limiting membrane, and subsequent ectasia of the central/paracentral cornea (most commonly in the inferior-temple corneal quadrant) [114]. Corneal topography, pachymetry, and slit lamp examination are the main methods used to detect keratoconus and are effective for the diagnosis of keratoconus in moderate to advanced phases [115], [116]. However, procedures based solely on corneal morphological changes are insufficient for detecting keratoconus in its incipient or preclinical stages [117]. Early stages of subclinical asymptomatic keratoconus and form-fruste (non-progressing) keratoconus [118], which may not be easily detectable by common clinical examination methods is regarded as a significant risk factor for the development of ectasia following laser refractive surgery [117]. Comprehensive evaluations that integrate corneal morphological and biomechanical measurements are required to detect keratoconus, particularly in its early or subclinical stages, and are advantageous for providing timely intervention [119].
Treatment for keratoconus differs depending on the severity of the disease and extent of progression. In mild, moderate, and severe forms of keratoconus, different strategies and methods are typically employed, including spectacles, rigid gas permeable contact lenses, scleral lenses, corneal collagen cross-linking (CXL), intracorneal ring implantation, and ultimately, corneal transplantation (keratoplasty). CXL uses riboflavin as a photosensitizer and ultraviolet-A (UVA) to increase the formation of intra- and interfibrillar covalent bonds by photosensitized oxidation. Among these methods, CXL is the only technique that directly modifies corneal rigidity (e.g., Young’s modulus of human cornea measured ex vivo has been shown to increase by a factor of 450% after CXL treatment [86]), and only CXL has been shown to slow or even stop keratoconus degeneration [120]. With early intervention, CXL is a treatment that has been shown to stop the progression of keratoconus by directly increasing the cornea’s biomechanical stability and stiffness, emphasizing the importance of early diagnosis and close monitoring [114].
3.2. Myopia and refractive surgeries
Myopia, also known as short- or near-sightedness, has become a major global public health issue [8]. In urban areas of east and southeast Asia, ∼80–90% of high school students are myopic, among whom, 10–20% are highly myopic [121]. It has been estimated that, by 2050, half of the global population will have myopia, and nearly one billion people will be highly myopic [122]. Myopia is characterized by an elongation of the ocular axial length, which prevents the eye from focusing light onto the retina, resulting in blurry images. Refractive surgery is recognized as an effective method for myopia treatment, which works by altering the corneal shape [12], [123]. In the United States, approximately 700,000 laser vision correction surgeries have been conducted annually for the past decade. The effect of refractive surgery on patients extends beyond spectacle independence resulting in improvements in the quality of life, working ability, and daily working experience [12], [124]. Nonetheless, myopic refractive surgery can reduce the tensile strength of the cornea, cause long-term instability [15], [125], and carries the risk of an infrequent, but severe complication known as iatrogenic corneal ectasia [19], [126], [127]. Corneal ectasia is associated with a thin residual corneal stromal bed following treatment (typically<300 µm) and progressive steepening of the cornea. Corneal ectasia is thought to be a result of biomechanical decompensation of the stroma when an inadequate residual stromal bed is left after surgery (e.g., in the case of high myopia treatment) or when the surgery is performed on corneas with inadequate strength (e.g., in the case of unidentified subclinical keratoconus). Corneal ectasia is an irreversible disease and ∼35% of ectatic cases finally require corneal transplantation to restore vision [128]. Since first reported by Seiler in 1998 [129], [130], the prevention of corneal ectasia has become a major concern for refractive surgeons [131]. A primary factor in iatrogenic corneal ectasia is the inability to identify compromised corneal biomechanics prior to surgery [132]; the pre-operative evaluation of corneal biomechanics is key to preventing ectasia as well as predicting and evaluating treatment outcomes [10]. Although the development of advanced screening strategies have already decreased the incidence of ectasia, from a relatively high level of 0.66% (reported by Pallikaris in 2001) [133] to 0.033% (reported by Bohac in 2018) [127], unexplained cases of ectasia have continued to confound clinicians and stimulate additional research in this field [131]. Developing more advanced imaging and quantitative methods to access corneal biomechanics more reliably in the clinic is an active research area in vision science and is of great importance to refractive surgery for myopia treatment [15], [131], [134].
3.3. Glaucoma and IOP measurement
IOP is the fluid pressure inside the eye and the primary source of mechanical stress for the ocular tissues. The normal IOP range is 10–21 mmH, and elevated IOP (ocular hypertension) is associated with an increasing prevalence of optic nerve damage in glaucoma - the second leading cause of blindness worldwide, which is irreversible [6], [135]. The Goldmann applanation tonometer is acknowledged as the gold standard for IOP measurement based on the Imbert-Fick law, which assumes that the pressure within an ideal dry, thin-walled sphere equals the force needed to flatten its surface divided by its area [136]. To date, the etiology of many forms of glaucomatous optic neuropathy are unclear and our current understanding of glaucoma remains insufficient [137]. Clearly, IOP is not the only risk factor in the development and progression of glaucoma, but IOP reduction is still the only proven treatment that has been shown to effectively halt the progression of glaucoma. However, many people with elevated IOP do not develop glaucoma, and a significant number of patients show progressive vision loss despite the reduction in IOP [135], [138].
Ocular biomechanics have recently gained more attention as a potential determinant of both IOP measurement and glaucoma risk prediction [6], [139]. First, the IOP measurement is widely known to be influenced by corneal biomechanics, and inaccurate IOP readings caused by abnormal corneal biomechanical properties might raise the risk for misdiagnosis of glaucoma, resulting in missed or delayed glaucoma identification [139]. Second, recent evidence reveals that ocular biomechanical features may have intrinsic and independent value for predicting glaucoma risk [140]. For instance, the biomechanics of optical nerve head tissues (particularly lamina cribrosa) might indicate the strain (deformation) limits that the tissues can bear under elevated IOPs and therefore play an important role in early diagnosis and better clinical management of glaucoma [141]. Further development of ocular biomechanical theories may help to explain why many people with elevated IOP do not develop glaucoma and why patients with normal tension glaucoma suffer optic neuropathy at normal IOP levels [141]. Although direct measurement of the structure and biomechanics of the optical nerve head tissues (e.g., lamina cribrosa) could become a strong biomarker to predict those at higher risks of developing glaucoma [142], [143], [144], [145], it remains difficult to measure the biomechanics of posterior ocular tissues in vivo. Corneal biomechanics are closely correlated with the biomechanics in the posterior eye, including the tissues in the optical nerve head [146], [147]; thus, an alternative and easier option is to measure the corneal biomechanics for the purposes of enhancing the measurement accuracy of IOP and glaucoma risk evaluation. As corneal biomechanics have been shown to have a strong correlation with biomechanics in the posterior eye, including the tissues in the optical nerve head [146], [147], an alternative and more feasible option is to measure the corneal biomechanics. Thereby, the measurement of corneal biomechanics can help to increase the IOP measurement accuracy and may serve as a viable glaucoma risk indicator [138].
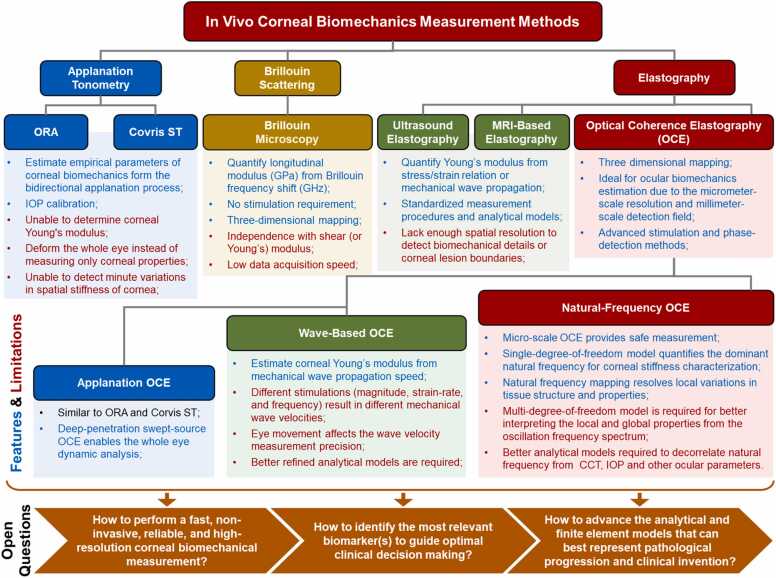
4. Methods of in vivo corneal biomechanics assessment
The in vivo estimation methods of corneal biomechanics are primarily derived from the following three approaches: applanation tonometer methods, such as the ocular response analyzer (ORA) and corneal visualization Scheimpflug technology (Corvis ST); Brillouin microscopy; and elastography methods, such as optical coherence elastography (OCE). Here, we introduce the basic concepts, applications, and limitations of these in vivo methods.
4.1. ORA and Corvis ST
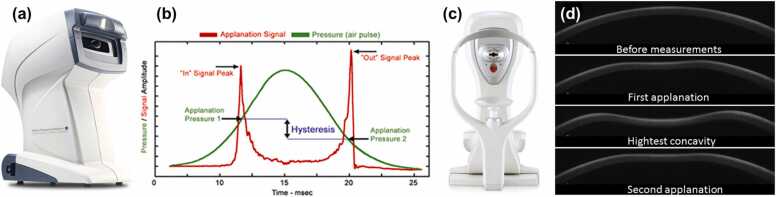
The first approach originated from the development of the ocular applanation tonometer. In 1957, Goldmann and Schmidt [148] invented the Goldmann applanation tonometer based on the Imbert-Fick law, which states that the IOP acting on a thin membrane sphere (cornea) is equal to the pressure required to flatten a small region of the membrane. So far, the Goldmann tonometer has been widely regarded as the gold standard for IOP measurement. In 1972, Grolman [149] designed the non-contact tonometer, which flattens the cornea for IOP calculation using an air puff rather than the contact probe (prism) used in the Goldmann tonometer. In 2005, Luce [39] developed the ocular response analyzer (ORA, Reichert Inc.; Buffalo, NY), which uses an air jet to induce the cornea to move inward, past applanation, through a small concavity, and then back to normal curvature, before recording the corneal deformation using an electro-optical infrared (IR) detection device (shown in Fig. 4a and b). ORA measurement is based on the pressures (P1 and P2) at the two applanation events, whereas P1 is greater than P2 because the cornea is viscoelastic and the stimulation energy is absorbed and dissipated. The Goldmann-correlated IOP value (IOPg) is denoted as the average of the two pressures, and corneal hysteresis (CH) is defined as the difference between P1 and P2. The corneal resistance factor (CRF) and corneal-compensated IOP (IOPcc) were then developed empirically. The CRF was designed to have the highest correlation with the central corneal thickness (CCT), while the IOPcc was designed to have minimal differences before and after refractive surgery [150], and has been recognized with more accurate intraocular pressure estimation than IOPg [151]. The equations are listed below [53].
| (1) |
Fig. 4.
Demonstration of the ocular response analyzer (ORA) and corneal visualization Scheimpflug technology (Corvis ST). (a) ORA system. (b) Applanation and air pressure signals for intraocular pressure and corneal biomechanics estimation. (c) Corvis ST system. (d) Corneal displacement dynamic profiles. (a, b) Reproduced from http://www.reichert.com/. (c) Reproduced from [156]. (d) Adapted from https://www.oculus.de/.
The formulas enclosed by brackets are the commonly accepted equations. However, the phenomenon of CRF> CH always appears in clinical measurement, which is contrary to common sense [53]. Thereby, the constants (a–e) in Eq. (1) are calibrated based on regression for better results. The value of CRF is highly correlated with CH and CCT, and CH is often considered a more clinically relevant biomarker than CRF. It should be noted that the cornea is nonlinearly viscoelastic, and the mechanical performance of the cornea depends not only on the magnitude but on the rate of the applied force [152]. Typically, a faster strain rate results in a stiffer corneal response [153]. Clinical experiments have shown that raising the pressure amplitude has little effect on P1 but does affect P2, which influences the assessment of CH [152]. To minimize this effect, the current ORA sets the maximum pressure Pmax in relation to an individual’s P1 value, as Pmax = 1.1713P1 + 28.106 (mmHg) [154]. In addition, CH is affected comprehensively by various combinations of corneal thickness, elasticity, viscosity, IOP, and hydration; thus, CH alone cannot represent corneal biomechanical properties, such as stiffness or Young’s modulus [155].
Based on the similar bidirectional corneal applanation concept, the Oculus corneal visualization Scheimpflug technology (Corvis ST, Scheimpflug Technology; Wetzlar, Germany) captures the air-jet-induced (maximal pressure: 25 kPa) corneal deformation of a single 8-mm horizontal slit with 140 frames in 31 ms using a high-speed (4300 frames per second) Scheimpflug camera (Fig. 4c and d) [40]. The IOP is determined based on the first applanation event; the deformation amplitude (DA) is calculated as the maximum displacement of the apex in the highest concavity moment (HC); and the applanation length (AL) and corneal velocity (CVel) are recorded during the ingoing and outgoing periods. It should be noted that the ORA sets the maximum pressure based on the P1 value, whereas the Corvis ST produces a consistent air puff that has a symmetrical configuration and fixed maximal internal pump pressure. Due to the interaction between the different air-puff profiles and the nonlinear viscoelasticity of the cornea, the detailed deformation features and the observed biomechanical parameters are likely to differ between these two devices, despite the similar biomechanical performance trend: for example, a stiffer cornea deforms more slowly, with less magnitude, and recovers more quickly [53].
To date, the ORA and Corvis ST are the only two clinically available devices for corneal biomechanics calculation, and both instruments have been used widely in the clinic for the diagnosis of corneal pathologies (keratoconus [157], [158], glaucoma [156], [159]) and evaluation of medical or surgical treatment (e.g., refractive surgery [160] and CXL [161], [162]). However, these two clinical instruments suffer from several limitations. First, they are unable to determine Young’s modulus of the cornea or analyze its elasticity, viscosity, or stiffness independently. Although some pioneering tonometer studies have claimed Young’s modulus estimate from corneal applanation process [103], [104], [105], [106], these estimation results are considered inaccurate due to being heavily dependent on IOP levels. For example, the tonometer results [103] in the estimations of corneal Young’s modulus with aging contradict prior studies [94], [95] (Fig. 3). Second, as the clinical measured parameters (such as CH and CRF) are affected by a combination of many factors (corneal thickness, elasticity, viscosity, IOP, and hydration), accurate assessment of corneal biomechanics using these observed parameters is usually not possible [53]. Third, the clinical air-puff approach employs large-magnitude (70–300 kPa) and long-duration (10–30 ms) stimulation, which not only results in corneal displacement from a convex to a concave form but also produces the motion of the entire ocular tissue and aqueous fluid [163], [164]. These factors confound measurements of corneal biomechanical properties and preclude any possibility of spatially resolved measurements that would be necessary to detect minute variations in spatial stiffness [165], such as in early stage keratoconus where local weakness occurs [166]. It is because of these limitations that clinical trials have shown conflicting outcomes, such as the measured corneal stiffness results for keratoconus patients undergoing CXL treatments [157], [158], [167], [168].
4.2. Brillouin optical microscopy
In 1922, Brillouin [169] first reported the acoustically generated inelastic light scattering effect, which provides non-contact, label-free, and direct measurement of the viscoelastic characteristics of a material, and has emerged as an attractive method during the past decade [170]. The phenomenon of Brillouin scattering is the result of an interaction between the light (photons) incident on a medium of interest and the spontaneous acoustic phonons (propagation of thermodynamic fluctuations) in the medium. As the propagation speeds of acoustic phonons are associated with the mechanical properties of the material, quantification of the frequency shift caused by the acousto-optic interaction can enable elastic parameter estimation. The resulting frequency shift Ω and the line width ∆Ω of the Brillouin spectrum are related to the longitudinal viscoelastic modulus M, which can be defined by the complex equation [171], [172].
| (2) |
where M’ and M’’ are the longitudinal elastic modulus and viscous modulus respectively, ρ is the mass density, λ is the optical wavelength, and n is the refractive index.
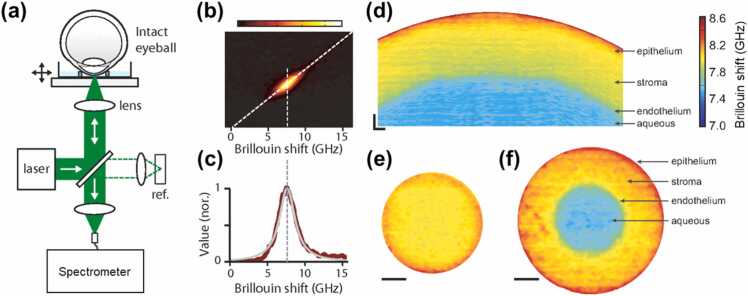
We have reproduced Fig. 5 from reference [173] to briefly illustrate the Brillouin optical microscopy and its imaging with Brillouin shift values (in the GHz range). As shown in Fig. 5a, Brillouin optical microscopy is mainly comprised of a confocal microscope and an optical spectrometer [174]. The Brillouin shift of typical materials is in the order of GHz (Fig. 5b and c), which corresponds to a wavelength of< 0.01 nm, providing difficulties for the development of a fast and high-resolution spectrometer. Multipass scanning Fabry–P é rot etalon interferometry [175] has been utilized for decades, such as in the material characterization of the cornea and crystalline lens of the eye [171], [176]. Early biological demonstrations were single-point and primarily ex vivo given that scanning Fabry–P é rot spectrometers capture spectral components sequentially and at limited throughput, resulting in extended data acquisition time [174]. The recently developed multistage virtually imaged phased array (VIPA) spectrometer [177] has enabled better throughput, less noise, faster imaging speed, and higher frequency resolution (sub-GHz range) of the Brillouin frequency shift, which has resulted in more precise measurements of the Brillouin longitudinal modulus (Eq. (2)). Cross-sectional Brillouin imaging of the cornea (Fig. 5d) reveals a noticeable depth-reduced Brillouin frequency shift, indicating that the Brillouin longitudinal modulus is greater in the anterior corneal area and decreases gradually toward the endothelium. Compared to the depth (axial) variation, the normal cornea has substantially less change laterally at the same depth from the corneal surface (Fig. 5e and f).
Fig. 5.
Brillouin optical microscopy and its corneal imaging reproduced from reference [173]. (a) Schematic of a Brillouin microscopy set-up. (b) A typical CCD output from the spectrometer displaying the Brillouin spectrum of the corneal stroma. (c) Brillouin spectrum (red trace) analysis using Lorentzian curve fit (gray trace). (d) Cross-sectional Brillouin image of the ex vivo bovine cornea. The Brillouin shift is a decrease in depth, revealing the depth-decreased longitudinal modulus. The horizontal (x) and vertical (z) span is 5 × 0.5 mm. Scale bars: 200 µm. (e) and (f) En face Brillouin image of the cornea at different depths. Scale bars: 1 mm.
Brillouin microscopy does not require any stimulation or corneal deformation and is capable of a three-dimensional Brillouin shift (longitudinal modulus) estimate with an optical resolution, making it a potential technique for clinical translation [41], [42], [43]. Ex vivo study of corneal Brillouin imaging has shown distinguishable Brillouin frequency shifts among normal and Keratoconus corneas [178], before and after collagen crosslinking [172], [179], [180]. Recently, Shao et al. [42] conducted a clinical study including 85 human individuals (93 eyes), including 47 healthy volunteers and 38 patients with varying degrees of keratoconus (stages I–IV). They demonstrated an increase in biomechanical inhomogeneity in the cornea as keratoconus progresses, as well as the biomechanical asymmetry between the left and right eyes during the outset of keratoconus [42].
Several limitations on the clinical applicability of this approach should be recognized. First, the Brillouin ophthalmic instrument requires> 0.2 s per depth point and ∼10–20 s per axial scan at a single point on the cornea. The total data acquisition time is very long depending on the sampling density (e.g., 4–8 min, 12 s per axial scan, 20–40 total axial scans [42]), making the measurement very susceptible to motion artifacts caused by patient eye movement during long-time data acquisition [41]. Second, the Brillouin longitudinal modulus does not directly correlate with the shear (or Young’s) modulus, whereas the latter can better describe the elasticity or stiffness a clinician can feel by touching the tissue [181]. Although longitudinal and Young’s moduli are independent, these two moduli may exhibit simultaneous changes (either increasing or decreasing) throughout physiological or pathological processes in vivo. For example, both moduli would increase (decrease) when the thickening (thinning) of collagen fibrils occurs in the cornea stroma [181]. Third, Brillouin microscopy measures a frequency shift in the cornea at gigahertz (GHz) frequencies, and the associated longitudinal modulus is in the gigapascals (GPa) range. This is orders of magnitude more than Young’s modulus (typically, the corneal Young’s modulus is in the kPa to tens of MPa range, Fig. 3). It is important to use caution when attempting to link longitudinal and shear moduli and interpret Brillouin outputs, as they are independent and have a large magnitude difference. Notably, it remains impossible to predict the value of one modulus from the other as of yet [170].
4.3. Elastography methods
For millennia, palpation has been used as a component of physical examination to diagnose and locate diseases by feeling the stiffness changes in tissue. Similarly, elastography methods can access tissue biomechanics by observing the tissue’s response (e.g., strain and mechanical wave) to the loading force and detect subtle alterations in tissue stiffness, which may be caused by the changes in tissue structure, health, aging, and function [182], [183], [184]. In general, tissue biomechanics are anisotropic, viscous, and nonlinear, with these measured parameters varying based on the direction, extent, and rate of deformation. The elastography method usually employs a simple first-order linear assumption of an elastic and isotropic material, where the tissue mechanical property can be more easily expressed using a simple elastic modulus [184]. Since 1990, when ultrasonic devices were first demonstrated in elastic imaging of tissues and whole organs [185], [186], multiple elastic imaging modalities have been developed to assess the changes in the mechanical properties at the organ, tissue, or cellular levels [187], [188], [189], and to diagnose diseases such as liver fibrosis [190], cardiovascular diseases [191], and breast [192] and prostate [193] cancers. Unlike the subjective nature of physical palpation, elastography uses non-invasive, high-resolution imaging methods to produce objective and quantitative diagnostic results. However, non-invasive in-vivo evaluation of human corneal biomechanical properties using the elastography method remains a great challenge [11].
The elastographic imaging resolution, field-of-view, imaging speed, and displacement sensitivity are majorly determined by the imaging modality (e.g., ultrasound, MRI, or OCT) [195]. Fig. 6 demonstrates a common classification scheme for the major elastic imaging modalities according to their relative spatial resolution and penetration depth. The detailed comparison among these modalities has been explained extensively in previous reviews [184], [194], [195]. In brief, AFM contributes to a wide variety of research in cell mechanics and cell biology by applying a sub-nano Newton contact force to load the cell membrane and detect the resulting deformation with nanometer-scale precision [36]. Due to its limited field of view and measuring process, AFM has been mainly applied to cultured cells [196], [197].
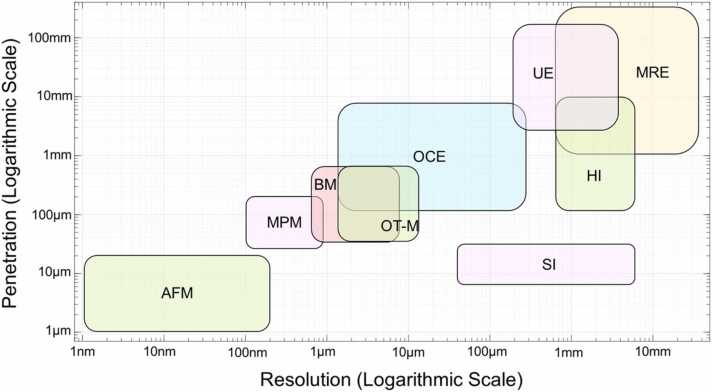
Fig. 6.
Comparison of elastic imaging modalities in the map of detection scale (penetration depth vs spatial resolution). AFM: Atomic force microscopy, MPM: Multiphoton microscopy, BM: Brillouin microscopy, OT-M: Optical tweezers-based microrheology, OCE: Optical coherence elastography, SI: Speckle Interferometry, HI: Holographic imaging, UE: Ultrasound elastography, MRE: Magnetic resonance elastography. This figure was modified based on previous review work [184], [194], [195].
Ultrasound elastography (UE), magnetic resonance elastography (MRE), laser speckle elastography (LSE), and holographic imaging (HI) have a macroscopic level of spatial resolution ranging from hundreds of micrometers to several millimeters [198], [199], [200], which prevents their further use in the imaging of the biomechanical details of the corneal substructure. UE and MRE have been extensively employed in today’s clinical settings, including for cancer diagnosis [201], [202]. Although their application in corneal biomechanical imaging has been reported [45], [46], [203], they are not widely adopted methods due to the lack of appropriate resolution and the difficulty in determining the boundaries of corneal lesions. Because of the sensitivity of the cornea to the applied force and the effect of eye motion, the development of micro-stimulation, non-invasive, high-speed, and high-resolution corneal elastography modalities represents the current trend in clinical corneal biomechanical evaluation [204]. Among these elastography modalities, optical coherence elastography (OCE) [205]—based on optical coherence tomography (OCT) imaging [206]—can provide micron-scale resolution in both the axial and lateral directions, which exceeds the resolution of UE or MRE. The phase-sensitive OCT detection techniques [207], [208], [209] can further enhance the dynamic mechanical response resolution into a sub-nanometer scale [49], [210]. The field of view and tissue penetration capability of the OCT/OCE system is in the range of up to ∼10 millimeters. The spatial coverage and resolution of the OCE system have bridged the gap between single-molecule biophysical techniques (e.g., AFM) and the organ-level medical elastographies (e.g., UE and MRE) [194], [211], making it an ideal device for ocular biomechanics estimation [204]. More recently, OCE methods have been used to characterize in vivo corneal biomechanical properties by observing shear-wave propagation [22], [47], local [212] or global tissue displacements [164], [213], [214], [215], and corneal mechanical resonance frequency [49], [50]. The detailed methodologies and the use of OCE for in vivo corneal biomechanics estimation are presented in Section 5.
5. In vivo OCE
5.1. OCE loading and detection strategies
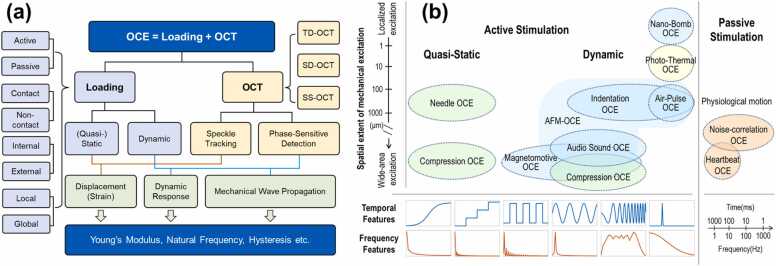
OCE employs a loading system to apply stimulation forces and an OCT system to observe the subsequent tissue displacements (strains) or mechanical waves for tissue biomechanical property estimation (OCE = Loading + OCT). Fig. 7a briefly summarizes the OCE system according to the loading method and OCT detection method. Numerous loading strategies have emerged as a result of the development of OCE for multiple applications, such as static [216], [217] or dynamic bulk compression [205], [218], [219], [220], needle probe compression [221], [222], magnetomotive [223], [224], nano-bomb [225], [226], audio sound [50], [227], pulsed laser (photothermal excitation) [228], [229], ultrasound [230], [231], [232], and air-coupled ultrasound [233], [234], [235]-induced acoustic radiation force (ARF), air puff/pulse indentation [236], [237], [238], and passive sources, such as the heartbeat [239] and noise-correlation approach [240]. These loading strategies can be sorted into different categories (Fig. 7a), such as active or passive loading, contact or non-contact loading, (quasi-)static or dynamic loading, internal or external loading, and local or global loading methods [194], [241].
Fig. 7.
Classification of the optical coherence elastography (OCE) technique based on (a) the loading and OCT detection strategies, and (b) the tempo-spatial characteristics of mechanical loading strategies in OCE techniques. (b) An update from previous reviews [195], [211]. ARF: Acoustic radiation force.
Based on the temporal, frequency, and spatial scales and characteristics of the excitation profiles, in addition to the associated OCT detection methodologies, the OCE detection methods can be divided into two categories: static (or quasi-static) OCE and dynamic OCE. The aforementioned loading methods can be organized into a tempo-spatial map, as illustrated in Fig. 7b. Previous reviews have delved into great detail addressing the contents of both static and dynamic imaging using ultrasound elastography [184], [242] and optical coherence elastography [195], [211]. These reviews provide further information for the readers. From a spatial extent, the wide-area excitation, such as bulk compression, loads the sample globally, while the local excitation, such as needle and indentation methods, can apply the force to a particular region. From the perspective of mechanical reconstruction, wide-area excitation may necessitate more information about the local stress distribution, which is dependent on the boundary conditions (such as the interface between layers or the presence of a stiff inclusion), which are typically outside the OCT detection fields [195]. Notably, OCT imaging only has a millimeter-scale field of view and penetration depth, so it can only image features close to the sample surface [243]. From the temporal and frequency contents, the (quasi-) static OCE characterizes the sample under very slow motion so that the time-dependent effects (e.g., viscosity) are small or negligible. In contrast, the dynamic OCE, including step, harmonic (sinusoid signal), spectroscopic (chirp signal), or impulse loading methods, characterize the sample response with faster motion features (such as resonation and wave propagation), and these induced motions are strain-rate- and frequency-dependent. Thus, it is essential to characterize the excitation method in the temporal and frequency domains to accurately analyze motion characteristics, such as the potential evoked frequency range [49], [50], [244], [245] and the phase velocity, which is frequency dependent in a viscoelastic sample such as the cornea.
OCT is a non-invasive imaging method developed from the principle of the Michelson interferometer. In the 30 years since Huang et al. initially proposed time-domain optical coherence tomography (TD-OCT) [206], OCT technology and its functional extension (such as OCT angiography) have continued to evolve and advance in addition to revolutionizing clinical eye care [246], [247], [248], [249]. The clinical applications of the original TD-OCT devices were limited by the low axial resolution (10–15 µm) and limited number of A-scans [250], while the advancement of spectral-domain OCT (SD-OCT) [251] has enabled better axial resolution (e.g., ∼3–5 µm) and faster imaging speed (e.g.,>100 kHz) with an increased number of A-scans. SD-OCT allowed the visualization of microstructures in the anterior [252] and posterior [253] segments of the eye to reach a level of detail comparable to histopathology [254], [255]. Swept-source OCT (SS-OCT) was first described as an alternative OCT approach in 1995 [256], although it has only lately advanced for ocular imaging [257]. Although both SD-OCT and SS-OCT are classified as Fourier-domain OCT (FD-OCT) technology, their configurations are different. The former employs a broadband diode light source and measures the interference spectrum with a spectrometer and a high-speed line scan camera, while the latter makes use of a tunable laser sweeping through a narrow range of wavelengths and a dual-balanced photodetector. Recently developed linear-in-wavenumber (linear-k) spectrometers [258], [259] allow for optical dispersion of the interference spectrum in k-space, which effectively enhances the detection sensitivity in depth for the SD-OCT system [260]. SS-OCT uses higher-speed swept sources (e.g.,>MHz A-scan rates [261], [262]), allowing faster data acquisition speed and minimal motion artifacts. SS-OCT also demonstrates superior axial resolution and depth penetration capability in tissue imaging. Due to the time jitter issue that exists in the swept-source, the present SD-OCT has greater phase stability than the SS-OCT when it comes to the application of phase-based detection [210].
Speckle tracking and phase-sensitive detection are the two primary detection methods in OCE. The former approach is primarily applied in the early stages of (quasi-) static OCE measurements, whereas the latter is mostly utilized in the more recent stages of dynamic OCE measurements. Early research has demonstrated that the reflection of a laser beam from a rough surface has a distinctive granular or mottled appearance (laser speckle), and the dark and bright speckles have no obvious relationship with the texture of the surface of the sample but tend to change their pattern whenever the sample moves slightly [263]. In OCT imaging of highly scattering biological tissues, speckles arise as a natural consequence of the limited spatial-frequency bandwidth of the interference signals measured in OCT. This phenomenon is affected by several factors, including the optical properties and motion of the sample, the size and temporal coherence of the light source, and multiple scattering and phase aberrations of the propagating beam [264]. As such, the speckle phenomenon serves a dual role as a source of noise and as a carrier of information on the tissue microstructure and motion. In speckle tracking OCE, the cross-correlation of a multi-pixel kernel among cross-sectional images from the same or nearby location is typically used to compute the vectorial displacement (strain) of the sample under quasi-static loading. This process necessarily reduces the spatial resolution of the elastogram, while the interpolation method can improve the displacement measurement sensitivity to a sub-pixel scale [265]. Thereby, the detection resolution of the speckle is several micrometers, similar to those of OCT spatial resolutions, with the axial resolution as , and the lateral resolution of , where is the central wavelength, is the bandwidth, and NA is the numerical aperture. The latterly developed digital volume correlation (similar to the widely used digital image correlation method, but developed for volumes instead of cross-sectional images) can efficiently avoid the out-of-plane deformation artifacts that exist in the cross-sectional images and enable measurement of the full strain tensor [266], [267]. Given the long data acquisition time and low spatial resolution, the combination of compression, TD-OCT, and speckle tracking method is primarily used in the early research of OCE [268], [269], [270], [271], [272], [273], [274].
Advances in the phase-sensitive detection technique [207], [208], [209] for OCT imaging provide much greater sample dynamic displacement sensitivity and enable the visualization and analysis of the shear wave propagation in dynamic OCE [219], [241]. Displacement values can be analyzed via the phase variation of successive scans for the same locations. is the phase difference between A-scan and the reference A-scan as
| (3) |
where represents the phase angle of the complex signal, is usually in the range of -π to π, and the unwrapped phase difference can be used to represent the displacement as
| (4) |
where n is the refractive index.
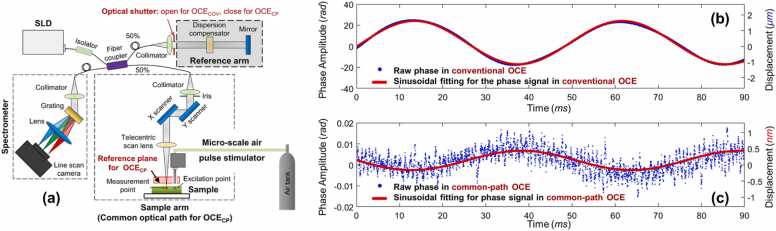
In phase-sensitive OCT, the detection sensitivity is determined by signal-to-noise ratio (SNR), as [275], as well as the phase stability. The phase stability can be affected by the environmental vibration existing between the sample and reference arms, which represents a major source of optical phase fluctuations. The common-path OCT configuration [210], [276], where the sample and reference arms share the same optical path (Fig. 8a), can provide intrinsic compensation for polarization and dispersion mismatches induced by optical elements (e.g. fibers and lenses), and can effectively reduce the imaging system’s susceptibility to vibration, thereby increasing the system’s physical stability and optical phase detection sensitivity (Fig. 8b and c).
Fig. 8.
Common-path configuration can effectively reduce phase instability. (a) Common-path OCE was made by blocking the reference arm in a conventional OCE while using a flat surface (sample-side optical surface of the reference plate) between the scan lens and sample as the new reference plane. (b) and (c) illustrate two examples of the low-frequency sinusoidal pattern of background noise measured in conventional OCE and common-path OCE, respectively (note the different y-axis scale).
Reproduced from [210].
5.2. Analytical models for OCE
5.2.1. Shear and Young’s moduli
The relationship between a sample’s response (e.g., displacements and mechanical waves) and mechanical loading is the basis for mechanical measurement, and the displacement at each spatial position of the sample is the most fundamental form of measurable sample response. In a homogeneous, linear elastic, and isotropic sample, the relationship between stress (σ, force per unit area) and strain (ɛ, proportional deformation) can be expressed through a generalized form of Hooke’s law for a simple mechanical spring, as [211], [277].
| (5) |
where σ is the stress tensor, ε is the strain tensor (, u is the displacement field, xi and xj are the spatial coordinates), and H is a fourth-order stiffness tensor connecting stress and strain. Eq. (5) takes the form of a 3D Cartesian space as
| (6) |
where K and G are the bulk and shear moduli that can be written in complex forms. The longitudinal modulus . The elastic modulus (or Young’s modulus E) refers to the ratio of the uniaxial stress to strain in the same direction (i = j), whereas the shear modulus (G) relates shear strain with stress in any ij-plane (i ≠ j). Young’s modulus E can be associated with the shear moduli using , where is Poisson’s ratio, defined as the ratio of transverse elongation to axial compression ( since most tissues are nearly incompressible). Thereby,
| (7) |
In wave-based measurement (as most elastography methods employed, Section 5.3.2), the shear waves velocity () is related to the shear modulus G and tissue density ρ, and under certain assumptions, to Young’s modulus E, which are important biomechanical parameters that have been used to characterize tissues in normal and pathological conditions, as
| (8) |
It should be noted that the shear, elastic moduli can be frequency-dependent and written in complex forms. The shear modulus of a viscoelastic tissue can be represented using a frequency-dependent, complex form
| (9) |
where and are the storage and loss moduli, respectively, and is the angular frequency (). Thereby, the shear wave speed and shear modulus in Eq. (8) can be represented using a complex form
| (10) |
The complex shear wave speed shows no physical meaning, but the frequency-dependent phase velocity can represent the shear wave profiles. The wave number can be written in a complex form as [278].
| (11) |
The frequency-dependent phase velocity , can be acquired from two dimensional Fourier transform from the tempo-spatial relation of the propagation waves. The imaginary part represents the attenuation factor of the shear wave during propagation. The shear complex modulus in Eq. (9) can also be represented by and , as
| (12) |
For harmonic steady-state excitation in a Kelvin-Voigt model, the time derivative becomes , and the shear modulus can be written as [277].
| (13) |
where is the real shear modulus and is the shear viscosity. and can be represented as
| (14) |
where , , and the phase velocity is
| (15) |
At low frequencies, ; when , . Thereby, is a transition frequency that divides the low-frequency region where the phase velocity is dominated by the stiffness from the high-frequency region where it is dominated by its viscosity [277].
The above equations are based on the assumption that the tissue is homogeneous, isotropic, and linear elastic (i.e., and are the same in any direction). Some other analytical models have been proposed in OCE applications, such as body waves (shear and compression waves), longitudinal shear waves (LSW) [279], and surface acoustic waves (SAW), which can be Rayleigh/Scholte or Lamb waves depending on the coupling media and boundary conditions. The detailed mathematical description of these mechanical wave models can be found in a recent review presented by Zvietcovich et al. [278].
5.2.2. Natural frequency
Natural frequency is an intrinsic property of a sample, which is defined as the frequency at which the sample tends to oscillate when disturbed [280]. Natural frequency oscillation in response to excitation force is intimately connected to tissue elastic properties [49], [244], [245]. It has been demonstrated that the natural frequency is linearly related to the square root of Young’s modulus in a simple elastic model.
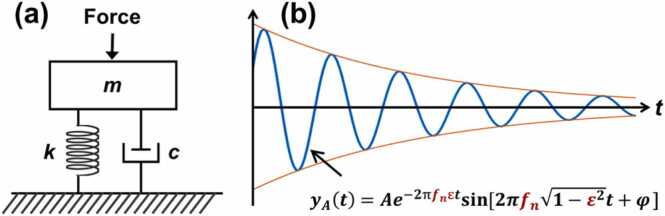
In a single degree of freedom (SDOF) model (as shown in Fig. 9 [244]), natural frequency fn can be calculated as , where k is spring stiffness and m is the mass; the damping ratio is defined as , where c refers to the viscous damping coefficient. In an under-damped condition (ε < 1), the motion of the free response of a SDOF system is described as [244].
| (16) |
where yA(t) is the time-dependent displacement profile of the center of mass. The solution of this equation (when ε < 1) in the time (t) domain is
| (17) |
where A is the initial amplitude, φ is a phase value, denotes the envelope decay function with time, and represents the resonant feature. The damped natural frequency (fd) is defined as , which can be acquired directly as the dominant resonant frequency via fast Fourier transform. Although the cornea is actually a multiple-degrees-of-freedom (MODF) oscillation system with multiple layers and boundaries, the SDOF analytical approach of Eq. (17) can be utilized to access the dominant oscillation features (i.e., the dominant natural frequency fn), which are related to the major property of the cornea.
Fig. 9.
Natural frequency oscillation in response to excitation force in a single degree of freedom (SDOF) spring-mass-damper system. (a) Schematic of a spring-mass-damper model. m: Mass, k: Spring stiffness coefficient, c: viscous damping coefficient. (b) Logarithmic decay oscillation response in an under-damping situation (0 ≤ ε < 1). fn: Natural frequency, fd: Damped natural frequency, ε: Damping ratio, A: Original oscillation amplitude, B: Decay coefficient.
Reproduced from [244].
5.3. In vivo corneal biomechanics assessment using OCE
The performance of OCE has been rapidly improved in the following ways since Schmidt first developed this technique in 1998: (1) The OCT resolution has been significantly enhanced, from micron-scale (speckle tracking method) to the sub-nanometer scale dynamic detection resolution (phase-sensitive detection); (2) the data acquisition speed has been increased by several orders of magnitude, with 1.5 million A-lines per second in the most recent advancement in SS-OCT; (3) various excitation methods have been developed, which expands the applicability of the OCE approach to broader fields and permits greater flexibility across a broad spectrum of temporal and spatial scales; and (4) the analytical and finite element models have been evolved from simple, isotropic models through inhomogeneous and viscoelastic models to complicated analytical and finite element models that account for corneal geometry, boundary conditions, and intraocular pressures, among others. Due to the recent developments in non-invasive, high-speed, and high-resolution OCE techniques, in vivo estimation of corneal biomechanics has been made possible through various OCE approaches, such as applanation OCE, wave-based OCE, and natural frequency OCE.
5.3.1. Applanation OCE
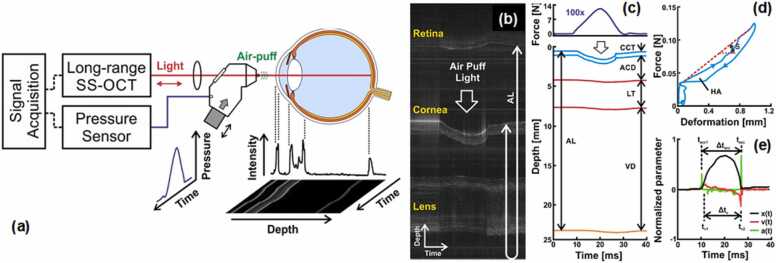
The first attempt at in vivo corneal OCE imaging involved combining the OCT system with a commercial air-puff device from a non-contact tonometer [281], which is similar to those of the ORA and Corvis ST tonometers (Section 4.1). The air pipe has a diameter of 3 mm and delivers an airflow that lasts ∼20 ms, deforming the cornea in a scale of several millimeters. In 2019, Maczynska et al. [164] measured 20 eyes of 20 healthy subjects using the air-puff applanation OCE method (See Fig. 10). Fig. 10a illustrates the OCE system setup. Fig. 10b demonstrates typical M-mode scan imaging of the induced dynamics of the ocular components (from top to bottom: retina, cornea, and lens) during the air-puff cycle, where the retinal signal is aliased at the top to cover the entire depth of the ocular tissue. Fig. 10c demonstrates the temporal displacement profile of the ocular components in response to the air-puff profiles (maximum force: ∼14 N). Fig. 10d demonstrates the hysteresis loop of the cornea, where HA represents the hysteresis area, and S represents the slope of the loading curve. Compared to the CH value measured by ORA (the pressure difference between the two corneal applanation events), OCT/OCE can record the whole hysteresis curve of the cornea during the loading and unloading process. In a more recent study, a micrometer scale (rather than a millimeter scale) tissue hysteresis method was provided by microliter air-pulse OCE; however, it has not yet been applied to the in vivo cornea measurement [85]. Fig. 10e shows the motion dynamic parameters of the corneal apex, including corneal apex displacement, velocity, and acceleration profiles. Although this method possesses the advantages of clinical instruments (ORA and Corvis ST), it also suffers similar limitations as discussed in Section 4.1. Briefly, these methods all involve a wide-area excitation method for corneal applanation, which not only deforms the cornea in the order of millimeters but also deforms all the ocular components up to the retina (Figs. 10b and 10c), making it difficult to quantify the minimal mechanical variations due to the lack of sufficient spatial resolution.
Fig. 10.
Estimation of corneal biomechanics by combining an SS-OCT with a commercial air-puff device from a non-contact tonometer. (a) Schematic of the air-puff OCE. (b–e) Representative air-pulse-induced dynamics of the ocular components (i.e., cornea, lens, and retina) from the right eye of a 23-year-old subject. (b) M-mode scan during the air-puff cycle. (c) Temporal force and displacement profiles. (d) Corneal hysteresis loop. (e) Air puff-induced corneal deformation, speed, and acceleration.
Reproduced from [164].
5.3.2. Wave-based OCE
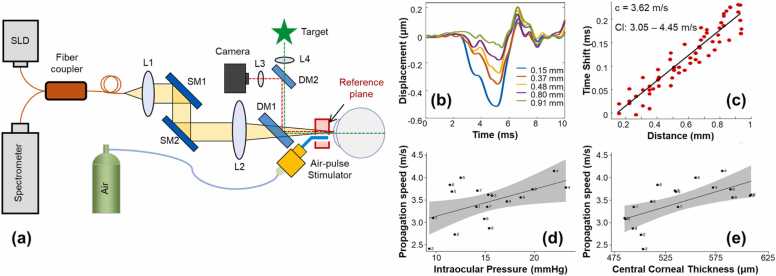
The wave-propagation-based OCE method is the most utilized OCE method to determine tissue Young’s modulus using different types of wave models, mainly in the shear direction. In 2020, Ramier et al. [47] utilized an OCE system with a vibrational contact probe (diameter: 2 mm) driven by a pair of acoustic transducers (20 mN, frequency: 2–16 kHz) to determine the shear modulus of human corneas. The measured Rayleigh-wave speed in 12 healthy subjects (age: 25–67 years, seven males and five females, IOP: 13–18 mmHg) was 7.86 ± 0.75 m/s, corresponding to a shear modulus of 72 ± 14 kPa (and a Young’s modulus of 216 ± 42 kPa using Eq. (7)). However, there was no correlation between the wave speed and IOP or central corneal thickness [47]. Also in 2020, Jin et al. [48] utilized the air-pulse based OCE method (pressure: ∼150 kPa, force: 1.73 mN) to measure 12 corneas from eight healthy subjects (four females, four males, age: 24 ± 1 years, IOP: 10.4–16.6 mmHg) and the measured Lamb (Scholte) wave velocity and Young’s modulus were 12.73 ± 1.46 m/s and 733 ± 164 kPa, respectively. In 2021, Lan et al. [22] combined high-resolution common-path OCT imaging with a microliter air-pulse stimulation (Fig. 11a) to induce submicron corneal surface displacement amplitude (Fig. 11b) and measure the surface wave propagation in the spatio-temporal domain (Fig. 11c) in 18 eyes from nine healthy participants (three females, six males, age: 27 ± 5 years, IOP: 9.3–23.2 mmHg). The air-pulse stimulation was similar to that of reference [48] but had much lower stimulation pressure (13 Pa). The group velocity of the surface waves was 2.4–4.2 m/s (mean: 3.5 m/s; 95% confidence interval: 3.2–3.8 m/s) and was correlated with the central corneal thickness (r = 0.64, P < 0.001) and IOP (r = 0.52, P = 0.02), as shown in Fig. 11(d, e) [22]. Although this paper did not connect the surface wave speed to Young’s modulus, an estimation of Young’s moduli can be made in the range of 14.6–58.2 kPa (mean: 40.43 kPa, 95% confidence interval: 33.8–47.7 kPa) using a surface wave equation , where represents the group velocity, and the density) and Passion’s ratio can be assumed as 1000 kg/m3 and 0.5, respectively.
Fig. 11.
In vivo corneal surface wave characterization using microliter common-path OCE. (a) The OCE system was combined with a fixation target and an iris camera to monitor the measured area, a microliter air-pulse stimulator (pressure: 13 Pa) was used to provide localized tissue excitation, and a common-path OCT was used to image the resulting mechanical waves and natural frequency oscillation behavior. SLD: 845 nm superluminescent laser diode, L1–L4: Lenses, DM1–2: Dichroic mirrors, SM1–2: Galvanometer scanning mirrors. (b–d) Corneal surface wave quantification. (b) Typical induced corneal displacement profiles that attenuate their magnitudes along the surface wave propagation path. (c) Typical estimation of the wave speed using a linear-fitting method in the spatio-temporal domain. (d) and (e) show the correlation between the group velocity of the corneal surface wave with the intraocular pressure and central corneal thickness, respectively.
Reproduced from [22].
Comparing the existing wave-based OCE results for in vivo human cornea imaging, the remaining limitations are obvious [22], [47], [48]. First, there remains no proper eye-tracking device designed for anterior segment OCT; therefore, the physiological eye-motion (from bulk motion, respiration, heartbeat, and ocular pulsations) [212] is a major source of noise when attempting to measure corneal mechanical wave propagations in vivo. Although the fixation target and iris camera are helpful to partially compensate the anterior segment motion (Fig. 11a), the average coefficient of variation for corneal displacement measurements was up to ∼ 17% when the induced displacements were –0.2 to –0.8 μm in amplitude [22]. Second, because of the nonlinear viscoelastic property of the cornea, different features (e.g., magnitude, strain-rate, and frequency) of stimulation approaches can evoke mechanical wave propagations with different velocities, even in the same cornea (Fig. 3 depicts the broad estimation range of the corneal Young’s modulus due to the nonlinear corneal property and different testing methodologies). These recent wave-based OCE studies have shown the following differences: wave propagation velocities and Young’s moduli of 7.86 ± 0.75 m/s and 216 ± 42 kPa (2-mm diameter vibrational contact probe, 20 mN, frequency: 2–16 kHz) in [47]; 12.73 ± 1.46 m/s and 733 ± 164 kPa (air-pulse, pressure: ∼150 kPa, force: 1.73 mN) in [48]; and 2.4–4.2 m/s and 14.6–58.2 kPa (microliter air-pulse, 13 Pa) in [22], respectively. In the future, it will be necessary to standardize the stimulation profile to distinguish between healthy and diseased corneas, as the wave propagation speeds and the interpretation of Young’s modulus are both influenced by the stimulation approach. Third, different analytical modeling may also result in different Young’s modulus estimation results. The shear wave model can be directly related to the shear or Young’s modulus and is widely applied by ultrasound- and MRI-based elastography in clinical applications such as diagnosing diseases of kidney and liver. However, the shear-wave model is insufficient to describe the biomechanical properties from the OCE observing mechanical wave propagation in the cornea due to the complicated layered geometry and boundary conditions of corneal tissue [282]. Moreover, the shear/Young’s moduli may be different under the same measured wave velocity, when the cornea is considered semi-infinite by the shear or surface acoustic model; a thin-plate, isotropic, and viscoelastic tissue by the Lamb wave model; or a thin-plate, transverse isotropic, and elastic tissue by the modified Lamb wave model [278]. A standardized analytical approach for mechanical wave propagation in the cornea is also required when attempting to apply wave-based OCE in clinical applications.
5.3.3. Natural-frequency OCE
Natural frequency refers to the frequency at which the sample tends to oscillate when disturbed [280]. For decades, ultrasound-based vibrational spectroscopy has been used to evoke and measure the resonant frequencies of samples with known size and mass [283], [284], but the detection resolution is still limited [285]. Phase-sensitive OCE approaches, with greater spatial and frequency resolutions, have been recently applied for vibrational or resonant response characterization by applying a variety of loading strategies, including an acoustic radiation force (ARF) ultrasound transducer [285], piezoelectric actuator [286] or mechanical wave driver [287], magnetomotive nanoparticle transducer [223], [288], [289], air pulse [49], [244], [245], and audio sound from a speaker [50], [227]. These dynamic OCE methods have demonstrated enhanced frequency contrast in the cross-sectional as well as volumetric imaging at certain excitation frequencies [285], [286], [287], [289], and high-resolution quantification of resonant natural frequencies by providing a wide-spectrum frequency stimulation simultaneously [49], [244], [245] or by sweeping the driving frequencies in step [223], [285], [286], [288], [289]. Natural frequency has been shown to be linearly correlated with the square root of Young’s modulus in a simple elastic model [223], [244], [285]. Spatially stimulated and measured natural frequency values can be used to recognize both the global and local features, including the locally variated mechanical properties of the heterogeneous samples [245].
Patient safety is a primary concern for clinical translation of the vibrational/natural frequency OCE technique. To avoid damaging the cornea or other ocular components, it is important to keep the force to a minimum value due to the resonance effect, which can induce relatively large corneal oscillations by relatively small forces. From the tempo-spatial characteristics point of view (Fig. 7b), the dynamic loading methods can be used to generate the corneal oscillation process. The spectroscopic method (i.e., using chirp signals that sweep the harmonic signals over a defined frequency range) can effectively evoke the oscillations in a specifical frequency range; however, this typically takes longer time and may cause discomfort or even harm during in vivo measurements of the human eye. In the tempo-frequency domain, a wider temporal stimulus duration results in narrower frequency bandwidth responses. In contrast, transient stimulation techniques (e.g., impulse indentation) can deliver broadband stimulation frequencies simultaneously, speeding up the data acquisition process while keeping patients at ease. In addition, non-contact, local stimulation methods are preferred for safety and high spatial resolution characterization of the corneal oscillation features.
In 2021, Lan et al. [49] proposed an air-pulse indentation OCE system (See Fig. 11a) for in vivo human corneal natural frequency quantification using a microliter air-pulse stimulator to provide low pressure (tens of Pa), transient, and broadband frequency excitation (∼0–1 kHz) with induced tissue damping oscillation magnitudes in the sub-micrometer to sub-nanometer range. Fig. 12a demonstrates the corneal deformation overlaid with the transient air pulse (up to 20 Pa, offline calibrated using 40 times measurement) in a time series. The oscillation features (red window) were characterized using a free response of the SDOF method, as described in Eq. (17), Section 5.2.2. Fig. 12b shows the FFT result, where the dominant resonant frequency () was 254 Hz, and the dominant corneal natural frequency () was 255 Hz. The natural frequency distribution, as well as the means and standard deviations in the horizontal and vertical directions, for the right corneas of two human subjects are displayed in Fig. 12(c–f). Fig. 12e illustrates the local variation of natural frequencies between the red-dash circle (241 ± 6 Hz) and the yellow-dash circle (260 ± 8 Hz). Fig. 12g shows the comparison results using different protocols with different measurement areas (from 2.5 × 2.5 mm2 to 1 × 1 mm2), sampling points (from 26 × 11 points to 3 × 3 points), and measurement times (from 28.6 s to 0.9 s). The natural frequencies ranged from 234 Hz to 277 Hz for the 20 corneas, and no obvious differences were observed among these three protocols. By comparing the in vivo corneal measurement that utilized the same optical system (Fig. 11a), the average coefficient of variations (CVs) were 17.0% for corneal displacements (magnitude: 0.2–0.8 µm) [212]), 19.3% for corneal surface wave speeds (2.4–4.2 m/s for 18 eyes) [22], and only 3.2% for corneal natural frequencies (234–277 Hz for 20 eyes) [49]). Thereby, the OCE natural frequency measurements have much better repeatability and reproducibility.
Fig. 12.
In vivo measurement of corneal natural frequency (NF) using a microliter air pulse OCE system (same as Fig. 11a) and the single degree of freedom (SDOF) modeling method (Section 5.2.2). (a) Typical profiles of air-pulse (20 Pa) and induced corneal displacement in a time series. The air pulse profile was calibrated as the means and standard deviations of 40 repeat measurements. The corneal damping oscillatory motion (in the red window) can be used for the SDOF analysis based on Eq. (7). (b) Fast Fourier transform for the corneal damping oscillations process. (c–f): Natural frequency (NF) characterization for ∼2.5 × 5 mm2 area (26 × 41 points; total time: 106.6 s) on the left and right corneas from two human subjects (air-pulse: 13 Pa). (g) Comparison of the NF (mean± SD) among three protocols with different measurement areas and time on 20 eyes from ten human subjects.
Reproduced from [49].
In 2022, Crespo et al. [50] utilized an OCE system with a spectrum of audio sound frequencies (50–250 Hz with 10-Hz steps) to stimulate and measure the corneal resonant responses with magnitudes in a millimeter scale. They observed five frequency peaks with the dominant frequencies as 148.7 ± 8.0 Hz (central cornea) and 147.2 ± 6.7 Hz (inferior cornea), respectively, from 32 eyes of 16 healthy adult participants. By utilizing an empirical equation (calibrated from soft tissue OCE measurement and uniaxial tensile testing [51]), the natural frequency () can be related to Young’s modulus (E) as
| (18) |
where d is the thickness of soft tissue. Using this equation, Crespo et al.’s work derived the in vivo human corneal Young’s moduli as 2.94 ± 0.40 MPa (central cornea) and 2.76 ± 0.28 MPa (inferior cornea) [50].
It is important to exercise caution when attempting to link the natural frequency to Young’s modulus using Eq. (18). While this is certainly an interesting concept, it should be noted that applying this first-order estimate to in vivo measurements of corneal biomechanics or clinical research could yield misleading results. Factors such as variations in stimulation methods, corneal curvature, boundary conditions, and intraocular pressures have not been addressed in this equation, and this could significantly impact the accuracy of the results. Notably, the cornea is non-linearly viscoelastic, and the Young's modulus estimated using natural frequency measurement should increase with the strain (force) applied to the cornea. Applying Eq. (18) directly to the results obtained by Lan et al.’s work [49] can overestimate Young’s modulus by as much as approximately 7.60–10.46 MPa (natural frequency: 234–277 Hz) when assuming a central corneal thickness of 0.5 mm. The work of Lan et al. [49], which used microliter air-pulse (13 Pa) OCE to stimulate sub-micrometer magnitude corneal displacements, should yield a much lower Young’s modulus value than the work (<3 MPa) of Crespo et al. [50], which generated millimeter-scale corneal displacements. However, results from these estimation methods disagree and could be off by an order of magnitude or more. One possible reason for this is that Eq. (18) was calibrated using macro-scale deformation OCE and tesile testing methods, whereas a micro-scale natural frequency empirical fitting equation should be specifically derived for the microliter OCE system that accounts for Young’s modulus, natural frequency, and tissue thickness. In addition, natural frequency is comprehensively affected by many factors, not only Young’s modulus and thickness, but also the mass, geometry, intraocular pressure, and, especially, tissue boundary conditions. To better understand the limitations and potential clinical use of the natural frequency measurements, more in-depth studies (e.g., more advanced analytical methods and more complex finite element eye models) are required to investigate the relationship between corneal natural frequencies and other ocular structural parameters (e.g., corneal center thickness, intraocular pressure, and corneal topography). Advancement in the analytical or finite element models can assist with understanding corneal biomechanics and improve the diagnosis of ocular diseases using the highly repeatable, reproducible, and sub-micrometer natural frequency measurements. Furthermore, natural frequency could be another alternative and complementary metric for characterizing corneal properties in clinical translation of the in vivo corneal OCE technique without the necessity to convert to Young’s modulus. However, this remains to be investigated through further natural frequency OCE studies, as the current literature provides only a limited number of studies on this topic.
6. Summary and outlook
Reliable assessment of corneal biomechanics can aid the diagnosis, classification, and treatment of ocular disease; however, the in vivo measurement of corneal biomechanical properties remains an open challenge. As the filed has progressed, our understanding of corneal biomechanics specifically and soft tissue biomechanics more generally has improved. There is a need for additional technical innovations related to elasticity imaging methods, mechanical stimulation methods, and the analytical models linking experimental observations to the underlying mechanical properties of interest. Current work on the cellular, molecular, and ultrastructural characteristics of corneal tissue continue to advance our understanding of the biological factors that drive normal and pathological clinical observations. Quantitative elasticity mapping for ocular tissues has great potential to advance our understanding of numerous clinical conditions affecting the eye such as glaucoma, cataracts, myopia, keratoconus, refractive surgery, and more. Nevertheless, these capabilities will have to address several challenges including the ability to quantify nonlinear viscoelasticity, complex boundary conditions, and soft tissue frequency dispersion characteristics just to name a few.
Current corneal biomechanics estimation methods were primarily derived from three approaches: the applanation tonometer methods (ORA and Corvis ST); Brillouin microscopy; and elastography methods, including OCE. The features and limitations of the existing methodologies are illustrated in Fig. 13 (4, 5). Although significant progress has been achieved since 2005 when the in vivo measurement of human corneal biomechanical properties started [39], this work is still in an early stage. As a result, there are three pressing open questions that remain to be solved in the future based on the current state of in vivo biomechanics assessment techniques and the requirements for their clinical applications.
Fig. 13.
Summary of the requirements and the present status for developing in vivo corneal biomechanical measurement methods, and the open questions for improving existing methods or creating new methods for effective clinical applications.
(1) How to perform a fast, non-invasive, reliable, and high-resolution corneal biomechanical examination? There is a growing appreciation for the need to identify regional/ spatial variations in corneal mechanical characteristics for early-stage keratoconus diagnosis [117], [118], [119] when focal degenerations appear prior to clinical symptom caused by gross corneal deformations [166]. Because both ORA and Corvis ST measure tissue responses to global deformation forces, it is not possible to assess regional differences in tissue properties with these devices [163], [164], [165]. The current ultrasound- or magnetic-resonance-based elastographies also lack sufficient spatial resolution [46], [203]. Because the cornea is one of the most heavily innervated tissues, which is sensitive to stimulation forces used for elasticity characterization [25], [26], non-contact, low-force stimulation is preferable for corneal elasticity estimation [236]. However, this presents significant challenges for the development of high-resolution imaging equipment required to image small amplitude, high-speed phenomena associated with microscopic corneal deformations or elastic wave propagation. OCE is a promising solution to this challenge with flexible tissue stimulation options and high dynamic spatial and temporal resolution, but it requires further refinement for translation from a laboratory tool to a clinical device. Although Brillion microscopy does not require any external mechanical stimulation, it does require long duration imaging (e.g., 4–8 min, 12 s per axial scan, 20–40 total axial scans [42]), which is prone to significant artifacts due to the patient’s eye movement [41]. Technical advances are required to address this as well as the analytical models used to link Brillloun scattering to tissue mechanical properties. Developing devices capable of accounting for individual variations in corneal structure and regional variations in biomechanical properties is a long-standing clinical need [11] that has yet to be satisfied.
(2) How to identify the most relevant biomarker(s) to guide optimal clinical decision-making? The cornea is well known for its nonlinear and complex viscoelasticity. The estimates of Young’s modulus range from ∼kPa to tens of MPa using existing devices and methods (Fig. 3). This wide estimation range is due to the different techniques and conditions under which the cornea has been studied (ex vivo versus in vivo; non-destructive versus destructive; dehydration states; the difference in amplitude or rate of the applied force). In this context, it is understandable that a simple/linear parameter to represent the complex nonlinear viscoelasticity of the cornea is unsatisfactory [53]. However, this has not prevented scientists and clinicians from attempting to find other useful biomarkers in the clinic to differentiate between diseased and healthy corneas. Many metrics have been observed or estimated in various devices to characterize corneal biomechanics, but none of the current metrics has been shown to be a reliable biomarker (or gold standard) for disease identification or therapy evaluation. ORA and the Corvis ST evaluate corneal biomechanics based on the global corneal deformation response to an air puff. CH and CRF from ORA measurement have been widely used in the eye clinic to explore ocular biomechanics in keratoconus and glaucoma, but as they are co-determined by many factors, such as corneal thickness, elasticity, viscosity, IOP, and hydration, they often result in conflicting findings [53]. The longitudinal modulus (∼GPa) estimated from the Brillouin microscope is independent of Young’s modulus, whereas the latter can better represent the elasticity or stiffness that a clinician can feel by palpating the tissue [181]. Wave-based elastographies characterize Young’s modulus from the group or phase velocity of mechanical waves in the cornea using a particular analytical model (e.g., shear wave [290], [291], Lamb wave [292], [293], etc.) The wave velocity is not only dependent upon corneal biomechanical properties but is also determined by the amplitude, rate, and the frequency of the applied mechanical stimulation force. Different research groups utilize various stimulation techniques and analytical models for wave-tracking and Young’s modulus estimation. The absence of a common approach yields a range of estimates for Young’s modulus across different elastography modalities and publications [22], [44], [45], [47], [48], [107]. Natural frequency could be another alternative and complementary metric for characterizing corneal properties [49], [50], [51], [108]. However, natural frequencies are determined not only by elasticity but also by other parameters, including boundary conditions, IOP, corneal thickness, and topography. The challenge of interpreting natural frequency responses has not been solved yet. The decay coefficient of the propagating wave magnitudes [294], the relaxation rate of the displacements [295], the whole corneal hysteresis loop [85], [164], and the damping ratio of the resonant magnitudes [244] have also been proposed as metrics to characterize corneal viscosity, although these are recent metrics that are not currently widely accepted. As investigations into these imaging, measurement, and analytical methods continues, collaboration with clinicians will be necessary to further refine and inform researchers seeking clinically useful approaches to quantifying soft tissue biomechanical properties.
(3) How to advance the analytical and finite element models that can best represent the pathological progression and clinical invention? Scientists, engineers, and doctors are working in parallel on two fronts for a better understanding and treatment of ocular diseases. First, by looking for a simple and representative metric for clinical use and second, by attempting to construct comprehensive analytical or finite element models that incorporate corneal anatomy, IOP, biomechanical properties, pathological changes, and clinical inventions such as surgical processes. Analytical models typically employ simplified geometry and boundary conditions, as well as linear approximations of the corneal nonlinear behavior in response to the applied force. Taking wave-based elastography as an example, even if the measured group or phase velocities are the same, the shear/Young’s moduli would be different when the cornea is considered semi-infinite by the shear or surface acoustic model; a thin-plate, isotropic, and viscoelastic tissue by the Lamb wave model; or a thin-plate, transverse isotropic, and elastic tissue by the modified Lamb wave model [278], [296]. The finite element (FE) model of the corneal mechanical response also has a wide range of complexity, from one simple layer structure to complicated models that even account for the fiber organization of the stroma. Thus, balancing the complexity is another challenge, which may also depend on the application, yet a well-accepted standard for a certain application is very beneficial. The lack of reliability of current FE models is also compounded by the difficulties in precisely measuring the corneal biomechanics in the macro-, micro-, or cellar-scales. The dynamic stimulation methods with various spatial, temporal, and frequency features often result in different dynamic responses of the cornea, which may require more specific analytical or FE models to decipher the dynamic process and their related corneal biomechanical properties. Another challenge related to reconstruction of corneal biomechanical properties from dynamic tissue responses is isolating the influence of IOP and corneal structure (including tissue boundaries). However, such reconstruction demands pose a nontrivial inverse problem because many factors, such as boundary conditions and applied stress field, are unknown or difficult to determine [195].
In summary, a rapid expansion of knowledge regarding the corneal structure and biomechanical properties has been achieved in recent decades. In part this is due to valuable interdisciplinary collaborations between investigators in optical engineering, analytical biomechanical modeling, and clinical research. These collaborations have led to innovations and new discoveries in testing methods (ex vivo, and recently, in vivo) across multi-spatial scales and stress/strain regions. High-resolution imaging technologies, new biomechanical metrics derived from more detailed analysis of the mechanical response, and the capability to analyze the corneal mechanical response in multiple temporal-spatial scales are all promising developments that add complementary information to our expanding knowledge of corneal biomechanics. These advances have further potential to broaden our understanding of corneal biomechanical properties and provide insights on how best to apply this knowledge for the detection and management of ocular diseases and to enhance the safety and efficacy of future clinical practice.
Funding
National Natural Science Foundation of China (61975030); Guangdong Basic and Applied Basic Research Foundation (2021A1515011981); Innovation and Entrepreneurship Teams Project of Guangdong Pearl River Talents Program (2019ZT08Y105); National Key Research and Development Program of China (2019YFC1604600); Guangdong-Hong Kong-Macao Intelligent Micro-Nano Optoelectronic Technology Joint Laboratory (2020B1212030010); National Institutes of Health/National Eye Institute (NIH/NEI) P30EY07551, R01EY022362, and R01EY022362.
CRediT authorship contribution statement
Gongpu Lan, Michael D. Twa: Conceptualization. Gongpu Lan, JinPing Feng, Chengjin Song: Data curation. Gongpu Lan, Chengjin Song: Formal analysis. Gongpu Lan, Michael D. Twa, Yanping Huang, Jingjiang Xu, Jia Qin, Lin An, Xunbin Wei: Funding acquisition. Gongpu Lan, Michael D. Twa: Methodology. All authors: Validation, Writing − review & editing. Gongpu Lan, Chengjin Song: Visualization. Gongpu Lan: Roles/Writing − original draft.
Declaration of interest
GL, YH, and JX are consultants at Weiren Meditech Co., Ltd. JQ and LA are currently working at Weiren Meditech Co., Ltd. Remaining authors have no disclosures.
Contributor Information
Gongpu Lan, Email: langongpu@fosu.edu.cn.
Michael D. Twa, Email: mdtwa@central.uh.edu.
References
- 1.Miguel Gonzalez-Andrades P.A., Gipson A.I. In: Corneal Regeneration: Therapy and Surgery. Jorge F.A.-M., Alió del Barrio L., editors. Springer Nature; 2019. Corneal anatomy. [Google Scholar]
- 2.Sridhar M.S. "Anatomy of cornea and ocular surface,". Indian J Ophthalmol. 2018;66:190–194. doi: 10.4103/ijo.IJO_646_17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kling S., Hafezi F. "Corneal biomechanics - a review,". Ophthal Physl Opt. 2017;37:240–252. doi: 10.1111/opo.12345. [DOI] [PubMed] [Google Scholar]
- 4.Wolffsohn J.S., Safeen S., Shah S., Laiquzzaman M. "Changes of corneal biomechanics with keratoconus,". Cornea. 2012;31:849–854. doi: 10.1097/ICO.0b013e318243e42d. [DOI] [PubMed] [Google Scholar]
- 5.Gokul A., Vellara H.R., Patel D.V. "Advanced anterior segment imaging in keratoconus: a review,". Clin Exp Ophthalmol. 2018;46:122–132. doi: 10.1111/ceo.13108. [DOI] [PubMed] [Google Scholar]
- 6.Jonas J.B., Aung T., Bourne R.R., Bron A.M., Ritch R., Panda-Jonas S. "Glaucoma,". Lancet. 2017;390:2183–2193. doi: 10.1016/S0140-6736(17)31469-1. [DOI] [PubMed] [Google Scholar]
- 7.Brown K.E., Congdon N.G. "Corneal structure and biomechanics: impact on the diagnosis and management of glaucoma,". Curr Opin Ophthalmol. 2006;17:338–343. doi: 10.1097/01.icu.0000233951.01971.5b. [DOI] [PubMed] [Google Scholar]
- 8.Resnikoff S., Pascolini D., Mariotti S.P., Pokharel G.P. "Global magnitude of visual impairment caused by uncorrected refractive errors in 2004,". Bull World Health Organ. 2008;86:63–70. doi: 10.2471/BLT.07.041210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shen M., Fan F., Xue A., Wang J., Zhou X., Lu F. "Biomechanical properties of the cornea in high myopia,". Vis Res. 2008;48:2167–2171. doi: 10.1016/j.visres.2008.06.020. [DOI] [PubMed] [Google Scholar]
- 10.Chansangpetch S., Panpruk R., Manassakorn A., Tantisevi V., Rojanapongpun P., Hurst C.P., Lin S.C. "Impact of myopia on corneal biomechanics in glaucoma and nonglaucoma patients,". Invest Ophthalmol Vis Sci. 2017;58:4990–4996. doi: 10.1167/iovs.17-22219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ruberti J.W., Sinha Roy A., Roberts C.J. "Corneal biomechanics and biomaterials,". Annu Rev Biomed Eng. 2011;13:269–295. doi: 10.1146/annurev-bioeng-070909-105243. [DOI] [PubMed] [Google Scholar]
- 12.Kim T.I., Alió Del Barrio J.L., Wilkins M., Cochener B., Ang M. "Refractive surgery,". Lancet. 2019;393:2085–2098. doi: 10.1016/S0140-6736(18)33209-4. [DOI] [PubMed] [Google Scholar]
- 13.Guo H., Hosseini-Moghaddam S.M., Hodge W. "Corneal biomechanical properties after SMILE versus FLEX, LASIK, LASEK, or PRK: a systematic review and meta-analysis,". BMC Ophthalmol. 2019;19:1–20. doi: 10.1186/s12886-019-1165-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang D., Liu M., Chen Y., Zhang X., Xu Y., Wang J., To C.-H., Liu Q. Differences in the corneal biomechanical changes after SMILE and LASIK. J Refract Surg. 2014;30:702–707. doi: 10.3928/1081597X-20140903-09. [DOI] [PubMed] [Google Scholar]
- 15.Shetty R., Francis M., Shroff R., Pahuja N., Khamar P., Girrish M., Nuijts R.M., Roy A.S. "Corneal biomechanical changes and tissue remodeling after SMILE and LASIK,". Invest Ophthalmol Vis Sci. 2017;58:5703–5712. doi: 10.1167/iovs.17-22864. [DOI] [PubMed] [Google Scholar]
- 16.Hammer A., Richoz O., Mosquera S.A., Tabibian D., Hoogewoud F., Hafezi F. "Corneal biomechanical properties at different corneal cross-linking (CXL) irradiances,". Invest Ophthalmol Vis Sci. 2014;55:2881–2884. doi: 10.1167/iovs.13-13748. [DOI] [PubMed] [Google Scholar]
- 17.Scarcelli G., Besner S., Pineda R., Yun S.H., Science V. Biomechanical characterization of keratoconus corneas ex vivo with Brillouin microscopy. Invest Ophthalmol Vis Sci. 2014;55:4490–4495. doi: 10.1167/iovs.14-14450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shah S., Laiquzzaman M., Bhojwani R., Mantry S., Cunliffe I. "Assessment of the biomechanical properties of the cornea with the ocular response analyzer in normal and keratoconic eyes,". Invest Ophthalmol Vis Sci. 2007;48:3026–3031. doi: 10.1167/iovs.04-0694. [DOI] [PubMed] [Google Scholar]
- 19.Kanellopoulos A.J. "Post-LASIK ectasia,". Ophthalmology. 2007;114:1230. doi: 10.1016/j.ophtha.2007.03.041. [DOI] [PubMed] [Google Scholar]
- 20.Binder P.S., Lindstrom R.L., Stulting R.D., Donnenfeld E., Wu H., McDonnell P., Rabinowitz Y. "Keratoconus and corneal ectasia after LASIK,". J Refract Surg. 2005;21:749–752. doi: 10.3928/1081-597X-20051101-15. [DOI] [PubMed] [Google Scholar]
- 21.Seven I., Vahdati A., De Stefano V.S., Krueger R.R., Dupps W.J., Jr. "Comparison of Patient-Specific Computational Modeling Predictions and Clinical Outcomes of LASIK for Myopia,". Invest Ophthalmol Vis Sci. 2016;57:6287–6297. doi: 10.1167/iovs.16-19948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lan G., Aglyamov S.R., Larin K.V., Twa M.D.J.O., Science V. In Vivo Human Corneal Shear-wave Optical Coherence Elastography. Optom Vis Sci. 2021;98:58–63. doi: 10.1097/OPX.0000000000001633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Petsche S.J., Chernyak D., Martiz J., Levenston M.E., Pinsky P.M. "Depth-dependent transverse shear properties of the human corneal stroma,". Invest Ophthalmol Vis Sci. 2012;53:873–880. doi: 10.1167/iovs.11-8611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Xue C., Xiang Y., Shen M., Wu D., Wang Y. "Preliminary investigation of the mechanical anisotropy of the normal human corneal stroma,". J Ophthalmol. 2018;2018:5392041. doi: 10.1155/2018/5392041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rozsa A.J., Beuerman R.W. "Density and organization of free nerve endings in the corneal epithelium of the rabbit,". Pain. 1982;14:105–120. doi: 10.1016/0304-3959(82)90092-6. [DOI] [PubMed] [Google Scholar]
- 26.Beuerman R.W., Pedroza L. "Ultrastructure of the human cornea,". Microsc Res Tech. 1996;33:320–335. doi: 10.1002/(SICI)1097-0029(19960301)33:4<320::AID-JEMT3>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 27.Woo S.L., Kobayashi A.S., Schlegel W.A., Lawrence C. "Nonlinear material properties of intact cornea and sclera,". Exp Eye Res. 1972;14:29–39. doi: 10.1016/0014-4835(72)90139-x. [DOI] [PubMed] [Google Scholar]
- 28.Kanellopoulos A.J. "Comparison of corneal biomechanics after myopic small-incision lenticule extraction compared to LASIK: an ex vivo study,". Clin Ophthalmol. 2018;12:237–245. doi: 10.2147/OPTH.S153509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hu Y., Huang Y., Chen Y., Ye C., Wei W., Feng Y., Mi S. "Study on patterned photodynamic cross-linking for keratoconus,". Exp Eye Res. 2021;204 doi: 10.1016/j.exer.2021.108450. [DOI] [PubMed] [Google Scholar]
- 30.Beshtawi I.M., O’Donnell C., Radhakrishnan H. "Biomechanical properties of corneal tissue after ultraviolet-A–riboflavin crosslinking,". J Cataract Refract Surg. 2013;39:451–462. doi: 10.1016/j.jcrs.2013.01.026. [DOI] [PubMed] [Google Scholar]
- 31.Wang J., Liu X., Bao F., Lopes B.T., Wang L., Eliasy A., Abass A., Elsheikh A. "Review of ex-vivo characterisation of corneal biomechanics,". Med Nov Technol Devices. 2021;11 [Google Scholar]
- 32.Elsheikh A., Anderson K. "Comparative study of corneal strip extensometry and inflation tests,". J R Soc Interface. 2005;2:177–185. doi: 10.1098/rsif.2005.0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nash I.S., Greene P.R., Foster C.S. "Comparison of mechanical properties of keratoconus and normal corneas,". Exp Eye Res. 1982;35:413–424. doi: 10.1016/0014-4835(82)90040-9. [DOI] [PubMed] [Google Scholar]
- 34.Abdshahzadeh H., Abrishamchi R., Torres-Netto E.A., Kling S., Hafezi N.L., Hillen M., Hafezi F. "Impact of hypothermia on the biomechanical effect of epithelium-off corneal cross-linking,". Eye Vis. 2021;8:4. doi: 10.1186/s40662-021-00229-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kling S., Remon L., Pérez-Escudero A., Merayo-Lloves J., Marcos S. "Corneal biomechanical changes after collagen cross-linking from porcine eye inflation experiments,". Invest Ophthalmol Vis Sci. 2010;51:3961–3968. doi: 10.1167/iovs.09-4536. [DOI] [PubMed] [Google Scholar]
- 36.Lombardo M., Lombardo G., Carbone G., De Santo M.P., Barberi R., Serrao S. "Biomechanics of the anterior human corneal tissue investigated with atomic force microscopy,". Invest Ophthalmol Vis Sci. 2012;53:1050–1057. doi: 10.1167/iovs.11-8720. [DOI] [PubMed] [Google Scholar]
- 37.Jayasuriya A.C., Ghosh S., Scheinbeim J.I., Lubkin V., Bennett G., Kramer P. "A study of piezoelectric and mechanical anisotropies of the human cornea,". Biosens Bioelectron. 2003;18:381–387. doi: 10.1016/s0956-5663(02)00144-6. [DOI] [PubMed] [Google Scholar]
- 38.Elsheikh A., Anderson K. "Comparative study of corneal strip extensometry and inflation tests,". J R Soc, Interface. 2005;2:177–185. doi: 10.1098/rsif.2005.0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Luce D., A Determining in vivo biomechanical properties of the cornea with an ocular response analyzer. J Cataract Refract Surg. 2005;31:156–162. doi: 10.1016/j.jcrs.2004.10.044. [DOI] [PubMed] [Google Scholar]
- 40.Ambrosio Jr. Renato, Isaac Ramos, Allan Luz, Correa Faria Fernando, Andreas Steinmueller, Matthias Krug, Michael W Belin, Jane R.C. "Dynamic ultra high speed Sheimpflug imaging for assessing corneal biomechanical properties,". Rev Bras Oftalmol. 2013;72:99–102. [Google Scholar]
- 41.Zhang H., Asroui L., Randleman J.B., Scarcelli G. "Motion-tracking Brillouin microscopy for in-vivo corneal biomechanics mapping,". Biomed Opt Express. 2022;13:6196–6210. doi: 10.1364/BOE.472053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shao P., Eltony A.M., Seiler T.G., Tavakol B., Pineda R., Koller T., Seiler T., Yun S.-H. "Spatially-resolved Brillouin spectroscopy reveals biomechanical abnormalities in mild to advanced keratoconus in vivo,". Sci Rep. 2019;9:7467. doi: 10.1038/s41598-019-43811-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Scarcelli G., Yun S.H. "In vivo Brillouin optical microscopy of the human eye,". Opt Express. 2012;20:9197–9202. doi: 10.1364/OE.20.009197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chen P.Y., Shih C.C., Lin W.C., Ma T., Zhou Q., Shung K.K., Huang C.C. "High-Resolution Shear Wave Imaging of the Human Cornea Using a Dual-Element Transducer,". Sensors. 2018;18:4224. doi: 10.3390/s18124244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sit A.J., Lin S.C., Kazemi A., McLaren J.W., Pruet C.M., Zhang X. "In Vivo Noninvasive Measurement of Young's Modulus of Elasticity in Human Eyes: A Feasibility Study,". J Glaucoma. 2017;26:967–973. doi: 10.1097/IJG.0000000000000774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Voorhees A.P., Ho L.C., Jan N., Tran H., van der Merwe Y., Chan K., Sigal I.A. "Whole-globe biomechanics using high-field MRI,". Exp Eye Res. 2017;160:85–95. doi: 10.1016/j.exer.2017.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ramier A., Eltony A.M., Chen Y., Clouser F., Birkenfeld J.S., Watts A., Yun S.H. "In vivo measurement of shear modulus of the human cornea using optical coherence elastography,". Sci Rep. 2020;10:1–10. doi: 10.1038/s41598-020-74383-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jin Z., Chen S., Dai Y., Bao C., Ye S., Zhou Y., Wang Y., Huang S., Wang Y., Shen M., Zhu D., Lu F. "In vivo noninvasive measurement of spatially resolved corneal elasticity in human eyes using Lamb wave optical coherence elastography,". J Biophotonics. 2020;13 doi: 10.1002/jbio.202000104. [DOI] [PubMed] [Google Scholar]
- 49.Lan G., Aglyamov S., Larin K.V., Twa M.D. "In vivo human corneal natural frequency quantification using dynamic optical coherence elastography: repeatability and reproducibility,". J Biomech. 2021;121 doi: 10.1016/j.jbiomech.2021.110427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Crespo M.A., Jimenez H.J., Deshmukh T., Pulido J.S., Saad A.S., Silver F.H., Benedetto D.A., Rapuano C.J., Syed Z.A. "In vivo determination of the human corneal elastic modulus using vibrational optical coherence tomography,". Transl Vis Sci Technol. 2022;11:11-11. doi: 10.1167/tvst.11.7.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Silver F.H., Kelkar N., Deshmukh T., Horvath I., Shah R.G. "Mechano-vibrational spectroscopy of tissues and materials using vibrational optical coherence tomography: a new non-invasive and non-destructive technique. Recent Prog Mater. 2020;2:010. [Google Scholar]
- 52.Yuhas P.T., Roberts C.J. "Clinical ocular biomechanics: where are we after 20 years of progress?,". Curr Eye Res. 2022:1–16. doi: 10.1080/02713683.2022.2125530. [DOI] [PubMed] [Google Scholar]
- 53.Roberts C.J. "Concepts and misconceptions in corneal biomechanics,". J Cataract Refract Surg. 2014;40:862–869. doi: 10.1016/j.jcrs.2014.04.019. [DOI] [PubMed] [Google Scholar]
- 54.Abahussin M., Hayes S., Knox Cartwright N.E., Kamma-Lorger C.S., Khan Y., Marshall J., Meek K.M. "3D Collagen Orientation Study of the Human Cornea Using X-ray Diffraction and Femtosecond Laser Technology,". Invest Ophthalmol Vis Sci. 2009;50:5159–5164. doi: 10.1167/iovs.09-3669. [DOI] [PubMed] [Google Scholar]
- 55.Rüfer F., Schröder A., Erb C. "White-to-white corneal diameter: normal values in healthy humans obtained with the Orbscan II topography system,". Cornea. 2005;24:259–261. doi: 10.1097/01.ico.0000148312.01805.53. [DOI] [PubMed] [Google Scholar]
- 56.Khng C., Osher R.H. "Evaluation of the relationship between corneal diameter and lens diameter,". J Cataract Refract Surg. 2008;34:475–479. doi: 10.1016/j.jcrs.2007.10.043. [DOI] [PubMed] [Google Scholar]
- 57.Lan G., Zeng J., Li W., Ma G., Shi Q., Shi Y., Wang Y., Xu J., Huang Y., Qin J., Feng J., Tan H., An L., Wei X. "Customized eye modeling for optical quality assessment in myopic femto-LASIK surgery,". Sci Rep. 2021;11:16049. doi: 10.1038/s41598-021-95730-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Doughty M.J., Jonuscheit S. "An assessment of regional differences in corneal thickness in normal human eyes, using the Orbscan II or ultrasound pachymetry,". Optometry. 2007;78:181–190. doi: 10.1016/j.optm.2006.08.018. [DOI] [PubMed] [Google Scholar]
- 59.Guérin L.-P., Le-Bel G., Desjardins P., Couture C., Gillard E., Boisselier É., Bazin R., Germain L., Guérin S.L. "The Human Tissue-Engineered Cornea (hTEC): Recent Progress. Int J Mol Sci. 2021;22:1291. doi: 10.3390/ijms22031291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Elsheikh A., Alhasso D., Rama P. "Assessment of the epithelium's contribution to corneal biomechanics,". Exp eye Res. 2008;86:445–451. doi: 10.1016/j.exer.2007.12.002. [DOI] [PubMed] [Google Scholar]
- 61.van Dijk K., Liarakos V.S., Parker J., Ham L., Lie J.T., Groeneveld-van Beek E.A., Melles G.R. Bowman layer transplantation to reduce and stabilize progressive, advanced keratoconus. Ophthalmology. 2015;122:909–917. doi: 10.1016/j.ophtha.2014.12.005. [DOI] [PubMed] [Google Scholar]
- 62.Dawson D.G., Grossniklaus H.E., McCarey B.E., Edelhauser H.F. "Biomechanical and wound healing characteristics of corneas after excimer laser keratorefractive surgery: is there a difference between advanced surface ablation and sub-Bowman's keratomileusis?,". J Refract Surg. 2008;24:S90–S96. doi: 10.3928/1081597X-20080101-16. [DOI] [PubMed] [Google Scholar]
- 63.Seiler T., Matallana M., Sendler S., Bende T. (SLACK Incorporated Thorofare, NJ,; 1992. Does Bowman's layer determine the biomechanical properties of the cornea? pp. 139–142. [PubMed] [Google Scholar]
- 64.Torres-Netto E.A., Hafezi F., Spiru B., Gilardoni F., Hafezi N.L., Gomes J.A.P., Randleman J.B., Sekundo W., Kling S. "Contribution of Bowman layer to corneal biomechanics,". J Cataract Refract Surg. 2021;47:927–932. doi: 10.1097/j.jcrs.0000000000000543. [DOI] [PubMed] [Google Scholar]
- 65.Kremer I., Eagle R.C., Rapuano C.J., Laibson P.R. "Histologic evidence of recurrent keratoconus seven years after keratoplasty,". Am J Ophthalmol. 1995;119:511–512. doi: 10.1016/s0002-9394(14)71239-5. [DOI] [PubMed] [Google Scholar]
- 66.Hashmani K., Branch M.J., Sidney L.E., Dhillon P.S., Verma M., McIntosh O.D., Hopkinson A., Dua H.S. "Characterization of corneal stromal stem cells with the potential for epithelial transdifferentiation,". Stem Cell Res Ther. 2013;4:75. doi: 10.1186/scrt226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Meek K.M., Fullwood N.J. "Corneal and scleral collagens—a microscopist’s perspective,". Micron. 2001;32:261–272. doi: 10.1016/s0968-4328(00)00041-x. [DOI] [PubMed] [Google Scholar]
- 68.Meek K.M., Leonard D.W. "Ultrastructure of the corneal stroma: a comparative study,". Biophys J. 1993;64:273–280. doi: 10.1016/S0006-3495(93)81364-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Newton R.H., Meek K.M. "The integration of the corneal and limbal fibrils in the human eye,". Biophys J. 1998;75:2508–2512. doi: 10.1016/S0006-3495(98)77695-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Meek K.M., Boote C. "The organization of collagen in the corneal stroma,". Exp Eye Res. 2004;78:503–512. doi: 10.1016/j.exer.2003.07.003. [DOI] [PubMed] [Google Scholar]
- 71.Abass A., Hayes S., White N., Sorensen T., Meek K.M. "Transverse depth-dependent changes in corneal collagen lamellar orientation and distribution,". J R Soc Interface. 2015;12:20140717. doi: 10.1098/rsif.2014.0717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Komai Y., Ushiki T. "The three-dimensional organization of collagen fibrils in the human cornea and sclera,". Invest Ophthalmol Vis Sci. 1991;32:2244–2258. [PubMed] [Google Scholar]
- 73.Bueno J.M., Gualda E.J., Artal P. "Analysis of corneal stroma organization with wavefront optimized nonlinear microscopy,". Cornea. 2011;30:692–701. doi: 10.1097/ICO.0b013e3182000f94. [DOI] [PubMed] [Google Scholar]
- 74.Ruberti J.W., Zieske J.D. "Prelude to corneal tissue engineering - gaining control of collagen organization,". Prog Retin Eye Res. 2008;27:549–577. doi: 10.1016/j.preteyeres.2008.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Randleman J.B., Dawson D.G., Grossniklaus H.E., McCarey B.E., Edelhauser H.F. "Depth-dependent cohesive tensile strength in human donor corneas: implications for refractive surgery,". J Refract Surg. 2008;24:S85–S89. doi: 10.3928/1081597X-20080101-15. [DOI] [PubMed] [Google Scholar]
- 76.Quantock A.J., Young R.D., Akama T.O. "Structural and biochemical aspects of keratan sulphate in the cornea,". Cell Mol Life Sci. 2010;67:891–906. doi: 10.1007/s00018-009-0228-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Murphy C.G., Alvarado J.A., Juster R.P. "Prenatal and postnatal growth of the human Descemet's membrane,". Invest Ophthalmol Vis Sci. 1984;25(12):1402–1415. [PubMed] [Google Scholar]
- 78.Kabosova A., Azar D.T., Bannikov G.A., Campbell K.P., Durbeej M., Ghohestani R.F., Jones J.C., Kenney M.C., Koch M., Ninomiya Y., Patton B.L., Paulsson M., Sado Y., Sage E.H., Sasaki T., Sorokin L.M., Steiner-Champliaud M.F., Sun T.T., Sundarraj N., Timpl R., Virtanen I., Ljubimov A.V. "Compositional differences between infant and adult human corneal basement membranes,". Invest Ophthalmol Vis Sci. 2007;48:4989–4999. doi: 10.1167/iovs.07-0654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Johnson D.H., Bourne W.M., Campbell R.J. "The ultrastructure of Descemet's membrane. I. Changes with age in normal corneas,". Arch Ophthalmol. 1982;100:1942–1947. doi: 10.1001/archopht.1982.01030040922011. [DOI] [PubMed] [Google Scholar]
- 80.Fitch J.M., Birk D.E., Linsenmayer C., Linsenmayer T.F. "The spatial organization of Descemet's membrane-associated type IV collagen in the avian cornea. J Cell Biol. 1990;110:1457–1468. doi: 10.1083/jcb.110.4.1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Srinivas S.P. "Dynamic regulation of barrier integrity of the corneal endothelium,". Optom Vis Sci. 2010;87:E239–E254. doi: 10.1097/OPX.0b013e3181d39464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Joyce N.C. "Proliferative capacity of corneal endothelial cells,". Exp Eye Res. 2012;95:16–23. doi: 10.1016/j.exer.2011.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Lakes R.S. "Viscoelastic measurement techniques,". Rev Sci Instrum. 2004;75:797–810. [Google Scholar]
- 84.Huang Y., Zheng Y. CRC Press,; 2015. Measurement of soft tissue elasticity in vivo: techniques and applications. [Google Scholar]
- 85.Li W., Feng J., Wang Y., Shi Q., Ma G., Aglyamov S., Larin K.V., Lan G., Twa M. "Micron-scale hysteresis measurement using dynamic optical coherence elastography,". Biomed Opt Express. 2022;13:3021–3041. doi: 10.1364/BOE.457617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Wollensak G., Spoerl E., Seiler T. "Stress-strain measurements of human and porcine corneas after riboflavin-ultraviolet-A-induced cross-linking,". J Cataract Refract Surg. 2003;29:1780–1785. doi: 10.1016/s0886-3350(03)00407-3. [DOI] [PubMed] [Google Scholar]
- 87.Kohlhaas M., Spoerl E., Schilde T., Unger G., Wittig C., Pillunat L.E. "Biomechanical evidence of the distribution of cross-links in corneas treated with riboflavin and ultraviolet A light,". J Cataract Refract Surg. 2006;32:279–283. doi: 10.1016/j.jcrs.2005.12.092. [DOI] [PubMed] [Google Scholar]
- 88.Chae J.J., Choi J.S., Lee J.D., Lu Q., Stark W.J., Kuo I.C., Elisseeff J.H. Physical and Biological Characterization of the Gamma-Irradiated Human Cornea. Cornea. 2015;34:1287–1294. doi: 10.1097/ICO.0000000000000555. [DOI] [PubMed] [Google Scholar]
- 89.Ramirez-Garcia M.A., Sloan S.R., Nidenberg B., Khalifa Y.M., Buckley M.R. "Depth-dependent out-of-plane Young's modulus of the human cornea,". Curr Eye Res. 2017;43:595–604. doi: 10.1080/02713683.2017.1411951. [DOI] [PubMed] [Google Scholar]
- 90.Søndergaard A.P., Ivarsen A., Hjortdal J. "Corneal resistance to shear force after UVA-riboflavin cross-linking,". Invest Ophthalmol Vis Sci. 2013;54:5059–5069. doi: 10.1167/iovs.12-10710. [DOI] [PubMed] [Google Scholar]
- 91.Sloan S.R., Jr., Khalifa Y.M., Buckley M.R. "The location- and depth-dependent mechanical response of the human cornea under shear loading,". Invest Ophthalmol Vis Sci. 2014;55:7919–7924. doi: 10.1167/iovs.14-14997. [DOI] [PubMed] [Google Scholar]
- 92.Hjortdal J.O., Ehlers N. "Effect of excimer laser keratectomy on the mechanical performance of the human cornea,". Acta Ophthalmol Scand. 1995;73:18–24. doi: 10.1111/j.1600-0420.1995.tb00006.x. [DOI] [PubMed] [Google Scholar]
- 93.Hjortdal J.O. "Regional elastic performance of the human cornea,". J Biomech. 1996;29:931–942. doi: 10.1016/0021-9290(95)00152-2. [DOI] [PubMed] [Google Scholar]
- 94.Elsheikh A., Wang D., Brown M., Rama P., Campanelli M., Pye D. "Assessment of corneal biomechanical properties and their variation with age,". Curr Eye Res. 2007;32:11–19. doi: 10.1080/02713680601077145. [DOI] [PubMed] [Google Scholar]
- 95.Elsheikh A., Alhasso D., Rama P. "Biomechanical properties of human and porcine corneas,". Exp Eye Res. 2008;86:783–790. doi: 10.1016/j.exer.2008.02.006. [DOI] [PubMed] [Google Scholar]
- 96.Kling S., Torres-Netto E.A., Spiru B., Sekundo W., Hafezi F. "Quasi-static optical coherence elastography to characterize human corneal biomechanical properties,". Invest Ophthalmol Vis Sci. 2020;61:29. doi: 10.1167/iovs.61.6.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Knox Cartwright N.E., Tyrer J.R., Marshall J. "Age-related differences in the elasticity of the human cornea,". Invest Ophthalmol Vis Sci. 2011;52:4324–4329. doi: 10.1167/iovs.09-4798. [DOI] [PubMed] [Google Scholar]
- 98.Ke L., Zhang L., Zhang N., Wu Q.Y.S., Leong H.S., Abdelaziem A., Mehta J.S., Liu Y.C. "Corneal elastic property investigated by terahertz technology,". Sci Rep. 2022;12:19229. doi: 10.1038/s41598-022-22033-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Diakonis V.F., Likht N.Y., Yesilirmak N., Delgado D., Karatapanis A.E., Yesilirmak Y., Fraker C., Yoo S.H., Ziebarth N.M. "Corneal elasticity after oxygen enriched high intensity corneal cross linking assessed using atomic force microscopy,". Exp Eye Res. 2016;153:51–55. doi: 10.1016/j.exer.2016.10.008. [DOI] [PubMed] [Google Scholar]
- 100.Dias J., Diakonis V.F., Kankariya V.P., Yoo S.H., Ziebarth N.M. "Anterior and posterior corneal stroma elasticity after corneal collagen crosslinking treatment,". Exp Eye Res. 2013;116:58–62. doi: 10.1016/j.exer.2013.07.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Labate C., Lombardo M., Lombardo G., De Santo M.P. Biomechanical Strengthening of the Human Cornea Induced by Nanoplatform-Based Transepithelial Riboflavin/UV-A Corneal Cross-Linking. Invest Ophthalmol Vis Sci. 2017;58:179–184. doi: 10.1167/iovs.16-20813. [DOI] [PubMed] [Google Scholar]
- 102.Last J.A., Thomasy S.M., Croasdale C.R., Russell P., Murphy C.J. "Compliance profile of the human cornea as measured by atomic force microscopy,". Micron. 2012;43:1293–1298. doi: 10.1016/j.micron.2012.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Shih P.J., Huang C.J., Huang T.H., Lin H.C., Yen J.Y., Wang I.J., Cao H.J., Shih W.P., Dai C.A. "Estimation of the Corneal Young's Modulus In Vivo Based on a Fluid-Filled Spherical-Shell Model with Scheimpflug Imaging,". J Ophthalmol. 2017;2017:5410143. doi: 10.1155/2017/5410143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Hamilton K.E., Pye D.C. "Young's modulus in normal corneas and the effect on applanation tonometry,". Optom Vis Sci. 2008;85:445–450. doi: 10.1097/OPX.0b013e3181783a70. [DOI] [PubMed] [Google Scholar]
- 105.Sjøntoft E., Edmund C. "In vivo determination of Young's modulus for the human cornea,". Bull Math Biol. 1987;49:217–232. doi: 10.1007/BF02459699. [DOI] [PubMed] [Google Scholar]
- 106.Lam A.K., Hon Y., Leung L.K., Lam D.C. "Repeatability of a novel corneal indentation device for corneal biomechanical measurement,". Ophthalmic Physiol Opt. 2015;35:455–461. doi: 10.1111/opo.12219. [DOI] [PubMed] [Google Scholar]
- 107.Mikula E.R., Jester J.V., Juhasz T. "Measurement of an elasticity map in the human cornea,". Invest Ophthalmol Vis Sci. 2016;57:3282–3286. doi: 10.1167/iovs.15-18248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Silver F.H., Shah R.G., Benedetto D. "Non-Invasive and Non-Destructive Determination of Corneal and Scleral Biomechanics Using Vibrational Optical Coherence Tomography: Preliminary Observations,". Mater Sci Appl. 2018;9:657–669. [Google Scholar]
- 109.Yuan A., Pineda R. "Developments in imaging of corneal biomechanics,". Int Ophthalmol Clin. 2019;59:1–17. doi: 10.1097/IIO.0000000000000286. [DOI] [PubMed] [Google Scholar]
- 110.Rabinowitz Y.S. "Keratoconus,". Surv Ophthalmol. 1998;42:297–319. doi: 10.1016/s0039-6257(97)00119-7. [DOI] [PubMed] [Google Scholar]
- 111.Mathew J.H., Goosey J.D., Söderberg P.G., Bergmanson J.P. "Lamellar changes in the keratoconic cornea,". Acta Ophthalmol. 2015;93:767–773. doi: 10.1111/aos.12811. [DOI] [PubMed] [Google Scholar]
- 112.Lu Y., Vitart V., Burdon K.P., Khor C.C., Bykhovskaya Y., Mirshahi A., Hewitt A.W., Koehn D., Hysi P.G., Ramdas W.D.J.N.G. Genome-wide association analyses identify multiple loci associated with central corneal thickness and keratoconus. Nat Genet. 2013;45:155. doi: 10.1038/ng.2506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Godefrooij D.A., de Wit G.A., Uiterwaal C.S., Imhof S.M., Wisse R.P. "Age-specific Incidence and Prevalence of Keratoconus: A Nationwide Registration Study,". Am J Ophthalmol. 2017;175:169–172. doi: 10.1016/j.ajo.2016.12.015. [DOI] [PubMed] [Google Scholar]
- 114.Santodomingo-Rubido J., Carracedo G., Suzaki A., Villa-Collar C., Vincent S.J., Wolffsohn J.S. "Keratoconus: An updated review,". Cont Lens Anterior Eye. 2022;45 doi: 10.1016/j.clae.2021.101559. [DOI] [PubMed] [Google Scholar]
- 115.Wilson S.E., Lin D., Klyce S.D. "Corneal topography of keratoconus,". Cornea. 1991;10:2–8. [PubMed] [Google Scholar]
- 116.Cavas-Martínez F., De la Cruz Sánchez E., Nieto Martínez J., Fernández Cañavate F., Fernández-Pacheco D. "Corneal topography in keratoconus: state of the art,". Eye Vis. 2016;3:1–12. doi: 10.1186/s40662-016-0036-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Martínez-Abad A., P. D. P New perspectives on the detection and progression of keratoconus. J Cataract Refract Surg. 2017;43:1213–1227. doi: 10.1016/j.jcrs.2017.07.021. [DOI] [PubMed] [Google Scholar]
- 118.Henriquez M.A., Hadid M., Izquierdo L., Jr "A systematic review of subclinical keratoconus and forme fruste keratoconus,". J Refract Surg. 2020;36:270–279. doi: 10.3928/1081597X-20200212-03. [DOI] [PubMed] [Google Scholar]
- 119.Esporcatte L.P.G., Salomão M.Q., Lopes B.T., Sena N., Ferreira É., Filho J., Machado A.P., Ambrósio R., Jr. "Biomechanics in Keratoconus Diagnosis,". Curr Eye Res. 2022:1–7. doi: 10.1080/02713683.2022.2041042. [DOI] [PubMed] [Google Scholar]
- 120.O’Brart D.P. "Corneal collagen cross-linking: a review,". J Optom. 2014;7:113–124. doi: 10.1016/j.optom.2013.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Lin L.L.K., Shih Y.F., Hsiao C.K., Chen C.J. "Prevalence of Myopia in Taiwanese Schoolchildren: 1983 to 2000,". Ann Acad Med Singap. 2004;33:27–33. [PubMed] [Google Scholar]
- 122.Holden B.A., Fricke T.R., Wilson D.A., Jong M., Naidoo K.S., Sankaridurg P., Wong T.Y., Naduvilath T.J., Resnikoff S. "Global Prevalence of Myopia and High Myopia and Temporal Trends from 2000 through 2050,". Ophthalmology. 2016;123:1036–1042. doi: 10.1016/j.ophtha.2016.01.006. [DOI] [PubMed] [Google Scholar]
- 123.Sakimoto T., Rosenblatt M.I., Azar D.T. "Laser eye surgery for refractive errors,". Lancet. 2006;367:1432–1447. doi: 10.1016/S0140-6736(06)68275-5. [DOI] [PubMed] [Google Scholar]
- 124.Sugar A., Hood C.T., Mian S.I. "Patient-Reported Outcomes Following LASIK: Quality of Life in the PROWL Studies,". JAMA. 2017;317:204–205. doi: 10.1001/jama.2016.19323. [DOI] [PubMed] [Google Scholar]
- 125.Stonecipher K., Ignacio T.S., Stonecipher M. "Advances in refractive surgery: microkeratome and femtosecond laser flap creation in relation to safety, efficacy, predictability, and biomechanical stability,". Curr Opin Ophthalmol. 2006;17:368–372. doi: 10.1097/01.icu.0000233957.88509.2d. [DOI] [PubMed] [Google Scholar]
- 126.Lamparter J., Dick H.B., K. F Complications after laser in situ keratomileusis (LASIK): results of a meta-analysis on incidences and expectable costs. Klin Monbl Augenheilkd. 2007;224:627–635. doi: 10.1055/s-2007-963336. [DOI] [PubMed] [Google Scholar]
- 127.Bohac M., Koncarevic M., Pasalic A., Biscevic A., Merlak M., Gabric N., Patel S. "Incidence and Clinical Characteristics of Post LASIK Ectasia: A Review of over 30,000 LASIK Cases,". Semin Ophthalmol. 2018;33:869–877. doi: 10.1080/08820538.2018.1539183. [DOI] [PubMed] [Google Scholar]
- 128.Twa M.D., Nichols J.J., Joslin C.E., Kollbaum P.S., Edrington T.B., Bullimore M.A., Mitchell G.L., Cruickshanks K.J., Schanzlin D.J. "Characteristics of corneal ectasia after LASIK for myopia,". Cornea. 2004;23:447–457. doi: 10.1097/01.ico.0000122702.49054.12. [DOI] [PubMed] [Google Scholar]
- 129.Seiler T., Koufala K., Richter G. "Iatrogenic keratectasia after laser in situ keratomileusis,". J Refract Surg. 1998;14:312–317. doi: 10.3928/1081-597X-19980501-15. [DOI] [PubMed] [Google Scholar]
- 130.Seiler T., Quurke A.W. "Iatrogenic keratectasia after LASIK in a case of forme fruste keratoconus,". J Cataract Refract Surg. 1998;24:1007–1009. doi: 10.1016/s0886-3350(98)80057-6. [DOI] [PubMed] [Google Scholar]
- 131.Ambrosio R., Jr. "Post-LASIK Ectasia: Twenty Years of a Conundrum,". Semin Ophthalmol. 2019;34:66–68. doi: 10.1080/08820538.2019.1569075. [DOI] [PubMed] [Google Scholar]
- 132.Jabbur N.S., Sakatani K., O'Brien T.P. "Survey of complications and recommendations for management in dissatisfied patients seeking a consultation after refractive surgery,". J Cataract Refract Surg. 2004;30:1867–1874. doi: 10.1016/j.jcrs.2004.01.020. [DOI] [PubMed] [Google Scholar]
- 133.Pallikaris I.G., Kymionis G.D., Astyrakakis N.I. "Corneal ectasia induced by laser in situ keratomileusis,". J Cataract Refract Surg. 2001;27:1796–1802. doi: 10.1016/s0886-3350(01)01090-2. [DOI] [PubMed] [Google Scholar]
- 134.Alvani A., Hashemi H., Pakravan M., Mahbod M., Seyedian M.A., Amanzadeh K., Khabazkhoob M., Jafarzadehpur E., F. A Post-LASIK Ectasia Versus Keratoconus: An In Vivo Confocal Microscopy Study. Cornea. 2020;39:1006–1012. doi: 10.1097/ICO.0000000000002318. [DOI] [PubMed] [Google Scholar]
- 135.Stein J.D., Khawaja A.P., Weizer J.S. "Glaucoma in Adults—Screening, Diagnosis, and Management: A Review,". JAMA. 2021;325:164–174. doi: 10.1001/jama.2020.21899. [DOI] [PubMed] [Google Scholar]
- 136.Silva F., Lira M. "Intraocular pressure measurement: A Review,". Surv Ophthalmol. 2022 doi: 10.1016/j.survophthal.2022.03.001. [DOI] [PubMed] [Google Scholar]
- 137.Baudouin C., Kolko M., Melik-Parsadaniantz S., Messmer E.M. "Inflammation in Glaucoma: From the back to the front of the eye, and beyond,". Prog Retin Eye Res. 2021;83 doi: 10.1016/j.preteyeres.2020.100916. [DOI] [PubMed] [Google Scholar]
- 138.Gordon M.O., Beiser J.A., Brandt J.D., Heuer D.K., Higginbotham E.J., Johnson C.A., Keltner J.L., Miller J.P., Parrish R.K., II, Wilson M.R., Kass M.A., Group O.H.T.S. The Ocular Hypertension Treatment Study: Baseline Factors That Predict the Onset of Primary Open-Angle Glaucoma. Arch Ophthalmol. 2002;120:714–720. doi: 10.1001/archopht.120.6.714. [DOI] [PubMed] [Google Scholar]
- 139.Liu J., Roberts C.J. "Influence of corneal biomechanical properties on intraocular pressure measurement: quantitative analysis,". J Refract Surg. 2005;31:146–155. doi: 10.1016/j.jcrs.2004.09.031. [DOI] [PubMed] [Google Scholar]
- 140.Congdon N.G., Broman A.T., Bandeen-Roche K., Grover D., Quigley H.A. Central corneal thickness and corneal hysteresis associated with glaucoma damage. Am J Ophthalmol. 2006;141:868–875. doi: 10.1016/j.ajo.2005.12.007. [DOI] [PubMed] [Google Scholar]
- 141.Beotra M.R., Wang X., Tun T.A., Zhang L., Baskaran M., Aung T., Strouthidis N.G., Girard M.J.A. "In Vivo Three-Dimensional Lamina Cribrosa Strains in Healthy, Ocular Hypertensive, and Glaucoma Eyes Following Acute Intraocular Pressure Elevation,". Invest Ophthalmol Vis Sci. 2018;59:260–272. doi: 10.1167/iovs.17-21982. [DOI] [PubMed] [Google Scholar]
- 142.Wang X., Rumpel H., Lim W.E.H., Baskaran M., Perera S.A., Nongpiur M.E., Aung T., Milea D., Girard M.J.A. "Finite Element Analysis Predicts Large Optic Nerve Head Strains During Horizontal Eye Movements,". Invest Ophthalmol Vis Sci. 2016;57:2452–2462. doi: 10.1167/iovs.15-18986. [DOI] [PubMed] [Google Scholar]
- 143.Sigal I.A., Flanagan J.G., Ethier C.R. "Factors Influencing Optic Nerve Head Biomechanics,". Invest Ophthalmol Vis Sci. 2005;46:4189–4199. doi: 10.1167/iovs.05-0541. [DOI] [PubMed] [Google Scholar]
- 144.Crawford Downs J., Roberts M.D., Sigal I.A. "Glaucomatous cupping of the lamina cribrosa: a review of the evidence for active progressive remodeling as a mechanism,". Exp Eye Res. 2011;93:133–140. doi: 10.1016/j.exer.2010.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Ivers K.M., Sredar N., Patel N.B., Rajagopalan L., Queener H.M., Twa M.D., Harwerth R.S., Porter J. "In Vivo Changes in Lamina Cribrosa Microarchitecture and Optic Nerve Head Structure in Early Experimental Glaucoma,". PLoS One. 2015;10 doi: 10.1371/journal.pone.0134223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Wells A.P., Garway-Heath D.F., Poostchi A., Wong T., Chan K.C.Y., Sachdev N. "Corneal Hysteresis but Not Corneal Thickness Correlates with Optic Nerve Surface Compliance in Glaucoma Patients,". Invest Ophthalmol Vis Sci. 2008;49:3262–3268. doi: 10.1167/iovs.07-1556. [DOI] [PubMed] [Google Scholar]
- 147.Safa B.N., Wong C.A., Ha J., Ethier C.R. "Glaucoma and biomechanics,". Curr Opin Ophthalmol. 2022;33:80–90. doi: 10.1097/ICU.0000000000000829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Goldmann H., S. T Applanation tonometry. Ophthalmol J Int D'Ophtalmol Int J Ophthalmol Z fur Augenheilkd. 1957;134:221–242. doi: 10.1159/000303213. [DOI] [PubMed] [Google Scholar]
- 149.Grolman B. "A new tonometer system,". Am J Optom Arch Am Acad Optom. 1972;49:646–660. doi: 10.1097/00006324-197208000-00005. [DOI] [PubMed] [Google Scholar]
- 150.Luce D. "Methodology for cornea compensated IOP and corneal resistance factor for the Reichert Ocular Response Analyzer,". Invest Ophthalmol Vis Sci. 2006;47:2266. [Google Scholar]
- 151.Luce D. "Methodology for Cornea Compensated IOP and Corneal Resistance Factor for the Reichert Ocular Response Analyzer,". Invest Ophthalmol Vis Sci. 2006;47:2266. [Google Scholar]
- 152.Kotecha A., Elsheikh A., Roberts C.R., Zhu H., Garway-Heath D.F. "Corneal Thickness- and Age-Related Biomechanical Properties of the Cornea Measured with the Ocular Response Analyzer,". Invest Ophthalmol Vis Sci. 2006;47:5337–5347. doi: 10.1167/iovs.06-0557. [DOI] [PubMed] [Google Scholar]
- 153.Elsheikh A., Wang D., Rama P., Campanelli M., Garway-Heath D. "Experimental assessment of human corneal hysteresis,". Curr Eye Res. 2008;33:205–213. doi: 10.1080/02713680701882519. [DOI] [PubMed] [Google Scholar]
- 154.Lopes B.T., Bao F., Wang J., Liu X., Wang L., Abass A., Eliasy A., Elsheikh A. "Review of in-vivo characterisation of corneal biomechanics,". Med Nov Technol Devices. 2021;11 [Google Scholar]
- 155.Glass D.H., Roberts C.J., Litsky A.S., Weber P.A. "A Viscoelastic Biomechanical Model of the Cornea Describing the Effect of Viscosity and Elasticity on Hysteresis,". Invest Ophthalmol Vis Sci. 2008;49:3919–3926. doi: 10.1167/iovs.07-1321. [DOI] [PubMed] [Google Scholar]
- 156.Matsuura M., Hirasawa K., Murata H., Nakakura S., Kiuchi Y., Asaoka R. "The usefulness of CorvisST Tonometry and the Ocular Response Analyzer to assess the progression of glaucoma,". Sci Rep. 2017;7:40798. doi: 10.1038/srep40798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Gkika M., Labiris G., Giarmoukakis A., Koutsogianni A., Kozobolis V. "Evaluation of corneal hysteresis and corneal resistance factor after corneal cross-linking for keratoconus,". Graefes Arch Clin Exp Ophthalmol. 2012;250:565–573. doi: 10.1007/s00417-011-1897-0. [DOI] [PubMed] [Google Scholar]
- 158.Bak-Nielsen S., Pedersen I.B., Ivarsen A., Hjortdal J. "Dynamic Scheimpflug-based assessment of keratoconus and the effects of corneal cross-linking,". J Refract Surg. 2014;30:408–414. doi: 10.3928/1081597X-20140513-02. [DOI] [PubMed] [Google Scholar]
- 159.Liang L., Zhang R., He L.-Y. "Corneal hysteresis and glaucoma,". Int Ophthalmol. 2019;39:1909–1916. doi: 10.1007/s10792-018-1011-2. [DOI] [PubMed] [Google Scholar]
- 160.Salouti R., Razeghinejad R., Eslami G., Zare M., Salouti K., Ghoreyshi M., Nowroozzadeh M.H. "Agreement of ocular response analyzer cornea compensated IOP with corvis ST biomechanical IOP following Femtosecond Laser-assisted LASIK,". Eye. 2023;37:263–266. doi: 10.1038/s41433-021-01928-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Salouti R., Khalili M.R., Zamani M., Ghoreyshi M., Nowroozzadeh M.H. Assessment of the changes in corneal biomechanical properties after collagen cross-linking in patients with keratoconus. J Curr Ophthalmol. 2019;31:262–267. doi: 10.1016/j.joco.2019.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Jabbarvand M., Moravvej Z., Shahraki K., Hashemian H., Ghasemi H., Berijani S., Amiri Z., Jamali A. "Corneal biomechanical outcome of collagen cross-linking in keratoconic patients evaluated by Corvis ST,". Eur J Ophthalmol. 2021;31:1577–1583. doi: 10.1177/1120672120944798. [DOI] [PubMed] [Google Scholar]
- 163.Boszczyk A., Kasprzak H., J. A Eye retraction and rotation during Corvis ST 'air puff' intraocular pressure measurement and its quantitative analysis. Ophthalmic Physiol Opt. 2017;37:253–262. doi: 10.1111/opo.12383. [DOI] [PubMed] [Google Scholar]
- 164.Maczynska E., Rzeszewska-Zamiara J., Jimenez Villar A., Wojtkowski M., Kaluzny B.J., G. I Air-Puff-Induced Dynamics of Ocular Components Measured with Optical Biometry. Invest Ophthalmol Vis Sci. 2019;60:1979–1986. doi: 10.1167/iovs.19-26681. [DOI] [PubMed] [Google Scholar]
- 165.Twa M.D., Li J., Vantipalli S., Singh M., Aglyamov S., Emelianov S., L. K. V Spatial characterization of corneal biomechanical properties with optical coherence elastography after UV cross-linking. Biomed Opt Express. 2014;5:1419–1427. doi: 10.1364/BOE.5.001419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Pahuja N., Kumar N.R., Shroff R., Shetty R., Nuijts R.M., Ghosh A., Sinha-Roy A., Chaurasia S.S., Mohan R.R., Ghosh A. "Differential molecular expression of extracellular matrix and inflammatory genes at the corneal cone apex drives focal weakening in keratoconus,". Invest Ophthalmol Vis Sci. 2016;57:5372–5382. doi: 10.1167/iovs.16-19677. [DOI] [PubMed] [Google Scholar]
- 167.Greenstein S.A., Fry K.L., Hersh P.S. "In vivo biomechanical changes after corneal collagen cross-linking for keratoconus and corneal ectasia: 1-year analysis of a randomized, controlled, clinical trial,". Cornea. 2012;31:21–25. doi: 10.1097/ICO.0b013e31821eea66. [DOI] [PubMed] [Google Scholar]
- 168.Goldich Y., Barkana Y., Morad Y., Hartstein M., Avni I., Zadok D. "Can we measure corneal biomechanical changes after collagen cross-linking in eyes with keratoconus?-a pilot study,". Cornea. 2009;28:498–502. doi: 10.1097/ICO.0b013e318190734d. [DOI] [PubMed] [Google Scholar]
- 169.Brillouin L. "Diffusion de la lumière et des rayons X par un corps transparent homogène," in. Ann Phys. 1922:88–122. [Google Scholar]
- 170.Antonacci G., Beck T., Bilenca A., Czarske J., Elsayad K., Guck J., Kim K., Krug B., Palombo F., Prevedel R., Scarcelli G. "Recent progress and current opinions in Brillouin microscopy for life science applications,". Biophys Rev. 2020;12:615–624. doi: 10.1007/s12551-020-00701-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Randall J., Vaughan J.M. The measurement and interpretation of Brillouin scattering in the lens of the eye. Proc R Soc Lond B Biol Sci. 1982;214:449–470. doi: 10.1098/rspb.1982.0021. [DOI] [PubMed] [Google Scholar]
- 172.Scarcelli G., Kling S., Quijano E., Pineda R., Marcos S., Yun S.H. "Brillouin Microscopy of Collagen Crosslinking: Noncontact Depth-Dependent Analysis of Corneal Elastic Modulus,". Invest Ophthalmol Vis Sci. 2013;54:1418–1425. doi: 10.1167/iovs.12-11387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Scarcelli G., Pineda R., Yun S.H. "Brillouin optical microscopy for corneal biomechanics,". Invest Ophthalmol Vis Sci. 2012;53:185–190. doi: 10.1167/iovs.11-8281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Zhang J., Scarcelli G. "Mapping mechanical properties of biological materials via an add-on Brillouin module to confocal microscopes,". Nat Protoc. 2021;16:1251–1275. doi: 10.1038/s41596-020-00457-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Lindsay S., Anderson M., Sandercock J. "Construction and alignment of a high performance multipass vernier tandem Fabry–Perot interferometer,". Rev Sci Instrum. 1981;52:1478–1486. [Google Scholar]
- 176.Vaughan J., Randall J. "Brillouin scattering, density and elastic properties of the lens and cornea of the eye,". Nature. 1980;284:489–491. doi: 10.1038/284489a0. [DOI] [PubMed] [Google Scholar]
- 177.Scarcelli G., Yun S.H. "Multistage VIPA etalons for high-extinction parallel Brillouin spectroscopy,". Opt Express. 2011;19:10913–10922. doi: 10.1364/OE.19.010913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 178.Scarcelli G., Besner S., Pineda R., Yun S.H. "Biomechanical Characterization of Keratoconus Corneas Ex Vivo With Brillouin Microscopy,". Invest Ophthalmol Vis Sci. 2014;55:4490–4495. doi: 10.1167/iovs.14-14450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179.Zhang H., Roozbahani M., Piccinini A.L., Hafezi F., Scarcelli G., Randleman J.B. "Brillouin microscopic depth-dependent analysis of corneal crosslinking performed over or under the LASIK flap,". J Cataract Refract Surg. 2020;46:1543–1547. doi: 10.1097/j.jcrs.0000000000000294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180.Zhang H., Roozbahani M., Piccinini A.L., Hafezi F., Scarcelli G., Randleman J.B. "Depth-dependent analysis of corneal cross-linking performed over or under the LASIK flap by Brillouin microscopy,". J Cataract Refract Surg. 2020;46:1543. doi: 10.1097/j.jcrs.0000000000000294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181.Yun S.H., Chernyak D. "Brillouin microscopy: assessing ocular tissue biomechanics,". Curr Opin Ophthalmol. 2018;29:299. doi: 10.1097/ICU.0000000000000489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182.Greenleaf J.F., Fatemi M., Insana M. "Selected methods for imaging elastic properties of biological tissues,". Annu Rev Biomed Eng. 2003;5:57–78. doi: 10.1146/annurev.bioeng.5.040202.121623. [DOI] [PubMed] [Google Scholar]
- 183.Sarvazyan A., Hall T.J., Urban M.W., Fatemi M., Aglyamov S.R., Garra B.S. "An Overview of Elastography - an Emerging Branch of Medical Imaging,". Curr Med Imaging Rev. 2011;7:255–282. doi: 10.2174/157340511798038684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184.Ormachea J., Parker K. Elastography imaging: the 30 year perspective. Phys Med Biol. 2020;65:24TR06. doi: 10.1088/1361-6560/abca00. [DOI] [PubMed] [Google Scholar]
- 185.Lerner R.M., Parker K.J., Holen J., Gramiak R., Waag R.C. Acoustical Imaging. Springer,; 1988. "Sono-elasticity: medical elasticity images derived from ultrasound signals in mechanically vibrated targets,"; pp. 317–327. [Google Scholar]
- 186.Ophir J., Cespedes I., Ponnekanti H., Yazdi Y., Li X. "Elastography: A quantitative method for imaging the elasticity of biological tissues,". Ultrason Imaging. 1991;13:111–134. doi: 10.1177/016173469101300201. [DOI] [PubMed] [Google Scholar]
- 187.Guillot C., Lecuit T. "Mechanics of epithelial tissue homeostasis and morphogenesis,". Science. 2013;340:1185–1189. doi: 10.1126/science.1235249. [DOI] [PubMed] [Google Scholar]
- 188.Butcher D.T., Alliston T., Weaver V.M. "A tense situation: forcing tumour progression,". Nat Rev Cancer. 2009;9:108–122. doi: 10.1038/nrc2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 189.Wu P.H., Aroush D.R.B., Asnacios A., Chen W.C., Dokukin M.E., Doss B.L., Durand Smet P., Ekpenyong A., Guck J., Guz N.V. "A comparison of methods to assess cell mechanical properties,". Nat Methods. 2018;15:491–498. doi: 10.1038/s41592-018-0015-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 190.De Lédinghen V., Vergniol J., Barthe C., Foucher J., Chermak F., Le Bail B., Merrouche W., Bernard P.H. "Non‐invasive tests for fibrosis and liver stiffness predict 5–year survival of patients chronically infected with hepatitis B virus,". Aliment Pharmacol Ther. 2013;37:979–988. doi: 10.1111/apt.12307. [DOI] [PubMed] [Google Scholar]
- 191.Khan S., Fakhouri F., Majeed W., Kolipaka A. "Cardiovascular magnetic resonance elastography: A review,". NMR Biomed. 2018;31 doi: 10.1002/nbm.3853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192.Samani A., Zubovits J., Plewes D. "Elastic moduli of normal and pathological human breast tissues: an inversion-technique-based investigation of 169 samples,". Phys Med Biol. 2007;52:1565. doi: 10.1088/0031-9155/52/6/002. [DOI] [PubMed] [Google Scholar]
- 193.Correas J.-M., Tissier A.-M., Khairoune A., Khoury G., Eiss D., Hélénon O. "Ultrasound elastography of the prostate: state of the art,". Diagn Interv Imaging. 2013;94:551–560. doi: 10.1016/j.diii.2013.01.017. [DOI] [PubMed] [Google Scholar]
- 194.Wang S., Larin K.V. "Optical coherence elastography for tissue characterization: a review,". J Biophotonics. 2015;8:279–302. doi: 10.1002/jbio.201400108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195.Mulligan J.A., Untracht G.R., Chandrasekaran S.N., Brown C.N., Adie S.G. "Emerging approaches for high-resolution imaging of tissue biomechanics with optical coherence elastography,". IEEE J Sel Top Quantum Electron. 2015;22:246–265. [Google Scholar]
- 196.Mahaffy R.E., Shih C.K., MacKintosh F.C., Käs J. "Scanning probe-based frequency-dependent microrheology of polymer gels and biological cells,". Phys Rev Lett. 2000;85:880–883. doi: 10.1103/PhysRevLett.85.880. [DOI] [PubMed] [Google Scholar]
- 197.Kirmizis D., Logothetidis S. "Atomic force microscopy probing in the measurement of cell mechanics,". Int J Nanomed. 2010;5:137–145. doi: 10.2147/ijn.s5787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 198.Righetti R., Ophir J., Ktonas P. "Axial resolution in elastography,". Ultrasound Med Biol. 2002;28:101–113. doi: 10.1016/s0301-5629(01)00495-1. [DOI] [PubMed] [Google Scholar]
- 199.Braun J., Guo J., Lützkendorf R., Stadler J.R., Papazoglou S., Hirsch S., Sack I., Bernarding J. High-resolution mechanical imaging of the human brain by three-dimensional multifrequency magnetic resonance elastography at 7T. Neuroimage. 2014;90:308–314. doi: 10.1016/j.neuroimage.2013.12.032. [DOI] [PubMed] [Google Scholar]
- 200.Johnson C.L., Mcgarry M.D., Van Houten E.E., Weaver J.B., Paulsen K.D., Sutton B.P., Georgiadis J.G. Magnetic resonance elastography of the brain using multishot spiral readouts with self-navigated motion correction. Magn Reson Med. 2013;70:404–412. doi: 10.1002/mrm.24473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 201.Itoh A., Ueno E., Tohno E., Kamma H., Takahashi H., Shiina T., Yamakawa M., Matsumura T. "Breast disease: clinical application of US elastography for diagnosis1,". Radiology. 2006;239:341–350. doi: 10.1148/radiol.2391041676. [DOI] [PubMed] [Google Scholar]
- 202.Mcknight A.L., Kugel J.L., Rossman P.J., Manduca A., Hartmann L.C., Ehman R.L. "MR elastography of breast cancer: preliminary results,". Am J Roentgenol. 2002;178:1411–1417. doi: 10.2214/ajr.178.6.1781411. [DOI] [PubMed] [Google Scholar]
- 203.Pavlatos E., Chen H., Clayson K., Pan X., Liu J. "Imaging corneal biomechanical responses to ocular pulse using high-frequency ultrasound,". IEEE Trans Med Imaging. 2018;37:663–670. doi: 10.1109/TMI.2017.2775146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 204.Kirby M.A., Pelivanov I., Song S., Ambrozinski L., Yoon S.J., Gao L., Li D., Shen T.T., Wang R.K., O'Donnell M. Optical coherence elastography in ophthalmology. J Biomed Opt. 2017;22 doi: 10.1117/1.JBO.22.12.121720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 205.Schmitt J. "OCT elastography: imaging microscopic deformation and strain of tissue,". Opt Express. 1998;3:199–211. doi: 10.1364/oe.3.000199. [DOI] [PubMed] [Google Scholar]
- 206.Huang D., Swanson E.A., Lin C.P., Schuman J.S., Stinson W.G., Chang W., Hee M.R., Flotte T., Gregory K., Puliafito C.A. "Optical coherence tomography,". Science. 1991;254:1178. doi: 10.1126/science.1957169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 207.Zhao Y., Chen Z., Saxer C., Xiang S., de Boer J.F., Nelson J.S. "Phase-resolved optical coherence tomography and optical Doppler tomography for imaging blood flow in human skin with fast scanning speed and high velocity sensitivity,". Opt Lett. 2000;25:114–116. doi: 10.1364/ol.25.000114. [DOI] [PubMed] [Google Scholar]
- 208.Sticker M., Hitzenberger C.K., Leitgeb R., Fercher A.F. Quantitative differential phase measurement and imaging in transparent and turbid media by optical coherence tomography. Opt Lett. 2001;26:518–520. doi: 10.1364/ol.26.000518. [DOI] [PubMed] [Google Scholar]
- 209.Kirkpatrick S.J., Wang R.K., Duncan D.D. "OCT-based elastography for large and small deformations,". Opt Express. 2006;14:11585–11597. doi: 10.1364/oe.14.011585. [DOI] [PubMed] [Google Scholar]
- 210.Lan G., Singh M., Larin K.V., Twa M.D. "Common-path phase-sensitive optical coherence tomography provides enhanced phase stability and detection sensitivity for dynamic elastography,". Biomed Opt Express. 2017;8:5253–5266. doi: 10.1364/BOE.8.005253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211.Leartprapun N., Adie S.G. "Recent advances in optical elastography and emerging opportunities in the basic sciences and translational medicine,". Biomed Opt Express. 2023;14:208–248. doi: 10.1364/BOE.468932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 212.Lan G., Gu B., Larin K.V., Twa M.D. "Clinical corneal optical coherence elastography measurement precision: effect of heartbeat and respiration,". Transl Vis Sci Technol. 2020;9:3. doi: 10.1167/tvst.9.5.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 213.Curatolo A., Birkenfeld J.S., Martinez-Enriquez E., Germann J.A., Muralidharan G., Palací J., Pascual D., Eliasy A., Abass A., Solarski J. "Multi-meridian corneal imaging of air-puff induced deformation for improved detection of biomechanical abnormalities,". Biomed Opt Express. 2020;11:6337–6355. doi: 10.1364/BOE.402402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 214.Maczynska E., Rzeszewska-Zamiara J., Villar A.J., Wojtkowski M., Kaluzny B.J., Grulkowski I. "Air-Puff-Induced Dynamics of Ocular Components Measured with Optical Biometry,". Invest Ophthalmol Vis Sci. 2019;60:1979–1986. doi: 10.1167/iovs.19-26681. [DOI] [PubMed] [Google Scholar]
- 215.Chen S., Jin Z., Zheng G., Ye S., Wang Y., Wang W., Wang Y., Zhu D., Shen M., Lu F. "Diurnal variation of corneal elasticity in healthy young human using air‐puff optical coherence elastography,". J Biophotonics. 2021 doi: 10.1002/jbio.202000440. [DOI] [PubMed] [Google Scholar]
- 216.Rogowska J., Patel N.A., Fujimoto J.G., Brezinski M.E. "Optical coherence tomographic elastography technique for measuring deformation and strain of atherosclerotic tissues,". Heart. 2004;90:556–562. doi: 10.1136/hrt.2003.016956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 217.Chan R., Chau A., Karl W., Nadkarni S., Khalil A., Iftimia N., Shishkov M., Tearney G., Kaazempur-Mofrad M., Bouma B. "OCT-based arterial elastography: robust estimation exploiting tissue biomechanics,". Opt Express. 2004;12:4558–4572. doi: 10.1364/opex.12.004558. [DOI] [PubMed] [Google Scholar]
- 218.Li C., Guan G., Reif R., Huang Z., Wang R.K. "Determining elastic properties of skin by measuring surface waves from an impulse mechanical stimulus using phase-sensitive optical coherence tomography,". J R Soc Interface. 2012;9:831–841. doi: 10.1098/rsif.2011.0583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 219.Song S., Huang Z., Nguyen T.-M., Wong E.Y., Arnal B., O’Donnell M., Wang R.K. "Shear modulus imaging by direct visualization of propagating shear waves with phase-sensitive optical coherence tomography,". J Biomed Opt. 2013;18 doi: 10.1117/1.JBO.18.12.121509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 220.Kennedy B.F., Hillman T.R., McLaughlin R.A., Quirk B.C., Sampson D.D. "In vivo dynamic optical coherence elastography using a ring actuator,". Opt Express. 2009;17:21762–21772. doi: 10.1364/OE.17.021762. [DOI] [PubMed] [Google Scholar]
- 221.Kennedy K.M., Kennedy B.F., McLaughlin R.A., Sampson D.D. "Needle optical coherence elastography for tissue boundary detection,". Opt Express. 2012;37:2310–2312. doi: 10.1364/OL.37.002310. [DOI] [PubMed] [Google Scholar]
- 222.Kennedy K.M., McLaughlin R.A., Kennedy B.F., Tien A., Latham B., Saunders C.M., Sampson D.D. Needle optical coherence elastography for the measurement of microscale mechanical contrast deep within human breast tissues. J Biomed Opt. 2013;18 doi: 10.1117/1.JBO.18.12.121510. [DOI] [PubMed] [Google Scholar]
- 223.Crecea V., Oldenburg A.L., Liang X., Ralston T.S., Boppart S.A. "Magnetomotive nanoparticle transducers for optical rheology of viscoelastic materials,". Opt Express. 2009;17:23114–23122. doi: 10.1364/OE.17.023114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 224.Ahmad A., Kim J., Sobh N.A., Shemonski N.D., Boppart S.A. "Magnetomotive optical coherence elastography using magnetic particles to induce mechanical waves,". Biomed Opt Express. 2014;5:2349–2361. doi: 10.1364/BOE.5.002349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 225.Liu C.-H., Nevozhay D., Schill A., Singh M., Das S., Nair A., Han Z., Aglyamov S., Larin K.V., Sokolov K.V. "Nanobomb optical coherence elastography,". Opt Express. 2018;43:2006–2009. doi: 10.1364/OL.43.002006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 226.Liu C.-H., Nevozhay D., Zhang H., Das S., Schill A., Singh M., Aglyamov S., Sokolov K.V., Larin K.V. "Longitudinal elastic wave imaging using nanobomb optical coherence elastography,". Opt Express. 2019;44:3162–3165. doi: 10.1364/OL.44.003162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 227.Akca B.I., Chang E.W., Kling S., Ramier A., Scarcelli G., Marcos S., Yun S.H. "Observation of sound-induced corneal vibrational modes by optical coherence tomography,". Biomed Opt Express. 2015;6:3313–3319. doi: 10.1364/BOE.6.003313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 228.Li C., Guan G., Huang Z., Johnstone M., Wang R.K. "Noncontact all-optical measurement of corneal elasticity,". Opt Lett. 2012;37:1625–1627. doi: 10.1364/OL.37.001625. [DOI] [PubMed] [Google Scholar]
- 229.Li C., Huang Z., Wang R.K. "Elastic properties of soft tissue-mimicking phantoms assessed by combined use of laser ultrasonics and low coherence interferometry,". Opt Express. 2011;19:10153–10163. doi: 10.1364/OE.19.010153. [DOI] [PubMed] [Google Scholar]
- 230.Kang H., Qian X., Chen R., Wodnicki R., Sun Y., Li R., Li Y., Shung K.K., Chen Z., Zhou Q. "2-D Ultrasonic Array-Based Optical Coherence Elastography,". IEEE Trans Ultrason Ferroelectr Freq Control. 2021;68:1096–1104. doi: 10.1109/TUFFC.2020.3033304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 231.Zhao Y., Zhu Y., Wang Y., Yang H., He X., Alvarez-Arenas T.G., Li Y., Huang G. "Quantitative Evaluation of In Vivo Corneal Biomechanical Properties after SMILE and FLEx Surgery by Acoustic Radiation Force Optical Coherence Elastography,". Sensors. 2023;23:181. doi: 10.3390/s23010181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 232.Ai S., Zhang Y., Shi G., Wang Y., Liu G., Han X., Zhao Y., Yang H., He X. "Acoustic radiation forces optical coherence elastography: a preliminary study on biomechanical properties of trabecular meshwork,". J Biophotonics. 2023 doi: 10.1002/jbio.202200317. [DOI] [PubMed] [Google Scholar]
- 233.Zvietcovich F., Nair A., Singh M., Aglyamov S.R., Twa M.D., Larin K.V. "In vivo assessment of corneal biomechanics under a localized cross-linking treatment using confocal air-coupled optical coherence elastography,". Biomed Opt Express. 2022;13:2644–2654. doi: 10.1364/BOE.456186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 234.Ambroziński Ł., Pelivanov I., Song S., Yoon S.J., Li D., Gao L., Shen T.T., Wang R.K., O'Donnell M. Air-coupled acoustic radiation force for non-contact generation of broadband mechanical waves in soft media. Appl Phys Lett. 2016;109 doi: 10.1063/1.4959827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 235.Jin Z., Khazaeinezhad R., Zhu J., Yu J., Qu Y., He Y., Li Y., Gomez Alvarez-Arenas T.E., Lu F., Chen Z. "In-vivo 3D corneal elasticity using air-coupled ultrasound optical coherence elastography,". Biomed Opt Express. 2019;10:6272–6285. doi: 10.1364/BOE.10.006272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 236.Wang S., Larin K.V., Li J., Vantipalli S., Manapuram R.K., Aglyamov S., Emelianov S., Twa M.D. "A focused air-pulse system for optical-coherence-tomography-based measurements of tissue elasticity,". Laser Phys Lett. 2013;10 doi: 10.1088/1612-2011/10/7/075605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 237.Wang S., Li J., Manapuram R.K., Menodiado F.M., Ingram D.R., Twa M.D., Lazar A.J., Lev D.C., Pollock R.E., Larin K.V. "Noncontact measurement of elasticity for the detection of soft-tissue tumors using phase-sensitive optical coherence tomography combined with a focused air-puff system,". Opt Lett. 2012;37:5184–5186. doi: 10.1364/OL.37.005184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 238.Dorronsoro C., Pascual D., Perez-Merino P., Kling S., Marcos S. "Dynamic OCT measurement of corneal deformation by an air puff in normal and cross-linked corneas,". Biomed Opt Express. 2012;3:473–487. doi: 10.1364/BOE.3.000473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 239.Nair A., Singh M., Aglyamov S.R., Larin K.V. "Multimodal heartbeat and compression optical coherence elastography for mapping corneal biomechanics,". Front Med. 2022;9 doi: 10.3389/fmed.2022.833597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 240.Nguyen T.-M., Zorgani A., Lescanne M., Boccara C., Fink M., Catheline S. Diffuse shear wave imaging: toward passive elastography using low-frame rate spectral-domain optical coherence tomography. J Biomed Opt. 2016;21 doi: 10.1117/1.JBO.21.12.126013. [DOI] [PubMed] [Google Scholar]
- 241.Larin K.V., Sampson D.D. "Optical coherence elastography–OCT at work in tissue biomechanics,". Biomed Opt Express. 2017;8:1172–1202. doi: 10.1364/BOE.8.001172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 242.Parker K.J., Doyley M.M., Rubens D.J. Imaging the elastic properties of tissue: the 20 year perspective. Phys Med Biol. 2010;56:R1. doi: 10.1088/0031-9155/56/1/R01. [DOI] [PubMed] [Google Scholar]
- 243.Kennedy K.M., Es’haghian S., Chin L., McLaughlin R.A., Sampson D.D., Kennedy B.F. "Optical palpation: optical coherence tomography-based tactile imaging using a compliant sensor,". Opt Express. 2014;39:3014–3017. doi: 10.1364/OL.39.003014. [DOI] [PubMed] [Google Scholar]
- 244.Lan G., Larin K.V., Aglyamov S., Twa M.D. "Characterization of natural frequencies from nanoscale tissue oscillations using dynamic optical coherence elastography,". Biomed Opt Express. 2020;11:3301–3318. doi: 10.1364/BOE.391324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 245.Lan G., Shi Q., Wang Y., Ma G., Cai J., Feng J., Huang Y., Gu B., An L., Xu J. "Spatial assessment of heterogeneous tissue natural frequency using micro-force optical coherence elastography,". Front Bioeng Biotechnol. 2022;382 doi: 10.3389/fbioe.2022.851094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 246.Lains I., Wang J.C., Cui Y., Katz R., Vingopoulos F., Staurenghi G., Vavvas D.G., Miller J.W., Miller J.B. "Retinal applications of swept source optical coherence tomography (OCT) and optical coherence tomography angiography (OCTA),". Prog Retin Eye Res. 2021;84 doi: 10.1016/j.preteyeres.2021.100951. [DOI] [PubMed] [Google Scholar]
- 247.Sampson D.M., Dubis A.M., Chen F.K., Zawadzki R.J., Sampson D.D. "Towards standardizing retinal optical coherence tomography angiography: a review,". Light Sci Appl. 2022;11:1–22. doi: 10.1038/s41377-022-00740-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 248.Fujimoto J., Swanson E. The development, commercialization, and impact of optical coherence tomography. Invest Ophthalmol Vis Sci. 2016;57:OCT1–OCT13. doi: 10.1167/iovs.16-19963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 249.Spaide R.F., Fujimoto J.G., Waheed N.K., Sadda S.R., Staurenghi G. "Optical coherence tomography angiography,". Prog Retin Eye Res. 2018;64:1–55. doi: 10.1016/j.preteyeres.2017.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 250.Puliafito C.A., Hee M.R., Lin C.P., Reichel E., Schuman J.S., Duker J.S., Izatt J.A., Swanson E.A., Fujimoto J.G. "Imaging of macular diseases with optical coherence tomography,". Ophthalmology. 1995;102:217–229. doi: 10.1016/s0161-6420(95)31032-9. [DOI] [PubMed] [Google Scholar]
- 251.Leitgeb R., Wojtkowski M., Kowalczyk A., Hitzenberger C.K., Sticker M., F. A. F Spectral measurement of absorption by spectroscopic frequency-domain optical coherence tomography. Opt Express. 2000;25:820–822. doi: 10.1364/ol.25.000820. [DOI] [PubMed] [Google Scholar]
- 252.Li P., An L., Lan G., Johnstone M., Malchow D., Wang R.K. Extended imaging depth to 12 mm for 1050-nm spectral domain optical coherence tomography for imaging the whole anterior segment of the human eye at 120-kHz A-scan rate. J Biomed Opt. 2013;18 doi: 10.1117/1.JBO.18.1.016012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 253.An L., Li P., Lan G., Malchow D., Wang R.K. "High-resolution 1050 nm spectral domain retinal optical coherence tomography at 120 kHz A-scan rate with 6.1 mm imaging depth,". Biomed Opt Express. 2013;4:245–259. doi: 10.1364/BOE.4.000245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 254.Gloesmann M., Hermann B., Schubert C., Sattmann H., Ahnelt P.K., Drexler W. "Histologic Correlation of Pig Retina Radial Stratification with Ultrahigh-Resolution Optical Coherence Tomography,". Invest Ophthalmol Vis Sci. 2003;44:1696–1703. doi: 10.1167/iovs.02-0654. [DOI] [PubMed] [Google Scholar]
- 255.Ko T.H., Fujimoto J.G., Schuman J.S., Paunescu L.A., Kowalevicz A.M., Hartl I., Drexler W., Wollstein G., Ishikawa H., Duker J.S. Comparison of ultrahigh-and standard-resolution optical coherence tomography for imaging macular pathology. Ophthalmology. 2005;112(1922):e1921–e1922. doi: 10.1016/j.ophtha.2005.05.027. e1915. e1915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 256.Fercher A.F., Hitzenberger C.K., Kamp G., El-Zaiat S.Y. "Measurement of intraocular distances by backscattering spectral interferometry,". Opt Commun. 1995;117:43–48. [Google Scholar]
- 257.Choma M.A., Sarunic M.V., Yang C., Izatt J.A. "Sensitivity advantage of swept source and Fourier domain optical coherence tomography,". Opt Express. 2003;11:2183–2189. doi: 10.1364/oe.11.002183. [DOI] [PubMed] [Google Scholar]
- 258.Lan G., Li G. "Design of a k-space spectrometer for ultra-broad waveband spectral domain optical coherence tomography,". Sci Rep. 2017;7:42353. doi: 10.1038/srep42353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 259.Hu Z., Rollins A.M. "Fourier domain optical coherence tomography with a linear-in-wavenumber spectrometer,". Opt Lett. 2007;32:3525–3527. doi: 10.1364/ol.32.003525. [DOI] [PubMed] [Google Scholar]
- 260.Lan G., Xu J., Hu Z., Huang Y., Wei Y., Yuan X., Liu H., Qin J., Wang Y., Shi Q., Zeng J., Shi Y., Feng J., Tan H., An L., Wei X. Design of 1300-nm spectral domain optical coherence tomography angiography system for iris microvascular imaging. J Phys D Appl Phys. 2021 [Google Scholar]
- 261.Singh M., Wu C., Liu C.H., Li J., Schill A., Nair A., Larin K.V. "Phase-sensitive optical coherence elastography at 1.5 million A-Lines per second,". Opt Lett. 2015;40:2588–2591. doi: 10.1364/OL.40.002588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 262.Song S., Wei W., Hsieh B.Y., Pelivanov I., Shen T.T., O'Donnell M., Wang R.K. "Strategies to improve phase-stability of ultrafast swept source optical coherence tomography for single shot imaging of transient mechanical waves at 16 kHz frame rate,". Appl Phys Lett. 2016;108 doi: 10.1063/1.4949469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 263.Rigden J., Gordon E. Granularity of scattered optical maser light. Proc Inst Radio Eng. 1962;50:2367. &. [Google Scholar]
- 264.Schmitt J.M., Xiang S.H., Yung K.M. Speckle in optical coherence tomography. J Biomed Opt. 1999;4:95–105. doi: 10.1117/1.429925. [DOI] [PubMed] [Google Scholar]
- 265.Sun C., Standish B.A., Vuong B., Wen X.-Y., Yang V.X. Digital image correlation–based optical coherence elastography. J Biomed Opt. 2013;18 doi: 10.1117/1.JBO.18.12.121515. [DOI] [PubMed] [Google Scholar]
- 266.Nahas A., Bauer M., Roux S., Boccara A.C. "3D static elastography at the micrometer scale using Full Field OCT,". Biomed Opt Express. 2013;4:2138–2149. doi: 10.1364/BOE.4.002138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 267.Fu J., Pierron F., Ruiz P.D. "Elastic stiffness characterization using three-dimensional full-field deformation obtained with optical coherence tomography and digital volume correlation,". J Biomed Opt. 2013;18 doi: 10.1117/1.JBO.18.12.121512. [DOI] [PubMed] [Google Scholar]
- 268.Schmitt J. "OCT elastography: imaging microscopic deformation and strain of tissue,". Opt Express. 1998;3:199–211. doi: 10.1364/oe.3.000199. [DOI] [PubMed] [Google Scholar]
- 269.Chau A.H., Chan R.C., Shishkov M., MacNeill B., Iftimia N., Tearney G.J., Kamm R.D., Bouma B.E., Kaazempur-Mofrad M.R. "Mechanical analysis of atherosclerotic plaques based on optical coherence tomography,". Ann Biomed Eng. 2004;32:1494–1503. doi: 10.1114/b:abme.0000049034.75368.4a. [DOI] [PubMed] [Google Scholar]
- 270.Chan R., Chau A., Karl W., Nadkarni S., Khalil A., Iftimia N., Shishkov M., Tearney G., Kaazempur-Mofrad M., Bouma B. "OCT-based arterial elastography: robust estimation exploiting tissue biomechanics,". Opt Express. 2004;12:4558–4572. doi: 10.1364/opex.12.004558. [DOI] [PubMed] [Google Scholar]
- 271.Liang X., Oldenburg A.L., Crecea V., Chaney E.J., Boppart S.A. "Optical micro-scale mapping of dynamic biomechanical tissue properties,". Opt Express. 2008;16:11052–11065. doi: 10.1364/oe.16.011052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 272.Hendriks F., Brokken D., Oomens C., Bader D., Baaijens F. "The relative contributions of different skin layers to the mechanical behavior of human skin in vivo using suction experiments,". Med Eng Phys. 2006;28:259–266. doi: 10.1016/j.medengphy.2005.07.001. [DOI] [PubMed] [Google Scholar]
- 273.Ko H.-J., Tan W., Stack R., Boppart S.A. "Optical coherence elastography of engineered and developing tissue,". Tissue Eng. 2006;12:63–73. doi: 10.1089/ten.2006.12.63. [DOI] [PubMed] [Google Scholar]
- 274.Rogowska J., Patel N., Plummer S., Brezinski M. "Quantitative optical coherence tomographic elastography: method for assessing arterial mechanical properties,". Br J Radiol. 2006;79:707–711. doi: 10.1259/bjr/22522280. [DOI] [PubMed] [Google Scholar]
- 275.Park B.H., Pierce M.C., Cense B., Yun S.-H., Mujat M., Tearney G.J., Bouma B.E., De Boer J.F. Real-time fiber-based multi-functional spectral-domain optical coherence tomography at 1.3 µm. Opt Express. 2005;13:3931–3944. doi: 10.1364/opex.13.003931. [DOI] [PubMed] [Google Scholar]
- 276.Li Y., Moon S., Chen J.J., Zhu Z., Chen Z. "Ultrahigh-sensitive optical coherence elastography,". Light Sci Appl. 2020;9:1–10. doi: 10.1038/s41377-020-0297-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 277.Carstensen E.L., Parker K.J. "Physical models of tissue in shear fields,". Ultrasound Med Biol. 2014;40:655–674. doi: 10.1016/j.ultrasmedbio.2013.11.001. [DOI] [PubMed] [Google Scholar]
- 278.Zvietcovich F., Larin K.V. "Wave-based optical coherence elastography: the 10-year perspective,". Prog Biomed Eng. 2022;4 doi: 10.1088/2516-1091/ac4512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 279.Zhu J., Yu J., Qu Y., He Y., Li Y., Yang Q., Huo T., He X., Chen Z. "Coaxial excitation longitudinal shear wave measurement for quantitative elasticity assessment using phase-resolved optical coherence elastography,". Opt Express. 2018;43:2388–2391. doi: 10.1364/OL.43.002388. [DOI] [PubMed] [Google Scholar]
- 280.Sokolnikoff I.S., Specht R.D. McGraw-Hill,; New York: 1956. Mathematical Theory of Elasticity. [Google Scholar]
- 281.Alonso-Caneiro D., Karnowski K., K. B. J Assessment of corneal dynamics with high-speed swept source optical coherence tomography combined with an air puff system. Opt Express. 2011;19:14188–14199. doi: 10.1364/OE.19.014188. [DOI] [PubMed] [Google Scholar]
- 282.Pelivanov I., Gao L., Pitre J., Kirby M.A., Song S., Li D., Shen T.T., Wang R.K., O'Donnell M. Does group velocity always reflect elastic modulus in shear wave elastography? J Biomed Opt. 2019;24 doi: 10.1117/1.JBO.24.7.076003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 283.Fatemi, M Ultrasound-stimulated vibro-acoustic spectrography. Science. 1998;280:82–85. doi: 10.1126/science.280.5360.82. [DOI] [PubMed] [Google Scholar]
- 284.Maynard J. "Resonant ultrasound spectroscopy,". Phys Today. 1996;49:26–31. [Google Scholar]
- 285.Qi W., Li R., Ma T., Li J., Kirk S.K., Zhou Q., Chen Z. "Resonant acoustic radiation force optical coherence elastography,". Appl Phys Lett. 2013;103:75–96. doi: 10.1063/1.4820252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 286.Adie S.G., Liang X., Kennedy B.F., John R., Sampson D.D., Boppart S.A. "Spectroscopic optical coherence elastography,". Opt Express. 2010;18:25519–25534. doi: 10.1364/OE.18.025519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 287.Liang X., Oldenburg A.L., Crecea V., Chaney E.J., Boppart S.A. "Optical micro-scale mapping of dynamic biomechanical tissue properties,". Opt Express. 2008;16:11052–11065. doi: 10.1364/oe.16.011052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 288.Oldenburg A.L., Boppart S.A., Biology Resonant acoustic spectroscopy of soft tissues using embedded magnetomotive nanotransducers and optical coherence tomography. Phys Med Biol. 2010;55:1189–1201. doi: 10.1088/0031-9155/55/4/019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 289.Fischer T.H. "Imaging and elastometry of blood clots using magnetomotive optical coherence tomography and labeled platelets,". IEEE J Sel Top Quantum Electron. 2011;18 doi: 10.1109/JSTQE.2011.2162580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 290.Wang S., Larin K.V. "Shear wave imaging optical coherence tomography (SWI-OCT) for ocular tissue biomechanics,". Opt Lett. 2014;39:41–44. doi: 10.1364/OL.39.000041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 291.Song S., Huang Z., Nguyen T.M., Wong E.Y., Arnal B., O'Donnell M., Wang R.K. "Shear modulus imaging by direct visualization of propagating shear waves with phase-sensitive optical coherence tomography. J Biomed Opt. 2013;18 doi: 10.1117/1.JBO.18.12.121509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 292.Shih C.-C., Qian X., Ma T., Han Z., Huang C.-C., Zhou Q., Shung K.K. "Quantitative assessment of thin-layer tissue viscoelastic properties using ultrasonic micro-elastography with Lamb wave model,". IEEE Trans Med Imaging. 2018;37:1887–1898. doi: 10.1109/TMI.2018.2820157. [DOI] [PubMed] [Google Scholar]
- 293.Han Z., Li J., Singh M., Wu C., Liu C., Raghunathan R., Aglyamov S.R., Vantipalli S., Twa M.D., Larin K.V. "Optical coherence elastography assessment of corneal viscoelasticity with a modified Rayleigh-Lamb wave model. J Mech Behav Biomed. 2017;66:87–94. doi: 10.1016/j.jmbbm.2016.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 294.Li J., Han Z., Singh M., Twa M.D., Larin K.V. "Differentiating untreated and cross-linked porcine corneas of the same measured stiffness with optical coherence elastography,". J Biomed Opt. 2014;19 doi: 10.1117/1.JBO.19.11.110502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 295.Wu C., Han Z., Wang S., Li J., Singh M., Liu C., Aglyamov S., Emelianov S., Manns F., Larin K.V. "Assessing age-related changes in the biomechanical properties of rabbit lens using a coaligned ultrasound and optical coherence elastography system,". Invest Ophthalmol Vis Sci. 2015;56:1292–1300. doi: 10.1167/iovs.14-15654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 296.Pitre J.J., Kirby M.A., Li D.S., Shen T.T., Wang R.K., O’Donnell M., Pelivanov I. "Nearly-incompressible transverse isotropy (NITI) of cornea elasticity: model and experiments with acoustic micro-tapping OCE,". Sci Rep. 2020;10:12983. doi: 10.1038/s41598-020-69909-9. [DOI] [PMC free article] [PubMed] [Google Scholar]