On the Need for Landmark Analysis or Time Dependent Covariates

As statistical editors for The Journal of Urology we have identified one of the most common serious statistical errors in recent submissions is ignoring the time-dependency of covariates in survival analyses, despite being identified and described as guideline 4.15¹ in the shared statistical guidelines published across the four major urological journals (The Journal of Urology, European Urology, BJUI and Urology). In this paper we seek to highlight this issue, provide examples of scenarios involving time-dependent covariates, and introduce appropriate statistical methods for use in this setting.

In many urological studies the primary endpoint is the time to an event of interest, such as death, recurrence, or progression. It is common that not all individuals in a study will have experienced the event of interest at the time of analysis, a phenomenon known as censoring. For time-to-event endpoints where some subjects are censored, specialized statistical methods known as survival analysis are used, in which the status and the time-to-event are analyzed simultaneously. The time to event is defined as the time from the start of follow-up (e.g. date of randomization, date of treatment initiation, date of diagnosis) to either the event of interest (among patients who experienced the event) or the last follow-up at which the subject was known to be event-free (among patients who did not yet experience the event) (for further description see guideline 4.13¹).

Common survival analysis techniques, such as Cox regression or the Kaplan-Meier method, assume that all covariates are known at the start of follow-up. However, at times we may wish to analyze the association between a covariate that is not known at the start of follow-up and a time-to-event endpoint. In 1983 a seminal paper by Anderson et al. in the Journal of Clinical Oncology drew attention to the issue of post-baseline covariates in survival analysis.⁶ The authors demonstrate that comparing survival between responders and non-responders using traditional survival analysis methods is biased in favor of responders due to “guarantee-time bias” (also known as immortal-time bias), in which responders must live long enough to eventually be evaluated as responders, whereas no such requirement is present for non-responders.⁶ They then outline statistical techniques to handle covariates whose value changes over the course of follow-up time, including landmark analysis and the use of time-dependent covariates.

The landmark analysis technique is appropriate when the covariate of interest is known within a relatively short period of time after the start of follow-up. In a landmark analysis, first a fixed time after baseline is selected to use as the landmark time. This will typically be a time by which the covariate of interest would be known for most patients. For example, in a study of the association between systemic therapy alone or in combination with cytoreductive nephrectomy and overall survival in patients with metastatic renal cell carcinoma, a 6-month landmark time was used since the study exclusion criteria required patients to have initiated systemic therapy within 6 months of diagnosis, so the group assignment would be fully known by this landmark time⁴. Second, the analysis cohort is limited to those who are still at risk for the event at the landmark time, meaning that subjects who were censored or experienced the event of interest prior to the landmark are excluded. For example, in a study of the association between PSA decline and metastasis-free survival in patients with prostate cancer, 407 patients who experienced metastasis or died prior to the 12-month landmark were excluded from the analysis². Third, follow-up time is calculated starting from the landmark time and standard survival analysis techniques like the log-rank test or Cox regression can be applied to examine associations between the covariate and time-to-event endpoint of interest. Continuing the previous example, the Kaplan-Meier method was used to estimate metastasis-free survival following the 12-month landmark for those who did and did not experience PSA decline by the landmark time². Lastly, results must be interpreted in the context of the landmark population. For example, in a study comparing time-to-metastasis between prostate cancer patients treated with active surveillance versus initial curative treatment, among patients who were followed for at least two years and had not yet developed metastases or been censored for any reason, active surveillance was associated with an increased hazard of metastasis as compared to initial curative treatment³.

Consider a hypothetical example where overall survival after surgery is compared between patients who did or did not receive adjuvant therapy. Figure 1 illustrates the differences when analyzing the data using the Kaplan-Meier method with the log-rank test to compare between groups (A) where follow-up time starts at the baseline date of surgery and (B) where follow-up time starts at a landmark time of 3 months after surgery. In the naïve approach when follow-up time starts at the date of surgery (A) we find a significant improvement in overall survival for patients who received adjuvant therapy versus those who did not (p<0.001) whereas using the landmark approach (B) we do not have sufficient evidence of a difference (p=0.12) (Figure 1). The guarantee-time bias described by Anderson et al⁶ is clear in (A), which demonstrates that in order to be in the adjuvant therapy group patients had to live long enough to undergo treatment. While the results of a landmark analysis may not always be so different as to impact the significance of association, this is an important concept to understand and address in analyses to avoid bias in estimates of association.

Figure 1.

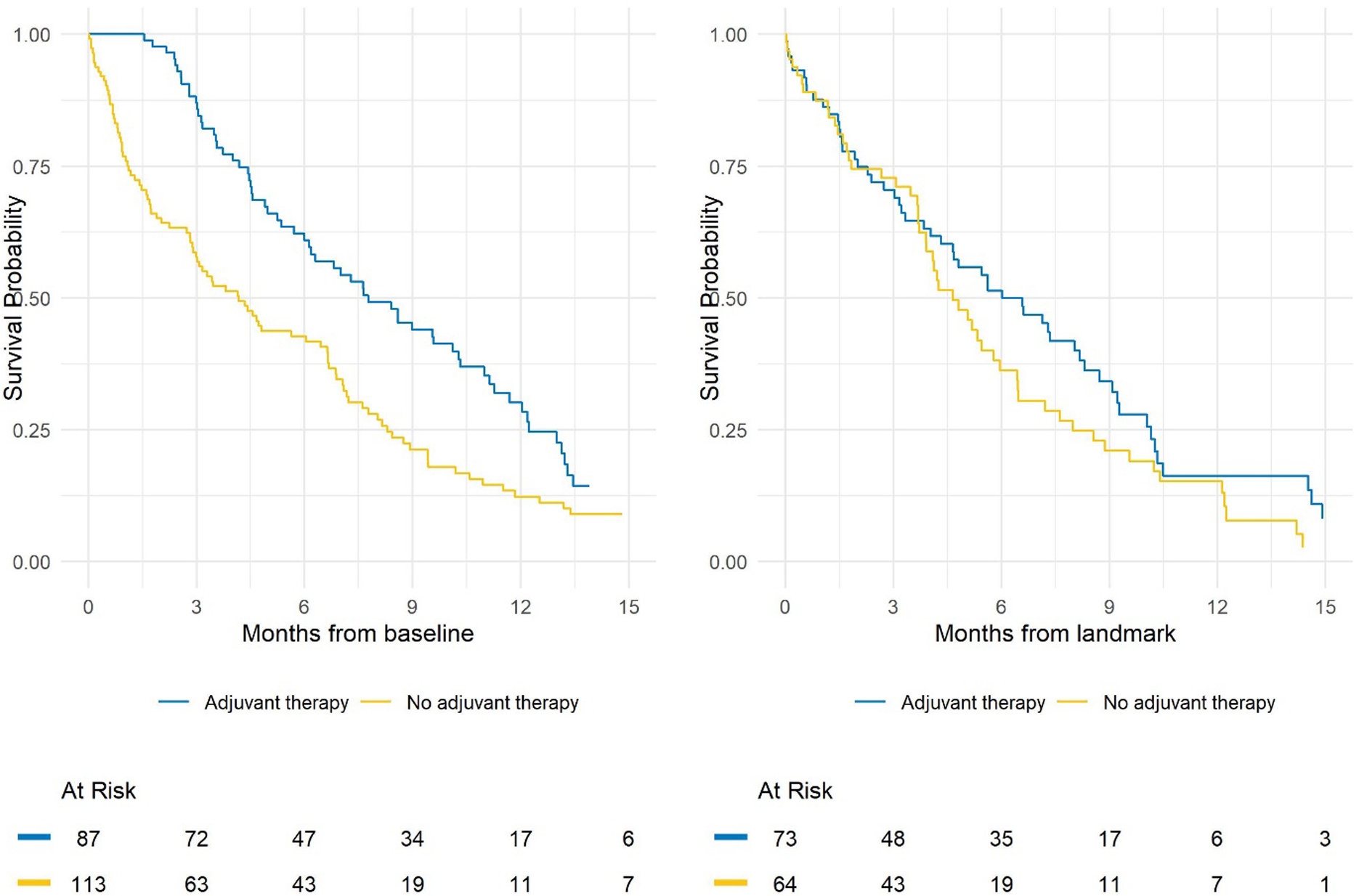
Comparison of Kaplan-Meier plots with follow-up starting at (A) baseline, resulting in a log-rank p-value <0.001, or (B) the landmark, resulting in a log-rank p-value of 0.12.

In addition to reporting the standard descriptives accompaying a survival analysis (see guidelines 4.11–4.13¹), when performing a landmark analysis it is essestial to report the number of subjects excluded in each group because they expeirenced the event of interest or were censored before the landmark, and the number of subjects whose covariate status changed after the landmark. For example, in our hypothetical example 4 patients were censored and 10 patients died prior to the 3-month landmark in the adjuvant therapy group, 3 patients were censored and 46 patients died prior to the 3-month landmark in the no adjuvant therapy group, and 10 patients received adjuvant therapy starting after the 3-month landmark and so were analyzed in the no adjuvant therapy group. Study-specific sensitivity analyses to assess potential biases that could be introduced due to exclusions prior to the landmark time should be conducted. These may include, but are not limited to, sensitivity analyses using different landmark times, comparison of patient characteristics between patients who were included and excluded, and comparison of events between groups prior to the landmark time.

Alternatively, the use of time-dependent covariates in Cox regression may be more appropriate than the landmark analysis approach when the value of a covariate changes during follow-up, when there is not an obvious landmark time, or when the use of a landmark time would lead to an unacceptable number of exclusions. For example, if interest is the association between estimated glomerular filtration rate (eGFR) following radical nephrectomy and overall survival, eGFR can be treated as a time-dependent covariate and the value of the covariate would change at each measurement time between surgery and the date of death or last follow-up. Analysis of a time-dependent covariate in a Cox regression model requires setup of a specialized dataset in a format known as counting process format, in which patients may have multiple rows of data corresponding to different time intervals. An example dataset is presented in Table 1, where we see that for subject 1, over the interval 0 to 67 days they had an eGFR of 75 and the interval did not end in death, over the interval 67 to 123 days they had an eGFR of 62 and the interval did not end in death, and over the interval 123 to 188 days they had an eGFR of 55 and the interval ended in death. If the changing value of a covariate over time is ignored, it is likely that the proportional hazards assumption, upon which Cox regression relies, is violated, which can lead to incorrect estimates and conclusions. An important drawback of the time-dependent covariate approach is that it cannot be used to generate prediction of survival over time, and intrepretation of the time-dependent coefficients can be difficult^7,8.

Table 1.

Example of the counting process format of data, to include a time-dependent covariate (here, eGFR) in a Cox regression model.

Subject ID	Time1	Time2	Death	eGFR
1	0	67	0	75
1	67	123	0	62
1	123	188	1	55
2	0	45	1	52
3	0	63	0	72
3	63	123	0	78
3	123	185	0	81
3	185	244	0	83
3	244	306	0	82
3	306	367	0	84

It is essential that each covariate for inclusion in the analysis is carefully considered to determine whether the value was fully known prior to the start of follow-up for the endpoint of interest. If that is not the case for any covariate of interest, then specialized statistical methods such as landmark analysis or time dependent covariates must be used to appropriately account for the post-baseline nature of the covariate. Analyses that do not appropriately handle time-dependent covariates violate the assumptions of the standard survival analyses and submissions which do not analyze time-dependent covariates appropriately will not pass statistical review at The Journal of Urology.

Take home points:

• The use of traditional survival analysis methods such as Cox regression or Kaplan-Meier analysis require that all covariates are known at the start of follow-up and remain constant throughout the follow-up period.

• Covariates whose status changes during follow-up are known as time-dependent covariates. When the time-dependency of covariates is ignored Kaplan-Meier estimates are subject to “guarantee-time bias” and the proportional hazards assumption of Cox regression may be violated.

• Cox regression can accommodate a time-varying covariate using a dataset in the appropriate specialized format. But this method cannot be used to generate survival estimates.

• Landmark analysis is useful when the covariate of interest is known within a relatively short period of time after the start of follow-up. A fixed landmark time is selected and the start of follow-up and covariates status is defined at the time of the landmark. This method can be used to generate survival estimates, but requires exclusion of patients who had the event or were censored prior to the landmark time.

• Analyses that do not appropriately handle time-dependent covariates violate the assumptions of the standard survival analyses and submissions that do not analyze time-dependent covariates appropriately will not pass statistical review at The Journal of Urology.