Structure-Function relationships in the skeletal muscle extracellular matrix

Abstract

The vast majority of skeletal muscle biomechanical studies have rightly focused on its active contractile properties. However, skeletal muscle passive biomechanical properties have significant clinical impact in aging and disease and are yet incompletely understood. This review focuses on the passive biomechanical properties of the skeletal muscle extracellular matrix (ECM) and suggests aspects of its structural basis. Structural features of the muscle ECM such as perimysial cables, collagen cross-links and endomysial structures have been described, but the way in which these structures combine to create passive biomechanical properties is not completely known. We highlight the presence and organization of perimysial cables. We also demonstrate that the analytical approaches that define passive biomechanical properties are not necessarily straight forward. For example, multiple equations, such as linear, exponential, and polynomial are commonly used to fit raw stress–strain data. Similarly, multiple definitions of zero strain exist that affect muscle biomechanical property calculations. Finally, the appropriate length range over which to measure the mechanical properties is not clear. Overall, this review summarizes our current state of knowledge in these areas and suggests experimental approaches to measuring the structural and functional properties of skeletal muscle.

1. Introduction

1.1. Background and historical perspective

The last century has seen an explosion in studies of skeletal muscle’s biomechanical properties. By far, the most studied aspects of muscle structure–function relationships have been the isometric and dynamic properties of activated skeletal muscle. These studies have revealed the exquisite “crystalline” nature of muscle structure (Huxley and Hanson, 1954) that gives rise to the highly predictable sarcomere length-tension relationship (Edman, 1966; Gordon et al., 1966a, b). Indeed, it was the sometimes-contentious studies of the 1950 s and 1960 s, in which sarcomere length was shown to and also shown not to (Buchthal and Knappies, 1940; Carlsen et al., 1961) explain muscle isometric properties, that finally settled in the late 1960 s on the classic length-tension curve, although some doubts of the details remain (Pollack, 1983; ter Keurs et al., 1978). Defining muscle dynamic properties proved more elusive, but the prescient studies by Nobel laureate AF Huxley posited the existence of a “cross-bridge” which was actually an ATPase enzyme that could cyclically produce force by serial attachment and detachment to other myofilaments (Huxley, 1957). For steady state dynamic contractions, the cross-bridge theory largely explains isotonic muscle force production doing especially well for muscle active shortening (Hill, 1953) but less well for active lengthening contractions (Katz, 1939; Morgan, 1990).

Throughout this age of “active muscle force investigation,” in the background, was the passive tension measured from muscle in resting conditions as it was stretched in the absence of activation. From a mechanical point-of-view, it was important to account for muscle passive tension in order to “correct” for changes in the force actively generated by the muscle because explaining total tension (active tension + passive tension) was confounded by conflation of active and passive processes (Zajac, 1989).

While investigating the isometric properties of single muscle fibers, Sybil Street and her colleagues made the provocative assertion (given the then lack of microscopic tools available to investigate structure) that different structures were responsible for the active compared to the passive mechanical properties of muscle (Ramsey and Street, 1940). While their explanation for passive mechanical properties ultimately proved not to be accurate (specifically, that the sarcolemma was a major muscle fiber load bearing structure), she used her insights into experimental measurement of small muscle fiber bundle mechanical experiments to make the radical, and now, clearly accurate, assertion, that skeletal muscle force is not only transmitted along a muscle fiber, but also laterally to adjacent fibers via interstitial tissue termed the extracellular connective tissue matrix (ECM, Street, 1983).

The definitive experiment Street et al. performed was to dissect a single frog muscle fiber from one end of the muscle and leave the fibers on the other end intact (Fig. 1). They first secured the bare end of the single muscle fiber and, using a carefully placed electrode that activated only the single fiber, measured the force generated by the single fiber. They then released the bare end of the single fiber and secured the remaining muscle fibers adjacent to the single fiber at the opposite end. Even when the single fiber was completely free at the isolated end, upon activation, they measured an isometric force nearly equivalent to that measured when the bare end of the single fiber was secured. Their interpretation of this experiment was that the physical interaction among adjacent fibers was sufficient so that the activated single fiber transmitted its force radially to adjacent fibers that were secured, and that force was then transmitted to the force-measuring end via these adjacent fibers. While the results of this experiment were generally accepted at the time, the biomechanics community was too preoccupied with the obvious importance of studying active muscle properties to put the same creativity and energy into ECM studies.

Fig. 1.

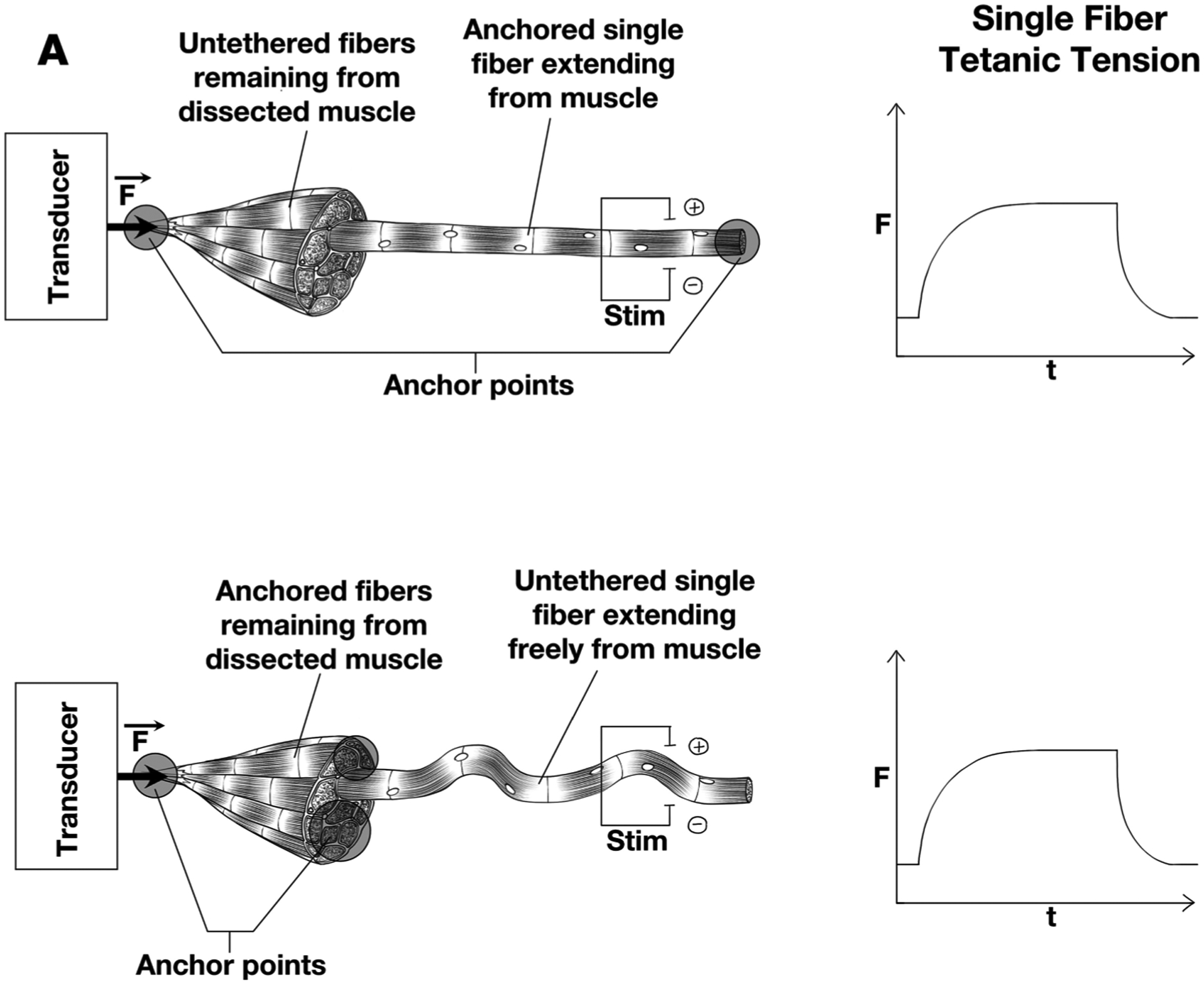
Schematic arrangement of experimental measurements on frog muscle to determine magnitude of force transmitted laterally between fibers. Experimental condition is shown on left and tetanic tension on the right, resulting from single fiber stimulation. Force is measured on the left end (solid circle) (A) The isolated fiber is secured at the bare end and at end still containing surrounding fibers. (B) The isolated fiber is secured only at end containing surrounding fibers. The surrounding fibers themselves are secured to the measuring device. Only the single fiber is activated in both cases and isometric force generation is essentially identical. (Modifed from Figs. 2–21 of reference Lieber, 2010).

As modern muscle physiology evolved and passive tension gained more interest, the seminal paper regarding the relationship between passive frog muscle mechanics and size scale was presented by Magid and Law (Magid and Law, 1985) who concluded that the source of passive tension in frog was intracellular, likely the giant protein titin (Labeit and Kolmerer, 1995; Maruyama, 1994). Numerous mechanistic studies of titin followed leading to a host of interesting biophysical discoveries about this giant molecular filament. However, because frog ECM is less dense compared to mammalian muscle (Meyer and Lieber, 2018), titin’s role in passive muscle mechanics turned out to be an anomaly compared to mammalian muscle. In fact, recent studies estimated that frog muscle ECM bears less than 5 % of passive tension while mammalian muscle ECM may bear of 50 % of passive tension—a ten -fold difference (Meyer and Lieber, 2018; Meyer and Lieber, 2011). Unfortunately, even though the ECM has been shown to bear very high passive tensions, the ECM structures and their organization that leads to such passive tensions has remained elusive.

This review first provides a historical perspective on the evolution of passive biomechanics research alongside major discoveries in active mechanics. It then describes our current understanding of skeletal muscle extracellular matrix (ECM) structure at different hierarchical levels from collagen cross-links to perimysial cables. In a point-counterpoint fashion, we delve into some hypotheses for the lack of clear structure–function relationships in passive muscle mechanics, beginning with limitations in the methodology to quantify structural changes in the ECM and ending with limitations in the methodology used to quantify changes in passive material properties. Finally, some perspectives are shared on how future studies can take advantage of emerging methodology to attain a more comprehensive picture of structure–function relationships in skeletal muscle ECM.

2. Structure of the extracellular matrix

Some attention has been directed toward ECM structure with the hope that high-resolution mapping will lead to an understanding of passive mechanical properties in the same way that sarcomere structural studies led to a mechanistic understanding of active muscle force generation. However, it appears that no such simple structure–function relationship exists. Regardless, there are a number of important studies that have begun to shed light on the structural properties of the ECM.

Scanning electron micrographs of muscle ECM reveal a beautiful matrix of interconnected tubes that surround muscle fibers (Fig. 2). Important seminal studies by Trotter and Purslow demonstrated that a model of passive force transmission in which muscle fibers were simply arranged in parallel with ECM was overly simplistic. This conclusion was based on the observation that many fibers actually tapered within the muscle belly (Trotter et al., 1981; Trotter and Purslow, 1992) and never reached the external tendon. For example, the animal model of muscular dystrophy (mdx), in which the subsarcolemmal dystrophin protein is missing and muscle fibrosis results, resulting in collagen accumulation, shows a relatively poor correlation (r² ranging from 0.1 to 0.3) between collagen content and passive stiffness (Brashear et al., 2021; Smith and Barton, 2014). Similarly, in human cerebral palsy, where fibrosis occurs, there is also a poor correlation between collagen content and passive stiffness (Data from references Chapman et al., 2014; Lieber and Friden, 2018; Smith et al., 2011b).

Fig. 2.

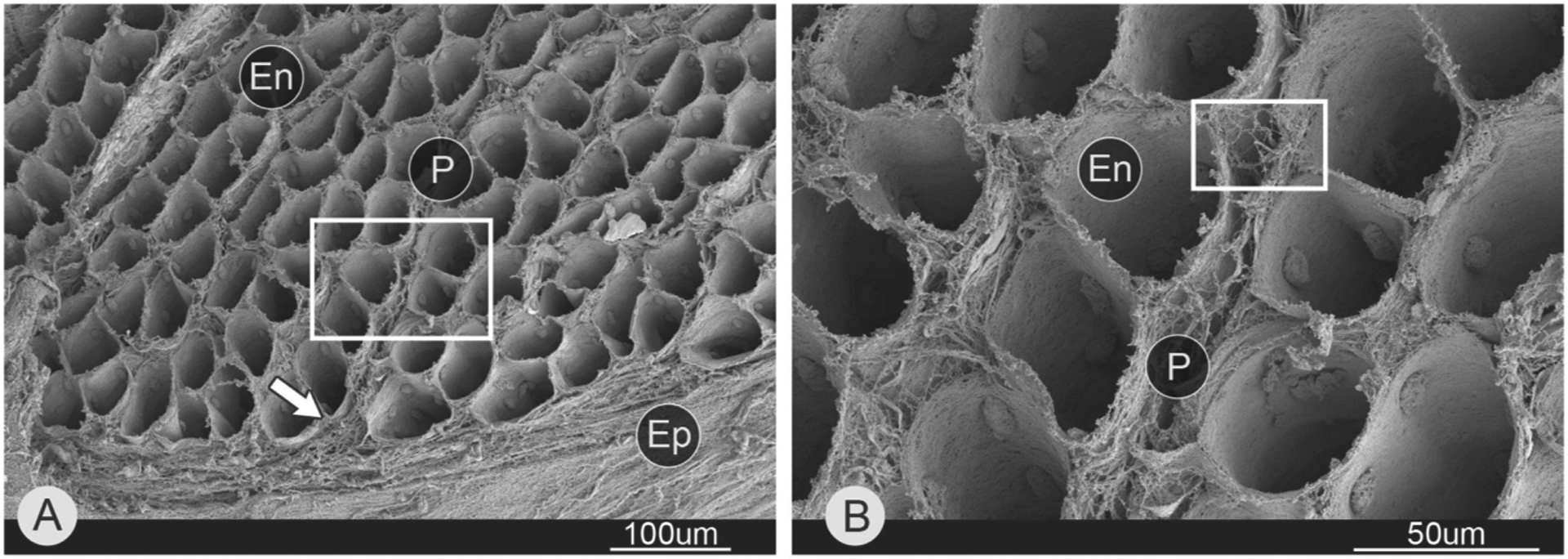
Scanning electron micrograph of endomysial connective tissue within skeletal muscle. This image was generated by scanning electron microscopy of a muscle whose fibers were removed by acid digestion. (A) Mouse lateral gastrocnemius. While boxed area shown in B. Arrow points to epimysium. (B) Magnified area from A. Abbreviations: endomysium (En), perimysium (P), and epimysium (Ep). (Micrograph reproduced from reference Sleboda et al., 2020).

3. Structure-function relationships in the extracellular matrix

The ECM is obviously more than just collagen. Indeed, as in other connective tissues, muscle ECM is composed primarily of type 1 and type 3 collagen (Smith and Barton, 2014; Smith et al., 2019) but also contains proteoglycans, that have been shown to affect mechanical properties in other connective tissues (Kjaer, 2004). Additionally, collagen is post-translationally enzymatically cross-linked which alters its mechanical properties. There has been a paucity of biochemical-biomechanical correlative studies that are designed to understand the differential biomechanical roles of collagen, collagen cross-links and proteoglycans.

As mentioned above, there is generally a poor correlation measured between collagen content, the major ECM component, and muscle stiffness. This may be due, in part, to the tremendous variation in collagen content along the length of the muscle (Binder-Markey et al., 2020). This complexity is compounded by the fact that collagen content inside muscle fiber bundles (referred to as endomysial connective tissue, Gillies and Lieber, 2011) is much lower compared to the true muscle tendon. In mouse muscle, average muscle fascicle contains ~ 5 μg/mg wet weight collagen, while tendon collagen content is ~ 300 μg/mg (Ker, 1981). This means that almost any “contamination” of muscle fascicle samples by aponeurosis, fascia, internal tendon or perimysial connective tissue will disproportionately affect a biochemical assay and confound elucidation of a structure–function relationship. A recent explicit study of the relationship between collagen content and intramuscular anatomy (Binder-Markey et al., 2020) revealed a well-defined relationship between anatomical structures, histological area fraction and muscle biochemical composition (Fig. 3). While it was possible to account for collagen content based on intramuscular anatomy, an adequate explanation of muscle biomechanical function, based on the location of all of the intramuscular connective tissue in these three muscles was not possible.

Fig. 3.

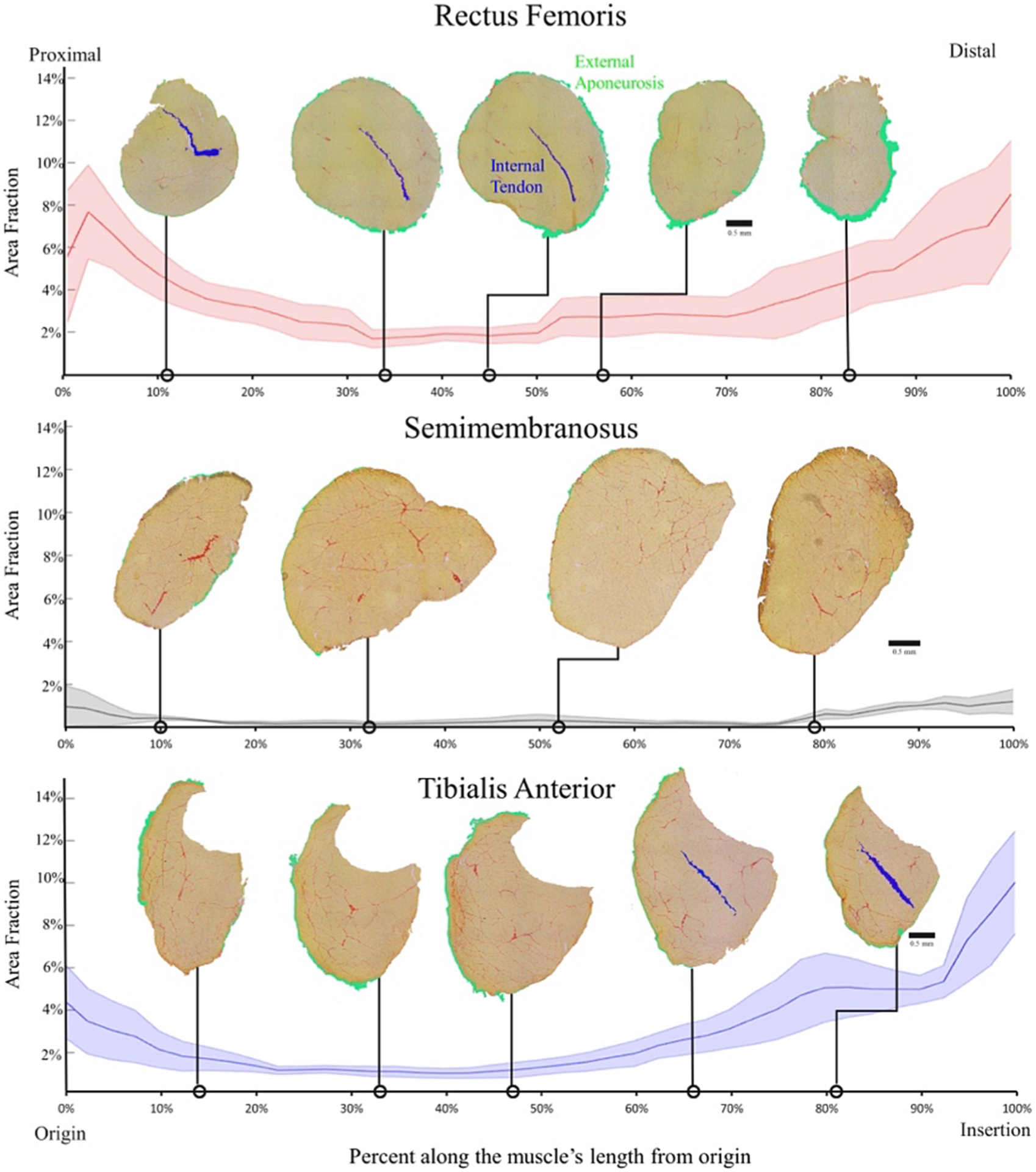
Average area fraction ± SEM (shaded region) along the normalized length of the mouse rectus femoris (top), semimembranosus (middle), and tibialis anterior (bottom) (n = 4/muscle). The area fraction of the rectus femoris and tibialis anterior demonstrate the pattern of higher area fraction at the proximal and distal ends with low area fraction in the middle. The semimembranosus demonstrates the same pattern but to a much smaller extent since there are minimal connective tissue structures within that muscle. External aponeurosis and internal tendon are color coded green and blue respectively. (Figure reproduced from reference Binder-Markey et al., 2020).

Collagen cross-links also do not appear to provide much of an explanation of muscle stiffness besides making a distinction between “normal” and “diseased” muscle (Brashear et al., 2022). In a recent study, we used our nesprin-desmin double knockout mouse (NDKO) model of skeletal muscle fibrosis to investigate the relationship between collagen content and muscle passive mechanical properties (Chapman et al., 2015; Chapman et al., 2014). NDKO mice had a sixfold increased tissue stiffness and a twofold increased collagen content but, as above, when we regressed tissue stiffness against collagen content, there was no significant correlation (Chapman et al., 2014).

If biochemical composition does not quantitatively explain passive stiffness, what does? There is not a clear answer, but there are suggestions that unique ECM structures may have functional significance (Gillies and Lieber, 2011). None of the methods previously described account in any way for the specific arrangement of collagen bundles which are rich in the perimysial space and can easily be appreciated in cross-sections of muscle viewed by transmission electron microscopy. These so-called “perimysial cables” run parallel to muscle fibers but this three-dimensional arrangement is not easily appreciated from a single section and the structures are completely invisible at the light microscopic level (the most commonly used method for muscle tissue-level structural analysis). Recently, a serial block face scanning electron microscopy method was developed to reconstruct skeletal muscle ECM with submicron resolution over hundreds of microns (Fig. 4). This technology holds great potential for determining collagen/ECM ultrastructure and could answer questions about whether tissue stiffness is related to ECM organization. In addition, micromechanical studies of small bundles of fibers show that these cables are appropriately located to bear passive loads and deform and rotate with sarcomere stretch (Fig. 5).

Fig. 4.

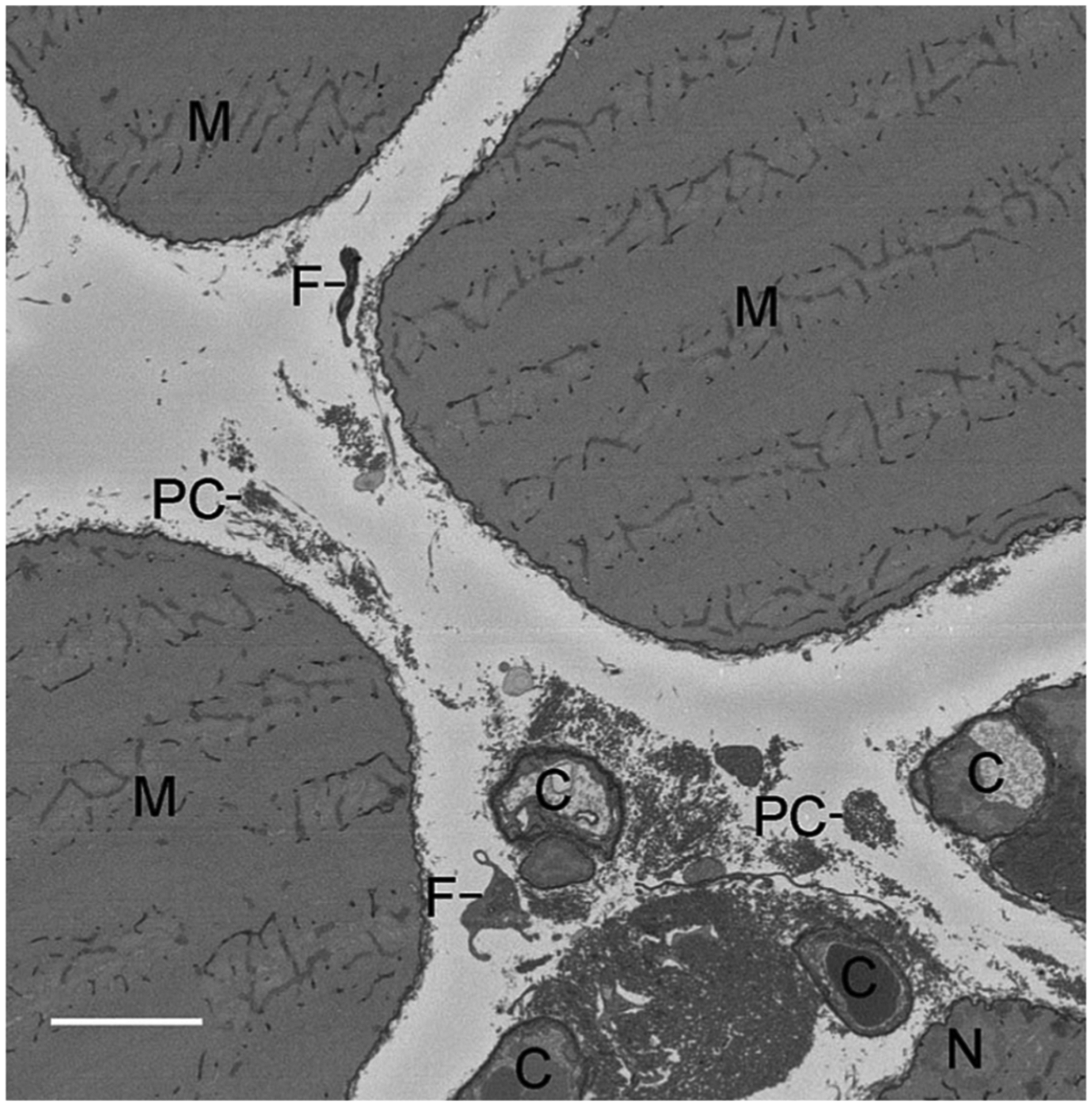
Representative single x-y slice obtained from serial block face scanning electron microscopy (SBEM) of mouse extensor digitorum longus muscle (z = 28 μm; z range 0–140 μm). Scale bar = 5 μm. M, myofiber; C, capillary; N, myonucleus; F, fibroblast; PC, perimysial collagen cable. (Figure reproduced from reference Gillies et al., 2014).

Fig. 5.

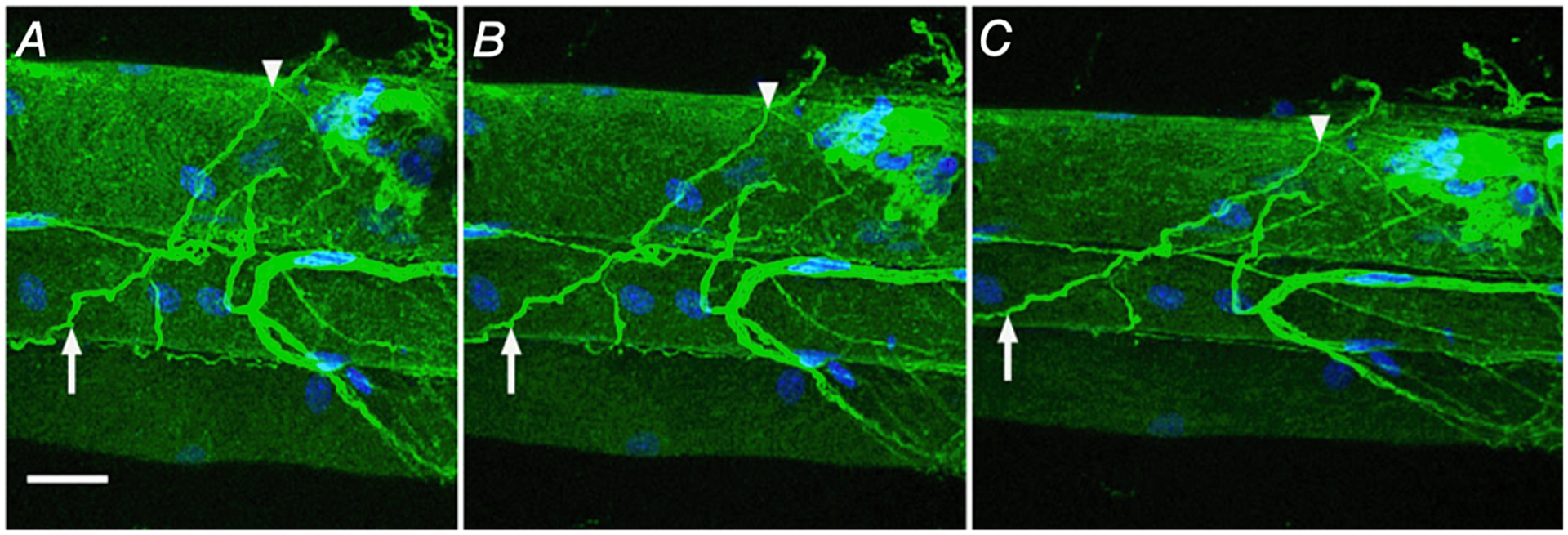
Collagen cables are composed of type I collagen and realign with increased strain. Mouse fiber bundle preparations were immunolabelled for type I collagen (green) and nuclei (blue). At slack length (0 % strain; A) intensely stained type I collagen positive structures that traverse multiple fibers are defined as collagen cables. Two points on a cable are identified in each preparation (arrow and arrowhead) and these points are again identified at 20 % strain (B) and 40 % strain (C) showing reorganization of cables with strain. Scale bar = 25 μm. (Figure reproduced from reference Gillies et al., 2017).

The global organization of collagen fibers within ECM can be determined using second harmonic generation microscopy and this has recently been applied to studies of passive muscle biomechanics (Brashear et al., 2021). These authors showed that collagen alignment in the ECM was correlated with passive mechanical properties in the mdx mouse model of fibrosis. Overall, selection of a specific methodology, each of which has advantages and disadvantages, must be made judiciously in light of the questions posed and the system studied.

4. Complexity in quantifying passive stiffness

It is tempting to conclude that the poor association between ECM structure and passive stiffness derives from the failure of molecular biology and imaging to capture the complexity of the ECM. Muscle ECM is composed of no less than 10 subtypes of collagen that link with elastin, laminin, fibronectin, proteoglycans and other glycoproteins to form complex structures that are unique at each hierarchical scale (Gillies and Lieber, 2011). It is hard to imagine describing such complexity with a single number (or even a set of numbers). On the other hand, tensile stiffness has been described with a single number for centuries and therefore seems established and straightforward by comparison. However, before pointing the finger at structural complexity, it is valuable to take another look at the standard practice of mechanical characterization which, in its relative simplicity, might be missing important features.

A recent systematic review of skeletal muscle passive mechanics reported that the majority of ex-vivo studies employ similar testing and analysis paradigms (Binder-Markey et al., 2021). On the testing side, these are almost exclusively uniaxial tension tests. On the analytic side, stress–strain data are typically fit with a simple linear, quadratic, or exponential elastic model. Considering ECM structural complexity, this approach likely suffers from the same oversimplicity as the biological measurements discussed above. If we agree that muscle ECM is a non-linear, anisotropic, non-uniform, viscoelastic structure, then we must also agree that, like “total collagen content,” tensile stiffness poorly characterizes all permutations of adaptation in age or disease. For example, tensile stiffness could miss changes in non-linearity due to altered collagen crimping, changes in anisotropy due to altered collagen cross-linking or changes in viscosity due to changes in proteoglycans – all of which are expected to impact in-vivo muscle behavior and human movement. However, comprehensive characterization of the directional-, time- and strain-dependent properties of muscle is experimentally and computationally burdensome at best and intractable at worst. Therefore, we seek a middle ground strategy—one that retains the most important features of passive mechanics but avoids experimental and/or mathematical complexity that makes findings difficult to interpret or compare across studies. The challenge is that such an approach makes assumptions about the system that, if incorrect, could bias the results (either finding a relationship that isn’t real or missing a relationship that is). Binder-Markey et al. provide an excellent discussion about how some of these assumptions may affect comparisons among scales (e.g., bundles vs whole muscles) and across studies (Binder-Markey et al., 2021). The next sections will discuss how these assumptions affect comparisons at the same scale in a single study if ECM changes are expected.

5. Sources of experimental bias in passive testing

Most muscle experimental and modelling approaches are built on the phenomenological model of A.V. Hill (Hill, 1938) which is comprised of a contractile element in parallel and series with linear elastic elements. In the passive state, the contractile element is inactive, and the model reduces to a linear elastic spring. However, as skeletal muscle is viscoelastic, this model only represents the passive behavior under full viscous relaxation. The phenomenological Hill model can be modified to include a viscous component, typically augmenting the contractile or series elastic element with a viscous damper (Anderson et al., 2002; Moss and Halpern, 1977; Wolff et al., 2006), but this poorly describes muscle viscosity (Meyer et al., 2011). Alternatively, a coefficient of damping can be calculated from the complex modulus obtained during dynamic testing (Moss and Halpern, 1977; Toscano et al., 2010). However, this is also expected to have poor predictive capacity as it does not capture either the strain or strain-rate dependence of muscle viscosity. A number of detailed models have been developed to better describe passive viscoelasticity with quasi-linear viscoelastic, visco-hyperelastic, thixotropic or pseudoplastic formulations (Alipour-Haghighi and Titze, 1985; Best et al., 1994; Lu et al., 2010; Meyer et al., 2011; Odegard et al., 2008; Quaia et al., 2009; Rehorn et al., 2014). However, these are mathematically complex and rarely implemented in practice. Of the 33 studies reviewed by Binder-Markey et al. that compare passive properties among groups, only 4 assessed viscous properties (Kammoun et al., 2016; Lim et al., 2019; Smith and Barton, 2014; Toscano et al., 2010). The vast majority of muscle passive mechanical studies use experimental conditions that approximate viscous relaxation and assume purely elastic behavior to avoid this complexity altogether. This approach takes two general forms, either a low-velocity ramp stretch or an incremental stress relaxation test (see Fig. 6).

Fig. 6.

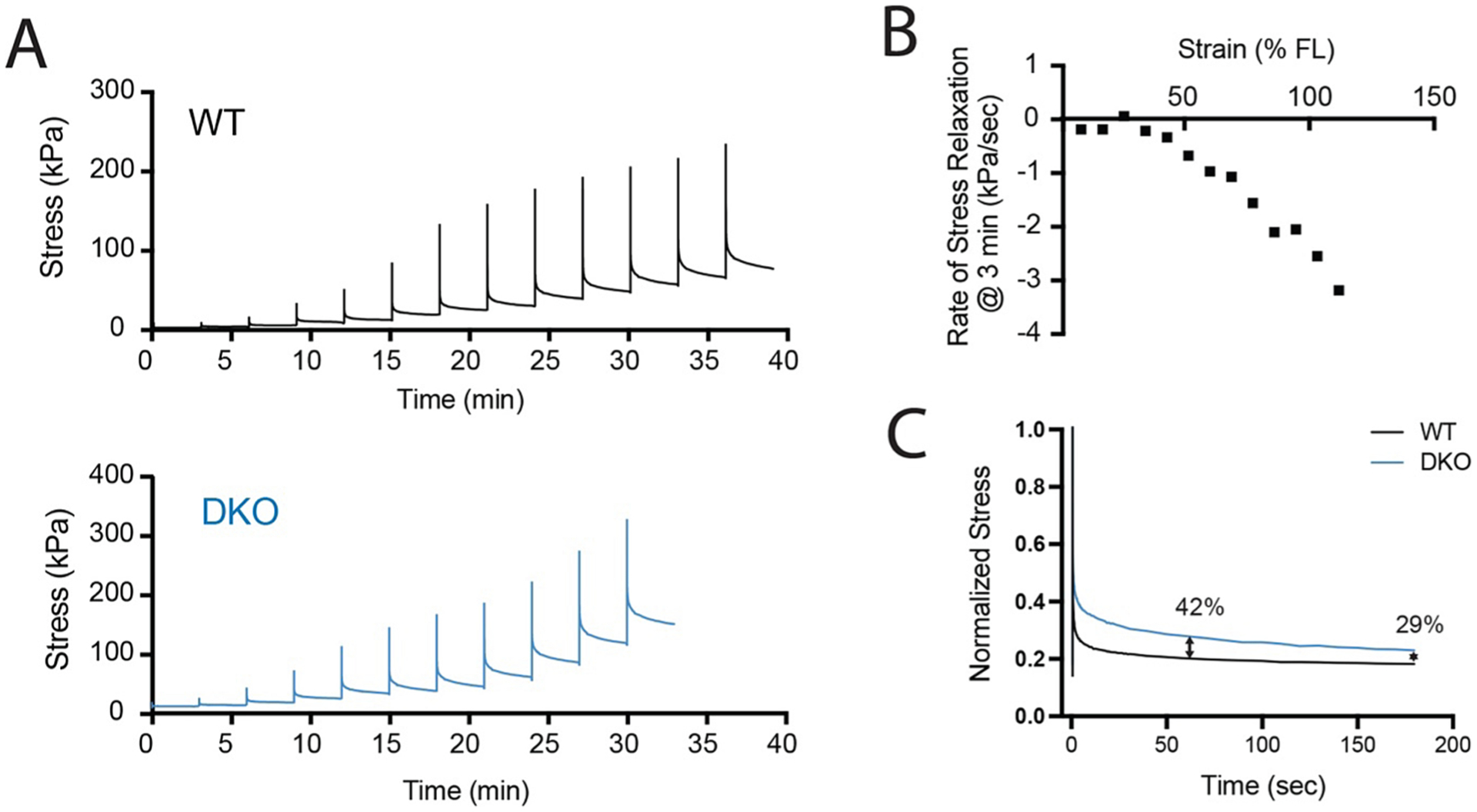
Representative incremental stress relaxation data from wildtype (WT) and desmin knockout (DKO) mouse muscles. (A) Force records normalized to physiological cross-sectional area for ex-vivo mouse 5^th toe EDL muscles stretched at 10% zero-strain fiber length (FL) every 3 min until failure. (B) Rate of stress relaxation for the final 20 s of each increment of WT data. (C) Overlay of normalized stress relaxation curves from WT and DKO at 70% strain with percent differences noted at 60 and 180 s.

To illustrate how the assumption of complete viscous relaxation can bias conclusions, consider the following actual experimental data acquired from wildtype (WT) and desmin knockout (DKO) 5th toe EDL muscles. These muscles were freshly excised, mounted in a bath of Mammalian Ringer’s solution and subjected to an incremental stress relaxation test (Fig. 6A). In the incremental stress relaxation test, muscle length was set to a zero-strain state where passive force first registers on the transducer, then stretched rapidly by 10 % of this fiber length and held for 3 min while viscous stress-relaxation occurs. This cycle is repeated until specimen failure. Note in Fig. 6B that viscous relaxation is not complete, even after 3 min in the later stretches. While the rate of stress decay is near zero at 3 min for the first 5 stretches, it increases to over 3 kPa/sec by the last stretch. This is because muscle viscosity is strain dependent (Meyer et al., 2011), which has been validated in studies where the hold phase exceeded 3 min (de Bruin et al., 2014; Pavan et al., 2020). This has two important implications for passive testing, 1) a low-velocity ramp stretch will always include significant viscosity because viscous relaxation is ongoing even after multiple minutes of rest and 2) even incremental stress relaxation tests include some viscous force at the final “relaxed stress” whose relative contribution depends on the duration of the hold phase. Alterations in ECM composition or structure most likely affect elastic and viscous properties, and these are difficult to fully separate in simple tests. This is evident in the example data. DKO muscle has significantly higher viscosity compared to WT muscle, leading to slower viscous relaxation and a higher relative contribution of viscous forces to “relaxed stress” compared to WT. At 70 % strain, with one minute of viscous relaxation, there is a 42 % difference in “relaxed stress” between WT and DKO. At 3 min, this difference is only 29 % (Fig. 6C). This biases conclusions about the relationship between passive properties and ECM composition because different components of the ECM probably contribute differentially to elasticity and viscosity. As an extreme hypothetical example, mistakenly attributing viscous forces to elasticity could make it appear that there was increased elastic stiffness even if there was no change in collagen content/organization, when instead there was actually increased viscosity due to increased glycosaminoglycans.

It is not strictly necessary to perform more complex dynamic testing or higher order modeling in the form of quasi-linear viscoelastic models to mitigate this bias. The beauty of an incremental stress relaxation test is that it includes data that allow estimation of both viscous and elastic components. The viscous relaxation phase is typically not analyzed, but even basic approaches such as comparing regions of local linearity (e.g., Fig. 6B) or overlaying normalized relaxation phases to observe differences (e.g., Fig. 6C) are likely to be informative. Not only does this type of testing test the assumption of full viscous relaxation, but it also provides a more complete data set from which to link structural and material properties. If we assume full viscous relaxation in the example data, then the stress at the end of each 3 min rest period can be plotted against strain to estimate passive elastic behavior (Fig. 7A). Passive stress is higher in the DKO muscle than WT and the discrepancy increases with strain indicating higher stiffness in DKO. However, if stiffness or size is significantly different between samples, it could cause a bias in the definition of zero-strain. Specifically, zero-strain is theoretically considered a zero-stress state, but practically speaking it is a “same-force” state because it is actually defined as the length at which passive force registers above transducer noise. Stiffer or larger muscle will have higher force at shorter lengths and thus begin zero-strain earlier (i.e., at a shorter sarcomere length). In this dataset, the DKO muscle is ~ 40 % smaller in physiological cross-sectional area compared to WT. Because sarcomere length was recorded by laser diffraction during this testing, zero-strain can be re-defined by an absolute, rather than a subjective, reference – in this case 2 μm. When relaxed stress is plotted against sarcomere strain, the differences between DKO and WT are less dramatic because some of the previous difference was due to the biased start point (Fig. 7B). This has particular significance for attempts to correlate material properties with ECM changes in intact muscles because many of these comparisons are made in transgenic or disease models with altered muscle size, like the mdx, DKO or sarcopenic mouse (Brashear et al., 2021; Sam et al., 2000; Xie et al., 2021). It is theoretically possible to observe no changes in passive tension between muscles because the zero-strain bias has offset the increased stiffness. This issue has gained increasing awareness and the majority of studies comparing specimens with expected differences in ECM composition (19 out of 25 reported by Binder-Markey et al.) either model stress vs sarcomere length (Meyer et al., 2011; Smith et al., 2011b), stress vs fiber strain (relative to fiber length at peak active tension) (Gosselin et al., 1994; Smith and Barton, 2014) or stress vs fiber strain (confirming no difference in sarcomere length at zero strain) (de Bruin et al., 2014; Ward et al., 2020).

Fig. 7.

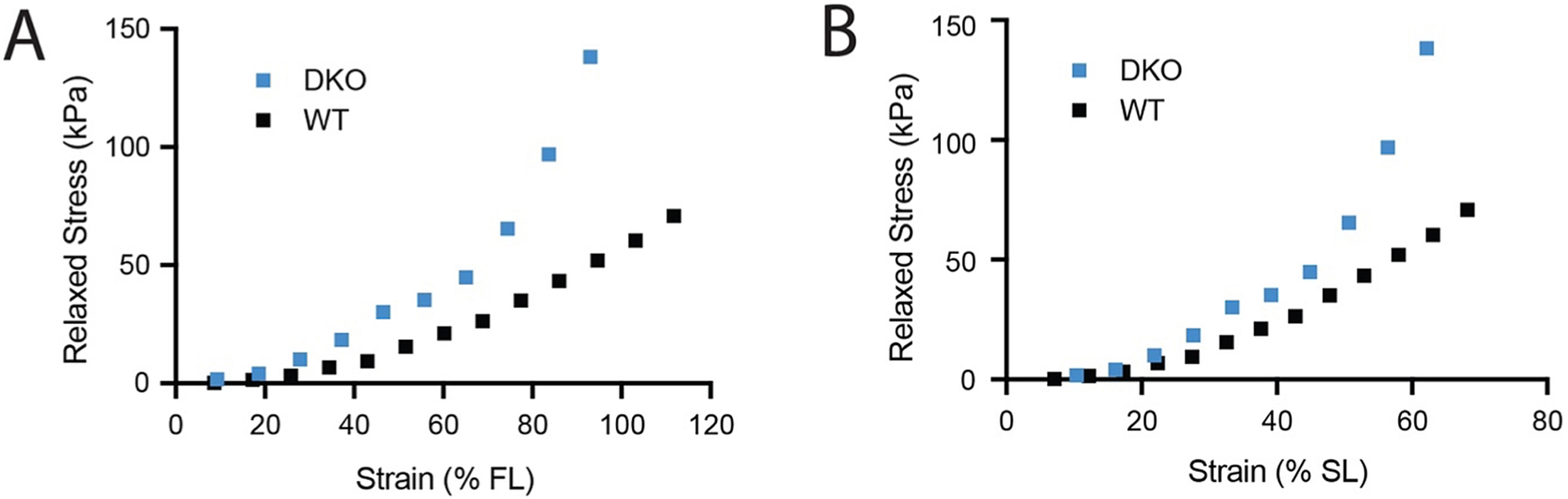
The same relaxed stress–strain data from representative WT and DKO mouse muscles incremental stress-relaxation tests plotted using two definitions of zero strain. (A) Stress at 3 min following stretch (relaxed) plotted against strain calculated as a percentage of the fiber length at the zero-strain state. (B) Same relaxed stress plotted against strain calculated as a percentage of sarcomere length relative to an absolute standard of 2 μm. Sarcomere length measured by laser diffraction (Lieber et al., 1984).

Additionally, differences in material properties can bias the testing endpoint. If an adaptation or pathology decreases strain to failure, then datasets for that group will consistently have fewer datapoints at high strains. Analysis of data against a different strain scale than what was used during acquisition (e.g., sarcomere strain vs fiber strain) can also cause some datasets to have fewer datapoints at low strains. Both of these are the case for the example data where the DKO dataset has one fewer point at the beginning and at the end of testing. This issue is also apparent in some studies that plot raw data curves (Brown et al., 2012; Danos and Azizi, 2015; Shah et al., 2012). Only about half of the studies reported by Binder-Markey et al. report limiting either the data range of testing or quantification (14 out of 33). The degree to which this affects quantification will depend on the data (e.g., number of datapoints, variability, degree of nonlinearity, etc.) and the model of fit used.

This point is easily illustrated by taking the previous DKO dataset and analyzing how fit parameters change with the subtraction of data (Fig. 8). The DKO dataset is non-linear but could be fit with linear model yielding an r² of 0.83. This approach is sometimes used to simplify analysis and interpretation (Anderson et al., 2002; Shah et al., 2012). Using one fewer datapoint at low strain (Fig. 8A green) changes the slope of the best fit line by 11 %, while using one fewer datapoint at high strain (Fig. 8B green) changes the slope by 20 %. The differences in slope increases as additional data are subtracted. A quadratic model does a better job fitting the nonlinear data with an r² of 0.98, but the parameters are even more sensitive to the range of data included (Fig. 8C, 8D). In contrast, the exponential model fits the data well (r² > 0.99) and is relatively insensitive to the range of data because it requires passive stress to be zero at zero strain (Fig. 8E, 8F). This variation in analytical approaches demonstrates that muscles from two experimental conditions, with the exact same passive stress–strain behavior could be concluded to have different stiffness if there was a systematic bias in the range of data in one group or the other. This could lead to the conclusion that changes in stiffness are not associated with changes in collagen, when, in fact, they may be.

Fig. 8.

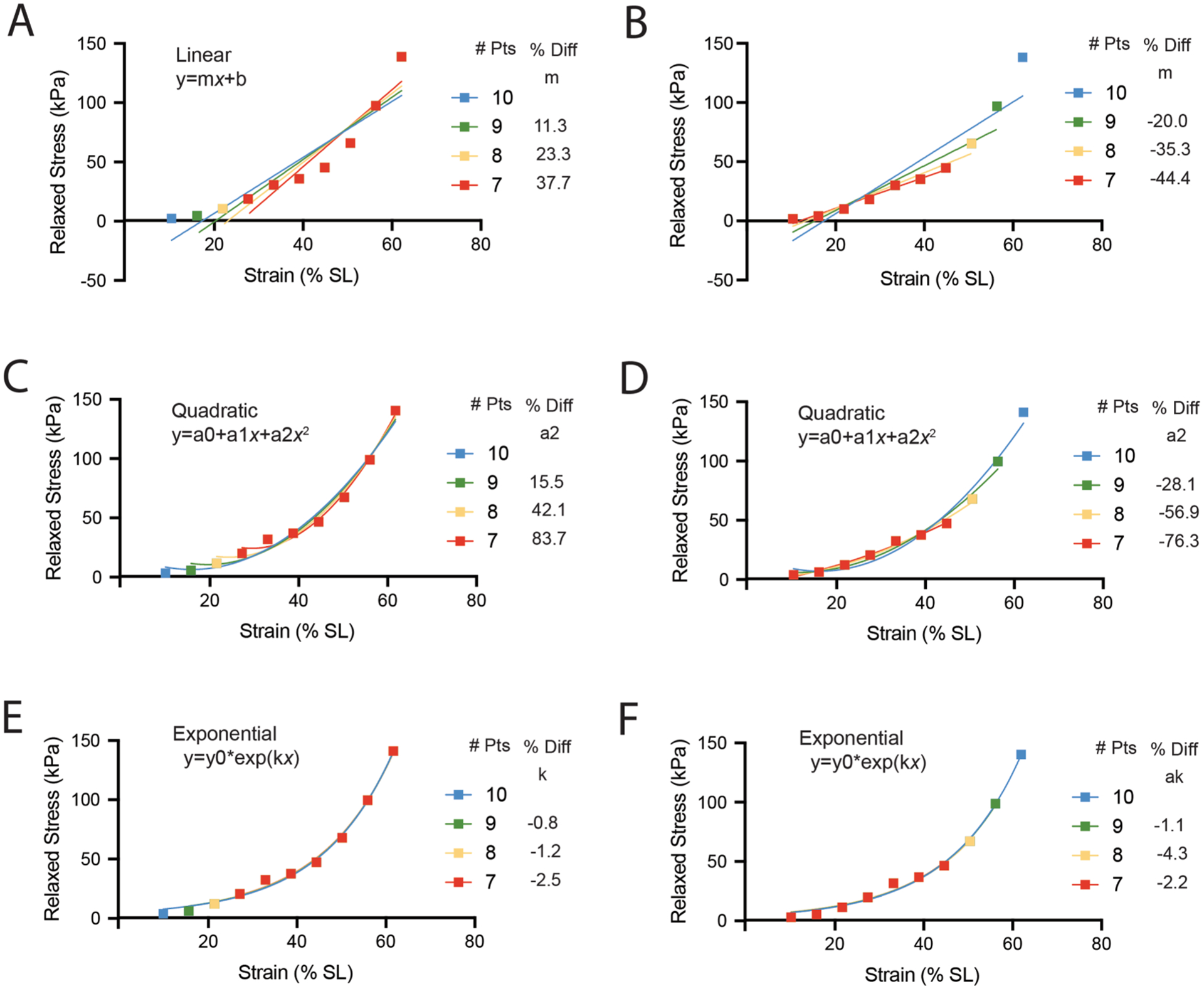
Illustration of the sensitivity of parameter estimation to data range for linear, quadratic, and exponential fits of mouse skeletal muscle. (A, C, E) DKO representative data (10) excluding one (9), two (8) or three (7) datapoints at low strain fit with linear, quadratic, and exponential relationships, respectively. The change in the most referenced parameter from each fit is listed alongside the legend (linear: linear modulus (m), quadratic: quadratic modulus (a2), exponential: linear natural log modulus (k)). (B, D, F) DKO representative data (10) excluding one (9), two (8) or three (7) datapoints at high strain fit with linear, quadratic, and exponential relationships, respectively.

Of course, this bias is easy to mitigate by limiting the analysis to a range where all samples have data. But even this example can be used to illustrates additional issues that arise when comparing between studies across different data ranges. Frequently, studies will limit data analysis to a physiologically meaningful range such as a region of the length-tension curve or sarcomere lengths reached during the range of motion of the joint (Brynnel et al., 2018; Pavan et al., 2020; Smith et al., 2011b; Ward et al., 2020). This approach typically limits the data range quite a bit because the muscle can easily be stretched supra-physiologically ex-vivo. Limiting range is appealing because it characterizes the behavior only under conditions experienced in-vivo and frequently data will exhibit better linearity over this range allowing a linear stiffness value to be extracted. Additionally, restricting range enables better physiological comparison among samples with different sarcomere length operating ranges (Brynnel et al., 2018; Smith et al., 2011b). However, this approach may also limit efforts to understand the relationship between ECM structure and passive properties because some structural changes may not be discernable in the stress response until supraphysiological strain. Some examples may be collagen crimping or sliding of perimysial cables such that structures don’t bear tension at low strain. Additionally, defining the actual physiological range is not trivial, especially in disease models.

In experimental measurement and quantification of passive tension, there is no reason that data need be discarded when more can be learned by analyzing data in multiple ways. A non-linear viscoelastic model can be applied to the entire dataset and a linear model can be fit to a physiological range. It is important to note that there is no single proper approach to analyzing these experimental data—the strategy should be dictated by the data and the question being addressed. For example, when examining the consistent range of data for all 3 wt and 4 DKO muscles tested (the range where all samples had data), the stress–strain relationship is clearly non-linear and fitting these data with a quadratic or exponential model is appropriate (Fig. 9A). However, the physiological range of data (sarcomere length over the full range of motion) is locally linear (Fig. 9B). Analysis of the major parameters of linear, quadratic, and exponential fits finds a significant difference between WT and DKO for all three fits in the consistent range, but only for the linear fit in the physiological range (Table 1).

Fig. 9.

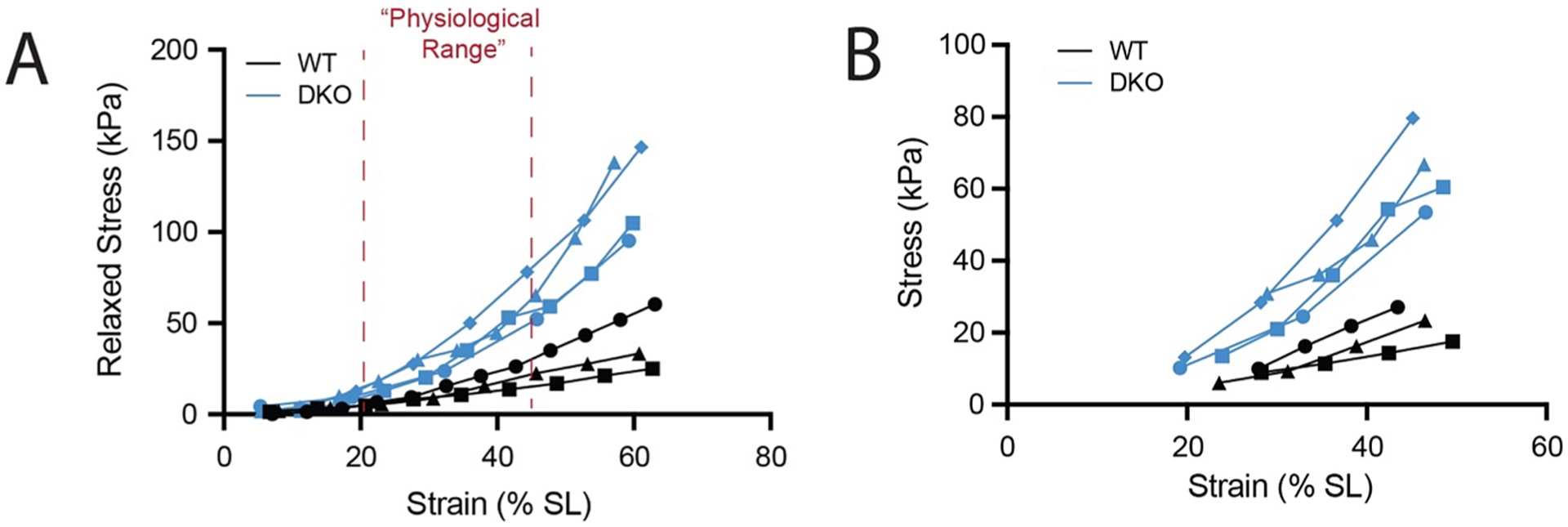
Relaxed Stress vs Strain for all WT and DKO mouse muscles tested. (A) Data are plotted over a “consistent range” which includes only strains where data exist for all samples. Red dotted lines mark a “physiological range” of sarcomere strains that the EDL would be expected to reach in-vivo during the full range of ankle and toe motions. (B) Data are plotted only over the “physiological range.”.

Table 1.

Parameter estimations for linear, quadratic, and exponential fits to all WT and DKO data over consistent and physiological ranges graphed in Fig. 9.

	Consistent Range Analyzed
	Linear (y = mx + b)			Quadratic (y = a0 + a1x + a2x2)				Exponential (y = y0exp(kx)
	m	b	r2	a0	a1	a2	r2	y0	k	r2
WT (n = 3)	0.72 ± 0.34	−8.46 ± 6.43	0.96 ± 0.24	−0.26 ± 0.24	0.09 ± 0.12	0.009 ± 0.007	1.00 ± 0.01	2.96 ± 0.19	0.04 ± 0.004	0.97 ± 0.01
DKO (n = 4)	2.21 ± 0.54	−28.51 ± 13.46	0.92 ± 0.04	4.43 ± 6.81	−0.41 ± 0.62	0.039 ± 0.014	0.99 ± 0.01	5.58 ± 1.91	0.053 ± 0.006	0.99 ± 0.01
	Physiological Range Analyzed
	Linear (y = mx + b)			Quadratic (y = a0 + a1x + a2x2)				Exponential (y = y0exp(kx)
	m	b	r2	a0	a1	a2	r2	y0	k	r2
WT (n = 3)	0.76 ± 0.35	−12.41 ± 8.86	0.99 ± 0.01	−8.08 ± 20.3	0.49 ± 1.10	0.004 ± 0.012	1.00 ± 0.01	2.33 ± 1.01	0.05 ± 0.02	0.099 ± 0.01
DKO (n = 4)	2.01 ± 0.54	−29.6 ± 14.65	0.97 ± 0.04	19.44 ± 72.4	−0.85 ± 4.03	0.040 ± 0.057	0.99 ± 0.01	6.28 ± 2.07	0.05 ± 0.01	0.97 ± 0.01

Significant differences by t-test are noted by bold blue type.

Importantly, this is because there is not enough nonlinearity in the data to guide the parameter estimations of the fits, not because there is no difference in passive stress–strain behavior in this range. This example highlights the importance of taking a data-driven rather than a one-size-fits all approach to modeling passive mechanics.

6. Perspectives on advancing passive mechanics and biological measurements

While it may seem that skeletal muscle ECM structure and passive mechanical behavior are of such complexity that uncovering meaningful relationships is in the domain of those with significant financial and mathematical prowess, additional and meaningful insight can be obtained simply by expanding traditional approaches. First, the majority of experimental protocols perform incremental stress relaxation tests that record viscous relaxation but don’t quantify the viscous component (Binder-Markey et al., 2021). This represents a missed opportunity to tie viscous changes between ECM composition and structural properties. Furthermore, the vast majority of passive muscle strain-rates during movement are expected to generate viscous forces, meaning that viscous forces likely represent a significant proportion of total passive force. It is worthwhile to at least qualitatively assess potential differences if not apply a simple (though incomplete) model. Second, if the specimen will not be used for further functional tests, it is useful to strain the specimen to failure. The material behavior at these supraphysiological lengths may better tie to ECM changes and strain to failure provides another measurement to consider. However, it is experimentally advantageous to measure ECM properties in the same sample that was mechanically tested in which case strain-to-failure might compromise subsequent structural measurements. Ideally, ECM structure and passive mechanics could be measured simultaneously using real-time microscopy techniques such as second harmonic generation, but technology and methodology for this is still in development. Third, more information can be gleaned moving beyond uniaxial tension testing. As discussed, ECM structure is layered and anisotropic, which means a significant portion of that structure will hold tension orthogonal to the axis of tension testing. Skeletal muscle has substantially different material properties in the fiber vs cross-fiber directions (Takaza et al., 2013) and both are important during material deformation and radial expansion (Smith et al., 2011a). Some changes in ECM structure with aging and disease may be more apparent in biaxial or compression testing than uniaxial testing. Finally, it is important to consider the mechanical role that the ECM plays beyond resisting tissue deformation. Muscle ECM is a scaffold for all muscle resident cells that operate in the interstitial space, including satellite cells (during regeneration), fibro/adipogenic progenitors, resident macrophages, etc. These cells sense and respond to micro-scale features of their extracellular environment including viscoelastic properties (Chaudhuri et al., 2020; Loomis et al., 2022). Multiscale measurements may shed light on the apparent dissociation of ECM structure and muscle passive tension.