Abstract
The accurate prediction of drug–target binding affinity (DTA) is an essential step in drug discovery and drug repositioning. Although deep learning methods have been widely adopted for DTA prediction, the complexity of extracting drug and target protein features hampers the accuracy of these predictions. In this study, we propose a novel model for DTA prediction named MSGNN-DTA, which leverages a fused multi-scale topological feature approach based on graph neural networks (GNNs). To address the challenge of accurately extracting drug and target protein features, we introduce a gated skip-connection mechanism during the feature learning process to fuse multi-scale topological features, resulting in information-rich representations of drugs and proteins. Our approach constructs drug atom graphs, motif graphs, and weighted protein graphs to fully extract topological information and provide a comprehensive understanding of underlying molecular interactions from multiple perspectives. Experimental results on two benchmark datasets demonstrate that MSGNN-DTA outperforms the state-of-the-art models in all evaluation metrics, showcasing the effectiveness of the proposed approach. Moreover, the study conducts a case study based on already FDA-approved drugs in the DrugBank dataset to highlight the potential of the MSGNN-DTA framework in identifying drug candidates for specific targets, which could accelerate the process of virtual screening and drug repositioning.
Keywords: drug–target binding affinity prediction, graph neural networks, feature representation learning
1. Introduction
Drug discovery is a complex and time-consuming process that may span more than a decade and cost billions of dollars from screening to market [1]. Contrarily, drug repositioning provides a promising approach to overcoming the temporal and financial bottlenecks of new drug discovery. This strategy involves identifying FDA-approved drugs that exhibit a binding affinity for specific targets, alter the expression of abnormal proteins, and exert pharmacological effects [2,3,4]. The accurate identification of potential drug–target interactions is crucial for successful drug repositioning [5], and the strength of drug–target binding affinity (DTA) serves as an important indicator for drug screening [6,7,8,9,10]. Traditional methods of measuring DTA are resource-intensive and time-consuming. The rapid advancement of computer technology has facilitated accurate and efficient prediction of DTA, thereby assisting biological experiments [11]. Currently, DTA prediction methods can be classified into three categories: structure-based methods, machine learning-based methods, and deep learning-based methods.
In computer experiments, structure-based approaches typically utilize molecular docking and molecular dynamics simulations for DTA prediction. Molecular docking explores potential binding sites by considering the 3D structure of the receptor and ligand, and a scoring function based on the molecular position is defined to calculate the binding energy [12]. For proteins with known structural information, binding affinity can be obtained directly by docking the drug molecule [13]. However, this approach necessitates high-precision 3D protein structures, which may be unattainable for a massive number of proteins with unknown structural information. Even with extensive homology modelling, reliable structural information may not be acquired [14].
Conventional machine learning methods have been applied for DTA prediction. Pahikkala et al. [15] proposed KronRLS, an approach based on Kronecker regularized least squares, which utilizes the Smith–Waterman algorithm and PubChem structural clustering server to build similarity matrices for proteins and drugs, and then calculate the Kronecker product to predict the DTA. He et al. [16] introduced Simboost, which utilizes a gradient booster to extract features from drugs, targets, and drug–target pairs. These methods have limitations in achieving significant performance improvement, as they heavily rely on intricate feature engineering, which typically requires a high level of domain expertise [17].
Deep learning is widely used in many research areas of bioinformatics [18], various deep learning-based methods have been applied in DTA prediction, where it can capture complex hidden information from massive data. Öztürk et al. [9] proposed DeepDTA, which employs two convolutional neural networks (CNNs) to extract local sequence information and then feed it into several fully connected layers for DTA prediction. Similarly, Öztürk et al. [19] proposed another CNN-based model, called WideDTA, which takes advantage of two additional text-based information sources, namely protein interaction domains and ligand maximum common structure words, obtaining four representations that further improve the DTA prediction performance. Furthermore, attention-based methods have been introduced to improve interpretability in DTA prediction. Chen et al. [20] proposed TransformerCPI, which retains the decoder of the transformer but modifies its encoder and the final linear layer to increase interpretability. In another work, Yang et al. [21] developed ML-DTI, which uses a mutual information mechanism to capture the interaction relationship between drug and protein encoders, bridging the gap between the two encoders and enabling the identification of new drug–target interactions.
Although CNN-based methods have demonstrated remarkable achievements in DTA prediction, their exclusive utilization of 1D representations of drugs and proteins fails to capture the spatial structural information of molecules, such as the distance and angle between residues that determine molecular function. Graph neural networks (GNNs), renowned for their efficacy in tackling an array of challenges, have been implemented in various models representing drugs as graphs for DTA prediction. Nguyen et al. [10] devised GraphDTA, a graph-based model encoding drugs as undirected graphs represented by a feature matrix and an adjacent matrix. Experimental results and theoretical analyses suggest that graph-based drug representations may further bolster performance. Lin et al. [22] proposed DeepGS, leveraging advanced embedding learning techniques that consider molecular topology, SMILES string, and protein sequence for DTA prediction. Yang et al. [23] developed MGraphDTA, constructing a 27-layer ultra-deep GNN that learns multi-scale features and capitalizes on topological information while avoiding gradient disappearance. Furthermore, Jiang et al. [24] created DGraphDTA, which predicts the contact map using amino acid sequence, thereby constructing the protein graph to boost prediction performance further. When producing the protein contact map, WGNN-DTA [25] obviates the need for sophisticated processes such as multiple sequence alignment (MSA), which effectively enhances the execution speed.
In general, graph-based DTA prediction models only employ a limited number of GNN layers, typically ranging from two to four layers. However, such shallow GNNs are incapable of capturing the intricate topological information of molecules, leading to insufficient representation learning. To fully capture topological information, multiple layers of GNN should be stacked, which is also infeasible due to the problems of vanishing gradients and node feature degradation [26]. Furthermore, motifs have special meanings in drug molecules, such as carbon rings and NO2 groups that are prone to mutagenesis [27]. The motifs can exert their practical value when considered as a whole, and it would be meaningless if the chemical bonds in the ring are isolated separately. Therefore, motifs deserve more attention during the feature extraction process. Additionally, topological features at different scales are extracted from various GNN layers, but previous models only used single-scale features for DTA prediction, resulting in a loss of prediction performance. Therefore, the fusion of multi-scale features is necessary, and the model should be capable of adaptively fusing essential features to improve prediction performance.
In response to the aforementioned challenge, we present a novel GNN-based model for DTA prediction that leverages multi-scale topological feature fusion. Our proposed approach underscores the significance of motifs by creating drug motif-level graphs, where motifs are viewed as holistic entities and mapped as graph vertices. This design choice captures the practical value of motifs and effectively extracts meaningful features that contribute to accurate predictions. To further exploit the topological information of drug molecules, we introduce a gated skip-connection mechanism during the GNN-based representation learning process. This mechanism enables the model to dynamically adapt and selectively fuse features from different scales, thus avoiding the problems of node gradient vanishing and feature degradation. The learned enhanced representations are informative and enable accurate predictions. The experimental evaluations demonstrate that our model outperforms existing models on benchmark datasets, with low prediction error and high stability. We believe that our approach has practical applications in drug discovery and development by providing a more comprehensive and interpretable approach to DTA prediction.
This paper’s significant contributions are summarized as follows:
To make full use of the topological information of drugs and proteins, we simultaneously construct drug atom graphs, motif graphs, and weighted protein graphs to learn drug and protein representations from multiple perspectives.
To extract and fuse multi-scale topological information, a gated skip-connection mechanism is introduced in the feature learning based on GNNs, and topological features at different scales are selectively preserved.
To improve the adaptive capability of the model, we incorporate an attention mechanism in the prediction phase, which enables the model to concentrate on the crucial features of multi-scale and further strengthen the DTA prediction performance.
2. Results
2.1. Evaluation Metrics
DTA prediction is a regression task using the mean squared error (MSE) as a loss function. MSE measures the error between the ground and predicted values, with a smaller MSE indicating that the predicted value is closer to the true value. MSE is defined as follows:
| (1) |
where is the true value of the ith sample and is the predicted value of the ith sample.
Another evaluation metric is the concordance index (CI), which measures whether the predicted values of two randomly selected drug–target pairs have a consistent relative order with the true dataset. A larger CI indicates better model prediction performance. It is defined as shown in Equation (2).
| (2) |
where is the prediction value for the larger affinity , is the prediction value for the smaller affinity , and is step function. Z is the normalization constant that maps the values to [0,1]. The step function is defined as shown in Equation (3).
| (3) |
The Pearson correlation coefficient was calculated by Equation (4). is the covariance between the predicted value p and true value y, and is the standard deviation. A higher Pearson coefficient suggests greater predictive accuracy.
| (4) |
Regression toward the mean () is a metric for evaluating the external predictive performance of a model. If a variable is extremely large or extremely small at this measurement, indicates how close to the mean it tends to be at the next measurement. The index calculation process is depicted in Equation (5).
| (5) |
where r is the correlation coefficient with intercept and is the correlation coefficient without intercept.
2.2. Experimental Setup
MSGNN-DTA is built with PyTorch [28], which is an open-source machine learning framework. The GNN models are implemented using PyTorch Geometric (PyG) [29]. We evaluated the performance of the proposed model on two benchmark datasets, the Davis [30] and KIBA datasets [31]. To ensure a fair comparison, we adopted the same strategy for data partitioning as DeepDTA [9], which randomly divided the datasets into six equal parts, with one part reserved for independent testing and the remaining five parts used for model training.The hyperparameter settings for our experimental part are shown in Table 1.
Table 1.
Experimental hyperparameter settings.
| Parameters | Setting |
|---|---|
| Epoch | 2000 |
| Batch size | 512 |
| Leaning rate | 0.0005 |
| Optimizer | Adam |
| Dropout rate | 0.2 |
| Graph convolutional layers | 3 |
| Input dimension of the three layers in GNN | N, 4 N, 4 N |
| Output dimension of the three layers in GNN | N, 4 N, 4 N |
| Fully connected layer hidden unit | 1024, 512 |
Note: N represents the dimension of the initial features.
2.3. Performance Comparison with Benchmark Models
To evaluate the superiority of MSGNN-DTA, we compared it with the state-of-the-art models on two benchmark datasets, Davis and KIBA, respectively. We compared MSGNN-DTA with KronRLS [15], SimBoost [16], DeepDTA [9], WideDTA [19], GraphDTA [10], MGraphDTA [23], GEFA [32], WGNN-DTA [25], and DGraphDTA [24], which are currently widely used benchmark methods for DTA prediction. To ensure a fair comparison, we adopted the same training and testing sets as well as performance metrics for evaluation. The performance results, along with those reported in the original publications for the baseline methods, are summarized in Table 2 and Table 3.
Table 2.
Performance evaluation of the DTA prediction models on the Davis dataset.
| Methods | Proteins | Compounds | MSE ↓ | CI ↑ | ↑ | Pearson ↑ |
|---|---|---|---|---|---|---|
| KronRLS | Smith–Waterman | Pubchem-Sim | 0.379 | 0.871 | 0.407 | - |
| SimBoost | Smith–Waterman | Pubchem-Sim | 0.282 | 0.872 | 0.644 | - |
| DeepDTA | CNN | CNN | 0.261 | 0.878 | 0.630 | - |
| WideDTA | CNN + PDM | CNN + LMCS | 0.262 | 0.886 | - | 0.820 |
| GraphDTA | CNN | GIN | 0.229 | 0.893 | - | - |
| GEFA | GCN | GCN | 0.228 | 0.893 | - | 0.847 |
| MGraphDTA | MCNN | MGNN | 0.207 | 0.900 | 0.710 | - |
| WGNN-DTA | GCN | GCN | 0.208 | 0.900 | 0.692 | 0.861 |
| WGNN-DTA | GAT | GAT | 0.208 | 0.903 | 0.691 | 0.863 |
| DGraphDTA | GCN | GCN | 0.202 | 0.904 | 0.700 | 0.867 |
| MSGNN-DTA | GAT | GAT + GAT | 0.195 | 0.906 | 0.719 | 0.871 |
Note: Bold indicates the best result in the evaluation metrics. These results are not reported from original studies.
Table 3.
Performance evaluation of the DTA prediction models on the KIBA dataset.
| Methods | Proteins | Compounds | MSE ↓ | CI ↑ | ↑ | Pearson ↑ |
|---|---|---|---|---|---|---|
| KronRLS | Smith–Waterman | Pubchem-Sim | 0.411 | 0.782 | 0.342 | - |
| SimBoost | Smith–Waterman | Pubchem-Sim | 0.222 | 0.836 | 0.629 | - |
| DeepDTA | CNN | CNN | 0.194 | 0.863 | 0.673 | - |
| WideDTA | CNN + PDM | CNN + LMCS | 0.179 | 0.875 | - | 0.856 |
| GraphDTA | CNN | GAT − GCN | 0.139 | 0.891 | - | - |
| MGraphDTA | MCNN | MGNN | 0.128 | 0.902 | 0.801 | - |
| WGNN-DTA | GCN | GCN | 0.144 | 0.885 | 0.781 | 0.888 |
| WGNN-DTA | GAT | GAT | 0.130 | 0.898 | 0.791 | 0.899 |
| DGraphDTA | GCN | GCN | 0.126 | 0.904 | 0.786 | 0.903 |
| MSGNN-DTA | GAT | GAT + GAT | 0.117 | 0.908 | 0.818 | 0.910 |
Note: Bold indicates the best result in the evaluation metrics. These results are not reported from original studies.
According to the experimental results, the proposed MSGNN-DTA achieved the best performance compared to state-of-the-art methods in all datasets, demonstrating its generalization and robustness. The model decreased the MSE by % and % and increased the CI by % and % on the Davis and KIBA datasets, respectively, underscoring the model’s ability to outperform other models in terms of predictive accuracy and reliability. Additionally, the model showed advantages in the other two evaluation metrics, and Pearson. The considerable improvements over the second best model of % and % in the Davis dataset and % and % in the KIBA dataset, respectively. Overall, the MSGNN-DTA model’s superior performance across all metrics and datasets makes it an essential tool for researchers seeking to predict drug–target affinity values.
Our proposed model achieves significant performance gains, which can be attributed to the following factors. Firstly, we utilize graph-based representations for both compounds and proteins, providing a more comprehensive and informative approach to encoding molecular structures compared to traditional sequence-based methods. By constructing three types of graphs, including drug molecule graphs, motif graphs, and protein graphs, our model captures the molecular structure and functional information from multiple perspectives, allowing for more accurate predictions of DTA. Secondly, during the feature representation learning stage, our model integrates multi-scale feature information using graph neural networks (GNNs). This enables the learning of enriched and informative molecular representations, leading to further improvements in predictive performance. Thirdly, the incorporation of attention mechanisms during the DTA prediction phase allows the model to adaptively fuse critical features, resulting in even higher accuracy. Importantly, experimental results demonstrate the potential of MSGNN-DTA for practical applications in drug discovery and development.
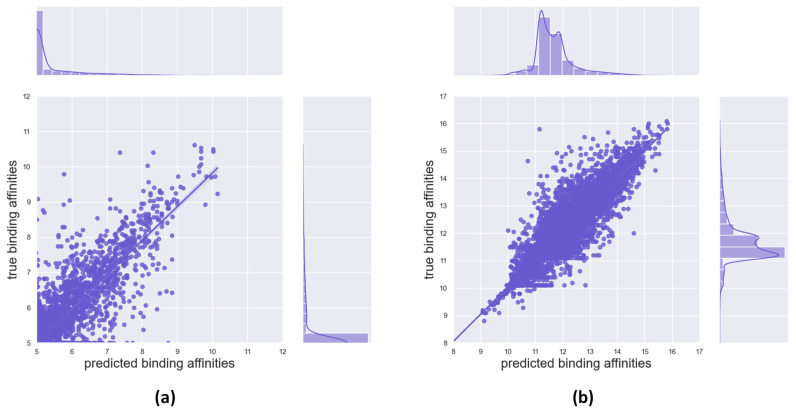
Figure 1 displays the relationship between the predicted binding affinity and the true value. Upon analysing the model prediction, the linear regression curves between the true and predicted values are almost indistinguishable from the diagonal line, indicating an excellent fit between the predicted and true values. Moreover, the distribution trend of the sample size between the predicted and actual values closely aligns, further validating the model’s accuracy in making precise predictions.
Figure 1.
Scatter plot of true and predicted values on the Davis (a) and KIBA datasets (b), in which the horizontal coordinates represent the predicted binding affinity and the vertical coordinates represent the true binding affinity. The bar charts above and right show the distribution of the sample size.
2.4. Performance Comparison of Various GNN Models and Pooling Methods
To achieve effective feature extraction with rich information during GNN-based representation learning, selecting the appropriate GNN model and pooling method is crucial. In this study, we conducted an evaluation of two different graph convolution methods, namely GCN and GAT, along with two distinct pooling methods, max pooling and average pooling, to obtain the graph-level representations of drugs and proteins, as presented in Table 4. Our experimental findings reveal that GAT-based feature extraction outperforms GCN-based feature extraction in almost all performance metrics. This superiority can be attributed to the multi-head attention mechanism employed by GAT, which aggregates neighbouring node features and considers node correlation by computing attention scores, whereas GCN assigns the same attention weight to different neighbouring nodes. Furthermore, we observed that the max pooling method yields higher prediction accuracy than the average pooling method on both benchmark datasets. This finding highlights the importance of selecting a suitable pooling method in GNN-based models for DTA prediction.
Table 4.
Performance comparison of different GNN models and pooling methods.
| Dataset | GNN Model | Pooling Method | MSE ↓ | CI ↑ | ↑ | Pearson ↑ |
|---|---|---|---|---|---|---|
| Davis | GCN | Max | 0.203 | 0.903 | 0.713 | 0.864 |
| GCN | Mean | 0.201 | 0.904 | 0.723 | 0.866 | |
| GAT | Max | 0.196 | 0.906 | 0.719 | 0.871 | |
| GAT | Mean | 0.202 | 0.905 | 0.716 | 0.865 | |
| KIBA | GCN | Max | 0.122 | 0.904 | 0.789 | 0.906 |
| GCN | Mean | 0.121 | 0.904 | 0.795 | 0.907 | |
| GAT | Max | 0.117 | 0.908 | 0.818 | 0.910 | |
| GAT | Mean | 0.122 | 0.906 | 0.794 | 0.906 |
Note: Bold indicates the best result of the evaluation metrics.
2.5. Ablation Experiments
To investigate the key factors influencing the predictive performance of our model, we conducted a series of ablation experiments using the following variants of MSGNN-DAT:
Without Attention: This model does not incorporate an attention mechanism to fuse the feature representations of the three channels, instead it directly concatenates the features to predict DTA, which is equivalent to giving the three parts equally important weight parameters.
Without Motif-Level: This model does not construct a motif graph to learn drug motif-level feature representation, instead it only constructs a drug atom graph and a weight protein graph, and fuses two parts to predict DTA
Without Skip-Connection: This model does not incorporate the gated skip-connection mechanism during the feature learning process, the node features of the previous-hop are not preserved when aggregating the next-hop neighbour information, and the hidden features at different scales are discarded.
Through these ablation experiments, we can gain insight into the relative importance of each component in our proposed model and the effectiveness of our design choices. Table 5 depicts the results of our ablation experiments on the two benchmark datasets, highlighting the superior performance of MSGNN-DTA over all other variants. Particularly noteworthy is the considerable performance gap between MSGNN-DTA and the other variants when the attention mechanism is not employed. This finding highlights the crucial role of attention in our model, as it permits the discerning integration of critical information during the feature aggregation process. Furthermore, we observe that the absence of motif-level results in comparatively poorer performance than MSGNN-DTA, emphasizing the importance of learning drug features from diverse perspectives and exploiting the topological information of drugs more comprehensively. Lastly, we note that the gated skip-connection mechanism can selectively preserve the features of different scales, resulting in further improvements in prediction performance.
Table 5.
Performance comparison of ablation experiments.
| Dataset | Variants | MSE ↓ | CI ↑ | ↑ | Pearson ↑ |
|---|---|---|---|---|---|
| Davis | Without Motif-Level | 0.200 | 0.903 | 0.715 | 0.867 |
| Without Skip-Connection | 0.201 | 0.903 | 0.728 | 0.866 | |
| Without Attension | 0.203 | 0.897 | 0.709 | 0.865 | |
| MSGNN-DTA | 0.195 | 0.906 | 0.719 | 0.871 | |
| KIBA | Without Motif-Level | 0.123 | 0.905 | 0.790 | 0.906 |
| Without Skip-Connection | 0.122 | 0.904 | 0.788 | 0.906 | |
| Without Attension | 0.124 | 0.906 | 0.808 | 0.905 | |
| MSGNN-DTA | 0.117 | 0.908 | 0.818 | 0.910 |
Note: Bold indicates the best result of the evaluation metrics.
2.6. Case Study
To evaluate the generalization capability of our model, we conducted experiments on a set of FDA-approved drug candidates from the DrugBank [33] database, excluding those contained in the KIBA dataset and retaining 2092 drug candidates. Subsequently, we selected a specific protein, epidermal growth factor receptor (), which is known to be associated with various types of cancer and is a popular target for cancer therapy. Among the 2092 candidates, 9 are known to have interactions with . We used the trained model on the KIBA dataset to calculate the interaction scores between all of the drug candidates with , ranked in descending order of scores for further analysis.
The results presented in Table 6 demonstrate that out of the top 11 small molecule compounds, 6 of them are inhibitors, while the remaining 3 compounds are ranked at positions 17, 32, and 43. Several other top-ranking drugs belong to tyrosine kinase inhibitors, which are targeted therapies for various types of cancer. Given that is a member of the tyrosine kinase family, these drugs possess a high possibility to be ligands for binding to . This assertion is supported by existing literature, where the mode of action of ibrutinib with mutant kinases has been investigated [34,35].
Table 6.
The predicted KIBA score ranking of drug candidates with .
| Rank | DrugBank ID | Drug Name | Predict KIBA Score |
|---|---|---|---|
| 1 | DB09053 | Ibrutinib | 12.98426 |
| 2 | DB00317 | Gefitinib | 12.94488 |
| 3 | DB12267 | Brigatinib | 12.91385 |
| 4 | DB09063 | Ceritinib | 12.86993 |
| 5 | DB12095 | Telotristat ethyl | 12.86020 |
| 6 | DB01254 | Dasatinib | 12.71807 |
| 7 | DB01259 | Lapatinib | 12.66030 |
| 8 | DB05294 | Vandetanib | 12.61738 |
| 9 | DB11828 | Neratinib | 12.61046 |
| 10 | DB01167 | Itraconazole | 12.60930 |
| 11 | DB00530 | Erlotinib | 12.58477 |
Note: Bold in the table denotes a drug that has known interactions with .
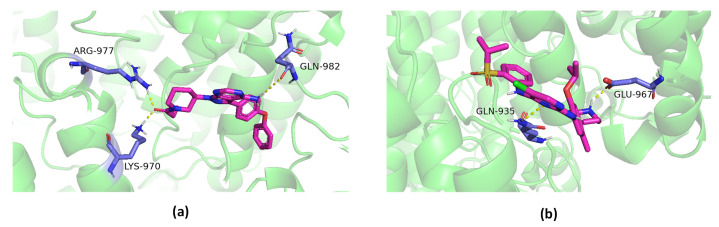
To further validate the predicted drug–target interactions, we downloaded the crystal structure of (UniProt P00533) with PDB ID from the Protein Data Bank (PDB) and performed molecular docking using Autodock [36]. We used the lowest affinity energy output as a candidate binding site for specific ligands and receptors, thereby visualizing the hydrogen bonds formed by docking between drug molecules and amino acids of proteins using Pymol, as shown in Figure 2.
Figure 2.
(a) Molecular docking and hydrogen bonding colouring results between and ibrutinib (DB09053). (b) Molecular docking and hydrogen bonding colouring results between and ceritinib (DB09063); the target protein is shown as a cartoon (green), the ligand molecule is shown as a stick structure (pink), the hydrogen bonding is shown in yellow, and the amino acid residues connected to the ligand by hydrogen bonding are shown as stick structures (purple).
Our results demonstrate that the MSGNN-DTA exhibits a strong generalization performance in identifying potential drug candidates that have a high likelihood of binding to specific targets among a massive number of candidates. This makes it a valuable tool for screening potential drug candidates and prioritizing those with a higher predicted binding affinity for further testing. Ultimately, this could lead to the development of more effective drugs with improved therapeutic outcomes and fewer side effects.
3. Discussion
In this study, we introduce a novel approach for predicting drug–target binding affinity named MSGNN-DTA. Our method utilizes a graph neural network that introduces a gated skip-connection mechanism, which integrates multi-scale topological features to improve the accuracy of predictions. Specifically, we construct drug atom-level graphs, motif-level graphs, and weighted protein graphs to capture more sufficient information about drugs and proteins. Additionally, we incorporate an attention mechanism to adaptively fuse the multi-scale features, which enhances the performance of DTA prediction. The proposed method has the potential to significantly advance drug discovery and contribute to the development of more effective treatments.
The results demonstrate that our proposed method significantly outperforms the baseline approach. In practical applications, our pre-trained model can predict the affinity value by simply inputting the SMILES string of the drug and the amino acid sequence of the protein. This provides a powerful tool for the virtual screening of target proteins, facilitating the discovery of lead compounds. Although MSGNN-DTA shows superior performance in DTA prediction, there is still scope for further improvements.
The overall 3D geometry of a compound plays a crucial role in the interactions between drugs and protein targets. For instance, the active site of a protein often has specific geometric constraints, and the overall 3D shape of a drug must match it to effectively bind and exert its function. Furthermore, for compounds with multiple chiral centres, different optical isomers can have distinct biological activities, particularly for compounds such as protein kinase inhibitors. Thus, the correct selection and optimization of optical isomers are crucial in drug design and discovery. In this study, we did not consider the optical isomers and the overall 3D geometry of compounds, which may limit the predictive ability of our method. Although our method achieved good results in predicting based on molecular topological structure, its predictive ability may be limited for some complex compounds.
In future research, we will further explore how to incorporate optical isomers and the overall 3D geometry of compounds into our model. This will include using advanced computational tools to simulate the 3D shape of molecules and developing new models to process this information. We believe that this work will help improve the predictive performance of our method and apply it to a wider range of compounds and proteins.
4. Materials and Methods
4.1. Datasets
In this research, we performed a comprehensive performance evaluation of MSGNN-DTA on two widely recognized and publicly available datasets, namely the Davis [30] and KIBA [31] datasets. To ensure a fair and objective comparison, we employed a standard dataset split approach by randomly dividing the dataset into five parts, out of which four parts were used for training purposes while the remaining part was reserved for testing. We conducted five-fold cross-validation and reported the average performance as the final evaluation.
The Davis dataset contains 442 kinase proteins and their associated 68 inhibitors, with the binding affinity obtained through the measurement of dissociation constants , which are expressed in units of nanomolar. To more graphically describe the relationship between and binding affinity, the was converted to logarithmic space with [16], and the process of taking the negative logarithm is expressed in Equation (6). The higher value of indicates a stronger binding affinity, with values ranging from 5.0 to 10.8. The boundary value 5.0 is considered the true negative drug–target pairs that exhibit either extremely weak binding affinities or are not detected in wet laboratory experiments.
| (6) |
The KIBA dataset is a comprehensive and expansive resource. The interaction value was recorded using the KIBA score, derived from the combination of heterogeneous information sources, including the inhibition constant (), , and the half-maximal inhibitory concentration (), with values ranging from 0.0 to 17.2. The dataset is of superior quality, as the integrated heterogeneous measurements mitigated the data inconsistency arising from relying on a single information source. For further clarity, Table 7 presents a comprehensive overview of both benchmark datasets.
Table 7.
Summary of the Davis and KIBA datasets.
| Dataset | Compounds | Proteins | Interactions |
|---|---|---|---|
| Davis | 68 | 442 | 30,056 |
| KIBA | 2111 | 229 | 118,254 |
4.2. Model Architecture
Our prediction task aims to predict the binding affinity between drug–target pairs, given the SMILES of drugs and the amino acid sequence of target proteins as the original input. To achieve this goal, we propose a new approach called MSGNN-DTA, which involves constructing drug and protein graphs from multiple perspectives. For each drug, we simultaneously construct an atom graph and a motif graph, where individual atoms and motifs are represented as nodes, respectively. Meanwhile, for each protein, we predict residue contact maps using a protein structure prediction model and construct a weighted protein graph accordingly. To obtain multi-scale topological feature representations of drugs and proteins, we parallelize the constructed graphs through a GNN-based feature learning module. This module enables us to obtain two representations of the drug and one representation of the protein. Subsequently, we apply an attention mechanism to adaptively fuse the drug–target representations and obtain a joint representation, which is then fed into multiple fully connected layers to predict DTA. The main architecture of our model is illustrated in Figure 3, which depicts the detailed workflow of each module. In the following sections, we will provide a comprehensive description of each module.
Figure 3.
The main architecture of MSGNN-DTA.
4.3. Graph Construction for Drugs and Proteins
4.3.1. Construction of Drug Atom-Level Graph
Drugs are commonly represented by SMILES (simplified molecular input line entry specification) [37]. The structural information of the molecule is missing when using the string representation directly. Therefore, we use the open-source molecular processing software Rdkit [38] to construct the atom-level graph of drugs based on SMILES, where nodes represent atoms, edges represent chemical bonds, and the graph topology is represented by an adjacency matrix A. The initial feature vector of each atom is obtained based on chemical and structural properties. The detailed meaning of node features is illustrated in Table 8, represented by a 78-dimensional vector.
Table 8.
The node features for a drug atom-level graph.
| Feature Name | Dimension |
|---|---|
| Atomic symbol | 44 |
| Degree of atom | 11 |
| Total number of connected hydrogen atoms (implicit and explicit) | 11 |
| Implicit valence of atoms | 11 |
| Whether the atom is aromatic or not | 1 |
4.3.2. Construction of Drug Motif-Level Graph
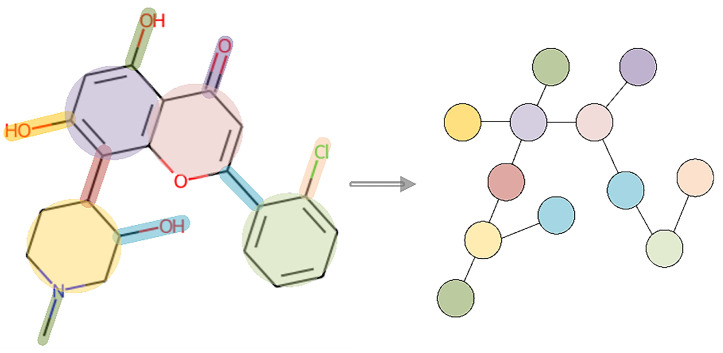
It is widely recognized that some motifs in drugs, such as the benzene ring, are intimately related to molecular properties. The benzene ring is meaningful when considered as a whole, but it loses meaning when the chemical bonds within the ring are separated individually. However, several layers of GNN cannot capture all of the information in the ring to which an atom belongs, resulting in incomplete information being extracted. Therefore, in MSGGN-DTA, the motif-level graph for drugs is constructed simultaneously. Cyclic structures and individual chemical bonds, which do not belong to any cyclic structures, along with their connected pairs of atoms, are considered the fundamental building blocks of molecules and are represented as nodes in the molecular motif graph [39]. Specifically, cyclic structure nodes represent a group of atoms and chemical bonds connected cyclically, while nodes representing individual chemical bonds along with their connected pairs of atoms represent the relationships between atoms and chemical bonds. This approach provides a better reflection of the structural information of the molecule, thus facilitating motif graph generation and model training. The edges represent whether two nodes are connected by a chemical bond. The construction process of a drug motif graph is depicted in Figure 4. Similar to the molecular graph, the initial features of nodes also need to be extracted. The detailed meaning is described in Table 9, represented by a 92-dimensional vector.
Figure 4.
The construction process of a drug motif-level graph, where the nodes represent motifs and edges represent whether two nodes are connected by a chemical bond.
Table 9.
The node features for a drug motif-level graph.
| Feature Name | Dimension |
|---|---|
| Atomic symbols contained in the motif | 44 |
| Number of atoms in the motif | 11 |
| Number of edges connecting to other motifs | 11 |
| Total number of hydrogen atoms connected by motif (implicit & explicit) | 12 |
| Implicit valence of motif | 12 |
| Whether the motif is a simple ring | 1 |
| Whether the motif is chemically bonded or not | 1 |
4.3.3. Construction of Weighted Protein Graph
Proteins are conventionally represented as 1D sequences consisting of 25 distinct amino acids, but such a representation fails to reflect the entire spatial structure information. The spatial structure of proteins is determined by various interactions, including hydrogen bonds, ionic bonds, and hydrophobic interactions, among others [40]. Consequently, sole reliance on a 1D representation proves inadequate to capture the intricate spatial structure information of proteins, thereby posing a challenge in extracting an effective protein representation. Despite the exponential growth of protein databases, the structures of the majority of proteins remain unknown. However, recent advances in natural language processing techniques have facilitated the development of several cutting-edge protein language models [41,42,43], which can accurately predict protein structures solely from the input protein sequences.
In this study, we employed the ESM-1b model proposed by Rives et al. [42] to predict the contact map of proteins. The ESM-1b model is an unsupervised protein language modelling approach based on transformer architecture that leverages large-scale protein sequence and structure exploration through pre-training. It can accurately and efficiently predict protein contact maps by directly inputting the 1D protein sequence. We selected this model because ESM-1b can predict protein contact maps accurately without requiring multiple sequence alignment (MSA), which greatly enhances the prediction efficiency.
The contact map predicted by the ESM-1b model is represented as a probability matrix, where each element represents the interaction probability between different residues, ranging from 0 to 1. According to the construction process of the weighted protein graph in the WGNN-DTA model [25], if a value in the probability matrix exceeds the threshold of 0.5 is retained, while those below are set to 0. The weighted protein graph is constructed using residues as nodes, residue interactions as edges, and probability values as the weight of the edges. Since the ESM-1b model is trained with a fixed context size of 1024 tokens for position embedding, the sequence length is limited. To handle longer protein sequences (over 1000 residues), WGNN-DTA employs a truncation and splicing strategy to construct the contact map. The entire sequence is divided into multiple fixed-length subsequences of length L with a step size of , and the contact map of each subsequence is predicted sequentially by the ESM-1b model, followed by splicing together, with overlapping parts averaged. Algorithm 1 describes the specific construction process of the contact map. Additionally, features of each residue node, such as residue type, polarity, hydrophobicity, weight, group dissociation constant, and more, are extracted to generate an initial feature vector for each node, represented by a 33-dimensional vector.
| Algorithm 1 Construction of a protein contact map |
|
Input: protein amino acid sequence: Output: contact map Initialization: contact map
|
4.4. Feature Learning Based on Graph Neural Networks
Through the process of graph construction, we obtain the drug atom-level graph, the motif-level graph, and the weighted protein graph. GNN can effectively extract hidden features using the spatial topological structure information of the graph, and obtain a graph-level representation by aggregating features of nodes. Below is a brief description of the graph convolutional network (GCN) [44] and the graph attention network (GAT) [45].
For a graph , V is the set of nodes and E is the set of edges. The initial feature vector of each atom is , a graph is represented by a feature matrix and an adjacency matrix , where N is the number of nodes, F is the feature dimension, and the adjacency matrix represents the interaction relationship between nodes. The propagation mechanism of the GCN layer is described in Equation (7).
| (7) |
where is the adjacency matrix added to a self-loop, is the degree matrix of the graph, and represents the feature matrix of the lth layer. represents the output of the feature representation after message propagation. is the ReLU activation function. W is a learnable weight matrix. The input layer is equal to the input feature matrix X.
GAT learns the hidden representation of nodes based on the self-attentive mechanism. First, the nodes are linearly transformed by a weight matrix , and denotes the feature dimension of hidden layer nodes. For a given node i, the attention coefficient with its neighbour j is calculated by Equations (8) and (9). The attention weights are then normalized with their neighbouring nodes using the Softmax function to ensure that the sum of attention weights of all neighbouring nodes is equal to one, indicating the importance between node pairs. The LeakyReLU activation function is used to improve the model’s stability and robustness, especially when processing negative inputs, outperforming the ReLU activation function [45]. Equation (10) aggregates the features of neighbouring nodes according to the attention score to obtain the feature representation of the hidden layer.
| (8) |
| (9) |
| (10) |
where is feature vector of node i, is the set of neighbouring nodes of node i, denotes the attention coefficient between node i and node j, denotes the normalized attention coefficient, is the hidden layer feature of node i, is the non-linear activation function, and a, W is the learnable weight matrix.
In MSGNN-DTA, node-level feature representations are learned through three consecutive GNN layers. To obtain representation vectors of the same length for drugs containing different atom numbers and proteins with different residue numbers, we add pooling layers after the last GNN layer, aggregating node-level features to obtain graph-level representations. Finally, a 128-dimensional vector is obtained by several fully connected and dropout layers.
Gated Skip-Connection Mechanism
To aggregate neighbour information at long distances in a specific central atom, stacking multiple GNN layers is necessary. However, the side effects of gradient disappearance and node degradation appear as the number of GNN layers increase. We incorporate a gated skip-connection mechanism [46] in the representation learning of each hidden layer, fusing features from different hidden states by adjusting the rate of forgetting and updating. Along with the increase in model depth, each node can aggregate the information carried by remote nodes and preserve the unique features of the node themselves.
The gated skip-connection mechanism is described in Equations (11) and (12).
| (11) |
| (12) |
where and are trainable parameters, b is bias, and denote the lth and l+1th layer feature vectors of node i, respectively, and is the learned proportion coefficient that retains the information of the previous hidden layer. Here we have chosen a sigmoid activation function to ensure that the learned proportion coefficient falls within the range of 0 to 1.
4.5. Prediction of Drug–Target Binding Affinity
With three representation learning modules running in parallel, we obtain drug atom-level (), drug motif-level (), and protein () representations. The three parts are concatenated into a complete vector and then fed into three consecutive fully connected layers to predict DTA.
Compared with many previous models that employ simple concatenation, the attention mechanism allows the model to adaptively integrate the critical features, further improving prediction accuracy. Let , , and denote the attention scores of , , and , respectively. Firstly, the weight scores , , and are calculated by Equation (13). Here we choose the tanh activation function, which increases the speed of model convergence.
| (13) |
where and are learnable weight vectors and can be adjusted during training, and then normalized using by the Softmax function to map the above-learned weight scores to the (0,1) interval to obtain the attention scores, which represent the importance of each part in determining the final prediction.
| (14) |
Finally, we connect the three components of the representation by the learning attention scores.
| (15) |
where denotes the connected feature vector of the drug–target pair.
5. Conclusions
The study proposes a novel approach, MSGNN-DTA, for predicting drug–target binding affinity that integrates multi-scale topological features using graph neural networks. We concurrently construct drug atom-level graphs, motif-level graphs, and weighted protein graphs for learning enhanced multi-scale features that represent the rich information of drugs and proteins. The novelty of this approach lies in its ability to capture the multi-scale topological features of drugs and proteins and fuse them adaptively using an attention mechanism. This allows for more a accurate prediction of the drug–target binding affinity and has the potential to aid in the development of more effective and safe drugs with fewer adverse effects.
The proposed method is evaluated through a series of experiments, which demonstrate it outperforms existing state-of-the-art models in all evaluation metrics, indicating its potential as a powerful tool for accurate DTA prediction. Furthermore, we conducted an analysis of candidate drugs for the epidermal growth factor receptor () based on FDA-approved drugs, and the predicted scores of drugs known to interact with were consistently ranked among the top positions, further validating the effectiveness and generalization ability of the proposed method. These results collectively highlight the potential of MSGNN-DTA as an efficient and reliable approach for advancing drug discovery and design. These results collectively highlight the potential of MSGNN-DTA as an efficient and reliable approach for advancing drug discovery and design.
In future work, we plan to investigate the feature representation learning process further by integrating a broader range of features, including evolutionary, structural, functional, and physicochemical features, among others. Additionally, we will explore the construction of networks using similarity matrices to enhance the accuracy of DTA prediction. Our research directions aim to continue advancing the field of drug–target interaction prediction and contribute to the development of more effective therapeutic interventions.
Acknowledgments
The authors are grateful to Wenhao Wu and Yu Zhang for advice and excellent technical assistance.
Abbreviations
The following abbreviations are used in this manuscript:
| DTA | Drug–Target Binding Affinity |
| GNNs | Graph Neural Networks |
| CNN | Convolutional Neural Networks |
| GCN | Graph Convolutional Network |
| GAT | Graph Attention Network |
| SMILES | Simplified Molecular Input Line Entry Specification |
| MSA | Multiple Sequence Alignment |
| MSE | Mean Squared Error |
| CI | Concordance Index |
| Regression Towards the Mean | |
| Dissociation Constants | |
| Inhibition Constant | |
| Half-Maximal Inhibitory Concentration | |
| PYG | PyTorch Geometric |
| Epidermal Growth Factor Receptor |
Author Contributions
Conceptualization, S.W. and Y.Z.; methodology, X.S.; software, X.S.; validation, X.S., Y.Z. and K.Z.; formal analysis, Y.Z., Y.L. and C.R.; investigation, Y.L. and C.R.; resources, S.W. and S.P.; data curation, X.S.; writing—original draft preparation, X.S.; writing—review and editing, X.S., Y.Z. and K.Z.; visualization, X.S.; supervision, Y.Z.; project administration, S.W.; funding acquisition, S.W., Y.Z. and S.P. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The source code and data of this study are available at https://github.com/songxuanmo/MSGNN-DTA (accessed on 1 May 2023).
Conflicts of Interest
The authors declare no conflict of interest.
Funding Statement
This research was funded by National Key Research and Development Project of China (2021YFA1000102, 2021YFA1000103), and the National Natural Science Foundation (Nos.61902430).
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Xue H., Li J., Xie H., Wang Y. Review of drug repositioning approaches and resources. Int. J. Biol. Sci. 2018;14:1232. doi: 10.7150/ijbs.24612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pang S., Zhang K., Wang S., Zhang Y., He S., Wu W., Qiao S. HGDD: A Drug-Disease High-Order Association Information Extraction Method for Drug Repurposing via Hypergraph; Proceedings of the Bioinformatics Research and Applications: 17th International Symposium (ISBRA 2021); Shenzhen, China. 26–28 November 2021; pp. 424–435. [Google Scholar]
- 3.Lee I., Keum J., Nam H. DeepConv-DTI: Prediction of drug-target interactions via deep learning with convolution on protein sequences. PLoS Comput. Biol. 2019;15:e1007129. doi: 10.1371/journal.pcbi.1007129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Huang K., Xiao C., Glass L.M., Sun J. MolTrans: Molecular interaction transformer for drug–target interaction prediction. Bioinformatics. 2021;37:830–836. doi: 10.1093/bioinformatics/btaa880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wen M., Zhang Z., Niu S., Sha H., Yang R., Yun Y., Lu H. Deep-learning-based drug–target interaction prediction. J. Proteome Res. 2017;16:1401–1409. doi: 10.1021/acs.jproteome.6b00618. [DOI] [PubMed] [Google Scholar]
- 6.Luo Y., Zhao X., Zhou J., Yang J., Zhang Y., Kuang W., Peng J., Chen L., Zeng J. A network integration approach for drug-target interaction prediction and computational drug repositioning from heterogeneous information. Nat. Commun. 2017;8:573. doi: 10.1038/s41467-017-00680-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Li Y., Qiao G., Wang K., Wang G. Drug–target interaction predication via multi-channel graph neural networks. Briefings Bioinform. 2022;23:bbab346. doi: 10.1093/bib/bbab346. [DOI] [PubMed] [Google Scholar]
- 8.Yue Y., He S. DTI-HeNE: A novel method for drug-target interaction prediction based on heterogeneous network embedding. BMC Bioinform. 2021;22:418. doi: 10.1186/s12859-021-04327-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Öztürk H., Özgür A., Ozkirimli E. DeepDTA: Deep drug–target binding affinity prediction. Bioinformatics. 2018;34:i821–i829. doi: 10.1093/bioinformatics/bty593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nguyen T., Le H., Quinn T.P., Nguyen T., Le T.D., Venkatesh S. GraphDTA: Predicting drug–target binding affinity with graph neural networks. Bioinformatics. 2021;37:1140–1147. doi: 10.1093/bioinformatics/btaa921. [DOI] [PubMed] [Google Scholar]
- 11.Lin X., Li X., Lin X. A review on applications of computational methods in drug screening and design. Molecules. 2020;25:1375. doi: 10.3390/molecules25061375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Morris G.M., Huey R., Lindstrom W., Sanner M.F., Belew R.K., Goodsell D.S., Olson A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009;30:2785–2791. doi: 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kairys V., Baranauskiene L., Kazlauskiene M., Matulis D., Kazlauskas E. Binding affinity in drug design: Experimental and computational techniques. Expert Opin. Drug Discov. 2019;14:755–768. doi: 10.1080/17460441.2019.1623202. [DOI] [PubMed] [Google Scholar]
- 14.Yadav A.R., Mohite S.K. Homology Modeling and Generation of 3D-structure of Protein. Res. J. Pharm. Dos. Forms Technol. 2020;12:313–320. doi: 10.5958/0975-4377.2020.00052.X. [DOI] [Google Scholar]
- 15.Pahikkala T., Airola A., Pietilä S., Shakyawar S., Szwajda A., Tang J., Aittokallio T. Toward more realistic drug–target interaction predictions. Briefings Bioinform. 2015;16:325–337. doi: 10.1093/bib/bbu010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.He T., Heidemeyer M., Ban F., Cherkasov A., Ester M. SimBoost: A read-across approach for predicting drug–target binding affinities using gradient boosting machines. J. Cheminform. 2017;9:24. doi: 10.1186/s13321-017-0209-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chu Z., Huang F., Fu H., Quan Y., Zhou X., Liu S., Zhang W. Hierarchical graph representation learning for the prediction of drug-target binding affinity. Inf. Sci. 2022;613:507–523. doi: 10.1016/j.ins.2022.09.043. [DOI] [Google Scholar]
- 18.Wang S., Lin B., Zhang Y., Qiao S., Wang F., Wu W., Ren C. SGAEMDA: Predicting miRNA-Disease Associations Based on Stacked Graph Autoencoder. Cells. 2022;11:3984. doi: 10.3390/cells11243984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Öztürk H., Ozkirimli E., Özgür A. WideDTA: Prediction of drug-target binding affinity. arXiv. 2019 doi: 10.1093/bioinformatics/bty593.1902.04166 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chen L., Tan X., Wang D., Zhong F., Liu X., Yang T., Luo X., Chen K., Jiang H., Zheng M. TransformerCPI: Improving compound–protein interaction prediction by sequence-based deep learning with self-attention mechanism and label reversal experiments. Bioinformatics. 2020;36:4406–4414. doi: 10.1093/bioinformatics/btaa524. [DOI] [PubMed] [Google Scholar]
- 21.Yang Z., Zhong W., Zhao L., Chen C.Y.C. ML-DTI: Mutual learning mechanism for interpretable drug–target interaction prediction. J. Phys. Chem. Lett. 2021;12:4247–4261. doi: 10.1021/acs.jpclett.1c00867. [DOI] [PubMed] [Google Scholar]
- 22.Lin X. DeepGS: Deep representation learning of graphs and sequences for drug-target binding affinity prediction. arXiv. 20202003.13902 [Google Scholar]
- 23.Yang Z., Zhong W., Zhao L., Chen C.Y.C. Mgraphdta: Deep multiscale graph neural network for explainable drug–target binding affinity prediction. Chem. Sci. 2022;13:816–833. doi: 10.1039/D1SC05180F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jiang M., Li Z., Zhang S., Wang S., Wang X., Yuan Q., Wei Z. Drug–target affinity prediction using graph neural network and contact maps. RSC Adv. 2020;10:20701–20712. doi: 10.1039/D0RA02297G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jiang M., Wang S., Zhang S., Zhou W., Zhang Y., Li Z. Sequence-based drug-target affinity prediction using weighted graph neural networks. BMC Genom. 2022;23:449. doi: 10.1186/s12864-022-08648-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li G., Muller M., Thabet A., Ghanem B. Deepgcns: Can gcns go as deep as cnns?; Proceedings of the IEEE/CVF international conference on computer vision; Seoul, Republic of Korea. 27 October–2 November 2019; pp. 9267–9276. [Google Scholar]
- 27.Debnath A.K., Lopez de Compadre R.L., Debnath G., Shusterman A.J., Hansch C. Structure-activity relationship of mutagenic aromatic and heteroaromatic nitro compounds: Correlation with molecular orbital energies and hydrophobicity. J. Med. Chem. 1991;34:786–797. doi: 10.1021/jm00106a046. [DOI] [PubMed] [Google Scholar]
- 28.Paszke A., Gross S., Massa F., Lerer A., Bradbury J., Chanan G., Killeen T., Lin Z., Gimelshein N., Antiga L., et al. Pytorch: An imperative style, high-performance deep learning library; Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019); Vancouver, BC, Canada. 8–14 December 2019. [Google Scholar]
- 29.Fey M., Lenssen J.E. Fast graph representation learning with PyTorch Geometric. arXiv. 20191903.02428 [Google Scholar]
- 30.Davis M.I., Hunt J.P., Herrgard S., Ciceri P., Wodicka L.M., Pallares G., Hocker M., Treiber D.K., Zarrinkar P.P. Comprehensive analysis of kinase inhibitor selectivity. Nat. Biotechnol. 2011;29:1046–1051. doi: 10.1038/nbt.1990. [DOI] [PubMed] [Google Scholar]
- 31.Tang J., Szwajda A., Shakyawar S., Xu T., Hintsanen P., Wennerberg K., Aittokallio T. Making sense of large-scale kinase inhibitor bioactivity data sets: A comparative and integrative analysis. J. Chem. Inf. Model. 2014;54:735–743. doi: 10.1021/ci400709d. [DOI] [PubMed] [Google Scholar]
- 32.Nguyen T.M., Nguyen T., Le T.M., Tran T. Gefa: Early fusion approach in drug-target affinity prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021;19:718–728. doi: 10.1109/TCBB.2021.3094217. [DOI] [PubMed] [Google Scholar]
- 33.Wishart D.S., Feunang Y.D., Guo A.C., Lo E.J., Marcu A., Grant J.R., Sajed T., Johnson D., Li C., Sayeeda Z., et al. DrugBank 5.0: A major update to the DrugBank database for 2018. Nucleic Acids Res. 2018;46:D1074–D1082. doi: 10.1093/nar/gkx1037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gao W., Wang M., Wang L., Lu H., Wu S., Dai B., Ou Z., Zhang L., Heymach J.V., Gold K.A., et al. Selective antitumor activity of ibrutinib in EGFR-mutant non–small cell lung cancer cells. J. Natl. Cancer Inst. 2014;106:dju204. doi: 10.1093/jnci/dju204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang A., Yan X.E., Wu H., Wang W., Hu C., Chen C., Zhao Z., Zhao P., Li X., Wang L., et al. Ibrutinib targets mutant-EGFR kinase with a distinct binding conformation. Oncotarget. 2016;7:69760. doi: 10.18632/oncotarget.11951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Trott O., Olson A.J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010;31:455–461. doi: 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Weininger D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 1988;28:31–36. doi: 10.1021/ci00057a005. [DOI] [Google Scholar]
- 38.Landrum G. RDKit: A Software Suite for Cheminformatics, Computational Chemistry, and Predictive Modeling. [(accessed on 1 December 2022)]. Available online: http://www.rdkit.org/RDKit_Overview.pdf.
- 39.Jin W., Barzilay R., Jaakkola T. Junction tree variational autoencoder for molecular graph generation; Proceedings of the International Conference on Machine Learning; Stockholm, Sweden. 10–15 July 2018; pp. 2323–2332. [Google Scholar]
- 40.Dill K.A., MacCallum J.L. The protein-folding problem, 50 years on. Science. 2012;338:1042–1046. doi: 10.1126/science.1219021. [DOI] [PubMed] [Google Scholar]
- 41.Jumper J., Evans R., Pritzel A., Green T., Figurnov M., Ronneberger O., Tunyasuvunakool K., Bates R., Žídek A., Potapenko A., et al. Highly accurate protein structure prediction with AlphaFold. Nature. 2021;596:583–589. doi: 10.1038/s41586-021-03819-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Rives A., Meier J., Sercu T., Goyal S., Lin Z., Liu J., Guo D., Ott M., Zitnick C.L., Ma J., et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl. Acad. Sci. USA. 2021;118:e2016239118. doi: 10.1073/pnas.2016239118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Baek M., DiMaio F., Anishchenko I., Dauparas J., Ovchinnikov S., Lee G.R., Wang J., Cong Q., Kinch L.N., Schaeffer R.D., et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science. 2021;373:871–876. doi: 10.1126/science.abj8754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kipf T.N., Welling M. Semi-supervised classification with graph convolutional networks. arXiv. 20161609.02907 [Google Scholar]
- 45.Veličković P., Cucurull G., Casanova A., Romero A., Lio P., Bengio Y. Graph attention networks. arXiv. 20171710.10903 [Google Scholar]
- 46.Ryu S., Lim J., Hong S.H., Kim W.Y. Deeply learning molecular structure-property relationships using attention-and gate-augmented graph convolutional network. arXiv. 20181805.10988 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The source code and data of this study are available at https://github.com/songxuanmo/MSGNN-DTA (accessed on 1 May 2023).