Abstract
The objective of this study was to evaluate the effect of imputation of single nucleotide polymorphisms (SNP) on the estimation of genomic inbreeding coefficients. Imputed genotypes of 68,127 Italian Holstein dairy cows were analyzed. Cows were initially genotyped with two high density (HD) SNP panels, namely the Illumina Infinium BovineHD BeadChip (678 cows; 777,962 SNP) and the Genomic Profiler HD-150K (641 cows; 139,914 SNP), and four medium density (MD): GeneSeek Genomic Profiler 3 (10,679 cows; 26,151 SNP), GeneSeek Genomic Profiler 4 (33,394 cows; 30,113 SNP), GeneSeek MD (12,030 cows; 47,850 SNP) and the Labogena MD (10,705 cows; 41,911 SNP). After imputation, all cows had genomic information on 84,445 SNP. Seven genomic inbreeding estimators were tested: (i) four PLINK v1.9 estimators (F, Fhat1,2,3), (ii) two genomic relationship matrix (grm) estimators [VanRaden's 1st method, but with observed allele frequencies (Fgrm) and VanRaden's 3rd method that is allelic free and pedigree dependent (Fgrm2)], and (iii) a runs of homozygosity (roh) – based estimator (Froh). Genomic inbreeding coefficients of each SNP panel were compared with genomic inbreeding coefficients derived from the 84,445 imputation SNP. Coefficients of the HD SNP panels were consistent between genotyped-imputed SNP (Pearson correlations ~99%), while variability across SNP panels and estimators was observed in the MD SNP panels, with Labogena MD providing, on average, more consistent estimates. The robustness of Labogena MD, can be partly explained by the fact that 97.85% of the SNP of this panel is included in the 84,445 SNP selected by ANAFIBJ for routine genomic imputations, while this percentage for the other MD SNP panels varied between 55 and 60%. Runs of homozygosity was the most robust estimator. Genomic inbreeding estimates using imputation SNP are influenced by the SNP number of the SNP panel that are included in the imputed SNP, and performance of genomic inbreeding estimators depends on the imputation.
Keywords: inbreeding, single nucleotide polymorphism (SNP), imputation, genomics, dairy cattle
1. Introduction
The evolution in recent years of genotyping technologies enabled a continuous drop in costs and increased availability in the market of various single nucleotide polymorphism (SNP) microarrays (hereafter denoted as SNP panels) for livestock species diverse in quantity (number of SNP) and quality (e.g., SNP targeting specific genes). This promoted advanced genomic tools in animal breeding, but also led many breeding companies to genotype, in time, different groups of animals with diverse SNP panels. Moreover, the combination of overlapping SNP among panels and imputation pipelines allows to further reduce costs. Nowadays, it is a common practice to genotype few core animals with high density (HD) SNP panels (or whole genome sequencing), genotype a high number of animals with low density or medium density (LD and MD, respectively) SNP panels and to impute the LD/MD to HD genotypes, hence ending up with a common number of imputed genotypes for all genotyped animals (1, 2). Very analogous is the imputation of low coverage sequencing data to high coverage (3). The imputation SNP data can be used for genomic predictions, genome-wide association analyses, genetic diversity studies within and across populations, etc. Moreover, imputation SNP data can be used for estimating genetic relationships among animals and inbreeding coefficients (termed as genomic inbreeding), that were traditionally estimated via pedigree data. For the latter, there are various factors that can influence genomic inbreeding coefficients, such as methodology (e.g., summing homozygosity over individual SNP vs. summing homozygous blocks), associated parameters within each estimator (e.g., parameters to define a homozygous block), SNP quality control, imputation method, etc. (4–6).
The imputation procedures in livestock breeding programs increased the interest to assess the effect of SNP panels in estimating inbreeding coefficients. The objective of this study was to evaluate the effect of imputation of SNP on the estimation of genomic inbreeding coefficients. Thus, we extended a previous work on genomic inbreeding with imputed SNP (6), aiming to quantify differences among SNP panels that cows were genotyped with (i.e., MD vs. HD). Two HD (Illumina Infinium BovineHD BeadChip and Genomic Profiler HD-150K) and four MD (GeneSeek Genomic Profiler 3, GeneSeek Genomic Profiler 4, GeneSeek Genomic MD and Labogena MD) SNP panels were analyzed. Genomic inbreeding coefficients were estimated with seven commonly used estimators. Comparisons between genotyped – imputation inbreeding coefficients were made for each SNP panel and estimator.
2. Materials and methods
2.1. Animals and genotypes
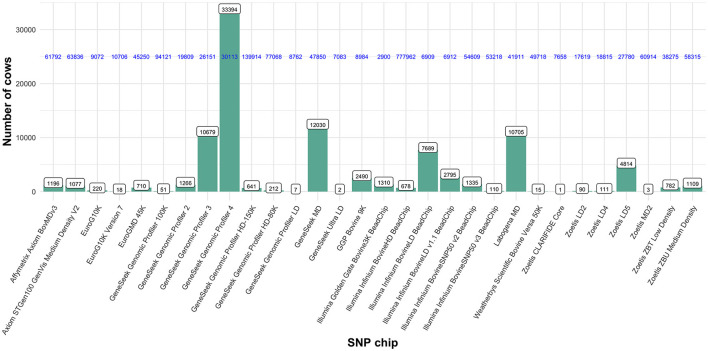
The available dataset contained 95,540 Italian Holstein dairy cows, all registered to the official herd book of the Italian National Association of Holstein, Brown and Jersey Breeders (ANAFIBJ). Cows were born between 1998 and 2020 and genotyped with 30 different SNP panels of varying densities (from 3k to 777k; Figure 1). From those, we selected 68,127 Italian Holstein dairy cows genotyped with two high density (HD) SNP panels, namely the Illumina Infinium BovineHD BeadChip (678 cows; 777,962 SNP) and the Genomic Profiler HD-150K (641 cows; 139,914 SNP), and four medium density (MD) SNP panels: GeneSeek Genomic Profiler 3 (10,679 cows; 26,151 SNP), GeneSeek Genomic Profiler 4 (33,394 cows; 30,113 SNP), GeneSeek MD (12,030 cows; 47,850 SNP) and the Labogena MD (10,705 cows; 41,911 SNP). A dataset of 84,445 common SNP (on the 29 autosomes) was created. Those SNP are pre-selected and used in the routine genomic evaluations of ANAFIBJ. Cows genotyped with the four MD SNP panels were imputed, while those with the two HD SNP panels were degraded to the 84,445 common SNP. The imputation was carried out in an improved version of the PedImpute software (7) for faster computations. After imputation, SNP quality control included: (i) call rate < 95%, (ii) parent-offspring SNP mismatch > 0.01, (iii) minor allele and genotype (< 0.02 and < 0.001, respectively) frequencies and (iv) extreme deviation from Hardy–Weinberg equilibrium (P < 0.005).
Figure 1.
Cows and genotype panels available from which were selected two high density SNP panels (Illumina Infinium BovineHD BeadChip and GeneSeek Genomic Profiler HD-150K) and four medium density SNP panels (GeneSeek Genomic Profiler 3, GeneSeekGenomic Profiler 4, GeneSeek MD and Labogena MD). Numbers on the top of the bars show the number of cows genotyped within each SNP panel. Horizontal numbers in blue show the total number of SNP included in each SNP panel.
2.2. Inbreeding coefficients
In scientific literature, inbreeding coefficient is abbreviated either as F or f. To be consistent with software abbreviation, we used F to denote the first genomic inbreeding estimator of PLINK v.1.9 software [(8); http://pngu.mgh.harvard.edu/purcell/plink/]. We adopted “f ” to denote inbreeding coefficient and fSNP for referring to whole genome SNP based inbreeding coefficients. Seven genomic inbreeding estimators were tested, and genomic inbreeding coefficients were calculated for the 68,127 cows for each estimator:
Four estimators (F, Fhat1,2,3) implemented in PLINK v1.9 [(8); http://pngu.mgh.harvard.edu/purcell/plink/]. F (flag –het in PLINK v1.9) was proposed by Li and Horvitz (1953) and counts the proportion of homozygous SNP. Fhat1 − 3 were primarily implemented in the GCTA software (9, 10) and can be obtained simultaneously with the flag –ibc in PLINK v1.9. More precisely, Fhat1 is estimated as , where X is the genotype matrix based on the number of copies of the defined reference allele, with p and q being the frequencies of the reference and alternative alleles, respectively and m is the number of SNP. Fhat2 measures the excess of homozygosity () and differs from F in the sense that Fhat2 is a sum of ratios, while F is a ratio of sums (11). Fhat3 is estimated as and reflects the inbreeding definition of Wright stated as correlation between uniting gametes (12, 13).
Two genomic relationship matrix (grm) – based inbreeding estimators (based on VanRaden's 1st and 3rd methods). The first method (Fgrm) (14– 16) was estimated as follows: grm = , where Z = X – 2(qm – 0.5); where Fgrm = diag(grm) – 1. To alleviate the problem of using observed allele frequencies in Fgrm, a simplified version of VanRaden's 3rd proposed method was used Fgrm2, where we regressed the diagonal of XX′ on pedigree inbreeding coefficients (Fped) to get the mean and the slope and then to obtain , where mean and slope are the estimates of the previous regression. Both estimators were determined without considering a base population or AI sire information to calibrate the diagonal elements of XX′, as, for e.g., reported by (17),
A roh-based estimator (Froh), where Froh expresses the sum of rohs identified in an individual to the total genome length. We used the consecutive runs method in the R software (v. 3.6.3) package detectRUNS v. 0.9.5 (18–20). To define a roh we set the minimum length of roh to 1 Mbp and a minimum of 15 SNPs/ROH. Moreover, we allowed one heterozygous SNP within a roh to account for possible genotyping errors. In a previous study (6), we focused on the differences among genomic inbreeding estimators. In that study, two more genomic inbreeding estimators were included that were simplifications of the F and Froh estimators, namely FPH and FROH2, respectively, as reported in (6). Due to their high correlations, we decided to exclude those estimators from the current study. Moreover, the grm-based estimator (FGRM05; with allele frequencies set to 0.5) described in (6) was highly correlated with F and was not considered in the current analysis.
In addition, pedigree based inbreeding coefficients (Fped) were also estimated in the pedigree R package (18, 21). This estimation does not consider genetic groups and assigns the value of 0 for missing ancestors. Pedigree consisted of 393,607 cattle with 10 generations depth with a pedigree completeness index (22), estimated in R package optiSel (23), of 0.99.
Pairwise comparisons were made between genotyped-imputation fSNP for each SNP panel and genomic inbreeding estimator. In each panel, only those genotyped SNP included in the preselected imputation set of 84,445 SNP were considered (because the rest of the SNP were automatically omitted from the imputation pipeline of ANAFIBJ). This means that the genotyped SNP per panel were 79,900 (Illumina Infinium BovineHD BeadChip), 77,085 (Genomic Profiler HD-150K), 13,870 (GeneSeek Genomic Profiler 3), 16,862 (GeneSeek Genomic Profiler 4), 27,331 (GeneSeek MD) and 40,218 (Labogena MD) (Table 1). Average SNP distance per chromosome for each panel and the imputation data was estimated. Results were also summarized over genomic inbreeding estimators across the different SNP panels. Pearson and Spearman correlations were considered for estimating the consistency of inbreeding coefficients between genotyped – imputation SNP for each SNP panel. The imputation data of 84,445 SNP was a mixture of genotyped and imputed SNP, hence the term imputation SNP was adopted herein rather imputed SNP.
Table 1.
Number of single nucleotide polymorphisms per chromosome in the imputed dataset and each genotype panel.
| Chr | Imputation | Illumina Infinium BovineHD BeadChip | GeneSeek Genomic Profiler HD-150K | GeneSeek Genomic Profiler 3 | GeneSeek Genomic Profiler 4 | GeneSeek MD | Labogena MD |
|---|---|---|---|---|---|---|---|
| 1 | 5,255 | 4,980 | 4,750 | 794 | 981 | 1,673 | 2,628 |
| 2 | 4,398 | 4,150 | 4,019 | 627 | 770 | 1,506 | 2,142 |
| 3 | 4,120 | 3,868 | 3,736 | 661 | 833 | 1,408 | 2,040 |
| 4 | 3,938 | 3,748 | 3,561 | 523 | 643 | 1,238 | 1,949 |
| 5 | 3,835 | 3,642 | 3,506 | 820 | 976 | 1,298 | 1,674 |
| 6 | 4,004 | 3,792 | 3,649 | 590 | 759 | 1,227 | 1,960 |
| 7 | 3,617 | 3,447 | 3,291 | 569 | 673 | 1,102 | 1,711 |
| 8 | 3,794 | 3,575 | 3,428 | 538 | 670 | 1,179 | 1,853 |
| 9 | 3,431 | 3,261 | 3,140 | 526 | 670 | 1,189 | 1,649 |
| 10 | 3,436 | 3,250 | 3,155 | 479 | 582 | 1,111 | 1,685 |
| 11 | 3,642 | 3,412 | 3,304 | 545 | 667 | 1,129 | 1,724 |
| 12 | 2,815 | 2,660 | 2,569 | 441 | 512 | 882 | 1,306 |
| 13 | 2,827 | 2,680 | 2,585 | 437 | 536 | 946 | 1,382 |
| 14 | 2,887 | 2,760 | 2,665 | 497 | 604 | 924 | 1,405 |
| 15 | 2,880 | 2,709 | 2,627 | 507 | 604 | 889 | 1,369 |
| 16 | 2,770 | 2,609 | 2,515 | 443 | 543 | 904 | 1,320 |
| 17 | 2,553 | 2,416 | 2,350 | 370 | 449 | 792 | 1,223 |
| 18 | 2,352 | 2,226 | 2,171 | 536 | 642 | 784 | 1,012 |
| 19 | 2,340 | 2,216 | 2,138 | 539 | 641 | 812 | 1,071 |
| 20 | 2,631 | 2,482 | 2,357 | 470 | 598 | 924 | 1,323 |
| 21 | 2,383 | 2,234 | 2,151 | 440 | 534 | 797 | 1,111 |
| 22 | 2,137 | 2,022 | 1,964 | 311 | 386 | 682 | 997 |
| 23 | 1,922 | 1,825 | 1,787 | 410 | 495 | 653 | 881 |
| 24 | 2,124 | 2,031 | 1,937 | 331 | 394 | 659 | 953 |
| 25 | 1,608 | 1,518 | 1,500 | 312 | 374 | 518 | 757 |
| 26 | 1,800 | 1,704 | 1,668 | 301 | 356 | 566 | 827 |
| 27 | 1,605 | 1,529 | 1,499 | 257 | 296 | 492 | 757 |
| 28 | 1,618 | 1,539 | 1,478 | 278 | 315 | 516 | 721 |
| 29 | 1,723 | 1,615 | 1,585 | 318 | 359 | 531 | 788 |
| Total | 84,445 | 79,900 | 77,085 | 13,870 | 16,862 | 27,331 | 40,218 |
| Percentagea | / | 94.62 | 91.28 | 16.42 | 19.97 | 32.37 | 47.63 |
Percentage of SNP of the SNP panel included in the imputation data.
3. Results
3.1. Similarities among the SNP panels and the imputed SNP data
Table 1 and Supplementary Figure 1 summarize the number and density, respectively, of SNP per chromosome for each SNP panel and the imputation data. The number of SNP included in the preselected 84,445 imputation SNP varied for each SNP panel from 79,900 (Illumina Infinium BovineHD BeadChip) to 13,870 (GeneSeek Genomic Profiler 3), that is corresponding to 94.6% and 16.4%, respectively.
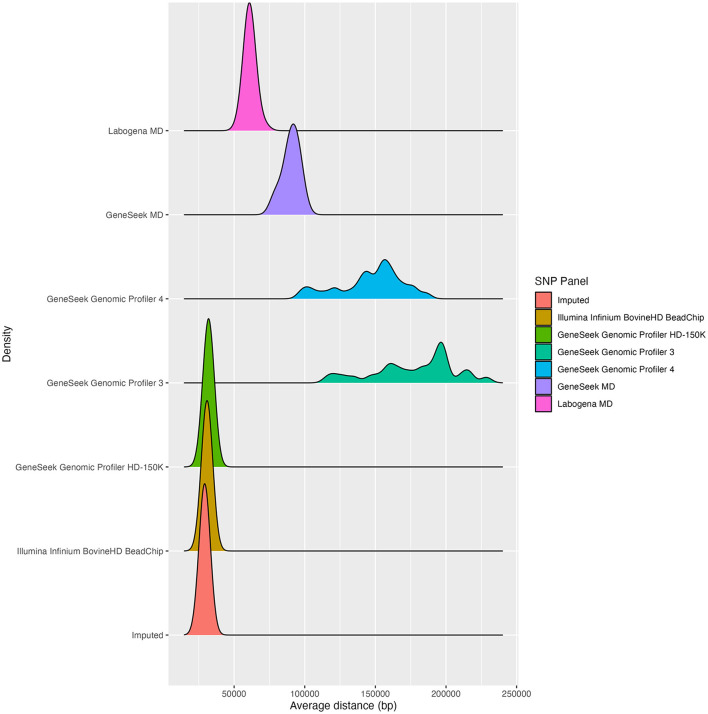
The average SNP distance over the 29 autosomes (Figure 2) was 29,138 bp for the imputation set, 30,791 bp for the Illumina Infinium BovineHD BeadChip and 31,867 bp for the Genomic Profiler HD-150K. Higher average SNP distances were observed for Labogena MD (61,119 bp), GeneSeek MD (90,200 bp), and the GeneSeek Genomic Profiler 4 and 3 (146,433 and 177,375 bp, respectively). The SNP distance distributions over the 29 autosomes were comparable for the two HD SNP panels and the imputation set. Regarding MD SNP panels, the Labogena MD was more closely to the HD SNP panels, followed by GeneSeek MD, while the GeneSeek Genomic Profiler 4 and GeneSeek Genomic Profiler 3 clearly diverged from the rest, with both SNP panels consisting of a mixture of distributions.
Figure 2.
SNP distance distribution over the 29 autosomes for each of the SNP panels.
3.2. Correlations of inbreeding coefficients between genotyped and imputation SNP
Descriptive statistics of the pedigree and SNP inbreeding coefficients are reported in Table 2. The average Fped was 0.05 for the cows genotyped with Illumina Infinium BovineHD BeadChip, 0.07 for GeneSeek Genomic Profiler 3, 4 and Labogena MD and 0.08 for Genomic Profiler HD-150K and GeneSeek MD. Average fSNP was close to 0 (for both genotyped and imputed SNP) for the genomic estimators, except for Fgrm2 and Froh. Specifically, average fSNP across all SNP panels for Fgrm2 varied between−0.92 and−0.95 with inbreeding coefficients being always negative. The highest mean fSNP across all SNP panels was observed for Froh (0.11 to 0.16). Moreover, although the mean fSNP was, in general, equal between genotyped – imputed SNP for all estimators, the space of the inbreeding coefficients differed when estimated using genotyped vs. imputation SNP. This was observed for all estimators and SNP panels. The most consistent results were found for the two HD SNP panels when fSNP was estimated with Froh. For e.g., F in the group of cows genotyped with the GeneSeek Genomic Profiler 3 varied between −0.35 to 0.26 for the genotyped and−0.16 to 0.82 for the imputation SNP data. Similarly, for the same group of cows, Froh ranged between 0.00–0.37 and 0.02–0.60 for the genotyped and imputation SNP, respectively.
Table 2.
Mean, standard deviation (superscript) and range (subscript) of the pedigree and the genomic inbreeding coefficients for each genotyping panel.
| Estimator | Genomic information | Illumina Infinium BovineHD BeadChip | GeneSeek Genomic Profiler HD-150K | GeneSeek Genomic Profiler 3 | GeneSeek Genomic Profiler 4 | GeneSeek MD | Labogena MD |
|---|---|---|---|---|---|---|---|
| Pedigree | |||||||
| Fped | |||||||
| PLINK a | |||||||
| F | Genotyped | ||||||
| Imputation | |||||||
| Fhat1 | Genotyped | ||||||
| Imputation | |||||||
| Fhat2 | Genotyped | ||||||
| Imputation | |||||||
| Fhat3 | Genotyped | ||||||
| Imputation | |||||||
| grm b | |||||||
| Fgrm | Genotyped | ||||||
| Imputation | |||||||
| Fgrm2 | Genotyped | ||||||
| Imputation | |||||||
| roh c | |||||||
| Froh | Genotyped | ||||||
| Imputation | |||||||
Genomic inbreeding estimates based on PLINKv1.9 software;
Genomic inbreeding estimates based on genomic relationship matrices (grm);
Genomic inbreeding estimates based on runs of homozygosity (roh).
Negative fSNP were found for all estimators, except Froh. Although with pedigree this cannot happen, with SNP data this is possible. Theoretically, inbreeding coefficients below zero reflect potential gain of genetic variability, given an unselected base population consisted of unrelated individuals. The interpretation and the theoretical background of inbreeding coefficients has been elaborated in previous studies (5, 6).
Pairwise comparisons between genotyped vs. imputation fSNP for each SNP panel were investigated (Supplementary Figure 2); Pearson correlations are reported, except if stated otherwise. For the two HD SNP panels correlations between genotyped-imputation fSNP were close to one (≥ 0.98) for all genomic inbreeding estimators (Supplementary Figures 2A, B). For the four MD SNP panels, correlations ranged between 0.65 (GeneSeek Genomic Profiler 3; Supplementary Figure 2C) and 0.85 (GeneSeek MD and Labogena MD; Supplementary Figures 2E, F). However, for MD SNP panels correlations between genotyped-imputation fSNP varied across estimators. More precisely, for the three GeneSeek SNP panels, Fhat2 had the lowest correlations, ranging between 0.51 (GeneSeek Genomic Profiler 4; Supplementary Figure 2D) to 0.68 (GeneSeek MD; Supplementary Figure 2E). For Labogena MD (Supplementary Figure 2F), Fhat3 had the lowest correlation (0.77) between genotyped-imputation fSNP. Moreover, for GeneSeek Genomic Profiler 3 the estimators F, Fhat3 and Fgrm2 had correlations ~0.60, Fhat1 and Fgrm values ranged between 0.68-0.75 with Froh being more consistent (~0.79) compared to the rest of the estimators. For GeneSeek Genomic Profiler 4, the lowest correlation (0.55) was observed for Fhat1, followed by Fhat3 and Fgrm (~0.62 for both), F (0.68), Froh (0.89) and Fgrm2 (0.98). For GeneSeek MD (Supplementary Figure 2E), the estimators F, Fgrm and Fgrm2 had correlations ~0.80 between genotyped-imputation fSNP, while Fhat1, Fhat3 and Froh had values close to one (~0.97). In this case, however, it should be noted that an extreme and influential inbreeding coefficient was observed for Fhat1 and Fhat3 that impacts the values of Pearson correlations. In the case of Labogena MD (Supplementary Figure 2F), all estimators except Fhat3 had correlations of between 0.82-0.89 with the highest (0.98) observed for Froh; correlations between genotyped – imputed fSNP for Fhat3 were at 0.77. Moreover, for Labogena MD the inbreeding coefficients of the imputed SNP had always greater variability and higher values than the genotyped SNP, across all estimators (Table 2). This, in general, was also observed for the three MD GeneSeek estimators. However, for the three MD GeneSeek panels there were cases, especially for Fhat1−3 were fSNP estimated from genotyped SNP showed greater variability.
To further investigate the differences between genotyped vs. imputation fSNP, pairwise comparison with Fped were made for all SNP panels and estimators (Supplementary Figure 3). We assume that the most accurate inbreeding coefficients should have higher correlation to Fped. In general, the genotyped data had higher correlations to Fped compared to the imputation set. Opposite results were found for Fhat1,2 for GeneSeek Genomic Profiler 4, where fSNP estimated from the imputation SNP were higher correlated to Fped compared to fSNP estimated using the only the genotyped SNP. No differences were found for the two HD SNP panels.
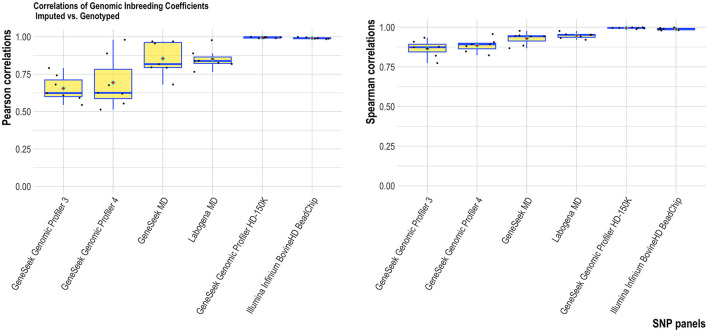
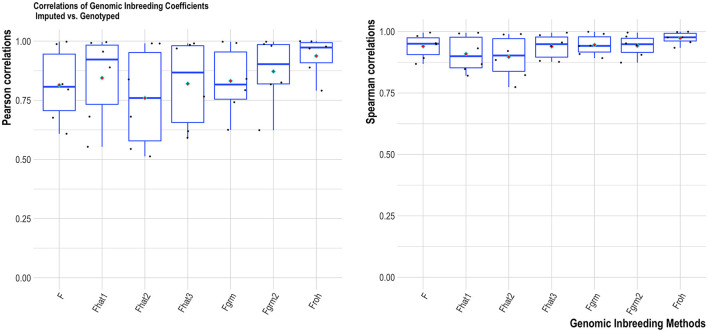
Overall, the two HD SNP panels had consistent results between genotyped-imputation fSNP (correlations close to one). For the four MD SNP panels, higher correlations were found for the Labogena MD (summarized over all estimators), followed by the GeneSeek MD, GeneSeek Genomic Profiler 4 and GeneSeek Genomic Profiler 3 (Figure 3). Froh provided the most robust results across all genomic inbreeding estimators tested (Figure 4). Spearman correlations were always higher compared to Pearson correlations (with the former being able to capture monotonic patterns).
Figure 3.
Average Pearson (left) and Spearman (right) correlations of the genomic inbreeding estimators tested for each SNP panel. Horizontal bars within each boxplot represent the median, and red rhombus the mean.
Figure 4.
Average Pearson (left) and Spearman (right) correlations of the tested SNP panels for each genomic inbreeding estimator. Horizontal bars within each boxplot represent the median, and red rhombus the mean.
4. Discussion
Inbreeding coefficients are traditionally estimated from pedigree data and used to characterize diversity, evolution, and population structure. The study of inbreeding can be applied to individual animals, herd, consortium (e.g., dairy chains or semen companies) and population levels (24–26). It is also used in livestock breeding and conservation programs to organize matings and manage the level of relationship among individuals of a given population. Whole genome SNP data allowed the estimation of the realized level of homozygosity of an individual, compared to the expectations derived from pedigree information. However, it is important to keep in mind that homozygosity might be caused by either common ancestors (homozygosity by descent; autozygosity) or by other evolutionary processes. In the latter case, homozygosity represents an identical by state situation termed allozygosity. The two forms of homozygosity practically are not straightforward to be distinguished.
The rationale of the present work was driven by applied methods of estimating genomic inbreeding coefficients with whole genome imputed SNP data, during routine genomic evaluations in dairy cattle breeding programs. Our work is not critical on the SNP panels evaluated herein per se, rather on the way they are applied in breeding programs. The rapid increase in number and quality of SNP panels in the market, the drastic drop for genotyping and novel imputation methods resulted in genotyping subgroups within breeding populations. For instance, in the ANAFIBJ genomic breeding program to date, 43 SNP panels have been utilized to genotype different groups of cattle. This situation is representative of other genomic breeding programs mainly in cattle (27, 28), broilers (29) and swine (30, 31).
In the dataset analyzed in the current study, 10,679 cows were genotyped with GeneSeek Genomic Profiler 3 (containing 26,151 SNP), and 33,394 cows with GeneSeek Genomic Profiler 4 (containing 30,113 SNP). However, for those cows only 13,870 and 16,862 SNP were used in the imputation data (representing 16.4 and 20% of the imputation set, respectively). Less SNPs of these chips were selected because they have a lower overlap with other DNA chips. This means, that (i) ~50% of the SNP of those panels are omitted and (ii) cows genotyped with those SNP panels have ~80–85% of their genotypes imputed. For some of those cows discrepancies were found between observed vs. imputed SNP genomic inbreeding coefficients, with the question being which estimates represent the real state. Moreover, results varied among estimators.
To address this question we used as a baseline the Fped, assuming that a higher correlation with Fped is favorable. Our results showed that, in general, the genotyped fSNP were strongly correlated to the Fped for all estimators (Supplementary Figure 3) in the MD SNP panels, compared to fSNP estimated with SNP from the imputation set. However, variability was observed among estimators on the the actual difference between genotyped – imputation fSNP. For e.g., for the GeneSeek Profilers 3 Pearson correlations between Fped and each of the genomic estimators were 0.56,−0.12, 0.45, 0.36, 0.04, 0.58 and 0.61, while with the imputation SNP correlations were of 0.38,−0.25, 0.45, 0.16, 0.03, 0.38 and 0.48 for F, Fhat1, Fhat2, Fhat3, Fgrm, Fgrm2 and Froh, respectively. Moreover, imputation increased the correlations between the pairwise comparison of the genomic inbreeding estimators. For instance, in the GeneSeek Genomic Profilers 3 the correlations of Froh with the other estimators were increased from 0.89 to 0.95, 0.02 to 0.11, 0.61 to 0.69, 0.69 to 0.79, 0.29 to 0.60 and from 0.90 to 0.96 (for F, Fhat1, Fhat2, Fhat3, Fgrm and Fgrm2, respectively). Furthermore, there where cows with inbreeding coefficients close to 0 with the genotyped SNP, and high inbreeding coefficients with the imputed SNP. This was observed even with Froh that was the most robust estimator. For instance, there was a group of cows genotyped with the GeneSeek Genomic Profiler 3 with inbreeding coefficients (based on genotyped SNP) ranging between ~0-0.15 while with imputation SNP the inbreeding coefficients were estimated between ~0.4 and 0.6 (Supplementary Figure 2C). Similar observation was made for cows genotyped with the GeneSeek Genomic Profiler 4 (Supplementary Figure 2D), where for few cows genotyped fSNP ranged between 0 and 0.15 while the imputation fSNP for those cows was >0.3. We could hypothesize that fSNP estimated from ~15k SNP (as was the case of GeneSeek Genomic Profilers 3 and 4 in our study) might be biased. However, it must be also very unlikely that cows could have 40–60% of their genome in homozygous state, as was found with fSNP estimated with imputation SNP. It is known that for a successful imputation three important components are (i) the distribution along the genome and the number of SNP in the LD/MD panels, (ii) the linkage disequilibrium between SNP in the MD and SNP in the HD (32–34) and (iii) the presence of genotypes from the parents and/or grandparents. For the GeneSeek Genomic Profilers 3 and 4, perhaps those could be hypothesized as limited parameters in our study.
5. Future perspectives
Passing through the second decade of applied genomic breeding programs, it is of interest that we still lack criteria to select a simple and optimal genomic inbreeding measure. In a recent work we showed that discrepancies among genomic inbreeding estimators exist (6) and some genomic inbreeding estimators can provide coefficients out of the range [-1, 1]; where negative coefficients reflect proportional gain of variability compared to a base unselected population of unrelated animals (5, 6, 35). Moreover, various parameters have to be considered when comparing genomic inbreeding estimators, such as SNP quality control, imputation methods, distinguishing between allozygosity – autozygosity, including SNP on the X-chromosome (28) to account for differences between males and females and better scale genomic inbreeding coefficients to pedigree inbreeding coefficients, to name some.
In the present study, we emphasized on the effect that imputation might have on the estimation of genomic inbreeding coefficients, relative to the density of SNP panels. Another important aspect of imputation relates to the relationship between animals genotyped with LD and MD SNP panels (to be imputed) and the animals that consist of the reference panel, and which were genotyped in HD. In a preliminary analysis, we have evidenced that indeed the correlation between genotyped – imputation fSNP drastically degrades for the cows that have none of the parents and/or the maternal grand sire genotyped in HD and belonging in the reference set of the imputation pipeline (data not shown). This degrade in accuracy varies across the SNP panels and has been observed even with cows genotyped in HD, albeit to a much lower degree compared to cows genotyped in MD. This needs further investigation and quantification.
6. Conclusion
We investigated the effect of imputation, regarding the density of SNP panels used to genotype cows, in a routine dairy cattle genomic breeding program on SNP inbreeding coefficients. Correlations between genotyped vs. imputation SNP inbreeding coefficients were high and consistent for the HD SNP panels. Accuracies were degraded for the four MD density SNP panels. This drop in accuracy was linked to the number of SNP of the SNP panel included in the imputation SNP set and the average distance of SNP on the genome. Assuming that high correlation with pedigree inbreeding coefficients reflects more realistic values, genomic inbreeding coefficients estimated from imputation SNP were biased for the cows genotyped with MD SNP panels, because they were less correlated to pedigree inbreeding coefficients compared to inbreeding coefficients estimated only from genotyped SNP.
We wish to state that our analysis is not critical on the quality of commercial SNP panels per se, but rather it highlights the effect that the imputation pipeline and the overall genotyping management might have on the genomic inbreeding coefficients. Our results indicate that SNP panels that contain more informative SNP for the population under study can have more genotyped SNP that remain in the imputation data and thereby provide with more robust results on the genomic inbreeding coefficients of the cows. Cows that were genotyped with MD SNP panels that had few SNP included in the final imputed SNP data were more likely to have biased genomic inbreeding estimates for some groups of cows. In such a concept, Froh can be considered as a more robust estimator, reflecting identity-by-descent, compared to estimators summing homozygosity over individual SNP, measuring identity-by-state.
Data availability statement
The data analyzed in this study is subject to the following licenses/restrictions: Data supporting this paper were obtained from ANAFIBJ. The genotype data are available only upon agreement with ANAFIBJ. Requests to access these datasets should be directed to J-TK, jtkaam@anafi.it.
Ethics statement
Ethical review and approval was not required for the animal study because no animals were used in this study, and ethical approval for the use of animals was thus deemed unnecessary.
Author contributions
CD, J-TK, CC-G, and MA conceived the idea and formulated the objectives of this study. J-TK helped in data preparation. CD conducted the analysis and wrote the first draft of the paper. ASu and ASa supervised the project. ASu, CC-G, ASa, MM, RF, and MC critically reviewed the text. All authors read and approved the final manuscript.
Funding Statement
This study was supported by the Latteco2 project, sottomisura 10.2 of the PSRNBiodiversity 2020–2023 (MIPAAF. D.M. no. 465907 del 24/09/2021, project unique code J12C21004080005). This research benefits from the High Performance Computing facility of the University of Parma, Italy (HPC.unipr.it).
Conflict of interest
The author MC declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fvets.2023.1142476/full#supplementary-material
SNP density per chromosome for the (A) imputed, (B) Illumina Infinium BovineHD BeadChip, (C) GeneSeek Genomic Profiler HD-150K, (D) GeneSeek Genomic Profiler 3, (E) GeneSeek Genomic Profiler 4, (F) GeneSeek MD, and (G) Labogena MD.
Comparison between genotyped and imputed SNP inbreeding coefficients for (A) Illumina Infinium BovineHD BeadChip, (B) GeneSeek GenomicProfiler HD-150K, (C) GeneSeek Genomic Profiler 3, (D) GeneSeek Genomic Profiler 4, (E) GeneSeek MD, and (F) Labogena MD.
Pairwise Pearson correlations (above diagonal) between each pair of the pedigree and the seven genomic inbreeding estimators analyzed for (A) Illumina Infinium BovineHD BeadChip, (B) GeneSeek Genomic Profiler HD-150K, (C) GeneSeek Genomic Profiler 3, (D) GeneSeek Genomic Profiler 4, (E) GeneSeek MD, and (F) Labogena MD. In gray color the overall correlation, in red correlations estimated from the genotyped SNP in each panel and in green correlations estimated from the imputation SNP.
References
- 1.Whalen A, Gorjanc G, Ros-Freixedes R, Hickey JM. Assessment of the performance of hidden Markov models for imputation in animal breeding. Genetics Selection Evol. (2018) 50:44. 10.1186/s12711-018-0416-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Whalen A, Gorjanc G, Hickey JM. Family-specific genotype arrays increase the accuracy of pedigree-based imputation at very low marker densities. Genetics Selection Evol. (2019) 51:33. 10.1186/s12711-019-0478-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Snelling WM, Hoff JL Li JH, Kuehn LA, Keel BN, Lindholm-Perry AK, Pickrell JK. Assessment of imputation from low-pass sequencing to predict merit of beef steers. Genes. (2020) 11:1312. 10.3390/genes11111312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Meyermans R, Gorssen W, Buys N, Janssens S. How to study runs of homozygosity using PLINK? A guide for analyzing medium density SNP data in livestock and pet species. BMC Genomics. (2020) 21:94. 10.1186/s12864-020-6463-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Villanueva B, Fernández A, Saura M, Caballero A, Fernández J, Morales-González E, et al. The value of genomic relationship matrices to estimate levels of inbreeding. Genetics Selection Evol. (2021) 53:42. 10.1186/s12711-021-00635-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dadousis C, Ablondi M, Cipolat-Gotet C, van Kaam J-T, Marusi M, Cassandro M, et al. Genomic inbreeding coefficients using imputed genotypes: Assessing different estimators in Holstein-Friesian dairy cows. J. Dairy Sci. (2022) 15:5926–45. 10.3168/jds.2021-21125 [DOI] [PubMed] [Google Scholar]
- 7.Nicolazzi EL, Biffani S, Jansen G. Short communication: Imputing genotypes using PedImpute fast algorithm combining pedigree and population information. J Dairy Sci. (2013) 96:2649–53. 10.3168/jds.2012-6062 [DOI] [PubMed] [Google Scholar]
- 8.Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. (2007) 81:559–75. 10.1086/519795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Li CC, Horvitz DG. Some methods of estimating the inbreeding coefficient. Am J Hum Genet. (1953) 5:107–17. [PMC free article] [PubMed] [Google Scholar]
- 10.Yang J, Lee SH, Goddard ME, Visscher PM, GCTA. A tool for genome-wide complex trait analysis. Am J Hum Genet. (2011) 88:76–82. 10.1016/j.ajhg.2010.11.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gazal S, Sahbatou M, Perdry H, Letort S, Génin E, Leutenegger A-L. Inbreeding coefficient estimation with dense SNP data: comparison of strategies and application to HapMap III. Hum Hered. (2014) 77:49–62. 10.1159/000358224 [DOI] [PubMed] [Google Scholar]
- 12.Wright S. Systems of mating. Genetics. (1921) 6:111–78. 10.1093/genetics/6.2.111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, et al. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. (2010) 42:565–9. 10.1038/ng.608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Leutenegger A-L, Prum B, Génin E, Verny C, Lemainque A, Clerget-Darpoux F, et al. Estimation of the inbreeding coefficient through use of genomic data. Am J Hum Genet. (2003) 73:516–23. 10.1086/378207 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Amin N, Duijn CM. van, Aulchenko YS. A genomic background based method for association analysis in related individuals. PLoS ONE. (2007) 2:e1274. 10.1371/journal.pone.0001274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.VanRaden PM. Efficient methods to compute genomic predictions. J Dairy Sci. (2008) 91:4414–23. 10.3168/jds.2007-0980 [DOI] [PubMed] [Google Scholar]
- 17.Rolf MM, Taylor JF, Schnabel RD, McKay SD, McClure MC, Northcutt SL, et al. Impact of reduced marker set estimation of genomic relationship matrices on genomic selection for feed efficiency in Angus cattle. BMC Genet. (2010) 11:24. 10.1186/1471-2156-11-24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.R Core Team . R: A Language and Environment for Statistical Computing, Vienna, Austria. (2021). [Google Scholar]
- 19.Marras G, Gaspa G, Sorbolini S, Dimauro C, Ajmone-Marsan P, Valentini A, et al. Analysis of runs of homozygosity and their relationship with inbreeding in five cattle breeds farmed in Italy. Anim Genet. (2015) 46:110–21. 10.1111/age.12259 [DOI] [PubMed] [Google Scholar]
- 20.Biscarini F, Cozzi P, Gaspa G, Marras G. detectRUNS: An R Package to Detect Runs of Homozygosity Heterozygosity in Diploid Genomes. R package version 0.9.6. (2019). Available online at: https://CRAN.R-project.org/package=detectRUNS
- 21.Coster A. Pedigree: Pedigree functions. R Package Version 1.4. (2013). Available online at: https://CRAN.R-project.org/package=pedigree
- 22.MacCluer JW, Boyce AJ, Dyke B, Weitkamp LR, Pfenning DW, Parsons CJ. Inbreeding and pedigree structure in Standardbred horses. J. Heredity. (1983) 74:394–9. 10.1093/oxfordjournals.jhered.a109824 [DOI] [Google Scholar]
- 23.Wellmann R. optiSel: Optimum Contribution Selection Population Genetics. R package version 2.0.5 (2021). Available online at: https://CRAN.R-project.org/package=optiSel
- 24.Howard JT, Pryce JE, Baes C, Maltecca C. Invited review: Inbreeding in the genomics era: Inbreeding, inbreeding depression, and management of genomic variability. J Dairy Sci. (2017) 100:6009–24. 10.3168/jds.2017-12787 [DOI] [PubMed] [Google Scholar]
- 25.Ablondi M, Malacarne M, Cipolat-Gotet C, van Kaam J-T, Sabbioni A, Summer A. Genome-wide scan reveals genetic divergence in Italian Holstein cows bred within PDO cheese production chains. Sci Rep. (2021) 11:12601. 10.1038/s41598-021-92168-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ablondi M, Sabbioni A, Stocco G, Cipolat-Gotet C, Dadousis C, Kaam J-T, et al. Genetic diversity in the italian holstein dairy cattle based on pedigree and SNP data prior and after genomic selection. Front Vet Sci. (2022) 8:773985. 10.3389/fvets.2021.773985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lozada-Soto EA, Maltecca C, Lu D, Miller S, Cole JB, Tiezzi F. Trends in genetic diversity and the effect of inbreeding in American Angus cattle under genomic selection. Genet Sel Evol. (2021) 53:50. 10.1186/s12711-021-00644-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nani JP, VanRaden, P. M. Accounting for X chromosome and allele frequencies in genomic inbreeding estimation. J. Dairy Sci. (2021). 104: 79–80 [Google Scholar]
- 29.Dadousis C, Somavilla A, Ilska JJ, Johnsson M, Batista L, Mellanby RJ, et al. A genome-wide association analysis for body weight at 35 days measured on 137,343 broiler chickens. Genet Sel Evol. (2021) 53:70. 10.1186/s12711-021-00663-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Salek Ardestani S, Jafarikia M, Sargolzaei M, Sullivan B, Miar Y. Genomic prediction of average daily gain, back-fat thickness, and loin muscle depth using different genomic tools in canadian swine populations. Front Genetics. (2021) 12:665344. 10.3389/fgene.2021.665344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ros-Freixedes R, Valente BD, Chen C-Y, Herring WO, Gorjanc G, Hickey JM, et al. Rare and population-specific functional variation across pig lines. Genet Selection Evol. (2022) 54:39. 10.1186/s12711-022-00732-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhang Z, Druet T. Marker imputation with low-density marker panels in Dutch Holstein cattle. J Dairy Sci. (2010) 93:5487–94. 10.3168/jds.2010-3501 [DOI] [PubMed] [Google Scholar]
- 33.Hickey JM, Kinghorn BP, Tier B, van der Werf JH, Cleveland MA, A. phasing and imputation method for pedigreed populations that results in a single-stage genomic evaluation. Genet Sel Evol. (2012) 44:9. 10.1186/1297-9686-44-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Huang Y, Hickey JM, Cleveland MA, Maltecca C. Assessment of alternative genotyping strategies to maximize imputation accuracy at minimal cost. Genet Sel Evol. (2012) 44:25. 10.1186/1297-9686-44-25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pryce JE, Hayes BJ, Goddard ME. Novel strategies to minimize progeny inbreeding while maximizing genetic gain using genomic information. J Dairy Sci. (2012) 95:377–88. 10.3168/jds.2011-4254 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
SNP density per chromosome for the (A) imputed, (B) Illumina Infinium BovineHD BeadChip, (C) GeneSeek Genomic Profiler HD-150K, (D) GeneSeek Genomic Profiler 3, (E) GeneSeek Genomic Profiler 4, (F) GeneSeek MD, and (G) Labogena MD.
Comparison between genotyped and imputed SNP inbreeding coefficients for (A) Illumina Infinium BovineHD BeadChip, (B) GeneSeek GenomicProfiler HD-150K, (C) GeneSeek Genomic Profiler 3, (D) GeneSeek Genomic Profiler 4, (E) GeneSeek MD, and (F) Labogena MD.
Pairwise Pearson correlations (above diagonal) between each pair of the pedigree and the seven genomic inbreeding estimators analyzed for (A) Illumina Infinium BovineHD BeadChip, (B) GeneSeek Genomic Profiler HD-150K, (C) GeneSeek Genomic Profiler 3, (D) GeneSeek Genomic Profiler 4, (E) GeneSeek MD, and (F) Labogena MD. In gray color the overall correlation, in red correlations estimated from the genotyped SNP in each panel and in green correlations estimated from the imputation SNP.
Data Availability Statement
The data analyzed in this study is subject to the following licenses/restrictions: Data supporting this paper were obtained from ANAFIBJ. The genotype data are available only upon agreement with ANAFIBJ. Requests to access these datasets should be directed to J-TK, jtkaam@anafi.it.