Abstract
Monte Carlo (MC) radiation transport methods are used for dose calculation as ‘gold standard.’ However, the method is computationally time-consuming and thus impractical for normal tissue dose reconstructions for the large number of proton therapy patients required for epidemiologic investigations of late health effects. In the present study, we developed a new dose calculation method for the rapid reconstruction of out-of-field neutron dose to patients undergoing pencil beam scanning (PBS) proton therapy. The new dose calculation method is based on neutron dose voxel kernels (DVKs) generated by MC simulations of a proton pencil beam irradiating a water phantom (60 × 60 × 300 cm3), which was conducted using a MC proton therapy simulation code, TOPAS. The DVKs were generated for 19 beam energies (from 70 to 250 MeV with the 10-MeV interval) and three range shifter thicknesses (1, 3, and 5 cm). An in-house program was written in C++ to superimpose the DVKs onto a patient CT images according to proton beam characteristics (energy, position, and direction) available in treatment plans. The DVK dose calculation method was tested by calculating organ/tissue-specific neutron doses of 1- and 5-year-old whole-body computational phantoms where intracranial and craniospinal irradiations were simulated. The DVK-based doses generally showed reasonable agreement with those calculated by direct MC simulations with a detailed PBS model that were previously published, with differences mostly less than 30% and 10% for the intracranial and craniospinal irradiations, respectively. The computation time of the DVK method for one patient ranged from 1 to 30 minutes on a single CPU core of a personal computer, demonstrating significant improvement over the direct MC dose calculation requiring several days on high-performance computing servers. Our DVK-based dose calculation method will be useful when dosimetry is needed for the large number of patients such as for epidemiologic or clinical research.
1. Introduction
Proton therapy is an emerging radiotherapy technique with great potential to enhance clinical outcomes by delivering smaller doses to organs at risk surrounding the tumor compared to conventional radiotherapy with photons (Gondi et al 2016). This benefit leads to the exponential growth of proton therapy patients worldwide (Jermann 2015). However, epidemiologic investigations of late health effects such as second cancers after proton treatment are sparse (Journy et al 2018). Understanding the late effects is crucial particularly for pediatric patients having higher radiosensitivity of tissues and longer life expectancy than adult patients (Xu et al 2008). In a dedicated effort to investigate the late health effects for pediatric patients in proton therapy, the Pediatric Proton/Photon Consortium Registry (PPCR) (http://www.pedsprotonregistry.org/) was launched in 2012 and has actively enrolled children and young adults (under the age of 22) treated by 17 US proton centers (Kasper et al 2014, Hess et al 2018). To expand this collaboration, Berrington de Gonzalez et al (2017) proposed an International Pediatric Proton Therapy Consortium for large-scale collaborative studies involving a large number of proton centers on an international level.
The risk assessment in epidemiologic investigations requires estimation of dose to the normal organs and tissues where adverse effects occurred. Dose to the normal organs and tissues in the field of primary proton beams can be estimated by a proton treatment planning system (TPS). Most existing TPSs, however, to enhance calculation efficiency, are designed for accurate in-field proton dose calculation but not for out-of-field secondary neutron dose to the normal organs and tissues at risk. In proton therapy, secondary neutrons are the main contribution to the out-of-field dose even for scanning beams (Kry et al 2017). Dose calculation based on a Monte Carlo (MC) radiation transport method, which is considered the ‘gold standard’ (Kozłowska et al 2019), has been used to estimate neutron dose to proton patients (Polf and Newhauser 2005, Athar et al 2010, Zheng et al 2008, Geng et al 2015). However, the MC dose calculation method is computationally time-consuming (Ma et al 2018) and therefore may not be a practical solution for individualized patient dose reconstruction in the context of large-scale epidemiologic investigations which must consider hundreds or thousands of patients to reach sufficient statistical power (Newhauser et al 2018).
In the present study, we developed a new dose calculation method that can rapidly reconstruct out-of-field neutron dose to patients undergoing proton pencil beam scanning (PBS) treatment using pre-generated neutron dose voxel kernels (DVK) from MC simulations of proton pencil beams irradiating a water phantom. We simulated intracranial and craniospinal irradiations for whole-body pediatric computational human phantoms (Lee et al 2010) and compared the DVK-based dose with those calculated by the direct MC simulation using a dedicated PBS MC model (Yeom et al 2020). Computation times were also recorded to evaluate performance improvement against the direct MC dose calculation.
2. Material and Methods
2.1. Generation of dose voxel kernels
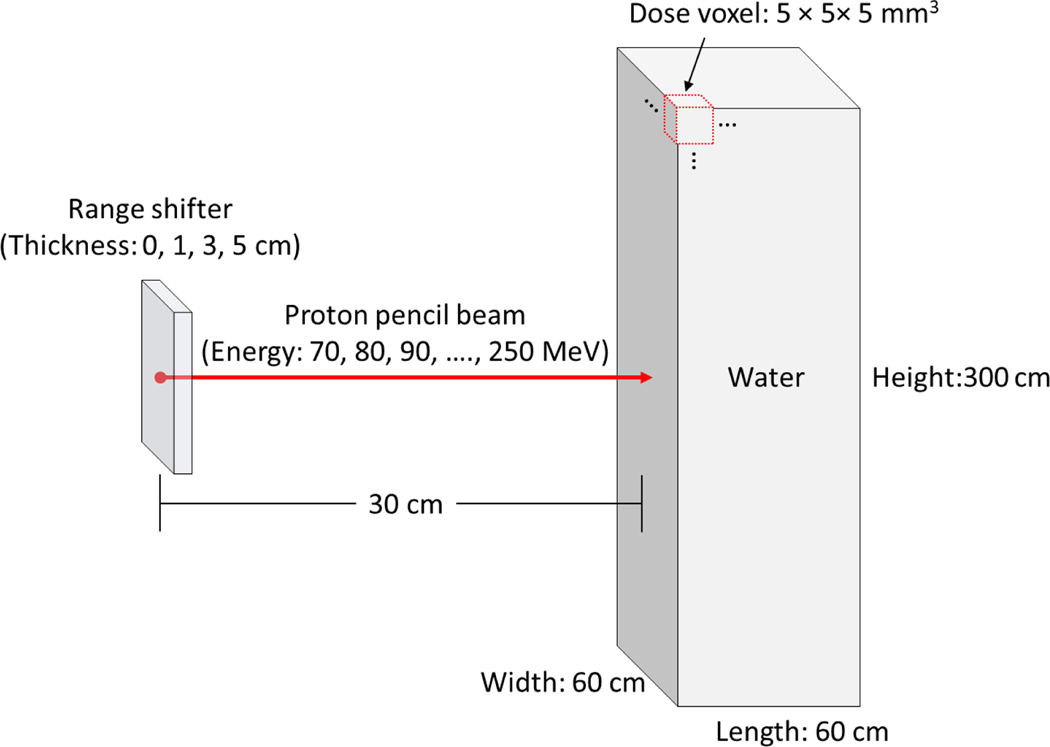
A comprehensive set of DVKs was generated by conducting MC simulations where proton pencil beams were irradiated onto a water phantom. The TOPAS MC code (ver. 3.1) (Perl et al 2012), an application built with the Geant4 MC toolkit (Allison et al 2016), was adopted for the DVK generations. The TOPAS MC code has been widely used in medical applications mainly for proton therapy (Shin et al 2017, Hartman et al 2018, Lin et al 2014) and validated against neutron measurements in proton treatment rooms (Lutz et al 2018, Prusator et al 2018). Figure 1 shows the beam irradiation conditions for the DVK generations. A proton pencil beam was simulated with the source located at 30 cm from the center of a water phantom of 60 × 60 × 300 cm3 to cover the body size of most pediatric patients. The beam energies (i.e., nominal energies) were simulated with the initial proton energy ranging from 70 to 250 MeV in 10-MeV increments, covering proton energies most commonly used for treatment. We used beam properties (i.e., spot size, spot divergence, mean energy, and energy spread) as a function of the nominal energy that were matched to the beam measurement data in the Varian ProBeam system installed at the Maryland Proton Treatment Center (MPTC) (Yeom et al 2020). The water phantom was fully binned with a dose scoring voxel of 5 × 5 × 5 mm3. The neutron doses were scored by setting the TOPAS filtering parameter of OnlyIncludeIfParticleOrAncestorNamed to “neutron.” Additional sets of the DVKs were generated for range shifters (RSs) in three different thicknesses (1, 3, and 5 cm) considered in the Varian ProBeam system (Langner et al 2017). The DVKs for the RSs were composed of two separate dose maps: one resulting from neutrons induced from the water phantoms and the other resulting from neutrons induced from the RSs. The number of primary protons simulated for each beam irradiation varied from 1011 to 1012 so that the statistical relative errors in the dose for most scored voxels (> 90%) was kept less than 10%. The default physics modules (g4em-standard_opt4, g4h-phys_QGSP_BIC_HP, g4decay, g4ion-binarycascade, g4h-elastic_HP, and g4stopping) and the default range value (0.05 mm) of secondary production cutoffs for all particles were used. The MC simulations were performed on Biowulf, the National Institutes of Health (NIH)’s high-performance Linux computing cluster (http://hpc.nih.gov).
Figure 1.
Illustration of MC simulations to generate neutron dose voxel kernels by irradiating a water phantom with proton pencil beams.
2.2. Development of dose calculation program
We developed an in-house program written in C++ that can calculate neutron dose to a patient by using the DVKs established in Section 2.1. The program imports the DVKs and patient treatment plan data (e.g., CT images and treatment plan) in the DICOM-RT (Digital Imaging and Communications in Medicine – Radiotherapy). From the DICOM-RT data, the beam information (e.g., direction, energy, and position) was extracted. According to the beam energies, the DVKs (70 to 250 MeV with the 10-MeV intervals) are linearly interpolated in energy to obtain a new set of DVKs (one for each beam). The obtained DVK is translated on the patient CT images by matching the location of the first DVK voxel irradiated by the proton beam, to that of the first voxel representing the skin surface of the patient located at the geometric center of the proton beam (see figure 2(b)). The first tissue voxel is found by tracing a ray in the direction of the proton beam incident on the patient. The ray tracing is conducted by using a fast ray-tracing algorithm in voxel geometry (Amanatides and Woo 1987). Considering the matched voxel location as a rotation center, the translated DVK is rotated according to the direction of the proton beam (see figure 2(c)). The aligned DVK is then accumulated on the patient CT images. Note that, due to the limited box shape, the aligned DVK cannot cover a part of the body for some cases, particularly when a proton beam in a lateral direction is irradiated to the head. To reduce the dosimetric bias due to this limitation, the DVK is mirrored as shown in figure 2(d), and the mirrored DVK is additionally accumulated on the CT images to approximate dose to the uncovered body part. This process for the DVK accumulation is repeated for all the proton beams, finally obtaining the neutron dose map to the patient.
Figure 2.
Illustration of superimposing of a dose voxel kernel (DVK) onto a patient for dose calculation: (a) example patient CT image and DVK; (b) translated DVK on patient CT image; (c) rotated DVK on patient CT image; (d) mirrored DVK to cover the body region not covered by (c).
In case of the RSs considered in the treatment, the distance between the RS and the patient may be different from that used when generating the DVKs in the water phantom (i.e., 30 cm – RS thickness) (see figure 1). The distance difference biases the contribution to the patient neutron dose by the neutrons induced from the RS. To minimize this bias, prior to the DVK accumulation, the RS-induced dose map in the DVK is adjusted with a scaling factor [= (distance between the RS and the water phantom)2 / (distance between the RS and the patient)2] considering the inverse-square law.
2.3. Performance evaluation
We evaluated the performance of the developed dose calculation method against a direct MC dose calculation. For this, neutron doses for example cases of pediatric patients undergoing intracranial and craniospinal irradiations were calculated and compared with the previous results calculated by the direct MC simulation using the TOPAS MC model dedicated for the Maryland Proton Treatment Center (MPTC) PBS system (Yeom et al 2020). Computation times for the DVK method were also recorded and compared with those of the MC simulations. Computational phantoms (1- and 5-year-old) developed in collaboration between the University of Florida and the National Cancer Institute (Lee et al 2010) were selected as surrogate patient anatomies and converted in the DICOM-RT format compatible with commercial treatment planning systems (TPSs) while maintaining the organ/tissue identities of the phantoms (Griffin et al 2019). The intracranial and craniospinal irradiations were created on the phantoms by a clinical medical physicist using the MTPC TPS (Eclipse v13.7, Varian Medical Systems, Palo Alto CA). No RS was used for the intracranial irradiations, whereas the 5-cm RS was used for the craniospinal irradiations. Four different patient cases were considered: Patient A (1-year-old phantom with intracranial irradiation; Patient B (5-year-old phantom with intracranial irradiation); Patient C (1-year-old phantom with craniospinal irradiation); and Patient D (5-year-old phantom with craniospinal irradiation). The dose calculations using the DVK method were conducted on a single CPU of the Intel® Xeon® Gold 5122 CPU (@3.60GHz) and 64 GB RAM in a personal computer.
3. Results
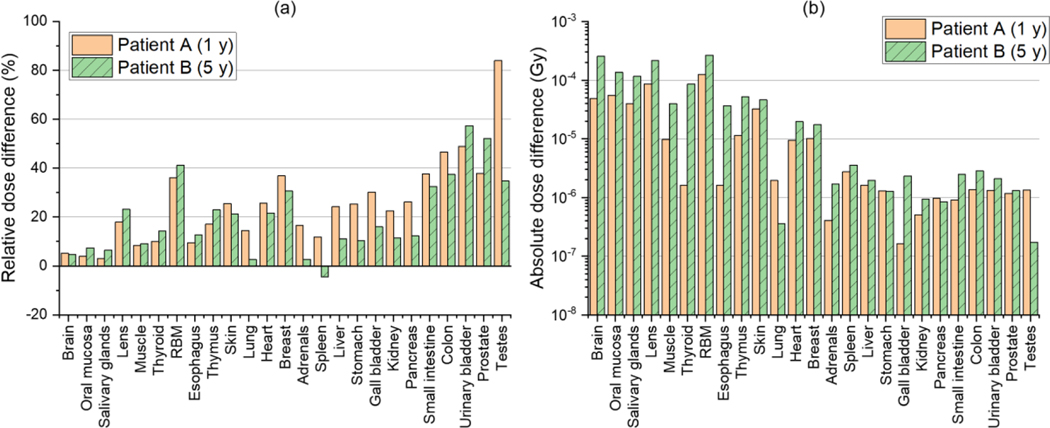
Figure 3(a) shows relative differences in the neutron doses for 25 organs and tissues of Patient A and Patient B (intracranial irradiations) calculated by using the DVK method from those calculated by using the direct MC simulation of Yeom et al (2020) [= (DVK – MC) / MC × 100] . The relative differences for most organs and tissues are less than 30%. The average absolute values of the relative differences for all the organs and tissues are 25% and 20% for Patient A and Patient B, respectively. The maximum relative difference is 84% for the testes of Patient A. Figure 3(b) shows absolute dose differences between the DVK method and the direct MC simulation [= |DVK – MC|], which are small, ranging from 0.2 μGy to 0.3 mGy.
Figure 3.
(a) Relative dose difference (%) in neutron doses for 25 organs and tissues between the DVK dose calculation method (DVK) and the detailed MC simulation (MC) [=(DVK – MC) / MC × 100] and (b) absolute dose difference (Gy) [= |DVK – MC|] for Patient A and Patient B undergoing intracranial irradiations
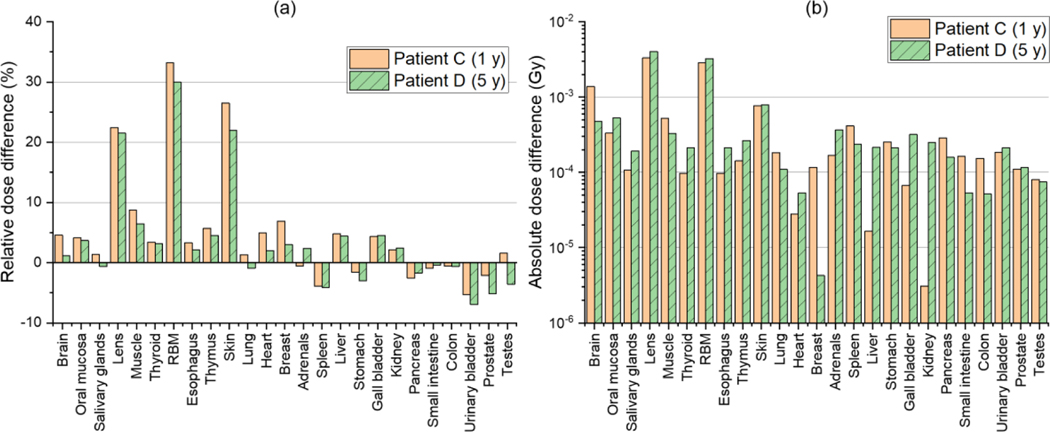
Figure 4(a) shows the relative dose differences for Patient C and Patient D, i.e., the craniospinal irradiation cases. The relative differences are generally less than those for the intracranial irradiation cases (Patient A and Patient B). The relative differences for most organs and tissues are less than 10%. The average of the absolute values of the relative differences for all the organs and tissues is 6% and 5% for Patient C and Patient D, respectively. Larger differences can be seen in the lens and red bone marrow for both Patient C and Patient D (20% – 30%), which are however in a similar level with those for the intracranial irradiation cases (see Figure 3(a)). Figure 4(b) shows the absolute dose differences in a range from 3 μGy to 4 mGy, which are also small but tend to be greater than those for the intracranial irradiation cases (see Figure 3(b)).
Figure 4.
(a) Relative dose difference (%) in neutron doses for 25 organs and tissues between the DVK dose calculation method (DVK) and the detailed MC simulation (MC) [=(DVK – MC) / MC × 100] and (b) absolute dose difference (Gy) [= |DVK – MC|] for Patient C and Patient D undergoing craniospinal irradiations
Table 1 shows the computation times of the DVK method for the dose calculations of the four patients. The computation times vary from 1 to 30 minutes depending on the patient. The computation times of the DVK method are significantly shorter than those of the direct MC simulations of Yeom et al (2020) (several days per patient treatment using 1,500 CPU cores of the NIH Biowulf high-performance computing cluster). The variation of the computation times in the different patients is associated with the different number of proton beams used for the treatment irradiation, which directly determines the number of loops of the repetitive process for the DVK accumulation (see Section 2.2). The number of proton beams for each patient case was also presented in Table 1.
Table 1.
Computation times of the DVK dose calculation model for dose calculations of four patients: Patient A (intracranial irradiation on 1-year-old phantom), Patient B (intracranial irradiation on 5-year-old phantom), Patient C (craniospinal irradiation on 1-year-old phantom), and Patient A (craniospinal irradiation on 5-year-old phantom).
| Patient | A | B | C | D |
|---|---|---|---|---|
| Computation time (minutes) | 1.0 | 4.5 | 15.8 | 30.3 |
| Number of proton beams | 179 | 1148 | 3947 | 7725 |
4. Discussion
Several studies (Polf and Newhauser 2005, Athar et al 2010, Zheng et al 2008, Geng et al 2015) estimated out-of-field neutron doses to patients in proton therapy by conducting direct MC simulation which is considered to be the gold standard dose calculation method. The MC approach, however, is computationally time-consuming and currently impractical for use in dose reconstructions of a large-scale patient cohort required for risk assessment in epidemiologic studies (Newhauser et al 2018). Therefore, it is important to develop and deploy a practical dose calculation approach that can quickly and accurately estimate out-of-field neutron doses to proton patients. In a dedicated effort to address this important issue, we developed the dose calculation method based on DVKs for the rapid dose reconstruction of pediatric patients in proton PBS treatments. Note that half of the proton pediatric patients treated worldwide in 2016 were found to be PBS treatment patients according to an international survey (Journy et al 2018).
The DVK method was generally in good agreement with those of the direct MC simulation, with the differences typically within several tens of percent (Figures 3 and 4). The relative dose differences between the DVK method and direct MC simulation tended to be larger for the intracranial irradiation cases than for the craniospinal irradiation cases. This tendency can be explained by the fact that the approximation of the patient’s body as a water box phantom for the DVK generation biases the calculated doses using the DVK method, mainly contributed by scattered neutrons (not by primary neutrons induced in the proton beam fields). The scattered-neutron dose contributions in the DVKs are greater than those found in the patient because the water phantom is larger than the patient to cover the entire body. These dose contributions become more important at further distances from the proton beam field. Organ/tissue distances from the intracranial irradiation beam fields are mostly longer than from the craniospinal irradiation beam fields. Nevertheless, the absolute dose differences for the intracranial irradiation cases were all smaller than those for the craniospinal irradiation cases because the neutron dose values for the intracranial irradiation cases were significantly lower than those for the craniospinal irradiation cases (Yeom et al 2020).
The scattered-neutron dose bias also explains why the relative dose differences between the DVK method and the direct MC simulation for the intracranial irradiation cases tended to be larger at the organs and tissues located farther from the brain. For example, organs and tissues in the pelvic region such as prostate, testes, and urinary bladder showed notable differences by up to about a factor of 2. Note that the water phantom (60 × 60 × 300 cm3) selected to cover the body size of most patients for large-scale cohort studies is fairly large compared to the reference body sizes of the 1- and 5-year-old patients. The dose differences could be reduced by using additional DVKs derived in smaller water phantoms closer to the patients. Nevertheless, the dosimetric errors due to the size of the water phantom may not be of great concern for dose response assessment because the dose values in the pelvic region for the intracranial irradiations are very small (microgray scale). Besides, actual patient CT images for intracranial irradiations usually only cover the head region and not the whole body. The missing body region can be predicted by using an anatomy extension method based on existing whole-body computational phantoms (Kuzmin et al 2018); however, the anatomical difference between the computational phantom and the patient inevitably exists and could result in more significant dosimetric biases than that of the DVK method.
We also observed the DVK method indeed dramatically improved computation efficiency against the direct MC dose calculation, which is the key advantage of the DVK method. The average of the computation times of the four patient cases was only 13 minutes using a personal computer (see Table 1). Therefore, the DVK method, when combined with an available high-performance computing system such as the NIH Biowulf cluster (equipped with ~95,000 CPU cores), can be a practical approach for conducting high-quality dose reconstructions of a large-scale patient cohort (e.g., 100,000) for the epidemiologic investigations within a reasonable time.
We acknowledged several limitations of the current work. We evaluated the performance (accuracy and computation efficiency) of the DVK method within a limited number of patient cases and treatment types (i.e., intracranial and craniospinal irradiations), although these irradiations are used mainly for central nervous system tumors diagnosed in the majority of pediatric patients (Journy et al 2018). Nevertheless, the overall performance of the DVK method may not be significantly different for other treatment irradiations because the field sizes for other treatments are mostly between that of intracranial and craniospinal irradiations. We ignored dosimetric bias due to the material difference between water (used for the DVK generation) and patient tissues. This bias, however, may not be significantly large considering that Söderberg and Carlsson (2000) derived neutron dose scaling factors (SF = Dwater / Dtissue) between water and different tissues (bone, muscle, adipose, soft tissue) at different energies (10, 40, 80 MeV) and depths (10, 15, 20 cm) via MC simulations and found that all the SF values were very close to unity (0.94 to 1.02). In the current work, the DVKs were generated with respect to the RS thicknesses (1, 3, and 5 cm) limited to the Varian ProBeam system (Langner et al 2017). When other PBS systems use RS thicknesses significantly different from the RS thicknesses considered in the current study, an additional set of the DVKs should be generated. In addition, the inverse-square law was considered to adjust the DVKs due to the different RS distance to the water phantom and the patient, but may not be the best assumption considering that neutrons induced in the RSs are predominantly emitted in a forward direction. Nevertheless, the calculated organ/tissue doses for the craniospinal irradiation cases involving the 5-cm RS showed good agreement with those of the direct MC simulation. Finally, the DVKs in the current work were generated using only one MC code (i.e., TOPAS) as our focus was on the development of the new dose calculation method. A further study should be conducted to quantify dosimetric variation due to different physics model and cross-section data against other MC codes such as MCNP (Goorley et al 2012) and FLUKA (Battistoni et al 2016).
5. Conclusion
In the present study, we developed a new dose calculation method for rapid reconstructions of out-of-field neutron doses of pediatric patients undergoing proton PBS treatment. Our method estimates neutron dose to a patient by directly using the DVKs pre-generated by MC simulations following the proton beam information in the treatment plan. The DVK method was tested by calculating neutron dose for example pediatric patients undergoing intracranial and craniospinal irradiations, showing that our method significantly improves computation efficiency and provides reasonable accuracy compared to direct MC simulation. Although the method was developed primarily for retrospective dose calculations to support epidemiologic studies, it could be also incorporated into clinical TPSs to estimate out-of-field normal organ/tissue dose to support clinical judgments in the stage of treatment planning.
Acknowledgments
This work was funded by the intramural program of the National Institutes of Health (NIH), National Cancer Institute, Division of Cancer Epidemiology and Genetics. One of the authors (Yeon Soo Yeom) was supported by a grant of the Korean Health Technology R&D Project through the Korean Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (Project No: H18C2257). The calculations in this work were performed on the NIH High-Performance Computing Biowulf Cluster (http://hpc.nih.gov).
References
- Allison J, Amako K, Apostolakis J, Arce P, Asai M, Aso T, Bagli E, Bagulya A, Banerjee S, Barrand G, Beck BR, Bogdanov AG, Brandt D, Brown JMC, Burkhardt H, Canal Ph, Cano-Ott D, Chauvie S, Cho K, Cirrone GAP, Cooperman G, Cortés-Giraldo MA, Cosmo G, Cuttone G, Depaola G, Desorgher L, Dong X, Dotti A, Elvira VD, Folger G, Francis Z, Galoyan A, Garnier L, Gayer M, Genser KL, Grichine VM, Guatelli S, Guèye P, Gumplinger P, Howard AS, Hřivnáčová I, Hwang S, Incerti S, Ivanchenko A, Ivanchenko VN, Jones FW, Jun SY, Kaitaniemi P, Karakatsanis N, Karamitros M, Kelsey M, Kimura A, Koi T, Kurashige H, Lechner A, Lee SB, Longo F, Maire M, Mancusi D, Mantero A, Mendoza E, Morgan B, Murakami K, Nikitina T, Pandola L, Paprocki P, Perl J, Petrović I, Pia MG, Pokorski W, Quesada JM, Raine M, Reis MA, Ribon A, Ristić Fira A, Romano F, Russo G, Santin G, Sasaki T, Sawkey D, Shin JI, Strakovsky II, Taborda A, Tanaka S, Tomé B, Toshito T, Tran HN, Truscott PR, Urban L, Uzhinsky V, Verbeke JM, Verderi M, Wendt BL, Wenzel H, Wright DH, Wright DM, Yamashita T, Yarba J, et al. 2016. Recent developments in Geant4 Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 835 186–225 [Google Scholar]
- Amanatides J and Woo A 1987. A Fast Voxel Traversal Algorithm for Ray Tracing Eurographics 87 3–10 [Google Scholar]
- Athar BS, Bednarz B, Seco J, Hancox C and Paganetti H 2010. Comparison of out-of-field photon doses in 6 MV IMRT and neutron doses in proton therapy for adult and pediatric patients Physics in Medicine and Biology 55 2879–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battistoni G, Bauer J, Boehlen TT, Cerutti F, Chin MPW, Dos Santos Augusto R, Ferrari A, Ortega PG, Kozłowska W, Magro G, Mairani A, Parodi K, Sala PR, Schoofs P, Tessonnier T and Vlachoudis V 2016. The FLUKA Code: An Accurate Simulation Tool for Particle Therapy Front Oncol 6 Online: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4863153/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berrington de Gonzalez A, Vikram B, Buchsbaum JC, de Vathaire F, Dörr W, Hass-Kogan D, Langendijk JA, Mahajan A, Newhauser W, Ottolenghi A, Ronckers C, Schulte R, Walsh L, Yock TI and Kleinerman RA 2017. A Clarion Call for Large-Scale Collaborative Studies of Pediatric Proton Therapy Int. J. Radiat. Oncol. Biol. Phys. 98 980–1 [DOI] [PubMed] [Google Scholar]
- Geng C, Moteabbed M, Seco J, Gao Y, George Xu X, Ramos-Méndez J, Faddegon B and Paganetti H 2015. Dose assessment for the fetus considering scattered and secondary radiation from photon and proton therapy when treating a brain tumor of the mother Physics in Medicine and Biology 61 683–95 [DOI] [PubMed] [Google Scholar]
- Gondi V, Yock TI and Mehta MP 2016. Proton therapy for paediatric CNS tumours — improving treatment-related outcomes Nat Rev Neurol 12 334–45 [DOI] [PubMed] [Google Scholar]
- Goorley T, James M, Booth T, Brown F, Bull J, Cox LJ, Durkee J, Elson J, Fensin M, Forster RA, Hendricks J, Hughes HG, Johns R, Kiedrowski B, Martz R, Mashnik S, McKinney G, Pelowitz D, Prael R, Sweezy J, Waters L, Wilcox T and Zukaitis T 2012. Initial MCNP6 Release Overview Nuclear Technology 180 298–315 [Google Scholar]
- Griffin KT, Mille MM, Pelletier C, Gopalakrishnan M, Jung JW, Lee C, Kalapurakal J, Pyakuryal A and Lee C 2019. Conversion of computational human phantoms into DICOM-RT for normal tissue dose assessment in radiotherapy patients Phys Med Biol 64 13NT02 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartman J, Zhang X, Zhu XR, Frank SJ, Lagendijk JJW and Raaymakers BW 2018. TOPAS Monte Carlo model of MD anderson scanning proton beam for simulation studies in proton therapy Biomed. Phys. Eng. Express 4 037001 [Google Scholar]
- Hess CB, Indelicato DJ, Paulino AC, Hartsell WF, Hill-Kayser CE, Perkins SM, Mahajan A, Laack NN, Ermoian RP, Chang AL, Wolden SL, Mangona VS, Kwok Y, Breneman JC, Perentesis JP, Gallotto SL, Weyman EA, Bajaj BVM, Lawell MP, Yeap BY and Yock TI 2018. An Update From the Pediatric Proton Consortium Registry Front. Oncol. 8 Online: 10.3389/fonc.2018.00165/full [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jermann M 2015. Particle Therapy Statistics in 2014 International Journal of Particle Therapy 2 50–4 [Google Scholar]
- Journy N, Indelicato DJ, Withrow DR, Akimoto T, Alapetite C, Araya M, Chang A, Chang JH-C, Chon B, Confer ME, Demizu Y, Dendale R, Doyen J, Ermoian R, Gurtner K, Hill-Kayser C, Iwata H, Kim J-Y, Kwok Y, Laack NN, Lee C, Lim DH, Loredo L, Mangona VS, Mansur DB, Murakami M, Murayama S, Ogino T, Ondrová B, Parikh RR, Paulino AC, Perkins S, Ramakrishna NR, Richter R, Rombi B, Shibata S, Shimizu S, Timmermann B, Vern-Gross T, Wang CJ, Weber DC, Wilkinson JB, Witt Nyström P, Yock TI, Kleinerman RA and Berrington de Gonzalez A 2018. Patterns of proton therapy use in pediatric cancer management in 2016: An international survey Radiotherapy and Oncology Online: http://www.sciencedirect.com/science/article/pii/S0167814018335461 [DOI] [PubMed] [Google Scholar]
- Kasper HB, Raeke L, Indelicato DJ, Symecko H, Hartsell W, Mahajan A, Hill-Kayser C, Perkins SM, Chang AL, Childs S, Buchsbaum JC, Laurie F, Khan AJ, Giraud C, Yeap BY and Yock TI 2014. The Pediatric Proton Consortium Registry: A Multi-institutional Collaboration in U.S. Proton Centers International Journal of Particle Therapy 1 323–33 [Google Scholar]
- Kozłowska WS, Böhlen TT, Cuccagna C, Ferrari A, Fracchiolla F, Georg D, Magro G, Mairani A, Schwarz M and Vlachoudis V 2019. FLUKA particle therapy tool for Monte Carlo independent calculation of scanned proton and carbon ion beam therapy Phys. Med. Biol. Online: 10.1088/1361-6560/ab02cb [DOI] [PubMed] [Google Scholar]
- Kry SF, Bednarz B, Howell RM, Dauer L, Followill D, Klein E, Paganetti H, Wang B, Wuu C-S and Xu XG 2017. AAPM TG 158: Measurement and calculation of doses outside the treated volume from external-beam radiation therapy Medical Physics 44 e391–429 [DOI] [PubMed] [Google Scholar]
- Kuzmin GA, Mille MM, Jung JW, Lee C, Pelletier C, Akabani G and Lee C 2018. A Novel Method to Extend a Partial-Body CT for the Reconstruction of Dose to Organs beyond the Scan Range Radiation Research 189 618–26 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langner UW, Eley JG, Dong L and Langen K 2017. Comparison of multi-institutional Varian ProBeam pencil beam scanning proton beam commissioning data Journal of Applied Clinical Medical Physics 18 96–107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee C, Lodwick D, Hurtado J, Pafundi D, Williams JL and Bolch WE 2010. The UF family of reference hybrid phantoms for computational radiation dosimetry. Physics in Medicine and Biology 55 339–63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin L, Kang M, Solberg TD, Ainsley CG and McDonough JE 2014. Experimentally validated pencil beam scanning source model in TOPAS Phys. Med. Biol. 59 6859. [DOI] [PubMed] [Google Scholar]
- Lutz B, Reginatto M, Zboril M, Dommert M, Swanson R, Enghardt W and Fiedler F 2018. Characterisation of the Secondary Neutron Radiation at the University Proton Therapy Dresden 2018 IEEE Nuclear Science Symposium and Medical Imaging Conference Proceedings (NSS/MIC) 2018 IEEE Nuclear Science Symposium and Medical Imaging Conference Proceedings (NSS/MIC) pp 1–6 [Google Scholar]
- Ma J, Tseung HSWC, Herman MG and Beltran C 2018. A robust intensity modulated proton therapy optimizer based on Monte Carlo dose calculation Medical Physics 45 4045–54 [DOI] [PubMed] [Google Scholar]
- Newhauser WD, Schneider C, Wilson L, Shrestha S and Donahue W 2018. A REVIEW OF ANALYTICAL MODELS OF STRAY RADIATION EXPOSURES FROM PHOTON- AND PROTON-BEAM RADIOTHERAPIES Radiat Prot Dosimetry 180 245–51 [DOI] [PubMed] [Google Scholar]
- Perl J, Shin J, Schümann J, Faddegon B and Paganetti H 2012. TOPAS: An innovative proton Monte Carlo platform for research and clinical applications Medical Physics 39 6818–37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polf JC and Newhauser WD 2005. Calculations of neutron dose equivalent exposures from range-modulated proton therapy beams Physics in Medicine and Biology 50 3859–73 [DOI] [PubMed] [Google Scholar]
- Prusator MT, Ahmad S and Chen Y 2018. Shielding verification and neutron dose evaluation of the Mevion S250 proton therapy unit Journal of Applied Clinical Medical Physics 19 305–10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin W-G, Testa M, Kim HS, Jeong JH, Lee SB, Kim Y-J and Min CH 2017. Independent dose verification system with Monte Carlo simulations using TOPAS for passive scattering proton therapy at the National Cancer Center in Korea Phys. Med. Biol. 62 7598 [DOI] [PubMed] [Google Scholar]
- Söderberg J and Carlsson GA 2000. Fast neutron absorbed dose distributions in the energy range 0.5–80 MeV - a Monte Carlo study Phys. Med. Biol. 45 2987–3007 [DOI] [PubMed] [Google Scholar]
- Xu XG, Bednarz B and Paganetti H 2008. A review of dosimetry studies on external-beam radiation treatment with respect to second cancer induction Physics in Medicine and Biology 53 R193–241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeom YS, Kuzmin G, Griffin K, Mille M, Polf J, Langner U, Jung JW, Lee C, Ellis D, Shin J and Lee C 2020. A Monte Carlo model for organ dose reconstruction of patients in pencil beam scanning (PBS) proton therapy for epidemiologic studies of late effects J. Radiol. Prot. 40 225–242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y, Taddei P, Mirkovic D, Fontenot J, Taddei P, Newhauser W, Mirkovic D and Newhauser W 2008. Monte Carlo simulations of neutron spectral fluence, radiation weighting factor and ambient dose equivalent for a passively scattered proton therapy unit Physics in Medicine and Biology 53 187. [DOI] [PubMed] [Google Scholar]