Deformable 3D-2D Registration of Known Components for Image Guidance in Spine Surgery

Abstract

A 3D-2D image registration method is reported for guiding the placement of surgical devices (e.g., K-wires). The solution registers preoperative CT (and planning data therein) to intraoperative radiographs and computes the pose, shape, and deformation parameters of devices (termed “components”) known to be in the radiographic scene. The deformable known-component registration (dKC-Reg) method was applied in experiments emulating spine surgery to register devices (K-wires and spinal fixation rods) undergoing realistic deformation. A two-stage registration process (i) resolves patient pose from individual radiographs and (ii) registers components represented as polygonal meshes based on a B-spline model. The registration result can be visualized as overlay of the component in CT analogous to surgical navigation but without conventional trackers or fiducials. Target registration error in the tip and orientation of deformable K-wires was $(1.5\pm 0.9)\text{mm}$ and $\left({0.6}^{\circ }\pm {0.2}^{\circ }\right)$, respectively. For spinal fixation rods, the registered components achieved Hausdorff distance of 3.4 mm. Future work includes testing in cadaver and clinical data and extension to more generalized deformation and component models.

1. Introduction

Intraoperative x-ray projection images (radiography and fluoroscopy) are commonly used in neurosurgery and orthopaedic surgery for up-to-date visualization of patient anatomy and surgical devices placed therein. However, accurate interpretation of the 3D orientation of devices within complex anatomy can challenge even experienced surgeons ∘ for example, assessing the trajectory of a K-wire within safe margins of a bone corridor in spine or pelvis surgery, which requires accuracies of 1 mm and $5^{°}$ [1]. Potential solutions include the use of tracking systems and fiducial markers for surgical navigation, but the additional workflow associated with tool calibration and patient registration in addition to the requirement for extrinsic fiducials are commonly cited as barriers to ease of use and broad utilization. Furthermore, many classes of trackers are limited to rigid bodies due to the affixed external markers. Electromagnetic trackers offer a potential solution to this problem by embedding markers at the tip of tools within the body (e.g., a flexible endoscope); however such systems tend to exhibit somewhat lower registration accuracy and may suffer from metal interference. Intraoperative 3D imaging systems, such as CT, cone-beam CT (CBCT), and MRI, can provide excellent 3D visualization of anatomy and the surgical product but carry additional expense, patient access, workflow, and (possibly) radiation dose that also challenge broad utilization.

An alternative approach can provide 3D localization from intraoperative 2D radiographic images via 3D-2D registration to preoperative 3D images and planning information therein [2]. Such registration methods can extend the functionality of intraoperative 2D imaging that is already common in the surgical arsenal, integrating more naturally with standard workflow and potentially absolving the aforementioned limitations associated with surgical tracking and intraoperative 3D imaging. These methods have recently been used in the context of spine surgery [3] as well as to solve for the pose of rigid implants [4, 5] as a means of verifying the surgical product. Accurate account of deformation remains a significant challenge, with promising results offered by statistical shape models to solve for interpatient anatomical differences [6].

In this work, we combine a 3D-2D image registration method with deformable models of surgical devices (“known components”) to resolve their pose and (deformed) shape within the patient. In a sense, the approach exploits the radiographic imaging system as a “tracker,” the patient as their own “reference marker,” and surgical components themselves as “tracked tools.” The method was applied within the context of spine surgery, using a phantom experiment and mobile C-arm to emulate a spinal fixation procedure. Surgical components (viz., K-wires and spinal fixation rods) were deformably registered based on three intraoperative radiographs. Geometric accuracy was analyzed in terms of target registration error (TRE) as well as concordance with the shape of the deformed component.

2. Methods

2.1. 3D-2D Registration Framework

The proposed solution involves a robust, gradient-based 3D-2D registration algorithm composed of two distinct stages that work in tandem to solve for the 3D pose of the patient as well as the components as shown in Fig. 1. In each stage, 2D intraoperative radiographic projections are registered to a particular source of prior information: (i) the patient registration stage (red in Fig. 1) computes the transformation relating one or more radiographs $\left(P_{\theta }\right)$ to the preoperative CT $\left(V\right)$ acquired for surgical planning; and (ii) the component registration stage (blue in Fig. 1) computes the pose and parameter vector relating two or more radiographs (the same $P_{\theta }$) to a parametric model $\left(C\right(p\left)\right)$ of surgical devices within the patient (referred to as “known components”). As detailed below, both stages iteratively optimize the gradient similarity between the radiographs $\left(P\right)$ and digitally reconstructed radiographs (DRRs) of the input 3D information $(V$ or $C)$. The patient registration stage is based on the method in [3] and can optionally include locally rigid/globally deformable transformation of patient information as in [7]. The component registration is based on the (rigid) “known-component” registration (KC-Reg) method in [5], with the main advance reported below involving a deformable transformation model of the known components – e.g., needles, rods, and catheters that would not follow a simple rigid transform.

Fig. 1.

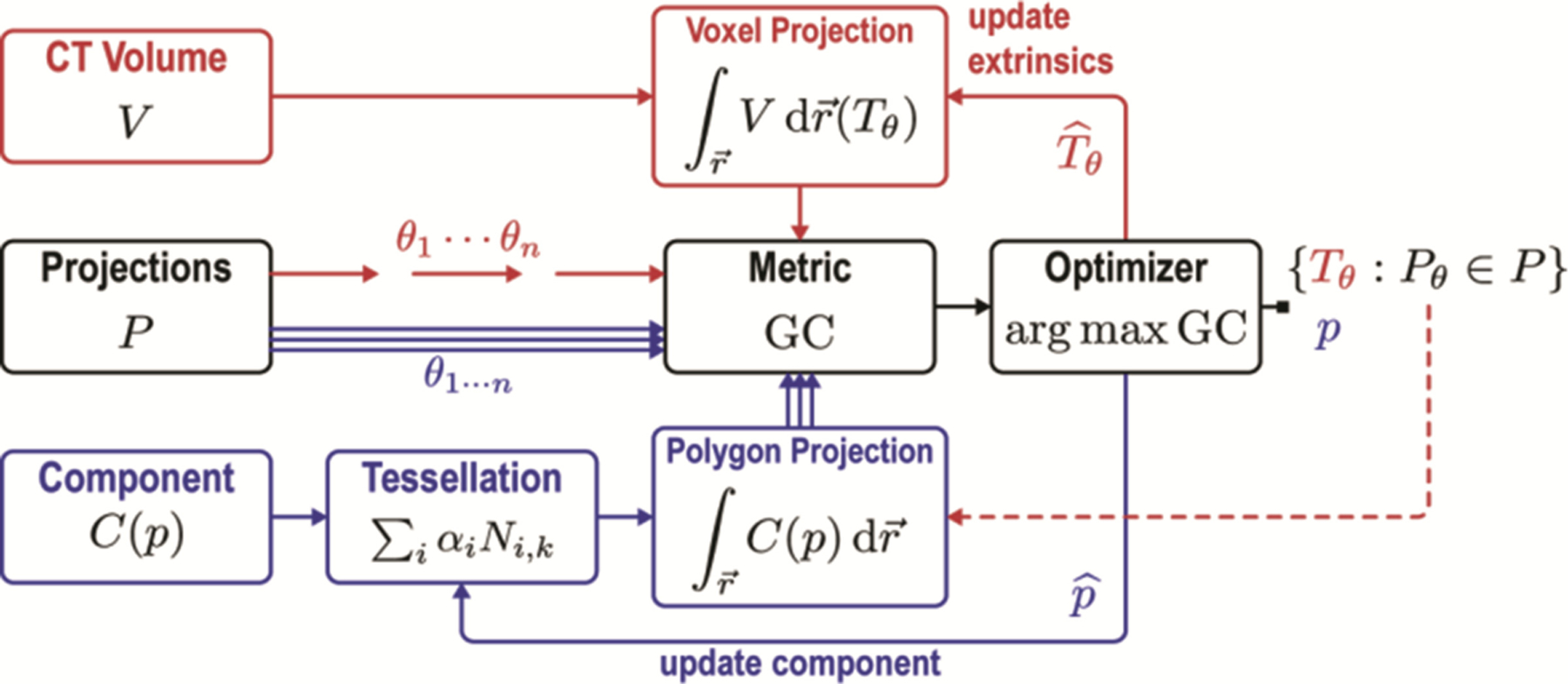
Flowchart for the deformable known-component registration (dKC-Reg) algorithm. Red: patient registration. Blue: registration of surgical components. The algorithm first solves for the transformation relating one or more radiograph $\left(P\right)$ to the patient CT $\left(V\right)$. The pose and deformation parameters of the component are then solved from one or more radiographs $\left(P_{\theta }\right)$. Note that the system operates free of conventional tracking/navigation systems and fiducial markers and employs simple mobile radiographic imaging systems already common in the operating room.

The algorithm uses radiographic projections $\left(P\right)$ (e.g., from a mobile C-arm) as normally acquired within the standard-of-care for anterior-posterior (AP), lateral, and oblique views $\left(\theta \right)$ of patient anatomy. Similarity between the projection and the DRR of the current estimate is then computed using pixel-wise gradient correlation (GC):

$$\text{GC}\left(f,m\right) =\frac{1}{2}\left\{\text{NCC}\left({\nabla }_{x}f,{\nabla }_{x}m\right)+\text{NCC}\left({\nabla }_{y}f,{\nabla }_{y}m\right)\right\}\text{}$$ (1)

where, $\text{NCC}\left(\nabla f,\nabla m\right) =\frac{\nabla f\nabla m}{\nabla f\nabla m}$ and $\nabla$ is the gradient operator applied to the fixed radiograph $\left(f\right)$ and moving DRR $\left(m\right)$ images. The similarity metric is iteratively optimized using the covariance matrix adaptation evolution strategy (CMA-ES [8]) with a population of $~200$ samples per iteration.

The optimization problem for the first stage uses the preoperative CT volume $\left(V\right)$ to establish the radiographic pose of a given projection view $\left(P_{\theta }\right)$, defined as:

$${\widehat{T}}_{\theta }=\underset{T}{\text{arg}\text{max}} \text{GC}\left(P_{\theta },\underset{\overrightarrow{r}}{\int }Vd\overrightarrow{r}\left(T_{\theta }\right)\right)$$ (2)

where $T_{\theta }$ are the rigid extrinsic parameters of projective geometry, governed by 6 degrees-of-freedom (DoF) representing translation and rotation (with extension to a globally deformable model in [7]). This process is repeated for each $P_{\theta }\in P$ to yield a set of transforms that describe radiographs with respect to the patient coordinate frame in lieu of a predetermined geometric calibration, thereby extending applicability beyond well-calibrated, computer-controlled C-arms and allowing increased DoF in C-arm positioning.

The second stage uses the parameterized component model $\left(C\right)$ and optimizes the parameter vector $\left(p\right)$ describing the pose, shape (e.g., diameter), and deformation via:

$$\widehat{p}=\underset{p}{\text{arg}\text{max}}{\sum }_{\theta }\text{GC}\left(P_{\theta },\underset{\overrightarrow{r}}{\int }C\left(p\right)d\overrightarrow{r}\left({\widehat{T}}_{\theta }\right)\right)$$ (3)

Note that the geometric relation established in the previous stage resolves the 3D component within the patient frame of reference and allows simultaneous projection of components and comparison to multiple (2–3) radiographs as expressed by the sum of their similarity. This is important for small, relatively simple surgical device components (unlike large, feature-rich anatomy), since the components have fewer characteristic features and may be ambiguous in certain views (e.g., end on view of a K-wire). This is especially important for deformable components to yield a unique (nondegenerate) solution for $\hat{p}$, and the use of multiple (2 or 3) views provides robustness to such degeneracy and accurate 3D localization.

2.2. Deformable Component Model

The component registration method uses a parametric description of surgical devices represented as polygonal meshes, providing a fairly general framework for modeling various 3D shapes and modes of deformation without manufacturer-specific (often proprietary) knowledge of device design. In this study, as illustrated in Fig. 2, we use a simple B-spline model for the component centerline with a tessellated mesh description of its radial extent, yielding a parametric description suitable to a broad range of devices presenting cylindrical symmetry (e.g., K-wires, needles, rods, shunts, catheters, flexible endoscopes, and some robotic manipulators).

Fig. 2.

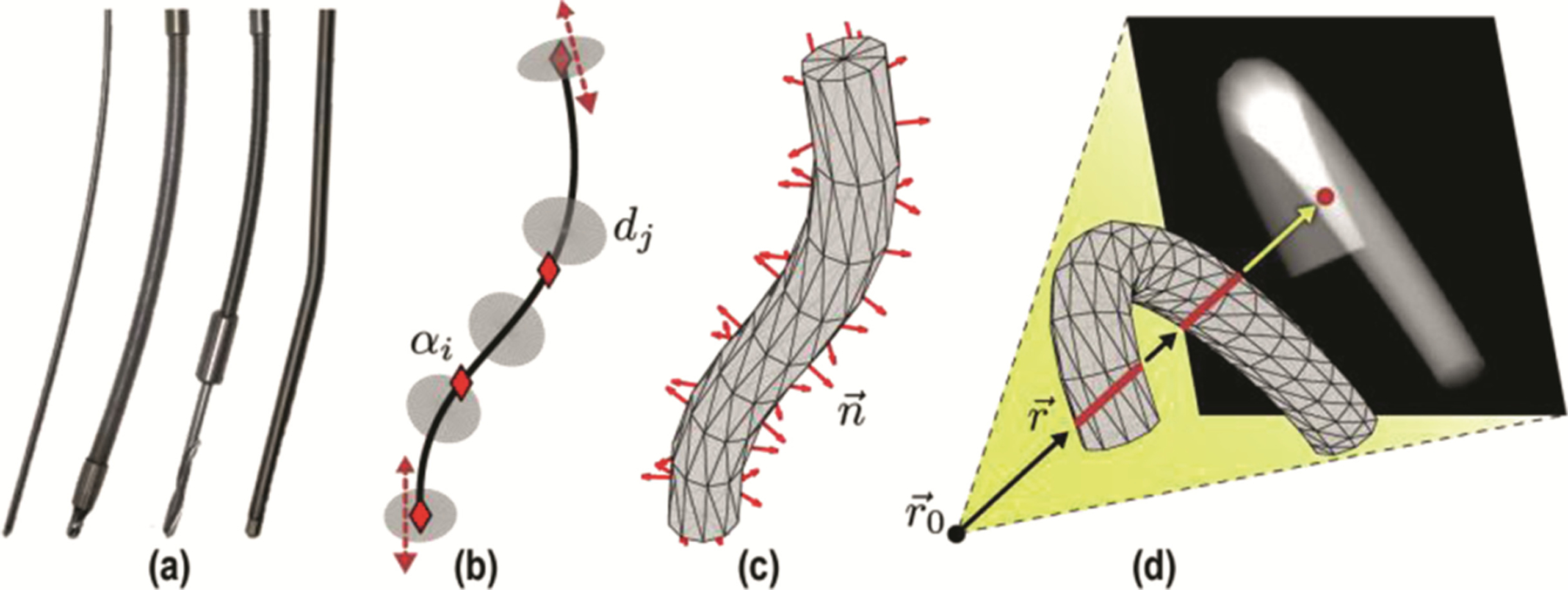
Deformable component models. (a) Example surgical tools (K-wire, flexible screwdriver, drill, and spinal fixation rod) presenting a cylindrical profile. (b) Parametric B-spline component model showing control points $\left({\alpha }_i\right)$, attached discs $\left(d_j\right)$, and tangent lines at clamped endpoints. (c) Tessellated 3D model with computed surface normals. (d) Non-convex polygon projection with multiple red line segments indicating line integrals through the mesh.

The B-spline model was chosen due to its locality and compatibility with the optimization framework, with individual control points (DoFs) that can be manipulated without changing the shape of the entire curve:

$$C\left(u\right)={\sum }_{i=0}^n {\alpha }_i{N}_{i,k}\left(u\right)$$ (4)

where control points ${\alpha }_i\in p$ are a subset of the component parameter vector, $\hat{p}$. Cubic splines $(k=3$) were used for orders $n>2$ (excepting the first order $[n=1]$ for which $k=1$ and second order $[n=2]$ for which $k=2$). The spline is clamped by constraining the first and last knots to $u_0=u_1\dots =u_k$ and $u_{n+1-k}=\dots =u_n=u_{n+1}$ such that the curve is tangent to the first and the last legs at the first and last control point. Such clamping ensures that the endpoint and approach angle of the device match that of the corresponding control point.

To construct the 3D cylindrical mesh about the centerline, the spline is sampled at locations $d_j$ corresponding to an arbitrary number of discs with radius $r\in p$, where $C\left(d_j\right)$ and $C\text{'}\left(d_j\right)$ define the position and orientation of each disc such that each disc is orthogonal to the spline as shown in Fig. 2. The discs are tessellated using triangles, and the surface normals of the resulting mesh are computed.

A novel polygon projector was defined to compute the DRR for the component model at each iteration of the optimization. The projector handles potential non-convex configurations that may occur (i.e., when the component bends on itself in the radiographic views) as follows:

$$\underset{\overrightarrow{r}}{\int }Cd\overrightarrow{r}\approx {\sum }_{t=1}^T\text{sgn}\left(\overrightarrow{r}\cdot \overrightarrow{n}\left\{C_t\right\}\right)\parallel \psi \left(\overrightarrow{r},C_t\right)-{\overrightarrow{r}}_0{\parallel }_2$$ (5)

which computes the line integral through the mesh by summing the contribution of all triangles $\left(T\right)$ for a given ray $\left(\overrightarrow{r}\right)$. The intersection point ($\text{ψ}$) between $\overrightarrow{r}$ and any given triangle on the component surface $\left(C_t\right)$ is computed using the Möller-Trumbore intersection algorithm. If a triangle is not intersected by $\overrightarrow{r}$, then $\text{ψ}={\overrightarrow{r}}_0$ (i.e., ray origin, which in this context is the x-ray source), thereby zeroing its contribution to the DRR. The sgn operation uses the surface normal $\overrightarrow{n}$ at $C_t$ to distinguish between and inbound and outbound rays on the mesh such that only the interior of the surface is integrated, thus handling non-convexity.

2.3. Experimental Evaluation

Experiments were conducted to test and evaluate the dKC-Reg algorithm in scenarios emulating the placement of transpedicle K-wires, pedicle screws, and spinal fixation rods in spine surgery. As shown in Fig. 3a, an anthropomorphic spine phantom placed within a soft-tissue holder (Sawbones, Pacific Research Laboratories, WA USA) formed the experimental model, with a CT scan acquired prior to placement of instrumentation (Toshiba Aquilion ONE CT scanner). Projection radiographs were acquired in the course of device placement using a mobile C-arm (Cios Alpha, Siemens, Erlangen Germany) yielding both the 1, 2, or 3 views employed for patient and component registration (Fig. 1) as well as a full orbital scan for CBCT “truth” definition following placement of each device. K-wires were placed in lumbar vertebrae (L1–L5) with the K-wire purposely bent to effect deformation. Device trajectories included medial (L1) and lateral (L2) breaches. Finally, spinal rods were bent to approximate correction of spinal curvature.

Fig. 3.

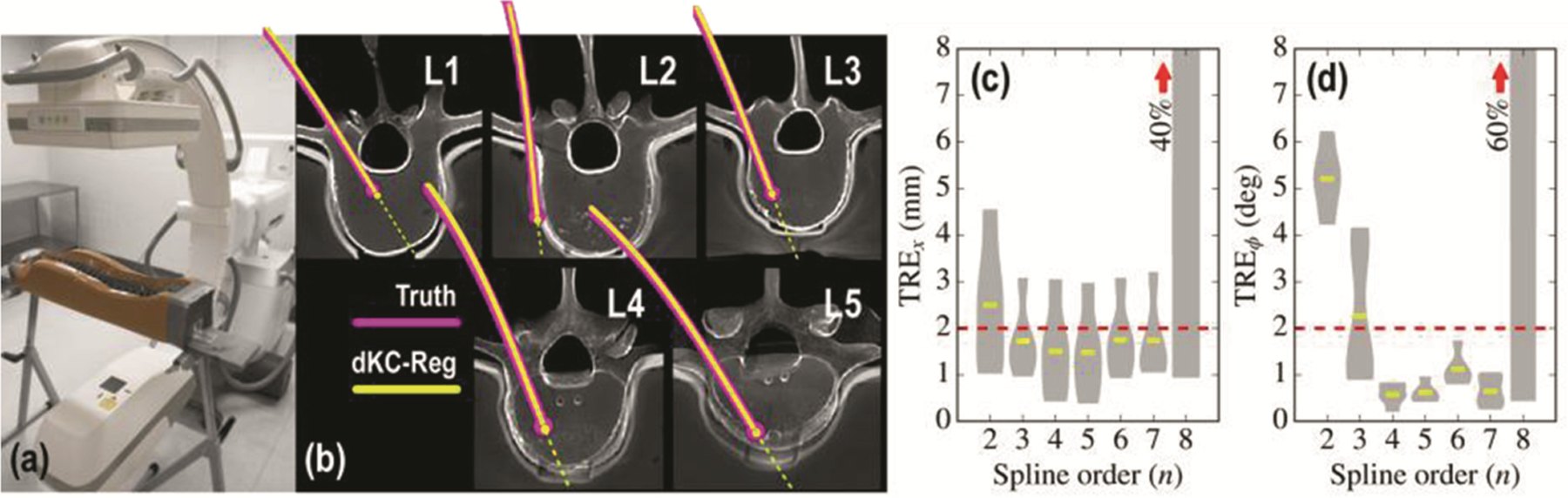
Deformable registration for K-wire guidance. (a) Experimental setup using a mobile C-arm and spine phantom. (b) Axial views of the pre-op CT showing the registered position of deformed registered components (yellow) in comparison to truth (magenta). (c–d) TRE of the K-wire tip $\left({\text{TRE}}_x,\text{ mm}\right)$ and trajectory $\left({\text{TRE}}_{\varphi },{ }^{°}\right)$ evaluated as a function of B-spline order. The deformable registration is found to be stable over a fairly broad range of spline order $(n=3-7)$ but fails from overfitting for order $\ge 8$.

Geometric accuracy of the registration was quantified in terms of targeting accuracy (at the tip of the K-wire) and proximity to the true shape of the component (for both the K-wire and fixation rods). The true position and shape were defined from thresholding, segmentation, and centerline extraction in a CBCT image acquired using the same C-arm for each device placement. The k-wire tips were conspicuous in these images, despite the usual metal artifacts. For the K-wires, registration accuracy was evaluated in terms of the error in component tip and angular trajectory, quantified using positional and angular variations on TRE:

$$\begin{gathered} {\text{TRE}}_x ={\Vert C\left({\alpha }_0\right)-C_{\text{true}}\left({\alpha }_0\right)\text{}\Vert }_2 \\ {\text{TRE}}_{\varphi } ={\cos }^{-1}\frac{C^{\prime }\left({\alpha }_0\right)\cdot C_{\text{true} }^{\text{'}}\left({\alpha }_0\right)}{\Vert C^{\prime }\left({\alpha }_0\right)\cdot C_{\text{true} }^{\text{'}}\left({\alpha }_0\right)\Vert } \end{gathered}$$ (6)

where ${\alpha }_0$ is the spline control point for the K-wire tip. For both the K-wires and spinal fixation rods, registration accuracy was also evaluated in terms of the concordance between the true centerline and spline registration result along the entire length of the device. At each point along the component, the distance to the true centerline was computed $\left({\text{Δ}}_x\right)$, as well as Hausdorff distance (HD) used to quantify the degree of overlap of the modeled component:

$$\text{HD}=\underset{a}{\text{max}}\left(\underset{b}{\min \parallel }C\left(a\right)-C_{\text{true}}\left(b\right){\parallel }_2\right)$$ (7)

where $C$ is the model and $C_{\text{true} }$ is the segmented medial line.

3. Results

3.1. K-Wires

Registration results for the K-wire guidance task are presented in Fig. 3b, demonstrating successful registration in each vertebral level with overall translational error $<2 \text{mm}$ and trajectory angulation error $<1^{°}$ [Fig. 3c–d].

The method also correctly indicated the suboptimal trajectories at L1 (medial breach) and L2 (lateral breach). The non-convex projector correctly handled retrograde curving of tools in generated samples prior to converging at the solution. Analysis of sensitivity to B-spline order $\left(n\right)$ showed robust performance for $n=4-7$; lower-order splines failed to model the deformation of the wire, and higher-order splines $(n\ge 8)$ were subject to sporadic excursions from a realistic curve. A nominal spline order $n=3$ or 4 yielded statistically significant improvement $(p<0.05)$ in ${\text{TRE}}_x(1.51\pm 0.90 \text{mm})$ and ${\text{TRE}}_{\varphi }\left(0.58\pm {0.22}^{°}\right)$ compared to a 2nd-order spline.

3.2. Spinal Rods

Applying the dKC-Reg method to curved spinal fixation rods also yielded good agreement with the true curvature of the component as visualized and quantified in Fig. 4. The convergence of the algorithm is illustrated in Fig. 4b, which shows GC similarity increasing monotonically and reaching a stable maximum for $>~50$ iterations, beyond which performance assessed in terms of Hausdorff distance is better than $5 \text{mm}$. Analysis of the results with respect to the B-spline order $\left(n\right)$ show agreement with the K-wire results. Similar to Fig. 3c–d, the registration results were stable for spline orders in the range $n=3-7$. For $n=3$, overall concordance was ${\text{Δ}}_{\text{x}}=(2.46\pm 0.72)\text{ mm}$, and $\text{HD}=3.35 \text{mm}$, which demarks the greatest separation from truth.

Fig. 4.

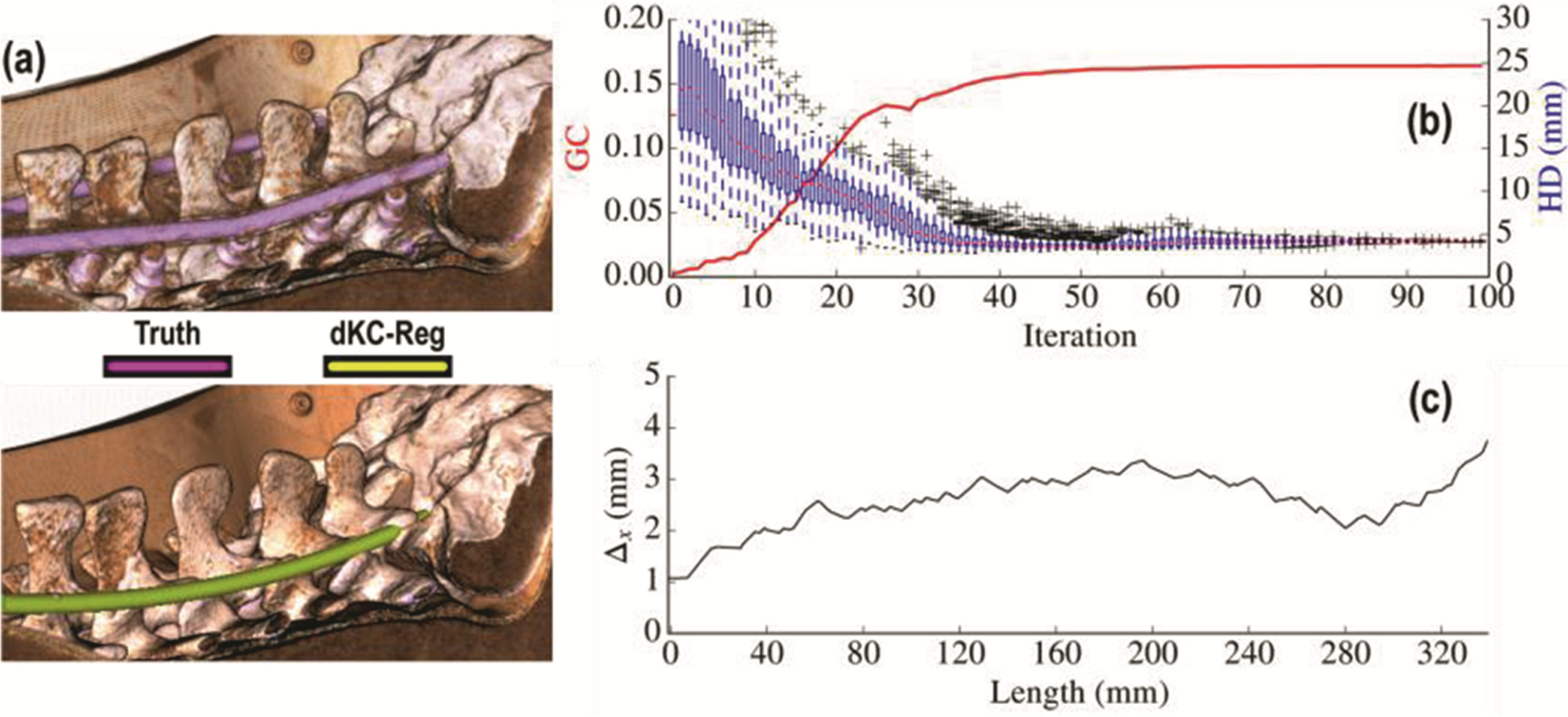
Deformable registration of spinal fixation rods. (a) Volumetric rendering of the post-op CT with the true component (top, magenta), and the registered component visualized in pre-op CT (bottom, yellow) for spline order $n=3$. (b) Convergence behavior of the optimizer illustrated in terms of the similarity metric (GC) and the HD measured as a function of iteration number. (c) Mean deviations from true position measured along the length of spinal rod.

4. Conclusion

A new method for 3D image guidance was presented that utilizes simple mobile radiography/fluoroscopy systems already common in the operating theatre to derive accurate localization and guidance of surgical devices within the body. The algorithm detailed in this work uses low-order parameterization of surgical components and includes deformation of the components (e.g., bending wire) within the solution. Experimental evaluation in a phantom emulating spine surgery yielded registration accuracy better than 2 mm and $2^{°}$ in the tip and orientation of (deformed) device components. The focus of the experiments were on the deformable component, and while the phantom used is admittedly simple, the patient registration have been shown to be very robust in clinical data that included anatomical deformation [7, 9]. While the system offers the means for navigation without the common workflow limitations of conventional tracking systems and assumption of rigid tools, it does not provide real-time visualization, rather updates with each radiographic view. Future work includes testing in clinical data and application to other clinical applications, such as the placement of catheters, shunts, or stents, where the cylindrical component model described above may be expected to hold. The framework will also be extended to support more general component shapes and modes of deformation, potentially employing more generalized deformation models, such as non-uniform rational basis splines (NURBS), which has shown promise in the field of computer-aided design.