Inferring equilibrium transition rates from nonequilibrium protocols

Abstract

We develop a theory for inferring equilibrium transition rates from trajectories driven by a time-dependent force using results from stochastic thermodynamics. Applying the Kawasaki relation to approximate the nonequilibrium distribution function in terms of the equilibrium distribution function and the excess dissipation, we formulate a nonequilibrium transition state theory to estimate the rate enhancement over the equilibrium rate due to the nonequilibrium protocol. We demonstrate the utility of our theory in examples of pulling of harmonically trapped particles in one and two dimensions, as well as a semiflexible polymer with a reactive linker in three dimensions. We expect our purely thermodynamic approach will find use in both molecular simulation and force spectroscopy experiments.

Significance

Biomolecules and molecular machines undergo conformational transitions that to large extent determine how they function, though model-free estimates of intrinsic transition rates via single-molecule force experiments and simulations are historically hard to come by. The transition rate theory we develop from stochastic thermodynamics allows us to generically infer these intrinsic rates with statistics from the distribution of heat dissipation, which are readily available from force-extension data.

Introduction

Extracting thermodynamic information from molecular systems through nonequilibrium processes was made possible with the revelation of Jarzynski’s equality (1,2,3,4). However, inference of kinetic information, such as the intrinsic rate of molecular transitions, has remained more elusive (5). Although useful ways of extracting transition rates from single-molecule force data exist, they often rely on fitting to phenomenological expressions (6) or specifying a low-dimensional model of the underlying conformational landscape (7,8). Such theories also typically assume that the driving forces are quasi-adiabatic, so that the molecule is assumed to locally equilibrate with the experimental forces imposed on it before a transition occurs. Here, we report that a molecule’s bare equilibrium transition rate can be inferred from the statistics of the excess heat released during a nonequilibrium protocol. This result derives from expressions from stochastic thermodynamics (9) and an extension of transition state theory into nonequilibrium regimes.

One of the most common methods for extracting rate information from nonequilibrium experiments and simulations employs Bell’s law (6). Bell’s phenomenological rate law postulates that the speed of a molecular transition is accelerated with an applied external force by a factor that varies exponentially:

$$k_{\lambda }\approx k_0{e}^{\beta {\lambda }^{†}{x}^{†}}\text{,}$$ (Equation 1)

where $k_{\lambda }$ is the rate in the presence of the external force λ, $k_0$ is the equilibrium rate, $x^{†}$ is the distance along the forcing direction between the reactant state and a putative transition state, ${\lambda }^{†}$ is the rupture force at the transition state, and β is the inverse temperature times Boltzmann’s constant. Evans and Richie showed that such a form emerges from Kramers’ theory for specific model potentials within a high friction limit (10). Dudko, Hummer, and Szabo (11) developed alternative rate expressions from Kramers’ theory, as well as expressions for other experimentally observable quantities, and more recently, they introduced a model-free method of estimating the force-dependent transition rate using statistics from the rupture force distribution (8). Using a nonequilibrium response relation for reaction rates, (12) we provide a general perspective on the origin of Bell’s law. We explore subsequent generalizations in a number of molecular systems with increasing complexity, and we study the utility of model-independent rate estimates that depend only on the statistics of the dissipation, a thermodynamic quantity that is measurable experimentally.

Materials and methods

To start, we demonstrate how Bell’s law can be understood as a consequence of two distinct approximations, a transition state theory approximation and a near equilibrium approximation. Within transition state theory, the rate of a transition between two metastable states is

$$k_{\lambda }=\nu p_{\lambda }\left(x^{†}\right)\text{,}$$ (Equation 2)

where ν is the probability flux through $x^{†}$ and $p_{\lambda }\left(x^{†}\right)$ the probability to reach a transition state, or dividing surface in phase space, starting from a metastable state (13). This expression is valid for any value of λ, but it is an approximation to the rate because ν in principle depends on $x^{†}$, and errors associated with this approximation can be minimized with a judicious choice of dividing surface (14). In equilibrium, the probability to reach a transition state is given by $p_0\left(x^{†}\right)\propto \exp \left[-\beta F\left(x^{†}\right)\right]$, where $F\left(x^{†}\right)$ is the free energy to reach $x^{†}$, resulting in the expected Arrhenius temperature dependence.

Although transition state theory is still applicable to systems away from equilibrium, (12,15,16) the likelihood of reaching the transition state is not generally known, rendering it difficult to employ. For a system initially in equilibrium and acted upon by an external force, the nonequilibrium distribution is encoded in the Kawasaki relation (17,18,19,20):

$$p_0\left(\mathbf{r}\right)=p_{\lambda }\left(\mathbf{r}\right){\langle e^{-\beta Q}\rangle }_{\lambda ,\mathbf{r}}\text{,}$$ (Equation 3)

where $p_0\left(\mathbf{r}\right)$ is the initial equilibrium probability of full configuration $\mathbf{r}$, $p_{\lambda }\left(\mathbf{r}\right)$ is the nonequilibrium probability, and the brackets ${\langle \dots \rangle }_{\lambda ,\mathbf{x}}$ denote a trajectory ensemble average evolved under the driving force λ conditioned on ending at $\mathbf{r}$. The likelihood of the transition state, $p_{\lambda }\left(x^{†}\right)$, is the marginalization of the full configurational probability onto the reaction coordinate. For any trajectory ending in rupture at time $t_{\text{rup}}$, the excess heat dissipated to the environment, Q, over that from the conservative force is given by

$$Q\left(t_{\text{rup}}\right)={\int }_0^{t_{\text{rup}}}dt\dot{\mathbf{r}}\left(t\right)·\mathit{\lambda }\left(\mathbf{r},t\right)\text{,}$$ (Equation 4)

which for a single molecule pulling experiment could be inferred from the force-extension curve.

In general, an applied time-dependent force can change the mechanism of the transition. Even if the mechanism is conserved, both the height of the relevant barrier as well as the location of the transition state can be altered (11). However, if the barrier to transitioning is large, we expect that the dominant change in the rate under an additional force is due to modulation of the transition state probability $p_{\lambda }\left(x^{†}\right)$, leaving the location and flux through the transition state unchanged. Under these assumptions, we employ the Kawasaki relationship, Eq. 3, together with transition state theory, Eq. 2, to relate the transition rates in the presence and absence of λ,

$$k_0\approx k_{\lambda }{\langle e^{-\beta Q}\rangle }_{\lambda ,x^{†}}\text{,}$$ (Equation 5)

to the statistics of the dissipated heat. In this limit, the Kawasaki response relation connects the transition rate amplification and the distribution of excess heat dissipated to the bath. A similar rate enhancement relation has been derived from path ensemble techniques (12). Although under the assumption of a conserved transition state, this is the best estimate of the rate enhancement, converging the exponential average requires significant data. The equilibrium rate can be approximated under an assumption of small applied force with a cumulant expansion. Expanding the logarithm of the relative rate for small values of the $\beta Q$,

$$\ln k_0\approx \ln k_{\lambda }-\beta \langle Q\rangle +\frac{{\beta }^2}{2}\langle \delta Q^2\rangle \text{,}$$ (Equation 6)

which is our first main result. For simplicity of notation, we drop the explicit condition on the heat averages. Eqs. 5 and 6 imply that by measuring the rate of a rare event, as determined by a mean first passage time $k_{\lambda }=1/\langle t_{\text{rup}}\rangle$ to $x^{†}$, and accompanying heat statistics in a driven system, we can infer the rate of a rare event in thermal equilibrium. These results can be considered as a nonlinear response theory for the rate, (21) in which frenetic contributions are neglected (22). Eq. 6 is similar to higher order corrections to Bell’s law valid for constant applied forces, (23,24) generalized to arbitrary protocols.

Near equilibrium, $\beta \langle Q\rangle \lesssim 1$, and for slow driving forces, $\dot{\lambda }\approx 0$, the heat dissipated until crossing the transition state $x^{†}$ is well approximated by ${\langle Q\rangle }_{\lambda ,x^{†}}\approx {\lambda }^{†}{x}^{†}$, where we have included only terms first order in λ and integrated Eq. 4 by parts. Such an approximation is good when the transition remains activated, so the transition path time is much shorter than the time over which $\lambda \left(t\right)$ varies. Substituting this approximation for the average heat into Eq. 6 and neglecting higher order heat statistics, we find Bell’s law.

Results

To understand the various rate inference expressions, we consider a hierarchy of models with increasing complexity. In each, we apply a simple force ramp, with constant velocity v so that $\lambda \propto v$, and we measure the rate under this driving protocol, $k_{\lambda }\to k_v$, as a mean first passage time to an absorbing boundary condition. The first model we consider is a simple overdamped particle trapped in a harmonic potential in one dimension, $\mathbf{r}\to x$. The equation of motion is

$$\dot{x}=\mu F\left(x\right)+\mu \lambda +\sqrt{2D}\eta \text{,}$$ (Equation 7)

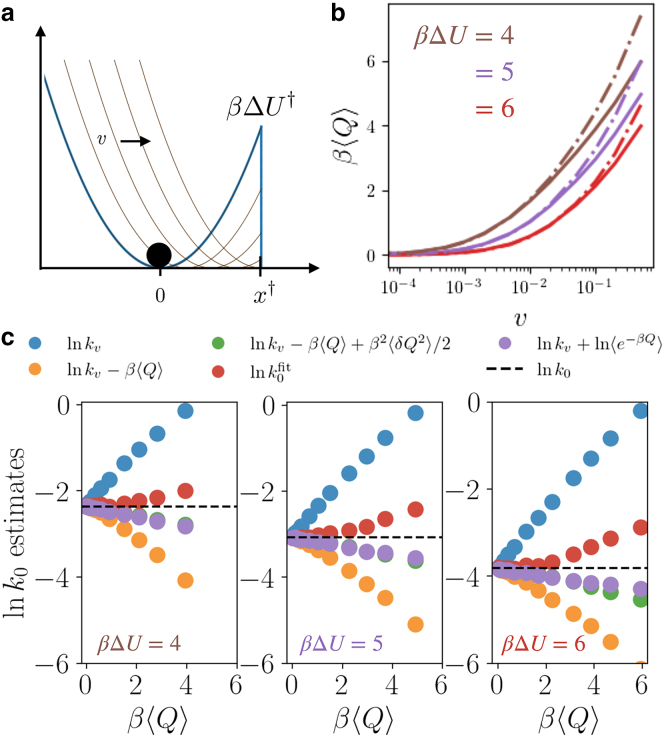
where the mobility μ and diffusivity D satisfy an Einstein relation $\beta D=\mu$, F is a conservative force, and η is a Gaussian random variable with $\langle \eta \rangle =0$ and $\langle \eta \left(t\right)\eta \left(t^{\prime }\right)\rangle =\delta \left(t-t^{\prime }\right)$. The conservative force is $F=-a\kappa x$, and the particle is pulled with a linear ramp at loading rate v, such that $\lambda =a\kappa vt\text{,}$ as depicted in Fig. 1 a. We fix $\kappa =x^{†}=\beta =\mu =1$ and vary $v=\left\{0,..,0.5\right\}$ and $a=\left\{\mathrm{8,10,12}\right\}$. Simulations are run from an initial condition at the origin and stopped upon crossing $x^{†}$ at $t=t_{\text{rup}}$, where $k_v=1/\langle t_{\text{rup}}\rangle$. Time is measured in units of $\tau =\kappa /\mu$. Associated with the location of the absorbing boundary condition is an increased potential energy, equal to $\Delta U^{†}=a\kappa x^{†2}/2$. We use a time step $t={10}^{-2}\tau$ and average over ${10}^4$ trajectories.

Figure 1.

Pulling on a harmonic molecule. (a) A cartoon of the time-dependent potential, initial barrier height $\beta \Delta U^{†}$, and absorbing boundary condition, $x^{†}$. (b) The heat dissipated gives Bell’s law in the small loading rate, long rupture time limit. Dashed curves are Bell’s law, and the solid curves represent the excess heat for three potential stiffnesses. (c) Estimates of the equilibrium escape rate for increasing barrier heights and a range of pulling velocities, each with a typical heat as in (b). To see this figure in color, go online.

In Fig. 1 b, we verify the relationship between the heat and the argument of the exponential in Bell’s law. Under a constant velocity force to lowest order in v, $Q\approx \kappa v{t}_{\text{rup}}{x}^{‡}$, which is plotted against the full expression for Q. As expected, for small v, in which $\beta \langle Q\rangle \lesssim 1$, both estimates agree. Note that $\langle Q\rangle$ does not vary linearly with v because $t_{\text{rup}}$ depends implicitly on loading rate. Fig. 1 c illustrates the convergence of the equilibrium rate employing different estimators, for a range of pulling velocities and barrier heights as $\langle Q\rangle \to 0$. The Bell’s law-like rate estimate, correcting the rate with just the mean heat, approaches the true equilibrium rate $\ln k_0$ from below. Within the validity of transition state theory, this behavior can be understood as a consequence of Jensen’s inequality, applied to Eq. 5. Including additional dissipation statistics as in the full expression in Eq. 5 yields a faster convergence to the equilibrium rate for all barrier heights considered. Significant deviations from Eq. 5 occur when the dissipation is comparable to the size of the energy barrier, in which case the barrier is degraded enough for the event to no longer be rare. The agreement between the full exponential average of the heat and its second order expansion is a result of the linearity of the model studied.

From Bell’s law, methods exist to extract the equilibrium rate from a forced measurement or simulation. A particularly accurate means of doing this is to perform maximum likelihood estimation on a known form of the rupture force distribution (7,25,26),

$$p_R\left({\lambda }^{‡}\right)=\frac{\beta k_0^{\text{fit}}}{a\kappa v}\exp \left[\beta {\lambda }^{‡}{x}^{‡}-\frac{k_0^{\text{fit}}}{a\kappa v{x}^{‡}}\left(e^{\beta {\lambda }^{‡}{x}^{‡}}-1\right)\right]\text{,}$$ (Equation 8)

to extract the equilibrium rate estimate $k_0^{\text{fit}}$ and transition state distance $x^{‡}$. Other state-of-the-art rupture force distributions exist, (27) but maximizing $p_R\left({\lambda }^{‡}\right)$ over $k_0^{\text{fit}}$ and $x^{‡}$ is a common method of inferring $k_0$ from single-molecule data, and it requires the least fitting parameters. We find $k_0^{\text{fit}}$ from fitting the rupture force distribution is comparable in accuracy to estimates from Eq. 6. For this system, all estimators that employ corrections to Bell’s law are accurate to within 30% across the full range of pulling speeds studied.

We now consider a simple model often adopted in force spectroscopy studies to understand the role of flexible linkers. Specifically, we consider overdamped motion in two spatial dimensions,

$$\dot{\mathbf{r}}=-\mathit{\mu }\nabla U\left(\mathbf{r}\right)+\mathit{\mu }\lambda +\sqrt{2\mathbf{D}}\mathit{\eta }\text{,}$$ (Equation 9)

where $\mathbf{r}=\left\{q,x\right\}$, and q is envisioned as a measured extension that is coupled to the true molecular extension, x, through a potential

$$U\left(\mathbf{r}\right)=\Delta U{x}^2{\left(x-2\right)}^2+{\kappa }_l{\left(x-q\right)}^2/2+{\kappa }_s{\mathbf{r}}^2/2\text{,}$$ (Equation 10)

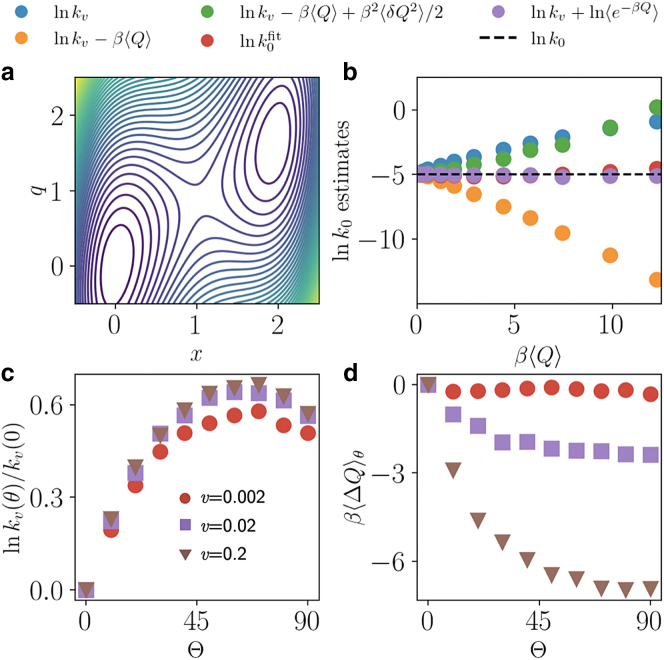
where $\Delta U$ denotes the height of the barrier in the molecular coordinate, and ${\kappa }_l$ and ${\kappa }_s$ are stiffnesses associated with the linker and trap, respectively (28,29,30,31,32). In this simplest multidimensional model of a single-molecule pulling experiment, the molecule undergoes diffusion in the 2D landscape as shown in Fig. 2 a. We perform force ramp simulations with an added force $\mathit{\lambda }={\kappa }_s{\mathbf{e}}_{\mathrm{\Theta }}vt$, parameterized by a pulling vector ${\mathbf{e}}_{\theta }=\left\{\cos \left(\mathrm{\Theta }\right),\sin \left(\mathrm{\Theta }\right)\right\}$ determined by the angle $\mathrm{\Theta }$ relative to the q axis. The rate of heat dissipation is computed from $\mathit{\lambda }·\dot{\mathbf{r}}$. We fix $\beta ={\mu }_q=1$, $x^{†}=1.5$, ${\kappa }_l={\kappa }_s=5$, and $\beta \Delta U=5$ and vary $v=\left\{0,..,0.5\right\}$ and $\mathrm{\Theta }$. As before, we estimate averages from 10 ${}^4$ trajectories with an absorbing boundary condition at $x^{†}$.

Figure 2.

Protocol dependence. (a) The potential energy surface in the molecular x and observed q coordinates with absorbing boundary placed at $x^{†}=1.5$. (b) Rate estimates labeled as in Fig. 1c. (c) Modulation of the nonequilibrium rate with pulling velocity and angle relative to the q axis where the reference rate is taken as pulling along the q direction. (d) Modulation of the dissipated heat with pulling velocity and angle relative to the q axis labeled as in (c) and reference analogously. To see this figure in color, go online.

We first consider the experimentally relevant case of $\mathrm{\Theta }=0$, where the q direction is slow, ${\mu }_q/{\mu }_x=1/20$, the opposite case, when x is slow, being treatable analytically (33). Note that when $\mathrm{\Theta }=0$, the heat is measured along the q direction only and is therefore experimentally accessible. Under these conditions, shown in Fig. 2 b, we observe that similar to the harmonic system, for small loading rates the dissipative second-cumulant estimate of Eq. 6 converges faster to the exact equilibrium rate $\ln k_0$ than either the bare driven rate or $\ln k_0\approx \ln k_v-\beta \langle Q\rangle$ as $\langle Q\rangle \to 0$. As before, the estimate from the mean dissipation converges from below; however in this case the inclusion of the second cumulant results in convergence from above. The fit from the rupture force distribution is found to perform better than Eq. 6 but is comparable to the exponential average from Eq. 5, even for higher v. This is a consequence of the nonlinear system considered in this example, where the non-Gaussian heat statistics manifest an enhanced variance and nonvanishing higher order cumulants. Estimates from both Eqs. 5 and 8 provide accuracies within 5% across the full range of pulling velocities, as pulling orthogonally to x does not degrade the barrier, allowing for transition state theory to remain accurate.

In order to understand the protocol dependence of our rate inference, we now imagine that both pulling directions are accessible. Although this is not typically experimentally practical, such a study provides insight into the convergence properties of the estimators. We consider the case ${\mu }_q/{\mu }_x=1$ and vary $\mathrm{\Theta }$ and v in Fig. 2 c and d. As expected, pulling along coordinate x, $\mathrm{\Theta }={90}^{\mathrm{o}}$, results in a faster process relative to $\mathrm{\Theta }=0^{\mathrm{o}}$, and one that dissipates less heat as quantified by $\Delta {\langle Q\rangle }_{\mathrm{\Theta }}={\langle Q\rangle }_{\mathrm{\Theta }}-{\langle Q\rangle }_0$. The rate within the driven dynamics is maximized near $\mathrm{\Theta }={60}^{\mathrm{o}}$, which is in reasonable agreement with the optimal transition state predicted by multidimensional transition state theory (34). For small v, near equilibrium, the dissipated heat approaches zero independent of $\mathrm{\Theta }$ as expected for a quasi-reversible process. These results suggest that in systems with multiple spatial dimensions, pulling along any direction may be sufficient to estimate $k_0$, but geometries that minimize the heat until rupture may lead to faster convergence of Eq. 5 and Eq. 6.

As an example of a nonlinear many-particle system, we consider stretching a semiflexible polymer with reactive ends (35) that attract each other with a strong, short-ranged potential. The configuration of the polymer consists of 3N dimensions, $\mathbf{r}=\left\{{\mathbf{r}}_1,\dots ,{\mathbf{r}}_N\right\}$, and it evolves with underdamped Langevin dynamics

$$m{\ddot{\mathbf{r}}}_i=-{\mu }^{-1}{\dot{\mathbf{r}}}_i-{\nabla }_{i}U\left(\mathbf{r}\right)+\mathit{\lambda }+{\mu }^{-1}\sqrt{2D}{\mathit{\eta }}_{\mathit{i}}\text{,}$$ (Equation 11)

where m is the mass of a monomer. The monomers interact through a potential that consists of $U\left(\mathbf{r}\right)=U_{\mathrm{b}}\left(\mathbf{r}\right)+U_{\mathrm{a}}\left(\mathbf{r}\right)+U_{\text{nb}}\left(\mathbf{r}\right)\text{,}$ where $U_{\mathrm{b}}\left(\mathbf{r}\right)$ is a harmonic bond potential between adjacent monomers,

$$U_{\mathrm{b}}\left(\mathbf{r}\right)=\frac{{\kappa }_{\mathrm{b}}}{2}\sum _{i=1}^{N-1}{\left({\mathbf{r}}_{i+1}-{\mathbf{r}}_i\right)}^2\text{,}$$ (Equation 12)

with stiffness ${\kappa }_{\mathrm{b}}$, and $U_{\mathrm{a}}\left(\mathbf{r}\right)$ is a harmonic angular potential that penalizes bending,

$$U_{\mathrm{a}}\left(\mathbf{r}\right)=\frac{{\kappa }_{\mathrm{a}}}{2}\sum _{i=2}^{N-1}{\left(\frac{{\mathbf{r}}_{i+1,i}·{\mathbf{r}}_{i,i-1}}{r_{i+1,i}{r}_{i,i-1}}-1\right)}^2\text{,}$$ (Equation 13)

where ${\mathbf{r}}_{i,i-1}={\mathbf{r}}_i-{\mathbf{r}}_{i-1}$ is the vector between two adjacent monomers, $r_{i,i-1}$ denotes its magnitude, and the potential has a stiffness ${\kappa }_{\mathrm{a}}$. The nonbonding potential $U_{\text{nb}}\left(\mathbf{r}\right)$ has a short-ranged form,

$$U_{\text{nb}}\left(\mathbf{r}\right)=\frac{1}{2}\sum _{i\ne j=1}^N{ϵ}_{ij}\left[5{\left(\frac{\sigma }{r_{i,j}}\right)}^{12}-6{\left(\frac{\sigma }{r_{i,j}}\right)}^{10}\right]\text{,}$$ (Equation 14)

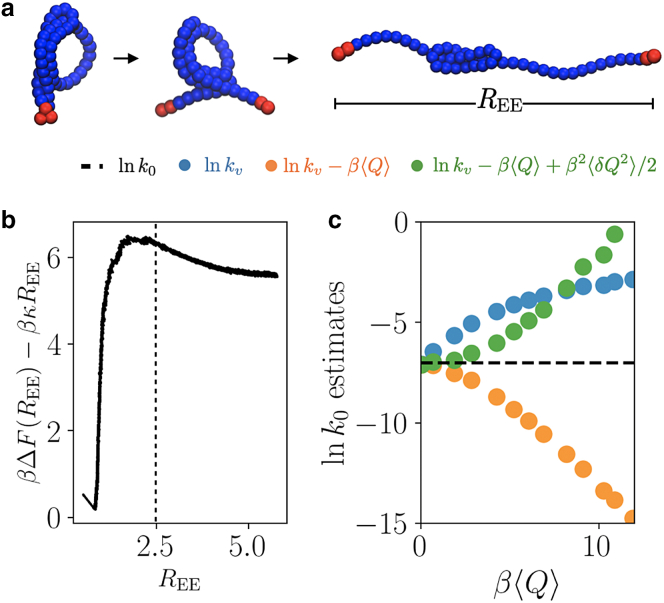
where σ sets the characteristic size of a monomer and ${\epsilon }_{ij}$ the interaction strength between monomer i and j. In order to model a reactive linker, we set the two monomers on each end to interact more strongly than the monomers in the interior of the polymer, and the cross interactions, between the linker and interior monomers, are neglected. We hold the first monomer fixed at the origin, so the end-to-end vector is ${\mathbf{R}}_{\mathbf{E}\mathbf{E}}={\mathbf{r}}_{\mathit{N}}$, and we pull the two ends apart with $\mathit{\lambda }=-\kappa \left({\mathbf{R}}_{\mathbf{E}\mathbf{E}}·\hat{\mathbf{x}}-vt\right)$, where $\hat{\mathbf{x}}$ is the unit vector in the x direction. Characteristic snapshots are shown in Fig. 3 a). We adopt a unit system with $\beta =m=\sigma =1$, with a natural timescale $\tau =1/\sqrt{\beta m{\sigma }^2}$. We set $\mu =5$, ${\kappa }_{\mathrm{b}}=110$, ${\kappa }_{\mathrm{a}}=4.5$, $\kappa =5.5$, end monomer interactions ${ϵ}_{1,N}=4.5$, and interior monomer interactions ${ϵ}_{3,N-3}=1.7$, $N=50$. We employ a time step of 10 ${}^{-2}\tau$ and estimate averages from 500 trajectories.

Figure 3.

(a) A semiflexible polymer with reactive ends, highlighted in red, mechanically unfolded to a large end-to-end distance during a force ramp experiment. (b) The free energy of the untethered polymer as a function of the end-to-end distance. The black dashed line denotes the absorbing boundary condition. (c) Rate estimates, labeled as in Fig 1c, as a function of heat. To see this figure in color, go online.

Under these conditions, the semiflexible polymer permits two types of conformations: a folded state for small $R_{\text{EE}}=\left|{\mathbf{R}}_{\mathbf{E}\mathbf{E}}\right|\text{,}$ where the linker monomers are bound, and an unfolded state for large $R_{\text{EE}}\text{,}$ where the linker monomers do not interact strongly. To differentiate between these two regimes, we first computed the work to pull $R_{\text{EE}}$ reversibly, denoted by $\beta \Delta F\left(R_{\text{EE}}\right)$. This is shown in Fig. 3 b and evaluated using the Jarzynski equality (1) within a steered Brownian dynamics framework (36). For the free energy calculation, we employed the same constant v protocols, including all of the simulation data shown in Fig. 3 c. The free energy exhibits a deep minimum for small end-to-end distances and a second shallow basin for large end-to-end distances. Under a small additional load, $-\kappa R_{\text{EE}}$, the two basins are separated by a barrier in the free energy. Using this biased free energy, we set an absorbing boundary condition for our pulling calculation to $R_{\text{EE}}^{†}=2.5\sigma$.

We pulled the polymer at loading rates over the interval $v=\left\{0.001-0.2\right\}\sigma /\tau$ and measured the dissipative heat and first passage time to $R_{\text{EE}}^{†}$. Shown in Fig. 3 c, we find that convergence to the true equilibrium rate is fastest using Eq. 6, and as in the 2D model the estimate converges from above upon the approach to equilibrium. As in both previous models, the incorporation of the variance of the heat provides an accurate estimate of the equilibrium over a range of heats that is comparable to a significant fraction of the native barrier, in this case as long as $\beta \langle Q\rangle <3$. The first-order estimate converges to the true equilibrium rate slowly from below, and slow convergence of the exponential average (37) in Eq. 5 prohibited its application in this example. Over the range of pulling velocities considered, if either the first-order estimate or the bare rate were fit and linearly extrapolated to $v=0$, both would overestimate the equilibrium rate by about an order of magnitude.

Discussion

Our results demonstrate an underlying stochastic thermodynamic basis for Bell’s law under nonequilibrium driving and a useful means for going beyond it to infer equilibrium transition rates. Within the context of single-molecule force ramp experiments, we have demonstrated a robust way to infer unfolding rates using the statistics of the heat distribution, conditioned on ending at an absorbing transition state. Although within transition state theory the full exponential estimator is most accurate, we suspect that in general its convergence will be cumbersome (37), and the perturbative expansions illustrated here will provide an intermediate means of rate estimation. In the future, this response method may be used to study the rare kinetics of more detailed protein models, protein unfolding in optical tweezing and atomic force microscopy experiments, and other rare molecular transitions that can be sped up by applied force (38,39,40,41). The nonequilibrium thermodynamic framework developed here works not only with constant velocity force ramps, but it could be used with more complex protocols. Indeed, protocols can be optimized to allow for rate inferences, (42) or could be used as a theoretical framework for understanding other approximate methods that use driven dynamics to infer rates with applied force (43,44,45,46).

Author contributions

B. K.-S. and D.T.L. designed and carried out the research, analyzed the data, and wrote the article.

Editor: Michael T. Woodside