Fast and accurate Bayesian polygenic risk modeling with variational inference

Summary

The advent of large-scale genome-wide association studies (GWASs) has motivated the development of statistical methods for phenotype prediction with single-nucleotide polymorphism (SNP) array data. These polygenic risk score (PRS) methods use a multiple linear regression framework to infer joint effect sizes of all genetic variants on the trait. Among the subset of PRS methods that operate on GWAS summary statistics, sparse Bayesian methods have shown competitive predictive ability. However, most existing Bayesian approaches employ Markov chain Monte Carlo (MCMC) algorithms, which are computationally inefficient and do not scale favorably to higher dimensions, for posterior inference. Here, we introduce variational inference of polygenic risk scores (VIPRS), a Bayesian summary statistics-based PRS method that utilizes variational inference techniques to approximate the posterior distribution for the effect sizes. Our experiments with 36 simulation configurations and 12 real phenotypes from the UK Biobank dataset demonstrated that VIPRS is consistently competitive with the state-of-the-art in prediction accuracy while being more than twice as fast as popular MCMC-based approaches. This performance advantage is robust across a variety of genetic architectures, SNP heritabilities, and independent GWAS cohorts. In addition to its competitive accuracy on the “White British” samples, VIPRS showed improved transferability when applied to other ethnic groups, with up to 1.7-fold increase in $R^2$ among individuals of Nigerian ancestry for low-density lipoprotein (LDL) cholesterol. To illustrate its scalability, we applied VIPRS to a dataset of 9.6 million genetic markers, which conferred further improvements in prediction accuracy for highly polygenic traits, such as height.

Graphical abstract

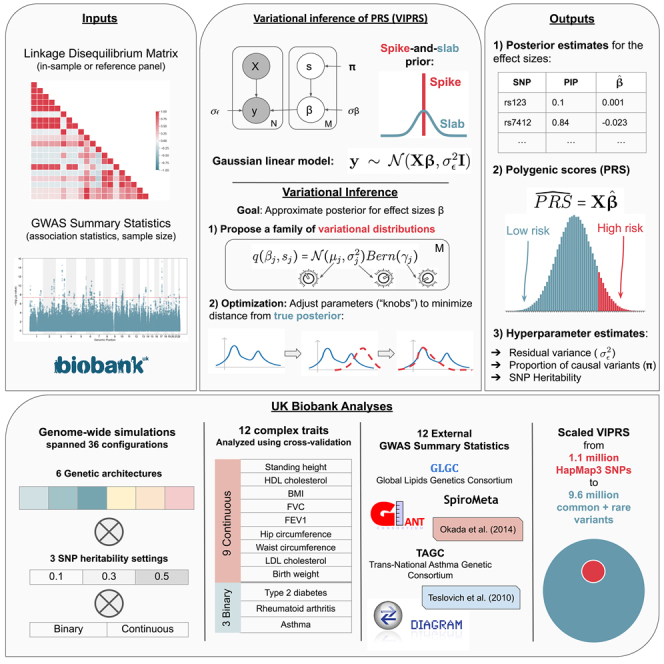
We present VIPRS, a fast and accurate variational Bayesian method for estimating polygenic risk scores from genome-wide association study (GWAS) data. The method is shown to be robust and competitively accurate against popular baselines and scales well to dense genotype array data.

Introduction

In recent years, with the rapid growth of large-scale biobank data with comprehensive genotyping and phenotyping efforts,^1,2,3 there has been growing interest in developing statistical methods to quantify an individual’s disease risk from their genotype data.^4,5,6,7,8 At the same time, these rich biobank data sources have powered many recent analyses of complex traits and diseases, revealing highly polygenic architectures^9,10,11 with a wide range of effect sizes across different genomic categories.^12,13,14 Linear models are an important framework for complex trait analysis that allow for the estimation of the additive genetic component of a phenotype, also known as a polygenic score (PGS) or polygenic risk score (PRS) in clinical contexts.^5,15 Even though many examples of genetic interactions have been documented, such additive effects capture much of the genetic variation underlying human complex traits.^16,17 Recent work has highlighted the clinical relevance of polygenic scores for some diseases and health conditions,^18,19 especially in applications related to disease risk stratification^20,21,22 and personalized medicine.²³

Estimating PGSs from genome-wide association study (GWAS) data has a long and rich history in the field of quantitative genetics as well as the animal and plant breeding literature.^24,25 In human and medical genetics, it remains an active area of research, with numerous methods recently developed.^{4,6,26,27,28,29,30,31,32,33,34} Standard PRS methods formulate the problem of polygenic risk estimation in terms of a multiple linear regression framework, where the goal is to infer the joint effect sizes of all genetic variants on the trait. The most common class of genetic variation considered in these analyses are single-nucleotide polymorphisms (SNPs), which are either measured by modern genotyping arrays or statistically imputed with reference haplotypes.^35,36

Genotyping arrays combined with imputation can accurately capture the genotype of an individual at millions of genetic markers. When paired with modern GWAS sample sizes routinely exceeding hundreds of thousands of individuals, high dimensional data of this scale present several computational and statistical challenges. Furthermore, most individual-level GWAS data sources are protected for privacy concerns.³⁷ These two factors motivated the development of a number of PRS methods that estimate PRSs on the basis of GWAS summary statistics,^{4,6,27,28,29,31,32,33,34} which are the marginal test statistic per SNP.

Within this class of summary statistics-based methods, Bayesian PRS models enable a principled way to incorporate prior knowledge as probability distributions over the genetic causal architecture of complex traits. In addition to providing meaningful estimates of parameter uncertainties,³⁸ Bayesian approaches have shown competitive predictive ability, exceeding the predictive performance of heuristic or penalized estimators in many settings.^{6,28,32,33,39,40} However, a major limitation of some existing Bayesian methods is that their scalability is hampered by slow and inefficient inference techniques. While heuristic methods such as clumping-and-thresholding (C+T) are routinely applied on millions of SNPs, Bayesian approaches are generally restricted to a smaller subset of approximately one million genetic markers. One of the main reasons for this limitation stems from computational considerations: most Bayesian PRS methods employ Markov chain Monte Carlo (MCMC) algorithms to approximate the posterior for the effect sizes.^4,6,28,32 MCMC algorithms are known to be asymptotically accurate but often slow to converge.^41,42 In practice, to obtain accurate posterior estimates, the MCMC chains need to be run for hundreds or thousands of iterations.^4,6 This challenge can be partially remedied with the help of efficient software implementation and enhanced linear algebra routines, which recently enabled scaling up two well-known MCMC-based Bayesian PRS methods to several million SNPs.^6,40 While this is an important advance, these variants still constitute a small fraction of the genetic variation that can be assayed by modern whole-genome-sequencing technologies.^3,43

An alternative scheme for approximating the posterior density for the effect sizes is variational inference (VI), a fast and deterministic class of algorithms that recast the problem of posterior inference in the form of an optimization problem.^41,42,44,45 Variational methods have seen a surge of interest in the machine learning literature in recent years as a result of significant advances in stochastic optimization techniques.^46,47 Methods that utilize VI have been explored in a wide variety of statistical genetics applications, specifically in the context of linear mixed models (LMMs),⁴⁸ association mapping,^49,50 fine-mapping,^51,52 and enrichment analysis,^53,54 among others. More recently, a number of studies examined the properties and relative accuracy of certain variational approximations to PRS by using both individual level data and summary statistics.^34,55,56,57

In this work, we present variational inference of polygenic risk scores(VIPRS), a Bayesian summary statistics-based PRS method that utilizes VI to approximate the posterior for the effect sizes. We conduct a comprehensive set of experiments by using simulated and real traits to assess the predictive ability of VIPRS in comparison with the some of the most popular Bayesian and non-Bayesian PRS methods. Overall, we show that VIPRS is a scalable and flexible method that enjoys the speed and efficiency of heuristic approaches, such as clumping-and-thresholding (C+T), while rivaling state-of-the-art Bayesian methods in terms of its predictive performance. We demonstrate the flexibility of the method by testing its predictions with different families of priors on the effect size, paired with four distinct strategies for tuning the hyperparameters of the model. To illustrate its scalability, we evaluate the predictive accuracy of VIPRS with approximately 9.6 million SNPs, almost an order of magnitude greater than the standard HapMap3 subset routinely used for this task. This allows us to examine the potential for phenotype prediction by using a more comprehensive set of genetic variants segregating in the human population.

Material and methods

Overview of the VIPRS model

Given a random sample of individuals from a general population with paired genotype and phenotype data, we model the dependence of the phenotype on the genotype via the standard linear model,

$$\mathbf{y}=\mathbf{X}\mathbf{\beta }+\mathbf{ϵ}\text{,}$$ (Equation 1)

where $\mathbf{y}$ is an $N\times 1$ vector of phenotypic measurements for $N$ individuals, $\mathbf{X}$ is the $N\times M$ genotype matrix that records the counts of alternative alleles for each individual at each genetic marker, $\mathbf{\beta }$ is a vector of effect sizes for each of the $M$ markers, and $\mathbf{ϵ}$ is an $N\times 1$ vector that captures the residual effects on the trait for each individual. Our model derivation assumes that both the genotype matrix $\mathbf{X}$ and phenotype vector $\mathbf{y}$ are column-wise standardized to have zero mean and unit variance. For quantitative traits, we assume that the phenotypes follow a Gaussian likelihood, such that $\mathbf{y}\sim \mathcal{N}\left(\mathbf{X}\mathbf{\beta },{\sigma }_{ϵ}^2\mathbf{I}\right)$, where ${\sigma }_{ϵ}^2$ is the residual variance. For case-control traits, we model the latent continuous liability underlying the disease,⁵⁸ which is assumed to follow the same Gaussian likelihood. Since our method operates on summary statistics, we followed the common practice of converting the marginal statistics of binary phenotypes from the log-odds to the liability scale.^4,59,60 Practically, a central goal of polygenic risk modeling is to arrive at a robust estimate for the effect sizes $\mathbf{\beta }$. In the Bayesian framework, this problem is tackled by imposing a prior distribution over the effect sizes and then deriving a solution for the posterior distribution given the data likelihood and the prior,

$$p\left(\mathbf{\beta }\mid \mathbf{X},\mathbf{y},\theta \right)\propto p\left(\mathbf{y}\mid \mathbf{X},\mathbf{\beta },\theta \right)p\left(\mathbf{\beta },\theta \right)\text{,}$$ (Equation 2)

where $\theta$ encapsulates all fixed hyperparameters in the model, i.e., parameters that we do not assign a prior. Here, the constant of proportionality is the marginal likelihood or the partition function for the posterior, $\int p\left(\mathbf{y}\mid \mathbf{X},\mathbf{\beta },\theta \right)p\left(\mathbf{\beta },\theta \right)d\mathbf{\beta }$, also known as the model evidence.^41,42 In recent years, considerable work has been devoted to deriving Bayesian PRS models with flexible priors on the effect sizes, such as the continuous shrinkage²⁸ and mixture priors.⁶ In this work, we follow the lead of earlier approaches, e.g., Vilhjálmsson et al.⁴ and Carbonetto and Stephens,⁵¹ and assign a spike-and-slab prior^61,62 on the effect sizes,

$${\beta }_j\sim \pi \mathcal{N}\left({\beta }_j;0,{\sigma }_{\beta }^2\right)+\left(1-\pi \right){\delta }_0\text{.}$$ (Equation 3)

Here, $\pi$ is a parameter that denotes the prior probability that a variant is causal, ${\sigma }_{\beta }^2$ is the prior variance on the effect size of each SNP, and ${\delta }_0$ is the Dirac delta function. In the simplest formulation of this model, we assume that $\pi$ and ${\sigma }_{\beta }^2$ are shared across all SNPs. Thus, $\pi$ may also be considered as the fraction of variants that are causal for the trait of interest, and the ${\sigma }_{\beta }^2$ parameter is related to the trait’s per-SNP heritability.^4,63 The spike-and-slab prior is a special case of the more general mixture prior:

$$p\left({\beta }_j\mid s_j\right)p\left(s_j\right)=\prod _{k=1}^K\mathcal{N}{\left({\beta }_j;0,{\sigma }_k^2\right)}^{s_{jk}}\prod _{k=1}^K{\pi }_k^{s_{jk}}\text{,}$$ (Equation 4)

where $s_{jk}$ is binary indicator for SNP $j$ belonging to the $k^{th}$ mixture component and ${\pi }_k$ and ${\sigma }_k^2$ denote the the mixing proportion and prior variance for component $k$, respectively. It is well known that Bayesian linear regression models with a spike-and-slab prior on the effect sizes result in an intractable posterior,^51,61,62 necessitating the use of approximate posterior inference schemes.

VIPRS model inference

In most of the previous Bayesian PRS formulations, the authors employ a Gibbs sampler, a MCMC technique that relies on conditional conjugacy between the prior and the likelihood, to approximate the posterior distribution of the effect sizes.^4,6,28,32 In this work, we instead leverage a technique known as Variational Inference (VI),⁴⁴ which approximates intractable densities by proposing a simple parametric distribution $q\left(\mathbf{\beta },\mathbf{s}\right)$ and optimizing its parameters to match the true posterior as closely as possible.⁴⁵ The closeness between the true posterior and the proposed distribution is measured by the Kullback-Leibler (KL) divergence,

$$KL\left[q\Vert p\right]={\mathbb{E}}_{q\left(\mathbf{\beta },\mathbf{s}\right)}\left[\log q\left(\mathbf{\beta },\mathbf{s}\right)\right]-{\mathbb{E}}_{q\left(\mathbf{\beta },\mathbf{s}\right)}\left[\log p\left(\mathbf{\beta },\mathbf{s}\mid \mathbf{X},\mathbf{y},\theta \right)\right]$$ (Equation 5)

$$={\mathbb{E}}_{q\left(\mathbf{\beta },\mathbf{s}\right)}\left[\log q\left(\mathbf{\beta },\mathbf{s}\right)\right]-{\mathbb{E}}_{q\left(\mathbf{\beta },\mathbf{s}\right)}\left[\log p\left(\mathbf{y},\mathbf{\beta },\mathbf{s}\mid \theta ,\mathbf{X}\right)\right]+\log p\left(\mathbf{y}\mid \mathbf{X},\theta \right)\text{,}$$ (Equation 6)

where ${\mathbb{E}}_{q\left(\mathbf{\beta },\mathbf{s}\right)}$ is the expectation taken with respect to the proposed distribution.^41,42 However, the KL divergence includes the normalizing constant that made the posterior intractable in the first place. Thus, practitioners typically optimize a surrogate objective known as the evidence lower bound (ELBO) of the log marginal likelihood^41,42,45:

$$\begin{array}{cc}& \mathcal{L}=\log p\left(\mathbf{y}\mid \mathbf{X},\theta \right)=\log \sum _{\mathbf{s}}\int \frac{p\left(\mathbf{y}\mid \mathbf{X},\mathbf{\beta },\theta \right)p\left(\mathbf{\beta },\mathbf{s}\mid \theta \right)}{q\left(\mathbf{\beta },\mathbf{s}\right)}q\left(\mathbf{\beta },\mathbf{s}\right)d\mathbf{\beta }\\ & \ge \sum _{\mathbf{s}}\int q\left(\mathbf{\beta },\mathbf{s}\right)\log p\left(\mathbf{y}\mid \mathbf{X},\mathbf{\beta },\mathbf{s},\mathbf{\theta }\right)p\left(\mathbf{\beta },\mathbf{s}\mid \mathbf{\theta }\right)d\mathbf{\beta }-\sum _{\mathbf{s}}\int q\left(\mathbf{\beta },\mathbf{s}\right)\log q\left(\mathbf{\beta },\mathbf{s}\right)d\mathbf{\beta }\\ & ={\mathbb{E}}_{q\left(\mathbf{\beta },\mathbf{s}\right)}\left[\log p\left(\mathbf{y},\mathbf{\beta },\mathbf{s}\mid \theta ,\mathbf{X}\right)\right]-{\mathbb{E}}_{q\left(\mathbf{\beta },\mathbf{s}\right)}\left[\log q\left(\mathbf{\beta },\mathbf{s}\right)\right]\equiv ELBO\end{array}$$ (Equation 7)

Here, the first term ${\mathbb{E}}_{q\left(\mathbf{\beta },\mathbf{s}\right)}\left[\log p\left(\mathbf{y},\mathbf{\beta },\mathbf{s}\mid \theta ,\mathbf{X}\right)\right]$ in Equation 7 is the expectation of the log joint likelihood of the phenotypes and the effect sizes and the second term $-{\mathbb{E}}_{q\left(\mathbf{\beta },\mathbf{s}\right)}\left[\log q\left(\mathbf{\beta },\mathbf{s}\right)\right]$ corresponds to the entropy of the variational distribution. The ELBO in Equation 7 and the KL-Divergence in Equation 6 add up to the marginal likelihood: $ELBO+KL\left[q\Vert p\right]=\mathcal{L}$. Therefore, maximizing ELBO is equivalent to minimizing the KL-Divergence.^41,42,45

The choice of approximating variational distribution $q\left(\mathbf{\beta },\mathbf{s}\right)$ is a central component in this setting. For simplicity and computational efficiency, we make use of the paired mean-field assumption,^41,42,64 whereby the density factorizes across the input coordinates, and model the effect size at each locus with a two-component Gaussian mixture density,^51,64,65

$$q\left(\mathbf{\beta },\mathbf{s}\right)=\prod _j^{M}q\left({\beta }_j,s_j\right)=\prod _j^M\mathcal{N}\left({\beta }_j;{\mu }_j,{\sigma }_j^2\right)\mathrm{Bern}\left(s_j;{\gamma }_j\right)\text{.}$$ (Equation 8)

Here, ${\mu }_j,{\sigma }_j^2,{\gamma }_j$ are the variational parameters defined for each variant in the dataset and $\mathrm{Bern}\left(s_j;{\gamma }_j\right)={\gamma }_j^{s_j}{\left(1-{\gamma }_j\right)}^{1-s_j}$ denotes a Bernoulli distribution with probability ${\gamma }_j$ for SNP $j$. Therefore, the Bernoulli indicator in the proposed distribution approximates the posterior probability that the variant is causal for the trait of interest and the Gaussian component approximates the posterior for the effect size.⁵¹ In the supplemental methods, we provide detailed derivations that show that, under certain assumptions, this variational family leads to the following closed-form updates that only depend on GWAS summary statistics and the SNP-by-SNP correlation or linkage disequilibrium (LD) matrix, which can be derived from an appropriately matched reference panel:

$${\sigma }_j^2=\frac{{\sigma }_{ϵ}^2}{N+{\sigma }_{ϵ}^2/{\sigma }_{\mathbf{\beta }}^2}$$ (Equation 9)

$${\mu }_j=\frac{N{\sigma }_j^2}{{\sigma }_{ϵ}^2}\left({\hat{\beta }}_j-\sum _{k\ne j}{\gamma }_k{\mu }_k{R}_{jk}\right)$$ (Equation 10)

$${\gamma }_j=\mathrm{Sigmoid}\left(\log \left(\frac{\pi }{1-\pi }\right)+\frac{1}{2}\log \left(\frac{{\sigma }_j^2}{{\sigma }_{\beta }^2}\right)+\frac{1}{2{\sigma }_j^2}{\mu }_j^2\right)\text{.}$$ (Equation 11)

Assuming standardized genotype and phenotype, ${\hat{\beta }}_j={\mathbf{y}}^{\top }{\mathbf{x}}_j/N$ is the marginal GWAS effect size of SNP $j$, $R_{jk}={\mathbf{x}}_j^{\top }{\mathbf{x}}_k/N$ is the LD between a pair of SNPs $j$ and $k$, and the sigmoid function is defined as $\mathrm{Sigmoid}\left(x\right)=1/\left(1+\exp \left(-x\right)\right)$. This formulation enables us to employ a fast coordinate ascent optimization algorithm to approximate the posterior distributions of the effect sizes. Related variational approaches have been explored in the context of fine mapping^51,52 and polygenic modeling^34,55,57 but differ in both conceptual and technical details—we discuss these similarities and differences in the supplemental methods section S2.7.

In addition, to perform inference given some of the unknown fixed parameters, i.e., $\theta =\left(\pi ,{\sigma }_{\beta }^2,{\sigma }_{ϵ}^2\right)$, the default formulation of the VIPRS model uses the variational expectation maximization (VEM) algorithm,^50,51,65 where in an alternating fashion, in the E-step we update the variational parameters given the hyperparameters and in the M-step we update the hyperparameters of the model. In both the E- and M-steps, we update the free parameters of the model to maximize our objective, the ELBO. In supplemental methods section S2.3, we show that updating the hyperparameters to maximize the ELBO also results in closed-form solutions for those parameters.

Once the VEM optimization procedure converges to a local maximum, we output the posterior mean for the effect sizes and use this quantity to weigh the contribution of each genetic marker to the polygenic score of a given sample. Concretely, under the spike-and-slab prior outlined above, the posterior mean for effect size of variant $j$ is given by ${\eta }_j:={\gamma }_j{\mu }_j$. Thus, the polygenic score for a new test sample $i$ can be defined as ${\widehat{PRS}}_i={\sum }_j{X}_{ij}{\eta }_j$. For case-control traits, this polygenic score approximates the latent continuous liability underlying the disease and can be thresholded or used as is along with other clinical and demographic data for downstream clinical applications.^20,21,22,23

Despite the conceptual simplicity of the framework described above, fitting such a model to biobank-scale data presents several computational challenges. For instance, the closed-form update equations for some of the variational parameters involve terms that relate to the LD between the focal variant and all other variants in the genome. This can be computationally prohibitive to compute for millions of variants and for hundreds of EM iterations. To overcome this, we follow the lead of other summary-statistics-based PRS methods and use a banded or shrunk LD matrix,^4,6,28,32 which results in substantial improvements in speed without substantially degrading predictive performance.

Hyperparameter tuning strategies

The standard VIPRS model employs a VEM framework to infer the hyperparameters $\mathbf{\theta }=\left(\pi ,{\sigma }_{\beta }^2,{\sigma }_{ϵ}^2\right)$, where in the M-step, we update each hyperparameter to maximize the surrogate objective, i.e., the ELBO.^51,65 This strategy works well in many settings, but it is prone to entrapment in local optima,⁶⁵ which may degrade overall predictive performance of the model. In this work, we explored three alternative strategies for tuning the hyperparameters of the model.

VIPRS-GS

In the first strategy, we performed grid search (GS) over the hyperparameters of the model, selecting the values that result in the best predictive performance on a held-out validation set.^27,29,32 We also explored a pseudo-validation variant of the model (supplemental methods) and showed that it results in almost identical prediction accuracy (Figures S6 and S7). The grid search was performed specifically over the proportion of causal variants $\pi$, with the remaining parameters updated according to their approximate maximum likelihood estimates. The grid for $\pi$ ranged from $\frac{1}{M}$ to $\frac{M-1}{M}$ with 30 equidistant values on a ${\log }_{10}$ scale, where $M$ is the number of variants included in the model.

VIPRS-BO

To search over the hyperparameter space without the constraint of a predefined and discrete grid, we experimented with a second hyperparameter tuning technique known as Bayesian optimization (BO).⁶⁶ In BO, we assume that there is an underlying unknown function $f\left(\mathbf{\theta }\right)$ that takes the hyperparameters as input and outputs a certain score that we wish to optimize, such as the training ELBO or the validation $R^2$. This unknown function is modeled with a Gaussian Process (GP) prior, which allows us to explore the parameter space efficiently while accounting for uncertainty in a principled manner. The other component in this framework is the acquisition function, a heuristic that maps from the GP posterior to information about the most promising regions in hyperparameter space.^66,67 In our experiments, we used the scikit-optimize python package to perform this optimization, with gp_hedge as the default acquisition function. The optimizer was allowed to sequentially evaluate up to 20 points in a bounded $1D$ space for the hyperparameter $\pi$.

VIPRS-BMA

In the third strategy, we used a Bayesian model-averaging (BMA) framework, where we use importance sampling to integrate out some of the hyperparameters of the model, as outlined in Carbonetto and Stephens.⁵¹ The main idea here is that instead of fixing $\pi$ to a particular value, we fit the VIPRS model along a grid of $\pi$ values, as in VIPRS-GS, and then take a weighted average of the effect size estimates for each SNP on the basis of each model’s ELBO.^50,51

Similar to previous work in this area, we note that these three strategies can be deployed in conjunction with the VEM framework,^50,51,68 where some of the hyperparameters are updated with their approximate maximum likelihood estimates while the remaining parameters are optimized via the user’s strategy of choice. This is important in practice because, with the three hyperparameters of the model, an exhaustive search will require searching over a three-dimensional grid, which can be computationally expensive. Therefore, in our experiments and analyses, for all of the three strategies that we explored, we only implemented a search over the fraction of causal variants $\pi$ and estimated the other two hyperparameters by using the closed-form updates in the M-step.

Data preprocessing

To assess the performance of VIPRS on a biobank-scale dataset, we made use of the UK Biobank (UKB), a large database of genomic and phenotypic measurements from 488,377 participants from the United Kingdom.¹ In its latest release, the UKB database has genotype information from 488,377 individuals, from which, after applying standard quality control procedures, we retained data for a total of 337,205 samples. We accessed the UKB data under IRB Study Number A10-M48-19B. Briefly, the sample quality controls involved selecting unrelated individuals with White British ancestry, defined by the UKB on the basis of self-reported ethnic background as well as principal-component analysis (PCA) of the GRM, and who were also included in the PCA and phasing procedures outlined in Bycroft et al.¹ We restricted our main analyses to the White British cohort in order to maximize power to detect causal effects while reducing confounding. In addition this, we filtered data for individuals with detected sex chromosome aneuploidy, excess relatedness, or missing genotype rate exceeding 5% from this analysis.

The genetic variants or SNPs included in the study were selected on the basis of a number of quality control filters applied at various stages in the analysis. For the base dataset, we excluded variants with duplicate rsIDs, ambiguous strand, imputation quality score $<$ 0.3, Hardy-Weinberg equilibrium p value $<{10}^{-10}$, or genotype missingness rate $>$ 0.05. We also removed multi-allelic variants as well as SNPs in long-range LD regions, as specified in supplemental table 13 of Bycroft et al. (2018).¹ In the GWAS analyses or LD matrix construction, we further filtered variants with minor allele count (MAC) < 5 or minor allele frequency (MAF) < 0.1%. This resulted in a total of 9,590,026 bi-allelic variants that were used in the expanded SNP set analyses. Finally, following standard practice in PRS methodologies,^6,32 for the base analyses with the VIPRS model, we restricted to the set of variants in the HapMap3 reference panel,³⁶ resulting in a total of 1,093,308 SNPs. Most of these quality control procedures were carried out with the genetic analysis software tool plink2.⁶⁹

Construction and efficient representation of LD matrices

An important quantity in the model is the LD or SNP-by-SNP correlation matrix $\mathbf{R}$. The matrix, or its columns, show up mainly in the update equations for the variational parameters ${\mu }_j$ of each SNP $j$ (Equation 10), the estimate of the residual variance ${\sigma }_{ϵ}^2$, as well as in the objective function (i.e., ELBO) (supplemental methods). In our model derivation, the LD matrix is assumed to be estimated in-sample from the same GWAS cohort. In practice, this information is generally not publicly available and working with dense LD matrices can be computationally inefficient. To get around these difficulties, we experimented with approximate and sparse LD estimators that were previously explored for in-sample or out-of-sample settings.^4,6,27 Our software supports a number of these approximate LD matrix estimators, including sample, block, shrinkage, and windowed estimators.

Sample estimator

In the sample estimator, we estimate the sample Pearson correlation coefficient between all SNPs on the same chromosome, which results in a dense matrix. For larger chromosomes and SNP sets, it is impractical to load dense matrices of this scale to memory. To handle data at that scale, we use compressed and chunked on-disk storage with Zarr arrays in python for fast, multi-threaded read and write access. Then, as we iterate through SNPs in the E-step, we load the matrix into memory one chunk at a time, thus allowing us to train VIPRS with extremely large LD matrices. In supplemental methods, we describe a procedure that allows us to load the LD matrix only once per iteration, resulting in improved speed and efficiency.

Block estimator

In the block LD estimator, we only estimate the sample LD between SNPs that are within the same LD block, as defined by, e.g., LDetect.⁷⁰ This is similar to what is done in the Lassosum and PRScs frameworks.^27,28

Shrinkage estimator

In the shrinkage estimator, we shrink and threshold the entries of the sample LD matrix according to procedure outlined by Lloyd-Jones et al.⁶ and Wen and Stephens⁷¹ and implemented in the gctb software. Briefly, for the shrinkage estimator, we shrink each element of the LD matrix by a quantity proportional to the distance between pairs of variants $j$ and $k$ in along the chromosome: ${\hat{R}}_{jk}=R_{jk}\cdot e^{c\cdot d\left(j,k\right)}$. In this context, $d\left(j,k\right)$ is the distance in centimorgans (cM) between variants $j$ and $k$ and the constant $c$ is related to sample size used to infer the genetic map as well as effective population size.^6,71

Windowed estimator

For the windowed LD estimator, we only consider the correlation between a focal variant with variants that are at most 3 cM away from it along the chromosome.^32,63 This estimator results in compact and banded LD matrices that can easily fit in memory on modern compute nodes.

To construct LD matrices for the main analyses of this paper, we selected a random subset of 50,000 individuals from the White British cohort described above. Within that group of individuals, we filtered SNPs with MAC < 5 or MAF < 0.1%, and again restricted to variants in the HapMap3 reference panel. For the analyses with the expanded set of variants, we only removed the HapMap3 filter. Unless explicitly stated otherwise, the analyses with the VIPRS model employed the windowed estimator for LD, with the distance cutoff set to 3 cM. The matrices are stored in compressed Zarr array format and are publicly available for download (see web resources).

Simulation study

To assess the predictive performance of VIPRS on large-scale datasets and for varying genetic architectures, we conducted a GWAS by using the pre-processed genotype data from the UK Biobank cohort. We simulated quantitative and binary traits according to six different genetic architectures and three settings for the additive genetic variance, $h_{SNP}^2=\left\{\mathrm{0.1,0.3,0.5}\right\}$, for a total of 18 simulation configurations for each trait category (continuous and case-control). For the first three genetic architectures, we simulated the effect size for each variant according to the generative model outlined previously in Equation 3, with three settings for the proportion of causal variants, $\pi =\left\{{10}^{-4},{10}^{-3},{10}^{-2}\right\}$. The next two simulation scenarios involved sampling the effect size for each variant from a scale mixture of Gaussians (supplemental methods), $p\left({\beta }_j\right)={\sum }_{k=1}^4{\pi }_k\mathcal{N}\left({\beta }_j;0,d_k{\sigma }_{\beta }^2\right)$, with the mixing proportions set to $\pi =\left\{\mathrm{0.95,0.02,0.02,0.01}\right\}$. The variance multipliers $d_k$ were set to $d=\left\{\mathrm{0.0,0.01,0.1,1}\right\}$ for the sparse mixture model and $d=\left\{\mathrm{0.001,0.01,0.1,1}\right\}$ for the infinitesimal mixture model. Finally, the last genetic architecture tested was the standard infinitesimal model, with the effect size drawn from a zero-centered Gaussian density $p\left({\beta }_j\right)=\mathcal{N}\left({\beta }_j;0,{\sigma }_{\beta }^2\right)$. For each configuration, we generated ten independent phenotypes for a total of 180 simulated traits. For the binary traits, we followed the same procedure but used the liability threshold model⁵⁸ to obtain case-control status, with prevalence set to $15\%$.

After we generated simulated phenotypes for all individuals in the study $\left(N=\mathrm{337,205}\right)$, we excluded the 50,000 samples used to generate the LD matrices and randomly split the remaining samples into 70% training $\left(N=\mathrm{201,043}\right)$, 15% validation, and 15% testing ($N=\mathrm{43,081}$ each). We then used the genotype and simulated phenotype data of the training samples to generate GWAS summary statistics with plink2.⁶⁹

Application to real traits from the UKB

To assess the predictive performance of VIPRS on real phenotypes, we extracted phenotypic measurements for nine quantitative and three case-control traits for the UKB cohort described previously. The quantitative phenotypes included log-transformed waist circumference (WC), log-transformed hip circumference (HC), standing height (HEIGHT), birth weight (BW), log-transformed body mass index (BMI), log-transformed high-density lipoprotein (HDL), low-density lipoprotein (LDL), forced vital capacity (FVC), and forced expiratory volume in the first second (FEV1). For each trait, we excluded samples with outlier or extreme values for the trait. For the remaining samples, within each sex separately, we corrected for age and the top ten principal components (PCs) of the genetic relationship matrix (GRM) and then applied a rank-based inverse normal transform (RINT) on the residuals.⁷² To assess the predictive performance on held-out test sets, we performed 5-fold cross-validation. For each split, we further split the training data into $90\%$ training and $10\%$ validation to facilitate running PRS methods that require a validation set to tune their hyperparameters.

The case-control phenotypes included in the analysis are asthma (prevalence $12.7\%$), type 2 diabetes (T2D) (prevalence $2.3\%$), and rheumatoid arthritis (RA) (prevalence $1.7\%$). To assess the predictive performance on held-out test sets, we performed stratified 5-fold cross-validation, followed by splitting the training data into $90\%$ training and $10\%$ validation in a stratified manner to keep the prevalence approximately the same for all subsets of the data.

The phenotypes and associated sample sizes in the UK Biobank are listed in Table 1. The detailed scripts with the extraction and transformation procedure for each phenotype are included in the public repository associated with this publication (web resources). The 5-fold cross-validation procedure was performed with the scikit-learn package in python.⁷³

Table 1.

The list of real phenotypes and GWAS data sources analyzed in this study

Phenotype	Description	GWAS source	GWAS sample size	Validation sample size	Test sample size
HEIGHT	standing height	UKB	242,213	26,913	67,282
HDL	high-density lipoprotein	UKB	211,856	23,540	58,849
BMI	body mass index	UKB	241,959	26,885	67,211
FVC	forced vital capacity	UKB	221,249	24,584	61,459
FEV1	forced expiratory volume in 1 s	UKB	221,265	24,586	61,463
HC	hip circumference	UKB	242,311	26,924	67,309
WC	waist circumference	UKB	242,340	26,927	67,317
LDL	low-density lipoprotein	UKB	230,995	25,667	64,166
BW	birth weight	UKB	138,300	15,367	38,417
T2D	type 2 diabetes	UKB	235,937	26,216	65,538
RA	rheumatoid arthritis	UKB	186,239	20,694	51,734
ASTHMA	asthma	UKB	229,031	25,448	63,620
LangoAllen2010_HEIGHT	standing height	Allen et al.74	131,547	26,913	67,282
Speliotes2010_BMI	body mass index	Speliotes et al.75	122,033	26,885	67,211
GLGC2021_HDL	high-density lipoprotein cholesterol	Graham et al.76	888,227	23,540	58,849
GLGC2021_LDL	low-density lipoprotein cholesterol	Graham et al.76	842,660	25,667	64,166
Teslovich2010_HDL	high-density lipoprotein cholesterol	Teslovich et al.77	97,749	23,540	58,849
Teslovich2010_LDL	low-density lipoprotein cholesterol	Teslovich et al.77	93,354	25,667	64,166
SpiroMeta2019_FVC	forced vital capacity	Shrine et al.78	79,005	24,584	61,459
SpiroMeta2019_FEV1	forced expiratory volume in 1 s	Shrine et al.78	79,005	24,586	61,463
Morris2012_T2D	type 2 diabetes	Morris et al.79	60,786	26,216	65,538
Scott2017_T2D	type 2 diabetes	Scott et al.80	159,208	26,216	65,538
Okada2014_RA	rheumatoid arthritis	Okada et al.81	37,681	20,694	51,734
Demenais2018_ASTHMA	asthma	Demenais et al.82	142,486	25,448	63,620

With each phenotype code, we provide the full phenotype name and description and the GWAS data source or cohort (UKB or external study) as well as the sample sizes for the training, validation, and test sets. The sample sizes for each subset may vary slightly across the five folds. For the external summary statistics, we prepended the phenotype codes with either the consortium name or the name of the first author as well as the year in which the GWAS was published. For analyses with the external GWAS summary statistics, the validation and test sets come from the UK Biobank.

Validation in minority populations in the UKB

To validate the relative predictive ability of VIPRS in individuals of different backgrounds, we used the approach of Privé et al.⁸³ to identify subgroups of relatively uniform ancestry and ethnicity. Using self-reported ethnic background as well as PCA medoids from Privé et al.,⁸³ we extracted genotype data for individuals of Italian $\left(N=\mathrm{6,177}\right)$, Indian $\left(N=\mathrm{6,011}\right)$, Chinese $\left(N=\mathrm{1,769}\right)$, and Nigerian $\left(N=\mathrm{3,825}\right)$ ancestry. In genetic analyses, those ancestry groups show various levels of allele frequency differentiation (Fst) when compared to the White British cohort.⁸³ The samples were selected after applying the same quality control filters as before. Mainly, we retained individuals who were used in the PCA and phasing procedures and filtered samples with detected sex chromosome aneuploidy or excess relatedness from this analysis.

For each individual in those target populations, we extracted phenotype data for the traits analyzed previously (Table 1). Then, we used effect size estimates derived from the 5-fold analyses on the White British cohort to generate polygenic scores for individuals in those minority populations. Given these polygenic score estimates, we computed the relative prediction $R^2$ as the incremental $R^2$ in the target population divided by the $R^2$ of the best performing PRS model on the test set in the White British cohort. This metric is designed to highlight the transferability of PRS estimates across different population and ancestry groups.

PRS method comparisons and specifications

To compare the predictive performance of VIPRS to state-of-the-art methods for polygenic risk prediction with summary statistics, we included a diverse collection of methods with different assumptions and implementations, including three stochastic Bayesian methods SBayesR (gctb 2.03),⁶ PRScs,²⁸ and LDPred2 (bigsnpr 1.9.11);³² a variational Bayesian PRS method MegaPRS (LDAK 5.2);³⁴ a penalized regression method (Lassosum 0.4.5²⁷); and finally, as a simple baseline, we included a C+T method (PRSice2 2.3.5²⁹). In addition to being widely used in practice, most of these methods were selected because they have been shown to be competitively accurate in recent comprehensive surveys.^39,40,84

For the main analyses presented in the text, our VIPRS method used the windowed LD estimator with 3 cM distance cutoff as well as the spike-and-slab prior family for the effect size. The hyperparameters of this model, $\theta =\left\{\pi ,{\sigma }_{ϵ}^2,{\sigma }_{\beta }^2\right\}$, were updated in the M-step of the VEM algorithm. For VIPRS-GS, we performed grid search over the proportion of causal variants $\pi$, where the grid spanned 30 points from $\frac{1}{M}$ to $\frac{M-1}{M}$ on a ${\log }_{10}$ scale, where $M$ is the number of genetic variants included in the model. Out of these 30 models, we selected the one that maximized the prediction accuracy in a held-out validation set. The remaining two hyperparameters, the residual variance ${\sigma }_{ϵ}^2$ and prior variance ${\sigma }_{\beta }^2$, were updated in the M-step via closed-form solutions as before.

For each external method, we provided the GWAS summary statistics for the simulated and real phenotypes and ran the model with default or recommended settings. Specifically, for SBayesR, we ran the MCMC chain for 10,000 iterations, with the first 2,000 taken as burn-in, and specified the default four component Gaussian mixture prior, with mixing proportions $\pi =\left\{\mathrm{0.95,0.02,0.02,0.01}\right\}$ and corresponding $\gamma$ parameters set to $\gamma =\left\{\mathrm{0.0,0.01,0.1,1}\right\}$.⁶ For PRScs, we used the PRScs-auto variant of the model, in which the $\phi$ hyperparameter is inferred automatically in a fully Bayesian fashion.²⁸ For the LDPred2 model, we ran the three variations of the method (LDPred2-inf, LDPred2-grid, and LDPred2-auto) and reported the performance for the grid model because it performed the best on average for the simulations and real traits. For the LDPred2-grid and LDPred2-auto models, we used the sparse model setting and the recommended grid over the two hyperparameters: (1) the SNP heritability $h^2\in \left\{0.7h_{LDSC}^2,h_{LDSC}^2,1.4h_{LDSC}^2\right\}$, where $h_{LDSC}^2$ is the LD score regression SNP heritability estimate^32,63 and (2) the proportion of causal variants $\pi$ ranging along 21 points on a log-scale from $\pi =1e-5$ to $\pi =1$. For MegaPRS, we used the BayesR variant of the model with the genome-wide complex trait analysis (GCTA) heritability model used to infer the prior variance for the effect size of each genetic marker.³⁴ As per the recommendations of the authors of that method, the inference in MegaPRS was performed within overlapping windows of 1 cM. For Lassosum, we used the default grid for the LASSO penalty parameter $\lambda$, which covers a 20-point grid on a log-scale from 0.001 to 0.1. Finally, for PRSice2, we used the default clumping and thresholding parameters.²⁹ For LD clumping, we used a window size of 250 kb and $r^2$ values greater than 0.1. For p value thresholding, we used a grid from 5e−8 to 0.5 with step size of 5e−5. For most of these external methods (SBayesR, LDPred2, PRScs, and Lassosum) we used pre-computed, publicly available LD matrices published by the authors and maintainers of each software. All of these LD matrices were pre-computed from large random samples in the UKB.^6,27,28,32 The LD matrices used by each method employed different LD estimators (e.g., block, windowed, or shrinkage) as well as different sample sizes within the UKB. For MegaPRS and PRSice2, we computed the LD matrices and associated files by using recommended or default parameters.

Some of the PRS methods included in our analyses require a held-out validation set to tune some of their hyperparameters while others only use data from the training set (i.e., the GWAS summary statistics). The former category of methods includes VIPRS-GS, Lassosum, LDPred2-grid, MegaPRS, and PRSice2 and the latter includes VIPRS, SBayesR, and PRScs. Thus, the methods that do not use cross-validation were effectively trained with a smaller subset of the data. In principle, the hyperparameters of PRScs and SBayesR can be tuned via cross-validation, but since this can be computationally expensive, we only include either the automated or default version of these two methods. Once the models converge, we output the effect size estimates and then generated polygenic scores for the samples in the test set. Given these polygenic scores, the models were then evaluated for the quality of their predictions. For quantitative traits, we reported the incremental prediction $R^2$, defined as the $R^2$ of a linear model with the PRS and covariates (age, sex, and top ten PCs) minus the $R^2$ obtained from a linear model with the covariates alone. For case-control phenotypes, we reported the area under the precision-recall curve (AUPRC) between the polygenic score and the binary phenotype.

In addition to these prediction metrics, we also compared the run-time (wall-clock time) of the different methods to gauge their scalability and computational efficiency. In all the experiments and analyses, each method was allocated eight cores and 16 GB of memory, and thus PRS methods that support parallel processing will have shorter wall-clock run-time but may have higher CPU utilization. The LDPred2 model was assigned an entire compute node (40 cores and >200 GB of memory) because we found that the sparse on-disk LD matrices were not working optimally in a shared computing environment. However, for fair comparisons, the method was restricted to using only eight cores.

The detailed specification of priors, grid values, hyperparameters, and computational resources for each PRS method is shown in the repository accompanying this manuscript (see web resources).

VIPRS software implementation

The data structures and inference algorithms for the VIPRS model are implemented in two python packages that are open source and publicly available on GitHub (see web resources). The first software package, magenpy, implements scripts and routines for computing LD matrices and transforming them to Zarr array format, simulating complex traits from genotype data and harmonizing multiple genetic data sources, such as GWAS summary statistics, LD reference panels, functional annotations, etc. The second software package, viprs, implements the optimized VI algorithms to obtain posterior estimates for the effect sizes. For optimal speed and efficiency, the coordinate ascent routine is written in cython, a compiled programming language that produces python-compatible modules with minimal overhead.⁸⁵ Both software packages follow object-oriented design principles to allow for streamlined user extensions and experimentation by experienced developers. We also provide runner scripts that allow users to perform inference with commandline interfaces.

Results

Genome-wide simulation results

To examine the predictive performance of the VIPRS model compared to existing PRS methods, we simulated quantitative and case-control traits with varying genetic architectures and heritability values. To align our simulations with the real trait analyses in terms of cohort size and composition, we used genotype data for a subset of $\approx \mathrm{340,000}$ unrelated White British individuals from the UKB (material and methods) and a HapMap3 subset of $\approx 1.1$ million genotyped and imputed SNPs. The simulations followed the generative models outlined in the material and methods section and supplemental methods, with the effect size of each variant drawn from different architectures and residuals for each individual sampled from an isotropic Gaussian density. For binary traits, we simulated case-control status following the liability threshold model,⁵⁸ with the prevalence set to $15\%$.

The simulations spanned six different genetic architectures, including both sparse and infinitesimal scenarios. In the first three scenarios, we simulated under the spike-and-slab model (material and methods), where the effect size for a given variant $j$ was drawn from $p\left({\beta }_j\right)=\pi \mathcal{N}\left({\beta }_j;0,{\sigma }_{\beta }^2\right)+\left(1-\pi \right){\delta }_0$, and the proportion of SNPs contribute to the variation in the trait ranging along a pre-specified grid $\pi \in \left\{{10}^{-4},{10}^{-3},{10}^{-2}\right\}$. In the next two simulation scenarios, the effect size is drawn from a scale mixture of Gaussians, $p\left({\beta }_j\right)={\sum }_{k=1}^4{\pi }_k\mathcal{N}\left({\beta }_j;0,d_k{\sigma }_{\beta }^2\right)$, with the mixing proportions set to $\pi =\left\{\mathrm{0.95,0.02,0.02,0.01}\right\}$. The variance multipliers $d_k$ were set to $d=\left\{\mathrm{0.0,0.01,0.1,1}\right\}$ for the sparse mixture model and $d=\left\{\mathrm{0.001,0.01,0.1,1}\right\}$ for the infinitesimal mixture model. Finally, for the infinitesimal model, we assumed that the effect size for all variants is drawn from a zero-centered Gaussian density, $p\left({\beta }_j\right)=\mathcal{N}\left({\beta }_j;0,{\sigma }_{\beta }^2\right)$. For each genetic architecture, we varied the proportion of additive genetic variance captured by all causal SNPs, $h_{SNP}^2\in \left\{\mathrm{0.1,0.3,0.5}\right\}$, such that the simulated traits range from the mildly to the highly heritable. For each unique configuration, we simulated ten independent phenotypes, for a total of 180 traits for each class (binary and continuous). Once the traits were simulated for all individuals in the dataset, we randomly split the sample into $70\%$ training, $15\%$ validation, and $15\%$ testing; we used the training set to generate GWAS summary statistics.

Next, we fit the VIPRS model to the summary statistics from the training data, along with other commonly used PRS methods. Given the many existing PRS approaches, we selected for comparison five methods that performed favorably in recent comprehensive surveys,^39,40,84 namely SBayesR,⁶ LDPred2,³² PRScs,²⁸ MegaPRS,³⁴ and Lassosum.²⁷ The first three methods use the Bayesian framework outlined above for approximate posterior inference, all employing a Gibbs sampling algorithm. They are mainly distinguished by the families of prior density they assign to the effect sizes, among many other algorithmic choices. The fourth model, MegaPRS, is similar to VIPRS in that it uses VI for polygenic risk estimation, though there are some fundamental differences in the details of the optimization algorithm (see supplemental methods). Lassosum is a penalized regression method that derived and implemented the LASSO estimator for PRS inference from GWAS summary statistics.²⁷ Finally, we included PRSice2,²⁹ which implements clumping and thresholding, a commonly used baseline method. After fitting each method on the summary statistics from the training data, we used the effect size estimates to generate polygenic scores for individuals in the held-out test set and evaluated their predictive performance. For quantitative traits, we computed the incremental prediction $R^2$ for each model, while for binary traits we show the AUPRC, a preferable metric in the presence of class imbalance.⁸⁶ In addition to the six external PRS models, we also examined the predictive performance of the basic VIPRS model trained with the VEM framework (material and methods) as well as a version of the VIPRS model, dubbed VIPRS-GS, in which we perform grid search and tune the hyperparameters on the basis of predictive performance on a held-out validation set.

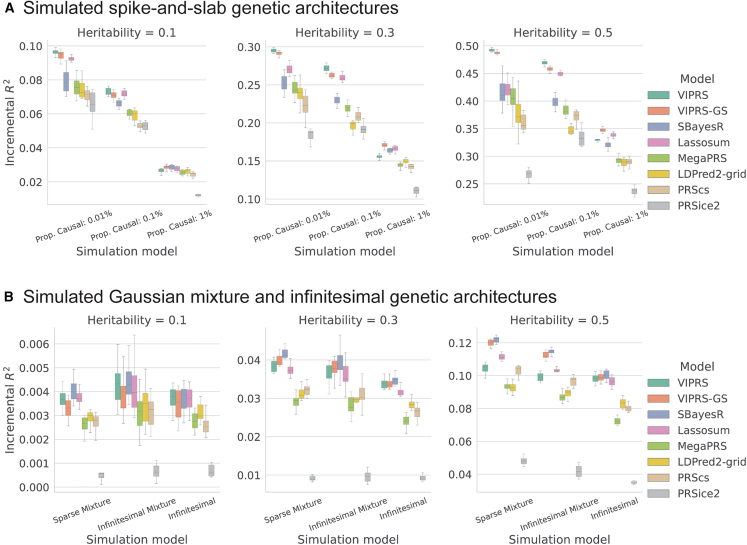
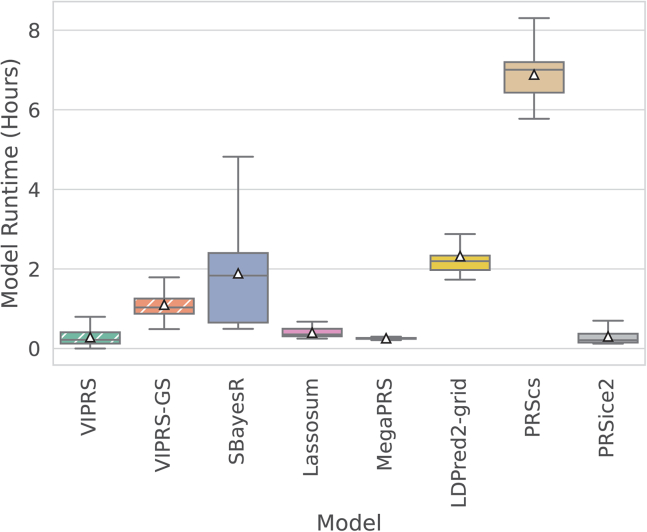
The predictive performance results for this simulation study are summarized in Figures 1 and S1, which show that VIPRS-GS outperforms or is on-par with state-of-the-art PRS methods in most of the scenarios tested. In particular, our analyses indicate that VIPRS provides the most benefit for more sparse architectures and highly heritable traits (leftmost panels in Figures 1A and S1A). Notably, in this particular setting, VIPRS is able to capture most of the additive genetic variance (as measured by the $R^2$ metric, which is upper-bounded by the heritability), while other Bayesian and non-Bayesian methods often lag behind. For infinitesimal and mixture-based architectures, VIPRS shows competitive predictive ability across the range, only lagging slightly behind SBayesR in those settings. For highly polygenic traits with the proportion of causal variants equal or greater than 1%, all models conferred lower prediction accuracy relative to the heritability values that we simulated with. This is because, under our simplified simulation scenario, the larger the number of causal variants, the smaller the effect size per SNP. Consequently, this makes it more difficult for PRS methods to pick up the true causal signals, at least given the training sample sizes available. Nonetheless, the VIPRS models conferred higher predictive performance relative to most competing methods in many of those scenarios. This pattern holds for both quantitative (Figure 1) as well as binary case-control phenotypes (Figure S1). This improvement in prediction accuracy comes also with improved computational efficiency, with the run-time of the standard VIPRS model rivaling other heuristic and deterministic methods, such as Lassosum, MegaPRS, and PRSice2 (Figure 2).

Figure 1.

Predictive performance of summary statistics-based PRS methods on simulated quantitative traits following spike-and-slab and Gaussian mixture or infinitesimal genetic architectures

The phenotypes were simulated with real genotype data from the White British cohort in the UK Biobank $\left(N=\mathrm{337,225}\right)$, leveraging a subset of 1.1 million HapMap3 variants. The simulation scenarios encompass a total of 18 configurations, spanning six genetic architectures and three values for SNP heritability. (A) shows prediction accuracy for traits simulated under the spike-and-slab model and (B) shows predictive performance for traits simulated under Gaussian mixture and infinitesimal genetic architectures. For each configuration, we simulated ten independent phenotypes. Each panel shows results for phenotypes simulated with the pre-specified SNP heritability and each column within a panel shows performance metrics for phenotypes simulated with a pre-specified genetic architecture. The performance metric shown is the incremental prediction $R^2$. The boxplot for each method and simulation configuration shows the quartiles of the $R^2$ scores for the ten simulated phenotypes. The PRS methods shown are our proposed VIPRSand VIPRS-GS (using grid search to tune model hyperparameters) as well as six other baseline models: SBayesR, Lassosum, MegaPRS, LDPred2 (grid), PRScs, and PRSice2 (C+T).

Figure 2.

The total runtime (in hours) of the summary statistics-based PRS methods included in the study

The boxplot for each method shows the quartiles of the runtime from a total of 420 independent experiments (360 simulated traits plus 60 experiments on real measured traits, comprising the 12 phenotypes analyzed multiplied by the five training folds). The white triangles indicate the mean runtime for each method. The PRS methods shown are our proposed VIPRS and VIPRS-GS (using grid search to tune model hyperparameters) as well as six other baseline models: SBayesR, Lassosum, MegaPRS, LDPred2 (grid), PRScs, and PRSice2 (C+T). Dashed lines highlight the models contributed in this work.

The prediction accuracy of PRS methods on simulated phenotypes may be over-optimistic as a result of the similarity between the generative process for the simulations and their model assumptions. Additionally, our simulations assume that all the causal SNPs are genotyped or imputed and thus present in the dataset, which is certainly not the case for real traits. Therefore, it is important to systematically evaluate these methods on real phenotypes as shown next.

Application on real phenotypes in the UK Biobank

Given its competitive performance on simulated traits, we next sought to assess the relative predictive ability of the VIPRS model on real phenotypes measured for a subset of $\approx \mathrm{340,000}$ unrelated White British individuals in the UKB. This focus on a large sub-cohort of relatively uniform ancestry helps us achieve sufficient power while reducing confounding due to population structure. A downside of this approach is that it is expected to yield PRS estimates that perform more poorly for individuals of other ancestries,^83,87 a limitation that we examine in more detail in the next section.

For this analysis, we extracted and processed phenotypic measurements for nine quantitative traits and three binary traits that are commonly used to benchmark PRS methods (Table 1). The traits considered have varying (inferred) genetic architectures and SNP heritabilities. To make full use of the data, we followed a 5-fold cross-validation study design, where in each iteration, $80\%$ of the samples with trait measurements were used to generate the GWAS summary statistics and training the PRS models and $20\%$ were used as an independent test set.

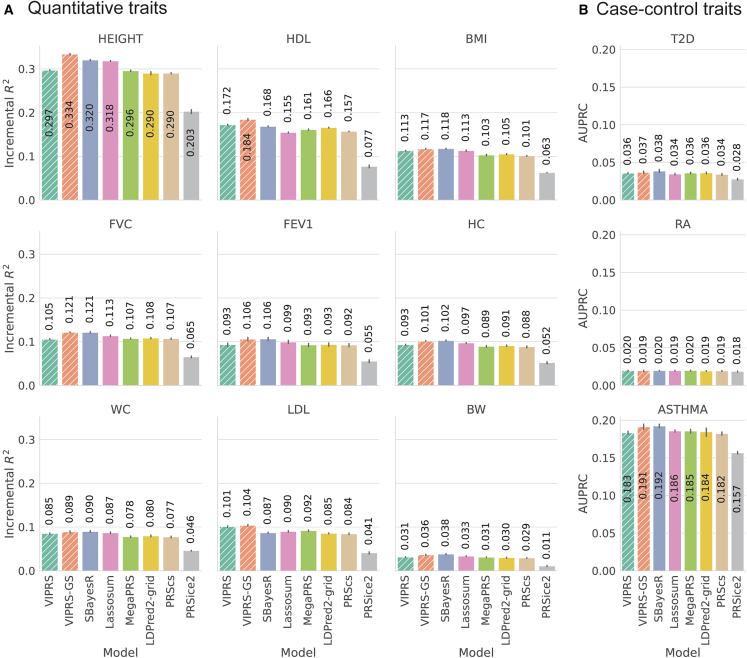
Our experiments show that, across a variety of different phenotypes, VIPRS is competitive with commonly used Bayesian PRS methods (Figure 3). Within the category of Bayesian PRS methods, the predictive performance of VIPRS is especially distinguished for anthropometric and blood lipid traits (Figure 3A). For instance, when compared to the LDPred2 model, which imposes the same spike-and-slab prior on the effect sizes, VIPRS shows an average of 4.6% improvement in prediction $R^2$ on continuous traits. However, in many cases the basic VIPRS model lags behind the SBayesR⁶ and Lassosum²⁷ models (Figure 3). In addition to the difference in posterior approximation strategy (VI versus Gibbs sampling), the SBayesR model differs from the VIPRS model in three other important respects: (1) the prior on the effect size, (2) the estimator for the linkage disequilibrium (LD) between variants, and finally (3) the approach for estimating the hyperparameters of the model. We sought to understand the effect of each of these modeling choices on the predictive performance of our model.

Figure 3.

Predictive performance of summary statistics-based PRS methods on real quantitative and case-control phenotypes in the UK Biobank

(A and B) The measured phenotypes were pre-processed and analyzed in a 5-fold cross-validation study design and the prediction metrics show the performance of each PRS method in predicting the phenotype in a held-out test set. Each panel shows the predictive performance, in terms of (A) incremental $R^2$ and (B) area under the precision recall curve (AUPRC), of various PRS methods when applied to a given phenotype. The bars show the mean of the prediction metrics across the five folds and the black lines show the corresponding standard errors. The quantitative phenotypes analyzed are standing height (HEIGHT), high-density lipoprotein (HDL), body mass index (BMI), forced vital capacity (FVC), forced expiratory volume in 1 s (FEV1), hip circumference (HC), waist circumference (WC), low-density lipoprotein (LDL), and birth weight (BW). The binary phenotypes analyzed are asthma (ASTHMA), type 2 diabetes (T2D), and rheumatoid arthritis (RA). The PRS methods shown are our proposed VIPRS and VIPRS-GS (using grid search to tune model hyperparameters) as well as six other baseline models: SBayesR, Lassosum, MegaPRS, LDPred2 (grid), PRScs, and PRSice2 (C+T). Dashed lines highlight the models contributed in this work.

To address the first point, we derived and implemented a version of VIPRS called VIPRSMix, where we replaced the spike-and-slab prior on the effect sizes with a sparse Gaussian mixture prior with four mixture components (supplemental methods).^6,26,50 Our experiments show that the more expressive mixture prior improves the performance of the standard VIPRS model on some traits, especially highly heritable and polygenic traits such as standing height and HDL (Figure S5), with an average of 2.4% increase in prediction $R^2$ on continuous traits. However, the improvement is not consistent across all traits and use of this prior does not fully bridge the gap between VIPRS and SBayesR.

Secondly, we assessed the impact of the LD estimator on the predictive performance of the VIPRS model by re-fitting the model with three commonly used estimators for LD: windowed,^32,63 shrinkage,^6,71 and block^28,70 (material and methods). Our experiments indicate that, on many of the traits tested, using the shrinkage estimator for LD results in slight improvements in prediction accuracy, though as in the case of the windowed LD estimator, it still slightly lags behind the SBayesR model (Figures S2 and S3). Notably, however, the shrinkage estimator tends to be more robust when the sample size of the LD reference panel is small (Figures S2 and S3).

Finally, and most importantly, the basic VIPRS model differs from the SBayesR model in terms of its hyperparameter estimation strategy. Most PRS methods have global hyperparameters, such as the residual variance ${\sigma }_{ϵ}^2$ or proportion of causal variants $\pi$, that need to be estimated or fixed to reasonable values. SBayesR follows a fully Bayesian approach for learning the hyperparameters of the model, assigning them priors and inferring their posterior distributions.⁶ By contrast, VIPRS follows a VEM framework where in the M-step we set the hyperparameters to their approximate maximum-likelihood estimates.^50,51 This latter strategy is known to be prone to overfitting or entrapment in local maxima.^{50,51,65,88,89} As an alternative to the VEM framework, we tested three other strategies for tuning the hyperparameters of the model, including grid search,⁹⁰ Bayesian optimization,⁶⁶ and Bayesian model averaging⁵¹ (see material and methods, Figures S6 and S7). In this context, similar to the Lassosum, MegaPRS, and LDPred2 methods, we found that by setting some of the hyperparameters of the model via grid search with an independent validation set, VIPRS-GS provides a powerful remedy in most settings (Figures 3, S6, and S7), resulting in a balanced trade-off between computational speed and predictive accuracy (Figures 2 and 3). Indeed, our results show that the VIPRS-GS model conferred the highest or second highest predictive performance on all traits tested (Figure 3), consistently exceeding the performance of the VEM-based VIPRS. At the same time, the main drawback of the grid search approach is that, despite the parallel software implementation, it results in a significant slowdown compared to the VEM approach (Figure 2). In terms of predictive performance, the advantage of the grid search is most prominent for highly heritable traits, such as standing height and HDL (Figure 3A). For the other traits, SBayesR is on-par or only marginally better. This indicates that the gap in predictive performance between SBayesR and the basic VIPRS model is mostly due to differences in hyperparameter estimation strategy, i.e., fully Bayesian inference of hyperparameters versus VEM approach.

PRS validation in minority populations in the UK Biobank

When trained on GWAS data from a single source population, transferability of PRS estimates across populations is limited,^83,87 and the degradation in prediction accuracy increases with the increase in allele frequency differentiation (Fst) between populations.⁸³ At the same time, recent studies of cross-population genetic correlations have demonstrated strong correlations in the genetic architectures of complex traits between various ancestry groups.^91,92 These correlations imply that PRS models that perform better in the source population will also tend to perform more favorably when applied to the target populations.

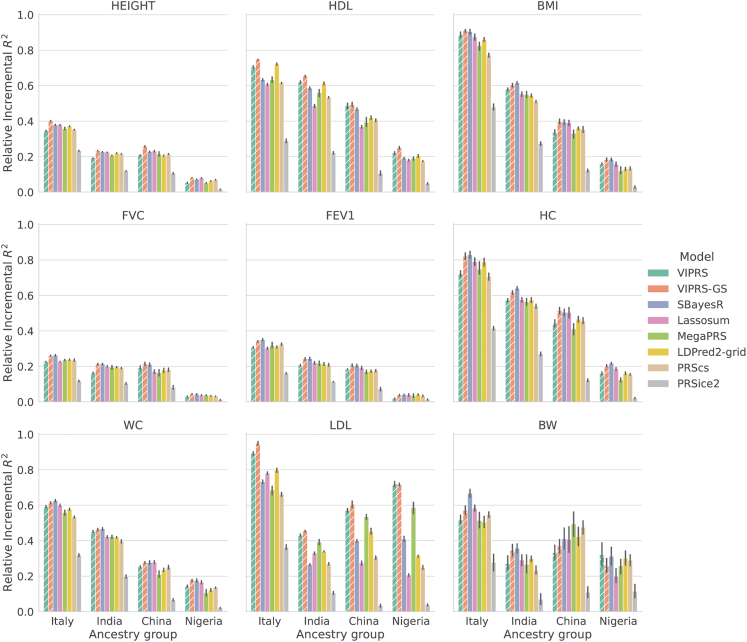
To assess this, we extracted genotype and phenotype data for individuals who self-identified as Italian $\left(N=\mathrm{6,177}\right)$, Indian $\left(N=\mathrm{6,011}\right)$, Chinese $\left(N=\mathrm{1,769}\right)$, and Nigerian $\left(N=\mathrm{3,825}\right)$. The self-reported ethnic backgrounds were further validated on the basis of the PCs of the GRM⁸³ (material and methods). Using the effect size estimates derived from training the PRS models on summary statistics from the White British cohort across the five training folds, we computed a PRS for each individual in the target population. Given the real phenotype measurements for these individuals, we evaluated the predictive performance by using relative incremental prediction $R^2$, where the $R^2$ in the target population was divided by the $R^2$ of the best performing model on the test set in the White British cohort.

Our results confirm that for most of the traits analyzed, the models with the best predictive performance on the source population (White British) tend to transfer better to the target populations (Figure 4). Furthermore, consistent with other analyses in this space,^83,87 the drop in prediction accuracy generally tracks with the Euclidean distance between the White British and the target populations in PC space. Interestingly, deviations from this general pattern were observed for LDL and birth weight, which may be due to gene-by-environment interactions.⁹² For LDL specifically, we observed strong differentiation in transferability between PRS methods, with models employing VI techniques, VIPRS and MegaPRS, attaining upwards of 1.5 times the prediction accuracy of the next competing PRS method in individuals of Nigerian and Chinese ancestry (Figure 4). We hypothesize that the high variance in accuracy and transferability for LDL is due, in part, to differences in effect size estimates for large effect APOE variants. For instance, rs7412, a known major determinant of LDL,⁷⁶ is assigned a large effect by VIPRS, while other methods either excluded this variant a priori (e.g., LDpred2, SBayesR) or assigned it a small effect (e.g., MegaPRS, PRScs).

Figure 4.

Relative predictive performance of summary statistics-based PRS methods on real quantitative phenotypes in minority populations in the UK Biobank

The PRS models were trained on summary statistics from the White British cohort in the UK Biobank using a 5-fold cross-validation design. Then, the effect size estimates from the five training folds were used to perform predictions in individuals of Italian, Indian, Chinese, and Nigerian ancestry. Each panel shows the incremental prediction $R^2$ in a given ancestry group relative to the prediction $R^2$ of the best performing model on the White British cohort. The bars show the mean of the relative prediction metric across the five training folds and the black lines show the corresponding standard errors. The quantitative phenotypes analyzed are standing height (HEIGHT), high-density lipoprotein (HDL), body mass index (BMI), forced vital capacity (FVC), forced expiratory volume in 1 s (FEV1), hip circumference (HC), waist circumference (WC), low-density lipoprotein (LDL), and birth weight (BW). The PRS methods shown are our proposed VIPRS and VIPRS-GS (using grid search to tune model hyperparameters) as well as six other baseline models: SBayesR, Lassosum, MegaPRS, LDPred2 (grid), PRScs, and PRSice2 (C+T). Dashed lines highlight the models contributed in this work.

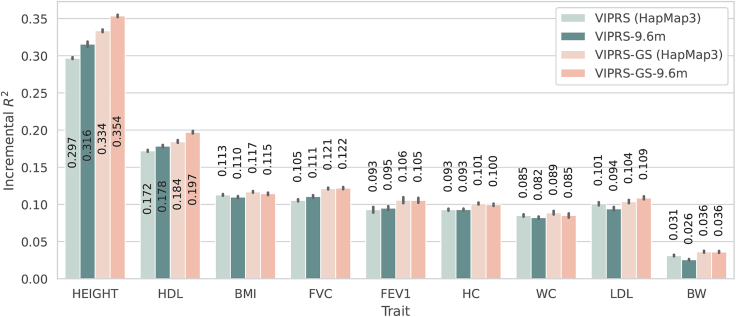
Scaling up VIPRS to 9.6 million variants

In recent years, with the advent of biobank-scale whole-genome sequencing efforts^3,43 and improved variant imputation pipelines,³⁵ there has been increasing interest in understanding the extent to which larger and larger sets of genetic variants enable us to better capture the genetic diversity underlying complex traits.⁹³ This is especially important in light of recent results that showed that a substantial proportion of the missing heritability is due to imperfect tagging of rare causal variants by common SNPs.⁹³ In this context, the main advantage of VIPRS is its speed and scalability (Figure 2); thus we wanted to understand the extent to which our method could benefit from modeling an expanded set of SNPs. Here, following recent efforts in this space,^34,40 we examine the predictive performance of VIPRS with approximately 9.6 million measured or imputed genetic variants, almost an order of magnitude greater than the HapMap3 subset analyzed previously. This includes all bi-allelic variants with MAF greater than 0.1% and MAC greater than 5 in the White British cohort in the UKB.

Following the same 5-fold cross-validation study design described earlier, we observed that modeling an expanded set of SNPs results in substantial improvements in prediction accuracy for highly heritable and polygenic traits, such as standing height and HDL, in comparison with the best performing PRS model using a subset of 1.1 million HapMap3 SNPs (Figure 3), which is consistent with previous studies⁶ (Figures 5 and S5). Concretely, for standing height and HDL in particular, including almost an order of magnitude more variants resulted in 3%–7% relative improvement in the predictive performance of VIPRS and VIPRS-GS. However, the improvement is not consistent across all traits, especially for the VEM-based VIPRS. Similar to previous studies,⁶ we saw that, in some cases, including more variants led to modest drop in prediction accuracy, perhaps because of increased noise in the PRS estimate. Presumably, imputation errors for rare variants could potentially degrade the performance of the model in this setting. Therefore, we believe that this analysis presents a lower-bound on what could be achieved with more accurate and complete whole-genome-sequencing data^3,43 (discussion).

Figure 5.

Comparing the predictive performance of the VIPRS method on real quantitative traits in the UK Biobank using the HapMap3 SNP set as well as an expanded set of 9.6 million genotyped and imputed variants

Each bar shows the predictive performance, in terms of incremental prediction $R^2$, of four different versions of the VIPRS model. From left to right, we have the standard VIPRS model trained on the HapMap3 subset (comprised of $\approx 1.1$ million variants), VIPRS-9.6m is the VIPRS model trained on 9.6 million variants, VIPRS-GS is VIPRS with grid search trained on the HapMap3 subset, and finally VIPRS-GS-9.6m is the VIPRS with grid search trained on the 9.6 million SNPs. The black vertical lines show the standard errors across the five folds from the 5-fold cross-validation scheme. The quantitative phenotypes analyzed are standing height (HEIGHT), high-density lipoprotein (HDL), body mass index (BMI), forced vital capacity (FVC), forced expiratory volume in 1 s (FEV1), hip circumference (HC), waist circumference (WC), low-density lipoprotein (LDL), and birth weight (BW).

PRS analysis with external GWAS summary statistics

A common use case in the inference of polygenic scores involves settings where the GWAS summary statistics and the LD reference panel are estimated from two different cohorts.^8,37 In other cases, the GWAS summary statistics may be derived from a meta-analysis that combines data from a number of different studies. These settings may present potential mismatches and heterogeneities between the LD reference panel and GWAS summary statistics and are thus challenging to model, often leading to substantial loss in predictive power.^32,33,94,95 In the case of meta-analyzed GWAS summary statistics, previous studies have also cautioned that various sources of heterogeneity between the source cohorts may introduce estimation errors and biases for summary statistics-based methods.^96,97

To systematically assess the robustness of VIPRS to potential heterogeneities and mismatches between the GWAS cohort and the LD reference panel, we conducted an analysis where we downloaded a number of publicly available GWAS summary statistics for some of the traits analyzed previously, including standing height,⁷⁴ BMI,⁷⁵ HDL and LDL cholesterol,⁷⁶ FVC and FEV1,⁷⁸ type 2 diabetes,⁸⁰ rheumatoid arthritis,⁸¹ and Asthma⁸² (Table 1, see web resources). These studies combined data from individuals of general European ancestry (excluding UKB participants), most in the form of meta-analysis. Therefore, we would expect some degree of differences between the LD reference panels derived exclusively from the White British cohort in the UKB and the in-sample LD from these GWAS cohorts, which are not available.

We fit VIPRS as well as other PRS methods to the external GWAS summary statistics, providing the same 5-fold validation and testing cohorts within the UK Biobank for the purposes of hyperparameter tuning and evaluation as in the previous analysis. Our results indicate that, for most of the studies analyzed, the VIPRS model is robust in the out-of-sample LD setting and achieves competitive prediction accuracy compared to popular baseline methods (Figure 6). In particular, VIPRS benefited substantially from the increased sample sizes $\left(N>\mathrm{800,000}\right)$ in the GLGC meta-analysis of blood lipid traits,⁷⁶ outperforming all competing methods by large margins and significantly improving its accuracy relative to the within-UKB analysis pipeline. For instance, when using the GLGC summary statistics, polygenic scores estimated with VIPRS can now explain up to 21.1% of the variance in HDL compared to 18.4% when using UKB summary statistics. However, there are some notable cases of older GWAS meta-analyses (ca. 2010) where VIPRS was sensitive to mismatches between the GWAS cohort and LD reference panel (Figures 6 and S14), though not to the same extent as SBayesR, which failed to converge for many of the quantitative traits analyzed, consistent with earlier work in this area.³³ The weak performance of both VIPRS and SBayesR in this setting is notable, since both models iteratively estimate the residual variance ${\sigma }_{ϵ}^2$, whereas recent work recommended fixing this hyperparameter in the out-of-sample LD setting.⁹⁷ In our experiments, we did not see significant differences between VIPRS with fixed versus estimated residual variance. However, when using a validation set to tune the hyperparameters of the model, VIPRS-GS recovered most of the drop in performance relative to other PRS methods and showed competitive predictive ability (Figures 6 and S14). This suggests that the VIPRS model trained to maximize the ELBO (material and methods) of the external GWAS data may not generalize well to the UKB individuals. Indeed, our experiments show a partial reversal in the correspondence between the training ELBO and the validation $R^2$ (the metric that VIPRS-GS is optimizing) in the analysis of some of the external summary statistics (Figure S13), which explains the poor predictive performance of the basic VIPRS model in those settings.

Figure 6.

Predictive performance of summary statistics-based PRS methods on real quantitative and case-control phenotypes using external GWAS summary statistics

(A and B) Each panel shows the predictive performance, in terms of (A) incremental $R^2$ and (B) area under the precision recall curve (AUPRC), of various PRS methods when applied to an independent test cohort in the UK Biobank. The bars show the mean and standard error of the prediction metrics across the five folds and the black lines show the corresponding standard errors. The quantitative phenotypes analyzed are high-density lipoprotein (GLGC2021_HDL⁷⁶), low-density lipoprotein (GLGC2021_LDL⁷⁶), standing height (LangoAllen2010_HEIGHT⁷⁴), body mass index (Speliotes2010_BMI⁷⁵), forced vital capacity (SpiroMeta2019_FVC⁷⁸), and forced expiratory volume in 1 s (SpitoMeta2019_FEV1⁷⁸). The binary phenotypes analyzed are type 2 diabetes (Scott2017_T2D⁸⁰), Rheumatoid arthritis (Okada2014_RA⁸¹), and asthma (Demenais2018_ASTHMA⁸²). The PRS methods shown are our proposed VIPRS and VIPRS-GS (using grid search to tune model hyperparameters) as well as six other baseline models: SBayesR, Lassosum, MegaPRS, LDPred2 (grid), PRScs, and PRSice2 (C+T). The asterisk (^∗) next to the SBayesR method in (A) indicates that it did not converge on some of those traits. Dashed lines highlight the models contributed in this work.

Given this observation, if an independent validation set is not available, we recommend that users of the VIPRS software run principled tests of LD mismatch and heterogeneity, such as the recently published DENTIST or SLALOM methods^95,96 before fitting the model to GWAS summary data. In the supplemental methods, we also derived a stochastic estimator of the DENTIST test statistic that can be computed efficiently and we provided that as a utility function in our software (see web resources).

Discussion

In this paper, we introduced VIPRS, a fast and flexible Bayesian PRS method that approximates the posterior for the effect sizes of genetic variants on the phenotype by using VI techniques. Our genome-wide simulation analyses using genotype data from the White British cohort in the UK Biobank demonstrated that variational approximations to the posterior are not only computationally efficient but they also provide highly accurate polygenic score estimates across diverse genetic architectures. Indeed, in some simulation scenarios, VIPRS exceeded the predictive performance of competing Bayesian and non-Bayesian methods by large margins. The competitive prediction accuracy of the VIPRS method replicated in our analyses of real quantitative and binary phenotypes measured for the same UKB participants, though the differences between the methods in this setup were more modest. Similar systematic but mostly modest benefits were observed when PRS methods were applied to individuals from ancestries not included in the training dataset, emphasizing the robustness of the approach. For example, the effect size estimates by VIPRS for LDL cholesterol showed a large enough improvement in performance across ancestries to have potential clinical relevance⁹⁸ and make a significant dent in the transferability problem for that trait.

As highlighted throughout the text, we found that many implementation and modeling choices can have a substantial impact on the performance of the VIPRS model in analyses with GWAS summary statistics for real measured traits: hyperparameter tuning strategies, LD estimators, and the prior on the effect size all influenced the predictive performance in ways that varied across phenotypes and experimental setups. Overall, in most of the setups and experimental conditions that we tested, the grid search approach for hyperparameter tuning combined with the spike-and-slab prior and windowed estimator of LD reliably outperformed or rivaled all the other variations of the model as well as previously described PRS methods. Notably, many of the individual modeling choices underpinning the VIPRS-GS model have been tried and tested in at least one other publication. Even the variational approximation that we derive bears some similarities to some existing methods that we compare against in our experiments, e.g., MegaPRS³⁴ (supplemental methods). However, crucial details in the variational algorithm and its implementation and how they are joined together can still have significant impact on the overall performance, as illustrated by our experimental results.

One of the main strengths of the VIPRS model is its computational efficiency, which we exploited to test the predictive performance of the model with approximately 9.6 million SNPs, almost an order of magnitude greater than the standard HapMap3 subset used to train PRS methods.^4,6,28,32 At this finer scale, we showed that modeling an expanded set of variants results in significant improvements in prediction accuracy for highly polygenic traits, such as standing height and HDL. This is consistent with recent whole-genome-sequencing analyses that showed that a considerable proportion of rare causal variants are not well tagged by common SNPs.⁹³ There are a number of reasons that lead us to believe that the performance metrics that we report here are a lower bound on what could be achieved in modeling large-scale SNP array data. First, the vast majority of the variants that we added beyond the HapMap3 subset are rare and statistically imputed. Rare variant imputation is still a challenging problem and existing algorithms are known to have elevated error rates.^99,100 We expect that these imputation errors can introduce substantial noise into the PRS estimate and thus result in decreased prediction accuracy, as we observed for a number of the traits that we analyzed. This difficulty can potentially be addressed by using whole-genome-sequencing data for GWASs, which may soon be enabled by recent large-scale initiatives by the UKB⁴³ and TOPMed.³ Second, residual confounding due to population structure may affect effect size estimation for rare variants.^93,101,102 In our GWAS pipeline, we corrected for population stratification by using only the top ten PCs of the GRM, which may not adequately capture the more recent demographic history reflected by rare variants.^102,103 This residual confounding effect may be addressed by increasing the number of PCs used in the GWAS analysis⁹³ or utilizing more genealogically informed estimates of the GRM.¹⁰⁴

Despite its competitive predictive ability, we believe that there are a number of modeling choices underlying VIPRS that can potentially be improved in future work. Firstly, compared to simulated phenotypes, the generative process for real traits is unknown and most likely involves complex and heterogeneous genetic architectures that are not well described by a two-component Gaussian mixture prior. The spike-and-slab prior assumes that all genetic variants have a uniform prior probability of being causal and that the causal SNPs have equal expected contribution to the heritability, which is a simplistic assumption given what is known about the genetic architectures of complex traits.^12,13,14 This motivated us to explore a more general and flexible Gaussian mixture prior with four mixture components.^6,26 Our experimental results show that adding mixture components improves accuracy for highly heritable and polygenic traits, such as standing height, but did not systematically improve accuracy for less heritable traits, perhaps because of reduced power to identify the larger number of parameters. Future work using priors informed by functional annotations (e.g., Zhang et al.³⁴ and Márquez-Luna et al.¹⁰⁵) is a promising avenue to improve accuracy in these cases. Second, our validation analyses in the UKB confirmed that, in general, VIPRS and other PRS methods do not transfer well across populations or ancestry groups, despite some notable differences between the methods. Recent work has highlighted that transferability in the context of summary statistics-based PRS methods is best achieved when we jointly model the effect sizes of multiple ancestrally homogeneous populations within the same framework.^57,106,107 This formulation has proved successful for some Bayesian PRS methods^57,107 and we believe that fast variational approximations to the posterior under such models will increasingly be shown to be effective and highly competitive.

Finally, while our results showed that variational approximations to the posterior are a promising alternative to MCMC techniques in predictive settings, it is important to highlight that mean-field variational approaches are known to underestimate the posterior variances and covariances in some cases.^45,108,109 In practice, this may result in miscalibrated PRS confidence intervals, if such a quantity is sought for some downstream applications.³⁸ This limitation can be addressed with more expressive variational families,¹¹⁰ such as those derived with variational boosting,¹¹¹ or alternatively, with the help of modern Bayesian inference techniques that combine variational methods and MCMC.¹¹²

Published: April 7, 2023

Web resources

• External GWAS summary statistics for asthma, http://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST006001-GCST007000/GCST006862/

• External GWAS summary statistics for GLGC lipid traits, http://csg.sph.umich.edu/willer/public/glgc-lipids2021/

• External GWAS summary statistics for SpiroMeta lung function traits, https://www.ebi.ac.uk/gwas/publications/30804560

• External GWAS summary statistics for standing height, BMI, and Rheumatoid arthritis, https://alkesgroup.broadinstitute.org/LDSCORE/all_sumstats/

• External GWAS summary statistics for type 2 diabetes, http://diagram-consortium.org/downloads.html

• LD matrices from the White British cohort in the UK Biobank in Zarr format, https://doi.org/10.5281/zenodo.7036625

• Modeling and Analysis of (Statistical) Genetics data in python, https://github.com/shz9/magenpy

• Variational Inference of Polygenic Risk Scores, https://github.com/shz9/viprs

• Reproducible code for running the analyses in the paper "Fast and Accurate Bayesian Polygenic Risk Modeling with Variational Inference" (2022), https://github.com/shz9/viprs-paper