Near-equilibrium glycolysis supports metabolic homeostasis and energy yield

Abstract

Glycolysis plays a central role in producing ATP and biomass. Its control principles, however, remain incompletely understood. Here, we develop a method that combines ²H and ¹³C tracers to determine glycolytic thermodynamics. Using this method, we show that, in conditions and organisms with relatively slow fluxes, multiple steps in glycolysis are near to equilibrium, reflecting spare enzyme capacity. In Escherichia coli, nitrogen or phosphorus upshift rapidly increases the thermodynamic driving force, deploying the spare enzyme capacity to increase flux. Similarly, respiration inhibition in mammalian cells rapidly increases both glycolytic flux and the thermodynamic driving force. The thermodynamic shift allows flux to increase with only small metabolite concentration changes. Finally, we find that the cellulose-degrading anaerobe Clostridium cellulolyticum exhibits slow, near-equilibrium glycolysis due to the use of pyrophosphate rather than ATP for fructose-bisphosphate production, resulting in enhanced per-glucose ATP yield. Thus, near-equilibrium steps of glycolysis promote both rapid flux adaptation and energy efficiency.

The steps of glycolysis have been known for nearly a century but the design principles and regulatory mechanisms of the pathway remain incompletely understood¹. A better understanding would benefit both metabolic engineering and medicine.

A key aspect of any metabolic pathway is its energetics. According to the second law of thermodynamics, every pathway step must have a negative Gibbs free energy (ΔG). Favorable ΔG is distributed across pathway steps². Steps with large absolute values of ΔG are irreversible and are preferred sites for pathway control via regulation of enzyme activity^3,4. Steps with small ΔG are near equilibrium, energy efficient and enable large changes in net flux with small changes in substrate and product levels⁵. On the flip side, steps with large absolute values of ΔG consume a larger share of the available pathway-driving force, while steps with small ΔG require spare enzyme capacity (extra enzyme relative to the minimum needed to catalyze only the forward pathway flux) to maintain the reaction near to equilibrium.

While advances in analytical capabilities have rendered the measurement of metabolite concentrations and fluxes increasingly straightforward^6–8, methods for measuring metabolic energetics remain less developed. One approach involves quantitating the concentrations of reaction substrates and products and inferring ΔG on the basis of the fundamental equation

$$\mathrm{\Delta }G=\mathrm{\Delta }G\prime °+RT\text{ln}Q$$ (1)

where R is the universal gas constant, T is the temperature in kelvin, Q is the reaction quotient, that is, the ratio of product-to-substrate activities, which are effective concentrations in a nonideal solution, and ΔG refers to the cellular context. At equilibrium, ΔG = 0 and the reaction quotient is equal to the equilibrium constant (K):

$$\mathrm{\Delta }G\prime °=-RT\text{ln}K$$ (2)

Challenges arise, however, because the concentrations of some substrates and products still cannot be reliably measured (for example, inorganic phosphate, where extracellular levels make it hard to determine intracellular ones accurately), concentrations may not perfectly align with activities due to variation in pH and ionic strength, mixing may be incomplete (especially in the case of compartmentalization) and small errors in measurement of ΔG′° or metabolite activities can lead to large fractional errors in measurement of ΔG for near-equilibrium reactions^6,9–12.

To address these concerns, one approach is to integrate information on both metabolite concentrations and reaction reversibility—here defined as the backward-to-forward flux ratio, J⁻/J⁺, as determined from isotope tracer studies—which relate to thermodynamics via equation (3)^13,14:

$$\mathrm{\Delta }G=\mathrm{\Delta }G\prime °+RT\ln Q=RT\ln \frac{Q}{K}=RT\ln \frac{J^{-}}{J^{+}}$$ (3)

Using this approach, we recently provided evidence that, in cells running glycolysis rapidly, most steps are sufficiently forward driven as to be reasonably enzyme efficient¹³.

Here, we explore the potential for more facile ΔG quantitation using only isotope-labeling data. The success of this approach—which we term GibbsIT (Gibbs energy from isotope tracing)—depends on the proper choice of tracers, so that metabolite-labeling patterns robustly depend on reaction ΔG. We show that a combination of [5-²H₁]- and [1,2-¹³C₂]glucose tracing enables effective assessment of glycolytic ΔG. We then use these tracers to explore glycolytic thermodynamics during nitrogen, phosphorus and oxygen upshift in Escherichia coli, respiration inhibition in a mammalian cell line and in two Clostridia species. We show that, on acute perturbations that accelerate glycolytic flux, several steps of glycolysis shift from being highly reversible towards being more forward driven. This enables substantial flux changes with only modest metabolite concentration changes. Moreover, we observe that Clostridium cellulolyticum, a microbe adapted to anaerobic life with low glucose availability, engages in a nearly fully reversible variant of glycolysis that extracts more ATP equivalents per glucose than the canonical glycolytic pathway. Collectively, these observations highlight the utility of near-equilibrium glycolytic steps for facilitating adaptation to changing environments and for enhancing metabolic energy yield.

Results

[5-²H₁]Glucose to trace glycolytic reversibility.

We set out to develop an isotope-tracing method for measuring glycolysis ΔG. We selected a glucose tracer harboring ²H at the fifth carbon. In glycolysis, [5-²H₁]glucose generates [5-²H₁]fructose-1,6-bisphosphate (FBP) and, subsequently via FBP aldolase, [2-²H₁]glyceraldehyde3-phosphate (M + 1 GAP) and unlabeled dihydroxyacetone phosphate (M + 0 DHAP). The deuterium can be lost at the following two steps of glycolysis: reverse triose phosphate isomerase (TPI) and forward enolase (ENO) (Fig. 1a). In the reverse TPI reaction, the M + 1 GAP loses deuterium to solvent and becomes M + 0 DHAP (Supplementary Fig. 1a)¹⁵. In the forward ENO reaction, [2-²H₁]2-phosphoglycerate (2PG) becomes unlabeled phosphoenolpyruvate (M + 0 PEP) (Supplementary Fig. 1b)¹⁶. If ENO were strongly forward driven (ΔG ≪ 0), the labeling of 1,3-bisphosphoglycerate (13BPG), 3-phosphoglycerate (3PG), 2,3-bisphosphoglycerate (23BPG) and 2PG would be identical to that of their precursor, GAP. With increasing reversibility of glycolytic reactions including ENO, unlabeled intermediates travel upstream. Therefore, [5-²H₁] glucose results in a monotonic decrease of ²H labeling down the glycolysis pathway that reflects the reversibility of the constituent reactions (Fig. 1b).

Fig. 1 |. Visualizing the extent of glycolysis reversibility using [5-²H₁]glucose.

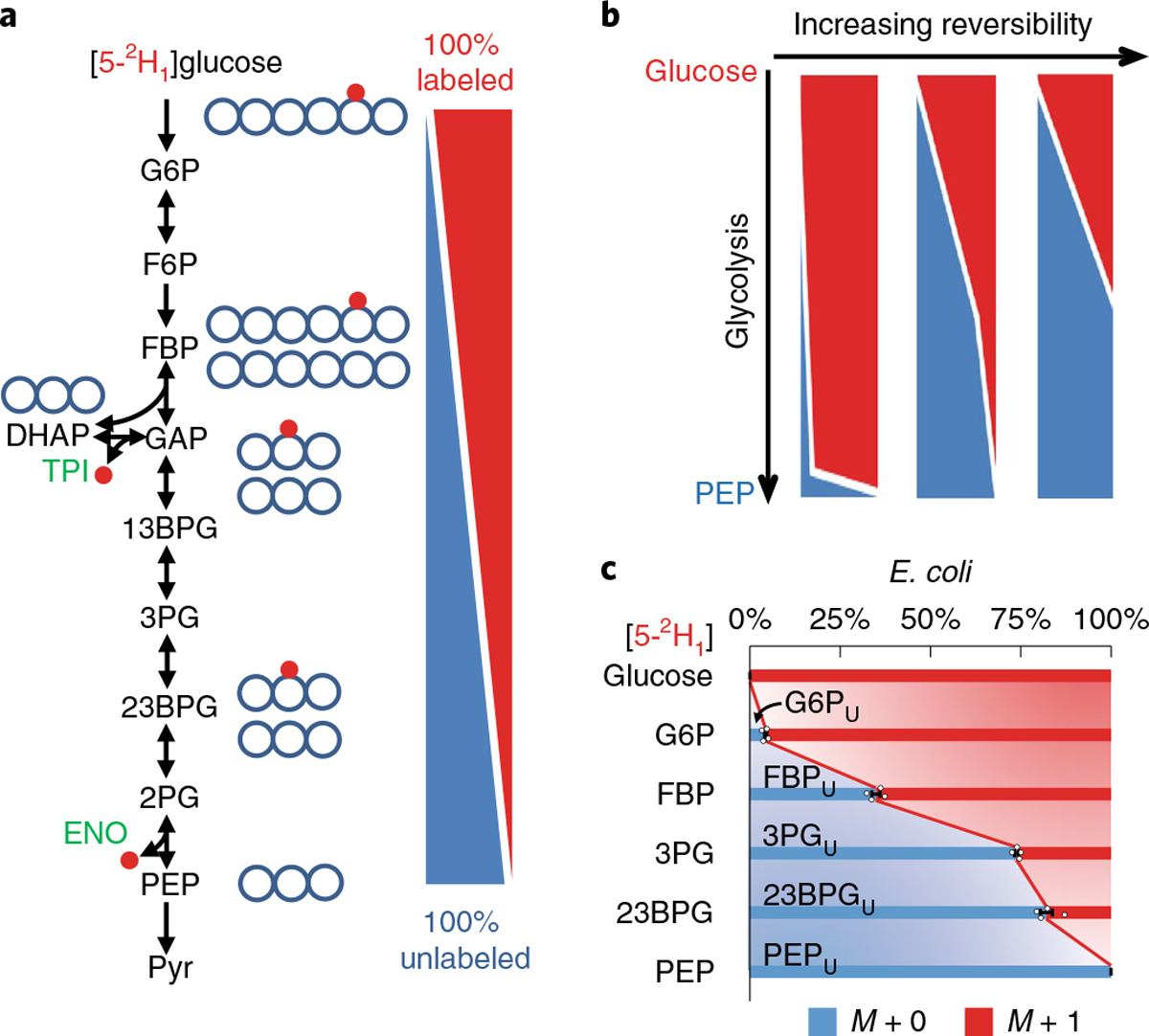
a, The deuterium of [5-²H₁]glucose is removed from glycolytic intermediates in the reverse triose phosphate isomerase (TPI: DHAP ⇌ GAP) and forward enolase (ENO: 2PG ⇌ PEP) reactions, leading to a descending gradient of ²H enrichment along glycolysis. b, Increasing reversibility of glycolysis results in ²H depleting earlier in the pathway. c, Labeling data from [5-²H₁]glucose in E. coli: metabolite names with subscript U indicate unlabeled fractions. The center and error bars represent the mean ± s.e.m. (n = 4, biologically independent samples).

To validate the ²H gradient, we cultured E. coli in the nutrient-rich (that is, high glucose and ammonia) minimal medium containing [5-²H₁]glucose. Using high-resolution liquid chromatography–mass spectrometry (LC–MS), we measured key glycolytic intermediates (unmeasured intermediates could not be readily quantified due to analytical interference, instability and/or low abundance¹⁷) (Fig. 1c and Supplementary Table 1). Efforts to compute the forward and backward fluxes of glycolytic reactions by modeling these labeling data¹⁸, however, failed, as various combinations of TPI and lower glycolysis reversibility resulted in indistinguishable ²H-labeling patterns (Supplementary Fig. 2). Hence, additional information is needed for accurate determination of thermodynamics.

Tracing both ²H and ¹³C reveals ΔG.

Using the [5-²H₁]glucose-tracing approach alone fell short because ²H-labeling loss may occur due to either TPI or lower glycolysis reversibility (Fig. 2a). To eliminate this degeneracy, we set out to quantitate TPI reversibility independently. For this purpose, we selected [1,2-¹³C₂]glucose¹³. If TPI is strongly forward driven, DHAP is made solely by aldolase, and thus from the first three carbons of glucose, resulting in M + 2 labeling. Reverse TPI flux introduces unlabeled carbons from the last three carbons of glucose, and thus can make unlabeled DHAP, with complete reversibility of TPI (ΔG_TPI ≈ 0) resulting in a 50:50 ratio of labeled and unlabeled DHAP (Fig. 2b). With [1,2-¹³C₂]glucose, TPI generated 60% M + 2 ¹³C-labeled DHAP, corresponding to substantial TPI reversibility (J⁻/J⁺ ≈ 0.7) (Fig. 2c and Supplementary Table 2). With these measurements in hand, we could express the reverse flux (and thus ΔG) of each glycolytic reaction step algebraically in terms of measured, unlabeled (nondeuterated) metabolite fractions from [5-²H₁]glucose and the reverse TPI flux (Fig. 2d and Supplementary Notes). The unlabeled GAP fraction (GAP_U) was required for determining the reversibility of lower glycolytic reactions. While GAP_U was not measured directly, the fraction of nondeuterated FBP (FBP_U) and FBP aldolase (FBA) reversibility allowed us to calculate this value (Supplementary Notes). Therefore, [5-²H₁]- and [1,2-¹³C₂]glucose together provide sufficient information for determining ΔG of key steps in glycolysis. In some cases, due to the inability to measure every glycolytic intermediate, individual reactions cannot be resolved, and we obtain ΔG for lumped pairs of sequential reactions instead. Specifically, we obtain ΔG for phosphoglucose isomerase (PGI): phosphofructokinase (PFK), FBA, TPI, GAP dehydrogenase (GAPDH): phosphoglycerate kinase (PGK) and phosphoglycerate mutase (PGM):ENO.

Fig. 2 |. Simultaneous ²H and ¹³C labeling reveals ΔG.

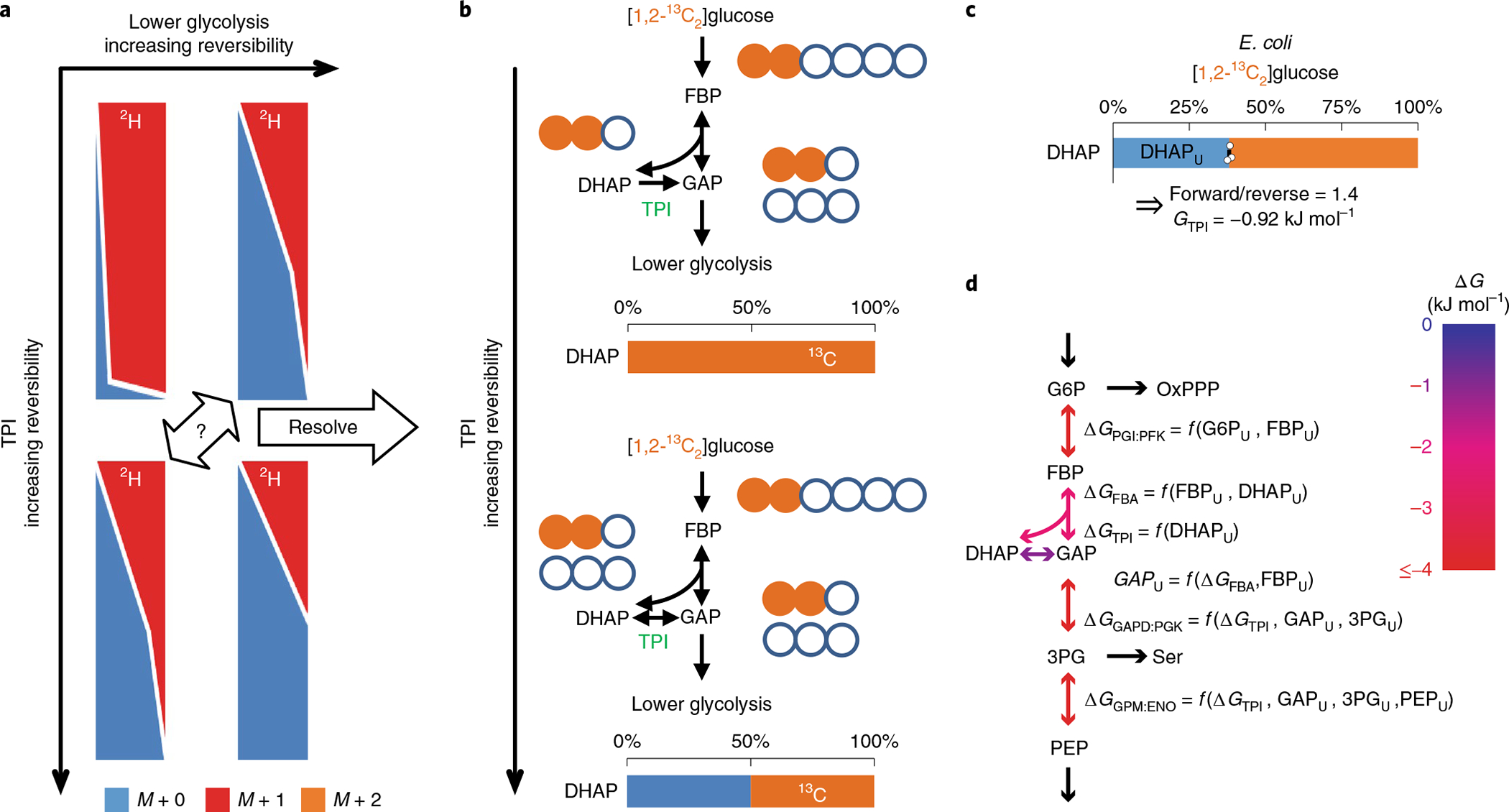
a, [5-²H₁]Glucose tracing alone falls short because each isotope labeling gradient could be the result of varying combinations of TPI and lower glycolysis reversibility. b, If TPI reversibility is known, the reversibility and ΔG of glycolysis can be determined. [1,2-¹³C₂]Glucose reveals TPI reversibility and ΔG. As the reverse TPI reaction introduces M + 0 DHAP, 0% M + 0 DHAP measurement implies no backward TPI flux (ΔG_TPI ≪ 0), while ~50% suggests a highly reversible reaction (ΔG_TPI ≈ 0). c, In E. coli, [1,2-¹³C₂]glucose generated 40% unlabeled DHAP (DHAP_U). The center and error bars represent the mean ± s.e.m. (n = 3, biologically independent samples). d, The ΔG of a reaction can be expressed as a function of the measured unlabeled fractions of primary substrate and product as well as GAP_U and ΔG_TPI. GAP_U was obtained from FBP aldolase reversibility and FBP_U. Using the ²H–¹³C labeling information and flux modeling, we determined the reversibility and ΔG of glycolytic reactions.

To compute ΔG also taking into account other relevant pathways, we used optimization tools and searched for flux distributions that simultaneously fit the [5-²H₁]- and [1,2-¹³C₂]glucose labeling data in a stoichiometric model encompassing glycolysis, the pentose phosphate pathway (PPP) and the Entner–Doudoroff pathway (EDP). We then used equation (2) to convert reaction reversibilities to ΔG (Fig. 2d and Supplementary Table 3). For measured reaction steps other than TPI (ΔG ≈ −0.9 kJ mol⁻¹), the absolute magnitude of ΔG was greater than 2 kJ mol⁻¹ (ΔG < −2 kJ mol⁻¹), indicative of enzymes catalyzing mainly forward reactions (J⁺/J⁻ > 2.1), confirming our prior observations that, in nutrient-replete E. coli, the thermodynamic driving force is partitioned to enable efficient enzyme use¹³.

Nitrogen upshift increases glycolytic driving force.

Balancing the use of different elemental nutrients is a fundamental challenge for metabolism. The three primary elemental nutrients, carbon, nitrogen and phosphorus, are particularly critical. In E. coli, a major regulatory mechanism enabling balancing of nitrogen and carbon is the inhibition of carbon use by α-ketoglutarate (αKG) (which contains carbon but not nitrogen, and builds up during nitrogen limitation). This inhibition occurs both at the level of transcription¹⁹ and by direct blockade of glucose uptake via enzyme I²⁰. When nitrogen availability increases, α-ketoglutarate falls, leading to immediate acceleration of glucose uptake²¹.

How this translates into increased flux through other steps in glycolysis, however, has remained unclear. Specifically, when fed arginine as the sole nitrogen source, E. coli grows and ferments slowly. On spiking the culture with ammonia, a superior nitrogen source, the growth and glucose uptake rates increase within minutes by 170% and 60% (from 0.34 h⁻¹ and 7.29 mmol gCDW⁻¹ h⁻¹ to 0.92 h⁻¹ and 11.70 mmol gCDW⁻¹ h⁻¹; CDW, cell dry weight)²⁰. The rapid upregulation of glucose uptake is triggered by decreased levels of α-ketoglutarate. But, despite the increase in glucose uptake, the levels of glycolytic intermediates do not change substantially, and how the rest of glycolysis keeps up with the increased glucose uptake remains a mystery.

We hypothesized that, if glycolysis is near to equilibrium in the nitrogen-limited state, small changes in the levels of glycolytic intermediates would be sufficient to substantially alter the thermodynamics and thereby the net flux. The net flux of a reaction is proportional to (1) active site occupancy by substrates and (2) thermodynamics, specifically, 1 − Q/K, as exemplified by the standard reversible Michaelis–Menten kinetics (k_s and k_p represent the Michaelis constants for substrate (S) and product (P), respectively):

$$v=v_{\text{m}}^{+}\frac{\frac{[\text{S}]}{k_{\text{s}}}}{1+\frac{[\text{S}]}{k_{\text{s}}}+\frac{[\text{P}]}{k_{\text{p}}}}\left(1-e^{\frac{\mathrm{\Delta }G}{RT}}\right)=v_{\text{m}}^{+}\frac{\frac{[\text{S}]}{k_{\text{s}}}}{1+\frac{[\text{S}]}{k_{\text{s}}}+\frac{[\text{P}]}{k_{\text{p}}}}\left(1-\frac{Q}{K}\right)$$ (4)

Small changes in metabolite levels imply small changes in active site occupancy, but in near-equilibrium reactions these small changes can result in large fold changes in the 1 − Q/K term, which is near zero.

To probe ΔG of glycolysis during the rapid nitrogen upshift, we cultured cells in labeled glucose media and measured how labeling changed in response to nitrogen upshift. On [5-²H₁]glucose and Arg, the depletion of ²H was extensive across glycolysis, and lower glycolytic intermediates retained less than 10% labeling, indicating high reversibility. Five minutes after addition of ammonia, most glycolytic intermediates gained substantial ²H labeling, indicating less glycolytic reversibility (Fig. 3a, Supplementary Fig. 3 and Supplementary Table 1). In labeling with [1,2-¹³C₂]glucose, the M + 0 DHAP fraction was ~50%, both before and after ammonia addition, reflecting near-equilibrium operation of TPI in both conditions (Supplementary Table 2). Together, the ²H and ¹³C tracing revealed that many glycolytic steps are highly reversible in the nitrogen-limited state, with nitrogen upshift nearly doubling glycolysis ΔG, rapidly shifting the pathway away from equilibrium to facilitate faster carbon utilization (Fig. 3b and Supplementary Table 3). The increased thermodynamic driving force in the ‘middle’ pathway steps complements the push–pull activation of the boundary steps: the glycolytic reactions between glucose-6-phosphate (G6P) and PEP become more forward driven, to keep up with increased enzyme I activity, which simultaneously produces G6P and consumes PEP. These mechanisms, in conjunction, allow the full pathway to respond rapidly to environmental changes while maintaining concentration homeostasis (Fig. 3c).

Fig. 3 |. Nitrogen upshift drives glycolysis forward.

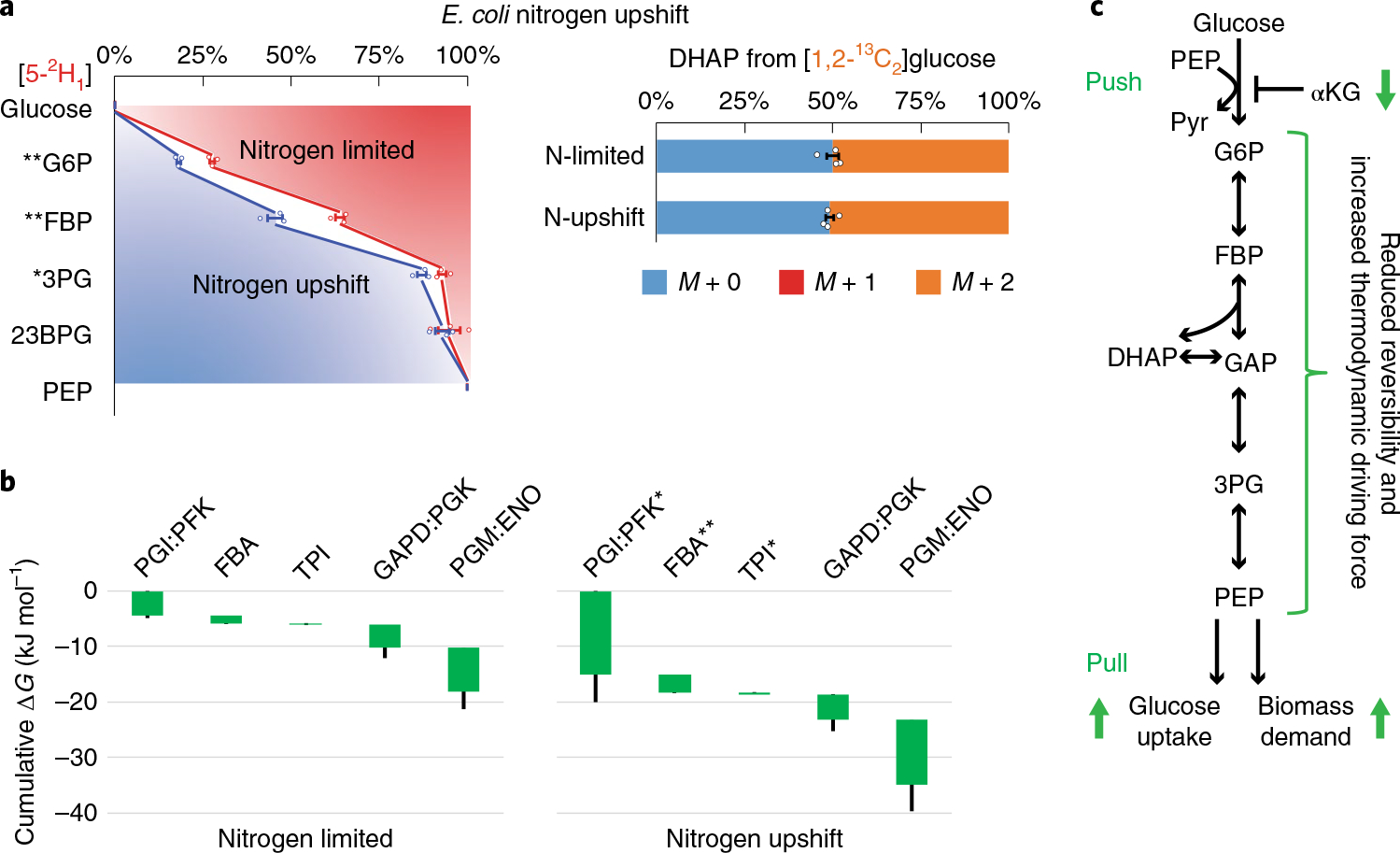
a, Isotope tracing of glycolytic reversibility in E. coli during nitrogen limitation and immediately following nitrogen upshift. E. coli were cultured on [5-²H₁]- or [1,2-¹³C₂]glucose with arginine as the sole nitrogen source, which supports slow cell growth (that is, nitrogen limitation). Glycolytic intermediates retained significantly less deuterium than in the NH₄Cl fast growth condition, indicating greater glycolytic reversibility. With [1,2-¹³C₂]glucose, DHAP was ~50% unlabeled, indicating high TPI reversibility. Five minutes after spiking in NH₄Cl (that is, nitrogen upshift), most glycolytic intermediates gained substantial deuterium labeling, while the DHAP labeling did not change. The center and error bars represent the mean ± s.e.m. (n = 3 or 4, biologically independent samples). b, Corresponding ΔG were inferred from the forward and backward fluxes that best simulated the observed ²H and ¹³C labeling. Each of the reaction(s) ΔG (<0) is represented by the height of the green bar. The bottom edges indicate the cumulative ΔG up to the corresponding step in glycolysis. Whiskers show s.e.m. (Methods). On nitrogen upshift, glycolysis shifted forward, with the most drastic free energy drops occurring near the beginning and the end of glycolysis. c, Schematic of glycolytic flux regulation during nitrogen upshift. Enzyme I is activated by the drop of αKG, accelerating G6P production and PEP consumption, with the middle of the pathway responding via decreased reversibility. *P < 0.05 and **P < 0.01 by two-tailed t-tests or bootstrapping (Methods).

Glycolytic response to phosphorus and oxygen upshift.

We similarly explored changes in metabolite concentrations, glycolytic flux and free energy during phosphorus upshift. Unlike nitrogen assimilation, which has been intensively studied^20,22,23, the metabolomics of phosphorus upshift have not been explored, in part because of the lack of a reliable ‘weak’ phosphorus source for E. coli. By culturing cells in an initial concentration of 0.15 mM PO₄³⁻, we induced a transient limitation response, as the phosphate was consumed from the medium as the cells reached higher optical density (OD₆₀₀ > 0.3).

In contrast to nitrogen upshift, where levels of glycolytic intermediates hardly change, there were rapid increases in glycolytic intermediates and nucleotide triphosphates on phosphorus upshift, as well as a decrease in NADH, which suggested activation of oxidative phosphorylation (Fig. 4a and Supplementary Fig. 4). The speed of these changes was highlighted by experiments using cells grown on the surface of a filter to collect multiple time points during the first minute following phosphorus upshift (Supplementary Fig. 4). [U-¹³C₆]glucose tracing revealed that the increase in metabolite levels involved incorporation of new carbon into glycolysis, but phosphorylation of pre-existing nucleotide precursors (Supplementary Fig. 5). Consistent with the dramatic increase in glycolytic metabolites, the glucose uptake rate increased from 3.0 ± 0.5 mmol gCDW⁻¹ h⁻¹ in phosphorus-limited conditions, to 12 ± 0.5 mmol gCDW⁻¹ h⁻¹, and cell growth accelerated (Supplementary Fig. 6). Thus, by increasing metabolite levels, phosphorus upshift increases enzyme active site occupancy to accelerate glycolysis.

Fig. 4 |. Phosphorus upshift drives glycolysis forward.

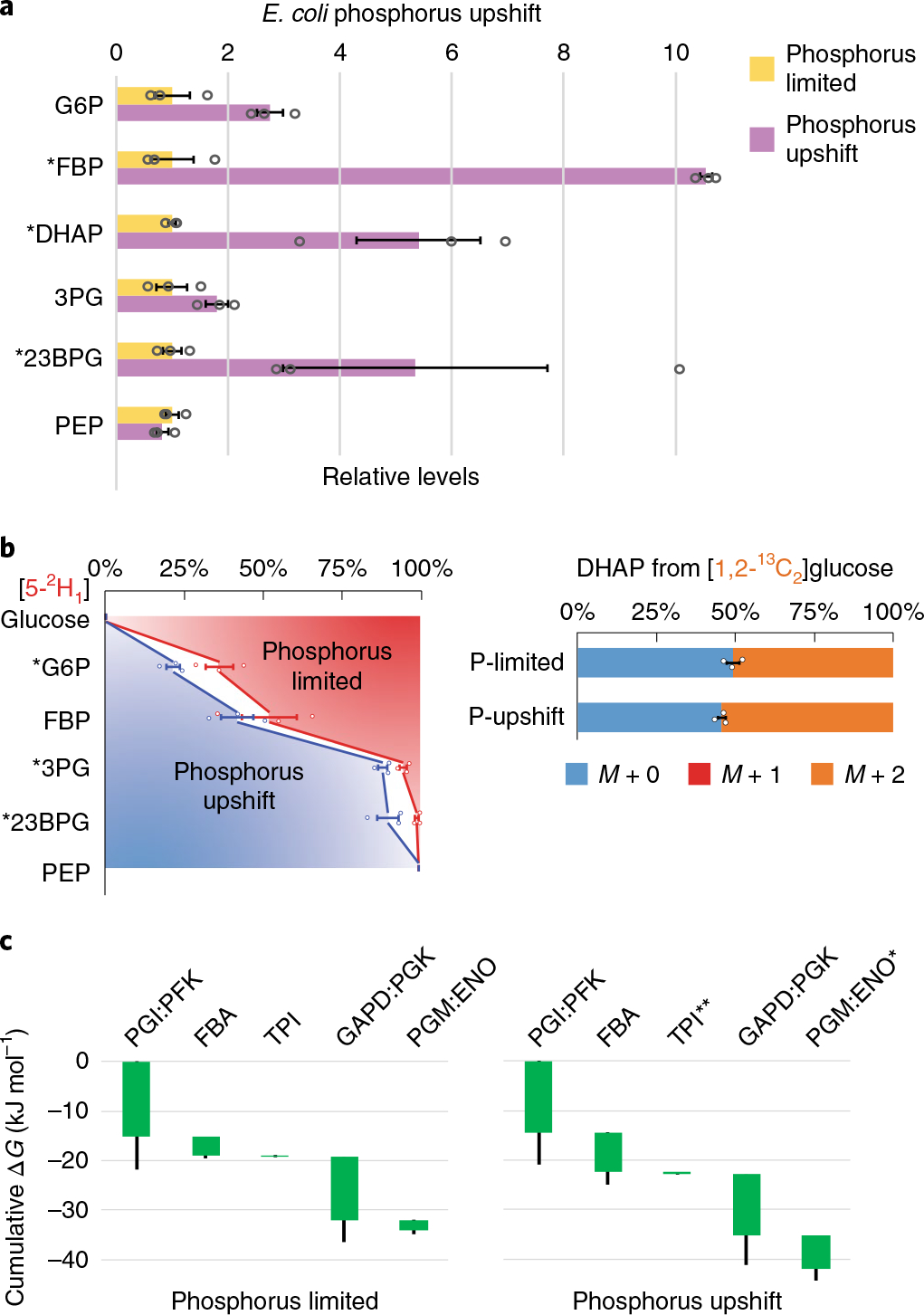
a, Changes in relative levels of glycolytic intermediates 5 min after spiking in 1.32 mM phosphate to E. coli phosphate-limited cultures. Measurements are normalized by means of the individual metabolites in the phosphorus-limited condition. The center and error bars represent the mean ± s.e.m. (n = 3, biologically independent samples). b, E. coli cultured on [5-²H₁]- or [1,2-¹³C₂]glucose during phosphate limitation and 5 min after spiking in 1.32 mM phosphate. G6P, 3PG and 23BPG gained substantial deuterium labeling, while the unlabeled DHAP pool decreased. The center and error bars represent the mean ± s.e.m. (n = 3, biologically independent samples). c, Corresponding ΔG were inferred from the flux-modeling results that best fit the observed ²H and ¹³C labeling. Each of the reaction(s) ΔG (<0) is represented by the height of the green bar. The bottom edges indicate the cumulative ΔG up to the corresponding step in glycolysis. Whiskers show s.e.m.; *P < 0.05 and **P < 0.01 by two-tailed t-tests or bootstrapping (Methods).

²H and ¹³C tracing revealed significant labeling changes within 5 min of phosphorus upshift in the direction of more forward-driven glycolysis (Fig. 4b and Supplementary Fig. 7). Although the GAPDH step in glycolysis directly assimilates inorganic phosphate, we did not observe a big increase in the forward driving force at this step. Instead, we observed a significant forward shift at TPI and at the PGM:ENO reaction sequence (Fig. 4c). The increased driving force between PGM and ENO was consistent with phosphorus upshift inducing a significant increase in 23BPG, but not PEP (Fig. 4a). In general, thermodynamic changes were smaller than in nitrogen upshift. Collectively, these data paint a picture where ATP synthesis, which, in aerobic E. coli normally occurs mainly via oxidative phosphorylation, is restricted by low phosphate. On phosphorus upshift, ATP levels increase, leading to increased FBP and enhanced glycolytic flux. Certain steps, such as GAPDH, are accelerated by higher substrate levels; others, such as phosphoenolpyruvate carboxylase, are accelerated by allostery²⁴; whereas yet others, such as TPI and enolase, are favored also by thermodynamics. The regulation of glucose uptake by enzyme I in response to phosphate remains unclear.

Oxygen impacts microbial growth in a fundamentally different manner from nitrogen and phosphorus, since it functions as an electron acceptor rather than as a biomass component. By enabling oxidative phosphorylation, oxygen decreases the demand for glycolysis. Consistent with this, anaerobic to aerobic O₂ upshift decreased the glucose uptake rate from 20 ± 3.0 mmol gCDW⁻¹ h⁻¹ to 13 ± 1.2 mmol gCDW⁻¹ h⁻¹. This was accompanied by a rapid fall in NADH and FBP levels, and a rise in lower glycolytic intermediates, including pyruvate (Pyr) (Supplementary Fig. 8). These observations are consistent with aerobic metabolism consuming NADH, which shifts the equilibrium of the aldolase–TPI–GAPDH reaction sequence away from FBP and towards lower glycolytic intermediates. Indeed, despite the glycolytic flux decreasing, we observed a forward shift (more negative ΔG) for the aldolase and TPI reactions (Supplementary Fig. 9).

Collectively, these data suggest that, on limitation for an elemental biomass component, decreased glycolytic flux results in spare enzymatic capacity. The situation is different with oxygen, since its presence slows, rather than accelerates, glycolysis (more detail in the Supplementary Notes). When an elemental biomass component reappears, the excess enzymatic capacity enables rapid acceleration of glycolysis. This occurs without disrupting homeostasis, as best exemplified by nitrogen upshift.

Thermodynamics-mediated acceleration of mammalian glycolysis.

We were curious as to whether a similar mechanism for rapid acceleration of glycolysis might also occur in mammalian cells. Here, rather than modulating nitrogen or phosphorus status, we used the inhibitor of respiratory ATP production, oligomycin, to trigger faster glycolysis. Culturing immortalized baby mouse kidney cells (iBMK cells) on [5-²H₁]- and [1,2-¹³C₂]glucose, we measured the concentrations and labeling fractions of glycolytic intermediates 30 min after oligomycin treatment. This short experimental timescale is sufficient for upregulation of glycolysis, while limiting enzyme concentration changes²⁵. The levels of glycolytic intermediates showed modest changes except for FBP, which increased more than threefold, and the ATP/ADP ratio decreased (Supplementary Fig. 10). Oligomycin-treated cells retained significantly more ²H in FBP and 3PG (Fig. 5a, Supplementary Fig. 11 and Supplementary Table 7). Similarly, DHAP was more M + 2 ¹³C-labeled (Supplementary Table 8). The total free energy change from G6P to PEP nearly doubled, with the greatest changes occurring in lower glycolysis (Fig. 5b and Supplementary Table 9). Thus, decreased reaction reversibility constitutes a general mechanism for rapidly enhancing glycolytic flux.

Fig. 5 |. Oligomycin enhances the forward driving force in glycolysis.

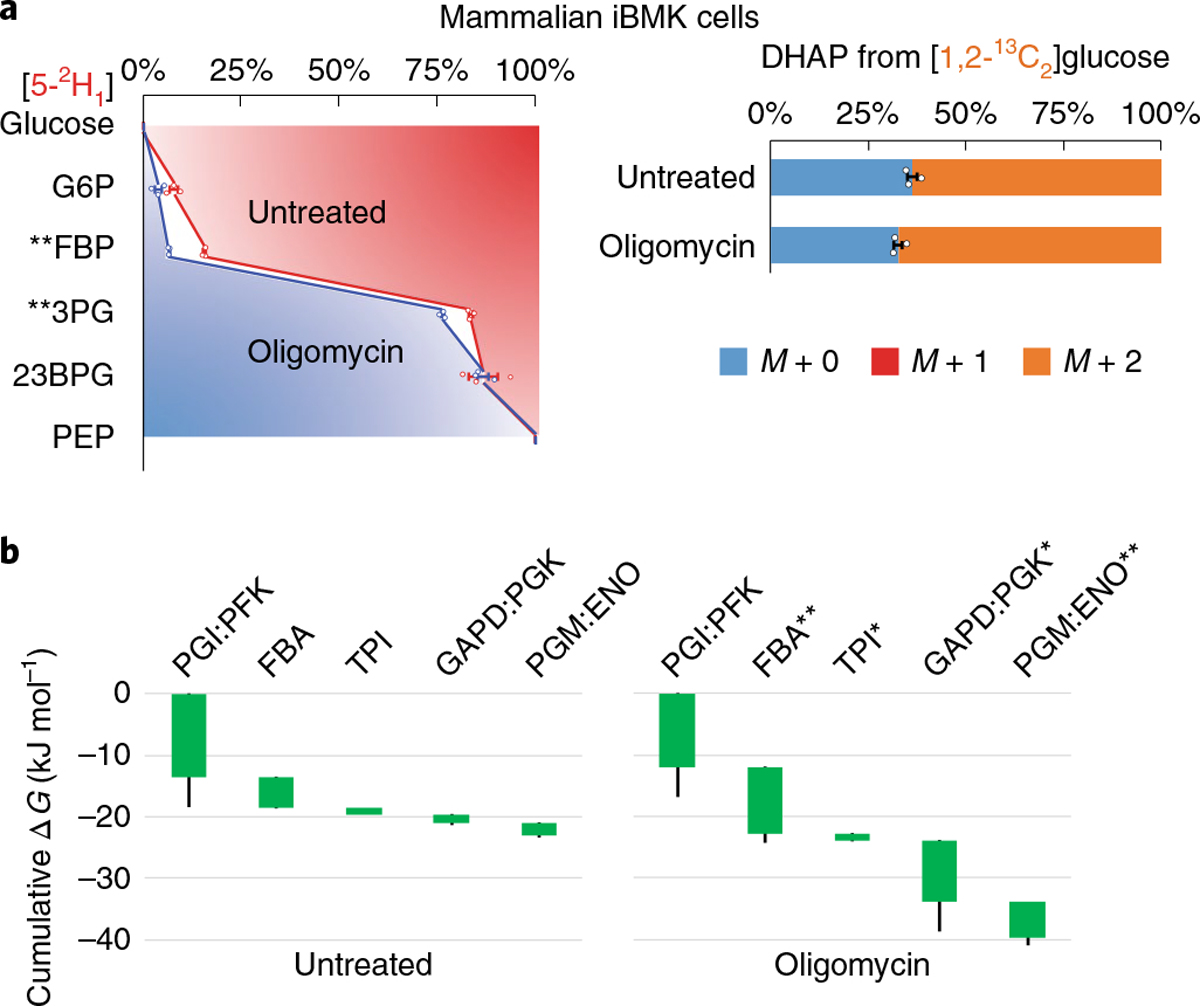
a, Mammalian iBMK cells cultured on [5-²H₁]- or [1,2-¹³C₂]glucose after addition of DMSO (untreated) or oligomycin for 30 min. On oligomycin treatment, the glycolytic intermediates retained more ²H and the unlabeled DHAP pool decreased, indicating less reversibility. The center and error bars represent the mean ± s.e.m. (n = 3, biologically independent samples). b, Corresponding ΔG were inferred from the flux-modeling results that best fit the observed ²H and ¹³C labeling. Each of the reaction(s) ΔG (<0) is represented by the height of the green bar. The bottom edges indicate the cumulative ΔG up to the corresponding step in glycolysis. Whiskers show s.e.m. (Methods). On oligomycin treatment, glycolysis shifted forward, towards a stronger thermodynamic force, especially at the aldolase and GAPD:PGK steps. *P < 0.05 and **P < 0.01 by two-tailed t-tests or bootstrapping (Methods).

Near-equilibrium glycolysis in C. cellulolyticum.

C. cellulolyticum is an obligate anaerobe capable of hydrolyzing cellulosic biomass into simple sugars and fermenting them into ethanol and other products²⁶. In contrast to model bacteria such as E. coli and to other Clostridia such as C. acetobutylicum, C. cellulolyticum displays slow glycolytic and growth rates, even when growing on simple sugars (glucose consumption rate = 1.9 ± 0.1 mmol gCDW⁻¹ h⁻¹, approximately one-sixth that of C. acetobutylicum or E. coli). Despite its capacity for cellulose degradation, slow fermentation has precluded the application of C. cellulolyticum for biofuel production. We observed that, in addition to slow fermentation, C. cellulolyticum has low concentrations of glycolytic intermediates (Fig. 6a).

Fig. 6 |. Slow glycolysis of C. cellulolyticum operates near equilibrium using PPi-dependent PFK.

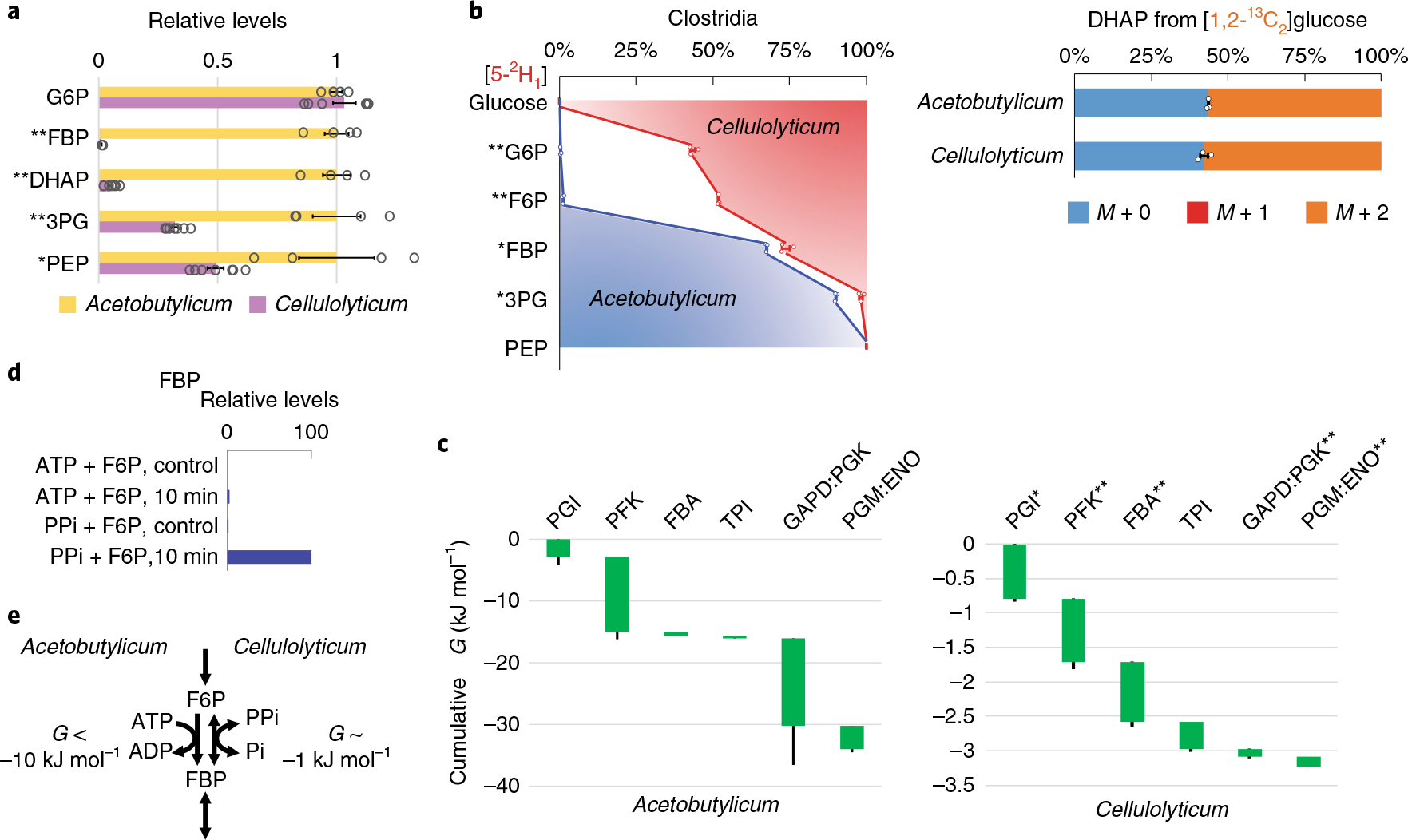
a, Relative levels of glycolytic intermediates in C. acetobutylicum versus C. cellulolyticum. Measurements are normalized by the means of the individual metabolites in C. acetobutylicum. The center and error bars represent the mean ± s.e.m. (n = 4 or 7, biologically independent samples). b, Isotope tracing of glycolytic reversibility in the obligate anaerobes C. cellulolyticum and C. acetobutylicum cultured on [5-²H₁]- or [1,2-¹³C₂]glucose. The center and error bars represent the mean ± s.e.m. (n = 3, biologically independent samples). c, All glycolytic reactions of C. cellulolyticum were close to equilibrium with ΔG > −1 kJ mol⁻¹. The resulting cumulative ΔG from G6P to PEP was approximately −3 kJ mol⁻¹, one-tenth of that of C. acetobutylicum. Each of the reaction(s) ΔG (<0) is represented by the height of the green bar. The bottom edges indicate the cumulative ΔG up to the corresponding step in glycolysis. Whiskers show s.e.m. (Methods). The most substantial differences between canonical (for example, E. coli, C. acetobutylicum and mammalian) and C. cellulolyticum glycolysis were in the ΔG of phosphofructokinase (PFK) and GAPD:PGK. d, In C. cellulolyticum cell lysate, fructose-1,6-bisphosphate (FBP) was produced in the presence of PPi but not ATP (10 min incubation). Control represents identical assays without cell lysate and the plotted results represent two replicate experiments. e, The weakly forward-driven PFK in C. cellulolyticum is due to the use of the PPi–Pi pair instead of the ATP–ADP pair. *P < 0.05 and **P < 0.01 by two-tailed t-tests or bootstrapping (Methods).

To explore the glycolytic thermodynamics, we cultured C. cellulolyticum in [5-²H₁]- and [1,2-¹³C₂]glucose. Interestingly, the ²H labeling of all glycolytic intermediates was substantially less than in E. coli, mammalian cells or its faster fermenting relative C. acetobutylicum (Fig. 6b, Supplementary Fig. 12 and Supplementary Table 10). The ¹³C labeling of DHAP was comparable across the organisms (Supplementary Table 11), and the total ΔG drop of C. cellulolyticum glycolysis from G6P to PEP was only −3 kJ mol⁻¹, roughly tenfold less than in mammalian cells, E. coli or C. acetobutylicum¹³ (Fig. 6c and Supplementary Table 12).

The PFK reaction is strongly forward driven in most organisms. However, the small ΔG for the full glycolytic sequence meant that it must be reversible in C. cellulolyticum. In another cellulolytic bacterium, C. thermocellum, this reaction step has been shown to be catalyzed by a PFK enzyme that uses pyrophosphate (PPi) instead of ATP²⁷. While futile cycling between PFK and fructose bisphosphatase could mimic labeling due to reversible PFK flux (Supplementary Notes), we were curious as to whether C. cellulolyticum may instead be using a PPi-dependent PFK that operates near equilibrium. We found two annotated PFK-encoding genes: Ccel_2223 with an unknown cofactor specificity and Ccel_2612 with ATP dependency. We assayed for cofactor specificity using C. cellulolyticum cell lysates and found that the conversion of fructose-6-phosphate (F6P) to FBP takes place only in the presence of PPi, but not in the presence of ATP (Fig. 6d). These observations suggested that Ccel_2612 is inactive and that Ccel_2223 encodes a PPi-dependent PFK.

PPi is thought to be produced mainly as a by-product of biomass synthesis (transfer RNA charging and nucleotide polymerization) and its levels within cells are expected to be ~1 mM (ref. ²⁸). The use of the PPi–Pi pair instead of the ATP–ADP pair explains the reversibility of the PFK step in C. cellulolyticum (Fig. 6e). This small driving force at PFK, in turn results in a very low FBP concentration (>50-fold lower compared with C. acetobutylicum, Fig. 6a), which limits the driving force available for the rest of glycolysis.

Advantageously, the use of PPi, instead of ATP, to produce FBP increases the energy yield of glycolysis from 2 to 3 ATP equivalents per glucose (Supplementary Fig. 13). This extra ATP generation would appear to be an important benefit for this anaerobe, in which oxidative phosphorylation is unavailable for ATP synthesis and glucose is scarce, coming mainly from cellulose degradation²⁹. The down side is a weaker driving force for glucose catabolism and thus slower net glycolysis. Thus, in C. cellulolyticum, the limited thermodynamic driving force translates into higher energy efficiency.

Discussion

The advancement of therapeutics, metabolic engineering and biofuel production relies on our understanding of metabolism in various cell types, diseased states and microorganisms. Over the past decades, stable isotope tracing has been increasingly employed to elucidate metabolic activity. In the present work, we augment the utility of isotope tracing by developing enhanced strategies for deciphering metabolic thermodynamics. With the proper choice of tracers, forward and backward reactions result in differential metabolite-labeling patterns, whose deconvolution reveals reaction reversibility and ΔG. This strategy works particularly well for reactions that are reasonably close to equilibrium, and hence labeling from reverse flux is readily detectable (Supplementary Notes). In addition to [5-²H₁]- and [1,2-¹³C₂]glucose, which we used here, other glucose tracers can be useful for determining ΔG of glycolytic reactions (for example, [2-²H₁]glucose for PGI and [4-²H₁] glucose for GAPDH). While presently demonstrated in glycolysis, with proper choice of tracers, this GibbsIT method can, in principle, be applied to other reactions and pathways.

The ΔG values presented here were obtained from fewer and easier experiments than in previous studies that required integration of absolute metabolite concentrations, ΔG′° and various ¹³C tracing data¹³. For the basal state of E. coli and iBMK cells, both approaches yielded similar quantitative answers. Importantly, the increased ease of obtaining the present measurements allows them to be made under conditions not previously explored. This expanded dataset revealed that glycolytic flux and thermodynamics do not always go hand-in-hand. Specifically, oxygen upshift was exceptional in that lower flux occurred with more driving force, reflecting a decreased need for glycolytic ATP even though the glycolytic product, NADH, was less abundant (see also Supplementary Notes). These data also revealed two important virtues of higher reaction reversibility in cells running glycolysis slowly: (1) ability to rapidly accelerate glycolysis and (2) potential for increased ATP yield.

From the perspective of resource allocation, thermodynamically forward-driven reactions, while energetically expensive, utilize enzymes at higher per-protein productivity (in terms of net flux per enzyme molecule)^30–34. In addition, high driving force reduces the risk of developing thermodynamic bottlenecks. Such bottlenecks have been suggested to occur at GAPDH in C. thermocellum, a relative to C. cellulolyticum, when the intracellular NADH level rises due to the addition of exogenous ethanol³⁵. Indeed, in rapidly fermenting cells, most steps of glycolysis are substantially forward driven¹³.

Yet, glycolysis with a substantial forward driving force has a practical drawback: when cellular demand for energy or biomass increases, each of the enzyme-efficient steps can become a kinetic bottleneck, requiring enzyme synthesis to accelerate the reaction. The benefits of inefficient enzyme usage during submaximal fermentation were highlighted using GibbsIT during oligomycin treatment and nitrogen and phosphorus upshift: by shifting from reversible to forward-driven thermodynamics, glycolysis was upregulated within minutes to meet increased energy and carbon demand.

Because of the high sensitivity of net flux through near-equilibrium reactions to substrate and product concentrations, these flux changes can be achieved, as exemplified by nitrogen upshift and oligomycin treatment, with only small deviations from metabolite concentration homeostasis. Quantitatively, to achieve a twofold flux increase solely via reaction thermodynamics, the reaction must initially be relatively close to equilibrium, with ΔG > −3 kJ mol⁻¹. This limit corresponds to J⁻/J⁺ ≈ 1/3, yielding a net forward flux of 2 flux units (J⁺ − J⁻ = 3 − 1), and the maximum capacity of 4 flux units (J⁺ + J⁻ = 3 + 1). In this scenario, however, the reaction must shift to being nearly irreversible (ΔG « 0) to achieve the required flux increase (as all 4 units of flux capacity need to run forward), and this requires large changes in metabolite levels. If the reaction is initially closer to equilibrium (ΔG > −2 kJ mol⁻¹), then net flux can double by only a modest (<2 kJ mol⁻¹) change in ΔG, which requires only a modest change in metabolite concentrations. For example, a 35% change is needed in each metabolite involved in a one-substrate-one-product reaction, such as TPI, PGM and ENO, and less if the reaction is initially closer to equilibrium or involves more substrates or products, as in GAPDH.

As the above calculations highlight, reactions transition from being mainly reversible to largely forward driven within a relatively narrow ΔG window (−1 to −4 kJ mol⁻¹). By shifting within this ‘goldilocks’ ΔG region, it is possible to accomplish large flux changes with small concentration changes, while still being reasonably enzyme efficient, especially in the higher flux state. GibbsIT enables precise measurement of ΔG changes in this key range.

The resulting observations show that cells employ an alternative to straightforward modulation of flux by changing enzyme levels^3,36,37. Indeed, while flux can be increased or decreased without altering metabolite levels or thermodynamics by proportionally increasing or decreasing the activity of every enzyme in the pathway, this approach is inflexible, since it requires substantial protein synthesis and degradation and/or hard-wired enzyme regulation. In contrast, by changing the reaction thermodynamics, pathways can adapt fluidly, regulating one or a few gating reactions whose products push on intervening near-equilibrium steps. The near-equilibrium steps disadvantageously require spare enzyme capacity (relative to the minimum needed to support the net forward flux), but advantageously increase the energy efficiency of the pathway. Thus, glycolysis strategically balances enzyme efficiency, energy yield and capacity to adapt to changing conditions.

Online content

Any methods, additional references, Nature Research reporting summaries, source data, statements of code and data availability and associated accession codes are available at https://doi.org/10.1038/s41589-019-0364-9.

Methods

Strains and culture conditions.

E. coli K-12 strain NCM3722 was grown at 37 °C in Gutnick minimal medium³⁸ containing 0.2% (w/v) glucose and 10 mM NH₄Cl or 2.5 mM arginine as the nitrogen source. For nitrogen upshift, NH₄Cl was spiked into the arginine culture to a final concentration of 2 mM (ref. ²⁰). For oxygen upshift, E. coli was inoculated anaerobically (OD₆₀₀ ≈ 0.03) into baffled flasks with magnetic stirring inside an anaerobic chamber (Coy Laboratory) with a 5% H₂, 5% CO₂, 90% N₂ atmosphere at 37 °C. During mid-log phase, oxygen upshift was performed by moving the flasks out of the anaerobic chamber and into an aerobic shaking incubator (300 r.p.m.). To ensure adequate oxygenation, liquid levels were kept at <20% of the baffled flask volume. Metabolite extractions were performed immediately before and 5 min after transferring cultures out of the anaerobic chamber. For phosphorus upshift experiments, E. coli RL3000 (MG1655 IlvG⁺ rph⁺ pyrE⁺ ΔglcB), a nonauxotrophic MG1655 derivative, was grown at 37 °C in MOPS minimal medium with the following adjustments: no tricine, 0.2 mM K₂HPO₄ and 2 g l⁻¹ glucose. Experimental cultures were inoculated (OD₆₀₀ ≈ 0.03) in MOPS minimal media containing 0.15 mM K₂HPO₄. Metabolite extractions were performed during mid-log phase immediately before and 5 min after addition of 1.32 mM K₂HPO₄. For rapid phosphorus upshift experiments, E. coli cultures were grown on top of nylon membrane filters on 0.15 mM K₂HPO₄ MOPS agarose plates³⁹. When cells reached OD₆₀₀ ≈ 0.4, the filters carrying cultures were placed onto new MOPS agarose plates containing 1.32 mM K₂HPO₄. Metabolite extractions were performed at various time points following this upshift.

For oligomycin treatment experiments in mammalian cells, BAX^−/−/BAK^−/−-immortalized baby mouse kidney epithelial cells (iBMK)⁴⁰ were grown at 37 °C, 5% CO₂ in DMEM without pyruvate supplemented with 10% dialyzed fetal bovine serum. At 48 h before oligomycin treatment, 1.5 μl (packed cell volume) of iBMK cells were seeded into 60-mm dishes. Cells were grown in DMEM containing 10% dialyzed fetal bovine serum at a volume of 3 ml per dish. Cells were incubated at 37 °C in a 5% CO₂ atmosphere. At 2 h before oligomycin treatment, medium was changed from unlabeled DMEM to DMEM with labeled glucose (4.5 g l⁻¹) at a volume of 2 ml per dish. After 2 h of incubation in labeled medium, 2 μl of 1 mM oligomycin was injected into the dishes for a final concentration of 1 μM oligomycin. DMSO (2 μl) was injected into the control plates. Cells were kept inside the incubator during injection to minimize perturbation. Metabolite extractions were performed 30 min after oligomycin treatment.

C. cellulolyticum (ATCC 35319) and C. acetobutylicum (ATCC 824) were grown anaerobically at 37 °C inside an anaerobic chamber with a 5% H₂, 5% CO₂, 90% N₂ atmosphere. Cells were cultured in minimal medium containing 0.5% glucose, 2 g l⁻¹ KH₂PO₄, 2 g l⁻¹ K₂HPO₄, 0.2 g l⁻¹ MgSO₄·7H₂O, 1.5 g l⁻¹ NH₄Cl, 0.13 mg l⁻¹ biotin, 32 mg l⁻¹ FeSO₄·7H₂O, supplemented with standard vitamin and mineral mixes. Metabolite extractions were performed during the mid-log phase.

For all organisms and growth conditions, labeling experiments were performed by substituting natural unlabeled glucose in culture media with [5-²H₁]- or [1,2-¹³C₂]glucose.

Metabolite extraction and measurements.

Metabolite extraction from bacterial and mammalian cells was performed as rapidly as possible to minimize perturbations in metabolism, and the extracts were analyzed by LC–MS⁷. Bacterial cultures (E. coli, C. acetobutylicum and C. cellulolyticum) were vacuum-filtered onto nylon membrane filters (0.45 μm; Millipore). The filters were quickly flipped cell-side down into cold (−20 °C) 40:40:20 HPLC-grade acetonitrile/methanol/ water in Petri dishes. After 20 min at −20 °C, filters were flipped and washed thoroughly with the extraction solvent. Mammalian cell metabolism was quenched and metabolites were extracted by quickly aspirating media from culture dishes and adding cold (−20 °C) 80:20 methanol/water. The plates were moved into a −20 °C freezer for 20 min. Then, cells were scraped off the culture dish surface. Note that, in all cases, quenching was performed without any washing steps that can perturb the metabolism.

Once obtained, all extracts were moved to Eppendorf tubes for centrifugation at 4 °C. The supernatants were dried under nitrogen flow and reconstituted in HPLC-grade water. These samples were analyzed by reversed-phase ion-pairing liquid chromatography coupled to a high-resolution orbitrap mass spectrometer with electrospray ionization in negative-ion mode and a resolution of at least 100,000 at m/z 200 (Exactive and Q Exactive, Thermo)^8,17,41. The LC–MS data were analyzed using the Metabolomic Analysis and Visualization Engine (MAVEN) with analyte peaks identified by authenticated standards⁴². Measured labeling fractions were corrected for the natural abundance of ¹³C and ²H, as well as the impurities in the labeled substrates⁴³.

E. coli nitrogen upshift and mammalian iBMK cell glucose uptake rates were obtained from Doucette et al.²⁰ and Fan et al.⁴⁴, respectively. E. coli oxygen upshift and phosphorus upshift, and C. cellulolyticum glucose uptake rates, were measured by sampling the culture medium over time and analyzing them via cryoprobe-assisted ¹H-NMR spectroscopy^45,46. Absolute metabolite concentrations for iBMK cells were obtained from Park et al.¹³ and the relative metabolite levels were used to compute the absolute metabolite concentrations on oligomycin treatment.

Cell lysate assay.

C. cellulolyticum cells were grown in 40 ml of rich medium to mid-exponential growth phase (OD₆₀₀ = 0.4–0.6). The cells were collected, washed twice by 10 ml Tris buffer (50 mM Tris HCl, 10 mM MgCl₂, 2 mM DTT at pH 7.4) and resuspended in 5 ml of the same buffer. After disruption of the cells by sonication and subsequent centrifugation for 10 min at 6,000g and 4 °C, the supernatant was used for assaying enzyme activities. Anaerobic conditions were maintained throughout the entire procedure, and all manipulations were performed under an oxygen-free nitrogen atmosphere. All assays were performed at 34 °C. The protein contents in the extracts were quantified by the Bradford method, with crystalline bovine serum albumin as calibrants. The reaction was carried out in 400 μl 50 mM Tris buffer, which included 100 μl cell extract and 5 mM substrates (F6P, ATP and pyrophosphate). Enzyme activities were measured by quantifying the changes in substrate and product concentrations using LC–MS, as described above. Control experiments were carried out by excluding cell lysate while keeping all other assay conditions identical. A single run is plotted in Fig. 6d. A replicate experiment reproduced the plotted results.

Metabolic flux and free energy analysis.

To estimate reaction reversibility and thus ΔG = −RTln(v_n,f/v_n,b), the backward reaction fluxes v_n,b were analytically computed by mass balancing unlabeled glycolytic metabolite fractions from [5-²H₁]- and [1,2-¹³C₂]glucose experiments. The unlabeled metabolite fractions are denoted by subscripts U and 0 from [5-²H₁] and [1,2-¹³C₂]glucose. Single-digit, nonzero subscripts denote the number of ¹³C atoms labeled from [1,2-¹³C₂]glucose. Below, v_0,b denotes the backward flux through lumped PGI:PFK reactions; v_1,b, FBA; v_2,b, TPI; v_3,b, GAPD:PGK; v_4,b, first half of PGM (3PG ⇌ 23BPG); and v_5,b, the latter half of PGM and ENO (Supplementary Fig. 14). Note that backward fluxes due to reaction reversibility versus due to an alternative enzyme with different cofactor usage are indistinguishable, as they result in the same labeling patterns (for example, reverse PFK versus fructose bisphosphatase; Supplementary Notes). All fluxes are normalized to the net upper glycolysis flux, and thus are dimensionless.

$$v_{0,\text{b}}=\frac{\text{G}6{\mathrm{P}}_{\mathrm{U}}}{{\text{FBP}}_{\text{U}}-\text{G}6{\mathrm{P}}_{\mathrm{U}}}$$

$$v_{1,\mathrm{b}}=\frac{\left(1+v_{0,\mathrm{b}}\right)\left({\text{FBP}}_0-{\text{G6P}}_0\right)}{{\text{DHAP}}_0\times {\text{GAP}}_0-{\text{FBP}}_0}$$

$$v_{2,\mathrm{b}}=\frac{\left({\text{DHAP}}_0-{\text{FBP}}_0/{\text{GAP}}_0\right)\left(1+v_{1,\mathrm{b}}\right)}{{\text{GAP}}_0-{\text{DHAP}}_0}$$

$$v_{3,\mathrm{b}}=\frac{2\times {\text{GAP}}_{\text{U}}-v_{2,b}\left(1-{\text{GAP}}_{\text{U}}\right)+v_{\text{PPP},\text{ED}}\left({\text{GAP}}_{\text{U}}-6{\text{PG}}_{\text{U}}\right)-1}{3{\text{PG}}_{\text{U}}-{\text{GAP}}_{\text{U}}}$$

$$v_{4,\mathrm{b}}=\frac{2\times 3{\text{PG}}_{\text{U}}-v_{2,\mathrm{b}}\left(1-{\text{GAP}}_{\text{U}}\right)+v_{\text{PPP},\text{ED}}\left(3{\text{PGU}}_{\text{U}}-6{\text{PG}}_{\text{U}}\right)-v_{\text{PPP}}\left(3{\text{PG}}_{\text{U}}-{\text{GAP}}_{\text{U}}\right)-1}{23{\text{BPG}}_{\text{U}}-3{\text{PG}}_{\text{U}}}$$

$$v_{5,\mathrm{b}}=\frac{2\times 23{\text{BPG}}_{\text{U}}-v_{2,\mathrm{b}}\left(1-{\text{GAP}}_{\text{U}}\right)+v_{\text{PPP},\text{ED}}\left(23{\text{BPG}}_{\text{U}}-6{\text{PG}}_{\text{U}}\right)-v_{\text{PPP}}\left(23{\text{BPG}}_{\text{U}}-{\text{GAP}}_{\text{U}}\right)-1}{1-23{\text{BPG}}_{\text{U}}}$$

$$v_{0,\text{f}}-v_{0,\mathrm{b}}=v_{1,\text{f}}-v_{1,\mathrm{b}}=v_{2,\text{f}}-v_{2,\mathrm{b}}=1$$

$$v_{3,\text{f}}-v_{3,\mathrm{b}}=v_{4,\text{f}}-v_{4,\mathrm{b}}=v_{5,\text{f}}-v_{5,\mathrm{b}}=2+v_{\text{PPP},\text{ED}}-v_{\text{PPP}}$$

$$v_{\text{PPP},\text{ED}}=\frac{\left(1-\frac{{\text{FBP}}_4}{{\text{DHAP}}_2}-{\text{GAP}}_0\right)\left(1+v_{1,\mathrm{b}}\right)+\left({\text{DHAP}}_0-{\text{GAP}}_0\right)\left(1+v_{2,\mathrm{b}}\right)}{{\text{GAP}}_0+6{\text{PG}}_4-1}$$

In E. coli, substantial flux through the PPP and the EDP may affect the labeling of glycolytic intermediates. These pathways were lumped into reactions to and from GAP. v_PPP,ED denotes the one-way flux from six-carbon molecules to three-carbon molecules via the PPP and, if applicable, the EDP (the lumped PPP and EDP fluxes that result in GAP). v_PPP denotes the sum of the GAP-consuming nonoxidative PPP reactions: the reverse transketolase (R5P + Xu5P ⇔ S7P + GAP and E4P + Xu5P ⇔ F6P + GAP) and the forward transaldolase (GAP + S7P ⇔ F6P + E4P). v_PPP,ED and v_PPP were treated as one-way fluxȝes. The difference between v_PPP,ED and v_PPP corresponds to the approximate five (and, for microbes, four) carbon requirements for nucleotide synthesis (and, for microbes, aromatic amino acids and histidine). All the labeling fractions above were directly measured by LC–MS except for GAP. GAP₀ (from ¹³C labeling) was inferred from the unlabeled fraction of the downstream metabolite 3PG, as there are no pathways that lead to differential ¹³C labeling of GAP and 3PG. GAP_U was solved using the following equation.

$${\text{GAP}}_{\text{U}}=\frac{{\text{FBP}}_{\text{U}}}{v_{1,\mathrm{b}}}+{\text{FBP}}_{\text{U}}$$

The full derivation can be found in the Supplementary Notes.

To complement the above approach, reaction reversibility and ΔG were computed using metabolic flux analysis^13,18. The model encompassed glycolysis and the PPP. As this approach is more rigorous in accounting for all relevant carbon transformations (at the expense of being more computationally complex), the ΔG reported in the text and figures were obtained in this manner. Carbon and hydrogen mappings were taken from standard textbooks and the enzymology literature (Supplementary Table 13). Isotopomer fractions were simulated by solving elementary metabolite unit mass balance equations¹⁸. This method relies on a stationary labeling assumption. We observe that glycolytic fluxes change rapidly to reach a new quasi-steady-state labeling (Supplementary Fig. 15). Under net flux balance constraints, optimal flux distributions were obtained by minimizing the variance-weighted sum-of-squared residuals (SSR) between the simulated and experimental isotope distributions and fluxes required for biomass production. The confidence interval of each forward-to-reverse flux ratio was determined by taking the maximum and minimum of flux ratios individually calculated from acceptable flux distributions¹³. The acceptable flux distributions were such that their SSR exceeded the SSR at the optimum by, at most, a fixed χ² cutoff with one degree of freedom (for example, 3.84 at 95% confidence level)⁴⁷. The algorithm was scripted in MATLAB.

Tests of statistical significance.

Tests compare measurements before versus after perturbations (for nitrogen, phosphorus and oxygen upshift and oligomycin addition) or between C. acetobutylicum and C. cellulolyticum. P values for labeling data and concentrations were determined by two-tailed t-test in Excel. For the labeling data, the t-test was performed on the log ratio of unlabeled to labeled fractions. For the concentration data, the t-test was performed on the log abundance data. P values for the ΔG measurements were based on extent of overlap of bootstrapped ΔG distributions. Specifically, for each reaction ΔG, random values were drawn from a uniform distribution, spanning the 99% confidence interval of that ΔG (on the basis of the 99% confidence interval χ² cutoff, 6.63, see section ‘Metabolic flux and free energy analysis’). These random values were then accepted or rejected probabilistically, with probability of acceptance Q = 100% − C, where C is the tightest ΔG confidence interval encompassing that value (on the basis of the χ² cutoff for that particular reaction and ΔG determined as in the previous section, with the confidence levels sampled in increments of 10%: 10%, 20%, …, 90%, and up to 99%). The average of three accepted values (three being the number of replicate labeling experiments) was then used as a single bootstrapped value of the ΔG distribution for that reaction, with the process repeated 1,000 times to generate the full ΔG distribution for that reaction. When comparing two ΔG distributions, P values were defined as the extent of overlap of the two distributions.

Reporting Summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Data availability

Source data for Figs. 1–6 are provided in Supplementary Tables 1–13 and on the GitHub public repository: https://github.com/jopark/GibbsIT

Code availability

The code for metabolic flux and free energy analysis is available on the GitHub public repository: https://github.com/jopark/GibbsIT