Abstract
Non-randomized studies of intervention effects (NRS), also called quasi-experiments, provide useful decision support about development impacts. However, the assumptions underpinning them are usually untestable, their verification resting on empirical replication. The internal replication study aims to do this by comparing results from a causal benchmark study, usually a randomized controlled trial (RCT), with those from an NRS conducted at the same time in the sampled population. We aimed to determine the credibility and generalizability of findings in internal replication studies in development economics, through a systematic review and meta-analysis. We systematically searched for internal replication studies of RCTs conducted on socioeconomic interventions in low- and middle-income countries. We critically appraised the benchmark randomized studies, using an adapted tool. We extracted and statistically synthesized empirical measures of bias. We included 600 estimates of correspondence between NRS and benchmark RCTs. All internal replication studies were found to have at least “some concerns” about bias and some had high risk of bias. We found that study designs with selection on unobservables, in particular regression discontinuity, on average produced absolute standardized bias estimates that were approximately zero, that is, equivalent to the estimates produced by RCTs. But study conduct also mattered. For example, matching using pre-tests and nearest neighbor algorithms corresponded more closely to the benchmarks. The findings from this systematic review confirm that NRS can produce unbiased estimates. Authors of internal replication studies should publish pre-analysis protocols to enhance their credibility.
Keywords: design replication, internal replication, meta-analysis, non-randomized study of interventions, quasi-experimental design, systematic review, within-study comparison
Introduction
In the past few decades there has been an explosion in the numbers of randomized controlled trials (RCTs) of development interventions, overall (Sabet & Brown, 2018) and in specific sectors like water, sanitation and hygiene (Chirgwin et al., 2021), and governance (Phillips et al., 2017). However, some types of relationship are not amenable to randomised assignment, for example, where program eligibility is universal or implementation has already begun, or where the primary measure of interest is an exposure, like use, rather than assignment to an intervention. In addition, some types of outcomes are measured with difficulty in prospective studies for ethical reasons (e.g., death in childhood). Contamination of controls threatens internal validity in trials, where measurement requires long follow-up periods. When effect sizes are small, it may be difficult to design studies prospectively to detect them (e.g., Bloom et al., 2008). There is interest in estimating causal effect magnitudes in all of these cases.
Theory is clear that under the right conditions—specifically that the selection process is completely known and has been perfectly measured 1 —non-randomized studies of intervention effects, also called quasi-experiments, can produce unbiased treatment effect estimates. It follows that if the selection process is reasonably well understood and measured, NRS should produce results that are reasonably close to those that would have been produced in a randomized experiment. The question is the extent to which this actually happens. To assess this, empirical studies of bias compare non-randomized study findings with those of a benchmark study, usually a randomized controlled trial (RCT) that is assumed to provide unbiased estimates. One type of benchmark study involves within-study comparison, or internal replication, in which the randomized and non-randomized estimates are drawn from the same population.
Internal replication studies on social science topics abound: we estimated there to be 133 such studies at the time our searches were completed. However, one needs to be careful when evaluating this literature because the studies may contain inherent biases. Researchers are not usually blinded to findings from the benchmark study and may therefore be influenced by those findings in specification searches. Measures of bias are confounded where different treatment effect estimands, representing different population samples, are used in benchmark and NRS. Systematic review and meta-analysis can help alleviate these concerns about bias, through systematic searches and screening of all relevant studies to avoid cherry-picking of findings, critical appraisal to assess risk of bias, and statistical synthesis to increase precision around estimates which, when well-designed and conducted, should be close to zero.
This paper presents the results of a systematic review of internal replication studies of economic and social programs in low- and middle-income countries (L&MICs). To our knowledge, it is the first review of these studies to use methods to identify, critically appraise, and synthesize evidence to systematic review standards (Campbell Collaboration, 2021). Section 2 presents the background and the systematic review approach. Section 3 presents the results of risk-of-bias assessment and quantitative estimates of bias using meta-analysis. Section 4 concludes.
Approach
Replication study design
Empirical approaches assess bias by comparing a given NRS estimator with an unbiased, causal benchmark estimator, usually an estimate produced by a well-conducted RCT (Bloom et al., 2002). One approach uses “cross-study” comparison (or external replication) of effect sizes from studies that are selected using systematic search methods and pooled using meta-analysis (e.g., Sterne et al., 2002; Vivalt, 2020). Cross-study comparisons are indirect as they use different underlying sample populations. They may therefore be subject to confounding due to context, intervention, comparator, participant group, and so on. Another approach is the “internal replication study” (Cook et al., 2008) or “design replication study” (Wong & Steiner, 2018). Like cross-study comparisons, these compare a particular estimator, usually a non-randomized comparison group, with a causal benchmark, usually an RCT, which is assumed to provide an unbiased estimate. However, the comparison arm used in the NRS may come from the same study, or data collection at the same time among the target population, hence they are also called “within-study comparisons” (Bloom et al., 2002; Glazerman et al., 2003). They have been undertaken in the social sciences since Lalonde (1986). A number of literature reviews of these studies exist (Glazerman et al., 2003; Cook et al., 2008; Hansen et al., 2013; Wong et al., 2017; Chaplin et al., 2018; Villar & Waddington, 2019).
There are different ways of doing internal replication studies (Wong & Steiner, 2018), the most commonly used—including all of the examples from development economics—being “simultaneous design.” In these studies, a non-equivalent comparison group is created, the mean of which is compared to the mean of the control group in the RCT. 2 In a standard simultaneous design, the NRS uses administrative data or an observational study from a sample of the population that did not participate in the RCT (e.g., Diaz & Handa, 2006). However, inference requires measurement of the same outcome at the same time, under the same study conditions, factors which are often difficult to satisfy (Smith & Todd, 2005) unless the experiment and NRS survey instruments are designed together (e.g., McKenzie et al., 2010). 3
Two types of simultaneous design are used to evaluate regression discontinuity designs (RDDs). The “tie-breaker” design (Chaplin et al., 2018) initially assigns clusters into the benchmark using an eligibility criterion, after which random assignment is done. Where the eligibility criterion is a threshold score, the design is used to compare observations within clusters immediately around the eligibility threshold in RDD—control observations from the RCT are compared to observations on the other side of the threshold which were ineligible for treatment (e.g., Buddelmeyer and Skoufias, 2004).
In “synthetic design,” the researcher simulates the RDD from existing RCT data by removing observations from the treatment and/or control arm to create non-equivalent groups. 4 For example, in cluster-RCTs in education, where schools are already using pre-test scores to assign students to remedial education, participants in remedial education from treated clusters of the RCT (which has been done to estimate the impact of a completely different intervention) are compared to those not assigned to remedial classes from control clusters (Barrera-Osorio et al., 2014). In this way, the RDD is constructed by researchers, and it may be applied to any threshold assignment variable measured at pre-test (Wong & Steiner, 2018). 5
Measuring Bias in Replication Studies
Bias in a particular estimate may arise from sampling error, study design and conduct (internal validity), and sampling bias (external validity) (Greenland, 2000). The extent to which evidence of statistical correspondence with RCT estimates adequately represents bias in NRS findings therefore depends only partly on internal validity of the RCT and NRS. Other factors affecting correspondence, which are sometimes inappropriately assumed to represent bias, include differences in the sampled population and specification searches. 6
Regarding internal validity, Cook et al. (2008) showed that NRS in which the method of treatment assignment is known, or carefully modeled using baseline data, produced very similar findings in direct comparisons with RCTs. Glazerman et al. (2003) found that the data source, the breadth of control variables, and evidence of statistical robustness tests were related to the magnitude of estimator bias in labor economics. In education, Wong et al. (2017) found that use of baseline outcomes, the geographical proximity of treatment and comparison, and breadth of control variables were associated with less bias. They also noted that NRS, which simply relied on a set of demographic variables or prioritized local matching when local comparisons were not comparable to treated cases, rarely replicated RCT estimates. One NRS approach that produces an internally valid estimator in expectation is the regression discontinuity design (Rubin, 1977). Chaplin et al. (2018) assessed the statistical correspondence of 15 internal replications comparing RDDs with RCTs at the cut-off, finding the average difference was 0.01 standard deviations. However, they warned larger samples and the choice of bandwidth may prove important in determining the degree of bias in individual study estimates. Hansen et al. (2013) noted that the difference between NRS estimates and RCTs was smaller where selection into treatment was done at the group level (hence individual participant self-selection into treatment was not the main source of variation). This finding is intuitively appealing, as group selection (by sex, age, geography, and so on) by implementers, also called “program placement bias,” may be easier to model than self-selection bias (which may be a function of individual aptitudes, capabilities and desires).
The second potential source of discrepancy between the findings of RCTs and NRS is in the effect size quantity or estimand due to differences in the target population in each study (external validity). For example, the correspondence between NRS and RCT may not represent bias when comparing an average treatment effect (ATE) estimate from an RCT with ATET from a double difference or matching study, or local average treatment effect (LATE) from an RDD (Cook et al., 2008). The ITT estimator, on which ATE is based in RCTs, becomes smaller as non-adherence increases, making raw comparison of the two estimators inappropriate, even if they are both unbiased. Similarly, when RDD is used to estimate the unbiased effect of an intervention amongst the population immediately around the treatment threshold, this may still differ from the RCT estimate due to heterogeneity in effects across the population receiving treatment. In other words, the interpretation of correspondence as bias may be confounded. An early review that found that NRS rarely replicated experimental estimates did not take this source of confounding into account (Glazerman et al., 2003).
A final factor is specification searches. Cook et al. (2008) argued that, due to the potential for results-based choices in the covariates and methods used, NRS analysts should be blinded to the results of the RCT they are replicating. These biases may serve to accentuate or diminish the differences between RCT and NRS depending on the replication study authors’ priors. Thus, Fretheim et al. (2016) “concealed the results and discussion sections in the retrieved articles using 3M Post-it notes and attempted to remain blinded to the original results until after our analyses had been completed” (p.326). Where it is not possible to blind replication researchers to the RCT findings, which would usually be the case, a reasonable expectation is that the internal replication report should contain sensitivity analysis documenting differences in effects due to changes in the specification (Hansen et al., 2013). An advantage of the latter approach, whether done openly or blinded, is to enable sensitivity analysis to different methods of conduct in the particular NRS.
Systematic Review approach
Most existing reviews of internal replication studies have not been done systematically—that is, based on systematic approaches to identify and critically appraise studies and statistically synthesize effect size findings. Exceptions include a review by Wong et al. (2017), which reported a systematic search strategy, and Glazerman et al. (2003) and Chaplin et al. (2018), which used statistical meta-analysis of effect sizes. This systematic review was registered (Waddington et al., 2018).
The eligibility criteria for inclusion in the review, alongside examples of excluded studies, are in Table 1. Eligible benchmark studies needed to use randomized assignment, whether controlled by researchers or administrators. Eligible within-study comparisons included any non-randomized approach to estimate the effect, including approaches with selection on unobservables and those using selection on observables only. These included methods with adjustment for unobservable confounding, such as difference-in-differences, also called double-differences (DD), instrumental variables (IV), RDD, and methods adjusting for observables such as statistical matching and adjusted regression estimation of the parametric model applied to cross-section data.
Table 1.
Systematic Review Inclusion Criteria.
| Criteria | Included studies | Excluded studies |
|---|---|---|
| Population | General program participants in L&MICs, where benchmark and NRS replication study draw on participants from the same target population and time period. | Between-study comparisons with no overlap in treatment group samples for causal benchmark and comparison (e.g., Glewwe et al., 2004). |
| Intervention and comparator | Any social or economic development intervention and any comparison condition (e.g., no intervention, wait-list, and alternate intervention). | Clinical or bio-medical interventions, or interventions conducted among populations in high-income country contexts (e.g., Fretheim et al., 2013) |
| Benchmark study design | Within-study comparisons reporting results of a benchmark randomised study, where randomisation was done by researchers or administratively. | Within-study comparisons where the causal benchmark did not use randomised assignment (e.g., Friedman et al., 2016). |
| NRS study design | Within-study comparisons reporting results of NRS comparison replication using any method (e.g., regression analysis applied to cross-section or panel data (DD), IV estimation, statistical matching, and RDD) from same target population and using the same outcome as benchmark study. | Within-study comparisons where target population differs from benchmark, for example, due to mismatch between ATE and LATE (Urquieta et al., 2009; Lamadrid-Figueroa et al., 2010). |
The NRS and benchmark needed to use the same treatment estimand. Where the bias estimator used the benchmark control and NRS comparison means only, data needed to be from the same sampled population. As discussed, this is important to avoid confounding. Evidence suggests that the assumption of constant treatment effects (treatment effect homogeneity) across sub-samples, which would be necessary to validate the comparison of different treatment estimands, should not be relied on. For example, Oosterbeek et al. (2008) showed positive impacts on school enrollment for the poorest quintile receiving benefits under the Bono de Desarrollo Humano (BDH) CCT program in Ecuador, but no impacts for the second poorest quintile.
Previous reviews noted several issues in systematically identifying internal replication studies due to a lack of common language used to index this evidence. Glazerman et al. (2003) indicated electronic searches failed to comprehensively identify many known studies, while Chaplin et al. (2018) stated that, despite attempting to search broadly, “we cannot even be sure of having found all past relevant studies” (p.424). Hence, a combination of search methods was used, including electronic searches of Research Papers in Economics (RePEc) database via EBSCO, where search terms were identified using “pearl harvesting” (using keywords from known eligible studies) (Sandieson, 2006) and 3ie′s Impact Evaluation Repository (Sabet & Brown, 2018); bibliographic back-referencing of bibliographies of included studies and reviews of internal replication studies; forward citation tracing of reviews of internal replication studies using three electronic tracking systems (Google Scholar, Web of Science, and Scopus); hand searches of the repository of a known institutional provider of internal replication studies (Manpower Demonstration Research Corporation, MDRC); and by contacting authors. Full details of the search strategy and results are in Villar and Waddington (2019).
Existing reviews of internal replication studies do not provide comprehensive assessments of the risk of bias to the effect estimate in the benchmark study using formal risk-of-bias tools. Partial exceptions are Glazerman et al. (2003), who commented on the likely validity of the benchmark RCTs (randomization oversight, performance bias, and attrition), and Chaplin et al. (2018) who coded information on use of covariates to control for pre-existing differences across groups and use of balance tests in estimation.
Modified applications of Cochrane’s tools for assessing risk of bias in RCTs were used to assess biases in benchmark cluster-randomized studies (Eldridge et al., 2016; Higgins et al., 2016). 7 For the individually randomized benchmark, which was analyzed using instrumental variables due to non-adherence, the risk-of-bias assessment drew on Hombrados and Waddington (2012), as well as relevant questions about selection bias into the study from Eldridge et al. (2016). 8 In addition, the appraisal of the benchmark took into account the relevance of the bias domains in determining internal validity of RCT estimate, as well as other factors that may have caused differences between the benchmark and NRS replication estimates. We also evaluated bias from specification searches using publication bias analysis at the review level.
Data collected from included papers included outcome means in control and comparison groups, outcome variances, sample sizes, and significance test values (e.g., t-statistics, confidence intervals, and p-values). These were used to calculate the distance metric measure of bias and its standard error. D is defined as the primary distance metric measuring the difference between the non-experimental and experimental means, interpreted as the size of the bias, calculated as
| (1) |
where and are the mean outcomes of the non-randomized comparison and randomized control groups and is the mean outcome of the randomized treatment group. Both numerical and absolute differences in D were calculated. Taking the absolute difference in D ensured that a measure of the overall deviation of randomized and non-randomized estimators was estimated, and not a measure based on the numerical difference that, on average “cancelled out” positive and negative deviations, potentially obscuring differences of interest. 9 Distance estimates were standardized by the standard deviation of the outcome, , as well as being compared as percentages of the treatment effect estimate and control and prima facie means to aid comparison. In total, six relative distance metrics were used to compare the difference between NRS and benchmark means, interpreted as the magnitude of bias in the NRS estimator: the standardised numerical difference; the standardised absolute difference; the percentage difference; the absolute difference as a percentage of the control mean; the percentage reduction in bias; and the mean-squared error. These are presented in Table 2.
Table 2.
Distance Metrics Used in Analysis.
| Estimator | Formula | Notes |
|---|---|---|
| Standardised numerical difference | = sample standard deviation of outcome in benchmark. | |
| Standardised absolute difference | ||
| Percentage of treatment effect estimate (percent difference) | ||
| Percentage of control mean (percent bias) | ||
| Percentage of remaining bias (percent bias removed) | = prima facie comparison mean. | |
| Mean-squared error | =variance of . |
The standard error of D s is given by the generic formulation of the difference between two independent estimates
| (2) |
where and are the standard errors of the non-randomized and randomized mean outcomes, respectively, which from equation (1) can be assumed independent.
In order to account for differences in precision across estimates, pooled means were calculated using fixed-effect inverse variance-weighted meta-analysis. The fixed effect model may be justified under the assumption that the estimates are from the same target populations, with the remaining bias being due to sampling error. However, each internal replication study reported multiple bias estimates using different methods of analysis and/or specifications. The weights w for each estimate needed to consider the different numbers of bias estimates each study contributed, using the following approach 10
| (3) |
where is the variance of distance estimate i and is the number of distance estimates provided by study k. The pooled weighted average of D was calculated as
| (4) |
Noting that the weight for a single study is equal to the inverse of the variance for each estimate adjusted for the total number of estimates, following Borenstein et al. (2009), it follows that the variance of the weighted average is the inverse of the sum of the weights across k included studies
| (5) |
We also tested the sensitivity of fixed effect meta-analysis estimates to different weighting schemes including simple averages and weighted averages using the inverse of the variance and the sample size.
Results
Information About the Sample
Eight eligible internal replications were included of randomized studies of social and economic programs (Table 3). All but one included study used a cluster-randomized controlled field trial as the benchmark. McKenzie et al. (2010) used administratively-randomized data, where program assignment was done individually by a lottery implemented by administrators, and the data itself were collected by the authors specifically to estimate the treatment effect of the lottery. Clusters were randomly assigned to the program in Galiani and McEwan (2013) and Galiani et al. (2017) as part of a field trial, and the study used census data to evaluate outcomes.
Table 3.
Eligible Within-Study Comparisons of Development Programs.
| Study | Intervention | Country | Outcome(s) | Benchmark | NRS replication | WSC type |
|---|---|---|---|---|---|---|
| Buddelmeyer and Skoufias (2004) | Cash transfer (PROGRESA) | Mexico | Reported school attendance and child labor | Cluster-RCT | RDD | Tiebreaker/synthetic |
| Diaz and Handa (2006) | Cash transfer (PROGRESA) | Mexico | Reported food expenditure, school enrollment, child labor | Cluster-RCT | Cross-section regression, matching | Simultaneous |
| Handa and Maluccio (2010) | Cash transfer (RPS) | Nicaragua | Reported expenditure, childcare, preventive health care, child illness | Cluster-RCT | Matching | Simultaneous |
| McKenzie et al. (2010) | Immigration entitlement | Tonga | Reported income | RCT | Cross-section regression, panel data regression (DD), IV regression, matching | Simultaneous |
| Galiani and McEwan (2013) | Cash transfer (PRAF) | Honduras | Census reported school enrollment and child labor | Cluster-RCT | RDD | Tiebreaker |
| Barrera-Osorio et al. (2014) | Scholarship | Cambodia | Grade completion and math test score | Cluster-RCT | RDD | Tiebreaker/synthetic |
| Chaplin et al. (2017) | Subsidy | Tanzania | Reported energy use and cost | Cluster-RCT | Matching | Simultaneous |
| Galiani et al. (2017) | Cash transfer (PRAF) | Honduras | Census reported school enrollment and child labor | Cluster-RCT | GDD | Tiebreaker |
Note. PROGRESA = Programa de Educación, Salud y Alimentación; RPS = Red de Protección Social; RCT = ; RDD = regression discontinuity design; DD = double-differences; GDD = geographical discontinuity design; PRAF = Programa de Asignación Familiar.
Four of the studies featured in a literature review of internal replication studies in development economics (Hansen et al., 2013). An additional four studies were located through the searches, including two of the Programa de Asignación Familiar (PRAF) in Honduras (Galiani & McEwan, 2013; Galiani et al., 2017) and one of a scholarship program in Cambodia (Barrera-Osorio et al., 2014), all of which examined discontinuity designs. A final study of electricity subsidies in Tanzania evaluated matching estimators (Chaplin et al., 2017).
The studies tested a range of non-randomized replication methods including cross-sectional and panel data regression, geographical discontinuity design (GDD), 12 IV, propensity score matching (PSM) and RDD.
Data were collected on treatment effects for the benchmark study, as well as each corresponding non-randomized replication. We calculated distance estimates from 586 specifications, of which 151 were estimated from test statistics due to incomplete information reported about standard deviations of the outcome in the benchmark (McKenzie et al., 2010; Galiani & McEwan, 2013; Barrera-Osorio et al., 2014; Galiani et al., 2017). The largest number of estimates was from matching and discontinuity designs, each totaling over 170 across four studies. The fewest estimates were from DD and IV estimation, with only 5 in total from a single study. The studies explored design and conduct, thus a range of matching estimators were tested, such as kernel matching (70 estimates) and nearest neighbor matching (59 estimates), or prospective RDD (92 estimates) and retrospectively designed RDD (81 estimates). The estimate of effect which most closely corresponded with the population for the non-randomized arm was taken from the RCT—the bandwidth around the treatment threshold for the replications using RDD (Buddelmeyer & Skoufias, 2004; Galiani & McEwan, 2013; Barrera-Osorio et al., 2014; Galiani et al., 2017) and the instrumental variables analysis of the administratively randomized study (McKenzie et al., 2010).
Bias in the Within-Study Comparisons
This section presents a summary of findings from the risk-of-bias assessment; the complete assessment is given in the Supplemental Appendix. Only one benchmark was estimated to have “low risk of bias” (Galiani & McEwan, 2013; Galiani et al., 2017). However, due to problems in implementing the NRS in those studies, there remained “some concerns” about confounding of the NRS-RCT distance estimate with respect to its interpretation as bias. The benchmark for PROGRESA was estimated to have “high risk of bias” due to attrition. 13 The remaining benchmark studies had “some concerns.” 14 Hence, all the within-study comparison estimates of bias in our sample may be confounded (Table 4).
Table 4.
Risk-of-Bias Assessment for Within Study Comparisons.
| Bias domain | Buddelmeyer and Skoufias (2004) * | Diaz and Handa (2006) * | Handa and Maluccio (2010) ** | McKenzie et al. (2010) *** | Barrera-Osorio et al. (2014) **** | Galiani and McEwan (2013) ; Galiani et al. (2017) ***** | Chaplin et al. (2017) |
|---|---|---|---|---|---|---|---|
| Bias arising from the randomisation process | Some concerns | Some concerns | Some concerns | Some concerns | Low risk | Low risk | Some concerns |
| Selection bias in recruitment | Some concerns | Some concerns | Some concerns | Some concerns | Low risk | Low risk | Some concerns |
| Departure from intended treatment^ | Some concerns | Some concerns | Low risk | Low risk | Low risk | Low risk | Some concerns |
| Attrition bias due to missing outcome data | High risk | High risk | Some concerns | Some concerns | Some concerns | Low risk | Low risk |
| Bias in measurement of the outcome^ | Some concerns | Some concerns | Some concerns | Some concerns | Low risk | Low risk | Low risk |
| Bias in selection of the reported result^ | Low risk | Low risk | Low risk | Low risk | Low risk | Low risk | Low risk |
| Bias in NRS estimate | Low risk | Some concerns | Some concerns | Low risk | Low risk | Some concerns | Low risk |
| Overall bias in within-study comparison | High risk | High risk | Some concerns | Some concerns | Some concerns | Some concerns | Some concerns |
Notes: * assessment draws on (Diaz & Handa, 2005), Behrman and Todd (1999), Skoufias et al. (2001), Angelucci and de Giorgi (2006) and Rubalcava et al. (2009); ** assessment draws on Maluccio and Flores (2004, 2005); *** assessment is of the instrumental variables estimate for the randomised sample; **** assessment draws on Barrera-Osorio and Filmer (2016); ***** assessment draws on Glewwe and Olinto (2004); ^ assessment takes into account relevance of the domain for relative bias regarding within-study comparison.
Source: authors using Higgins et al. (2016), Eldridge et al. (2016) and (Hombrados & Waddington, 2012).
Concerns about the benchmarks often arose from a lack of information, such as in the case of attrition in the PROGRESA benchmark experiment, or in assessing imbalance of baseline characteristics using distance metrics. In other instances, concerns were more difficult to address. For example, none of the studies was able to blind participants to intervention, and outcomes were mainly collected through self-report, a possible source of bias in open (unblinded) studies (Savović et al., 2012). For benchmark studies using cluster-randomization, where informed consent often does not necessarily alert participants to the intervention, this source of bias may be less problematic (Schmidt, 2017). Also, where participants are identified after cluster assignment it is not clear that evaluations can sufficiently capture data on non-adherence due to participant migration into, out of, or between study clusters.
However, it was not always clear whether the risk of bias arising in the benchmark estimate would cause bias in the difference estimate. For example, a threat to validity due to incomplete treatment implementation (“departures from intended treatment” domain) is not a threat to validity in the distance estimate for within-study comparisons that compare the randomised control and NRS comparison means only, which do not depend on treatment fidelity, as in the cases reviewed here. Similarly, biases arising due to the collection of reported outcomes data (“bias in measurement of the outcome” domain) in open trials may not cause bias in the internal replication estimate if the NRS uses the same data collection methods, and the potential sources of bias in benchmark and observational study are considered to be equivalent (e.g., there are no additional threats to validity due to motivational biases from participating in, or repeated measurement as part of, a trial). Multiple specifications, outcomes, and sub-groups were included to provide diversity in the estimates in all studies, hence selective reporting that may have affected benchmark trials (under “selection of the reported result” domain) was not judged problematic in the context of within-study comparisons.
Finally, bias in the difference estimate may be caused by bias in the NRS, confounding of the relationship and specification searches. Bias in the NRS is captured in the meta-analysis of different specifications. Confounding of the relationship may occur due to differences in the survey (e.g., outcome measurement) and target population. 15 All discontinuity design replications included were able to restrict the RCT samples to create localized randomized estimates in the vicinity of the discontinuity and compared the distance between the two treatment effect estimates (Buddelmeyer & Skoufias, 2004; Galiani & McEwan, 2013; Barrera-Osorio et al., 2014; Galiani et al., 2017). In the case of Galiani and McEwan (2013), where program eligibility was set for localities below a threshold on mean height-for-age z-score (HAZ), the RDD comparison was generated for untreated localities just above the threshold, where HAZ was predicted due to limited data. In Buddelmeyer and Skoufias (2004), there were four groups of households that enabled the RDD estimator to be compared to the RCT. The groups were differentiated by treatment status of the cluster, determined by randomization across those clusters below a maximum discriminant score (poverty index); and eligibility of households within clusters for treatment, determined by the household’s discriminant score. The RCT treatment estimand was calculated over households within the same bandwidth as the RDDs to ensure comparability of the target population. Other studies used statistical methods to compare NRS comparison groups with randomized control group means (Diaz & Handa, 2006; Handa & Maluccio, 2010; McKenzie et al., 2010; Chaplin et al., 2017).
Quantitative Estimates of Bias
NRS with selection on observables
Table 5 compares the distance estimates obtained from the different methods of calculating the pooled effect. Two within-study comparisons reported distance using regression-based estimators (Diaz & Handa, 2006; McKenzie et al., 2010). The cross-section regression specifications may perhaps be one benchmark against which other estimators may be compared. As expected, these distance estimators tended to be larger than those using other methods, including double differences, credible instrumental variables, and statistical matching. 16
Table 5.
Pooled Standardised Bias Estimates.
| NRS Estimator | (1) Standardized Numerical Difference* | (2) Standardized Absolute Difference* | (3) Standardized Absolute Difference** | (4) Standardized Absolute Difference*** | (5) Mean-Squared Error*** | (6) Percent Difference*** | (7) Percent Bias*** | (8) Percent Bias Removed*** | Number of Distance estimates$ |
|---|---|---|---|---|---|---|---|---|---|
| Cross-section regression | 0.232 | 0.236 | 0.229 | 0.290 | 0.180 | 340.8 | 26.3 | 33.9 | 10 |
| IV regression | 0.206 | 0.206 | 0.104 | 0.206 | 0.095 | 31.8 | 83.8 | −29.6 | 3 |
| IV (appropriate instrument) | 0.007 | 0.007 | 0.007 | 0.007 | 0.000 | 1.1 | 3.0 | 95.4 | 1 |
| IV (inappropriate instrument) | 0.305 | 0.305 | 0.184 | 0.305 | 0.142 | 47.2 | 124.2 | −92.1 | 2 |
| Panel data regression (DD) | 0.137 | 0.137 | 0.137 | 0.137 | 0.019 | 21.2 | 55.9 | 55.9 | 2 |
| Matching | 0.084 | 0.280 | 0.059 | 0.246 | 0.183 | 210.3 | 13.1 | 58.3 | 177 |
| Matching on baseline outcome | 0.120 | 0.120 | 0.039 | 0.044 | 0.004 | 1.6 | 4.3 | 55.9 | 14 |
| Matching on local comparison | −0.001 | 0.200 | 0.043 | 0.088 | 0.028 | −9.0 | −8.4 | 53.1 | 66 |
| Matching with rich controls | 0.025 | 0.282 | 0.031 | 0.232 | 0.124 | 178.4 | 8.4 | 81.3 | 116 |
| Matching with parsimonious controls | 0.208 | 0.321 | 0.087 | 0.354 | 0.305 | 353.8 | 25.9 | 44.9 | 44 |
| Kernel matching | 0.022 | 0.284 | 0.139 | 0.282 | 0.149 | 255.3 | 4.3 | 34.3 | 70 |
| Local linear matching | 0.179 | 0.257 | 0.201 | 0.285 | 0.133 | 267.8 | 18.3 | 21.4 | 6 |
| Nearest neighbor matching | 0.011 | 0.273 | 0.040 | 0.125 | 0.069 | 54.9 | −2.4 | 51.5 | 58 |
| Radius matching | 0.154 | 0.256 | 0.215 | 0.280 | 0.143 | 100.8 | 11.0 | 236.6 | 6 |
| RDD | −0.015 | 0.048 | 0.025 | 0.012 | 0.000 | 7.3 | 8.0 | 94.2 | 173 |
| RDD (prospective design) | −0.037 | 0.073 | 0.052 | 0.064 | 0.008 | −580.0 | 33.4 | 383.8 | 92 |
| RDD (retrospective design) | 0.009 | 0.020 | 0.014 | 0.010 | 0.000 | 33.1 | 6.9 | 81.5 | 81 |
| RDD (ATE comparison)^ | −0.057 | 0.091 | 0.038 | 0.029 | 0.002 | 34.4 | 17.6 | 0.1 | 71 |
Note. RDD = regression discontinuity design; DD = double-differences.
Notes: * simple average used to calculate pooled estimate; ** weighted average calculated using the inverse of the variance multiplied by the inverse of the number of estimates in the study; *** weighted average calculated using the benchmark sample size multiplied by the inverse of the number of estimates in the study; ^ indicates RDD estimate compared with RCT average treatment effect (ATE comparisons also incorporated Urquieta et al., 2009 and Lamadrid-Figueroa et al., 2010); $ sample size is for calculations in (1-7), calculations in (8) use a smaller number of studies owing to more limited availability of a prima facie estimate.
Matching produced small to medium sized estimates on average—between 0.10 and 0.30 in simple weighting (Table 5 columns 1–2), <0.10 for some specifications in more complex weighting (Table 5 columns 3–4)—but conduct mattered. Using more parsimonious matching by reducing the covariates in the matching equation to social and demographic characteristics that would be available in a typical household survey, usually led to bigger distance estimates than matching using rich control variables in the data available (Diaz & Handa, 2006; Chaplin et al., 2017). Matching on pre-test outcomes provided smaller distance metrics on average (Chaplin et al., 2017; McKenzie et al., 2010). Finally, smaller distance metrics were estimated when matching on local comparisons (Chaplin et al., 2017; Handa & Maluccio, 2010; McKenzie et al., 2010). 17
The remaining columns of Table 5 attempt to translate the findings into metrics that better indicate the substantive importance of the bias, Column 5 gives the mean-squared error, column 6 presents the bias as a percentage of the benchmark treatment effect, and column 7 gives bias as a percentage of the benchmark control mean.
Matching tended to produce estimates that differed from the RCT treatment effect by large percentages, on average 200% bigger than the RCT estimate (Table 5 column 6). However, matching would be expected to present a larger treatment estimate where it estimates ATET, which is bigger than the intent-to-treat estimate under non-adherence. Presenting bias as a percentage of the control mean (column 7), the estimates were smaller. In addition, as noted above, where the control mean was close to zero, or small relative to the treatment estimate, the percentage difference estimator was large, as was the case in many of the matching estimators presented by Handa and Maluccio (2010). The most important aspect of study conduct in matching was the use of “rich controls,” leading to 83% bias reduction on average across 116 estimates from four studies, although with a relatively high expected MSE of 0.15 (Table 5 column 5). Nearest neighbor matching also outperformed other matching methods, accounting for 52% of bias with expected MSE of 0.07, based on 59 estimates from four studies. Matching on the baseline measure, which is similar to DD estimation, on average removed 56% of bias with expected MSE less than 0.001, across 15 estimates.
In contrast, across 10 estimates from two studies, regression analysis applied to cross-section data removed 34% of bias with an expected MSE of 0.18.
NRS With Selection on Unobservables
The studies examining discontinuity designs produced distance metrics that were typically less than 0.1 standard deviations. These relatively small distance metrics, compared with the other NRS estimators, varied by the bandwidth used (Buddelmeyer & Skoufias, 2004), as shown in the comparison of LATE and ATE estimators. 18 It is notable that the sample includes RDDs designed both prospectively (Buddelmeyer & Skoufias, 2004; Barrera-Osorio et al., 2014) and retrospectively (Galiani & McEwan, 2013; Galiani et al., 2017), providing tests of both types of RDD implemented in practice. These findings are useful, given that potential sources of bias in prospective and retrospective RDDs are different—for example, retrospective studies are potentially more susceptible to biased selection into the study (due to missing data), whereas prospectively designed studies may be more susceptible to motivation bias (e.g., Hawthorne effects).
Regression discontinuity design estimation produced bias estimates that were on average different from the RCT treatment effect by 7%, and 8% of the control mean. However, when RDD was compared to ATE estimates, it produced distance estimates that are on average 20% different from the RCT estimate, providing evidence for heterogenous impacts. These findings were strengthened by the inclusion of distance estimates from two studies that were excluded from previous analysis (Urquieta et al., 2009; Lamadrid-Figueroa et al., 2010), which compared RDD estimates to RCT ATEs. Regarding the statistical significance of the findings, RDDs are also usually of lesser power because they are estimated for a sub-sample around the cut-off. 19 However, the strongest evidence for accuracy were for RDD, which across 173 separate estimates from four studies, removed 94% of bias on average, with expected MSE less than 0.001.
McKenzie et al. (2010) examined the correspondence of two DD regression estimates, which removed an estimated 56% of bias with expected MSE less than 0.02 compared to the RCT. In two-stage least squares (2SLS) instrumental variables estimation, one instrument was the migrant’s network (indicated by number of relatives in the country of immigration). This was shown to be correlated with migration (albeit with F-statistic = 6, which is below the satisfactory threshold of F = 10; Bound et al., 1995), but produced a treatment effect distance metric exceeding that for single differences, based on pre-test post-test or cross-section adjustment. This supports the theoretical prediction that inappropriate instruments produce 2SLS findings that are more biased than OLS. The authors argued it was unlikely to satisfy the exclusion restriction since it was very likely correlated with income after immigration, despite being commonly used in the field of migration. Another instrument, distance to the application center, produced the smallest distance metric of any within-study comparison, effectively equal to zero. The instrument was highly correlated with migration (F-statistic = 40) and, it was argued, satisfied the exclusion restriction as it was unlikely to determine income for participants on the main island where “there is only a single labor market… where all villages are within 1 hour of the capital city” (p.939). While distance may provide a plausible source of exogenous variation in some IV studies, it is also not possible to rule out the possibility that the arguments being made for the success of the instrument were based on results. Distance would not provide an appropriate instrument where program participants move to obtain access to services.
Sensitivity analysis
The matching estimates were sensitive to the choice of weighting scheme. It can be seen that the simple unweighted average of the numerical bias tended to produce the smallest distance metric where the individual underlying difference estimates were distributed above and below the null effect, on average “cancelling out” each other (Table 5, column 1). Using absolute mean differences accentuates the difference between the RCT and NRS mean, by definition exceeding zero. The corollary is that taking the simple (unweighted) average of the absolute difference produced distance estimates that tended to be bigger (Table 5, column 2). This explains why the findings from this review are different from those found in other within-study comparison papers, which, sometimes implicitly, used unweighted averages of the numerical difference when discussing their findings (e.g., Hansen et al., 2013).
On the other hand, using the adjusted inverse-variance weighted average produced distance metrics between these two extremes (Table 5, column 3). Even the metrics for matching are below 0.1 in these cases, although this is due to the large number of small distance metrics produced by Chaplin et al. (2017). When the studies were instead weighted by RCT sample size, 20 rather than inverse of the variance, the matching distance metrics reverted to magnitudes presented above, although remaining small for baseline measurement, local comparison, and nearest neighbor algorithm (Table 5, column 4). RDD estimates did not appear sensitive to the choice of study weights.
Meta-regressions were estimated to explore differences across findings by NRS design and conduct simultaneously, alongside factors that might affect correspondence between NRS and benchmark, including type of outcome measure and risk of bias. 21 Use of income measures of the outcome and high risk of bias in the estimate were significantly associated with greater differences between NRS and benchmark estimates (Table 6). Variables associated substantively with smaller differences were use of RDD, matching, and binary outcomes. 22 The estimated between-study variance is also equal to zero (Tau-sq = 0.000); hence, we are unable to reject the null hypothesis of homogeneity in the true effect sizes. While we chose the fixed effects model on conceptual grounds, this finding provides some empirical reassurance that our model choice was reasonable.
Table 6.
Meta-Regression of Standardized Absolute Bias.
| Coefficient | 95%CI | ||
|---|---|---|---|
| Constant | 0.13 | −0.07 | 0.32 |
| Regression estimation* | |||
| Regression discontinuity design | −0.12 | −0.31 | 0.07 |
| Matching | −0.16 | −0.36 | 0.04 |
| No baseline measure* | |||
| Baseline measure | −0.01 | −0.06 | 0.03 |
| Non-local comparison* | |||
| Local comparisons | −0.01 | −0.06 | 0.03 |
| Parsimonious controls* | |||
| Rich control variables | −0.05 | −0.09 | −0.01 |
| Nearest-neighbor matching | −0.02 | −0.10 | 0.06 |
| Kernel matching | 0.12 | −0.06 | 0.30 |
| Other matching algorithm* | |||
| Education outcome* | |||
| Health outcome | 0.08 | −0.03 | 0.18 |
| Income outcome | 0.14 | 0.02 | 0.27 |
| Some concerns about bias* | |||
| High risk of bias | 0.07 | 0.01 | 0.13 |
| Number of obs | 586 | ||
| Tau-squared | 0.00 | ||
| I-squared | 0.0% | ||
| F | 2.48 | ||
| Prob > F | 0.01 | ||
Notes: * base category. Standard errors use cluster adjustment (equation (5)).
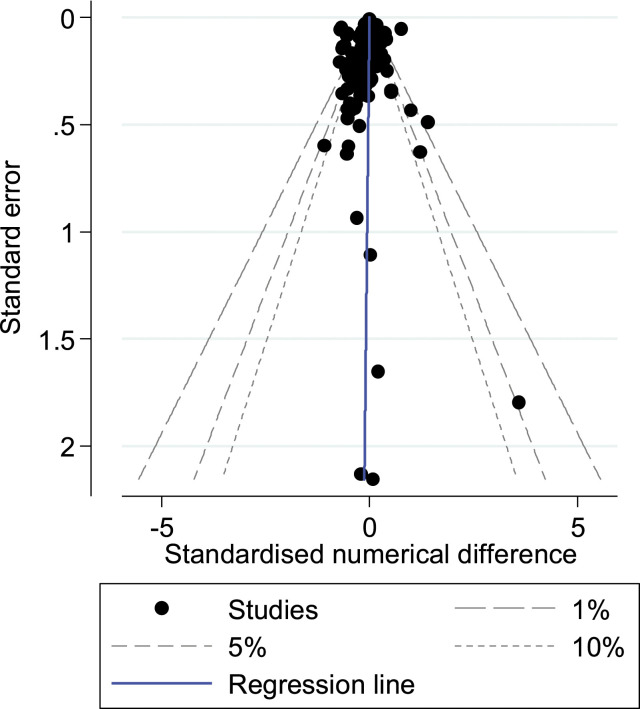
A funnel graph was plotted of the standardized numerical difference against the standard error to evaluate bias from specification searches (Figure 1). There was symmetry in the plot and regression line intercept passed through the origin, indicating no statistical evidence for specification searches. Since studies were designed to conduct and report results from multiple tests, regardless of findings, this evidence supports the validity of internal replication studies, even when authors are unblinded to the benchmark effect.
Figure 1.
Funnel graph with confidence intervals and regression line.
Conclusions
In this article, we aimed to provide empirical evidence on bias in non-randomized studies of intervention effects, or quasi-experiments, in development economics. We conducted a systematic review of evidence from internal replication studies on the correspondence between NRS and benchmark RCTs, and critically appraised the design and conduct of the studies. We conclude that NRS can provide unbiased effect estimates, supporting the findings of other researchers, notably (Cook et al., 2008). This is a useful finding for instances where causal inference is needed but randomized design infeasible to answer the evaluation questions. The analysis suggests that study design is probably the most important factor in determining bias. The most accurate findings, with large enough samples to generalize from, were from RDD, which were examined in four studies. Both prospective and retrospectively designed RDDs provided credible estimates. As predicted by theory, the bias properties of some estimators were dependent on effective study conduct, such as the choice of the instrument or the incorporation of baseline measures, geographically local matches, or matching algorithms. The strong performance of nearest neighbor matching algorithms on MSE is consistent with Busso et al.’s (2014) findings from Monte Carlo analysis, although these authors also found a trade-off between bias and variance.
The findings have implications for critical appraisal tools commonly used to assess risk of bias (e.g., Sterne et al., 2016), such as on the value of particular designs like regression discontinuity, the use of baseline covariates, or the methods of selecting matches. With regards to selection on observables more generally, matching sometimes produced almost identical bias coefficients to cross-section regression, but other times did not. Where matching used baseline adjustment, local matches, and nearest neighbor algorithms, the biases were smaller. The cause of selection bias is also likely to be important. As noted by Hansen et al. (2013), the estimates from McKenzie et al. (2010) are a case where the main source is participant self-selection, which is thought more difficult to control for directly than program placement bias at geographic level. It is possible, therefore, that program placement modeled using selection on observables may be able to provide more accurate findings, although the study in our sample of a group targeted program did not suggest findings using cross-section regression or matching were particularly accurate (Diaz & Handa, 2006).
Indeed, Smith and Todd (2005) warned against “searching for ‘the’ nonexperimental estimator that will always solve the selection bias problem inherent in nonexperimental evaluations” (p.306). Instead, they argued research should seek to map and understand the contexts that may influence studies’ degrees of bias. For instance, Hansen et al. (2013) noted the potential importance of the type of dependent variable examined in studies, suggesting simple variables (such as binary indicators of school attendance) may be easier to model relative to more complex outcome variables (such as consumption expenditure or earnings). Our meta-regressions support this finding. Additionally, complexity may not be a problem in and of itself, but rather simply magnify other problems, in particular missingness (easier to measure means probably less potential for missing data) and lower reliability.
On the magnitudes of the standardised distance metrics, which were found to be negligible in the case of discontinuity designs and, by conventional standards, small to medium for matching, recent attempts to examine effects sizes observed in empirical research show that these conventional values may provide a poor comparison of the magnitude of effects that seen in applied research. Reviews of education interventions in high-income countries and in L&MICs have shown that very few have effects that would be classified as anything but small according to Cohen’s approximations (Coe, 2002; McEwan, 2015). Averaging the effects of 76 meta-analyses of past education interventions, Hill et al. (2008) found the mean effect size ranged between 0.2 and 0.3 standard deviations. But there are also concerns about percentage distance metrics which depend on the magnitude of the baseline value, as seen here. Hence, it may be useful to compare distance based on both standardization and percentages, as done here.
A comment is warranted about generalizability, given the relatively small number of internal replication studies that exist in development economics and the small numbers of estimates for particular estimators. First, the interventions are restricted largely to conditional cash transfers, an approach that has been extensively tested using cluster-randomization. With the exception of the studies in Cambodia, Tanzania, and Tonga, most evidence from internal replications is from Latin America. There may therefore be legitimate concerns about the transferability of the evidence to other contexts and sectors. Furthermore, risk-of-bias assessments found that all of the studies had “some concerns” about bias, and those with “high risk of bias” were found to demonstrate less correspondence between NRS and RCT, confirming that conduct of the internal replication study itself is important in estimating bias (Cook et al., 2008).
A final comment concerns the conduct of further internal replication studies. We noted that it may be difficult to blind NRS replication researchers convincingly to the benchmark study findings, but that multiple model specifications, outcomes, and subgroups may help to provide sufficient variation in hypothesis testing. However, even though we were not able to find evidence of publication bias, reporting bias may clearly be problematic in these studies. The final implication, therefore, is that analysis protocols for future internal replication studies should be published. This should specify the findings from the benchmark study for which replication is sought, together with the proposed NRS designs and methods of analysis. It does not need to artificially constrain the NRS, in an area where pre-specifying all possible analyses may be difficult. As in evidence synthesis research, sensible deviations from protocol are acceptable provided the reasons for doing so are clearly articulated.
Supplemental Material
Supplemental material for Can Non-Randomised Studies of Interventions Provide Unbiased Effect Estimates? A Systematic Review of Internal Replication Studies by Hugh Sharma Waddington, Paul Fenton Villar, and Jeffrey C. Valentine in Evaluation Review
Notes
In regression discontinuity design, random error in measurement of the assignment variable can be incorporated to produce strong causal identification at the assignment threshold (Lee & Lemieux, 2010).
Simultaneous designs are dependent designs where the RCT treatment arm in dependent studies is common across study arms, and hence “differenced out” in distance estimator calculations (see equations 1) and 2) below).
“Multi-site simultaneous design” attempts to account for this by using data from an RCT based on multiple selected sites, within each of which participants are randomly assigned to treatment and control. Bias is inferred by comparing average outcomes from the treatment group in one site to the control observations from another site (Wong & Steiner, 2018).
For example, Fretheim et al. (2013) discarded control group data from a cluster-RCT with 12 months of outcome data points available from health administrative records before and after the intervention, in order to compare the RCT findings with interrupted time series analysis.
This approach was also used in the group A (eligible households in treated clusters) versus group D (ineligible households in control clusters) comparisons in Buddelmeyer and Skoufias (2004), and in the “pure control” group comparisons in Barrera-Osorio et al. (2014). The key difference between simultaneous tie-breaker and synthetic design is that, in the latter, the researcher removes observations to generate a “synthetic RDD,” whereas the former requires knowledge about the threshold decision rule used to assign groups into the RCT.
Where there is non-compliance due to no-shows in the treatment group, it is possible that the intervention “target population” could be included in the control group in the NRS in some within-study comparison designs. Furthermore, the sample used in NRS may differ from the RCT sample depending on whether observations are dropped non-randomly (e.g., to satisfy common support in PSM), which is sometimes referred to as sampling bias (Greenland, 2000), and similar to the problem of comparing population average treatment effects with local average treatment effects from discontinuity designs and instrumental variables estimation.
It was not considered necessary to blind coders to results following Cook et al. (2008), for example, by removing the numeric results and the descriptions of results (including relevant text from abstract and conclusion), as well as any identifying items such as author’s names, study titles, year of study, and details of publication. All studies reported multiple within-study comparisons and all data were extracted and analyzed by the authors.
Cochrane’s risk of bias tool for RCTs does not enable the reviewer to discern the validity of the application of IV to correct for non-compliance.
In practice, the standardized difference calculated as the subtraction of RCT numerical estimate from that of the NRS was frequently either side of zero, which did tend to “cancel out” across specifications, as shown in the results for simple subtracted standardized bias (Table 5 Column 1).
The generalized approach presented in Tanner-Smith and Tipton (2014) simplifies to equation (3) as follows
where the weighting considers the between-studies error in a random effects model, (equal to zero in the fixed effect case), and the estimated correlation between effects, (equal to 1 where all NRS comparisons draw on the same sample and the benchmark control is the same across all distance estimates).
The visas enabled Tongans to take permanent residency in New Zealand under New Zealand’s immigration policy which allows an annual quota of Tongans to migrate.
Galiani et al. (2017) stated that it was unlikely that households from the indigenous Lenca group migrated to obtain benefits under the CCT program, suggesting validity of the benchmark control group. However, there remained differences in shares of Lenca populations across the geographical discontinuity in cash transfer treatment and control communities, potentially invalidating the GDD comparison. Therefore, in this study the potential outcomes are assumed independent of treatment assignment, conditional on observed covariates.
The studies of PROGRESA were awarded as having “high risk of bias” due to high overall attrition and limited information about differential attrition in published reports available. For example, Rubalcava et al. (2009) noted “one-third of households left the sample during the study period” and “no attempt was made to follow movers” (p.515). Differential attrition in PROGRESA is discussed in Faulkner (2014).
There were two instances of “high risk of bias” in the NRS replications due to differences in the definition of outcomes relative to the benchmark survey questions (Diaz & Handa, 2006; Handa & Maluccio, 2010)—see Appendix.
In two studies there was risk of bias in the distance estimate due to differences in survey questionnaire for the expenditure and child labor outcomes (Diaz & Handa, 2006) and preventive health check-ups (Handa & Maluccio, 2010).
McKenzie et al. (2010) also reported the single difference estimator, taken from the difference between pre-test and post-test. This was found to be a less accurate predictor of the counterfactual outcome than matching on baseline outcome, double-differences and credible instrumental variables, but more accurate than cross-section regression and statistical matching which excluded the baseline measure.
McKenzie et al. (2010) implicitly used local matches, by choosing NRS comparisons from geographically proximate households in the same villages as treated households. Due to the reduced risk of contamination, as the treated households had emigrated already, matches in McKenzie et al. (2010) could be from the same villages, unlike in other matched studies (for an intervention where there is a risk of contamination or spillover effects), where matches would need to be geographically separate.
In Barrera-Osorio et al. (2014), the bias in test scores estimate was substantially smaller than the bias in grade completion, which the authors noted was estimated by enumerators and may therefore have been measured with error.
For example, Goldberger (1972) originally estimated that the sampling variance for an early conception of RDD would be 2.75 times larger than an RCT of equivalent sample size. See also Schochet (2008).
Sample size weighting uses the following formula: where n i is the sample size for difference estimate i and m j the number of estimates contributed by study k.
We used three regression specifications: meta-regression, OLS regression and Tobit regression (to account for censoring of the standardised absolute difference below 0). All models produced the same coefficient estimates. Results available on request from authors.
The meta-regression coefficient on a dummy variable equal to 1 when the study measured a binary outcome, was −0.10 (95%CI = −0.2, 0.0). When both binary outcome and income outcome dummies were included simultaneously, neither coefficient was statistically significant.
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: we gratefully received funding from the American Institutes for Research under Campbell Methods Grant CMG1.11.
Supplemental Material: Supplemental material for this article is available online.
References
- Angelucci M., de Giorgi G. (2006). Indirect effects of an aid program: the case of PROGRESA and consumption. IZA. Discussion Paper No. 1955, January 2006. [Google Scholar]
- Barrera-Osorio F., Filmer D. (2016). Incentivizing schooling for learning evidence on the impact of alternative targeting approaches. Journal of Human Resources, 51(2), 461–499. 10.3368/jhr.51.2.0114-6118r1 [DOI] [Google Scholar]
- Barrera-Osorio F., Filmer D., McIntyre J. (2014). An empirical comparison of randomized control trials and regression discontinuity estimations. SREE Conference Abstract, Society for Research on Educational Effectiveness. [Google Scholar]
- Behrman J., Todd P. (1999). Randomness in the experimental samples of PROGRESA. International Food Policy Research Institute. [Google Scholar]
- Bloom H., Hill C., Black A., Lipsey M. (2008). Performance trajectories and performance gaps as achievement effect-size benchmarks for educational interventions. Journal of Research on Educational Effectiveness, 1(4), 289–328. 10.1080/19345740802400072 [DOI] [Google Scholar]
- Bloom H. S., Michalopoulos C., Hill C.J., Lei Y. (2002). Can nonexperimental comparison group methods match the findings from a random assignment evaluation of mandatory welfare-to-work programs? MDRC working papers on research methodology. Manpower Demonstration Research Corporation. [Google Scholar]
- Borenstein M., Hedges L. V., Higgins J. P. T., Rothstein H. (2009). Introduction to meta-analysis. John Wiley and Sons. [Google Scholar]
- Bound J., Jaeger D. A., Baker R. (1995). Problems with instrumental variables estimation when the correlation between the instruments and the endogenous explanatory variable is weak. Journal of the American Statistical Association, 90(430), 443–450. 10.1080/01621459.1995.10476536 [DOI] [Google Scholar]
- Buddelmeyer H., Skoufias E. (2004). An evaluation of the performance of regression discontinuity design on PROGRESA World Bank Policy Research Working Paper 3386. The World Bank. [Google Scholar]
- Busso M., DiNardo J., McCrary J. (2014). New evidence on the finite sample properties of propensity score reweighting and matching estimators. The Review of Economics and Statistics, 96(5), 885–897. 10.1162/rest_a_00431 [DOI] [Google Scholar]
- Campbell Collaboration (2021). Campbell systematic reviews: policies and guidelines. Version 1.8. Campbell Policies and Guidelines Series 1. Campbell Collaboration. 10.4073/cpg.2016.1 [DOI] [Google Scholar]
- Chaplin D., Cook T., Zurovac J., Coopersmith J., Finucane M., Vollmer L., Morris R. (2018). The internal and external validity of the regression discontinuity design: A meta-analysis of 15 within-study comparisons: Methods for policy analysis. Journal of Policy Analysis and Management, 37(2), 403–429. 10.1002/pam.22051 [DOI] [Google Scholar]
- Chaplin D., Mamun A., Protik A., Schurrer J., Vohra D., Bos K., Burak H., Meyer L., Dumitrescu A., Ksoll A., Cook T. (2017). Grid electricity expansion in Tanzania by MCC: Findings from a rigorous impact evaluation. MPR Report, Mathematica Research Policy. [Google Scholar]
- Chirgwin H., Cairncross S., Zehra D., Sharma Waddington H. (2021). Interventions promoting uptake of water, sanitation and hygiene (WASH) technologies in low- and middle-income countries: An evidence and gap map of effectiveness studies. Campbell Systematic Reviews, 17(4), Article e1194. 10.1002/cl2.1194 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coe R. (2002). It's the effect size, stupid: What effect size is and why it is important. In Presented at: The annual conference of the British educational research association, England, 12–14 September 2002. University of Exeter. [Google Scholar]
- Cook T. D., Shadish W., Wong V. (2008). Three conditions under which experiments and observational studies produce comparable causal estimates: New findings from within-study comparisons. Journal of policy analysis and management, 27(4), 724–750. 10.1002/pam.20375 [DOI] [Google Scholar]
- Diaz J. J., Handa S. (2005). An assessment of propensity score matching as a nonexperimental impact estimator: Estimates from Mexico’s PROGRESA program. Working paper OVE/WP-04/05 July 22, 2005, Office of Evaluation and Oversight, Inter-American Development Bank, Washington, D.C. [Google Scholar]
- Diaz J. J., Handa S. (2006). An assessment of propensity score matching as a nonexperimental impact estimator: Estimates from Mexico’s PROGRESA program. The Journal of Human Resources, 41(2), 319–345. 10.3368/jhr.xli.2.319 [DOI] [Google Scholar]
- Eldridge S., Campbell M., Campbell M., Drahota A., Giraudeau B., Higgins J., Reeves B., Siegfried N. (2016) Revised Cochrane risk of bias tool for randomized trials (RoB 2.0) Additional considerations for cluster-randomized trials. Available at: https://www.riskofbias.info/welcome/rob-2-0-tool/archive-rob-2-0-cluster-randomized-trials-2016 (accessed 28 October 2020).
- Faulkner W. (2014). A critical analysis of a randomized controlled trial evaluation in Mexico: Norm, mistake or exemplar? Evaluation, 20(2), 230–243. 10.1177/1356389014528602 [DOI] [Google Scholar]
- Fretheim A., Soumerai S. B., Zhang F., Oxman A. D., Ross-Degnan D. (2013). Interrupted time-series analysis yielded an effect estimate concordant with the cluster-randomized controlled trial result. Journal of Clinical Epidemiology, 66(8), 883–887. 10.1016/j.jclinepi.2013.03.016 [DOI] [PubMed] [Google Scholar]
- Friedman W., Kremer M., Miguel E., Thornton R. (2016). Education as liberation? Economica, 83(329), 1–30. 10.1111/ecca.12168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galiani S., McEwan P. (2013). The heterogeneous impact of conditional cash transfers. Journal of Public Economics, 103(C), 85–96. 10.1016/j.jpubeco.2013.04.004 [DOI] [Google Scholar]
- Galiani S., McEwan P., Quistorff B. (2017). External and internal validity of a geographic quasi-experiment embedded in a cluster-randomized experiment. In Cattaneo M. D., Escanciano J. C. (Eds.), Regression discontinuity designs: Theory and applications. Advances in econometrics (Volume 38, pp. 195–236). Emerald Publishing Limited. [Google Scholar]
- Glazerman S., Levy D.M., Myers D. (2003). Nonexperimental versus experimental estimates of earnings impacts. The Annals of the American Academy of Political and Social Science, 589(1), 63–93. 10.1177/0002716203254879 [DOI] [Google Scholar]
- Glewwe P., Kremer M., Moulin S., Zitzewitz E. (2004). Retrospective vs. prospective analyses of school inputs: The case of flip charts in Kenya. Journal of Development Economics, 74(1), 251–268. 10.1016/j.jdeveco.2003.12.010 [DOI] [Google Scholar]
- Glewwe P., Olinto P. (2004). Evaluating the impact of conditional cash transfers on schooling: An experimental analysis of Honduras’ PRAF program. Final report for USAID January 2004 Washington, D.C. [Google Scholar]
- Goldberger A. (1972). Selection bias in evaluation of treatment effects: the case of interaction. Unpublished Manuscript. [Google Scholar]
- Greenland S. (2000). Principles of multilevel modelling. International Journal of Epidemiology, 29(1), 158–167. 10.1093/ije/29.1.158 [DOI] [PubMed] [Google Scholar]
- Handa S., Maluccio J.A. (2010). Matching the gold standard: Comparing experimental and nonexperimental evaluation techniques for a geographically targeted program. Economic Development and Cultural Change, 58(3), 415–447. 10.1086/650421 [DOI] [Google Scholar]
- Hansen H., Klejnstrup N. R., Andersen O. W. (2013). A Comparison of model-based and design-based impact evaluations of interventions in developing countries. American Journal of Evaluation, 34(3), 320–338. 10.1177/1098214013476915 [DOI] [Google Scholar]
- Higgins J. P. T., Sterne J. A. C., Savović J., Page M. J., Hróbjartsson A., Boutron I., Reeves B., Eldridge S. (2016). A revised tool for assessing risk of bias in randomized trials. In Chandler J., McKenzie J., Boutron I., Welch V. (Eds), Cochrane methods. Cochrane database of systematic reviews 2016 Issue 10 (Suppl 1). 10.1002/14651858.CD201601 [DOI] [Google Scholar]
- Hill C., Bloom H., Black A., Lipsey M. (2008). Empirical benchmarks for interpreting effect sizes in research. Child Development Perspectives, 2(3), 172–177. 10.1111/j.1750-8606.2008.00061.x [DOI] [Google Scholar]
- Hombrados J. G., Waddington H. (2012). A tool to assess risk of bias for experiments and quasi-experiments in development research. Mimeo. International Initiative for Impact Evaluation. [Google Scholar]
- Lalonde R. (1986). Evaluating the econometric evaluations of training with experimental data. American Economic Review, 76(4), 604–620. [Google Scholar]
- Lamadrid-Figueroa H., Ángeles G., Mroz T., Urquieta-Salomón J., Hernández-Prado B., Cruz-Valdez A., Téllez-Rojo M. M. (2010). Heterogeneous impact of the social programme Oportunidades on use of contraceptive methods by young adult women living in rural areas. Journal of Development Effectiveness, 2(1), 74–86. 10.1080/19439341003599726 [DOI] [Google Scholar]
- Lee D. S., Lemieux T. (2010). Regression discontinuity designs in economics. Journal of Economic Literature, 48(2), 281–355. 10.1257/jel.48.2.281 [DOI] [Google Scholar]
- Maluccio J., Flores R. (2004). Impact evaluation of a conditional cash transfer program: The Nicaraguan red de Protección social. FCND Discussion Paper No. 184, Food consumption and nutrition division. International Food Policy Research Institute, Washington, D.C. [Google Scholar]
- Maluccio J., Flores R. (2005). Impact evaluation of a conditional cash transfer program: The Nicaraguan red de Protección social. Research report No. 141. International Food Policy Research Institute. [Google Scholar]
- McEwan P. J. (2015). Improving learning in primary schools of developing countries: A meta-analysis of randomized experiments. Review of Educational Research, 85(3), 353–394. 10.3102/0034654314553127 [DOI] [Google Scholar]
- McKenzie D., Stillman S., Gibson J. (2010). How important is selection? Experimental vs nonexperimental measures of the income gains from migration. Journal of the European Economic Association, 8(4), 913–945. 10.1111/j.1542-4774.2010.tb00544.x [DOI] [Google Scholar]
- Oosterbeek H., Ponce J., Schady N. (2008). The impact of cash transfers on school enrolment: Evidence from Ecuador. Policy research working paper No. 4645. World Bank. [Google Scholar]
- Phillips D., Coffey C., Gallagher E., Villar P.F., Stevenson J., Tsoli S., Dhanasekar S., Eyers J. (2017). State-society relations in low- and middle-income countries: An evidence gap map. 3ie evidence gap map 7. The International Initiative for Impact Evaluation. [Google Scholar]
- Rubalcava L., Teruel G., Thomas D. (2009). Investments, time preferences and public transfers paid to women. Economic Development and Cultural Change, 57(3), 507–538. 10.1086/596617 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin D. B. (1977). Assignment to treatment on the basis of a covariate. Journal of Educational Statistics, 2, 1–26. 10.2307/1164933 [DOI] [Google Scholar]
- Sabet S.M., Brown A. (2018). Is impact evaluation still on the rise? The new trends in 2010-2015. Journal of Development Effectiveness, 10(3), 291–304. 10.1080/19439342.2018.1483414 [DOI] [Google Scholar]
- Sandieson R. (2006). Pathfinding in the research forest: The pearl harvesting method for effective information retrieval. Education and Training in Developmental Disabilities, 41(4), 401–409. http://www.jstor.org/stable/23879666 [Google Scholar]
- Savović J., Jones H., Altman D., Harris R., Jűni P., Pildal J., Als-Nielsen B., Balk E., Gluud C., Gluud L., Ioannidis J., Schulz K., Beynon R., Welton N., Wood L., Moher D., Deeks J., Sterne J. (2012). Influence of reported study design characteristics on intervention effect estimates from randomised controlled trials: Combined analysis of meta-epidemiological studies. Health Technology Assessment, 16(35), 1–82. 10.3310/hta16350 [DOI] [PubMed] [Google Scholar]
- Schmidt W.-P. (2017). Randomised and non-randomised studies to estimate the effect of community-level public health interventions: Definitions and methodological considerations. Emerging Themes in Epidemiology, 14(9), 1–11. 10.1186/s12982-017-0063-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schochet P. Z. (2008). Technical methods report: Statistical power for regression discontinuity designs in education evaluations (NCEE 2008-4026). National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. [Google Scholar]
- Skoufias E., David B., de la Vega S. (2001). Targeting the poor in Mexico: An evaluation of the selection of households into PROGRESA. World Development, 29(10), 1769–1784. 10.1016/s0305-750x(01)00060-2 [DOI] [Google Scholar]
- Smith J. C., Todd P. (2005). Does matching overcome LaLonde’s critique of nonexperimental estimators? Journal of Econometrics, 125(1–2), 303–353. 10.1016/j.jeconom.2004.04.011 [DOI] [Google Scholar]
- Steiner P. M., Wong V. (2018). Assessing correspondence between experimental and non-experimental results in within-study-comparisons. Evaluation Review, 42(2), 214–247. 10.1177/0193841x18773807 [DOI] [PubMed] [Google Scholar]
- Sterne J. A. C., Hernán M., Reeves B. C., Savovic J., Berkman N. D., Viswanathan M., Henry D., Altman D. G., Ansari M. T., Boutron I., Carpenter J. R., Chan A. W., Churchill R., Deeks J. J., Hrobjartsson A., Kirkham J., Juni P., Loke Y. K., Pigott T. D., Higgins J. P. (2016). ROBINS-I: A tool for assessing risk of bias in non-randomised studies of interventions. British Medical Journal, 355, i4919. 10.1136/bmj.i4919 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sterne J. A. C ., Juni P., Schulz K. F., Altman D. G., Bartlett C., Egger M. (2002). Statistical methods for assessing the influence of study characteristics on treatment effects in ‘meta-epidemiological’ research. Statistics in Medicine, 21(11), 1513–1524. 10.1002/sim.1184 [DOI] [PubMed] [Google Scholar]
- Tanner-Smith E., Tipton E. (2014). Robust variance estimation with dependent effect sizes: Practical considerations including a software tutorial in stata and SPSS. Research Synthesis Methods, 5(1), 13–30. 10.1002/jrsm.1091 [DOI] [PubMed] [Google Scholar]
- Urquieta J., Angeles G., Mroz T., Lamadrid-Figueroa H., Hernández B. (2009). Impact of Oportunidades on skilled attendance at delivery in rural areas. Economic Development and Cultural Change, 57(3), 539–558. 10.1086/596598 [DOI] [Google Scholar]
- Villar P. F., Waddington H. (2019). Within-study comparison and risk of bias in international development: Systematic review and critical appraisal. Methods research paper. Campbell Systematic Reviews, 15(1–2), Article e1027. 10.1002/cl2.1027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vivalt E. (2020). How Much Can We Generalize From Impact Evaluations?. Journal of the European Economic Association, 18(6), 3045–3089. 10.1086/596598 [DOI] [Google Scholar]
- Waddington H., Villar P. F., Valentine J. (2018). Within-study design replications of social and economic interventions: Map and systematic review (title registration). The Campbell Collaboration. [Google Scholar]
- Wong V., Steiner P. (2018). Designs of empirical evaluations of nonexperimental methods in field settings. Evaluation Review, 42(2), 176–213. 10.1177/0193841X18778918 [DOI] [PubMed] [Google Scholar]
- Wong V., Valentine J., Miller-Bains K. (2017). Empirical performance of covariates in education observational studies. Journal of Research on Educational Effectiveness, 10(1), 207–236. 10.1080/19345747.2016.1164781 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental material for Can Non-Randomised Studies of Interventions Provide Unbiased Effect Estimates? A Systematic Review of Internal Replication Studies by Hugh Sharma Waddington, Paul Fenton Villar, and Jeffrey C. Valentine in Evaluation Review