Abstract
Background:
Functional magnetic resonance imaging (fMRI) has been implemented widely to study brain connectivity. In particular, time-varying connectivity analysis has emerged as an important measure to uncover essential knowledge within the network. On the other hand, independent component analysis (ICA) has served as a powerful tool to preprocess fMRI data before performing network analysis. Together, they may lead to novel findings.
Methods:
We propose a new framework (GICA-TVGL) that combines group ICA (GICA) with time-varying graphical LASSO (TVGL) to improve the power of analyzing functional connectivity (FNC) changes, which is then applied for neuro-developmental study. To investigate the performance of our proposed approach, we apply it to capture dynamic FNC using both the Philadelphia Neurodevelopmental Cohort (PNC) and the Pediatric Imaging, Neurocognition, and Genetics (PING) datasets.
Results:
Our results indicate that females and males in young adult group possess substantial difference related to visual network. In addition, some other consistent conclusions have been reached by using these two datasets. Furthermore, the GICA-TVGL model indicated that females had a higher probability to stay in a stable state. Males had a higher tendency to remain in a globally disconnected mode.
Comparison with existing method:
The performance of sliding window approach is largely affected by the window size selection. In addition, it also assumes temporal locality hypothesis.
Conclusion:
Our proposed framework provides a feasible method to investigate brain dynamics and has the potential to become a widely used tool in neuroimaging studies.
Keywords: Dynamic functional connectivity, Resting state fMRI, GICA-TVGL framework, Sex difference
I. Introduction
Over the past decade, functional magnetic resonance imaging (fMRI) has attracted increasing attention, and has been widely used for mapping brain activity and studying neuronal connectivity in the human brain [1], [2]. By tracking the blood oxygenation level dependent (BOLD) responses of fMRI through both spatial and temporal scales, functionally important networks and their connectivity can be identified and investigated, where many computational approaches have been proposed. One classical method is seed-based analysis. In this approach, functional networks are defined as a collection of voxels that strongly correlated with the predefined seed regions [3]. As a result, it requires the prior knowledge of the brain and is sensitive to the selection of seed regions. Inappropriate choosing of seed regions may result in specific, small or overlapping networks [4]. By contrast, data-driven approaches can measure functional connectivity from the data directly without requiring prior information about the location of the network. For instance, nonnegative matrix factorization (NMF) allows the BOLD responses to be represented as a weighted linear combination of basis functions to reveal intrinsic networks [5], [6]. Sparse connectivity patterns (SCPs) and related approaches utilize the spatial sparsity property to identify functional network connectivity [7], [8], [9].
As a data-driven technique, independent component analysis (ICA) has become an important tool in fMRI studies [10], [11], [12]. The advantage of ICA is that it extracts separate independent sources mixed in original signals. Calhoun et al. extended the classical ICA approach into a group ICA (GICA) model to perform ICA analysis at the group level, which has been widely used in the fMRI community [13], [14], [15], [16], [17], [18]. Until recently, functional connectivity studies focussed primarily on static FNC patterns extracted from the whole fMRI scan session. While informative time-varying analysis of functional connectivity may uncover essential information within networks due to the dynamic nature of the human brain [19], [20]. A pipeline based on GICA was proposed by Allen et al. to assess resting-state FNC dynamics across the whole brain through analyzing dynamic functional network connectivity (dFNC) matrices [21]. This framework has shown great potential to investigate differences in functional connectivity induced by brain development and mental disorders [22], [23], [24], [25], [26]. The sliding window model as a common technique was used in this pipeline to capture FNC dynamics from the resting-state fMRI (rsfMRI) data. It assumes that FNC at a given time point can be calculated through the signal within the selected window. Window size selection can affect the performance of this approach. That is, an undersized window may cause unreliable estimation and spurious variability in dynamic FNC, while an oversized window may not reflect FNC dynamics well [27]. To address this limitation, various alternative methods have been proposed. For instance, Hidden Markov models (HMMs) were implemented without a window operation [28]. However, the HMM model assumes that transition probability among states is stationary in time and also assumes temporal locality. Yaesoubi et al. also provided a window-less model based on sparse dictionary learning algorithm to estimate time-varying FNC in rsfMRI data [29]. However, state transition sequences can only be detected via post hoc analysis in this approach. Recently, a time-varying graphical LASSO (TVGL) model was introduced by Hallac et al. to infer dynamic networks from time series data [30]. Because the TVGL can reveal interdependencies in dynamic systems, transitions in FNC dynamics can be detected. In our previous work, the ability of TVGL to estimate dFNC from resting-state fMRI data was validated [31].
In this article, we propose a data-driven framework by combining GICA and time-varying graphical LASSO to analyze dynamic functional network connectivity. Note that the TVGL requires that input data should follow a Gaussian distribution. However, component-level data generated by GICA does not necessarily satisfy this requirement. To improve the performance, we introduce a Gaussian copula model, which ensures components in the data follow a Gaussian distribution more closely without affecting the undirected graphical structure. In this paper, we first describe the details of the GICA-TVGL framework in Section 2. Then, we validate the reproducibility of our framework using both the PNC and PING datasets in Section 3. In particular, we apply our framework on both two large fMRI datasets to assess dynamic FNC differences between females and males. Some discussions and concluding remarks are given in Sections 4 and 5.
II. Methods
In this section, the algorithms involved in the GICA-TVGL framework are introduced, and the selection of key parameters is also described. The details are presented as follows.
A. Group ICA analysis
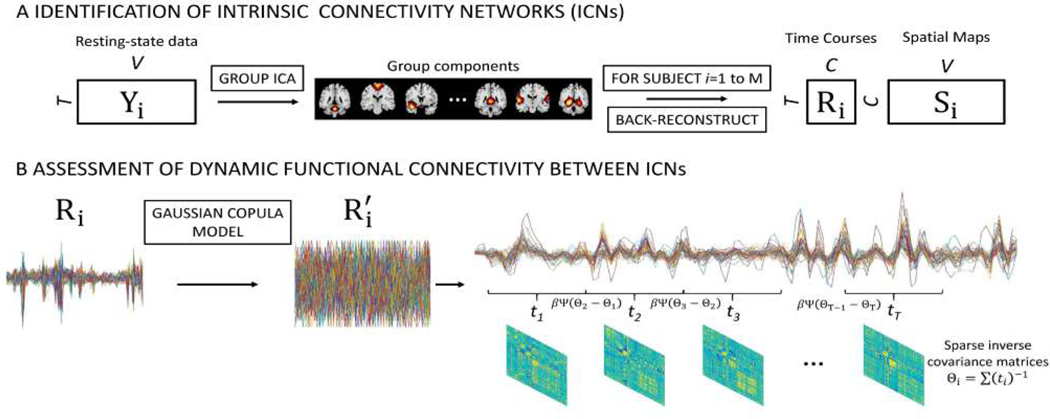
Group ICA (GICA), as a data-driven approach, can achieve parcellation of brain activity without any prior knowledge about the network location or its temporal activity. Herein, the data were decomposed into spatially independent sources and corresponding time series via group-level spatial independent component analysis (ICA) implemented in the GIFT toolbox (http://mialab.mrn.org/software/gift). The pipeline adopted here was proposed by Allen et al. with a relatively high model order (number of components, ) [21]. GICA was implemented in several steps. First, a subject-specific principal component analysis (PCA) was used to reduce subject data temporal dimension to 120 principal components (PCs). Next, the subject data (, M is the total number of participants) were concatenated along the time dimension and passed through group-level PCA to retain 100 PCs. After that, ICA was run on the compressed group-level data using the Infomax ICA algorithm [32]. To find the stable spatial maps (SMs), the ICA was repeated 10 times and clustered via ICASSO [33]. Subject-specific spatial maps (SMs, ) and time courses (TCs, ) were estimated through the GICA1 back-reconstruction algorithm [13], [34]. An overview of intrinsic connectivity networks (ICNs) identification is shown in Fig.1(A).
Fig. 1.
An illustration of the GICA-TVGL framework. (A) Group ICA (GICA) decomposes resting-state fMRI data into components. 50 of them are identified as intrinsic connectivity networks (ICNs). GICA1 back reconstruction is used to estimate the spatial maps (SMs, ) and time courses (TCs, ) for each subject. (B) Following the GICA analysis, time courses (TCs) are transformed by the Gaussian copula model into for each item. Then, dynamic functional connectivity is assessed through the TVGL model.
B. Gaussian copula model
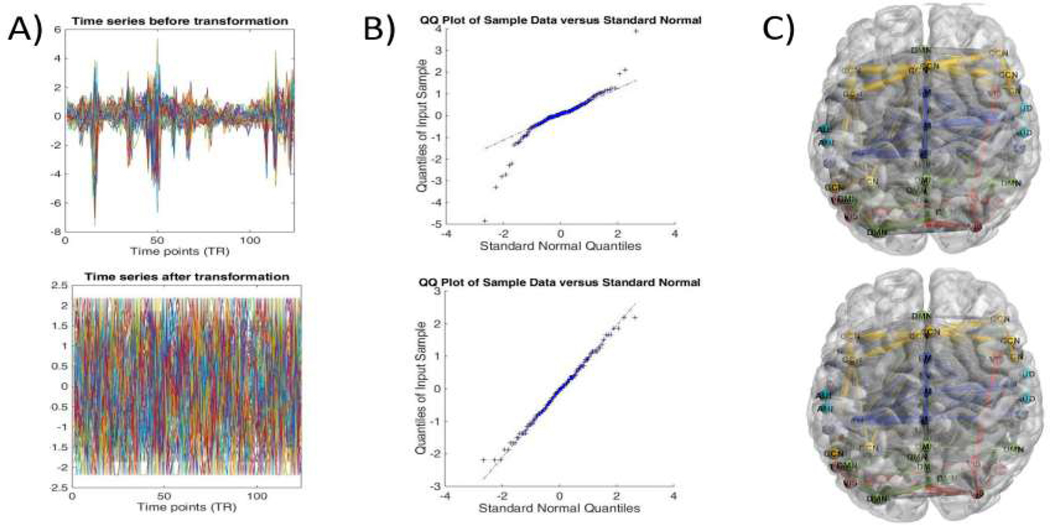
Following the GICA analysis, dynamic functional network connectivity (dFNC) was calculated from the component-level data. To this end, we implemented a method named time-varying graphical LASSO to catch dFNC. For the sake of adopting the TVGL, observations of input data are required to follow the Gaussian distribution. The quantile-quantile plot was implemented to check whether the components followed the normal distribution. As shown in Fig.2(B), component-level data obtained from the GICA do not conform well to a Gaussian distribution.
Fig. 2.
Gaussian copula model transformation for time courses extracted by the GICA. Here, the 40th subject from the PNC dataset is adopted as an example. The comparison of before (top) and after transformation (bottom) for the input data is shown. A) Description of the time courses for 50 components. B) A component is randomly selected from the pool and checked if this component follows the normal distribution applying the quantile-quantile plot. C) Functional connectivity within the brain estimated by the Pearson correlation and visualized using the BrainNet toolbox [36].
To address this problem, we introduced a Gaussian copula model proposed by Han Liu et al.[35]. This model is defined by the following equation:
| (1) |
where is the correlation matrix of the transformed data, is a set of monotone univariate functions and is the input data . Here, , where is the scaled empirical cumulative distribution function of , is a Winsorization (or truncation) operator and is the standard Gaussian quantile function [35]. Then, the nonparanormal estimate of the inverse correlation matrix can be obtained by plugging the correlation matrix into the graphical LASSO. Through this method, high-dimensional undirected graphical models can be efficiently and robustly estimated. This model is available in the R package (huge). The illustration of transformation with Gaussian copula model and time-varying graphical LASSO (TVGL) is shown in Fig.1(B).
We transformed time courses utilizing the Gaussian copula model to ensure they obey the normal distribution. As can be seen in Fig.2(B), time courses after the transformation follow the normal distribution. In addition, it can be shown in Fig.2(A) that time courses were transformed in the time domain. However, we find that functional connectivity estimated by time courses almost stay the same after the transformation, apart from some slight changes in the connectivity strength between different components in Fig.2(C). In other words, the Gaussian copula model can bridge the gap between the GICA algorithm and time-varying graphical LASSO.
C. Time-varying graphical LASSO
Time-varying graphical LASSO (TVGL) defined by Hallac et al. was extended from the classical graphical LASSO model and adopted to infer dynamic networks [30], [37], [38]. Let us assume that for each subject, we have a sequence of BOLD time series . For each time point , we have observation vectors for all independent components. Here, the observations follow the multivariate Gaussian distribution with mean zero and covariance . We aim to estimate the underlying covariance matrix , which changes over time. Hence, a sequence of graphical LASSO models are used to infer sparse inverse covariance matrices at times , where . As for these graphical LASSO problems, each one is coupled with others in a chain to penalize the deviations during the estimating process. Thus, we can estimate the covariance matrices by solving the following optimization problem:
| (2) |
where is the log likelihood of
| (3) |
denotes the off-diagonal norm, which enforces the element-wise sparsity for the solution of . Since the brain networks are known to be sparse and highly clustered, it is reasonable to enforce the off-diagonal norm to incorporate the sparsity of networks [39], [40]. is a convex penalty function, and is the number of the observations and is the empirical covariance matrix. For extracting time-varying changes from rsfMRI data, a Laplacian penalty (where ) is enforced to ensure that functional connectivity transitions in a smooth way, where refers to the row, column in the matrix . Due to the short time interval during the scanning session, we assume that adjacent graphs will change gradually in a smooth way, which is achieved with the use of the Laplacian penalty. and are nonnegative penalty parameters, which affect the sparsity level of the networks and the correlated level between adjacent networks respectively. It should be noted that the smaller is, the better the network matches with the empirical data. However, it will lead to dense functional connectivity which is hard to interpret. Meanwhile, with the increase of value, the estimated adjacent networks change smoothly over time. The number of the observations controls the ability to estimate dynamic changes. Smaller value of can better reflect the dynamic information.
In the TVGL model, , and are the key parameters which need to be determined. Since we want to analyze time-varying FNC using rsfMRI, the parameter should be as small as possible to describe dynamic FNC. Thus, in this study, the was set to be 2. Following the recommendation provided by Hallac et al., the regularization terms ( and ) are optimized by applying the Akaike Information Criteria (AIC) individually [30]. Here, the AIC is described as follows:
| (4) |
where is the parameter to be optimized ( and ), is the estimated precision matrix. is the empirical matrix, is the number of observations, and is the number of nonzero entries in the upper diagonal of . As a consequence, these parameters change from one subject to another. However, slightly fluctuates around the value of 0.01, and varies around 0.1 to a small extent. The TVGL is illustrated in Fig.1(B) and details for the solution algorithm can be found in related work [30], [31].
III. Results
In this section, we perform the GICA-TVGL pipeline to capture dynamic FNC using both the PNC and PING datasets. We analyze the dynamic connectivity and assess the group differences between females and males. Therein, the state dwell time and state transition matrix for both groups are examined. The details are described below.
A. Data acquisition and preprocessing
To validate the proposed framework, two different datasets were employed in this study. The PNC (Philadelphia Neurodevelopmental Cohort) dataset is a large-scale collaborative project between the Brain Behaviour Laboratory at the University of Pennsylvania and the Children’s Hospital of Philadelphia [41]. It contains resting-state fMRI for around 900 subjects with ages ranging from 8 to 21. In this work, some samples were removed due to missing information (age or sex). Eventually, 838 subjects remained. We also analyzed the Pediatric Imaging, Neurocognition, and Genetics (PING) dataset (http://ping.chd.ucsd.edu) [42]. For this specific study, only participants with complete rsfMRI scans were considered. Similarly, some subjects were discarded for the same reason as in the PNC dataset. This resulted in 410 subjects between 3 and 21 years of age. Multiple studies have shown that brain development is strongly related to functional connectivity [43], [44], [45], [46], [47], [48], [49]. To focus on sex differences, we minimized the variation of other possible confounding factors. We only included participants whose age was from 16 to 20, that is, young adults. This resulted in 316 subjects of the PNC dataset (age 17.86 ± 1.20 years, 135 male and 181 female), and 118 subjects of the PING dataset (age 18.41±1.22 years, 59 male and 59 female). Then we divided them into two subsets based on their sex. Note that in the following analysis, 124 TRs and 128 TRs were retained for PNC and PING dataset, respectively.
The preprocessing used here was an automated pipeline based on SPM 12 (http://www.fil.ion.ucl.ac.uk/spm/). Initially, first 4 volumes were discarded to avoid T1 equilibration effects. Then, slice timing correction and the motion correction were performed. For the slice timing correction, the middle slice was used as the reference. Using a nonlinear registration, EPI data were spatially normalized to standard Montreal Neurological Institute (MNI) space with the voxel size of and smoothed with a Gaussian kernel (). The influence of motion was further addressed using a regression procedure. Finally, a 0.01Hz - 0.1Hz band-pass filter was applied to the functional time series.
B. Postprocessing and results of resting state fMRI data
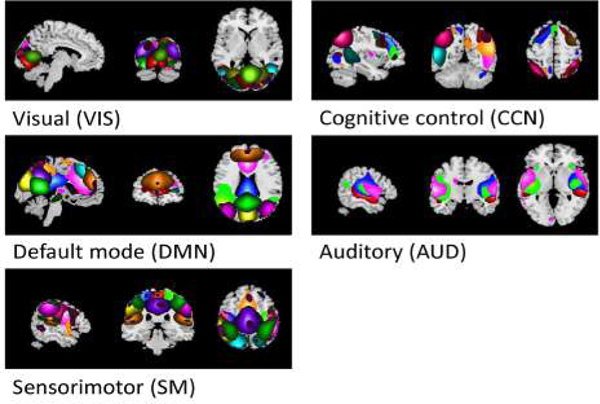
As mentioned previously, GICA was used to extract independent components from the resting-state fMRI data in our framework. By checking all of the 100 components from the results, those related to movement, imaging artifact or those that exhibited peak activations in white matter were removed [50]. After this, 50 components were retained and used for subsequent analysis. To better explain the functional connectivity within brains, these components were sorted into 5 functional networks based on previous work [21]. More specifically, we labeled components using the Component Labeler with the resting state networks (RSN) template (GIFT toolbox, http://mialab.mrn.org/software/gift) and referred the information on the Neurosynth (https://neurosynth.org/). Each component was assigned into the functional network which has the maximum correlation value with the component. These networks included the visual network (’VIS’), cognitive control network (’CCN’), default mode network (’DMN’), auditory network (’AUD’) and sensorimotor network (’SM’). Each of these networks was manually identified according to related literature [21] and depicted in Fig.3.
Fig. 3.
Functional networks spatial maps. 50 selected components are visualized and grouped into 5 functional networks based on previous literature. Each component is described by a specific color within the network.
1). Static and dynamic functional network connectivity:
To examine the reoccurring functional connectivity patterns, k-means clustering was applied to the time-varying precision matrices calculated by the TVGL. Due to the symmetric nature of precision matrices, only half of the off-diagonal elements contain unique information (that is, elements for each matrix). Hence, we performed the k-means clustering on these individual elements. Following the recommendation proposed by Allen et al., the distance function (Manhattan distance) was adopted here [21]. The number of centroids was set to be 4 by employing the elbow criterion defined as the ratio of within-cluster distances and between-cluster distances. The clustering was first applied on those subject exemplars which have the local maxima in FNC variance [21]. Next, the clustering results of these subject exemplars were chosen as the starting point to initialize the clustering process for all data.
Static FNCs or group mean FNC between ICN timecourses are shown in Fig.4(A). By applying the L1-norm penalized graphical LASSO to the Pearson correlation matrix estimated by signals across the whole scanning period, we obtained the precision matrix for each subject. Here, the static FNC for each group is represented as the mean of subjects’ precision matrices. The static connectivity matrices extracted from both the PNC and PING data demonstrate strong positive connectivity within the VIS, CCN, DMN, AUD and SM networks. Furthermore, a lot of regions in the AUD also show the positive connectivity with the SM network. Some unique relationships remain in each dataset. For instance, static FNC estimated by the PNC shows that some components in the DMN have positive connectivity with the SM network. Nevertheless, this positive connectivity between the DMN and CCN systems can be only detected in the static FNC based on the PING data. In regards to sex differences, the static FNC matrices suggested that such differences are relatively rare.
Fig. 4.
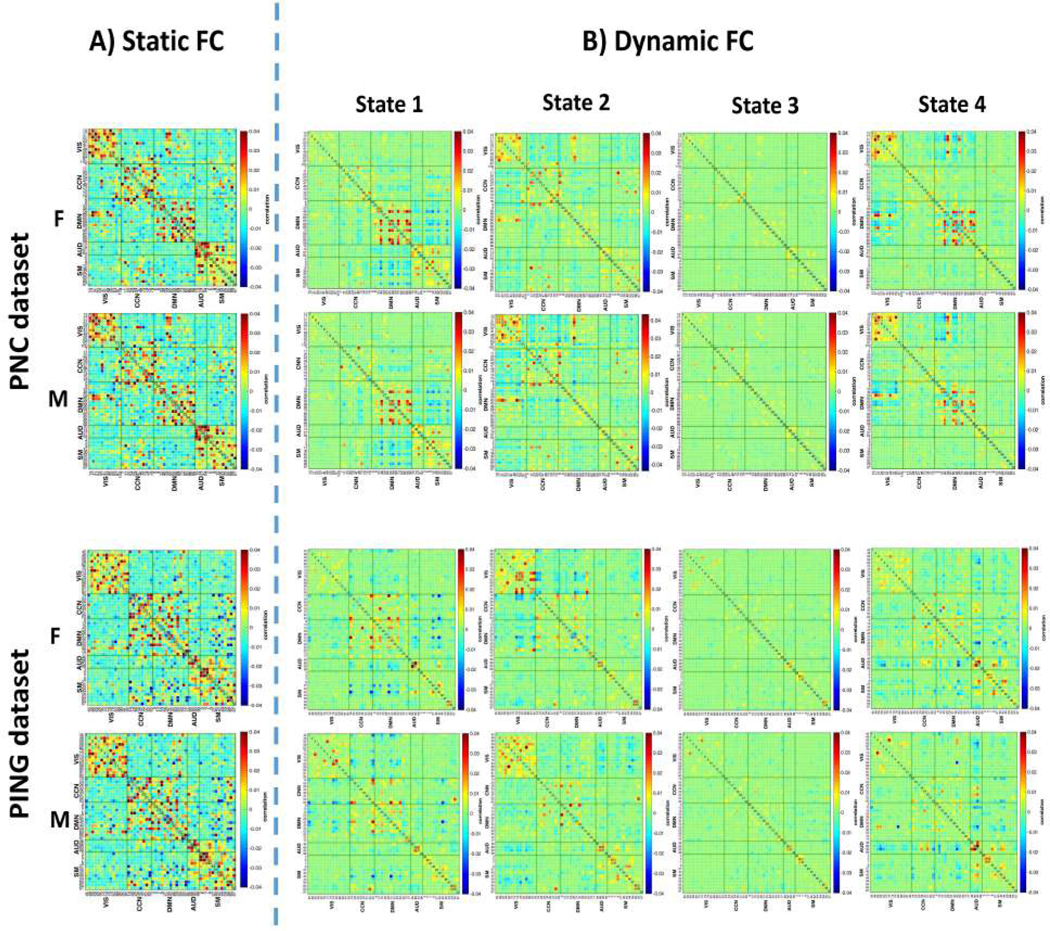
Static and dynamic functional network connectivity (FNC) for the female (F, top) and male groups (M, bottom) estimated by both the PNC and PING datasets. A) The L1 norm graphical LASSO was applied to the Pearson correlation matrices which calculated by time series across the whole scanning period for each subject. The mean of these precision matrices was considered as the static FNC for each group. B) Dynamic functional connectivity was described by the group specific centroids of states (from state 1 to state 4). These states were obtained from the k-means clustering.
We used the k-means clustering method to identify dynamic FNC patterns reoccurring throughout the scan sessions and across all the subjects for each group. As a result, 4 dynamic states were detected and these are shown in Fig.4(B). For both datasets, the dynamic connectivity analysis identified two modularized states (State 1: default mode modularized, i.e. intra-domain positive connectivity and inter-domain negative connectivity in DMN, and State 4: globally modularized, i.e. modularized FNCs present in globally intra-domain and inter-domain connectivity). In addition, one stable state (State 2: connectivity pattern is pretty similar to the corresponding static FNC) and one globally disconnected state (Static 3: intra-domain and inter-domain are connected loosely in this pattern) are detected. Except for the stable state, other patterns found in the dynamic analysis were not observed in the static FNC. This demonstrates the dynamic nature of the human brain and that time-varying investigation can help us to understand it better. Meanwhile, similar functional connectivity patterns captured by the two different datasets helps validate our proposed pipeline.
However, the dynamic patterns captured by our framework suggest some differences between the PNC and PING datasets. To figure out the cause, we repeated the analysis using the sliding window based pipeline proposed by Allen et al. to do the cross-validation [21]. Results depicting the patterns estimated by the sliding window method are shown in Fig.S1 of the supplementary materials. From that, we found that differences between these two datasets in the dynamic states still exist. Hence, we believe that the different datasets lead to these differences in the patterns instead of our approach. In addition, the dynamic patterns extracted by the sliding window approach resemble those captured by the GICA-TVGL framework. This phenomenon further confirms the feasibility of our GICA-TVGL approach. Furthermore, we also compared the sparsity level of the FNC patterns estimated by the GICA-TVGL and sliding window approaches. During the procedure, we used the number of connections to assess the sparsity level. By checking the results in Fig.S2, we found that the dynamic patterns obtained by the sliding window model were much denser than those evaluated by the GICA-TVGL. In our framework, the partial correlations are calculated instead of Pearson correlations as used in the sliding window approach. In this way, only the direct connection between two different ROIs will be considered. More importantly, applying the TVGL model, the prior knowledge of the brain network (e.g., sparsity, local temporal transition) is incorporated, resulting in the extraction of essential characteristics of brain network dynamics. Hence, we only implement our proposed model to conduct the subsequent analysis. It can give sparse solutions, which are easier to interpret.
2). Sex differences in dynamic functional network connectivity:
For identifying sex differences, an element-wise subject median was computed for each state (centroid) by using the unique elements of each matrix. Then, a univariate analysis pipeline developed by Allen et al. was applied to these median matrices [25]. Next, a Welch’s t-test was performed on the regression coefficients calculated by the univariate analysis to examine group differences. During this process, Benjamini-Hochberg correction with a significance level of 0.05 was implemented. Then, the results were visualized by drawing the log of values with the sign of statistics, . Besides, to validate the results generated by the Welch’s t-test, we also investigate the effect size (Cohen’s d) to examine the group differences (Fig.S4 in supplementary materials).
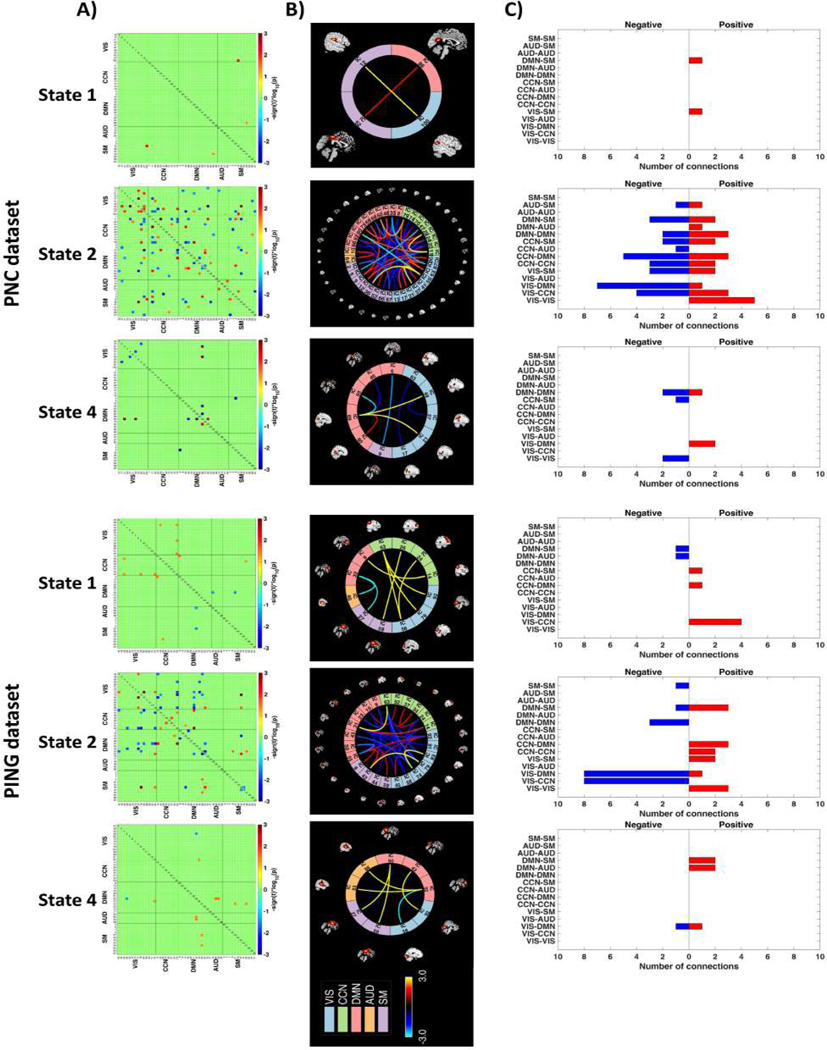
Essential group differences between females and males among these four dynamic states are shown in Fig.5(A). For the purpose of better visualization, a brain connectome for each of the significant dynamic states is also shown in Fig.5(B). It should be noted that only those states with significant differences are depicted here. During the GICA procedure, the PNC and PING dataset were processed individually. Hence, the independent components generated from the two datasets cannot match perfectly. To describe the results in a clearer way, we also calculated the number of connections between functional brain networks. As shown in Fig.5, some common conclusions can be reached from both the PNC and PING datasets. First, most of the sex differences show up in state 2, whose pattern is similar to the static FNC. Globally disconnected state (state 3) does not have any significant connections. Second, females have increased connectivity within the VIS networks relative to males. In comparison with females, males show stronger connectivity for the VIS-CCN and VIS-DMN. The results also suggest that no significant differences remain among the pairs of VIS-AUD, AUD-AUD, and AUD-SM.
Fig. 5.
Differences in dynamic states. Group differences in dynamic FNC states were obtained by using a two-sample t-test between females and males for both the PNC and PING datasets. These variations were visualized by plotting the log of -value with the sign of statistics, . The red/blue cells have survived the Benjamini-Hochberg correction with a significant level of 0.05. To show these differences clearly, the variations were depicted with both (A) heatmap, (B) their corresponding brain connectome and (C) summary of connection amounts between functional brain networks. Note that only dynamic states with essential differences were displayed in this figure. For certain relationship between two networks within the (C) (such as VIS-CCN), if the number of positive connections is more than the negative ones, we believe that females possess stronger connectivity, and vice versa.
Despite the similarity, we also detect some inconsistent results between these two datasets. Specifically, for the PNC dataset, the decreased correlations between the DMN and SM, CCN systems were detected for females in state 2. Additionally, females demonstrated stronger connectivity within the DMN network relative to males in state 2. By comparison, for the connections discussed above, the results generated by the PING dataset possessed the opposite circumstance. Note that the results generated by the effect size (Cohen’s d > 0.8) are completely contained by those achieved by Welch’s t-test.
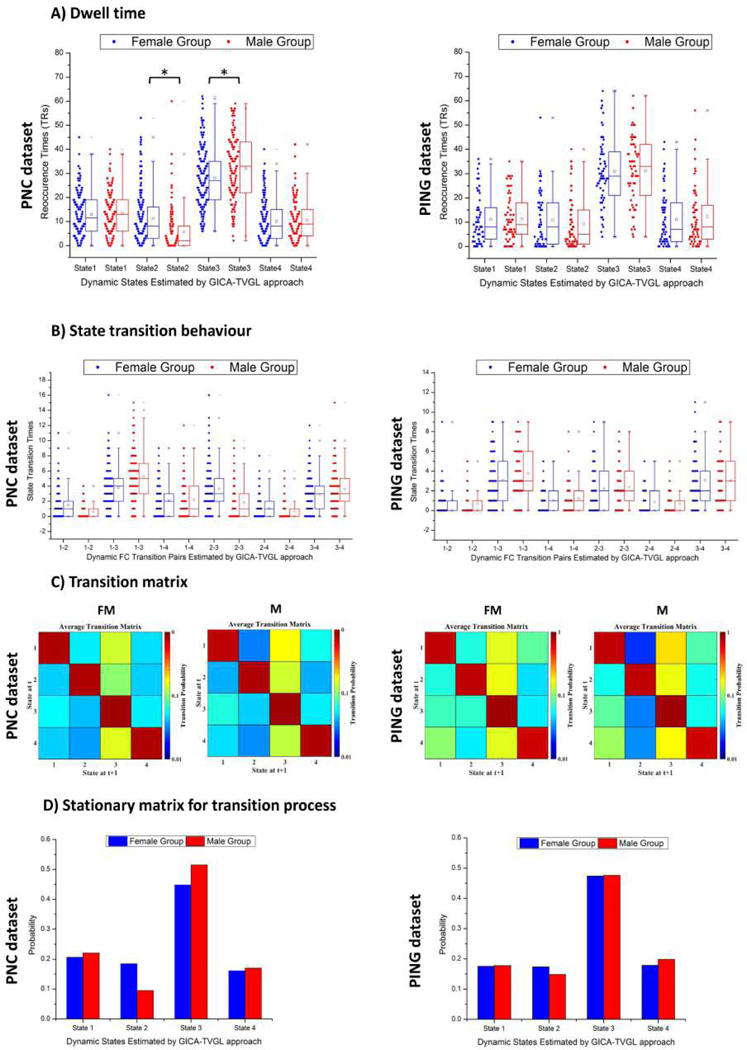
3). Dwell times and state transitions:
In addition to describing the connectivity differences for these networks, the time occupied by each state and transition behaviours for each group was also investigated. Dwell times were represented by the reoccurrence times of all the dynamic FNC states. For each subject, the reoccurrence time for each dynamic FNC pattern was defined as the total number of precision matrices assigned to that state. Since adjacent precision matrices are non-overlapping in time series, it is easy to calculate the dwell time of each state. As to the transition behaviour, the transition frequency among all the pairs of dynamic FNC patterns was considered. The transition frequency counts how many times the dynamic FNC changes between a pair of states for each individual (e.g., the transition frequency between state 1 and state 2 counts if the dynamic FNC alters its allegiance from state 1 to state 2 or vice versa). In addition, the sequence of transition was also considered as a one order Markov chain (MC) system, and the corresponding pattern was described by the transition probability from one state to another. Thus, an asymmetric matrix was generated for each group.
The dwell times for females and males in Fig.6(A) show a similar pattern. That is, they more often stay at the globally disconnected state (state 3) for a longer time and are in other states for a shorter period. Furthermore, males tend to spend more time in state 3 and less time in state 2 compared with females, although it can only be captured by the PNC dataset.
Fig. 6.
A) Dwell times represented by reoccurrence times of the dynamic functional connectivity states. Reoccurrence times of each individual in female and male group were presented in blue and red, respectively. Note that the symbol ’*’ means statistic significance (p-value=8.26e-7 for State 2 and p-value=4.7e-3 for State 3). B) Transition frequency of the dynamic functional connectivity states for two groups. The ticks on the horizontal axis indicate the state transition pairs, e.g., ”1−2” refers to the transition between state 1 and state 2. The state transition times of each individual in female and male were marked in blue and red, respectively. C) The state transition matrix for each group was averaged over subjects. Transition probability between two states ranging from 0 to 1 was on a log-scale in this map. D) Stationary matrices for transition matrices of the Markov chain shown in C). Note that the above analysis was performed on both the PNC and PING datasets.
By looking at the results in Fig.6(B), we discover that transition behaviour related to the state 3 possesses higher transition frequency relative to other states. It demonstrates that during the whole scanning session, the brain connectivity tends to stay at the globally disconnected state. This inclination is much stronger for male groups. Meanwhile, it is interesting to determine that the transition between default mode modularized (state 1) and the globally disconnected state (state 3) has the highest frequency for both groups. Due to the resting-state, the DMN is assumed to be most commonly active. However, unmatched transition behaviours were observed for two different datasets. For instance, in the PNC dataset, females hold higher frequency to transit from state 2 to state 3 (or from state 3 to state 2). However, this circumstance cannot be found for the PING dataset.
We characterized transition behaviour by considering FNC as a one order Markov chain (MC) and averaged transition matrices for this system were displayed in Fig.6 (B). Red squares along the diagonal demonstrate a very high probability of remaining in the same state. For the off-diagonal elements, a hotter color means a higher likelihood to be entered from other states in contrast with a cooler color. Based on transition matrices, functional connectivity is more inclined to remain unchanged. As to the transition between different patterns, the transition from other states to state 3 has a higher likelihood. This point is congruent with the finding that subjects tend to stay in state 3 much longer as mentioned above. Overall, the transition behaviour of females does not show obvious differences from males. However, by contrast with males, females have a higher chance to enter the stable state (state 2) from other states. Likewise, males possess more substantial probability to transition into the globally disconnected state (state 3) relative to females. Hence, we believe that the brain activity of males is slightly less connected than females during the scanning time-courses.
To further investigate the transition process between different FNC patterns, we evaluated the stationary property for transition matrices displayed in Fig.6(C). The results were shown in Fig.6(D). We obtain that in the long run, the functional connectivity has the highest chance to stay at the globally disconnected state (state 3) for both females and males (the probability is around 0.5). In contrast, the other states are much less stationary (the probability is around 0.2). It should be noted that the same outcome is observed at both the PNC and PING datasets.
IV. Discussion
In this study, we presented a framework named GICA-TVGL to estimate dynamic functional network connectivity patterns. This new data-driven approach was generated by combining group independent component analysis (GICA) and time-varying graphical LASSO [13], [30]. To link GICA and TVGL, a Gaussian copula model was introduced. Specifically, we examined resting-state fMRI data (PNC and PING dataset) to study functional network connectivity within the brain. We first validated the feasibility of our framework through assessing time-varying functional connectivity. We then investigated the difference in dynamic functional connectivity between females and males using these two datasets. In particular, both dwell times and transition behaviours were analyzed to further uncover the disparity caused by sex.
The GICA pipeline has become widely used to analyze resting-state dynamics across the human brain [21]. Moreover, the ability of TVGL to estimate dFNC from rsfMRI has been described in our previous work [31]. Thus, we believe that the proposed approach merging these two models would improve performance for capturing dFNC patterns from rsfMRI data. To prove our point, we estimated the dynamic FNC patterns from rsfMRI data using our framework and represented them using 4 different states. These states include two modularized modes (states 1 and 4), one stable (state 2) and one globally disconnected modes (state 3), which are congruent with the results in previous work [51]. In particular, for both females and males, the stable state (state 2) is similar to the static one, assessed by applying the L1-norm graphical LASSO to the Pearson correlation matrix. However, other states within the dynamic study cannot be reflected in the static analysis. Hence, the experiments validate our proposed framework and demonstrate that it can detect changes in fMRI signals.
Additionally, we found some differences between the PNC and PING datasets in the dynamic patterns captured by our proposed framework. Thus, we used the sliding window based pipeline to do cross-validation. As a consequence, similar differences remained in the results estimated by the sliding window method. Recently, Finn et al. pointed out that the individual’s connectivity profiles can be used as a ”fingerprint” to identify subjects from a large group [52]. Gratton et al. mentioned that functional brain connectivity patterns were dominated by both group and individual factors. [53]. Hence, we believe that the differences in the dynamic states are caused by the various individual effects remaining in these two datasets. In the next stage, the individual influence on the dynamic functional network connectivity needs to be considered. In addition, the difference remaining in the collection parameters between these two datasets may also lead to the inconsistent results (PNC/PING: , , , , ). On the other hand, the dynamic states captured by the sliding window method are quite similar to those estimated by our pipeline. This fact further validates the feasibility of our framework. Also, by comparing with the sliding window method, the dynamic patterns generated by the GICA-TVGL are much sparser. In our proposed framework, instead of the Pearson correlation, the partial correlation is assessed. This makes the results to be easier to interpret. In addition, the prior knowledge of the brain network (e.g., sparsity, local temporal transition) is incorporated into the analysis. Thus, we believe that the GICA-TVGL model is very powerful for capturing the dynamic FNC patterns. Note that as a commonly used approach, the partial correlation can also be investigated in the classical sliding window method. We may perform this part of the work in our future analysis.
Furthermore, we tested our GICA-TVGL model on two datasets to study the FNC differences between females and males. Overall, our analyses suggest that females and males have substantial differences in functional connectivity related to the visual network. More specifically, females have increased connectivity within the VIS networks relative to males. In comparison with females, males display stronger connectivity for the VIS-CCN and VIS-DMN networks. We postulate this is associated with the differences of visual center in the brain between males and females. Previous studies have found that males had greater sensitivity to fine details and rapidly moving stimuli, but females were better at discriminating between colors [54], [55]. Also, most of the sex differences are obtained from the stable state (state 2), and globally disconnected state (state 3) cannot represent significant discrimination. It demonstrates that the stable state has a powerful effect on the brain connectivity during the scan period. The fact that the stable state resembles the static pattern can explain this point as well. Furthermore, we also found that females displayed greater connectivity among occipital-frontal components in some particular states, which is in agreement with the results of a similar study [51]. Meanwhile, we also observed that a lof of mismatched results from the PNC and PING datasets were involved with the DMN networks (such as DMN-SM, DMN-CCN, and DMN-DMN). Traditionally, the DMN network is assumed to be most active when subjects have no external stimuli. On account of this characteristic, the individual distinction may have a large influence on the DMN network and lead to this outcome.
In brief, we have detected that sex has a small but significant influence on the dwell times and state transitions. Specifically, we observed that both females and males tended to spend more time on the disconnected state (state 3). Likewise, functional connectivity is more likely to transit from other states to state 3. However, females have a higher probability to stay at the stable state, while males possess a higher chance to remain in the globally disconnected mode. In this way, we believe that the FNC within the brain is less connected and active in males than females during the scan period.
Of note, GICA as a data-driven approach, has become a significant tool and widely used in fMRI analyses [14], [15], [16], [17]. To reveal the dynamic nature of the brain, Allen et al. proposed a GICA based pipeline to examine time-varying FNC in rsfMRI [21]. This framework combines the GICA with the sliding window model which is the most common strategy to assess brain dynamics. However, the window size selection has primarily affected the performance of the method to capture time-varying FNC. Compared with that, our proposed framework merges the GICA with TVGL instead of the sliding window approach. For the TVGL model, it can estimate the network even when the observation interval is only one time point. Hence, we believe that our pipeline can capture the dynamic changes within the brain well.
One potential limitation of our framework is the usage of a Laplacian penalty in the TVGL. By inferring the dynamic networks, we consider that the systems change smoothly. Under this condition, some abrupt variations are suppressed and hard to obtain. On the other hand, to detect the timevarying information, the time interval is pretty small () relative to the sliding window method. However, it is inevitable to capture time-varying noise despite our attempts to minimize it through several data preprocessing procedures. Additionally, due to we perform the GICA on the PNC and PING datasets independently, components generated by these two datasets cannot match perfectly. Hence, it is difficult to reach completely consistent results from various datasets. In the future, we may apply the seed-based FC to overcome this limitation.
V. Conclusion
We propose a framework named GICA-TVGL to assess dynamic FNC from the rsfMRI data. Our approach combines the GICA and TVGL to improve the ability to capture time-varying information. Two different datasets were used to demonstrate the validity and feasibility of our model to analyze dynamic connectivity within the brain. In addition, the sliding window based approach was used to perform both the cross-validation and comparison. Results for the FNC networks revealed remarkable differences between females and males, which were in connection with the visual network. In particular, we observed that males were more inclined to stay at the globally disconnected state relative to females. In summary, we demonstrate that the GICA-TVGL framework can facilitate the analysis of brain dynamics and therefore can find widespread applications in neuroimaging studies.
Supplementary Material
Acknowledgment
The authors would like to thank the partial support by NIH (R01 GM109068, R01 EB020407, R01 MH104680, R01 MH107354, R01 MH103220) and NSF (#1539067).
Footnotes
Propose GICA-TVGL, a data-driven approach to assess dynamic FNC from the rsfMRI data.
Validate GICA-TVGL using two different neuroimaging datasets (e.g., PNC and PING).
Reveal gender differences that can be confirmed with existing studies.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Bandettini PA et al. , “Time course epi of human brain function during task activation,” Magnetic resonance in medicine, vol. 25, no. 2, pp. 390–397, 1992. [DOI] [PubMed] [Google Scholar]
- [2].Menon RS et al. , “Functional brain mapping using magnetic resonance imaging. signal changes accompanying visual stimulation.” Investigative radiology, vol. 27, pp. S47–53, 1992. [DOI] [PubMed] [Google Scholar]
- [3].Bullmore E. et al. , “Complex brain networks: graph theoretical analysis of structural and functional systems,” Nature Reviews Neuroscience, vol. 10, no. 3, p. 186, 2009. [DOI] [PubMed] [Google Scholar]
- [4].Buckner R. et al. , “The brains default network: anatomy, function, and relevance to disease ann ny acad sci 2008; 1124: 1–38.” [DOI] [PubMed] [Google Scholar]
- [5].Lohmann G. et al. , “Using non-negative matrix factorization for single-trial analysis of fmri data,” Neuroimage, vol. 37, no. 4, pp. 1148–1160, 2007. [DOI] [PubMed] [Google Scholar]
- [6].Anderson A. et al. , “Non-negative matrix factorization of multimodal mri, fmri and phenotypic data reveals differential changes in default mode subnetworks in adhd,” NeuroImage, vol. 102, pp. 207–219, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Eavani H. et al. , “Identifying sparse connectivity patterns in the brain using resting-state fmri,” Neuroimage, vol. 105, pp. 286–299, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Zille P. et al. , “Fused estimation of sparse connectivity patterns from rest fmri. application to comparison of children and adult brains,” IEEE transactions on medical imaging, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Cai B. et al. , “Estimation of dynamic sparse connectivity patterns from resting state fmri,” IEEE transactions on medical imaging, vol. 37, no. 5, pp. 1224–1234, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Calhoun V. et al. , “Spatial and temporal independent component analysis of functional mri data containing a pair of task-related waveforms,” Human brain mapping, vol. 13, no. 1, pp. 43–53, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Kiviniemi V. et al. , “Independent component analysis of nondeterministic fmri signal sources,” Neuroimage, vol. 19, no. 2, pp. 253–260, 2003. [DOI] [PubMed] [Google Scholar]
- [12].Damoiseaux J. et al. , “Consistent resting-state networks across healthy subjects,” Proceedings of the national academy of sciences, vol. 103, no. 37, pp. 13848–13853, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Calhoun VD et al. , “A method for making group inferences from functional mri data using independent component analysis,” Human brain mapping, vol. 14, no. 3, pp. 140–151, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Calhoun V. et al. , “Latency (in) sensitive ica: group independent component analysis of fmri data in the temporal frequency domain,” NeuroImage, vol. 20, no. 3, pp. 1661–1669, 2003. [DOI] [PubMed] [Google Scholar]
- [15].Correa N. et al. , “Performance of blind source separation algorithms for fmri analysis using a group ica method,” Magnetic resonance imaging, vol. 25, no. 5, pp. 684–694, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Beckmann CF et al. , “Group comparison of resting-state fmri data using multi-subject ica and dual regression,” Neuroimage, vol. 47, no. Suppl 1, p. S148, 2009. [Google Scholar]
- [17].Abou Elseoud A. et al. , “Group-ica model order highlights patterns of functional brain connectivity,” Frontiers in systems neuroscience, vol. 5, p. 37–2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Calhoun VD et al. , “Multisubject independent component analysis of fmri: a decade of intrinsic networks, default mode, and neurodiagnostic discovery,” IEEE reviews in biomedical engineering, vol. 5, pp. 60–73, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Hutchison RM et al. , “Dynamic functional connectivity: promise, issues, and interpretations,” Neuroimage, vol. 80, pp. 360–378, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Sakoğlu Ü et al. , “A method for evaluating dynamic functional network connectivity and task-modulation: application to schizophrenia,” Magnetic Resonance Materials in Physics, Biology and Medicine, vol. 23, no. 5–6, pp. 351–366, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Allen EA et al. , “Tracking whole-brain connectivity dynamics in the resting state,” Cerebral cortex, vol. 24, no. 3, pp. 663–676, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Du Y. et al. , “Exploring difference and overlap between schizophrenia, schizoaffective and bipolar disorders using resting-state brain functional networks,” in Engineering in Medicine and Biology Society (EMBC), 2014 36th Annual International Conference of the IEEE. IEEE, 2014, pp. 1517–1520. [DOI] [PubMed] [Google Scholar]
- [23].Du Y. et al. , “A group ica based framework for evaluating resting fmri markers when disease categories are unclear: application to schizophrenia, bipolar, and schizoaffective disorders,” Neuroimage, vol. 122, pp. 272–280, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Khadka S. et al. , “Is aberrant functional connectivity a psychosis endophenotype? a resting state functional magnetic resonance imaging study,” Biological psychiatry, vol. 74, no. 6, pp. 458–466, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Allen EA et al. , “A baseline for the multivariate comparison of resting-state networks,” Frontiers in systems neuroscience, vol. 5, p. 2–2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Qin J. et al. , “Predicting individual brain maturity using dynamic functional connectivity,” Frontiers in human neuroscience, vol. 9, p. 418–2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Hutchison RM et al. , “Resting-state networks show dynamic functional connectivity in awake humans and anesthetized macaques,” Human brain mapping, vol. 34, no. 9, pp. 2154–2177, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Eavani H. et al. , “Unsupervised learning of functional network dynamics in resting state fmri,” in International Conference on Information Processing in Medical Imaging. Springer, 2013, pp. 426–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Yaesoubi M. et al. , “A window-less approach for capturing time-varying connectivity in f mri data reveals the presence of states with variable rates of change,” Human brain mapping, vol. 39, no. 4, pp. 1626–1636, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Hallac D. et al. , “Network inference via the time-varying graphical lasso,” in Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2017, pp. 205–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Cai B. et al. , “Capturing dynamic connectivity from resting state fmri using time-varying graphical lasso,” IEEE Transactions on Biomedical Engineering, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Bell AJ et al. , “An information-maximization approach to blind separation and blind deconvolution,” Neural computation, vol. 7, no. 6, pp. 1129–1159, 1995. [DOI] [PubMed] [Google Scholar]
- [33].Himberg J. et al. , “Validating the independent components of neuroimaging time series via clustering and visualization,” Neuroimage, vol. 22, no. 3, pp. 1214–1222, 2004. [DOI] [PubMed] [Google Scholar]
- [34].Erhardt EB et al. , “Comparison of multi-subject ica methods for analysis of fmri data,” Human brain mapping, vol. 32, no. 12, pp. 2075–2095, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Liu H. et al. , “High-dimensional semiparametric gaussian copula graphical models,” The Annals of Statistics, vol. 40, no. 4, pp. 2293–2326, 2012. [Google Scholar]
- [36].Xia M. et al. , “Brainnet viewer: a network visualization tool for human brain connectomics,” PloS one, vol. 8, no. 7, p. e68910, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Yuan M. et al. , “Model selection and estimation in the gaussian graphical model,” Biometrika, vol. 94, no. 1, pp. 19–35, 2007. [Google Scholar]
- [38].Friedman J. et al. , “Sparse inverse covariance estimation with the graphical lasso,” Biostatistics, vol. 9, no. 3, pp. 432–441, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].He Y. et al. , “Small-world anatomical networks in the human brain revealed by cortical thickness from mri,” Cerebral cortex, vol. 17, no. 10, pp. 2407–2419, 2007. [DOI] [PubMed] [Google Scholar]
- [40].Achard S. et al. , “Efficiency and cost of economical brain functional networks,” PLoS computational biology, vol. 3, no. 2, p. e17, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Satterthwaite TD et al. , “The philadelphia neurodevelopmental cohort: a publicly available resource for the study of normal and abnormal brain development in youth,” Neuroimage, vol. 124, pp. 1115–1119, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Jernigan TL et al. , “The pediatric imaging, neurocognition, and genetics (ping) data repository,” Neuroimage, vol. 124, pp. 1149–1154, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Cai B. et al. , “Estimation of dynamic sparse connectivity patterns from resting state fmri,” IEEE Transactions on Medical Imaging, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Faghiri A. et al. , “Changing brain connectivity dynamics: From early childhood to adulthood,” Human brain mapping, vol. 39, no. 3, pp. 1108–1117, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Dosenbach NU et al. , “Prediction of individual brain maturity using fmri,” Science, vol. 329, no. 5997, pp. 1358–1361, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Jolles DD et al. , “A comprehensive study of whole-brain functional connectivity in children and young adults,” Cerebral cortex, vol. 21, no. 2, pp. 385–391, 2011. [DOI] [PubMed] [Google Scholar]
- [47].Onoda K. et al. , “Decreased functional connectivity by aging is associated with cognitive decline,” Journal of cognitive neuroscience, vol. 24, no. 11, pp. 2186–2198, 2012. [DOI] [PubMed] [Google Scholar]
- [48].Zhang H-Y et al. , “Selective vulnerability related to aging in large-scale resting brain networks,” PloS one, vol. 9, no. 10, p. e108807, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Zille P. et al. , “Fused estimation of sparse connectivity patterns from rest fmri. application to comparison of children and adult brains,” IEEE Transactions on Medical Imaging, vol. PP, no. 99, pp. 1–1, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Cordes D. et al. , “Mapping functionally related regions of brain with functional connectivity mr imaging,” American Journal of Neuroradiology, vol. 21, no. 9, pp. 1636–1644, 2000. [PMC free article] [PubMed] [Google Scholar]
- [51].Blanken L, On the spectrum: The neurobiology of psychiatric symptoms in the general population, 2016. [Google Scholar]
- [52].Finn ES et al. , “Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity,” Nature neuroscience, vol. 18, no. 11, p. 1664, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Gratton C. et al. , “Functional brain networks are dominated by stable group and individual factors, not cognitive or daily variation,” Neuron, vol. 98, no. 2, pp. 439–452, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Abramov I. et al. , “Sex & vision i: Spatio-temporal resolution,” Biology of Sex Differences, vol. 3, no. 1, p. 20, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Abramov I. et al. , “Sex and vision ii: color appearance of monochromatic lights,” Biology of sex differences, vol. 3, no. 1, p. 21, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.