Predicting new mineral occurrences and planetary analog environments via mineral association analysis

Abstract

The locations of minerals and mineral-forming environments, despite being of great scientific importance and economic interest, are often difficult to predict due to the complex nature of natural systems. In this work, we embrace the complexity and inherent “messiness” of our planet's intertwined geological, chemical, and biological systems by employing machine learning to characterize patterns embedded in the multidimensionality of mineral occurrence and associations. These patterns are a product of, and therefore offer insight into, the Earth's dynamic evolutionary history. Mineral association analysis quantifies high-dimensional multicorrelations in mineral localities across the globe, enabling the identification of previously unknown mineral occurrences, as well as mineral assemblages and their associated paragenetic modes. In this study, we have predicted (i) the previously unknown mineral inventory of the Mars analogue site, Tecopa Basin, (ii) new locations of uranium minerals, particularly those important to understanding the oxidation–hydration history of uraninite, (iii) new deposits of critical minerals, specifically rare earth element (REE)- and Li-bearing phases, and (iv) changes in mineralization and mineral associations through deep time, including a discussion of possible biases in mineralogical data and sampling; furthermore, we have (v) tested and confirmed several of these mineral occurrence predictions in nature, thereby providing ground truth of the predictive method. Mineral association analysis is a predictive method that will enhance our understanding of mineralization and mineralizing environments on Earth, across our solar system, and through deep time.

Significance Statement.

The search for mineral resources and the quest for the underlying principles of their origins and distributions have been major preoccupations of geology for centuries. In the past, most discoveries have resulted from accumulated experience in the field and laboratory, implemented by perseverance and luck. Large and growing mineral data resources, coupled with the multidimensional analytical capabilities of machine learning, facilitate a new data-driven strategy for mineral discovery, by which known associations of suites of mineral species in distinctive geological settings allow prediction of as-yet-unknown deposits. These predictive association methods, furthermore, hold the promise of elucidating mineral origins in the contexts of their tectonic, environmental, and perhaps microbiological settings—insights that highlight the coevolving geosphere and biosphere.

Introduction

Minerals contribute essential raw materials for a technological society, while also providing the oldest surviving records from the formation and evolution of our solar system and, therefore, the only lasting evidence for many geologic events and ancient environments. As mineralogical data resources grow, so do opportunities for integration with other scientific domains and for exploration of outstanding scientific questions. Motivations to better understand large-scale geologic processes and transitions, such as the initiation of plate tectonics, the timing and rate of formation of the granitic crust, the gradual oxidation of the Earth's atmosphere, the mechanisms and distribution of ore system formation, and the coevolution of the geosphere and biosphere, have inspired researchers to characterize the spatial and temporal diversity and distribution of mineral species. Extensive and expanding mineralogical data resources enable predictive analytical methods, such as network analysis, cluster analysis, and the methods of mineral ecology (1–5).

Here, we develop and apply mineral association analysis to identify locations of as-yet-unknown mineral occurrences, deposits, or geologic environments and to predict the mineral inventory at any given locality on the Earth's surface or, if suitable data are available, other planetary bodies (6, 7). Furthermore, results generated by this method can be explored, interpreted, and curated using interactive visualizations built as part of this work. As a consequence, machine learning methods hold the promise to predict as yet undiscovered locations of mineral species or mineral-forming environments, such as analogue sites, geologic settings featuring specific paragenetic modes, or astrobiologically relevant localities. We demonstrate that machine learning is able to consolidate multidimensional field and laboratory experience and data, while limiting potential human-imposed biases and increasing the efficiency of discovery. In this study, we present four use cases employing association analysis, which is a machine learning method that performs association rule learning (8–13) to predict previously unknown mineral occurrences based on association rules, and test the results to ground truth this powerful predictive method.

Association analysis is not based simply on querying a database to find a locality match to a list of minerals. Rather, mineral association analysis predicts previously unknown localities, as well as their probabilities of success, based on the simultaneous analysis of numerous system attributes that have been derived from characteristics of known mineral assemblages. Consequently, association analysis exploits the power of multidimensional machine learning methods to make predictions related to mineral diversity and distribution through space and time.

By employing association rule learning and its metrics, mineral association analysis can be used to answer many questions of scientific interest, including the following: (i) What is the mineral inventory at a location of interest? (ii) What are the most likely locations to find a new occurrence of a specific mineral species? (iii) What are the most likely locations to find a mineral assemblage corresponding to a certain geologic setting, planetary environment, or deposit type? (iv) How do the diagnostic association rules differ for minerals from different geological time intervals? In particular, the flexibility of association analysis allows researchers interested in locating planetary analogue sites, exploring and assessing economic resources, or collecting specimens of a desirable mineral species, to identify locations that are not currently known to host the mineral or mineral assemblage of interest.

Results

Mineral occurrence matrix generation and data subset selection

The mineral occurrence matrix used in this study was generated from the Mineral Evolution Database (MED) (14–16), which incorporates 295,583 mineral localities, 45,472 of which have an associated age, representing 5,478 mineral species (as of 2020 October). Mineral species are as defined by the International Mineralogical Association (IMA)—a full list of the approved mineral species is available at RRUFF.info/IMA. This combination of mineral species and localities results in 810,907 mineral-locality pairs, of which 210,037 are dated. The large dimensionality of this data set makes it computationally intensive to consume and analyze. Therefore, we have chosen to subset the data to explore smaller, constrained mineral systems and provide proof of concept. These subsets represent distinct aspects of the large data set and help to highlight relationships among different mineral environments. For this preliminary exploration, we chose the following three mineral occurrence subsets:

Geographical subset: the United States

In this study, we selected the United States due to its high mineralogical diversity, well-documented and extensive geographic coverage, and broad range of geologic environments, making this region an optimal choice for exploration of mineral relationships. There are 2,622 mineral species, 93,419 localities, and 8,139,004 association rules in the US subset.

Geochemical subset: U minerals

In this work, we examine uranium (U)-bearing mineral phases by analyzing all mineral species (i.e. not only U-bearing phases) at localities at which one or more minerals with U as an essential element occur. U minerals are of particular interest in nuclear energy and nuclear forensics applications, as well as for understanding the redox history of various geological deposit types, including deposits formed directly or indirectly through biological processes. The U-mineral subset contains 5,439 mineral species, 11,729 localities, and 60,589,982 association rules.

Temporal subset: Archean, Proterozoic, and Phanerozoic Eons

Here, we selected three time slices, the Archean Eon (>2.5 Ga), Proterozoic Eon (2.5–0.54 Ga), and/or Phanerozoic Eon (<0.54 Ga), and all minerals and mineral localities dated to those time periods. At each locality, we included only the minerals from the selected time period, excluding any younger or older phases. This subset allows researchers to examine mineral associations through deep time and to compare mineral relationships at different stages of planetary evolution, thereby enabling exploration of questions related to the effects of biological evolution on mineral-forming environments through time, specifically the influence of the Great Oxidation Event (GOE) on mineral formation or how the rise of the terrestrial biosphere affected ore body formation. There are 2,683 mineral species, 1,498 localities, and 30,916,618 association rules in the Archean subset; 3,527 mineral species, 3,100 localities, and 52,435,569 association rules in the Proterozoic subset; and 2,882 mineral species, 4,644 localities, and 45,727,343 association rules in the Phanerozoic subset.

Mineral association rule generation

Association analysis is a machine learning method that reveals relationships among various items (e.g. mineral species) within the data. This method analyzes cooccurrence and identifies rules based on associations, from high correlation (i.e. strong association) to weak or no correlation/association, among these items. The method was first introduced by Agrawal and Srikant (1994) (17), who presented two algorithms, Apriori and AprioriTid, to create association rules. The Apriori algorithm uses a bottom-up approach where frequently cooccurring itemsets (e.g. mineral assemblages) are extracted as candidates for testing against the overall data set. The pattern and frequency of occurrence of an itemset are used to generate rules that quantify the likelihood of occurrence. In mineral association analysis, these rules can be queried to predict the occurrence likelihood of a mineral or mineral assemblage (i.e. itemset) of interest.

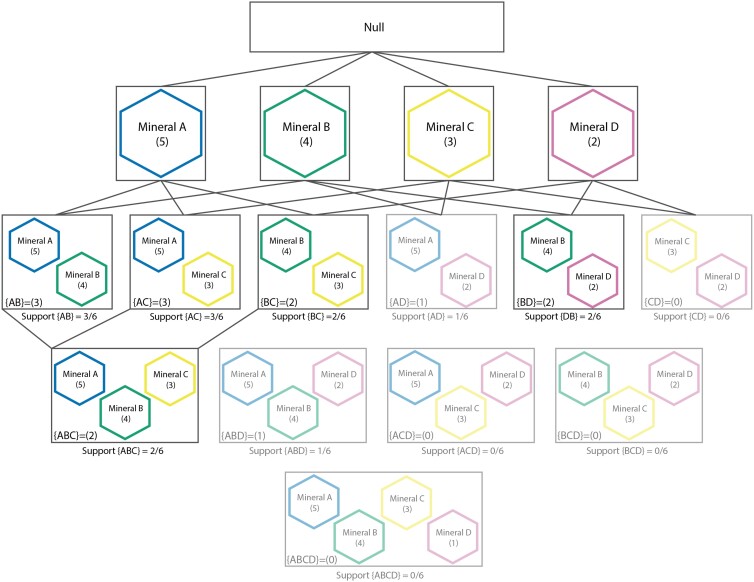
Consider a locality and the set of mineral species that occur there—this is referred to as a transaction in association analysis. The term transaction is derived from the algorithm's original and popular use as recommendation systems in sales for anticipating customer behavior based on purchase habits (e.g. which items are frequently purchased together and which items are rarely or never purchased together) (9). The set of transactions in a system (e.g. a set of all localities and their mineral occurrences on Earth) is combined into a transaction table, T. With T as the input, the Apriori algorithm generates and characterizes lists of frequently occurring itemsets (e.g. mineral assemblages), referred to as large itemsets, L_n, with the frequency cutoff value specified by a user-defined support threshold (see probability metrics below), ε (18). The support threshold is determined by a combination of domain expert decision-making and computational feasibility. The algorithm generates these lists of frequently occurring itemsets by the following steps (Fig. 1) (18):

Fig. 1.

Example of the first step in mineral association analysis. All possible itemsets are generated from the set (mineral A, mineral B, mineral C, and mineral D), with infrequent (support threshold < 2/6; see Metrics section) itemsets excluded (shown as transparent).

• Step 1. Generate L_k−1

Each L_n (large itemset, i.e. list of frequently occurring itemsets) contains itemsets of a specific length, with itemset length denoted as k. In order to create the first large itemset (step 1), the algorithm first extracts all itemsets of length k − 1, support (see metrics below) is then calculated for each itemset in the extracted list, and those with a support greater than the support threshold, ε, are compiled into the first large itemset, L_k−1.

• Step 2. Generate C_k

Next, the algorithm extracts from T all candidate itemsets of length k that contain the itemsets in L_k−1 and places them in a candidate set, C_k.

• Step 3. Generate L_k

The algorithm calculates support for each itemset in C_k, extracts itemsets that fall above ε, and places the extracted itemsets into a new large itemset, L_k.

• Step 4. Iterate to generate L_k−1 … L_{k + n,} while L_{k + n} ≠ ∅.

Iterate over steps 2 and 3 until step 2, C_{k + n}, results in an empty set, thus resulting in a series of large itemsets, L_k−1 … L_{k + n}.

Note that once an item or itemset is determined to be below ε, that item(set) will not be considered in any subsequent candidate sets [e.g. if the mineral itemset (abelsonite, tinnunculite) was found to be below ε in L₂, no itemset in C₃ (or any subsequent candidate sets) with itemset (abelsonite, tinnunculite) would be considered by the algorithm] because if an itemset occurs too infrequently, so too will any supersets of that itemset.

The resulting association rules take the form of if then statements with a left hand side (LHS) of a mineral or minerals known to occur at a locality and a right hand side (RHS) of a mineral or minerals predicted to occur at a locality [i.e. (mineral A, mineral B, mineral C) ≥ (mineral D)]. The provided example can be read as “If minerals A, B, and C occur at a locality, it is likely mineral D will also be found at that locality.”

We use the R package “arules” to run the Apriori algorithm (19). Hahsler (2017) (20) created an extension to the arules package called “arulesViz” that visualizes the rules generated by the association rule learning algorithm.

Association rule likelihood metrics

Association rules are first constrained during generation by adjustable measures of significance and interest—the user sets the thresholds for each metric in order to generate the desired list of rules. Later, these same significance and interest metrics are used to evaluate the likelihood of the prediction as well as to characterize the statistical nature of cooccurrence (see Table 1). The metrics used by the Apriori algorithm in the mineral association analysis experiment (9) are as follows:

Table 1.

Likelihood metrics for the most frequent (support threshold > 2/6) mineral associations from the example in Fig. 1.

Rule	Support	Confidence	Lift
(Mineral A) → (mineral B)	3/6	3/5	0.9
(Mineral A) → (mineral C)	3/6	3/5	1.2
(Mineral B) → (mineral A)	3/6	3/4	0.9
(Mineral B) → (mineral C)	2/6	2/4	1.0
(Mineral B) → (mineral D)	2/6	2/4	1.5
(Mineral C) → (mineral A)	3/6	3/3	1.2
(Mineral C) → (mineral B)	2/6	2/3	1.0
(Mineral D) → (mineral B)	2/6	2/2	1.5
(Mineral A, mineral B) → (mineral C)	2/6	2/3	1.3
(Mineral A, mineral C) → (mineral B)	2/6	2/3	1.0
(Mineral B, mineral C) → (mineral A)	2/6	2/2	1.2

Support

Support is a measure of how frequently an itemset (e.g. mineral or mineral assemblage) is observed in the data. Support for the itemset X and itemset Y, Support (X ∪ Y), is the ratio of the number of times they cooccur at a locality in the data set, frequency (X ∪ Y), to the total number of localities in the data set, N.

$$Support(X\cup Y)={\displaystyle \frac{frequency(X\cup Y)}{N}.}$$

Support provides a relative measure of how common the cooccurrence of a specified set of minerals is within our data set, providing some insight into the likelihood of finding this set of minerals at localities where they are not currently known to exist.

Confidence

Confidence is a measure of the accuracy of a rule, which indicates the probability of the occurrence of itemset Y, when itemset X occurs. Confidence for the itemset X and itemset Y, confidence (X → Y), is the ratio of the number of times they cooccur at a locality in the data set, frequency (X ∪ Y), to the number of times itemset X occurs in the data set, frequency (X).

$$Confidence(X\to Y)={\displaystyle \frac{frequency(X\cup Y)}{frequency(X)}.}$$

Confidence demonstrates how frequently the selected mineral group occurs together, rather than separately, providing a probability for how likely one is to find one mineral cooccurring with another elsewhere.

Lift

Lift is a measure of the statistical dependence of the rule over the entire data set, by relating the observed frequency of occurrence of a mineral itemset to the expected frequency of occurrence of the unique items in the itemset, if the items were mathematically independent (21, 22). The higher the lift, the more “interesting” the rule because the frequency of cooccurrence is higher than expected relative to the frequency of occurrence of the individual items in the itemset across the system. The observed frequency of occurrence of a mineral itemset is the support of the items cooccurring [support (X ∪ Y)]. The expected frequency is the product of the support of each unique item [i.e. support (X) * support (Y)]. Lift of item Y occurring when item X occurs, Lift (X → Y), is measured as the ratio of the support of the cooccurring items X and Y, support (X ∪ Y), to the expected (independent) frequency of occurrence of items X and Y, support (X) * support (Y).

$$Lift(X\to Y)={\displaystyle \frac{support(X\cup Y)}{support(X)*support(Y)}.}$$

Lift provides a means to characterize the “interestingness” or strength of association of the mineral cooccurrence behavior. If a combination of minerals occurs together more frequently than one would expect if mineral cooccurrence was independent, this indicates a stronger association than random. Mineralization, of course, is not random and is the result of the complex interplay of chemical, physical, and evolutionary processes and materials through deep time, which has generated high-dimensional patterns of correlation (and anticorrelation) related to their formational environments and subsequent weathering and alteration. This metric enables researchers to identify mineral assemblages that show very strong affinity and potentially signifying unique or interesting mineral-forming environments or geologic histories.

These metrics can be used not only in statistical evaluation of the data but also in gaining insight to the mineralizing processes that led to the observed occurrence and cooccurrence relationships. Support provides insight into how common a mineral assemblage is: do we want to identify and investigate mineralogical relationships that are ubiquitous across a planet, or are we interested in focusing on rare mineralogical occurrences that symbolize very unique paragenetic modes? Confidence enables understanding of how rare a mineral assemblage is relative to the overall behavior of the individual mineral species: do these minerals form in many different environments and through many different mechanisms, or is this the expected mineralizing mode and therefore the type of geologic setting where we should generally expect to find these phases? Lastly, lift provides a measure of the strength of this mineral cooccurrence relationship and how statistically unexpected or “interesting” it is across the mineralizing system: do these minerals form together as a consequence of the overall geochemical composition and physical conditions of our planet, or is there another driving force, such as geologic processes or biology, that is leading to this stronger association of mineral species?

Predicting mineral occurrence via mineral association rules

Predicting the occurrence of any mineral species, mineral assemblage, mineralizing environment, and/or mineral inventory of any locality is performed by mining and querying the mineral association rules generated in the above sections. In this study, we generated association rules for each data subset listed above, specifically the geographical, geochemical, and temporal subsets. Here, we explore these rules and make predictions of which locations to find previously unknown minerals and mineral inventories.

In order to make these predictions, we use the generated association rules to query the mineral occurrence data. To predict minerals occurring at a specific locality, we first extract all mineral occurrences at that locality and compare them with our mineral association rules. In our example below, we predict minerals that can be found at the Tecopa Basin in California, United States of America. Due to computational limitations (see section on overcoming big data problems), we can generate association rules of up to four minerals only. Therefore, the LHS of the rule has only three minerals. Thus, we take every three-item permutation of minerals occurring at Tecopa Basin and find rules that predict the likelihood of occurrence of an unknown mineral at the locality.

To predict localities for a given mineral, we examine association rules for the mineral of interest. In the two case studies below, we have selected U minerals of geologic importance and several critical minerals related to high-tech advancement. To predict new localities of these mineral phases, we select rules with the mineral of interest occurring on the RHS of the rule. Next, we query our mineral localities to identify those that contain all the minerals on the LHS of each rule but do not contain the mineral of interest (RHS). We perform this query for each rule of interest, generating a list of localities likely to contain the mineral of interest. Several of these predictions have been confirmed since their assertion in 2022 October—providing ground truth of the predictive capacity of mineral association analysis.

Lastly, we can compare association rules and how they have changed through deep time. In order to make this comparison, we explore summaries of the association rules generated over Archean, Proterozoic, and Phanerozoic Eons. We can do this by creating summary visualizations of the association rules and their metrics (see examples below). We are also currently developing metrics to evaluate change in association rules and methods to compare association rule bases (see future work for more details) (23).

Select results are shown below, and the full set of association rules is provided at https://www.odr.io/med-MAA.

Science Driver: Can we gain a better understanding of the mineralogy of a Mars analogue location on Earth?

Query type: Mineral inventory at selected locality

Data subset: Geographical (USA)

Locality: Tecopa Basin, Inyo Co., California, USA (35°48′25.5″N, 116°11′24.9″W)

Mindat ID: 255486

Rules: See Supplementary material for complete list

Hyperparameters: Minimum support = 0.0002, minimum confidence = 0.7, maximum rule length = 4

The site selected is a Mars analog environment in the Mojave Desert. This site has been the focus of extensive chemical, mineralogical, and geological study, including that of the NASA Mars 2020 rover scientific payload testing and ground truthing (24). The Tecopa Basin site, located near the China Ranch in Inyo County, California, is a paleolake environment with volcanic ash and travertine deposits (25) with basaltic lava flows in the near vicinity. This environment is relevant to the recent Mars 2020 Perseverance rover landing site, Jezero crater, which is also thought to be a paleolake emplaced within the basaltic terrain of Mars (26, 27). Further defining the mineralogy of this locality can offer insight into the processes and characteristics of this type of environment on Earth and, possibly, on Mars.

The minerals currently known to be found in this area are saponite [(Ca,Na)_0.3(Mg,Fe²⁺)₃(Si,Al)₄O₁₀(OH)₂·4H₂O], analcime (NaAlSi₂O₆·H₂O), calcite (CaCO₃), cristobalite (SiO₂), montmorillonite [(Na,Ca)_0.3(Al,Mg)₂Si₄O₁₀(OH)₂·nH₂O], muscovite [KAl₂(Si₃Al)O₁₀(OH)₂], opal (SiO₂·nH₂O), searlesite [NaBSi₂O₅(OH)₂], and tridymite (SiO₂). Based on examination of these mineral occurrences in the rules generated by association analysis of the mineralogy of the United States, the minerals shown in Table 2 are likely to be found in this locality and possibly in similar paleolake environments on Mars. Some of these phases may be of astrobiological interest, given that they can form through biomediated processes, specifically hematite, pyrite, gypsum, magnetite, and sphalerite (28). Finding and further characterizing these phases may offer insight into the geologic and biologic history of this area while also providing information about the potential astrobiological implications of identifying these minerals on the Martian surface.

Table 2.

Mineral species predicted to occur at Tecopa Basin, California—a Mars analogue locality.

Mineral	Mineral formula	Confidence	Lift
Hematite*	Fe3+2O3	0.76	8.8
Quartz*	SiO2	0.94	2.5
Kaolinite*	Al2Si2O5(OH)4	0.75	23.3
Pyrite*	Fe2+(S2)2−	0.88	3.7
Gypsum*	CaS6+O4·2H2O	0.74	18.1
Albite	NaAlSi3O8	0.71	18.3
Magnetite*	Fe2+Fe3+2O4	0.74	8.3
Chalcopyrite*	Cu1+Fe3+S2−2	0.74	4.5
Sphalerite	Zn2+S2−	0.71	5.1

The mineral species likely to occur at Mars analogue site, Tecopa Basin, Inyo Co., California, United States of America, along with the associated confidence and lift metrics for the association rules on which these predictions are based. For minerals with multiple relevant association rules, denoted by *, the highest confidence and lift values were reported.

Science Driver: Where can we find locations to study oxidation–hydration alteration of uraninite?

Query: List of localities where a selected minerals can be found

Data subset: Geochemical (U)

Minerals: Rutherfordine (UO₂CO₃), andersonite [Na₂Ca(UO₂)(CO₃)₃·6H₂O], schröckingerite [NaCa₃(UO₂)(CO₃)₃(SO₄)F·10H₂O], bayleyite [Mg₂(U⁶⁺O₂)(CO₃)₃·18H₂O], and zippeite [K₂[(U⁶⁺O₂)₄(S⁶⁺O₄)₂O₂(OH)₂](H₂O)₄]

Rules: {Saleeite, Schoepite, Torbernite}=>{Rutherfordine}; {Bayleyite, Natrozippeite, Schrockingerite}=>{Andersonite}; {Andersonite, Bayleyite, Natrozippeite}=>{Schröckingerite}; {Carnotite, Natrozippeite, Schrockingerite}=>{Bayleyite}; {Carnotite, Chalcocite, Schrockingerite}=>{Bayleyite}; {Andersonite, Schrockingerite, Uraninite}=>{Zippeite}

Hyperparameters: Minimum support = 0.002, minimum confidence = 0.7, maximum rule length = 4

Uranyl carbonates and uranyl sulfates represent different stages of uraninite oxidation–hydration alteration (29–31). During the initial stages of uraninite alteration, as the primary minerals of the system oxidize, the system pH is buffered by the dissolution of carbonates and alkali-element–containing minerals (29). The dissolution of carbonates and uraninite in neutral to alkaline pH ground water results in uranyl carbonate complexes forming in solution that can crystallize into uranyl carbonates when the water evaporates. Minerals representative of this stage include rutherfordine, andersonite, and schröckingerite. As alteration of the primary minerals continues, the carbonates in the system are eventually depleted and the primary sulfides oxidize with the primary U minerals. The sulfuric acid released begins acid mine conditions, and the dissolved sulfate will complex with the uranyl ion. The uranyl–sulfate complexes can travel some distance and often form ephemeral crusts on the walls of mine adits (29).

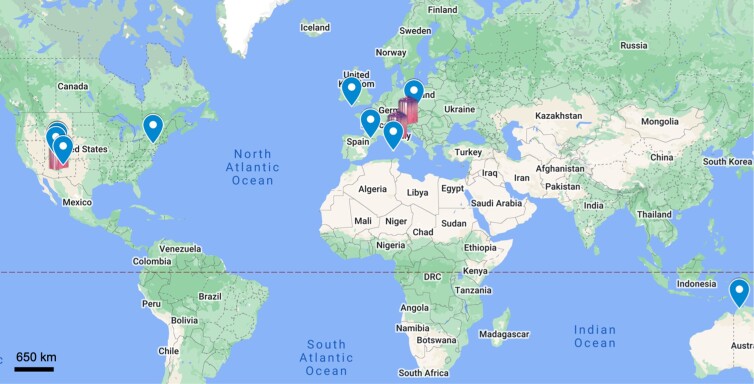
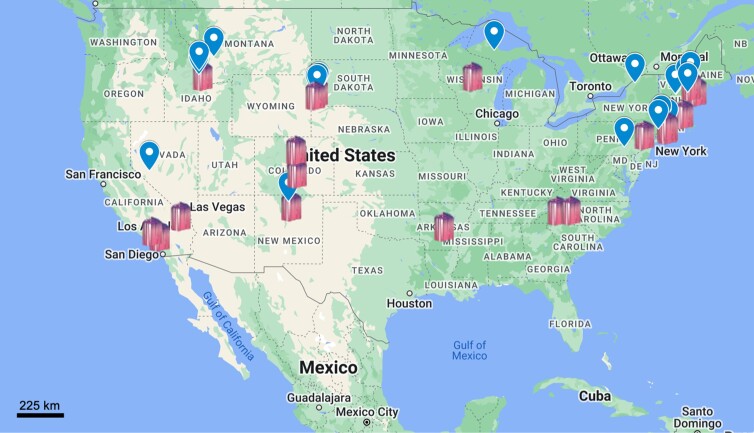
Below, we give examples of likely new, currently unknown localities of selected U mineral phases, specifically those associated with uraninite alteration, rutherfordine, andersonite, and schröckingerite, as well as the two phases with the highest lift in our data set, bayleyite, and zippeite (Fig. 2). Table 3 provides predictions of previously unrecognized localities of a mineral of interest, including whether or not the prediction of that mineral occurrence has been ground truthed since its assertion in 2020 October. A mineral at a locality is considered “ground-truthed” when it has been discovered, published in the scientific literature, and reported on the Mindat website.

Fig. 2.

Map of predicted new localities of selected U mineral species, rutherfordine, andersonite, schröckingerite, bayleyite, and zippeite (see Table 2). Locations ground-truthed as of October 2021 are marked by a Mindat logo, whereas unverified localities are signified with a marker. An interactive Google Earth map (*.kmz) can be found in Supplementary material.

Table 3.

Predictions of new localities of selected U mineral species.

Mineral	Rule	Predicted localities	Mindat ID	Ground truthed?
Rutherfordine	(Saleeite, schoepite, torbernite) ≥ (rutherfordine)	White's Mine, Rum Jungle, Batchelor, Coomalie Shire, Northern Territory, Australia	257,518	No
	Support = 0.002	Arcu Su Linnarbu, Capoterra, Cagliari Metropolitan City, Sardinia, Italy	2,123	No
	Confidence = 0.74	Giudicarie Valleys, Trento Province, Trentino-Alto Adige, Italy	130,590	Preliminary
	Lift = 61.4	Laguna District, Cibola Co., New Mexico, United States of America	21,688	No
Andersonite	(Bayleyite, natrozippeite, schröckingerite) ≥ (andersonite)	Deer Flat, White Canyon, White Canyon District, San Juan Co., Utah, United States of America	46,083	No
	Support = 0.002
	Confidence = 0.92
	Lift = 89.0
Schröckingerite	(Andersonite, bayleyite, natrozippeite) ≥ (schröckingerite)	Slick Rock District, San Miguel Co., Colorado, United States of America	73,134	Yes
	Support = 0.002
	Confidence = 1.00
	Lift = 41.6
Bayleyite	(Carnotite, natrozippeite, schröckingerite) ≥ (bayleyite)	Parco Mine Group, Yellow Cat Mesa, Thompsons District, Grand Co., Utah, United States of America	183,008	No†
	Support = 0.002
	Confidence = 0.88
	Lift = 107.0
	(Carnotite, chalcocite, schröckingerite) ≥ (bayleyite)	Shinarump Nos. 1–3 Mines, Seven Mile District, Grand Co., Utah, United States of America	21,766	No†
	Support = 0.002
	Confidence = 0.91
	Lift = 111.6
Zippeite	(Andersonite, schröckingerite, uraninite) ≥ (zippeite)	Předbořice Deposit, Předbořice, Kutná Hora District, Central Bohemian Region, Czech Republic	771	Yes
	Support = 0.003	Rožná I Mine, Rožná Deposit, Rožná, Žďár Nad Sázavou District, Vysočina Region, Czech Republic	135,187	No†
	Confidence = 0.72	Eureka Mine, Castell-estaó, La Torre De Cabdella, La Vall Fosca, El Pallars Jussà, Lleida, Catalonia, Spain	53,316	No
	Lift = 21.1	Geevor Mine, Pendeen, St Just, Cornwall, England, UK	1,296	No†
		Section 22 Deposit, Ambrosia Lake Sub-district, Grants District, McKinley Co., New Mexico, United States of America	47,967	No†
		Jim Thorpe, Carbon Co., Pennsylvania, United States of America	212,583	No
		Little Eva Mine, Yellow Cat Mesa, Thompsons District , Grand Co., Utah, United States of America	182,338	No†

This summary table provides the mineral species of interest, the association rule on which the prediction is based and its associated likelihood metrics (lift and confidence), the predicted localities, their associated Mindat IDs, and whether or not each mineral-locality prediction has been ground-truthed since its assertion in 2020 October. Localities with an occurrence of the selected mineral at the county (or equivalent) level are denoted with^†.

Science Driver: Where can we find new deposits of critical minerals in the United States?

Query: List of localities where a selected minerals can be found

Data subset: Geographic (USA)

Minerals: Monazite–(Ce) (CePO₄), allanite–(Ce) [CaCeAl₂Fe²⁺(Si₂O₇)(SiO₄)O(OH)], spodumene (LiAlSi₂O₆)

Rules: {Elbaite, Rutile, Sphalerite}=>{Monazite-(Ce)}; {Gadolinite-(Y), Microcline, Muscovite}=>{Allanite-(Ce)}; {Beryl, Mitridatite, Pyrite}=>{Spodumene}

Hyperparameters: Minimum support = 0.0002, minimum confidence = 0.7, maximum rule length = 4

Critical minerals are those deemed important to strategic and technological development that have the potential for significant supply chain disruptions in the future (32). These strategic materials include rare earth element (REE) minerals and lithium minerals, which are essential components in many high-tech devices and infrastructure, including green technologies such as batteries and magnets used in wind turbines and high-speed rail. Here, we demonstrate the ability to find new deposits of critical minerals in the United States, specifically focusing on selected REE minerals, monazite–(Ce), and allanite–(Ce), and spodumene. Monazite–(Ce) (CePO₄) is one of the major focuses of REE mining and extraction and, like all other REE-bearing minerals, does not only contain its namesake element, Ce, but also bears a large proportion of other REEs. Due to advances in REE silicate processing and extraction, allanite–(Ce) [CaCeAl₂Fe²⁺(Si₂O₇)(SiO₄)O(OH)] represents a potentially important future resource of REEs (33, 34). The United States currently produces 15% of the world's REEs, while thought to contain only 2% of global REE reserves (35). Spodumene (LiAlSi₂O₆) is the primary hard rock source of lithium, with the other major source of lithium being brine extraction. The United States currently accounts for 1% of global Li production, with 3.5% of the world's Li reserves and less and 10% of the world's known Li resources (35).

Below, we give examples of likely new, currently unknown localities of selected critical minerals, REE-bearing phases, monazite–(Ce) and allanite–(Ce), and the Li-bearing mineral, spodumene (Fig. 3). Table 4 provides predictions of previously unrecognized localities of these critical minerals, including whether or not the prediction of that mineral occurrence has been ground truthed since its assertion in 2020 October.

Fig. 3.

Map of predicted new localities of selected critical minerals, monazite–(Ce), allanite–(Ce), and spodumene (see Table 3). Locations ground-truthed as of October 2021 are marked by a Mindat logo, whereas unverified localities are signified with a marker. An interactive Google Earth map (*.kmz) can be found in Supplementary material.

Table 4.

Predictions of new localities for selected critical minerals.

Mineral	Rule	Predicted localities	Mindat ID	Ground truthed?
Monazite–(Ce)	(Elbaite, rutile, sphalerite) ≥ [monazite–(Ce)]	Jensen Quarry, Jurupa Mts, Jurupa Valley, Riverside Co., California, United States of America	3,525	Yes
	Support = 0.0002	U. S. Route 7 Expressway, Brookfield, Fairfield Co., Connecticut, United States of America	213,273	No
	Confidence = 0.76	Glastonbury, Hartford Co., Connecticut, United States of America	24,899	Yes
	Lift = 222.4	East Hampton, Middlesex Co., Connecticut, United States of America	23,094	Yes
		Haddam, Middlesex Co., Connecticut, United States of America	4,574	Yes
		Strickland Quarry, Strickland Pegmatite, Collins Hill, Portland, Middlesex Co., Connecticut, United States of America	3,708	Yes
		Mount Mica Quarry, Paris, Oxford Co., Maine, United States of America	3,784	Yes
		Topsham, Sagadahoc Co., Maine, United States of America	3,792	Yes
		Butte Mining District, Silver Bow Co., Montana, United States of America	3,873	No
		Hiddenite, Alexander Co., North Carolina, United States of America	4,034	Yes
		Ray Mica Mine, Hurricane Mountain, Burnsville, Spruce Pine District, Yancey Co., North Carolina, United States of America	5,494	Yes
		Cornwall Mines, Cornwall Borough, Lebanon Co., Pennsylvania, United States of America	3,653	No
		Custer District, Custer Co., South Dakota, United States of America	4,111	Preliminary
		Etta Mine, Keystone, Keystone District, Pennington Co., South Dakota, United States of America	4,106	Yes
		Rotten Granite Quarries, Wausau Intrusive Complex, Marathon Co., Wisconsin, United States of America	26,807	Preliminary
Allanite–(Ce)	[Gadolinite–(Y), microcline, muscovite] ≥ [allanite–(Ce)]	Little Rock, Pulaski Co., Arkansas, United States of America	24,253	Yes
	Support = 0.0002	San Gabriel Mts, Los Angeles Co., California, United States of America	28,941	Yes
	Confidence = 0.83	Commercial Quarry, Sky Blue Hill, Crestmore Quarries, Crestmore, Riverside Co., California, United States of America	6,801	Yes
	Lift = 249.4	Mountain Pass Mine, Mountain Pass District, Clark Mountain Range, San Bernardino Co., California, United States of America	11,616	Yes
		Jamestown District, Boulder Co., Colorado, United States of America	28,929	Yes
		Eight Mile Park Pegmatite District, Fremont Co., Colorado, United States of America	14,217	Preliminary
		Clear Creek Pegmatite Province, Jefferson Co., Colorado, United States of America	66,742	Yes
		Haddam, Middlesex Co., Connecticut, United States of America	4,574	Yes
		Eureka District, Lemhi Co., Idaho, United States of America	39,586	No
		Lemhi Pass District, Lemhi Co., Idaho, United States of America	39,593	No†
		McDevitt District, Lemhi Co., Idaho, United States of America	39,596	Preliminary
		Blueberry Mountain Quarry, Woburn, Middlesex Co., Massachusetts, United States of America	4,516	Yes
		Marquette Iron Range, Marquette Co., Michigan, United States of America	125,421	No
		Fitting District, Mineral Co., Nevada, United States of America	14,359	No
		Franklin Mine, Franklin, Franklin Mining District, Sussex Co., New Jersey, United States of America	8,541	Yes
		Petaca District, Rio Arriba Co., New Mexico, United States of America	21,886	No
		Picuris District, Taos Co., New Mexico, United States of America	21,698	Yes
		Harding Mine, Picuris District, Taos Co., New Mexico, United States of America	13,724	Yes
		De Kalb Township, St. Lawrence Co., New York, United States of America	23,672	No†
Spodumene	(Beryl, mitridatite, pyrite) ≥ (spodumene)	State Route 8 And State Route 118 Interchange, Harwinton, Litchfield Co., Connecticut, United States of America	253,331	No
	Support = 0.0005	Anderson No. 1 Mica Mine, East Hampton, Middlesex Co., Connecticut, United States of America	6,782	No†
	Confidence = 0.70	Estes Quarry, West Baldwin, Baldwin, Cumberland Co., Maine, United States of America	6,164	No†
	Lift = 169.6	Ryerson Hill Quarries, Paris, Oxford Co., Maine, United States of America	6,101	Yes
		Lookout Quarry, Rumford, Oxford Co., Maine, United States of America	193,451	No†
		Lord Hill Quarry, Stoneham, Oxford Co., Maine, United States of America	3,782	No†
		Palermo No. 1 Mine, Groton, Grafton Co., New Hampshire, United States of America	3,942	No
		Palermo No. 16 Mine, Groton, Grafton Co., New Hampshire, United States of America	77,251	No
		Palermo No. 2 Mine, Groton, Grafton Co., New Hampshire, United States of America	8,928	No
		Bull Moose Mine, Custer, Custer District, Custer Co., South Dakota, United States of America	4,107	No†
		Tip Top Mine, Fourmile, Custer District, Custer Co., South Dakota, United States of America	4,122	No†
		Big Chief Mine, Glendale, Keystone District, Pennington Co., South Dakota, United States of America	4,105	No†

This summary table provides the mineral species of interest [monazite–(Ce), allanite–(Ce), and spodumene], the association rule on which the prediction is based and its associated likelihood metrics (lift and confidence), the predicted localities, their associated Mindat33 IDs, and whether or not each mineral-locality prediction has been ground-truthed since its assertion in 2020 October. Localities with an occurrence of the selected mineral at the county (or equivalent) level are denoted with †.

• Science Driver: How has mineralization and mineral associations changed through deep time?

Query type: Subset and explore all rules from selected time periods

Data subsets: Archean, Proterozoic, Phanerozoic Eons

Hyperparameters:

Archean: Minimum support = 0.009, minimum Confidence = 0.7, maximum rule length = 4

Proterozoic: Minimum support = 0.008, minimum Confidence = 0.7, maximum rule length = 4

Phanerozoic: Minimum support = 0.004, minimum Confidence = 0.7, maximum rule length = 4

Mineralization, mineralizing environments, and mineral associations have changed through deep time (2, 28). In an effort to further characterize the changes in mineral occurrence throughout the Earth’s history, here, we examine the mineral association rules of selected time periods, specifically the Archean Eon (>2.5 Ga), Proterozoic Eon (2.5–0.54 Ga), and Phanerozoic Eon (<0.54 Ga). The Archean Eon was host to the Earth's earliest continental crust (36), the onset of plate tectonics (37), and the most ancient forms of life (38). The Proterozoic Eon saw the rise of global free oxygen (39), which dramatically altered the near-surface chemical landscape and made way for aerobic microorganisms and eukaryotes (40). The Phanerozoic Eon, representing the shortest of the three time periods, has seen a transformation in the Earth's surface, beginning with the Cambrian explosion (41), which resulted in the rapid biodiversification of multicellular life, moving through several mass extinction events (42), glaciation periods (42, 43), and the assembly and breakup of the last of the supercontinents, Pangea (44), on into the modern day, which has seen the rise of humans and the Anthropocene Epoch (45, 46).

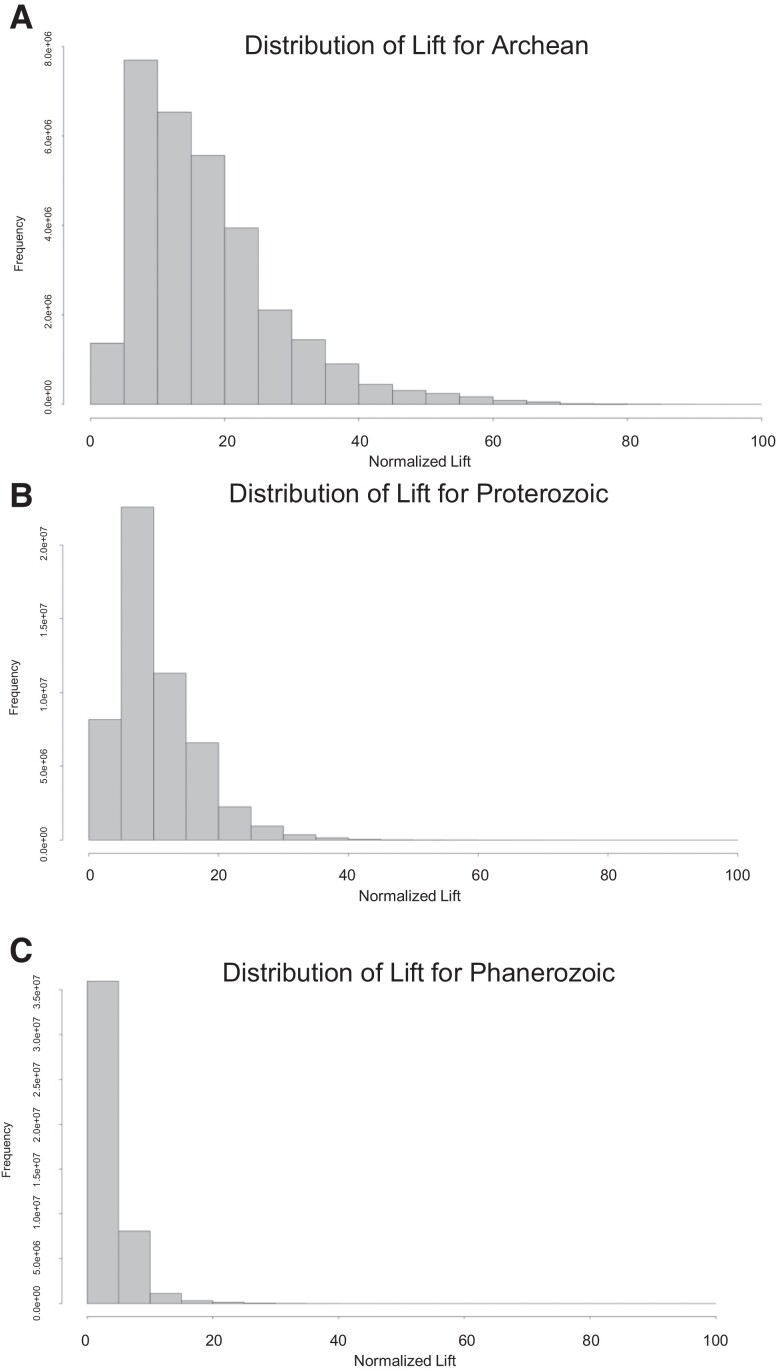
Lift represents the strength of association between mineral groups, which offers insight into mineralizing systems, specifically (i) the diversity of mineral species and their modes of mineralization, (ii) the number of mineralizing environments and processes, and (iii) the impact of sampling bias. There are clear differences between the distribution of lift across the three eons (Fig. 4A–C). The Archean Eon (Fig. 4A) shows the most significant skew toward high lift values, whereas the Phanerozoic Eon (Fig. 4C) shows a strong skew toward low lift values, with the Proterozoic (Fig. 4B) showing a moderate trend between the two extremes. This decrease in mineral association strength could be due to several, possibly overlapping, factors. These factors include the following: (i) the increase in mineralizing environments and diversity of mineral species, (ii) the increasing ubiquity of common minerals in the Phanerozoic, and (iii) a bias in sampling and/or preservation that results in underrepresentation of rare minerals and mineral occurrences in rare environments from older terrains, overrepresentation of robust minerals resistant to weathering and alteration in ancient samples, and an overall overrepresentation of minerals of scientific (e.g. age dating) and economic (e.g. ore bodies) significance. This unexpected decrease in the strength of mineral associations on Earth from the Archean to the Phanerozoic Eon opens a venue for exploration into the drivers behind this change, several of which are highlighted above. Future work will involve exploring better ways to characterize the changes in mineral association rules (23) and explore the effects of formational environments on the strength of mineral associations.

Fig. 4.

A) The distribution of mineral association lift in the Archean Eon, B) the Proterozoic Eon, and C) the Phanerozoic Eon. Lift values are normalized between 0 and 100 for comparison between time periods. Frequency is the number of mineral association rules within a given range of lift.

Discussion

Mineral association analysis adds a powerful predictive tool to the arsenal of mineralogists, petrologists, economic geologists, and planetary scientists. Through centuries of empirical observations, Earth materials researchers have developed numerous “rules of thumb” for discovering new deposits based on such diverse factors as colorful secondary phases, unusual detrital minerals, diagnostic geochemical anomalies, patterns of vegetation, and other environmental indicators. Recognition of such tracers requires years of experience, close observation, and intuitive leaps to connect one set of variables to others. Association analysis of mineral systems builds on that long tradition by probing simultaneously numerous attributes of many different geological occurrences to yield a multidimensional framework of associations far more comprehensive and quantitative than that possible by human intuition alone.

We suggest that useful and revealing patterns of association lie hidden in the extensive, multidimensional information of mineral data resources—patterns that reflect the phase equilibria and geochemical evolution of complex multicomponent systems. Immediate applications of association analysis, as shown above, include the following: (i) the prediction of new localities for target mineral species, (ii) the prediction of new locations of paragenetic environments of interest, including ore-forming processes and planetary analogues, based on suites of minerals that signal these regimes, (iii) the prediction of mineral inventories at localities of interest, and (iv) the comparison of mineralization and mineral occurrence relationships across different ages, tectonic settings, climate zones, and other contextual variables.

Ultimately, we anticipate a time when the collective data of centuries of Earth materials investigations will allow mineralogy to transition from its traditional role as a descriptive science to a more predictive endeavor. Implementation of the analytical techniques and visualization methods of data-driven discovery are central to that ambition because of the intrinsic multivariate character of rocks and minerals. Most natural deposits incorporate a dozen or more major elements, with scores of more trace and minor elements. The minerals of natural systems have been subjected to a succession of changes in pressure and temperature, exposed to diagenetic fluids, altered by tectonic processes, and, in many instances, transformed by biological influences. Such higher-dimensional complexities are not easily grasped by the unaided human mind but are the essence of data-driven discovery.

Future directions

Data science challenges and opportunities

Overcoming the “Big Data” problem: association analysis has established itself as a valuable algorithm in the fields of marketing, sales, and customer relations (8, 9, 47). Entering the era of Big Data, these algorithms faced scalability issues that limited their use to smaller data sets (i.e. “market baskets”) (11, 12). This limitation led to the development of techniques, modifications, and methods to make Apriori-like algorithms scalable to large data sets (10, 12, 48), but most of the work on scalability has been in scaling the number of transactions in the market basket data, which is equivalent to scaling up the number of mineral localities, but not the number of minerals in the system. As a consequence, association analysis is currently too computationally intensive to run this algorithm on all known mineral occurrences on Earth or to allow predictions of localities for the thousands of rarer mineral species that are currently known from 5 or fewer localities.

Our data set contains a large number of minerals in some localities (up to 433 in a single locality and 5,476 minerals overall, as of 2020 October), which presents an as-yet-unsolved scalability problem. Therefore, future work will include the scaling of association analysis algorithms to accept large numbers of items in its transactions (i.e. large combinations of minerals in query) and to continue work in finding a solution to the long tail problem (11) as it applies to mineral data (i.e. that many rare minerals occur at few localities). Progress in these areas will allow predictions on larger data sets, including all of Earth's mineralogy simultaneously, while reducing the support further to include rare minerals in the recommendations.

Evaluating association rules: while we have been using mineral association rules to predict unknown mineral occurrences for a given locality and to predict localities to find a given mineral, association analysis and more specifically the association rule mining are inherently an unsupervised method used to generate association rules based on cooccurrence data. Thus, most of the metrics used to evaluate the results of association analysis methods focus on either the ability of the model to ingest large amounts of data (49), or using a metric-based comparison of various algorithms used for association rule mining (50), or on evaluating the rules mined to more efficiently generate association rules (51). However, when patterns generated in an unsupervised method are used to predict the occurrences of entities such as minerals, there needs to be a way to evaluate the predictions made by the model. Because there is very little work done in this research area, we are currently developing a new method to evaluate the results of association rules, specifically when these rules are used in a predictive setting (23).

Characterizing mineral systems

The algorithms can further be expanded by including information beyond mineral cooccurrence, such as tectonic settings, geologic parameters, formation ages, and other attributes (e.g. climate zones, vegetation patterns, microbial metagenomes, and groundwater chemistry) to further aid predictions. These additional parameters and characteristics will further increase the precision of the association rules and will result in more accurate and informed predictions. Addition of these locality attributes will also expand the type of predictions that can be made—currently, we perform queries based on minerals and mineral assemblages, but with the proposed advances, we will be able to query the rule base on tectonic setting, geology, age, chemistry, and other attributes, providing previously unknown information about poorly characterized mineral occurrences.

Reaching the Solar System

Likewise, these data sets, algorithms, and predictions can be extended to other terrestrial worlds, particularly Mars, the Moon, Vesta, and other bodies for which we have mineralogical information (e.g. from meteorites, returned sample data, surface mission analyses, and remote sensing observations). With the data currently incorporated in this method, we can identify planetary analog environments on Earth, but with the inclusion of mineralogical profiles of other planets, moons, and asteroids, we will be able to predict the location of minerals of interest on those bodies. In addition to furthering our understanding of the environments as well as the geological and astrobiological histories of other planetary objects, these analyses will aid in landing site selection during future mission planning as it will allow for the targeting of specific locations of geological, geochemical, and astrobiological relevance. In advancing these facets, mineral association analysis, specifically the inclusion of contextual data and the extension to other celestial objects, has the potential to become the most advanced mineralogical tool for exploring the geology, geochemistry, and astrobiology of our planet and other planetary bodies in our solar system.

Expanding beyond minerals

Additionally, the application of this method is not restricted solely to mineral associations but can be applied to cooccurring fossils, microbes, molecules, and other attributes of geological environments. The extendibility and transferability of this association analysis method make it widely applicable and impactful in many realms of data-driven discovery of evolving Earth and planetary systems. Furthermore, a significantly more ambitious exploration using this method would be the combining of mineral and microbe occurrences, characterized by their physical, chemical, biological, and geological parameters. For example, rules generated using this method could elucidate roles that mineral occurrences play in microbial populations and functions, as well as roles of microbial communities in modifying mineral-forming environments, thus offering new insight into the coevolution of the geosphere and biosphere in planetary systems.

Materials and methods

Data resources

In recent years, efforts have been made to collect, curate, and make publicly available mineralogical and geochemical data resources existing in peer-reviewed literature, supplementary tables, and dark sources, such as undigitized journals and spreadsheets on private hard drives. These data collection efforts, such as the RRUFF Project (rruff.info), Mindat (mindat.org), and EarthChem (earthchem.org), are driven by unanswered scientific questions related to the formation and evolution of our planet and other planetary bodies in our solar system. FAIR (findable, accessible, interoperable, and reusable) (52, 53) data resources are foundational for successful data-driven scientific exploration. Below, we describe the databases employed in this study.

The IMA list of mineral species

The IMA list of mineral species (RRUFF.info/IMA) is part of the RRUFF Project (54)—a mineral library and series of databases with the goal of providing robust, diverse mineralogical data, including high-quality chemical, spectral, and diffraction data that is openly available for scientific research. In addition to the IMA list of approved mineral species, the RRUFF Project also houses the American Mineralogist Crystal Structure Database (AMCSD; RRUFF.geo.arizona.edu/AMS/amcsd.php), the Evolutionary System of Mineralogy Database (ESMD; odr.io/ESMD), the Mineral Properties Database (MPD; odr.io/MPD), mineral-locality age information (see Mineral Evolution Database section below), and more. The IMA list allows users to search the nearly 5,829 mineral species (as of 2022 August) by name, chemical composition, unit cell parameters and crystallography, crystal structure group, paragenetic mode, and the availability of associated data, including crystal structure files in the AMCSD or direct RRUFF Project analyses. This database also provides useful information about each mineral species, including composition, oldest known age, and number of documented localities on Earth, all of which can be downloaded in a number of machine-readable file formats. Lastly, this site offers an interface for querying a number of other websites and databases, including the Handbook of Mineralogy, Mindat, and the MED.

The Mineral Evolution Database

The MED (RRUFF.info/Evolution) (14–16, 55) was created to support studies in mineral evolution and ecology, focusing on characterizing and understanding the spatial and temporal mineral diversity and distribution in relation to geologic, biologic, and planetary processes (2, 3, 56–62). The MED contains mineral locality and age information extracted from primary literature and the mineral-locality database, mindat.org. As of 2020 February 3, 16,553 unique ages for 6,483 directly dated localities, documenting 810,907 mineral-locality pairs and 210,037 mineral-locality–age triples, are available in the MED. These data have been curated and documented to maximize the accuracy and transparency of age associations, which include data on specific mineral formations, mineralization events, element concentrations, and/or deposit formations. The MED interface allows download in various file formats and many sorting and displaying options.

Mindat.org

Mindat.org is an interactive mineral occurrence database with mineral localities from around the globe, as well as Apollo Lunar samples and meteorites. Mindat contains nearly 400,000 localities and over 1.4 million mineral-locality pairs (2022 August). The majority of mineral occurrence information on mindat.org is from published literature, but a crowd-sourcing option also exists, by which users can add localities, mineral-locality pairs, photographs, and references. The MED directly interfaces with Mindat, incorporating mineral-locality pair information and providing URL links to relevant Mindat locality pages.

Global Earth Mineral Inventory

The Global Earth Mineral Inventory (GEMI) is a faceted, searchable knowledge graph that allows interactive access to the MED, Mindat, and various other mineralogical data resources (55). GEMI is a Deep Carbon Observatory (DCO) data legacy project designed to integrate and provide access to the diverse data types collected in conjunction with the DCO's broad range of scientific driving questions (55). GEMI supports and facilitates scientific discovery by merging DCO data products, such as the MPD and MED, into a digestible, accessible, and user-friendly format for exploration, statistical analysis, and visualization. The GEMI data service can be found at https://doi.org/10.5281/zenodo.7897248.

Data processing

The data used in this paper were retrieved from the MED (14–16), which contains information on mineral occurrences, their localities with their geographical coordinates, and age information for many mineral-locality occurrences. Cooccurrence matrices were generated from subsets of these data using the “plyr” package (63).

Supplementary material

Supplementary material is available at PNAS Nexus online.

Funding

Funding for this project was provided by the Carnegie Institution for Science, the 4D Initiative (4d.carnegiescience.edu), the Alfred P. Sloan Foundation, the W. M. Keck Foundation via the Deep Time Data Infrastructure project (dtdi.carnegiescience.edu), a private foundation, and the NASA Astrobiology Institute (Cycle 8) ENIGMA: Evolution of Nanomachines In Geospheres and Microbial Ancestors (80NSSC18M0093).

Author contributions

S.M.M., A.P., J.R., and R.M.H. conceptualized the project; S.M.M., R.M.H., J.J.G., R.T.D., S.P., P.C.B., and J.R., generated the data; S.M.M., A.P., A.E., and P.F. designed the methodology and analyzed the data; S.M.M. and A.P. wrote the manuscript with sections and edits contributed by all authors.

Data availability

The mineral-locality data used in this study were derived from the Mineral Evolution Database and Mindat (14–16, 64) and are available for download at rruff.info/evolution. The overall rule set generated in this study is located at https://www.odr.io/MED-MAA. All source codes generated and used in this study are available on https://github.com/anirudhprabhu/Mineral-Association-Analysis. An interactive Google Earth map (*.kmz) of Figs. 2 and 3 can be found in Supplementary material.