An illustration of model agnostic explainability methods applied to environmental data

Abstract

Historically, two primary criticisms statisticians have of machine learning and deep neural models is their lack of uncertainty quantification and the inability to do inference (i.e., to explain what inputs are important). Explainable AI has developed in the last few years as a sub-discipline of computer science and machine learning to mitigate these concerns (as well as concerns of fairness and transparency in deep modeling). In this article, our focus is on explaining which inputs are important in models for predicting environmental data. In particular, we focus on three general methods for explainability that are model agnostic and thus applicable across a breadth of models without internal explainability: “feature shuffling”, “interpretable local surrogates”, and “occlusion analysis”. We describe particular implementations of each of these and illustrate their use with a variety of models, all applied to the problem of long-lead forecasting monthly soil moisture in the North American corn belt given sea surface temperature anomalies in the Pacific Ocean.

1 |. INTRODUCTION

A long-standing criticism of many algorithmic-motivated machine learning methods and modern deep neural network “artificial intelligence (AI)” methods has been the “black-box” nature of the models that prohibit uncertainty quantification and inference in the context of understanding which inputs are important for producing model predictions and/or classifications. In recent years, the sub-discipline of computer science known as explainable AI (sometimes referred to as XAI) has arisen to address these concerns. The literature on related topics has been expanding rapidly in recent years. Two recent papers describe modern approaches for uncertainty quantification (Abdar et al., 2021) and explainability (Samek et al., 2021). Comprehensive overviews are also given in Rudin et al. (2022) and Molnar (2022). Our focus in this work is on the explainability component, primarily because some of these explainability methods are not well-known in statistics, yet have broad application across a variety of models (i.e., they are “model agnostic”). In particular, we are interested in their application to predictive models used for environmental data.

Environmental statistics is concerned with a wide variety of problems such as: estimating ecological abundance, spatial and spatio-temporal prediction, climatological downscaling, long-lead prediction, and understanding health effects of environmental exposures, to name a few. Here, we are interested in problems for which a specified set of inputs are related to a specified set of outputs. In recent years, spatial and spatio-temporal prediction (interpolation) has been a big part of the environmental statistics literature. We are not particularly interested in those methods here because traditional best linear unbiased prediction approaches (e.g., kriging and its variants) provide a built-in estimate of the “weight” associated with each observation that is used to predict a given observation. Indeed, this is true of any predictive model that can be formulated as a linear model. Rather, here we are primarily interested in explaining models for which the response is modeled as a nonlinear function of the inputs. For example, we would like to know which geographic regions in the Pacific Ocean are most relevant to predicting soil moisture in the “corn belt” region of the midwest United States (US).

We illustrate three model agnostic explainability approaches in this manuscript. First, we consider simple feature shuffling methods where feature importance is determined by how much the prediction error of a model varies as individual features are shuffled, randomized, or perturbed (Section 2.1). The second approach we consider is the local interpretable model-agnostic explanations (LIME) method (Section 2.2), which is perhaps the best known local interpretable surrogate approach. Finally, we consider Shapley values (Section 2.3), a sophisticated occlusion analysis method that takes a game theoretic approach to explaining the output of any machine learning model. These and other related occlusion analysis methods are still underutilized in statistics.

The article is organized as follows. Section 2 gives an overview of the methods associated with implementation and interpretation of feature shuffling, LIME, and Shapley values. This is followed in Section 3 by an introduction to the long-lead forecasting environmental data example that is used to demonstrate the utility of these methods. Section 4 gives an overview of the machine learning algorithms and statistical models that will be used as frameworks to demonstrate the application of the explainability methods. Section 5 then demonstrates the use of these explainability approaches on a variety of models applied to the long-lead forecasting environmental data set. We conclude in Section 6 with a discussion, providing recommendations for the use of these algorithms in general, and an outline of future work needed for effective use of these methods and approaches in environmental statistics.

2 |. MODEL AGNOSTIC EXPLAINABILITY METHODS

The essential problem of interest here is using general methods to distribute or explain the prediction score of a model output given known input features. It is then assumed that the attribution to these input features can be interpreted as the “importance” of the feature to the prediction. We treat all models as black boxes, even if we understand some aspects of their internal connections. The goal is that by understanding why a model makes a specific prediction, it will help the model user determine how much the model can be trusted and/or provide mechanistic insight and possibly causality.

As mentioned in Section 1, the methods we are concerned with here fall under the area of machine learning research known as explainable AI (XAI). This is distinct from the more recent area of research known as “Interpretable AI”, which is focused on constructing models that are inherently interpretable by humans (see Rudin et al., 2022, for an overview and connections to XAI). In that work, the authors make the point that techniques such as those discussed below, tools for explaining black box models, are not needed for inherently interpretable models because models that are interpretable explicitly show what variables are being used, and how. The recent interest in building physical constraints into deep neural networks is an example of an interpretable AI model (e.g., Huang et al., 2021; Mohan et al., 2020; Reichstein et al., 2019). Rudin et al. (2022) further make clear that Interpretable AI is not a subset of XAI, although the two are often used interchangeably. We agree that interpretable models are the “gold standard”, but black box methods have proven quite useful for many prediction and classification tasks and they are not going away; thus, we should strive to explain them as much as possible.

Many statistical and machine learning methods have algorithm-specific approaches to facilitate explainability. For example, “attention mechanisms” or “pixel attribution saliency maps” in neural networks (Molnar, 2022). This is also true of tree-based methods such as random forests and boosting, for which there are well-established approaches to determine feature importance based on which variables are used in the splits associated with the tree construction (Breiman, 2001a). Our interest here is on flexible methods that are model agnostic, or at least largely so, and can be applied to a wide variety of models used to predict environmental data. In general, model-agnostic methods can be characterized as “global” or “local”. Global approaches describe the importance or effect of features on model behavior on average. Examples of such methods include “partial dependence plots”, “accumulated local effects plots”, “functional decomposition”, “permutation feature importance”, “global surrogates”, and others (see Chapter 8 of Molnar, 2022, for these and other approaches). For example, in our environmental example discussed in Section 3, we are interested in which predictors (locations) in the tropical Pacific Sea Surface Temperature Anomaly (SSTA) data set are most important, on average, for forecasting soil moisture in the US corn belt 3 months in the future across all years. Local approaches, as the name suggests, describes the importance of features on particular instances of the data. In our environmental example, this might be to identify SSTA locations that are important for predicting soil moisture in spring 2016 (at the end of strong El Niño event). There are several local model agnostic procedures such as “local surrogates” (e.g., LIME) and “occlusion analysis” (e.g., Shapley values) that have proven useful (see Chapter 9 of Molnar, 2022, for a comprehensive discussion). We note that in some cases it is possible to use a traditionally global procedure for local analysis (e.g., permutation feature importance) and local procedures (such as LIME and Shapley values) can be averaged across instances to give a global interpretation.

The remainder of this section describes the three model agnostic approaches we consider in our environmental forecasting application: feature shuffling, LIME, and Shapley values. We implement them from both a global and local perspective in our analysis in Section 5.

2.1 |. Feature shuffling

Variable importance, or more specifically, permutation feature importance (also called “feature shuffling”), was initially developed in the context of machine learning algorithms for random forests by Breiman (2001a), under the impetus of understanding the interaction of variables providing classification accuracy. Similar work was done on neural networks and perturbation of inputs around the same time (e.g., Gevrey et al., 2003; Recknagel et al., 1997). More recently, Fisher et al. (2019) proposed a general framework suitable to any input-output model, which we briefly summarize here using the same notation as in the original work, and assuming, without loss of generality, only two covariates. In this framework, the authors focused on the problem of how much prediction models rely on specific covariates to achieve their accuracy. The authors emphasized that existing variable importance measures do not account for the fact that multiple prediction models can fit the data equally (or near-equally) well, a phenomenon labeled the “Rashomon Effect” (introduced into statistics by Breiman (2001b) as the multiplicity of good models that may consider the predictors in different ways).

Consider the random variable Z = (Y, X₁, X₂) for outcome Y and two predictors, X₁, X₂. Now, consider two independent random variates from the same distribution as Z, $Z^{(a)}=(Y^{(a)},X_1^{(a)},X_2^{(a)})$ and $Z^{(b)}=(Y^{(b)},X_1^{(b)},X_2^{(b)})$, Let f be a fixed prediction model of interest. Then the question is how much f relies on covariate X₁ to predict Y. All prediction models are considered as measurable functions f from the predictor space $𝒳$ to the response space $𝒴$, and we may evaluate model performance using non-negative loss functions, say,$ℒ$. So in this case of two observed random variates (realizations or instances), we are interested in assessing $ℒ$ for model f if random variate (b) is considered, but with the first covariate substituted with the random variate (a). In particular we are interested in assessing the expected value, $e_{\text{switch}}(f)=\text{E}\left[ℒ\left(f,\left(Y^{(b)},X_1^{(a)},X_2^{(b)}\right)\right)\right]$, and comparing it with the expected value of the same loss without replacing the covariate: that is, $e_{\text{orig}}(f)=\text{E}\left[ℒ\left(f,\left(Y^{(b)},X_1^{(b)},X_2^{(b)}\right)\right)\right]=\text{E}[ℒ(f,Z)]$, as Z^(b) and Z follow the same distribution. From these two quantities, the model reliance (MR) is then defined as

$$\mathrm{MR}(f)\equiv \frac{e_{\text{switch}}(f)}{e_{\text{orig}}(f)},$$ (1)

although an alternative definition can be provided using the difference instead (Fisher et al., 2019, Appendix A.5). This MR has fairly intuitive interpretation: higher values of MR(f) signify greater reliance of f on the covariate swapped (X₁ in this case).

In terms of estimation, if we assume observations ${\mathbf{Z}}^{(i)}=(Y^{(i)},X_1^{(i)},X_2^{(i)})$, i = 1, … , n, then e_orig(f) can be inferred from a sample mean of the loss function across the observations,

$${\widehat{e}}_{\text{orig}}(f)=\frac{1}{n}\sum _{i=1}^nℒ\left(f,{\mathbf{Z}}^{(i)}\right),$$

whereas e_switch(f) can be estimated by considering the sample mean of the loss functions evaluated at all permutations where the first covariate is swapped with other observations:

$${\widehat{e}}_{\text{switch}}(f)=\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j\ne i}ℒ(f,(Y^{(j)},X_1^{(i)},X_2^{(j)})).$$

Then, MR(f) can be estimated by considering the ratio of these two estimates. As both estimates are U-statistics, unbiasedness and asymptotic normality can be retrieved with some mild conditions of finite moments (Fisheretal., 2019).

2.1.1 |. Feature perturbation

Feature shuffling is useful, but can be difficult to implement in some cases (e.g., with time-dependent features). A related, but simpler, alternative is to consider perturbing features in a systematic way to determine their influence. This intuitive idea has long been used in modeling nonlinear systems (sensitivity analysis; e.g., Werbos, 1982) and in regression diagnostics (covariate perturbation; e.g., Cook & Weisberg, 1991). More recently, this approach has been used in deep neural modeling to increase explainability (feature perturbation; e.g., Hassan et al., 2021; Wang et al., 2020; Wickramasinghe et al., 2021).

The idea is quite simple. Our interest is in explaining the importance of particular features in the prediction of our response. That is, we consider the effect of input features, X, on a response Y given a fitted model, $\widehat{f}(X,\theta )$, with parameters θ. One way to do this is simply to see how much the predicted response, $\widehat{Y}$, changes as the fitted model is interrogated with perturbed features, where the features are perturbed by adding some value to one feature (or group of features) at time. The added value can be a random draw from an appropriate distribution, or may simply be an additive constant (e.g., one standard deviation). A prediction summary, such as mean square error (MSE), is calculated for the predictions from the perturbed input, say MSE_pert, and for the predictions from the unperturbed input, say MSE_pred. One can then calculate model reliance metrics as in Equation (1). It is often useful to plot these metrics. For example, differences or ratios of the prediction metrics can be plotted as function of the feature label to visualize the impact of each feature. In the context of spatial predictors, one would simply visualize the ratio of prediction metrics as a function of location (e.g., see Section 5.3).

2.2 |. Local interpretable model-agnostic explanations (LIME)

The LIME approach to model explainability was developed by Ribeiro et al. (2016). The most important aspect of LIME is the surrogate model. Generally, a surrogate model is a model that emulates a complex black-box model. A local surrogate model is one that only needs to emulate the black-box model in local areas of the data’s input/output space. LIME trains many local surrogate models in order to explain individual predictions rather than a more global surrogate model. For this to work, the local surrogate models must perform similarly to the black-box model in the neighborhood of each input output pair being explained. This is sometimes referred to as “local faithfulness.” Thus, it is important how the surrogate models are trained. Similar to the notions of feature shuffling described in Section 2.1, the LIME procedure builds local surrogates by first perturbing the dataset to get the black-box predictions for the data points one is interested in explaining. These perturbed samples are weighted according to their proximity to the data point of interest. Then, one trains a weighted, interpretable model, such as a linear regression, on the perturbed data set, where the black-box predictions are used as the response. Finally, the prediction can be explained by interpreting this fitted local model. Molnar (2022) provides an accessible introduction to LIME.

Specifically, LIME taps the decision making process of the black-box model to generate a measure of the relative positive/negative importance assigned by the model to each of the features that enters its decision making process. Ribeiro et al. (2016) give the following examples distinguishing between features and interpretable data representations: the presence/absence of particular words (in contrast with the less easily humanly understandable features like word embeddings) in text classification problems, and the presence/absence of a contiguous patch of similar pixels (while the classifier may be representing the image as a tensor with three color channels per pixel) in image classification problems. LIME generates explanations by approximating the model ($f:{ℝ}^d\to ℝ$; e.g., a neural net model) locally with an interpretable model ($g:{ℝ}^{d^{\prime }}\to ℝ$; e.g., a linear model) and repeating this for several individual representative predictions to provide a global understanding. It learns an interpretable model locally around the prediction. The method itself is summarized below using the same notation as in Ribeiro et al. (2016). The explanation provided by LIME is obtained by the following formulation:

$$\xi (x)=\arg \underset{g\in G}{\min }ℒ\left(f,g,{\pi }_x\right)+\mathrm{\Omega }(g).$$ (2)

Here, the class of potentially interpretable models G (e.g., the class of linear models such that g(z^′) = β_g z^′), fidelity functions $ℒ$ (locality-aware loss, where π_x represents the locality function; see below), and complexity measures Ω(g) may be chosen suitably and the search may be conducted, using perturbations. For $x\in {ℝ}^d$ in the original representation of an instance being explained and $x^{\prime }\in {\{0,1\}}^{d^{\prime }}$ a binary vector denoting an interpretable representation of x, the domain of g is ${\{0,1\}}^{d^{\prime }}$. That is, g acts over the presence/absence of interpretable components. Every g ϵ G may not be simple enough to be interpretable and the complexity measure Ω(g) is a penalty for complexity (e.g., the time needed to compute f(x) along with the number of samples examined, the number of non-zero weights in the case of linear models, etc.). An example for the locality-aware loss function $ℒ$ (a measure of how unfaithful g is in approximating f in the locality defined by π_x(z)) is

$$ℒ\left(f,g,{\pi }_x\right)=\sum _{z,z^{\prime }\in 𝒵}{\pi }_x(z){\left(f(z)-g\left(z^{\prime }\right)\right)}^2,$$

with weight π_x(z) = exp(−D(x, z)²∕σ²), where D is a suitable distance function between observations in data space, σ is a width measure, and z and z^′ are set as follows. For an instance x, instances around x^′ are sampled by drawing non-zero elements uniformly at random (with the number of such draws also uniformly sampled) to get a perturbed sample $z^{\prime }\in {\{0,1\}}^{d^{\prime }}$ from which the sample in the original representation $z\in {ℝ}^d$ is obtained and f(z) determined. Note that f(z) is called a label for the explanation model. Given the dataset $𝒵$ of perturbed models and their associated labels, Equation (2) may be optimized to get an explanation ξ(x). The coefficients of the linear model, β_g, are recovered by weighted linear regression.

In practice, N “perturbed” samples $z_i^{\prime }$, i = 1,2, … , N are drawn from x^′, the interpretable version of the instance x being explained. The “perturbed” instances are recovered in the original feature space as z. The labels f(z) are generated and hence the explanation. Note that the choice of G, such as sparse linear models, means that if the underlying model is highly non-linear, even in the locality of the prediction, LIME may not return a faithful explanation.

LIME has only recently started to be used in environmental and ecological applications (e.g., Cha et al., 2021; Ryo et al., 2021; Taconet et al., 2021).

2.3 |. Shapley values

The Shapley value, coined by Shapley (Roth, 1988; Shapley, 1953), is a metric from game theory for assigning credit to players in a fair manner depending on their contribution to the total payout from a game. In the game-theoretic context, “players” cooperate in a coalition and receive a certain profit from this cooperation. The use of Shapley values for features in models such as regression or machine learning is a more recent development, with the first connection being the work of Lipovetsky and Conklin (2001) (starting in 1998 and leading up to this article), the proposal for use in some machine learning models by Cohen et al. (2005), and a full generalized model development in the form used in current software packages by Štrumbelj and Kononenko (2014). This work led to the development of the SHAP package for Python (Lundberg & Lee, 2017), which also has an R wrapper (Maksymiuk et al., 2020), leading to widespread use. Work continues on adaptation and expansion of the method (e.g., Merrick & Taly, 2020) and the values themselves are widely used in applied machine learning areas such as: medicine (e.g., Ibrahim et al., 2020; Smith & Alvarez, 2021), chemistry and pharmaceutical research (e.g., Rodríguez-Pérez & Bajorath, 2019, 2020), and economics (e.g., Antipov & Pokryshevskaya, 2020), among many others.

Shapley values were proposed for use in learning models for quantification of the contribution of each feature value to the prediction, as compared to a baseline of the average prediction. When considering classical linear models (i.e., linear or generalized linear), such quantification is simple: each feature is the product of the weight of the feature and the value of the feature, due to the linearity of the model. Black-box models such as neural networks are more complex (e.g., non-linear regression analogues), and this simple quantification does not work. To connect the game-theoretic context to machine learning predictions for interpretability, consider the “game” as a prediction task for a single instance of the dataset. The corresponding “gain” is the actual prediction for this instance minus the average prediction for all instances, and the “players” are the feature values of the instance that collaborate to receive the gain (i.e., predict a certain value).

As in Štrumbelj and Kononenko (2014), we may formally define the contribution of p different features relative to a model’s average prediction conditional on a subset Q of feature values being known: f_Q(x) = E[f|X_i = x_i, i ϵ Q], for Q ⊆ S = {1 2 … p} any subset of features and f the model. This then provides the contribution of a subset, namely: Δ_Q(x) = f_Q(x)− f_{}(x), the difference of the contribution of set Q as compared to the empty set. This is the change in prediction for a model connected to the observation of the values of a subset Q of features. Mapping back to the linear contribution approach valid for additive models requires mapping 2^p terms into p total contributions, one for each feature’s value. Adding defined interactions, the authors then give the explicit definition (proved in Štrumbelj & Kononenko, 2010):

$${\varphi }_i(x)=\sum _{Q\subseteq S\backslash \left\{i\right\}}\frac{\left|Q\right|!(|S|-|Q|-1)!}{\left|S\right|!}\left({\mathrm{\Delta }}_{Q\cup \left\{i\right\}}(x)-{\mathrm{\Delta }}_Q(x)\right),$$ (3)

which is equivalent to the Shapley value (Shapley, 1953). Generally speaking, the p features have a “grand coalition” that has a certain “worth” (predictive power), Δ_S. We are (from above) able to determine how much each subset coalition is worth (Δ_Q). The goal is to distribute the prediction among the features in a fair way, taking into account all sub-coalitions (subsets of features). Shapley values are one such solution, satisfying certain desirable properties—they are a partition; the contributions are normalized; any feature with no impact on prediction is assigned a zero contribution; and local contributions are additive.

Practically, Equation (3) is exponential in complexity, making it impractical for use on interesting data sets of reasonable feature set size. Štrumbelj and Kononenko (2014) detail a computational approximation in a form of Monte Carlo integration, and also propose the use of quasi-random sampling (for the variance on the estimate of the Shapley value see Molnar, 2022). They further adapt the number of samples drawn for each feature relative to the feature’s variance, keeping approximation error consistent across features despite differing population variances. These improvements are included in the Maksymiuk et al. (2020) and Lundberg and Lee (2017) implementations for R and Python. In model-building, Shapley values are useful for assigning weight (worth, as discussed above) to elements of a model, allowing an analyst to determine which elements, components, or aspects of a black-box model are most important to the predictive power of the model. Note that packages used for the estimation of Shapley values may use methods that are model-specific. For example, Aas et al. (2021) propose packages that take dependence into account for several models with various degrees of feature dependence. In the case of regression, the Shapley value and the Owen value reflect the average marginal contribution of individual regressor variables and individual groups of regressor variables to R², respectively (Hüttner & Sunder, 2011).

3 |. ENVIRONMENTAL DATA EXAMPLE: LONG-LEAD FORECASTING OF SOIL MOISTURE

Soil moisture is an important driver of processes such as agricultural production, wildfire intensity, and hydrological runoff, to name a few. Thus, for management purposes, it can be useful to have skillful long-lead forecasts of anywhere from 3 months to a year in advance. Here, “skillful” refers to showing improvement over a baseline model (see Section 5.1 for a formal definition). Successful long-lead forecasts are usually tied to the longer-time scale dynamics of the ocean, and the long-distance atmospheric teleconnections induced by anomalous heating or cooling at the ocean surface. In the context of the Pacific Ocean, this is most represented by the El Niño—Southern Oscillation (ENSO) phenomenon, a quasi-periodic variation in anomalously warmer than normal ocean states in the central and eastern tropical Pacific Ocean (El Niño) and colder than normal ocean states in the central tropical Pacific (La Niña). As has been known for quite some time, ENSO can serve as an effective predictor of atmospheric-derived conditions in North America and Oceania because of the associated teleconnection-based changes in the atmospheric circulation (e.g., Philander, 1990). Operationally, it has been demonstrated for nearly three decades that skillful long-lead forecasts based on statistical models that incorporate this relationship are as good as, and typically better than, deterministic models (e.g., Barnston et al., 1999; van Oldenborgh et al., 2005). Although linear models can be skillful in these settings (e.g., Penland & Magorian, 1993), nonlinear statistical methods often perform better than deterministic forecast models at least for some spatial regions and lead times (e.g., see the overview in McDermott and Wikle (2019) for references).

Here we consider long-lead soil moisture (SM) forecasts with lead times of 3 months, with a particular emphasis on predictions in the US corn belt in May given observations up to the previous February. We focus on SM forecasts because it is well-known that the amount of SM available to corn (and other crops) at certain phases of their phenology can significantly affect yield, and thus is of major interest to producers (e.g., Carleton et al., 2008). In addition, McDermott and Wikle (2016, 2019) showed that nonlinear spatio-temporal analog forecasts and deep echo state networks can yield skillful long-lead predictions for May across some regions of the corn belt (also, note that the US Climate Prediction Center produces seasonal outlooks (forecasts) for soil moisture¹).

We use monthly SSTA in the Pacific Ocean region from 124E to 70W (every 2°) longitude and 30S to 60N (every 2°) latitude for the period January 1948–December 2021, where the anomalies are location-specific, based on deviations from the monthly climatology for the period 1971–2000. The data were obtained from the IRI/LDEO Climate Data Library²; specifically, the “NOAA NCDC ERSST version5: Extended Reconstructed SST” data as described in Huang et al. (2017)³. For SM, we extract monthly North America data but focus on the US corn belt region, here defined from 101.5W to 80.5W (every 0.5°) longitude and 35.5N to 48.5N (every 0.5°) latitude) for the period January 1948–December 2021. These data were also obtained from the global monthly high resolution soil moisture dataset originally produced by the Climate Prediction Center as described in Fan and Van Den Dool (2004)⁴.

Summary statistics for the data are given in Table 1. As described in the Supporting Information section, all of the data used in the analyses presented below can be found on Zenodo (Simmons & Burr, 2022). The analysis code can be found on GitHub (Boone et al., 2022). This code provides details regarding normalization/standardization, preprocessing, input and output of the various models, and model architecture.

TABLE 1.

Summary statistics for the data sets used to demonstrate the explainable AI methods in this article: Sea Surface Temperature anomalies (SSTA) in the Pacific Ocean, and soil moisture (SM) in the central continental United States.

	Sea surface temperature
Summary statistic	Anomalies (SSTA) (°C)	Soil moisture (SM) (mm)
Total number of locations	3186	1125
Region	Pacific Ocean region	US corn belt
Latitude range	30S to 60N	35.5N to 48.5N
Longitude range	124E to 70W	101.5W to 80.5W
Resolution of data grid	2 deg × 2 deg	0.5 deg × 0.5 deg
Year range	1948–2021	1948–2021
Training data	1948–2013	1948–2013
Test data	2013–2021	2013–2021
Mean	0.00522	325.198
Median	−0.0116	328.431
Standard deviation	1.153	158.514
Skew	19.113	0.0411
Kurtosis	893.75	−0.885
Number of data-points	3186 × 888	1125 × 888

4 |. MODEL-BUILDING METHODS

In this section, we describe briefly several models and model-building methods that we use to illustrate the explainability methods described above. We also describe some of the implementation decisions for these methods, but leave the details to the implementations in Section 5. First, we describe a spatial functional linear regression model to serve as a baseline, followed by the machine learning models that we will use to demonstrate the utility of the explainability approaches. There are a very large number of possible candidate models, so this set of models is a non-comprehensive convenience choice rather than an exhaustive coverage of all possible application areas, combinations of models, and explainability methods.

4.1 |. Spatial functional linear regression

As a baseline, we consider a linear statistical model as a candidate that is rich enough to capture the main features of the data while retaining the simple interpretability of linear models. A naive linear model for predicting SM using the 3-month lagged SSTA data is given by

$$Y_t=\alpha +\sum _{s=1}^S\beta (s)X_{t-3}(s)+{ϵ}_t,$$ (4)

where Y_t is the SM at a land location at time t, X_t−3(s) is the 3-month lagged SSTA data at sea location s, α is the intercept, β(s) is the regression coefficient corresponding to lagged SSTA data at sea location s for predicting SM at the specified land location, and ϵ_t are errors.

The naive model in Equation (4) has multiple shortcomings. Most importantly, it does not account for the spatial structure in the covariates {X_t−3(s) : s = 1, … , S} by treating them as separate independent predictors as opposed to treating them as one predictor surface. Since SSTA is observed at S = 3186 locations, this leads to an over-parametrized model with S = 3186 unknown parameters. Since there are on the order of 800 training data-points (66 years of monthly data in the training period) for each land location and S = 3186 parameters, the linear model becomes unidentifiable and requires some dimension reduction or regularization.

Machine learning methods like CNNs (see Section 4.4) explicitly accommodate this dimension reduction by accounting for the spatial nature of the covariates. That is, CNNs achieve this by treating {X_t−3(s) : s = 1, … , S} as an image and subsequently uses block convolution with shared weights and pooling to reduce dimensionality of the predictor and parameter space. The key observation for such dimension reduction in CNNs is that the functional relationship connecting the SSTA X_t−3(s) to SM Y_t should be similar for nearby locations s because SSTA exhibits spatial dependence. Thus, we consider a functional regression model that uses the same principles within the linear setting by assuming that the β(s) for nearby locations s should be similar. This ensures dimensional reduction while retaining the interpretability of the linear model. Specifically, we treat {X_t−3(s) : s = 1, … , S} as a single spatial surface (a function in two-dimensional Euclidean space) instead of as 3186 separate predictors, and consider the traditional functional linear model

$$Y_t=\alpha +\rho Y_{t-3}+\sum _{m=2}^{12}{\eta }_m+\int \beta (s)X_{t-3}(s)ds+{ϵ}_t,$$ (5)

where β(s) is now a coefficient function on the ocean locations connecting the functional SSTA data to the SM outcome. This is analogous to the transition operator in integro-difference equation (IDE) models for spatio-temporal processes (e.g., see the review in Wikle et al., 2019) and integral projection models used in ecology (e.g., Merow et al., 2014). Additionally, the 3-month lagged SM Y_t−3 is included in (5) to account for auto-correlation, while the η_m are introduced as month-specific intercept parameters to account for periodicity.

As is common in functional regression and IDE models, dimension reduction in Equation (5) is accomplished by expanding the coefficient function β(s) in terms of basis function coefficients as $\beta (s)={\sum }_{k=1}^K{\gamma }_k{\varphi }_k(s)$, where {ϕ_k(·)|k = 1, …, K} is a set of basis functions appropriate for the analysis. Because K ≪ S = 3186, this achieves considerable dimension reduction as the model can now be written as a linear model in terms of the unknown γ_k’s

$$Y_t=\alpha +\rho Y_{t-3}+\sum _{m=2}^{12}{\eta }_m+\sum _{k=1}^K{\gamma }_k\int {\varphi }_k(s)X_{t-3}(s)ds+{ϵ}_t=\alpha +\rho Y_{t-3}+\sum _{m=2}^{12}{\eta }_m+\sum _{k=1}^K{\gamma }_k{X}_{t-3,k}^{*}+{ϵ}_t,$$ (6)

where for the given choice of bases ϕ_k(s), ${\varphi }_k(s),X_{t-3,k}^{*}$ can be pre-computed as $\int {\varphi }_k(s)X_{t-3}(s)ds\approx \frac{1}{s}{\sum }_{s=1}^S{\varphi }_k(s)X_{t-3}(s)$. Thus, the functional linear regression in Equation (6) becomes the traditional multiple linear regression in the parameters α,{η_m m = 2, …, 12}, and {γ_k| k = 1, … , K}. This facilitates easy implementation of the model while accommodating the important aspects of the data (e.g., spatially structured covariates, autocorrelation, and periodicity). Interpretability is also straightforward in the linear paradigm. The effect of the lagged sea surface temperature X_t−3(s) on the soil moisture data can be assessed by simply looking at the estimate $\widehat{\beta }(s)={\sum }_{k=1}^K{\widehat{\gamma }}_k{\varphi }_k(s)$. This is demonstrated in Section 5.1.

While the functional linear model offers direct interpretability on the importance of SSTA at each ocean location s via the coefficient surface $\widehat{\beta }(s)$, we can also compute more model-free measures of feature importance. We calculated the model reliance (MR) of the functional linear model using Equation (1) in Section 2.1 as follows. Let z_t denote the set of all covariates used to predict SM Y_t at hold-out time t. For the linear model, z_t includes an autoregressive term, month indicators and 3-month lagged SSTA. Let f denote the fitted linear model that takes the covariates z_t and predicts Y_t. Let $Z_{\text{out}}={(z_1^{\prime },z_2^{\prime },\dots ,z_{T_{\text{out}}}^{\prime })}^{\prime }$ denote the full matrix of features for the hold-out dataset and $Y_{\text{out}}={\left(Y_1,\dots ,Y_{T_{\text{out}}}\right)}^{\prime }$ denote the hold-out SM data where 1, … , T_out denotes the time-points in the hold-out data. The denominator e_orig in MR is calculated as

$$e_{\text{orig}}=\frac{1}{T_{\text{out}}}\sum _{t=1}^{T_{\text{out}}}{\left(Y_t-f\left(z_t\right)\right)}^2=\frac{1}{T_{\text{out}}}{\Vert Y_{\text{out}}-f\left(Z_{\text{out}}\right)\Vert }_2^2\text{.}$$

This yields e_orig for one land location in the corn-belt. Repeating this process on the SM data for each of the land locations in the corn-belt and averaging yields the overall e_orig. This is simply the MSPE over the entire hold-out time-period and over all the locations in the corn-belt.

To calculate e_switch we use eq. (3.3) of Fisher et al. (2019). Due to computational demands, instead of calculating MR for each SSTA location s, we calculate MR for sets of SSTA locations that are in the same cluster. For a cluster c, let z_c,t denote the subset of z_t that corresponds to the SSTA locations s in cluster c and z_−c,t denote the rest of the covariates for that time. Without loss of generality, we write $z_t^{\prime }=\left(z_{c,t}^{\prime },z_{-c,t}^{\prime }\right)$. For hold-out time t₀ and cluster c, we then create a shuffled covariate set $z_{\text{switch},t}^{\prime }\left(c,t_0\right)=\left(z_{c,t_0}^{\prime },z_{-c,t}^{\prime }\right)$. Stacking $z_{\text{switch},t}^{\prime }\left(c,t_0\right)$ for t = 1, 2, … , t₀ − 1, t₀ + 1, … , T_out we have our shuffled covariate matrix Z_switch(c, t₀) (note that t = t₀ is excluded). Now, e_switch for cluster c and time point t₀ can be calculated as

$$e_{\text{switch}}\left(c,t_0\right)=\frac{1}{T_{\text{out}}-1}\sum _{t\in \left\{1,\dots ,T_{\text{out}}\right\},t\ne t_0}{\left(Y_t-f\left(z_{\text{switch},t}\left(c,t_0\right)\right)\right)}^2=\frac{1}{T_{\text{out}}-1}{\Vert Y_{\text{out},-t_0}-f\left(Z_{\text{switch}}\left(c,t_0\right)\right)\Vert }_2^2,$$

where Y_out,−t0 denotes the vector Y_out with the data point for time t₀ removed. We repeat and average over all hold-out time points to obtain

$$e_{\text{switch}}(c)=\frac{1}{T_{\text{out}}}\sum _{t_0=1}^{T_{\text{out}}}{e}_{\text{switch}}\left(c,t_0\right)=\frac{1}{T_{\text{out}}}\frac{1}{\left(T_{\text{out}}-1\right)}\sum _{t_0=1}^{T_{\text{out}}}{\Vert Y_{\text{out},-t_0}-f\left(Z_{\text{switch}}\left(c,t_0\right)\right)\Vert }_2^2.$$

Finally, we repeat this over all the land locations in the corn-belt and average to get the overall e_switch(c). The MR for cluster c is then calculated as the ratio of e_switch(c) and e_orig.

4.2 |. Extreme gradient boosting

We consider machine learning boosting trees to demonstrate the Shapely value explainability method in Section 5.2. Boosted trees, originally developed by Freund and Schapire (1996) and expanded upon by Friedman (2001), are ubiquitous in modern data analysis. The idea is to create a committee of weak learners in the form of shallow trees to learn the signal in the data. The trees are sequentially created such that each new tree created is based on residuals from previous learners. Each new tree builds upon the information from the previous trees and slowly improves the prediction. The success of the algorithm is dependent upon identifying features that appropriately capture the information in the data and the hyperparameters defining the algorithm. One of the most popular implementations of gradient boosted trees was developed by Chen and Guestrin (2016) in their eXtreme Gradient Boosting (XGBoost) algorithm. This algorithm has been shown to be fast and efficient with good predictability (for example, XGBoost was used by most of the top 10 teams in the 2015 KDDCup competition) and has been implemented in several environmental studies (e.g., Liu et al., 2022; Ma et al., 2021; Zhang et al., 2020). Although there are many hyperparameters that can be tuned (see Xgboost Developers, 2021, for a complete list), we list a few of the most impactful ones in Table 2.

TABLE 2.

Some of the important parameters that are controllable by the analyst in the XGBoost algorithm implementation in Python and R.

Parameter	Description
booster	The booster defines the overall structure of the model. The gbtree and dart boosters are tree-based models and the gblinear booster uses linear functions; the default is gbtree.
Eta or learning_rate	This specifies the rate at which the boosting model is allowed to learn (i.e., it is the shrinkage imposed on tree’s nodes as they are added to the model). The value for the learning rate is between 0 and 1, where 1 does not impose any penalty. Usually, the learning rate is less than 0.3; the default is 0.3.
max_depth	This specifies the maximum depth each tree in the ensemble is allowed to grow. Allowing trees to go too deep will overfit the data. This parameter is usually between 4 and 6, with the default at 6.
nrounds	This specifies the number of trees in the ensemble of trees.
objective	There are various objective or loss functions that can be specified; the default is squared error loss.
Gamma	This parameter prevents overfitting by setting a minimum loss reduction threshold that must be met in order to further partition a leaf node. The larger Gamma is, the more conservative the algorithm is. Gamma ranges from 0 to infinity; default is 0.
Lambda	The L2 regularization term on weights. Larger values will make algorithm more conservative; default is 1.
min_child_weight	This is the minimum sum allowed in order for a tree to be further partitioned. The algorithm will not allow a partition to occur if the sum of the instance weights are lower than this threshold; default is 1.
Sampling	The XGBoost algorithm allows various ways to sample from the data to train the model. For example, subsample allows one to sample observations in the creation of the trees, while colsample_bynode is one of the options that samples features.

4.3 |. Artificial neural networks

Artificial neural networks (ANNs) date back to the development of the perceptron (Rosenblatt, 1958) and multiple-layer networks to Ivakhnenko and Lapa (1967), although their use stagnated until computer architectures developed sufficiently to allow them to be fit in practice. Since the availability of GPU processing (circa 2009), ANNs have been increasingly used for predicting or classifying complex datasets such as images, text and other phenomena (e.g., Zou et al., 2008). These models are often what one thinks of when hearing the phrase “artificial intelligence” as they are associated with deep neural networks, deep learning and so forth. ANNs are nonlinear mathematical models inspired by the structure of the human brain with a network of layered hidden units (neurons) that transform information at each layer and pass it onto the next layer (e.g., see the statistics-friendly review in Fan et al., 2021). This structure allows for data with complex relationships to be fit and predicted. The biggest criticism of these models is that the parameters (weights) that govern the model are not readily interpretable given there are so many of them and they are not uniquely identifiable.

ANNs have been used extensively in environmental research. For example, Rahimikhoob (2010) considered estimating solar radiation in semi-arid environments, Amaratunga et al. (2020) and Guo et al. (2021) used ANNs to predict rice paddy production based on climate data, Dogan et al. (2008) used ANNs to predict groundwater level using climate data, and many authors have used ANNs for air pollution modeling and monitoring (e.g., Alimissis et al., 2018; Araujo et al., 2020; Cabaneros et al., 2019; Pawul & liwka, 2016).

To specify an ANN for the examples presented here we use the following notation:

$$\text{ANN}(\text{Input}\text{Size},\text{Nodes}\text{Layer}{1}_{a{f}_1},\text{Nodes}\text{Layer}{2}_{a{f}_2},\dots ,\text{Nodes}\text{Layer}{k}_{a{f}_k},\text{Output}\text{Size}),$$

where af_i corresponds to the activation (transfer) functions employed in all nodes for layer i. There are many choices for activation functions (e.g., Abadi et al., 2015; Zou et al., 2008). The models used in this article use hyperbolic tangent (tanh) and linear (lin) activation functions. All ANNs were fit using the Keras package (Chollet, 2015) for Tensor-flow (version 2.4.0, Abadi et al. (2015)) with a mean square error objective function and the Adam, optimizer using Python 3.8.8. For smaller models, 1000 epochs⁵ were used for training, and for larger models, 2000 epochs were used. We demonstrate the feature perturbation explainability approach (Section 2.1.1) with ANNs in Section 5.3. Training details and application-specific details are given there.

4.4 |. Convolutional neural networks

Convolutional neural networks (CNNs) are regularized ANNs, originally designed to analyze visual imagery or spatial data. Their first appearance in the literature can be dated back to 1980s and early 1990s (Fukushima & Miyake, 1982; Waibel et al., 1989; Zhang et al., 1988; Zhang et al., 1990). These earlier forms of CNNs were largely inspired by the physiological work of Hubel and Wiesel (1968). CNNs experienced a similar stagnation as ANNs due to computational challenges with their implementation, including the large computational complexity and vanishing gradients (Goodfellow et al., 2016). These problems have been solved by the use of ReLU activation functions (Krizhevsky et al., 2017) and availability of advanced GPUs (Steinkraus et al., 2005). Since the early 2010s, CNNs have been used for a wide range of image classification (e.g., Ciregan et al., 2012) and video analysis (e.g., Ji et al., 2012) problems. CNNs are frequently used in environmental research because of their ability to extract informative features from spatial data, which are common in environmental sciences (e.g., Anderson & Radio, 2022; Kattenborn et al., 2021; Pan et al., 2019; Wang et al., 2021). In addition, CNNs have been employed to predict ground water potential maps from ground water conditioning factors by Panahi et al. (2020), and in real-time prediction of particulate matter in the atmosphere (Chae et al., 2021).

A typical CNN consists of two parts: (i) a feature extraction part composed of alternating convolutional and pooling layers; and (ii) a nonlinear regression part with the standard ANN layers (see the overview in Fan et al., 2021). A convolutional layer takes images or spatial data as input and generates multiple feature maps as output through convolution using filters (weights). Unlike classical approaches, the filters used for convolution are estimated based on training data, rather than pre-specified as one of the commonly used basis functions such as the radial basis functions. The generated feature maps are then supplied to pooling layers, which conduct downsampling by partitioning the feature map into sub-regions and finding a summary value (such as the average or the maximum value) within each partition. At the end of the final feature extraction part, all the feature maps are collected and vectorized into one long vector and then supplied to the final ANN layers.

In this article, a CNN model was trained with scaled input and output data for the SM forecast problem. LIME (Section 2.2) and Shapley values (Section 2.3) were used to evaluate the impact of each input location of SSTA on the SM output locations with respect to the trained model. As described above, this problem considers a 3 month lead-time prediction. SSTA data are mapped onto a 46 × 84 grid, with zero padding for locations that do not have associated data (e.g., land locations for SSTA data). The data are then flattened (vectorized) before being input into the model and reshaped back internally in the model. This is to aid the LIME and Shapley value calculations. All hidden layers in the model use a tanh for the activation function. A sigmoid is used as the activation function for the output layer as the output (soil moisture) values are normalized between 0 and 1. A dropout layer is included before each dense layer (used only during training). The full network structure is given in Table 3. The model is compiled with mean square error as the loss function and with the Adam optimizer (Kingma & Ba, 2015). We also consider a CNN model with both SSTA and lagged SM as inputs. The structure of this model is shown in Figure 1.

TABLE 3.

Network structure corresponding to type of input layer, shape of the output from each layer, and the number of parameters associated with each layer of the CNN model which takes SSTA as input.

Layer (type)	Output shape	Parameters
reshape (Reshape)	(None, 46, 84)	0
lambda (Lambda)	(None, 46, 84, 1)	0
conv2d (Conv2D)	(None, 46, 84, 64)	320
average_pooling2d	(None, 23, 42, 64)	0
(AveragePooling2D)
conv2d_1 (Conv2D)	(None, 23, 42, 16)	4112
average_pooling2d_1	(None, 11, 21, 16)	0
(AveragePooling2D)
flatten (Flatten)	(None, 3696)	0
dropout (Dropout)	(None, 3696)	0
dense (Dense)	(None, 2250)	8,318,250
dropout_1 (Dropout)	(None, 2250)	0
dense_1 (Dense)	(None, 1125)	2,532,375

FIGURE 1.

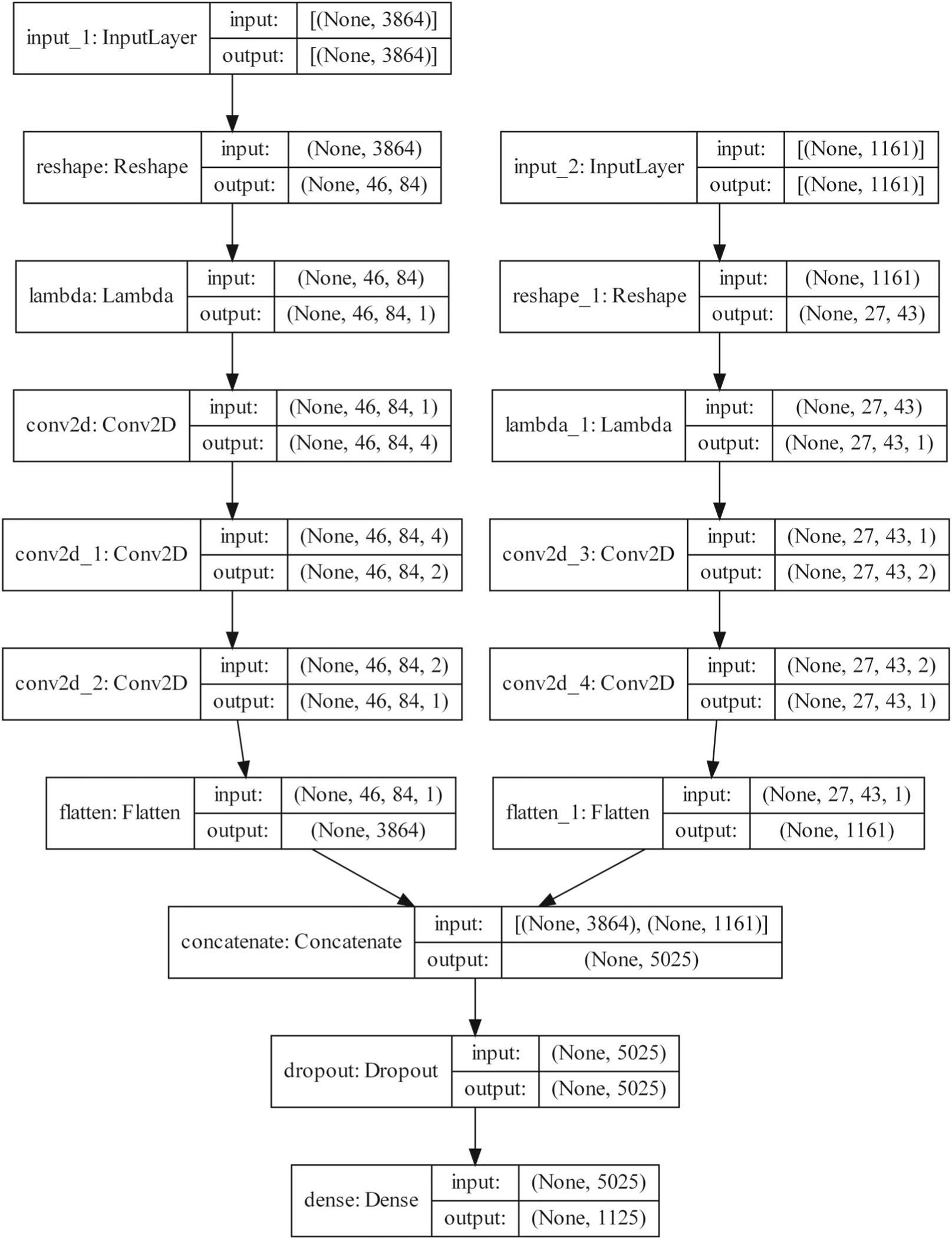
Network structure of the CNN model which takes SSTA and SM as inputs.

4.5 |. Reference approaches and model comparison metrics

In addition to the statistical and machine learning approaches described above, we also consider two simple approaches for prediction that serve as baselines for evaluating the performances of the more sophisticated algorithms. As the most basic prediction approach, we consider the SM prediction at a location simply to be the SM value at that location 3 months before. This is known as a “persistence” forecast and is a common reference forecast in climate forecasting (e.g., Wilks, 2011). The second reference method we consider is simply predicting the SM at each location by the monthly average of SM for that location based on the entire training data. This type of forecast is referred to as “climatology”.

We compare all the models based on the hold-out performance of the model forecasts for two test sets—the entire hold-out data, and more specifically, for the month of May in all of the years of the holdout period as described in Section 3. We present both mean square prediction error (MSPE) and test R² (i.e., the R² when the predicted SM is regressed on the true SM). Additionally, we also look at the skill score that compares a predictive metric for a model of interest to that from a reference model (see Wikle et al., 2019, for a general formulation). The skill score compares the MSPE between the reference model (MSPE_ref) and the statistical or machine learning model M of interest (MSPE_M) as Skill Score = (MSPE_ref − MSPE_M)∕MSPE_ref. We will use the persistence predictions as the reference for the skill score to assess the predictive performance of the other statistical and machine learning models applied in this article. Thus, models that include SSTA compared to persistence will help us understand the incremental contribution of SSTA to SM predictions relative to the lagged SM reference forecast. In this case, skill scores above zero show the model of interest has forecast skill relative to the reference, and skill scores less than zero indicate that forecasts from the model of interest have less skill than the reference.

5 |. RESULTS

The following sections show the results of applying the models and explainability methods discussed above to the problem of long-lead forecasting SM in the US corn belt given 3-month lagged SSTA in the Pacific Ocean. Table 4 summarizes the input, output, and explainability methods used for each example. Reproducible code for all examples can be found on GitHub (Boone et al., 2022).

TABLE 4.

Metadata for the spatial functional linear model (FLM), XGBoost, ANN, and CNN models: t = 1, 2, …, 12 corresponds to the index for the month for which the values are quoted; SHAP stands for Shapley value and LIME for the LIME value.

Model	Input	Output	Explainability approach
Spatial FLM	SSTAt−3, SMt−3	SMt	${\widehat{\beta }}_t\left(s\right)={\sum }_k{\gamma }_k\left(t\right){\varphi }_k\left(s,t\right),\widehat{M{R}_t}\left(c\right)={\widehat{e}}_{\text{switch}}\left(f\right)/{\widehat{e}}_{\text{orig}}\left(f\right)$
XGBoost	SSTAt−3, SMt−3	SMt	SHAPt(PCA75)
ANN	SSTAt−3	SMt	${\overline{MSE}}_t\left(s\right)={〈A{E}_{pert}/S{E}_{unpert}〉}_l$
CNN	SSTAt−3	SMt	〈SHAPt〉l(s), 〈LIMEt〉l(s)
CNN	SSTAt−3, SMt−3	SMt	〈SHAPt〉l(s), 〈SHAPt〉l(l)

As discussed in Section 3, we consider monthly predictions of SM data from the US corn belt between 35.5N and 48.5N latitude and between 101.5W and 80.5W longitude. Figure 2 (left) shows the 1125 distinct spatial locations with SM data available within this region. Data from 1948 to 2013 are used for training while data from 2014 to 2021 are used to assess model performance. Due to the use of 3-month lagged predictor variables in the models, the first 3 months of data from 1948 are not used.

FIGURE 2.

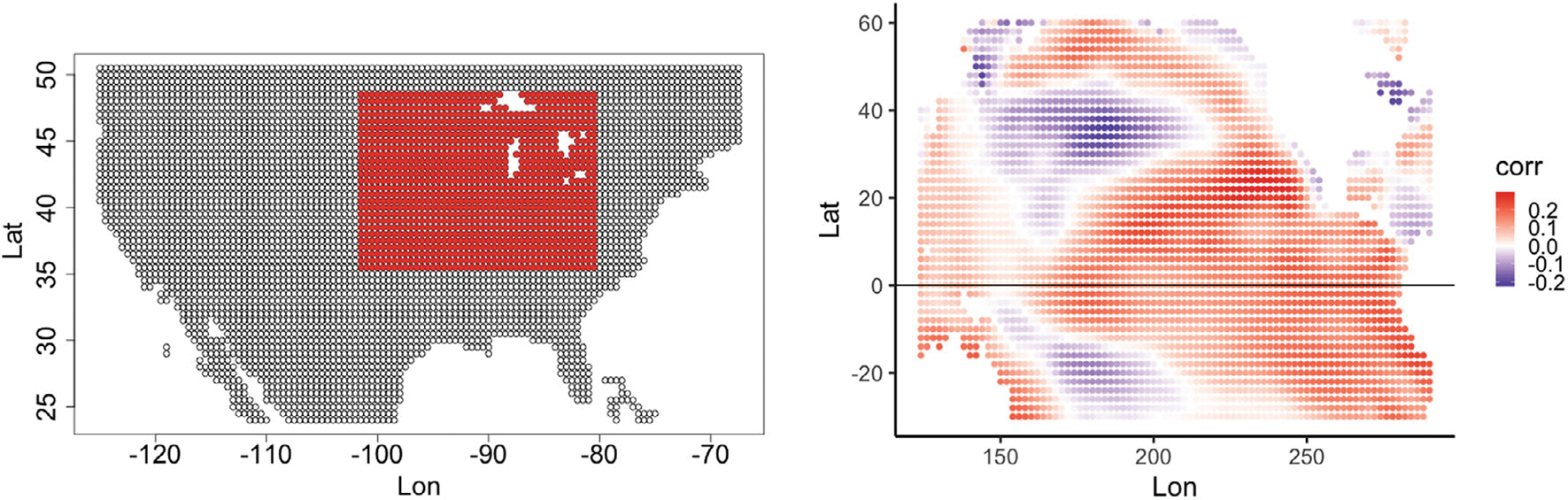
(Left) Locations (red) for the soil moisture (SM) data in the US corn belt. The white regions in the red box correspond to the Great Lakes of North America (note, the other white regions correspond to ocean locations). (Right) Average marginal correlation of 3-month lagged sea surface temperature anomalies (SSTA) at each ocean location with all of the SM data in the corn belt. The map runs from Australia in the southwest to Greenland in the northeast.

For the predictors we consider 3-month lagged SSTA. Figure 2 (right) shows the map of average marginal correlation of the 3-month lagged SSTA at each location with all of the SM data in the corn belt. We observe some regional patches of positive and negative correlations with the SM data, with highest positive correlations in the central Pacific and Northern Pacific, likely tied to the ENSO and Pacific decadal oscillations, respectively.

We first present the results of the persistence model as the forecast baseline in Table 5. We see that persistence generally offers considerably improved prediction when only restricted to May. This is not surprising given that there are years where there is little change in SM over a three-month span in the northern hemisphere spring. We also present the performance of the simple climatology forecasts in Table 5. We see that for both test sets the climatology forecasts have considerable negative skill scores with respect to persistence suggesting that seasonality alone is not sufficient in explaining the variation in the SM data.

TABLE 5.

Performance metrics (MSPE, test R², and skill score relative to the persistence forecast; see text) for the climatology, spatial functional linear model (FLM), XGBoost, ANN (Raw), ANN (PCA₆₀), ANN (Wide Raw), and ANN (Wide PCA₆₀), CNN (SSTA), CNN (SSTA, SM) forecasts of SM in the US corn belt for all months in test period (2014–2021) and for just the May months in the test period.

	All months			May months
	MSPE	Test R2	Skill score	MSPE	Test R2	Skill score
Persistence	3979	0.65	–	2562	0.83	–
Climatology	5116	0.54	−29%	4945	0.63	−93%
Spatial FLM	2252	0.79	43%	1880	0.86	27%
XGBoost	2642	0.74	34%	2519	0.82	2%
ANN (Raw)	5695	0.53	−43%	4995	0.66	−94%
ANN(PCA60)	5779	0.53	−45%	4690	0.69	−83%
ANN (Wide Raw)	6535	0.47	−64%	5856	0.34	−128%
ANN (Wide PCA60)	6299	0.45	−58%	5163	0.32	−101%
CNN (SSTA)	4862	0.55	−22%	4323	0.68	−69%
CNN (SSTA, SM)	3824	0.63	4%	3352	0.74	−31%

Note: See Section 4 for additional details about each forecast model.

5.1 |. Spatial functional linear model

As discussed in Section 4.1, a functional linear model makes a nice comparison model for the black-box machine learning models considered here because linear models are inherently interpretable, while still being more complex than simple statistical models. The model was implemented using PCA (empirical orthogonal function, EOF) basis functions (see Wikle et al., 2019, for an overview of spatial principal component/EOF analysis). The first 21 PC time series were used as inputs since they explain 80% of the variation in the SST data. From the 22nd PC onwards, every PC contributes less than 1% of the total variance explained. If considering a cutoff much higher than 80% one would need to include many more PCs. For example, 95% variance is explained by 47 PCs, leading to 60 total parameters. With only a training sample size of 790 we decided against such over parameterization. Note that other unsupervised dimension reduction procedures could be considered here as well. Indeed, machine learning approaches have been demonstrated to be superior to PCA in some environmental applications (e.g., Raza et al., 2019; Zhong et al., 2021). We focus on PCA because of their ubiquitous use in previous SSTA forecasting applications.

Figure 3 presents the scatterplot of true SM values and predictions from the functional linear model (Equation (5), Section 4.1) for the two test sets. We note that the predictions are generally better for May than for the test set spanning all months. There is no noticeable trend in the fits as a function of the year.

FIGURE 3.

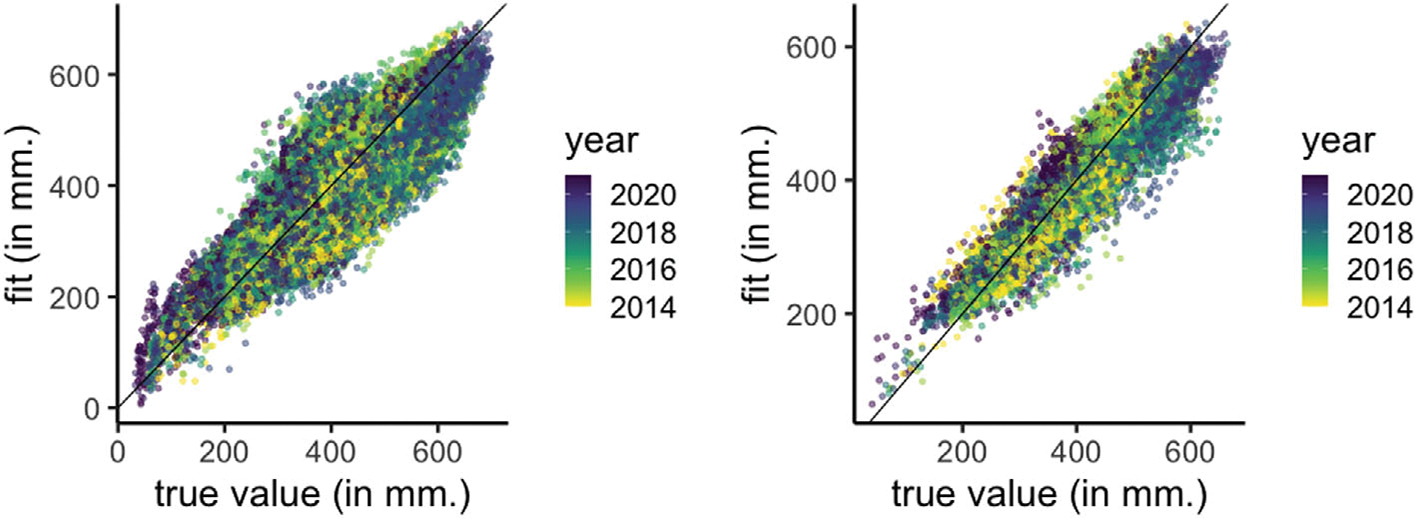
Scatterplot of true SM values and predictions from the functional linear model for the two test sets—all months (left) and May months (right).

Table 5 presents the summary metrics for the predictions. We see a 43% skill score (improvement in MSPE over that of persistence) for the functional linear model for the test set spanning all months, and the skill score for test set that only includes data from May months is 27%. The results suggest consistent improvement in the model fits from the functional linear model compared to the persistence predictions. Both the functional linear model and persistence fits are better for the months of May than when considering all months in the test set. Consequently the improvement of the functional linear model over persistence is relatively less for May as persistence predictions for May already offer a high test R² of 83% (Table 5).

Figure 4 shows maps of the MSPE from the functional linear model for each SM data location in the US corn belt. We note that when considering average MSPE over all months (left figure) the lowest MSPEs (best forecasts) are in the areas south and east of the Great Lakes and in the north west portion of the domain. When predicting only for May (right) we see again that the best forecasts are in the southeast and northwest portions of the domain, but note that MSPE is much higher for the southwest corner of the corn belt than when considering all months.

FIGURE 4.

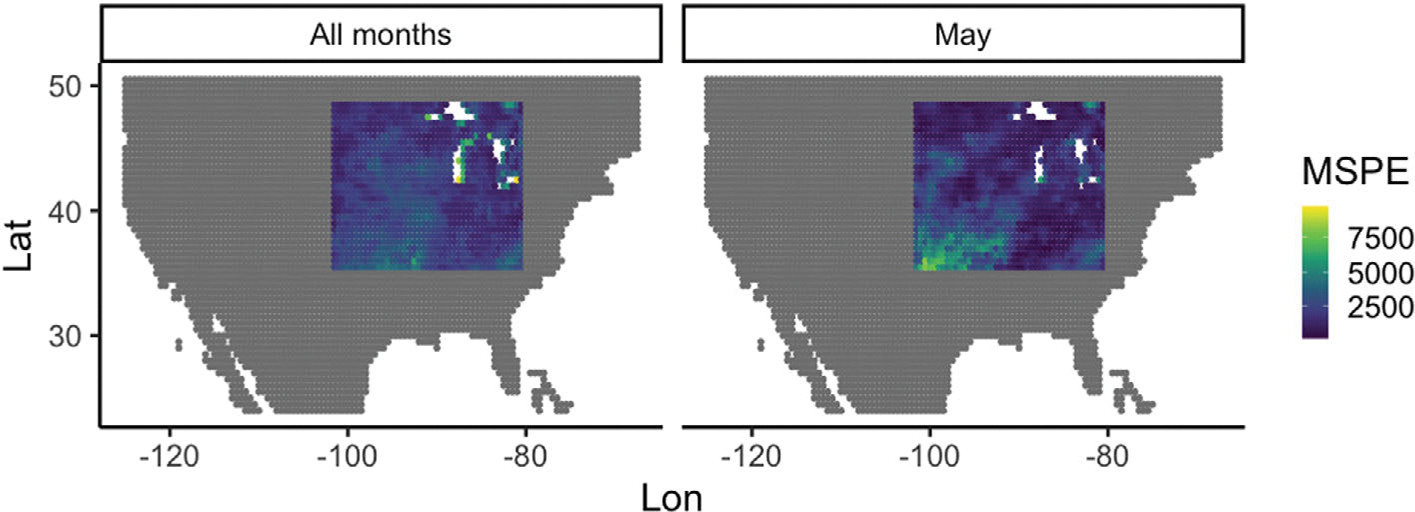
Map of MSPE for SM data from the functional linear model at each location in the US corn belt for all months (left) and only May months (right). Note the agreement (low error) is quite good in large swaths of belt for all months, and similarly good in all but the southwest region for the May months.

The purpose of this analysis is to examine the contribution of lagged SSTA at a particular ocean location s on the SM predictions from the functional linear model. Figure 5 shows maps of two different variable important measures for the functional linear model. The left figure gives the maps of the model reliance (MR) metric (Section 2.1) on the log-scale for each sea location. We observe that a large majority of the SSTA locations have log(MR) ≤ 0 (i.e., MR ≤ 1) implying that they had little importance in the final model. Notable areas with positive log(MR) include patches off the west coast of North and South America and a patch between 30N–40N latitude and 150E–175E longitude.

FIGURE 5.

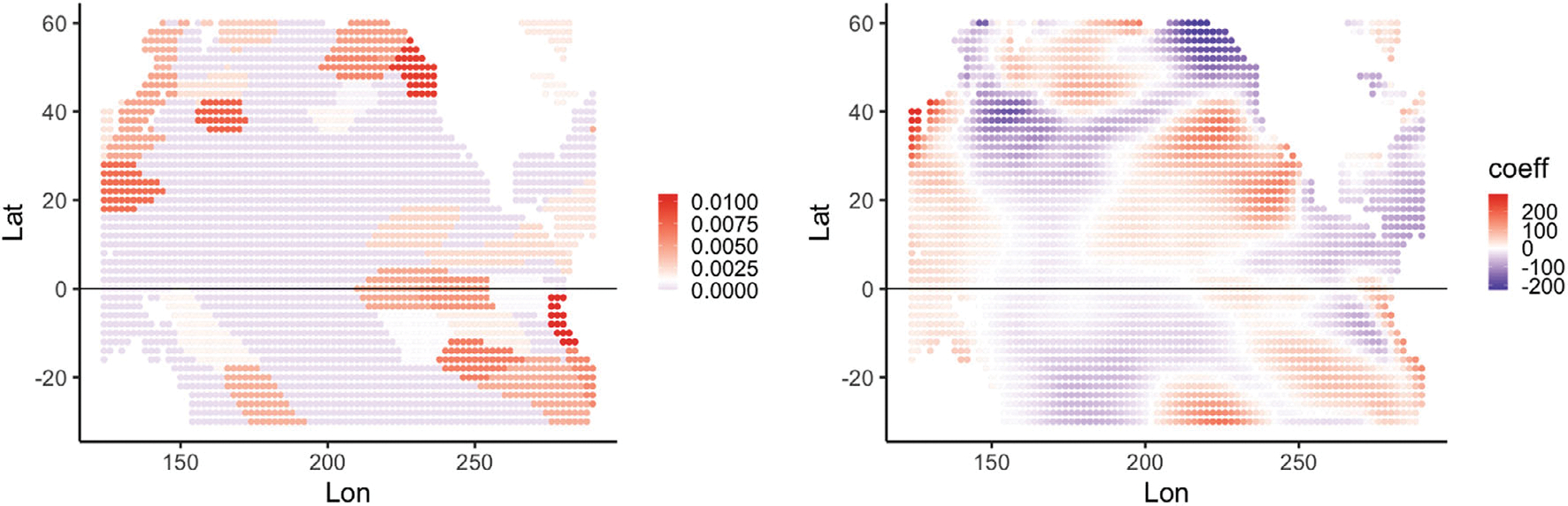
Variable importance maps for the spatial functional linear model: (Left) Map of the model reliance metric in log-scale for predicting SM in the months of May (Section 2.1); (Right) Map of the functional regression coefficient $\widehat{\beta }(s)$ for the functional linear model at a sea surface location s, averaged for all SM locations in the corn belt.

While the MR metrics allow comparison of the linear model to black-box machine learning models, the linear model also offers a more direct measure of interpretability through the regression coefficient β(s). Figure 5 (right) provides a plot of the average $\widehat{\beta }(s)$ for all the SM locations for each SSTA location s. There are some agreements with the marginal correlation map in Figure 2 (right), for example, a large patch of negative coefficients between 20N–40N latitude and 150E–200E longitude, and large patch of positive coefficients off the coast of California. There are also notable differences (much of the equatorial region and south of it). This is expected because, unlike the marginal correlations in Figure 2 (right), β(s) is essentially the partial correlation of SSTA at an ocean location with SM after adjusting for SSTA among the nearby ocean locations. The interpretation of a partial correlation is contingent upon the set of explanatory variables used (e.g., the lagged SM covariates) and hence partial correlations for different choices of covariates may not be directly comparable without standardization. Note also that the model reliance metric and spatially-varying coefficients show some areas of agreement—particularly, the near coast of South America up through the central tropical Pacific, the northern coast of North America and the far eastern coast of Asia. Differences include a region in the southern ocean for the reliance metric that does not show up in the spatially-varying parameter plot, and an area from the central Pacific to coastal North America in the parameter plot that does not show up in the reliance metric plot. Note that an advantage of the spatially-varying parameter plot is that one can see the sign of the impact (i.e., negative and positive parameter values).

5.2 |. Extreme gradient boosting

As mentioned in Section 4.2, it can be helpful to manually create features that better capture the signal in the data or provide dimension reduction or decorrelation. Thus, instead of using the raw SSTA data, we created clusters by first reducing the dimensionality through spatial PCA (EOFs) and then using a “partition around medoids” (PAM) clustering algorithm (e.g., Van der Laan et al., 2003). This identified 75 clusters for the SSTA data. Using the clustered data, the following features were created using 3-month lagged information: (1) means within the 3-month lagged clusters; (2) variances within the 3-month lagged clusters; (3) difference from last year’s mean (mean of the most recent 3 month period minus the mean of the previous year’s 3 month period at the same time of year); and (4) ratio of current variance to last year’s variance (ratio of the most recent 3 month variance to the previous year’s 3 month variance at the same time of year). This gave a total of 300 (4 × 75) features. In addition to these features, the monthly information was one hot encoded (converted to dummy variables), and the 3 month lagged SM data was also used as a predictor. This brought the total number of features to 315. The response being predicted is the SM 3 months into the future. The XGBoost algorithm was trained on the hyperparameters listed in Section 4.2. The tuning produced a learning rate of 0.05 with 70% of observations sampled in the creation of each tree and 80% of the features randomly selected. The maximum depth of each tree was set to 6 with a Gamma value of 2, the number of trees was set to 400 and the minimum sum allowed for a tree to split was set to 1. The default squared error loss function was used.

Table 5 shows that the XGBoost model performed well, but did not do as well as the spatial functional linear model with regards to its skill, yet it does show a similar pattern in that there is less skill for the May predictions relative to persistence than for all months combined.

The XGBoost algorithm has several internal measures of feature importance. One commonly used measure is the gain of each feature, which is the relative contribution of that feature to the model across all trees. Contribution is measured by the amount of information gained when that variable is used to split the data in a tree. This information is then averaged across all trees. Based upon the gain for all features, the means within the 3-month lagged clusters showed the most influence across all created features and was used to compare to the Shapley values from the same model. The gain for these features can be seen in the top left panel of Figure 6. All gains in this plot are positive, with larger values (darker red) indicating more influential areas. We compare this information to the corresponding mean absolute Shapley values averaged for all periods as shown in the top right panel of Figure 6. The scaled colors vary from white to dark red with the darker red values indicating a larger affect of the SSTA data. The Shapley value shows very similar patterns, especially the very influential areas in the south central Pacific.

FIGURE 6.

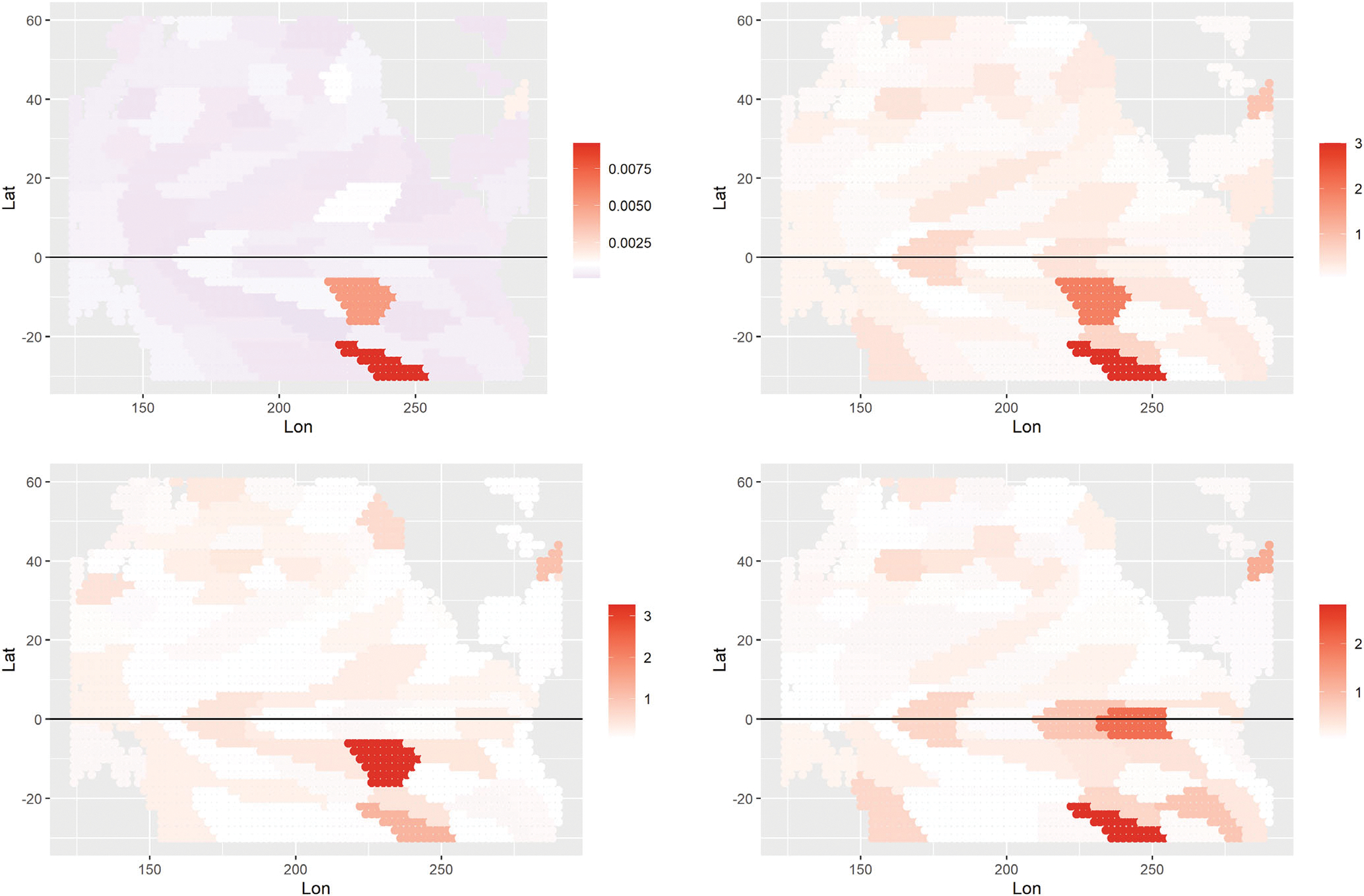
Interpretability plots for the XGBoost model for 3-month long lead forecasts of SM in the corn belt: (Top left) the overall gain for SSTA features in the XGBoost model; (Top right) mean absolute Shapley values over all months; (Bottom) absolute values of the Shapley values for the XGboost model for 2016 (left) and 2021 (right), with darker red indicating higher SSTA increasing the SM in the corn belt. These values are averaged over all locations in the corn belt. The scale bars vary with instance to facilitate interpretation.

An advantage of the Shapley value is its localness, that is, its ability to examine the influence for a particular instance. To illustrate this, the bottom panels in Figure 6 show the Shapley values for predicting May SM in 2016 (left) and 2021 (right). Note the similarity in the 2016 plot with the two average plots in the top panels of the figure. Given that 2016 was a strong El Niño year, this suggests that the overall influence of SSTA is driven mostly by ENSO events, as one would expect.

Thus, the Shapley plots may be helpful for climate scientists who are interested in understanding teleconnections between SSTA and SM on a year-to-year basis. Certain regions show consistent importance across the test years, including the central tropical Pacific and coastal South America regions that are typical for ENSO events. One might get additional insight by comparing these plots to the various climate indices associated with the Pacific region (note: NOAA makes available updated monthly values for a large number of climate indices⁶).

5.3 |. Artificial neural networks

We consider four models here that predict standardized SM observations using Z-score transformations at each spatial location. Note that the specification of the number of layers and the number of nodes in each hidden layer is chosen by trial and error, as is the case for most deep model implementations. We did evaluate the sensitivity to different choices of the number of hidden layers and nodes per layer, and found that the predictive performance was not monotonic with increasing depth, as expected. Models for each prediction month are fit separately using 1000 epochs.

The first model is a naive approach that uses the data from all 3186 SSTA locations in February as the input, and predicts all 1224 corn belt SM locations the following May; we call this the “Raw” model and specify it by ANN (3186_tanh, 2000_tanh, 2000_tanh, 1224_lin, 1224). The second model is the same as the first except it uses 6 months of lagged SSTA as predictors (i.e., September through February) to predict SM the following May. This model is given by: ANN(19,116, 19,116_tanh, 7000_tanh, 5000_tanh, 1224_lin, 1224); we call this the “Wide Raw” model. The third and fourth models considered here are based on dimension reduced input features. While the naive Raw model approach is viable, it is computationally intensive due to the high dimension of the parameter space. To reduce the high dimensionality associated with ANNs and hence, the computational burden, Migenda et al. (2021) suggest employing PCA to pre-process the input data. In essence, this forms an additional layer to the ANN with a linear activation function. However, this layer is “pretrained” (i.e., the PCA weights are unsupervised) and does not get updated during the training of the ANN. Specifically, to obtain the PCA projection, the SSTA data from the beginning of the dataset to November 2012 were used and 60 components were selected (note that 60 components account for 95.7% of the variation in the SSTA data for this period). We use ANN(60, 100_tanh, 100_tanh, 500_tanh, 1224_lin, 1224) to fit the data and refer to this model as the “PCA₆₀” model. The fourth model is a wide version of this the PCA model but using PCA input features from September through February. To implement this model we use: ANN(360, 420_tanh, 400_tanh, 1224_lin, 1224), and call this the “Wide PCA₆₀” model. As shown in Table 5, these ANN models are among the poorest performers in terms of MSPE, test R² and skill score relative to persistence.

We illustrate the random perturbation explainability approach (Section 2.1.1) here using the ANN predictions. This involves perturbing the SSTA input data and examining the influence on the model predictions via MSE_pred. In particular, for each SSTA location the corresponding sample standard deviation for each site and month (calculated over time) is then added to the observed SSTA value for that site, leaving all other SSTA values fixed. These perturbed data are then used to predict SM and the MSPE is calculated. This is done for every SSTA site and the ratio of the perturbed to unperturbed MSPE is recorded; recall, this is the model reliance metric in feature shuffling methods (Equation (1) in Section 2.1). For the PCA models, the PCA transformation was applied to the perturbed data.

Figure 7 shows maps of the model reliance ratios for 2014 for the Raw and PCA₆₀ models, and Figure 8 shows the model reliance ratios for three input months (December 2013–February 2014) for the Wide Raw and Wide PCA₆₀ models when applied to forecast SM in May 2014. The model reliance results in Figure 7 show that the equatorial “warm pool” region off the west coast of South America in the Pacific Ocean appears to influence the MSPE ratio for the Raw model more than the PCA₆₀ model, as evidenced by the red region. This is suggestive of an El Niño signal in SSTA, but this is interesting since February and May of 2014 do not correspond to an ENSO year. We do note, however, that the Pacific North America (PNA) statistic for those times show a strong negative influence (see the PNA statistic from the NOAA website⁷. Both models show an area of influence of the western coast of Mexico. In general, the Raw and PCA₆₀ models suggest somewhat different areas of influence, and there are even larger differences between years (not shown here).

FIGURE 7.

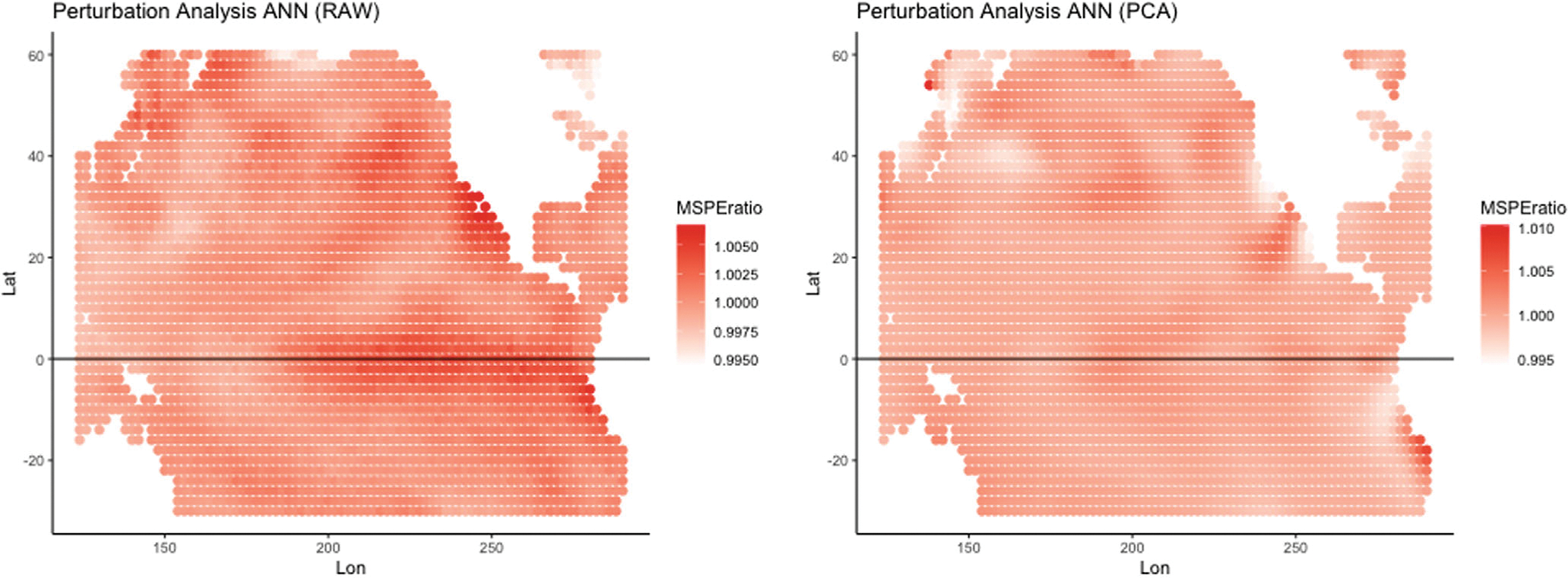
Model reliance perturbation results for the naïve approach using: (Left) Raw; and (Right) PCA₆₀ transformed SSTA data with 60 components using February alone to predict May 2014. Note that the scales differ between plots to facilitate interpretation.

FIGURE 8.

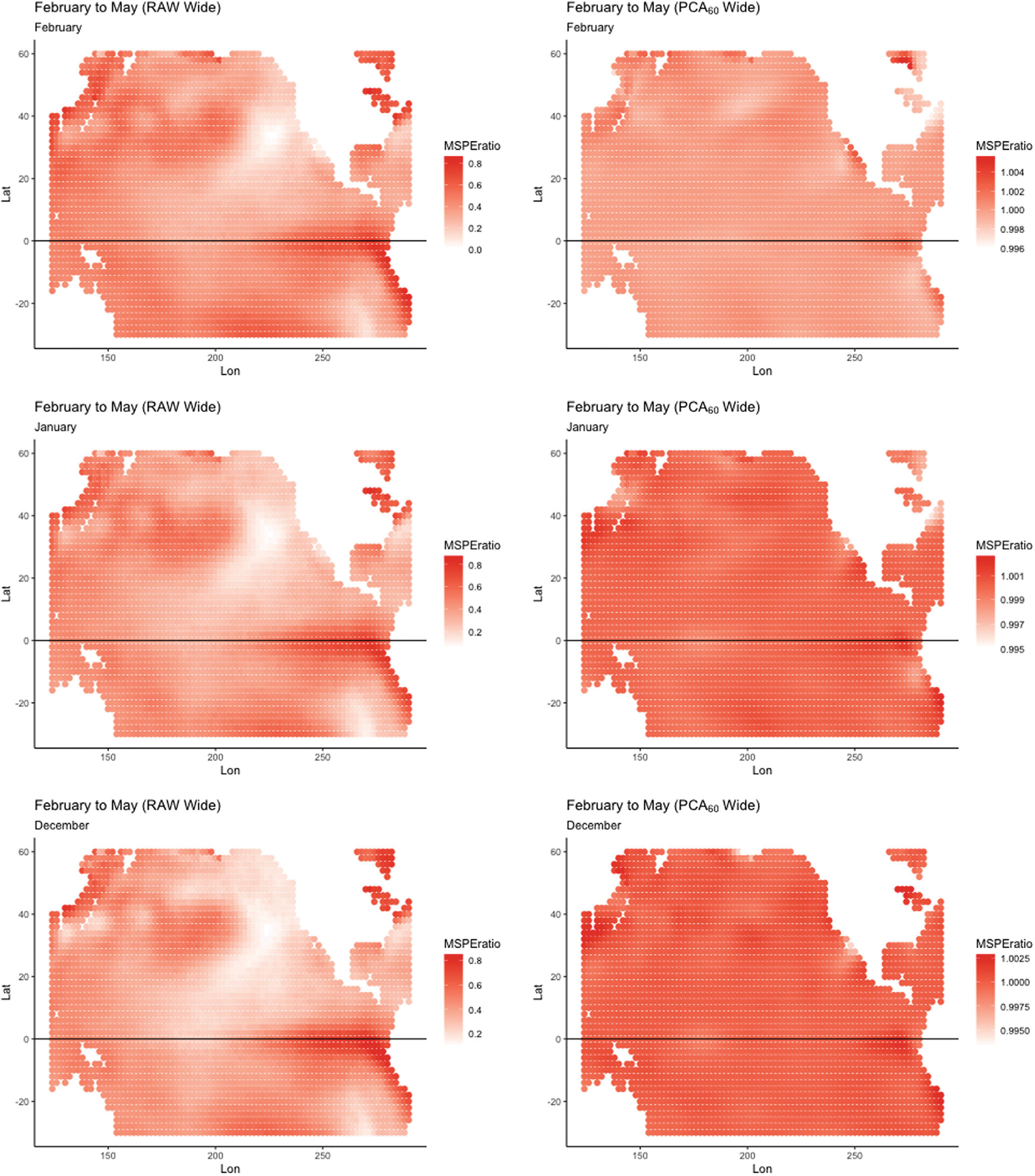
Model reliance perturbation results for the wide approach using Wide Raw (left) and Wide PCA₆₀ (right) for transformed SSTA data with 60 PCA components. Here, May 2014 is predicted using September 2013 to February 2014 data (note, the plots for September, October, and November are omitted). The scales on the plots vary to facilitate interpretation.

The plots for the Wide models shown in Figure 8 suggest a somewhat different story. The pattern for each lag for the Wide Raw model is indicative of an ENSO pattern in the central tropical Pacific, and includes an extension through coastal North America. However, the plots for the Wide PCA₆₀ do not exhibit this structure and vary from across each lag.

5.4 |. Convolutional neural networks

A CNN model was implemented to predict SM with SSTA data as input along with Shapley values and LIME as explainers. Table 5 gives the prediction summary metrics (test R², MSPE, and skill scores relative to persistence) for the forecasts corresponding to all months and for May months. Although the summary statistics show that the forecasts from the CNN model for this example are not as skillful as persistence (excepting CNN (SSTA, SM) for predictions for all months alone), the spatial functional linear model, and XGBoost, the CNN approach does yield useful interpretations when paired with LIME and Shapley values as described below.

Figure 9 shows heatmaps at SSTA locations for the absolute value of the LIME summaries for May averaged over the years 2014–2021 (left) and for May 2016 (right), corresponding to the mean of all SM prediction locations. The top panels of Figure 10 show the corresponding heatmap plots for the average of the absolute Shapley value summaries for SSTA over the years 2014–2021 (left) and the absolute Shapley value summaries for SSTA for May 2016 (right). The middle panels of Figure 10 show heatmaps of the absolute Shapley values for CNN model trained with both SSTA and SM as input; the left panel shows the SSTA contribution and the right panel shows the SM contribution for the year 2016. The bottom panels of Figure 10 show heatmaps of the absolute Shapley values for CNN model trained with both SSTA and SM as input; the left panel shows the average of the absolute Shapley value summaries for SSTA over the years 2014–2021 and the right panel shows the average of the absolute Shapley value summaries for SM over the years 2014–2021. The LIME results are not as clear as for the XGBoost results, but do suggest that regions off of Oceania, the central tropical Pacific, and the near coastal waters off of North and South America may be important predictors for SM. Shapley values are easier to interpret with respect to the CNN predictions given they exhibit substantially more spatial smoothness. They show many of the same regions being important as presented earlier, but notably, show a very strong indication that the ENSO region from tropical South America through the central Pacific is quite important for the prediction of SM in May 2016. Recall that ocean conditions in February 2016 suggested a strong El Niño.

FIGURE 9.

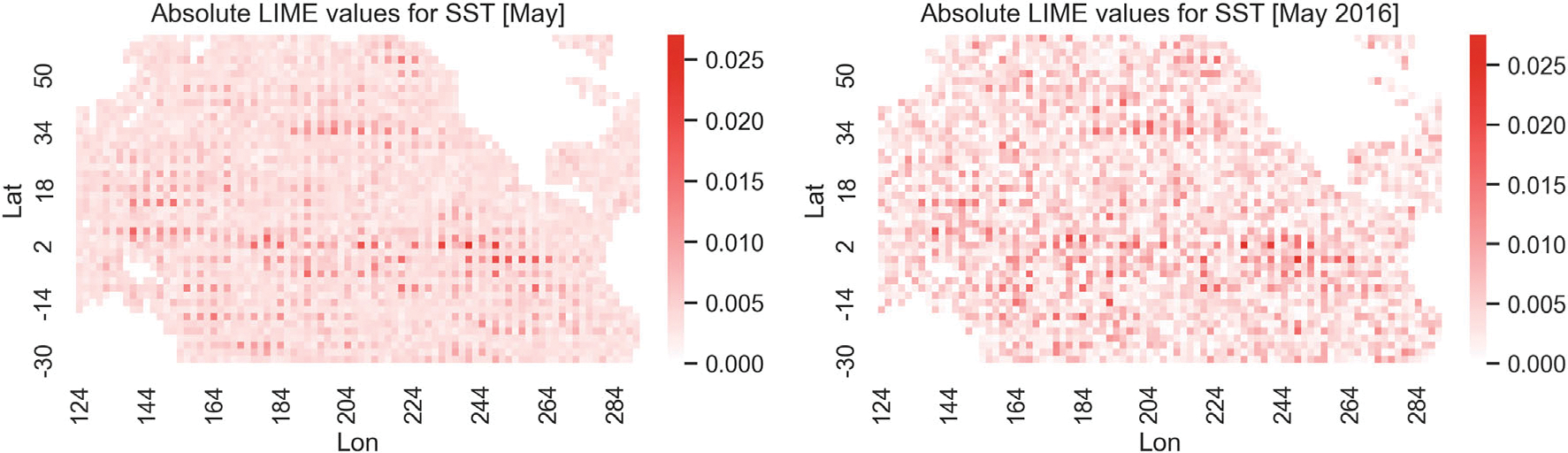
Absolute LIME values averaged across the years 2014–2021 (left) and absolute LIME values for the year 2016 (right). The CNN model used here takes SSTA data as input.

FIGURE 10.

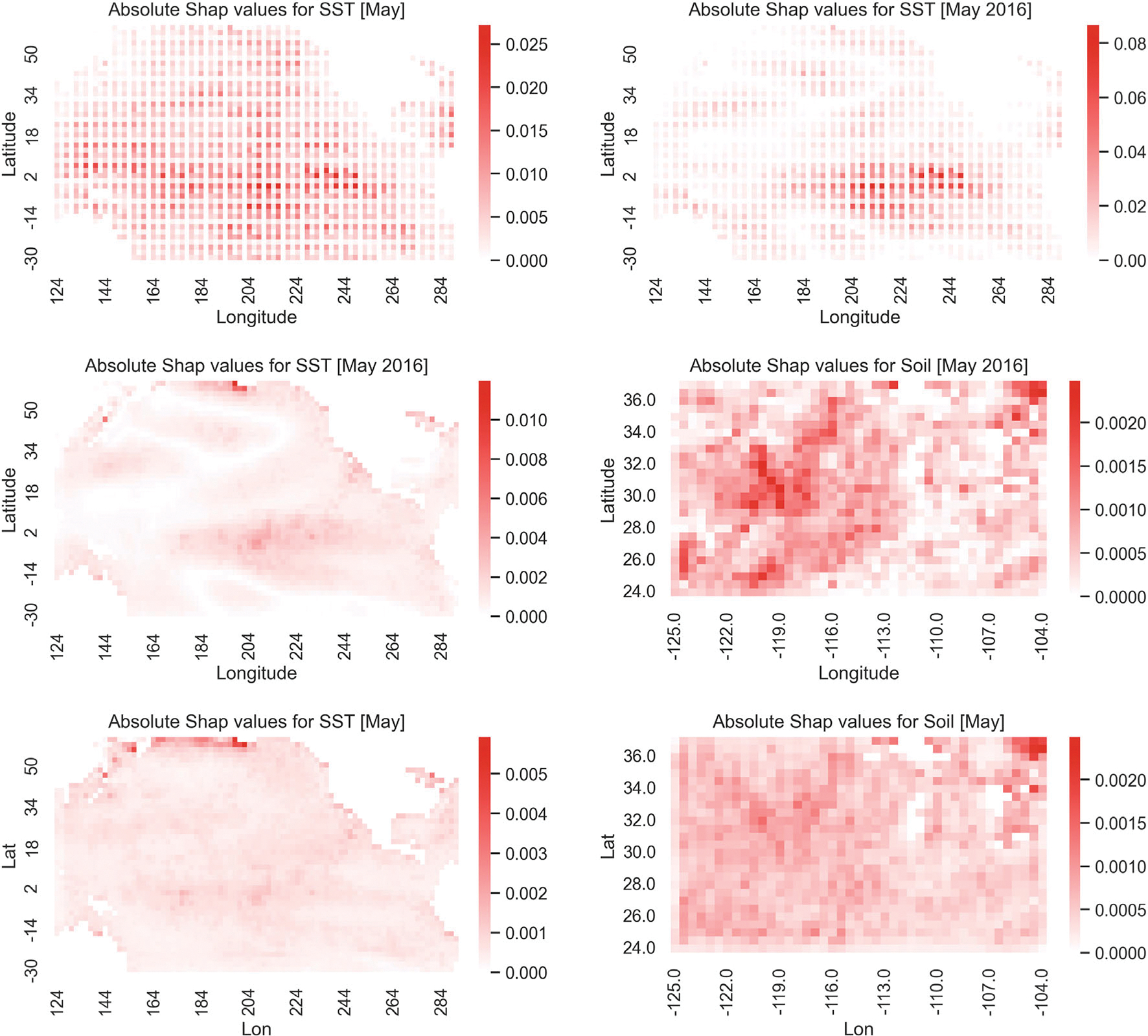
Upper panels: (Left) Absolute Shapley values averaged across the years 2014–2021; and (Right) the absolute Shapley values for the year 2016 for the CNN model for the month of May with SSTA as input. Middle panels: (Left) Absolute Shapley values, SSTA part; and (Right) SM part, for the year 2016, for the CNN model for the month of May trained with both SSTA and SM as input. Bottom panels: (Left) Absolute Shapley values, SSTA part; and (Right) SM part, averaged over the years 2014–2021, for the CNN model for the month of May trained with both SSTA and SM as input. The scales on the plots vary to facilitate interpretation.

6 |. DISCUSSION

We have illustrated how one can use three model-agnostic explainability approaches on various models applied to an environmental prediction problem. In particular, we consider feature shuffling, LIME, and Shapley values as explainability approaches and consider spatial functional regression, XGboost, ANNs, and CNNs to perform prediction of SM over the US corn belt region given SSTA predictors lagged at least 3 months.

The functional linear model gave the best predictions in terms of MSPE relative to a persistence forecast, followed by the XGboost model; the CNN (SSTA, SM) model performed marginally better for predictions for all months alone. We note that all three of these models considered 3 month lagged SM in addition to the lagged SSTA data as predictors. The network neural models, excepting CNN (SSTA, SM) for predictions for all months alone, all performed substantially worse than persistence, which would imply that they would not be reasonable forecasts for operational consideration. There was considerable spatial and year-to-year variability in the forecast quality, which has also been demonstrated in previous studies (e.g., McDermott & Wikle, 2016). It is not surprising that the linear model and the XGBoost models were skillful. Linear models for long lead prediction have been used operationally for quite some time, and Figure 2 shows that there is a strong linear association between Pacific SSTA and corn belt SM. Further, McDermott and Wikle (2019) showed that for some regions of the corn belt nonlinear models performed well, and for other regions they did not. We still find it surprising that the neural models did not perform better in general in the examples presented here. We recognize that given there is a wide range of potential architectures and modeling choices for such models, it is quite possible that other neural models might provide skillful forecasts. We conjecture that the primary limitation here was the relatively small training sample—it is well known that deep neural models often require a great deal of data, or pre-training to be successful.

In terms of explainability, each model considered one or two explainability approaches for the out-of-sample predictions. Although these methods tended to find coherent regions in the SSTA features that were important for the predictions, they were not always in agreement. There are many possible reasons for this, including the presence of additional predictors that were confounding the interpretation, as well as inherent differences in the explainability procedures themselves (e.g., LIME relies on the quality of its local surrogate models). Nevertheless, the explainability metrics did provide suggestions for particular regions in the SSTA feature space that were important for individual instances (forecast years) and could be investigated by climate scientists for potential physical mechanisms (e.g., ENSO or PNA patterns).

We note that there are several challenges with the approaches we present here. First, the explainability methods all have difficulty when there is dependence in the predictors. As we illustrate, this can be mitigated to some extent by pre-clustering and/or dimension reduction (e.g., PCA/EOF). In addition, deep models such as the ANN and CNN models, require the user to select many different hyperparameters with respect to model architecture (e.g., number of hidden layers, number of units per layer, activation functions, etc.) and whether input or output features should be reduced in dimension a priori. This is always a challenge with such models, but it is not clear how much this affects explainability. For example, we showed with the ANN implementation that feature perturbation results differed depending on whether we first consider a PCA dimension reduction on the input features. In addition, although the CNN models were not uniformly skillful, they did capture strong ENSO SSTA patterns of importance.

We also note that the implementation of these explainability methods is very computationally expensive for models where there are many input features and multivariate responses. Furthermore, although one of the strengths of these procedures is that they can be applied to explain individual instances, it can be quite labor intensive to manually evaluate each instance and summarize overall effects.

Finally, the predictive models considered here do not explicitly account for the temporal dynamics of the underlying SSTA and SM processes. Models such as spatio-temporal dynamic models (e.g., Cressie & Wikle, 2011) or combinations of CNNs and RNNs (e.g., Khaki et al., 2020; Zhu et al., 2021) could be used for this purpose and it would be interesting future research to investigate their use here, as well as their interpretability. Furthermore, future research may include exploring situations where the explainability approaches agree and disagree and to gain an understanding of why they are performing this way (i.e., “explain the explainer”). Finally, more research may be devoted to implementing and interpreting these explainability methods more efficiently with high-dimensional input and output spaces.