Functional Network Connectivity in high-frequency fMRI: An Eyes open, Eyes closed resting state study

Abstract

Background:

Resting-state fMRI (rs-fMRI) is employed to assess “functional connections” of signal between brain regions. However, multiple rs-fMRI paradigms and data-filtering strategies have been used, highlighting the need to explore BOLD signal across the spectrum. Rs-fMRI data is typically filtered at frequencies ranging between 0.008~0.2 Hz to mitigate nuisance signal (e.g. cardiac, respiratory) and maximize neuronal BOLD signal. However, some argue neuronal BOLD signal may be parsed at higher frequencies.

New method:

To assess the contributions of rs-fMRI along the BOLD spectra on functional network connectivity (FNC) matrices, a spatially constrained independent component analysis (ICA) was performed at seven different frequency “bins”, after which FNC values and FNC measures of matrix-randomness were assessed using linear mixed models.

Results:

Results show FNCs at higher-frequency bins display similar randomness to those from the typical frequency bins (0.01–0.15), while the largest values are in the 0.31–0.46 Hz bin. Eyes open (EO) vs eyes closed (EC) comparison found EC was less random than EO across most frequency bins. Further, FNC was greater in EC across auditory and cognitive control pairings while EO values were greater in somatomotor, visual, and default mode FNC.

Comparison with existing methods:

Effect sizes of frequency and resting-state paradigm vary from small to large, but the most notable results are specific to frequency ranges and resting-state paradigm with artifacts like motion displaying negligible effect sizes.

Conclusions:

These suggest unique information may be derived from FNC matrices across frequencies and paradigms, but additional data is necessary prior to any definitive conclusions.

Introduction:

Resting-state functional network connectivity (FNC) derived from brain networks informed by spatial independent component analysis (sICA), has become a ubiquitous approach for assessing brain function and probing diagnostic biomarkers. The primary assumption girding these findings is the observations of non-random FNC brain patterns and links of deviations from non-random FNC patterns to neuropathic and neurodivergent populations (Buckner, Andrews-Hanna, & Schacter, 2008; Nelson, Bassett, Camchong, Bullmore, & Lim, 2017; van den Heuvel, Bullmore, & Sporns, 2016; van den Heuvel & Fornito, 2014; van den Heuvel & Hulshoff Pol, 2010; Yeo et al., 2011). The signal of interest in most resting-state FNC studies is generally extracted after temporal filtering up-to the ~0.2 Hz range (Biswal, DeYoe, & Hyde, 1996), which is assumed to mitigate the contribution of nuisance signal in BOLD timeseries, including respiration (0.3–1.0 Hz), cardiovascular activity (≥1 Hz), scanner drift (≤ 0.01 Hz), and motion (varies) (Birn, Diamond, Smith, & Bandettini, 2006; Birn, Smith, Jones, & Bandettini, 2008; Biswal et al., 1996; Chang, Cunningham, & Glover, 2009; Cordes et al., 2001; Niazy, Xie, Miller, Beckmann, & Smith, 2011; Satterthwaite et al., 2013; Shmueli et al., 2007; Wise, Ide, Poulin, & Tracey, 2004). However, some have argued there is evidence that BOLD signal of neuronal origin may be present at higher frequencies up to the limit allowed by the sampling rate (1/[2*Repetition Time])(Chen & Glover, 2015). Further, differences in FNC across the frequency spectra may provide useful information in clinical populations (Morgan, Rogers, & Abou-Khalil, 2015; Sours et al., 2015; Wang et al., 2015).

However, Chen, Jahanian, & Glover, 2017 and others have noted that many studies examining FNC patterns across broader frequency ranges used preprocessing strategies for their data, resulting in the majority of high-frequency findings being attributed to sequential nuisance regression of artifact (Chen et al., 2017; Lindquist, Geuter, Wager, & Caffo, 2019). This calls into question results from previous analyses on higher-frequency data and their relevance for extracting diagnostically useful information. As such, it is worth re-visiting frequency-specific contributions regarding BOLD-based FNC.

Based on the observations of non-random organization of the human brain, FNC patterns generally reveal a degree of “modularity,” or grid-like organization with discrete and overlapping temporal and/or topological properties (Ferrarini et al., 2009; Newman, 2006; Sporns, 2003; Yu et al., 2011). However, few of these studies have assessed such organization across a range of frequencies, and one has done so without the use of graph-theory based measures, which are not without limitations (Vergara & Calhoun, 2016; Vergara, Yu, & Calhoun, 2018a, 2018b). Further, few studies have examined the effects of simple design choices such as resting-state paradigm (e.g. eyes open vs. eyes closed) on FNC outside of traditionally used filtering ranges (0.008~0.2 Hz; varies across the literature). This is despite previous research demonstrating significant alterations in FNC between eyes open (EO) vs eyes closed (EC) resting-state paradigms (Agcaoglu, Wilson, Wang, Stephen, & Calhoun, 2020, 2019; Liu, Dong, Zuo, Wang, & Zang, 2013; Patriat et al., 2013; Wang et al., 2015; Yuan, Wang, Zang, & Liu, 2014; Zou et al., 2009). Studies where participants serve as their own controls while the same filtering approaches are applied across different resting-state paradigms provide a clearer window into the contribution of neural-derived higher frequency BOLD signals.

To explore FNC measures at higher-frequency BOLD signals, the authors utilized sICA (Du & Fan, 2013; Li & Adali, 2010a, 2010b; S. Ma et al., 2011) to extract corresponding components across subsections of the frequency spectra. Resting-state functional magnetic resonance imaging (rs-fMRI) was collected with participants lying in the scanner with their eyes open attending to a fixation cross (EO), and eyes closed while told to think about nothing and not to sleep (EC) (counter-balanced across individuals). This analysis will, to the authors’ knowledge, be the first to examine differences in high-frequency BOLD FNC analyses within an ICA framework. The primary goal of this research is two-fold. First, we aimed to probe meaningful fluctuations in FNC, by utilizing matrix randomness estimations FNC patterns among high frequency BOLD signal as a proxy for BOLD signal of neuronal origin. This is achieved using the matrix randomness estimation method proposed by Vergara and colleagues (Vergara & Calhoun, 2016; Vergara et al., 2018a, 2018b). Second, the authors explored differences in FNCs and matrix-randomness measures from FNC matrices between EO and EC rs-fMRI paradigms across bins. The first objective establishes degrees of deviation and mutual information in FNC values derived from different temporal filters across the BOLD signal, while the latter explores interactions between signal-filtering on FNCs with resting-state paradigm.

Methods:

Participants:

Participants included 174 children with no reported clinical diagnoses from the greater Albuquerque, New Mexico (92) and Omaha, Nebraska (82) areas as part of the collaborative developmental chronnecto-genomics consortium (Dev-CoG; http://devcog.mrn.org/), between the Mind Research Network (MRN), University of Nebraska Medical Center (UNMC), and Tulane (Stephen et al., 2020). All parents signed informed consent forms, and youth signed assent forms approved by each participating site’s institutional review board before participating in the study. The appropriate institutional review board for each study site approved all procedures. Of the participants, 89 reported as male, 84 reported as female, and one did not report sex or gender (appears missing at random). No significant differences were identified regarding age and Full-Scale Intelligence Quotient (FSIQ) between participants who reported as male or female. However, comparisons between acquisition sites identified significantly higher FSIQs in participants from UNMC compared to MRN. There were no other significant differences across age or gender composition between MRN and UNMC. The comparisons are summarized in Table 1.

Table 1.

Demographic comparisons of participants

	N	Range	Difference (W )	Means(t )	Test Statistic	p -value	CI95%	Eff size
F vs M	89/84
Age		9.2–15.1 vs 9.1–15.5	−0.1		W = 3607	p = 0.691	−0.7 0.4	r = −0.03
FSIQ		72–140 vs 68–148		108.605 vs 112.138	t (165.429) = −1.557	p = 0.121	−8.014 : 0.948	g = −0.238
MRN vs UNMC	92/82
Age		9.1–15.5 vs 9.4–15.5	−0.2		W = 3520	p = 0.531	−0.8 : 0.4	r = −0.048
F vs M	46/46 vs 38/43				χ2 (1,174) = 0.0639452	p = 0.8		φ = 0.031
* FSIQ		72–139 vs 68–148	−0.883	108.272 vs 112.813	t (165.205) = −2.002	p = 0.046	−9.0179 : −0.062	g = −0.307

Note:

^*Indicates statistical significance at or below a 0.05 threshold.

W represents the rank-difference statistic from a Wilcoxon rank-sum test, quantified using the difference in ranks and an r effect size

t represents the difference in means derived from a Welch's two or paired sample t -test, effect size is quantified using Hedge's g

χ² Represents the goodness-of-fit from a Pearson chi-squared test. Effect size is displayed using ϕ.

V Represents the Wilcoxon signed-rank test pseudo median, effect size is quantified using a paired r.

Positive g & r values indicate greater values in females or MRN, while negative values indicate greater values males or UNMC.

Imaging data collection:

Imaging data collected at MRN utilized a 3T Siemens TIM Trio scanner, while a 3T Siemens Skyra scanner was used at the UNMC site. One single-band-reference image (SBref), followed by a total of 650 volumes rs-fMRI echo-planar imaging BOLD data and were collected for both EC and EO for each participant. Rs-fMRI scans were acquired using a standard gradient-echo echo planar imaging paradigm with a repetition time (TR) of 0.46 s, echo time (TE) = 29 ms, flip angle (FA) = 44°, and a slice thickness of 3 mm with no gap. The acquisition parameter for the MRN site used a field of view (FOV) of 246 × 246 mm (82 × 82 matrix), and 56 sequential axial slices, while the UNMC site utilized a FOV of 268 × 268 mm (82 × 82 matrix), and 48 sequential axial slices. The order of the EO and EC resting-state sessions were counter-balanced across participants at each site.

Data Quality Analyses:

Analyses were conducted on images from both EC and EO conditions for each participant to assess potential differences due to data quality. Median temporal signal-to-noise ratio (tSNR; median value of the mean timeseries image divided by the standard deviation of the timeseries), the standard deviation of outlier voxels by image (calculated using AFNI’s 3dToutcount), head motion quantified using the Euclidean norm (ENORM, the square-root of the sum-of-squares for mm of motion in each of the 6 directions) calculated with AFNI’s 3dvolreg on despiked data, and inherent smoothness (FWHM) using AFNI’s 3dFWHMx were used for comparisons across gender, site, and resting-state paradigm. Finally, EC and EO only differed on inherent smoothness and no other calculated metrics. The results of each statistical test are reported in Supplementary Table 1 and Supplementary Figure 1.

Preprocessing:

Images were pre-processed utilizing a hybrid pipeline of FSL 5.0.5 (Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012; Smith et al., 2004), AFNI (Cox, 1996) and ANTs (Brian B. Avants, Tustison, & Song, 2009). First, images were distortion corrected using FSL’s topup using AP-PA phase encoding. Second, ANTs’ antsMultivariateTemplateConstruction2.sh (Brian B Avants, Tustison, Wu, Cook, & Gee, 2011; Brian B Avants, Tustison, Song, et al., 2011; Sanchez, Richards, & Almli, 2012) was used to create a custom pediatric template from the distortion-corrected single-band reference (SBRef) images. Second, the first 10 of the 650 images in the distortion-corrected timeseries for each participant were removed to facilitate magnetization equilibrium relative to the first scans. Third, the distortion-corrected timeseries were then despiked using AFNI’s 3dDespike -NEW flag for multi-band data to increase registration accuracy (Caballero-Gaudes & Reynolds, 2017; Jo et al., 2013). Fourth, the data were realigned to the first image in the timeseries (after the first 10 images were discarded). Finally, the first image in each participant’s timeseries was non-linearly registered using ANT’s greedy SyN diffeomorphic registration (B B Avants, Epstein, Grossman, & Gee, 2008; Klein et al., 2009) to a 3mm isometric custom template constructed from all participant’s single-band reference (SBRef) images. Transformations were computed from the study-specific template to an MNI-space template constructed from warps of averaged timeseries data transformed directly to an isometric 3mm MNI space (via SPM8 (Friston et al., 1994)), and participant-to-template and template-to-MNI transformations were performed on the first image in each timeseries for all participants. No co-registration to anatomical images was performed in this workflow. Following normalization, AFNI’s 3dTproject was utilized to apply a regression model to simultaneously perform: 1) linear detrending, 2) second- and third-order Legendre polynomials to remove polynomials across the timeseries, 3) sine and cosine functions modeling frequencies outside the evenly spaced bins between 0.01–1.76 Hz (mimicking a passband filter using regression) and smoothing the residuals with a 6mm FWHM kernel. The residuals of BOLD timeseries from each set of 640 images (for each resting-state paradigm for each participant) were variance normalized (timeseries are linearly detrended and converted to z-scores for each voxel) prior to ICA.

Independent Component Analysis:

The network templates used in the current study were computed from previous work by (Agcaoglu et al., 2019), who performed ICA on the full frequency spectrum of the this dataset previously with no no filters were applied prior to ICA using the GIFT toolbox (http://trendscenter.org/software/gift/) in Matlab. First, EC and EO scans were pooled across participants and principal component analyses (PCAs) were employed for each set of images for each participant timeseries to reduce the dimensionality across 646 (as opposed to 640 for the current study) time points to 200 maximally variable directions. The principal components for each participant for EC and EO were concatenated across the time dimension, and a group PCA was applied to further reduce the dimensionality to 150 maximally variable directions (Erhardt et al., 2011). One hundred and fifty independent components were estimated from the group PCA matrix with the infomax algorithm (Bell & Sejnowski, 1995), repeated 20 times in ICASSO (Himberg & Hyvarinen, 2003) ( http://www.cis.hut.fi/projects/ica/icasso) with the most central runs selected from the resulting 20 runs to ensure stability of the estimated components (S. Ma et al., 2011).

The workflow utilizes a spatially constrained multivariate objective optimization ICA with reference (MOO-ICAR) to estimate sources using component maps as spatial priors (Du & Fan, 2013; Du et al., 2016). For this study, the gICA components from Agcaoglu et al., 2019 (see supplementary material for an html-based component viewer) were used to extract independent component maps and their timecourses from EC and EO for each frequency bin (Agcaoglu et al., 2019). Fifty components were identified as meaningful intrinsic connectivity networks (ICNs) and arranged into different functional domains using visual inspection and atlas labels from the “whereami” function in AFNI at the peak coordinates for each component. These include: 3 auditory (AUD), 2 cerebellar (CB), 12 cognitive control (CC), 4 default mode (DM), 4 subcortical (SC), 8 somatomotor (SM), and 17 visual (VS) components. FNC matrices from each pairwise combination of components totaled to 1225 possible combinations, with 20% consisting of within-domain (e.g. one DM component to another DM component), and 80% constituting between-domain(e.g. DM to SC components) correlations.

Functions from the GIFT toolbox (http://trendscenter.org/software/gift/) in Matlab were deployed with in-house workflows distributed across the TReNDs high-performance computing (HPC) environment (for specifications, see: https://help.rs.gsu.edu/display/PD/Advanced+Research+Computing+Technology+and+Innovation+Core+%28ARCTIC%29+resources) using a SLURM (Yoo, Jette, & Grondona, 2003) scheduler and resource manager. Software framework, versions, and builds by study are listed in Supplementary Table 2.

Randomness Estimations:

As described in (Vergara & Calhoun, 2016; Vergara et al., 2018a, 2018b), randomness of FNC matrices can be quantified using the mathematical framework first set forth by Girko (1985) which is now known as the circle law (Girko, 1985; Marčenko & Pastur, 1967; Trotter, 1984). Unlike graph-theory based measures (Rubinov & Sporns, 2010), the value associated with each edge in a random matrix is not weighted or binarized but is assumed to follow a Gaussian distribution with properties like the Fisher r-to-z transformed correlation. The randomness test fails (depending on hypothesis testing and statistical significance) if matrix edge values do not follow a random distribution. The proposed randomness test utilizes the characteristics of the FNC matrix using matrix singular value-spectrums. For each participant’s FNC matrix, a singular value decomposition (SVD) is computed. Assessing matrix randomness is achieved by comparing the FNC singular values (SVs) of each participant against the SVs of random matrices, where a participant’s FNC SVs are compared against SVs of randomly generated matrices M with Gaussian matrix elements. The distance ($L$) between the singular FNC vector and the randomly generated vector computed using Equation 1.

$$L={ }^2\sqrt{{{\sum }_{i\in N}\left(\frac{{\lambda }_i-{\mu }_i}{{\sigma }_i}\right)}^2}$$ 1

Where N is the total number of functional networks which make up the matrix of interest (for each participant), $i$ is a member of $N$ matrix, ${\mu }_i$ represents the mean and ${\sigma }_i$ the standard deviation of the FNC matrix of interest, and ${\lambda }_i$ is the vector with SVs for the (participant) FNC matrix of interest. Figure 1 adapted from (Vergara et al., 2018a) displays a brief illustration of the relationship between variables in the singular value spectra. The computations were performed using in-house Matlab workflow distributed across the TReNDs HPC environment described previously in the ICA section.

Figure 1.

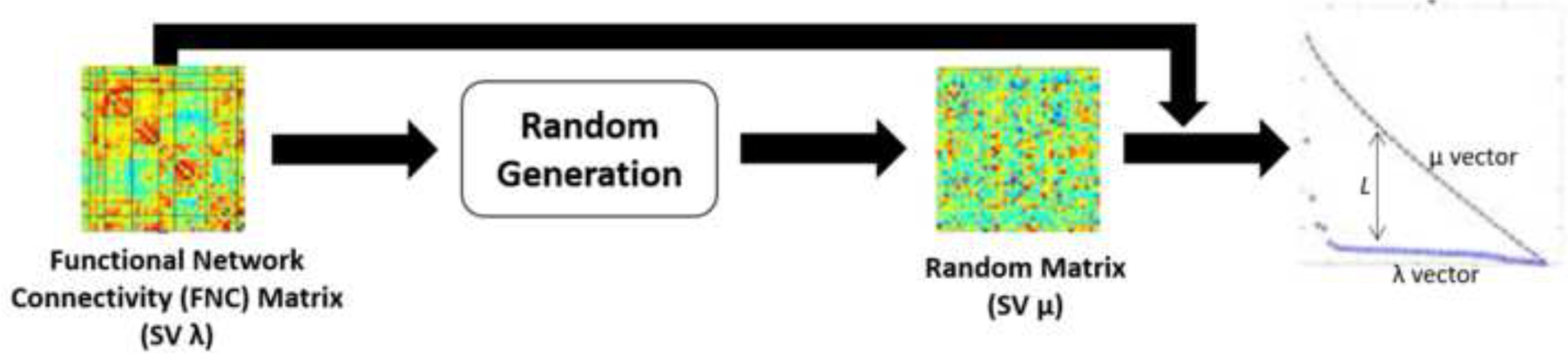
(Left) A functional network connectivity (FNC) with 𝑛!/2!(𝑛−2)! pairwise component combinations scaled to singular values (SV) $\lambda$.

(Middle) A randomly generated, gaussian-based connectivity matrix, scaled to SV $\mu$.

(Right) The $L$ distance between the plotted SVs for the randomly generated (upper $\mu$ plot), and FNC SV $\lambda$ plot. A greater value for $L$ indicates less randomness.

Once $L$ values are recorded for each participant across each resting-state paradigm and frequency bin, a single linear mixed effect (LME) model is performed on all $L$ values using the lmer function in the lme4 (Bates, Mächler, Bolker, & Walker, 2015) R package (R Core team, 2015; Team, 2019) a permutation-based LME model with age, gender, FSIQ, EC vs EO order, data acquisition site (MRN vs UNMC), resting-state paradigm (EC vs EO), frequency bin, motion, the interaction of frequency and motion, and the interaction between frequency bin and resting-state paradigm, as fixed effects using the permanova.lmer function in the lmerTest and predictmeans R packages (Bates et al., 2015; Kuznetsova, Brockhoff, & Christensen, 2017; Luo, Ganesh, & Koolaard, 2020). The permanova.lmer produces 5000 permutations of $L$ values to generate a p-distribution for the data for significance testing when the assumption of normally distributed residuals is not met. As the frequency bin is the factor of interest, and the effect of resting-state paradigm is shared within participants, pairwise comparisons of the residuals between frequencies were split across (with the effects of all other variable regressed out) resting-state paradigm and Holm corrected across all comparisons. The R version and package builds are also listed in Supplementary Table 2.

Linear Mixed-Effect model for FNC matrices:

Several LME models were fit to each pairwise r-to-z transformed FNC value within the FNC matrix using the same lmer function in the lme4 (Bates, Mächler, Bolker, & Walker, 2015) package in R, producing a total of 1225 individual analyses. This approach was selected to minimize the number of multiple comparison corrections across all frequency bins (7*1225 for FNC), for individual cell-wise regressions or pairwise contrasts. Like the previous model used for randomness, the FNC based LME model included participants as a random effect, and age, gender, FSIQ, acquisition site, resting-state paradigm, resting-state paradigm order, frequency bin (with 0.01–0.15 Hz as the reference), motion calculated using ENORM, and the interaction between frequency bin and motion as fixed effects. P-distributions for each FNC pairing were estimated using the permanova.lmer function within the predicmeans (Luo et al., 2020) package, with 5000 permuted FNC values per pairing. The effect of frequency on the FNC pairings between networks serves as the variable of interest and is false discovery rate (FDR) corrected at the level of the p-value for the omnibus F-value for each frequency bin across all FNC pairs. Interactions with motion and frequency bin (and other variables of no interest) are reported at factor-wise FDR corrected p-values to identify potential confounds and their influence on the model. The FDR corrected p-values by factor results for these variables are presented in the supplemental material.

Pairwise comparisons across the residuals of FNC pairs across frequency bin with nuisance variables removed were assessed using a Wilcoxon signed-rank test (R Core team, 2015; Team, 2019; Wilcoxon, 1946). Significant interactions between frequency bin and motion are examined using post-hoc pairwise t-tests of slopes using the emmeans (Lenth, 2019) and interactions (Long, 2019) packages in R using the emtrends function within the emmeans library.

As with the models for the $L$ variable computed in equation 1, pairwise comparisons between frequency residuals were split across resting-state paradigm and Holm corrected (Holm, 1979; Lenth, 2019; Torchiano, 2016) across all comparisons as the frequency bin is the effect of interest and the effect of resting-state paradigm is shared within participants. R version and package builds are described in Supplementary Table 2.

Results:

Matrix Randomness $L$ values for contrasts of interest:

The effects of frequency bin ($F_{\left(6,2163.5\right)}=254.401$, $p_{perm}=0.0002$, ${ }_{\text{p}}{\text{ώ}}^2=0.964$), acquisition site ($F_{\left(1,162.1\right)}=8.79$, $p_{perm}=0.0028$, ${ }_{\text{p}}{\text{ώ}}^2=0.2850$), resting-state paradigm ($F_{\left[1,2163.5\right]}=13.73$, $p_{perm}=0.0056$, ${ }_{\text{p}}{\text{ώ}}^2=0.0743$), the interaction of resting-state by frequency bin ($F_{\left(6,2163.5\right)}=4.765$, $p_{perm}=0.0004$, ${ }_{\text{p}}{\text{ώ}}^2=0.0084$) and the interaction of frequency bin and motion ($F_{\left(6,2163.5\right)}=4.84$, $p_{perm}=0.0002$, ${ }_{\text{p}}{\text{ώ}}^2=0.0082$) displayed significant differences in the model, suggesting each factor influenced noticeable changes in the $L$ randomness value. However, motion ($F_{\left(1,338.80\right)}=0.0018$, $p_{perm}=1$, ${ }_{\text{p}}{\text{ώ}}^2=-5.28\times {10}^{-6}$), age ($F_{\left(1,162.1\right)}=0.2677$, $p_{perm}=0.6106$, ${ }_{\text{p}}{\text{ώ}}^2=-0.0012$), gender ($F_{\left(1,162.1\right)}=0.0041$, $p_{perm}=1$, ${ }_{\text{p}}{\text{ώ}}^2=-2.5\times {10}^{-5}$), FSIQ ($F_{\left(1,162.1\right)}=0.0182$, $p_{perm}=1$, ${ }_{\text{p}}{\text{ώ}}^2=-1.0946\times {10}^{-5}$), or resting-state paradigm order ($F_{\left(1,2169.5\right)}=0.0098$, $p_{perm}=0.9314$, ${ }_{\text{p}}{\text{ώ}}^2=-4.48\times {10}^{-6}$) did not display statistically significant influences on the model, suggesting these factors contributed little to the variations in $L$. The conditional $R^2$ of 0.4697, and a marginal $R^2$ of 0.3680 for the model suggest a relatively short distance between the observed values and those fit by the LME model (Johnson, 2014; Nakagawa & Schielzeth, 2013), suggesting the number of factors and variables of interest in the model are not unreasonably low or high.

Despite the statistically significant effect of frequency bin in the LME model, pairwise comparisons across the main effect of frequency bin (between individual frequency bins, averaged across resting-state paradigm, e.g. 0.01–0.15 vs 0.46–0.61) were not significantly different between one another even at an uncorrected threshold for multiple comparisons. Like the frequency bin comparisons, contrast of the main effect of EC vs EO (averaged across all frequency bins) did not display statistically significant differences even at an uncorrected threshold (p = 0.7568, r = 0.0034).

When comparing within each resting-state paradigm across frequency bins (e.g. 0.15–0.31 vs 0.31–0.46 EO, 0.31–0.46 vs 0.91–1.07 EO), significant differences were identified between 0.46–0.61 vs other frequency bins in EO. For frequency bins below 0.46 Hz, most contrasts favored greater $L$ in the higher frequency bin relative to the lower bin. The exception to this trend occurred in the 0.46–0.61 Hz frequency range, which displayed significantly greater $L$ across comparisons with all other bins. The Hedge’s g effect size for each contrast is summarized in Figure 2 (left).

Figure 2.

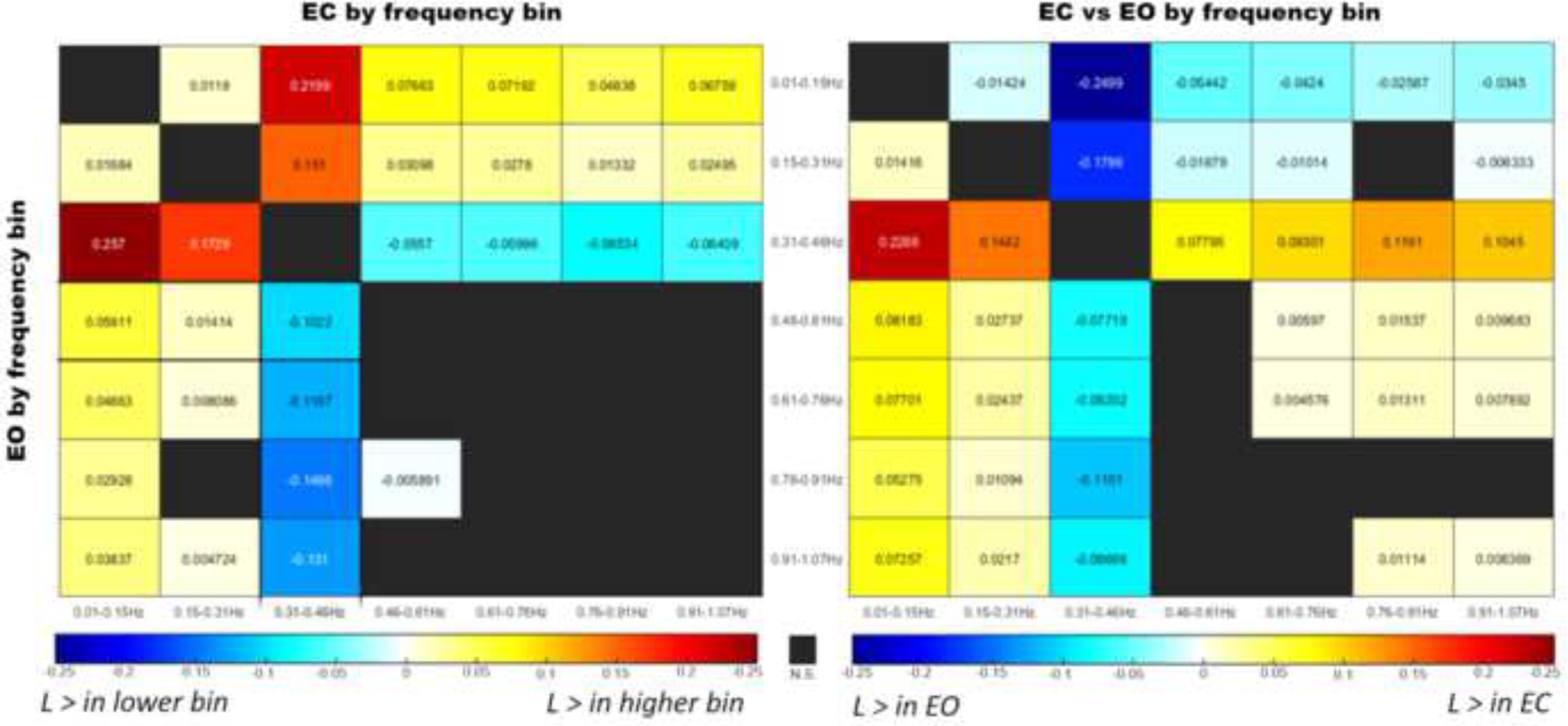
Hedge’s g measure of effect size values of pairwise slope comparisons of between-task randomness ($L$) residuals across frequency bands.

(Left) Comparisons $L$ residuals with resting-state paradigm across frequency bins with EC in the upper triangular and EO on the lower triangular. Cool colors indicate a higher $L$ value in the lower frequency bin, while warm colors indicate a higher $L$ value in the higher frequency bin

(Right) EC vs EO comparisons with EC as the reference across the seven frequency bins. Warm colors indicate greater $L$ values in the EC condition, while cool colors indicate greater $L$ values in EO.

When comparing between resting-state paradigms within the same frequency bins (e.g. 0.031–0.46 EC vs 0.31–0.46 EO), significantly increased $L$ was found in the EC matrices for the 0.61–0.76 (p = 0.0409, r = 0.0046) and 0.91–1.07 Hz bins (p = 0.006, r = 0.0064), but no other pairings. When applying the same paradigm comparison across frequency bins (e.g. 0.01–0.15 EC vs 0.15–0.31 EO), FC was noticeably less random in EC compared to EO (23 contrasts with significantly greater EC vs 14 with greater EO) across most of the contrasts. The contrasts with EO > EC occurred primarily at the lower frequency bins (0.01–0.31 Hz) and when EO from the 0.31–0.46 frequency bin was compared to any EC not within the 0.31–0.46 Hz bin. These results are summarized in Figure 2 (right).

Supplementary Pairwise Artifact Comparisons:

Motion measured using ENORM did not significantly influence the LME model used for $L$. However, significantly greater randomness in motion-by-frequency-bin slopes was found in the 0.01–0.15 Hz (p_Holm = 4.032 x 10⁻⁴, g = 0.0110) and 0.15–0.31 Hz (p_Holm = 0.0140, g = 0.0079) relative to the 0.31–0.46 Hz bin. These results are depicted in Supplementary Figure 2. No significant differences in data acquisition site were noted when contrasts were averaged across frequency bin and resting-state paradigm.

FNC comparisons for factors of interest:

Cell-wise LME models across each unique FNC paring reported marginal (fixed-effect only) $R^2$ for ranging from 0.0282–0.5435 (mean = 0.1916) and conditional (random and fixed-effects) $R^2$ from 0.1578–0.6517 (mean = 0.3645). The variability in $R^2$ suggests large, model-wise variability in fits for each FNC pair (Jaeger, 2017; Johnson, 2014; Nakagawa & Schielzeth, 2013). The linear mixed effect models found all the 1225 FNC pairs were significantly influenced (following FDR correction) by the frequency bin through which the data was filtered prior to MOO-ICAR. Partial ${\text{ώ}}^2$ values for frequency bin were also variable, ranging from 0.0003–0.9910, with 1090 (89%) meeting the criteria for a large effect for frequency bin when variance from all other independent variables are removed. For contrasts between EC vs EO (averaged across all frequency bins), roughly 712 (~58%) of the models were significantly influenced by the resting-state paradigm, with ${ }_{\text{p}}{\text{ώ}}^2$ values ranging 0.0028–0.9761, with 267 (~23%) meeting the criteria for a large effect size. When examining the interactions between the frequency bin by resting-state paradigm, 774 (~63%) of the 1225 models were significantly influenced by the relationship between resting-state paradigm and frequency bin, with ${ }_{\text{p}}{\text{ώ}}^2$ values ranging from 0.0006–0.4867, and 27 (~2%) displaying large effect sizes. Figure 3 displays both $R^2$ and ${ }_{\text{p}}{\text{ώ}}^2$ values for the bin and resting-state paradigm for all models across FNC pairs.

Figure 3.

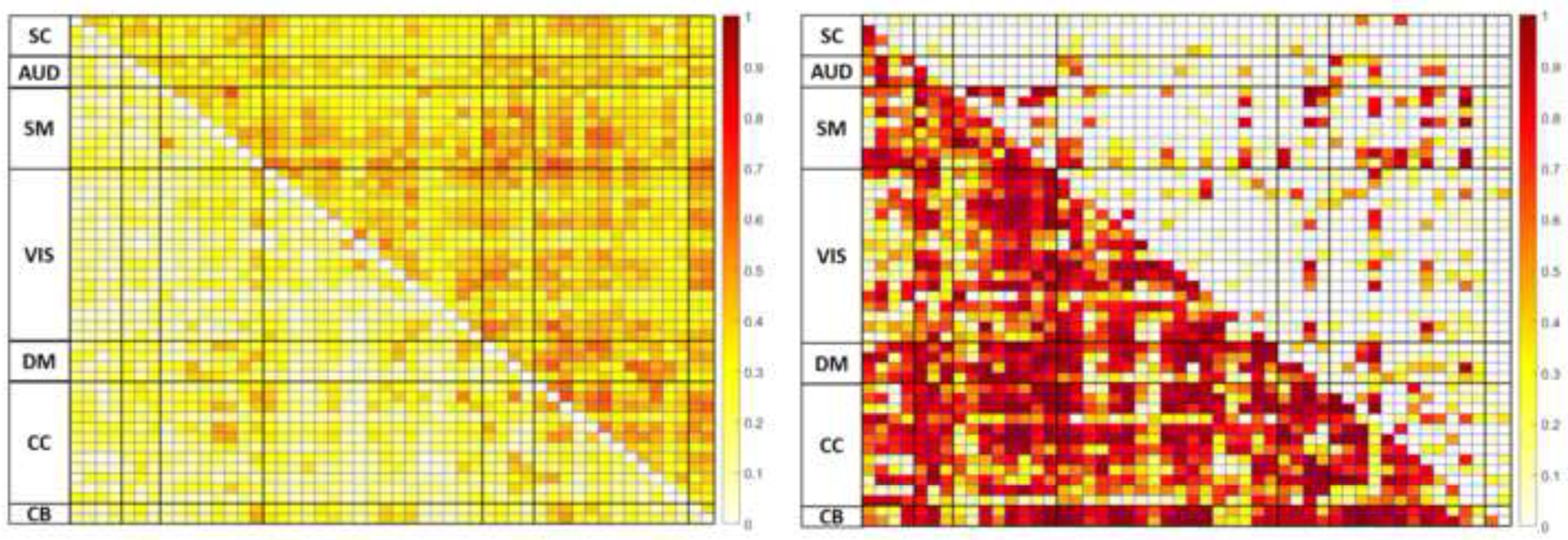
Model-fit summaries of Cell-wise FNC matrices

(Left) $R^2$ marginal (fixed-effects only, lower triangular) and $R^2$ conditional (fixed and random effects, upper triangular) indicative of model fit.

(Right) indicating ${ }_{\text{p}}{\text{ώ}}^2$ for statistically significant effects for frequency band (lower triangular) and resting-state paradigm (upper triangular).

Influences of artifact on cellwise FNC:

Statistically significant influences on FNC from data acquisition site were identified in 965 pairings (~79%), displaying effects sizes ranging from 0.0075–0.9919 ${ }_{\text{p}}{\text{ώ}}^2$, 745 of which met the criteria for large effect sizes. ENORM motion significantly influenced the LME models of 555 FC pairs (~45%), with ${ }_{\text{p}}{\text{ώ}}^2$ ranging from 0.0166–0.9504, 293 of which met criteria for a large effect size. Interactions between frequency bin and motion were identified for 836 (~68%) FC pairs, with effect sizes ranging from 0.0004–0.3314, but only 5 of which met criteria for large ${ }_{\text{p}}{\text{ώ}}^2$. These findings are discussed further in the pairwise comparisons section below.

Pairwise Comparisons:

Main effects of frequency bin and resting-state paradigm

Neither the subsequent pairwise comparisons of frequency bins averaged across both EC and EO (e.g. EC+EO 0.01–0.15 vs 0.15–0.31 Hz) analyses across frequency bins EC vs EO contrasts averaged across all frequency bins displayed statistically significant differences following pairwise EC vs EO contrasts for resting-state paradigm, or Holm corrected comparisons across frequency bins averaged across resting-state paradigms (21 contrasts). While pairwise comparisons of the main effects of resting-state paradigm or frequency bin did not appear significant when averaged, multiple contrasts of resting-state paradigm across frequency bin (91 comparisons per FC pair) were statistically significant following a Holm correction. The average r-to-z transformation for EC and EO values are displayed on the top row in Figure 4. The bottom row of Figure 4 depicts the Pearson r effect sizes of all within-frequency contrasts of EC vs EO.

Figure 4.

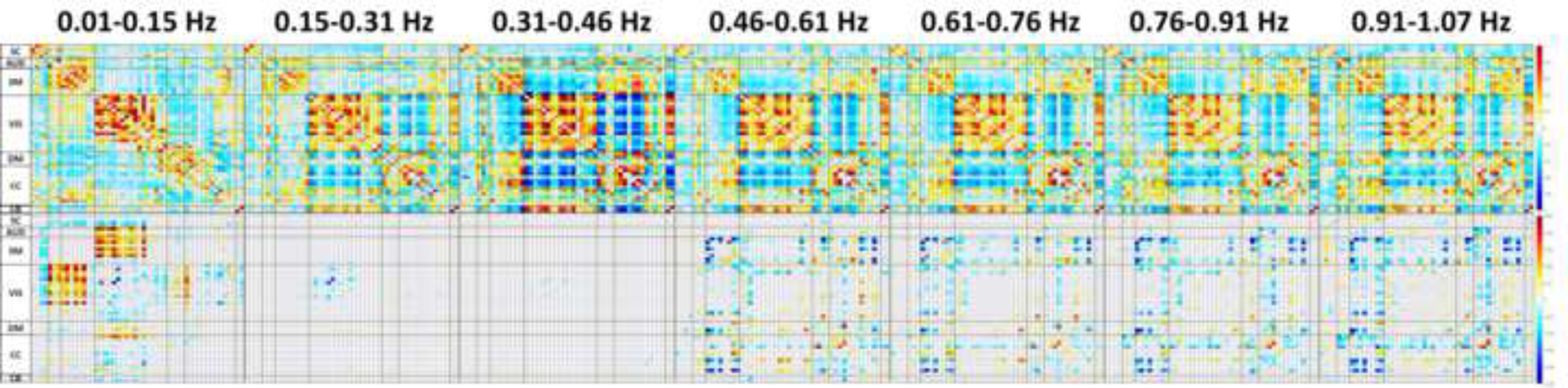
(Top) The color indicates the average value of the positive (red) or negative (blue) correlation represented with the r-to-z transform. The lower triangular matrix is averaged across EC, while the upper is averaged across EO.

(Bottom) FNC matrices of r effect sizes for FDR corrected LME models and Holm corrected pairwise tests between EC and EO within frequency bins, +r (red) indicates the value is greater in EC condition, while –r (blue) indicates greater values in the EO condition.

Note the differences in scaling between the average FC values and effect sizes.

Within resting-state paradigm across frequency bins:

For contrasts across frequency bins for EC (e.g. 0.15–0.31 EC vs 0.46–0.61 EC), within domain (FNC between one visual network and another visual network) connections were more likely to be greater in lower frequency bins for SC, SM, VS, and DM regions, with the opposite displayed in AUD and CC regions. For EO, within domain connections were more likely to be greater in lower frequencies in SC, AUD, SM, and DM pairs, with greater FC in higher frequencies more likely to occur in VIS and CC connections. Between-network connections in EC were more likely to be greater in lower frequencies in SC, AUD, SM, DMN, and CC regions and greater in higher frequencies in VIS and CB connections. For EO, lower frequencies were more likely to display increases in FC across SC, AUD, and CC regions, and greater in higher frequency bins in SM, VS, DM, and CB pairings. The distribution of these results quantified using difference scores in total results is displayed in Figure 5. In Figure 5, warm colors indicate connections where FNC values are more likely to be larger in lower frequencies, and cool colors indicate where FNC values are greater in higher frequencies compared to lower frequencies.

Figure 5.

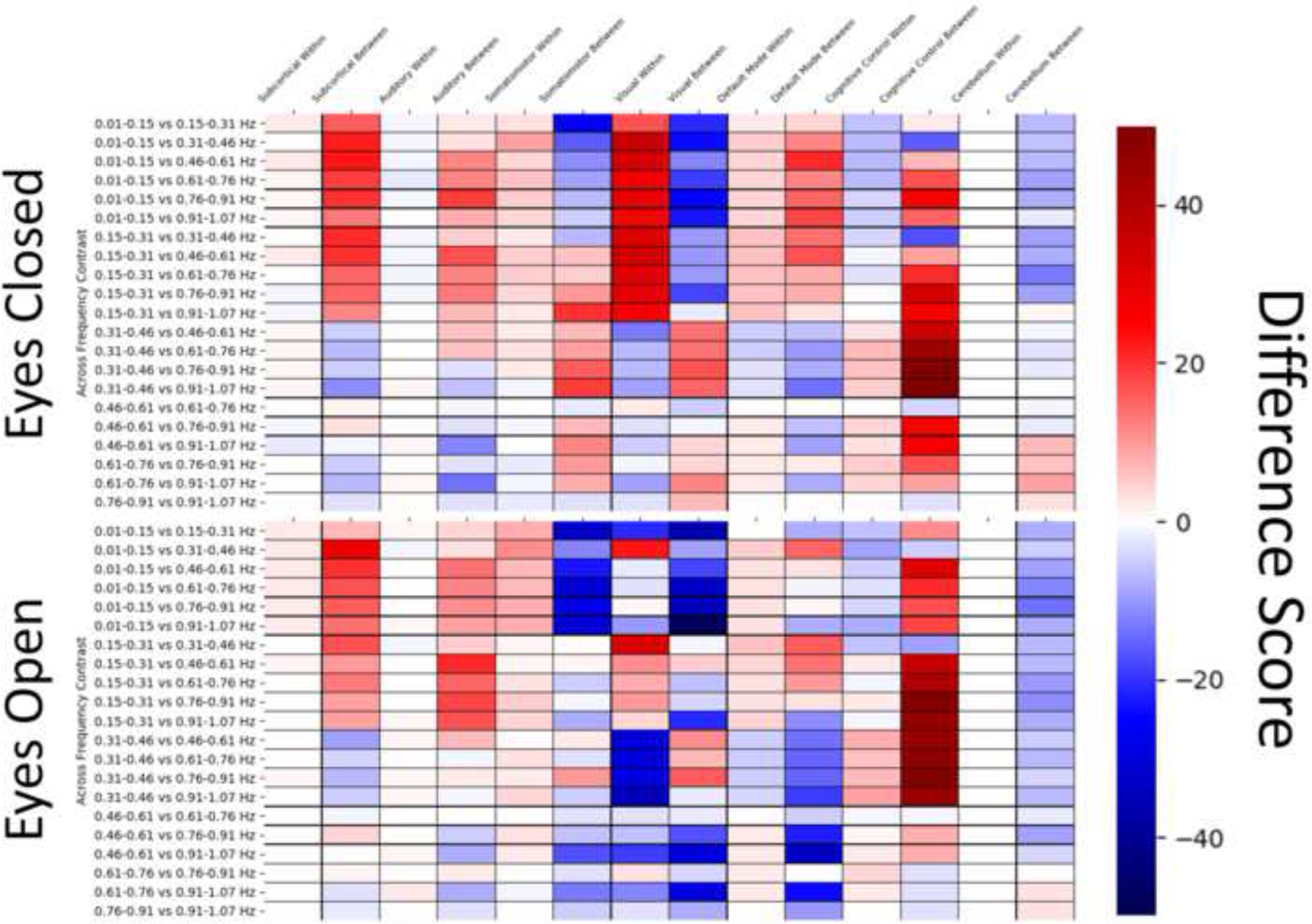
Difference scores between the total number of connections within or between a domain to quantify trends across frequency bins. Warm colors indicate that of the that more of the statistically significant results display FNC values that are greater in lower frequency bins compared to the higher frequencies, while cool colors indicate that of the total number of significant results, more tend towards greater FC in the higher frequencies.

The Top figure display the counts across the eyes open condition, while the bottom displays the eyes closed condition.

Between resting-state paradigm across frequency bins:

Of the total number of pairwise contrasts of EC vs EO results across frequency bins (60025), roughly 52% were identified as statistically significant differences between EC vs EO across the 7 frequency bins. Of these 52%, EC r-to-z values were more likely to be greater within SC, AUD, and CC pairs and between AUD and CC pairs, while EO r-to-z values were typically greater within network SM, VIS, and DM, and between network SC, SM, VIS, DM, and CB connections. Quantification using differences scores to illustrate the number of results trending towards EC vs EO are summarized in the top of Figure 6. The bottom of Figure 6 summarizes the significant results as a function of the total number of contrasts, where the number heatmap illustrates the results as a percentage of the total (111475 contrasts) across the pairwise testing of interactions between frequency bin and resting-state paradigm.

Figure 6.

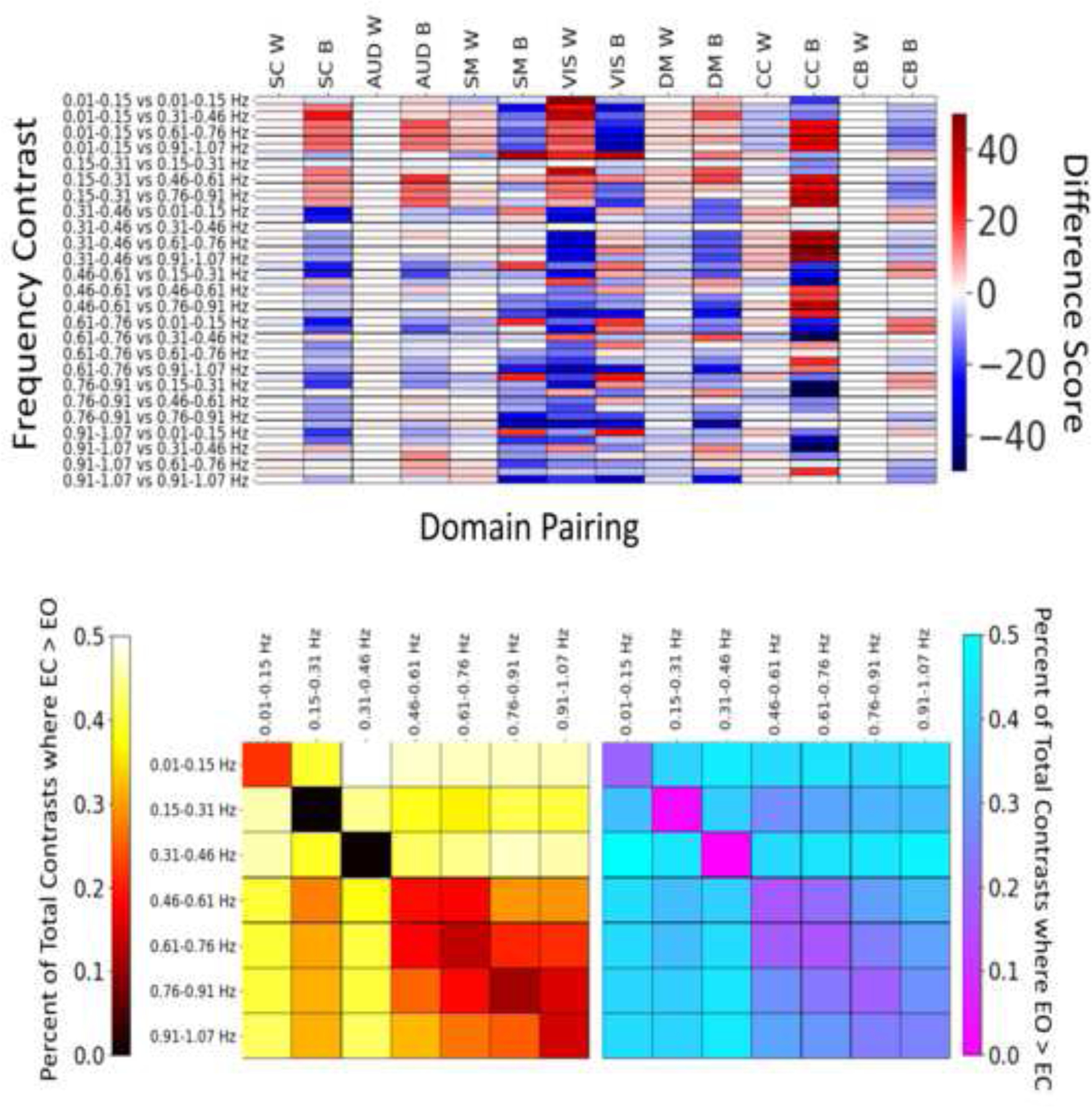
(Top) Difference scores by statistically significant result counts by domain (W indicating within domain, B indicating between domain). Warm colors indicate that a contrast trends towards FC values being greater in EC, while cool colors indicate greater values in EO.

(Bottom) Quantification of the percentages of significant results by the total number of contrasts across each frequency bin comparison. The left graph with the warm colors display contrasts where effects are greater in EC compared to EO, while the figure on the right and the cool colors indicate where EO is greater to EC. Note that the scale is in raw percentages, not fractions of the total.

LME effect sizes and unstandardized model slopes for these pairwise comparisons are illustrated in Figure 7(1). The top of Figure 7(2) depicts the slopes between resting-state-paradigm and frequency bin, while the bottom of Figure 7(2) depicts the slopes ENORM motion and frequency bin. All are relative to the 0.015–0.31 Hz filter bin serving as a base for the model. Motion-by-frequency slopes were more likely to be greater in lower frequency bins compared to higher frequencies in all types of FNC pairs except for within AUD and CB pairings.

Figure 7.

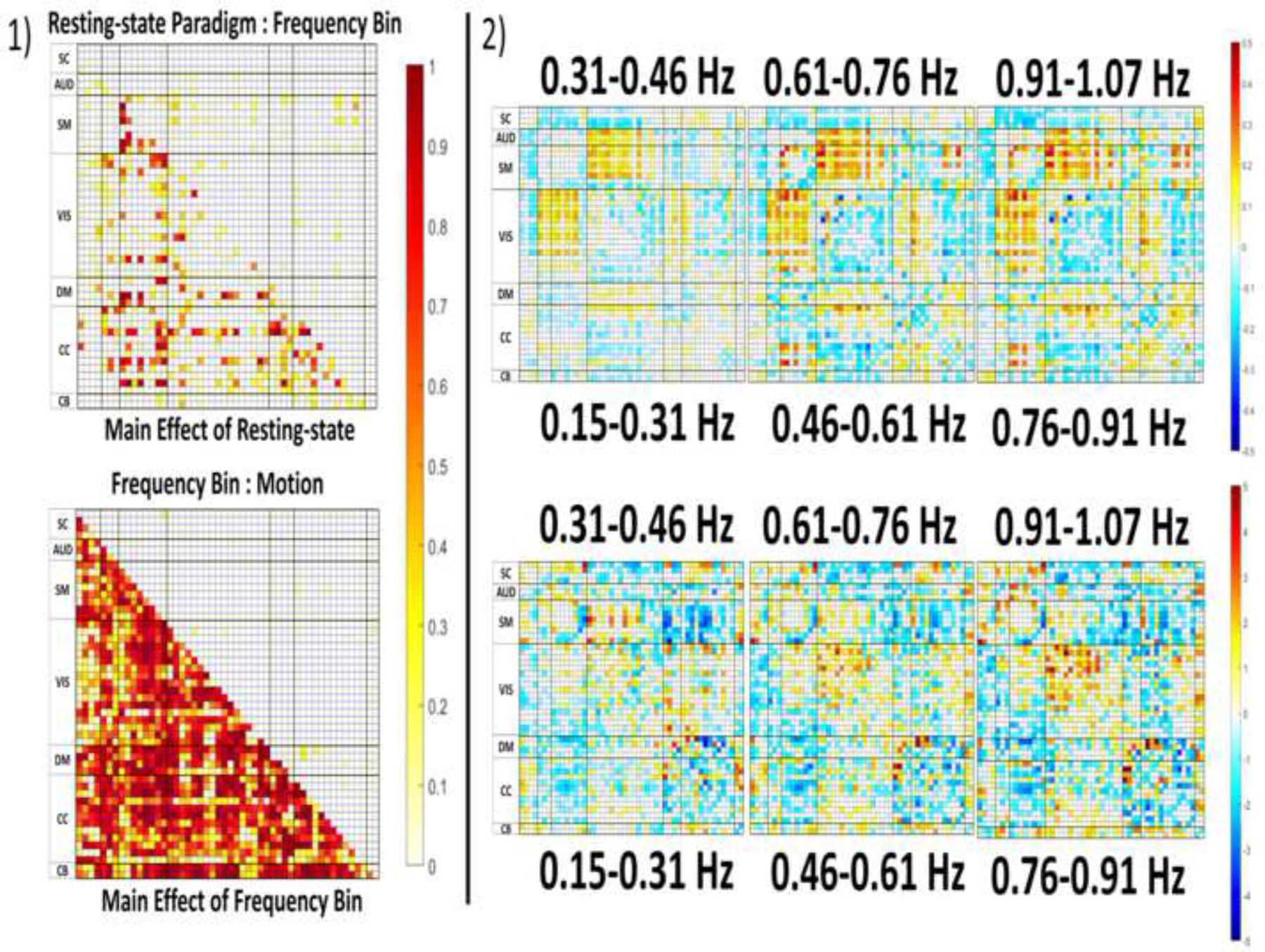
1) FNC matrices of partial ${\omega }^2$ from the linear mixed effect models.

The top image displays the partial ${\omega }^2$ for the main effect of resting-state paradigm (lower triangular), and interaction between frequency bin and resting-state paradigm (upper triangular). The bottom figure displays the ${\omega }^2$ value for the main effect of frequency bin (lower triangular) relative to the interaction between frequency bin and motion (upper triangular).

2) Top: The slopes for the interactions of resting-state paradigm by each frequency bin relative to the 0.01–0.15 frequency bin.

Bottom: The slopes of the interaction between frequency bin and motion each frequency bin above 0.01–0.15 Hz.

The slopes are unstandardized, note the differences in scale between the frequency bin slopes (−0.5, 0.05), and frequency bin by motion interaction (−5,5).

Discussion:

While the LME models indicated there are large main effects of resting-state paradigm and frequency on both matrix randomness and raw r-to-z FNC values, none of the pairwise follow-up contrasts indicated significant differences in resting-state paradigm or frequency bin. However, notable patterns were identified on randomness and FNC as functions of frequency bin and resting-state. The results suggest FNC non-randomness is greater in lower frequencies compared to higher frequencies, peaking at 0.31–0.46 Hz before displaying negligible differences across higher frequencies. However, differences between resting-state conditions are considerably less prevalent at lower frequencies compared to higher frequencies, except for the range typically employed by standard analyses. This observation suggests while both resting-state paradigm and frequency bin have significant influence on the FNC matrices, the influence is primarily within specific frequency ranges and FNC pairs. As such, studies wishing to assess fluctuations in FNC at higher frequencies will have to take differences in resting-state paradigms into account, especially in large databases where mixtures of EC vs EO paradigms are present.

Similar to the findings from Agcaoglu et al., 2019, there were significant differences in FNC between EO and EC in the lowest frequency bin (0.01–0.15 Hz). Interestingly however, few differences were found in lower-to-middle frequency bin, but differences were prevalent at frequencies above 0.46 Hz. VIS, CC and SM connections were more likely to be influenced by resting-state condition regardless of contrast, but these had much larger numbers of components/pairings relative to others so generalizations by network should consider this and may need to be replicated across datasets. However, further work using task-based (non-resting-state) fMRI would be required before such claims could be applied to cognitive research and clinical populations. Furthermore, if such information were to be utilized, it would need to be robust to acquisition parameters such as the Nyquist frequency limits set by the TR. If non-randomness can serve as a proxy for meaningful, potentially informative functional connectivity, information can be found at BOLD signal frequencies (up to the Nyquist frequency limit) higher than is typically selected for fMRI FNC analyses. Should the information in distinct BOLD frequency ranges be neural in origin, FNC matrices and other methods could serve as useful neural correlates for estimating FC coupling strength at lower frequencies, and differences across resting-state paradigms at higher frequencies.

Multiples studies using both simulated brains and real-time brain stimulation in humans and non-humans support neuronally-modulated temporal correlations between brain regions in the absence of tasks (Chan, Mohajerani, LeDue, Wang, & Murphy, 2015; Honey, Kötter, Breakspear, & Sporns, 2007; Kucyi et al., 2018; Y. Ma et al., 2016; Mateo, Knutsen, Tsai, Shih, & Kleinfeld, 2017; Matsui et al., 2011; Sporns & Betzel, 2016; Vanni, Chan, Balbi, Silasi, & Murphy, 2017). In the absence of invasive recordings, the observed synchrony among these regions have been quantified using various measures of network-quantification and randomness/coherence that frequently resemble measures from direct neural recordings (Hagmann et al., 2008; Honey et al., 2007; Kucyi et al., 2018; Y. Ma et al., 2016; Rubinov & Sporns, 2010; Sporns, 2003, 2011; Vanni et al., 2017; Vergara & Calhoun, 2016). Non-human studies have suggested FNC strength may be moderated within specific frequencies relative to the functional domain linked to the neural signal of origin, particularly those within visuomotor and the “default” network proposed by (Buckner et al., 2008) (Gohel & Biswal, 2015; Y. Ma et al., 2016; Vanni et al., 2017). Our findings of frequency-dependent alterations in somatomotor, visual, and DM domains mirror such previously reported trends. It has been noted in previous work that recordings at rest in humans or under anesthesia in non-humans vs wakefulness can alter the information at certain frequency ranges, but the findings of increased FNC values in EC goes against the suggestion that participants may engage in sleep in EC (Kucyi et al., 2018; Y. Ma et al., 2016). As such, the findings suggesting there may be frequency-dependent differences based on the resting-state paradigm are novel and warrant further exploration.

However, it is worth noting that these BOLD-based measures may be influenced by multiple artifacts. Several FNCs were significantly influenced by average participant motion even after correction for multiple comparisons. Most of these findings occurred in higher-frequencies relative to lower frequencies, and were more prevalent in SC, AUD, SM, VIS, and CC pairings. As such, careful consideration should be applied to interpretations made regarding results within these domains. The implications of this relationship is discussed further in the first paragraph of the limitations section but briefly, the 0.31–0.46 Hz range described in the results is typically a frequency range where motion from respiration aliases with framewise displacement in fMRI timeseries (Fair et al., 2020; Gratton et al., 2019). This has the unfortunate possibility of generating non-random, but artifactual, fluctuations in the signal. While the models used in this study suggest that the direct contribution of motion is minimal, the notable interactions with motion and frequency bin (summarized in Supplementary Figure 2) obligate the authors to urge caution linking non-random patterns of BOLD signal to neuronal sources alone. Future work would benefit from combinations of ICA, nuisance spectra (Fair et al., 2020; Gratton et al., 2019) and data-driven optimization not only to isolate signal of interest, but also design objective filters to minimize artifact, as artifact and signal of interest may not be compartmentalized to the evenly-spaced frequency bins selected for this analysis.

These results are the first to the author’s knowledge to examine differences in high-frequency BOLD FNC analyses within an ICA framework. While it has been explored in other work (Chen et al., 2017), the focus of that study was on high-frequency contamination from sequential nuisance regression, an approach that was eschewed in within the current study. The results presented here provide a starting point for the development of tools to assess and tune BOLD-based resting-state paradigm and FNC analyses, with the potential to expand into temporal dynamics once specific trends have been isolated and replicated across datasets. Further, the “bin-based” approach common within the high-frequency literature may be sub-optimal and implementing data-driven methods for filtering may expand on the results presented here.

Limitations:

As with any fMRI study, the effects of motion may significantly contribute to the measured BOLD signal, particularly long vs short range FNC values. Furthermore, recent work has identified that short TR multi-band sequences have respiration artifacts that alias with motion estimates, and without information specific to respiration (e.g. waist bellows) notch filtering is recommended to mitigate respiration (Fair et al., 2020; Gratton et al., 2019). For the current study however, motion measures likely mixed with respiration were fitted as a single regressor, both to avoid the loss of frequency specific information associated with notch filtering, and because respiration information was not collected in the dataset. It is an unfortunate reality that many of even the largest and most well-curated databases (e.g. most of the INDI databases like ABIDE and ADI) and even in large, well-curated databases like OpenNeuro.org, (as of this manuscript) only 15 datasets have physiological information available. As such, the authors suggest that follow-up research using datasets with respiratory information would significantly improve interpretation regarding the contribution of nuisance variables across the frequency spectrum. Further, the authors suggest that researchers utilizing multi-band for data collection include methods to record respiratory signal.

Previous work by Chen et al. 2017 and others identified a relationship in which stepwise nuisance regression may negatively influence signal at higher frequencies. The authors attempted to avoid this problem by applying the filtering directly to the data with no nuisance regressions, but included covariates and nuisance variables (variance and effect sizes for motion and the motion by bin interactions were relatively small, with a minimal number of the LMEs returning as statistically significant). However, it should be noted that partial ${ }_{\text{p}}{\text{ώ}}^2$ does not take correlations for within-participant measures into account, producing 25–50% inflation within the total ${ }_{\text{p}}{\text{ώ}}^2$. While generalized (${ }_g{\text{ώ}}^2$) addresses this limitation, its computation is not intuitive for models with many factors. While the authors acknowledge this limitation, it is worth noting that even with a conservative 50–75% reduction in ${ }_{\text{p}}{\text{ώ}}^2$, the effect size of frequency bin is still quite large (${ }_{\text{p}}{\text{ώ}}^2>0.14$), and the nuisance variable ${ }_{\text{p}}{\text{ώ}}^2$ values are small. As such, the authors conclude that while motion may have influenced the signal within some connections, the effect seems minimal within the overall results.

It is worth noting the FNC patterns and $L$ increasing up to the 0.31–0.46 Hz frequency bin and decreasing as the frequency continued to increase likely varies depending of the type (single vs multi-band) and TR of the data. As such, while the authors conclude visually that randomness and FNC patterns appear to be modular, generalization of this pattern across variable TRs and acquisition parameters has yet to be established.

The method used to remove frequency information outside of the “bins” of interest is not a true digital filter of the data, but rather a regression model where all signal outside of the bin of interest is treated as nuisance information. While this approach is advocated by research groups performing nuisance regression with fMRI data (Chen et al., 2017; Lindquist et al., 2019), the effect on the frequency from a phase perspective, the degree of ripple, and the speed of the transition from passband to stopband has not been studied in detail. Effects of the nuisance-regression approach will need to be examined before broader conclusions are made.

Even when considering these limitations, the results of this research indicate there is paradigm-mediated variability in higher-frequency component FNC, which may be developmentally, cognitively, and diagnostically useful. When spatially constraining independent component analyses derived from full-spectrum data to selective “bins” across higher frequencies, large differences in the FNC measures and randomness were identified even when the effects of some nuisance variables were considered. Identifying frequency-specific components has the potential to improve heuristic classification approaches, and the authors encourage the development of data-driven measures for BOLD filter design and applications with this goal in mind.

Highlights.

• fMRI matrix randomness decreases in lower BOLD frequencies compared to higher frequencies.

• BOLD signal appears least random in the 0.31–0.46 Hz range of those examined.

• Eyes closed vs open rsfMRI produce different results.

• Eyes closed vs open differences are greater above the 0.46 Hz range.