Riccati transfer equations for fluid structure interaction in liquid-filled piping systems

Abstract

In this paper, based on the Riccati transfer matrix method (RTMM), the Riccati fluid structure interaction transfer equations (FSIRTE) are established to improve the numerical stability of the classical fluid structure interaction transfer matrix method (FSITMM). Combined with numerical algorithms for eliminating the singularity points of the Riccati equations, the spare root problem in the calculation process is solved. This method can be used for the natural frequency calculation of liquid-filled piping systems. Compared with finite element method (FEM), it has the characteristics of high calculation efficiency; meanwhile, good numerical stability, compared with FSITMM; and accurate calculation results, compared with method of characteristics (MOC). Numerical simulation results of typical classical examples are given.

Highlights

• •Riccati transfer matrix method is used for fluid-structure interaction analysis.
• •Riccati fluid structure interaction transfer equations are provided to simulate a fluid-filled piping system.
• •Numerical methods for eliminating the singularity points of the Riccati equations were added to improve numerical stability of Riccati fluid structure interaction transfer equation.

1. Introduction

The fluid structure interaction (FSI) phenomenon exists in various mechanical equipment such as oil pipelines, aircraft, and shield tunneling machine. Pressure pulsations and mechanical vibrations in liquid-filled piping systems strongly affect system performance and safety. Therefore, people's enthusiasm for the study of FSI has been unabated.

In 1939, Bourrieres first derived the differential equation of motion of the cantilever liquid-filled tube [1]. Joukowsky published the famous paper “On the hydraulic hammer in water supply pipes” through research on the Moscow water supply system [2], and proposed the theory of water hammer for the first time. Up to now, there are three main numerical methods for FSI dynamic simulation: 1) Method of characteristics (MOC). Since both the liquid pulsations and the pipe vibrations in the liquid-filled piping system can be represented by a set of partial differential equations (i.e., wave equations), they can be effectively transformed into a set of special ordinary differential equations by MOC, and then by the numerical integration method, it is convenient to use computer for calculation, so MOC has been widely used in pipeline response calculation. Wiggert et al. [[3], [4], [5]] studied the calculation of the axial vibration response of the liquid-filled piping system considering FSI, and extended it to the bending and torsional vibration of the pipe. They also pointed out the error caused by the interpolation calculation. Tijsseling considered the axial and transverse bending vibrations of a straight pipe, and studied the effect of the coupling between the liquid and the pipe during the in-plane vibration of a single-elbow pipe system [6]. Zhang et al. [[7], [8], [9]] proposed the L-MOC based on Laplace transform to solve the FSI problem of a single straight pipe, and this method partially improved the numerical accuracy. MOC can directly solve the vibration wave equation in the pipe system, and the physical meaning is clear. However, due to the existence of various waves in the pipe system, when MOC is used, there are many characteristic lines, and there must be characteristic lines that do not pass through the calculation grid. The parameter values on these nodes must be obtained through interpolation methods, resulting in interpolation errors. Tijsseling [10] had to “slightly adjust” the wave speed to achieve the intersection of the characteristic lines. The multi-characteristic lines interpolation error problem has not been well solved, and it has become the main factor restricting the further development of MOC in calculating the vibration response of the liquid-filled piping systems. 2) Finite element method (FEM). FEM is a relatively mature method for structural modal analysis and response calculation [11,12]. The semi-analytical method combined with large-scale engineering software has also solved many complex piping problems [13,14]. Now many large-scale software, such as ANSYS FLUENT, have FSI modules for calculation and analysis. However, due to the complicated coupling between the pipeline and the fluid, modeling is difficult. FEM has low calculation efficiency and long calculation time, that is not suitable for design and optimization in engineering practice. 3) Transfer matrix method (TMM). TMM is an effective method for modal analysis of chained systems. Dupuis and Rousselet [15] considers the initial deformation of the pipeline under the action of the liquid, the shear of the pipeline, the curvature changes of the axial deformation and the bending, and establishes the differential equation of motion of the pipeline, then, uses the TMM to calculate it. Lesmez et al. considers Poisson coupling and connection coupling between pipes and liquids [16]. They established the transfer matrix of the liquid-filled straight pipe and gave the treatment method of the curved pipe. Variational iteration method is also applied to investigate the dynamic behavior and stability of pipe. TMM is used to assemble the system of equations resulting from applying the boundary conditions [17,18]. The advantage of TMM is that the calculation efficiency is high, the dimension of the total transfer matrix remains unchanged with the increase of elements. However, the total transfer matrix is obtained by matrix-chain multiplication. When the system frequency is very high, the elements of the total transfer matrix become very large. This can lead to numerical instability when solving the overall transfer equation of the system [[19], [20], [21]]. In order to improve the numerical stability of TMM, Horner and Pilkey proposed Riccati transfer matrix method (RTMM) for chained multibody systems [22]. By adding the Riccati transfer matrix, the original two-point boundary value problem was transformed into a one-point initial value problem. This approach retains the advantages of the usual transfer matrix while improving numerical stability. RTMM is widely used in the eigenvalue solution of chained systems. Rui and Bestle proposed a decoupling method for hinge elements, which solved the calculation problem in the presence of a closed loop and expanded the application range of RTMM [23]. However, the RTMM may introduce two more problems, first, there are singularity points in the characteristic equation of the system established by RTMM, and these singularity points are often very close to the zero point of the characteristic equation. Therefore, using a general search step to solve will get spare roots, and reducing the search step will greatly reduce the computational efficiency. The existing literature on the RTMM to study the FSITMM rarely discusses how to eliminate singularities. Gu et al. established a method to eliminate singularity points, which effectively improved the eigenvalue search efficiency of RTMM [21]. In this paper, this method is also used for numerical simulation of the Riccati fluid structure interaction transfer equations (FSIRTE). Second, the RTMM can hardly deal with complex boundary conditions [24]. Since the model in this paper is still a chain system, the complex boundary problem is not obvious. For complex systems, tree system models [21] using improved RTMM will be built to solve complex boundary problems in the next study.

Actively generated high frequency waves are studied widely and applied in transient-based leak detection for pipe systems. but the model of the pipeline is still a rigid body model [25], it is not seen as a fluid structure interaction model, there is no study of the impact of high-frequency waves on the pipeline using the FSI, which will result in less accurate damage location. The impact of high-frequency seismic waves on the pipeline is being paid more and more attention to, most of the research has adopted the finite element method [[26], [27], [28]], and the study of the high-frequency vibration characteristics of the pipeline system itself is not in-depth. Therefore, it is of practical significance to study the high frequency vibration of piping system.

In section 2 of this paper, the traditional fluid structure interaction transfer matrix method (FSITMM) is derived to obtain the transfer equation for the straight pipe. In section 3, with the help of RTMM, FSIRTE are derived, and method to improve the efficiency of searching for roots are introduced. In section 4, taking Dundee tube model as an example, numerical simulation is given to verify the correctness of FSIRTE. The conclusions given in the last section show the possibility of applying our method to FSI.

2. Classical FSITMM

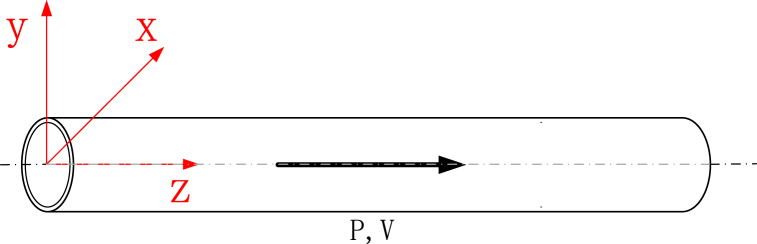
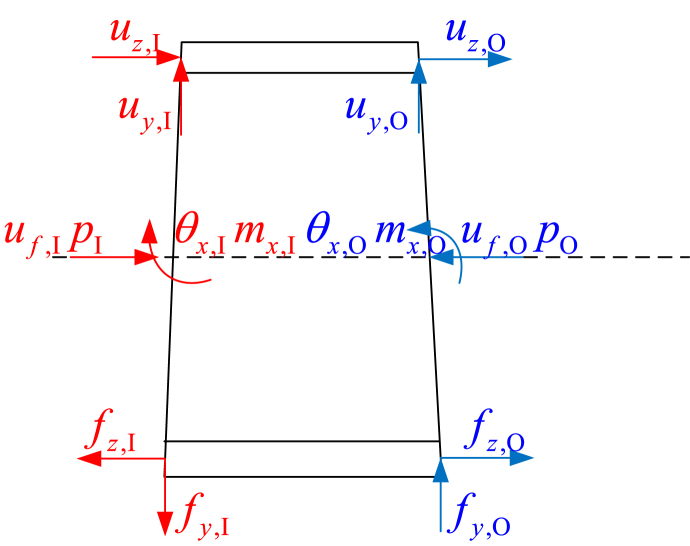
The equations discussed in this paper are in the frequency domain and are based on the physical model of Fig. 1. The model follows the assumptions: The model is based on Timoshenko beam theory. Straight pipes are placed horizontally. The wall material is linear, uniform and isotropic. The pipe deformation is within the elastic range. The pipe transports compressible Newtonian fluid. The fluid flows uniformly in one dimension without cavitation. Gravity of the pipe and fluid is ignored. The damping value is considered as additional stiffness, which is not represented independently in the matrix. The coordinate axis Z axis is along the neutral axis of the pipe when it is not deformed, and points to the direction of fluid flow; the Y axis is vertically upward; the X axis is given by the right-hand Cartesian coordinate system criterion. As shown in Fig. 2, a basic element in the FSITMM is defined, including the pipe wall and the fluid in it. The element is subjected to four generalized forces ($f_z$ is the pipe axial stress, $p$ is the fluid pressure, $f_y$ is the pipe vertical stress, $m_x$ is the pipe bending moment), which produce four generalized displacements ($u_z$ is the axial displacement of the pipe, $u_f$ is the fluid displacement, $u_y$ is the pipe vertical displacement, ${\theta }_x$ is the pipe bend angle) under the action of the generalized forces. In Fig. 2, the subscripts $\mathrm{I}$ denote input and $\mathrm{O}$ denote output. These eight quantities will be discussed in the next section as the state vectors of the system.

Fig. 1.

Physical model of liquid-filled straight pipe.

Fig. 2.

Basic element in the FSITMM.

2.1. Axial vibration

The axial vibration equation considering friction coupling and Poisson coupling [16] can be expressed as

$$\frac{{\partial }^2{u}_f}{\partial t^2}+\frac{1}{{\rho }_f}\frac{\partial p}{\partial z}+\frac{C_f\mu }{4R^2}\left(\frac{\partial u_f}{\partial t}-\frac{\partial u_z}{\partial t}\right)=0$$ (1)

$$\frac{1}{{\rho }_f{a}_f^2}\frac{\partial p}{\partial t}+\frac{{\partial }^2{u}_f}{\partial z\partial t}-2v\frac{{\partial }^2{u}_z}{\partial z\partial t}=0$$ (2)

$$\frac{{\partial }^2{u}_z}{\partial t^2}-\frac{1}{{\rho }_p{A}_p}\frac{\partial f_z}{\partial z}+\frac{C_z}{{\rho }_p{A}_p}\frac{\partial u_z}{\partial t}-\frac{{\rho }_f}{{\rho }_p}\frac{R}{e}\frac{C_f\mu }{8R^2}\left(\frac{\partial u_f}{\partial t}-\frac{\partial u_z}{\partial t}\right)=0$$ (3)

$$\frac{1}{E{A}_p}\frac{\partial f_z}{\partial t}-\frac{{\partial }^2{u}_z}{\partial z\partial t}-\frac{vR}{Ee}\frac{\partial p}{\partial t}=0$$ (4)

where $\mu$ is viscosity, $v$ is Poisson's ratio, ${\rho }_f$ is the fluid mass density, ${\rho }_p$ is the pipe mass density, $R$ is the inner diameter of the pipe, $e$ is the pipe wall thickness, $A_p$ is the pipe cross-sectional area, $E$ is the pipe Bulk Modulus, $K$ is the fluid Bulk Modulus, $a_f=\sqrt{KEe{\left[{\rho }_f\left(Ee+2KR\left(1-v^2\right)\right)\right]}^{-1}}$ is the liquid pressure wave velocity, $C_z$ and $C_f$ are damping coefficients [29].

By observing the four Eqs. (1), (2), (3), (4), simplifying towards $u_z,p$ is found to be more convenient,

$$2v\frac{{\partial }^3{u}_z}{\partial z\partial t^2}+\left(2v-1\right){\bar{C}}_f\frac{{\partial }^2{u}_z}{\partial z\partial t}-\frac{1}{{\rho }_f{a}_f^2}\frac{{\partial }^{2}p}{\partial t^2}-\frac{{\bar{C}}_f}{{\rho }_f{a}_f^2}\frac{\partial p}{\partial t}+\frac{1}{{\rho }_f}\frac{{\partial }^{2}p}{\partial z^2}=0$$ (5)

$$\frac{{\partial }^3{u}_z}{\partial z\partial t^2}+\left(\frac{c_z}{{\rho }_p{A}_p}+\frac{{\rho }_f}{{\rho }_p}\frac{R}{e}\frac{{\bar{C}}_f}{2}-v{\bar{C}}_f\frac{{\rho }_f}{{\rho }_p}\frac{R}{e}\right)\frac{{\partial }^2{u}_z}{\partial z\partial t}-a_p^2\frac{{\partial }^3{u}_z}{\partial z^3}+\frac{R}{e}\frac{{\bar{C}}_f}{2{\rho }_p{a}_f^2}\frac{\partial p}{\partial t}-\frac{vR}{{\rho }_{p}e}\frac{{\partial }^{2}p}{\partial t^2}=0$$ (6)

where ${\bar{C}}_f=C_f\mu /4R^2$.

The mode separation method is used, letting $u_z=U_z\left(z\right)\exp \left(st\right)$, $p=P\left(z\right)\exp \left(st\right)$,

$$\left[2v\left(s^2+s{\bar{C}}_f\right)-s{\bar{C}}_f\right]\frac{\partial U_z}{\partial z}-\frac{s^2+s{\bar{C}}_f}{{\rho }_f{a}_f^2}P+\frac{1}{{\rho }_f}\frac{{\partial }^{2}P}{\partial z^2}=0$$ (7)

$$a_p^2\frac{{\partial }^3{U}_z}{\partial z^3}-\left[s^2+\frac{c_{z}s}{{\rho }_p{A}_p}+\frac{1}{2}\left(1+2v\right)bd{\bar{C}}_{f}s\right]\frac{\partial U_z}{\partial z}+\frac{vb}{{\rho }_p}\frac{{\partial }^{2}P}{\partial z^2}-\frac{b{\bar{C}}_{f}s}{2{\rho }_p{a}_f^2}P=0$$ (8)

After the damping terms are ignored, Eqs. (7), (8) can be combined as

$$\frac{{\partial }^{4}P}{\partial z^4}-\left(\frac{s^2}{a_f^2}+\frac{s^2}{a_p^2}+\frac{2v^{2}bd}{a_p^2}{s}^2\right)\frac{{\partial }^{2}P}{\partial z^2}+\left(\frac{s^4}{a_f^2{a}_p^2}\right)P=0$$ (9)

$P$ is defined as $P=\bar{C}\exp \left(\lambda \eta \right)$, in which $\eta =z/L$ is the relative position, and substitute it into the characteristic Eq. (9)

$${\lambda }^4-\left(\alpha +\beta +\gamma \right){\lambda }^2+\alpha \beta =0$$ (10)

where $\alpha ={\left(sL\right)}^2/a_f^2$, $\beta ={\left(sL\right)}^2/a_p^2,\gamma =2v^{2}bd\beta$.

The solution to Eq. (10) has the form as

$$P=Q_1\cos \left({\lambda }_1\eta \right)+Q_2\sin \left({\lambda }_1\eta \right)+Q_3\cos \left({\lambda }_2\eta \right)+Q_4\sin \left({\lambda }_2\eta \right)$$ (11)

where $Q_i$ are undetermined coefficients.

Similarly, by simplifying Eqs. (1), (2), (3), (4) to variables $f_z,u_f,u_z$, and then performing modal transformation in the same way, an equation similar to Eq. (11) with undetermined coefficients can be obtained.

In order to facilitate the solution, $F$ is regarded as the reference state vector

$$F=A_1\cos \left({\lambda }_1\eta \right)+A_2\sin \left({\lambda }_1\eta \right)+A_3\cos \left({\lambda }_2\eta \right)+A_4\sin \left({\lambda }_2\eta \right)$$ (12)

$A_i$ are also undetermined coefficients.

During the simplification process, multiple sets of equations containing only two unknowns are obtained, such as Eq. (7). Substituting Eq. (12) into these equations, equations expressed in $A_i$ are presented, respectively, yielding the three equations below

$$V_f=B_1\left[A_1\sin \left({\lambda }_1\eta \right)-A_2\cos \left({\lambda }_1\eta \right)\right]+B_2\left[A_3\sin \left({\lambda }_2\eta \right)-A_4\cos \left({\lambda }_2\eta \right)\right]$$ (13)

$$V_z=B_3\left[A_1\sin \left({\lambda }_1\eta \right)-A_2\cos \left({\lambda }_1\eta \right)\right]+B_4\left[A_3\sin \left({\lambda }_2\eta \right)-A_4\cos \left({\lambda }_2\eta \right)\right]$$ (14)

$$P=B_5\left[A_1\cos \left({\lambda }_1\eta \right)+A_2\sin \left({\lambda }_1\eta \right)\right]+B_6\left[A_3\cos \left({\lambda }_2\eta \right)+A_4\sin \left({\lambda }_2\eta \right)\right]$$ (15)

where

$$B_1=L{\lambda }_1\left(\beta +{\lambda }_1^2\right)/\left(K\alpha \beta vb{A}_p\right),B_2=L{\lambda }_2\left(\beta +{\lambda }_2^2\right)/\left(K\alpha \beta vb{A}_p\right),B_3=-L{\lambda }_1/\left(E\beta A_p\right),B_4=-L{\lambda }_2/\left(E\beta A_p\right),B_5=\left(\beta +{\lambda }_1^2\right)/\left(\beta vb{A}_p\right),B_6=\left(\beta +{\lambda }_2^2\right)/\left(\beta vb{A}_p\right)$$

Further, Eqs. (12), (13), (14), (15) can be arranged into matrix form as

$$\left[\begin{array}{c}{V}_f\\ V_z\\ F\\ P\end{array}\right]=\underset{\mathit{B}\left(\eta \right)}{\underbrace{\left[\begin{array}{cccc}{B}_1\sin \left({\lambda }_1\eta \right)& -B_1\cos \left({\lambda }_1\eta \right)& B_2\sin \left({\lambda }_2\eta \right)& -B_2\cos \left({\lambda }_2\eta \right)\\ B_3\sin \left({\lambda }_1\eta \right)& -B_3\cos \left({\lambda }_1\eta \right)& B_4\sin \left({\lambda }_2\eta \right)& -B_4\cos \left({\lambda }_2\eta \right)\\ \cos \left({\lambda }_1\eta \right)& \sin \left({\lambda }_1\eta \right)& \cos \left({\lambda }_2\eta \right)& \sin \left({\lambda }_2\eta \right)\\ B_5\cos \left({\lambda }_1\eta \right)& B_5\sin \left({\lambda }_1\eta \right)& B_6\cos \left({\lambda }_2\eta \right)& B_6\sin \left({\lambda }_2\eta \right)\end{array}\right]}}\left[\begin{array}{c}{A}_1\\ A_2\\ A_3\\ A_4\end{array}\right]$$ (16)

Eq. (16) holds for any position, of course for $\eta =0$, $\eta =1$,

$${\left[\begin{array}{cccc}{V}_f& V_z& F& P\end{array}\right]}_{\mathrm{i}\mathrm{n}}^{\mathrm{T}}=\mathit{B}\left(0\right){\left[\begin{array}{cccc}{A}_1& A_2& A_3& A_4\end{array}\right]}^{\mathrm{T}}$$ (17)

$${\left[\begin{array}{cccc}{V}_f& V_z& F& P\end{array}\right]}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{T}}=\mathit{B}\left(1\right){\left[\begin{array}{cccc}{A}_1& A_2& A_3& A_4\end{array}\right]}^{\mathrm{T}}$$ (18)

In order to remove the undetermined coefficients $A_i$, Eqs. (17), (18) are combined to obtain a new equation as

$${\left[\begin{array}{cccc}{V}_f& V_z& F& P\end{array}\right]}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{T}}=\mathit{U}{\left[\begin{array}{cccc}{V}_f& V_z& F& P\end{array}\right]}_{\mathrm{i}\mathrm{n}}^{\mathrm{T}}$$ (19)

where

$$\mathit{U}=\mathit{B}\left(1\right){\mathit{B}}^{-1}\left(0\right)=\left[\begin{array}{cccc}{B}_1\sin \left({\lambda }_1\right)& -B_1\cos \left({\lambda }_1\right)& B_2\sin \left({\lambda }_2\right)& -B_2\cos \left({\lambda }_2\right)\\ B_3\sin \left({\lambda }_1\right)& -B_3\cos \left({\lambda }_1\right)& B_4\sin \left({\lambda }_2\right)& -B_4\cos \left({\lambda }_2\right)\\ \cos \left({\lambda }_1\right)& \sin \left({\lambda }_1\right)& \cos \left({\lambda }_2\right)& \sin \left({\lambda }_2\right)\\ B_5\cos \left({\lambda }_1\right)& B_5\sin \left({\lambda }_1\right)& B_6\cos \left({\lambda }_2\right)& B_6\sin \left({\lambda }_2\right)\end{array}\right]{\left[\begin{array}{cccc}0& -B_1& 0& -B_2\\ 0& -B_3& 0& -B_4\\ 1& 0& 1& 0\\ B_5& 0& B_6& 0\end{array}\right]}^{-1}$$

In the process of numerical simulation of Eq. (19), there is a large difference in the order of magnitudes of the elements. Therefore, people often normalize them for numerical stability

$${\left[\begin{array}{cccc}{\bar{V}}_f& {\bar{V}}_z& \bar{F}& \bar{P}\end{array}\right]}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{T}}=\bar{\mathit{U}}{\left[\begin{array}{cccc}{\bar{V}}_f& {\bar{V}}_z& \bar{F}& \bar{P}\end{array}\right]}_{\mathrm{i}\mathrm{n}}^{\mathrm{T}}$$ (20)

where

$$\bar{\mathit{U}}=\left[\begin{array}{cccc}{C}_0-\left({\alpha }_1+{\gamma }_1\right)C_2& -2v{\beta }_1{C}_2& 2v\left[C_1-\left({\alpha }_1+{\beta }_1+{\gamma }_1\right)C_3\right]& U_{14}\\ -vb{\alpha }_1{C}_2{h}^{-1}& C_0-{\beta }_1{C}_2& C_1-\left({\beta }_1+{\gamma }_1\right)C_3& vb{h}^{-1}\left[\left({\alpha }_1+{\beta }_1+{\gamma }_1\right)C_3-C_1\right]\\ vb{\alpha }_1{\beta }_1{C}_3{h}^{-1}& {\beta }_1\left({\beta }_1{C}_3-C_1\right)& C_0-{\beta }_1{C}_2& vb{\beta }_1{C}_2{h}^{-1}\\ {\alpha }_1\left[C_1-\left({\alpha }_1+{\gamma }_1\right)C_3\right]& -2v{\alpha }_1{\beta }_1{C}_3& -2v{\alpha }_1{C}_2& C_0-\left({\alpha }_1+{\gamma }_1\right)C_2\end{array}\right]$$

$$U_{14}=\left[{\left({\alpha }_1+{\gamma }_1\right)}^2+{\beta }_1{\gamma }_1\right]{\alpha }_1^{-1}{C}_3-\left({\alpha }_1+{\gamma }_1\right){\alpha }_1^{-1}{C}_1$$

$${\alpha }_1=\frac{{\left(\omega L\right)}^2}{a_f^2},{\beta }_1=\frac{{\left(\omega L\right)}^2}{a_p^2},{\gamma }_1=2v^{2}bd{\beta }_1,b=\frac{R}{e},d=\frac{{\rho }_f}{{\rho }_p},h=E/K$$

$$C_0={\Delta }_1\left[{\lambda }_2^2\cos \left({\lambda }_1\right)-{\lambda }_1^2\cos \left({\lambda }_2\right)\right],C_1={\Delta }_1\left[\left({\lambda }_2^2/{\lambda }_1\right)\sin \left({\lambda }_1\right)-\left({\lambda }_1^2/{\lambda }_2\right)\sin \left({\lambda }_2\right)\right]$$

$$C_2={\Delta }_1\left[\cos \left({\lambda }_1\right)-\cos \left({\lambda }_2\right)\right],C_3={\Delta }_1\left[\sin \left({\lambda }_1\right)/{\lambda }_1-\sin \left({\lambda }_2\right)/{\lambda }_2\right],{\Delta }_1={\left({\lambda }_1^2-{\lambda }_2^2\right)}^{-1}$$

$${\lambda }_1^2=\frac{1}{2}\left({\alpha }_1+{\beta }_1+{\gamma }_1\right)-\frac{1}{2}\sqrt{{\left({\alpha }_1+{\beta }_1+{\gamma }_1\right)}^2-4{\alpha }_1{\beta }_1},{\lambda }_2^2=\frac{1}{2}\left({\alpha }_1+{\beta }_1+{\gamma }_1\right)+\frac{1}{2}\sqrt{{\left({\alpha }_1+{\beta }_1+{\gamma }_1\right)}^2-4{\alpha }_1{\beta }_1}$$

$${\left[\begin{array}{cccc}{\bar{V}}_f& {\bar{V}}_z& {\bar{F}}_z& \bar{P}\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{cccc}{V}_f/L& V_z/L& F_z/\left(A_{p}E\right)& P/K\end{array}\right]}^{\mathrm{T}}$$

$s$ in the characteristic equation is actually the natural frequency, so it is recorded as $\omega$ .

2.2. Vertical vibration

For vertical vibration, a set of four equations can also be proposed [16],

$$\frac{\partial f_y}{\partial z}-C_y\frac{\partial u_y}{\partial t}-\left({\rho }_f{A}_f+{\rho }_p{A}_p\right)\frac{{\partial }^2{u}_y}{\partial t^2}=0$$ (21)

$$f_y=kG{A}_p\left(\frac{\partial u_y}{\partial z}+{\theta }_x\right)$$ (22)

$$\frac{\partial m_x}{\partial z}-f_y-\left({\rho }_f{A}_f+{\rho }_f{A}_f\right)\frac{{\partial }^2{\theta }_x}{\partial t^2}=0$$ (23)

$$m_x=E{I}_p\frac{\partial {\theta }_x}{\partial z}$$ (24)

where $f_y$ is the pipe vertical stress, $u_y$ is the pipe vertical displacement, ${\theta }_x$ is the pipe bend angle, $m_x$ is the pipe bending moment, $A_f$ is the fluid cross-sectional area, $k$ is the distribution coefficient of shear force in circular section, $G$ is the pipe shear modulus, $I_p$ is the moment of inertia of the pipeline, $C_y$ is damping coefficient [29].

Using the same method as part 2.1, the transfer matrix can be arranged as

$${\left[\begin{array}{c}{\bar{V}}_y\\ {\bar{\mathrm{\Theta }}}_x\\ {\bar{M}}_x\\ {\bar{F}}_y\end{array}\right]}_{\mathrm{o}\mathrm{u}\mathrm{t}}=\left[\begin{array}{cccc}{D}_0-{\alpha }_2{D}_2& \left({\alpha }_2+{\beta }_2\right)D_3-D_1& -D_2& {\alpha }_2{\gamma }_2^{-1}{D}_1-\left({\gamma }_2+{{\alpha }_2}^2\right){\gamma }_2^{-1}{D}_3\\ -{\gamma }_2{D}_3& D_0-{\beta }_2{D}_2& D_1-{\beta }_2{D}_3& D_2\\ -{\gamma }_2{D}_2& \left({\gamma }_2+{{\beta }_2}^2\right)D_3-{\beta }_2{D}_1& D_0-{\beta }_2{D}_2& D_1-\left({\alpha }_2+{\beta }_2\right)D_3\\ {\gamma }_2\left({\alpha }_2{D}_3-D_1\right)& {\gamma }_2{D}_2& {\gamma }_2{D}_3& D_0-{\alpha }_2{D}_2\end{array}\right]{\left[\begin{array}{c}{\bar{V}}_y\\ {\bar{\mathrm{\Theta }}}_x\\ {\bar{M}}_x\\ {\bar{F}}_y\end{array}\right]}_{\mathrm{i}\mathrm{n}}$$ (25)

where

$${\alpha }_2={\left(\omega L\right)}^2/a_s^2,{\beta }_2={\left(\omega L\right)}^2/a_b^2,{\gamma }_2=m{\omega }^2{L}^4/\left(E{I}_p\right),m=A_f{\rho }_f+A_p{\rho }_p,G=E{\left(1+v\right)}^{-1}/2$$

$$D_0={\Delta }_2\left[{\lambda }_4^2\cosh \left({\lambda }_3\right)+{\lambda }_3^2\cos \left({\lambda }_4\right)\right],D_1={\Delta }_2\left[\left({\lambda }_4^2/{\lambda }_3\right)\sinh \left({\lambda }_3\right)+\left({\lambda }_3^2/{\lambda }_4\right)\sin \left({\lambda }_4\right)\right]$$

$$D_2={\Delta }_2\left[\cosh \left({\lambda }_3\right)-\cos \left({\lambda }_4\right)\right],D_3={\Delta }_2\left[\sinh \left({\lambda }_3\right)/{\lambda }_3-\sin \left({\lambda }_4\right)/{\lambda }_4\right],{\Delta }_2={\left({\lambda }_3^2+{\lambda }_4^2\right)}^{-1}$$

$${\lambda }_3^2=\sqrt{{\left({\alpha }_2-{\beta }_2\right)}^2/4+{\gamma }_2}-\left({\alpha }_2+{\beta }_2\right)/2,{\lambda }_4^2=\sqrt{{\left({\alpha }_2-{\beta }_2\right)}^2/4+{\gamma }_2}+\left({\alpha }_2+{\beta }_2\right)/2$$

$${\left[\begin{array}{cccc}{\bar{V}}_y& {\bar{\mathrm{\Theta }}}_x& {\bar{M}}_x& {\bar{F}}_y\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{cccc}{V}_y/L& {\mathrm{\Theta }}_x& M_{x}L/\left(E{I}_p\right)& F_y{L}^2/\left(E{I}_p\right)\end{array}\right]}^{\mathrm{T}}$$

3. Riccati fluid structure interaction transfer equations

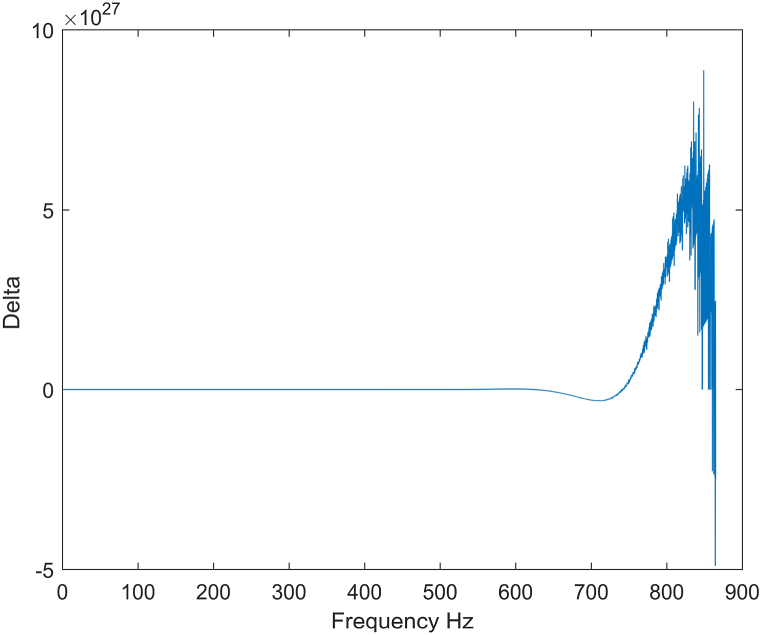
When calculating the vertical vibration, FSITMM has good numerical stability at low frequencies, but at high frequencies, it fails to calculate, as shown in Fig. 3(The definition of delta is given in section 3.4). This is due to the hyperbolic functions (cosh, sinh) contained in Eq. (25). During the numerical simulation, the terms containing hyperbolic functions in the element matrix will produce numerical errors. When the system frequency is high, the total matrix, obtained after matrix-chain multiplication, accumulates this error and eventually causes the calculation to fail. RTMM is employed to improve numerical stability.

Fig. 3.

Numerical stability of FSITMM.

3.1. Basic equations derivation

The content of this chapter has a detailed derivation process in Book [30]. The transfer matrix (20) or (25)obtained in Section 2, for the i-th element, can always be written in the form as

$${\mathit{Z}}_{O,i}={\mathit{U}}_i{\mathit{Z}}_{I,i}$$ (26)

where $\mathit{Z}$ is the $N$-dimensional state vector, $\mathit{U}$ is a $N\times N$ dimension transfer matrix, $\mathit{f}$ is an $N$-dimensional loading function independent of the state vector.

When $N$ is even, using the RTMM, Eq. (26) is divided into blocks as

$${\left[\begin{array}{c}{\mathit{Z}}_a\\ {\mathit{Z}}_b\end{array}\right]}_{O,i}={\left[\begin{array}{cc}{\mathit{T}}_{11}& {\mathit{T}}_{12}\\ {\mathit{T}}_{21}& {\mathit{T}}_{22}\end{array}\right]}_i{\left[\begin{array}{c}{\mathit{Z}}_a\\ {\mathit{Z}}_b\end{array}\right]}_{I,i}$$ (27)

where ${\mathit{Z}}_a,{\mathit{Z}}_b$ each contain half of the state vector elements, and their division method will be discussed in section 3.2, matrix $\mathit{T}$ is divided into matrix $\mathit{U}$ after rearrangement according to ${\mathit{Z}}_a,{\mathit{Z}}_b$.

The Riccati transform is defined as

$${\mathit{Z}}_{aI,i}={\mathit{S}}_i{\mathit{Z}}_{bI,i}$$ (28)

By Eq. (28), ${\mathit{Z}}_{aI,i}$ and ${\mathit{Z}}_{bI,i}$ are connected. The $\left(N/2\right)\times \left(N/2\right)$ dimension matrix ${\mathit{S}}_i$ is called the Riccati transfer matrix (RTM) at the input point $P_{I,i}$.

Eq. (27) is expanded as

$${\mathit{Z}}_{aO,i}={\mathit{T}}_{11,i}{\mathit{Z}}_{aI,i}+{\mathit{T}}_{12,i}{\mathit{Z}}_{bI,i}$$ (29)

$${\mathit{Z}}_{bO,i}={\mathit{T}}_{21,i}{\mathit{Z}}_{aI,i}+{\mathit{T}}_{22,i}{\mathit{Z}}_{bI,i}$$ (30)

Substituting Eq. (28) into Eq. (30), one can obtain

$${\mathit{Z}}_{bI,i}={\left({\mathit{T}}_{21,i}{\mathit{S}}_i+{\mathit{T}}_{22,i}\right)}^{-1}{\mathit{Z}}_{bO,i}$$ (31)

Further, Substituting Eq. (31) into Eq. (29) leads to

$${\mathit{Z}}_{aO,i}=\left({\mathit{T}}_{11,i}{\mathit{S}}_i+{\mathit{T}}_{12,i}\right){\left({\mathit{T}}_{21,i}{\mathit{S}}_i+{\mathit{T}}_{22,i}\right)}^{-1}{\mathit{Z}}_{bO,i}$$ (32)

can also be abbreviated as

$${\mathit{Z}}_{aO,i}={\mathit{S}}_{i+1}{\mathit{Z}}_{bO,i}$$

where

$${\mathit{S}}_{i+1}=\left({\mathit{T}}_{11,i}{\mathit{S}}_i+{\mathit{T}}_{12,i}\right){\left({\mathit{T}}_{21,i}{\mathit{S}}_i+{\mathit{T}}_{22,i}\right)}^{-1}$$

3.2. The basis for dividing ${\mathit{Z}}_a$ and ${\mathit{Z}}_b$

The division of ${\mathit{Z}}_a$ and ${\mathit{Z}}_b$ is determined by boundary conditions. Typically, boundary conditions come in two forms. 1) If the equations are homogeneous, then half of the state vector known by the boundary conditions there should be put into ${\mathit{Z}}_a$ and the unknown into ${\mathit{Z}}_b$. 2) If the equation is inhomogeneous, the two state vectors that are linearly related should be placed in ${\mathit{Z}}_a$ and ${\mathit{Z}}_b$, respectively.

After rearranging ${\mathit{Z}}_a$ and ${\mathit{Z}}_b$, matrix $\mathit{T}$ and vectors ${\mathit{f}}_a,{\mathit{f}}_b$ will be obtained elegantly.

3.3. Calculation process

Assuming that the system boundaries are homogeneous, ${\mathit{Z}}_{aI,1}=\mathbf{0},{\mathit{Z}}_{bI,1}\ne \mathbf{0}$ are obtained from the boundary conditions at the input of the system. Substituting ${\mathit{Z}}_{aI,1}=\mathbf{0},{\mathit{Z}}_{bI,1}\ne \mathbf{0}$ into Eq. (28), one can obtain

$${\mathit{S}}_1=\mathbf{0},{\mathit{e}}_1=\mathbf{0}$$ (33)

If it is a chain system, Eq. (32) can be used to obtain ${\mathit{S}}_i$, ${\mathit{e}}_i$ of the whole system.

If the system consists of n elements, then for another boundary of the system, the output point $P_{O,n}$, there is the equation

$${\mathit{Z}}_{aO,n}={\mathit{S}}_{n+1}{\mathit{Z}}_{bO,n}+{\mathit{e}}_{n+1}$$ (34)

Substituting the boundary conditions here, the frequency equation corresponding to the eigenvalue is obtained. Then the value of the state vector of the output point is calculated. Further, scanning backward from the output point to the input point, the value of the state vector at any point in the system is obtained.

3.4. Improved root search method

From Eq. (31), matrix inversion exists in the process of RTMM recursion. When the determinant of $\left({\mathit{T}}_{21,i}{\mathit{S}}_i+{\mathit{T}}_{22,i}\right)$ is 0, the frequency $\omega$ is the pole of the equation $\Delta \left(\omega \right)=\left|{\mathit{S}}_{n+1}\right|$. On either side of the pole, $\Delta \left(\omega \right)$ will have opposite signs. If the calculation program uses the dichotomy method to scan the roots of the equation, the singularity points are mistakenly considered to be the roots of the equation. Therefore, this paper adopts the method of literature [21] to scan the root of

$$\Delta \left(\omega \right)=\left|{\mathit{S}}_{n+1}\right|\prod _{i=1}^n\left|{\mathit{\Gamma }}_i\right|$$ (35)

where ${\mathit{\Gamma }}_i={\mathit{T}}_{21,i}{\mathit{S}}_i+{\mathit{T}}_{22,i}$. $\prod _{i=1}^n\left|{\mathit{\Gamma }}_i\right|$ is all the denominators in ${\mathit{S}}_{n+1}$, so equation Eq.(35) no longer contains singularity points.

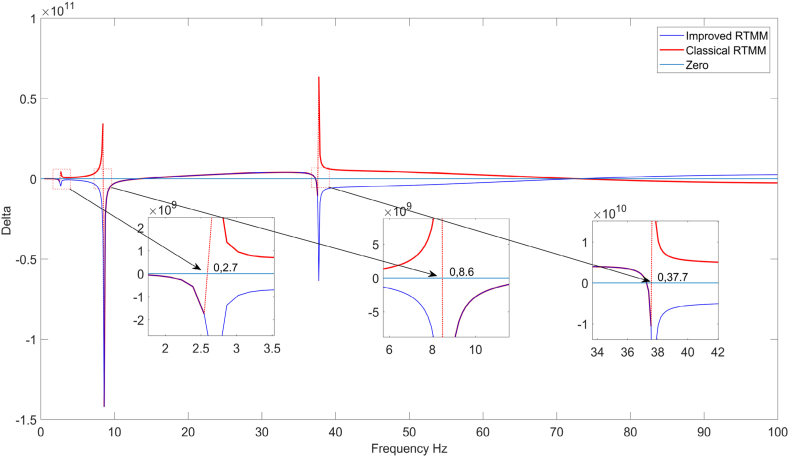
For example, in the tube model used in section 4, the numerical simulation shows three singularities in the first 100 Hz when calculating the vertical vibration, which is unacceptable. If the classical RTMM is applied, these intermittent points need to be found manually and then removed. These problems are avoided by using the improved RTMM method, which is shown in Fig. 4.

Fig. 4.

Elimination of singularities using improved RTMM.

4. Numerical simulation and discussion

The simulation example adopts the classic example named Dundee tube model [31], shown in Fig. 5.

Fig. 5.

Dundee tube model.

A straight liquid-filled pipe is closed at both ends and suspended from the ceiling soft springs. The tube can be considered as unaffected by the support and is able to move freely in the plane. regardless of the mass of the plug. The specific parameters are shown in Table 1.

Table 1.

Tube parameters.

Tube Parameters
Length (m)	4.502
Inside Diameter (m)	2.601e-2
Tube Wall Thickness (m)	3.933e-3
Poisson's Ratio	0.29
Tube Bulk Modulus (Gpa)	168
Tube Mass Density (kg/m3)	7985
Fluid Bulk Modulus (Gpa)	2.14
Fluid Mass Density (kg/m3)	999

Natural frequencies below 1000 Hz in different directions are calculated. Case A: Axial. Case B: Vertical.

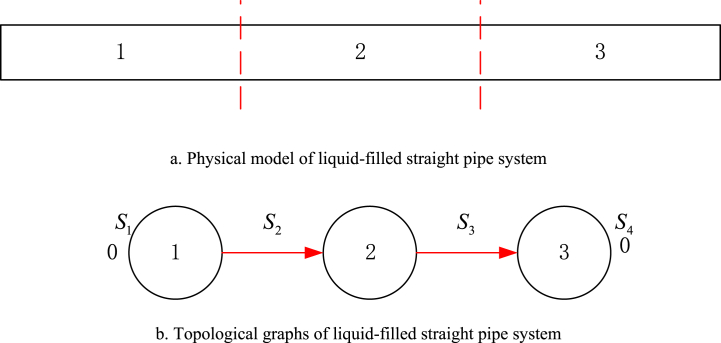
According to Fig. 5, the physical model of Fig. 6(a) is given. The FSI equations are a set of Quasilinear equations, which are not completely linearized, some nonlinear factors in the matrix are approximated as linear factors, and the error caused by the approximation will become larger if the pipe section is longer. Therefore, increasing the number of segments will increase the numerical accuracy, but more transfer matrices will decrease the computational speed [32]. The unit division process is a process of finding the balance position of accuracy and computational speed. The pipe was divided into different sections, including four cases from one section to four sections. The calculation results of vertical vibration frequency are shown in Table 2. In the case of only one section, the high frequency cannot be calculated. The results obtained from the two-to four-section calculations are stable. To ensure the success of the calculations, the pipeline was divided into three equal sections.

Fig. 6.

Physical model and topological graphs of liquid-filled straight pipe system.

Table 2.

Vertical Natural Frequencies of liquid-filled straight pipe with different sections.

	One section	Two sections	Three sections	Four sections
1	13.69	13.69	13.69	13.69
2	37.40	37.40	37.40	37.40
3	72.89	72.89	72.89	72.89
4	120.0	120.0	120.0	120.0
5	178.3	178.3	178.3	178.3
6	247.5	247.5	247.5	247.5
7	327.2	327.2	327.2	327.2
8	416.8	416.8	416.8	416.8
9	516.1	516.1	516.1	516.1
10	624.5	624.5	624.5	624.5
11	–	741.5	741.5	741.5
12	–	866.6	866.6	866.6
13	–	999.3	999.3	999.3

According to the theory of topological graphs [33], the transitive relationship is shown in Fig. 6(b).

4.1. Case A: Axial

The natural frequencies are shown in Table 3. It can be seen that the calculated results of FSITMM, L-MOC or FSIRTE are in good agreement with the experimental data, which proves the correctness of FSIRTE.

Table 3.

Axial Natural Frequencies of liquid-filled straight pipe system.

	Experiment [31]	L-MOC [9]	FSITMM	FSIRTE
1	173	172	172.4	172.4
2	289	286	284.6	284.6
3	459	453	453.9	453.9
4	485	493	489.2	489.2
5	636	633	634.2	634.2
6	750	741	741.2	741.2
7	918	907	907.3	907.3
8	968	980	976.4	976.4

4.2. Case B: Vertical

As shown in Table 4, it can be seen that when the frequency is too high, FSITMM cannot obtain the natural frequency due to poor numerical stability. Compared with the improved MOC(L-MOC), FSIRTE are still competitive. For FSIRTE, not only the natural frequencies are obtained, but also it is in good agreement with the experimental value. The numerical stability of FSIRTE is demonstrated.

Table 4.

Vertical Natural Frequencies of liquid-filled straight pipe system.

	Experiment [31]	L-MOC [9]	FSITMM	FSIRTE
1	13	14	13.69	13.69
2	36	37	37.40	37.40
3	70	73	72.89	72.89
4	116	120	120.0	120.0
5	173	179	178.3	178.3
6	241	248	247.5	247.5
7	320	328	327.2	327.2
8	411	418	416.8	416.8
9	510	518	516.1	516.1
10	619	627	624.5	624.5
11	737	744	–	741.5
12	864	870	–	866.6
13	999	1003	–	999.3

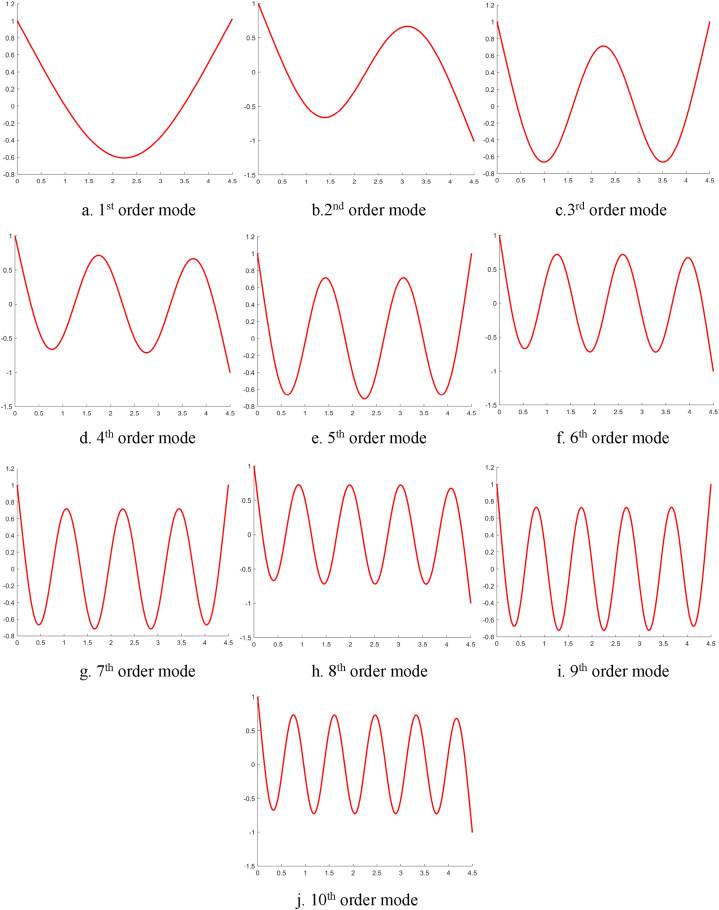
For beam models, more attention has been paid to the modes of vertical vibrations. The first ten vibration modes of the liquid filled pipeline are shown in Fig. 7. From the figure, it can be seen that the vertical vibration modes of the liquid-filled straight pipe system with both ends free have similar shapes to the vertical vibration modes of the solid beam with both ends free. For each order of frequency increase, the vibration mode will increase by one peak. This also verifies that the calculated natural frequency does not omit or add roots.

Fig. 7.

Vertical vibration mode of liquid-filled straight pipe system.

The simulation results of FSIRTE for a liquid-filled straight pipe system are satisfactory. The future work includes several aspects.

• 1.The calculation of the vibration characteristics of the liquid-filled pipe by FSIRTE method for complex boundary.
• 2.The dynamic response of the pipe under forced vibration.
• 3.The rapid determination of the number of pipe segments by mathematical methods.

5. Conclusion

In this paper, by introducing the Riccati transfer matrix method into the study of fluid structure interaction vibration characteristics of liquid-filled pipes, the Riccati transfer equations of fluid structure interaction of liquid-filled pipes are established. In this way, the numerical stability of the classical transfer matrix method when evaluating the vibration characteristics of liquid-filled pipes, especially in the high-frequency domain, is improved.

Meanwhile, the improved algorithm of removing the singular points of the Riccati transfer matrix significantly improves the computational efficiency of the Riccati transfer matrix method, as relative larger scanning steps are applicable.

Theoretically, the numerical instability of the dynamic model in this paper is caused by hyperbolic function; The calculation strategy introduced in this paper may be extended to many other calculation models containing hyperbolic functions, such as the Timoshenko beam model and its related models, which has reference significance and potential application value for the study of high-frequency vibration characteristics of other calculation models in the field of fluid structure coupling.

Author contribution statement

Li Tang: conceived and designed the experiments; performed the experiments; wrote the paper; contributed reagents, materials, analysis tools or data; analyzed and interpreted the data.

Rui Xiaoting: contributed reagents, materials, analysis tools or data; analyzed and interpreted the data.

Zhang Jianshu: wrote the paper; analyzed and interpreted the data.

Zhang Lina: performed the experiments; analyzed and interpreted the data.

Data availability statement

Data included in article/supp. material/referenced in article.ly098.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.