Computational Model of Shoe Wear Progression: Comparison with Experimental Results

Abstract

Worn shoes increase the risk of slip and fall accidents. Few research efforts have attempted to predict the progression of shoe wear. This study presents a computational modeling framework that simulates wear progression in footwear outsoles based on finite element analysis and Archard’s equation for wear. The results of the computational model were qualitatively and quantitatively compared with experimental results from shoes subjected to an accelerated wear protocol. Key variables of interest were the order in which individual tread blocks were worn and the size of the worn region. The order in which shoe treads became completely worn were strongly correlated between the models and experiments (r_s > 0.74, p < 0.005 for all of the shoes). The ability of the model to predict the size of the worn region varied across the shoe designs. Findings demonstrate the capability of the computational modeling methodology to provide realistic predictions of shoe wear progression. This model represents a promising first step to developing a model that can guide footwear replacement programs and footwear design with durable slip-resistance.

1. Introduction

Slips and falls continue to be among the leading causes of occupational injuries and a serious public health issue. In addition to the human suffering caused by falls, the overall annual financial burden to the United States is $180 billion [1] and the direct workers’ compensation costs due to slips and falls are approximately $18.5 billion annually [2]. Roughly half of occupational falling accidents are caused by a slipping event [3]. Low available friction between the shoe and flooring increases the risk of slips and subsequent falls [4, 5]. Shoe tread design characteristics such as tread depth [6], tread width [7], the size of the region without tread [8], and the available contact area between shoe and flooring [9] influence the available friction at the shoe-floor interface and therefore affect the risk of slips and falls [6–8, 10]. These properties change across a shoe’s lifetime as tread becomes worn. Specifically, severely worn shoes have been reported to decrease the available friction [11, 12], increase under-shoe fluid pressures [12, 13], and increase the slipping risk in occupational and laboratory settings [13, 14].

Elastomer wear is a complex phenomenon, which is influenced by multiple mechanisms. Specifically, elastomers can wear due to adhesion and tearing [15], abrasion [16, 17], or fatigue [18]. A common starting point in the investigation of such a complex phenomenon is Archard’s wear equation [19, 20], in which the worn volume is directly proportional to sliding distance and load. Archard’s wear equation has been shown to describe wear behavior across a wide variety of materials [21]. Shoe outsoles are typically made of elastomers. Specifically, Archard’s wear equation has been utilized to describe wear of elastomers based on the contact pressure in applications such as seals and tires [22–24]. The present study aimed to apply Archard’s equation in order to model the wear of shoe outsoles based on contact pressure.

Previous studies have used finite element analysis to predict wear progression, especially in metallic components [25–28], tires [24], and seals [23, 29]. These models employ the finite element method to predict the distribution of contact pressure at the interface. Wear is simulated by modifying the geometry using Archard’s equation based on the distribution of contact pressure. The modeling of contact pressures and updating of the geometry are performed using iterative methods. These approaches have been applied to elastomers for life prediction in tires and seals [22–24, 29], typically based on simple geometries with mild wear. However, there has not been substantial research to extend elastomer wear modeling to three-dimensional elastomers with complex geometries like whole-shoe tread geometry. Furthermore, some elastomer products like footwear tread go through substantial changes in their geometry caused by wear [11, 14] and specific modeling techniques are needed that can predict these changes. In this paper, we present a modeling workflow for applying Archard’s equation to shoe outsoles.

Finite element analysis has emerged as a useful tool for assessing the frictional performance of footwear and informing design choices. Previous research has demonstrated agreement between model-predicted traction and experimental values [30–32]. While these models show promise, they are not designed to assess changes in footwear performance as the tread wears throughout its life. A validated computational model is needed for the progression of shoe wear, which characterizes the relationship between the design properties and changes in the shoe tread over time. When merged with existing models of footwear friction performance, this could enable the prediction of friction throughout the life of a given shoe design. This modeling could then allow for further efforts in order to guide design improvements that extend the amount of time that a shoe is slip-resistant, analogous to the wear modeling studies on seals and tires [22, 24, 29]. Furthermore, this method is likely to predict the regions of the shoe in which wear is initiated and thus, identify shoe regions that could benefit from redesign.

The purpose of this study was to develop a computational model of the progression of shoe wear using Archard’s equation and finite element analysis. The validity of the model was assessed by comparing predictions to an experimental protocol for shoe wear.

2. Methods

2.1. Computational wear model

Modeling of the contact interface was performed in the explicit finite element package, LS-Dyna® (version R10.0.0, LSTC, Livermore, California, USA). The capability of this software in modeling shoe-floor contact has been previously demonstrated [30]. An automatic, segment-based soft contact was used in which the contact stiffness is determined based on timestep size to ensure stability. The shoe and floor surfaces were designated as slave and master, respectively, for the contact pair given the difference in their elastic moduli. The finite element modeling method simulated the contact pressure distribution at the contact interface of the shoe (Figure 1). The output of the finite element model was the nodal contact pressures at the interface. These pressures were used to calculate the nodal wear depths in each iteration by assuming that the wear depth for each node in each wear iteration was proportional to the interfacial contact pressure based on Archard’s equation (Equation 1). Therefore, the wear process was simulated by moving the respective nodes [29] in a direction perpendicular to the contact interface based on the amount of calculated wear. Specifically, the wear depth at the i-th node (Δh_i), was a function of the wear constant (k), the contact pressure at the i-th node (p_i), and the sliding distance on the counter-surface (s), (Equation 1).

Figure 1.

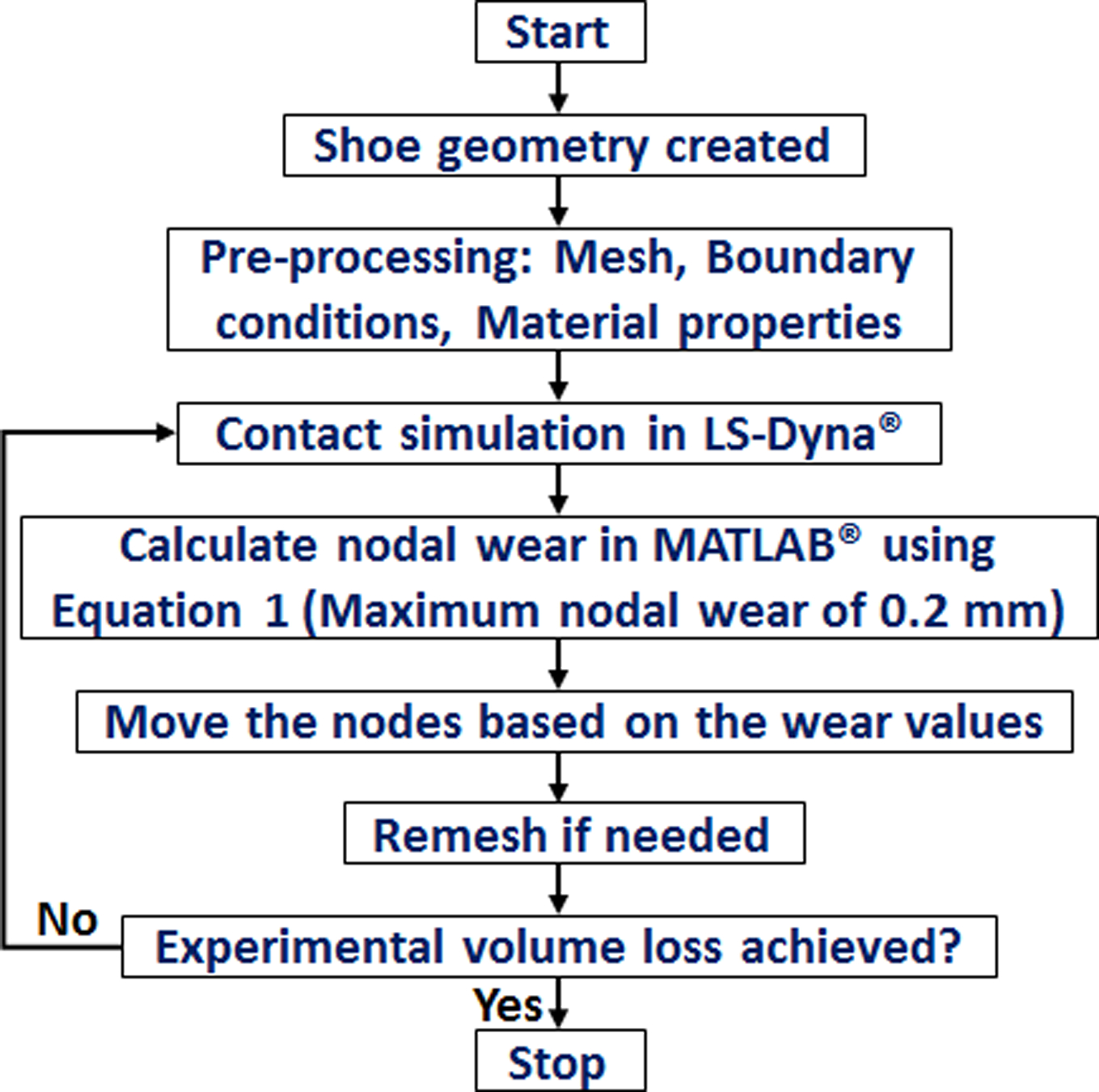
Flowchart of the iterative process for modeling wear.

$${\Delta h}_i=k{p}_{i}s$$ Equation 1.

This study was focused on developing a model that predict the locations of the wear as opposed to the overall wear rate. Therefore, the product of the wear constant and sliding distance (ks in Equation 1), was set for each iteration such that the maximum nodal wear depth (Δh_imax) in each iteration was 0.2 mm. This is equivalent to varying the amount of sliding distance in each wear iteration to achieve maximum local wear depth of 0.2 mm. Our preliminary modeling efforts, similar to the observations of Mukras et al. [27], determined that limiting the maximum nodal wear in each iteration was needed to achieve stability and convergence in wear progression simulations. Preliminary models also demonstrated that choosing values of less than 0.2 mm for the maximum nodal wear in each iteration, would result in unnecessarily long computational times, given the severity of wear that was expected to occur in shoes (Section 2.2). A custom script (MATLAB®, MathWorks, Natick, Massachusetts, USA) was developed that calculated wear depths across the contact nodes based upon nodal pressures at each iteration to guide positional changes in these nodes. The amount of wear during the simulation and subsequent deformations that occurred necessitated the use of global remeshing techniques to discretize the shoe geometry throughout the wear modeling cycles [29]. Meshing software (ANSYS®, ANSYS Inc., Canonsburg, Pennsylvania, USA) was used to perform the global-geometry remeshing when errors in the next wear iteration resulted due to a severely deformed finite element mesh.

The computational models of wear included heel geometries of five shoes that were also examined experimentally (Section 2.2). Computer Aided Design (CAD) models of the shoes were created in ANSYS DesignModeler® (ANSYS Inc., Canonsburg, Pennsylvania, USA), based on the measurements taken from the shoe outsoles. For shoes with a textured tread, texturing was not included in the CAD models as the preliminary experimental results (Section 2.2) revealed that texturing quickly wore off. Shoes were modeled as a linear elastic material for computational efficiency [30]. Linear-elastic material properties for the shoes were obtained using hardness readings of the shoes [30] (Section 2.2) based on methods described by Giacomin and Mix and Ghent [33, 34] (Equation 2). In Equation 2, S represents hardness (shore A durometer) and E represents the elastic modulus (MPa) of the shoe. Shoe tread was modeled as a nearly incompressible material with a Poisson’s ratio of 0.499 [35, 36].

$$\mathrm{E}=\frac{0.0981(56+7.6233S)}{0.1375(254-2.54S)}$$ Equation 2.

Finite element models were used to simulate contact between the shoe and a smooth, rigid counter-surface. Key parameters were consistent with the experimental wear protocol, including: shoe-floor angles of 17, 7, and 2 degrees, a sliding velocity of 9.65 m/s, a normal force of 40 N, and a lateral tilt angle that was consistent with the experimental wear protocol (Section 2.2). Normal force in the finite element models was controlled using the vertical displacement boundary conditions that were applied to nodes at the top surface of the shoe outsole models [30]. The shoe was pressed against the counter-surface until the desired normal force was achieved and then the horizontal sliding velocity boundary condition was applied. Other displacements and rotations of the nodes at the top surface of the shoes were constrained. Shoe models were meshed using tetrahedral elements that are recommended for simulating rubber-like (nearly-incompressible) materials with complex geometries [37]. This type of element overcomes the issue of volumetric locking by defining nodal volumes and representing the nodal pressures in terms of those volumes [38]. Mesh size for the shoes were determined based on the following criteria: (1) Mesh size was reduced until the first occurrence where the difference between the predicted normal force of one model and a subsequent model (with smaller mesh sizes) was less than 4 N. (2) All of the shoe elements had element qualities (the ratio of volume of the element to the edge length [39]) that were greater than 0.1 in the baseline iteration. (3) Mesh refinement was applied only to the elements in the contact region of the shoe to reduce the computational cost without losing accuracy in those regions. (4) The aforementioned mesh settings were used anytime that global remeshing was performed.

2.2. Experimental shoe wear protocol

Five shoes were worn using a custom-developed accelerated wear apparatus. This apparatus utilized a sliding abrasion belt [8] to wear shoes in angles that approximated the shoe angles of the gait cycle. For each wear iteration, the shoe was worn for 193 m (equal to 20 seconds on the abrasion belt) at three different shoe angles of 17, 7, and 2 degrees in the sagittal plane. Sliding speed of 9.65 m/s and a normal load of 40 N were consistent with the modeling conditions (Section 2.1). These wear angles mimic the variation in shoe-floor angles during gait cycle [40, 41]. The abrasion techniques are similar to previous methods for abrasively removing shoe tread and also measuring abrasion resistance for footwear [8, 42].

After each wear trial, volume loss of the shoes was measured and imprints of the shoe treads were generated using a silicone rubber mold [8]. The cavities in these molds were then filled with water and the mass of the water was weighed to deduce the volume of the water in the tread cavities, and thus the volume loss between the trials. Between wear trials, experimental measurements were made to determine the traction performance of the shoe and record fluid pressures at the shoe-floor interface during shoe sliding experiments [8, 12, 43, 44]. Experimental wear trials were stopped when it was determined that the shoe tread was no longer functional at draining out the fluid contaminant in the shoe-floor interface during the lubricated sliding experiments. Increases in the interfacial fluid pressure measurements were used as an indicator that the shoe lacked functional drainage [8, 12, 43, 44]. The method for making this determination is described in more detail in our other publications [8, 12]. The wear coefficient (k in Equation 1) was defined by the total wear volume (numerator), the sliding distance (denominator), and the normal force (denominator) for each shoe. Material properties were also collected as an input to the finite element models. Shore A hardness values of the shoes [45] were measured using a durometer (Intercomp®, Minneapolis, Minnesota, USA), which were converted to Young’s moduli of the shoe materials [30, 34] for computational models (Section 2.1). Durometer readings were conducted on nine different portions of the heel for each shoe and the average value was used. Table 1 summarizes the elastic moduli values that were derived from the hardness readings.

Table 1.

Elastic modulus of the shoes.

Shoe	S1	S2	S3	S4	S5
Elastic Modulus (MPa)	7.50	9.36	9.27	8.20	11.01

2.3. Data and statistical analysis

A statistical analysis was performed to evaluate the prediction quality of the model to identify the location of wear. For this analysis, tread blocks on the physical shoe and modeled shoe were ranked according to the order that they became completely worn. Agreement between the model and experiments in predicting regional geometrical wear was then assessed using Spearman’s rank-order correlation coefficient (r_s), which quantified how successfully the model predicted the order of tread wear observed in the experiment (Figure 2). The worn region area was approximated by calculating the product of the largest length without tread in the anteroposterior (major axis) and mediolateral (minor axis) directions [8]. Iterations were continued for the model until the total volume loss reached the experimental volume loss observed for each shoe. For each experimental wear trial, the modeling iteration that had the closest volume loss value to that experimental wear trial was picked as that trial’s matched modeling counterpart. Afterwards, the volume loss at each modeling iteration was used along with the Archard’s wear coefficient (See Section 2.2) to calculate sliding distance for each modeling iteration. The area of the worn region as a function of sliding distance in experiments and models were then compared. This analysis assessed the accuracy of the model in predicting the worn region area since this area has been demonstrated to be a predictor of the change in shoe-floor coefficient of friction due to wear [8]. Furthermore, a linear regression model quantified the correlation between the area of worn region in the model and experiment. Goodness of fit was assessed using the Pearson correlation coefficient (r) value for each shoe.

Figure 2.

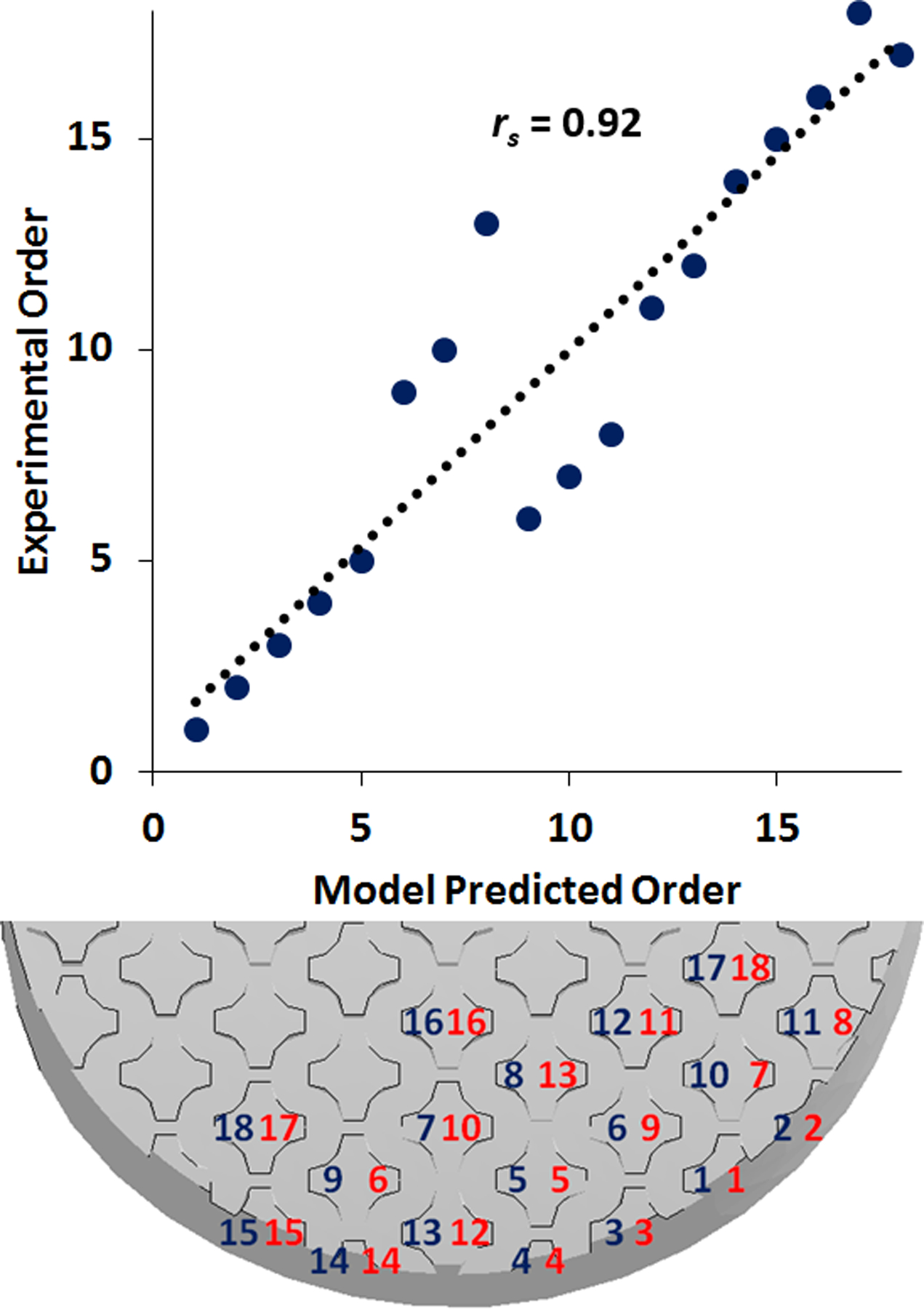
Top: the model and experimental wear order and correlation for this shoe. Bottom: the order that shoe (S4) tread wore down in the model (blue/left) and the experiment (red/right).

3. Results

Table 2 summarizes the distance that each shoe was worn on the experimental wear apparatus, the resulting volume loss, the experimental wear constant, the total number of elements and nodes, and the number of modeling iterations it took to simulate the experimentally-measured volume loss for each shoe. Shoes experienced extensive wear in both the experiments and the models and similar regions wore in the models and experiments (Figure 3). For S1, a majority of the wear occurred in the posterior section of the shoe in both the model and the experiment. For S2, a majority of the wear occurred in the lateral and posterior region of the shoe in the model and in the lateral and medial portion of the shoe in the experiment. For S3, wear in the posterior region of the outsole was observed in both the model and the experiment. For S4, wear was dominant in the posterior and medial portions of the shoe in both the model and the experiment. For S5, the model experienced wear mainly in the posterior region of the shoe and the experimental wear trials resulted in wear of the shoe in the medial region. The progression of wear is demonstrated in videos of the shoe wear progression in shoe models (Supplementary Videos S1–S5 (The numbers below the shoes correspond to the distance in kilometers)).

Table 2.

Distance on the experimental wear apparatus, the resulting volume loss, wear constant, total number of elements, nodes, and modeling iterations for the shoes.

Shoe	S1	S2	S3	S4	S5
Distance on wear apparatus (km)	9.8	11.6	13.3	8.7	20.3
Total volume loss (mm 3 )	3345	7046	3460	3593	3762
k (mm 3 /Nm)	0.0085	0.0138	0.0065	0.0103	0.0046
Total number of elements (at baseline)	102539	43463	23429	75993	54066
Total number of nodes (at baseline)	24485	12979	5970	16608	12283
Total number of modeling iterations	47	130	30	35	49

Figure 3.

Pictures of the shoes at the end of the experimental wear protocol (top) and final models of wear of the shoes (bottom).

Based on the rank correlation analysis of the order that tread blocks became fully worn, a strong, positive, and monotonic correlation existed between the wear model predictions and the accelerated wear experiment (Table 3, p < 0.005 for all of the shoes.). The strongest and weakest rank order correlations were observed in S1 (r_s = 0.98) and S5 (r_s = 0.74), respectively. The percentage of the tread blocks that wore down in both the model and experiment was greater than the percentage of the tread blocks that wore down only in the model for all shoes except S5, and greater than the percentage of the tread blocks that wore down only in the experiments for all shoes (Figure 4). For S1, a complete agreement in the number of worn tread blocks between the model prediction and experiment results was observed.

Table 3.

Results of the statistical analysis on the order of tread wear.

Shoe	S1	S2	S3	S4	S5
Number of tread blocks	8	10	17	18	15
Spearman’s Rho (r s )	0.98	0.87	0.94	0.92	0.74
t-score (p-value)	12.06 (0.000)	4.99 (0.001)	10.67 (0.000)	9.39 (0.000)	3.97 (0.002)

Figure 4.

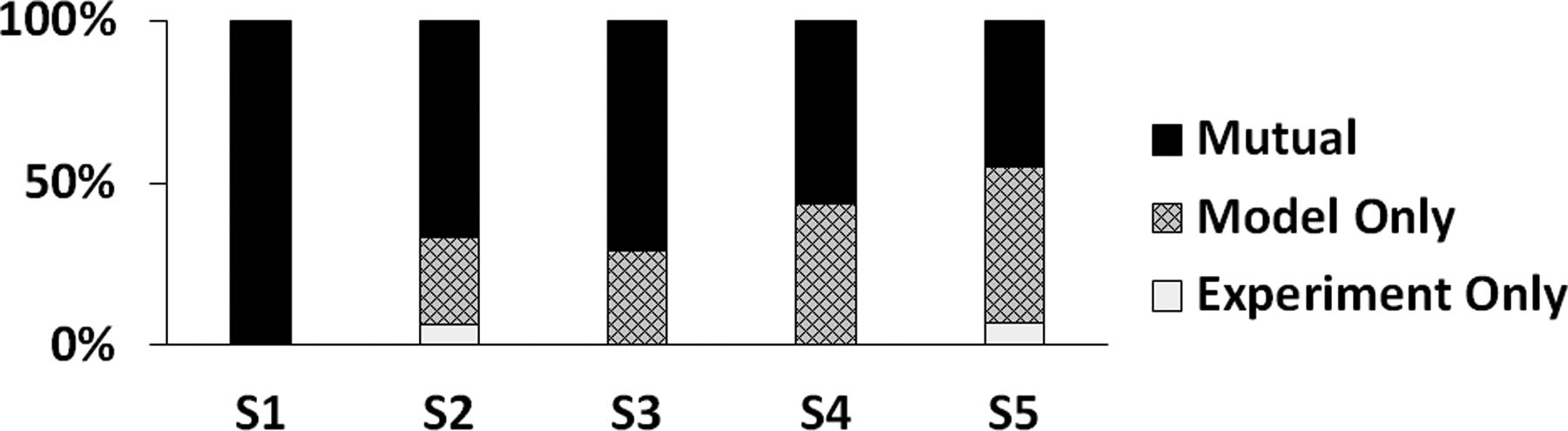
Percentage of the tread blocks that wore down in both models and experiments, only in the model, and only in the experiment

The size of the worn region area observed in the experiments was somewhat predicted by the model (Figure 5). For S1, the model predictions of the worn region area were of similar magnitudes to the experimentally-observed worn region areas (r=0.76 and with a slope of 0.97). For S2 and S3, the model under-predicted the experimentally-observed worn region areas (r=0.90 and 0.93 and with slopes of 0.47 and 0.34, respectively). For S4, the model over-predicted the experimentally-observed worn region areas (r=0.89 and a slope of 1.30). Simulations of S5 appeared not to be particularly successful in predicting the worn region area, as they over predicted the model worn region areas by a factor of 3.4 (r=0.72).

Figure 5.

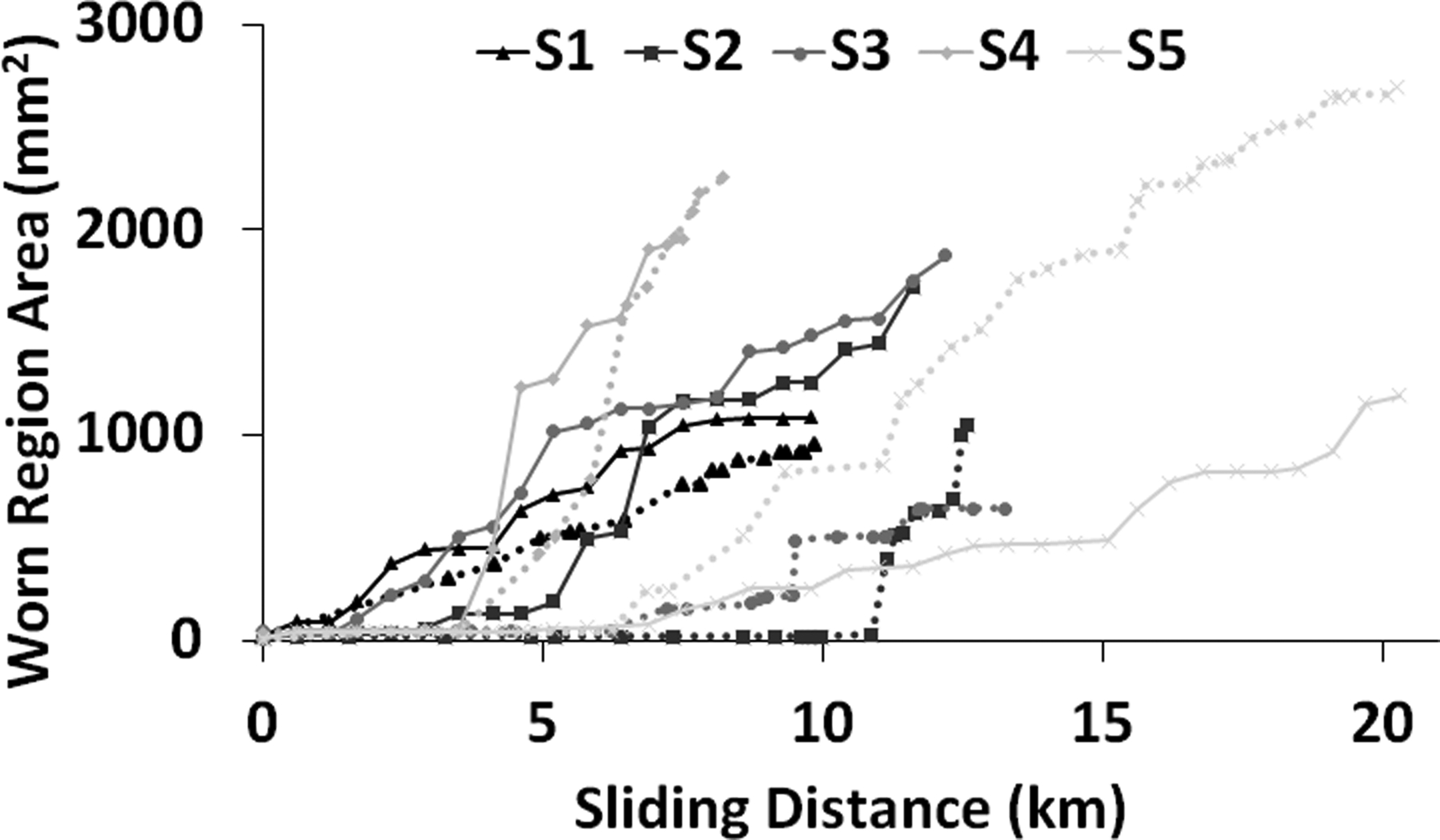
Rectangular worn region areas as a function of sliding distance. Solid and dashed lines demonstrate the experimentally-observed and model worn region areas, respectively.

4. Discussion

The computational model developed in this paper demonstrates the feasibility of using Archard’s equation and finite element analysis in predicting wear progression in footwear. Qualitative and quantitative agreement were observed between the outcomes of the computational model and the results of the experimental wear testing. The findings of this study demonstrate the potential for applying the described modeling framework for shoe wear given its preliminary success in predicting experimentally-observed wear of the outsoles. This modeling approach may offer potential for modeling wear in complex geometries with elastomeric materials.

The results of this study are consistent with the earlier qualitative experimental studies on shoe wear that demonstrate development of worn region areas [11, 14] at the regions of the shoe with higher contact pressures [8, 11, 46]. Findings of the present study are also in agreement with the previously developed computational models of wear in other applications such as disc brakes [47], seals [23], and pin-on-disk wear experiments [48] that use Archard’s equation for describing the relationship between wear depth and interfacial pressure. Specifically, the present findings demonstrate that wear of the shoe material can be simulated using Archard’s equation, global remeshing, and finite element analysis, similar to the procedures that were developed based on elastomers and metals [22, 23, 29, 47, 48]. The Archard’s wear coefficients that were calculated for shoes using the experimental volume loss, normal force and sliding distance were within the range of 0.004–0.014 mm³/(Nm). These values are in line with values available in the literature for the abrasive wear of elastomers on rough surfaces. However, the present values (4×10⁻³ to 1.4×10⁻² mm³/(Nm)) demonstrate a range that is two orders of magnitude less than prior measurements (5×10⁻⁴ to 1×10⁻¹ mm³/(Nm)) [49–51]. This narrow range is likely to due to the smaller set of test conditions considered in this study, while previous studies considered a variety of elastomers against a variety of rough surfaces. This narrower range may also indicate that elastomer materials that are commonly used in footwear have more consistent durability than the full range of possible elastomers. Once the Archard’s wear coefficient of these shoes has been quantified (Table 2), then the sliding distances were extracted from the model data (which previously only enabled the determination of the combined parameter ks). With this quantitative measure of the sliding distance, the worn region area across two shoes at a similar point in their life can be compared. For example, tread design S4 was predicted to have a larger worn area than the others at approximately 7 kilometers. Therefore, these findings demonstrate a strong potential application of the proposed model: the predictive comparison of the worn tread region across different tread designs.

While the outcomes of the model for some shoes were well-described by the model, other shoes were less accurately predicted. These discrepancies included the exact shape and area of the worn region, and the precise order of shoe tread wear in some of the shoes. One possible reason is the use of Archard’s equation and its assumption of a linear relationship between the contact pressure and wear depth. While Archard’s equation is widely used and has a large body of empirical support, some previous studies have suggested a phenomenological relationship based on power-law equations [21, 52]. Assuming the power-law form for the equation between contact pressure and wear depth would result in a higher difference between the wear depth of the regions with higher and lower contact pressures and would lead to a less uniform wear region in models. The phenomenon of highly localized wear is observed in the wear experiments, but is absent in the model. In our experiments (Figure 3), S1 had a small local wear region in the posterior portion of the shoe, S2 demonstrated local wear regions in the lateral and posteromedial portions of the shoe, S3 had a local wear region in the posterior portion of the shoe, S4 demonstrated a local wear region in the posterolateral region of the shoe, and S5 was locally worn in the medial region of the shoe in the experiments. However, the wear models demonstrated a more uniform wear region (i.e. wear region distributed over a larger portion of the shoe) in comparison to their experimental pairs. Another possible explanation for the differences that were observed between the models and experiments is the method used to define the orientation of the shoe in the model. For the current version of the model, sagittal and frontal plane angles were matched to the experiments based on goniometer measurements of the shoe tilt against the abrasive surface. However, changes in center of pressure can occur with minimal changes in the frontal plane angle [53, 54]. For future versions of this wear model, this approach could be improved by matching the two-dimensional location of the center of pressure [55] to achieve more realistic contact regions. Modifying these biomechanical parameters also offers an opportunity to assess how different gait patterns influence wear patterns. A final possible reason for differences between experimental and model results arises from the discrete nature of wear in the modeling. For example, if one of the tread blocks in the experiment gets worn while the matching tread block in the model is not worn yet, there will be a mismatch between the worn region areas in the model and experiment for a few trials until the matching tread block in the model gets worn down. This mismatch will further intensify at greater wear distances as this phenomenon is likely to occur multiple times.

A computational model can be particularly useful in guiding the design of durable, slip-resistant shoes by estimating the impact of design modifications (e.g., increasing tread depth in regions that become worn) on the durability of shoes. Furthermore, tread could be designed to spread the contact pressures and wear across a larger region which would increase the coefficient of friction [30, 56, 57] and durability. The computational model for wear can also be used to describe the “running-in” phenomenon [29, 47] that leads to an increase of coefficient of friction for slightly worn shoes [8, 58]. A post-hoc revealed that slightly worn shoes had an increase in contact area relative to the unworn condition both in the models (Figure 6) and experiments [8]. This increase in contact area led to a more distributed contact pressure (Figure 6) over the surface of the shoe [30]. As predicted in previous models [30, 57] and experiments [59], increased contact area and decreased contact pressures led to increased hysteresis friction. This explains the initial increase in shoe-floor coefficient of friction that is common in the early stages of wear [8].

Figure 6.

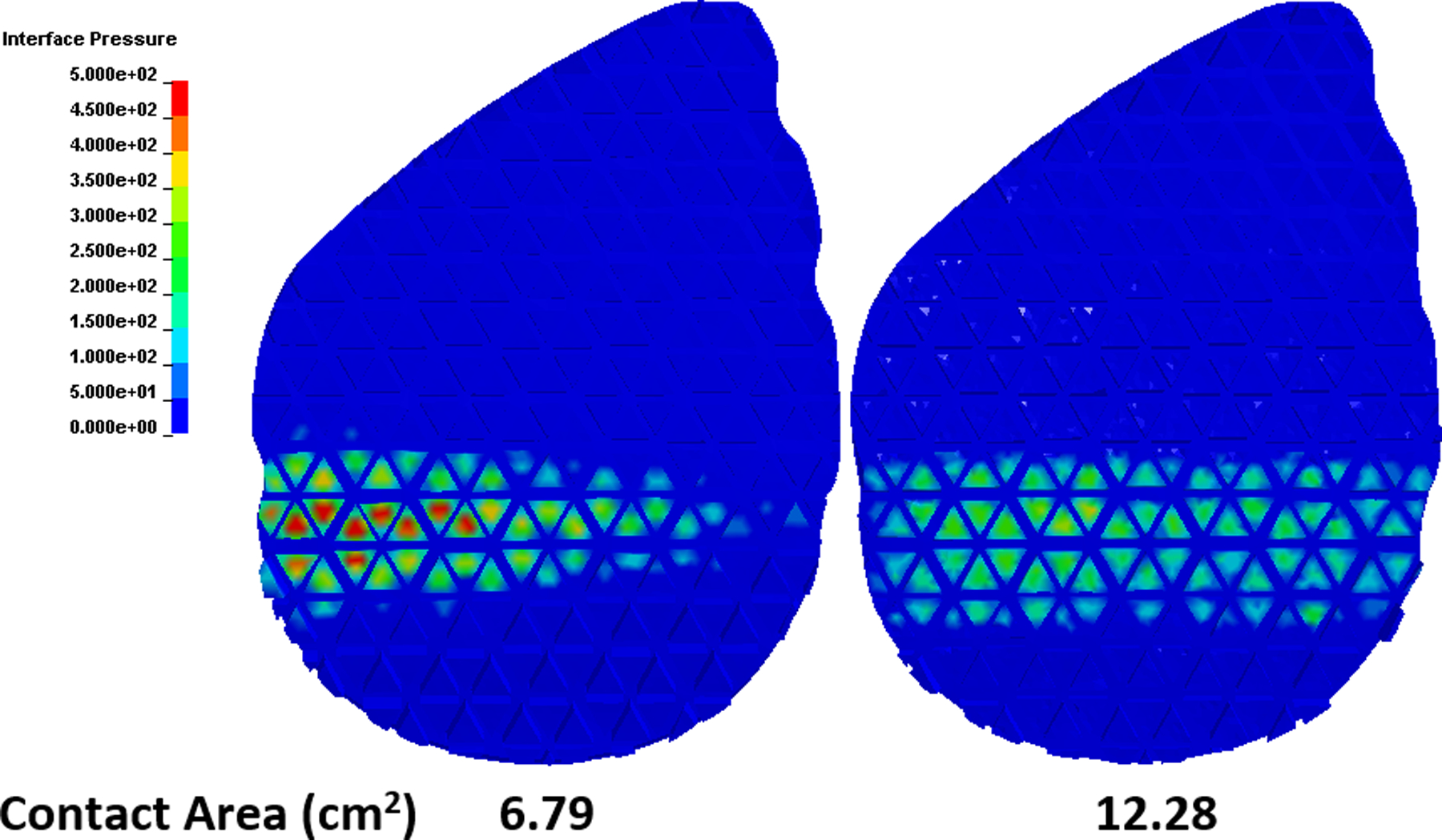
Under-shoe contact pressure in kiloPascals (S2) and contact areas of the shoe at 250 N and 7° shoe angle at the baseline (Left) and after 5.2 kilometers of simulated wear (Right). Total contact area of the shoe in each case is reported below the shoe.

The computational model for wear demonstrates an important first step toward developing more sophisticated models of shoe wear. The current version of the model can be used to predict the spatial distribution and rates of tread wear across the shoe. Future versions of this wear model should advance this framework by using wear coefficients (k) which can be obtained a priori using shoe material wear testing [8]. Future versions should also aim to include whole-shoe geometry to simulate changes to the forefoot and subject-specific boundary conditions (i.e. linear and angular kinematics and kinetics) based on each person’s gait parameters. This inclusion and individualization based on one’s gait profile will allow predictions to quantify a shoe’s duration of usage until the shoe becomes too worn and the risk of a slip and fall increases [12, 13]. Once these models become available, more reliable predictions on shoe wear and durable slip-resistant designs will become feasible. This result will promote the long-term goal of reducing slip and fall injuries.