Abstract
Purpose:
To design a pulse sequence for efficient 3D T2-weighted imaging and T2 mapping.
Methods:
A stack-of-stars turbo spin echo pulse sequence with variable refocusing flip angles and a flexible pseudorandom view ordering is proposed for simultaneous T2-weighted imaging and T2 mapping. An analytical framework is introduced for the selection of refocusing flip angles to maximize relative tissue contrast while minimizing T2 estimation errors and maintaining low specific absorption rate. Images at different echo times are generated using a subspace constrained iterative reconstruction algorithm. T2 maps are obtained by modeling the signal evolution using the extended phase graph model. The technique is evaluated using phantoms and demonstrated in vivo for brain, knee, and carotid imaging.
Results:
Numerical simulations demonstrate an improved point spread function with the proposed pseudorandom view ordering compared to golden angle view ordering. Phantom experiments show that T2 values estimated from the stack-of-stars turbo spin echo pulse sequence with variable refocusing flip angles have good concordance with spin echo reference values. In vivo results show the proposed pulse sequence can generate qualitatively comparable T2-weighted images as conventional Cartesian 3D SPACE in addition to simultaneously generating 3D T2 maps.
Conclusion:
The proposed stack-of-stars turbo spin echo pulse sequence with pseudorandom view ordering and variable refocusing flip angles allows high resolution isotropic T2 mapping in clinically acceptable scan times. The optimization framework for the selection of refocusing flip angles improves T2 estimation accuracy while generating T2-weighted contrast comparable to conventional Cartesian imaging.
Keywords: 3D T2 mapping, stack-of-stars, turbo spin echo, variable refocusing flip angles
1 |. INTRODUCTION
T2-weighted (T2w) imaging pulse sequences are routinely used for the diagnosis of various pathologies and the turbo spin echo (TSE) pulse sequence has been a “clinical workhorse” for 2D acquisitions. The desired T2w contrast can be achieved by selecting an appropriate echo time (TE) and interleaving data for multiple slices within each repetition time (TR) allows for clinically acceptable scan times. However, 2D pulse sequences are limited in the minimum slice thickness achievable due to signal-to-noise ratio (SNR) and gradient restrictions making 2D TSE unsuitable for high resolution isotropic imaging commonly preferred in neuro and musculoskeletal (MSK) imaging applications. 3D acquisitions circumvent this limitation and may provide higher SNR than 2D methods.
3D T2w imaging protocols based on single-slab 3D TSE/FSE pulse sequences1,2 (e.g., CUBE, SPACE) are commonly used for high resolution isotropic imaging. They make use of very long echo train lengths (ETLs) to reduce the overall scan time and employ variable refocusing flip angles to control the signal evolution along the echo train. Data are acquired using Cartesian sampling and the view ordering is chosen to minimize blurring from T2 decay.1 The utility of this pulse sequence has been successfully demonstrated for brain,1,3 knee,4,5 and spine6 imaging. Tamir et al7 proposed a 3D TSE pulse sequence that enables the generation of T2w images at multiple TEs from a single acquisition. This approach uses a random phase encode reordering in the ky-kz plane along with subspace constraints to reconstruct the different T2 contrasts without image blurring. As an alternative to full Cartesian acquisition, a stack-of-stars TSE pulse sequence was proposed for motion robust T2w imaging and demonstrated for brain8 and abdomen imaging.9
T2 mapping is a parametric imaging approach that provides quantification of T2w images for a more accurate diagnosis of pathology. It requires generation of T2w images at multiple TE times in order to obtain a T2 map. 3D T2 mapping techniques have been proposed using gradient echo,10,11 dual echo in the steady state,12 T2-prepared gradient echo13–16 and TSE based pulse sequences17,18 TSE based T2 mapping approaches involve acquisition of the 3D volume at 3 or more TE times, making the scan times very inefficient for clinical imaging.18–20 Recently, Yuan et al17 proposed a T2 mapping technique for carotid vessel wall imaging which acquires 3 different T2w images in an interleaved manner using compressed sensing and parallel imaging to reduce scan time. All these techniques tradeoff scan time with the number of TE times acquired and generate T2 maps assuming an exponential model for the T2 signal decay. The coarse sampling of the signal evolution caused by the limited number of TEs can affect T2 estimation. This is more pronounced when the signal model deviates from a single exponential, as it is the case when the refocusing RF pulses deviate from the ideal 180°.21
In this work, we propose an efficient 3D stack-of-stars TSE pulse sequence for the simultaneous generation of multiple T2w images and 3D T2 maps. We introduce an efficient radial view ordering to enable reconstruction of echo images and T2 maps from highly undersampled data. We also developed an analytical framework to design the refocusing flip angle trains that maximizes tissue relative contrast and minimizes T2 estimation error. Images are reconstructed at multiple TEs from highly undersampled data using a subspace constrained iterative algorithm. Performance of the sequence is evaluated using phantoms and demonstrated in vivo for brain, knee, and carotid imaging.
2 |. METHODS
2.1 |. Technique
2.1.1 |. Pulse sequence
In the proposed 3D stack-of stars TSE, each kz partition is sampled using a radial trajectory and Cartesian phase encoding is applied along the kz dimension. Each partition is filled up in consecutive TRs before moving to the next, with the same set of angles acquired in all the partitions. A flip back pulse22 is played at the end of the echo train to restore the longitudinal magnetization in order to enable the use of shorter TRs to improve scan efficiency. To suppress the free induction decay signal generated from outside the excited slab, crusher gradients are added around the refocusing pulse.23–25
2.1.2 |. Pseudorandom radial view ordering
In a TSE pulse sequence, the ETL and the number of shots are known a priori for each kz partition allowing the design of efficient k-space coverage schemes. In this work, we introduce a pseudorandom radial view ordering scheme to meet the following goals: (i) allow uniform coverage of k-space for each TE time, (ii) distribute radial views to reduce artifacts from T2 decay, and (iii) allow flexibility in the choice of ETL for very long ETL imaging. The angle acquired at and the from the proposed view ordering scheme is given by:
where, is the total number of radial views, and is the optimal angular separation between radial views for each TE.
While the previously proposed bit-reversed view ordering scheme26 fulfills requirements (i) and (ii) it restricts the ETL to powers of 2 thereby reducing flexibility of the pulse sequence. Another alternative is the golden angle view ordering scheme27 often used in radial gradient echo pulse sequences. The golden angle view ordering does not restrict the choice of ETL; however, at very high acceleration rates (such as 3–4 views per TE), it yields a nonuniform coverage of k-space. The proposed pseudorandom view ordering scheme ensures uniform distribution of views for each TE by incrementing Δ based on the specific TR and TE being acquired. The angles are computed for odd and even echoes in a pseudorandom manner to ensure good radial coverage without restrictions on the ETL.
2.1.3 |. Refocusing flip angle design
In Cartesian imaging, refocusing flip angle designs have traditionally focused on minimizing spatial blurring while maintaining low specific absorption rate (SAR).1,28,29 One proposed design parametrizes the refocusing flip angles by 4 control angles which are computed using a prospective extended phase graph (EPG) algorithm.1 The control angles are used to set the target signal intensity for the pseudosteady state signal along the echo train. In this work, we propose an analytical framework to design the refocusing flip angles that maximizes the relative contrast between 2 species at the desired contrast equivalent , enables accurate T2 estimation, and reduces SAR. As described by Busse et al,29 is defined as the TE of a pulse sequence with a train of 180° refocusing flip angles that yields the same contrast as the variable refocusing flip angle train.
The analytical framework is based on the following objective function
| (1) |
where, is the relative contrast between 2 tissue types and is the signal at for the respective tissues.
In order to enable accurate T2 estimation, the unconstrained objective function is augmented by constraints to (i) decrease the T2 estimation error within an acceptable threshold and (ii) increase the SNR, measured as the area under the T2 decay curve, by prolonging the signal evolution curve to ensure the latter echoes are not corrupted by noise. In addition, constraints are added to maintain SAR within acceptable limits. Thus, the flip angle design problem can be expressed as a constrained optimization:
| (2) |
where, is the analytical Cramer-Rao lower bound (CRLB) with being the acceptable bound on the variance of the estimator and is defined as the area under decay curve (AUDC). is used as a subject independent measure of SAR and is defined as a function of the total RF power and the total scan time of the pulse sequence: . An additional lower bound constraint is added to reduce motion-related signal dephasing at very low refocusing flip angles.30,31
At very long ETLs, the shorter T2 species is more susceptible to estimation error due to the rapid signal decay. Thus, the CRLB was computed for the short T2 species and added as a constraint. The CRLB was derived from the Fisher information matrix using the EPG based signal model with an independent and identically distributed noise assumption. Derivatives of the EPG were computed numerically based on the recursive relationship described by Layton et al.32 The resultant CRLB was expressed as a function of the tissue relaxation times and the control angles.
2.1.4 |. T2 estimation
The highly undersampled TE k-space data sets from the stack-of-stars TSE pulse sequence are reconstructed using a subspace constrained algorithm33 with locally low rank regularization.7,34 In this technique, the signal evolution is constrained to a lower dimensional subspace using principal component (PC) analysis on a basis of curves generated using the forward EPG model. The signal at the ith echo when using shorter TRs and flip back pulses is modeled as follows35:
| (3) |
where, is the steady state longitudinal magnetization, is the recovery period from the last echo to the end of the TR and corresponds to the normalized value used to account for flip angle deviations due to RF field inhomogeneity. The function is the EPG model given by
| (4) |
Here, is the excitation flip angle along the slab obtained by discretizing the excitation RF slice profile based on the number of slices within the slab, is the refocusing flip angle for the echo and esp is the echo spacing between the refocusing pulses. is assumed to be a constant function for nonselective excitations. The slice profiles were computed using Bloch simulations and considered the effect of relaxation between the RF pulses.
The PC subspace basis is generated by simulating the TSE signal using the model in Equation 3. Signal redundancy across the temporal dimension can be exploited by approximating the TE images in a lower dimensional subspace,
| (5) |
where, is the matrix such that the rows are the different echoes and the columns are the pixels in each TE image, is a dimensional PC subspace such that , and are the PC coefficients. The constrained reconstruction recovers the individual PC coefficients which are then projected on to the basis to obtain the individual TE images. T2 maps are generated from the reconstructed TE images by fitting them to a library of precomputed T2 evolution curves.36
2.2 |. Simulations
All simulations were implemented in MATLAB (MathWorks, MA).
Point spread function (PSF) simulations were performed to compare the different view ordering schemes. 2D Radial PSFs were computed for each TE assuming an ETL of 64, 256 radial views (resulting in 4 views per TE), and 256 points along each view. To evaluate PSF behavior over the different TE times, a temporal maximum intensity projection (t-MIP) of the individual PSFs was computed as outlined in Chan et al.37 The t-MIP was created from the individual PSFs by computing the maximum intensity for each pixel over the different TEs. In addition, the temporal standard deviation of the PSFs were also computed to capture variations in the PSF over the TEs. To quantitatively compare the PSFs, the full-width-half-maximum (FWHM) and the mean side lobe amplitudes were calculated for the center line profile of the t-MIP image.
The objective function and constraints for the flip angle design optimization problem were computed for the specific imaging application using relaxation values from the literature. The SNR and CRLB constraint functions were computed using tissue specific values of T1 and T2 values . The control angles were obtained by solving the optimization problem using the augmented Lagrangian genetic algorithm.38 The solver was implemented using the Genetic Algorithm Toolbox (MATLAB) using 500 generations and a function tolerance of 1e-7 as the stopping criteria. This resulted in a computation time of 420 seconds on a server with 44 physical cores (2.4 GHz Intel Xeon processor E5-2699A). The computational complexity of the flip angle design requires offline calculation of the control angles for each imaging application.
Numerical simulations were performed to study the T1 sensitivity due to the use of variable refocusing flip angles and flip back pulses on the T2 estimation accuracy. The TSE signal was generated for a range of T1 and T2 values using a Bloch equation simulator assuming the following parameters: ETL = 70, echo spacing = 6 ms, . In order to evaluate the performance in the presence of flip angle variations due to RF field inhomogeneity, the simulations were performed assuming the following values for normalized , 1.0, and 1.2. Gaussian noise was added to the generated signal and 2 different types of fitting were performed using the EPG based model: (i) 2-parameter fitting to estimate T2 and assuming a fixed T1 = 1000 ms and (ii) 3-parameter fitting to estimate T2, , and T1. This was repeated for 100 noise realizations and the mean and standard deviation of the estimated T2 were computed for the 2 different fitting approaches. T2 values from 20 ms to 220 ms and T1 values from 250 ms to 2500 ms were used for the simulation.
Monte Carlo simulations were performed to verify the error in T2 estimation due to subspace projection (Equation 5). A PC subspace basis was generated using Equation 3 with T2 values in the range of 20 ms to 300 ms in steps of 1 ms, T1 values in the range of 500 ms to 2500 ms in steps of 250 ms, and values from 0.5 to 1.3 in steps of 0.05. The 3D TSE signals were generated for a range of T2 values from 20 ms to 220 ms for 9 different T1 values assuming ETL = 70, echo spacing = 6 ms, and 100 noise realizations. The signal was projected onto the subspace and a variable number of PC coefficients were retained. T2 was estimated from the reconstructed signal and the mean estimation error was computed.
Simulations were performed using a digital computer phantom to study the effect of the number of PC coefficients (L) on reconstructed image quality and T2 estimation. A digital BrainWeb phantom39 was used to synthesize T1 and T2 maps corresponding to gray matter, white matter, CSF, and scalp using T2 values from the literature. The T2 maps were used to synthesize TSE images at different TEs using the EPG forward model, assuming ETL = 130, radial views = 260, and echo spacing = 6 ms. The following control angles were used to generate the variable refocusing flip angle train: . Stack-of-stars k-space data were generated using a 1D Fourier transform operator along the slices and in-plane radial sampling using the pseudorandom view ordering. Coil sensitivities from a 20-channel head coil were used to create multi-coil data. A Monte-Carlo experiment was setup for 100 noise realizations (with Gaussian noise added to the real and imaginary components of k-space) and data were reconstructed using the proposed reconstruction framework for PC coefficients of length L = 2–7. For each choice of L, the T2 map was estimated using a library of precomputed signal evolutions. The library was generated for T2, T1, and values in the range of 20 to 350 ms, 500 to 2500 ms, and 0.5 to 1.6, respectively. Performance of the reconstruction was evaluated by computing the normalized error in the T2 map and the image, and , across the noise realizations.
2.3 |. MRI Experiments
The stack-of-stars TSE pulse sequence was implemented on a 3T MRI scanner (Skyra, Siemens, Erlangen, Germany).
2.3.1 |. Phantom experiments
The T2 estimation accuracy of the proposed sequence was evaluated using 5 agarose gel tubes with the following T2 and T1 values (ms): 129.1/1000, 81.9/611, 73.5/437, 61.1/745, 54/900 and 40.5/951. Reference estimates of T2 were obtained using a single slice single-echo spin-echo pulse sequence with: field of view (FOV) = 12 cm, acquisition matrix = 128 × 128, TR = 5 s, and 12 different TEs from 8 ms to 96 ms. The reference T1 estimates were obtained using a single slice inversion-recovery single-echo spin-echo pulse sequence with: FOV = 12 cm, acquisition matrix = 128 × 128, TR = 8 s, and 7 different inversion times (ms): 300, 700, 1200, 1800, 2500, 3200, 4200. The stack-of-stars TSE pulse sequence was used to acquire data using the following parameters: FOV = 120 cm, base resolution = 256, radial views = 384, ETL = 96, TR = 2000 ms, echo spacing = 7.1 ms, and 1-mm-thick slices with nonselective excitation.
2.3.2 |. In vivo experiments
Subjects were imaged after obtaining informed consent in agreement with the institutional review board requirements.
In vivo brain data (whole brain coverage) were acquired on 3 normal volunteers (male, mean age = 27.3 years) using the stack-of-stars pulse sequence in the sagittal orientation with nonselective excitation and the following parameters: 1.0 × 1.0 × 1.0 mm resolution, FOV = 25 cm, base resolution = 256, radial views = 260, ETL = 130, echo spacing = 5.84 ms, and slice parallel imaging factor = 2 (32 reference partitions). Data were acquired at 2 TRs (1300 ms and 2600 ms) resulting in scan times of 5.3 min and 6.7 min, respectively. For comparison, data were acquired with the Cartesian 3D SPACE pulse sequence with FOV = 25 cm, base resolution = 256, 1.0 × 1.0 × 1.0 mm resolution, ETL = 220, echo spacing = 3.6 ms, TR = 2600 ms for a total scan time of 4.8 min.
Data were also acquired on a clinical patient (male, 64 years) as part of a brain tumor protocol. The protocol included the short TR stack-of-stars TSE pulse sequence before the injection of contrast along with a postcontrast T1-weighted Cartesian 3D SPACE pulse sequence. Postcontrast SPACE data were acquired with the following parameters: FOV = 25 cm, base resolution = 300, 0.8 × 0.8 × 0.8 mm resolution, ETL = 43, TE = 21 ms, and TR = 600 ms.
In vivo knee data were acquired on 3 normal volunteers (2 male, 1 female, mean age = 29 years) in the sagittal orientation with 0.63 × 0.63 × 0.75 mm resolution and nonselective excitation in a 6.2 min scan. The acquisition parameters were: TR = 1200 ms, ETL = 70, echo spacing = 6.76 ms, FOV = 16 cm, radial views = 210, base resolution = 256, slice parallel imaging factor = 2 (32 reference partitions). Additional data were acquired with the Cartesian 3D SPACE pulse sequence with matching slice coverage and resolution with FOV = 16 cm, TR = 1200 ms, ETL = 64, echo spacing = 4.62 ms, and total scan time = 5.6 min.
In vivo carotid vessel wall data were acquired on a subject (56 year old male) with the following parameters: ETL = 64, echo spacing = 7.1 ms, TR = 1300 ms, base resolution = 256, radial views = 256, in-plane resolution = 0.53 × 0.53 mm2, slice thickness = 2 mm, and slab thickness = 72 mm. Data were acquired using a dedicated carotid coil40 and slab-selective excitation. The acquisition was performed with motion sensitizing gradient preparation41 to suppress signal from blood flow and using adiabatic RF pulses for fat suppression. To reduce artifacts caused by the free induction decays resulting from combining a slab-selective excitation with nonselective refocusing pulses, phase cycled measurements were used.42,43 To reduce the total scan time, only the central 60% of the cylinder was acquired for the phase cycled measurement.
2.3.3 |. Image reconstruction
The acquired k-space data with slice parallel imaging was reconstructed using 1D-GRAPPA along the slice dimension to fill the missing kz partitions. The TE images were then reconstructed using the iterative reconstruction algorithm. The subspace constrained reconstruction problem was solved using the alternating direction method of multipliers (ADMM)44 using 5 PCs. The T2, T1, and ranges for the subspace basis were 20–350 ms, 500–2500 ms, and 0.5–1.6, respectively. For slab-selective excitation, the excitation RF slice profile was computed using the Shinnar-Le Roux algorithm45 and used to generate a slice dependent basis. All reconstruction algorithms were implemented offline using MATLAB (MathWorks, MA) and the Gadgetron framework46 in a hybrid central processing unit/graphics processing unit (CPU-GPU) approach. The ADMM algorithm was implemented on the CPU with the nonuniform fast Fourier transform computed on a GPU at each iteration and the slices were processed in parallel. This resulted in a reconstruction time of ~15 min/slice on a server with 44 cores (2.4 GHz Intel Xeon processor E5-2699A), 440GB RAM, and 8-NVIDIA Tesla P100 GPUs.
2.3.4 |. Image quality analysis
Quantitative evaluation of the stack-of-stars pulse sequence was performed in vivo using both brain and knee imaging data. For brain imaging, region of interests were drawn in the gray matter (GM), white matter (WM) and CSF on the sagittal cross section images from the stack-of-stars and Cartesian SPACE acquisitions. Signal intensities were measured on 5 mid-slices for each subject and the relative contrast was calculated between GM-WM, WM-CSF, and GM-CSF. For knee imaging, signal intensities were measured in the muscle and cartilage tissues on 5 slices for each subject and the muscle-cartilage relative contrast was computed for both pulse sequences.
3 |. RESULTS
3.1 |. View ordering
To evaluate the PSF behavior over the different TE times, the temporal MIP and temporal standard deviation images were computed from the 2D radial PSFs for the different view ordering schemes and are shown in Figure 1. The figure also shows the center line profile of the t-MIP and standard deviation images. From the t-MIP image note that both the bit-reversed and proposed pseudorandom ordering schemes demonstrate less aliasing compared to golden angle ordering which presents increased streaking artifact (arrow). The proposed view ordering scheme has comparable main lobe width and side lobe amplitude (FWHM = 1.22, mean side lobe = 0.64e-3) as the bit-reversed scheme (FWHM = 1.22, mean side lobe = 0.64e-3). The golden angle view ordering has a much higher mean side lobe amplitude (FWHM = 1.65, mean side lobe = 1.2e-3) resulting in increased aliasing near the central PSF peak. The zero intensity at the central circular region of the standard deviation images indicates that the bit-reversed and pseudorandom view ordering schemes have a constant PSF intensity in the central region over the different TEs, indicative of uniform coverage across the TEs. Note that the proposed view ordering scheme is more flexible and removes the power of 2 restriction on the ETL, present in the bit-reversed scheme.
FIGURE 1.
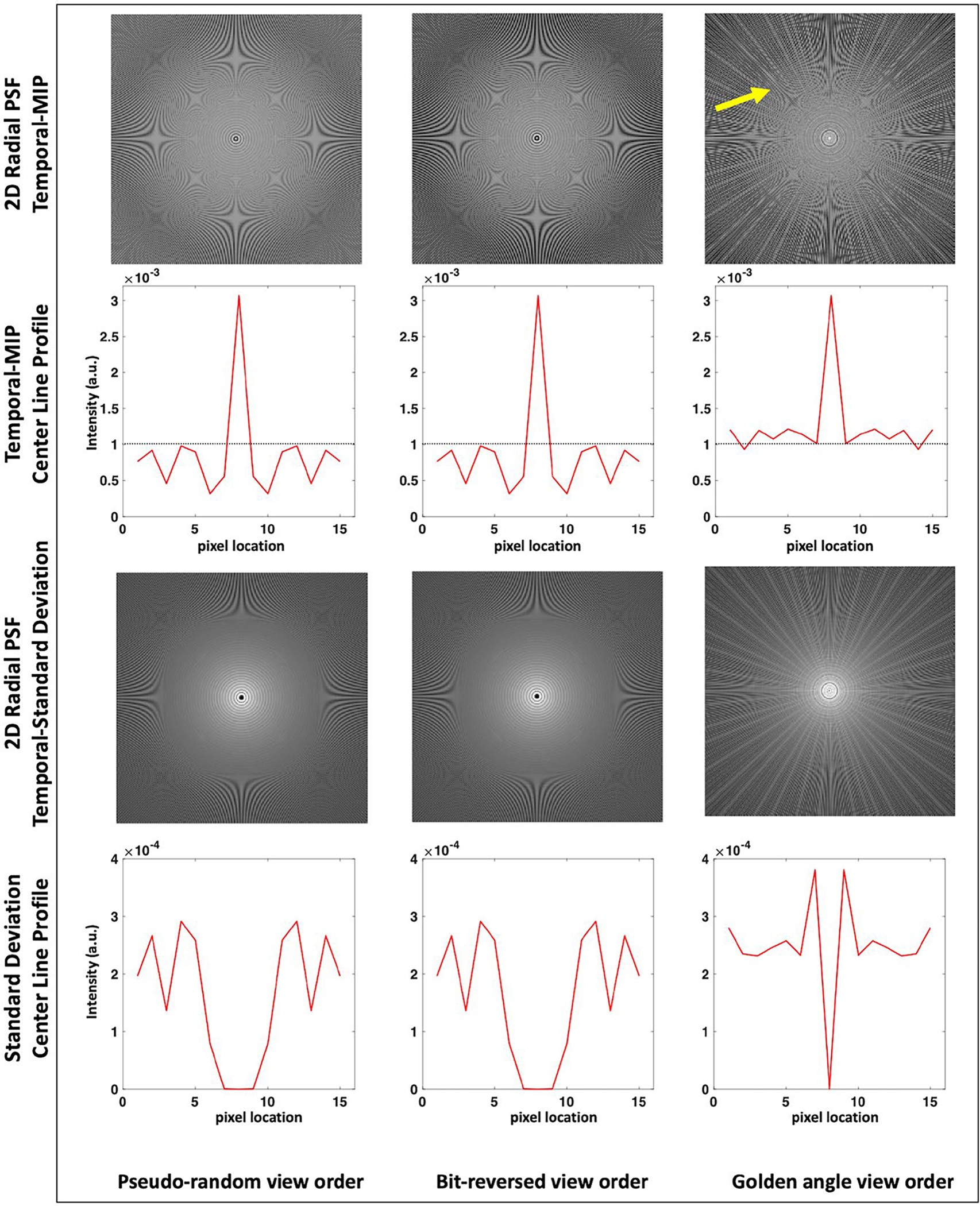
Temporal MIP and standard deviation images computed from the 2D radial PSF are shown for the pseudorandom, bit-reversed, and golden angle view ordering schemes for ETL = 64 and 256 radial views. From the t-MIP images note that both the bit-reversed and the proposed pseudorandom ordering schemes demonstrate reduced aliasing artifacts compared to the golden angle ordering which presents increased streaking artifacts (arrow). This is also indicated by the reduced mean side lobe amplitude in the line profile plots for the proposed scheme. The zero intensity at the central circular region of the standard deviation images indicate that the bit-reversed and pseudorandom view ordering schemes have a uniform coverage over the different echoes
3.2 |. Flip angle optimization
Figure 2 shows the flip angle design (top) and signal evolutions (bottom) for muscle and cartilage using 3 different refocusing flip angle schemes for ETL = 64. The flip angles were derived using the following control angles: (A) , (B) , (C) . The vertical dashed line shows the echo corresponding to , the effective TE typically used in Cartesian T2w imaging47 for making radiological decisions. The signal evolutions in Figures 2A,B illustrate that decreasing causes a slight drop in relative contrast between cartilage and muscle for the same . Note that the use of a higher (Figure 2C) results in an increased relative contrast compared to Figure 2A. However, the rapid signal decay leads to a reduced AUDC.
FIGURE 2.
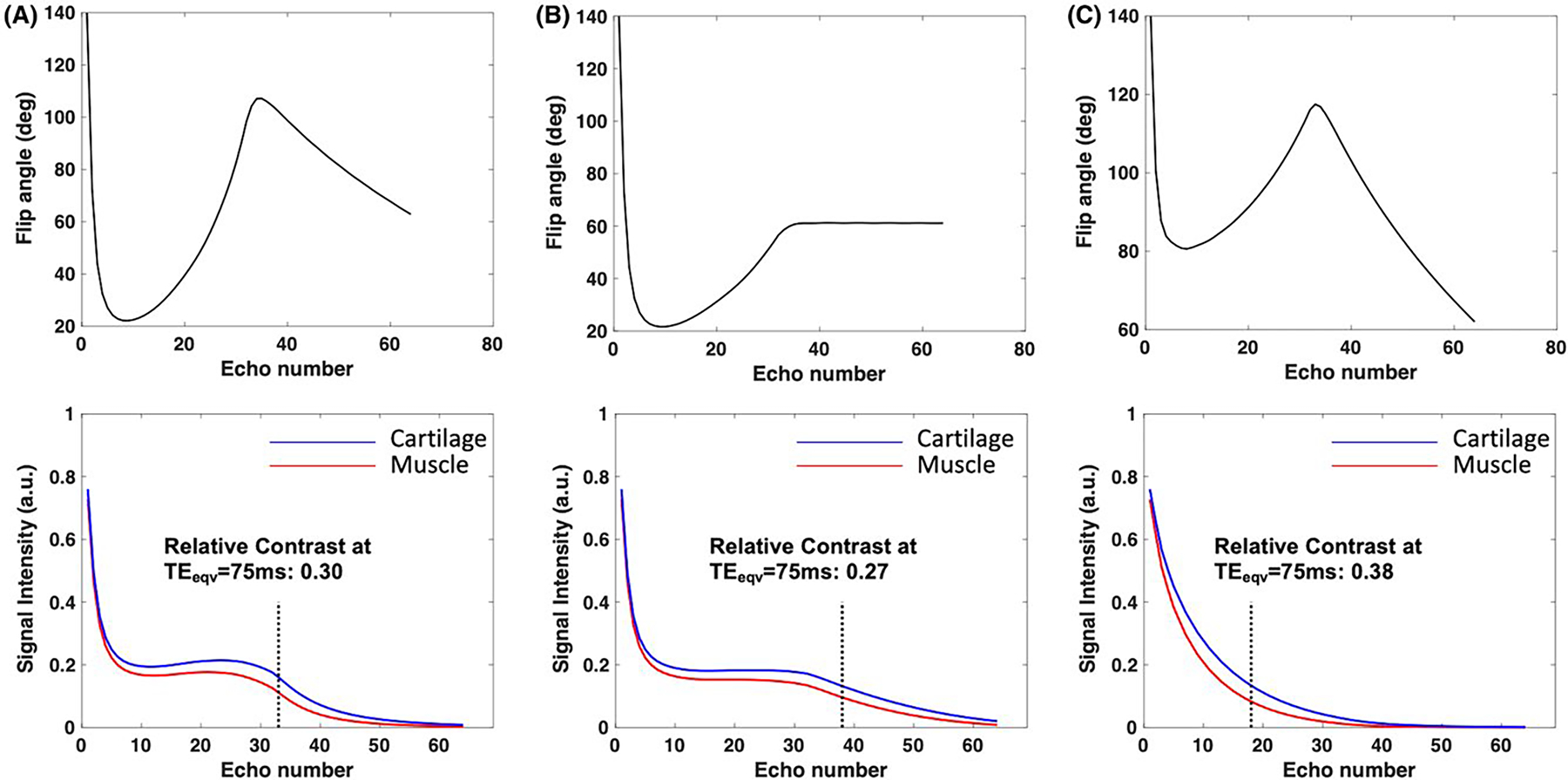
Refocusing flip angles (top) and signal evolutions (bottom) for muscle and cartilage using 3 different refocusing flip angle schemes for ETL = 64. The flip angles were derived using the following control angles: (A) , (B) , (C) . The relative contrast is also shown for the contrast equivalent of 75 ms
While Figure 2 illustrates the ability to tailor refocusing flip angles to improve relative contrast between tissues, it also demonstrates the tradeoff between contrast and SNR. The curves in Figure 2C have a lower AUDC, making the latter echoes more susceptible to noise which would in turn affect T2 estimation accuracy. In order to improve the estimation accuracy, additional constraints were added to the objective function as indicated in Equation 2. The effect of these constraints is illustrated in Figure 3 for 3 different applications: MSK, neuro, and carotid vessel wall imaging. Figure 3A shows a 2D plot of the objective function for the relative contrast between the following tissues: muscle and cartilage at (row 1), GM and WM at (row 2), and carotid vessel wall and recent intraplaque hemorrhage at (row 3). Note that the relative contrast distribution varies across the tissues considered since it is a function of the T1 and T2 of the tissues. Figure 3B shows the cumulative AUDC (from both tissues) used as a metric of SNR across the TEs. From the plot, it can be observed that the AUDC is predominantly determined by . In order to minimize noise in the latter echoes, we want to operate in regions of high AUDC which corresponds to lower values of . A plot of the CRLB lower bound on the variance of the T2 estimator is shown in Figure 3C. Note that the T2 estimation performance is a nonlinear function of the design parameters and . Figure 3D shows a plot of the computed metric that is used as a subject weight independent measure of SAR. Since the is proportional to the total RF power in the pulse sequence, it linearly increases with the control angles and is the same for all 3 tissue types. Based on the constraints shown in Figure 3, one possible feasible region for the search space of and would be and for MSK and neuro imaging, respectively. While the vessel wall imaging case could have a similar feasible region as muscle and cartilage, the anatomy is susceptible to swallowing motion that would result in signal dephasing at low values of . Based on in vivo volunteer experiments, was found to be a robust lower bound for carotid imaging.31,48
FIGURE 3.
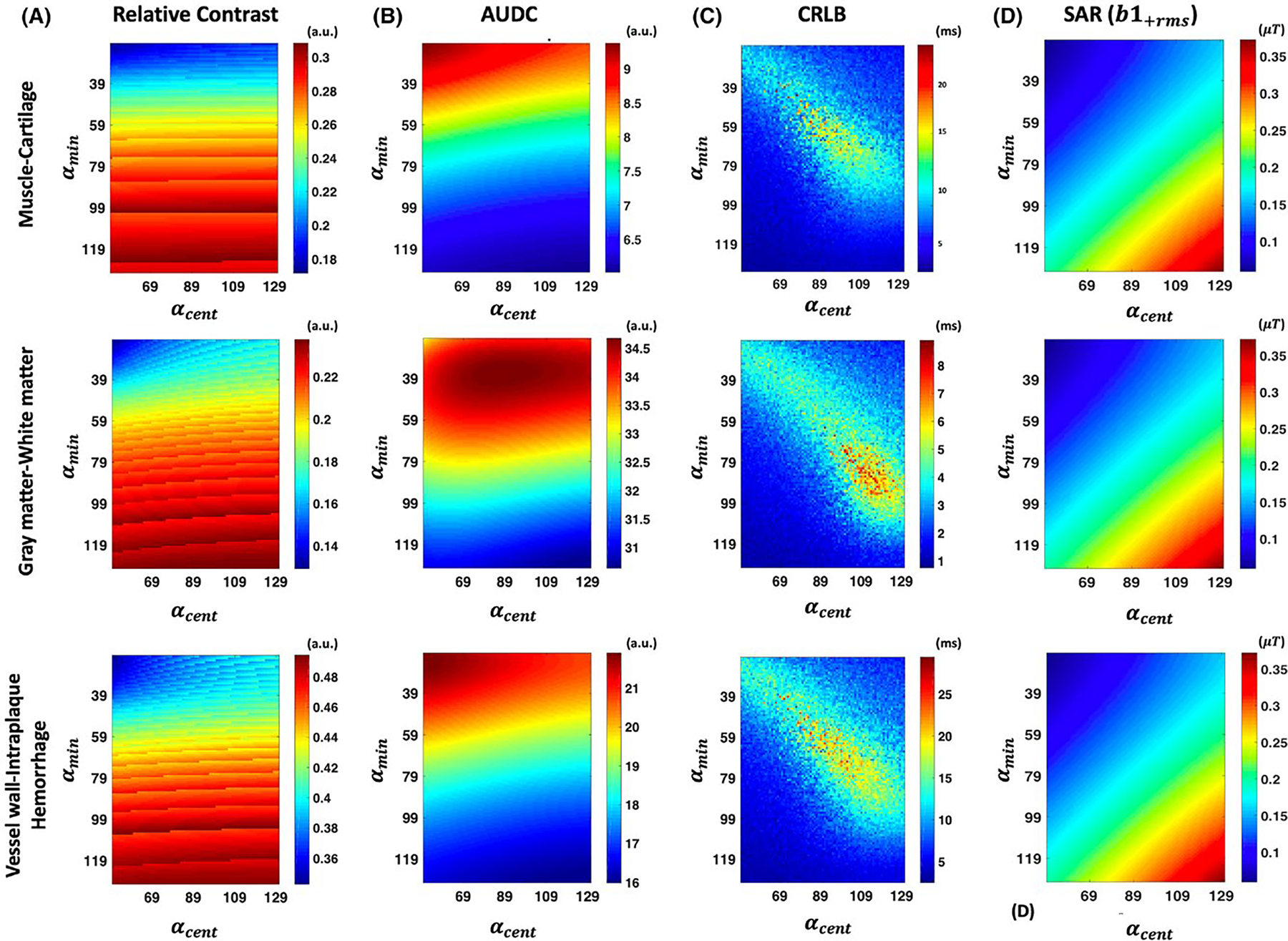
Two-dimensional plots of the objective function and constraints for MSK (top row), neuro (middle row), and carotid vessel wall imaging (bottom row) applications. A, The relative contrast as a function of and . The T2 estimation related cumulative AUDC and CRLB constraints are shown in (B) and (C), respectively. The SAR related is shown in (D)
3.3 |. Numerical simulations T2 estimation
To study the effect of T1 sensitivity on the estimated T2 accuracy, simulations were performed by fitting the TSE signal to 2 different signal models. The 2-parameter fit, which estimates T2 and while assuming a fixed T1, and the 3-parameter fit, which estimates T2, T1, and . Plots of the percent T2 estimation error along with standard deviation of the estimate are shown in Figure 4 for the 3-parameter and 2-parameter fit for the range of T2 and T1 values typically found in vivo. We can observe that the 3-parameter fit has an overall reduced relative error as it accounts for T1 effects arising from the use of variable refocusing flip angles and the flip back pulses. The 2-parameter fit has a low error only for T1 values close to the value assumed during fitting (1000 ms), however, the standard deviation is lower than the 3-parameter fit as fewer parameters are being estimated. Note that a similar trend in estimation performance is observed across the different normalized values.
FIGURE 4.
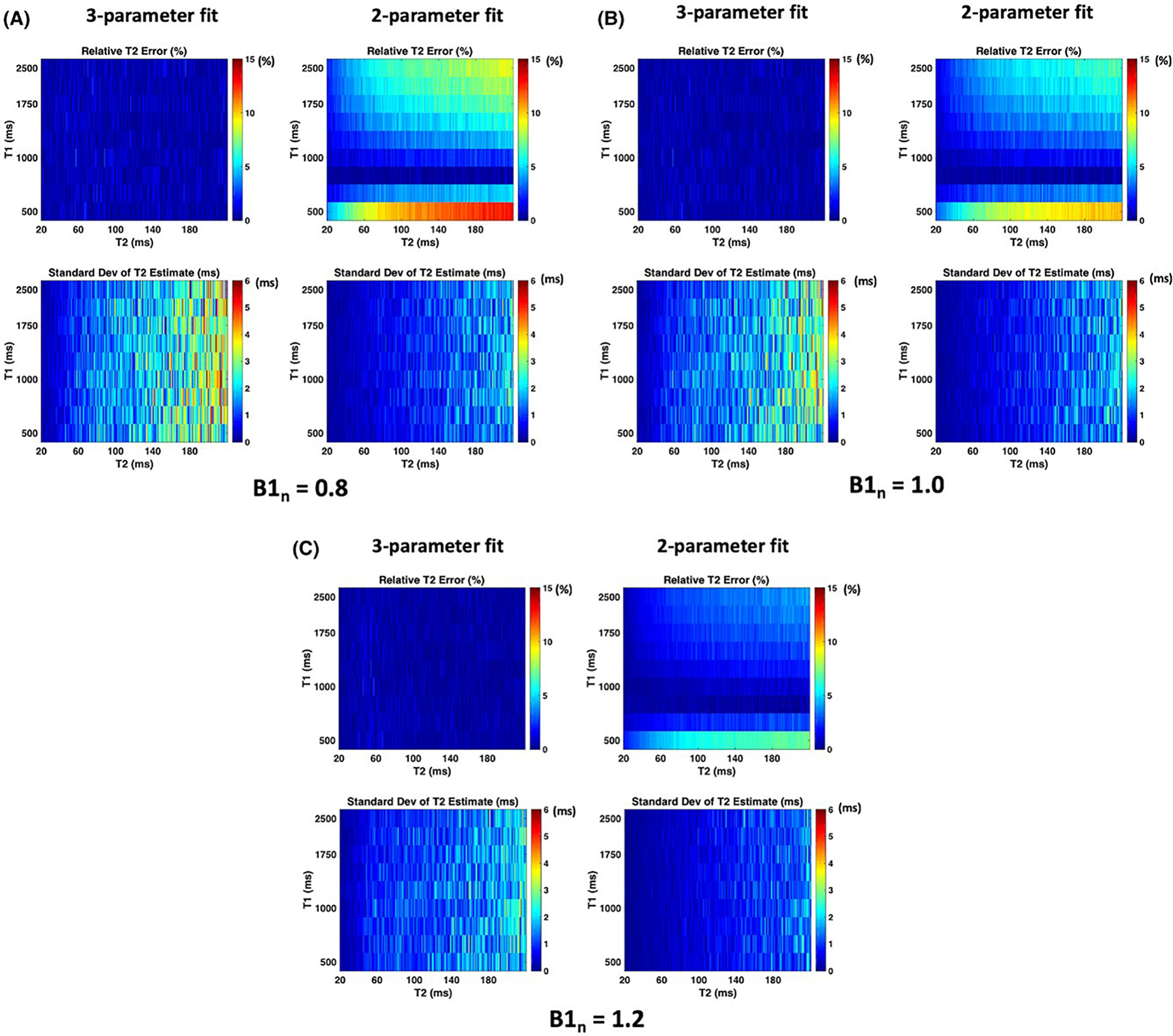
Results from numerical simulations to study the effect of T1 sensitivity on T2 estimation accuracy. The relative error and standard deviation of the T2 estimates from the 3-parameter fit and the 2-parameter fit are shown for (A), (B), and (C)
Results from the Monte-Carlo simulations performed to study the effect of the number of PCs used in the subspace reconstruction on T2 estimation accuracy are shown in Supporting Information Figure S1, which is available online. The figure shows plots of the percent T2 error according to the number of PCs used for a range of T2 values typically found in vivo and for 3 different T1 values (500 ms, 1250 ms, and 2500 ms). Note that the estimation error decreases when the number of PCs ≥ 5 for all the T2 values considered.
Figure 5 shows results from simulations performed to study the effect of the number of PCs on the estimated T2 map accuracy. The figure shows estimated T2 maps for different choices of L. Also shown are normalized T2 estimation error maps along with the mean normalized error (bottom left). Observe that the T2 estimation error decreases with increasing L due to better representation of the temporal signal evolution. However, a higher estimation error was observed in the CSF region due to the use of a restricted range of T2 values (20–350 ms) in the library of curves used for T2 estimation.
FIGURE 5.
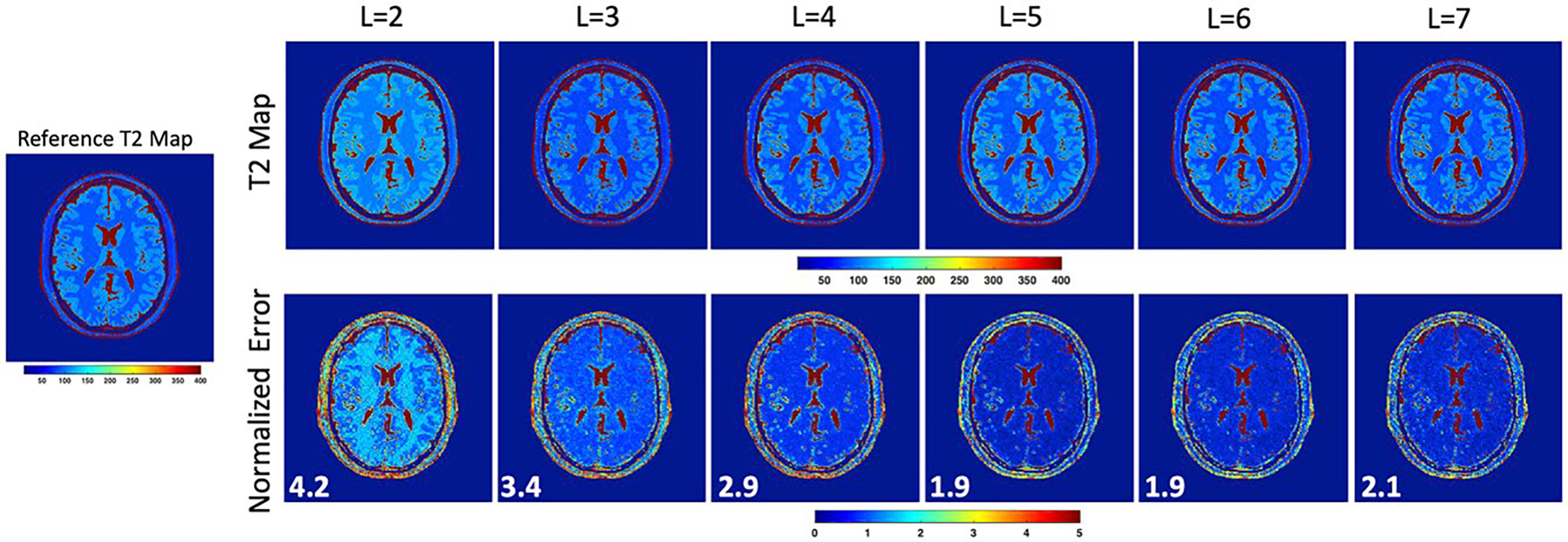
Results from digital phantom simulations to study the effect of number of PCs on T2 estimation accuracy. The reconstructed T2 maps are shown for different values of L along with the normalized error in T2 estimation. The mean normalized error is indicated at the bottom left of the error maps. Increasing L leads to a reduction in T2 estimation error due to better representation of the temporal signal evolution
The effect of L on the reconstructed TE image quality is shown in Supporting Information Figure S2. This figure shows the reconstructed image for different choices of L along with the normalized error map. At lower values of L, differences in TE image contrast can be observed compared to the reference resulting in higher normalized error values. On the other hand, at a high value of L (L = 7), there is noise amplification in the reconstructed TE image. This explains the noisy appearance of the corresponding T2 map in Figure 5. We chose L = 5 for our reconstructions to allow a reasonable tradeoff between TE image quality and T2 estimation accuracy.
The results of our Monte-Carlo simulations are consistent with earlier observations on the tradeoff between model error and noise amplification due to the choice of L.7,49 While simulations using noiseless data show that the model error decreases with larger L,49 the presence of noise leads to poor recovery of the TE images due to noise amplification with increasing L.7
3.4 |. Phantom imaging
T2 values estimated using the stack-of-stars TSE pulse sequence for 5 agarose phantoms are shown in Table 1 along with the percent T2 error compared to the reference single-echo spin-echo pulse sequence. The 2-parameter fit was performed assuming T1 = 1000 ms for all voxels. Consistent with the simulation results from Figure 4, T2 values estimated using the 3-parameter fit have a relative error < 5% for all the samples. Despite the accuracy in T2 estimation, the T1 values estimated from the fit were not accurate, indicating insufficient sensitivity for T1 estimation.
TABLE 1.
T2 estimation accuracy of stack-of-stars TSE from physical phantom experiments
| Phantom | Reference T2 & T1 (ms) | Stack-of-stars 3D TSE (3-parameter fit) (ms) | Percent error (%) | Stack-of-stars 3D TSE (2-parameter fit) (ms) | Percent error (%) |
|---|---|---|---|---|---|
| 1 | 129.1/1000 | 132.3 ± 2.8 | −2.5 | 133 ± 0.6 | −3.2 |
| 2 | 81.9/611 | 84.2 ± 0.6 | −2.8 | 93.0 ± 0.3 | −13.5 |
| 3 | 73.5 / 437 | 76.1 ± 0.5 | −3.5 | 81.9 ± 0.2 | −11.4 |
| 4 | 61.1/745 | 63.2 ± 0.9 | −3.4 | 66.5 ± 0.3 | −8.8 |
| 5 | 54.0/900 | 56.5 ± 0.8 | −4.6 | 56.9 ± 0.6 | −5.3 |
| 6 | 40.5/951 | 42.8 ± 0.4 | −5.6 | 42.3 ± 0.2 | −4.4 |
Abbreviations: 3D, 3-dimensional; TSE, turbo spin echo
3.5 |. In vivo imaging
Figure 6 shows reformatted cross sections of the brain for a normal volunteer from a 1 mm isotropic acquisition. The figure shows T2-weighted images from the stack-of-stars pulse sequence at acquired using both long and short TRs (2600 ms and 1300 ms) along with the conventional Cartesian SPACE acquisition at TR = 2600 ms. The advantage of the shorter TR is that full brain data can be acquired in 5.3 min whereas the longer TR requires 6.7 min. However, in the images obtained with the long TR, the CSF is brighter and the image contrast matches more closely the Cartesian SPACE images. Also, in the shorter TR stack-of-stars images, there is loss of signal in the CSF near the brain stem which leads to an apparent shorter T2. This could be attributed to flow related signal dephasing.
FIGURE 6.
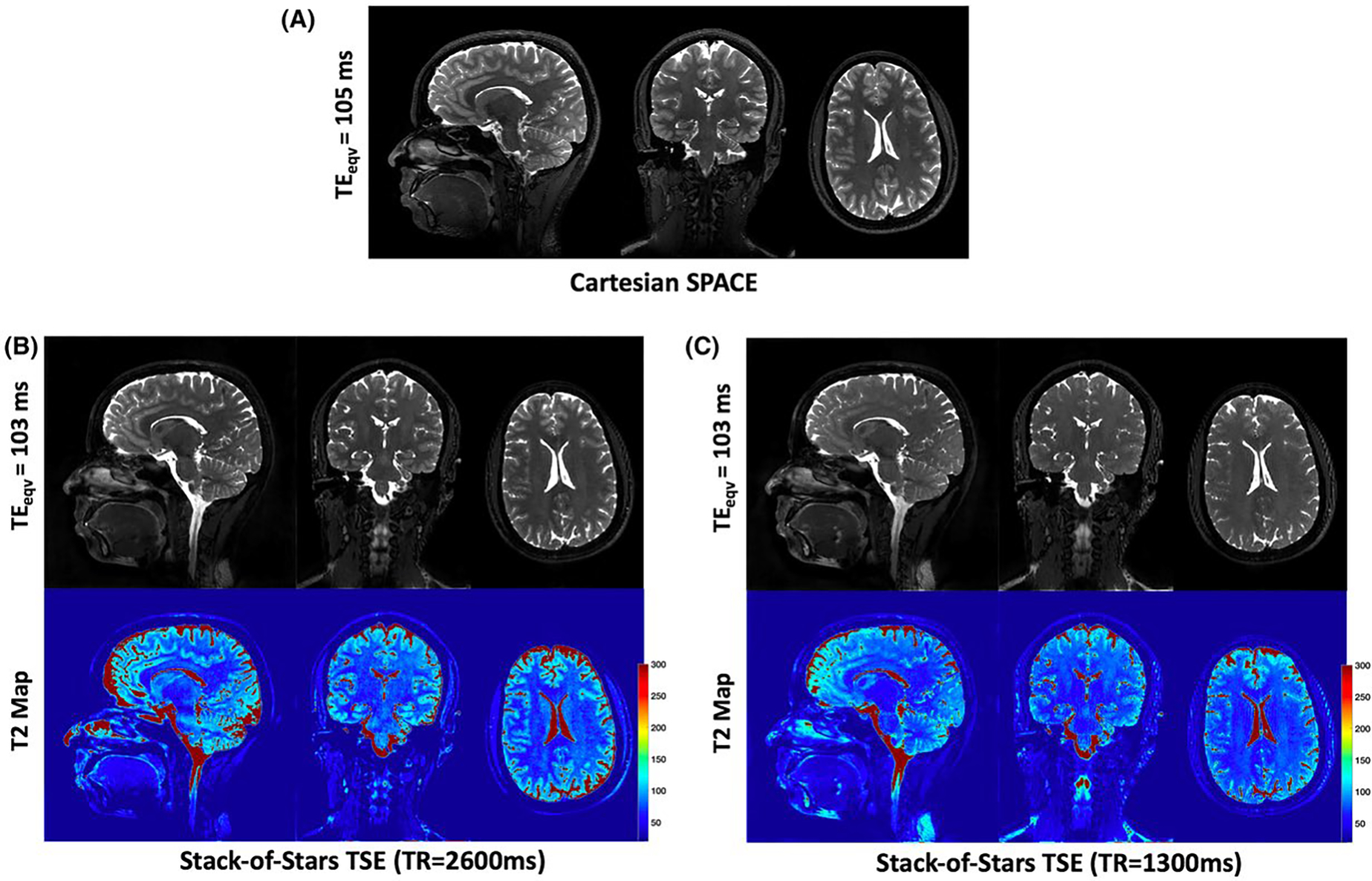
Reformatted cross-sections of the brain for a normal volunteer from the stack-of-stars TSE and Cartesian SPACE. A, T2w images from the conventional Cartesian SPACE sequence. T2w images from the stack-of-stars TSE are shown for long TR (B) and short TR (C) along with the corresponding T2 maps. The long TR images demonstrate higher CSF signal and better image contrast than the short TR acquisition
Figure 7 shows images from a patient diagnosed with brain metastasis, confirmed by the post contrast T1-weighted SPACE image which shows the enhancing lesions (red arrows) along with the region of edema. The metastatic lesion has hyperintense T2 signal (corresponding to high T2 values) in regions of edema, as demonstrated in the stack-of-stars TSE T2w images and T2 maps obtained from data acquired precontrast. Note that edema is more conspicuous in the T2 maps than in the image at . This is an advantage over Cartesian SPACE methods which only generate data at 1 effective .
FIGURE 7.
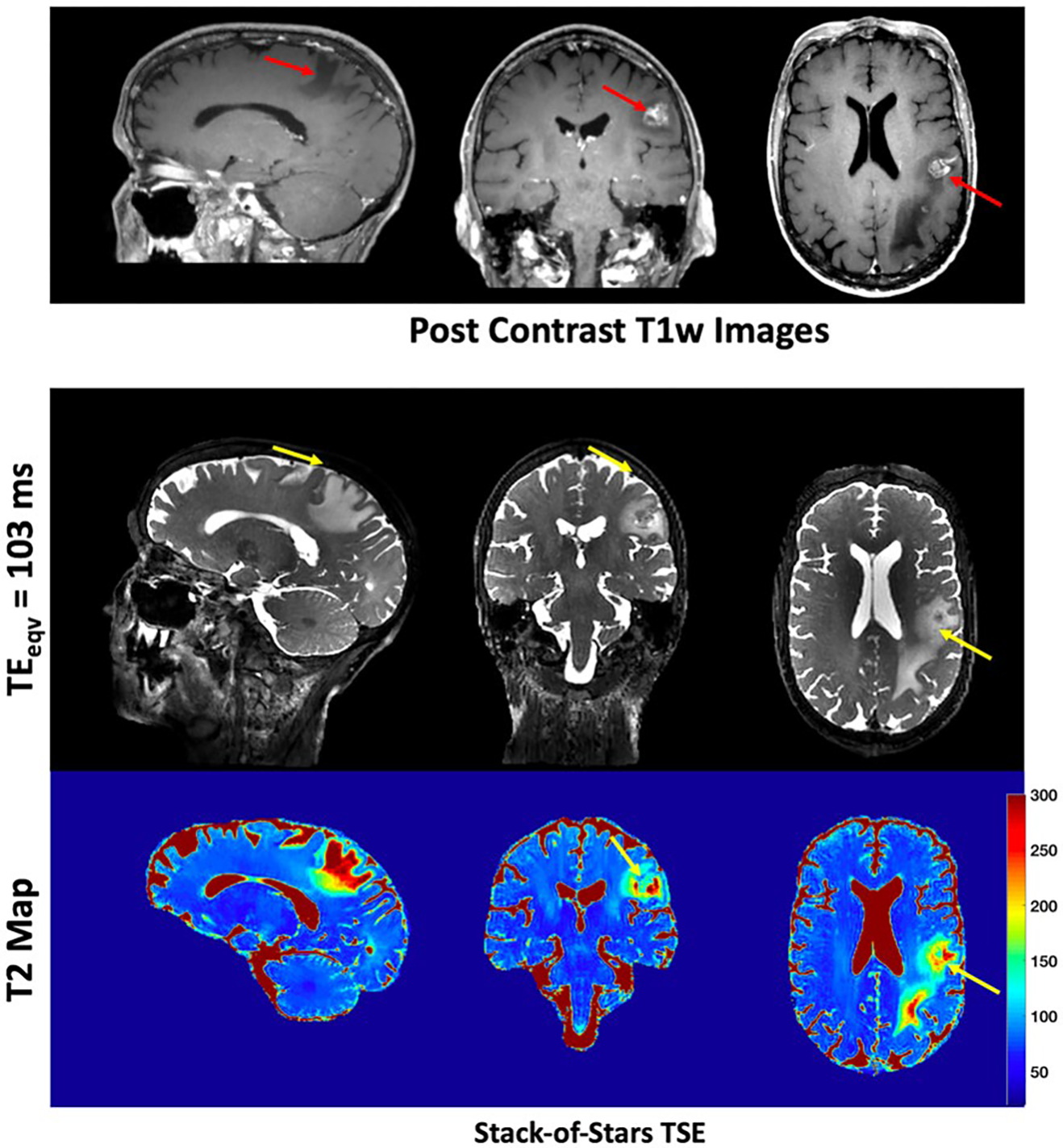
T2w images from precontrast stack-of-stars TSE are shown for a patient with brain metastasis. Also shown are the post contrast T1w Cartesian SPACE images that show the enhancing lesions (red arrows) along with the region of edema. The metastatic lesion has hyperintense T2 signal, corresponding to high T2 values, as demonstrated in the precontrast stack-of-stars TSE images and maps
Figure 8 shows reformatted T2-weighted images of the knee at from both the stack-of-stars TSE and the Cartesian SPACE pulse sequences. The refocusing flip angles were designed to generate good T2w contrast between cartilage and muscle tissues without compromising the T2 estimation accuracy. T2 maps of the cartilage are shown overlaid on the 3 cross-sections of the stack-of-stars TSE. The latter generates images at comparable image quality to the conventional SPACE with the advantage of providing T2 information. The mean T2 of the cartilage is 42.4 ± 3.6 ms and is comparable to values reported in the literature for healthy subjects.20,50
FIGURE 8.
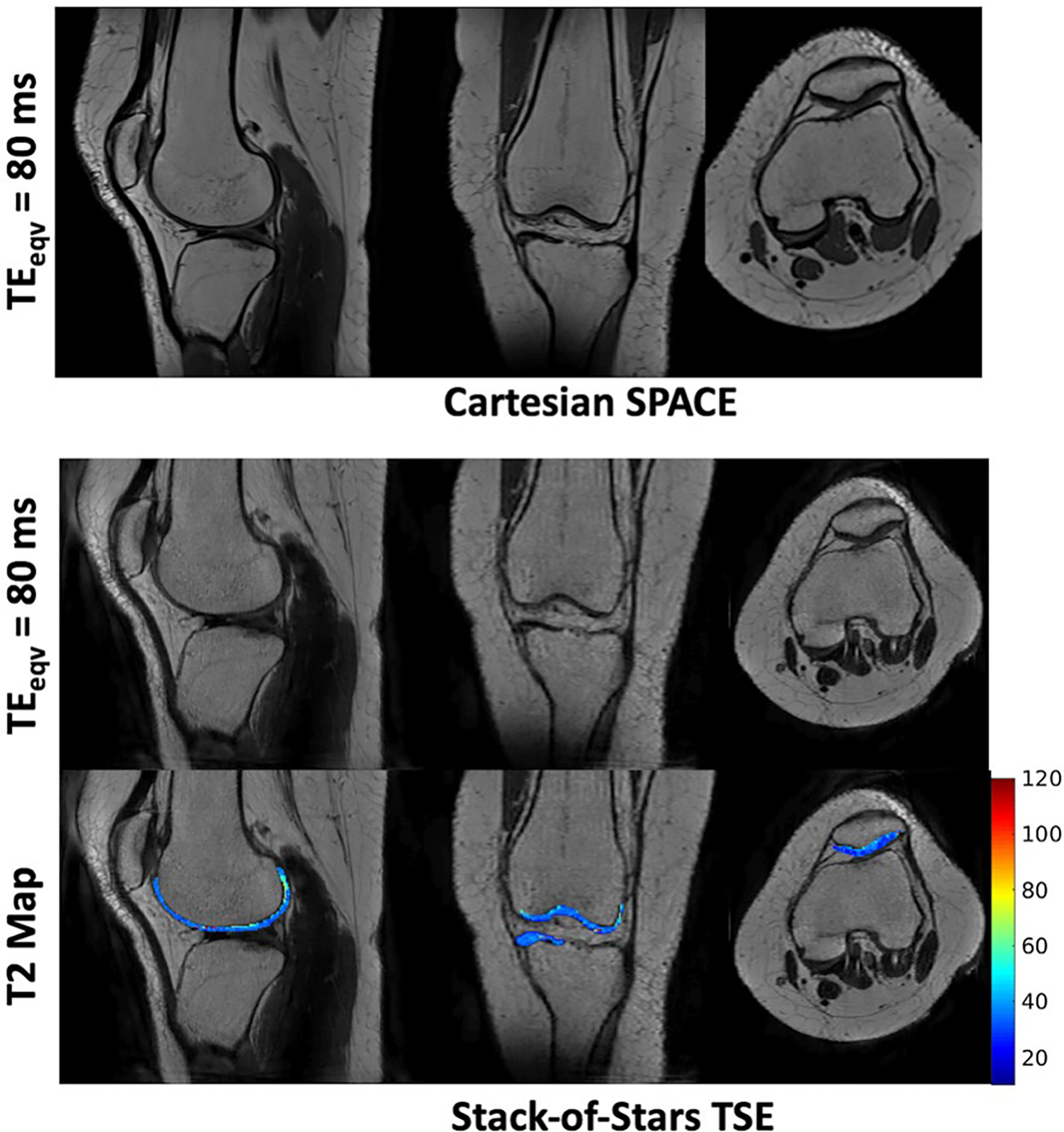
Reformatted cross-sections of the knee for a normal volunteer from the stack-of-stars TSE and Cartesian SPACE. The T2 map of the cartilage overlaid on the anatomical image is also shown. The refocusing flip angles were designed to generate good T2w contrast between cartilage and muscle tissues without compromising the T2 estimation accuracy. Note that the cartilage has a mean T2 of 42.4 ± 3.6 ms
The region of interest based quantitative analysis of brain images indicated comparable GM – WM relative contrast for the stack-of-stars (0.464 ± 0.056) and Cartesian SPACE (0.451 ± 0.065) pulse sequences. The stack-of-stars technique had a slightly lower GM – CSF contrast (0.671 ± 0.037 versus 0.714 ± 0.042) and WM – CSF contrast (0.825 ± 0.018 versus 0.843 ± 0.025). However, a significantly lower GM-CSF and WM-CSF contrast was observed with the short TR stack-of-stars acquisition. The mean cartilage to muscle relative contrast from 3 healthy volunteers was 0.234 ± 0.102 and 0.229 ± 0.11 from the stack-of-stars and Cartesian SPACE, respectively. The proposed pulse sequence can generate images with comparable image quality to the conventional SPACE in addition to simultaneously generating a T2 map for each slice, at a slightly longer scan time.
Use of the slab selective variant of the pulse sequence for carotid vessel wall imaging is demonstrated in Figure 9. In this case, the flip angles were designed to better visualize plaque components from the surrounding vessel wall. Dark blood T2w images at and for 4 different slices from a 72-mm slab are shown along with the T2 map in the slices of suspected pathology. The proposed pulse sequence enables the acquisition of TE images and T2 maps with excellent coverage of the anatomy within a 4.4-min scan.
FIGURE 9.
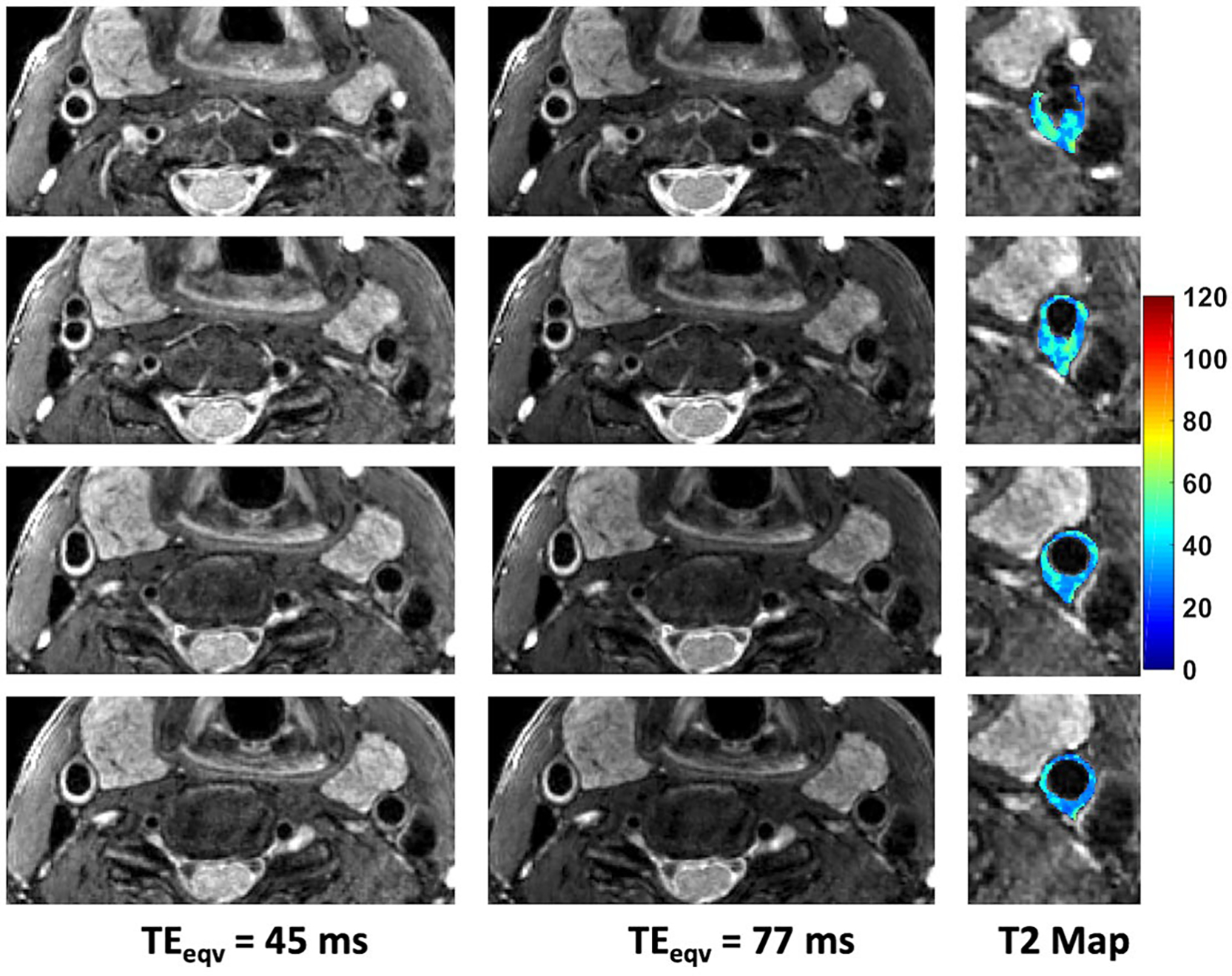
Dark blood T2w images of the carotid vessel wall acquired using the stack-of-stars TSE pulse sequence. Shown are 4 slices (2 mm thick) from a 72 mm selectively excited slab along with the corresponding T2 maps for the vessel wall
4 |. DISCUSSION
We have demonstrated a stack-of-stars TSE pulse sequence for high resolution 3D T2w imaging and T2 mapping. The pulse sequence uses a flexible pseudorandom view ordering scheme that ensures uniform coverage of k-space for each TE while distributing the views to reduce artifacts from T2 decay. The view ordering scheme allows for the acquisition of highly undersampled data (3 to 4 views per TE) with good radial coverage. The use of highly undersampled radial data and a subspace constrained reconstruction enables the generation of T2w images at different TE times (e.g., 64–70 TE time points) and the corresponding T2 map in a time efficient manner. Radial sampling has the added advantage of being motion robust.8
The refocusing flip angles were designed to maximize the relative contrast between tissues of interest while reducing T2 estimation error and SAR. The proposed pulse sequence with tailored refocusing flip angles can generate T2w images with spatial resolution and contrast comparable to the Cartesian 3D TSE with the added benefit of T2 mapping with only a minimal increase in imaging time. The acquisition scheme combined with appropriate modeling of the signal evolution (which considers RF pulses that are less than 180° and RF imperfections due to slice profile effects) and a subspace reconstruction algorithm allows for accurate 3D T2 mapping.
The optimized flip angles also result in a lower SAR (up to 3× lower) compared to a constant flip angle scheme for the same ETL. While lower flip angles along the echo train can further reduce SAR, low values of cause signal dephasing in the presence of significant motion.31,48 To overcome this the lower bound for the minimum flip angle has to be chosen on a per application basis.
As demonstrated, the stack-of-stars TSE pulse sequence can generate isotropic T2w images and T2 maps of the whole brain and the whole knee with a scan time of 6.7 min and 6.2 min, respectively. While the scan times are slightly longer (~2 min) than the conventional T2w SPACE pulse sequence, they are comparable to the recently proposed compressed sensing based T2 shuffling technique.7 Yuan et al17 recently proposed a Cartesian 3D TSE approach for carotid vessel wall T2 mapping that uses data from 3 TEs to generate T2 maps for 40 slices in a 7.8-min acquisition. The stack-of-stars TSE pulse sequence can achieve comparable slice coverage in 4.9 min in addition to providing higher temporal sampling (64 to 128 TEs) of the signal evolution. This is made possible by the use of very long ETLs along with in-plane radial undersampling and through slice parallel imaging. Efficient T2 mapping, which is illustrated here for brain, cartilage, and carotid atherosclerotic plaque, should enable the quantitative evaluation of pathologies in a clinical setting.
As shown in Figure 4, the use of a 3-parameter fit improves T2 estimation accuracy but also leads to an increase in the standard deviation of the fit. If the T1 values of the species of interest are known a priori, the estimation performance can be improved by performing a region-of-interest based fitting with fixed T1 values. While the T2 values in this work were estimated assuming a single compartment model, the signal model can be extended to perform multicomponent fitting51 for applications such as myelin-water fraction imaging52 and cartilage imaging.53
As observed in Figures 6 and 7, there is under-estimation in the CSF T2 relaxation times. The reconstruction subspace basis was generated for T2 values in the range of 20–350 ms as the goal was to obtain accurate estimates of gray matter and white matter tissues. This forces the T2 estimates of CSF pixels to 350 ms. Note that the T2 maps in Figure 6 and 7 are displayed using a scale of (10 – 300) ms to illustrate contrast variations between the short T2 species. Furthermore, the temporal sampling of the signal evolution using the stack-of-stars pulse sequence was restricted to 800 ms (echo spacing of 5.8 ms and an ETL of 130). This temporal sampling may not be sufficient to accurately estimate T2 relaxation times of CSF.
The proposed stack-of-stars trajectory acquires different radial views in the same kz partition along the echo train. An alternative approach would be to sample different kz partitions along the echo train such that the center of k-space is sampled at a specific echo to allow reconstruction of images at a specific T2w contrast.9 To reconstruct images at multiple T2w contrasts, we are interested in acquiring the same number of radial views for each TE for each partition, therefore the latter sampling scheme does not offer any advantage in scan time reduction.
While the current work explores the use of in-plane radial sampling, efficiency of the pulse sequence could be further improved using alternative non-Cartesian trajectories such as spiral, GRASE or bent radial readout schemes.54–56 These trajectories would allow the acquisition of sufficient k-space samples in a single shot, reducing further the scan time. However, these schemes also require additional corrections to reduce their sensitivity to artifacts arising from off-resonance effects and readout gradient delays.
Radial sampling results in a circular FOV, which is not ideal for applications such as spine imaging. However, the use of anisotropic radial trajectories57 would circumvent this issue.
Finally, the iterative algorithms used for data reconstruction are computationally intensive due to the radial re-gridding performed in each iteration. In the current implementation, the ADMM algorithm was implemented on the CPU and the nonuniform fast Fourier transform was computed on a GPU at each iteration. While this offers about 4× acceleration compared to a CPU-only implementation, it is sub-optimal in particular due to the data transfer over-head during each ADMM iteration. An optimal implementation to bring the reconstruction times within a clinically acceptable range would involve performing the entire ADMM algorithm (together with the NUFFT operations) on the GPU to avoid unnecessary data transfer between the GPU and the CPU at each iteration. Furthermore, deep learning techniques have recently been proposed to efficiently solve subspace constrained iterative reconstruction problems resulting in 2 orders of magnitude reduction in reconstruction times.58
5 |. CONCLUSIONS
A stack-of-stars TSE pulse sequence has been introduced for simultaneous T2w imaging and T2 mapping. The sequence allows high resolution isotropic T2 mapping in clinically acceptable scan times. We have presented an optimization framework for the selection of refocusing flip angles to improve T2 estimation accuracy and reduce SAR while generating T2w contrast comparable to conventional Cartesian pulse sequences. The utility of the sequence has been demonstrated for neuro, MSK, and carotid vessel wall imaging.
Supplementary Material
Funding information
The authors would like to acknowledge support from the Arizona Biomedical Research Commission (Grant ADHS14-082996) and the Technology and Research Initiative Fund (TRIF) Improving Health Initiative.
Footnotes
SUPPORTING INFORMATION
Additional supporting information may be found online in the Supporting Information section at the end of the article.
REFERENCES
- 1.Busse RF, Brau ACS, Vu A, et al. Effects of refocusing flip angle modulation and view ordering in 3D fast spin echo. Magn Reson Med. 2008;60:640–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mugler JP, Kiefer B, Brookeman JR. Three-dimensional T2-weighted imaging of the brain using very long spin-echo trains. In: Proceedings of the 8th Annual Meeting of ISMRM, Denver, Colorado, 2000. Abstract 687. [Google Scholar]
- 3.Lummel N, Schoepf V, Burke M, Brueckmann H, Linn J. 3D fluid-attenuated inversion recovery imaging: reduced CSF artifacts and enhanced sensitivity and specificity for subarachnoid hemorrhage. AJNR Am J Neuroradiol. 2011;32:2054–2060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kijowski R, Davis KW, Woods MA, et al. Knee joint: comprehensive assessment with 3D isotropic resolution fast spin-echo MR imaging—diagnostic performance compared with that of conventional MR imaging at 3.0 T. Radiology. 2009;252:486–495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Li CQ, Chen W, Rosenberg JK, et al. Optimizing isotropic three-dimensional fast spin-echo methods for imaging the knee. J Magn Reson Imaging. 2014;39:1417–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lee S, Jee W-H, Jung J-Y, Lee S-Y, Ryu K-S, Ha K-Y. MRI of the lumbar spine: comparison of 3D isotropic turbo spin-echo SPACE sequence versus conventional 2D sequences at 3.0 T. Acta Radiol. 2015;56:174–181. [DOI] [PubMed] [Google Scholar]
- 7.Tamir JI, Uecker M, Chen W, et al. T2 shuffling: sharp, multi-contrast, volumetric fast spin-echo imaging. Magn Reson Med. 2017;77:180–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mugler JP, Bauer S, Paul D, Stemmer A, Kiefer B. Radial Single-slab 3D Turbo Spin Echo (SPACE). In: Proceedings of the 21st Annual Meeting of ISMRM, Salt Lake City, Utah, 2013. Abstract 2368. [Google Scholar]
- 9.Benkert T, Mugler JP III, Rigie DS, Sodickson DK, Chandarana H, Block KT. Hybrid T2- and T1-weighted radial acquisition for free-breathing abdominal examination. Magn Reson Med. 2018;80:1935–1948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Deoni S, Rutt BK, Peters TM. Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state. Magn Reson Med. 2003;49:515–526. [DOI] [PubMed] [Google Scholar]
- 11.Coolen BF, Poot D, Liem MI, et al. Three-dimensional quantitative T1 and T2 mapping of the carotid artery: sequence design and in vivo feasibility. Magn Reson Med. 2015;75:1008–1017. [DOI] [PubMed] [Google Scholar]
- 12.Welsch GH, Scheffler K, Mamisch TC, et al. Rapid estimation of cartilage T2 based on double echo at steady state (DESS) with 3 Tesla. Magn Reson Med. 2009;62:544–549. [DOI] [PubMed] [Google Scholar]
- 13.Ding H, Fernandez-de-Manuel L, Schär M, et al. Three-dimensional whole-heart T2 mapping at 3T. Magn Reson Med. 2014;74:803–816. [DOI] [PubMed] [Google Scholar]
- 14.Van Heeswijk RB, Piccini D, Feliciano H, Hullin R, Schwitter J, Stuber M. Self-navigated isotropic three-dimensional cardiac T2 mapping. Magn Reson Med. 2015;73:1549–1554. [DOI] [PubMed] [Google Scholar]
- 15.Mussard EPC, Hilbert T, Forman C, Meuli R, Thiran J-P, Kober T. High-resolution 3D T2 mapping of the brain using T2-prepared Cartesian spiral phyllotaxis FLASH and compressed sensing. In: Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, Hawaii, 2017. Abstract 3725. [Google Scholar]
- 16.Colotti R, Omoumi P, Bonanno G, Ledoux J-B, van Heeswijk RB. Isotropic three-dimensional T2 mapping of knee cartilage: development and validation. J Magn Reson Imaging. 2018;47:362–371. [DOI] [PubMed] [Google Scholar]
- 17.Yuan J, Usman A, Reid SA, et al. Three-dimensional black-blood T2 mapping with compressed sensing and data-driven parallel imaging in the carotid artery. Magn Reson Imaging. 2017;37:62–69. [DOI] [PubMed] [Google Scholar]
- 18.Weidlich D, Schlaeger S, Kooijman H, et al. T2 mapping with magnetization-prepared 3D TSE based on a modified BIR-4~T2 preparation. NMR Biomed. 2017;30:e3773. [DOI] [PubMed] [Google Scholar]
- 19.Mädler B, Harris T, MacKay AL. 3D-relaxometry—quantitative T1 and T2 brain mapping at 3T. In: Proceedings of the 14th Annual Meeting of ISMRM, Seattle, Washington, 2006. Abstract 958. [Google Scholar]
- 20.Juras V, Bohndorf K, Heule R, et al. A comparison of multi-echo spin-echo and triple-echo steady-state T2 mapping for in vivo evaluation of articular cartilage. Eur Radiol. 2016;26:1905–1912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pell GS, Briellmann RS, Waites AB, Abbott DF, Lewis DP, Jackson GD. Optimized clinical T2 relaxometry with a standard CPMG sequence. J Magn Reson Imaging. 2006;23:248–252. [DOI] [PubMed] [Google Scholar]
- 22.Melhem ER, Itoh R, Folkers P. Cervical spine: three-dimensional fast spin-echo MR imaging—improved recovery of longitudinal magnetization with driven equilibrium pulse. Radiology. 2001;218:283–288. [DOI] [PubMed] [Google Scholar]
- 23.Han M, Chiba K, Banerjee S, Carballido-Gamio J, Krug R. Variable flip angle three-dimensional fast spin-echo sequence combined with outer volume suppression for imaging trabecular bone structure of the proximal femur. J Magn Reson Imaging. 2015;41:1300–1310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yuan C, Schmiedl UP, Weinberger E, Krueck WR, Rand SD. Three-dimensional fast spin-echo imaging: pulse sequence and in vivo image evaluation. J Magn Reson Imaging. 1993;3:894–899. [DOI] [PubMed] [Google Scholar]
- 25.Mugler JP, Bao S, Mulkern RV, et al. Optimized single-slab three-dimensional spin-echo MR imaging of the brain. Radiology. 2000;216:891–899. [DOI] [PubMed] [Google Scholar]
- 26.Theilmann RJ, Gmitro AF, Altbach MI, Trouard TP. View-ordering in radial fast spin-echo imaging. Magn Reson Med. 2004;51:768–774. [DOI] [PubMed] [Google Scholar]
- 27.Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the golden ratio for time-resolved MRI. IEEE Trans Med Imaging. 2007;26:68–76. [DOI] [PubMed] [Google Scholar]
- 28.Mugler JP. Optimized three-dimensional fast-spin-echo MRI. J Magn Reson Imaging. 2014;39:745–767. [DOI] [PubMed] [Google Scholar]
- 29.Busse RF, Hariharan H, Vu A, Brittain JH. Fast spin echo sequences with very long echo trains: design of variable refocusing flip angle schedules and generation of clinical T2 contrast. Magn Reson Med. 2006;55:1030–1037. [DOI] [PubMed] [Google Scholar]
- 30.Madhuranthakam AJ, Busse RF, Brittain JH, Rofsky NM, Alsop DC. Sensitivity of low flip angle SSFSE of the abdomen to cardiac motion. In: Proceedings of the 15th Annual Meeting of ISMRM, Berlin, Germany, 2007. Abstract 2523. [Google Scholar]
- 31.Litwiller DV, Holmes JH, Saranathan M, et al. Sensitivity of modulated refocusing flip angle single-shot fast spin echo to impulsive cardiac-like motion. In: Proceedings of the 22nd Annual Meeting of ISMRM, Milan, Italy, 2014. Abstract 1613. [Google Scholar]
- 32.Layton KJ, Morelande M, Wright D, Farrell PM, Moran B, Johnston LA. Modelling and estimation of multicomponent T2 distributions. IEEE Trans Med Imaging. 2013;32:1423–1434. [DOI] [PubMed] [Google Scholar]
- 33.Huang C, Bilgin A, Barr T, Altbach MI. T2 relaxometry with indirect echo compensation from highly undersampled data. Magn Reson Med. 2012;70:1026–1037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang Z-P. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn Reson Med. 2014;74:489–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Malik SJ, Beqiri A, Padormo F, Hajnal JV. Direct signal control of the steady-state response of 3D-FSE sequences. Magn Reson Med. 2014;73:951–963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Huang C, Altbach MI, Fakhri G El . Pattern recognition for rapid T2 mapping with stimulated echo compensation. Magn Reson Imaging. 2014;32:969–974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chan RW, Ramsay EA, Cheung EY, Plewes DB. The influence of radial undersampling schemes on compressed sensing reconstruction in breast MRI. Magn Reson Med. 2012;67:363–377. [DOI] [PubMed] [Google Scholar]
- 38.Conn A, Gould N, Toint P. A globally convergent Lagrangian barrier algorithm for optimization with general inequality constraints and simple bounds. Math Comput Am Math Soc. 1997;66:261–288. [Google Scholar]
- 39.Dl Collins, Ap Zijdenbos, Kollokian V, et al. Design and construction of a realistic digital brain phantom. IEEE Trans Med Imaging. 1998;17:463–468. [DOI] [PubMed] [Google Scholar]
- 40.Beck MJ, Parker DL, Bolster BD, et al. Interchangeable neck shape–specific coils for a clinically realizable anterior neck phased array system. Magn Reson Med. 2017;78:2460–2468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang J, Yarnykh VL, Hatsukami T, Chu B, Balu N, Yuan C. Improved suppression of plaque-mimicking artifacts in black-blood carotid atherosclerosis imaging using a multislice motion-sensitized driven-equilibrium (MSDE) turbo spin-echo (TSE) sequence. Magn Reson Med. 2007;58:973–981. [DOI] [PubMed] [Google Scholar]
- 42.Magland JF, Rajapakse CS, Wright AC, Acciavatti R, Wehrli FW. 3D fast spin echo with out-of-slab cancellation: a technique for high-resolution structural imaging of trabecular bone at 7 tesla. Magn Reson Med. 2010;63:719–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mugler JPIII Brookeman JR. Efficient spatially-selective single-slab 3D turbo-spin-echo imaging. In: Proceedings of the 12th Annual Meeting of ISMRM, Kyoto, Japan, 2004. Abstract 695. [Google Scholar]
- 44.Ramani S, Fessler JA. Parallel MR image reconstruction using augmented Lagrangian methods. IEEE Trans Med Imaging. 2011;30:694–706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pauly J, Le Roux P, Nishimura D, Macovski A. Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm (NMR imaging). IEEE Trans Med Imaging. 1991;10:53–65. [DOI] [PubMed] [Google Scholar]
- 46.Hansen MS, Sørensen TS. Gadgetron: an open source framework for medical image reconstruction. Magn Reson Med. 2013;69:1768–1776. [DOI] [PubMed] [Google Scholar]
- 47.Subhas N, Kao A, Freire M, Polster JM, Obuchowski NA, Winalski CS. MRI of the knee ligaments and menisci: comparison of isotropic-resolution 3D and conventional 2D fast spin-echo sequences at 3 T. AJR Am J Roentgenol. 2011;197:442–450. [DOI] [PubMed] [Google Scholar]
- 48.Busse RF . Flow sensitivity of CPMG sequences with variable flip refocusing and implications for CSF signal uniformity in 3D-FSE imaging. Proceedings of International Society for Magnetic Resonance in Medicine. In: Proceedings of the 14th Annual Meeting of ISMRM, Seattle, Washington, 2006. Abstract 2930. [Google Scholar]
- 49.Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI. T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. Magn Reson Med. 2012;67:1355–1366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mamisch TC, Trattnig S, Quirbach S, Marlovits S, White LM, Welsch GH. Quantitative T2 mapping of knee cartilage: differentiation of healthy control cartilage and cartilage repair tissue in the knee with unloading—initial results. Radiology. 2010;254:818–826. [DOI] [PubMed] [Google Scholar]
- 51.Prasloski T, Mädler B, Xiang Q-S, MacKay A, Jones C. Applications of stimulated echo correction to multicomponent T2 analysis. Magn Reson Med. 2011;67:1803–1814. [DOI] [PubMed] [Google Scholar]
- 52.Mackay A, Whittall K, Adler J, Li D, Paty D, Graeb D. In vivo visualization of myelin water in brain by magnetic resonance. Magn Reson Med. 1994;31:673–677. [DOI] [PubMed] [Google Scholar]
- 53.Reiter DA, Lin P-C, Fishbein KW, Spencer RG. Multicomponent T2 relaxation analysis in cartilage. Magn Reson Med. 2009;61:803–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Li Z, Hu Hh, Miller Jh, et al. A spiral spin-echo MR imaging technique for improved flow artifact suppression in T1-weighted postcontrast brain imaging: a comparison with cartesian turbo spin-echo. AJNR Am J Neuroradiol. 2016;37:642–647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bilgin A, Gmitro AF, Block WF, Altbach MI. A half Fourier radial fast spin-echo method using a bent radial trajectory. In: Proceedings of the 13th Annual Meeting of ISMRM, Miami Beach, Florid, 2005. Abstract 2404. [Google Scholar]
- 56.Gmitro AF, Kono M, Theilmann RJ, Altbach MI, Li Z, Trouard TP. Radial GRASE: 1mplementation and applications. Magn Reson Med. 2005;53:1363–1371. [DOI] [PubMed] [Google Scholar]
- 57.Wu Z, Han F, Hu P, Nayak KS. Anisotropic field-of-view support for golden angle radial imaging. Magn Reson Med. 2016;76:229–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Fu Z, Mandava S, Keerthivasan MB, Martin DR, Altbach MI, Bilgin A. A multi-scale deep ResNet for MR parameter mapping. In: Proceedings of the 26th Annual Meeting of ISMRM, Paris, France, 2018. Abstract 568. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


