Effects of rare-earth magnetism on the superconducting upper critical field in infinite-layer nickelates

Abstract

The search for superconductivity in infinite-layer nickelates was motivated by analogy to the cuprates, and this perspective has framed much of the initial consideration of this material. However, a growing number of studies have highlighted the involvement of rare-earth orbitals; in that context, the consequences of varying the rare-earth element in the superconducting nickelates have been much debated. Here, we show notable differences in the magnitude and anisotropy of the superconducting upper critical field across the La-, Pr-, and Nd-nickelates. These distinctions originate from the 4f electron characteristics of the rare-earth ions in the lattice: They are absent for La³⁺, nonmagnetic for the Pr³⁺ singlet ground state, and magnetic for the Nd³⁺ Kramer’s doublet. The unique polar and azimuthal angle-dependent magnetoresistance found in the Nd-nickelates can be understood to arise from the magnetic contribution of the Nd³⁺ 4f moments. Such robust and tunable superconductivity suggests potential in future high-field applications.

Rare-earth moments control the magnitude and anisotropy of superconducting upper critical fields in layered nickelates.

INTRODUCTION

Following the initial discovery of superconductivity in Nd_0.8Sr_0.2NiO₂ (1), the subsequent development of rare-earth (R) variants with Pr and La in place of Nd (2–5) has created an emerging family of superconducting infinite-layer nickelates (Fig. 1A) (6–8). Unlike the cuprates, with which the nickelates are often compared, R-site variations are expected to have appreciable impact beyond ionic size effects. Specifically, rare-earth effects in cuprates are usually overshadowed by the much larger energy scale of superconductivity (9, 10). One exception is in PrBa₂Cu₃O_7−δ, where coincidental hybridization between the Pr 4f and oxygen 2p states is believed to compete with the emergence of superconductivity (11). In contrast, in the nickelate superconductors, there is consistent transport, spectroscopic, and theoretical evidence for hybridization between a broad range of R 5d orbitals and the Ni 3d orbitals (2–8, 12–24). An open question currently under debate is the potential role of the R 4f electrons (25–28). Here, we report that the R-site directly controls the magnitude and anisotropy of the superconducting upper critical field H_c2.

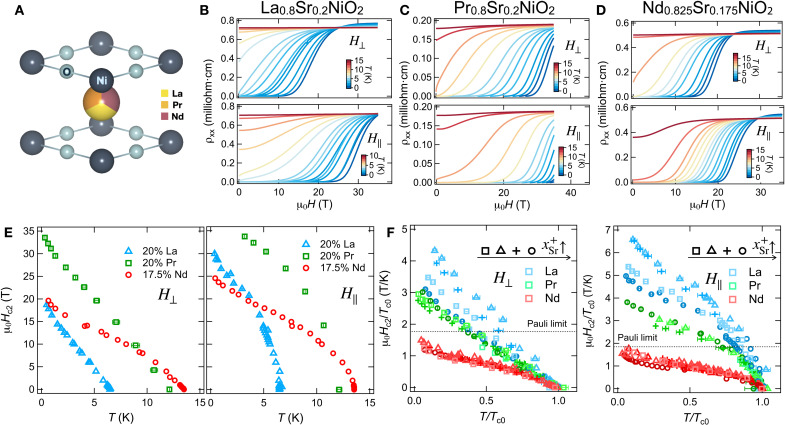
Fig. 1. Structure, magnetotransport, and H_c2 properties of (R,Sr)NiO₂.

(A) Schematic unit cell structure of (R,Sr)NiO₂ (R = La, Pr, or Nd; Sr substitution not indicated). (B to D) Magnetoresistance of representative samples near optimal doping: La_0.8Sr_0.2NiO₂, Pr_0.8Sr_0.2NiO₂, and Nd_0.825Sr_0.175NiO₂ (20) respectively, at temperatures ranging from 0.34 to 18 K for out-of-plane (H_⊥) and in-plane (H_||) field orientations. (E) Temperature dependence of H_c2 determined from data shown in (B) to (D). (F) Normalized H_c2/T_c0 against reduced temperature T/T_c0 of R_1−xSr_xNiO₂ for H_⊥ and H_|| orientations, respectively. Here, x = 0.15, 0.175, 0.2, and 0.225 (20, 29) for Nd, x = 0.16, 0.18, 0.20, and 0.24 for Pr, and x = 0.15, 0.16, 0.18, and 0.20 for La. The dashed lines indicate the Pauli limit of H_c2 = 1.86 T_c0.

RESULTS

Figure 1 shows a central result motivating this study—that the magnetic field suppression of superconductivity differs widely among R-variants, which does not scale with T_c0, the superconducting transition temperature in zero external magnetic field. Magnetoresistance measurements up to 35 T of representative (R,Sr)NiO₂ (R = La, Pr, Nd) samples at optimal doping are shown in Fig. 1 (B to D), for both out-of-plane (H_⊥) and in-plane (H_||) field orientations. The corresponding resistively determined upper critical fields (H_c2⊥ and H_c2||; defined as 50% of the normal-state resistivity) are shown (Fig. 1E), where the drastically different scales for H_c2 are evident.

For a superconductor in the dirty limit, which describes the nickelates (19, 29), the effective Ginzburg-Landau coherence length ξ is the geometric mean of the Pippard coherence length ξ₀ and the mean free path (30). Then, as $H_{\mathrm{c}2\perp }=\frac{{\mathrm{\varphi }}_0}{2\mathrm{\pi }{\mathrm{\xi }}^2}(1-\frac{T}{T_{\mathrm{c}0}})$, H_c2⊥ ∝ 1/ξ₀ ∝ Δ₀ ∝ T_c0. Here, ϕ₀ is the magnetic flux quantum and Δ₀ the superconducting gap. As for H_c2||, the observed (1 − T/T_c0)^1/2 temperature dependence indicates dominant paramagnetic depairing near T_c0 (19, 29). H_c2|| is also proportional to T_c0 at temperatures near T_c0, described by $-\ln \left(\frac{T}{T_{\mathrm{c}0}}\right)=7\mathrm{\eta }(3){\left(\frac{{\mathrm{\mu }}_0{H}_{\mathrm{c}2\Vert }}{2\mathrm{\pi }{k}_{\mathrm{B}}{T}_{\mathrm{c}0}}\right)}^2$(31), where k_B is the Boltzmann constant, μ₀ is the vacuum magnetic permeability, and η(x) is the Riemann zeta function. Therefore, we normalize both H_c2 and T by T_c0 (Fig. 1F) for all samples. We observe a systematic variation in H_c2/T_c0, which is largest for La-nickelates, somewhat smaller for Pr, and substantially reduced for Nd. Furthermore, this variation between R-sites is persistent across the respective superconducting domes via Sr doping (Fig. 1F; see figs. S1 and S2 for complete datasets).

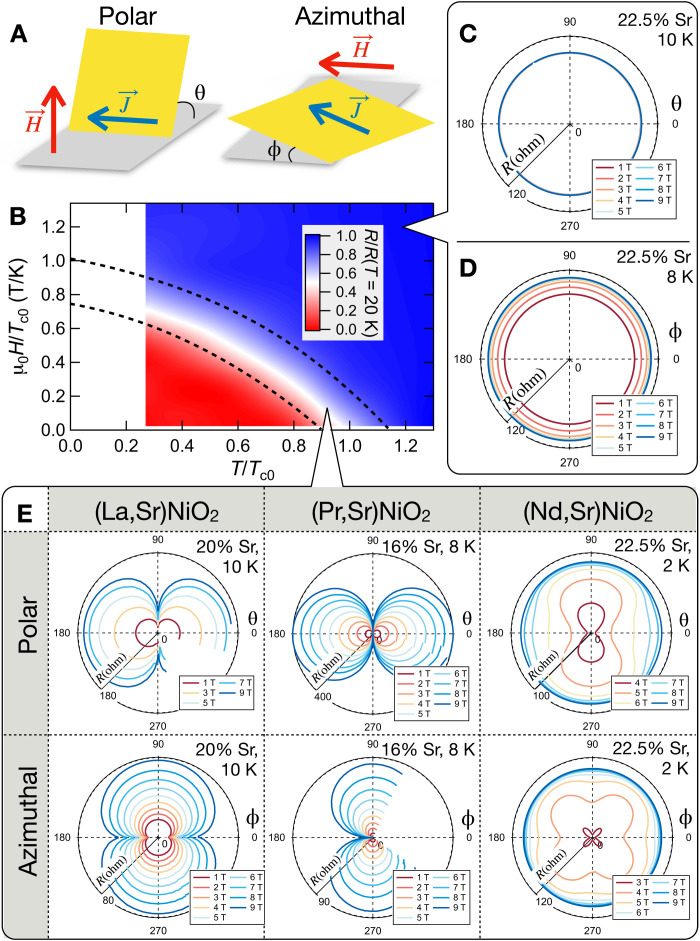
To probe the origin of this large variation in H_c2, we measure in detail the magnetoresistance as a function of the polar (θ) and azimuthal (ϕ) angle of the applied magnetic field direction, as illustrated in Fig. 2A. In the normal state, negligible angular dependence is observed for all samples (Fig. 2, C and D). Therefore, we focus on the superconducting transition region with finite sample resistance below the normal-state value. We first present the characteristic features through representative measurements (Fig. 2E; see figs. S3 to S5 for complete datasets). The La- and Pr-nickelates both show conventional angular dependence; their “∞”-shaped θ-dependence shows that superconductivity is more robust to in-plane magnetic fields than perpendicular fields, as commonly seen in layered superconductors (32). Their “figure-of-eight”–shaped ϕ-dependence, arising from vortex motion, also follows previous studies of other type II superconductors (32, 33). In sharp contrast, the Nd-nickelates show qualitatively distinct magnetoresistance. The orientation of the θ-dependence is opposite to that of La-/Pr-nickelates and other layered superconductors, i.e., superconductivity is more suppressed by an in-plane magnetic field, indicating a complete reversal of the superconducting anisotropy. Furthermore, a pronounced clover-leaf ϕ-dependence is observed for Nd. As shown in fig. S6, we can rule out a vortex-related origin of these features.

Fig. 2. Representative characteristics of the angular magnetoresistance in (R,Sr)NiO₂.

(A) Schematic of the measurement geometry with respect to the sample (yellow square). The blue and red arrows represent the directions of the measurement current and the external magnetic field, respectively. (B) Magnetic field versus temperature phase diagram of a representative Nd_0.775Sr_0.225NiO₂ sample (T_c0 = 7.4 K). (C and D) Representative polar (θ) and azimuthal (ϕ) angle dependence of the magnetoresistance in the normal state for Nd_0.775Sr_0.225NiO₂. (E) Representative polar and azimuthal angle dependence of magnetoresistance in the superconducting transition region for La-, Pr-, and Nd-nickelates, with the specific doping and temperature indicated at the top right corner of each panel.

How can we understand this clear difference between the Nd-nickelates versus the La-/Pr-nickelates? In all cases, the in-plane lattice parameters are clamped to that of the SrTiO₃ substrate, while for a specific Sr doping, the c-axis variations reflect the average R-site ionic radii (1–3): La³⁺ is the largest, ~4.5% larger than the closely similar Pr³⁺ and Nd³⁺ (within 1.5% of each other) (34). In addition, the range of the c-axis lattice constant variation of the three R-variants across the superconducting dome substantially overlap. Thus, cation size effects do not seem to account for the unique H_c2 features in Nd. Rather, the clover-leaf ϕ-dependent magnetoresistance in Nd is more suggestive of a potential role of local magnetic moments, leading to a consideration of the 4f electrons and their crystal electric field (CEF) structure.

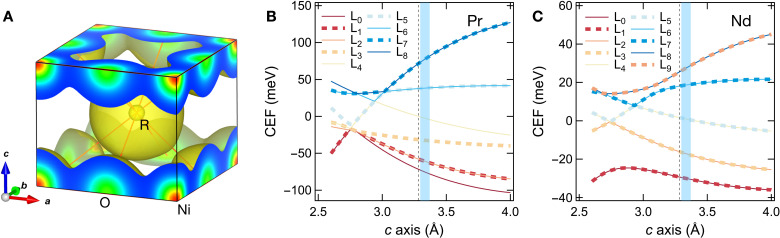
To examine this, we use theoretical approaches including ab initio density functional theory (DFT) calculations (35, 36), Bader charge analysis (37), and symmetry arguments to determine the 4f levels split by the tetragonal CEF (see the Supplementary Materials for details). In Fig. 3A, we show the electron density isosurface of the Ni 3d, 4s, O 2p, and R 5d, 6s orbital electrons within a unit cell where the contours correspond to 2.5% of the maximum electron density. Despite the hybridization, especially between the O 2p and Ni 3d orbitals, most of the electron density remains within the vicinity of the parent ion. This motivates the use of a point charge approximation in determining the CEF-split 4f energy levels, as shown for Pr³⁺ and Nd³⁺ as a function of c-axis lattice constant (Fig. 3, B and C), where the range of experimental values is highlighted by the vertical blue bands and the bulk values are marked by dashed lines (38). While La³⁺ has no 4f electrons, we find a singlet crystal field ground state for Pr³⁺ that to first order is also nonmagnetic. By contrast, Nd³⁺ has a doublet ground state as expected for a Kramer’s ion, making this the lone magnetic R-site ion among the three. Furthermore, by adding an external field term to the CEF perturbation Hamiltonian, we find that the Nd 4f moment shows an easy-plane magnetic anisotropy (fig. S7). All of these conclusions are robust to a very large variation of the c-axis lattice parameter, far exceeding the experimentally observed range (Fig. 3).

Fig. 3. Calculation of 4f CEF levels.

(A) DFT-calculated electron density distribution of NdNiO₂, with the valence including Nd 5d, 6s, Ni 3d, 4s, and O 2p electrons. The yellow isosurface gives the contour corresponding to 2.5% of the maximum electron density. DFT calculations using a Pr pseudopotential result in a visually indistinguishable charge distribution. (B and C) Calculated CEF splitting as a function of c-axis lattice constant for Pr- and Nd-nickelates, respectively. The blue shaded region marks the range of experimental c-lattice constant values, and the vertical dashed line marks the undoped bulk value (38). The crystal field levels L_x are expanded in table S1.

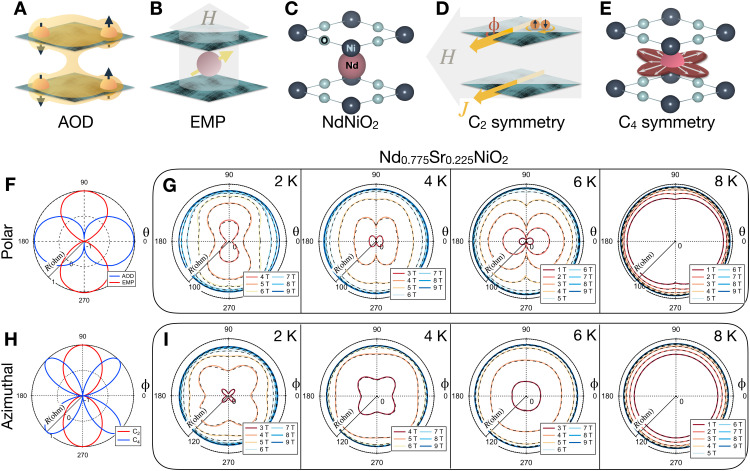
Following these CEF considerations, we can construct a simple model that quantitatively describes all of the angular magnetoresistance data, based on the assumption that the Nd 4f moment contributes purely to the background magnetization and magnetic permeability of the lattice. For the θ-dependent magnetoresistance, all the nickelates have in common anisotropic orbital depairing (AOD; Fig. 4A) as a natural consequence of the shorter c-axis coherence length (30), and hence an H_c2|| larger than H_c2⊥. This can be seen to dominate at all temperatures for La-/Pr-nickelates (fig. S3). For Nd-nickelates, there is an additional competing term due to the enhanced magnetic permeability (EMP; Fig. 4B) arising from the 4f moments, which has crucially the opposite anisotropy given the easy-plane magnetic anisotropy.

Fig. 4. Competing effects in the angular magnetoresistance.

(A to E) Schematic illustrations of (A) AOD, (B) EMP, and the origin of the (D) C₂ and (E) C₄ symmetric azimuthal response. (C) Corresponding unit cell. (F and H) Fitting functions corresponding to the AOD and EMP effects for θ-dependence and C₂ and C₄ symmetric ϕ-dependence, respectively. (G and I) Temperature and magnetic field dependence of the θ- and ϕ-dependence of magnetoresistance of Nd_0.775Sr_0.225NiO₂. Fits based on Eqs. 1 and 2 are shown in black dashed lines.

The temperature-dependent balance of this competition (Fig. 4F) underlies the remarkable reversal of the θ-dependent magnetoresistance anisotropy we observe for highly doped Nd-nickelates (Fig. 4G)—i.e., the temperature-dependent crossing of H_c2⊥ and H_c2||. Our minimal model is unexpectedly quantitative; the measured magnetoresistance of all samples (La, Pr, and Nd), doping levels, temperatures, and magnetic fields can be described by one generic form for the resistance R_AOD(θ) arising from AOD and another generic form for the resistance R_EMP(θ) from EMP for Nd, such that the total θ-dependent resistance R^PL(θ) can be expressed as

$$R^{PL}(\mathrm{\theta })=C+{\mathrm{\alpha }}_{\mathrm{AOD}}{R}_{\mathrm{AOD}}(\mathrm{\theta })+{\mathrm{\alpha }}_{\mathrm{EMP}}{R}_{\mathrm{EMP}}(\mathrm{\theta })$$ (1)

Here, C is a constant, and α_AOD and α_EMP are the temperature- and magnetic field–dependent coefficients of the two functional forms (fig. S8). The dashed lines in Fig. 4G and fig. S4 show the accuracy of this two-component description. In particular, as the polar anisotropy reverses with temperature, the competing AOD and EMP terms produce complex θ-dependences with up to 6 local resistance maxima (fig. S4), which can be well described by Eq. 1.

As for the ϕ-dependent magnetoresistance, we see a competition between a twofold symmetric (C₂) ϕ-dependence and a fourfold symmetric (C₄) ϕ-dependence (Fig. 4D, E, and H). The C₂ response has been seen previously (32, 33) and is a generic result of the ϕ-dependence of the Lorentz force exerted by the measurement current on vortices, because only the perpendicular component contributes. Thus, this ϕ-dependence is seen in all R-variants of the nickelates. However, uniquely in the Nd-nickelates, we observe an additional sin(4ϕ) component (clover-leaf pattern, Fig. 4I), such that the total ϕ-dependent resistance R^AZ(ϕ) can be then expressed as

$$R^{AZ}(\mathrm{\varphi })=C+{\mathrm{\alpha }}_{\mathrm{c}2}\sin [2(\mathrm{\varphi }-{\mathrm{\varphi }}_{\mathrm{c}2})]+{\mathrm{\alpha }}_{\mathrm{c}4}\sin [4(\mathrm{\varphi }-{\mathrm{\varphi }}_{\mathrm{c}4})]$$ (2)

Here, C, ϕ_c2, and ϕ_c4 are constants, and α_c2 and α_c4 are the temperature- and magnetic field–dependent coefficients (figs. S5 and S8). We attribute the C₄ symmetric dependence again to the 4f moments, because the occupied CEF levels are necessarily invariant to C₄ symmetry operations. This implies an in-plane magnetic easy axis along the [110] and equivalent directions. This interpretation is bolstered by the experimental observation that ϕ_c2 follows the applied current direction, while ϕ_c4 is locked to the lattice (fig. S9).

The extracted coefficients α_AOD, α_EMP, α_c2, and α_c4 exhibit peaks in magnetic field for a given constant temperature (fig. S8), which is a natural result of the boundary conditions: In either the fully superconducting or normal state, no angle-dependent magnetoresistance is seen. With decreasing temperature, both the peaks in α_EMP and α_AOD shift to higher magnetic fields, tracing the superconducting phase boundary in the temperature-field plane (Fig. 2B). However, the magnitude of α_AOD drops substantially with decreasing temperature, contrasting with the increase in α_EMP.

DISCUSSION

The pair-breaking framework of superconductivity is useful to discuss these observations. To leading order, the external magnetic field suppresses superconductivity through either orbital or paramagnetic depairing (30). While orbital depairing has an intrinsic θ-dependence rooted in the superconducting anisotropy, paramagnetic depairing is largely isotropic as it suppresses superconductivity by the Zeeman energy cost. Therefore, although both effects are enhanced by the local magnetic field arising from the Nd 4f moments, an underlying θ-dependence of the local magnetic field intensity is more readily visible when paramagnetic depairing is dominant. With this in mind, we can associate α_AODR_AOD(θ) with orbital depairing, and α_EMPR_EMP(θ) with paramagnetic depairing, which dominates at low temperatures.

In contrast, neither depairing effect has intrinsic ϕ-dependence, and both would faithfully exhibit the structure of the local magnetic field. Therefore, the clover-leaf pattern is a direct manifestation of the ϕ-dependence of the local magnetic field intensity, particularly because α_c4 is consistently an order of magnitude larger than α_c2 where it is observed (figs. S8 and S10; see the Supplementary Materials for more details on an additional C₂ symmetric response). With decreasing temperature, the onset and marked increase of α_c4 signal the growing contribution of the 4f moments, which in turn enhances α_EMP. Note that while the magnetic response of the 4f moments likely exists over a broader range of temperature and magnetic field, it only appears in the magnetoresistance in the vicinity of H_c2 through pair-breaking effects and, in this process, becomes intertwined with the superconducting response. Therefore, the exact temperature or field dependence of the 4f magnetic moment magnetization cannot be simply extracted from these data. However, the impact of Nd on H_c2 is suggestive of low-temperature Nd 4f antiferromagnetic exchange, as is typically observed for complex materials hosting magnetic R-sites (fig. S11) (39).

With these developments, we lastly return to the differences in H_c2 across R-variants shown in Fig. 1. With important 4f moment enhancements of the field, Nd has the lowest H_c2/T_c0; in their absence, H_c2/T_c0 is highest for La. Pr is intermediate, consistent with the contribution of a Pr³⁺ 4f moment induced by magnetic field. Thus, we see that the underlying intrinsic behavior of H_c2 appears to be similar across the infinite-layer nickelates, once the additional suppression due to the R-site magnetism has been taken into account. This leads to the conclusion that the conventional weak-coupling Pauli limit H_c2 = 1.86 T_c0 (40) is broadly exceeded, at least with respect to T_c0. Although the (Nd,Sr)NiO₂ samples obey this limit (Fig. 1F) (29), we now understand this to occur because of Nd 4f moment contributions. We observe that the Pauli limit is surpassed by up to a factor of 3.5 in the La series (Fig. 1F). Note that we use a 50% resistance criterion for H_c2, to minimize contributions from superconducting fluctuations and vortex creep (29); adopting higher resistance thresholds would make this discrepancy even larger.

While the magnitude of H_c2 presents an important question for future research, we discuss potentially relevant scenarios. We observe that the angular magnetoresistance in the Nd-nickelates can be fully captured by considering only the 4f moment contribution to the background magnetization and magnetic permeability. However, it is important to note that this does not preclude other contributions from the hybridization between the R 5d and the Ni 3d orbitals—in the presence of finite spin-orbit coupling, multiorbital mixing could enhance H_c2. Perhaps the most straightforward explanation is that the experimentally observed T_c0 via transport occurs in the presence of substantial phase fluctuations/disorder and does not reflect the pairing scale Δ₀. Tunneling spectroscopy indicates a large Δ₀-to-T_c0 ratio, although surface effects and variations remain to be clarified (41). Further evidence for this scenario may be found in a recent study of La_0.8Sr_0.2NiO₂ with higher T_c0 but comparable extrapolations of H_c2 to what we observe (42). The fact that experimentally, nickelate superconductivity is in the dirty limit appears to us to disfavor more exotic mean-field enhancements. Independent of origin, the unusually large H_c2/T_c0 ratios in the nickelates, combined with sensitive control through the R-site, give properties that would be useful for high-field applications. Provided that substantial further advances can be made in materials synthesis, nickelates could be used for superconducting wires and components, particularly in chemically reducing environments (43).

MATERIALS AND METHODS

Materials

Thin-film nickelate samples (7 nm thick) were grown on SrTiO₃ substrates using pulsed-laser deposition under growth and reduction conditions previously reported (1, 2, 3, 44).

Methods

For angular magnetoresistance measurements, the samples were contacted using wire-bonded aluminum wires in a 6-point Hall bar geometry. The 50% resistive criterion is applied to both temperature-sweep and field-sweep data to determine T_c0 and H_c2. For high-field measurements, transport measurements were performed using the standard four-probe lock-in technique, with an alternating current excitation between 1 and 10 μA. Continuous magnetic fields up to 35 T were generated using a Bitter magnet, coupled with a He-3 cryostat, at the High Field Magnet Laboratory at Nijmegen, the Netherlands. The magnetic field angle was varied in situ using a customized rotator stage.

Note

During the preparation and review of this manuscript, we became aware of two reports on H_c2 in La-nickelates (42, 45) and three reports on Nd-nickelates (46–48). All the reported behavior is qualitatively consistent with our results, independent of variations in the magnitude of the resistivity (see also fig. S12), and they further demonstrate that the presence or absence of a capping layer has minimal impact on the observed angular magnetoresistance. We also note that our crystal field assignment for the doped Nd system is very consistent with recent bulk neutron diffraction measurements (49).

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S12

Table S1