Autonomous, untethered gait-like synchronization of lobed loops made from liquid crystal elastomer fibers via spontaneous snap-through

Abstract

The transition from one equilibrium state to another via rapid snap-through can store elastic energy and release it as kinetic energy for rapid motion as seen in Venus flytrap and hummingbird to catch insects mid-flight. They are explored in soft robotics for repeated and autonomous motions. In this study, we synthesize curved liquid crystal elastomer (LCE) fibers as the building blocks that can undergo buckling instability upon heated on a hot surface, leading to autonomous snap-through and rolling behaviors. When they are connected into lobed loops, where each fiber is geometrically constrained by the neighboring ones, they demonstrate autonomous, self-regulated, and repeated synchronization with a frequency of ~1.8 Hz. By adding a rigid bead on the fiber, we can fine-tune the actuation direction and speed (up to ~2.4 mm/s). Last, we demonstrate various gait-like locomotion patterns using the loops as the robot’s legs.

Connecting pre-bent liquid crystal elastomer fibers into a loop generates a self-regulated synchronized motion with snap through.

INTRODUCTION

In nature, froghoppers, water striders, flea, and locusts use elastic muscles to store elastic energy with latch-like structure of the legs and release the stored energy quickly to generate rapid and forceful locomotion (1–5) such as jumping or launching into flight. Venus flytraps (6) and bladderworts (7), on the other hand, achieve rapid and agile movement between two equilibrium states by sudden inversion of their internal structures without muscles, referred as a snap-through transition. Both the latch-mediated spring mechanism and the snap-through instabilities store elastic strain energy to their compliant bodies, then releasing it by overcoming the elastic potential barrier under external stimuli. Because snap-through mechanism can be achieved in a compliant body without external interlocks or use of muscles, it offers soft robots a simple and attractive way to achieve fast, agile, and autonomous locomotion (8–14) using elastomeric materials, including silicone (14, 15), hydrogels (16, 17), soft composites (18, 19), shape memory polymers (20, 21), liquid crystal elastomers (LCEs) (9, 22–25), and dielectric elastomers (26, 27). However, most of the snap-through behaviors are one-time deployment due to the potential energy barrier between the two equilibrium states (28). For repeated snap-through, multiple controllers and power sources are needed, thus limiting the degrees of freedom (29, 30). It becomes even more challenging when the materials become softer and when the device is miniaturized. In addition, realization of snap-through is highly dependent on the contact surface; thus, few have demonstrated directional motions. It will be highly desired for a soft robot to realize autonomous, fast, and repeated; autonomous and self-regulated; untethered; and gaited motions (31, 32).

Introducing structural instabilities on one-dimensional (1D) elements such as filaments or fibers is more favorable than the 2D or 3D geometries due to higher degrees of freedom in deformation. One of the effective ways to attain the snap-through feature of a filament is to rotate a curved one while constraining its ends; the twist-driven buckling of the filament then leads to its rapid flipping to release the stored elastic energy (33). Among various responsive materials, LCEs with intrinsic anisotropy and programmable director fields are a promising class of soft actuators: They are compliant (Young’s modulus, ~1 to 10 MPa) and exhibit large and reversible axial strains (up to 500%) along the mesogenic alignment direction upon heated from an ordered state to a disordered state. It has been shown that curved LCE fibers, rings, and ribbons can autonomously roll on the heated surfaces (9, 25, 34, 35). The temperature gradient of the internal fiber body can generate strain mismatch vertically along the fiber thickness, forcing it to bend out of plane (35) or snap-through (9, 25), leading to continuous rolling. These motions, although autonomous and untethered, lack directionality: The flipping of the fibers depends on the local contact of the fiber with the substrate, where the fiber needs to gain sufficient energy to snap though. Recently, Zhao et al. (25) demonstrated a wavy LCE ring capable of flipping by temperature-stimulated snap-through. Because the wavy ring is molded from monolithic LCE, the flipping motion is irregular similar to a simple elastic ring where a part of it rotates driven by twisting induced stress. As a result, the motion is slow (~0.16 Hz) compared with that of the photoresponsive LCE actuators (up to ~2.5 Hz) (22).

Horses are known for their gaited motions, including the walk, trot, canter, and gallop (36). The horse moves its two diagonal legs in the opposite side in perfect, two-beat or four-beat synchrony with suspension/concussion in between each stride. Gait planning has been demonstrated in multi-legged robots such as quadruped for lifting off and placing the feet with special sequences to direct the locomotion and adapt to unpredicted environment (37). Nevertheless, these gaits are stiff and require a myriad central control systems. It has been shown that when rigid hinges are inserted into an elastic ring, regular deformations emerge in the rotational motion as the ring is under conformational constraints (38, 39). Here, we investigate the possibilities to achieve gaited motions using a set of prebent LCE fibers connected into lobed loops, where the deformation of each fiber is confined by the neighboring ones in the loop. While the unconstrained individual fiber with a cylindrical cross section undergoes heat-induced buckling and rolling, the lobed loop achieves self-regulated, highly agile (up to ~1.8 Hz), sustainable, gait-like synchronization in an untethered fashion on the hot plate by snapping-through. By introducing a rigid bead on one of fibers in the loop as a rigid anchor, which increases the friction between the fiber and the substrate, the synchrony of flipping is broken, leading to a directional propulsion such that the loop jumps forward at a speed of up to ~2.4 mm/s. On the basis of this strategy, we program the lobed LCE loops that can travel on sloped, sandy surfaces and bumpy terrains; transport cargos; and potentially act as energy harvesters.

RESULTS AND DISCUSSION

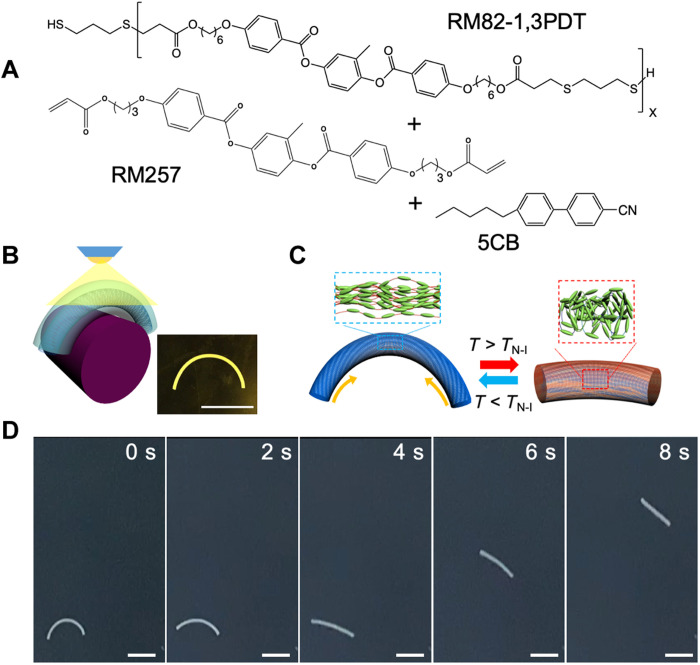
The LCE precursor is prepared by mixing a nonreactive mesogen [4-cyano-4-pentylbiphenyl (5CB)] with reactive mesogens consisting of an thiol-terminated LC oligomer (LCO), 1,4-bis-[4-(6-acryloyloxy-hexyloxy)benzoyloxy]-2-methylbenzene (RM82)–1,3 propanedithiol (RM82-1,3PDT), and reactive mesogenic monomer {1,4-bis-[4-(6-acryloyloxypropyloxy)benzoyloxy]-2-methylbenzene (RM257)} (1.3:1 molar ratio) (Fig. 1A). The LCO is prepared from RM257 and 1,3-propanedithiol (1,3PDT), referred to as RM257-1,3PDT via oxygen-mediated step-growth polymerization (40). We used a flexible polytetrafluoroethylene (PTFE) tube (diameter, 800 μm) to facilitate the deformation of the fiber, as illustrated in fig. S1. The LCE mixture was filled into the PTFE tube and bent around a cylinder, followed by ultraviolet (UV) curing via thiol-acrylate click chemistry (Fig. 1B). After the photocuring was completed, the fiber was removed from the tube, exhibiting a prebent shape that remained unchanged even after the removal of 5CB (see fig. S2). Here, 5CB does not participate in polymerization but (i) lowering the viscosity of the precursor to facilitate infiltration of the precursors inside the tube and (ii) increasing surface anchoring strength to assist the alignment of the precursor along the tube because the diameter of the tube is large (41). The cured LCE fiber has a bent shape with diameter of ~680 μm (Fig. 1B and fig. S3). It has a nematic to isotropic transition temperature (T_N-I), ~143°C as measured by differential scanning calorimetry (DSC) (fig. S4). Above T_N-I, the fiber rapidly shrinks in length and becomes straightened starting from 90°C due to the broad transition of T_N-I (Fig. 1C). Small and wide-angle x-ray scattering and polarized optical microscopy images (fig. S5) confirm that mesogens are aligned in parallel along the long axis of fiber. The intermolecular spacing is ~4.6 Å, consistent with the typical π-π stacking distance between mesogens as shown in LC polymers obtained from RM257 (42).

Fig. 1. Fabrication of a prebent LCE fiber and its locomotion on a hot plate.

(A) Chemical structures of LCE precursors, including RM82-1,3PDT (the LCO) and RM257 (the reactive mesogenic monomer), and 5CB (the nonreactive mesogen). (B) Illustration of the UV curing and a photograph of a prebent LCE fiber. Scale bar, 1 cm. (C) Schematic illustrations of the reversible axial actuation of the prebent fiber during the heating and cooling cycle. Insets: Mesogenic ordering in the nematic and isotropic phases, respectively. (D) Snapshots of a prebent fiber rolling on a hot plate at 200°C. Scale bars, 1 cm.

When placed onto a hot plate at 200°C, the prebent LCE fiber rolls automatously: First, it gradually shrinks and straightens along the arc of the fiber, as the originally bent director field undergoes phase transition into an isotropic state [Fig. 1D, fig. S6A, (0 to 4 s), and movie S1]. The fiber begins to roll when it is nearly straightened. The resistance of rolling per length of a cylindrical rod (M_f) is known to be linearly proportional to the curvature (κ) and internal bending moment (M_Ι) (35)

$$M_{\mathrm{f}}=\frac{2}{3}\mathrm{\kappa }{M}_{\mathrm{I}}$$ (1)

When the torque generated in the LCE fiber overcomes the resistance, which gradually decreases due to the reduction of the lateral bending curvature, the fiber starts to roll spontaneously in a direction perpendicular to the long axis of the fiber (Fig. 1D and fig. S5A; 4 to 8 s). The rolling of LCE fiber can be attributed to the nonuniform thermal stress generated within the fiber. Above T_N-I, the bottom part of the LCE fiber in contact with the hot plate begin to contract. However, because of the relatively large fiber diameter, ~680 μm, there is a temperature gradient along the diameter of fiber with the top part of the fiber in the ambient environment as schematically illustrated in fig. S6B. This thermal gradient has been reported in literature (25). As a result, the strain mismatch emerges where the axial contraction of the bottom is larger than that of the top part, and the fiber bends out of plane (fig. S6C). As soon as the fiber bends, it leaves the hot plate. The cooler top of the fiber attempts to return to the original state, leading to instability that the fiber falls in the direction of convex curvature. When the fiber hits the hot plate, it shrinks and buckles again. The cycle of bending and falling of the fiber is rapid and iterative, leading to continuous rolling forward or background depending on the initial stress stored in the prebent fiber (fig. S6, B to D). We note that the cylindrical geometry of the fiber is essential in our experiments to realize the rapid rotation with minimal resistance. In contrast, a LCE fiber with a square cross section cannot roll because the angled edge generates large friction between the fiber and the substrate (see movie S2). The rolling is highly autonomous and sustainable due to self-regulation of the heat flux, where the top and bottom areas are cooled and heated, respectively. This is different from the autonomous dancing rings with square cross sections and much larger curvatures reported by Zhao et al. (25), which are fabricated by molding, followed by radial stretching and UV curing, where stretching aligns the mesogens in the fibers and thus directs the instability of the fibers. As the temperature increases, the rate of rolling increases because larger heat flux induces higher internal bending moment (35). However, when the entire LCE fiber turns into isotropic (~6 s at ~200°C), the fiber eventually stops rolling.

Because the LCE fiber is relatively thick (~680 μm), the formation of cross-linking gradient along the thickness might be considered (41). To clarify this, we created LCE fibers that were UV irradiated in the opposite of the bent direction as shown in fig. S7 and found that their forms followed the bent shape of the PTFE tube, regardless of the direction of UV irradiation. Furthermore, we did not observe any void in the cross section of the LCE fiber, as shown in fig. S7 (B and E), which may be due to the soft nature of LCEs. Therefore, we assumed that the modulus of the prebent LCE fiber remained constant throughout its thickness. Last, we observed no difference in terms of the thermal responsiveness of the prebent fibers, as shown in fig. S7 (C and F). To sum up, the prebent shape of the LCE fiber is determined by the templating of the PTFE tube, and our proposed mechanism is not affected by the potential inhomogeneity of the cross-linking density across the fiber thickness.

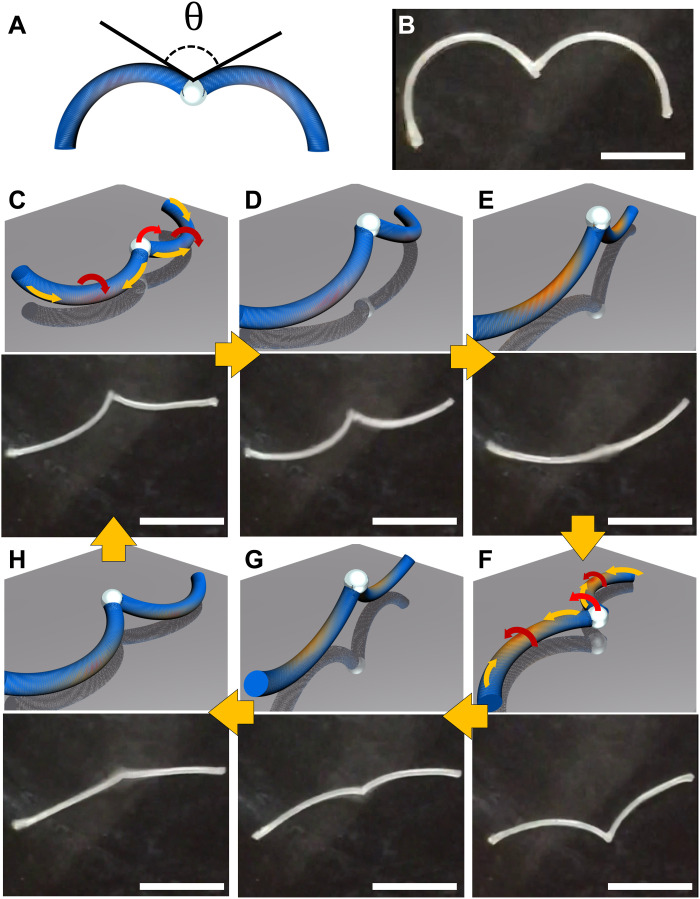
We note that the single LCE fiber is not constrained. Because the rolling motion relies on axial contraction induced by thermal phase transition, it is only temporary (<10 s), and it stops once the fiber leaves the hot surface. The fiber also has a limited ability to craw or roll over rough or sloped terrains. To test the potential of gaited motions via collected buckling behaviors of LCE fibers, we connect the prebent LCE fibers into a loop. First, we connect two prebent LCE fibers, referred as 2-lobed fiber, by gluing the edges together using a UV curable adhesive (NOA63) in a dot, which has a Young’s modulus of ~1.65 GPa (Fig. 2, A and B) (43). The 2-lobed fiber flips back and forth laterally, much like a waddling gait (movie S3 and see illustration in Fig. 2, C to F). Similar to the single fiber, the 2-lobed fiber flips over 180° due to the rolling moment generated by the internal temperature gradient. Unlike the single fiber that rolls over in the same direction several times, the pointy junction constrains the 2-lobed fiber from further rolling in the same direction (Fig. 2F). Instead, the 2-lobed fiber waddles back and forth with each of the lobed fibers repeatedly touch down and reverse back on the hot plate; as they hold “hands” together at the junction, they waddle in the same direction. As illustrated in Fig. 2, C to H, the upper part of the fiber that initially faces the ambient air touches down and then faces the hot plate and contracts, while the lower part increases in length when it returns to the nematic phase by ambient cooling. Movie S3 shows that most of the fiber bodies touch the hot plate during the waddling, which is important to enable highly effective heat transfer from LCE fiber to ambient, thus improving the self-sustained locomotion at such a high temperature.

Fig. 2. Waddling gaits of a 2-lobed LCE fiber.

(A and B) Illustration and the corresponding photos of the 2-lobed fiber. (C to H) Illustrations and the corresponding snapshots of 2-lobed fiber during waddling gait, showing flipping back and forth laterally on a hot plate of 170°C. Scale bars, 1 cm.

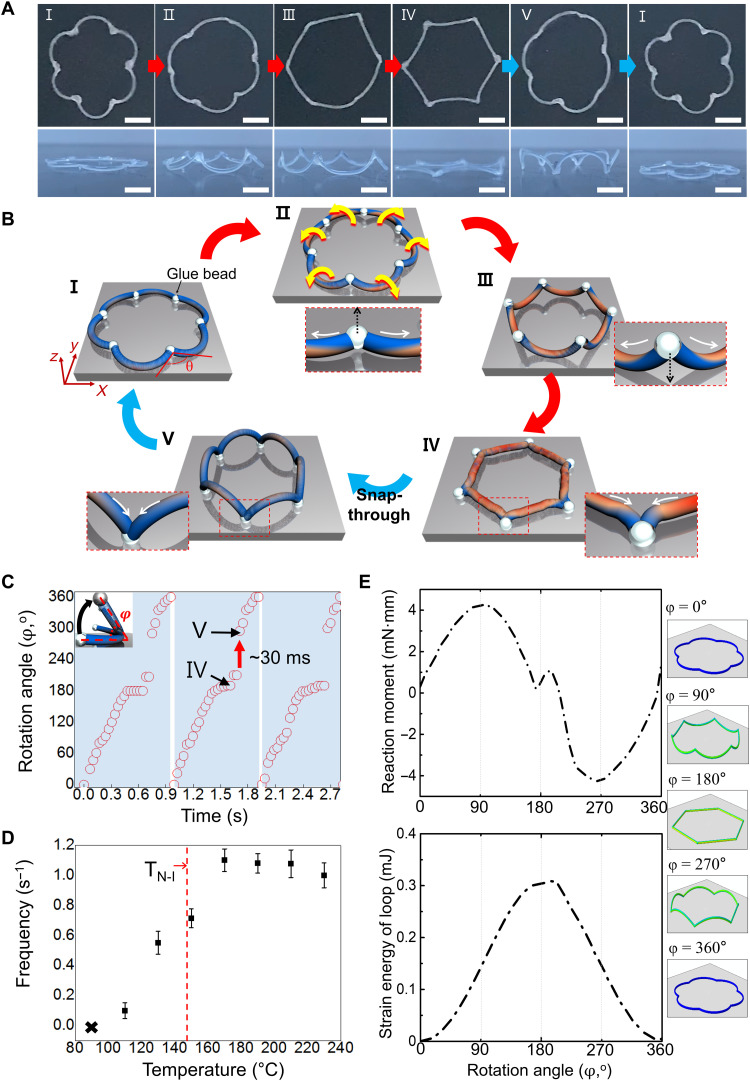
Next, we create a closed, symmetric loop of several prebent LCE fibers. Figure 3A shows snapshots for one cycle of synchronized flipping of a six-fiber loop (fig. S8) on the hot plate at 170°C, demonstrating autonomously regulated out-of-plane rotation at a frequency of ~1.1 Hz (movie S4). High-frequency and macroscopic deformation have been achieved from a light-responsive LCE thin film (20 μm thick, up to ~2.5 Hz) consisting of azobenzene derivatives (22) or electrospun LCE microfiber bundles via photothermal effect (diameter, 35 to 68 μm, 1.3 to 16.7 Hz) (44) but yet to be attained from a heat-activated thick film or a large diameter filament because heat is very lossy. We note the rapid rotation demonstrated here is an order of magnitude faster than that from the molded, wavy LCE ring (~0.16 Hz) (25). We illustrate each state, I to V, observed in Fig. 3 (A and B), showing the direction of the acting force and moment in each fiber, denoted by yellow arrows, and the temperature contour, where the blue and red regions correspond to most of the mesogens in nematic and isotropic phase, respectively. At the initial state I, rolling moments at the fiber and the pulling force on both sides of the junction (denoted by the white arrows, state II) are generated due to the shortening of the LCE fiber. The symmetric geometry together with six rigid junctions lead to simultaneous rise and rolling of the fibers by 180° from inward to outward of the loop (states III to IV), followed by snap-through, that is the loop actuator rolls more than 180° (state V), in contrast to the 2-lobed fiber actuation, where the connected fibers roll back to the initial state. Clearly, the difference is caused by the constrained edges. Both ends of the 2-lobed fiber are free, so the junction can rotate without imposing stress. On the other hand, the junction in the 6-lobed loop pulls the neighboring fibers to maintain the closed loop geometry when trying to rotate outward (state IV in Fig. 3B). Therefore, when the loop rolls 180°, an axial tensile stress is generated around the junction that drags the fibers to move inward of the loop. As shown in the state IV in Fig. 3 (A and B), each straightened fiber also supports the axial tensile stress generation, while such a notable curvature change is not observed in the 2-lobed fiber during waddling. Then, the 180° flipped fibers in the loop are now subjected to bending upward due to the reversal of the temperature gradient inside the loop body, resulting in creation of the force directing the junction downward (state V in Fig. 3, A and B). Therefore, the net force applied to the junction directing inward and downward makes the prebent fiber roll 360° instead of rolling backwards.

Fig. 3. Gait-like synchronization of a 6-lobed LCE loop.

(A) Sequential images of the synchronized motion of the 6-lobed loop during a single cycle in top and side views, respectively. (B) Corresponding schematic illustrations of (A), where color gradient shows heated and ambient regions. (C) Displacement of the center of the prebent fiber, indicated by the rotation angle, ϕ, as a function of time during the locomotion at 170°C. (D) Average frequency of the synchronized locomotion as a function of temperature. (E) Finite element method simulation results of the rolling moment of a prebent fiber and the strain energy profile of the LCE loop with varying rotation angles. Scale bars, 1 cm.

A snap-through jumping occurs when the loop turns over 180°. Figure 3C shows the rotation angle of the fiber, ϕ, as a function of time. A large angle displacement of ~100° within 30 ms is observed at 0.7, 1.6, and 2.5 s, corresponding to the states from IV to V of the first, second and third cycles. As a result of the snap-through, the entire body of LCE loop pushes up and leaves the hot plate with only the junctions remain in contact with the surface as shown in state V in Fig. 3 (A and B), promoting the heat transfer from the LCE loop to ambient, and thus its rapid return to the initial state I. Although the magnitude of the displacement moment decreases as the rotation approaches 180°, the sign remains the same. This preference for rotation in the initial direction allows for continuous storage of strain energy within the loop. However, when the sign of the moment changes from positive to negative, the fiber prefers to rotate in the opposite direction. At this point, the stored strain energy is released, leading to snapping.

Unexpectedly, our loop can autonomously actuate more than an hour at 170°C on the hot plate in the ambient air (~25°C) (see movie S5); such a high sustainable motion has not been experimentally demonstrated in thermally stimulated LCE actuators. Note that 170°C is well above T_N-I (143°C), meaning that the lobed loop is efficiently heat-fueled and released in a self-regulation manner, thereby generating the continuous gait motion.

The temperature influences the speed of the gait synchronization because since the heat influx drives the internal bending moment (34). As shown in Fig. 3D, for a sample heated above 170°C, a frequency up to ~1.1 Hz is reached. When the temperature is decreased to 110°C, below the T_N-I, the frequency decreases to ~0.1 Hz (see movie S6). The motion stops entirely at T < 110°C, owing to the insufficient thermal flux. It is noticed that the synchronized motion of the LCE loop is stable in a much broader temperature range (110° to 230°C) than that of the single LCE fiber, which we hypothesize as a result of efficient heat and stress transfer among each other under the constraints. Moreover, we used an infrared (IR) camera to monitor the temperature changes of the LCE loop and the hot plate during the flipping, as shown in fig. S9. The result revealed that the qualitative temperature of the LCE loop remained almost constant at approximately 114.6°C throughout the duration of the flipping actuation.

To better understand the actuation mechanism, we conduct finite element method (FEM) to simulate the snap-through behaviors of the LCE loop. Figure 3E shows the rolling moment and the strain energy profile of the 6-lobed LCE loop according to ϕ. A series of snapshots of the simulated LCE loop is provided at every 90° rotation (see movie S7). To reduce the computation cost, FEM is conducted by applying angular displacement to the middle point of the six prebent fibers instead of thermal conduction method. Details are provided in the Supplementary Materials. The reaction moment gradually increases as ϕ reaches 90° due to the friction between the fiber and the hot plate and then decreases until 180° because the junctions fall by gravity force, and the stored strain energy in the fiber reaches the maximum (~0.3 mJ). When the snap-through jumping occurs, the reaction moment is converted to a negative value, and the stored strain energy in the loop is released. Here, the frictional force generated by the contact between the junction and the hot plate acts as an energy barrier to add a stored strain energy in the loop, which is applied fairly over the loop. The snap-through jumping could enable loop actuator to smoothly travel on sand or grooved terrains, on which the frictional force reduces, while symmetry breaking of the frictional force over the loop enables the loop moving toward the direction where the frictional force is the highest. This will be discussed in more details in the next section.

To achieve the autonomous gait synchronization of the LCE lobed loops, the thermal gradient between the hot plate and the ambient environment is the most critical factor. To confirm this, we convolve the lobed LCE loop with a copper wire that provide thermal energy to the loop by joule heating. In this case, heat is uniformly transferred to the LCE loop, and the loop only shrinks and expands in circumferential direction without rotation (movie S8). In addition to the thermal gradient, the angle θ between the two adjacent fibers (denoted in Fig. 3B) in the LCE loop is another critical factor to trigger the gait motion. As described earlier, the junctions are directed outward by the pulling force and the torque driven by the gradient of phase transitions along the diameter of LCE fiber. Both forces are directed outward from the LCE loop, synergistically generating the rotational locomotion. For the proof of concept, we prepare two types of 2-lobed LCE loops with varying θ, 250° and 109°, which is above and below 180°, respectively (fig. S10). For θ = 250°, the length of the loop actuator only shrinks circumferentially without performing any motion, while the loop with θ = 109° shows autonomous rotation (fig. S10 and movie S9). When θ > 180°, the net force acting on the junction pulls the junction inward the loop, which is opposite to the direction of the rolling moment that pulls the junction outward the loop. Therefore, the two conflicting forces prevent the loop from rotating. For example, when the initial fibers were straight, the loop forms a hexagonal structure similar to a benzene ring, as shown in fig. S11. Since θ in the hexagonal ring is ~240°, which violates the geometrical rule, the hexagon loop placed on a hot plate (170°C) did not rotate or flip but simply shrank. When θ < 180°, the pulling force and the rolling moment act synergistically in the direction of rotating the loop. Following the geometric design rules, the lobed LCE loop actuator can have a variety of structures by the on-demand assembly of the prebent fibers. For example, the loop can have two- to sevenfold symmetries (fig. S12 and movie S10) or different global shapes such as elliptical, rhombus, and triangular ones (fig. S13 and movie S11). They all show circular contour at flipping by 180°, although the initial contour of the lobed loop is not circular. The presence of the circular contour during flipping is possibly because the loops prefer to distribute the twist-driven stress equally throughout the curved fibers.

Furthermore, we examine the flipping behaviors of the sixfold lobed LCE loops with varying aspect ratios (ARs) (AR = length/diameter) by changing the fiber length but fixing the diameter at ~680 μm (fig. S14). The flipping rate decreases with an increase of the aspect ratio as long as θ < 180° due to increased weight and steric hindrance between LCE fibers in the loop. It is noteworthy that the lobed loop of the largest aspect ratio (AR4 = 3.77) has the fibers overlapped with each other, and exhibits delayed but nevertheless flipping behaviors. This can be attributed to the fact that the structure of loop AR4 falls in the geometrical rule that is θ should be smaller than 180°. We also investigate the flipping efficiency of the sixfold lobed LCE loops as a function of the radius of curvature of the LCE fibers with fixed AR = 18.5 (fig. S15). Because the radius of curvature varies with AR, the 6-lobed loop with the largest curvature (k1 = 0.33 mm⁻¹) shows an overlapped loop form similar to that seen in fig. S14 with AR4 and k = 0.20 mm⁻¹. Accordingly, increase of radius of curvature impedes the flipping efficiency. Furthermore, the flipping rate decreases when the curvature becomes small enough such that θ > 180° (see k4 = 0.10 mm⁻¹ in fig. S15).

Our method is versatile and highly scalable, where the diameter and length of the fibers can be conveniently adjusted. For example, we show a 6-lobed loop fabricated from prebent fibers of ~240 μm in diameter and 4 mm in length; the volume of the single fiber is ~38 times smaller than that of the larger prebent fiber of ~680 μm in diameter and 19 mm in length (figs. S3 and S16). Because the smaller 6-lobed loop is much smaller and lighter, each fiber in the loop applies less frictional force to the surface and thus shows a rapid flipping motion with a frequency of ~1.8 Hz at 170°C, which is about two times faster than the larger one (movie S12).

Because the prebent fiber has a larger radius of rotation at the central axis than that of a straight fiber during rolling, the loop can travel even on a bumpy surface such as aligned metal bars, as seen in fig. S17A and the first part of movie S13. Here, the diameter of the metal bar (14.6 mm) is ~18 times larger than that of LCE fiber (0.8 mm), thus the aligned metal bars form a rough terrain with deep and wide valleys. We then investigate if the loop can move on a sandy surface where the surface topography of sand continues to change as the loop moves around. On a rough sand surface with grain size of 50 to 200 μm at ~170°C, the LCE loop can move up and down with gait synchronization even with sand grains stick to the loop and it leaves its footprint on the surface (see fig. S17B and second part of movie S13). These demonstrations prove the adaptability and versatility of our LCE loops working on various kinds of environments due to little contact with the substrate. Similar behaviors have been reported from a single pre-twisted LCE ribbon at much larger sizes (9 cm in length, 3 mm in width, and 1 mm in depth) (9).

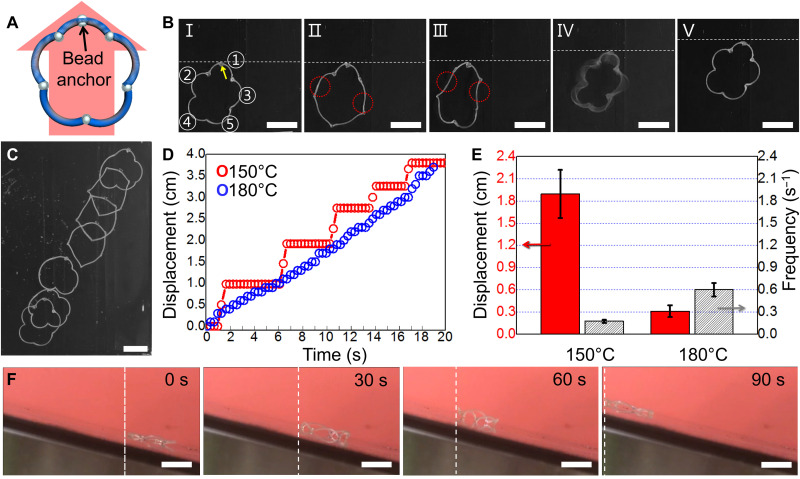
We now investigate how to propel the LCE loop in a certain direction. To do so, we add a NOA63 glue bead at the center of one of the fibers of a 5-lobed loop (Fig. 4A), which acts as an anchor to generate larger resistance to fiber rolling than those without the bead. When placed onto the 150°C hot plate, the loop moves forward in the direction where the glue bead faces (see first half of movie S14 and the yellow arrow indicates the bead attached on fiber ① in Fig. 4B). Upon heating, initially fibers ④ and ⑤ rotates 180,° while fiber ① is anchored (Fig. 4B, snapshot II). This unbalanced constrain then leads to twist of fibers ② and ③, which pushes fiber ① forward. The twisted fibers are denoted by red dotted circles in Fig. 4B. Further rotation of fibers ④ and ⑤ twists more fibers ② and ③, pushing fiber ① harder (snapshot III). Once the pushing force combined with rolling moment applied to fiber ① overcomes the anchoring constrain, twisted fibers ② and ③ are released in an instant, and the anchored fiber ① is also quickly rotated by 360° (snapshot IV in Fig. 4B). As a result, the loop leaps forward (snapshot V in Fig. 4B). Note that the gait motion changes from synchronized rotations to sequential rotations of the fibers so that the LCE loop propagates. The overlaid snapshots present the jumping path of the LCE loop led by the bead (Fig. 4C). As a result of the instant leap forward, the travel distance versus travel time presents a stepped profile (see Fig. 4D and the first half of movie S14), showing a displacement of ~1 cm per step at a rate of 2.4 mm/s at 150°C. At 180°C, the loop leaps at a rate of 1.9 mm/s with smoother steps (Fig. 4, D and E, and the latter half of movie S14). The snap-through jumping is obvious at 150°C but less so at 180°C. The temperature-dependent snap-through feature can be explained by variation of the torsion elastic modulus with temperature. In terms of torsion energy that obeys the angular form of Hooke’s law, 𝜀ϕ²/2, where 𝜀 is torsion elastic modulus and ϕ is the angle of twist from its equilibrium position, the elastic modulus of a polymer decreases as the temperature increases (33); thereby, the torsion energy that can be stored in the loop should be lower at 180°C than that at 150°C. Meanwhile, the higher temperature field induces a larger thermal influx, leading to a faster motion. Consequentially, the gait speed and gait stride of the lobed LCE loop with a glue bead can be qualitatively controlled by the temperature (Fig. 4E). Moreover, an efficiency of the directional movement between 5- and 6-lobed LCE loops was investigated, consequently where the 5-lobed loop moves faster than 6-lobed loop (fig. S18). The movement of a 6-lobed LCE loop is more hindered when moving toward the fiber with bead anchor due to the existence of its corresponding pair of fibers in diametrically opposite directions, as compared to a 5-lobed loop. In addition, the 6-lobed loop weighs 20% more than the 5-lobed loop, which may also affect the speed of its directional movement.

Fig. 4. Directional jumping from a symmetry breaking 5-lobed LCE loop.

(A) Schematic illustrations of a 5-lobed LCE loop with an urethan acrylate glue bead crosslinked at the center of the one of the fibers in the loop and the big red arrow indicates the jumping direction. (B) Sequential images of the fibers during the one-step forward movement. (C) Overlaid sequential images showing the trajectory of the translational movement. (D) Moving distance of the loop as a function of time at 150° and 180°C, respectively. (E) Average displacement (red column) of a single jumping step moving forward and the average frequency (gray column) of the flipping motion at 150° and 180°C, respectively. (F) Sequential images of the 5-lobed LCE loop climbing up a 18° inclined hot plate. White dashed lines are used to guide the eyes. Scale bars, 2 cm.

Taking advantage of the instant leaping in a certain direction at 150°C, the LCE loop can climb up a sloped heating surface, where the speed decreases as the surface becomes inclined. At a slope angle of 18°, the moving speed decreases to 0.1 cm/s, which is half that on the flat surface (Fig. 4F and movie S15).

Last, we construct a “soft propulsion leg” that can be integrated into a soft robot to use the heat-powered gait motion for tasks such as transportation, oscillation, and bending. As seen in Fig. 5A, we prepare a ring made from aluminum (Al) foil as a linker between the LCE loop and the robot body. Al foil is chosen because it is lightweight and a good heat conductor. The ring is designed such that it will not impede the motion of the LCE fiber loop. To realize translational and rotational motion, two LCE loops, with and without the glue bead anchor, are connected to a cargo body, which is constructed by wood sticks (Fig. 5, B to D). Propelled by the two “gait legs,” the soft cargo robot can travel as directed depending on where the additional glue is placed. For examples, it can turn clockwise (Fig. 5B), anti-clockwise (Fig. 5C), or go straight (Fig. 5D and see the first part of movie S16). When two LCE fibers in the 5-lobed LCE loop are integrated to a bird-shaped Al sheet, which we refer as a “nodding-bot,” it oscillates up and down, which is attributed by the presence of friction between the Al linker and LCE fiber during the flipping of the “leg” (Fig. 5E and the second part of movie S16). Last, reversible bending of a robot body made from the Al sheet is demonstrated using the 6-lobed loop, which we refer as a “bending-bot.” The bending-bot uses the variation in distance between two facing-fibers in a 6-lobed LCE loop leg, where an Al foil canopy is placed on top to bridge the two fibers (Fig. 5F). During the gait synchronization, the reversible bending and recovery of the Al canopy is achieved when the LCE loop reaches the states IV and I defined in Fig. 3C, respectively (Fig. 5F and last part of movie S16). Such a bending-bot could be potentially used as a mechanoelectrical energy harvester, for example, by embedding piezoelectric materials in the canopy capable of repeated bending and releases.

Fig. 5. Demonstration of soft robotic tasks using the 6-lobed LCE loops as propulsion legs.

(A) Schematic illustration of the 6-lobed LCE loop with a linker, referred as the leg, where the linker is used to connect to the robot body. (B to D) A soft cargo-carrying robot with two propulsion legs, showing directional movement depending on where the glue bead is placed on the fiber. (E) A bird-shaped Al sheet with one leg showing the nodding motion reversibly as the leg flips. (F) Bending and straightening of an Al sheet connected to the two linkers in the loop facing each other.

In summary, we have fabricated lobed loops by connecting prebent LCE fibers with a rigid adhesive bead, demonstrating self-regulated, gait synchronization upon heating above the nematic-to-isotropic phase transition. It exploits structural instability and physical constraints in cylindrical LCE fibers for gait-like motions with a frequency (~1.1 or ~1.8 Hz for large or small one, respectively). So far, LCE actuators that show a high-frequency actuation with macroscopic deformation are photostimulated from LCEs with azobenzene derivatives or electrospun LCE microfiber bundles (22, 44). Yet, none has shown synchronized gait-like motions. Here, our actuators are fast and sustainable, which can repeat the gait motions over a couple of hours in an autonomous manner on a hot surface using heat as fuel but with little contact. Moreover, the lobed LCE loop can travel in a specific direction simply by introducing a rigid anchor on the fiber that breaks the symmetry of the synchronized locomotion. The resulting LCE loop can climb a sloped hot plate or travel on the bumpy terrains. Last, we construct the lobed LCE loop as a propulsion leg to perform series robotic tasks, including untethered and autonomous cargo transport, self-sustainable reversible motion producers such as nodding- and bending-bot. We believe that the lobed loop design and the resulting gait synchronization via snap-through instability open a route to effectively design autonomous and agile soft robots capable of using the extreme environment or wasted heat.

MATERIALS AND METHODS

Materials

1,3PDT (>99%), (3-aminopropyl)triethoxysilane (99%), butylhydroxytoluene (BHT; analytical standard), 1,8-diazabicyclo[5.4.0]undec-7-ene (98%), dichloromethane (DCM; anhydrous, ≥ 99.8%), N,N-dimethyl-n-octadecyl-3-aminopropyltrimethoxtsilyl chloride (42 wt% in methanol), 2,2-dimethoxy-2-phenylacetophenone (DMPA; 99%), poly(vinyl alcohol) (cold water soluble, molecular weight of 31,000 to 50,000, 98 to 99% hydrolyzed) were purchased from Sigma-Aldrich. Hydrochloric acid (HCl; certified ACS Plus, 36.5 to 38.0%), magnesium sulfate (anhydrous powder) (MgSO₄), and tetrahydrofuran (high-performance liquid chromatography grade) were purchased from Thermo Fisher Scientific. RM82 and RM257 were purchased from Wilshire Technologies. 5CB were purchased from Tokyo Chemical Industry. NOA63 was purchased from Noland Optical Adhesive. SilcPigTM was purchased from Smooth-On. Photoinitiator, Irgacure 369, was purchased from Ciba. All chemicals were used as received. PTFE tubing for templating LCE fiber was purchased from Cole-Parmer.

Preparation of the prebent LCE fibers

LCO, RM82-1,3PDT, was first synthesized according to the literature (40). Briefly, LCE precursor was prepared by mixing a 1:1 molar ratio LCO and RM257 and 40 wt % 5CB with respect to the amount of mixture of LCO and RM 257. Then, 2 wt % DMPA as a photoinitiator and 0.2 wt % BHT as an inhibitor with respect to whole amount of LCE mixture were dissolved in DCM and mixed with LCE precursor. DCM was completely evaporated under magnetic stirring at 40°C for a few hours. The prebent LCE fibers were prepared by injecting the mixtures into the PTFE tubing using a syringe pump (Pump 11 Pico Elite, Harvard Apparatus) with a rate of 4 ml/hour, followed by bending the tube and photopolymerization under 365-nm UV light exposure (Newport Hg 97435 Oriel Flood Exposure Source), although a photomask at the same total dosage of 8.0 J/cm². Last, the fibers were extruded, of which lengths are ~4 or ~19 mm for ~240 or 680 μm in diameter, respectively, followed by washing with ethanol to remove nonreacted 5CB and residual monomers and oligomers. The average gel fraction of the LCE fiber was ~84% by calculating the weight ratio before and after washing with ethanol.

Preparation of the lobed LCE loop

The prebent fibers were connected in lobed loop form using UV curable optical adhesive (NOA63, Norland Products, Inc.). All loops were UV cured at 365 nm (10 mJ/cm² for 5 min). The lobed LCE loops present an average adjacent angle (θ) of ~219.5°, 167.7°, 140.3°, 123.2°, 118.8°, and 114.4° for 2-, 3-, 4-, 5-, 6-, and 7-lobed loops, respectively (fig. S10).

Characterization of LCE and the locomotion of LCE fibers and loops

The thermal transition temperatures of LCEs were measured by DSC on a TA Instruments Q2000 using an aluminum hermetic crucible. Samples were heated and cooled at a ramping rate of 10°C /min for two cycles, and data from the second cycle were reported here. Alignments of LC mesogens within the fibers were characterized by an Olympus BX61 motorized optical microscope with crossed polarizers using cellSens software. All digital images and videos were taken by iPhone 13 Pro. X-ray scattering experiments were performed on the Dual Source and Environmental X-ray Scattering (DEXS) facility at the University of Pennsylvania. A Xeuss 2.0 with a GeniX3D S4 source (Cu Kα, λ = 1.54 Å) and a PILATUS3 1 M detector (981 × 1043 pixels, pixel dimension of 172 μm) was used with the sample-to-detector distance of 16 cm. The LCE fiber is placed in the same direction relative to the beam direction in a transmission configuration. IR images of LCE loops flipping were taken by spot finder IR camera (Xi 400, Optris).

Finite element simulation of the rolling 6-lobed LCE loop

FEM simulation is conducted through Abaqus/computer-aided engineering(CAE) with explicit solver (Dassault systems). C3D8 meshes are applied to the LCE loop model, and discrete rigid body is applied to the hot plate. The Young’s modulus and Poisson’s ratio of LCE are set to 4 MPa and 0.4, respectively. To accurately simulate the experimental results, the input boundary conditions (BCs) such as heat convection and radiation on the hot plate are required. However, these thermal parameters are difficult to measure experimentally. In addition, reflecting the phase change of the LCE materials results in the convergence issue especially at the transition of different phases due to the huge difference of the physical properties. Therefore, to reduce the complexity of the simulation, we used the angular displacement as the input BCs instead of the thermal properties and phase transformation. Even if we substitute the angular displacement as inputs, the snapping behavior of fiber loop can be analyzed via energy/moment profile. In experiments, the rotating motion (and the angular displacement) can be generated by temperature gradient induced partial phase transition of the LC fiber.

Gravity is applied to the whole simulation model. Hard contact option is chosen for normal contact, and penalty contact is chosen for tangential contact with friction constant of 0.2. The reaction moment of the rotating fiber and the strain energy of the LCE loop are extracted to reveal the snap-through feature of the LCE loop.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S18

Legends for movies S1 to S16

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S16