Abstract
The detailed reaction mechanism and kinetics of the C3H3 + CH2OO system have been thoroughly investigated. The CBS-QB3 method in conjunction with the ME/vRRKM theory has been applied to figure out the potential energy surface and rate constants for the C3H3 + CH2OO system. The C3H3 + CH2OO reaction leading to the CH2-[cyc-CCHCHOO] + H product dominates compared to the others. Rate constants of the reaction are dependent on temperatures (300–2000 K) and pressures (1–76,000 Torr), for which the rate constant of the channel C3H3 + CH2OO → CH2-[cyc-CCHCHOO] + H decreases at low pressures (1–76 Torr), but it increases with rising temperature if the pressure P ≥ 760 Torr. Rate constants of the three reaction channels C3H3 + CH2OO → CHCCH2CHO + OH, C3H3 + CH2OO → OCHCHCHCHO + H, and C3H3 + CH2OO → CHCHCHO + CH2O fluctuate with temperatures. The branching ratio of the C3H3 + CH2OO → CH2-[cyc-CCHCHOO] + H channel is the highest, accounting for 51–98.7% in the temperature range of 300–2000 K and 760 Torr pressure, while those of the channels forming the products PR10 (OCHCHCHCHO + H) and PR11 (CHCHCHO + CH2O) are the lowest, less than 0.1%, indicating that the contribution of these two reaction paths to the title reaction is insignificant. The proposed temperature- and pressure-dependent rate constants, together with the thermodynamic data of the species involved, can be confidently used for modeling CH2OO-related systems under atmospheric and combustion conditions.
1. Introduction
A Criegee intermediate (also called a Criegee zwitterion or Criegee biradical) known as a carbonyl oxide with two charge centers was produced by alkene ozonolysis. This process goes through an ozonide intermediate before generating the Criegee intermediate and a carbonyl species.1 Horie and Moortgat2 also indicated that, after forming from the reaction of ozone with an alkene, the very energy-rich ozonide intermediate transforms into two fragments (a stable carbonyl compound and a vibrationally excited Criegee intermediate), in which the second one can either undergo unimolecular decomposition or can form a stabilized Criegee intermediate via collisional relaxation. According to the study of Khan et al.,3 a stabilized Criegee intermediate can also be generated in the troposphere via radical–radical reactions such as CH3O2 + BrO, CH3O2 + OH, and CH3O2 + Cl; however, these reactions can be ignored due to their negligible contribution to the total stabilized Criegee intermediate. Due to the high reactivity of the stabilized Criegee intermediate, it can chemically interact with various species such as SOx and NOx in the earth’s atmosphere and is connected with the formation of aerosols, which play a critical role in the global climate regulation.4,5 In addition, the Criegee intermediate is a substance that also has the ability in improving air quality by producing a strong oxidizing agent, OH, in the troposphere. By using a global atmospheric chemistry and transport model, Khan et al.3 have indicated that the decomposition of the stabilized Criegee intermediate in the terrestrial rainforest and boreal forest areas can lead to a significant source of OH (up to 13%), especially during nighttime and winter months. Therefore, it can be said that the amount of OH radicals generated from Criegee intermediate consumptions in these regions has an obvious impact on the oxidizing capacity in the troposphere.
Experimentally, several early studies have been done, but the uncertainties of their experimental results were often very large, which was explained to be the short lifetime of the Criegee intermediate and lack of direct precursors. On the other hand, the measured experimental results are also far different from those calculated by theory. Until 2012, those limitations were first addressed by a ground-breaking research of Welz and co-workers.4 Since then, there have been numerous studies on the structures and reactivity of Criegee compounds with different species,6−22 for which mechanisms and kinetics of several reaction systems CH2OO + CH3CHO20 and CH2OO + (CH3)2O21 have been carefully examined. The common feature of these reactions was the addition of CH2OO to the C=O double bond of the carbonyl compounds in the first stage to form ozonides, which were isomerized or dissociated to give organic acids and other carbonyl compounds in the second stage. At high pressure, the channel CH2OO + CH3CHO → ozonide is favorable,20 whereas the reactions forming CH3COOH prevail at low pressure.21
Theoretically, it can be said that, among the reactions of the Criegee intermediate, there are reactions that cannot be carried out under experimental conditions due to various reasons. However, those difficulties have been and are being solved with the effective help of the modern quantum chemical methods. Therefore, so far, a vast amount of data exists in the literature on the mechanisms and rate constants of the reactions related to the Criegee species.23−35 Among these theoretical studies, the addition reaction of Criegee to the C=C pi bond is worth noting, which has been indicated in the studies of Vereecken et al.,23 Crehuet et al.,35 and Eskola et al.36
As mentioned above, the experimental studies have focused on the reaction of Criegee with a carbonyl compound, which were featured by the addition reaction of Criegee to the C=O bond, while the theoretical investigations have examined the addition reaction of Criegee to the C=C bond. We all know that both the pi bonds, C=C and C=O, belong to the family of unsaturated hydrocarbon substances, which have a critical role in the atmospheric environment because they have high reactivity and occupy a large percentage in the troposphere. Among the unsaturated hydrocarbons, propargyl radical (C3H3) emerged as a highly reactive precursor, which has been proved by many previous studies.37−44 Therefore, a detailed study of the mechanism and kinetics of the reaction between Criegee and C3H3 is much essential. It will help us better understand the reactivity of Criegee with the unsaturated hydrocarbons containing double bonds such as the C3H3 organic compound.
To our knowledge, up to this point there is no research on the reaction between Criegee and the propargyl radical. That is the reason why, in the present study, we have decided to explore the reaction mechanism and kinetics of the C3H3 + CH2OO system. It must also be added that, due to the time limit, only the simplest Criegee intermediate CH2OO is considered in this work, and larger Criegee intermediates such as CH3CHOO and (CH3)2COO will be considered in our next study. The reaction mechanism in detail has been implemented by the CBS-QB3 high-level quantum chemical method. The calculated high accuracy relative energy values in conjunction with state-of-the-art RRKM model and the master equation (ME) were utilized to predict information about the temperature- and pressure-dependent rate constants and product branching ratios for the dominant reaction channels on the C3H3 + CH2OO potential energy profile. The temperature and pressure ranges, 300–2000 K and 1–76,000 Torr, respectively, were applied. This investigation is the premise basis to supply new information for further studies of the reactions of the Criegee intermediate with unsaturated hydrocarbons in the gas phase.
2. Calculations
2.1. Quantum Chemical Calculations
The potential energy surface (PES) of the C3H3 + CH2OO bimolecular reaction has been established by quantum chemical calculations at the CBS-QB3 level of theory.45 The average, mean absolute, and root mean square errors for the CBS-QB3 method were known to be 0.2, 0.87, and 1.08 kcal/mol, respectively.45 There are several steps conducted in the CBS-QB3 computations. First, the B3LYP/CBSB7 level was utilized to optimize and calculate frequencies. Thereafter, the CCSD(T)/6-31+G(d′) and MP4SDQ/CBSB4 levels were used to predict single-point energies. Lastly, pair natural orbital energies at the MP2/CBSB3 level and an additive correction to the CCSD(T) level were employed for extrapolation to the infinite-basis-set limit to obtain the total energy. It should be noted that the CBS-QB3 method has also been used widely for open-shell singlet ground state species in recent years.46−52 In addition, the wave functions used in this method were clarified to have no multireference character, and the spin contamination can be ignored.46 These feasible results motivate us to use the CBS-QB3 method in this study. Harmonic vibrational frequencies of all species (reactants, intermediates, transition states, and products) located on the PES were employed to characterize stationary points (a local minimum possessing all real frequencies and a transition state holding an imaginary frequency). Those frequencies were then used for rate constant computations. The relationship between a transition state and preferred points (reactants, intermediates, and/or products) has also been thoroughly confirmed by using intrinsic reaction coordinate predictions.53 The Gaussian 16 electronic structure code54 was used to optimize and calculate single-point energies for all species involved in this system.
2.2. Kinetic Calculations
The MESMER code55 with the variational Rice–Ramsperger–Kassel–Marcus (RRKM)56−58 was utilized to calculate the second-order P-dependent rate constants and product branching ratios for the C3H3 + CH2O2 system. Multistep vibrational energy transfers for the excited intermediate (C4H5O2)* occurring in the system were thoroughly examined by solving the master equation (ME).59−61 The tunneling effect62 in conjunction with a one-dimensional asymmetrical Eckart potential was also used to calculate rate constants for the reaction paths related to H-shift processes. The Beyer–Swinehart algorithm63,64 was employed to compute the sum of states and density of states with the use of energy barriers, moments of inertia, and vibrational frequencies of species involved as the input parameters. The intermediates containing single bonds such as C–C and C–O with the low-frequency vibrational modes were treated by hindered internal rotors (HIRs). In this treatment, the V(θ) hindrance potentials were predicted at the CBS-QB3 level via the relaxed scans with the interval size of 10° for dihedral angles related to the rotations. The temperature-dependent exponential-down model, ⟨ΔEdown⟩ = 250 × (T/298)0.8 cm–1, was used to compute the energy-transfer scheme utilizing the Ar bath gas.65 The L–J parameters of Ar were quoted from ref (66) with ε/kB = 113.50 K and σ = 3.465 Å, while the values ε/kB = 412.3 K and σ = 5.349 Å were applied for the C4H5O2 intermediates.67 The second-order rate constants for the prior reaction paths of the studied system were computed under the conditions of 300–2000 K and 1–760,000 Torr with the use of the calculated CBS-QB3 energy values.
3. Results and Discussion
3.1. Potential Energy Surface and Reaction Mechanism
All geometric structures involved in the C3H3 + CH2O2 system including reactants, intermediate states, transition states, and products optimized at the B3LYP/CBSB7 level of theory are exhibited in Figure S1 in the Supporting Information (SI) file. Frequencies, moments of inertia, and rotational constants of all species calculated at the same level are shown in Table S1, while Cartesian coordinates are listed in Table S2 of the SI file. The detailed PES containing all reaction paths is illustrated in Figure S2, whereas the simplified PES holding favorable channels is indicated in Figure 1.
Figure 1.

Simplified potential energy surface for the C3H3 + CH2O2 reaction leading to various products. Energies (in units of kcal/mol) calculated at the CBS-QB3 level.
As can be seen from Figures 1 and S2, the reaction between propargyl radical and Criegee can lead to different products either by direct H-abstraction or through addition intermediates, in which only one product (PR1) has been created by the H-abstraction case (see Figure S2), while remaining products (PR2–PR11) have been generated by the addition channels. In the direct H atom abstraction mechanism, the CH2OO Criegee abstracts a hydrogen atom from the CH2 group of the propargyl radical, forming propynylidene (HCCCH) and the CH3OO radical. The structure of the TS1 transition state shown in Figure S1 reveals that the H atom is moving away from the CH2 group and coming close to the C atom of the CH2OO radical at the distances of 1.482 and 1.231 Å, respectively. However, this process needs to consume quite much energy to overcome the 36.7 kcal/mol activation barrier, cf.Figure S2, and the PR1 product formed in this case is not thermodynamically stable with ∼23 kcal/mol higher than the entrance points. In contrast, in the addition mechanism, the first two intermediates, namely, IS1(HCCCH2CH2OO) and IS2(CH2CCHCH2OO), can be formed as the CH2OO Criegee attacks two ends of the C3H3 radical. Both processes are exothermic with a similar energy level of ∼51.5 kcal/mol at the CBS-QB3 level, indicating that the addition capability of CH2OO on the two sides of C3H3 is the same. Nevertheless, these two channels can be considered as barrierless processes because two transition states TS01 and TS02 connecting the reactants with IS1 and IS2 locate under the starting point about 2.7 and 2.8 kcal/mol, respectively.
From IS1 and IS2, many isomers and/or products can be created by H-shift and/or H-, O-, OH-, and O2-abstraction. Among those isomers, the CHCCHCH2OOH intermediate denoted as IS3 may be obtained directly from both IS1 and IS2 by H-shift processes via TS2 and TS4, respectively. The TS2 transition state shows the displacement of a hydrogen atom from the CH2 group to the terminal O atom with the respective C–H and H–O bond distances of 1.351 and 1.255 Å, while the TS4 saddle point presents the same transfer of an H atom with the C–H and H–O bond lengths of 1.332 and 1.283 Å, respectively. Because the H atom in IS2 must travel a longer distance than the H-shift distance in IS1, which are 3.596 and 2.599 Å, respectively, the relative energy of TS4 (−17.8 kcal/mol) is therefore much higher than the TS2 (−23.6 kcal/mol) relative energy, suggesting that the IS1 → IS3 channel via TS2 takes place more easily than the IS2 → IS3 one via TS4. Compared to the IS1 and IS2 adducts, the IS3 isomer is energetically less stable, being about 2 kcal/mol higher, cf.Figure 1. From the IS3 (CHCCHCH2OOH) intermediate, the PR5 (CHCCH2CHO + OH) product has been found at the position of 76.9 kcal/mol below the reactants. It can be seen in Figure S1 that the geometric structure of TS6, a transition state of the IS3 → PR5 channel, includes two processes of H-shift (from the CH2 group to the adjacent CH group) and OH-abstraction, which makes the TS6 energy barrier larger than that of a process containing only one H-shift or one OH-abstraction. However, the TS6 relative energy still locates 12.5 kcal/mol below the entrance point; thus, the reaction channel going from C3H3 + CH2OO to CHCCH2CHO + OH is considered to be energetically favorable and used for kinetic calculations.
Next, it is interesting to see that the oxygen molecule can appear in both the PR2 (CH2CH2CCH + O2) and PR3 (CH2CCHCH2 + O2) products, in which O2 of PR2 was directly abstracted from IS1 by a barrierless process IS1 → PR2, while O2 of PR3 was created from IS2 by an elementary channel IS2 → PR3 proceeding via a TS22 tight transition state. In the TS22 geometry (see Figure S1), the bond length of C–O was stretching at a 2.207 Å distance, 0.759 Å longer compared to itself in the IS2 geometry; at the same time, the CCOO dihedral angle increased almost twice (θ = 162 vs 81°) as IS2 transformed into the structure of TS22, which facilitated for breaking of the C–O bond. Although PR2 and PR3 are the two isomer products, PR2 is thermodynamically less stable than PR3 (−16.7 kcal/mol compared to −33.0 kcal/mol). However, the competitiveness of these two products may be the same because the IS1 → PR2 process is barrier-free, while the IS2 → PR3 process must overcome a rather high energy barrier, being about 20 kcal/mol. Furthermore, an oxygen molecule can also be formed in the PR9 (CH2CHCHCH + O2) product; still, the reaction path leading to this product from IS2 must surpass through two very high transition states, namely, TS7 and TS17, located at the respective energy levels of ∼11 and ∼13 kcal/mol on the full PES as displayed in Figure S2 of the SI file. Hence, the channel starting from IS2 via the two saddle points TS2 and TS17 as well as via two intermediates IS6 (CH2CHCCH2OO, 3.2 kcal/mol) and IS12 (CH2CHCHCHOO, −64.5 kcal/mol) to the PR9 product has not been used for kinetic estimations.
Similar to the O2-loss, the H-loss processes can be found in the channels forming three products PR6 (CHCCHCHOOH + H), PR7 (CH2-[cyc-CCHCHOO] + H), and PR10 (OCHCHCHCHO + H) as shown in Figures 1 and S2. It is easy to see that reaction paths running from the reactants to the products PR6, PR7, and PR10 proceed exothermicity by 8.2, 38.9, and 94.9 kcal/mol, respectively. Among these products, the former can be produced from IS1, while the two latter can be generated from both IS1 and IS2. In order to form PR6, the IS1 intermediate needs to pass through two energy barriers TS5 and TS9 with the heights of around 41.5 and 35.5 kcal/mol, respectively. The TS5 is a transition state connecting between two isomers IS1 and IS5, which is showing an H-shift from the CH2O group to the outermost O atom with the C–H and H–O distances of 1.333 and 1.275 Å, respectively; simultaneously, the ∠COO bond angle was bent to 89.2° from 111.4° to facilitate for transferring of the H atom. In contrast to the TS5, the transition state TS9 presents an H-loss from the CH2 group of the IS5 (CHCCH2CHOOH) structure lying roughly 40 kcal/mol under the starting points, with the breaking C–H bond length of 2.031 Å. Though the reaction channel giving rise to the PR6 product is exothermic by 8.2 kcal/mol, it has still not been considered for kinetic calculations because the energy required for the TS5 and TS9 transition states was very high compared to that of the most energetically favorable reaction channel, which will be considered hereinafter. Therefore, this channel has been eliminated from the simplified PES as depicted in Figure 1. The PR7 product can be made directly from a five-membered ring structure denoted as IS9 via an H-loss transition state TS12 located a 37 kcal/mol energy level below the entrance points, in which the IS9 intermediate can be generated directly and/or indirectly from IS2 and/or IS1, respectively. If going from IS2, the channel goes through only one ring transition state, namely, TS11, but if going from IS1, it must proceed via two transition states being a closed-ring TS (TS20) and an H-shift TS (TS21). In terms of energy, the IS2 → IS9 branch is much favorable than the IS1 → IS9 branch because the relative energy of TS11 is much lower than that of TS21, being −38.65 and −0.4 kcal/mol, respectively. As can be seen in Figure 1, the energy level of IS9 is fairly lower than that of IS1 and/or IS2 (E = −77 vs −51.5 kcal/mol), indicating that the structure of IS9 is more stable than the IS1 and IS2 structures. This explains that IS9 is the ring structure, while IS1 and IS2 are the open ones (cf.Figure S1). It is worth noting that both the transition states TS11 and TS12 are the lowest-lying TSs compared to all other TSs on the full PES; the reaction channel proceeding via two intermediates (IS2 and IS9) and three TSs (TS02, TS11, and TS12) giving rise to PR7 (−38.9 kcal/mol) is, therefore, the most energetically and kinetically favorable channel on the whole PES. Similar to the PR7 product, the most stable product, namely, PR10 (OCHCHCHCHO + H), can also be established from two different channels as abovementioned. As shown in Figure 1, the first channel goes through (IS1, IS10, and IS11) and (TS14, TS16, and TS18), while the second one proceeds via (IS2, IS7, and IS11) and (TS8, TS13, and TS18). It is possible to see that both these channels are energetically equivalent because the energies of (IS1, IS10, TS14, and TS16) on the first channel are similar to those of (IS2, IS7, TS8, and TS13) on the second one, being (−51.5, −50.4, −32.8, and −9.2 kcal/mol) and (−51.2, −51.4, −34.3, and −10.85 kcal/mol), respectively, calculated at the CBS-QB3 level. In addition, before moving to the stabilized PR10 product, both these channels converge to the lowest point on the PES located at the IS11 (OCH2CHCHCHO) with a relative energy of −111.3 kcal/mol; thus, it can be said that these two reaction channels compete with each other in the formation of the PR10 product. Moreover, the IS11 → PR10 last step of both channels is predicted to occur easily because the energy released in the previous stages can help them quickly overcome an energy barrier of ∼20 kcal/mol at the TS18 transition state. The TS18 geometry (Figure S1) shows that one hydrogen atom of the CH2 group is abstracting at a long distance of 1.879 Å, which is characterized by only one negative frequency of −754 cm–1, suggesting that this is a correct H-loss process. The PR10 product created consisting of a two-functional aldehyde whose chemical formula is OCH–CHCH–CHO and a H atom has been found to be the most thermodynamically stable product compared to all others of the title reaction. In addition to the product PR10, the two abovementioned reaction channels have also produced the PR11 product. As can be seen in Figure 1, from the position of IS11 (OCH2CHCHCHO), instead of producing PR10, the reaction can generate PR11 (CHCHCHO + CH2O) through the transition state TS19. The TS19 structure shows that the CH2O moiety is eliminating from the CHCHCHO moiety at a loose connection of 2.219 Å characterized by an imaginary frequency of −299.4893 cm–1, indicating that this process occurs by CH2O-loss. Undoubtedly, the H-loss mechanism is similar to the CH2O-loss mechanism, and the energy of the transition state TS18 (−90.8 kcal/mol) is therefore not significantly different from that of the TS19 (88 kcal/mol) transition state. Furthermore, the energy of the product PR10 (−94.9 kcal/mol) is only slightly lower than that of the PR11 (−88.5 kcal/mol) product. This proves that these two products have the same contribution to the general product formation of the C3H3 + CH2OO system.
Another point to be considered here is that the O-abstraction process from the structure of IS4 (CH2CCH2CHOO, −15.9 kcal/mol), which was isomerized directly from IS2 via the TS3 transition state can bring out the CH2CCH2CHO product belonging to PR4 (−10.2 kcal/mol). The structure of TS3 shown in Figure S1 reveals that the H atom is going far away from the CH2OO group and is coming closer to the neighbor CH group with the corresponding loose bond distances of 1.445 and 1.285 Å, whereas the ∠CCOO torsional angle decreases nearly 81° to facilitate the movement of the CH2OO hydrogen atom. Because the relative energy of TS3 is nearly 10 kcal/mol higher than that of the initial reactants (cf.Figure S2), the IS2 → PR4 channel is not advantageous in energy and can be ignored in kinetic predictions.
Last but not least, from the IS1 intermediate state, the bimolecular product PR8 (HCCH + CH2CHOO) can be made indirectly via an H-shift transition state TS10 and a C2H2-loss transition state TS15 with a dissociation barrier heights of nearly 72 and 14 kcal/mol, respectively. The structure of TS10 reveals that the H atom is 1.6 Å moving far away from the CH2 group and is 1.332 Å coming close to the C atom, whereas in the TS15 structure, the C–C bond length increases to 1.932 Å from 1.458 Å to facilitate the abstraction of two moieties HCCH and CH2CHOO. The calculated results point out that each TS (TS10 and TS15) contains only one imaginary frequency, being −1914 and −722 cm–1, respectively, and the predicted IRCs for those TSs also confirmed that the TS10 connects with both IS1 (CHCCH2CH2OO, −51.5 kcal/mol) and IS8 (CHCHCH2CHOO, −17.3 kcal/mol), while the TS15 connects with both IS8 and the PR8 product. Even though the C3H3 + CH2OO → PR8 reaction path is much exothermic by approximately 28 kcal/mol, this channel is considered to be unfavorable in energy because it must surpass the very high transition state TS10 located at about 20 kcal/mol above the reactants. Therefore, it can be ignored in the kinetic calculations presented hereinafter.
3.2. Thermochemical Properties
To increase the reliability of the calculations in this study, thermodynamic properties (ΔH298K) for all species involved in the C3H3 + CH2OO system have been investigated as shown in Table 1, in which the values of several limited species (e.g., C3H3, CH2OO, HCCH, CH2O, C2H2, and OH) have been benchmarked against the available literature data. It can be observed from Table 1 that the computed values for some above-listed species are in good agreement with the available literature data. The maximum deviation between our values and the ATcT data was recorded to be less than 1.0 kcal/mol, indicating that the methods utilized in the present study are extremely reasonable for the title reaction.
Table 1. Standard Enthalpies of Formation (at 298 K, in kcal/mol) of All Species Related to the C3H3 + CH2OO Systema in Comparison with Literature Datab.
| species | ΔH298K | species | ΔH298K |
|---|---|---|---|
| C3H3 (propargyl radical) | 83.56 | TS12 | –38.00 |
| 84.02 ± 0.39b | |||
| CH2OO (Criegee biradical) | 25.32 | TS13 | –9.81 |
| 25.48 ± 0.29b | |||
| IS1 | –46.98 | TS14 | –29.37 |
| IS2 | –47.18 | TS15 | –2.19 |
| IS3 | –45.88 | TS16 | –7.65 |
| IS4 | –12.95 | TS17 | 13.47 |
| IS5 | –36.63 | TS18 | –91.52 |
| IS6 | 5.90 | TS19 | –86.45 |
| IS7 | –46.45 | TS20 | –31.17 |
| IS8 | –14.05 | TS21 | 0.06 |
| IS9 | –73.33 | TS22 | –29.43 |
| IS10 | –45.35 | PR1 | 21.35 |
| IS11 | –107.65 | PR2 | –15.65 |
| IS12 | –60.13 | PR3 | –32.04 |
| IS13 | –46.34 | PR4 | –10.02 |
| TS01 | –1.97 | PR5 | –75.64 |
| TS02 | –2.21 | PR6 | –9.55 |
| TS1 | 34.64 | PR7 | –39.69 |
| TS2 | –23.03 | PR8 | –26.92 |
| TS3 | 9.74 | PR9 | –17.27 |
| TS4 | –17.71 | PR10 | –95.32 |
| TS5 | –9.62 | PR11 | –87.58 |
| TS6 | –12.88 | CH3OO | 2.43 |
| 2.89 ± 0.24b | |||
| TS7 | 11.69 | HCCCH | 130.22 |
| 130.52 ± 0.16b | |||
| TS8 | –31.11 | C2H2 | 54.91 |
| 54.57 ± 0.03b | |||
| TS9 | –7.04 | CH2O | –25.63 |
| –26.10 ± 0.01b | |||
| TS10 | 19.68 | OH | 8.15 |
| TS11 | –36.09 | 8.96 ± 0.01b |
4. Chemical Kinetic Calculations
All of the reaction channels displayed on the simplified PES (see Figure 1) were used to calculate rate constants for the C3H3 + CH2OO system. For convenience, each channel is denoted as follows:
| k1 |
| k2 |
| k3 |
| k4 |
| k5 |
| k6 |
The RRKM theory was used to predict bimolecular rate constants of the six channels (k1–k6) above with a variational treatment of the entrance channels. All of the variational RRKM rate constant calculations were conducted by the MESMER program. The calculated results (k1–k6) in the 300–2000 K temperature range at various pressures ranging from 1 to 76,000 Torr (corresponding to ∼0.001–100 atm) are shown in Tables S3–S8 of the SI file, while the plots of the temperature- and pressure-dependent rate constants and the branching ratios for the channels indicated are graphically shown in Figures 2–8. It should be noted that the kinetic calculation in this work aims to help to understand the chemical process for the troposphere (0.001–1 atm). In addition, the calculated results should also be used as a database for further related studies; therefore, the considered temperature and pressure ranges are relatively wide (up to 2000 K and 76,000 Torr, respectively) as shown above.
Figure 2.

Plot of rate constants of the C3H3 + CH2OO system calculated at P = 1 Torr (Ar) in the temperature range of 300–2000 K.
Figure 8.

Branching ratios of the C3H3 + CH2OO system calculated at P = 760 Torr (Ar) in the temperature range of 300–2000 K.
Figure 3.
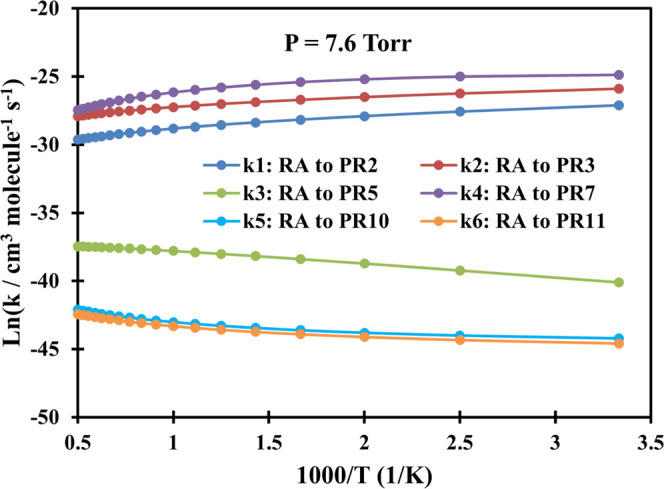
Plot of rate constants of the C3H3 + CH2OO system calculated at P = 7.6 Torr (Ar) in the temperature range of 300–2000 K.
Figure 4.
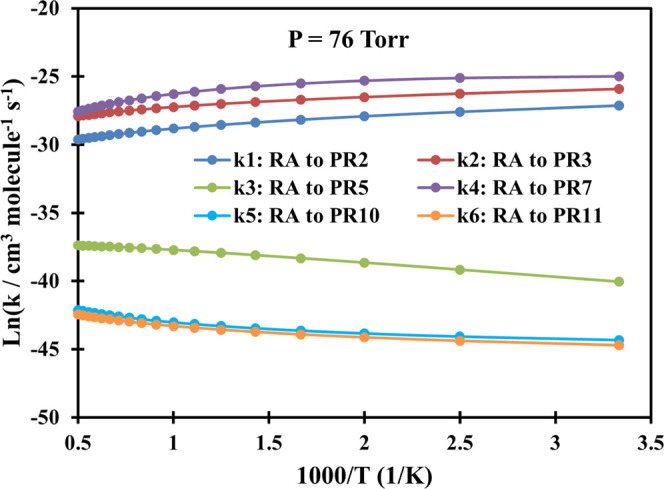
Plot of rate constants of the C3H3 + CH2OO system calculated at P = 76 Torr (Ar) in the temperature range of 300–2000 K.
Figure 5.

Plot of rate constants of the C3H3 + CH2OO system calculated at P = 760 Torr (Ar) in the temperature range of 300–2000 K.
Figure 6.
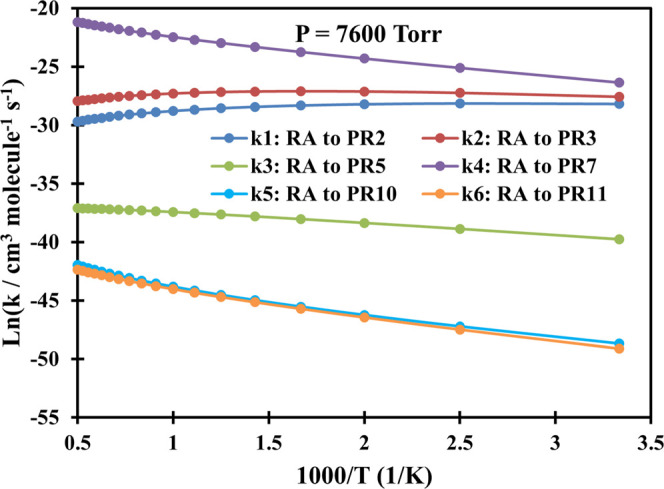
Plot of rate constants of the C3H3 + CH2OO system calculated at P = 7600 Torr (Ar) in the temperature range of 300–2000 K.
Overall, as can be seen from Figures 2–7, the bimolecular rate constants (k1–k6) of the C3H3 + CH2OO system are pressure- and temperature-dependent. For the first two channels C3H3 + CH2OO → PR2 and C3H3 + CH2OO → PR3, their rate constants mostly decrease with rising temperatures in the range of 300–2000 K. The fourth channel C3H3 + CH2OO → PR7 has the same trend as the first two channels in the low-pressure range of 1–76 Torr; however, its rate constant will increase with rising temperature if the pressure reaches or exceeds 760 Torr. In contrast to the first two reaction paths, the rate constants of the remaining three reaction channels (k3, k5, and k6) are proportional to the temperatures.
Figure 7.

Plot of rate constants of the C3H3 + CH2OO system calculated at P = 76,000 Torr (Ar) in the temperature range of 300–2000 K.
Particularly, in the low-pressure region P = 1–760 Torr, the second-order rate constants of the first channel decrease from 1.66 × 10–12 to 1.33 × 10–13 cm3 molecule–1 s–1, while those of the second channel reduce in the range of 5.72 × 10–12–7.46 × 10–13 cm3 molecule–1 s–1 as the temperature goes up covering the considered T-range. At P = 7600 Torr, the value of the first channel increases slightly from 5.77 × 10–13 to 6.00 × 10–13 cm3 molecule–1 s–1 in the range T = 300–400 K before slowly going down to 1.27 × 10–13 cm3 molecule–1 s–1 at T = 2000 K, while the value of the second path increases in the range of 1.06 × 10–12–1.69 × 10–12 cm3 molecule–1 s–1 (T = 300–600 K) before reducing to 7.34 × 10–13 cm3 molecule–1 s–1 at T = 2000 K. At P = 76,000 Torr, the k1 value increases from 6.15 × 10–14 to 2.80 × 10–13 cm3 molecule–1 s–1 in the temperature range of 300–700 K before going down to 1.35 × 10–13 cm3 molecule–1 s–1 at 2000 K, whereas the k2 value moderately rises from 9.80 × 10–14–9.12 × 10–13 cm3 molecule–1 s–1 in the whole considered temperature range. From the calculated data above, it is easy to observe that the rate constants of the k2 channel are always larger than those of the k1 channel with the branching ratios decreasing in the ranges of 37–1% and 12–0.2%, respectively, at P = 760 Torr and T = 300–2000 K.
As mentioned above, the k4 channel forming the PR7 (CH2-[cyc-CCHCHOO] + H) product is considered to be the most favorable reaction path on the PES. The calculated result also indicates that the rate constants of this channel are always larger than those of the others (see Figures 2–7); e.g., at P = 760 Torr, its rate constant lies in the range of 6.44 × 10–12–6.75 × 10–11 cm3 molecule–1 s–1 with the branching ratio increasing from 51 to 98.7% corresponding to T = 300–2000 K (see Figure 8). Therefore, the predicted rate constants for the k4 reaction pathway has correctly reflected the reaction mechanism as shown in the PES. Furthermore, it is worth noting that the k4 value reduces with rising pressure in the 1–76 Torr range as can be seen in Tables S3–S5 of the SI file. At higher pressures (P ≥ 760 Torr), this value only reduces with an increase in pressure if the temperature is less than 500 K, but it increases as the pressure goes up if the temperature is larger than 500 K. Thus, it can be said that the reaction path leading to the PR7 product depends strongly on both temperature and pressure.
Last but not least, from Figures 2–7, it is easy to see that the rate constants of the two last reaction channels, namely, k5 and k6, always compete with each other at any temperature and pressure, in which the values of the k5 channel are slightly larger than those of the k6 channel. This is completely consistent with the results of the energy calculation for the two reaction channels (k5 and k6) as analyzed above. For example, at 760 Torr, the k5 value varies from 1.54 × 10–20 to 5.00 × 10–19 cm3 molecule–1 s–1, while the k6 value ranges from 1.20 × 10–20 to 3.63 × 10–19 cm3 molecule–1 s–1; the maximum deviation between them is only 1.38 times. It is worth noting that both the k5 and k6 values decrease with rising pressure in the 1–76,000 Torr range. In particular, at low temperatures these two values are strongly dependent on pressure; e.g., at 300 K, the 76 Torr values of the k5 and k6 were calculated as 3.81 × 10–20 and 5.64 × 10–20 cm3 molecule–1 s–1, respectively, while the 7600 Torr values of them in order were 7.14 × 10–22 and 4.64 × 10–22 cm3 molecule–1 s–1. At very high temperatures, however, the effect of pressures on rate constants is really minor. Compared to the other rate constants, obviously, the k5 and k6 values are considered to occupy the lowest positions at any temperature and pressure. The total branching ratio for these two channels, at 760 Torr, was recorded to be less than 0.1%, indicating that the contribution of these two reaction pathways to the overall product formation of the title reaction is negligible.
For the convenience of tracking and using the calculated results, in the present study, the modified Arrhenius equation has been utilized to express for the individual and total rate constants (in units of cm3 molecule–1 s–1) of the bimolecular reaction, C3H3 + CH2OO, in the temperature range of 300–2000 K at 760 Torr (Ar):
5. Concluding Remarks
In this study, the CBS-QB3 level of theory was used to investigate the mechanism of the C3H3 + CH2OO reaction, while the rigorous ME/vRRKM theory was utilized to calculate rate constants for the preferred channels on the PES of the reaction. The obtained PES has revealed that the C3H3 + CH2OO system can proceed via the abstraction mechanism to create the PR1 (HCCCH + CH3OO) product and/or via the addition mechanism to possibly form the bimolecular products, namely, PR2–PR11, in which the PR7 (CH2-[cyc-CCHCHOO] + H) product has been found to be the most favorable product of the title reaction. All of the reaction channels and the bimolecular products have been found in this study for the first time.
Based on the received data, it can be concluded that the rate constants for the key channels of the title reaction depend vigorously on both temperature and pressure, in which the values of the two channels, C3H3 + CH2OO → CH2CH2CCH + O2 and C3H3 + CH2OO → CH2CCHCH2 + O2, decrease gradually when the temperature increases in the 300–2000 K range. At low pressures in the region of 1–76 Torr, the rate constant of the channel C3H3 + CH2OO → CH2-[cyc-CCHCHOO] + H also decreases as the first two channels, but its value will increase with rising temperature if the pressure is greater than or equal to 760 Torr. Rate constants of the three reaction pathways leading to the bimolecular products CHCCH2CHO + OH, OCHCHCHCHO + H, and CHCHCHO + CH2O have been found to be proportional to the temperatures.
The calculated data also confirmed that the rate constants of the k4 channel giving rise to the PR7 (CH2-[cyc-CCHCHOO] + H) product are the highest values compared to the others. At P = 760 Torr, the values of this channel increase from 6.44 × 10–12 to 6.75 × 10–11 cm3 molecule–1 s–1 corresponding to the branching ratio of 51–98.7% in the temperature range of 300–2000 K. The rate constants of the channels forming the products PR10 (OCHCHCHCHO + H) and PR11 (CHCHCHO + CH2O) are found to be the lowest values at any temperature and pressure. The total branching ratio for these two channels, at 760 Torr, does not exceed 0.1%, showing that the contribution of these two reaction paths to the title reaction is insignificant.
It is recommended that the given detailed kinetic mechanism along with the computed rate constants and thermodynamic properties of the title reaction help to understand the chemical process for the troposphere in the pressure range of 1–760 Torr and also should be used for modeling/simulation of both atmospheric and combustion applications at high temperature and pressure.
Acknowledgments
This research is funded by Hanoi University of Science and Technology (HUST) under Grant Number T2022-PC-069. The authors also acknowledge the National Center for High-Performing Computers in Taiwan for the use of its facility.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c00491.
Frequencies, moments of inertia, and rotational constants of reactants, intermediates, transition states, and products of the C3H3 + CH2OO reaction at the B3LYP/CBSB7 level; Cartesian coordinates of reactants, intermediates, transition states, and products of the C3H3 + CH2OO combination reaction optimized at the B3LYP/CBSB7 level; calculated rate constants of the C3H3 + CH2OO reaction at P = 1–76,000 Torr (Ar) and T = 300–2000 K; geometry of reactants, intermediates, transition states, and products involved in the C3H3 + CH2OO reaction optimized at the CBS-QB3 level of theory; bond angles and bond lengths are in degree (°) and angstroms (Å), respectively; detailed PES for the C3H3 + CH2OO reaction calculated at the CBS-QB3 level of theory; energies are in kcal/mol; and scanned file for the IS1 → CH2CH2CCH + O2 (PR2) channel optimized at the CBS-QB3 level of theory (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Marston G.; Johnson D. The gas-phase ozonolysis of unsaturated volatile organic compounds in the troposphere. Chem. Soc. Rev. 2008, 37, 699–716. 10.1039/b704260b. [DOI] [PubMed] [Google Scholar]
- Horie O.; Moortgat G. K. Decomposition pathways of the excited Criegee intermediates in the ozonolysis of simple alkenes. Atmos. Environ., Part A 1991, 25, 1881–1896. 10.1016/0960-1686(91)90271-8. [DOI] [Google Scholar]
- Khan M. A. H.; Percival C. J.; Caravan R. L.; Taatjes C. A.; Shallcross D. E. Criegee intermediates and their impacts on the troposphere. Environ. Sci.: Processes Impacts 2018, 20, 437. 10.1039/C7EM00585G. [DOI] [PubMed] [Google Scholar]
- Welz O.; Savee J. D.; Osborn D. L.; Vasu S. S.; Percival C. J.; Shallcross D. E.; Taatjes C. A. Direct Kinetic Measurements of Criegee Intermediate (CH2OO) Formed by Reaction of C2I with O2. Science 2012, 335, 204–207. 10.1126/science.1213229. [DOI] [PubMed] [Google Scholar]
- Vereecken L.; Francisco J. S. Theoretical Studies of Atmospheric Reaction Mechanisms in the Troposphere. Chem. Soc. Rev. 2012, 41, 6259–6293. 10.1039/c2cs35070j. [DOI] [PubMed] [Google Scholar]
- Ouyang B.; McLeod M. W.; Jones R. L.; Bloss W. J. NO3 Radical Production from the Reaction between the Criegee Intermediate CH2OO and NO2. Phys. Chem. Chem. Phys. 2013, 15, 17070–17075. 10.1039/c3cp53024h. [DOI] [PubMed] [Google Scholar]
- Taatjes C. A.; Welz O.; Eskola A. J.; Savee J. D.; Scheer A. M.; Shallcross D. E.; Rotavera B.; Lee E. P.; Dyke J. M.; Mok D. K.; et al. Direct Measurements of Conformer-Dependent Reactivity of the Criegee Intermediate CH3CHOO. Science 2013, 340, 177–180. 10.1126/science.1234689. [DOI] [PubMed] [Google Scholar]
- Berndt T.; Voigtlander J.; Stratmann F.; Junninen H.; Mauldin R. L. 3rd; Sipila M.; Kulmala M.; Herrmann H. Competing Atmospheric Reactions of CH2OO with SO2 and Water Vapour. Phys. Chem. Chem. Phys. 2014, 16, 19130–19136. 10.1039/C4CP02345E. [DOI] [PubMed] [Google Scholar]
- Stone D.; Blitz M.; Daubney L.; Howes N. U.; Seakins P. Kinetics of CH2OO Reactions with SO2, NO2, NO, H2O and CH3CHO as a Function of Pressure. Phys. Chem. Chem. Phys. 2014, 16, 1139–1149. 10.1039/C3CP54391A. [DOI] [PubMed] [Google Scholar]
- Chao W.; Hsieh J. T.; Chang C. H.; Lin J. J. Direct Kinetic Measurement of the Reaction of the Simplest Criegee Intermediate with Water Vapor. Science 2015, 347, 751–754. 10.1126/science.1261549. [DOI] [PubMed] [Google Scholar]
- Lewis T. R.; Blitz M. A.; Heard D. E.; Seakins P. W. Direct Evidence for a Substantive Reaction between the Criegee Intermediate, CH2OO, and the Water Vapour Dimer. Phys. Chem. Chem. Phys. 2015, 17, 4859–4863. 10.1039/C4CP04750H. [DOI] [PubMed] [Google Scholar]
- Newland M. J.; Rickard A. R.; Alam M. S.; Vereecken L.; Munoz A.; Rodenas M.; Bloss W. J. Kinetics of Stabilised Criegee Intermediates Derived from Alkene Ozonolysis: Reactions with SO2, H2O and Decomposition under Boundary Layer Conditions. Phys. Chem. Chem. Phys. 2015, 17, 4076–4088. 10.1039/C4CP04186K. [DOI] [PubMed] [Google Scholar]
- Caravan R. L.; Khan M. A. H.; Rotavera B.; Papajak E.; Antonov I. O.; Chen M. W.; Au K.; Chao W.; Osborn D. L.; Lin J. J.; et al. Products of Criegee Intermediate Reactions with NO2: Experimental Measurements and Tropospheric Implications. Faraday Discuss. 2017, 200, 313–330. 10.1039/C7FD00007C. [DOI] [PubMed] [Google Scholar]
- Liu Y.; Liu F.; Liu S.; Dai D.; Dong W.; Yang X. A Kinetic Study of the CH2OO Criegee Intermediate Reaction with SO2, (H2O)2, CH2I2 and I Atoms Using OH Laser Induced Fluorescence. Phys. Chem. Chem. Phys. 2017, 19, 20786–20794. 10.1039/C7CP04336H. [DOI] [PubMed] [Google Scholar]
- Ting W.-L.; Chang C.-H.; Lee Y.-F.; Matsui H.; Lee Y.-P.; Lin J. J.-M. Detailed Mechanism of the CH2I + O2 Reaction: Yield and Self-Reaction of the Simplest Criegee Intermediate CH2OO. J. Chem. Phys. 2014, 141, 104308 10.1063/1.4894405. [DOI] [PubMed] [Google Scholar]
- Ahrens J.; Carlsson Philip T. M.; Hertl N.; Olzmann M.; Pfeifle M.; Wolf J. L.; Zeuch T. Infrared Detection of Criegee Intermediates Formed During the Ozonolysis of β-Pinene and Their Reactivity Towards Sulfur Dioxide. Angew. Chem., Int. Ed. 2014, 53, 715–719. 10.1002/anie.201307327. [DOI] [PubMed] [Google Scholar]
- Buras Z. J.; Elsamra R. M.; Green W. H. Direct Determination of the Simplest Criegee Intermediate (CH2OO) Self Reaction Rate. J. Phys. Chem. Lett. 2014, 5, 2224–2228. 10.1021/jz5008406. [DOI] [PubMed] [Google Scholar]
- Berndt T.; Jokinen T.; Mauldin R. L.; Petäjä T.; Herrmann H.; Junninen H.; Paasonen P.; Worsnop D. R.; Sipilä M. Gas-Phase Ozonolysis of Selected Olefins: The Yield of Stabilized Criegee Intermediate and the Reactivity toward SO2. J. Phys. Chem. Lett. 2012, 3, 2892–2896. 10.1021/jz301158u. [DOI] [Google Scholar]
- Welz O.; Eskola Arkke J.; Sheps L.; Rotavera B.; Savee John D.; Scheer Adam M.; Osborn David L.; Lowe D.; Murray Booth A.; Xiao P.; et al. Rate Coefficients of C1 and C2 Criegee Intermediate Reactions with Formic and Acetic Acid near the Collision Limit: Direct Kinetics Measurements and Atmospheric Implications. Angew. Chem. 2014, 126, 4635–4638. 10.1002/ange.201400964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taatjes C. A.; Welz O.; Eskola A. J.; Savee J. D.; Osborn D. L.; Lee E. P.; Dyke J. M.; Mok D. W.; Shallcross D. E.; Percival C. J. Direct Measurement of Criegee Intermediate (CH2OO) Reactions with Acetone, Acetaldehyde, and Hexafluoroacetone. Phys. Chem. Chem. Phys. 2012, 14, 10391–10400. 10.1039/c2cp40294g. [DOI] [PubMed] [Google Scholar]
- Jalan A.; Allen J. W.; Green W. H. Chemically Activated Formation of Organic Acids in Reactions of the Criegee Intermediate with Aldehydes and Ketones. Phys. Chem. Chem. Phys. 2013, 15, 16841–16852. 10.1039/c3cp52598h. [DOI] [PubMed] [Google Scholar]
- Buras Z. J.; Elsamra R. M.; Jalan A.; Middaugh J. E.; Green W. H. Direct Kinetic Measurements of Reactions between the Simplest Criegee Intermediate CH2OO and Alkenes. J. Phys. Chem. A 2014, 118, 1997–2006. 10.1021/jp4118985. [DOI] [PubMed] [Google Scholar]
- Vereecken L.; Harder H.; Novelli A. The Reactions of Criegee Intermediates with Alkenes, Ozone, and Carbonyl Oxides. Phys. Chem. Chem. Phys. 2014, 16, 4039–4049. 10.1039/c3cp54514h. [DOI] [PubMed] [Google Scholar]
- Kurtén T.; Lane J. R.; Jorgensen S.; Kjaergaard H. G. A Computational Study of the Oxidation of SO2 to SO3 by Gas-Phase Organic Oxidants. J. Phys. Chem. A 2011, 115, 8669–8681. 10.1021/jp203907d. [DOI] [PubMed] [Google Scholar]
- Long B.; Tan X. F.; Long Z. W.; Wang Y. B.; Ren D. S.; Zhang W. J. Theoretical Studies on Reactions of the Stabilized H2COO with HO2 and the HO2···H2O Complex. J. Phys. Chem. A 2011, 115, 6559–6567. 10.1021/jp200729q. [DOI] [PubMed] [Google Scholar]
- Vereecken L.; Harder H.; Novelli A. The Reaction of Criegee Intermediates with NO, RO2, and SO2, and Their Fate in the Atmosphere. Phys. Chem. Chem. Phys. 2012, 14, 14682–14695. 10.1039/c2cp42300f. [DOI] [PubMed] [Google Scholar]
- Berndt T.; Kaethner R.; Voigtlander J.; Stratmann F.; Pfeifle M.; Reichle P.; Sipila M.; Kulmala M.; Olzmann M. Kinetics of the Unimolecular Reaction of CH2OO and the Bimolecular Reactions with the Water Monomer, Acetaldehyde and Acetone under Atmospheric Conditions. Phys. Chem. Chem. Phys. 2015, 17, 19862–19873. 10.1039/C5CP02224J. [DOI] [PubMed] [Google Scholar]
- Kuwata K. T.; Guinn E. J.; Hermes M. R.; Fernandez J. A.; Mathison J. M.; Huang K. A Computational Re-Examination of the Criegee Intermediate-Sulfur Dioxide Reaction. J. Phys. Chem. A 2015, 119, 10316–10335. 10.1021/acs.jpca.5b06565. [DOI] [PubMed] [Google Scholar]
- Vereecken L.; Rickard A. R.; Newland M. J.; Bloss W. J. Theoretical Study of the Reactions of Criegee Intermediates with Ozone, Alkylhydroperoxides, and Carbon Monoxide. Phys. Chem. Chem. Phys. 2015, 17, 23847–23858. 10.1039/C5CP03862F. [DOI] [PubMed] [Google Scholar]
- Chen L.; Huang Y.; Xue Y.; Cao J.; Wang W. Competition between HO2 and H2O2 Reactions with CH2OO/anti-CH3CHOO in the Oligomer Formation: A Theoretical Perspective. J. Phys. Chem. A 2017, 121, 6981–6991. 10.1021/acs.jpca.7b05951. [DOI] [PubMed] [Google Scholar]
- Vereecken L.; Nguyen H. M. T. Theoretical Study of the Reaction of Carbonyl Oxide with Nitrogen Dioxide: CH2OO + NO2. Int. J. Chem. Kinet. 2017, 49, 752–760. 10.1002/kin.21112. [DOI] [Google Scholar]
- Xu K.; Wang W.; Wei W.; Feng W.; Sun Q.; Li P. Insights into the Reaction Mechanism of Criegee Intermediate CH2OO with Methane and Implications for the Formation of Methanol. J. Phys. Chem. A 2017, 121, 7236–7245. 10.1021/acs.jpca.7b05858. [DOI] [PubMed] [Google Scholar]
- Zhao Q.; Liu F.; Wang W.; Li C.; Lu J.; Wang W. Reactions between Hydroxyl-Substituted Alkylperoxy Radicals and Criegee Intermediates: Correlations of the Electronic Characteristics of Methyl Substituents and the Reactivity. Phys. Chem. Chem. Phys. 2017, 19, 15073–15083. 10.1039/C7CP00869D. [DOI] [PubMed] [Google Scholar]
- Raghunath P.; Lee Y. P.; Lin M. C. Computational Chemical Kinetics for the Reaction of Criegee Intermediate CH2OO with HNO3 and Its Catalytic Conversion to OH and HCO. J. Phys. Chem. A 2017, 121, 3871–3878. 10.1021/acs.jpca.7b02196. [DOI] [PubMed] [Google Scholar]
- Crehuet R.; Anglada J. M.; Cremer D.; Bofill J. M. Reaction Modes of Carbonyl Oxide, Dioxirane, and Methylenebis(oxy) with Ethylene: A New Reaction Mechanism. J. Phys. Chem. A 2002, 106, 3917–3929. 10.1021/jp0142031. [DOI] [Google Scholar]
- Eskola A. J.; Dontgen M.; Rotavera B.; Caravan R. L.; Welz O.; Savee J. D.; Osborn D. L.; Shallcross D. E.; Percival C. J.; Taatjes C. A. Direct Kinetics Study of CH2OO + Methyl Vinyl Ketone and CH2OO + Methacrolein Reactions and an Upper Limit Determination for CH2OO + CO Reaction. Phys. Chem. Chem. Phys. 2018, 20, 19373–19381. 10.1039/C8CP03606C. [DOI] [PubMed] [Google Scholar]
- Pham T. V. Theoretical Investigation on Mechanism, Thermochemistry, and Kinetics of the Gas-phase Reaction of 2-Propargyl Radical with Formaldehyde. Chem. Res. Chin. Univ. 2019, 35, 884–891. 10.1007/s40242-019-9054-0. [DOI] [Google Scholar]
- Pham T. V.; Trang H. T. T. Combination Reactions of Propargyl Radical with Hydroxyl Radical and the Isomerization and Dissociation of trans-Propenal. J. Phys. Chem. A 2020, 124, 6144–6157. 10.1021/acs.jpca.0c05106. [DOI] [PubMed] [Google Scholar]
- Pham T. V.; Trang H. T. T.; Ngo C. T.; Nguyen H. M. T. A quantum chemical study of the mechanisms and kinetics of the reaction between propargyl (C3H3) and methyl (CH3) radicals. Chem. Phys. Lett. 2021, 762, 138126 10.1016/j.cplett.2020.138126. [DOI] [Google Scholar]
- Nguyen H. M. T.; Pham T. V.; Hung V. H.; Pham T. H.; Ngo T. C. Mechanism and kinetics of the reaction of the 2-propargyl radical with ammonia. Int. J. Chem. Kinet. 2020, 52, 84–91. 10.1002/kin.21332. [DOI] [Google Scholar]
- Pham T. V.; Trang H. T. T. Theoretical Investigation of the Mechanisms and Kinetics of the Bimolecular and Unimolecular Reactions Involving in the C4H6 Species. J. Phys. Chem. A 2021, 125, 585–596. 10.1021/acs.jpca.0c08983. [DOI] [PubMed] [Google Scholar]
- Pham T. V.; Trang H. T. T.; Nguyen H. M. T. Temperature and Pressure-Dependent Rate Constants for the Reaction of the Propargyl Radical with Molecular Oxygen. ACS Omega 2022, 7, 33470–33481. 10.1021/acsomega.2c04316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen T. N.; Trang H. T. T.; Nghia T. N.; Pham T. V. Computational Study of the Reaction of C3H3 with HNCO and the Decomposition of C4H4NO radicals. Int. J. Kinet. 2022, 54, 447–460. 10.1002/kin.21573. [DOI] [Google Scholar]
- Van Pham T.; Nguyen N. N.; Trang H. T. T. Computational Investigation on the Formation and Decomposition Reactions of the C4H3O Compound. ACS Omega 2021, 6, 17965–17976. 10.1021/acsomega.1c01663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montgomery J. A. Jr.; Frisch M. J.; Ochterski J. W.; Petersson G. A. A complete basis set model chemistry. VI. Use of density functional geometries and frequencies. J. Chem. Phys. 1999, 110, 2822. 10.1063/1.477924. [DOI] [Google Scholar]
- Kuzhanthaivelan S.; Rajakumar B. Computational investigations on the thermochemistry and kinetics for the autoignition of 2-pentanone. Combust. Flame 2020, 219, 147–160. 10.1016/j.combustflame.2020.05.009. [DOI] [Google Scholar]
- Mahmoud M. A. M.; El-Demerdash S. H.; EL Gogary T. M.; El-Nahas A. M. Oxidation of Methyl Propanoate by the OH Radical. Russ. J. Phys. Chem. A 2018, 92, 2476–2484. 10.1134/S0036024418120294. [DOI] [Google Scholar]
- Jiao Y.; Zhang F.; Dibble T. S. Quantum Chemical Study of Autoignition of Methyl Butanoate. J. Phys. Chem. A 2015, 119, 7282–7292. 10.1021/jp5122118. [DOI] [PubMed] [Google Scholar]
- Antonov I. O.; Zador J.; Rotavera B.; Papajak E.; Osborn D. L.; Taatjes C. A.; Sheps L. Pressure-Dependent competition among reaction pathways from First- and Second O2 additions in the Low-temperature oxidation of tetrahydrofuran. J. Phys. Chem. A 2016, 120, 6582–6595. 10.1021/acs.jpca.6b05411. [DOI] [PubMed] [Google Scholar]
- Parab P. R.; Sakade N.; Sakai Y.; Fernandes R.; Heyfer K. A. A computational kinetics study on the intramolecular hydrogen shift reactions of alkylperoxy radicals in 2-Methyltetrahydrofuran Oxidation. Int. J. Chem. Kinet. 2017, 49, 419–437. 10.1002/kin.21087. [DOI] [Google Scholar]
- Koritzke A. L.; Davis J. C.; Caravan R. L.; Christianson M. G.; Osborn D. L.; Taat- jes C. A.; Rotavera B. QOOH-mediated reactions in cyclohexene oxidation. Proc. Combust. Inst. 2019, 37, 323–335. 10.1016/j.proci.2018.05.029. [DOI] [Google Scholar]
- Khanniche S.; Green W. H. Reaction pathways, Thermodynamics and kinetics of cyclopentanone oxidation intermediates: A theoretical approach. J. Phys. Chem. A 2019, 123, 9644–9657. 10.1021/acs.jpca.9b05806. [DOI] [PubMed] [Google Scholar]
- Gonzalez C.; Schlegel H. B. An Improved Algorithm for Reaction Path Following. J. Phys. Chem. A 1989, 90, 2154–2161. 10.1063/1.456010. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.. et al. Gaussian 16; Gaussian, Inc.: Wallingford CT, USA, 2016.
- Glowacki D. R.; Liang C. H.; Morley C.; Pilling M. J.; Robertson S. H. MESMER: an open-source master equation solver for multi-energy well reactions. J. Phys. Chem. A 2012, 116, 9545–9560. 10.1021/jp3051033. [DOI] [PubMed] [Google Scholar]
- Holbrook K. A.; Pilling M. J.; Robertson S. H.. Unimolecular Reactions; Wiley, 1996. [Google Scholar]
- Wardlaw D. M.; Marcus R. A. RRKM reaction rate theory for transition states of any looseness. Chem. Phys. Lett. 1984, 110, 230–234. 10.1016/0009-2614(84)85219-7. [DOI] [Google Scholar]
- Klippenstein S. J.; Marcus R. A. Unimolecular Reaction Rate Theory for Highly Flexible Transition States. 2. Conventional Coordinate Formulas for the Various Possible Fragment Combinations. Miscellaneous Topics. J. Phys. Chem. B 1988, 92, 5412–5417. 10.1021/j100330a018. [DOI] [Google Scholar]
- Gilbert R. G.; Smith S. C.. Theory of Unimolecular and Recombination Reactions; Blackwell Scientific: Carlton, Australia, 1990. [Google Scholar]
- Holbrook K. A.; Pilling M. J.; Robertson S. H.. Unimolecular Reactions; Wiley: New York, 1996. [Google Scholar]
- Troe J. Theory of thermal unimolecular reactions at low pressures. I. Solutions of the master equation. J. Chem. Phys. 1977, 66, 4745. 10.1063/1.433837. [DOI] [Google Scholar]
- Eckart C. The Penetration of a Potential Barrier by Electrons. Phys. Rev. 1930, 35, 1303–1309. 10.1103/PhysRev.35.1303. [DOI] [Google Scholar]
- Stein S. E.; Rabinovitch B. S. Accurate evaluation of internal energy level sums and densities including anharmonic oscillators and hindered rotors. J. Chem. Phys. 1973, 58, 2438–2445. 10.1063/1.1679522. [DOI] [Google Scholar]
- Beyer T.; Swinehart D. F. Algorithm 448: number of multiply-restricted partitions. Commun. ACM 1973, 16, 379. 10.1145/362248.362275. [DOI] [Google Scholar]
- Tan T.; Yang X.; Ju Y.; Carter E. A. Ab Initio Reaction Kinetics of CH3OĊ(=O) and ĊH2OC(=O)H Radicals. J. Phys. Chem. B 2016, 120, 1590–1600. 10.1021/acs.jpcb.5b07959. [DOI] [PubMed] [Google Scholar]
- Hippler H.; Troe J.; Wendelken H. J. Collisional deactivation of vibrationally highly excited polyatomic molecules. II. Direct observations for excited toluene. J. Chem. Phys. 1983, 78, 6709–6717. 10.1063/1.444670. [DOI] [Google Scholar]
- Mourits F. M.; Rummens F. H. A. A critical evaluation of Lennard-Jones and stockmayer potential parameters and of some correlation methods. Can. J. Chem. 1977, 55, 3007. 10.1139/v77-418. [DOI] [Google Scholar]
- Ruscic B.; Pinzon R. E.; von Laszewski G.; Kodeboyina D.; Burcat A.; Leahy D.; Montoya D.; Wagner A. F. Active Thermochemical Tables: thermochemistry for the 21st century. J. Phys.: Conf. Ser. 2005, 16, 561–570. 10.1088/1742-6596/16/1/078. [DOI] [Google Scholar]
- Ruscic B.; Pinzon R. E.; Morton M. L.; Srinivasan N. K.; Su M. C.; Sutherland J. W.; Michael J. V. Active Thermochemical Tables: Accurate Enthalpy of Formation of Hydroperoxyl Radical, HO2. J. Phys. Chem. A 2006, 110, 6592–6601. 10.1021/jp056311j. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


