Abstract
Purpose:
To develop a deep neural network for respiratory motion compensation in free-breathing cine MRI and evaluate its performance.
Methods:
An adversarial autoencoder network was trained using un-paired training data from healthy volunteers and patients who underwent clinically indicated cardiac MRI examinations. A U-net structure was used for the encoder and decoder parts of the network and the code space was regularized by an adversarial objective. The autoencoder learns the identity map for the free-breathing motion-corrupted images and preserves the structural content of the images, while the discriminator, which interacts with the output of the encoder, forces the encoder to remove motion artifacts. The network was first evaluated based on data that were artificially corrupted with simulated rigid motion with regard to motion correction accuracy and presence of any artificially created structures. Subsequently, to demonstrate the feasibility of the proposed approach in vivo, our network was trained on respiratory motion-corrupted images in an unpaired manner and was tested on volunteer and patient data.
Results:
In the simulation study, mean structural similarity index (SSIM) for the synthesized motion-corrupted images, and motion-corrected images were 0.76, and 0.93 (out of 1), respectively. The proposed method increased the Tenengrad focus measure of the motion-corrupted images by 12% in the simulation study and by 7% in the in-vivo study. The average overall subjective image quality for the motion-corrupted images, motion-corrected images, and breath-hold images were 2.5, 3.5, and 4.1(out of 5.0), respectively. Non-parametric paired comparisons showed that there was a significant difference between the image quality scores of the motion-corrupted and breath-held images (P<0.05), however after correction there was no significant difference between the image quality scores of motion-corrected and breath-held images.
Conclusion:
This feasibility study demonstrates the potential of an adversarial autoencoder network for correcting respiratory motion-related image artifacts without requiring paired data.
Keywords: Magnetic Resonance Imaging, Cardiovascular Magnetic Resonance, Deep Learning, Respiratory Motion Correction, Adversarial Autoencoder
INTRODUCTION
In current clinical practice of thoracic and abdominal MRI, images are commonly acquired during a breath-hold to compensate for respiratory motion. Physiological limitations of breath-holding constrain the data acquisition window to approximately 15–20 seconds in relatively healthy patient populations. In clinical practice, many patients undergoing MRI have impaired breath-holding abilities, further limiting the acquisition window. As a result, 3D acquisitions are not routinely performed during a single breath-hold, despite previous efforts1–4. Many approaches have been proposed to enable free-breathing thoracic and abdominal MRI, including real-time single-shot cine imaging5–7 and the use of non-Cartesian sampling (e.g. radial), which tends to be less sensitive to respiratory motion8–10. However, the use of these approaches is not without compromise. For example, single-shot imaging approaches are generally of inferior image quality, signal-to-noise ratio or resolution when compared to their corresponding k-space segmented techniques. Non-Cartesian sampling, although relatively immune to motion, is prone to various other types of image artifacts, including streaking, off-resonance blurring and issues related to gradient delays. Alternative methods for respiratory motion compensation include respiratory bellows gating11–13, diaphragm navigators14, and MR self-gating15. These techniques, as a whole, result in prolonged scan time and reduced scanning efficiency, as a significant portion of the data is discarded. In addition to longer acquisition times, these techniques each suffer from their own respective drawbacks. Respiratory bellows rely on air pressure signal, which may not always have a well-defined correlation with the respiratory position of various anatomical structures. Diaphragmatic navigators and MR self-gating navigators have enabled high quality imaging of the coronary arteries16,17; however, their adoption in routine clinical imaging remains limited, in part because irregular and abrupt breathing pattern changes often reduce image quality and reliability. Multiple methods have been proposed for motion correction18–20, where motion is corrected in k-space using well-known relationships between affine motion and the corresponding k-space. However, these corrections are often inadequate because of significant non-rigid and deformable motion, which does not have well-defined k-space correction methods.
In this work, we sought to investigate the use of deep neural networks (DNNs) for respiratory motion compensation in MRI to alleviate some of the aforementioned problems. DNNs, particularly convolutional DNNs, have presented new possibilities for tackling a wide range of inverse problems including image inpainting, super resolution21–24, denoising and deblurring25–31 in an efficient manner. The main advantage of DNNs over classical data processing approaches is that it learns the effective features and priors in a data-driven fashion. To date, few studies have implemented DNNs for motion compensation31–35. Recent studies have shown that DNN can correct rigid-motion artifacts in brain imaging 32,33,36. They mainly trained convolutional neural networks with pixel-wise objective functions in a supervised manner. Haskell et al. combined a deep convolutional network with model-based motion estimation approach in an iterative manner to reduce the rigid motion artifacts from the 2D T2-weighted rapid acquisition with refocused echoes (RARE) brain images36. Their algorithm is of iterative nature, and in each iteration, the output of the convolutional neural network (CNN) was used to estimate the motion parameters and to correct the image k-space. They used time series registration information from fMRI scans to create the realistic motion trajectories. Then, they modified motion-free raw k-space brain data to synthesize realistic rigid-motion-corrupted images, and subsequently they estimated the motion parameters and forced the data consistency.
However, for DNN-based respiratory motion compensation in cardiac and abdominal imaging, supervised learning approaches are generally not feasible because the ground truth non-rigid motion data, which is needed for training the network, is either extremely challenging to obtain or simply not available. Kustner et al. reported a feasibility study to correct rigid and non-rigid motion artifacts by implementing a conditional generative adversarial network (GAN) (MedGAN), in which the generative network consists of eight cascaded U-nets31. The network was trained using a combination of adversarial, style transferring, and perceptual loss functions37. Among the loss functions used by Kustner et al.31, the perceptual loss function requires paired data, which is challenging to obtain, especially for non-rigid motion correction tasks. In addition, there are >108 trainable parameters in the network architecture used by Küstner et al31. Armanious et al. used a cycle consistency approach to extend the MedGAN in a way that can be trained in unsupervised manner38. They incorporated an attention module in their generator network to capture long-range dependencies. They mainly focused on reducing rigid simulated artifacts from brain datasets and achieved promising results.
The goal of this study was to develop and validate a DNN-based platform to remove respiratory motion artifacts in free-breathing imaging. We chose 2D cardiac cine imaging as an exemplary target application to validate our technique. In particular, based on the numerous challenges associated with obtaining the ground truth non-rigid motion data, we aimed to develop a network that can be trained in an unsupervised manner. In particular, our DNN is based on an adversarial autoencoder39–41 network structure to take advantage of its ability to be trained in a self-supervised manner without access to paired training data or the ground truth motion data. In our work, the encoder and decoder part of the adversarial autoencoder are both convolutional U-nets. The autoencoder’s code space is regularized with an adversarial loss network. The autoencoder preserves anatomical accuracy and consistency during the motion correction process while the adversarial network regularizes the encoder and drives the code space to be as close as possible to a motion artifact-free image. By leveraging the intrinsic competition between these two networks during the training process, we expect motion-corrected, artifact-free images to preserve their fidelity with regard to the overall anatomical structure and consistency.
METHODS
Theory
An autoencoder is a neural network that reconstructs an output that is almost identical to its input with the goal of learning useful representations of the input data42. Figure 1(a) shows a general architecture of an autoencoder. It consists of two parts, the encoder and the decoder. The encoder and decoder can be expressed as , : where, represents the code space and are the learnable parameters of the encoder and decoder networks, respectively. Equation 1 formulates the objective function of the autoencoder network as an L1-norm minimization problem:
| [1] |
where, is a batch of the data selected from dataset . In general, putting constraints on the autoencoder, such as limiting the dimension of code space or adding regularization to the code space prevents them from learning a trivial identity mapping. In our problem, the code space has the same dimension as the input data. Therefore, a proper approach is to add a special regularizer to the code space to produce the motion-corrected images. Equation 2 describes the objective function of the regularized autoencoder:
| [2] |
where is the tuning parameter for the regularizer. Such a regularizer needs to be capable of assessing the presence and extent of significant motion artifacts in the image and the regularizer needs to be differentiable. Although without access to paired data, an explicit form of the metrics to be used for such assessment may not exist, it can be learnt via the neural network. Such a neural network uses an adversarial loss to force the code space to be similar to the motion-free images. Figure 1(b) shows a graphical view of the proposed platform. As can be seen in the Figure 1(b), an adversarial objective is added to the conventional autoencoder structure to regularize the output of the encoder. The input of the encoder is the motion-corrupted image acquired during free breathing without any means of motion compensation. The output of the encoder is one of the inputs of the discriminator network during network training. In addition, the discriminator has access to motion artifact-free images Y that are not necessarily paired with the input X for the encoder. Through the training process, the discriminator drives the encoder to correct motion artifact in such a way that the discriminator network is not able to distinguish between unpaired high-quality images acquired during breath-holds that are free of motion artifacts and the motion-corrected images generated by the encoder. Equation 3 shows the adversarial regularizer of the network:
| [3] |
where and are the trainable parameters of the encoder and discriminator network. Equation 4 shows the full objective function of the entire proposed network with regularizer weight :
| [4] |
The first term in the Eq. 4 represents the reconstruction objective and it preserved the overall accuracy of the motion-corrected images with regard to anatomical structure and image content. The second term in Eq. 4 is the regularizer and its role is to force the encoder part to produce the images with similar appearance as motion-free images. The detailed network structure, including the layers and number of kernels, are shown in the Figure A1 (Online Supplemental Materials). In our cardiac cine imaging validation, the input for the encoder was motion-corrupted free-breathing cardiac cine data acquired with a conventional k-space segmented cardiac cine imaging sequence during free breathing. The high-quality imaging data were obtained using standard clinical breath-held cardiac cine data from patients who underwent clinically indicated cardiac MRI. Because the proposed platform does not require paired data for training and can be trained in a self-supervised fashion, the high-quality breath-held data could be obtained from a cohort of subjects separate from the motion-corrupted data.
Figure 1.
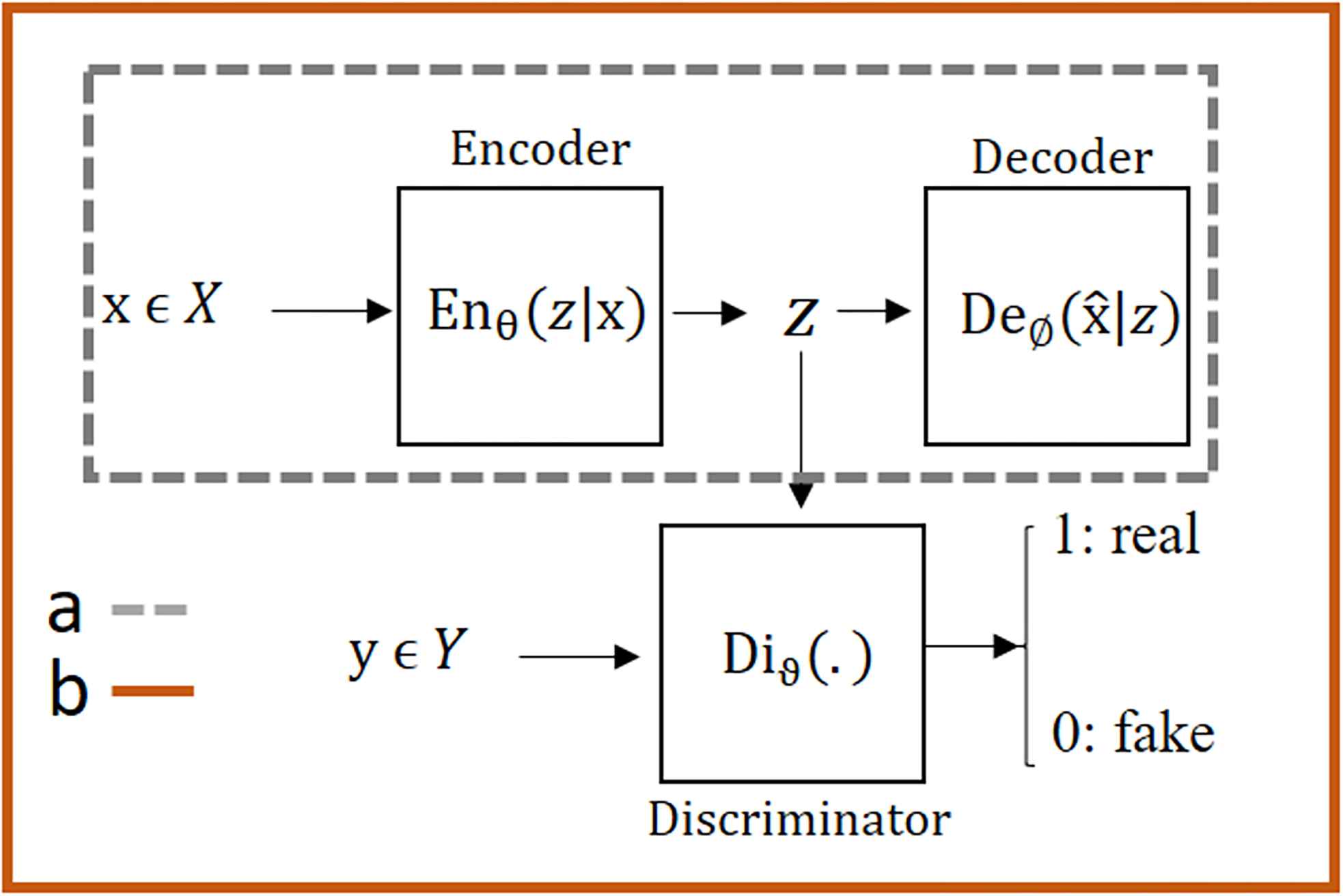
Various structures of the autoencoder: a) A simple autoencoder which encodes the high dimensional inputs into the code space data, which is usually of substantially reduced dimensions, by applying a series of convolutional layers. The decoder recovers the same input data from the code space data. b) An adversarial autoencoder (AAE) combines a simple autoencoder with an adversarial regularizer called discriminator to the code space. The discriminator is trained with the goal of accurately differentiating between data generated for the code space of the autoencoder and the data from the external data source Y. The adversarial autoencoder is trained with the goal of generating the code space data that resemble the external source data Y. The end result of the AAE network is that the code space data are driven to represent the external data source as much as possible during the adversarial (and competing) training processes between the encoder part of the autoencoder and the discriminator. In the context of our motion correction work using AAE, the encoder and decoder networks are each a convolutional U-net, the input x of the autoencoder is a free-breathing motion-corrupted image, the code space data is the corresponding motion-corrected image of the same dimensions, and the external data source Y is unpaired standard breath-hold motion-free reference images. The code space is driven by the discriminator network to be motion-corrected images such that they resemble the motion-free images from the external source Y. More details about the structure of our network are included in Figure A1.
Training Procedures:
In the training phase, the autoencoder and the discriminator network were trained with Stochastic Gradient Descent (SGD) in two phases – the accuracy phase and the correction phase. In the accuracy phase, the autoencoder updates its encoder U-net and the decoder U-net to minimize the reconstruction error of the input. In the correction phase, the discriminator and the encoder U-net were trained in an adversarial manner, where the discriminator first updates its structure to distinguish between the high-quality cardiac cine data and the samples from the output of the encoder; subsequently, the encoder U-net was updated to produce images that are as similar as possible to the high-quality cardiac cine data. Both networks, autoencoder and the discriminator, were trained in an end-to-end fashion and updated in the training phase sequentially mini-batch after mini-batch. Our training algorithm is summarized in Table 1.
Table 1.
Training algorithm: De(.), En(.), and Di(.) stands for the Decoder, Encoder, and Discriminator, respectively. First two lines belong to the accuracy phase of the training process and the remaining lines belong to the correction phase.
| Algorithm 1 Minibatch stochastic gradient descent training of adversarial autoencoder network. |
|
|
|
For number of training iterations do: • Sample minibatch of m motion corrupted examples from motion-corrupted set . • Update the Encoder and the Decoder by ascending its stochastic gradient: • Sample minibatch of m motion corrupted examples from motion-corrupted set . • Sample minibatch of m breath-hold examples from motion-free set . • Update the discriminator by ascending its stochastic gradient: • Sample minibatch of m motion corrupted examples from motion-corrupted set . • Update the Encoder by descending its stochastic gradient: |
Relatively large image patch size of 128×128 was used as the input to the autoencoder network. Previous studies show that generation of large size image in an adversarial manner is difficult compared to smaller size i.e. 64×64, because larger image patch size generally makes it easier for the discriminator to differentiate between the images provided by the generator and the high-quality data43,44. Most stable adversarial training methods were based on 64×64 patch size51. In order to stabilize the adversarial training process, a Markovian-patch-based approach was used to train the correction phase network46. During the training process, the output of the encoder for each epoch was divided into 4 patches of size 64×64 and the discriminator either accepts or rejects the decision based on the average probability calculated for the 4 patches.
To update the weights of the correction (encoder + discriminator) and accuracy network (autoencoder), the Adam optimizer was used with the momentum parameter β =0.9, mini-batch size= 64, and initial learning rate 0.0001 that is halved every 15,000 iterations. All the weights were initiated with random normal distributions with a variance of σ = 0.01 and mean μ=0. The first iteration was started by updating the accuracy network and for the second iteration, the decoder part was kept frozen with no updates while the correction network was updated. This process was continued and, in each epoch, we produced the test results to make decision for stopping criteria. The training was performed with the Tensorflow interface on a commercially available graphics processing unit (GPU) (NVIDIA Titan XP, 12GB RAM). We allowed 125 epochs that took approximately 11 hours for training.
Data Acquisitions
To evaluate the performance of the proposed neural network and demonstrate its utility, we tested our strategy for cardiac cine imaging. Our institutional review board approved the study, and each subject provided written informed consent. The datasets used to train and test our network consisted of three groups:
Free breathing 2D multi-slice, retrospective EKG-triggered, balanced steady state free precession (bSSFP) cardiac cine MR images in the short- and long-axis views from 20 healthy volunteers (Avanto Fit, Siemens Healthineers). The sequence parameters included TR(repetition time)/TE(echo time)=42.45/1.19 ms, FOV(field of view)=271 × 300 mm2, resolution= 1.74 × 1.92 mm2, 25 cardiac phases, slice thickness=6 mm, 3–10 slices, acquisition time=8–12s. As the data were acquired using standard clinical cardiac cine imaging sequences but during free breathing, they were contaminated by respiratory motion artifacts. For comparison purposes, the same sequence was repeated during breath-hold for each healthy volunteer. The free-breathing acquisition time was similar to breath-hold.
Standard clinical breath-held 2D multi-slice, retrospective electrocardiogram (ECG)-triggered, bSSFP cardiac cine MR images in the short-axis, horizontal long-axis, and vertical long-axis views from 162 patients. These images were acquired as part of clinically indicated cardiac MRI scans and were collected retrospectively. These images were acquired during breath-holds, had 10–14 slices (one slice per breath-hold of 8–12s), and were used as the high-quality imaging data for the adversarial network.
Standard ECG-triggered, bSSFP breath-held cardiac cine images in the short-axis and horizontal long-axis views were acquired from 10 additional patients as part of their clinically indicated cardiac MRI examination. In addition, in each of the 10 patients, we performed the same cardiac cine imaging sequence during free-breathing.
Before the network was trained and tested during our in-vivo study, we performed a simulation study based on data from Group 2 with simulated rigid motion. The goal of the simulation study was to confirm our technique’s motion correction accuracy by commonly used metrics such as peak signal to noise ratio (PSNR) and structural similarity index (SSIM), which would not be possible for the in vivo study due to lack of ground truth data. More details of the simulation study are in the Evaluations section.
For the in vivo network training and validation, we used 15 out of the 20 volunteers’ data from Group 1 and all of the breath-held cardiac cine imaging data from the 162 patients in Group 2. Our network training process was performed in an un-paired fashion. All the breath-held data from Groups 1&2 were shuffled randomly in each training batch before they were used as input data for the discriminator network. All the free-breathing data from Group 1 were randomly shuffled as well before they were used as input data for the autoencoder network. The anatomical orientation (short axis or long axis) was matched between the input data for the autoencoder and the input data for the discriminator network for each training batch. Our network testing was based on the remaining 5 volunteers’ data in Group 1 and all the data from Group 3.
To increase the flexibility of the network in correcting the motion artifact for arbitrary image sizes, our network was trained based on 128 × 128 patches extracted from the datasets. Each data set was reconstructed by applying adaptive coil combination to a single complex image and normalized to −1 to 1. Each single complex image was formatted as a real tensor with real and imaginary channels. In total, 125000 patches were used to train and validate the network and 25300 patches were used to test the network.
Evaluations
Evaluation of the network performance consisted of four main parts:
-
Motion Correction Accuracy:
One major concern is whether the reconstructed image is consistent with the breath-held reference. Due to the generative nature of the adversarial autoencoders, it is important to ensure motion accuracy with regard to structural and anatomical content. To evaluate the motion correction accuracy and confirm that the proposed platform is capable of correcting the motion-corrupted datasets in un-paired training process, a simulation study was conducted. 1D translational respiratory motion of the diaphragm with variable displacements ranging from 10 to 20 pixels was introduced to corrupt the k-space data from Group 2 using a well-known relationship between k-space and the image space as shown in Eq. 5, where the simulated translation vector is (x0, y0), M1 and M2 are the k-space data before and after motion corruption, respectively.[5] In our simulation, k-space of the Group 2 was divided into 16 segments. To find the diaphragm position for each segment, the respiratory signal was divided to 800-ms cardiac cycles and each cycle was divided into 20 cardiac segments. Inferior-superior diaphragm position was expressed as a function of time47 in Eq. 6
where are the position of diaphragm during end-exhalation and end inhalation, are the period and initial phase of the respiratory cycle, and n controls the shape of the simulated motion curve. For average diaphragm motion as described in47, , , and were selected. Our simulated motion assumed that each pixel had an isotropic size of 1mm2, and b varied from 10 to 20 pixels.[6] Figure 2(a) shows details of simulation process for an image with 256 phase-encoding k-space lines. The respiratory cycle was divided into 5 cardiac cycles, where each cycle was further divided into 20 cardiac phases. In Figure 2(a), only the first cardiac phase in each cardiac cycle is shown as a dashed-rectangle. To simulate the motion-corrupted image, each data were divided to 16 k-space segments and each segment was multiplied by the phase term corresponding to its motion on the simulated motion curve shown in Fig. 2(a) according to Eq. 5.
In our simulation study, all clinical breath-held cine data in Group 2 were used to synthesize the motion corrupted datasets. Out of the 162 synthesized motion-corrupted data sets, 20 were randomly chosen as testing data and were excluded from the training process. The remaining 142 data sets were used to train the network in an unpaired manner. Figure 2 (b) shows an example of the synthesized images and artifacts. These images with synthesized artifact also enabled us to partially prove that our network does not produce extra structures. Assessment of motion correction accuracy was performed by calculating Tenengrad focus measure, PSNR and SSIM for the simulated test data on the image level.
- Quantitative Sharpness: To quantify the sharpness of an image, the Tenengrad focus measure was used48,49. To calculate the Tenengrad focus measure, the image is convolved with a Sobel operator and the square of all the magnitudes greater than a threshold is reported as a focus measure. Equation 7 formulates the Tenengrad measure:
where shows the image and is the Sobel operator: . Because of difference in the size of the test cases in both simulation and in-vivo studies, the mean of the Tenengrad measure without threshold was calculated and normalized based on the breath-hold value.[7] Subjective Image Quality Scoring: The motion-corrupted test data from the 5 testing volunteer data sets in Group 1 and the 10 patient testing data sets in Group 3, their corresponding motion-corrected images after our network, and the corresponding breath-held reference cardiac cine images were randomized and presented to an experienced reader with >5 years of experience in reading clinical cardiac MRI who was blinded to the acquisition technique or patient information. The reader scored each of the images, which were presented as cine movies, with regard to image quality with an emphasis on motion artifacts according to the criteria in Table A1 (Online Supplementary Materials)50,51.
Cardiac Function Analysis: Motion-corrected images were further evaluated with regard to indices of cardiac function measurements, including left ventricular end-diastolic volume (EDV), end systolic volume (ESV), stroke volume (SV), and ejection fraction (LVEF). These indices were measured from automatic segmentations of epicardial and endocardial left ventricular borders using a commercial tool (Arterys Cardio DL, Arterys Inc, San Francisco, CA). The cardiac function analysis was based on 5 of the test cases, which had full stack of short-axis-view images covering from the apex to the base. The same cardiac function measurements were repeated for the clinical standard breath-hold cardiac cine images acquired on the same 5 subjects.
Figure 2.
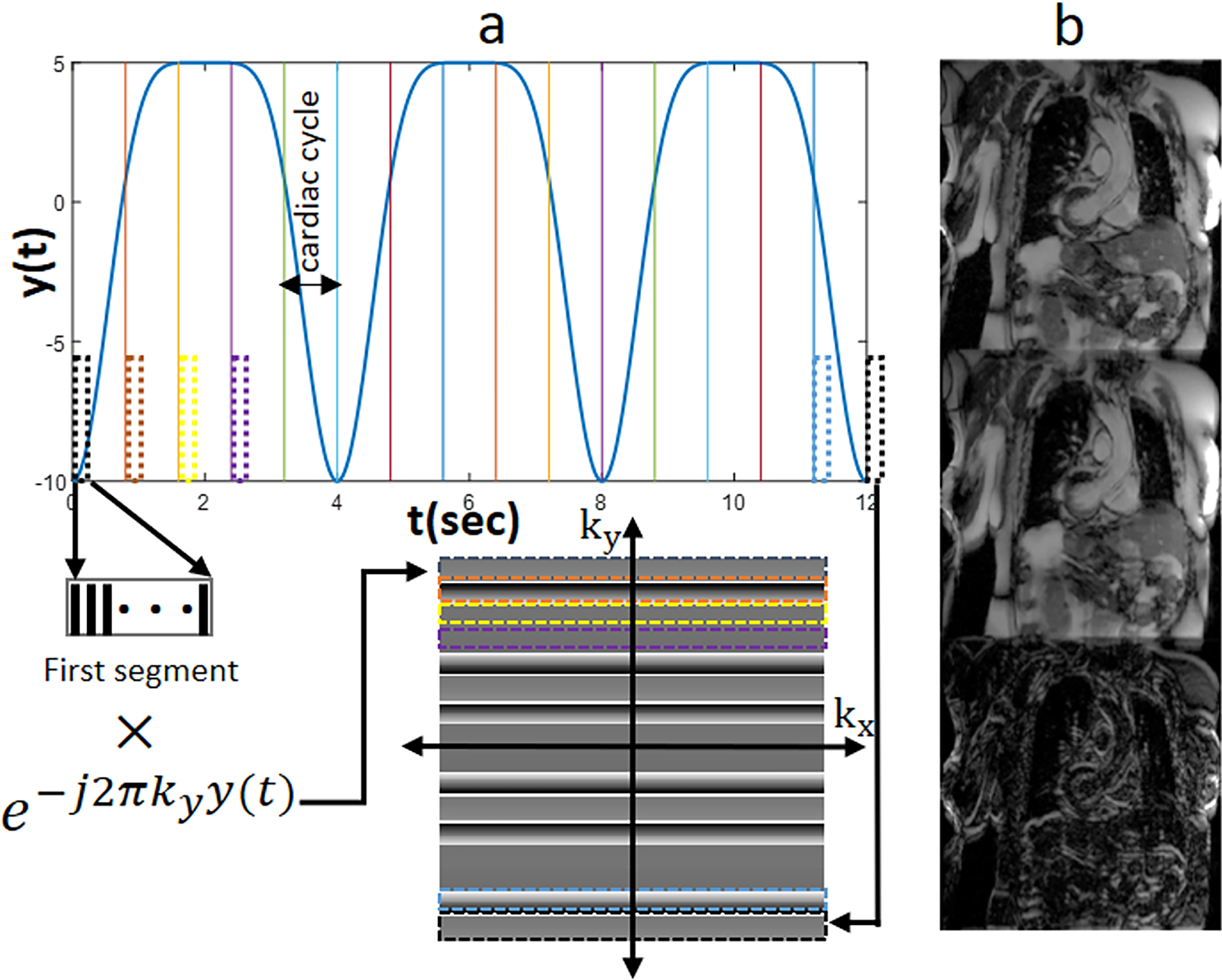
Motion simulation process of the Simulation Study. a) respiratory motion pattern and corruption process. Each k-space line is intentionally corrupted by adding a signal phase term that corresponds to the simulated motion distance for the line. b) (From top to bottom) Sample of the original motion-free image, the synthesized respiratory motion-corrupted image, and the error map between them.
Statistical Analysis
Statistical analysis was performed using R (version 3.5.3). Statistical tests were applied on the subjective image quality scores to answer two main questions: 1) was there any statistical difference between the motion-corrected, breath-held, and motion-corrupted images? 2) If yes, among the mentioned groups, which pairs had statistically significant difference? To answer these questions, Friedman’s two-way analysis52,53 and non-parametric paired comparison tests were applied. Significance level for all statistical test was assumed at α = 0.05.
RESULTS
Simulation Study
Figure 3 shows representative examples of artifact-free images, artificially motion-corrupted images, and motion-corrected images. Based on the absolute error map, the proposed network was able to sharpen the edge and remove the ghosting artifact without generating extra structures.
Figure 3.
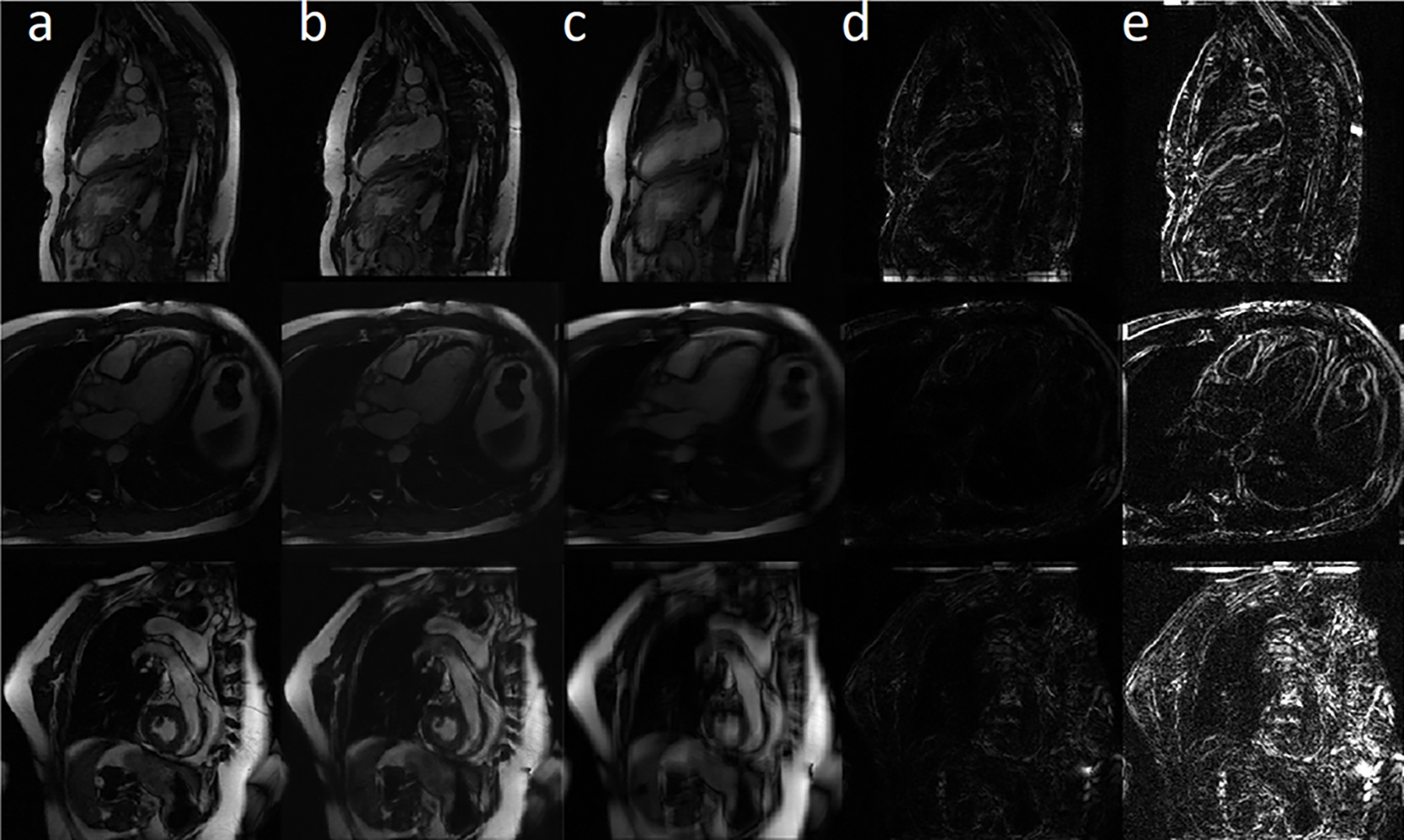
Motion accuracy simulation study results. Columns a, b, and c are the ground truth, motion-corrected, and synthetically motion-corrupted images. Absolute error map between ground truth and the motion-corrected/motion-corrupted images are shown in columns d and e, respectively. The first row shows an example for the vertical long-axis view, the second row presents a horizontal long-axis view, and the third row represents the short-axis view.
Figure 4 shows the frequency plot of SSIM and PSNR scores for the simulated test datasets. Mean value (green circles) and 95% confidence interval (black lines) were also added to the top of each chart. Based on the SSIM scores, the proposed network produced images that were structurally similar to the ground truth and increase the SSIM 22% in comparison to motion-corrupted images. Also, the PSNR results show that our motion correction network was able to reduce the residual errors and improve PSNR by 25% in comparison to motion-corrupted images. The normalized Tenengrad focus measure was 0.82±0.06 for the motion-corrupted images and 0.92±0.04 for the motion-corrected images, representing a 12% increase using the proposed technique.
Figure 4.
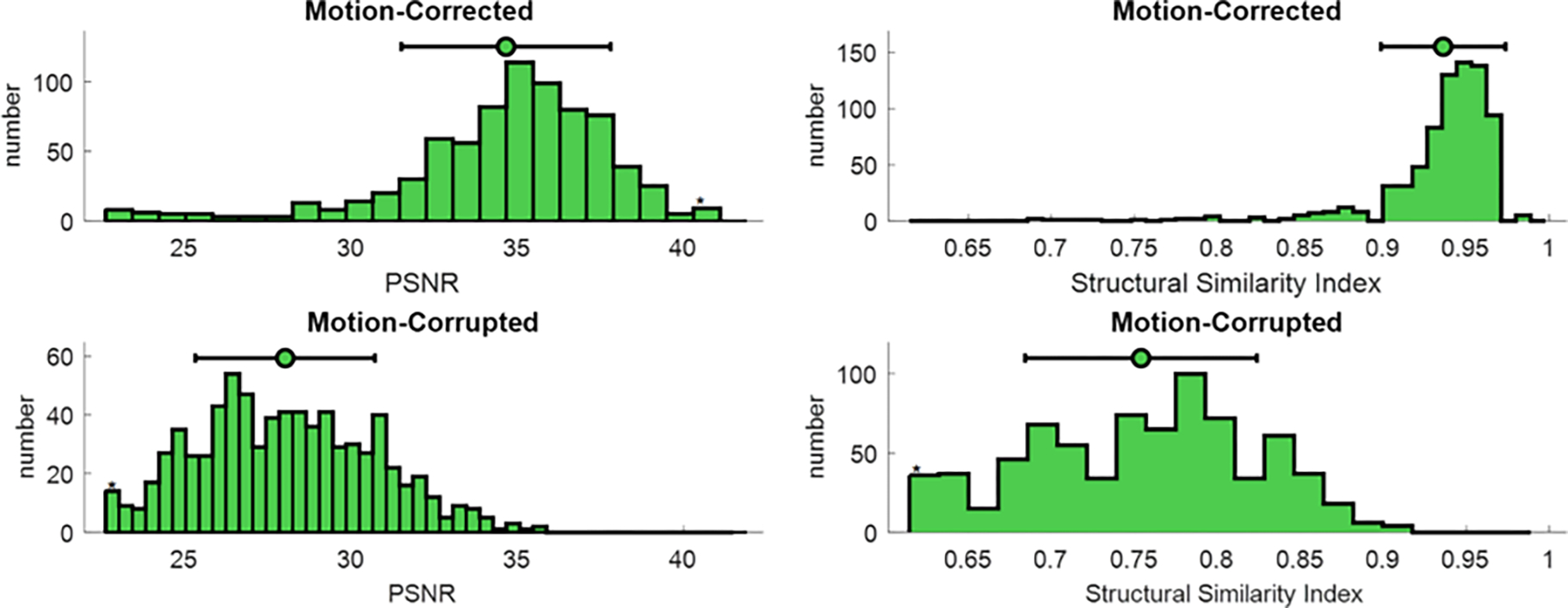
Quantitative simulation analysis. SSIM and PSNR, common metrics for image evaluation, were calculated for the simulated motion-corrupted data sets (bottom row) and motion-corrected images (top row). Both scores were reported by frequency plot and 95% of confidence interval. Mean values are shown with green circles; 95% of confidence intervals are depicted by black lines.
In Vivo Study
After validating the proposed method’s performance in correcting synthesized motion, the network was trained and tested based on in vivo motion-corrupted datasets. Throughout the training process, intermediate output in each epoch was exported to monitor the training process. Figure 5 shows improvement in quality of the output image through the training process. After 5 epochs, the outputs were blurry and had substantial artifacts, which would easily enable the discriminator network to classify unequivocally as fake images. However, as the training went on, the image quality of the encoder output was progressively improved. After 125 epochs, the quality of the images was sufficiently high for the discriminator to label them as real images.
Figure 5.
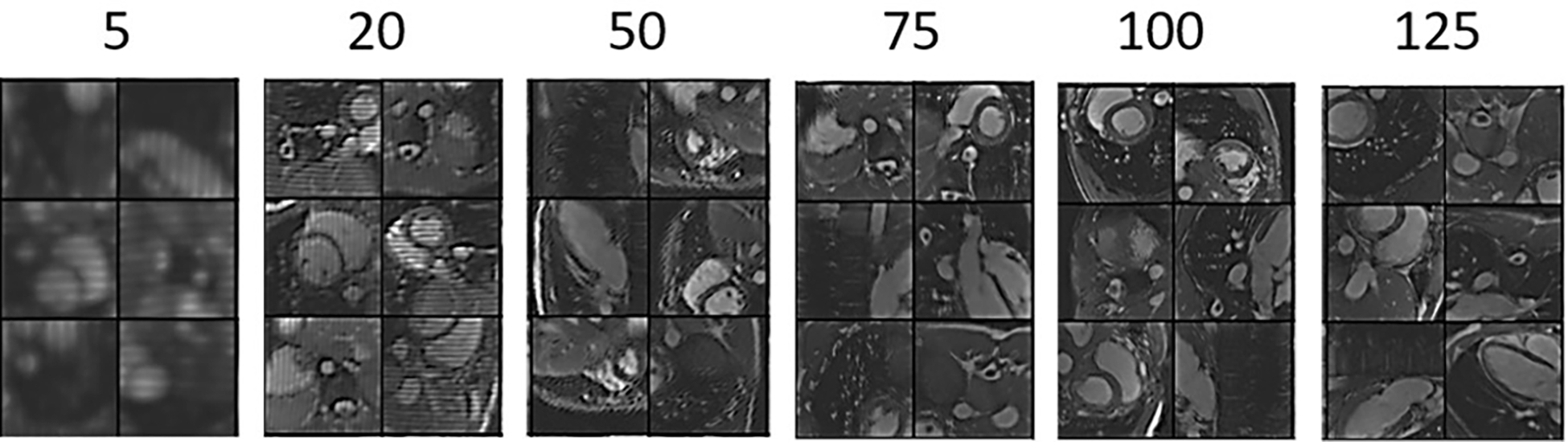
Image quality of the encoder output image with respect to the number of training epochs. As the training progresses, the image quality increases steadily.
Figure 6 shows representative images from two test volunteers’ data. The motion-corrected image (column b) reduced the motion artifact from the motion-corrupted image (column c) and provided visually sharper images at the interventricular septum and better visualization of the heart and adjacent structures. Residual minor blurring still exists for smaller structures, however.
Figure 6.
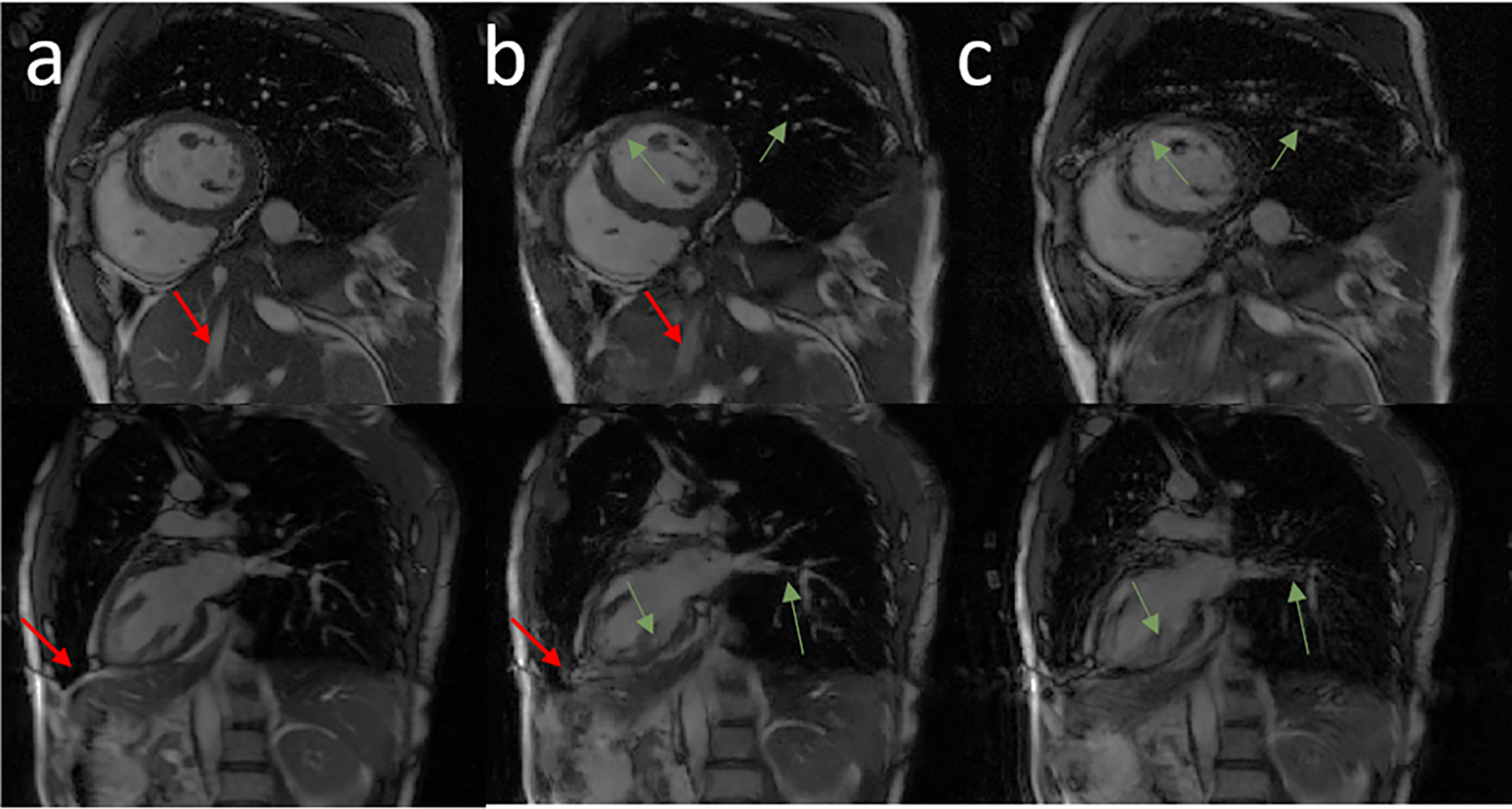
Representative images in the short-axis view, and vertical long-axis view from two volunteer subjects. Columns a, b, and c show the breath-held cine, motion-corrected free-breathing cine, and motion-corrupted free-breathing cine images, respectively. Green arrows highlight structures that were recovered completely by the network. Red arrows point to regions of residual blurring.
Figure 7 shows representative examples of breath-held cine (a), motion-corrected free-breathing cine (b), and motion-corrupted free-breathing (c) images from a patient who underwent a clinically indicated cardiac MRI exam. The network was able to eliminate the motion artifact seen at the left ventricular myocardium and the right ventricle. The motion-corrected images overall resemble the breath-held cine images. Supporting videos S2 (S2-1, S2-2, S2-3) provide 3 cardiac cine movie examples for motion-corrupted, motion-corrected and breath-held data. The normalized Tenengrad focus measure was 0.86±0.13 for the motion-corrupted images and 0.92±0.11 for the motion-corrected images, which represent a 7% increase using the proposed motion correction network.
Figure 7.
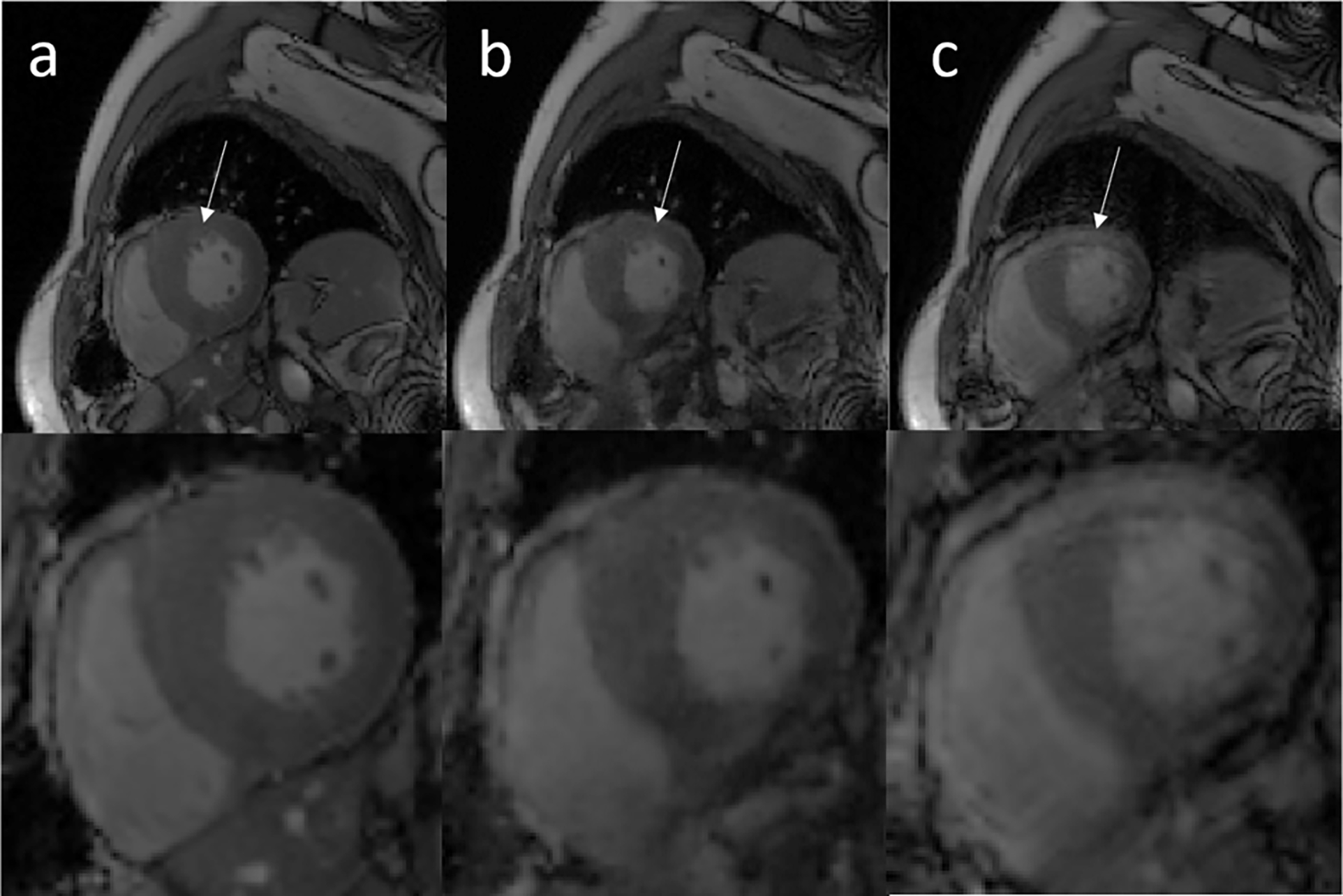
Representative cardiac cine images from a testing data acquired on a patient. Columns a, b, and c show standard clinical breath-held cine, the motion-corrected cine based on free-breathing data, and motion-corrupted cine data, respectively. White arrows show that the left ventricle region is significantly affected by motion artifacts and these artifacts were removed by the proposed network.
Figure 8 shows Bland-Altman plots of the left ventricular SV, ESV, EDV, and LVEF for the cardiac functional analysis. The cardiac function parameters calculated based on our motion-corrected images were in good agreement with standard breath-hold images.
Figure 8.
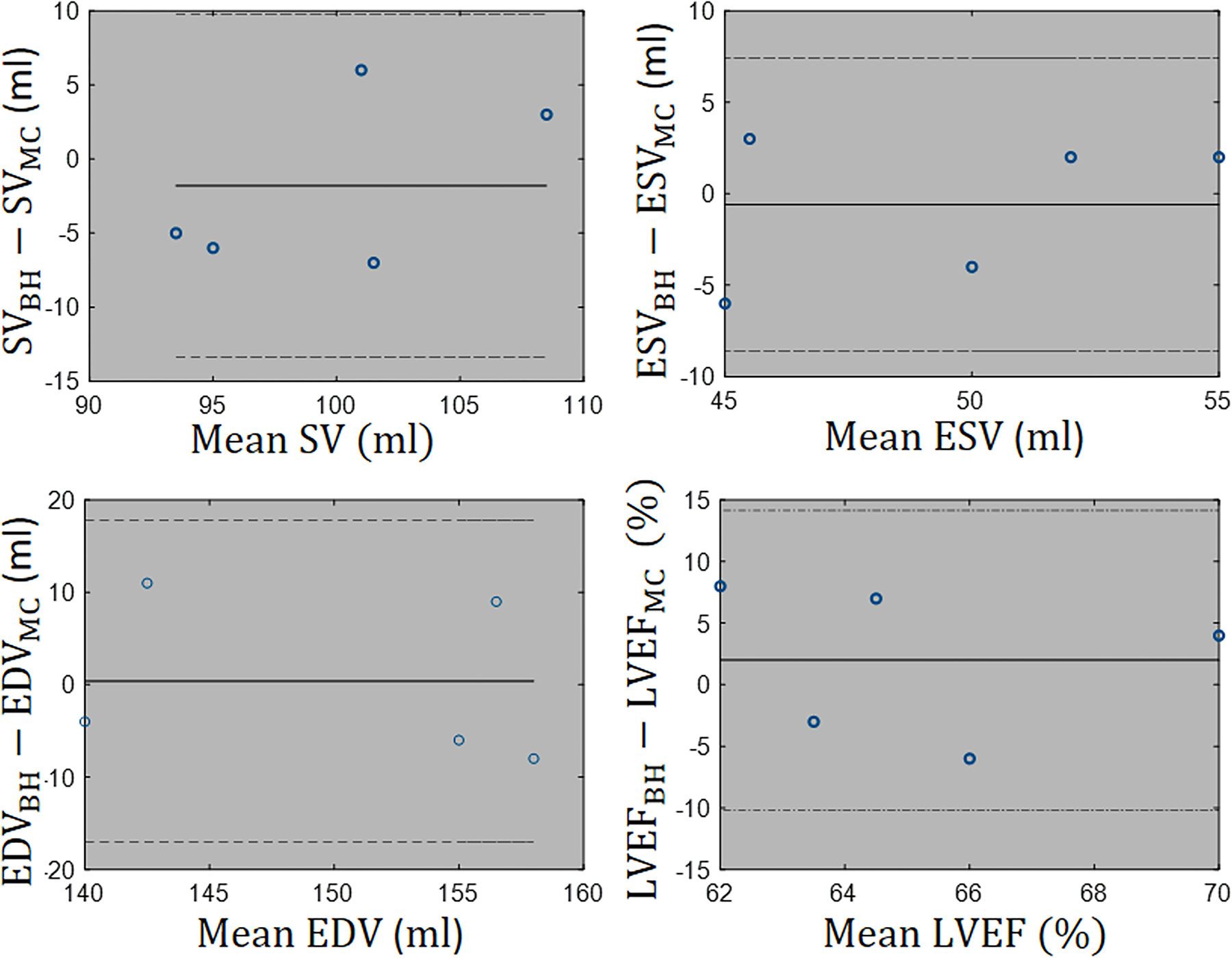
Functional analysis: Left ventricular endocardial borders are automatically segmented to compute stroke volume (SV), end-systolic volume (ESV), end-diastolic volume (EDV), and ejection fraction (LVEF) for 5 test cases. Bland-Altman plots confirm that there is agreement with 95% confidential level between functional metrics measured from breath-hold free of the motion images and motion-corrected images.
Figure 9(a) summarizes image quality scores. To identify any statistically significant difference in the overall image quality of breath-held cine, motion-corrected, and motion-corrupted groups, the null hypothesis assumed that the rank distribution of groups is the same. The null hypothesis was rejected significantly () by applying Friedman’s two-way analysis on the rank scores of different groups. Figure 9(b) reports paired comparisons between the mentioned groups. As can be seen, there was no statistically significant difference between the qualitative scores of motion-corrected and breath-held groups. Due to the statistically significant difference between the scores of motion-corrected and motion corrupted groups as highlighted by yellow edge, we conclude that the proposed method, increases the overall image quality of the motion-corrupted images.
Figure 9.
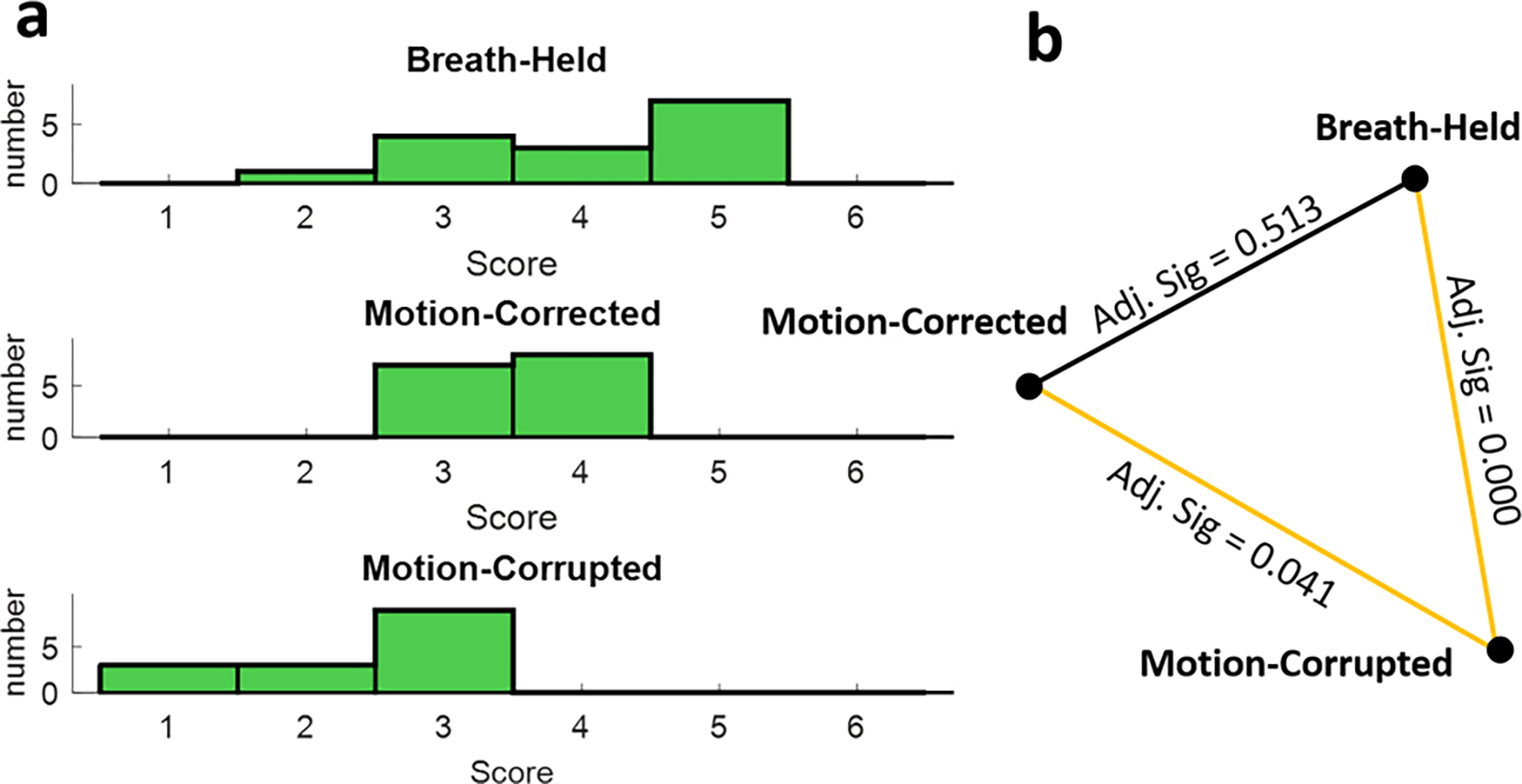
Blinded overall image quality reading and non-parametric paired comparison. (a) Frequency of overall image quality scores for each group. (b) Results from non-parametric paired comparisons. Statistically significant differences between pairs are highlighted by yellow lines.
DISCUSSION
We proposed a deep learning-based method to reduce respiratory motion artifacts and tested it for free-breathing cardiac cine imaging. The proposed method was evaluated in terms of SSIM, PSNR, image sharpness score and subjective image quality. We showed that our adversarial autoencoder technique can effectively reduce or eliminate blurring and ghosting artifacts associated with respiratory motion while enabling free-breathing scanning. Using an adversarial autoencoder neural network in the proposed scheme has several advantages over the conditional generative adversarial networks for motion correction. First, the network does not require paired data because network training can be performed in a self-supervised manner. Second, image data consistency and anatomical accuracy was enforced implicitly in training process using an autoencoder network to ensure the motion-corrected image retains the important anatomical and structural content of the image. It is worth noting that the data consistency and anatomical accuracy may be enforced explicitly if the process of non-rigid motion-corruption is well-defined mathematically or if we had access to strictly paired motion-corrupted/motion-free data.
In medical imaging applications, acquiring large amounts of paired data for motion correction tasks can be highly challenging and time consuming. Other approaches, such as conditional GANs, usually use L1 or perceptual loss functions for the generator network, which requires paired data to stabilize the training process. In our adversarial autoencoder, the autoencoder path preserves the overall structural content accuracy, which is mandatory for medical imaging applications; while the adversarial path forces the encoder network to correct the motion artifacts in the images.
Typical motion-induced effects in MRI include blurring, ghosting, regional signal loss, and appearance of other unphysical signals54. Based on the quantitative sharpness analysis, the proposed method was able to increase the sharpness score in the simulation study by 12% and in the in-vivo study by 7%. It seems that there is a drop in the improvement of the sharpness score from the simulation study to the in-vivo study. It may be explained by considering the difference between the simulation and the in-vivo study. Realistically, motion corruption for Cartesian cine images under free breathing tends to cause more ghosting effect than blurring. Therefore, baseline normalized Tenengrad focus measure is expected to be higher for the real motion affected images than the simulated motion affected images, which was predominantly blurred by the simulated motion.
Two important concerns for our type of technique are: 1) whether the pathologies were preserved in the proposed motion correction network; 2) whether our adversarial-based network introduced new spurious anatomical features in the images. Based on our expert radiologist’s evaluation of 3 test set images, we did not find any cases where any of these two scenarios occurred. However, we caution that larger scale evaluations in future studies are clearly warranted before a definitive conclusion can be made.
One of the innovations of this work with regard to the network architecture is that we used convolutional U-Nets for the Encoder and Decoder. In other commonly used autoencoders, the code space is often of smaller dimension/size compared to the input. However, for our application, the code space is the motion-corrected image and needs to have exactly the same size as the input images. Therefore, both the encoder and decoder parts of the autoencoder need to be networks that produce an output that is of the same size as the input. Convolutional U-Net has this desirable property. We note that there are many other potential network structures that also have this property (input size = output size), residual networks and dense networks being just two examples. However, several nice characteristics of U-Net made it a suitable choice: 1) It covers a large receptive field without increasing the depth of the network. 2) It is able to extract the features in multi-scale levels of the resolution. 3) The dense connections between the different levels of the U-Net make its training process very stable and effective.
Several further enhancements of the network may help improve its performance. First, we did not exploit all available information in MR data. Exploiting the multi-channel data as well as acquisition details could increase the capability of the network to correct respiratory motion artifacts. Several conventional motion correction methods identify k-space data that are corrupted by motion, often by leveraging redundant k-space signal afforded by multiple receiver coils55,56. The proposed technique operates more in the image space. The input data are motion-corrupted images that have already been reconstructed from motion-corrupted k-space. Therefore, our approach is fundamentally different from the aforementioned methods. As is with many other types of deep neural networks, our technique cannot be mathematically fully understood in analytical forms. We speculate that our network relies on learning and recognizing the underlying patterns of motion artifacts that are typically present in a free-breathing scan in order to improve the image quality and remove motion contamination. We expect our approach could be applied in tandem after conventional motion correction methods are finished to remove any residual motion artifacts. Second, we focused on correcting motion under normal free breathing condition. The performance of our technique in the presence of deeper than normal breathing remains to be evaluated. Using prior information about the characteristics of the motion may constrain the degrees of motion and correct the motion more effectively. For example, incorporating the respiratory bellows signal could afford us extra information about the motion-corrupted k-space lines. This extra information could enable us to incorporate the explicit data consistency term in the network, which could further improve the performance of our technique. Third, our platform is a 2D network, which performs correction in-plane. For through-plane motion, implementing a 3D adversarial autoencoder may be considered. Fourth, we did not take into account the differences in image FOV between the training data and the testing data when training the network. Therefore, motion correction capability of our network for arbitrary FOV should be investigated. Fifth, we did not compare our method with other free-breathing imaging methods, such as self-gated and real-time imaging. Such a comparison is clearly warranted in future studies.
Our study has limitations. It is possible that our technique might not fully remove any motion-related artifacts in our image. A larger study with more clinical validation is clearly needed. For future work, focusing on data augmentation may be very beneficial if we could realistically simulate in vivo motion patterns and their associated MR signal, which is currently challenging. In the absence of this, an alternate approach is to use unpaired high-quality data to train an adversarial autoencoder network.
Supplementary Material
Funding Support:
National Institutes of Health under award numbers R01HL127153
References
- 1.Kressler B, Spincemaille P, Nguyen TD, Cheng L, Xi Hai Z, Prince MR, Wang Y. Three-dimensional cine imaging using variable-density spiral trajectories and SSFP with application to coronary artery angiography. Magnetic resonance in medicine 2007;58(3):535–543. [DOI] [PubMed] [Google Scholar]
- 2.Wetzl J, Schmidt M, Pontana F, Longère B, Lugauer F, Maier A, Hornegger J, Forman C. Single-breath-hold 3-D CINE imaging of the left ventricle using Cartesian sampling. Magnetic Resonance Materials in Physics, Biology and Medicine 2018;31(1):19–31. [DOI] [PubMed] [Google Scholar]
- 3.Barkauskas KJ, Rajiah P, Ashwath R, Hamilton JI, Chen Y, Ma D, Wright KL, Gulani V, Griswold MA, Seiberlich N. Quantification of left ventricular functional parameter values using 3D spiral bSSFP and through-time non-Cartesian GRAPPA. Journal of Cardiovascular Magnetic Resonance 2014;16:65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Küstner T, Bustin A, Neji R, Botnar R, Priet C. 3D Cartesian Whole-heart CINE MRI Exploiting Patch-based Spatial and Temporal Redundancies. ESMRMB 2019. [Google Scholar]
- 5.Weiger M, Pruessmann KP, Boesiger P. Cardiac Real-Time Imaging Using SENSE. Magn Reson Med. 2000; 43: 177–184. [DOI] [PubMed] [Google Scholar]
- 6.Cui C, Yin G, Lu M, et al. Retrospective Electrocardiography-Gated Real-Time Cardiac Cine MRI at 3T: Comparison with Conventional Segmented Cine MRI. Korean J Radiol. 2019;20(1):114–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Uecker M, Zhang S, Voit D, Karaus A, Merboldt K and Frahm J. Real -time MRI at a resolution of 20 ms. NMR Biomed. 2010; 23: 986–994. [DOI] [PubMed] [Google Scholar]
- 8.Feng X, Salerno M, Kramer CM, Meyer CH. Non-Cartesian Balanced Steady-State Free Precession Pulse Sequences for Real-Time Cardiac MRI. Magn Reson Med. 2016;75:1546–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Stehning C, Bornert P, Nehrke K, Eggers H, Stuber M. Free-Breathing Whole-Heart Coronary MRA With 3D Radial SSFP and Self-Navigated Image Reconstruction. Magn Reson Med. 2005;54:476–480. [DOI] [PubMed] [Google Scholar]
- 10.Feng L, Axel L, Chandarana H, Block KT, Sodickson D.K, Otazo R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn Reson Med. 2016;75:775–788 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yuan Q, Axel L, Hernandez EH, et al. Cardiac-Respiratory Gating Method for Magnetic Resonance Imaging of the Heart. Magn Reson Med. 2000; 43:314–318. [DOI] [PubMed] [Google Scholar]
- 12.Wang Y, Christy PS, Korosec FR, et al. Coronary MRI with a Respiratory Feedback Monitor : The 2D Imaging Case. Magn Reson Med. 1995; 33:116–121. [DOI] [PubMed] [Google Scholar]
- 13.Santelli C, Nezafat R, Goddu B, et al. Respiratory Bellows Revisited for Motion Compensation : Preliminary Experience for Cardiovascular MR. Magn Reson Med. 2011; 65:1097–1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ehman RL, Felmlee JP. Adaptive Technique for High-Definition MR Imaging of Moving Structures. Radiology. 1989; 173(1): 255–263. [DOI] [PubMed] [Google Scholar]
- 15.Larson AC, Kellman P, Arai A, et al. Preliminary investigation of respiratory self -gating for free -breathing segmented cine MRI. Magn Reson Med. 2005; 53:159–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang Y, Riederer SJ, Ehman RL. Respiratory Motion of the Heart : Kinematics and the Implications for the Spatial Resolution in Coronary Imaging. Magn Reson Med. 1995; 33:713–719. [DOI] [PubMed] [Google Scholar]
- 17.Wang Y, Ehman RL. Retrospective Adaptive Motion Correction for Navigator-Gated 3D Coronary MR Angiography. Magn Reson Imaging. 2000; 11:208–214. [DOI] [PubMed] [Google Scholar]
- 18.Atkinson D, Hill DLG, Stoyle PNR, Summers PE, Keevil S. Automatic correction of motion artifacts in magnetic resonance images using an entropy focus criterion. IEEE Trans Med Imaging. 1997; 16(6): 903–910. [DOI] [PubMed] [Google Scholar]
- 19.Cheng JY, Alley MT, Cunningham CH, Vasanawala SS, Pauly JM, Lustig M. Nonrigid Motion Correction in 3D Using Autofocusing With Localized Linear Translations. Magn Reson Med. 2012; 68:1785–1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cruz G, Atkinson D, Buerger C, Schaeffter T, Prieto C. Accelerated Motion Corrected Three-Dimensional Abdominal MRI Using Total Variation Regularized SENSE Reconstruction. Magn Reson Med. 2016; 75:1484–1498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang Z, Liu D, Yang J, Han W, Huang T. Deep Networks for Image Super-Resolution with Sparse Prior. In: IEEE International Conference on Computer Vision (ICCV). Santiago, Chile: IEEE Computer Society; 2015:370–378. [Google Scholar]
- 22.Cui Z, Chang H, Shan S, Zhong B, Chen X. Deep Network Cascade for Image Super-resolution. In: Proceeding of Computer Vision -- ECCV. Zurich, Switzerland: Springer International Publishing; 2014:49–64. [Google Scholar]
- 23.Kim J, Lee JK, Lee KM. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA: IEEE Computer Society; 2016(1):1646–1654. [Google Scholar]
- 24.Dong C, Loy CC, He K, Tang X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans Pattern Anal Mach Intell. 2016; 38(2):295–307. [DOI] [PubMed] [Google Scholar]
- 25.Jain V, Seung S. Natural Image Denoising with Convolutional Networks. In: Proccedings of Advances in Neural Information Processing Systems (NIPS). Vancouver, B.C., Canada: Curran Associates, Inc; 2008: 769–776 [Google Scholar]
- 26.Xie J, Xu L, Chen E. Image Denoising and Inpainting with Deep Neural Networks. In: Proccedings of Advances in Neural Information Processing Systems (NIPS). Harrah’s Lake Tahoe, USA: Curran Associates, Inc; 2012: 341–349. [Google Scholar]
- 27.Zhang K, Zuo W, Chen Y, Meng D, Zhang L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans Image Process. 2017;26(7):3142–3155. [DOI] [PubMed] [Google Scholar]
- 28.Chen H, Zhang Y, Kalra MK, et al. Low-Dose CT With a Residual Encoder-Decoder Convolutional Neural Network. IEEE Trans Med Imaging. 2017;36(12):2524–2535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Xu L, Ren JS, Liu C, Jia J. Deep Convolutional Neural Network for Image Deconvolution. In: Proccedings of Advances in Neural Information Processing Systems (NIPS). Montreal, Canada: Curran Associates, Inc; 2014: 1790–1798. [Google Scholar]
- 30.Nishio M, Nagashima C, Hirabayashi S, et al. Convolutional auto-encoder for image denoising of ultra-low-dose CT. Heliyon. 2017;3(8):e00393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Küstner T, Schick F, et al. Retrospective correction of motion - affected MR images using deep learning frameworks. Magn Reson Med. 2019; 82: 1527–1540. [DOI] [PubMed] [Google Scholar]
- 32.Pawar K, Chen Z, Shah NJ, Egan GF. Motion Correction in MRI using Deep Convolutional Neural. arXive: arXive: 1807.10831, preprint, 2018. [Google Scholar]
- 33.Sommer K, Brosch T, Wiemker R, Harder T, Saalbach A, Hall C, Andre J. In: Proccedings of International Society of Magnetic Resonance in Medicine (ISMRM). Paris, France; 2018. [Google Scholar]
- 34.Duffy BA, Zhang W, Tang H, Zhao L, Law M, Toga AW, Kim. Retrospective correction of motion artifact affected structural MRI images using deep learning of simulated motion. In: Medical Imaging with Deep Learning (MIDL). Amesterdam, Netherlands; 2018. [Google Scholar]
- 35.Lv J, Yang M, Zhang J, Wang X. Respiratory motion correction for free-breathing 3D abdominal MRI using CNN-based image registration: a feasibility study. Br J Radiol. 2018;91(1083):20170788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Haskell MW, Cauley SF, Bilgic B, et al. Network Accelerated Motion Estimation and Reduction (NAMER): Convolutional neural network guided retrospective motion correction using a separable motion model. Magn Reson Med. 2019; 82: 1452–1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Johnson J, Alahi A, Li F-F. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. arXive: arXive: 1603.08155, preprint, 2016. [Google Scholar]
- 38.Armanious K, Tanwar A, Abdulatif S, Kustner T, Gatidis S, Yang B. Unsupervised Adversarial Correction of Rigid MR Motion Artifacts. arXive: arXive: 1910.05597, preprint, 2019. [Google Scholar]
- 39.Makhzani A Implicit Autoencoders. arXive: arXive: 1805.09804, preprint, 2019. [Google Scholar]
- 40.Makhzani A, Frey B, Goodfellow I. Adversarial Autoencoders. arXive: arXive:1511.05644, preprint, 2016. [Google Scholar]
- 41.Zhu J-Y, Park T, Isola P, Efros AA. Unpaired image-to-image translation using cycle-consistent adversarial networks. arXive: arXive: 1703.10593, preprint, 2016. [Google Scholar]
- 42.Goodfellow I, Bengio Y, Courville A, Bengio Y. Autoencoders. Deep Learning. Vol 1. MIT press Cambridge; 2016:493–515. [Google Scholar]
- 43.Odena A, Olah C, Shlens J. Conditional Image Synthesis with Auxiliary Classifier GANs. arXive: arXive: 1610.09585, preprint, 2017. [Google Scholar]
- 44.Karras T, Aila T, Laine S, Lehtinen J. Progressive Growing of GANs for Improved Quality, Stability, and Variation. arXive: arXive: 1710.10196, preprint, 2018. [Google Scholar]
- 45.Radford A, Metz L, Chintala S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. arXive: arXive: 1511.06434, preprint, 2016. [Google Scholar]
- 46.Li C, Wand M. Precomputed Real-Time Texture Synthesis with Markovian Generative Adversarial Networks. arXive: arXive: 1604.04382, preprint, 2016. [Google Scholar]
- 47.Xanthis CG, Venetis IE, Aletras AH High performance MRI simulations of motion on multi-GPU systems. J Cardiovasc Magn Reson 16, 48 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Focusing Krotkov E. Int J Comput Vision 1, 223–237 (1988). [Google Scholar]
- 49.Mir Hashim, Xu Peter, Peter van Beek, “An extensive empirical evaluation of focus measures for digital photography,” Proc. SPIE 9023, Digital Photography X, 90230I (7 March 2014). [Google Scholar]
- 50.Nguyen KL, Khan SN, Moriarty JM, et al. High-field MR imaging in pediatric congenital heart disease: initial results. Pediatr Radiol. 2015; 45(1):42–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Gwet KL. Computing inter-rater reliability and its variance in the presence of high agreement. British Journal of Mathematical and Statistical Psychology. 2008; 61(1) 29–48. [DOI] [PubMed] [Google Scholar]
- 52.Forthover RN, Lee SL, Hernandez M. Biostatistics: A Guide to Design, Analysis, and Discovery. 2nd ed. San Diego: Academic Press, 2007: 249–68. [Google Scholar]
- 53.Ghodrati V, Shao J, Bydder M, Zhou Z, Yin W, Nguyen K.L, Yang Y, Hu P. MR image reconstruction using deep learning: evaluation of network structure and loss functions. Quant Imaging Med Surg. 2019;9(9):1516–1527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zaitsev M, Maclaren J, Herbst M. Motion artifacts in MRI: A complex problem with many partial solutions. J Magn Reson Imaging. 2015;42(4):887–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bydder M, Larkman D and Hajnal J (2002), Detection and elimination of motion artifacts by regeneration of k -space. Magn. Reson. Med, 47: 677–686. [DOI] [PubMed] [Google Scholar]
- 56.Samsonov AA, Velikina J, Jung Y, Kholmovski EG, Johnson CR, Block WF. POCS-enhanced correction of motion artifacts in parallel MRI. Magn Reson Med. 2010;63(4):1104–1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Yang G et al. , “DAGAN: Deep De-Aliasing Generative Adversarial Networks for Fast Compressed Sensing MRI Reconstruction,” in IEEE Transactions on Medical Imaging, vol. 37, no. 6, pp. 1310–1321, June 2018. [DOI] [PubMed] [Google Scholar]
- 58.Mardani M et al. , “Deep Generative Adversarial Neural Networks for Compressive Sensing MRI,” in IEEE Transactions on Medical Imaging, vol. 38, no. 1, pp. 167–179, Jan. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


