Carbon isotope fractionation by an ancestral rubisco suggests that biological proxies for CO₂ through geologic time should be reevaluated

Significance

Earth scientists rely on chemical fossils like the carbon isotope record to derive ancient atmospheric CO₂concentrations, but interpretation of this record is calibrated using modern organisms. We tested this assumption by measuring the carbon isotope fractionation of a reconstructed ancestral rubisco enzyme (>1 billion years old) in vivo and in vitro. Our results contradicted prevailing models of carbon flow in Cyanobacteria, but our data could be rationalized if light-driven uptake of CO₂is considered. Our study suggests that the carbon isotope record tracks both the evolution of photosynthetic physiology as well as changes in atmospheric CO₂, highlighting the importance of considering both evolution and physiology for comparative biological approaches to understanding Earth’s history.

Abstract

The history of Earth’s carbon cycle reflects trends in atmospheric composition convolved with the evolution of photosynthesis. Fortunately, key parts of the carbon cycle have been recorded in the carbon isotope ratios of sedimentary rocks. The dominant model used to interpret this record as a proxy for ancient atmospheric CO₂ is based on carbon isotope fractionations of modern photoautotrophs, and longstanding questions remain about how their evolution might have impacted the record. Therefore, we measured both biomass (ε_p) and enzymatic (ε_Rubisco) carbon isotope fractionations of a cyanobacterial strain (Synechococcus elongatus PCC 7942) solely expressing a putative ancestral Form 1B rubisco dating to ≫1 Ga. This strain, nicknamed ANC, grows in ambient pCO₂ and displays larger ε_p values than WT, despite having a much smaller ε_Rubisco (17.23 ± 0.61‰ vs. 25.18 ± 0.31‰, respectively). Surprisingly, ANC ε_p exceeded ANC ε_Rubisco in all conditions tested, contradicting prevailing models of cyanobacterial carbon isotope fractionation. Such models can be rectified by introducing additional isotopic fractionation associated with powered inorganic carbon uptake mechanisms present in Cyanobacteria, but this amendment hinders the ability to accurately estimate historical pCO₂ from geological data. Understanding the evolution of rubisco and the CO₂ concentrating mechanism is therefore critical for interpreting the carbon isotope record, and fluctuations in the record may reflect the evolving efficiency of carbon fixing metabolisms in addition to changes in atmospheric CO₂.

Photoautotrophs have evolved over geologic time to harness energy from the sun in order to “fix” external, inorganic carbon (C_i) into reduced, organic carbon (C_o), thereby creating biomass for growth and energy storage. Today, and likely for much of Earth’s history (1), the most widespread strategy for carbon fixation is the Calvin–Benson–Bassham (CBB) cycle, where the key carbon fixation step is catalyzed by ribulose-1,5-bisphosphate (RuBP) carboxylase/oxygenase (rubisco) (2, 3). But rubisco’s central role in the CBB cycle and oxygenic photosynthesis poses a conundrum because it is usually considered to be a nonspecific and slow enzyme. The first issue concerns rubisco’s dual carboxylase and oxygenase activities: The RuBP intermediate (enediolate) is susceptible to both O₂ and CO₂ attacks (4). Consequently, instead of fixing a CO₂ molecule during photosynthesis, rubisco can instead assimilate O₂ to yield 2-phosphoglycolate (2-PG), which is not part of the CBB cycle and therefore must be salvaged through photorespiratory pathways that consume adenosine triphosphate (ATP), reducing power, and carbon (5). The second issue concerns rubisco’s maximum carboxylation rate (V_C), which is ≈7 to 10 times slower than other central metabolic enzymes (6), and displays very limited variation across large phylogenetic distances (7).

Both issues—its dual carboxylase/oxygenase activity and limited maximum carboxylation rate—are typically rationalized by considering its evolutionary history in the context of long-term changes in environmental CO₂ and O₂ concentrations. Rubisco is thought to have been the primary carboxylating enzyme of global photosynthesis since the Great Oxygenation Event and potentially far prior (1). It is also thought to have evolved when there was trace O₂ and much higher CO₂ concentrations in the atmosphere, in contrast to the modern atmosphere where O₂ is roughly 20% while CO₂ is only about 0.04% by partial pressure (1).

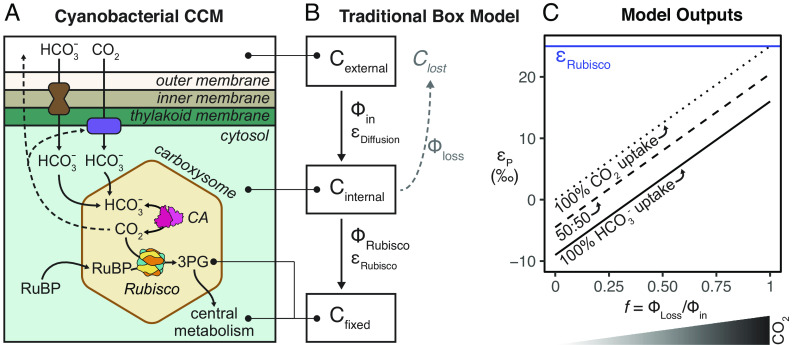
Likely in response to these changing environmental concentrations, many aquatic photoautotrophs evolved CO₂ concentrating mechanisms (CCMs) that enhance carboxylation and suppress oxygenation by immersing rubisco in a high-CO₂ environment. Even with CCMs, the effective in vivo rates of extant rubiscos are estimated to be lower (≈1% for terrestrial and ≈15% for marine rubiscos) than the maximal catalytic rates measured at 25 °C (2). Today, all known Cyanobacteria have CCMs, as do many bacterial chemolithoautotrophs, many aquatic algae and some plants (8). The bacterial CCM has two main components: i) C_i pumps producing high cytosolic HCO₃⁻ concentrations, and ii) coencapsulation of carbonic anhydrase (CA) and rubisco inside proteinaceous organelles known as carboxysomes (Fig. 1A) (9–11). These C_i pumps include BCT1 (ATP-dependent powered HCO₃⁻ transporter), SbtA (Na⁺/HCO₃⁻ symporters), BicA (Na-dependent HCO₃⁻ transporter), NDH-1MS, and NDH-1MS’ (NADPH-dependent powered CO₂ uptake; see ref. 12 for review). It is unclear exactly when the bacterial CCM arose, with proposals ranging from the Proterozoic to the Phanerozoic Eon (8, 13). Therefore, for up to half of Earth’s history, cyanobacterial rubiscos have functioned in concert with a system that pumps C_i into and around the cell.

Fig. 1.

Comparing the cyanobacterial CO₂ concentrating mechanism (CCM) to the traditional box model of photosynthetic C isotope discrimination. (A) Cyanobacterial CCMs rely on i) active C_i uptake into the cell, and ii) coencapsulation of carbonic anhydrase (CA) and rubisco within the carboxysome. Independent, powered transporters for HCO₃⁻ and CO₂ are shown in brown and purple; both work to increase cytosolic concentrations of HCO₃⁻ (see ref. 12 for review). All CCM components work to produce a high carboxysomal CO₂ concentration that enhances CO₂ fixation by rubisco and suppresses oxygenation. Limited CO₂ escapes from the carboxysome—some is scavenged by CO₂ pumps while the rest leaves the cell. (B) Architecture of the traditional box model based on (14–17); see SI Appendix for full discussion of this model. Boxes denote carbon pools of interest, and fluxes between boxes are denoted by Φ. Each flux has its own isotopic fractionation denoted by ε; no fractionation is assumed for Φ_loss. Model assumes an infinitely large external carbon pool, that carbon not fixed by rubisco (C_lost) returns to this pool, and that fluxes are at steady state. Note that this architecture does not include a box for the carboxysome. (C) Model solution for the traditional model is ε_P = a*ε_equil + f*ε_Rubisco (Eq. 2), where ε_P is defined as the difference in δ¹³C of C_external and C_fixed, f is defined as the fraction of C_i lost (Φ_loss/Φ_in), and a is the fractional contribution of HCO₃⁻ to total C_i uptake. When a = 0, all C_i uptake is as CO₂ (dotted line); when a = 1, all C_i uptake is as HCO₃⁻ (solid line). This model is presented in ref. 18, which is a generalization of (19) that accounts for the fact that C_i uptake (Φ_in in Panel B) ranges in composition between CO₂ and HCO₃⁻ based on which C_i uptake system is used. Values of ε_Rubisco = 25‰ and ε_equil = −9‰ were used for this illustration (20). Model outputs indicate that at high external CO₂ concentrations (dark wedge under graph), there is greater net C_i leakage (larger f values) from the cell.

Rubisco displays a kinetic isotope effect (KIE) where it preferentially fixes ¹²CO₂ over ¹³CO₂ due in part to the V_C being slightly faster for ¹²CO₂ than ¹³CO₂ (21), leading the reaction product, 3-phosphoglycerate (3-PG), to be relatively depleted in ¹³C by several percent (tens of ‰) relative to the isotopic composition of the CO₂ substrate. This effect is typically reported in delta (δ¹³C) and epsilon (ε) notation in units of per mille (‰), where δ¹³C = [¹³R_sa/¹³R_ref - 1]*1000 and ¹³R is the ratio of ¹³C/¹²C in the sample or reference, respectively; see Materials and Methods. The difference in δ¹³C of the CO₂ substrate and the 3-PG product is reported as ε_Rubisco and varies between 18 and 30‰ for extant rubiscos (22, 23), with the exception of the coccolithophore E. huxleyi with ε_Rubisco ≈ 11‰ (24). Because autotrophs utilizing the CBB cycle synthesize biomass from 3-PG, biomass is ¹³C-depleted compared to external C_i pools—the magnitude of this difference is called ε_p.

The KIE of rubisco, along with other and more minor processes that affect carbon isotope ratios, is recorded in the carbon isotope record, which is comprised of measurements of the relative ratios of ¹³C to ¹²C isotopes in C-bearing phases of sedimentary rocks over time (25). Carbon isotope data have been assembled globally from myriad of ancient environments to cover ≈3.8 billion years (Ga) of Earth’s 4.5 Ga history (26). Contemporaneous C_i pools are preserved as carbonate salts (e.g., limestones and dolomites), while contemporaneous biomass and C_o pools are preserved in the organic-rich components (e.g., kerogen) of many different lithologies and are measured as rock total organic carbon (TOC) (25). There are additional fractionations associated with the preservation of biomass and C_i as rocks, so the magnitude of fractionation between rock C_i and C_o is termed ε_TOC and differs slightly from ε_p (27). Therefore, if one can derive ε_p from the rock record (ε_TOC) and pair it with a model relating ε_p to pCO₂, in principle one can infer the history of atmospheric pCO₂ from the carbon isotope record.

The carbon isotope record is particularly important for constraining ancient atmospheric pCO₂ (28, 29) because direct observations of the past atmosphere from trapped gas in ice cores only extends back ≈1 million years (30). One notable feature of the record from ≈3.8 Ga to the present is that rock C_o is depleted in ¹³C by ≈25‰ compared to C_i (23, 25, 26), and this offset roughly matches the KIE of extant rubiscos (25). The dominant model used to derive ancient atmospheric CO₂ from the geological record (referred to as the “C Isotope Record Model” here; SI Appendix, Fig. S7 and Eq. 1) reflects this observation by fixing the maximum possible fractionation of biomass to be that of rubisco:

$${\epsilon }_p={\epsilon }_f-\frac{b}{\left[C{O}_2\left(aq\right)\right]},$$ [1]

where ε_f is the maximum isotopic fractionation for carbon fixation and is typically set to equal ε_Rubisco, [CO₂(aq)] is the concentration of dissolved CO₂ in solution around the cells, and b is a fitted parameter derived from experiments (31). This physiological factor, b (‰ kg μM⁻¹), is fit from pure culture experiments of eukaryotic and bacterial algae, and encompasses all physiological effects that may affect cellular isotopic fractionation including the CCM, growth rate, cell size and geometry, membrane permeability, growth medium composition (e.g., pH, salinity, limiting nutrient), strain genetics, and physiological state (31–35). In the limit of high [CO₂(aq)], the term b/[CO₂(aq)] goes to zero and ε_P = ε_f, which is assumed to equal ε_Rubisco. Therefore, with this model framework the maximum value of ε_P is ε_Rubisco, and the term b sets how quickly ε_P approaches the limit of ε_Rubisco.

The term b and the assumption that ε_Rubisco sets the upper limit of ε_P directly follows from the “traditional model” (Fig. 1 B and C and Eq. 2) that was developed by measuring ε_P of plants and algae while parameters like pCO₂ were varied:

$${\epsilon }_p=f\ast {\epsilon }_{\mathit{Rubisco}}+a\ast {\epsilon }_{\mathit{equil}},$$ [2]

where f is a ratio describing how much C_i exits vs. enters the organism (f = 1 is all C_i that enters is lost), ε_equil is the equilibrium isotope effect, and a is the fraction of C_i entering the cell as CO₂ (a = 0) or HCO₃⁻ (a = 1) (18, 19). The diffusion isotope effect (ε_Diffusion) is considered negligible. This model (Fig. 1 B and C and Eq. 2) is therefore the physiological underpinning Eq. 1 and subsequent interpretations of the C isotope record; both show a limit where the maximum ε_P is ε_Rubisco.

This traditional model was originally developed from studies of C isotope fractionation in plants (dotted line in Fig. 1C; all C_i uptake is as CO₂ for plants) and was later adapted to eukaryotic and bacterial algae. The primary architecture of the traditional model stems from a seminal study by Park and Epstein (16) who proposed a “two step model” to explain ε_P of tomato plants grown in varied CO₂ concentrations and light levels. In this model, carbon can be viewed as residing in one of three pools or “boxes” (Fig. 1B)—C_i outside the cell (C_ext), C_i inside the cell (C_internal), or C_o as biomass (C_fixed). A “leakiness” term, f, is defined as the ratio of fluxes (Φ) of C_i exiting or entering the plant, where all of the C_i that entered the cell is lost when f = 1. In this simplified model, ε_p is determined by the isotopic effect of two distinct steps: i) the diffusion of CO₂ into the plant [ε_Diffusion; <1‰ across a diaphragm cell in water at 25 °C (36)]; and ii) the carbon fixation step catalyzed by rubisco (ε_Rubisco; ≈18 to 30‰). Notably, Park and Epstein proposed that the isotopic fractionations of these two steps are not additive in vivo (i.e., ε_p ≠ ε_Diffusion + ε_Rubisco) but instead reflects the process by which photosynthesis is limited, either entry of CO₂ into the cell (ε_p = ε_Diffusion) or CO₂ fixation by rubisco (ε_p = ε_Rubisco) (16).

Solving the traditional model at steady state results in a linear relationship between ε_p and f where the minimum and maximum ε_p values are ε_Diffusion and ε_Rubisco, respectively (Fig. 1C). This allows experimentally measured values of ε_p to be used to solve for CO₂ leakage (f, Fig. 1C). When ε_p ≈ ε_Diffusion, nearly all carbon entering the cell is used (f ≈ 0) and rubisco’s ¹²C preference is not “expressed”; conversely, when ε_p ≈ ε_Rubisco, very little of the carbon entering the cell is fixed (f ≈ 1, nearly all carbon leaks from the cell) and rubisco can “choose” between ¹²C and ¹³C substrates so that rubisco’s KIE is fully expressed. Farquhar et al. (17) later derived a relationship between ε_p and the ratio of external vs. intracellular CO₂ partial pressures, allowing CO₂ concentrations at the site of rubisco to be roughly estimated from ε_p. Therefore, given the assumption that C_i is taken up passively, it is possible to derive an increasing relationship between C_ext and ε_P from this model, where large ε_P indicates that high external CO₂ concentrations generate excess CO₂ at rubisco and ultimately cause more CO₂ to leak out of the cell than can be fixed [see SI Appendix and (15)].

This model was later adapted to algae to account for CCMs—mainly active uptake of C_i as HCO₃⁻ and/or CO₂—and physiological parameters including growth rate and cell geometry (19, 32, 33, 37, 38). These studies grew eukaryotic and bacterial algae in a range of pCO₂ and culturing conditions to test if the linear relationship between ε_p and pCO₂ observed in plants still held. Interestingly, cyanobacterial ε_p was found to be roughly constant independent of environmental pCO₂ and growth rate (32). Because cyanobacterial ε_p values were less than known corresponding ε_Rubisco values, additional isotopic fractionation factors were not needed to explain ε_p, even though some active C_i transport processes, which may fractionate carbon isotopes, were known in cyanobacteria at the time (39–41). Therefore, though different versions of this “traditional model” exist, all variations essentially modified the plant model by shifting the y-intercept of Fig. 1C to account for uptake of HCO₃⁻ in addition to CO₂. If C_i entering the cell is primarily CO₂, the model effectively represents plants (dotted line in Fig. 1C). If C_i is taken up primarily as HCO₃⁻, as in many algae, ε_p is shifted to lower values (solid line in Fig. 1C) because of the equilibrium isotopic effect (ε_equil) between CO₂ and HCO₃⁻ [≈ −9‰ (20)]. In Fig. 1C, we plot the traditional model as derived in Eichner et al. (18), which is an adaptation of (19).

The C Isotope Record Model (Eq. 1 and SI Appendix, Fig. S7) and the traditional model (Eq. 2 and Fig. 1C) have a limit where ε_p cannot exceed ε_Rubisco. Yet, the largest ε_p values observed in the Archaean Eon exceed 30‰ (25, 26) and also exceed all current measurements of ε_Rubisco (23). In addition, recent studies in dinoflagellates have shown that ε_p can regularly exceed ε_Rubisco under certain growth conditions (22), and detailed studies of Cyanobacteria imply that leakage estimates derived from ε_p are not physiologically possible (18). These studies motivated updated models of algal carbon isotope fractionation that account for the isotopic fractionations associated with different C_i uptake mechanisms in order to rationalize anomalous ε_p values (18, 22).

These experiments made clear that the physiology of algae and Cyanobacteria—e.g., how they take up C_i as CO₂ or HCO₃⁻ and by which mechanism—affects the C isotopic content of biomass, ε_p. Further, these C_i transporters and other integral components of modern CCMs were once absent from ancient autotrophs, who used various forms of rubisco alone to grow in Archaean or Proterozoic atmospheres (42). Efforts to draw inferences about the ancient Earth from the C isotope record must, therefore, include some understanding of the physiology and evolution of CCMs in Cyanobacteria and eukaryotic algae (22, 42, 43). Recent studies have attempted to address this issue by characterizing model organisms that may better resemble an ancestral counterpart, including a cyanobacterial strain lacking a CCM (43), a strain that overexpresses rubisco (44), and a strain expressing an inferred ancestral rubisco dating from ≈1 to 3 Ga (45, 46).

Here, we measured the ε_p of a control strain of Synechococcus elongatus PCC 7942 expressing the wild-type rubisco (NS2-KanR, referred to as “WT” for "wild-type", see Materials and Methods), as well as a strain, nicknamed “ANC” for "ancestral", engineered to express an inferred ancestral Form 1B enzyme (dating to >1 Ga) as its sole rubisco (47) in varied CO₂ and light conditions. This putative ancestral rubisco was previously purified and its kinetics were characterized in vitro. Its sequence was then inserted into the genome of a modern cyanobacterium, though the genome of the strain in that study contained both extant and ancestral rubisco sequences (47). Here we study a strain where the extant rubisco was fully removed and replaced with the reconstructed ancestor. In contrast to (46), we also measured ε_Rubisco of the present-day and ancestral rubiscos in vitro. We observed that: i) biomass ε_p is greater for ANC than WT for all conditions tested, even though ANC ε_Rubisco (17.23 ± 0.61‰) is considerably smaller than WT ε_Rubisco (25.18 ± 0.31‰); ii) ANC ε_p increases with light levels while WT ε_p increases with CO₂; iii) ANC displays a growth defect at ambient pCO₂ that is rescued at high pCO₂; and iv) ANC growth is severely inhibited in high light. Consistent with recent studies of eukaryotic algae (18, 22), ANC ε_p exceeding ε_Rubisco in all conditions implies that the traditional box model is incomplete and additional isotope fractionations are needed to rationalize measured ε_p. In addition, modulation of ANC ε_p with light suggests that some light-powered component of the CCM is responsible for excess fractionation beyond ε_Rubisco. We posit that fractionation due to C_i uptake might explain isotopic measurements that deviate from traditional model predictions in both extant and ancient organisms.

Results and Discussion

Ancestral Rubisco Enzyme Fractionates Less Than the Modern Rubisco.

We measured the carbon isotope fractionations of WT and ANC rubiscos in vitro using the substrate depletion method (48–51). Note that there exists experimental variation in ε_Rubisco measurements, both within and across studies, and its cause remains uncertain at present [see SI Appendix, section 4a and (52)]; so we employed the same general approach as others (the substrate depletion method) to be consistent with prior literature. Previous work on rubisco isotope discrimination predicted that ε_Rubsico should correlate positively with specificity (S_C/O), a unitless measure of the relative preference for CO₂ over O₂ (53). We therefore expected ANC and WT ε_Rubisco values to be the same within uncertainty because of their similar S_C/O values (previously measured in ref. 47), but found that the fractionation factor (ε_Rubisco) of the ancestral rubisco (17.23 ± 0.61‰) was about 8‰ lower than that of the extant rubisco (25.18 ± 0.31‰, Table 1).

Table 1.

Rubisco characteristics

Rubisco	εRubsico (‰)	VC (s−1)	KCAir (μM)	VC/KCAir (s−1mM−1)	SC/O
Ancestral form IB	17.23 ± 0.61	4.72 ± 0.14	168.7	28	49.6 ± 1.8
Modern form IB	25.18 ± 0.31*	9.78 ± 0.48*	184.1*	53.1*	50.3 ± 2.0*

Starred values (*) for the modern Form 1B were measured in rubiscos purified from Synechococcus sp. PCC 6301, which has the same small and large subunit (RbcS RbcL) sequences as our working WT strain, Synechococcus sp. PCC 7942 (47). Kinetic isotope effect (ε_Rubisco, avg. ± SE) was measured in this study using the substrate depletion method (48–51). Carboxylation turnover under substrate-saturated conditions (V_C); Michaelis constant for CO₂ in ambient levels of O₂ (K_C^Air); the catalytic efficiency toward CO₂ in ambient air (V_C/K_C^Air); and specificity, a unitless measure of the relative preference for CO₂ over O₂; (S_C/O) are from ref. 47.

Ancestral Rubisco Strain Grows at Ambient CO₂ Concentrations.

Working in S.elongatus PCC 7942, we produced a mutant strain lacking the native Form 1B rubisco and expressing instead an ancestral Form 1B rubisco produced by computational ancestral sequence reconstruction (47) as its sole rubisco enzyme. We then grew this strain, termed ANC, and a control strain, termed wild-type or “WT” (Materials and Methods), in a variety of light and CO₂ levels: i) a reference condition (ambient pCO₂ of 0.04% v/v, standard light flux (120 µE)); ii) high CO₂ (5% pCO₂, 120 µE); and iii) high light (0.04% pCO₂, 500 µE). The CO₂ gas at ambient and high CO₂ conditions had δ¹³C values of −12.46‰ and −36.84‰, respectively.

Remarkably, as in ref. 46, the ANC strain managed to grow in ambient pCO₂ and standard light conditions (Fig. 2), even though the ancestral rubisco has a V_C roughly half that of WT (Table 1). This implies that its rubisco enzyme is properly encapsulated in the carboxysome, since improper carboxysome formation prohibits growth in ambient air (54, 55). Additional characterization of the physiology of the ANC could be valuable, but our inference of proper carboxysome encapsulation is supported by several experiments and analyses as follows. First, electron micrographs of WT and ANC cells grown in ambient CO₂ and light conditions (Materials and Methods) showed multiple carboxysomes per cell in both strains (Fig. 3 and SI Appendix, Fig. S13). Rubisco density can be seen within some of the carboxysomes (Fig. 3C). Second, the rubisco amino acid residues necessary for protein interactions mediating β-carboxysome encapsulation were recently identified (56), and the ANC sequence retains fourteen of the sixteen residues involved (SI Appendix, Tables S8 and S9 and Fig. S14). In addition, WT and ANC strains harvested during exponential growth in the reference condition exhibit similar photosystem stoichiometry, as indicated by absorbance spectra (SI Appendix, Fig. S15). Taken together, these data indicated that carboxysomes form in ANC and the ancestral rubisco is encapsulated within these structures.

Fig. 2.

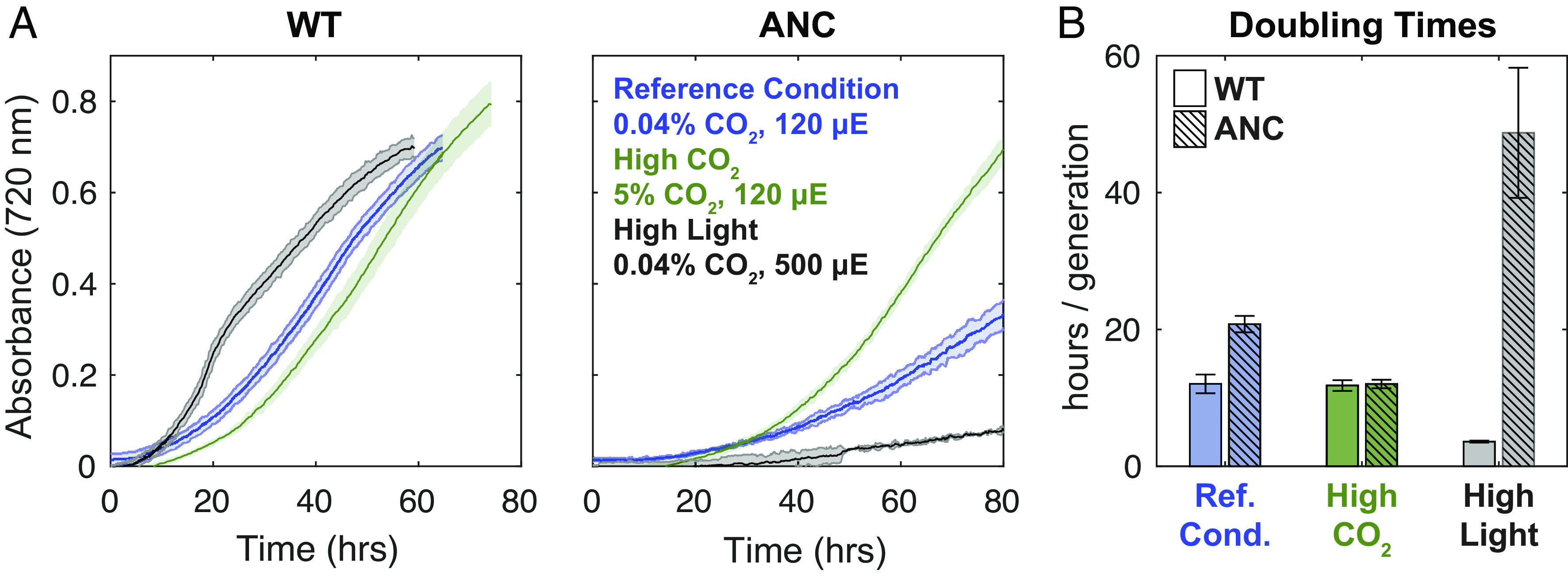
Growth curves for WT and ANC strains across experimental conditions. (A) Averaged growth curves shown for WT and ANC strains to 80 h, colored by growth condition as indicated in figure. Data were smoothed with a rolling median (Materials and Methods); see full ANC growth curves in SI Appendix, Fig. S12. (B) Average doubling times with SDs. See SI Appendix for details of doubling time calculation. ANC displayed a growth defect relative to the WT at the reference condition, which was rescued by high CO₂. ANC grew slowest in high light, while WT grew fastest in that condition.

Fig. 3.

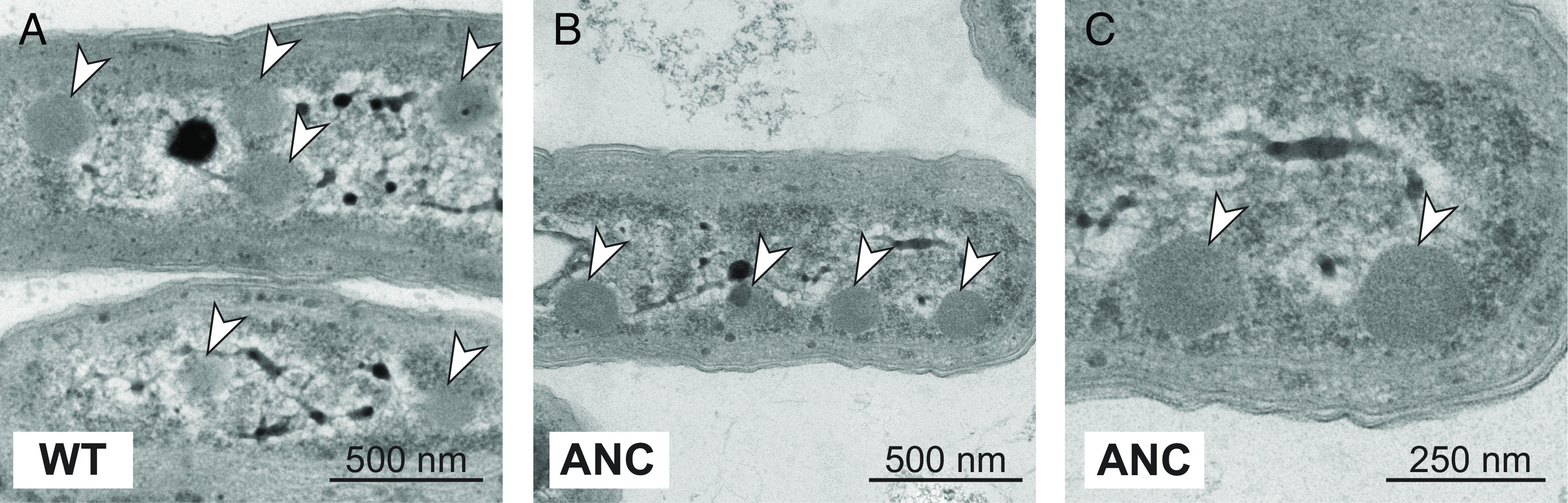
WT and ANC strains both produce carboxysomes at ambient pCO₂. Transmission electron micrographs of WT (A) and ANC (B and C) strains that were harvested during exponential growth in the reference condition (ambient pCO₂, standard light flux). Both strains show multiple carboxysomes per cell, as indicated by white arrows, and carboxysomes exhibit the typical hexagonal shape (55). (C) is the same image as in (B) but enlarged to show that rubisco density seen can be within the carboxysomes of ANC. The dark internal body in (A) is likely a polyphosphate body (57). See SI Appendix, Fig. S13 for additional images.

In addition, the difference in V_C between the ancestral and modern rubiscos was mirrored in the doubling times of WT and ANC strains (Fig. 2B and SI Appendix, Table S2), where ANC doubling times were roughly twice that of WT in the reference condition (20.8 ± 1.2 vs. 12.0 ± 1.4 h, respectively). This suggested that ANC’s growth was limited by its ability to fix CO₂ from ambient air. This growth defect was ameliorated by high pCO₂, where doubling times for both strains were the same within uncertainty (WT 11.8 ± 0.8 h; ANC 12.0 ± 0.6 h). In contrast to WT, elevated CO₂ greatly accelerated the growth of ANC, reducing its doubling time from ≈21 to ≈12 h (Fig. 2B), supporting our inference that CO₂ availability limits the growth of ANC in ambient air, implicating the CCM in its growth defect. Similar results were found in ref. 46.

We observed the greatest differences in doubling times between ANC and WT when the strains were grown in high light (500 µmol photons m⁻² s⁻¹, Fig. 2 and SI Appendix, Table S2). In these conditions, WT cultures were a dark, blue-green color typical of healthy cyanobacterial cells while ANC cultures were yellow-green (SI Appendix, Fig. S11), suggesting degradation of phycobilisomes via a known starvation pathway to reduce the cell’s capacity for light harvesting and photochemical electron transport (58, 59). Note that this is a very high light intensity for Cyanobacteria and may induce a severe photoinhibitory response (60). We therefore inferred that ANC could not fix CO₂ at a rate matching its light harvesting capability, and hence expressed this regulatory pathway to decrease light harvesting capacity. WT, in contrast, grew rapidly in high light.

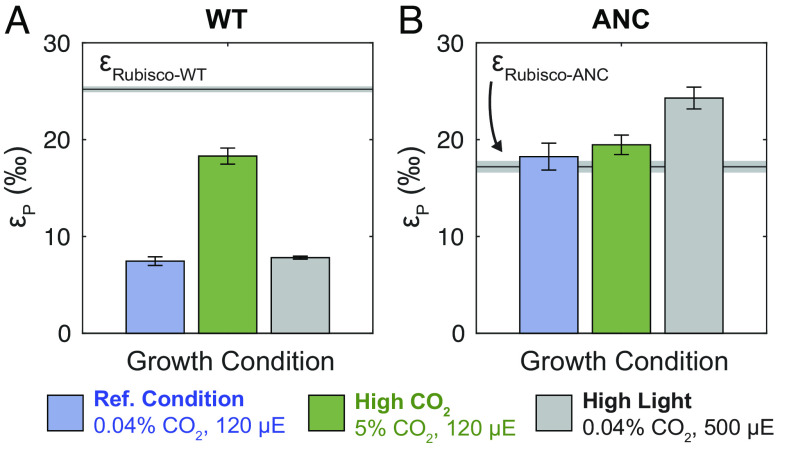
The ANC Strain Fractionates More than WT.

Counter to expectations based on ε_Rubisco (Table 1), ANC ε_p was as large or larger than WT ε_p in all conditions tested (Fig. 4). This was consistent with recent results from a similar ancestral mutant, where that mutant’s ε_p values exceeded WT in ambient and elevated CO₂ levels (46). In this study, the highest ANC ε_p values were observed for cultures grown in high light, where growth was significantly slower than the WT (doubling time ≈ 50 vs. 4 h, respectively, Fig. 3 and SI Appendix, Table S3). ANC ε_p values were also modulated differently by light and CO₂ compared to WT. Compared to the reference condition, WT ε_p values were indifferent to high light and only increased in high CO₂ (Fig. 4A). In contrast, ANC ε_p values did not increase in high CO₂ and only increased in high light (Fig. 4B). This result contrasted with the ancestral mutant in ref. 46 where ε_p values increased by ≈10‰ at 2% CO₂.

Fig. 4.

Whole-cell carbon isotope fractionation by WT and ANC strains. ε_p (‰) values (avg. ± SE) for (A) WT and (B) ANC strains across growth conditions. For each strain, the maximum ε_p possible based on the traditional model (ε_p = ε_Rubisco) is shown as a gray line (avg. ± SE). Most measured ANC ε_P values exceed the theoretical limit (ε_p > ε_Rubisco-ANC + SE), while WT ε_p values do not (ε_p < ε_Rubisco-WT + SE). WT ε_p values increase in response to elevated CO₂ concentrations, while ANC ε_p values increase in response to elevated light flux. See SI Appendix, Table S3 for full results.

As discussed above, the traditional box model cannot accommodate ε_p values in excess of ε_Rubisco (Fig. 1C). However, average ANC ε_p values exceeded ANC ε_Rubisco in all growth conditions (Fig. 4), particularly under high-light conditions where the largest difference was seen (ε_p = 24.30 ± 0.12‰ vs. ε_Rubisco = 17.23 ± 0.61‰). The traditional box model also states that ε_p values are solely modulated by changing external pCO₂ concentrations, which is plainly contradicted by Fig. 4B.

Proposed Influence of a Light-Powered, Vectoral Carbonic-Anhydrase.

Recent studies in extant bacterial and eukaryotic algae have shown that ε_p can regularly exceed ε_Rubisco under certain growth conditions (22), motivating updated models of carbon isotope fractionation in both eukaryotic and bacterial algae (18, 22, 61). Taken together, these studies indicated that observed ε_p values could only be rationalized if an additional fractionation factor was present. Several studies argued that this factor is an energy-coupled CA catalyzing the vectoral hydration of intracellular CO₂ to HCO₃⁻, as this reaction is calculated to have a large isotopic effect and would allow ε_p to exceed ε_Rubisco (18, 22, 61). Energy-coupled CAs can facilitate CO₂ uptake by converting extracellular CO₂ that passively translocates the membrane to intracellular HCO₃⁻ (Fig. 1A), which is advantageous in acidic conditions where CO₂ is the dominant form of extracellular C_i (10, 62, 63). Vectoral CAs are also thought to potentially “recycle” CO₂ that leaks from the carboxysome by converting it to HCO₃⁻ (12).

Cyanobacteria and eukaryotic algae have two general modes of active C_i uptake: uptake of hydrated C_i (predominantly H₂CO₃ and HCO₃⁻) and of CO₂ (63). In order for the CCM to function, either mode must produce a high, nonequilibrium concentration of HCO₃⁻ in the cytoplasm (8, 10). This is thought to be achieved by coupling CA to an energy source (e.g., light or an ion gradient) that drives the vectoral hydration of CO₂ to HCO₃⁻ in the cytoplasm (64). There is now excellent data supporting this hypothesis in Cyanobacteria, where accessory proteins that bind to the NDH complex, the cyanobacterial homolog of the respiratory Complex I NADH-dehydrogenase, are known to mediate CO₂ uptake specifically (65–67). Additionally, one of these accessory proteins, CupA/B, is reminiscent of a CA and contains a telltale zinc active site situated near a proton channel in a membrane subunit (68). The prevailing understanding of these data is, therefore, that these complexes couple C_i uptake to energy supplied by photochemical electron transport (68, 69). Moreover, a similar protein complex has been described in proteobacterial chemoautotrophs, suggesting that energy-coupled CO₂ hydration is widespread (62).

A vectoral CA would affect ε_p for two reasons. First, CO₂ and HCO₃⁻ are isotopically distinct. At equilibrium in standard conditions, HCO₃⁻ is ≈9‰ more enriched in ¹³C than CO₂ (20, 70, 71). Therefore, if a cyanobacterium is predominantly taking up CO₂, the internal C_i pool from which biomass is formed would be isotopically lighter (¹³C-depleted) than if HCO₃⁻ is the dominant source of C_i. We focused only on C_i uptake as CO₂ because we were interested in a modification to the traditional model that could achieve large ε_p values (indicating ¹³C-depleted biomass) to account for at least an additional ~8‰ of fractionation in ε_p (maximum of ~25‰ in the high-light condition) greater than ε_Rubisco (~17‰) in ANC. Though HCO₃^- uptake through bicarbonate transporters (e.g., SbtA) was likely occurring under our experimental conditions (65), isotopically it would not help us achieve the measured large ε_p values because it would shift all ε_p values to be maximally 9‰ more negative (i.e., ¹³C-enriched biomass, Fig. 1C) when we seek to explain values that are ~8‰ more positive. Second, unidirectional CO₂ hydration (CO₂ + H₂O → HCO₃^– + H⁺) is expected to impart a substantial KIE, with calculated values ranging from ≈19 to 32‰ (70, 72–75). Therefore, there are two mechanistic reasons (CO₂ vs. HCO₃⁻ uptake; unidirectional CO₂ hydration) that ε_p could exceed ε_Rubisco in conditions where energized CO₂ uptake and hydration is active. Indeed, a recent model of C-isotope fractionation in Cyanobacteria specifically invoked the NDH complex to rationalize ε_p values that exceed ε_Rubisco (18).

Because energy-coupled CO₂ uptake and hydration by the NDH complex is driven by light energy, e.g., via cyclic electron flow around photosystem I (68), and because the vectoral hydration of CO₂ to HCO₃⁻ is thought to have a large carbon isotope fractionation (70, 72–75), ε_p should increase with light intensity. Indeed, we observed the largest ANC ε_p values in the high-light condition and found that ANC ε_p varies primarily with light and not CO₂ (Fig. 4). This observation is counter to the traditional model, which proposes ε_p as a direct correlate of external pCO₂ (14, 15). Furthermore, on short timescales (≈minutes) cyanobacterial C_i uptake can be modulated by light intensity alone, fully independent of external C_i concentrations (76), and CO₂ uptake can occur in the absence of carbon fixation (77, 78). Based on these physiological and isotopic observations, our study also supports the hypothesis that an energy-coupled vectoral CA like the NDH complex permits ε_p > ε_Rubisco, as observed here for ANC in all growth conditions.

Conceptual Model for Carbon Isotope Fractionation in Cyanobacteria.

As discussed above, the traditional box model cannot produce ε_p > ε_Rubisco (Fig. 1C). In this model, the C_i leakage term (f  ) is fit from measured ε_p values and f = 1 implies that all carbon uptake leaks out of the cell. Though the traditional box model can accommodate both CO₂ and HCO₃^- uptake, which differ in their equilibrium isotopic composition, it does not account for the isotopic effect of vectoral CO₂ hydration. As such, even modeling 100% CO₂ uptake gave physiologically infeasible values of f > 1 for ANC in all conditions (Fig. 5A and SI Appendix, Fig. S8), yet ANC grew reproducibly in all conditions tested (Fig. 2). We also encountered challenges using the traditional model to rationalize WT data: fitting the model gave f < 1 in ambient pCO₂ conditions, but high-CO₂ conditions yielded f > 1 unless all C_i uptake was assumed to be as HCO₃⁻ (see SI Appendix, Fig. S8 for discussion). Therefore, to rationalize our results, we developed a simple modified box model that permits ε_p > ε_Rubisco by including fractionation due to C_i uptake through vectoral CAs.

Fig. 5.

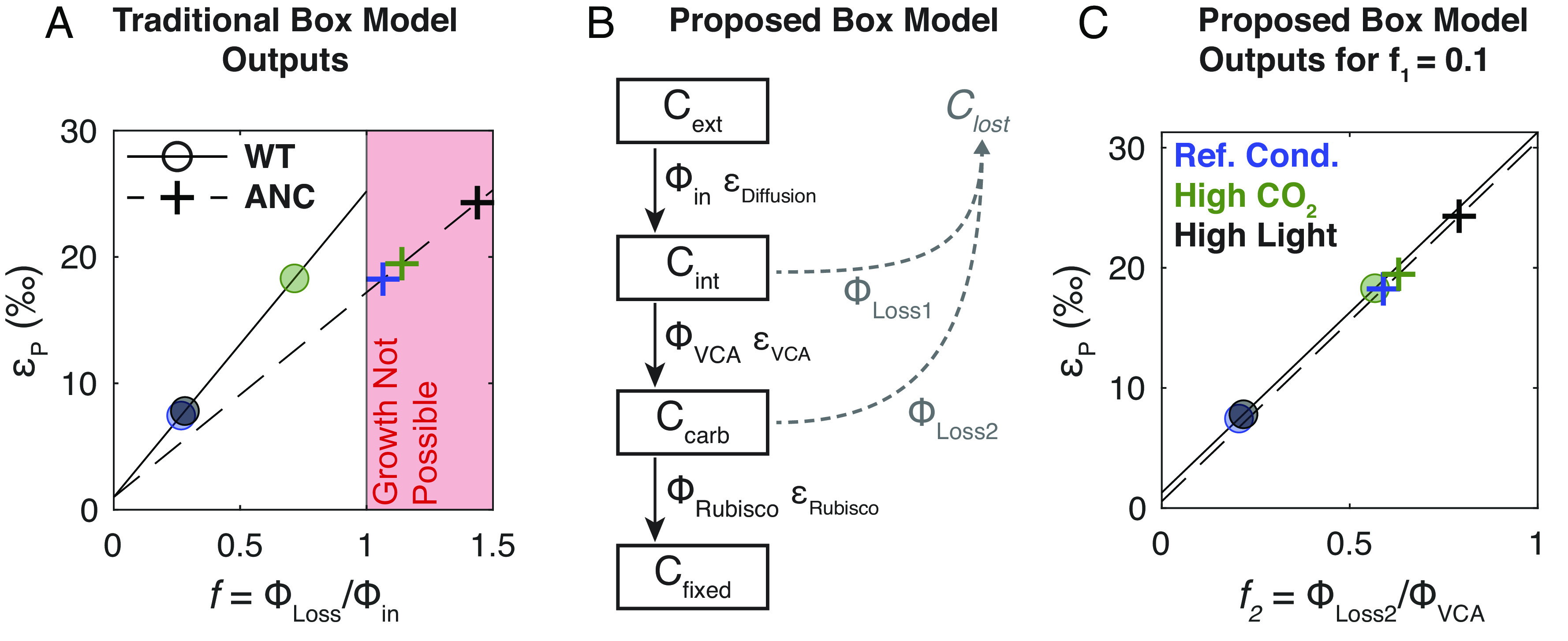
Proposed box model based on experimental results. (A) Experimental results (circles and crosses) plotted onto traditional box model outputs (solid and dashed lines) for WT and ANC, respectively, if C_i uptake is all CO₂. See SI Appendix, Table S11 for quantification of uncertainty. Colors indicate growth conditions as in Fig. 2. The red shaded region demarcates the physiologically infeasible region where f > 1. (B) Our proposed box model architecture. Subscripts indicate external (ext), internal (int), carboxysome (carb), and fixed (fixed) carbon pools. Fluxes are denoted by Φ where subscripts indicate fluxes into the cell (in), out of the cell (Loss1, Loss2), into the carboxysome (VCA for Vectoral Carbonic Anhydrase), and into fixed biomass (Rubisco), each with a corresponding isotopic fractionation denoted with ε. Loss fluxes were assumed to have no isotopic fractionation. In this model, f₁ is defined as Φ_Loss1/Φ_in, and f₂ is defined as Φ_Loss2/Φ_VCA. (C) Experimental results plotted onto proposed box model outputs for f₁ = 0.1; colors and symbols are the same as Panel A; see SI Appendix, Table S11 for quantification of uncertainty. ε_p is defined as the difference in δ¹³C between C_ext and C_fixed. Here only results for f₁ = 0.1 are shown; see SI Appendix, Supplementary Text for full description of model assumptions and results.

In this modified model, we explicitly represent the CCM by distinguishing between carbon in the cytosol (C_int) and carbon in the carboxysome (C_carb), allowing carbon to be lost from the carboxysome (Φ_Loss2, Fig. 5B). Therefore, external C_i enters the cell (flux Φ_in) where it can either leak out (flux Φ_Loss1) or undergo active hydration (flux Φ_VCA, where VCA denotes Vectoral CA). Intracellular C_i can then enter the carboxysome, where it is either fixed (flux Φ_Rubisco) or ultimately leaks out of the cell (flux Φ_Loss2).

We made similar simplifying assumptions as the traditional box model: i) an infinite supply of external carbon, ii) no isotopic fractionation for carbon lost from the cell, iii) Φ_in has the isotopic fractionation associated with ε_Diffusion, and iv) the system is at steady state. We did not add an explicit term for light energy used to power C_i uptake. Instead, the model included an energized CA (denoted VCA) and its associated isotopic fractionation as free parameters. In modeling each strain, we used the appropriate ε_Rubisco measurements (Table 1). We do not know the true value for ε_VCA, but used a value of 30‰ similar to a recent model that explicitly invoked the NDH complex in Cyanobacteria (18). For comparison with the traditional model, we plotted Fig. 5C with f₁ = 0.1 so that it could be represented in two dimensions; see SI Appendix, Fig. S10 for full model outputs. In this updated model, each value of ε_p corresponds to a set of feasible f₁ and f₂ values that fall along a line (SI Appendix, Fig. S10). Therefore, our model constrains but does not uniquely determine f₁ and f₂, nor does it allow for estimation of external C_i levels because many pairs of f₁ and f₂ values can produce the same ε_p.

The modified model was able to rationalize our experimental data of ε_p > ε_Rubisco with leakage values compatible with cell growth (f₂ < 1, Fig. 5C). It may also explain why ANC and WT responded so differently to high light. Our model results implied that ANC lost more carbon than WT at the branch point before rubisco (Φ_Loss2); i.e., even though carbon was present in the cell, it could not be fixed by the ancestral rubisco, perhaps due to its lower V_C (Table 1). Excess CO₂ allowed rubisco’s KIE (ε_Rubisco) to be expressed in ε_p. These results indicated that, in high light, the vectoral CA was delivering high amounts of CO₂ to both the WT and ANC rubiscos. The faster WT rubisco was able to match this flux, which was reflected in its fast growth rate (Fig. 2) and no change in ε_p vs. the reference condition (Fig. 4). However, the slower ANC rubisco was not, which led to its slowest growth rate (Fig. 2), and highest ε_p values across all conditions (Fig. 4). Conditions where ε_p exceeded ε_Rubisco in ANC suggested that, in addition to Φ_Loss2 being large (allowing ε_Rubisco to be expressed), Φ_Loss1 was high as well, which allows ε_VCA to be expressed. However, since we could not independently determine Φ_Loss1 and Φ_Loss2 —i.e., what proportion of ε_p reflects the contribution of ε_Rubisco vs. ε_VCA —we could only conclude that overall the slower ANC rubisco created a “backup” where leakage increased all along the CO₂ fixation pathway and that this effect was exaggerated at high light.

We also note that our use of the term “vectoral” CO₂ hydration connotes a net flux that is dominantly in the direction of CO₂ hydration (CO₂ + H₂O → HCO₃⁻ + H⁺), rather than implying that the flux of HCO₃⁻ dehydration (HCO₃⁻ + H⁺ → CO₂ + H₂O) is zero. As such, there is likely some bidirectional activity (CO₂ + H₂O ⇌ HCO₃⁻ + H⁺) of the NDH complex. It is difficult to experimentally measure the isotope effect associated with the CO₂ hydration reaction, but transition state theory and quantum chemical modeling (70, 71, 74) suggest that the value is large (roughly 25‰, see ref. 22 for review). HCO₃⁻ dehydration, and equilibration in general, would tend to reduce the isotopic fractionation (70). Our results here do not require a larger isotopic effect, however. Rather, a smaller value of ε_VCA = 10‰ (SI Appendix, Fig. S10) would have allowed us to rationalize our measurements, as we need only account for an additional ≈8‰ of fractionation in ε_p (maximum of ≈25‰) above ε_Rubsico (≈17‰) in ANC. See SI Appendix, Fig. S10 for further discussion.

In addition, ours is not the only model structure that can permit ε_p > ε_Rubisco. We tested other models by fitting our data to them (SI Appendix, Fig. S9). Models that incorporated an explicitly one-way, “CA-like” enzyme (61) or the NDH complex specifically (18) were mostly able to rationalize our data as well. The poorest fits are when C_i uptake was mostly as HCO₃⁻ (SI Appendix, Fig. S9) which is not surprising since we need more positive ε_p values and HCO₃⁻ uptake would shift all ε_p values to be 9‰ more negative (Fig. 1C). Altogether, model fitting indicates adding an additional carbon isotope fractionation step produces a model capable of rationalizing our data by enabling ε_p > ε_Rubisco with plausible leakage values f < 1.

Consequences for Understanding the Evolution of Carbon-Fixing Metabolisms.

Our goal was to test if prevailing models of carbon fixation and isotopic fractionation apply to an ancestral analogue strain that may be relevant to understanding the carbon cycle over geologic time. We did so by measuring the isotopic fractionation of a reconstructed ancestral rubisco both inside and outside a living cyanobacterium. We emphasize that ANC is not a true ancestral Cyanobacteria; rather it is a chimeric construct—a modern strain saddled with a predicted Precambrian enzyme. This reconstructed ancestral rubisco is characterized by slower carboxylation kinetics (47) and a much lower ε_rubisco than the modern strain’s native enzyme (17.23 ± 0.61‰ vs. 25.18 ± 0.31‰, Table 1).

Recent studies in extant bacterial (18) and eukaryotic algae (22) have motivated updated models of C isotope fractionation in cells; these models address observations that: i) ε_p can exceed ε_Rubisco in certain conditions; ii) factors other than pCO₂ can modulate ε_p. Our results emphasize that similar caveats apply to Cyanobacteria, where ANC ε_p exceeded ε_Rubisco in all conditions tested. Inference of Archaean and early Proterozoic pCO₂ from the C isotopic record relies intimately on models of cyanobacterial physiology due to their distinction as the oldest oxygenic photoautotrophs (1). Yet, our results show that the traditional form of these models is not generally reliable.

To date, such anomalous ε_p values have been observed during relatively slow growth; in ref. 61 ε_p > ε_Rubisco occurred early in the growth curve as cells were acclimating to fresh culture media, in ref. 22 ε_p > ε_Rubisco occurred during nitrogen and phosphorus limitation, and in this study ε_p > ε_Rubisco was observed in a mutant strain growing slowly while expressing a reconstructed ancestral rubisco. These observations indicated that growth physiology affects isotopic fractionation by photosynthetic algae and, in all cases, motivated a rethinking of the traditional box model (Fig. 1 B and C) to include more physiological detail relating to the presence of a CCM.

As high light consistently slowed growth of ANC, induced chlorosis (yellowing of cultures, SI Appendix, Fig. S11), and increased ε_p, we were motivated to consider the effects of light-related physiology on ε_p. The yellowing of ANC cultures in high light was consistent with starvation and taken to indicate that light levels exceeded the downstream capacity for CO₂ fixation (79, 80). We interpreted these observations as indicating that the replacement of the native rubisco with a slower enzyme decreased capacity for CO₂ fixation (Table 1).

Low-CO₂ fixation capacity would not, on its own, explain anomalously high ε_p values, however. An additional fractionating process is required to explain ε_p values in excess of ε_Rubisco, which we assume is due to light-coupled vectoral hydration of CO₂, which has a large calculated isotope effect (70, 72–75). It is well established that modern Cyanobacteria have light-coupled CO₂ uptake systems (65, 68) and in model Cyanobacteria, this activity is due to the Cup proteins (CupAS/B, also known as Chp proteins), which bind the NDH complex (68, 81). In order for CO₂ uptake to drive the CCM and promote CO₂ fixation, it would need to produce a high, nonequilibrium HCO₃⁻ concentration in the cytoplasm (8, 10). We and others therefore assumed that the complex of NDH-1 and CupAS/B couples light energy to the vectoral hydration of CO₂ to HCO₃⁻ at a CA-like active site (68). Disruption of a Cup protein by point mutation was also shown to largely affect cell growth (69), suggesting that the energy-induced directionality is important for Cyanobacteria.

It is apparent from our experiments that ε_Rubisco does not set an upper bound on ε_p, nor does it predict which strains will have larger ε_p values (Fig. 4). This was only apparent because we measured the isotopic fractionation due to the ancestral rubisco enzyme (ε_Rubisco) and compared it to ANC strain biomass (ε_p), in contrast with (46), which measured ε_p but not ε_Rubisco. While our ANC ε_p values (≈18 to 24‰) fell within the range of ε_p values derived from the carbon isotope record (43), they exceeded ANC ε_Rubisco (Fig. 2). Attention has been paid to outliers in the carbon isotope record where ε_p exceeds ε_Rubisco precisely because they violate the assumptions underlying the dominant models Eqs. 1 and 2) used to interpret the record (22). In addition, ANC ε_Rubsico (17.23 ± 0.61‰) is anomalously low; not only is it ≈8‰ less than WT ε_Rubsico (25.18 ± 0.31‰) but it is among the lowest measured rubisco KIEs. However, only thirteen unique rubisco KIEs have been measured thus far (23) while ≈300 distinct rubiscos have been kinetically characterized (7, 82), suggesting that measuring the isotopic effects of several well-chosen rubisco variants is worthwhile.

Turning to trends in carbon isotope data from the geological record, our results suggested there are at least two nonunique ways to achieve the large ε_p values observed earlier in Earth history: i) High external concentrations of C_i, or ii) Active CO₂ uptake driven by photochemical electron transport. Our proposed model (an idealized extension of the traditional model, Eq. 2) cannot be applied readily to the C Isotope Record Model (Eq. 1). Doing so currently gives nonsensical values of b because ANC ε_p > ε_Rubisco (see SI Appendix, section 6 and Fig. S16 for further discussion), and because we cannot independently constrain the extra degree of freedom introduced (two loss fluxes, Φ_Loss1 and Φ_Loss2, instead of one, f  ). In addition, these parameters could vary over evolutionary history as the CCM and the efficiency of carbon fixation evolves. Additional measurements that constrain these parameters (i.e., Φ_Loss1 and Φ_Loss2) could enable pCO₂ to be back-calculated from ε_p, but further work must be done to then adapt those observations to the C Isotope Record Model (Eq. 2). Importantly, the modified model framework proposed here is not the only approach to producing ε_p > ε_Rubisco with physiologically feasible leakage fluxes. Rather than advocating for our specific model, we offer it as an example form of a solution – showing that ε_p can only exceed ε_Rubisco if additional fractionating process is considered. As shown in SI Appendix, Fig. S9, several approaches to extending the traditional box model can accommodate ε_p > ε_Rubisco (18, 61), yet all of these models represent substantial simplifications of bacterial and algal CCMs. Overall, our study supports the conclusion of prior studies (18, 22) that a modified traditional model that engages more fully with photosynthetic physiology, like the CCM, is required to more accurately constrain environmental C_i concentrations from ε_p.

In addition, this study and other recent work (43, 46) have raised a greater question for the Earth Sciences: What is uniformitarianism for biology? Earth scientists often apply uniformitarian assumptions—assuming that physical and chemical processes behave the same now as they did billions of years ago—in order to reason about the past. This approach is powerful, but these assumptions are challenged by biological processes that undergo substantial evolution on geologic timescales. Ongoing discoveries of novel metabolisms have supported some principles like “the principle of microbial infallibility”—that microbes will always find a way to take advantage of available energy sources (83)—but it is not clear what principles apply to the details of metabolism. Take rubisco, for example – most extant autotrophs use rubisco to fix carbon, but rubisco sits within a variety of physiologies—e.g., C3, C4, CAM in plants—that temper the effect of ε_Rubisco on ε_p (23). We are far from having a clear answer to this question, but recent work at the interface of molecular biology and isotope geochemistry show that these ideas can be tested in the lab. Here and in other recent papers (42, 43, 46), we used synthetic biology to construct organisms with ancestral components so that specific aspects of ancient organisms can be isolated and tested. These “ancestral-like” organisms helped sharpen our understanding of the physiological and environmental factors determining growth (42) and isotopic fractionation (this work) in both ancient and modern autotrophs, showing that models rigidly based on modern taxa are likely not universally applicable across geologic time.

Overall, carbon fixation was a fundamental challenge that autotrophs overcame early in the history of Earth’s biosphere (1). These early processes were recorded in some fashion in the carbon isotope record, but robust interpretation of this record must grapple with the fact that the carbon cycle is an amalgam of both environmental changes and evolutionary processes, mediated by physiology. We now have synthetic biological approaches that offer a way to probe these long timescale coevolutionary problems by producing ancient process analogs of carbon fixation in the laboratory. Utilizing these tools will enable us to better understand how the evolution of key metabolisms have shaped Earth’s chemistry over time.

Materials and Methods

Ancestral Enzyme Reconstruction.

Ancestral Rubisco enzyme sequences were previously reported and characterized by Shih et al. (47). Briefly, for both the large subunit and small subunit of Rubisco, encoded by rbcL and rbcS, respectively, the most recent common ancestor (MRCA) for Form 1A (α), 1B (β), and 1A/B (α/ β) clades were predicted from independently derived phylogenetic trees for RbcL and RbcS containing a broad diversity of Form 1A and 1B Rubisco (>100 sequences). Maximum-likelihood algorithms were used to reconstruct the most probable ancestral sequence for each clade. Ancestral sequences were then expressed in Escherichia coli and purified, and enzyme kinetics were measured.

ANC Strain Generation.

The “ANC” strain studied here was generated by replacing the native large and small rubisco subunits (cbbL and cbbS, respectively) of the parent strain (Synechococcus elongatus PCC 7942) with the reconstructed β ancestral cbbL and cbbS sequences. The NS2-KanR (“WT” strain) was generated by inserting a KanR cassette into neutral site 2 (NS2) (GenBank: U44761.1). This was done as a control for having the KanR in the neutral site. Synechococcus elongatus PCC 7942 were transformed from the WT strain using the approach of Golden and Sherman (84). Briefly, cultures were grown to OD750 nm = 0.5. Cultures were centrifuged at 18,000 x g for 2 min. Pellets were washed with 100 mM CaCl₂ and spun again at 18,000 x g for 2 min. Pellets were resuspended in BG-11 media followed by addition of plasmid and grown for 16 h in the dark at 30 °C. Transformants were then plated onto BG-11 + KAN100 agar plates and placed under 100 µE of light at 30 °C. Single colonies were selected in media with antibiotic until segregation and then genotyped by PCR amplification of the rubisco locus followed by sequencing to confirm homoplasmic ANC strain rubisco sequence. SI Appendix, Table S1 lists plasmids and primers used in this study.

Growth Conditions.

For ambient CO₂ growth, NS2-KanR (“WT”) and β Ancestral Rubisco-KanR (“ANC”) strains were grown in quadruplicate in a photobioreactor (Photon Systems Instruments–MC 1000) at the University of California, Berkeley (UC Berkeley) for four biological replicates total. Cultures were grown in buffered BG-11 media with 50mM HEPES at pH 8. Cultures were inoculated at a starting OD720 nm = 0.015 and cultivated at 120 µmol photons m⁻² s⁻¹, 30 °C, and bubbled with ambient air. High CO₂ growth was performed using the same conditions as ambient growth with the exception of placing the photobioreactor in a 5% CO₂ chamber (Percival AR22L) and bubbling in air from the chamber. High-light growth was performed using the ambient conditions above with the exception of using 500 µmol photons m⁻² s⁻¹ for light intensity. Cells were harvested by centrifugation at 6000 x g for 20 min at 4 °C. Decanted pellets were then flash frozen with liquid N₂ and lyophilized overnight with the Millrock Technology Model BT85A freeze dryer. Doubling time was calculated by fitting the exponential phase of growth (k) using a Markov Chain Monte Carlo (MCMC) approach, using the generic model y = a*EXP(k*x)+b. Growth curves displayed in Fig. 3 were smoothed with a rolling median (n = 12) to remove errant readings caused by bubbles advected in front of the detector. See SI Appendix for more information.

Carbon Isotope Analysis.

Carbon isotope data are reported using delta notation (δ¹³C) in units of per mille (‰) where δ¹³C = [(¹³C/¹²C)_sa/(¹³C/¹²C)_ref-1]*1000, where the subscripts “sa” and “ref” denote sample and reference respectively. The reference used is the Vienna Pee Dee Belemnite (VPDB). δ¹³C values of cyanobacterial cells were measured on an EA-IRMS (Elemental Analyzer Isotope Ratio Mass Spectrometer; Costech Thermo Delta-V) at the California Institute of Technology (Caltech) in Pasadena, CA. Each biological replicate was run four times with two different isotope standards—urea (−27.8‰) and sucrose (−10.45‰). A suite of urea and sucrose standards were run at the beginning, middle, and end of run for sample bracketing and to assess drift throughout the run. An average δ¹³C and SE were calculated and reported for each biological replicate (see SI Appendix for more information). The δ¹³C of the starting CO₂ gas was measured on the Thermo Mat 253 Ultra at Caltech; the CALT-2049C standard was used, which has a δ¹³C_VPDB value of −3.62‰. CO₂ gas from high-pCO₂ experiments was sourced from a CO₂ tank, while the CO₂ gas in ambient pCO₂ experiments was distilled from ambient lab air through cryogenic distillation at Caltech. In addition, we labored to keep gas pressures approximately constant during our experiments (i.e., equilibrating to ambient pressure by bubbling) because of potential unwanted isotopic pressure effects. ε_p, the carbon isotope fractionation between CO₂ gas and bulk cyanobacterial cells, was calculated as (α_CO2/bio - 1)*1000, where α_CO2/bio = ¹³R_CO2/¹³R_bio, where ¹³R is the ratio of ¹³C to ¹²C in the analyte. We note this in contrast to other isotope literature where ε_p is calculated as α_bio/CO2 - 1)*1000, which would cause the positive values in this study to be negative. In this study, more positive ε_p values indicate more ¹³C-depleted; see SI Appendix for more detail.

Rubisco KIE Assay.

Syn6301 and β-MRCA rubisco were purified according to previous methodologies (85, 86) at University of California, Davis and then shipped on dry ice to Caltech. Clarified lysate from a BL21 DE3 Star E. coli culture expressing rubisco was subjected to ammonium sulfate precipitation, at the 30 to 40% cut for Syn6301 and at the 40 to 50% cut for β-MRCA, followed by anion exchange chromatography and size exclusion chromatography. We then used the substrate depletion method to measure the KIE of the Syn6301 and β-MRCA rubiscos (ε_Rubisco), as used previously in similar studies (48–51). Briefly, an assay mix of HCO₃⁻, bovine CA, rubisco, ribulose 1,5-bisphosphate (RuBP), MgCl₂, bicine, and dithiothreitol (DTT) was prepared. As the reaction progressed to completion, aliquots of that assay mix were injected into prefilled exetainers containing phosphoric acid that both stopped the reaction and converted all inorganic carbon species to gaseous CO₂. The δ¹³C of these CO₂ aliquots was then measured on a Delta-V Advantage with Gas Bench and Costech elemental analyzer at Caltech. Here, instead of RuBP being given in excess, CO₂ was given in excess. In addition, instead of determining the fraction of CO₂ (f ) consumed independently to create a Rayleigh plot, we fit the curvature of the δ¹³C results to find f before converting to a Rayleigh plot to calculate ε_Rubisco, similar to previous studies (49). See SI Appendix for more information.

Transmission Electron Microscopy Imaging of Whole Cells.

WT and ANC strains were grown in the reference condition—buffered BG-11 media, shaking at 250 rpm, with white cool fluorescent light at 120 µE, 30 °C, ambient air (0.04% CO₂ (v/v). WT and ANC cells were collected at mid-log (40 and 80 h, respectively) at OD730 nm = 0.4 and pelleted by centrifugation (10,000 x g for 10 min). Pelleted cells were then resuspended in 1 mL cold solution 2.5% Glutaraldehyde in 0.1M Sodium Cacodylate Buffer, pH 7.4 (Electron Microscopy Sciences) and stored in the fixative solution at 4 °C until imaging. Sample preparation and sectioning were performed in the Electron Microscope Laboratory core facility at the University of California Berkeley. Briefly, samples were stabilized in 1% low melting-point agarose, cut into small cubes, and then washed at room temperature with 0.1 M sodium cacodylate buffer, pH 7. Samples were then mixed with 1% osmium tetroxide, 1.6% potassium ferricyanide and 0.1 M cacodylate buffer pH 7.2 for an hour in the dark with rotation. These were washed again with a cacodylate buffer pH 7.2, then DI water, and subjected to a 1-h incubation with uranyl acetate 0.5% solution. After a new wash with DI water, samples were dehydrated by an ascending series of acetone concentration (35%, 50%, 75%, 80%, 90%, 100%, 100%). Later, samples were progressively infiltrated in resin (Epon solution: Eponate 12, DDSA NMA and BDMA (Electron Microscopy Sciences) with rotation, followed by a final step at 60˚C until polymerized. Thin sections (70 nm) were cut using a Reichert Ultracut E (Leica Microsystems) and collected on 100 mesh formvar-coated copper grids. Sections were poststained using 2% uranyl acetate in 70% methanol and followed with Reynold’s lead citrate. The sections were imaged using a FEI Tecnai 12 transmission electron microscope operated at 120 kV (FEI). Images were collected using UltraScan 1000 digital micrograph software (Gatan Inc).

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.