The nervous system tunes sensorimotor gains when reaching in variable mechanical environments

Summary

Humans often move in the presence of mechanical disturbances that can vary in direction and amplitude throughout movement. These disturbances can jeopardize the outcomes of our actions, such as when drinking from a glass of water on a turbulent flight or carrying a cup of coffee while walking on a busy sidewalk. Here, we examine control strategies that allow the nervous system to maintain performance when reaching in the presence of mechanical disturbances that vary randomly throughout movement. Healthy participants altered their control strategies to make movements more robust against disturbances. The change in control was associated with faster reaching movements and increased responses to proprioceptive and visual feedback that were tuned to the variability of the disturbances. Our findings highlight that the nervous system exploits a continuum of control strategies to increase its responsiveness to sensory feedback when reaching in the presence of increasingly variable physical disturbances.

Graphical abstract

Highlights

• •The control of reaching is altered when facing time-varying physical disturbances
• •The changes in control increase responses to proprioceptive and visual feedback
• •Responses to feedback are tuned to the variability of the time-varying disturbances

Biological sciences; Neuroscience; Sensory neuroscience; Cognitive neuroscience

Introduction

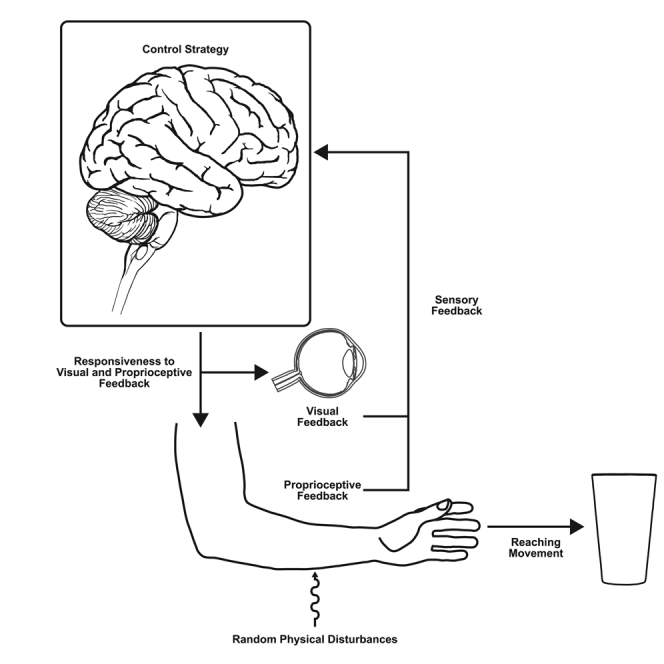
We often interact with environments where there is the potential for our actions to be disturbed. These disturbances create a challenge for the nervous system because they are difficult to anticipate and have the potential to jeopardize task performance. Consider the task of drinking from a cup of water—a task that can vary in difficulty when performed at the dinner table versus a bumpy train ride or turbulent flight. While disturbances are unlikely at the dinner table, successful performance on a train or plane would require sensory feedback to correct for environmental disturbances that vary randomly in amplitude and direction throughout movement. This raises the question: How does the nervous system alter the control of reaching in environments when there is the potential to be disturbed throughout movement?

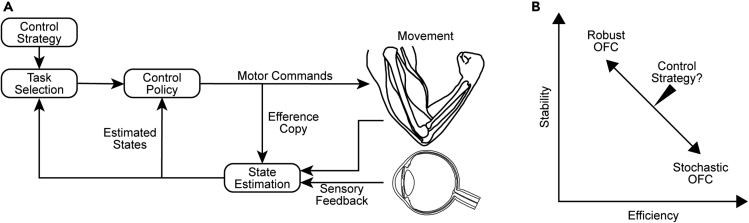
Optimal feedback control (OFC) theory (Figure 1A) can provide insight into how the nervous system ought to deal with disturbances that arise during movement.^1,3,4 In addition to the task demands (e.g., time and accuracy) and movement costs emphasized in stochastic OFC, robust OFC imposes a trade-off between the stability and efficiency of movement (Figure 1B).² Consequently, robust OFC increases the sensitivity to sensory feedback (i.e., feedback gains) to minimize the impact of disturbances arising from errors in modeling properties of the body or variable disturbances that emerge from interactions with the environment. Increased feedback gains will lead to faster peak forward velocities and increased responsiveness to disturbances (e.g., muscle stretch) for movements with fixed time constraints.² This control strategy should lead to an increase in sensitivity to both proprioceptive and visual feedback.

Figure 1.

Optimal feedback control (OFC) framework

(A) The control policy consists of time-varying feedback gains that transform the estimated states into motor commands. According to stochastic OFC, the feedback gains depend on a cost function that accounts for the goal of the task (task selection) while minimizing the motor cost. Efference copies of motor commands are combined with delayed sensory feedback to estimate the current state of the limb. The estimated states are continuously fed into the control policy to update the outgoing motor commands (modified from¹). Robust OFC extends the framework and imposes an additional cost to maximize the controller’s response to disturbances that may arise from unmodeled dynamics or variable external disturbances. In turn, the controller’s time-varying feedback gains increase (control policy) and the influences of internal feedback (efference copy) are downregulated during state estimation.²

(B) Robust OFC and stochastic OFC lie on opposite ends of a continuum of control strategies that trade-off the controller’s movement efficiency and stability against errors (modified from²).

Robust OFC (formulated in H_∞-control) is a model-free strategy that increases feedback gains to minimize the impact of any arbitrary disturbance. As a result, the strategy is both conservative and costly.² Past evidence suggests the nervous system changes its control policy when reaching in environments with disturbances that vary between movements. Indeed, participants make movements with larger peak forward velocities,⁵ increase their grip forces,⁶ reduce their hand displacements,⁷ and generate larger muscle responses² when encountering velocity-dependent forces that vary in strength and direction between movements. The changes in control imply that the nervous system may not use a default, model-free strategy to counter any disturbances but may instead tune control so that it becomes more robust-like when exposed to more variable disturbances. Although the results seem consistent with the idea that the nervous system increases feedback gains to counter disturbances, the studies did not measure feedback gains by imposing controlled limb displacements or visual cursor jump perturbations. Moreover, past work was not designed to examine how feedback gains change with the variability of potential disturbances that arise throughout movement. Answering these questions will provide a fundamental test of the control strategies that support human movements.

Here, we examined how healthy human participants controlled their movements while reaching in the presence of random, time-varying torque disturbances that changed in amplitude and direction throughout movement. We demonstrate that individuals increased their feedback gains, resulting in faster peak movement velocities and larger muscle responses to the same limb (mechanical probe) or cursor displacement (visual probe) when interacting with increasingly variable disturbances. The results demonstrate that the nervous system modifies control for the variability of mechanical disturbances encountered during upper limb reaching movements.

Results

Voluntary reaching movements and corrective responses to mechanical probes are altered in the presence of random, time-varying disturbances

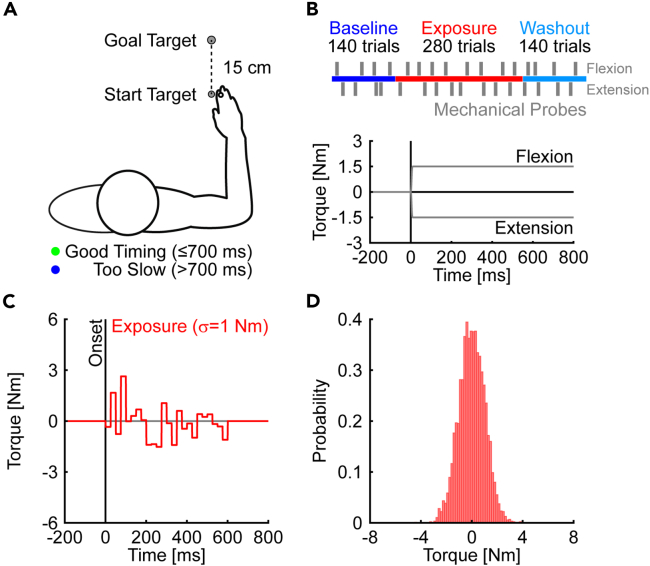
We tested the predictions in healthy human participants (N = 16, 1 left-handed). Participants performed planar reaching movements (15 cm; Figure 2A) with their dominant arm supported in a Kinarm exoskeleton robot.^8,9 The movements were time constrained (<700 ms) and participants received explicit feedback about their movement time (see STAR Methods for further details). The experiment was divided into baseline, exposure, and washout phases. Participants reached to the goal target in the baseline phase (Figure 2A). In the exposure phase, they encountered random, time-varying disturbances (step torques at the elbow, 1 ms ramp-up) that could change in amplitude and direction throughout movement. The torques were sampled from a normal distribution (Figure 2C; μ = 0, σ = 1 Nm, every 25 ms) from the instant that participants left the start target (i.e., movement onset) until they entered the goal target (Figure 2D). The random disturbances were removed in the washout phase. Constant step-torque perturbations (±1.5 Nm at the shoulder and elbow, 10 ms sigmoidal ramp-to-hold profile) were applied at the onset of randomly selected movements throughout the experiment (Figure 2B).^10,11,12 We refer to these perturbations as mechanical probes since they allowed us to measure the gain of responses to torque perturbations.^13,14 The mechanical probes disturbed the motion of the elbow and displaced the hand laterally relative to a straight line between the start and goal target.

Figure 2.

Behavioral task and time course of experiment 1

(A) Participants performed planar reaching movements with their dominant arm. Color-coded timing feedback was provided at the end of each trial.

(B) The experiment consisted of baseline, exposure, and washout phases. During the exposure phase, random, time-varying disturbances displaced the hand lateral to the goal target. Vertical gray lines denote constant step-torque perturbations (mechanical probes) that were used to probe the control policy (i.e., feedback gains) on randomly selected trials. Positive torques cause flexion motion of the elbow joint and displace the hand leftward of the target. The mechanical probes were applied at movement onset, at the instant the participant left the start target, and ramped down after participants held the goal target position.

(C) Time course of a representative trial. The random disturbances were sampled every 25 ms from a normal distribution (μ = 0, σ = 1 Nm).

(D) Distribution of random disturbances encountered by an exemplar participant across trials in the exposure phase.

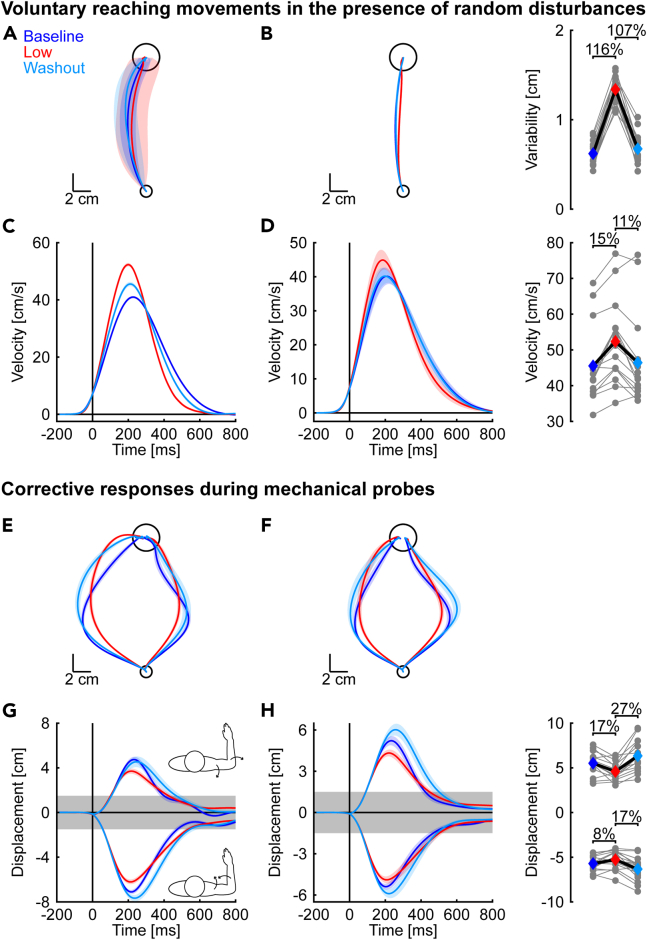
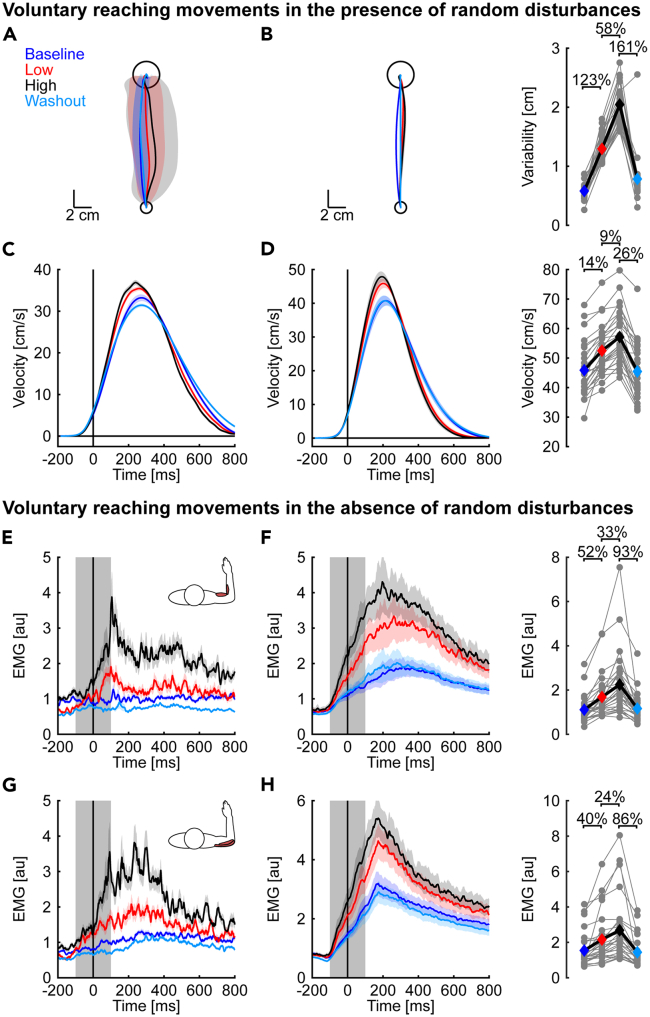
We first examined how the random, time-varying disturbances affected the variability of voluntary reaching movements. Figure 3A displays the hand paths of an exemplar participant. Note the participant reached the target with little change in the spatial properties of their average hand paths across the baseline, exposure, and washout phases. However, the participant’s movements became more variable during the exposure phase. Similar results were observed at the group level. We quantified the variability of hand paths by averaging the pointwise standard deviation of each participant’s lateral hand displacements. We then used a contrast analysis to test if hand path variability increased in the exposure phase relative to baseline and washout (quadratic contrast; see STAR Methods for further details).^15,16,17 Note that contrast analyses are statistical procedures that assess specific questions and are often better suited than omnibus analyses of variance with subsequent post-hoc comparisons.^15,16,17 Contrast analysis revealed an increase in the variability of hand paths in the exposure phase (quadratic trend: t(15) = 18.42, p < 0.001, d = 9.5).

Figure 3.

Properties of voluntary reaching movements and corrective responses during mechanical probes

(A) Hand paths displayed by a representative participant during reaching movements with random, time-varying disturbances. Solid lines represent the average hand path in each phase of the experiment. Shaded regions represent the corresponding pointwise standard deviation in the lateral direction.

(B) Group mean and SE hand paths. Gray dots represent the hand path variability, averaged pointwise SD in the lateral direction, for each participant. Colored diamonds indicate the means of each phase.

(C) Mean and SE forward velocities of the same exemplar participant are shown in the same format as (A). The data are aligned with movement onset (t = 0 ms).

(D) Group mean and SE forward velocities. Gray dots represent the average peak forward velocities displayed by individual participants. Colored diamonds show the mean of each phase.

(E) Mean and SE hand paths in mechanical probes displayed by the same exemplar participant as in (A).

(F) Group mean and SE hand paths across phases of the experiment.

(G) Mean and SE lateral hand displacements of the same exemplar participant as in (E). The data are aligned with the onset of the mechanical probes which corresponded to the time the participant left the start target (t = 0 ms). Shaded gray area indicates the width of the goal target.

(H) Group mean and SE lateral displacements. Gray dots represent individual averages in each phase of the experiment. Colored diamonds are the corresponding group averages.

Statistically significant effects are highlighted with %-changes in the outcome variable.

Next, we focused on the vigor of voluntary reaching movements. We used the forward hand velocity as a proxy for the feedback gains arising from the neural control policy (Figures 3C and 3D). Note that we compared the forward velocity of movements performed in the presence of random disturbances in the exposure phase against unperturbed reaching movements during baseline and washout. We expected participants would display larger and earlier peak forward velocities when encountering the random disturbances in the exposure phase. Such changes in movement velocity are aligned with robust OFC strategies that increase feedback gains to make the arm more responsive to disturbances.² Representative participant and group averages are shown in Figures 3C and 3D. Peak forward velocities increased in the exposure phase (quadratic trend: t(15) = 5.97, p < 0.001, d = 3.1, Figure 3D) and shifted to earlier in movement (quadratic trend: t(15) = 4.74, p < 0.001, d = 2.5). Participants decreased their forward velocity when nearing the target in the exposure phase, such that the increase and shift in peak forward velocity occurred in the absence of statistical differences in average movement times (quadratic trend: t(15) = -1.22, p = 0.240, d = −0.63).

We also disturbed the arm with constant step torques (mechanical probes) to examine how the feedback gains changed when interacting with the random disturbances. The mechanical probes were identical throughout the experiment and provided an assay of the feedback gains by measuring the nervous system’s responsiveness to similar evoked limb motion (Figure 2B). The combined elbow and shoulder torques displaced the elbow while leaving shoulder motion unaltered for >100 ms after the onset of the probe.^10,11,12 The combined torque perturbations displaced the hand predominantly lateral to the goal target and required rapid corrective responses to complete the movement successfully. Behavioral responses were assessed using the peak lateral displacement of the hand relative to a straight line joining the start and goal targets (Figures 3E–3H).^18,19 Exemplar participant data and averaged group responses suggest the arm was displaced less in the exposure phase (Figures 3G and 3H). Quadratic contrasts revealed a statistically significant reduction in peak hand displacements in extension (t(15) = 5.79, p < 0.001, d = 2.9) and flexion probe trials (t(15) = 4.88, p < 0.001, d = 2.5) during the exposure phase. Taken together, the results indicate that participants increased their feedback gains and reduced the peak displacement of the hand when interacting with the random, time-varying disturbances.

Voluntary reaching movements and muscle activity are tuned to the variability of random disturbances

Experiment 1 revealed an increase in feedback gains when participants encountered random mechanical disturbances during upper limb reaching movements. The increased gains were associated with larger and earlier peaks in the forward hand velocity and a reduction in the peak hand displacement when disturbed by the same mechanical probes in the exposure phase. Collectively, the results indicate that behavior more closely resembled robust OFC when interacting with random disturbances that varied during reaching. Motivated by the findings from experiment 1, we conducted a second experiment to examine if the nervous system tunes its feedback gains to the variability of the disturbances encountered during reaching. We expected that participants would systematically increase their feedback gains to make the arm more robust to disturbances in phases of the experiment that imposed more variable disturbances. The lack of a systematic increase in gains would show that the nervous system uses a default, model-free strategy to increase feedback gains and make the arm robust when moving in the presence of random disturbances.²

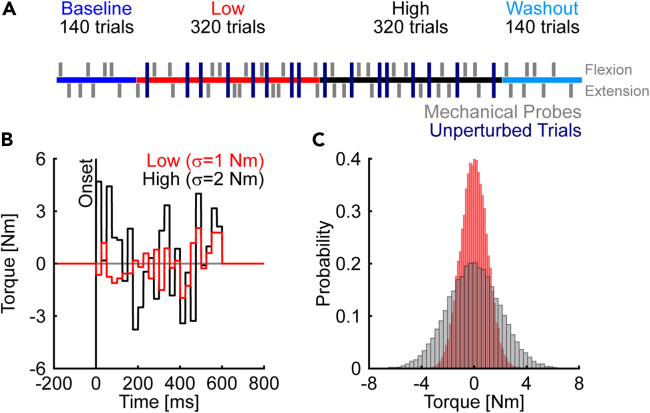
Participants (N = 28, all right-handed) performed reaching movements using the same arm and target configuration as in experiment 1. The baseline phase was followed by an exposure phase where the arm was disturbed by random, time-varying perturbations with low and high variability (Figure 4A). As in experiment 1, the disturbances in the low variability condition were sampled every 25 ms from a normal distribution with μ = 0 and σ = 1 Nm (Figure 4B). In contrast, σ of the high variability condition was changed to 2 Nm to increase the likelihood of encountering large disturbances (Figure 4B). The order of the low and high variability conditions was counterbalanced across participants. Figure 4B displays the time course of representative trials performed by an exemplar participant in the low and high variability conditions. Distributions of random disturbances encountered by the same exemplar participant across all trials of the exposure phases are shown in Figure 4C. Unperturbed trials were also randomly interleaved throughout the exposure phase. These trials align our analysis with past work^2,20 and allowed us to examine the forward velocities and movement times in the absence of random, time-varying disturbances. We recorded the activity of mono- (brachioradialis and triceps lateralis) and biarticular elbow muscles (biceps and triceps longus) using surface electromyography (EMG). We used EMG to quantify the activity of agonist and antagonist muscles during unperturbed voluntary movements and the amplitude and timing of rapid muscle responses in mechanical probes.

Figure 4.

Time course of experiment 2

(A) The experiment was divided into baseline, exposure, and washout phases. Participants encountered random disturbances with low and high levels of variability in the exposure phase. The order of the low and high variability conditions was counterbalanced across participants. Gray vertical lines denote step-torque perturbation trials (mechanical probes) that were used to probe the feedback gains on randomly selected trials throughout the experiment. Participants also performed unperturbed trials (navy blue vertical lines).

(B) Time course of representative trials. The random disturbances were sampled every 25 ms from distributions with low (μ = 0, σ = 1 Nm) and high variability (μ = 0, σ = 2 Nm).

(C) Distributions of random disturbances encountered by an exemplar participant across trials during the exposure phase.

We first examined how hand paths were affected by the random torque disturbances in the exposure phase. Despite the similarity of the spatial properties of the average hand paths, the representative participant’s hand paths (measured by the standard deviation of hand paths in the lateral direction) became more variable when moving in the presence of increasingly variable disturbances (Figure 5A). This observation was also supported at the group level, where participants displayed more variable hand paths in the high compared to the low variability condition (Figure 5B). We extended the contrast analysis to account for the expected increase in hand path variability from the low to high variability conditions (scaled quadratic trend, see STAR Methods for further details). The analysis revealed that the variability of hand paths paralleled the variability of the mechanical disturbances (scaled quadratic trend: t(27) = 19.21, p < 0.001, d = 7.4).

Figure 5.

Properties of voluntary reaching movements and associated muscle activity in experiment 2

(A) Hand paths displayed by a representative participant (mean ± SD in the x-direction) when encountering random disturbances.

(B) Group mean and SE hand paths in each phase of the experiment. Gray dots represent the averaged pointwise SD in the x-direction displayed by individual participants in each phase of the experiment. Colored diamonds represent the group mean.

(C) Mean and SE forward velocities of the same exemplar participant as in (A). Forward velocities of the low and high variability conditions are based on trials where participants encountered the random disturbances. The data are aligned with movement onset (t = 0 ms).

(D) Group mean and SE forward velocities. Data are plotted in the same format as (C). Gray dots show the peak forward velocity for each participant. The colored diamonds indicate the group averages in each phase of the experiment.

(E) Mean and SE elbow flexor (brachioradialis & biceps) muscle activity of the same exemplar participant as in (A). Note that we display the muscle activity of unperturbed reaching movements across all experimental phases to avoid reflexive increases in muscle responses elicited by the random disturbances. Shaded gray area indicates the muscle activity associated with the planning and initiation of voluntary reaching movements (−100 to 100 ms aligned with movement onset). Note that we smoothed the muscle activity traces using a 10 sample (10 ms), zero-delay moving average for display purposes.

(F) Group mean and SE elbow flexor muscle activity are shown in each phase of the experiment. The data are plotted in the same format as (E). Gray dots represent the means of the elbow flexor muscle activity. Colored diamonds indicate the group means in each phase of the experiment.

(G and H) Elbow extensor (triceps lateralis & triceps longus) muscle activity is displayed following the same layout as (E) and (F).

Statistically significant effects are highlighted with %-changes in the outcome variable.

See also Figure S1.

We again used the amplitude and timing of the peak forward velocity to measure the vigor of voluntary reaching movements. We expected that peak forward velocities would increase and shift to earlier in movement when participants moved in the presence of increasingly variable disturbances. We first compared reaching movements when encountering random disturbances with low and high variability against unperturbed reaching movements during baseline and washout. Indeed, peak forward velocities increased in the exposure phase. We also observed a systematic increase in peak velocity from the low to high variability condition (Figures 5C and 5D; scaled quadratic trend: t(27) = 13.16, p < 0.001, d = 5.1). Increases in movement velocity were paired with a systematic shift in peak velocity to earlier in movement, such that participants displayed earlier peaks in the high variability condition (scaled quadratic trend: t(27) = 6.67, p < 0.001, d = 2.6). Similar to experiment 1, participants tended to decrease their forward velocity when nearing the goal target in the exposure phase. As a result, the changes in amplitude and timing of the peak forward velocity occurred in the absence of statistical differences in movement time (scaled quadratic trend: t(27) = -0.03, p = 0.978, d = −0.01). We compared the same outcome variables in unperturbed trials that were randomly interleaved throughout the exposure phase (Figure 4A; Figure S1). The peak forward velocities also increased (scaled quadratic trend: t(27) = 8.80, p < 0.001, d = 3.4) with the peaks occurring earlier in movement in the exposure phase (scaled quadratic trend: t(27) = 4.89, p < 0.001, d = 1.9). However, the movement times of unperturbed reaching movements were reduced during the exposure phase (scaled quadratic trend: t(27) = 5.74, p < 0.001, d = 2.2). Taken together, the results reveal systematically faster and earlier peaks in forward hand velocity and a reduction in the time to complete unperturbed reaching movements in the exposure phase.

We further assessed the vigor of voluntary reaching movements by quantifying the muscle activity surrounding movement onset (−100 to 100 ms).^{18,21,22,23,24} We averaged the activity of the elbow flexors (brachioradialis & biceps) and extensors (triceps lateralis & triceps longus) to simplify the analysis²⁵ as similar trends were observed in the activity of individual muscles. We based the analysis on unperturbed trials to extract the activity associated with the planned movement while avoiding reflexive increases in muscle activity when interacting with the random disturbances. We expected the muscle activity surrounding movement onset to parallel changes in movement velocity and increase with the variability of the random, time-varying disturbances. In line with our prediction, increases in muscle activity were evident in both exemplar participant and group-averaged patterns of muscle activity (Figures 5E–5H). Increases in muscle activity were evident in the low variability condition and most pronounced in the high variability condition. Scaled quadratic contrast analyses revealed an increase in both the elbow flexor (Figures 5E and 5F; t(27) = 5.54, p < 0.001, d = 2.1) and extensor muscles (Figures 5G and 5H; t(27) = 4.77, p < 0.001, d = 1.8). Indeed, muscle activity increased with the variability of the random disturbances and returned to near baseline levels when removed in the washout phase. Collectively, the results indicate that participants altered their control policy and increased their feedback gains with the variability of the random disturbances they encountered during reaching.

Corrective responses and muscle activity to mechanical probes are tuned to the variability of random disturbances

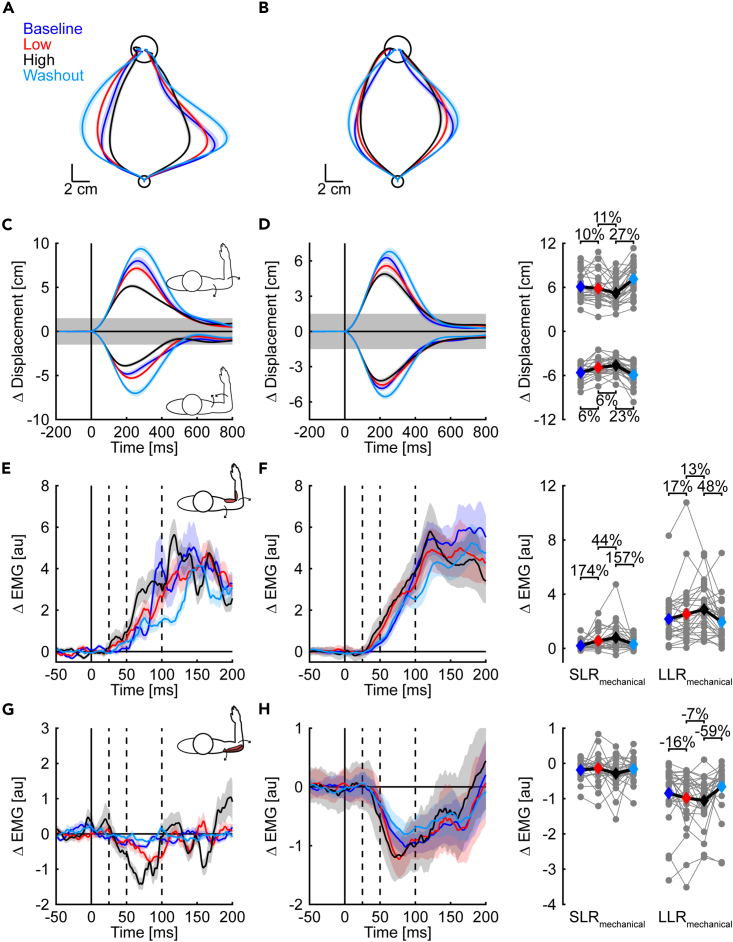
We next examined how responses to mechanical probes changed throughout the experiment. Similar to experiment 1, mechanical probes were interleaved on randomly selected trials and provided an assay of how the nervous system alters control when encountering disturbances with different levels of variability (Figure 6). The exemplar participant’s hand was displaced less when countering the same mechanical probes in the exposure phase. Importantly, reductions in peak hand displacement were more pronounced in the high variability condition (Figures 6A and 6C). At the group level, the hand was displaced farther in the baseline and washout phases, less in the low variability condition, and least in the high variability condition. The reductions in peak lateral hand displacements were evident in both extension (scaled quadratic trend, t(27) = 7.17, p < 0.001, d = 2.8) and flexion probe trials (t(27) = 5.98, p < 0.001, d = 2.3; Figure 6D).

Figure 6.

Hand paths, corrective responses, and muscle activity during mechanical probes

(A) Mean and SE hand paths of the same exemplar participant in each phase of the experiment.

(B) Group mean and SE hand paths in each phase of the experiment.

(C) Mean and SE lateral hand displacements of the same exemplar participant as in (A). The data are aligned with movement onset (t = 0 ms). Shaded gray area indicates the width of the goal target.

(D) Group mean and SE lateral displacements are shown for each experimental phase following the same layout as (C). Gray dots represent the peak lateral displacement displayed by individual participants in each phase of the experiment. Colored diamonds represent the corresponding group-level averages.

(E) Mean and SE stretch response of the elbow flexor muscles (agonists) of the same exemplar participant as in (A). The data are plotted as muscle stretch responses (ΔEMG) and correspond to the difference in muscle activity between mechanical probes and unperturbed trials in each phase of the experiment. The data are aligned with the probe onset (t = 0 ms). Dashed vertical lines separate short-latency (SLR_mechanical: 25 to 50 ms) and long-latency (LLR_mechanical: 50 to 100 ms) muscle stretch responses.

(F) Group mean and SE stretch response of the elbow flexor muscles. The data are plotted in the same format as (E). Gray dots represent the mean SLR_mechanical and LLR_mechanical of the flexor muscles of each participant. Colored diamonds are the group averages.

(G and H) Shortening responses of elbow extensor muscles (antagonists) are displayed following the same layout as (E and F).

Statistically significant effects are highlighted with %-changes in the outcome variable.

See also Figure S2.

We then extracted muscle responses in pre-determined time windows after the onset of the mechanical probes. The approach can provide insight into the neural implementation of the control policies by determining the timing of the upregulated corrective responses.^2,26 Modulation in the short-latency time window (SLR_mechanical: 25 to 50 ms) would reveal the involvement of spinal circuitry,^{27,28,29,30,31} whereas changes that emerge in the long-latency time window (LLR_mechanical: 50 to 100 ms) would implicate transcortical processing.^{13,14,32,33,34,35,36,37,38,39,40} Figures 6E–6H displays exemplar and group-averaged muscle responses during mechanical probes that extended the elbow. The average muscle responses are plotted as the change in activity relative to unperturbed trials in each phase of the experiment (ΔEMG). In agreement with our prediction, the stretch responses of the elbow flexors increased with the variability of the disturbances. Upregulation of the flexor muscles was evident both in the SLR_mechanical (scaled quadratic trend, t(27) = 3.05, p = 0.005, d = 1.2) and LLR_mechanical time windows (t(27) = 3.82, p < 0.001, d = 1.5), such that responses in both time windows were largest in the high variability condition. Inhibition of the antagonist elbow extensor muscles emerged in the LLR_mechanical time window (scaled quadratic trend, SLR_mechanical: t(27) = 1.01, p = 0.324, d = 0.4; LLR_mechanical: t(27) = 2.38, p = 0.024, d = 0.9) with the muscles being most inhibited in the high variability condition. Collectively, paired increases in the excitation of the agonist (stretched) muscles and inhibition of the antagonist (shortened) muscles would increase the amplitude of the corrective responses and lead to a reduction in joint motion when interacting with increasingly variable disturbances.

In contrast to mechanical probes that extended the elbow, the modulation of responses occurred largely in elbow flexor muscles that were shortened by mechanical probes that displaced the elbow into flexion (Figure S2). Larger inhibition of the elbow flexor muscles was evident in the SLR_mechanical (t(27) = 2.09, p = 0.046, d = 0.8) and LLR_mechanical time windows (t(27) = 3.71, p < 0.001, d = 1.4) when interacting with increasingly variable disturbances. In contrast, excitatory responses of the stretched elbow extensor muscles did not show statistically significant modulation (SLR_mechanical: t(27) = 1.59, p = 0.124, d = 0.6; LLR_mechanical: t(27) = 1.04, p = 0.309, d = 0.4). Taken together, the findings support the main prediction that the nervous system increases feedback gains to make the control of the arm more robust to the effects of random disturbances that change throughout movement.

Corrective responses and muscle activity to visual probes are tuned to the variability of random disturbances

Experiment 2 revealed a systematic increase and shift in the timing of peak forward velocities, with increased co-activation surrounding the onset of movements when encountering disturbances with low and high variability. The amplitude of corrective responses in mechanical probes also paralleled the variability of the disturbances encountered during reaching. Muscle co-activation has been associated with increases in the stiffness of the arm.^41,42,43,44 The challenge is that methods for estimating the stiffness of the arm average displacement for >200 ms post-perturbation and include contributions from neural feedback loops that engage rapidly following limb displacements.^{13,14,32,33,45}

We conducted a third experiment to examine changes in responsiveness to visual “cursor jump” probes.^46,47,48,49 Muscle stiffness limits the mobility of the arm by making muscles more resistant to stretch. We reasoned that stiffness would have little benefit when responding to cursor jumps and could hamper the corrective responses. In contrast, co-activation may increase the range of potential feedback responses by making the agonist, antagonist, or both muscles available for control.^2,50,51,52 In short, the approach allowed us to measure feedback gains independent of contributions of limb stiffness that may make the arm more resistant to the random torque disturbances. Moreover, the experiment enabled us to verify that the results are coupled with a change in control rather than a selective increase in responsiveness to proprioceptive feedback resulting from a reweighting of this feedback during state estimation (cf.^53,54,55).

We tested these ideas using a similar design as experiment 2 (Figure 4) with the exception that participants (N = 26, 3 left-handed) encountered the low (σ = 1 Nm) followed by the high variability condition (σ = 2 Nm). This simplified design was justified given the lack of statistical evidence supporting order effects in experiment 2 (see Table S1). We probed the gain of rapid feedback responses using visual cursor jumps (i.e., visual probes) on randomly selected trials. During these trials, the hand-aligned cursor jumped laterally relative to a straight line joining the start and goal target at the onset of movement (±4 cm; Figure 7A). In some of these visual probes, an error clamp restricted hand motion to a straight path between the targets.^46,47,49 The cursor displacement was transient and was realigned with the hand position after 250 ms. This setup measures the forces that participants exert against the error clamp and provides a proxy for the feedback gains.^46,47 The amplitude of the applied forces was assessed in early (Force_early: 180 to 230 ms) and late time windows (Force_late: 230 to 280 ms) after the onset of the transient visual probes. Clamp trials without visual probes were also interleaved to determine the forces associated with unperturbed movements throughout the experiment. We also interleaved visual probes where the lateral cursor displacement was maintained throughout movement in the absence of an error clamp. These persistent visual probes helped to avoid a decrease in visuomotor feedback gains when transient cursor jumps were encountered repeatedly in the clamp^47,56 and provided a means to quantify kinematic properties of corrective responses throughout the experiment. We predicted that feedback gains would parallel the variability of the random, time-varying disturbances and result in more forceful rapid responses when countering the same visual probes in the high variability condition.

Figure 7.

Lateral forces and muscle responses during transient visual probes

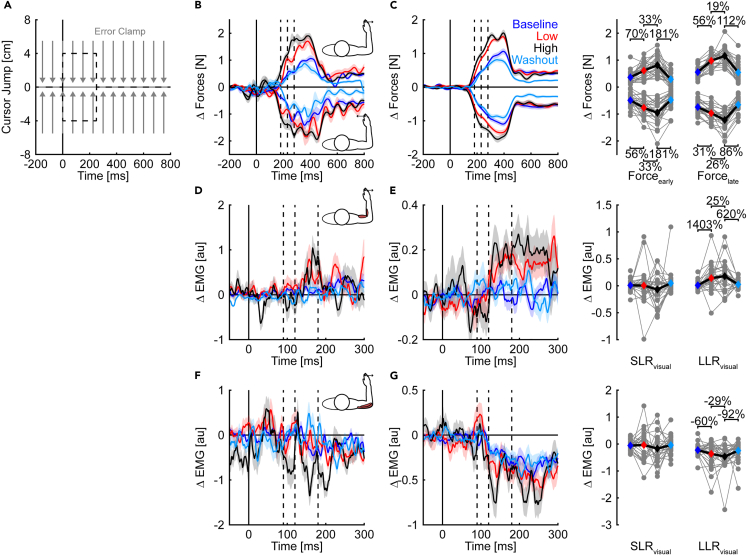
(A) Visual probes were randomly interleaved throughout the entire experiment. The hand-aligned cursor (black dashed line) jumped perpendicular to the reach direction (±4 cm) with movement onset (t = 0 ms). After 250 ms, the cursor was realigned with the true hand position. Hand paths (gray solid line) were restricted to a straight line connecting the start with the goal target by an error clamp (gray arrows).

(B) Mean and SE forces of an exemplar participant are shown for each phase of the experiment. The data are aligned with perturbation onset. The dashed vertical lines separate the Force_early (180–230 ms) and Force_late (230–280 ms) responses.

(C) Group mean and SE forces are shown for each experimental phase (same layout as (B)). Gray dots represent the means of the individual forces of each participant across the experimental phases for the Force_early and Force_late. Colored diamonds indicate the means.

(D) Mean and SE muscle response of the elbow flexor muscles (agonists) of the same exemplar participant as in (B) during rightward cursor jumps across the different experimental phases. Muscle activity of unperturbed reaches of each experimental phase was subtracted from the corresponding muscle responses. The data are aligned with the onset of the cursor jump (t = 0 ms). Dashed vertical lines separate the short-latency (SLR_visual: 90 to 120 ms) and long-latency (LLR_visual: 120 to 180 ms) responses to visual probes.

(E) Group mean and SE muscle response of elbow flexor muscles are shown for each experimental phase (same layout as (D)). Gray dots represent the mean SLR_visual and LLR_visual of the elbow flexor muscles of each participant across the experimental phases. Colored diamonds indicate the means.

(F and G) Responses of elbow extensor muscles (antagonists) are displayed following the same layout as (D) & (E).

Statistically significant effects are highlighted with %-changes in the outcome variable.

See also Figures S3, S4, and S5.

Lateral forces in clamped cursor jump trials are shown in Figures 7B and 7C. In agreement with our prediction, lateral forces in the Force_early and Force_late time windows increased with the variability of the random, time-varying torque disturbances encountered during reaching (scaled quadratic trends, rightward – Force_early: t(25) = 7.67, p < 0.001, d = 3.1, Force_late: t(25) = 13.05, p < 0.001, d = 5.2; leftward Force_early: t(25) = 6.73, p < 0.001, d = 2.7, Force_late: t(25) = 9.07, p < 0.001, d = 3.6). Similar results were evident in the lateral hand velocities when the cursor jump persisted throughout movement and required a corrective response to complete the trial (Figure S3). Together, the results indicate that participants increased their feedback gains and made their movements more closely resemble robust OFC strategies when interacting with time-varying disturbances with greater variability.

Figures 7D–7G display exemplar and group-averaged responses of the elbow muscles in transient visual probes in the rightward direction. We focused our analysis on the SLR_visual (90–120 ms) and LLR_visual (120–180 ms) time windows that provide information about the neural implementation of the corrective responses.^46,48 Changes in the SLR_visual are thought to involve subcortical feedback processing, while changes in the LLR_visual would implicate cortical feedback processing.^{33,48,57,58,59} Larger muscle responses emerged during the LLR_visual in the elbow flexors (scaled quadratic trend, t(25) = 3.23, p = 0.003, d = 1.3), with the largest responses occurring in the high variability condition. Similar modulation of the LLR_visual was evident in the inhibition of the elbow extensor muscles (t(25) = 2.42, p = 0.023, d = 0.9). We did not observe statistically significant modulation in the SLR_visual when examining excitation of the flexor muscles (t(25) = -1.24, p = 0.226, d = −0.5) or inhibition of the extensor muscles (t(25) = 0.99, p = 0.331, d = 0.4). Following transient visual probes in the leftward direction (Figure S4), larger muscle responses were evident in both the SLR_visual and LLR_visual time windows in the elbow extensor muscles (SLR_visual: t(25) = 2.69, p = 0.012, d = 1.1; LLR_visual: t(25) = 3.85, p < 0.001, d = 1.5) that acted as agonists to counter the visual probes. We did not observe statistically significant modulation of the antagonist elbow flexor muscles in either the SLR_visual (t(25) = 0.18, p = 0.858, d = 0.1) or LLR_visual time windows (t(25) = 1.60, p = 0.122, d = 0.6). Similar modulation of muscle responses was observed during persistent visual probes that required corrective responses to reach the goal target and complete the trial successfully (Figure S5). Collectively, the findings show significant modulation of visuomotor feedback gains when interacting with variable torque disturbances.

Discussion

Humans often interact with environments where there is the chance of being disturbed during movement. Despite the potential to jeopardize task performance, the nervous system is often able to counter such disturbances and produce successful actions, such as when drinking from a glass on a bumpy train ride or turbulent flight. Here, we tested how the healthy human nervous system regulates feedback gains when reaching in the presence of disturbances that vary in amplitude and direction throughout movement. We found that participants produced larger and earlier peak forward velocities and increased muscle co-activation when reaching in the presence of random torque disturbances. Changes in voluntary behavior were coupled with an increase in the vigor of rapid responses to mechanical and visual probes. The changes in voluntary reaching movements and corrective responses increased with the variability of the random disturbances and returned to baseline levels following their removal. The findings support the hypothesis that the nervous system modifies control to counter random, time-varying torque disturbances during reaching movements.

Our findings are in line with recent advances in optimal feedback control (OFC).² Robust OFC increases feedback gains to minimize the impact of disturbances arising from unmodeled dynamics of the body or environment or random disturbances external to the controller, like the random, time-varying step torques used in our experiments. The resulting control policy minimizes the cost to achieve the task goal while maximizing the controller’s response to any disturbances that arise during movement.² Thus, robust OFC imposes a trade-off where increases in feedback gains inherently increase the cost of movement. In support of this trade-off, we found that participants generated larger muscle activity during voluntary movements (cf.^60,61,62) and greater rapid feedback responses when disturbed by the same mechanical and visual probes. Moreover, participants increased their forward reaching velocities with the peaks occurring earlier in movement. In the absence of any disturbances (i.e., unperturbed reaching movements), movement times were reduced in the exposure phase. Although the changes in movement times were consistent across participants, they were relatively small compared to the change in movement time required to modulate feedback responses.^18,63 In addition to modulating the control policy, the theory downregulates the reliance on internal feedback since this information is derived from efference copies of the control signal (motor commands) that may be corrupted by unmodeled dynamics or external disturbances. This mechanism differs from altering the uncertainty of motor commands,⁶⁴ although both result in state estimates that rely more heavily on sensory feedback.

Robust OFC is a default, model-free strategy that increases the feedback gains to minimize the impact of any disturbance encountered during movement.² This would allow the nervous system to mitigate the effect of disturbances arising from unmodeled dynamics of the body (i.e., plant) or environment (i.e., external disturbances). Robust OFC differs from stochastic OFC strategies that minimize the cost of goal-directed movements but require an accurate model of the body and environment.^1,3,4 While both stochastic and robust OFC are capable of producing flexible, goal-oriented control, they lie on opposite ends of a continuum of strategies that prioritize efficiency versus stability. Our results suggest the nervous system takes advantage of this inherent continuum by tuning the control of the arm to properties of the environment (cf.⁶⁵).

Our findings highlight that the nervous system tunes its sensitivity to sensory feedback to the variability of environmental disturbances. We previously exposed participants to velocity-dependent loads where the nature and direction of the applied forces varied between trials.² Unperturbed trials were interleaved with force-fields that were proportional to the velocity of movement and deviated the hand to the left or right of the target. The design imposed an unmodelled bias in the forces encountered in most trials. Similar to the current results, participants increased their peak forward velocities and responsiveness to muscle stretch (and shortening) when exposed to mechanical disturbances that varied between trials.² However, the experiment was not designed to examine control strategies that allow the nervous system to counter variable environmental disturbances that arise throughout movement. In the current study, we demonstrate that the nervous system increases its responsiveness to proprioceptive and visual feedback in a way that depends on the statistical properties of the disturbances encountered during reaching. Collectively, these studies suggest the nervous system can take on strategies that more closely resemble robust OFC to mitigate the consequences of variable disturbances encountered while interacting with the environment.

The results complement a growing body of work that emphasizes the flexible control of goal-directed reaching movements. Recent studies have demonstrated that participants can increase their feedback gains to produce faster movements and more vigorous corrections when reaching to targets with higher probability of reward.²⁰ Other work has highlighted online updates in control to accommodate a change in target size,^66,67 avoid obstacles,⁶⁶ or accommodate different applied loads.^68,69 Here, we have shown that participants increase their feedback gains and opt for strategies that more closely resemble robust OFC when moving in the presence of more variable environmental disturbances that change in amplitude and direction throughout movement. Other frameworks could be used to understand the changes in responsiveness to sensory feedback. Perceptual control theory uses hierarchical feedback loops^{70,71,72,73,74} and reference signals that can be modified based on intent or task goal to influence the nervous system’s response to disturbances. Studies on perceptual control theory have focused on continuous tracking tasks that require participants to minimize deviations from a trajectory by moving targets or displacing a cursor relative to the target.⁷¹ However, the need to produce specific trajectories differs from the control of discrete reaching movements, where the nervous system will generate flexible solutions to attain the goal of the task.^{3,11,19,28,47,75,76,77,78,79,80,81,82,83,84} Although it is unlikely that the nervous system uses the formalisms of optimal control theory,¹³ growing evidence suggests it can approximate a range of strategies depending on the goal of the task, reward, and features of the environment.

Increases in muscle co-activation were prominent in our experiments. These changes in muscle activity can make it difficult to dissociate feedback gains from reductions in limb motion arising from muscle stiffness,^41,44,85 automatic gain-scaling of muscle stretch responses,^{27,28,29,30,31} or α-γ co-activation.^86,87 However, it is important to note that the observed muscle responses cannot solely reflect the influence of automatic gain-scaling^{27,28,29,30,31} or α-γ co-activation.^86,87 Automatic gain-scaling is thought to arise from the recruitment properties of pools of spinal motor neurons. Thus, increased muscle activity should amplify short-latency and, to a lesser extent, long-latency responses in the stretched muscle,²⁷ while leading to increased inhibition in the shortened muscle in the same response windows.²⁸ In contrast, α-γ co-activation would be expected to potentiate short- and long-latency responses in stretched muscles and increase inhibition in muscles shortened (unloaded) by the mechanical probe.⁸⁸ Despite changes in co-activation, we did not observe any statistical differences in the modulation of short-latency responses of the elbow extensors during both muscle stretch and shortening, thereby ruling out the general influences of automatic gain-scaling and α-γ co-activation. Instead, the gain modulation was largely evident in the elbow flexors, particularly when they acted as antagonists and were shortened by the mechanical probe. Since the modulated muscle responses were largely evident during the long-latency time window, our findings highlight the involvement of transcortical feedback processing.^{13,14,32,33,34,35,36,37,38,39,40} Thus, co-activation of agonist and antagonist muscles may increase the nervous system’s range of feedback responses by enabling excitation of agonist muscles, inhibition of antagonist muscles, or both.^2,50

We further addressed these concerns in experiment 3 using visual cursor jumps to assess changes in the nervous system’s sensitivity to sensory feedback. This experiment provided two important lines of evidence supporting the regulation of feedback gains. First, we found that participants responded more vigorously to visual feedback when interacting with random torque disturbances. The upregulated muscle responses largely emerged in the visual long-latency time window that has been associated with transcortical feedback processing.^14,33,48 However, subcortical feedback processing may also be involved in the gain modulation^{33,48,57,58,59} as highlighted by upregulated muscle responses in the visual short-latency time window in some conditions. The increased responses resulted in larger applied forces when the participant’s hand was constrained by a virtual error clamp. We also observed greater lateral velocities in trials where persistent cursor jumps required corrective responses to return the cursor to the target. Importantly, the amplitude of the responses increased with the variability of disturbances and revealed that exposure to the random, time-varying disturbances led to an increase in the gain of responses to both visual and proprioceptive feedback. The findings support a general increase in feedback gains compared to a selective increase in responsiveness to proprioceptive feedback when reaching in the presence of the physical disturbances (cf.^53,54,55). Second, the upregulation of visual responses helps to rule out the alternative explanation that corrective responses are solely driven by increases in background muscle activity. Indeed, past studies have shown that visuomotor corrections are less sensitive to changes in background loads than responses to muscle stretch.^49,89 The results reveal flexible and distributed sensorimotor gain control at latencies that are consistent with spinal, subcortical, and cortical processing (cf.^90,91). Our findings emphasize the importance of both agonist and antagonist muscles in the flexible control of sensorimotor gains in variable mechanical environments. Collectively, the data support the hypothesis that the nervous system alters its control policy when moving in the presence of random, time-varying disturbances.

Limitations of study

The findings highlight that the nervous system can modify control to deal with random, time-varying disturbances. OFC is a normative framework that captures many features of human and animal movements.^{2,3,18,75,80,82,83,92} Although our findings align with the predictions of stochastic OFC and its extension robust OFC, it is unclear how the nervous system implements such changes in control.^13,38 Several brain areas, such as the primary motor cortex,^34,35,36,37 the cerebellum,^93,94,95 and the brainstem,⁹⁶ may be involved in shaping the control of reaching movements since these areas receive sensory information and communicate with the spinal cord. Future work should examine the neural circuitry that gives rise to the changes in control that emerge when dealing with random disturbances² or altered movement reward.²⁰

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
MATLAB (R2020b)	MathWorks	RRID: SCR_001622
RStudio (1.1.463)	RStudio Inc.	RRID: SCR_000432
Other
Kinarm exoskeleton	Kinarm	https://kinarm.com/
Delsys Bagnoli DE-2.1 EMG Sensors	Delsys	https://delsys.com/

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Tyler Cluff (tyler.cluff@ucalgary.ca).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

A total of 70 adults participated in one of three experiments (35 males, 35 females, between 18 and 51 years of age, 4 left-handed individuals). Sixteen individuals participated in experiment 1, 28 individuals participated in experiment 2, and 26 individuals participated in experiment 3. All participants had normal or corrected-to-normal vision and reported no musculoskeletal or neurological impairments. Participants provided written informed consent prior to participation. The experimental procedures were approved by the University of Calgary’s Conjoint Health and Research Ethics Board (REB16-1670). The experiments took between 90 and 150 min to complete, and participants were compensated for their time ($20 CAD).

Method details

Apparatus and Motor Task

Participants sat in a robotic exoskeleton device (Kinarm Exoskeleton Lab; Kinarm, Kingston, ON, Canada).^8,9 The device supported the dominant arm against gravity and enabled near frictionless motion of the upper limb in a horizontal plane. The robotic device can selectively apply mechanical loads at the shoulder and/or elbow joints. Visual targets and a real time, hand-aligned feedback cursor (white, 0.5 cm radius) were projected into the participant’s workspace using an LCD monitor and semi-silvered mirror. Direct vision of the arm was blocked by a metal barrier throughout the experiments.

Participants performed 15 cm reaching movements from a start target (radius = 0.65 cm) to goal target (radius = 1.5 cm; Figure 2A). The start target was located at a shoulder angle of 0° (relative to the frontal plane) and elbow angle of 90° (relative to the upper arm). The goal target was positioned directly in front of the start target. At the beginning of each trial, participants moved their hand-aligned feedback cursor into the start target. After a brief hold period (800–1200 ms, uniform distribution), the goal target was displayed in red. Participants were instructed to reach to the goal target within 700 ms of movement onset and hold this position for 750 ms. Movement onset was defined as the instant in time when the center of the hand-aligned feedback cursor left the start target. Movement time was determined as the time difference between movement onset and when the cursor entered the goal target.^18,45,97 The trials were self-paced without any constraints on reaction time. Participants received explicit timing feedback on each trial. The goal target turned green and ‘Good Timing!’ was displayed on the screen if participants completed the movement on time and held the target position. The goal target turned blue and ‘Speed Up!’ was displayed on the screen if the participant’s reach was too slow or they did not maintain their feedback cursor in the goal target. The start target then reappeared on the screen, and participants returned the cursor into the start target.

Experiment 1

The goal of this experiment was to assess whether feedback gains are modulated when participants interact with random disturbances. We probed the feedback gains by applying mechanical perturbations that rapidly displaced the elbow joint on randomly interleaved trials (i.e., mechanical probes).^13,14 The perturbations (±1.5 Nm at the shoulder and elbow joint, 10 ms sigmoidal ramp-up) were applied at movement onset. The mechanical probes displaced the hand lateral to the goal target by selectively disturbing the elbow joint into flexion or extension. Shoulder motion was relatively unaltered for >100 ms after perturbation onset due to the nature of the multi-joint torque perturbations.^10,11,12 Participants were instructed to counter the mechanical probes and reach the goal target given the same time demands as unperturbed trials. The same explicit feedback was presented while participants held the target position.

Before starting the experiment, participants familiarized themselves with the testing conditions by performing 105 practice trials. The main experiment was split into baseline, exposure, and washout phases. During baseline, participants performed 140 trials. In the exposure phase, participants were exposed to randomly changing step torques while reaching to the goal target (exposure trials). The torque magnitude was sampled from a normal distribution (μ = 0, σ = 1 Nm) and changed every 25 ms (Figure 2C). The torques were turned off as soon as participants entered the goal target. Participants performed 280 trials in the exposure phase. Lastly, the random disturbances were unexpectedly removed during washout, where participants performed 140 trials. Note that all trials were presented in blocks of 5 unperturbed reaching trials or exposure trials and 2 mechanical probes (1 flexion & 1 extension).

Experiment 2

We conducted a follow-up experiment to assess whether feedback gains increase with the variability of random disturbances during reaching (Figure 4). Experiment 2 followed a similar design to experiment 1. Participants first familiarized themselves with the task by performing 140 practice trials. Next, participants performed 140 trials during baseline. In contrast to experiment 1, participants encountered step torques with low and high variability during the exposure phase. The disturbances in the low variability condition were sampled from a normal distribution with μ = 0 and σ = 1 Nm. The disturbances in the high variability condition were sampled from a distribution with μ = 0 and σ = 2 Nm to increase the likelihood of encountering larger disturbances during reaching movements. The low and high variability conditions were counterbalanced across all participants. In addition, we interleaved unperturbed reaching trials throughout the exposure phase to assess the forward velocities, movement times, and changes in muscle activity surrounding movement onset in the absence of random disturbances (see emg recordings and analysis).^21,22,23,24 The low and high variability conditions consisted of 280 trials each. Finally, participants performed 140 trials during washout. Note that trials were presented in blocks of 10 unperturbed reaching trials or exposure trials and 4 mechanical probes (2 flexion & 2 extension). Furthermore, each block also included 2 unperturbed reaching trials throughout the exposure phase.

Experiment 3

We conducted a third experiment to rule out influences of increased background muscle activity and/or muscle stiffness that could influence the responses to mechanical perturbations.^41,42 The experiment also allowed us to ensure that the results are linked to a change in control instead of a selective increase in responsiveness to proprioceptive feedback due to a reweighting of feedback during state estimation (cf.^53,54,55). In experiment 3, we probed feedback gains by applying sudden shifts in cursor feedback on randomly selected trials (i.e., visual probes).^46,47,48,49 Throughout the experiment, we used constant and transient visual probes during which the cursor position shifted lateral to the reach direction (±4 cm) when leaving the start target. Following constant visual probes, participants were required to respond to the visual perturbation. The veridical cursor position was restored at the end of the trial. Following transient visual probes, the veridical cursor position was restored after 250 ms. Importantly, we also restricted hand motion to a straight path connecting the start and goal targets by an error clamp.⁴⁷ The forces of the error clamp ramped up as soon as the goal target was shown (400 ms sigmoidal ramp-up). The error clamp had a stiffness of 600 N/m and a viscosity of 15 N/m.⁹⁸ Past work has shown that feedback responses following cursor jump trials are largely unaffected by changes in background loads.^49,89 Moreover, we reasoned that stiffness of the antagonist muscles due to changes in co-activation would have little benefit to visual disturbances or could impede responses to cursor jumps by resisting the corrective response (stretch of the antagonist muscles). Thus, this approach allowed us to quantify changes in feedback gains when interacting with random torque disturbances. We included both constant and transient visual probes throughout the experiment to avoid a downregulation of feedback gains.^47,56

Experiment 3 followed a similar design to experiment 2. First, participants performed 105 trials to familiarize themselves with the task. Then, they performed 225 trials during baseline. In the exposure phase, participants encountered random disturbances with low (μ = 0, σ = 1 Nm) and high (μ = 0, σ = 2 Nm) variability akin to experiment 2. Since we did not observe any statistical evidence (no reliable interaction effects of mixed analyses of variance; Table S1) suggesting order effects in experiment 2, all participants encountered the low variability condition first. Participants performed 480 trials in both the low and high variability conditions. Finally, they performed 225 trials during washout. Note that the trials were presented in blocks of 10 unperturbed reaching trials or exposure trials, 1 error clamp trial, 2 constant visual probes, and 2 transient visual probes. Similar to experiment 2, each block also included 1 unperturbed reaching trial throughout the low and high variability conditions.

Quantification and statistical analysis

Kinematic and kinetic recordings and analysis

Elbow and shoulder kinematics and kinetics were recorded by the robotic exoskeleton at 1000 Hz.^8,9 The kinematic and kinetic data were filtered (low-pass, second order, dual-pass Butterworth filter, 30 Hz cutoff) before further analysis.^98,99 Across all experiments, we assessed the vigor of voluntary movements by calculating the amplitude and timing of the peak forward hand velocity and movement times during unperturbed reaching and exposure trials.² Moreover, we quantified hand path variability perpendicular to the reach direction in unperturbed and exposure trials by averaging the standard deviation from movement onset to offset. During mechanical probes, we examined the vigor of corrective responses by extracting the peak lateral hand displacements.^18,19 During transient visual probes, we quantified the vigor of corrective responses by subtracting the averaged forces during unperturbed error clamp trials from the forces measured following the cursor jumps.^46,47 Similarly, we subtracted the averaged lateral velocities during unperturbed trials from the lateral velocities observed during constant visual probes.⁴⁸ We extracted the average channel forces and lateral velocities in an early (Force_early & Velocity_early: 180 to 230 ms after cursor jump onset) and late (Force_late & Velocity_late: 230 to 280 ms after cursor jump onset) time window.^46,48 Note that the data of visual probes were aligned with the perturbation onset while considering the delays of the video display. We mapped these delays using a photodiode.

EMG recordings and analysis

We recorded electromyographic activity (EMG) from mono-articular (brachioradialis, triceps lateralis) and biarticular (biceps brachii, triceps longus) elbow muscles using bipolar surface electrodes (DE 2.1 Single Differential Electrode, Delsys, Boston, MA, USA).^10,76 Before placing the electrodes, we prepared the recording sites by removing hair and cleaning the skin surface with isopropyl alcohol. The electrodes were placed on the skin surface overlying the belly of each muscle and parallel to the orientation of muscle fibers. A reference electrode was placed over the right olecranon process or lateral epicondyle. EMG signals were amplified online (gain = 10³-10⁴) and sampled at 1 kHz. EMG data were band-pass filtered (third order, dual-pass Butterworth filter, 20 and 450 Hz) and full-wave rectified prior to further analysis.^10,76 Each muscle’s activity was normalized to the average activity required to counter ±1 Nm reference loads.⁹⁹ The loads excited either the elbow flexor or extensor muscles by displacing the elbow joint into extension or flexion (2 conditions). Participants performed 5 trials for each condition, during which they countered the reference loads for 15 s. The normalization task was performed after experiments 1 and 2 and before experiment 3. Following the EMG normalization, we averaged the activity of elbow flexor or extensor muscles to simplify our analysis since the individual muscles displayed qualitatively similar changes in activity.²⁵

We extracted the average muscle activity surrounding the onset of unperturbed reaching trials (−100 to 100 ms), which has been used to quantify the planning and initiation of voluntary movements.^21,22,23,24 In experiment 2, muscle activity observed during the interleaved unperturbed reaching trials during the exposure phase and reaching trials in baseline and washout was subtracted from the muscle activity recorded during mechanical probes (ΔEMG).^11,18,19 Subsequently, we quantified muscle stretch and shortening responses associated with rapid feedback responses. We focused our analyses on the short-latency (SLR_mechanical: 25 to 50 ms after perturbation onset) and long-latency (LLR_mechnical: 50 to 100 ms after perturbation onset) responses.^2,26 Since experiment 1 did not include unperturbed reaching trials in the exposure phase and muscle activity is biased in exposure trials due to the randomly applied loads, we did not further investigate EMG data in experiment 1. In experiment 3, we subtracted the muscle activity during interleaved error clamp trials without cursor jumps from the activity recorded during transient visual probes⁴⁶ or the activity during unperturbed trials from the muscle activity measured during constant visual probes.⁴⁸ Based on the ΔEMG, we quantified the feedback gains by extracting the average muscle responses in the short-latency (SLR_visual: 90 to 120 ms after cursor jump onset) and long-latency (LLR_visual: 120 to 180 ms after cursor jump onset) response.^{46,48,57,58,59} The kinematic, kinetic, and EMG analyses were performed in MATLAB (R2020b, Mathworks, Natick, MA).

Statistical analysis

We conducted planned contrast analyses to test our hypotheses.^15,16,17 Contrast analyses are statistical procedures that test specific questions.^15,16,17 In short, fixed weights (λ-weights) are assigned to the means of the testing conditions of interest (e.g., baseline, exposure, & washout) that represent a hypothesized trend (e.g., quadratic trend) with the sum of all weights equaling zero. Rosenthal and colleagues^15,16,17 have highlighted that contrast analyses have greater statistical power and are more specific in answering research questions compared to omnibus analyses of variance with subsequent post-hoc comparisons. Recent research has utilized contrast analyses for their statistical analyses.^18,79,100

In experiment 1, we expected an increase (e.g., forward hand velocity) or decrease (e.g., peak lateral displacement) in outcome measures when interacting in the exposure phase and a return to baseline levels during washout. Thus, we examined a quadratic trend. The following weights were assigned to each experimental phase to indicate an increase during the exposure phase: λ_baseline = −0.5, λ_exposure = 1, & λ_washout = −0.5. The signs of the weights were flipped to indicate a decrease in the outcome measure. In experiments 2 and 3, we expected an increase in outcome measure paralleling the variability of the random physical disturbances with a return to baseline levels during washout. Therefore, we expanded the quadratic trend with a linear component representing the scaling effects. The following weights were used to assess an increase in the outcome measure: λ_baseline = −0.5, λ_low = 0.25, λ_high = 0.75, & λ_washout = −0.5. Again, the signs of the weights were flipped to indicate a decrease in the outcome measure. All t-statistics, degrees of freedom, and effect sizes based on Cohen’s d were reported in the main text.^15,16 Effect sizes in agreement with our hypotheses are positive. The statistical analyses and hypotheses are justified in light of past research.^2,5 The α-level threshold was set to 0.05. The contrast analyses were performed in RStudio (1.1.463; RStudio Inc.).

Published: April 27, 2023

Data and code availability

• •All data reported in this paper will be shared by the lead contact upon request.
• •This paper does not report original code. We used MATLAB (R2020b) and RStudio (1.1.463) to analyze the data in line with past research.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.