Abstract
Various neurological diseases affect the morphology of myelinated axons. Quantitative analysis of these structures and changes occurring due to neurodegeneration or neuroregeneration is of great importance for characterization of disease state and treatment response. This paper proposes a robust, meta-learning based pipeline for segmentation of axons and surrounding myelin sheaths in electron microscopy images. This is the first step towards computation of electron microscopy related bio-markers of hypoglossal nerve degeneration/regeneration. This segmentation task is challenging due to large variations in morphology and texture of myelinated axons at different levels of degeneration and very limited availability of annotated data. To overcome these difficulties, the proposed pipeline uses a meta learning-based training strategy and a U-net like encoder decoder deep neural network. Experiments on unseen test data collected at different magnification levels (i.e, trained on 500X and 1200X images, and tested on 250X and 2500X images) showed improved segmentation performance by 5% to 7% compared to a regularly trained, comparable deep learning network.
Keywords: myelin, axon, electron microscopy, meta learning
I. INTRODUCTION
An axon is a cable-like structure that extends from a neuron. Axons are responsible for the transmission of electrical signals between neurons and peripheral tissues. In the central and peripheral nervous systems, most axons are wrapped in a spiral fashion with a myelin sheath [1], as illustrated in Figure 1. A myelin sheath is an extended and modified plasma membrane that functions as an insulator [2]. Various neurological diseases affect the morphology of axons and the myelin sheaths surrounding them. High-resolution electron microscopy is used to capture the subtle morphological changes in the nervous system in general and in myelinated axons in particular (Figure 2). Quantitative analysis of these structures is of great importance for characterization of disease state and treatment response [3]–[6]. Image segmentation is the first step towards this goal. Various segmentation methods using deep learning approaches have been proposed for segmentation of axons and myelin sheaths around them. For example, [7] created a framework based on U-net for segmentation of axons and myelin sheaths in 2D images of scanning electron microscopy (SEM) and transmission electron microscopy (TEM); [8]–[10] proposed a software package using a deep neural network for 3D instance segmentation of axons and myelin; [11] introduced a 3D image dataset, AxonEM, for instance segmentation of axons in brain cortical regions. These models rely on the availability of large amounts of annotated data for training. This is a problem due to: (1) labor-intensive and expertise-required nature of the image segmentation process; (2) limited availability of diseased samples; (3) different imaging parameters for the existing data; and (4) large appearance variations in the data caused by neurodegeneration/regeneration.
Fig. 1:
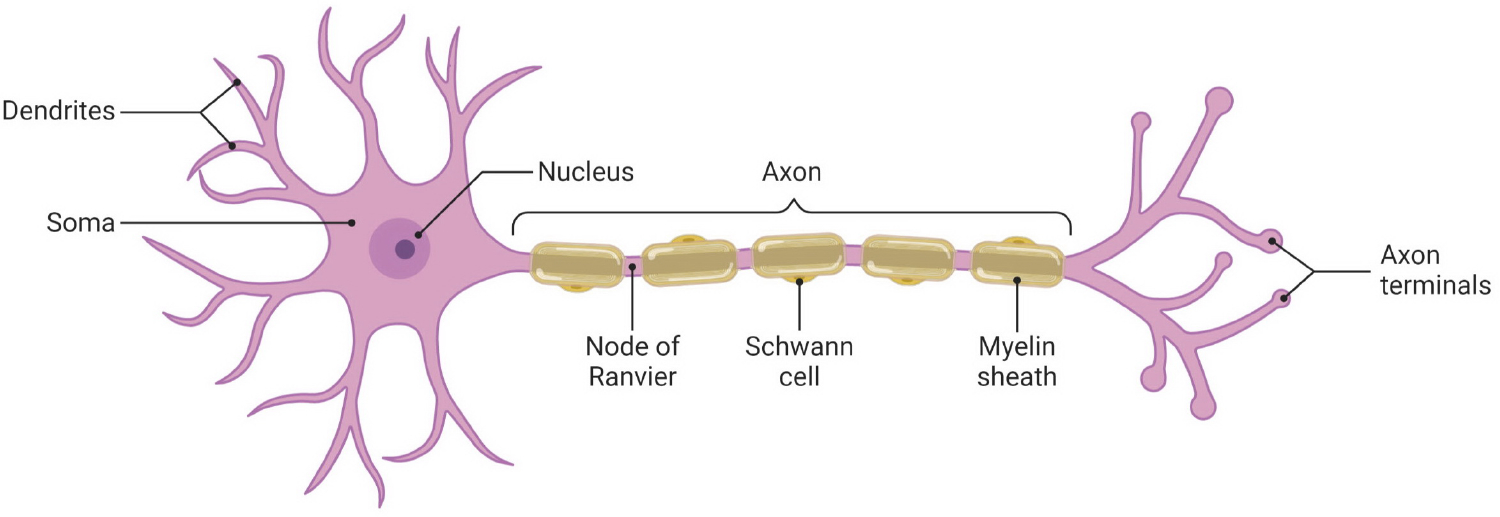
Neuron anatomy illustrated by using BioRender app [19]
Fig. 2:
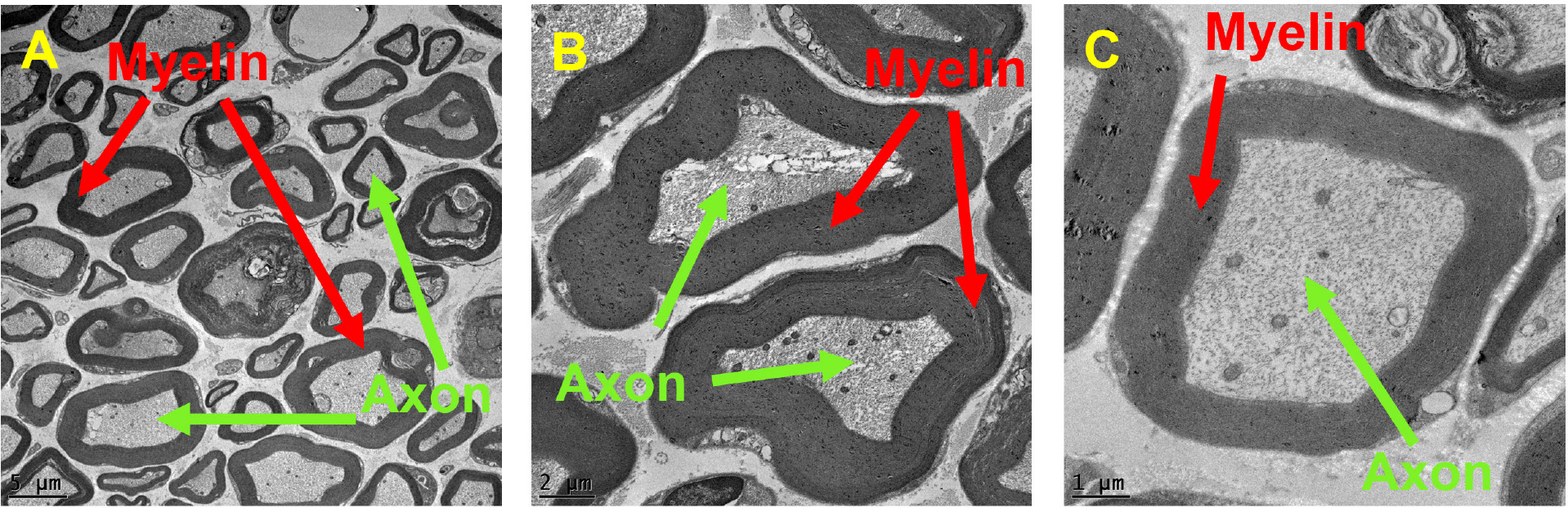
Electron microscopy images of axons and myelin sheaths surrounding them at different magnification levels: (A) 500X, (B) 1200X, and (C)2500X.
Recently, few-shot learning and meta learning methods have been introduced to improve the generalization capabilities of deep learning models to improve performance on unseen data [12]–[16]. [17] proposed a self-supervised few shot learning scheme to address scarce annotated data for medical image segmentation. [18] proposed a meta learning algorithm to capture the variety between slides for volumetric segmentation of medical images. This model was trained and tested on different sets of organs.
In this work, we present a meta learning-based deep learning system (Figure 3) for robust segmentation of axons and myelin sheaths in electron microscopy images of distal axons of hypoglossal neurons. Our group previously published qualitative evidence that distal axons of hypoglossal neurons exhibited degenerative changes following CTB-SAP-induced hypoglossal degeneration [20]. The proposed system will be used to enable effective quantitative analysis of electron microscopy-related bio-markers (myelin thickness and morphology, as well as axon number, size, and morphology) of hypoglossal degeneration and regeneration.
Fig. 3:
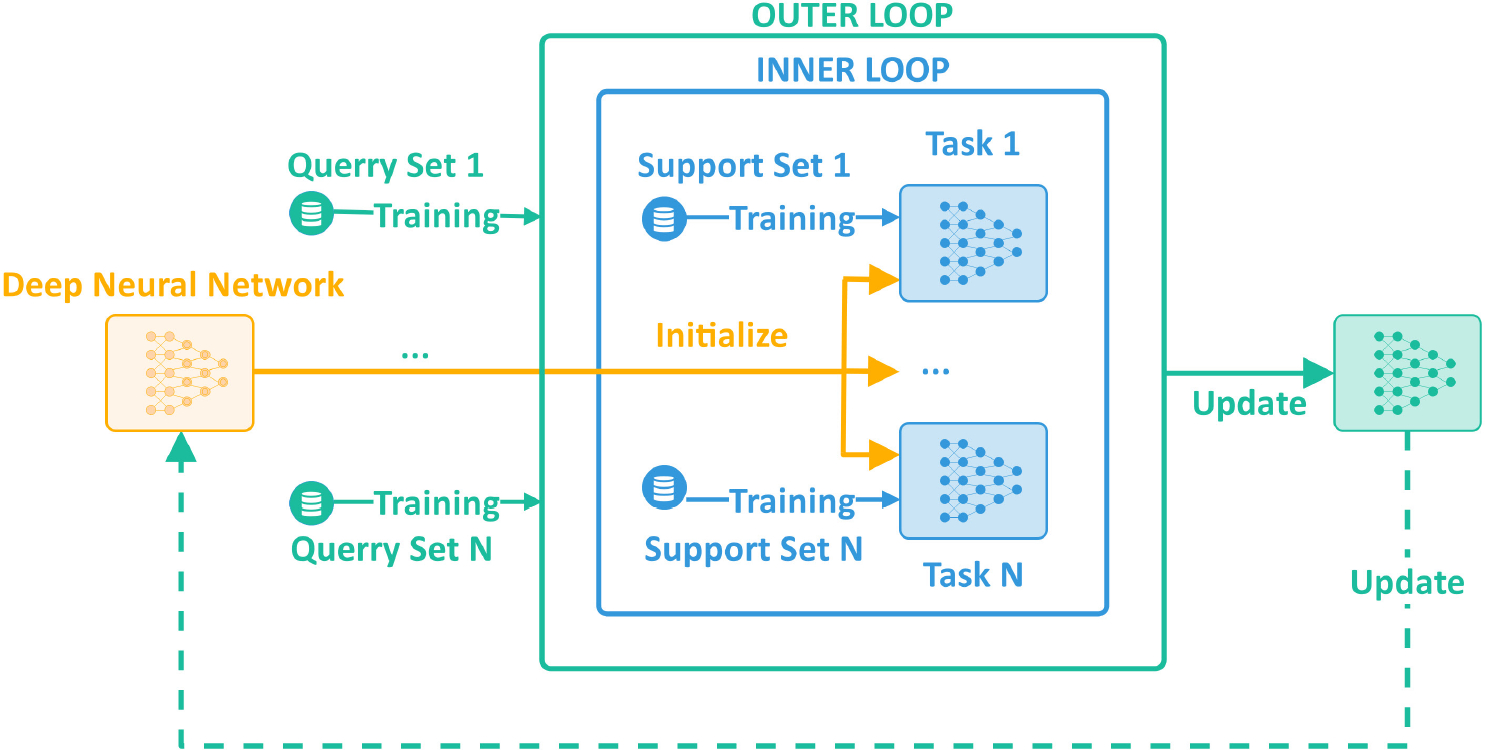
General training pipeline of meta learning for deep neural network.
II. METHODS
A. Core deep neural network
We used U-net network [21] as the core model for our segmentation pipeline. Input to the network is a single channel 2D grayscale image. Output from the network is a 3-channel 2D segmentation mask corresponding to axon, myelin, and background regions in the input image. The network’s encoder uses the ResNet-34 model [22] as the backbone. It’s a fully convolutional deep neural network with shortcut connections to learn residual features. The encoder includes three primary layers with 16, 32, and 64 filters, respectively.
B. Meta learning optimization
Meta-learning algorithms can be categorized into three main groups: (1) metric-based, (2) model-based, and (3) optimization-based [15], [16], [23] approaches. The metric-based approaches learn data representations by comparing two feature mappings, one corresponding to a support item, the other to a query item. These approaches rely on siamese networks [24], matching networks [25], relation networks [26], or prototypical networks [27] for comparison. The model-based approaches accomplish rapid learning by updating only a subset of network parameters based on value-memory location relationships. In order to generate a prediction, artificial neural networks (ANN) typically employ all of their parameters. This process necessitates updating of all these parameters in each training cycle. Unlike the regular ANNs, the model-based approaches employ a human-like learning mechanism. They bind the learned values (contents) to some specific locations of memory using Memory-Augmented Neural Networks (MANN) [28] enabling updating of specific network parameters. The optimization-based approaches enhance model generalization by utilizing a complex pipeline for training. In this work, we utilize an optimization-based approach that improves the generalization capabilities of a U-net [21] like encoder-decoder network architecture designed for image segmentation. This method begins by sampling a batch of tasks (N-ways) following a distribution . Then each task randomly selects a subdataset including data points (m-shots) from the whole dataset. These subdatasets do not overlap with one another. We partition each subdataset into two disjoint sets: a support set and a query set . The neural network is trained with an interleaved training procedure, comprised of inner and outer update loops [23]. First, the neural network is trained on the support sets in the inner loop. Then, it is fine-tuned using prior information extracted from query sets in the outer loop. Figure 3 illustrates the general overview of the optimization based training approach. Practical implementation for this approach can use algorithms such as Model-Agnostic Meta-Learning (MAML) [23], [29] or Reptile learning [30].
Assuming that our neural network model has a set of parameters , the inner loop in MAML optimizes the parameters of this network for each task individually by minimizing the loss over the task’s support set in steps. Specifically, the parameter set is updated for each task and step as following:
where denotes the parameter set for task at step denotes the gradient with respect to the parameter set denotes the loss function of task i on the support set at the current step; and is the inner loop learning rate.
After these initial updates, the outer loop fine-tunes the network parameters by minimizing the loss across the query sets of all tasks. Figure 4 illustrates the update sequence of MAML. Each iteration of the outer loop updates the network parameters using the following equation:
where denotes the parameter set for task at step generated by the inner loop; denotes the loss function of task on the query set; and is the outer loop learning rate.
Fig. 4:
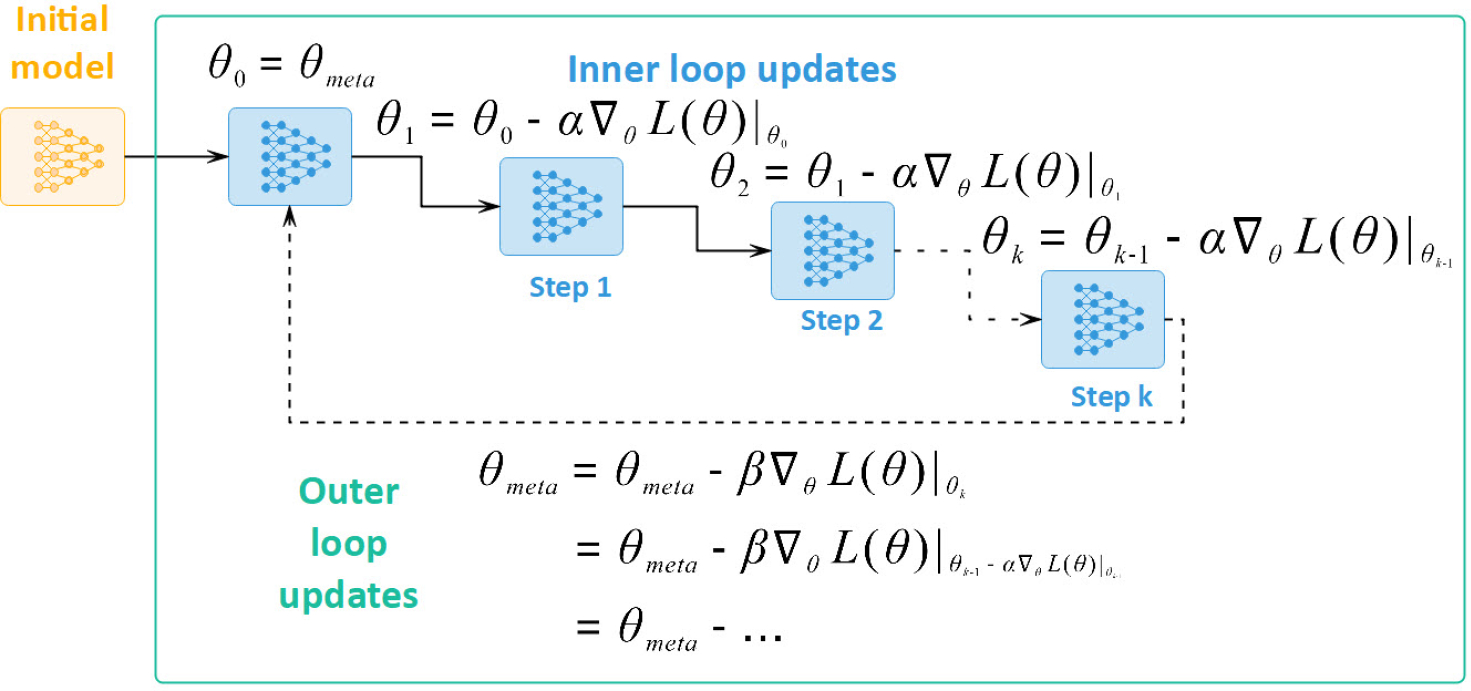
Unrolling gradient updates between inner loop and outer loop in MAML [23], [29].
The analytical relationship between gradient updates in the inner loop and the outer loop can be derived as following [23], [29]. In the inner loop of task , we perform gradient update steps on its support set as follows:
where denotes the parameter set for task at step denotes the gradient with respect to the parameter set denotes the loss function of task i on the support set at the current step; and is the inner loop learning rate.
Then the outer loop relies on those updated parameters to work on the query sets as illustrated in Figure 4 and shown below:
where
MAML is simplified to First Order MAML (FO-MAML) if we ignore the last term in the final equation. In other words, FO-MAML only keeps the last level of gradient in the inner loop and applies it to update parameters in the outer loop. In the Reptile algorithm [30], if the inner loop only performs a single step , then the outer loop works as minimizing the expected loss over all the query sets.
For this paper, we selected to use the MAML learning scheme to optimize our model because of its high-order optimization approach.
III. EXPERIMENTAL RESULTS
A. Dataset
The dataset used in this study consists of electron microscopy images of distal axons of hypoglossal neurons. Samples were prepared as described in [20]. Images were acquired at University of Missouri Electron Microscopy Core with a TEM microscope (JEM 1400; JEOL, Ltd, Tokyo, Japan) at 80 kV using a CCD camera (Ultrascan 1000; Gatan, Inc, Pleasanton, California). Control and CTB-SAP (CTB–saporin, cholera toxin B conjugated to saporin) injected rats were used in the study. Hypoglossal motor neuron death via CTB–SAP injections mimic aspects of amyotrophic lateral sclerosis (ALS) related to dysphagia (swallowing difficulties) [7]. For training, we used three data subsets: our image samples at 500X and 1200X magnification levels (197 images with dimension 2048 × 2048), and an additional publicly available TEM dataset of axons and myelin [7] at ~500X magnification level (157 images with dimension 3762×2286). Our other two data subsets at magnification levels 250X and 2500X (52 images with dimension 2048 × 2048) were used as unseen data for testing. The training data were split into tasks for the meta learning training pipeline.
B. Results and evaluation
We have evaluated the axon and myelin segmentation performance of the proposed meta learning-based pipeline and compared to a similar deep neural network (with U-net architecture [21]) trained using a regular training approach where a single training loop and a single training task was used. We utilized dice score [31] to assess image segmentation performance. Given a predicted segmentation mask and a ground truth segmentation mask , dice score is computed as:
Table I shows segmentation performance on the training set in which the regular training slightly outperforms the meta learning pipeline with 90% versus 89% dice scores, respectively. However, when both systems were tested on unseen data with different characteristics (magnification levels 250X and 2500X), the proposed axon and myelin segmentation pipeline with meta learning resulted in significant performance improvements against regular training. Table II illustrates the test results where the meta learning-based pipeline outperforms regular training by 5% to 7%, in terms of dice scores, for two subsets with magnification levels of 250X and 2500X and for both categories of control and diseased samples. For both of the training schemes, better segmentation performances were obtained on the control samples compared to the diseased samples due to the abnormal structures and textures on these cases.
TABLE I:
Training results
| Zoom Level | Training Dice Scores (%) | |||
|---|---|---|---|---|
| Regular Training | Meta Learning | |||
| Control | Disease | Control | Disease | |
| 500X | 90 | 89 | ||
| 1200X | ||||
| TEM | ||||
TABLE II:
Test results
| Zoom Level | Test Dice Scores (%) | |||
|---|---|---|---|---|
| Regular Training | Meta Learning | |||
| Control | Disease | Control | Disease | |
| 250X | 77 | 76 | 84 (+7) | 82 (+6) |
| 2500X | 86 | 83 | 91 (+5) | 90 (+7) |
Figure 5 illustrates sample segmentation results on the training data with 500X and 1200X magnification levels and on the test data with 250X and 2500X magnification levels. As expected and as can be seen from the raw images, different magnification levels reveal different size, shape, and texture characteristics. In Figure 5, yellow and purple overlays mark the detected axon and myelin regions, respectively. Blue arrows point to missed myelin regions either due to misclassification as background or as axon, and red arrows point to false myelin detections. While mostly satisfactory results were obtained for the training magnification levels, partially missed myelin layers and some axon regions misclassified as myelin are observed for test magnification levels in regular training results. These issues are largely reduced after using the proposed meta learning-based segmentation scheme.
Fig. 5:
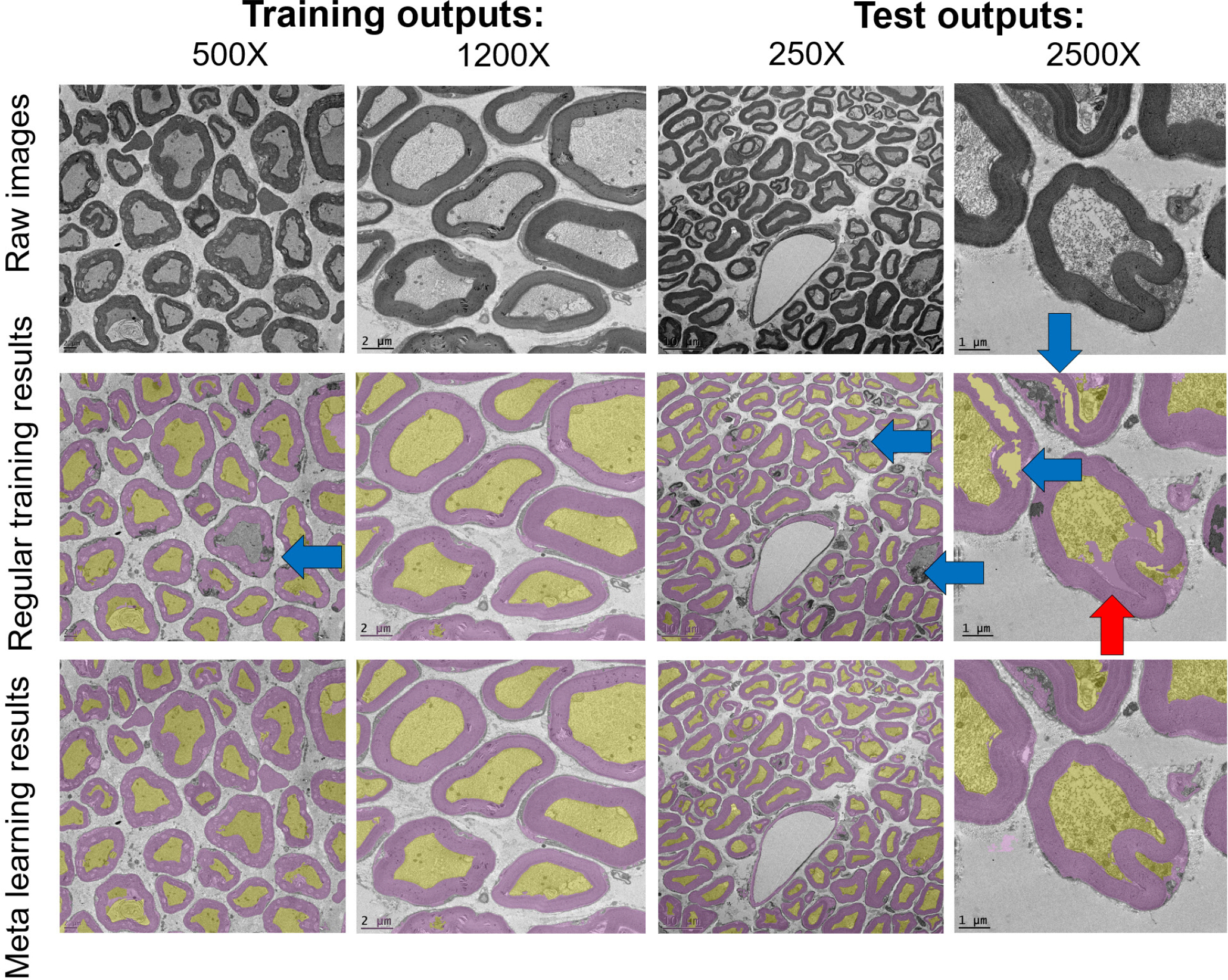
Segmentation outputs for training and test stages: axons (yellow areas) and myelin (purple areas). Blue arrow: false negative, red arrow: false positive.
These results demonstrate generalization capabilities of meta learning. These capabilities are critical for problems with scarce annotated data and for problems with largely varying data characteristics due to imaging parameters (e.g., zoom levels) or sample characteristics (e.g., different levels of neurodegeneration). The proposed pipeline using meta learning leads to a promising solution for segmentation of axons and myelin in electron microscopy images, particularly at high image resolutions (magnification levels 1200X and 2500X) where axon, myelin, and background textures are better observed.
IV. CONCLUSIONS
In this study, we proposed a meta learning-based deep learning system for robust segmentation of axons and myelin sheaths in electron microscopy images. The proposed meta learning-based system lead to 5% to 7% performance improvement compared to regular training. This image segmentation scheme will be our first step towards computation of medically relevant, image analytics-based outcome measures describing size, shape, and texture properties of axons and surrounding myelin layers. These outcome measures will be used to quantify neurodegenerative changes and to characterize disease-state and treatment response. Of particular interest to this study is degeneration and regeneration of hypoglossal motor neurons and resulting swallowing function impairment and improvement respectively.
Acknowledgement.
This work was partially supported by the National Institutes of Health Grant R01HL153612-03 and MU VRSP (Veterinary Research Scholars Program). The authors would like to acknowledge DeAna Grant at the University of Missouri Electron Microscopy Core for her assistance with processing and imaging of the nerve samples.
REFERENCES
- [1].Stassart RM, Möbius W, Nave K-A, and Edgar JM, “The axon-myelin unit in development and degenerative disease,” Frontiers in neuroscience, p. 467, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Raine CS, “Morphology of myelin and myelination,” in Myelin. Springer, 1984, pp. 1–50. [Google Scholar]
- [3].Robertson AM, Huxley C, King RH, and Thomas PK, “Development of early postnatal peripheral nerve abnormalities in Trembler-J and PMP22 transgenic mice,” J. Anat, vol. 195, no. Pt, p. 3, Oct. 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Verhamme C, King RHM, Asbroek A. L. M. A. t., Muddle JR, Nourallah M, Wolterman R, Baas F, and van Schaik IN, “Myelin and axon pathology in a long-term study of PMP22-overexpressing mice,” J. Neuropathol. Exp. Neurol, vol. 70, no. 5, pp. 386–398, May 2011. [DOI] [PubMed] [Google Scholar]
- [5].Zhao HT, Damle S, Ikeda-Lee K, Kuntz S, Li J, Mohan A, Kim A, Hung G, Scheideler MA, Scherer SS, Svaren J, Swayze EE, and Kordasiewicz HB, “PMP22 antisense oligonucleotides reverse Charcot-Marie-Tooth disease type 1A features in rodent models,” J. Clin. Invest, vol. 128, no. 1, pp. 359–368, Jan. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Kaiser T, Allen HM, Kwon O, Barak B, Wang J, He Z, Jiang M, and Feng G, “MyelTracer: A Semi-Automated Software for Myelin g-Ratio Quantification,” eNeuro, vol. 8, no. 4, Jul. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Zaimi A, Wabartha M, Herman V, Antonsanti P-L, Perone CS, and Cohen-Adad J, “AxonDeepSeg: automatic axon and myelin segmentation from microscopy data using convolutional neural networks,” Sci. Rep, vol. 8, no. 3816, pp. 1–11, Feb. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Abdollahzadeh A, Belevich I, Jokitalo E, Tohka J, and Sierra A, “Automated 3D Axonal Morphometry of White Matter,” Sci. Rep, vol. 9, no. 6084, pp. 1–16, Apr. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Abdollahzadeh A, Belevich I, Jokitalo E, Sierra A, and Tohka J, “DeepACSON automated segmentation of white matter in 3D electron microscopy,” Commun. Biol, vol. 4, no. 179, pp. 1–14, Feb. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Behanova A, Abdollahzadeh A, Belevich I, Jokitalo E, Sierra A, and Tohka J, “gACSON software for automated segmentation and morphology analyses of myelinated axons in 3D electron microscopy,” Comput. Methods Programs Biomed, vol. 220, p. 106802, Jun. 2022. [DOI] [PubMed] [Google Scholar]
- [11].Wei D, Lee K, Li H, Lu R, Bae JA, Liu Z, Zhang L, dos Santos M, Lin Z, Uram T, Wang X, Arganda-Carreras I, Matejek B,Kasthuri N, Lichtman J, and Pfister H, “AxonEM Dataset: 3D Axon Instance Segmentation of Brain Cortical Regions,” in Medical Image Computing and Computer Assisted Intervention – MICCAI 2021. Cham, Switzerland: Springer, Sep. 2021, pp. 175–185. [Google Scholar]
- [12].Wang Y, Yao Q, Kwok JT, and Ni LM, “Generalizing from a Few Examples: A Survey on Few-shot Learning,” ACM Comput. Surv, vol. 53, no. 3, pp. 1–34, Jun. 2020. [Google Scholar]
- [13].Sun J and Li Y, “MetaSeg: A survey of meta-learning for image segmentation,” Cognitive Robotics, vol. 1, pp. 83–91, Jan. 2021. [Google Scholar]
- [14].Huisman M, van Rijn JN, and Plaat A, “A survey of deep meta-learning,” Artif. Intell. Rev, vol. 54, no. 6, pp. 4483–4541, Aug. 2021. [Google Scholar]
- [15].Song Y, Wang T, Mondal SK, and Sahoo JP, “A Comprehensive Survey of Few-shot Learning: Evolution, Applications, Challenges, and Opportunities,” arXiv, May 2022. [Google Scholar]
- [16].Hospedales T, Antoniou A, Micaelli P, and Storkey A, “Meta-Learning in Neural Networks: A Survey,” IEEE Trans. Pattern Anal. Mach. Intell, vol. 44, no. 09, pp. 5149–5169, Sep. 2022. [DOI] [PubMed] [Google Scholar]
- [17].Ouyang C, Biffi C, Chen C, Kart T, Qiu H, and Rueckert D, “Self-Supervised Learning for Few-Shot Medical Image Segmentation,” IEEE Trans. Med. Imaging, vol. 41, no. 7, pp. 1837–1848, Feb. 2022. [DOI] [PubMed] [Google Scholar]
- [18].Farshad A, Makarevich A, Belagiannis V, and Navab N, “MetaMed-Seg: Volumetric Meta-learning for Few-Shot Organ Segmentation,” in Domain Adaptation and Representation Transfer. Cham, Switzerland: Springer, Sep. 2022, pp. 45–55. [Google Scholar]
- [19].“BioRender,” Nov. 2022, [Online; accessed 15. Nov. 2022]. [Online]. Available: https://biorender.com
- [20].Lind LA, Lever TE, and Nichols NL, “Tongue and hypoglossal morphology after intralingual cholera toxin b–saporin injection,” Muscle & nerve, vol. 63, no. 3, pp. 413–420, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Ronneberger O, Fischer P, and Brox T, “U-Net: Convolutional Networks for Biomedical Image Segmentation,” in Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. Cham, Switzerland: Springer, Nov. 2015, pp. 234–241. [Google Scholar]
- [22].He K, Zhang X, Ren S, and Sun J, “Deep residual learning for image recognition,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, pp. 770–778. [Google Scholar]
- [23].Weng L, “Meta-Learning: Learning to Learn Fast,” Nov. 2018, [Online; accessed 9. Nov. 2022]. [Online]. Available: https://lilianweng.github.io/posts/2018-11-30-meta-learning
- [24].Koch G, Zemel R, and Salakhutdinov R, “Siamese neural networks for one-shot image recognition,” 2015. [Google Scholar]
- [25].Vinyals O, Blundell C, Lillicrap T, Kavukcuoglu K, and Wierstra D, “Matching Networks for One Shot Learning,” Advances in Neural Information Processing Systems, vol. 29, 2016. [Online]. Available: https://papers.nips.cc/paper/2016/hash/90e1357833654983612fb05e3ec9148c-Abstract.html [Google Scholar]
- [26].Sung F, Yang Y, Zhang L, Xiang T, Torr PHS, and Hospedales TM, “Learning to compare: Relation network for few-shot learning,” 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 1199–1208, 2018. [Google Scholar]
- [27].Snell J, Swersky K, and Zemel RS, “Prototypical networks for few-shot learning.” in NIPS, Guyon I, von Luxburg U, Bengio S, Wallach HM, Fergus R, Vishwanathan SVN, and Garnett R, Eds., 2017, pp. 4077–4087. [Online]. Available: http://dblp.uni-trier.de/db/conf/nips/nips2017.html#SnellSZ17 [Google Scholar]
- [28].Santoro A, Bartunov S, Botvinick M, Wierstra D, and Lillicrap T, “Meta-Learning with Memory-Augmented Neural Networks,” in International Conference on Machine Learning. PMLR, Jun. 2016, pp. 1842–1850. [Online]. Available: http://proceedings.mlr.press/v48/santoro16.html [Google Scholar]
- [29].Finn C, Abbeel P, and Levine S, “Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks,” in International Conference on Machine Learning. PMLR, Jul. 2017, pp. 1126–1135. [Online]. Available: http://proceedings.mlr.press/v70/finn17a [Google Scholar]
- [30].Nichol A, Achiam J, and Schulman J, “On first-order meta-learning algorithms.” CoRR, vol. abs/1803.02999, 2018. [Online]. Available: http://dblp.uni-trier.de/db/journals/corr/corr1803.html#abs-1803-02999 [Google Scholar]
- [31].Zou KH, Warfield SK, Bharatha A, Tempany CMC, Kaus MR, Haker SJ, William I, Wells M, Jolesz FA, and Kikinis R, “Statistical Validation of Image Segmentation Quality Based on a Spatial Overlap Index: Scientific Reports,” Acad. Radiol, vol. 11, no. 2, p. 178, Feb. 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]


