Abstract
Minimally-invasive surgeries using transcatheter approaches and sophisticated imaging modalities are gaining popularity to treat mitral regurgitation (MR). This paper proposes the next generation of a robotic catheter to deliver an implant onto the mitral valve (MV) through a transseptal approach. The proposed robot has an outer diameter (OD) of 5.7 mm, a rigid distal end length of 20 mm, a prismatic tube that can be advanced by 50-60 mm, and a bending joint that can easily bend 120° to reach the valve opening. The implant can be rotated 75° bidirectionally by the distal torsion joint to orient it with the MV leaflet for precise implantation. The robotic joints are modeled individually, the forward and inverse kinematics are derived, and the robot motion validation is carried out through experimentation. A modified kinematics (MK) model, Prandtl-Ishlinskii (PI) hysteresis model, and hybrid of MK and PI model are used to compensate for the catheter nonlinearities. A preliminary study is conducted to evaluate if force sensing can be used to compensate for the effects of fluid flow. Also, the implantation procedure is demonstrated in a phantom heart.
I. Introduction
Mitral regurgitation (MR) is a commonly occurring heart condition where the valve between the left atrium (LA) and left ventricle (LV) does not close properly during systole, allowing the backflow of blood from the LV to LA. MR increases pressure in the pulmonary venous channel and the left atrial chamber, weakening the heart walls, causing shortness of breath, fatigue, lightheadedness, and in chronic cases, even heart failure. 1.7 % of US adult population and 9.3 % of adults over the age of 75 suffer from MR [1], [2]. If left untreated, the mortality rate of patients can increase to 57 % [3]. Open-heart surgery can provide immediate relief unlike medication, but 50 % of the MR patients are not recommended an open-heart surgery due to their age and possibilities of post-operative complications [4]. Minimally-invasive surgeries, aided by sophisticated imaging modalities, are becoming popular as a solution [5]-[8] due to reduced post-operative pain, fewer complications, and faster recovery time.
To address the problem of MR, transcatheter mitral valve repair (TMVr) is preferred over transcatheter mitral valve replacement (TMVR) to avoid LV outflow tract (LVOT) obstruction [9], valve thrombosis, structural degeneration over time, and complications due to inadequate anchoring and sealing. For primary (functional) MR, caused due to abnormalities in the mitral valve apparatus, TMVr techniques can be classified into two groups: edge-to-edge repair of mitral leaflets and chordae tendineae repair. The only CE marked and FDA approved transcatheter edge-to-edge repair system is the MitraClip™ device (Abbott Laboratories, IL). However, with CE approval and an ongoing investigational device exemption (IDE) trial, the Edwards Pascal transcatheter valve repair system (Edwards Lifesciences, CA) has better features like a central spacer, independently controlled clasps, and improved grasping capabilities [10]. For chordae tendineae repair, the Neochord DS 1000 (NeoChord, MN) and Harpoon TDS-5 (Edward Lifesciences, CA) systems perform transapical off-pump beating heart neochordae implantation [11] to hold the mitral valve (MV) leaflets in position. Moreover, modification of the mitral annulus, using the Cardioband™ system (Edwards Lifesciences, CA) and Carillon® mitral contour system™ (Cardiac Dimensions, WA), is another TMVr technique used in the case of structural and functional abnormalities of the left ventricle (secondary MR). However, since all pathologies are not repairable, TMVR techniques, like Intrepid (Medtronics, MN), Tendyne (Abbott Laboratories, IL), and Tiara (Neovasc, MN), are needed [12]. Dexterous manipulation of the catheter is required to deliver the implant onto the MV precisely [13] to treat primary MR. Proper bending and torquing capabilities of the catheter’s distal end to position and orient the implant are necessary for successful implantation. However, commercially available catheter systems have one catheter for steering (bending) and another catheter, put through the first, for remote torquing. Remote torquing causes less transmission efficiency and torque build-up (needs dottering) that may result in unwanted implant orientation change during grasping [14].
Furthermore, performing manual minimally-invasive surgeries for this application has three main challenges, i.e., over-exposure of surgeon and staff to radiation [15]-[17], surgeries following failed procedures in high-risk patients can be complex [18], [19], and the operators must be adequately trained to use the technology [20]. Robotic endoscopic systems can help overcome these obstacles while also increasing dexterity [21], hand-eye coordination, and visualization [16]. With a robotic system, lesser operators are required and the surgeons can work from a distance reducing exposure to radiation [17]. Also, the repeatability of robotic systems will encourage the development of standardized procedures, which are intuitive and less prone to human error.
To improve the commercially available catheter design, we have, in our prior work [22], developed a steerable robot to manipulate the mitral valve implant. In work following this, we reduced the dimensions (to 5.7 mm outer diameter (OD) of the steerable robot, automated it, and improved its torsion capabilities [23]. This paper presents the next generation design of the robotic catheter, which is clinically more relevant than the previous designs [22] [23]. The design reduction and modification of the sub-components of the robot structure, as mentioned below, are a significant improvement over our previous work:
The robot’s rigid distal end (RDE) length is 20 mm (previously 27 mm) to avoid collision with the left atrial wall. The compact design of the RDE is a challenge as it should: 1) accommodate the implant, which is 13 mm long, provide a significant moment arm to open the implant, and 3) also include a torsion joint to align the implant with the MV leaflet successfully.
The implant’s prismatic motion is increased from 18 mm to 60 mm, to effectively get under the MV leaflet by replacing the robot’s prismatic RDE section with a flexible prismatic quadlumen tube. This design modification aids in achieving the previous objective (limited RDE) and makes the prismatic motion limitation a characteristic of the actuation system that can be easily modified. Using the quadlumen tube makes dedicated tendon routing possible for the implant manipulation tendons.
Ultra-high-molecular-weight polyethylene (UHMWPE) tendons are used instead of nylon for higher strength, low friction, and insignificant elongation.
A new hyper-redundant bending joint design achieves a smoother continuous bend with internal tendon routing.
The working of the torsion joint is improved by using two metal tubes instead of a torsion spring hence avoiding pitching at higher angles under high tendon tension.
The robot is not actuated directly unlike in [22] [23] but through a 0.61 m long tube to access the heart chamber from the femoral vein. The increase in friction due to the tube is reduced by proper routing and design modifications, and the remaining nonlinearity is compensated using a hysteresis model.
A compact design is adopted with all the force exerting tendons, routed internally, unlike in [22] [23], to avoid tendon interaction with the internal heart structures. Also, the quadlumen tube provides dedicated paths for the implant manipulation tendons, thereby reducing friction and entanglement between the different tendons.
Also, the proposed design is used to find the position and orientation of the clip using C-Arm fluoroscopy through a deep learning semantic segmentation framework and an SVM classifier, respectively [24]. Additionally, the new bending joint that can bend to 120° (max 264°) facilitates reaching the mitral valve opening without kinking or any permanent deformation. Furthermore, the forward and inverse kinematics for this robot is derived, and the robot motion validation is performed through experimentation. The modified kinematics (MK) model, Prandtl-Ishlinskii (PI) hysteresis model, and a hybrid model using a combination of both are compared and used to compensate for the nonlinearities. We also did a preliminary study to evaluate if force sensing can be used to record and compensate for the effect of fluid flow at the actuation end. Also, the feasibility of the robotic catheter is demonstrated in a phantom heart model by steering the robot, clipping the implant onto the MV, and detaching the implant successfully from the robot. The paper is organized as follows: Section II explains the design and kinematics of the robotic system, section III describes the control system used to implement joint space control, section IV contains experiments and results. Finally, the conclusions and future work are covered in section V, followed by acknowledgments in section VI.
II. Design and Kinematics of the Robotic System
The robotic catheter proposed in this paper has two main parts: the steerable guide and the prismatic tube (Figure 1(a)). The steerable guide consisting of the proximal torsion and bending joint (Figure 1(b)) positions the robot tip to face the MV opening. The prismatic tube consists of the implant actuator that orients the implant and the quadlumen tube that advances the implant below the MV leaflet. The tendons in the implant holder manipulate (open and close) the implant for proper implantation (Figure 1(c)). The tendons from the steerable guide joints and the quadlumen tube carrying the implant manipulation tendons to the actuation system are routed through the inner tube that is 0.61 m long, as shown in Fig. 1(b). The flexible inner tube (Nylon, ID 3 mm, OD 5 mm) is held in a straight configuration for all the experiments performed in this paper, except the experiments in sections IV-D and IV-E. The robotic catheter component dimensions and joint capabilities are given in TABLE. I.
Fig. 1:
Schematic of entire robotic catheter. (a) Prismatic tube motion shown and robotic catheter parts labeled, (b) parts of robot labeled, and (c) tendon routing for implant manipulation shown at the: implant actuator, quadlumen tube, and implant manipulation actuator (actuation system).
TABLE I:
Robotic catheter component dimensions and joint capabilities.
| Proximal torsion module | Bending ring | Prismatic quad lumen tube | Distal torsion module | ||||
|---|---|---|---|---|---|---|---|
| r | 2.85 mm | t | 0.52 mm | OD | 1.68 mm | r | 2.85 mm |
| h | 2.5 mm | n | 10 | Lumen ID | 0.51 mm | h | 2 mm |
| a t | 120° | a b | 1.8 mm | Hardness | 72D | a t | 120° |
| length (TM) | 15mm | length | 2.04 mm | PE OD | 0.12 mm | length (TM) | 4.5 mm |
| length (BM) | 5mm | ID | 1.9 mm | length (BM) | 6 mm | ||
| Proximal torsion | ±75° | Bending | ±120° | Translation | 5-6 cm | Distal torsion | ±75° |
A. Steerable Guide
Bending Joint:
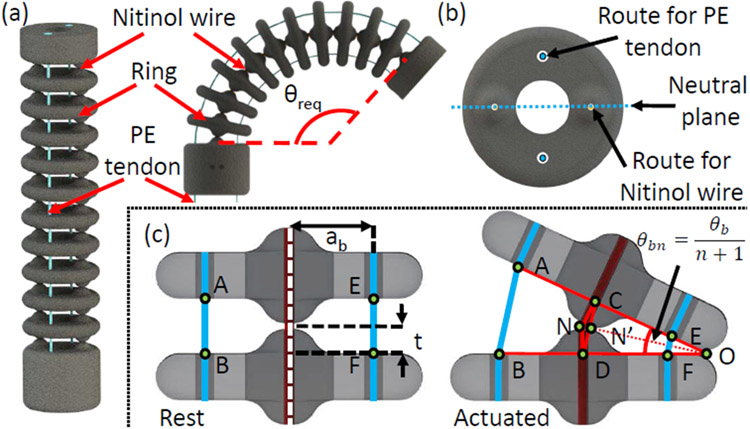
The bending joint is a stack of 10 rings connected concentrically by two superelastic 0.13 mm Nitinol wires (Confluent Medical, AZ) as shown in Figure 2(a). The two superelastic wires keep the joint straight when no external force is applied and pass vertically through diametrically opposite passages in the rings. The plane containing the Nitinol wires does not undergo any compression or expansion (neutral plane). A plane perpendicular to the neutral plane contains the routing passage of tendons to actuate the bending joint. The bending joint can be actuated to obtain the required angle, θb, by controlling the motion of the antagonistic PE tendons. The groove in each ring is introduced to accommodate the coupling wire (explained in section II-C).
Fig. 2:
Schematic of the bending joint. (a) Joint parts labeled: Nitinol wire, Ring and PE tendon. Route for tendon, route of the Nitinol wire, neutral plane, and groove for the coupling wire illustrated in the top view of a ring, and (b) joint parameters labeled.
In Figure 2(b), two rings: at rest and in the actuated state, are shown. At rest, and are equal to 2t, t being half the gap maintained in between the rings. However, when the joint is actuated, shortens and elongates. As ΔCOD is similar to ΔEOF and ΔAOB in the actuated state, we obtain:
| (1) |
and
| (2) |
where, ab, and θbn are the moment arm and the angle between two rings, respectively. The number of rings in the bending joint is n. To bend the joint by θb = θbn(n + 1), as (n + 1) is the total number of gaps, one tendon is pulled by and the other tendon is released by .
| (3) |
| (4) |
Here lpb and lrb are the required tendon pull and release lengths, respectively, and are a function of θb. The absolute value of lrb is always less than lpb. So, the joint can be bent using a single motor with a pulley to control the antagonistic tendons simultaneously [23]. The difference between lrb and lpb appears as slack on the expansion side which does not affect the bending angle. This bending joint can theoretically bend up to , which is ≈ 264°, far exceeding the clinically required value of 120°. The length of the bending joint can be adjusted by varying n.
Additionally, given the bending tendon displacement lb ≜ rpθpulley (pulling: lpb and releasing: lrb), where rp=7.19 mm is the radius of the pulley and θpulley is the motor actuation angle, we find θb using the inverse functions of (3) and (4) which are given by:
| (5) |
where , , , , , .
Torsion Joint:
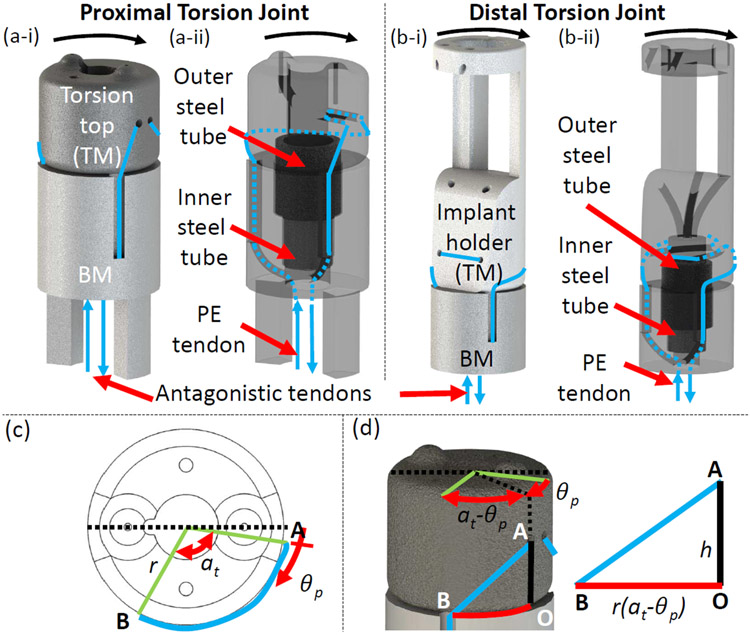
There are two torsion joints in the robot: proximal and distal (see Figure 3(a) and 3(b)). The proximal torsion joint is part of the steerable guide and the distal torsion joint is part of the prismatic tube (Figure 1(b)). Each torsion joint has four parts: top module (TM), bottom module (BM), inner steel tube, and outer steel tube. The TM and BM are held concentric to each other by the two steel tubes. In Fig. 3(a-i), the top (torsion top) and bottom modules of the proximal torsion joint are labeled, and the displacement of the antagonistic tendons is shown for the torsion motion indicated. Also, in Fig. 3(a-ii), the steel tubes (outer and inner) and the routing of the PE tendons through the proximal torsion joint are illustrated by making the top and bottom modules translucent. Similarly, in Fig. 3(b-i), the top (implant holder) and bottom modules of the distal torsion joint are labeled, and the displacement of the antagonistic tendons is shown for the torsion motion indicated. Moreover, in Fig. 3(b-ii), the steel tubes (outer and inner) and the routing of the PE tendons through the distal torsion joint are illustrated by making the top and bottom modules translucent. Buckling of the joint is avoided by using the steel tubes which is an improvement over the last design [23]. The two antagonistic PE tendons (shown in blue) connected to TM (Proximal: Torsion Top, Distal: Implant Holder) are wrapped around it and then routed along the wall of BM into the hollow lumen of the robot. Pulling one tendon by lp rotates TM. As shown in Figure 3(c) and 3(d), at home position the length of the tendon wrapped around TM of radius, r, is . When the joint is actuated by θp, the length of the tendon wrapped around TM is . Therefore, for the proximal torsion joint:
| (6) |
Fig. 3:
Schematic of the torsion joints. (a) Proximal torsion parts labeled and motion shown, (b) distal torsion joint parts labeled and motion shown, (c) joint parameters labeled, and (d) geometry of the joint shown.
The same equations hold for the distal torsion joint by replacing θp with θd. Ideally the torsion joint can achieve an angle of at=120° bidirectionally (see Figure 3(c)), but ±75° is practically achievable. However, ±75° is well above the clinically required ±45° for fine refinement. The proximal torsion joint aligns the robot’s bending plane with the plane containing the transseptal puncture point and MV annulus center. The distal torsion joint aligns the implant with the MV leaflet for proper coaptation.
Given the tendon displacement lp (pulley angle is lp/rp), we can find the inverse functions of (6) as follows:
| (7) |
where rp is the radius of the pulley.
B. Prismatic Tube
The prismatic motion of the prismatic tube controlled by the actuation system is shown in Figure 1(a).
Implant actuator:
The implant actuator comprises three parts: implant holder (TM), implant, and distal torsion joint (BM) as shown in Figure 1(b). As shown in Figure 1(c-i), the implant is held in position by an open-loop of (yellow) tendon routed through the implant base notches and opened by an open-loop of (green) tendon routed through a PE loop (white) on the implant arm. The two ends of each open-loop (yellow and green) are routed through the implant holder into the quadlumen tube. One end of each open-loop (yellow and green) is pulled to deploy the implant. Also, a pair of antagonistic (red) tendons that actuate the distal torsion joint is routed through the implant actuator followed by the quadlumen tube as shown in Figure 1(c-i). To easily disengage the implant from the robot during deployment, the PE loop (white) is added to the implant arm.
Quadlumen tube:
A coupling wire (0.3 mm, Nitinol tendon) is attached parallel to the quadlumen tube (Figure 1(b)), giving the quadlumen tube a prismatic profile. The coupling wire, engaging with the grooves in the bending joint rings (Figure 2(a)), enables rotational coupling between the proximal torsion joint and the implant actuator. The six tendons from the implant actuator (Figure 1(c-i)) are routed through the quadlumen tube to the actuation system in the arrangement shown in Figure 1(c-ii). Each of the implant anchoring tendons is routed through different lumens to reduce friction while disengaging the implant. The same routing principle is followed for the implant opening and distal torsion joint tendons. The tendons attach to the actuation system as shown in Figure 1(c-iii). The implant manipulations (anchoring and opening) are achieved by manually controlling the slider, and actuating the distal torsion joint using a motor. The quadlumen tube starts at the implant actuator and goes in sequence as follows: steerable guide → inner tube → connector → guide → stiff tube. A prismatic tube guide and stiff tube have been used to prevent the quadlumen tube from kinking when it is advanced.
C. Routing and Actuation System
The actuation system consists of two parts (see Figure 1(a)): steerable guide actuator (red dotted line box) and implant manipulation actuator (blue dotted line box). The steerable guide actuator consists of: bending joint actuator, proximal torsion joint actuator, connector, and guide. The implant manipulation actuator consists of a stiff tube, implant manipulator, distal torsion joint actuator, and guide rails. Each of the three actuators: bending, proximal torsion, and distal torsion, has a pulley, a motor ( Micro Metal Gearmotor 380:1, Pololu robotics and electronics, NV), and a motor housing unit as shown in Figure 1(a). A pair of antagonistic tendons from one joint are connected to a pulley (Figure 1(a) and Figure 1(c-iii)), in turn actuated by the motor [23]. Only one motor is needed to actuate a joint using antagonistic tendons with the actuation module.
The end of the quadlumen tube, described in subsection II-B, is housed inside the stiff tube. The tendons from the quadlumen tube are routed to the distal torsion joint actuator and implant manipulator as shown in Figure 1(c-ii). It is important to note that the entire implant manipulation actuator slides on the guide rails, thereby advancing the prismatic tube. Finally, the tendons from the steerable guide travel through the inner tube and split at the connector to their respective joint actuators.
D. Forward and Inverse Kinematics
Forward Kinematics:
The robot has four joints: proximal torsion θp, bending θb, prismatic θe and distal torsion θd. In Figure 4(a), the kinematic configuration of the robot is shown when all the joint parameters (given in TABLE. II), are equal to 0 (home configuration). The frames ({Fn}, n = 0,1,2,3,4,5,6) are used to derive the robot’s forward and inverse kinematics. The X, Y and Z axes are shown as green, blue, and red line segments, respectively. Also, the joint parameters θp, θb/2, θc, θb/2, θe, θd are shown in this figure to visualize the motion of the robot. The joint parameters θb/2, θc, and θb/2 are dependent and together actuate the bending joint, which is explained in detail below. The dotted black lines in Figure 4(a) connect the frames to their actual position on the robot. For example, {F1} and {F2} have the same origin. The frames in the home configuration are as follows:
Fig. 4:
Forward and inverse kinematics of the robot. (a) Kinematic configuration, (b) Link lengths, (c-i). Bending joint made up of three joints : revolute-1, prismatic, and revolute-2 (RPR), and (c-ii). Joint parameters labeled.
TABLE II:
Table of frames and their corresponding parameters
| {Fn} | Name | Parameter | Description |
|---|---|---|---|
| 0 | Proximal torsion | θ p | Revolution about Z0 |
| 1 | Bending revolute-1 | θ b/2 | Revolution about Z1 |
| 2 | Bending prismatic | θ c | Translation along Z2 |
| 3 | Bending revolute-2 | θ b/2 | Revolution about Z3 |
| 4 | Prismatic | θ e | Translation about Z4 |
| 5 | Distal torsion | θ d | Revolution about Z5 |
| 6 | Tool | - | End point of robot |
{F0} is attached to the proximal torsion joint,
{F1}-{F2}-{F3} are attached to the bending joint,
{F4} is attached to the prismatic tube,
{F5} is attached to the distal torsion joint, and
{F6} is attached to the end tip of the robot.
In Figure 4(b), the link lengths of the robot are shown: po, pt, bl, dt, and h are the lengths of the proximal torsion (BM), proximal torsion (TM), bending, distal torsion (BM) and implant holder respectively. Figure 4(c-i) and 4(c-ii), shows the modeling of the bending joint in its actuated state. The length of the bending joint is at rest and when actuated as shown in Figs. 4(c-i) and 4(c-ii). Constant curvature of the bending joint is assumed while deriving the robot kinematics. When the bending joint is actuated, its overall length changes by . Also, by geometry, the angle between a chord and a tangent at the end of a chord is half the angle subtended by that chord at the center. In the case of the bending joint, the angle subtended by at the center is θb. Hence, the angle between the chord and the tangent is θb/2 as shown in Figure 4(c-i). Hence, the flexible bending joint can be modeled as a revolute-prismatic-revolute (RPR) joint with joint parameters equal to θb/2, θc, and θb/2. The 6 joint parameters, {θp, θb/2, θc, θb/2, θe, θd}, and their direction of actuation are also shown in Figs. 4(c-i) and 4(c-ii).
The transformation from the tool frame, {F6}, to the base frame, {F0}, when all joint parameters are zero, is given by:
| (8) |
The unit angular velocity for the each revolute joint in home configuration is given by:
| (9) |
The position vectors to the origins of the various frames for the revolute joint in the home configuration is given by:
| (10) |
The twist for a revolute joint is given by ξ = [−ω × q, ω]T and for a prismatic joint is given by ξ = [v, 0]T, where v is the velocity of a point attached to the prismatic joint moving with unit velocity [25]. The resultant twists are found to be:
| (11) |
Through the product of exponentials, the forward kinematics map of the robot is given by [25]:
| (12) |
where, the joint parameters as shown in Figs. 4(c-i) and 3(c-ii) are, {θ1, θ2, θ3, θ4, θ5, θ6} = {θp, θb/2, θc, θb/2, θe, θd}.
Inverse Kinematics:
On expanding (12) we get:
| (13) |
where, R(θ) and p(θ) ≜ [px, py, pz]T are the orientation and position of {F6} with respect to the base frame {F0}, respectively.
| (14) |
| (15) |
where, ci = cos θi and si = sin θi. When the orientation of the tool frame, R(θ), is known, we can calculate the following joint angles: bending angle (θb), proximal torsion angle (θp), and distal torsion angle (θd). Solving for the bending joint angle:
| (16) |
For each value of θb, we can calculate θp and θd, assuming θb ≠ 0, π and is given by:
| (17) |
| (18) |
So we get two sets of values for {θp, θb, θd} given R(θ). To choose the right set of values we look at the constraints of the joints. As discussed in the design and modeling of the bending and torsion joint (subsection II-A), the maximum bending joint angle required for our application is 120° bidirectionally, i.e., ∣θb∣ ≤ 120°. Also, the maximum torsion joint angle achieved by the torsion joint is 75° bidirectionally i.e., ∣θp∣ ≤ 75° and ∣θd∣ ≤ 75°. Applying these constraints gives us unique feasible values for {θp, θb, θd}. When θb = 0,
| (19) |
This condition gives infinite solutions for θp and θd in our case and hence we avoid this configuration in robot motion.
The next step is to find the corresponding θc and θe. The prismatic component of the bending joint is θc (Figure 4(c-i)) and the motion of the prismatic joint is given by θe (Figure 4(c-ii)). From Figs. 4(b) and 4(c), we obtain:
| (20) |
Therefore, we can compute θc, since θb is known. Finally, θe is given by:
| (21) |
where, p(θ) is the known position vector to the origin of {F6}, given as [px, py, pz]T in (13) and p′(θ) is the position vector to the origin of {F6} computed using (12) with actuation angles:
Here θp, θb, θc, and θd, have been computed using Eqs.(16)-(20) and θe is considered to be zero. Hence, θe is the magnitude of the difference between p(θ) and p′(θ). The constraints to θc and θe are: θc ≤ 0 mm, as the length of (shown in Figure 4(c-i)) is always less than lb and 0 mm ≤ θe ≤ 60 mm, as the actuation system is designed to work in that range.
III. Control System
In Figure 5, a control diagram with a feedforward controller is shown to manipulate the joints of the proposed robotic catheter. The feedforward controller actuates the joints by providing reference pulley angles (same as motor shaft angle or pulley angle) to achieve the desired joint angles. These reference pulley angles to control the bending and torsion joint can be obtained by dividing the pulley radius, rp, from the respective tendon displacement equations, (3) and (6), given the desired joint angles. The feedforward controller uses proportional-derivative control and a disturbance observer to compensate for the external forces to provide robust motor control. Here Q(s), Gm(s), and Kg are a 2nd-order lowpass filter, a nominal motor plant model, and the gear ratio (1/380), respectively. and . A feedback controller can be used for compensation control, as done for joint control in [23] using an EM tracker.
Fig. 5:

Control block diagram of the joint space
IV. Experiment
In this section, the following experiments are performed: 1) The bending and torsion joint models derived above are validated for no prismatic tube backbone (section IV-A and section IV-B). 2) Introducing the prismatic tube stiffens the bending joint, and therefore we need to use modified kinematics, and PI modeling approaches discussed in section IV-C to perform robot motion validation. 3) The effect of introducing path tortuosity is discussed in section IV-D. 4) Finally, the feasibility of using the robotic system is demonstrated in a phantom heart model, and the effect of a simulated flow on the robotic end tip of the catheter are explored in section IV-E and IV-F, respectively
A. Bending Joint Model Validation
In this experiment, the theoretical model of the bending joint, derived in subsection II-A, is verified experimentally. The model is derived for the case with no prismatic tube. As shown in Figure 6(a-i) the experimental data gathered using an EM tracker (red line) follows the theoretically derived data (black dashed line) with an R2-value of: 0.9972 during loading and 0.995 during unloading, when actuated antagonistically. Ten cycles of this experiment are run to demonstrate repeatability. The hysteresis observed occurs due to friction in the tendon path and slacking of the antagonistic tendons. This slacking can be reduced by attaching prestressed tension springs to the antagonistic tendons close to the actuation system. This removes the slack and reduces hysteresis (blue line) as observed in Figure 6(a). However, significant deviation from the model is observed when the prismatic tube is introduced into the hollow lumen of the robot. This deviation is compensated using a physics-based and data-driven model explained in subsection IV-C.
Fig. 6:
Experimental results: (a) verification of theoretical model of bending and torsion joint. (b) Schematic of setup for robot motion validation
B. Torsion Joint Model Validation
The relationship between the torsion angle and tendon displacement as derived in subsection II-A is experimentally verified in this section. In Figure 6(a-ii), the theoretical data (black dashed line) and experimental data (red line) are shown. The experimental data follows the model with an R2-value of 0.962 during loading and 0.9134 during unloading. The hysteresis seen in the graph can be reduced by adding a spring into the actuation tendons to remove slack from the system. The spring improves the performance of the torsion joint significantly when there is no tube. The resultant curve is shown as a blue line in Figure 6(a). We still observe hysteresis in the torsion joint due to a backlash error in the coupling of the pulley slot and motor shaft or the Pololu motor gear system. Also, we assume that the PE tendons must take the shortest path around the top module, which is shown in Fig. 3(c)-(d) and described in (6). However, it is observed that the tendons may take a longer path due to friction between the top module and the PE tendons. These deviations due to backlash and change in the tendon path are compensated using data-driven modeling in subsection IV-C.
C. Robot Motion Validation
In this section, we validate the entire robot’s kinematics using (12). Due to problems like hysteresis (see subsection IV-A and subsection IV-B), the position accuracy of the bending joint, torsion joint, and consequently the robot tip gets affected. To improve the accuracy, we propose a modified kinematics model for the bending and torsion joints. Also, as hysteresis compensation approaches like Bouc-Wen [26], Preisach [27], and Prandtl-Ishlinskii (PI) [28] do exist, we use the PI method to model the hysteresis in the joints and compare it to the modified kinematics model. The PI method is chosen for the following reasons: 1) it is based on summing many elementary hysteresis backlash operators, and 2) it is known for its simplicity, ease of implementation, and accuracy. The experimental setup is shown in Fig. 7. The proposed robot is being actuated using a model in Simulink Real-Time (MATLAB 2021a, The Mathworks Inc., MA) designed to control the individual joints of the robot, as shown in Fig. 5. The user can control the robotic joints by entering the desired joint angles into the Simulink program.
Fig. 7:
Experimental setup: (a) actuation system with steerable guide actuator and implant manipulation actuator and (b) robot with an EM tracker attached for tracking.
Modified Kinematics of Bending Joint:
In (3), since n is equal to 10, varies over a small range of values in the feasible region θb = [−120°, 120°]. Hence, we can simplify (3) as follows: and , and the kinematics of the bending joint (3), pure kinematics (PK), can be given by:
| (22) |
(22) is simplified to a linear equation with the slope and intercept equal to ab and 0, respectively. We can write (22) in a general form:
| (23) |
where α, β are coefficients that can be obtained by calibration. Using (22) and (23), the inverse kinematics of the bending joint is computed as
| (24) |
To find the relationship between θb and lpb for the robot, we conducted a similar experiment as that in subsection IV-A. In this experiment, the quadlumen tube was installed in the robot and the bending joint was given a repetitive motion (10 cycles). The results (see Figure 8(a)) show that the actual trajectory (green lines) can be separated into two segments: deadband and linear segment. The first segment is nearly horizontal (i.e., small change in bending angle θb) whereas, the second segment θb is linearly related to lpb. We can apply (24) to the two segments and get
| (25) |
where parameters α1, β1, α2, β2, and can be obtained from Figure 8(a). Here, we apply the least square linear regression method to the data gathered (green lines) to find the following values: , α1 = 0.1246, β1 = 0.9498, α2 = 0.0290, and β2 = 1.5849. The modified kinematics (25) provides a better result (red lines) as compared to the pure kinematics (3) (blue line).
Fig. 8:
Comparison between the pure kinematics (PK), the modified kinematics (MK), and the Prandtl-Ishlinskii (PI) model applied to the (a) bending joint, (b) proximal torsion joint, and (c) distal torsion joint.
Modified Kinematics of Torsion Joints:
For the torsion joint, since both the proximal and distal torsion joints have the same actuation mechanism, we focus on analyzing the proximal joint. We conducted a similar experiment as that for the bending joint above, and the results are shown in Figure 8(b). The torsion joint’s trajectory (green lines) in Figure 8(b) can be separated into four segments: 1) deadband 1 → 2) nonlinear segment 1 → 3) deadband 2 → 4) nonlinear segment 2. The modified kinematics we propose is as follows: the deadbands are linear equations with slope equal to zero (red lines 1 and 3), and the nonlinear segments (red lines 2 and 4), can be obtained by shifting (yellow arrow) the theoretical curve (blue line, using (6)) to the match experimental data (green lines):
| (26) |
where,
| (27) |
| (28) |
is a discrete expression of the pure kinematics formulation (7), in terms of the tendon displacement . s is 1 during loading and 0 during unloading. ϒL and ϒU are the torsion angle values of the deadbands 1 and 3 (linear equation with zero slope), respectively, and db is the deadband width. ϒU, ϒL, and db can be obtained by calibration. In Figure 8(b), ϒU, ϒL, and db are equal to 58.8°, 10.0°, and 1.35 mm, respectively. Hence, (26) is used to calculate θp[k] (proximal torsion angle using modified kinematics).
Using the same procedure above, we can obtain the modified kinematics of the distal torsion joint, i.e., replacing lp and θp (in (26)) with ld and θd, respectively. The result shown in Figure 8(c), is obtained by manually tuning the parameters ϒU, ϒL, and db which are given by 73.0°, 12.0°, and 0.83 mm, respectively. Additionally, in Figure 8(b) and Figure 8(c), we observe some deviation of the experimental data (green lines) from the modified kinematics (red lines), which we hypothesize to be a result of backlash in the Pololu motor gearbox and joints, assembly errors, friction between the prismatic tube and joints, and coupling of torsion and bending joints.
Prandtl-Ishlinskii Model:
The elementary operator in the PI hysteresis is used to model backlash between gears. The discrete expression of a backlash operator [28] is given by:
| (29) |
where ℓ[k], ϑ[k], and r are the input, output, and threshold (magnitude of the backlash), respectively. The initial condition is given by:
| (30) |
where ϑ0 represents the initial output. Introducing a weighting value wh, the gain of the backlash of the operator, into (29) gives:
| (31) |
The more complicated hysteresis behavior can be modeled by summing m elementary hysteresis backlash operators , i.e.,
| (32) |
where wh = [wh0,…, whm]T, r = [r0,…, rm]T, and ϑ0 = [ϑ01,…, ϑ0m]T are vectors of weighting value, threshold, initial output. Hr(ℓ, ϑ0)[k] = [Hr0(ℓ, ϑ00)[k],…, Hrm(ℓ, ϑ0m)[k]]T. The ith input threshold, ri, is given by:
| (33) |
The parameters wh = [wh0,…, whm]T can be identified by
| (34) |
where ϑ and are the model output (using (32)) and the measured value, respectively. We conduct the same experiments as those for the pure kinematics and modified kinematics and evaluate the performance of the PI model by applying (29)-(34) (see Figure 8). Equations (29)-(34) can be applied to the different joints in which the input ℓ and output ϑ are replaced with the corresponding joint variables (bending joint: lb and θb; proximal joint: lp and θp; distal joint: ld and θd). Due to space constraints, the experimental procedure and weights are not included as the approach is well known [29]. We choose m is equal to 10 (32) to fit experimental data and then r and wh can be computed by using (33) and (34), respectively. Here we use a nonlinear optimization solver, fmincon (MATLAB 2021a, The Mathworks Inc., Natick, MA, USA), to solve (34).
In Figure 8, we observe that the PI model (blue dot lines, see Figure 8(a)) deviates from the experiment results (green lines) but can successfully estimate the hysteresis in the proximal and distal torsion joints (see Figure 8(b)-(c)). Also, we hypothesize that the complex mechanism of the bending joint causes asymmetric hysteresis which is not modeled well using the PI modeling approach explained above.
Robot Motion Validation:
To verify the performance of the robot motion, we substitute the pure kinematics ((3) and (6)), the modified kinematics ((25) and (26)), and the lookup tables generated by the PI model (32) into (15) to find the position of the robot tip, respectively. The experimental setup consists of mounting two EM trackers, one on the stationary proximal torsion joint and the other on the implant holder (see Figure 6(b)), to gather the positions of the robot base and tip. Since the prismatic joint is actuated manually, three scenarios are considered, namely prismatic joint displacement θe of 0 mm, 10 mm, and 20 mm, respectively. Simultaneously, the bending joint, the proximal torsion, and the distal torsion joints are given time-varying trajectories. For brevity, we show the plot for θe equal to 20 mm (see Figure 9). However, TABLE. III shows the RMSE values for all three prismatic joint displacements considered. When the robot is actuated by a given pulley angle for the various joints as shown in Figure 9, we obtain the robot tip position (px, py, and pz are with respect to frame {Fb} as in Figure 6(d)) as well as the RMSE values using the pure kinematics and the modified kinematics formulations.
Fig. 9:
Robot motion validation experiment II. (a) Robot states at 5 s intervals from 0 s to 15 s (one cycle) and (b) Inputs and tip position of the robot using pure kinematics, modified kinematics, Prandtl-Ishlinskii method and hybrid method, where θe equals 20 mm.
TABLE III:
RMSE values by using different methods.
| θe (mm) | Method | X (mm) | Y (mm) | Z (mm) | 3D (mm) |
|---|---|---|---|---|---|
| 0.0 | PK | 14.67 | 19.49 | 38.37 | 45.47 |
| MK | 2.51 | 1.81 | 2.52 | 4.00 | |
| PI | 2.45 | 5.37 | 5.76 | 8.25 | |
| Hybrid | 2.35 | 1.77 | 2.52 | 3.88 | |
| 10.0 | PK | 18.00 | 25.01 | 49.21 | 58.06 |
| MK | 3.62 | 2.41 | 2.25 | 4.90 | |
| PI | 2.59 | 7.19 | 6.40 | 9.96 | |
| Hybrid | 3.41 | 2.29 | 2.25 | 4.69 | |
| 20.0 | PK | 20.05 | 29.67 | 58.44 | 68.54 |
| MK | 4.05 | 2.53 | 3.63 | 6.00 | |
| PI | 3.98 | 8.22 | 8.66 | 12.59 | |
| Hybrid | 3.81 | 2.43 | 3.63 | 5.79 |
To demonstrate repeatability of the motion of the robot in 3D space, nine cycles of motion, with each cycle being 35 s long, were executed (see Figure 9). In Figure 9(a), we depict the robot states at an interval of 5 s from 0 s (initial state) to 15 s. The results (see Figure 9(b) and Table III) show that in the X, Y, and Z directions, the pure kinematics-based trajectory does not match the experimental result as the quadlumen tube changes the robot stiffness (X: RMSE = 20.05 mm, Y: RMSE = 29.67 mm, Z: RMSE = 58.44 mm). However, the modified kinematics-based trajectory matches the experimental result better (X: RMSE = 4.05 mm, Y: RMSE = 2.53 mm, Z: RMSE = 3.63 mm). Therefore, a much higher position accuracy of the tip is obtained while using the modified kinematics (RMSE = 6.00 mm) than the pure kinematics (RMSE = 68.54 mm) when the prismatic tube is integrated into the system. Comparing the modified kinematics RMSE values from the results in TABLE. III, we observe that the overall errors increase by ~2 mm. We hypothesize that this error arises due to the precurvature of the prismatic tube and the force of gravity acting on it, and therefore, reducing θe should result in a smaller error. As a verification, it is observed that when θe = 10 mm (< 20 mm), the overall error reduces by ~1 mm.
Compared to the results from the modified kinematics (physics-based model), the PI model (data-driven model) has a lower position accuracy (see Figure 9 and Table III). Also the RMSEs of the PI model (RMSE = 12.59 mm) increase significantly when θe = 20 mm. We hypothesize that this occurs due to deviation of the bending joint (see the aforementioned analysis). To overcome this issue, it is possible to combine the physics-based (MK) and data-driven models (PI), to improve the accuracy, i.e., we use the modified kinematics for the bending joint and the PI model for the proximal and distal torsion joints. We observe that the 3D RMSEs reduce significantly when the hybrid model is used. The RMSEs are 3.88 mm, 4.69 mm, and 5.79 mm when θe is equal to 0 mm, 10 mm, and 20 mm, respectively.
D. Introducing Path Tortuosity
In this section, we guide the robotic catheter from the inferior vena cava (IVC) to the left atrium through the transseptal puncture location using a rigid curved phantom, as shown in Fig. 10(a). The curved phantom functions like a steerable outer sheath used for catheter introduction. The rigidity of the outer sheath straightens the path from the femoral vein to the IVC. Therefore, the only tortuosity the catheter experiences is emulated by the 3D printed curved phantom (Form 3 printer, Formlabs, MA), as shown in Fig. 10(b).
Fig. 10:
Experimental setup implementing path tortuosity.
The path tortuosity increases the friction in the tendon routing inner tube. This friction increases joint hysteresis and leads to compression of the routing tubes. Hence, we use a tension spring to reinforce the inner tube (see Fig. 10(c)), increasing its compressive stiffness without increasing the bending stiffness. To evaluate the accuracy with which we can predict the robot tip position, we use the experimental setup shown in Fig. 10(b) (top view) and Fig. 10(c) (side view).
Similar to the robot motion validation experiments described in section IV-C, we use pure kinematics ((5), (7), and (15)) and PI models ((29)-(34)), with m equal to 10, to find the robotic tip position. Unlike, the results when the inner tube is in a straight configuration, the bending joint trajectory is best emulated by a PI model. Using the MK model here (and consequently the hybrid model) leads to large RMSE values. This could be because of the increase in friction and hysteresis in the joint. Hence, only PI modelling is used in this demonstration as it emulates the joint trajectories sufficiently well. The RMSE values for these experiments performed for prismatic joint displacements of θe equal to 0 mm, 10 mm and 20 mm are given in Table IV. We observed that the lowest 3D RMSE obtained (see Table IV and Fig. 11, PI model) in the bent configuration was similar to the lowest 3D RMSE obtained in the straight configuration (see Table III and Fig. 9, Hybrid model). Fig. 11 show the robot motion validation results for θe equal to 20 mm. Hence, PI models can be used to compensate for the increased joint hysteresis due to path tortuosities encountered during this procedure.
TABLE IV:
RMSE values for path tortuosity experiments.
| θe (mm) | Method | X (mm) | Y (mm) | Z (mm) | 3D (mm) |
|---|---|---|---|---|---|
| 0.0 | PK | 7.34 | 10.23 | 20.99 | 24.47 |
| PI | 3.40 | 0.83 | 1.26 | 3.72 | |
| 10.0 | PK | 11.53 | 15.21 | 26.02 | 32.37 |
| PI | 3.12 | 2.91 | 1.53 | 4.53 | |
| 20.0 | PK | 16.06 | 18.99 | 33.76 | 41.93 |
| PI | 2.92 | 5.59 | 1.76 | 6.54 |
Fig. 11:
Results for robot motion validation, when introduced through a tortuous path, for prismatic motion being 20 mm.
E. Demonstration of Robotic System in a Phantom Heart
In this section, the actuation system shown in Figure 7 is used to actuate the 0.609 m long robotic catheter to deliver the implant onto the MV of the phantom heart model, while the inner tube is kept in a straight configuration. The same experiment is performed again to assess the maneuverability of the robotic catheter when routed through the rigid curved phantom. As shown in Fig. 12, the following steps were followed in both the experiments: a) The robot is introduced into the left atrium. b) The robot’s bending plane is aligned with the MV opening by actuating the proximal torsion joint (20°-40°). c) The robot is bent by around 60° to reach the MV opening. d) The prismatic tube (see Figure 1(a)) is advanced by 25-35 mm to get the implant holder under the MV leaflets. e) The distal torsion joint is actuated to align the implant to the leaflets f) The implant is manipulated (opened, closed, rotated and advanced) with the help of the implant manipulation actuator to clip onto the MV leaflet. Once the implant is attached to the leaflet, it is deployed from the robot by pulling one end of the opening and closing tendons (green and yellow tendon in Figure 1(c)). In practice, the implant has pointed edges to hold onto the leaflet so that the robot can be pulled back without disturbing the implant. The robot must be pulled back from its previous position, but this step was not implemented as the implant was not designed to hold onto the valve. Also, step (f) was only implemented with the inner tube in a straight configuration as we were only testing the maneuverability of the joints when the catheter was put through a tortuosity path. We observed that increasing the tortuosity increased the hysteresis in the bending joint, and hence a larger input was needed to achieve similar bending angles when the catheter was put through the rigid curved phantom. Overall, the steerable guide of the catheter is automated and the prismatic tube is manually controlled to provide more control to the surgeon.
Fig. 12:
Demonstration in a phantom heart model
For adequate implantation, the grasping arm (see Fig. 12(f)) of the implant must be aligned perpendicular to the plane of coaptation of the anterior and posterior leaflets. Using the proposed design, we can position (bending, proximal torsion, and prismatic) and fine-tune the implant’s orientation (distal torsion) to the mitral valve leaflet for proper implantation. As per the clinical requirement, the distal torsion joint can be actuated by 45° bidirectionally, as shown in Fig. 8(c). However, according to the design description of the joint given in Sec. II-A and joint motion demonstrated in Fig. 6(a-ii), the joint can be actuated up to ±75°. In this experiment, the implant is successfully detached, and the feasibility of the robotic transcatheter is demonstrated.
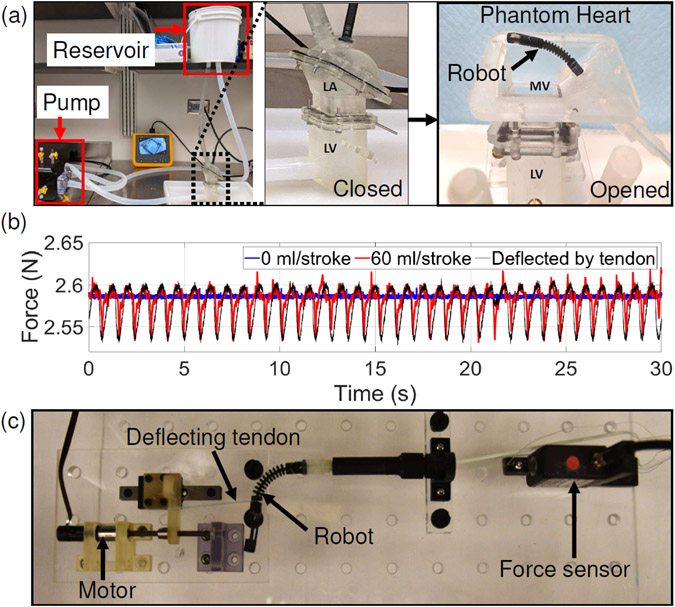
F. Deflection of Robot in a Simulated Pulsatile Flow
In this experiment, we estimate the robot’s deflection in a simulated pulsatile flow system by sensing the tension in the bending joint actuation tendon (BJAT), as follows: 1) The robot is introduced into a waterproofed phantom of the left heart chambers (see Figure 13(a)). 2) The phantom of the left heart chambers is connected to a pulsatile flow system (Endovascular simulator, ViVitro Labs, BC, Canada) wherein the robot can be viewed using an endoscope (DS-701, Fluke Corporation, WA). 3) The robot is held at a bending angle of 90° and the tension in the BJAT is recorded using a force sensor (MDB-5, Transducer Techniques®, CA) for flowrates varying from 0 ml/stroke to 60 ml/stroke (70 strokes/min, Physio70 waveform), as shown in Figure 13(b) (blue and red lines). 4) Next, the robot is held at 90° in free air (see Figure 13(c)) with the BJAT tension recorded by the same force sensor while small external deflections are applied to the bending joint using a tendon connected to a motor. This helps us calculate the relationship between the tendon tension (BJAT) and the amount of external deflection applied, which is calculated to be 1.814 mm/N. 5) Using the value calculated in the previous step, the robot bent at 90°, is externally actuated by a periodic input of Amp = 0.13 mm and Frequency = 70 min−1, and the BJAT tension is recorded and plotted against the force experienced by the robot within the phantom of the left heart chambers at 60 ml/stroke (RMSE = 0.02 N) (see Figure 13(b) black line). This experiment is carried out to approximately estimate the deflection that the robot tip underwent when subjected to a pulsatile flow of 60 ml/stroke which is around 0.13 mm. The aim of the experiment is to demonstrate that the bending joint tendon can be actuated to compensate for the deflection that the robot undergoes in a pulsatile flow system by applying the required counter force.
Fig. 13:
(a) Experimental setup to sense the robot’s deflection in a simulated pulsatile flow and images of the waterproofed phantom of the left heart chambers (left atrium closed and opened). (b) Setup to calculate the relation between the tendon tension and the robot deflection. (c) Plot of bending joint actuation tendon tension versus time when the robot is in a pulsatile flow of 0 ml/stroke, 60 ml/stroke, and when a tendon in free air deflects it.
V. Conclusions and Future Work
This paper proposed an improved robotically steerable transcatheter design to achieve highly articulated maneuvers needed for transcatheter intervention procedures for the treatment of MR. The robot joints were modeled, and the forward and inverse kinematics of the robot was derived and verified. We conducted experiments to verify the position accuracy of the robot motion using appropriate models derived in this paper: the modified kinematics model, PI hysteresis model, and the hybrid model (combination of PI and MK models), with and without path tortuosity. A preliminary study is conducted to evaluate if force sensing can be used to compensate for the effects of fluid flow. Also, the implant was successfully detached from the robot onto the artificial MV in the phantom heart, verifying the feasibility of the robotic catheter. We observed some key factors that affect the position accuracy, such as 1) the nonlinearity of the prismatic tube, 2) friction between the prismatic tube and steerable guide, 3) motor and joint backlash, and 4) coupling between the torsion and the bending joints. In our future work, we plan to model the effects of these factors on the robot’s performance. Also, we will conduct experiments to estimate the joint motion resolution for varying bending joint angles, and introduce further refinements in the design and the controller. our future work also involves using ultrasound imaging as compensation control feedback and demonstrating the procedure in a porcine heart model. Finally, for the section where we introduced path tortuosity, a tension spring is used inside our inner tube to increase the compressive stiffness to improve our results. This feature will be optimized and used in the prototypes we fabricate in our future work.
VI. Acknowledgments
We thank Dr. Muralidhar Padala, Associate Professor, Division of Cardiothoracic Surgery, Emory University, for providing us with the mitral valve implant, feedback on the manuscript, inputs on how to house the implant at the catheter tip, and the suggestion to introduce a loop into the implant arm to disengage the implant from the robot with ease.
This work was supported in part by the National Heart, Lung, And Blood Institute of the National Institutes of Health under Award Number R01HL140325. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
References
- [1].Nkomo VT, Gardin JM et al. , “Burden of valvular heart diseases: a population-based study,” The Lancet, vol. 368, no. 9540, pp. 1005–1011, 2006. [DOI] [PubMed] [Google Scholar]
- [2].Mozaffarian D, Benjamin EJ et al. , “Executive summary: heart disease and stroke statistics2016 update: a report from the american heart association,” Circulation, vol. 133, no. 4, pp. 447–454, 2016. [DOI] [PubMed] [Google Scholar]
- [3].Cioffi G, Tarantini L et al. , “Functional mitral regurgitation predicts 1-year mortality in elderly patients with systolic chronic heart failure,” Eur. J. Heart Fail, vol. 7, no. 7, pp. 1112–1117, 2005. [DOI] [PubMed] [Google Scholar]
- [4].Mirabel M, Iung B et al. , “What are the characteristics of patients with severe, symptomatic, mitral regurgitation who are denied surgery?” Eur. Heart J, vol. 28, no. 11, pp. 1358–1365, 2007. [DOI] [PubMed] [Google Scholar]
- [5].Cosgrove DM, Sabik JF, and Navia JL, “Minimally invasive valve operations,” Ann. Thorac. Surg, vol. 65, no. 6, pp. 1535–1539, 1998. [DOI] [PubMed] [Google Scholar]
- [6].Cohn LH, Adams et al. , “Minimally invasive cardiac valve surgery improves patient satisfaction while reducing costs of cardiac valve replacement and repair.” Ann. Surg, vol. 226, no. 4, p. 421, 1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Goldstone AB, Atluri etal P, “Minimally invasive approach provides at least equivalent results for surgical correction of mitral regurgitation: a propensity-matched comparison,” J. Thorac. Cardiovasc. Surg, vol. 145, no. 3, pp. 748–756, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Meier S, Seeburger J, and Borger MA, “Advances in mitral valve surgery,” Curr. Treat. Options Cardio. Med, vol. 20, 2018. [DOI] [PubMed] [Google Scholar]
- [9].Yoon SH, Whisenant BK et al. , “Outcomes of transcatheter mitral valve replacement for degenerated bioprostheses, failed annuloplasty rings, and mitral annular calcification,” Eur Heart J., vol. 40, pp. 441–451, 2019. [DOI] [PubMed] [Google Scholar]
- [10].Kansara T, Kumar A et al. , “Mitral regurgitation following PASCAL mitral valve repair system: A single arm meta-analysis,” Indian Heart Journal, vol. 73, no. 1, pp. 129–131, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Fiocco A, Nadali M et al. , “Transcatheter mitral valve chordal repair: Current indications and future perspectives,” Front. Cardiovasc. Med, vol. 6, p. 128, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Dahle G, “Current devices in TMVI and their limitations: Focus on Tendyne,” Frontiers in Cardiovascular Medicine, vol. 7, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Sharma RP, Makar M, and Kar S, “An overview of the mitraclip procedure,” J. Struct. Heart Dis, vol. 1, no. 3, pp. 127–136, 2015. [Google Scholar]
- [14].MitraClip®. MitraClip® Clip Delivery System. [Accessed: Jan 24, 2021]. [Online]. Available: https://www.accessdata.fda.gov/cdrh_docs/pdf10/P100009c.pdf. [Google Scholar]
- [15].Godzik J, Mastorakos GM et al. , “Surgeon and staff radiation exposure in minimally invasive spinal surgery: prospective series using a personal dosimeter,” J. Neurosurg.: Spine, Feb 2020. [DOI] [PubMed] [Google Scholar]
- [16].Lanfranco AR, Castellanos AE et al. , “Robotic surgery: a current perspective,” Ann. Surg, vol. 239, no. 1, pp. 14–21, Jan 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Ragosta M and Singh KP, “Robotic-Assisted Percutaneous Coronary Intervention: Rationale, Implementation, Case Selection and Limitations of Current Technology,” J. Clin. Med, vol. 7, no. 3, Jan 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Mkalaluh S, Szczechowicz M et al. , “Failed MitraClip therapy: surgical revision in high-risk patients,” J. Cardiothorac. Surg, vol. 14, no. 75, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Rader F, Siegel RJ et al. , “Mitral Valve Surgery After Failed MitraClip: A Single-Center Experience,” J. Interv. Cardiol, Apr 2021. [DOI] [PubMed] [Google Scholar]
- [20].Adams DH and Anyanwu A, “Pitfalls and limitations in measuring and interpreting the outcomes of mitral valve repair,” J. Cardiothorac. Surg, vol. 131, no. 3, Mar 2006. [DOI] [PubMed] [Google Scholar]
- [21].Kato T, King F et al. , “Robotized catheter with enhanced distal targeting for peripheral pulmonary biopsy,” IEEE/ASME Trans. Mechatronics, vol. 26, no. 5, pp. 2451–2461, 2021. [Google Scholar]
- [22].Nayar N, Jeong S, and Desai JP, “Towards the development of a robotic transcatheter delivery system for mitral valve implant,” in 2020 IEEE/RSJ Int. Conf. on Intell. Robots and Syst. (IROS), 2020, pp. 3172–3177. [Google Scholar]
- [23].Nayar N, Jeong S, and Desai JP, “Design and control of 5-dof robotically steerable catheter for the delivery of the mitral valve implant,” in 2021 IEEE Int. Conf. on Robotics and Autom. (ICRA), 2021, pp. 12268–12274. [Google Scholar]
- [24].Ravigopal SR, Nayar NU, and Desai JP, “Toward real-time pose estimation of the mitral valve robot under c-arm x-ray fluoroscopy,” IEEE Trans. Med. Robot. Bionics, vol. 3, no. 4, pp. 928–935, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Murray RM, Li Z, and Sastry SS, A Mathematical Introduction to Robotic Manipulation. CRC press, 1994. [Google Scholar]
- [26].Ikhouane F and Rodellar J, Systems with Hysteresis: Analysis, Identification and Control using the BoucWen Model. John Wiley & Sons Ltd, Chichester, West Sussex, England, 2007. [Google Scholar]
- [27].Liu L and Yang Y, Modeling And Precision Control Of Systems With Hysteresis. Waltham, MA, USA: Elsevier Inc., 2016. [Google Scholar]
- [28].Kuhnen K, “Modeling, identification and compensation of complex hysteretic nonlinearities: A modified prandtl-ishlinskii approach,” Eur. J. Control, vol. 9, no. 4, pp. 407–418, 2003. [Google Scholar]
- [29].Zhang J, Iyer K et al. , “Modeling and inverse compensation of hysteresis in supercoiled polymer artificial muscles,” IEEE Robot. Autom. Lett, vol. 2, no. 2, pp. 773–780, 2017. [Google Scholar]