Intrinsic Neural Timescales in the Temporal Lobe Support an Auditory Processing Hierarchy

Abstract

During rest, intrinsic neural dynamics manifest at multiple timescales, which progressively increase along visual and somatosensory hierarchies. Theoretically, intrinsic timescales are thought to facilitate processing of external stimuli at multiple stages. However, direct links between timescales at rest and sensory processing, as well as translation to the auditory system are lacking. Here, we measured intracranial EEG in 11 human patients with epilepsy (4 women), while listening to pure tones. We show that, in the auditory network, intrinsic neural timescales progressively increase, while the spectral exponent flattens, from temporal to entorhinal cortex, hippocampus, and amygdala. Within the neocortex, intrinsic timescales exhibit spatial gradients that follow the temporal lobe anatomy. Crucially, intrinsic timescales at baseline can explain the latency of auditory responses: as intrinsic timescales increase, so do the single-electrode response onset and peak latencies. Our results suggest that the human auditory network exhibits a repertoire of intrinsic neural dynamics, which manifest in cortical gradients with millimeter resolution and may provide a variety of temporal windows to support auditory processing.

SIGNIFICANCE STATEMENT Endogenous neural dynamics are often characterized by their intrinsic timescales. These are thought to facilitate processing of external stimuli. However, a direct link between intrinsic timing at rest and sensory processing is missing. Here, with intracranial EEG, we show that intrinsic timescales progressively increase from temporal to entorhinal cortex, hippocampus, and amygdala. Intrinsic timescales at baseline can explain the variability in the timing of intracranial EEG responses to sounds: cortical electrodes with fast timescales also show fast- and short-lasting responses to auditory stimuli, which progressively increase in the hippocampus and amygdala. Our results suggest that a hierarchy of neural dynamics in the temporal lobe manifests across cortical and limbic structures and can explain the temporal richness of auditory responses.

Introduction

The human brain gives rise to rich neural dynamics, which play a fundamental role in processing sensory information. Intrinsic dynamics of the brain operate at multiple timescales (Hasson et al., 2008; Honey et al., 2012; Murray et al., 2014; Raut et al., 2020) through oscillatory (Frauscher et al., 2018; Mahjoory et al., 2020; Vezoli et al., 2021) and nonoscillatory (Gao et al., 2020) processes. In the visual and somatosensory systems, intrinsic timescales manifest at rest, in ongoing neural activity: primary areas exhibit short timescales that may facilitate a quick reaction to incoming stimuli (Murray et al., 2014; Siegle et al., 2021). These progressively increase while advancing through the cortical hierarchy, supporting integration of information (Murray et al., 2014; Chaudhuri et al., 2015). Whether a similar hierarchy of intrinsic dynamics exists in the auditory system, and in particular within the temporal lobe, a hub for auditory processing, remains underexplored.

In the auditory system, evidence for processing of external stimuli at multiple latencies stems from studying evoked responses (Honey et al., 2012; Norman-Haignere et al., 2022). Primary auditory areas show fast- and short-lasting responses to sounds (Camalier et al., 2012). Response latencies progressively increase while advancing in a processing hierarchy, from primary to secondary areas, as, for example, the superior temporal gyrus (Nourski et al., 2014). Beyond this “classical” auditory cortex circuitry of the temporal lobe, an extensive network of adjacent cortical and deeper regions is also sensitive to auditory input and exhibits diverse response profiles and latencies. At a cortical level, the insula, for example, shows relatively fast auditory responses (Blenkmann et al., 2019), while deeper structures, such as the hippocampus and amygdala, show slower, long-lasting responses to auditory stimuli (Halgren et al., 1980), possibly mediating the integration of sensory information (Zuo et al., 2020).

This richness in auditory responses suggests that, when stimulated with sounds, the temporal lobe facilitates auditory processing at multiple timescales (Stephens et al., 2013). These are thought to reflect temporal “integration” windows that manifest in response to external stimuli (Lerner et al., 2011; Honey et al., 2012; Norman-Haignere et al., 2022). Whether a similar temporal lobe hierarchical organization also exists during rest and contributes to auditory processing remains underexplored. Importantly, there is a critical lack of studies that simultaneously assess neural timescales not only in the temporal cortex, but also in the hippocampus and amygdala, which are key, yet underexplored regions in processing of auditory information (Billig et al., 2022). The question of how these structures are positioned in a hierarchy of intrinsic timescales remains therefore open. In humans, in particular, a fine-grained measurement of neural dynamics in the temporal lobe can be challenging with noninvasive techniques (Tzovara et al., 2019; Johnson et al., 2020; Raut et al., 2020), but evidence from invasive recordings remains limited.

Here, we aimed at characterizing spontaneous intrinsic neural dynamics within cortical and limbic structures of the extended auditory system, covering the temporal lobe and insula, and their contribution to auditory processing. We focused on this network, which is relatively accessible through intracranial EEG (iEEG) recordings in patients with pharmaco-resistant epilepsies. We hypothesized that spontaneous intrinsic neural timescales, estimated via the autocorrelation function (ACF) (Golesorkhi et al., 2021b; Zeraati et al., 2022), or via the knee frequency of the power spectral density (PSD) (Gao et al., 2020) of iEEG signals, would show a hierarchical organization within an extended auditory network, which could, in turn, explain a hierarchy of neural responses to incoming auditory stimuli. We additionally hypothesized that nonoscillatory brain dynamics, characterized by the spectral exponent of aperiodic neural activity, which has been suggested to reflect a proxy of the excitation to inhibition balance (Gao et al., 2017), would also reveal a hierarchical organization across the temporal lobe.

Materials and Methods

Patients

We recorded iEEG in 11 neurosurgical patients (4 women, median age = 32 years, minimum = 27, maximum = 56 years) with drug-refractory epilepsy who had been implanted with depth electrodes to identify seizure foci (for a detailed patient description, Table 1). Electrode locations were based on clinical criteria only. Recordings took place at the EPI Clinic, Zurich, and at the Inselspital, Bern. The number of patients included in this study is following standards in the field and is in line with, or larger than, existing intracranial studies investigating intrinsic neural dynamics (Honey et al., 2012; Hullett et al., 2016; Lendner et al., 2020; Mercier et al., 2022). Patients provided written informed consent before participation in this research study, approved by institutional ethics review boards of the Canton of Zurich (PB-2016-02055), and Inselspital, Bern (#2018-01387). All experiments were performed in accordance with the 6th Declaration of Helsinki.

Table 1.

Overview of patient dataset^a

Patient ID	Gender	Age (yr)	Clinic	No. of electrodes analyzed	Hemisphere	Regions
1	M	31	Zürich	25	L + R	CTX, ENT, HIP, AMY
2	F	33	Bern	17	R	CTX, ENT, HIP
3	F	29	Zürich	34	L + R	CTX, ENT, HIP, AMY
4	F	30	Zürich	30	L + R	CTX, ENT, HIP, AMY
5	M	56	Zürich	28	L + R	CTX, ENT, HIP, AMY
6	M	42	Zürich	20	L	CTX, ENT, HIP, AMY
7	M	34	Zürich	37	L + R	CTX, ENT, HIP, AMY
8	F	45	Bern	24	L	CTX, ENT, HIP
9	M	29	Zürich	28	L + R	CTX, ENT, HIP, AMY
10	M	27	Zürich	19	R	CTX, ENT, HIP, AMY
11	M	32	Bern	8	L	CTX, HIP

^aWe collected data from a total of 270 electrodes from 11 patients, with a median of 25 electrodes per patient and minimum and maximum of 8 and 37 electrodes, respectively. For each patient, we report gender, age, the hospital where the data were collected, the number of electrodes used for our analyses, the hemisphere(s) where the electrodes were implanted, and the regions sampled from the retained electrodes.

Experimental protocol

Patients were presented with auditory stimuli consisting of pure tones at three frequencies (500, 1250, 2500 Hz) with a random interstimulus interval between 0.9 and 19 s. Each tone had a duration of 100 ms with 5 ms on/off ramps to avoid clicks. Interstimulus interval and tone frequency were drawn from a pseudorandom distribution such that each was played 120 times per hour (in total, 360 tones per hour). Auditory stimuli were presented via in-ear headphones, and their intensity was adjusted individually for each patient at a comfortable level. Patients were instructed to relax and ignore the sounds. Some of the patients were additionally presented with the auditory stimuli during sleep, at a later session, which was not analyzed in the context of the present study.

iEEG recordings and preprocessing

Depth electrodes were used for iEEG recordings (DIXI Medical, 3 patients; Ad-Tech Medical, 8 patients) targeting different brain regions and varying from 8 to 18 platinum iEEG contacts along their shaft. Data were recorded at 4096 or 1024 Hz. Recordings with 4096 Hz sampling rate were downsampled offline to 1024 Hz.

All data were visually inspected to exclude electrodes with persistent spiking activity. Continuous data were notch filtered at ∼50 Hz and harmonics, and rereferenced with a bipolar scheme (i.e., each electrode to the closest one in the same electrode lead outwardly) to remove any source of widespread noise. This was done to retain a local signal and mitigate effects of volume conduction, following recommendations in the analysis of iEEG data (Lachaux et al., 2012; Mercier et al., 2022). Peristimulus epochs were then extracted, spanning from −5 s before the sounds' onset to 5 s after stimulus onset. Only epochs that did not overlap with another sound in this period were kept. All epochs were then visually inspected, and any epochs with remaining artifacts were rejected. The baseline period of each epoch was defined as the interval [−1, 0] s preceding the sounds. For studying auditory responses (see Responsive electrodes), the raw signal from all electrodes was additionally bandpass filtered between 1 and 40 Hz. Processing of iEEG data was performed using MNE-Python (Gramfort et al., 2013).

Electrode localization

Electrodes were localized on postimplant CT scans using the Lead-DBS toolbox (Horn and Kühn, 2015) and transformed into standard MNI coordinates for group analyses. The postimplant CT scan was registered to a preimplant structural T1-weighted MRI scan from which anatomic labels were reconstructed using the FreeSurfer toolbox and the Destrieux atlas. Subsequently, electrode coordinates identified on the postimplant CT scans were mapped to their corresponding anatomic regions identified on the preimplant MRI. Anatomical label assignment was validated for all electrodes by an expert neurologist, who verified their location and additionally ensured that none of the electrodes that were included in our analyses were in white matter. The available electrodes were divided across four regions of interest (ROIs), covering the temporal cortex, the insula because of its prominent auditory responses (included in temporal cortex), entorhinal cortex, hippocampus, and amygdala. This resulted in N = 270 electrodes in total, with a median = 25, minimum = 8 and maximum = 37 electrodes per patient (Table 1).

Intrinsic neural timescales

For estimating spontaneous intrinsic neural timescales, we first computed the ACF on each epoch during 1 s baseline period (function acf from Python's statsmodels) (Seabold and Perktold, 2010). The resulting ACFs across epochs were then averaged to yield a single ACF for each electrode. We then defined the “intrinsic timescale” of each electrode as the time lag at which the ACF reaches the value 1/e, consistent with an analytical decay of the form f(t) = exp(–t/τ). The precise time lag was computed by interpolating with a spline fit to the ACF, as in Raut et al. (2020).

To ensure that the estimation of timescales was not trivially driven by neural oscillations, we performed two additional control analyses, following previous literature (Murray et al., 2014; Chaudhuri et al., 2015; Gao et al., 2020; Zeraati et al., 2022). First, we fitted a curve of the form f(t) = a*exp(–t/τ) + (1 – a)*cos(2πft) to the ACF with (a, τ, f) as parameters to be optimized (Zeraati et al., 2022); a represents the amplitude parameter, f the putative oscillatory frequency, and τ the estimated timescale. In a second control analysis, we computed timescales as the inverse of the knee frequency in power spectra, estimated as f_k = k^1/exp with k being the knee parameter and exp the spectral exponent, as implemented in the specparam toolbox (Donoghue et al., 2020) in “knee” mode. We fitted power spectra from 2 to 35 Hz, to have a reliable power estimate on the lower limit and to keep consistency with the “fixed” spectral parametrization for the higher limit (for a discussion on the choice of frequency band, see PSD and spectral exponent). Electrodes where the algorithm could not find a knee frequency were excluded.

PSD and spectral exponent

For estimating the spectral exponent we computed power spectra with a Hann-windowed and detrended Fourier transform on the baseline period (function spectrogram from Python's scipy) (Virtanen et al., 2020). Power spectra were averaged using a “meanlog” approach (i.e., taking the mean of the logarithm of the power spectra across epochs) to yield a single power spectrum density for each electrode. The spectral exponent was then computed on each electrode's average power spectrum density using the standard implementation of the spectral parameterization algorithm (Donoghue et al., 2020) in the “fixed” mode (linear fit in log-log plot) in two different frequency ranges: a lower one, at 20-35 Hz, and a higher one, at 80-150 Hz. The lower range was chosen following a large body of literature to avoid low-frequency knees, high-power peaks, and spectral plateaus (Gerster et al., 2021), and has been previously linked with individual variations to excitation to inhibition balance (Gao et al., 2017; Lendner et al., 2020). Different alternative, but related, frequency ranges were tested in exploratory analyses on a subset of patients (e.g., 30-45 Hz, or 20-40 Hz). All of those gave comparable results, and we used 20-35 Hz for our analysis, as it was the band that more consistently avoided the above-mentioned problems. The higher range was chosen as a typical high-frequency range that is often computed in iEEG studies (Lachaux et al., 2012).

The spectral exponent was computed as the slope of nonperiodic parts of the power spectra observed at each electrode via a standardized approach with the specparam toolbox (Donoghue et al., 2020) (parameters for the fitting: peak_threshold = 2, min_peak_height: 0.1, peak_width_limits: [1, 10], with max_n_peaks = 2 for the lower range and 0 for the higher one). Fits for every electrode were visually inspected, and any electrodes with clear artifacts on the power spectra, or where the fit was particularly noisy, were excluded to ensure an accurate estimation of the spectral exponent. After this step, all remaining electrodes (N = 270) had fits with R² of at least 0.8. Amygdalar electrodes from 2 patients had a prominent peak in their power spectra at ∼40 Hz (see Fig. 5A). This was found for electrodes of the amygdala only, and not other electrodes, and to the best of our knowledge was unrelated to any sources of noise, or pathologic findings in these patients. We confirmed that fitting of the spectral exponent was not affected by these peaks in any of the 2 patients, which were outside the range of our fits.

Figure 5.

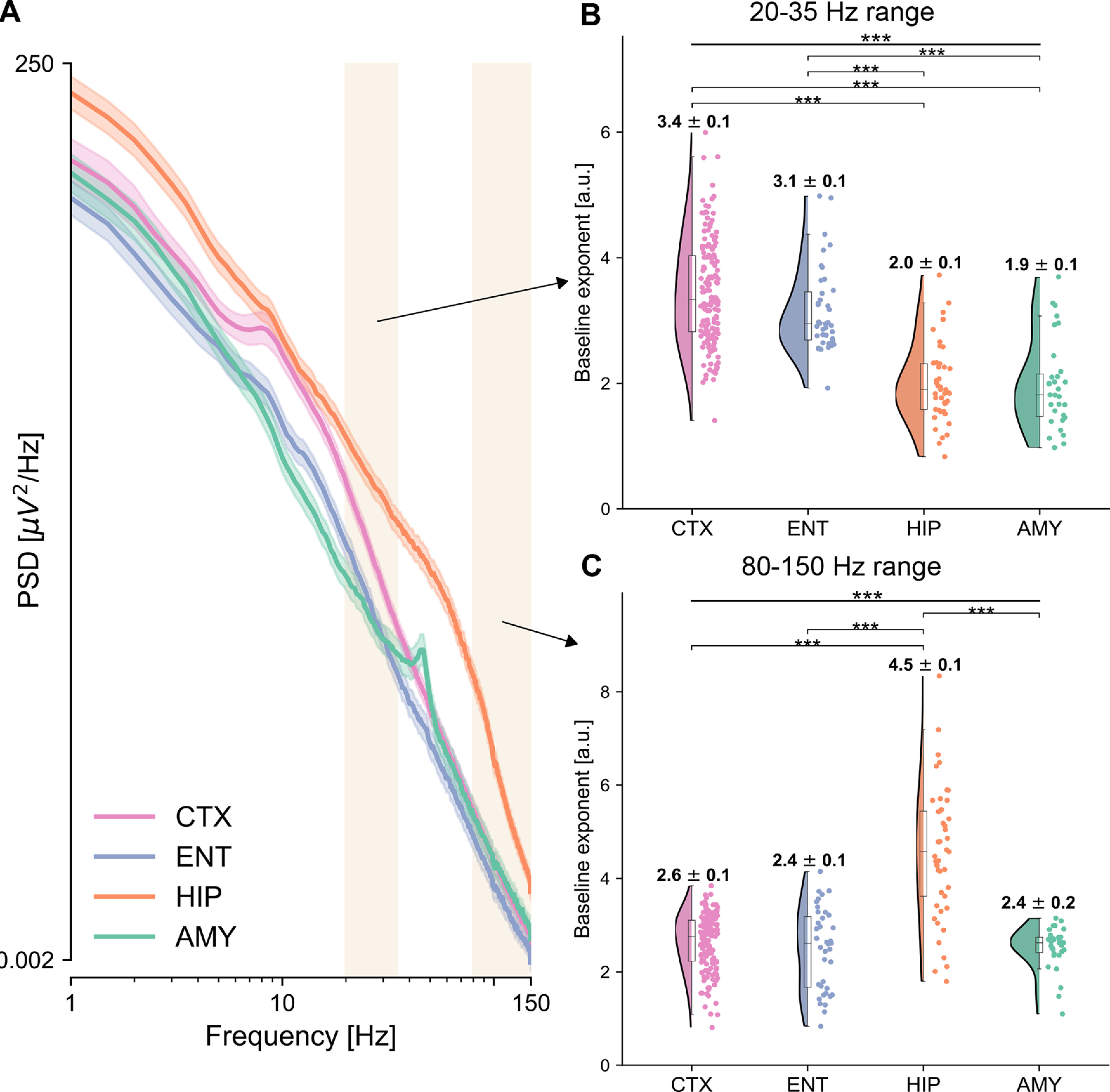
Power spectra and spectral exponents across brain regions. A, Average power spectra are displayed for the four ROIs. Cortex (pink) exhibits a characteristic oscillatory peak at ∼10 Hz, and a relatively fast decay, while the hippocampus (orange) displays the strongest power, which for low frequencies decay relatively gently, but after 70 Hz much faster. Shaded rectangles represent the two frequency ranges for which the spectral exponent is computed, at 20-35 Hz, and at 80-150 Hz. x and y axes are plotted in logarithmic scales. B, C, Spectral exponent at 20-35 Hz (B) and 80-150 Hz (C), for each electrode and ROI. The spectral exponent in the 20-35 Hz range shows a significant main effect of region, with the temporal cortex having the steepest exponent followed by the entorhinal cortex, the hippocampus, and amygdala, which have flatter exponents. The spectral exponent at 80-150 Hz also shows a significant effect of region, with the hippocampus having the steepest exponent among all other regions, compatible with the knee observed in the average power spectra (A).

Responsive electrodes

Responsive electrodes were identified following common approaches in the field of iEEG (Dürschmid et al., 2016). Briefly, differences between the average signal in poststimulus time points $\overline{\mathrm{A}}\left(t\right)$, and over the entire baseline $\overline{\mathrm{B}}$, were compared with surrogate distributions computed by randomly shifting the original epochs for i = 1,…,1000 iterations ({A_i(t) – B_i}_{i = 1…1000}). Response time points were considered significantly different from the baseline if $\overline{\mathrm{A}}\left(t\right)–\overline{\mathrm{B}}$ fell outside the outer 5% interval of the permuted distribution. Additionally, only electrodes with at least one consecutive response lasting >50 ms were kept, to correct for multiple comparisons, as commonly done in the field (Guthrie and Buchwald, 1991; Haller et al., 2018; Kam et al., 2021). The poststimulus time points were restricted to the interval [10, 600] ms, to control for too early and too late onsets that would be biologically implausible. We defined the onset latency as the time between the sound onset and the first responsive time point, and the peak latency as the time between the sound onset and the maximum absolute voltage difference from baseline.

Statistical analyses

Statistical tests were conducted in R version 4.2.0 (R Development Core Team, 2020) using linear mixed-effects models with a random intercepts term corresponding to the patient. The random intercepts term captures interpatient variability, which is needed when analyzing electrodes from multiple patients together. This ensured that any identified effects were not trivially driven by the fact that the electrodes were recorded from multiple patients (Yu et al., 2022) (implemented with nlme package) (Lindstrom and Bates, 1990). The omnibus tests for the “brain region” factor were computed with F tests, while post hoc pairwise comparisons were computed with Tukey's range test, controlling for multiple comparisons (implemented with emmeans package). In the case of omnibus tests on multiple time lags (see Fig. 2A) and tests over multiple MNI coordinates, p values were Bonferroni-corrected. For regression analyses, we used linear mixed-effects models with a continuous predictor and random intercepts accounting for across-patient variability. We computed correlation values starting from R² as described by Nakagawa and Schielzeth (2013) and took the square root, mimicking a fixed-effects-only linear model (implemented with MuMIn package) (Barton, 2020). p values were computed with F tests, correcting with Bonferroni when regressing on each level of the region factor separately (p_corr).

Figure 2.

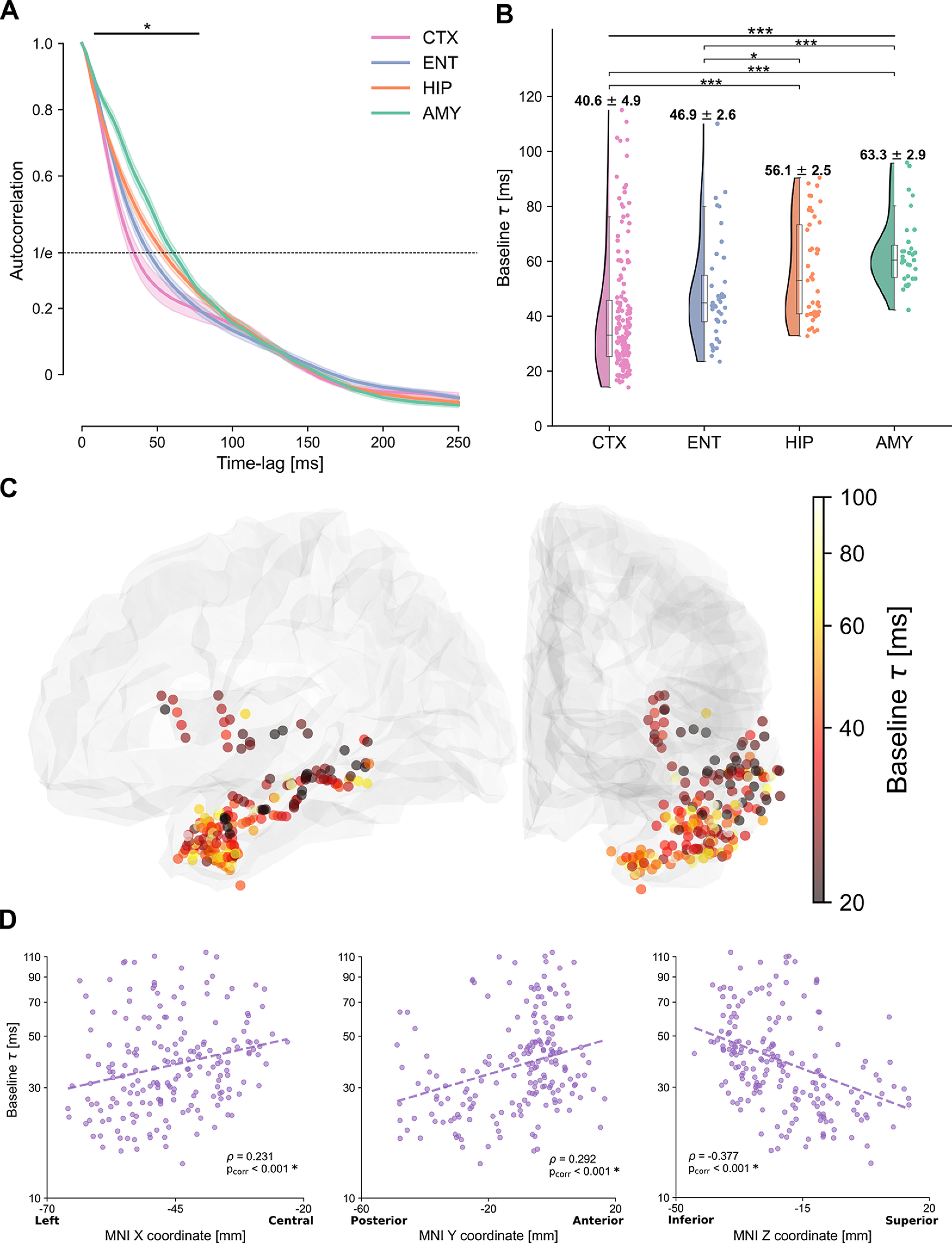
Autocorrelation function and intrinsic cortical neural timescales at baseline. A, Average autocorrelation function at baseline across electrodes and patients, for electrodes in the temporal (pink) and entorhinal (light blue) cortices, hippocampus (orange), and amygdala (green). The autocorrelation shows a significant main effect of region for time lags between 10 and 80 ms (horizontal solid bar). Dashed horizontal line at 1/e (inverse of natural logarithm) indicates the value of the autocorrelation for which the characteristic timescales are extracted. B, Intrinsic timescales at baseline (τ), plotted for each electrode, show a main effect of region, with significantly faster timescales for the temporal and entorhinal cortices compared with the hippocampus and amygdala. C, The spatial organization of intrinsic timescales follows the cortical anatomy. Electrodes in the posterior/superior temporal cortex exhibit the fastest timescales, which progressively increase along the anterior/inferior axis. Color map represents the intrinsic timescale for each electrode on a logarithmic scale. For display purposes, all electrodes were projected to the left hemisphere. D, Gradients of timescales spanning the cortex, plotted as timescales along the X, Y, and Z directions of MNI coordinates of each electrode. Timescales significantly correlate with MNI coordinates in all three dimensions, tracking the cortical anatomy.

Data and code availability

Because of the sensitive nature of the data, data and code can be made available from the corresponding author on reasonable request.

Results

We analyzed iEEG signals in 270 electrodes from 11 epilepsy patients (median = 25, minimum = 8, maximum = 37 electrodes per patient, Table 1). In a first step, we assessed a macroscopic organization of neural dynamics by dividing electrodes into four ROIs, selected based on the most consistent implantation schemes across patients. These were targeting the entorhinal cortex (ENT), hippocampus (HIP), and amygdala (AMY) in their innermost electrodes, and had additional electrodes covering the temporal and adjacent cortices (CTX) (for an exemplar implantation, see Fig. 1A). In a second step, we grouped all available electrodes together (for full electrode coverage, see Fig. 1B), regardless of ROIs, and assessed their spatial organization at a finer level, with respect to cortical and limbic anatomies.

Figure 1.

Experimental paradigm, electrode coverage, and exemplar iEEG traces. A, Summary of the main analyses and methodology. Left, Schematic of the auditory stimulation protocol. Patients were presented with 100 ms pure tones, occurring at random intervals between 0.9 and 19 s. Middle, Example of implanted iEEG electrodes and exemplar raw trace of spontaneous neural activity from one electrode, before sound presentation, which is used to estimate intrinsic timescales and spectral exponents. Right, iERPs are extracted in response to the sounds. These are displayed for a schematic illustration of our protocol, for three exemplar electrodes, presented in more detail in Figure 4. B, Illustration of recorded electrodes (N = 270) over the group of 11 patients. Black-circled electrodes are responsive to the auditory stimulation. As exemplar signals, we show iEEG traces from the transverse and superior temporal gyri (TTG and STG, pink), the entorhinal cortex (light blue), the hippocampus (orange), and the amygdala (green). Each of these regions exhibits characteristic and distinct spontaneous dynamics, displayed here over a 6 s segment.

iEEG signals in the four ROIs present striking qualitative differences already in their ongoing neural activity before sound presentation (for exemplar iEEG recordings, see Fig. 1B). To characterize ongoing neural dynamics, we computed their intrinsic timescales before the presentation of sounds (Fig. 1A, middle). For each electrode, we computed the autocorrelation function of baseline iEEG signals, which quantifies how similar a time series is to its past values across multiple time lags. The mean autocorrelation, computed across patients and brain regions, shows a characteristic decay as the time lag increases (Fig. 2A). For short time lags, the mean autocorrelation follows an ordering: electrodes in the temporal cortex have the most rapid decay, followed by electrodes in the entorhinal cortex, the hippocampus, and last, the amygdala (Fig. 2A), with significant differences across the four regions at time lags between 10 and 80 ms (mixed-effects models, accounting for different patients, p_corr < 0.05 with Bonferroni correction) (Fig. 2A, solid horizontal line).

We next computed intrinsic neural timescales (τ). These were defined as the time lag at which the autocorrelation of each electrode decayed to a fixed value (in our case, 1/e, Fig. 2A, dashed horizontal line). The extracted intrinsic timescales τ confirm the macroscopic hierarchy observed via the autocorrelation function and show a significant difference across brain regions (F_(3,256) = 27.313, p = 2.33 × 10⁻¹⁵, mixed-effects model with random intercepts) (Fig. 2B). The temporal cortex exhibits significantly faster intrinsic timescales, at 40.6 ms on average compared with both the hippocampus and amygdala, which have slower timescales, at 56.1 and 63.3 ms, respectively (for a detailed report of all paired statistical comparisons, based on t tests derived via the linear mixed-effects models, see Table 2). Within subregions of the cortex, intrinsic timescales tend to be slower in the pole, and faster in the transverse gyrus, while the superior, middle, and inferior temporal cortex, and the insula lie in between (Table 3). The entorhinal cortex (46.9 ms) is also significantly faster compared with other limbic areas, but not different from the temporal cortex (Table 2).

Table 2.

Pairwise comparisons of intrinsic neural timescales across ROIs^a

Comparison	df	t	p
CTX-ENT	192	−2.383	0.083
CTX-HIP	198	−6.099	2.34 × 10−8
CTX-AMY	184	−7.716	1.69 × 10−12
ENT-HIP	82	−2.817	0.027
ENT-AMY	68	−4.635	3.36 × 10−5
HIP-AMY	74	−2.067	0.167

^aThe first column lists each of the six pairwise comparisons, the second one the relative degrees of freedom (df) of the test, the third one the t values of the post hoc t test, and the last column the related p values. All pairs of cortical-limbic areas have significant differences in their intrinsic timescales, while the differences between temporal/entorhinal cortex and hippocampus/amygdala are nonsignificant. The timescale values per region are computed through a mixed-effects model with a patient-specific random effect. p values are corrected for multiple comparisons via the Tukey range test.

Table 3.

Intrinsic neural timescales, iERP latencies, and the spectral exponent across cortical subregions^a

Cortical subregion	No. of electrodes (responsive)	Median timescale (ms)	Median iERP onset (ms)	Median iERP peak (ms)	Median exponent (a.u.)
TTG	3 (3)	16.7	42.0	80.1	2.1
STG + STS	54 (13)	31.2	83.0	168.9	3.4
MTG	18 (2)	30.0	189.0	293.5	3.5
ITG + ITS	19 (2)	32.1	133.8	286.6	3.4
Insula	22 (8)	31.3	131.3	276.9	2.7
Pole	13 (3)	41.4	260.7	438.5	3.9

^aThe number of total and responsive electrodes across all recordings is reported for each subregion, together with median values of timescales, auditory latencies, and 20-35 Hz exponent. The fastest timescales and lower response latencies are observed for the transverse temporal gyrus, while the opposite is true for the temporal pole. TTG, Transverse temporal gyrus; STG, superior temporal gyrus; STS, superior temporal sulcus; MTG, middle temporal gyrus; ITG, inferior temporal gyrus; ITS, inferior temporal sulcus.

These results were confirmed with two additional control analyses, which accounted for potential biases because of oscillations. First, when estimating timescales by a direct exponential decay fit to the ACFs, similar to previous studies (Murray et al., 2014; Siegle et al., 2021), but accounting for oscillations (Zeraati et al., 2022), the same macroscopic hierarchy was observed, highlighted by a significant difference of timescales across regions (F_(3,256) = 16.789, p = 5.49 × 10⁻¹⁰). Second, the same hierarchy was also observed when estimating timescales as the inverse of the knee frequency in power spectra, similar to Gao et al. (2020) (F_(3,197) = 28.769, p = 1.78 × 10⁻¹⁵). Both of these control analyses replicate the same ordering of timescales as reported in Figure 2B. These findings reveal a robust macroscopic hierarchy in spontaneous neural activity, confirmed with three different methods, where the temporal cortex shows short intrinsic timescales, while limbic areas exhibit slower dynamics.

We then delved into a finer characterization of timescales by exploring their spatial organization within anatomic regions (for an overview of cortical subregions, see Table 3). Within the temporal and entorhinal cortices, intrinsic timescales show a gradient that spans the temporal lobe through the posterolateral (fast timescales) to the anteromedial (slow timescales) axis, following the temporal lobe anatomy (Fig. 2C). This gradient is particularly prominent in the Y and Z directions that mostly define the temporal lobe orientation (Fig. 2D, correlation between coordinates in MNI space and intrinsic timescales: ρ_X = 0.231, p_X = 2.44 × 10⁻⁶; ρ_Y = 0.292, p_Y = 1.83 × 10⁻⁹; ρ_Z = −0.377, p_Z = 2.94 × 10⁻¹², mixed-effects models and Bonferroni-corrected).

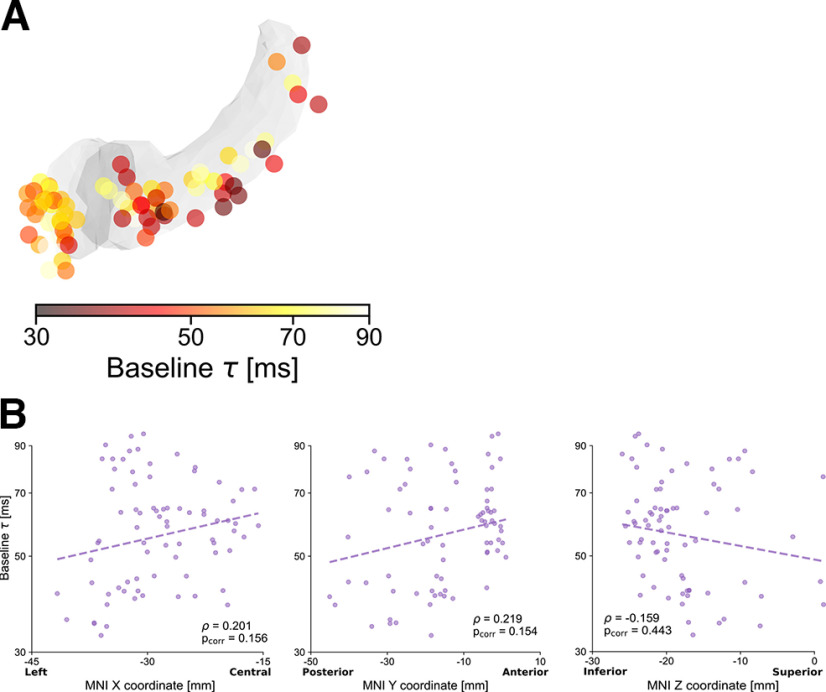
The spatial distribution of timescales in the hippocampus and amygdala, on the contrary, is less defined, with no significant correlation along any of the MNI coordinates after correcting for multiple comparisons (ρ_X = 0.201, p_X = 0.156; ρ_Y = 0.219, p_Y = 0.154; ρ_Z = −0.159, p_Z = 0.443, mixed-effects models and Bonferroni-corrected; Fig. 3). These findings support a fine-grained intrinsic organization of spontaneous neural dynamics in the extended auditory network that manifests across cortical and limbic regions and exhibits an anatomic gradient spanning the temporal cortex from posterior to anterior.

Figure 3.

Intrinsic hippocampal and amygdalar neural timescales at baseline. A, Anatomical organization of intrinsic timescales at baseline throughout the hippocampus and amygdala, displaying generally shorter timescales in hippocampus (darker colors) than in amygdala, as in Figure 2B. Color map represents the intrinsic timescale for each electrode on a logarithmic scale. For display purposes, all electrodes were projected to the left hemisphere. B, Correlations between MNI coordinates and intrinsic timescale (τ) across electrodes. Although τ tends to be slower for anterior electrodes, and in particular for the amygdala, correlations in the X, Y, and Z directions are not significant when accounting for different patients and after Bonferroni correction.

We next investigated whether intrinsic timescales at baseline could explain the timing of auditory processing. At a qualitative level, auditory intracranial event-related potentials (iERPs) show striking differences throughout the temporal lobe (Fig. 4A). iERPs in primary auditory regions (e.g., the transverse gyrus, Fig. 4A, top row) show early, short-lasting, and high-amplitude responses, while iERPs in the superior temporal gyrus have a later onset and duration (Fig. 4A, second row). By contrast, auditory responses in the hippocampus, amygdala, and entorhinal cortex are smoother and long-lasting (Fig. 4A, third to fifth rows), similar to previous reports (Halgren et al., 1980).

Figure 4.

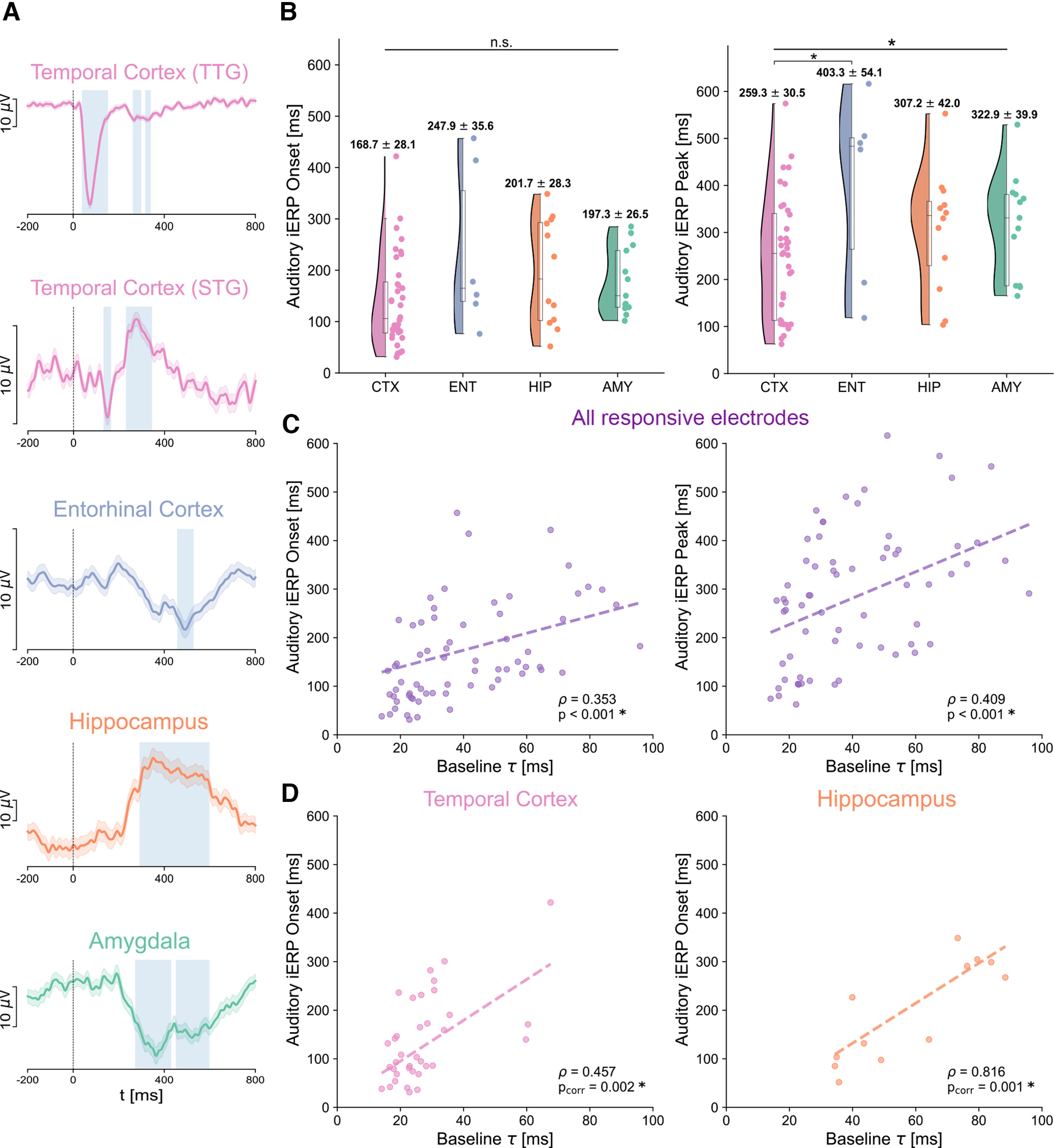
Onset and peak latencies of auditory responses across brain regions and their relation to intrinsic timescales at baseline. A, Exemplar auditory responses for each of the recorded regions (1-40 Hz iERPs). Time 0 corresponds to sound onset. Auditory responses in the transverse temporal gyrus (TTG) are the earliest, shortest-lasting, and exhibit the largest amplitude (top plot). Responses in other cortical regions, for example, the superior temporal gyrus (STG), have a relatively early onset, and later peak, while responses in the entorhinal cortex, hippocampus, and amygdala (third to fifth row) are typically smoother, long-lasting, and with later peaks. Blue represents significant response periods compared with the prestimulus baseline. The variability in response amplitudes is indicated by the different spans of a 10 μV scale on the y axis. B, Auditory response onset (left) and peak (right) latencies for all responsive electrodes. The temporal cortex shows the earliest onset and peak latencies across all brain regions, with responses starting on average at 168.7 ms, and peaking at 259 ms after sound onset, followed by the hippocampus/amygdala, and entorhinal cortex. C, Regression of auditory iERP onset (y axis, left) and peak (y axis, right) latencies on intrinsic timescales τ at baseline (x axis) across all responsive electrodes. Regressions of both onsets and peaks on intrinsic timescales are highly significant, accounting for across-patient variations, suggesting that intrinsic timescales can explain the timing of auditory responses at the single electrode level. D, A significant regression of iERP onsets on intrinsic timescales also persists within the temporal cortex (left), and hippocampus only (right), but not in the amygdala or entorhinal cortex.

To quantify these response profiles, we restricted our analysis to electrodes that showed a significant 1-40 Hz iEEG response to the auditory stimuli compared with a prestimulus baseline (see Responsive electrodes, N = 67 of 270 total electrodes). For each responsive electrode, we computed its response onset and peak latencies (Fig. 4B). Cortical electrodes show generally faster responses than hippocampal and amygdalar ones both for onset (30 ms faster) and peak (50-60 ms faster). At the group level though, there is no significant effect of brain region on onset latency (F(3,55) = 1.867, p = 0.146) and just barely on peak latency (F(3,55) = 2.774, p = 0.0499, both mixed-effects models). In cortical subregions, the transverse gyrus shows the earliest responses, followed by the superior temporal gyrus/sulcus, inferior and middle temporal gyri (Table 3).

Interestingly, this variability in onset and peak latencies within and between brain regions can be partially explained when accounting for differences in intrinsic timescales (Fig. 4C). We computed a regression of response latencies on intrinsic timescales, which shows a highly significant main effect of timescale at baseline both on response onset (ρ = 0.353, p = 0.0009) and peak latency (ρ = 0.409, p = 0.0005, both mixed-effects models with random intercepts, to account for different patients). The strong regression of the onset of auditory responses on intrinsic timescales at baseline holds for electrodes within the temporal cortex (ρ = 0.457, p_corr = 0.0017) and hippocampus (ρ = 0.816, p_corr = 0.0013, Fig. 4D) (mixed-effect models and Bonferroni-corrected). The other within-region regressions do not reach significance, except for the peak latency in the hippocampus (ρ = 0.734, p_corr = 0.031). Moreover, a significant regression result persists when splitting each patient's trials into two experimental halves, suggesting that the observed results are robust across the experimental session (ρ₁ = 0.429, p₁ = 0.001; ρ₂ = 0.364, p₂ = 0.01 for the first and second half of the experiment, respectively). These results show that intrinsic timescales at baseline can explain both the onset and peak latencies of auditory responses throughout the temporal lobe: regions that are characterized by fast intrinsic timescales exhibit a fast reaction to incoming auditory stimuli, while the hippocampus, amygdala, and entorhinal cortex are mediated by slower ongoing dynamics and show slower auditory responses.

To further explore and confirm the observed hierarchy of intrinsic neural timescales, we additionally characterized their aperiodic neural activity via the spectral exponent (Fig. 5). The average PSD shows qualitative differences across the four ROIs (Fig. 5A). The cortex exhibits a characteristic oscillatory peak at ∼10 Hz, and a relatively fast decay, while the hippocampus displays the strongest power, which for low frequencies decays relatively gently, but after 70 Hz much faster (Fig. 5A). We quantified the nonoscillatory part of the power spectra for each electrode via the spectral exponent (i.e., the slope in log-log space) in a lower (20-35 Hz, as commonly reported in the literature) (Gao et al., 2017; Miskovic et al., 2019; Lendner et al., 2020) and upper range (80-150 Hz), corresponding to high γ-power (Lachaux et al., 2012). The lower range was chosen after considering typical ranges used in the literature, which vary across studies, and compromising between consistency with previous studies and recommended methodological considerations (for a detailed explanation of the choice of the frequency band and control analyses, see PSD and spectral exponent).

The spectral exponent in the 20-35 Hz range shows a strong ordering, with electrodes in the temporal cortex having the steepest exponent, followed by electrodes in the entorhinal cortex, hippocampus, and amygdala (Fig. 5B), with a significant effect of region (F_(3,256) = 80.665, p = 1.11 × 10⁻¹⁶). This result confirms the ordering observed for intrinsic timescales (Fig. 2B), with a different and complementary measure. Moreover, all pairs of cortical-limbic areas have significant differences in their 20-35 Hz exponent (Table 4), while the difference between temporal and entorhinal cortex is slightly below significance threshold (Table 4, p_CTX-ENT = 0.054). Exponents in cortical subregions do not show marked differences from each other (Table 3).

Table 4.

Pairwise comparisons of spectral exponents among the four ROIs in the two analyzed frequency ranges (20-35 Hz and 80-150 Hz)^a

Comparison	df	t (20-35 Hz)	p (20-35 Hz)	t (80-150 Hz)	p (80-150 Hz)
CTX-ENT	192	2.557	0.054	1.551	0.408
CTX-HIP	198	12.421	4.34 × 10−14	−14.214	4.31 × 10−14
CTX-AMY	184	11.409	5.35 × 10−14	1.631	0.363
ENT-HIP	82	7.591	3.63 × 10−12	−12.321	4.35 × 10−14
ENT-AMY	68	7.564	4.27 × 10−12	0.195	0.997
HIP-AMY	74	0.608	0.929	11.650	4.90 × 10−14

^aThe first column lists each of the six pairwise comparisons, the second one the relative degrees of freedom (df) of the test, the third and fourth ones the t values and p values of the post hoc t test for the 20-35 Hz range, respectively, and the last two columns the t values and p values for the 80-150 Hz range, respectively. All pairs of cortical-limbic areas have significant differences in their 20-35 Hz exponent, while the difference between temporal and entorhinal cortex is slightly below significance threshold. For the 80-150 Hz range, only the comparisons between hippocampus and the other areas are significant because of the very steep slope of hippocampal electrodes in the high-γ range. The spectral exponent values are computed through a mixed-effects model with a patient-specific random effect. p values are corrected for multiple comparisons via the Tukey range test.

The spectral exponent in the 80-150 Hz range also shows a significant main effect of region (F_(3,256) = 79.156, p = 1.11 × 10⁻¹⁶) (Fig. 5C). This effect is mainly driven by the difference between the hippocampus (with an exponent of 4.5 on average across electrodes) and all other regions (Table 4), which instead have very similar exponent values, ranging between 2.4 and 2.6 on average (Fig. 5C). The particularly steep hippocampal spectral exponent for high frequencies reflects the abrupt change of slope in the power spectrum, which forms a knee at ∼70 Hz (Fig. 5A).

As the lower range spectral exponent reflects the same ordering of brain regions as intrinsic timescales, we explored its spatial organization. Similar to the intrinsic timescales, we observe an anatomic modulation of spectral exponents along the temporal lobe, indicated by a significant, albeit weaker, correlation between spectral exponent and MNI X coordinates (ρ_X = −0.188, p_X = 9.99 × 10⁻⁴, mixed-effects model and Bonferroni-corrected), but no significant correlation along other axes (p > 0.12). This information provides further support for a gradient organization of neural dynamics within the extended auditory cortical network.

Last, the spectral exponent within the hippocampus/amygdala only shows a weak correlation along the X axis (ρ_X = −0.252, p_X = 0.029, mixed-effects model and Bonferroni-corrected). When correlating the lower spectral exponent with response onset or peak latencies, there is no significant correlation, neither in all responsive electrodes grouped together (ρ_onset = 0.066, p_onset = 0.529; ρ_peak = −0.096, p_peak = 0.430, mixed-effects models) nor within any of the individual brain regions (Table 5).

Table 5.

Regressions of iERP auditory latencies on the 20-35 Hz spectral exponent at baseline^a

Region	Correlation ρ (iERP onset)	p (iERP onset)	Correlation ρ (iERP peak)	p (iERP peak)
All	0.066	0.53	−0.096	0.43
CTX	0.381	0.12	0.345	0.21
ENT	0.669	0.73	−0.276	1.0
HIP	0.313	1.0	0.215	1.0
AMY	−0.237	1.0	−0.340	0.93

^aThe correlation coefficients and relative p values are summarized when regressing onset and peak iERP latencies on the spectral exponent, for all responsive electrodes. Regressions are computed with mixed-effects models with a patient-specific random effect. p values for the four regions are Bonferroni-corrected.

Discussion

We provide evidence for a hierarchy of spontaneous intrinsic neural dynamics in the extended human auditory network, which in turn explains a hierarchy in the processing of incoming auditory stimuli. At a macroscopic level, the temporal cortex assumes a “low” position along this hierarchy, highlighted by a steep spectral exponent and short intrinsic timescales, which likely mediate short temporal receptive windows (Honey et al., 2012; Norman-Haignere et al., 2022). On the contrary, the hippocampus and amygdala exhibit longer intrinsic timescales and have flatter spectral exponents. This suggests that the hippocampus and amygdala assume a “higher,” or integrative, function in a temporal lobe hierarchy, as longer receptive time windows, indicated by longer timescales, may be necessary for information integration (Murray et al., 2014; Golesorkhi et al., 2021b). By contrast, a flatter exponent may indicate a shift toward excitation (Gao et al., 2017), or increased neural noise (Alnes et al., 2021).

Intrinsic timescales and spectral exponent reveal a hierarchy in the temporal lobe

Our findings are in line with previous reports of a hierarchical organization in the visual and somatosensory modalities (Murray et al., 2014; Wang, 2020), where neural timescales progressively increase along the cortical hierarchy. Previous investigations of intrinsic timescales in humans have mainly relied on hemodynamic and magnetoencephalographic measures, and have shown fast spontaneous dynamics in the temporal lobe compared with higher-level areas, such as the Prefrontal cortex, albeit only at a macroscopic level (Raut et al., 2020; Golesorkhi et al., 2021a). Apart from timescales, oscillatory power and the spectral exponent also show an intrinsic organization (Frauscher et al., 2018; Mahjoory et al., 2020). iEEG oscillatory peaks transition from faster to slower frequencies along the posterior-to-anterior temporal cortex (Frauscher et al., 2018), while primary auditory regions show weaker α and stronger high-γ power in their baseline activity compared with secondary auditory areas (Billig et al., 2019). Here, we refine these observations by exploring the hierarchy of intrinsic timescales within the extended auditory network of the temporal lobe.

From a signal processing perspective, timescales quantify the autocorrelation decay of neural signals, while the spectral exponent measures the power decay of aperiodic neural activity (He et al., 2010; Hasson et al., 2015). A steeper exponent may reflect decreased higher-frequency activity, a rotation in the power spectra (Podvalny et al., 2015), or lower levels of neural noise (Voytek et al., 2015; Alnes et al., 2021). As several mechanisms can explain changes in the steepness of power spectra, associating those to neural timescales is neither trivial nor unambiguous. At a physiological level, timescales are considered an indicator of a neural system's memory capacity (Hasson et al., 2015), while the steepness of the spectral exponent around the lower range we studied here is considered a proxy of excitation-to-inhibition balance (Gao et al., 2017).

Importantly, similar to timescales, synaptic excitation and inhibition also manifest hierarchically: while advancing through the visual hierarchy, excitatory connections increase, myelin content decreases, and the expression of genes involved in synaptic transmission increases (Wang, 2020). In our data, the 20-35 Hz spectral exponent was steeper in the temporal cortex than in the hippocampus or amygdala, similar to previous reports (Frauscher et al., 2018), and possibly reflecting higher levels of inhibition, compatible with previous reports of increased inhibition in sensory regions (Wang, 2020).

In our results, the macroscopic ordering that we identify via timescales is mirrored by the spectral exponent and reflects the neurobiological proximity that one would expect between the temporal/entorhinal cortex and hippocampus, which are all characterized by a laminar organization of pyramidal neurons, as opposed to the amygdala whose basolateral nucleus consists primarily of pyramidal cells without preferential orientation, and with a much higher neural density (Dumas et al., 2011).

Overall, our findings support the notion that properties of neural dynamics are intrinsic (Wainio-Theberge et al., 2022); to this, we add that they are also local in nature. Taking advantage of the fine spatial resolution of intracranial recordings in humans, we show that a hierarchy of intrinsic neural dynamics of the extended auditory network manifests as a continuous gradient along the posterolateral to anteromedial axis, following the anatomy of the temporal lobe, both for intrinsic timescales and spectral exponent.

Extending the hierarchy of intrinsic timescales to hippocampus and amygdala

Importantly, contrary to the vast majority of existing studies (Honey et al., 2012; Murray et al., 2014; Gao et al., 2020; Norman-Haignere et al., 2022), we extend the characterization of intrinsic neural dynamics beyond cortical electrodes by including limbic structures, such as the hippocampus and the amygdala. Previous studies have shown that prefrontal or parietal regions assume the role of “higher-order” areas (Honey et al., 2012; Rocchi et al., 2021). Here, we expand these well-studied hierarchies by showing that the hippocampus and amygdala can also be positioned in a “higher” order compared with sensory areas, both in terms of intrinsic dynamics (slower timescales and flatter exponent) and auditory response latencies.

To date, only few studies have attempted to characterize intrinsic timescales in the human hippocampus and amygdala. These report intermixed results, with one MRI study showing gradients of timescales in the hippocampus in the range of few seconds (Raut et al., 2020), and a study of neural firing reporting no differences in timescales between the two structures (Hagemann et al., 2022). In our work, we did not find evidence for gradients of timescales within the hippocampus and amygdala. There are several possible explanations for these diverging results across studies, including the different overall temporal sensitivity of the recorded signals, ranging from seconds to milliseconds, the electrode coverage, or, in the case of hemodynamic responses, signal dropout (Raut et al., 2020), which all together make the comparison of timescales extracted from different recording modalities nontrivial (Manea et al., 2022).

Additionally, the extended auditory network includes the “what” and “where” pathways, comprising prefrontal and parietal areas (Rauschecker and Scott, 2009). The “what,” or rostral, pathway typically shows sustained responses and longer response latencies than the “where,” or caudal, pathway (Jasmin et al., 2019). This dissociation can be observed in nonhuman and human primates (Scott et al., 2011; Camalier et al., 2012; Hamilton et al., 2018). The lack of frontal or parietal electrode coverage in our patient cohort did not allow investigating how timescales are organized along the full extent of these pathways and how they would be positioned relative to hippocampus/amygdala in a putative hierarchy. Future investigations could expand beyond the temporal lobe, allowing a direct comparison of intrinsic timescales in limbic structures and frontal or parietal cortex.

Linking spontaneous intrinsic timescales and auditory processing

Although several studies have posited that short intrinsic timescales may mediate fast responses to incoming stimuli, we now provide direct evidence for the auditory system. Previous studies have either analyzed intrinsic timescales in the auditory system while assessing whole-brain dynamics (Gao et al., 2020; Raut et al., 2020; Golesorkhi et al., 2021a), without the specificity of our work for the auditory system, or have investigated intrinsic timescales during complex auditory stimuli such as speech, as they unfold over time (Honey et al., 2012; Norman-Haignere et al., 2022). Here, we show, for the first time, specifically for the extended auditory system, that a hierarchical organization in spontaneous neural activity is strongly related to the timing of processing short, evoked auditory stimuli.

Importantly, we show, in the same patients and recordings, that the diversity of intrinsic timescales partially explains the richness of auditory responses that are observed in temporal areas in terms of onset and peak latencies, at the single electrode level, with high spatial resolution. Although our analyses are correlational, we posit that this repertoire of spontaneous intrinsic timescales may support the auditory process itself, providing a variety of processing windows (Golesorkhi et al., 2021b) both at a macroscopic level across brain regions, and also at the millimeter level, following the anatomic organization of the temporal cortex. Here, we used pure tones as a simple experimental model of auditory processing. Future studies can examine how the characteristics of auditory stimuli, for example, their frequency or complexity, affect the interplay between spontaneous and evoked activity, and whether trial-by-trial changes in timescales may affect auditory processing and perception of individual sounds.

Last, although the spectral exponent mirrors the macroscopic hierarchy observed via intrinsic timescales, in our data there was no direct link to the timing of auditory responses. Although the spectral exponent is sensitive to auditory processing (Gyurkovics et al., 2022), or levels of attention (Waschke et al., 2021), it does not seem to directly relate to their timing. We speculate that the exponent may capture frequency-specific modulations in neural activity, rather than the response latency itself, which may be better explained by the temporal “memory” of a signal.

In conclusion, our results show a hierarchy of neural dynamics in the extended human auditory network that manifests across cortical and limbic structures, exhibits anatomic gradients with millimeter resolution, and can explain the temporal richness of neural responses to auditory stimuli.