Abstract
This decade had witnessed the tremendous progress in miniaturizing optical imaging systems. Despite the advancements in 3D printing optical lenses at increasingly smaller dimensions, challenges remain in precisely manufacturing the dimensionally compatible optomechanical components and assembling them into a functional imaging system. To tackle this issue, here we report the use of 3D printing to enable digitalized optomechanical components manufacturing, part-count-reduction design, and the inclusion of passive alignment features, all for the ease of system assembly. We 3D printed the key optomechanical components of a penny-sized accommodating optical microscope in 50 minutes at a significantly reduced unit cost near $4. By actuating a built-in voice-coil-motor, we validated its accommodating capability to focus on specimens located at different distances, and further utilized a focus stacking function to greatly extended depth-of-field. The microscope can be readily customized and rapidly manufactured to respond to task-specific needs in form-factor and optical characteristics.
Keywords: additive manufacturing, 3D printing, optical imaging system, low cost, miniature accommodating optical microscope, micro-continues liquid interface production
Graphical Abstract
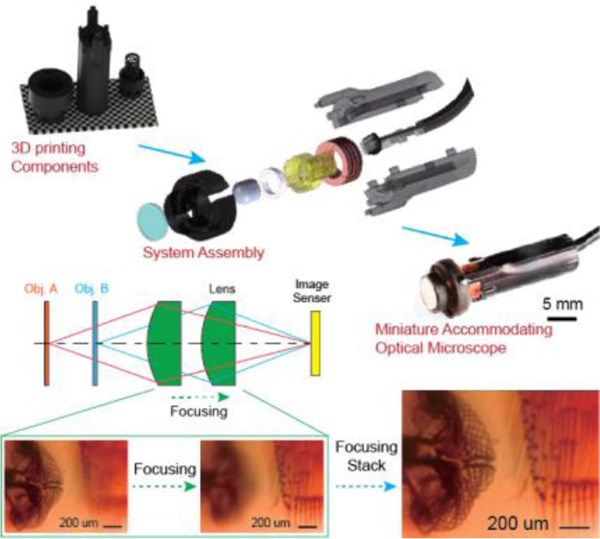
Key optical and optomechanical components of a miniature accommodating optical microscope are 3D printed in 50 minutes for less than $4. Synergizing the built-in voice-coil-motor and compliant optomechanics facilitates focus stacking functionality for extending imaging depth. 3D printing enables digitized component manufacturing, part-count reduction, and passive alignment for the ease of system assembly and alignment, allowing rapid customizability towards task-specific needs.
1. Introduction
There are growing interests in miniaturing imaging platforms for potential commercial, research, and educational applications [1]. However, dealing with optical and optomechanical components with increasingly smaller size requires high manufacturing precision and tight system assembly tolerances to achieve diffraction-limited performance. Traditional lens manufacturing relies on costly and time-consuming lapping, grinding, and polishing processes. Injection molding can produce low-cost polymer lenses, but still requires precision machined molds for the high-performance features needed for optical applications[2]. Such applications also necessitate equally strict tolerances for system assembly and the alignment of numerous components; labor-intensive and costly tasks which often require highly trained personnel and precision alignment equipment.
Breaking this cost barrier calls for a cost-effective and scalable manufacturing solution. In contrast to traditional manufacturing processes, additive manufacturing (AM), also referred to as 3D printing, produces complex volumetric structures by the successive addition of building layers[3]. The evolution of AM has seen a rapid growth in satisfying the ever-increasing demands in producing geometrically complex parts and assemblies in a wide range of industries, including automobile[4], aerospace[5], biomedical[6], and architecture[7]. This has the potential to transform existing optical manufacturing processes by allowing for design customization directly from digital models without sacrificing manufacturing speed and cost. Its inherent geometric complexity advantages enable a part count reduction (PCR) design for producing a single monolithic part to replace existing multi-component assemblies, reducing lifecycle cost, improving performance, and eliminating further alignment[8].
AM has made great strides over the years to miniaturize optical components. Two-photon direct laser writing with sub-100 nm voxel resolution has demonstrated the fabrication of micro-lenses and lens-assemblies, but at a rather slow “point-by-point” patterning nature[9]. Inkjet printing benefits from the viscosity and surface tension of larger liquid resin droplets to more quickly 3D print optically smooth surfaces on a solid substrate[10]. However, additional molding steps are required for free-standing optical elements[11]. A significant step in tackling this speed/accuracy trade-off was reported by us and other groups by using projection micro-stereolithography (PμSL) and its derivatives[12]. PμSL parallelizes the 3D printing process by curing an entire fabrication layer in a single exposure, being capable of printing millimeter-sized aspherical lenses in an hour[12c]. Micro-continuous Liquid Interface Production (μCLIP) reported further fabrication speed improvements by eliminating the lengthy resin-recoating step between the printing layers[13], further reducing fabrication time to minutes[12a, 12d]. Apart from photopolymer optics, direct ink writing (DIW) and computed axial lithography (CAL) have been used to fabricate gradient index (GRIN) and free form optics from silica-based materials, although they require a sintering process utilizing high temperature over 1000 ˚C[14]. In addition to 3D printed optical components, filament deposition 3D printers have been used to fabricate the optomechanics for the OpenFlexure Microscope design which provides precise mechanical sample manipulation in a lightweight and compact device[15]. These advancements have made AM optical lenses more economically favorable, however, there are still unsolved challenges in precisely manufacturing and assembling the dimensionally compatible optomechanical components into a miniaturized optical imaging system.
Unifying the fabrication processes for optics and optomechanics using AM would retain the low-cost, small-size benefit of the previously mentioned methods while improving the scalability and design customizability through additive manufacturing. In this article, we demonstrate the capability to AM the essential optical and optomechanical components for a miniaturized imaging platform featuring an aspherical lens and voice coil motor (VCM). System configuration can be tailored for a range of lens focal lengths or procurement sources. Furthermore, the VCM features a near-zero Poisson’s ratio 3D printed compliant foundation to minimize interference during focusing, preserving customizability in imaging magnification. All optomechanical components are 3D printed in a single batch within 50 minutes with minimal assembly requirements, at a system cost of less than $4. We have experimentally compared the imaging characteristics of 3D printed lenses with commercial polymer lenses. Finally, we demonstrate the active focusing through actuating the built-in VCM, and further implement the focus stacking function by combining multiple images taken while axially translating the imaging lens, to greatly extended the depth of field (DOF).
2. Results and Discussion
2.1. System Design of Miniature Optical Microscope
Figure 1 illustrates the modular design of the miniaturized accommodating microscope. A focusing motor translates the imaging lens along the optical axis to form magnified images onto the CMOS sensor for objects A and B located at different positions (Figure 1a). Optical magnification requires translating the imaging lens further away from the CMOS sensor, and thus, the planar configurations commonly found in the cell-phone cameras are not applicable. While the static DOF is shallow, successively acquired frames along the optical axis can be digitally combined using a focus stacking function, thereby extending the DOF. The system design (Figure 1b) incorporates two primary strategies - PCR and passive alignment features - to simplify assembly (details in Supporting Information).
Figure 1. System design and assembly flowchart of the 3D printed miniature accommodating optical microscope.

a) Conceptual illustration of focal plane adjustment principle and key components. b) Exploded view of the CAD model of the miniaturized optical microscope. c) Microscope components used in the assembly, including lenses with different focal length and corresponding elastic lens mount, IR-cutoff filter, enclosure components, focusing motor components and CMOS imaging sensor. d) Schematic illustration of microscope assembly process. e) Photo of packaged endoscope with 3D printed components. Scale bar: 10 mm.
PCR strategy reduces system part count to only five 3D printed components (lens, elastic lens mount, front cap and clamshells) and four off-the-shelf components (IR-cutoff filter, ring magnet, coil and CMOS sensor) (Figure 1b), with a full assembly chart of several customizable options shown in Figure 1c. The fabrication of all shown 3D printed components is unified using the homemade μCLIP system[12a] (Figure S1). AM offers customizable options in two progressive steps. Firstly, imaging lens effective focal length (EFL) can be tailored for specific working distances and imaging magnifications. Two options (EFL = 4.3 mm and EFL = 3.0 mm) are shown in Figure 1c. The digital design model of the elastic lens mount can be readily modified, and 3D printed with a desirable offset between the lens and CMOS sensor. Secondly, taking the design for EFL = 3 mm as an example, 3D printed lens (AM30) can be interchanged with off-the-shelf polymer lenses (“T30” and “E30” in Figure 1c). We intentionally constrained EFL and lens outer diameter to be compatible with commercial polymer lenses to improve design modularity. All the components are snapped into place using passive alignment features without the needs for a dedicate fixture and machines (Figure 1d, detailed assembly procedure in Supporting Information, and Supplementary Movie S1). The assembled miniature microscope shown in Figure 1e has the outer dimension of 8.10×8.10×29.85 mm3, comparable to a penny. Such methods also led to the dramatic cost reductions shown in Table 1 (Detailed cost analysis can be found in Supporting Information). The estimated unit cost of the whole system is $3.74, making it potentially disposable.
Table 1.
Itemized price for each component.
| Component | Unit Cost ($) | 3D Printing Time |
|---|---|---|
| Optomechanics | 1.079 | 45 min. 21 s |
| Aspherical lens | 0.069 | 3 min. |
| Ring magnet | 0.65 | N/A |
| Coil | 0.47 | N/A |
| CMOS sensor | 1.371 | N/A |
| IR cutoff filter | 0.10 | N/A |
| Total cost | 3.739 |
2.2. Design, Fabrication and Characterization of Optical Imaging Lenses
We experimentally characterized each interchangeable lens option shown for Design 1 (FL=3.0 mm): AM30 (Aspherical lens 3D printed in house), E30 (15–271, Edmund Optics) and T30 (APL0303, Thorlabs Inc.) (Figure 2). Optical properties of photocurable resin (detailed recipe in Method) were measured using a spectroscopic ellipsometer (J. A. Woollam M2000U). The wavelength-dependent refractive index of photocurable resin was extracted from ellipsometry measurements and was further used as inputs to optimize the aspherical profile of AM30 using Zemax OpticStudio (optimized profile in Method). The wavelength-dependent refractive index determines the aspherical coefficients of 3D printed lens with a given aperture and focal distance. Figure 2a and Figure 2b depict the simulated ray diagram and point spread function (PSF), respectively. The optimized lens profile was loaded into µCLIP to fabricate AM30, whose scanning electron microscope (SEM, FEI Quanta 650 ESEM) image is shown in Figure 2c. For comparison, we show the SEM images of E30 and T30 in Figure 2d and 2e, respectively. All three lenses have smooth aspherical surfaces, but with additional surface asperities found on E30 and T30. The distinct structural defects along the circumferences of E30 and T30 are common to all the lenses (N>10) we purchased from both vendors. The smooth surface profiles are further confirmed by optical profiler (Nexview, Zygo) measurement (Figure 2f-h). Images captured with a 240-μm-diameter aperture for all three lenses illustrate smooth surface profiles. We extracted linear profiles (dashed lines I and II in Figure 2f-h) for quantitative comparison. AM30 has the best surface smoothness (Ra = 7.63 nm, Figure 2i), in comparison with E30 (Ra = 8.67 nm, Figure 2j) and T30 (Ra = 11.39 nm, Figure 2k). Notably, at a volumetric printing speed of 1.25×104 mm3 h−1, the 3-mm-high AM30 was 3D printed in just 3 minutes.
Figure 2. Design and characterization of imaging lenses used on 3D printed optical microscope.
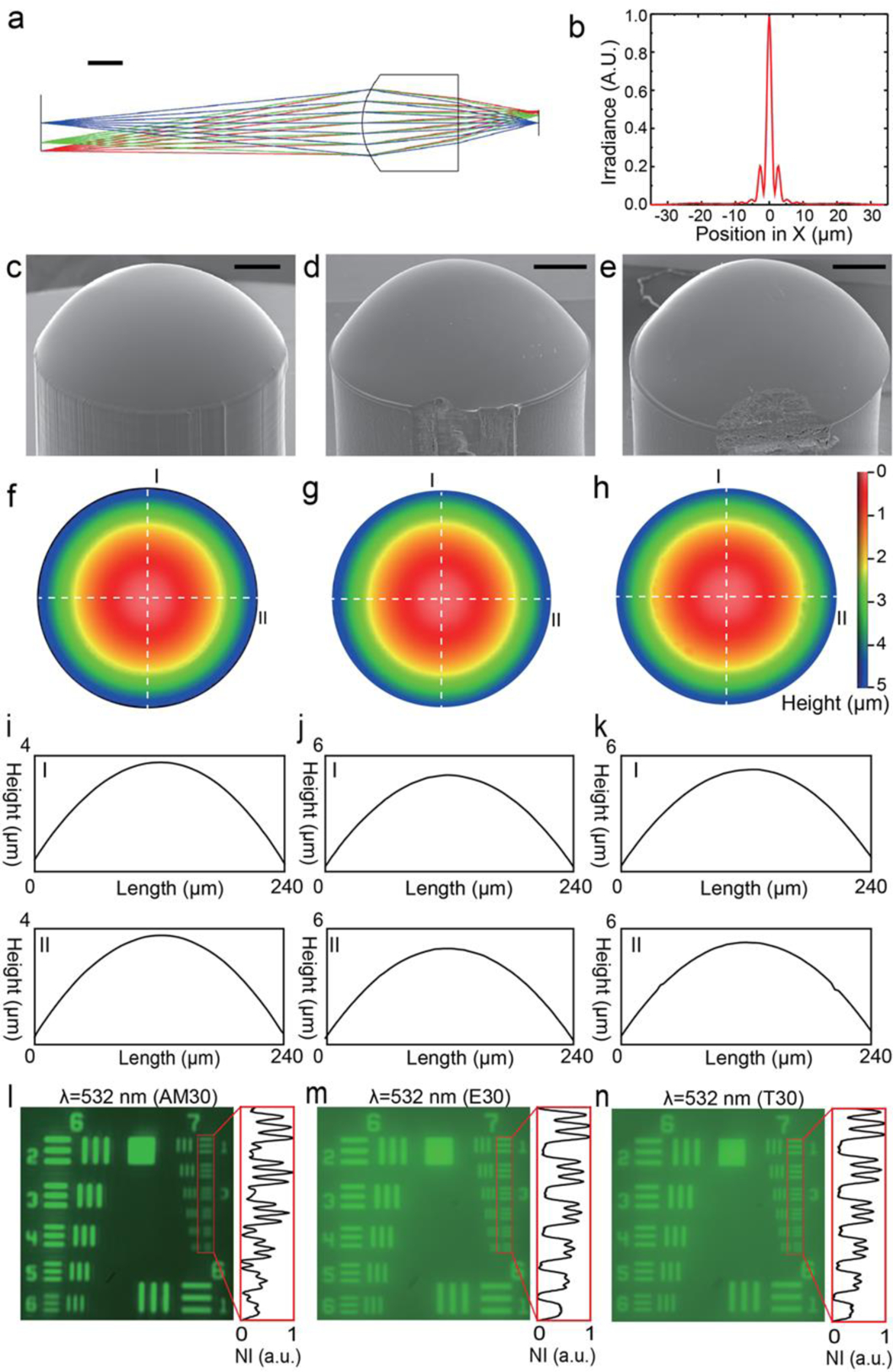
a) Imaging characteristic of the aspherical lens optimized under 532 nm illumination in Zemax. Scale bar: 1 mm. b) Simulated point spread function (PSF) for the optimized aspherical lens. c) to e): Tilted view of c) 3D printed aspherical lens, d) plastic aspherical lens from Edmund Optics (15–271) and e) molded acrylic aspherical lens from Thorlabs, Inc. (APL0303) respectively. Scale bars: 500 µm. f) to h): surface profile measured by white light interferometry for f) 3D printed lens, g) Edmund lens and h) Thorlabs lens, respectively. i) to k): extracted line profiles corresponding to the dashed lines I and II in f) to h) for i) 3D printed lens, j) Edmund lens and k) Thorlabs lens, respectively. l) to n): Images of USAF 1951 resolution target acquired under 532 nm (green light) illumination using l) 3D printed lens, m) Edmund lens and n) Thorlabs lens, respectively.
We experimentally compared imaging resolution for all three lenses (Figure S2 and description in Supporting Information). Captured images of the USAF 1951 resolution target illuminated with green light (λ = 532 nm) for AM30, E30, and T30 are shown in Figure 2l, 2m, and 2n, respectively. All three lenses exhibit a comparable imaging resolution capable resolving Element 3 of Group 7, corresponding to a 3.10-μm spatial resolution which optimizes the overall performance of the imaging system as the highest spatial frequency of the lens shall not exceed the Nyquist frequency of the CMOS sensor (OV09734-H16A, Omnivision) to avoid aliasing. Images acquired using E30 and T30 show relatively poor contrast, which might be correlated to the aforementioned structural defects found in Figure 2d,e. Similar behavior is also observed under different illumination conditions (Figure S3 and description in Supporting Information). For the interest of customization, we also characterized the imaging resolution of AM43 with EFL of 4.3 mm (Figure S4 and description in Supporting Information).
2.3. Design, Fabrication and Characterization of VCM Assembly
The VCM assembly (Figure 3a) was designed to focus the imaging lens through electromagnetic actuation. It contains an electromagnetic coil, a ring magnet, a compliant foundation, and the imaging lens mount. The components were carefully designed to ease the assembly process. To better illustrate the assembly process, relative positions of elastic lens mount, lens, ring magnet and coil are illustrated in Fig. 3a). The elastic lens mount consists of three components: lens mount, ring magnet mount, and compliant foundation from top to bottom, as shown in Fig. 3b). Grooves on the top and at bottom of the mount were designed for mounting the lens and ring magnet, respectively. To allow for the use of tweezers during the assembly process, we designed the interspace on the top of the lens mount to provide clearance. Two large sliding blocks on the side of the mount correspond with the sliding rails in the upper shell, to calibrate the movement of the mount. Meanwhile, four half-cylinder lug bosses were designed to reduce friction during translating of the mount. We implement PCR design to integrate three distinct optomechanical components - lens mount, ring magnet mount, and compliant foundation - into a monolithic elastic lens mount. The axial translation of the imaging lens is determined by the balance between electromagnetic forces from the coil and magnet and resilient forces from the compliant foundation. Figure 3b shows the boundary conditions used in a simulated compression test in ANSYS (details see Method Section). The primary design variable in the compliant foundation is the strut angle (θ), which was varied between −4.5° to +10° (Inset, Figure 3b). We optimize θ to achieve sufficient axial deformation (>1.0 mm) while reducing radial deformation to minimize its interference during VCM actuation. An optimal 0˚ strut angle exhibits the lowest Poisson’s ratio of 0.051, achieving a largest axial displacement of 1.17 mm (Figure 3c). The fabricated compliant foundation demonstrated a highly linear behavior during compression testing (Figure 3d), corroborating the numerical simulation. We further simulate the magnetic force (details in Experimental Section) that a N50 Neodymium ring magnet (R0545, SuperMagnetMan) bears as a function of axial distance and input voltage (Figure 3e) obtained by a previously reported algorithm[16]. ANSYS simulation suggests that the force of 52.96 mN - an amount readily available from the coil/magnet over the designed displacement range - is required to reach the largest axial deformation of 1.17 mm, validating the feasibility of our proposed axial translation mechanism. The simulated displacement fields in the lens mount during the cyclic contracting and extending motion are predominantly translational along the optical axis (Figure 3f).
Figure 3. Working principle and optimization of the elastic lens mount.
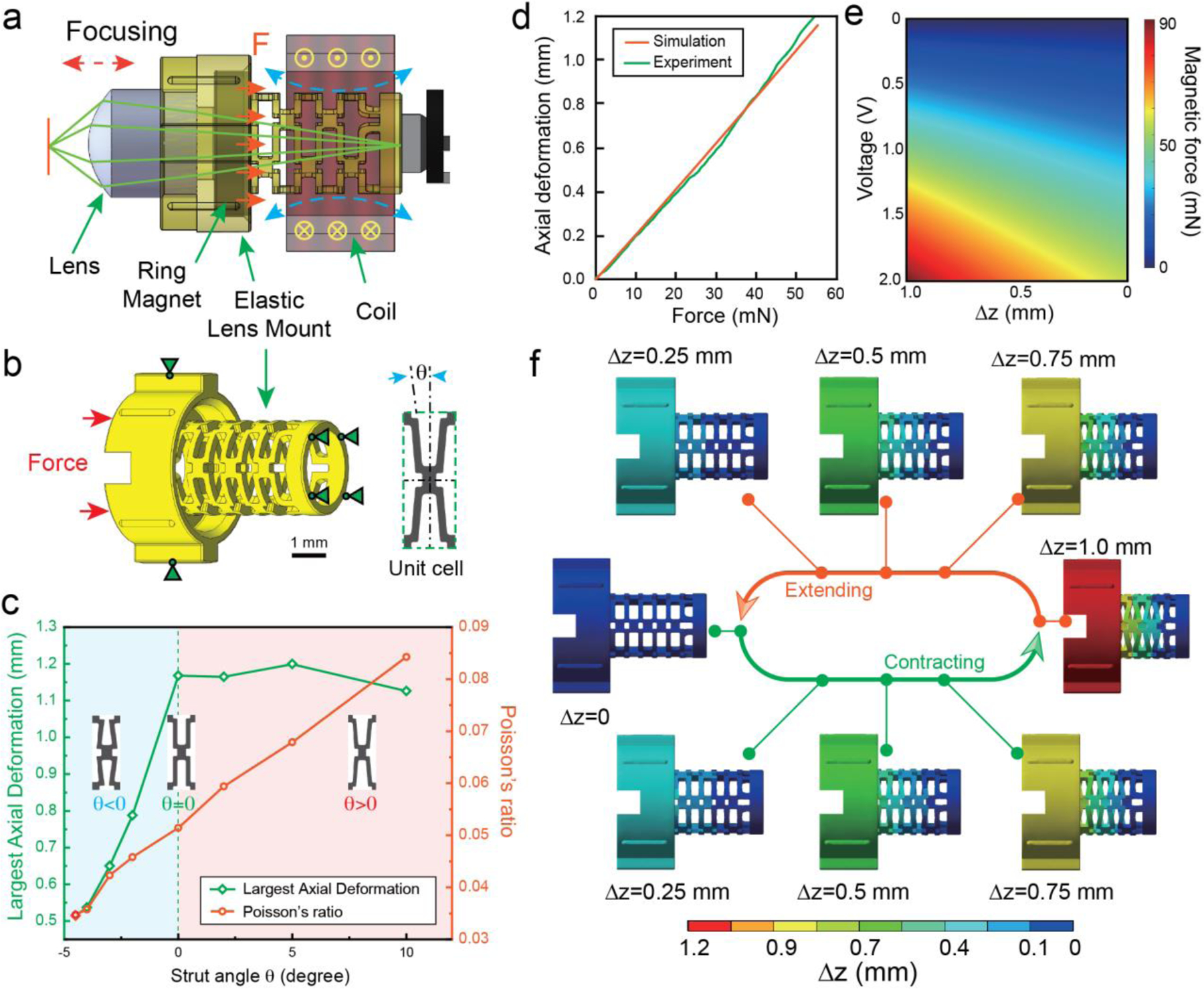
a) Working principle of VCM. b) CAD model and boundary conditions of the elastic lens mount used for simulated compression testing in ANSYS. Scale bar: 1 mm. Insets: the unwrapped unit cell design illustrating the definition of strut angle. c) Comparison of maximum axial deformation and Poisson ratio for different lens mount designs. Insets: zoomed-in view of designs featuring negative, 0 and positive strut angles, respectively. d) Comparison of experimental and simulated elastic response of lens mount in compression tests. e) Magnetic force exerted on elastic lens mount as a function of axial distance and applied voltage. f) Axial displacement of the elastic lens mount during compression and extension.
2.4. Performance Validation of Assembled Miniature Microscope
We experimentally validated the performance of the assembled miniaturized microscope using AM30 (Figure 1e). The test objects used in this study are a pair of biological specimens (NEW-BRE1003, NOCOEX Company) indicated by object A and B in Figure 1a that are spatially offset by 1.0 mm axially and 0.8–1.2 mm laterally. As the axial offset is greater than system DOF, we can actuate the VCM to translate the imaging lens to bring the desirable object in focus (Figure 4a,b). The ability to axially scan the imaging lens further enable us to implement the focusing stack function to effectively extend the DOF (Figure 4c). We used the pair of house fly labellum (object A) and honeybee barsitarsus (object B) specimens as test Case I. Figure 4a illustrates the scenario where the VCM is used to bring object A in focus, while leaving object B out of focus. Only the network structure of the house fly labellum can be clearly resolved (Figure 4d). The VCM can then translate the imaging lens backwards to acquire clear images of object B (Figure 4e) and the recorded image is shown in Figure 4d. A series of images can be acquired covering the axial positions of objects A and B and processed using the stack function in Adobe Photoshop with defaults settings (Supplementary Movie S2). After focus-stacking, both objects are brought into focus simultaneously without any degradation compared with single frames, thereby extending system DOF (Figure 4f).
Figure 4. Demonstration of active focusing and extended depth of field via focus stacking.
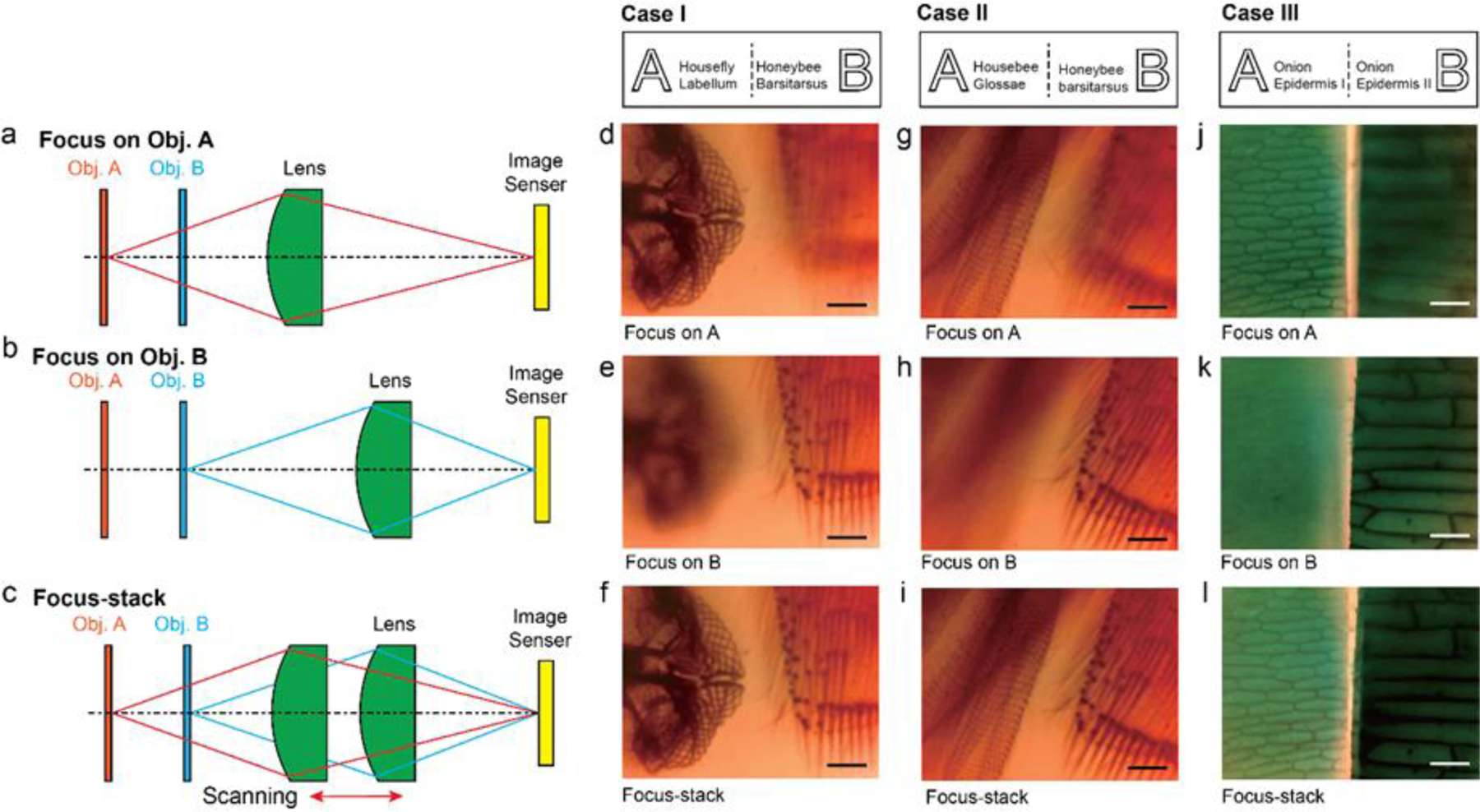
Schematic illustrations of three distinct imaging modes: (a) Lens focusing on the distal object A; (b) lens focusing of the closer object B; and (c) focus-stacking mode by capturing a series of images while axially scanning the imaging lens. Those images can be digitally combined to render a clear image of both Objects A and B with greatly extended imaging depth. Case I: Schematic illustration of object A (housefly labellum) and object B (honeybee barsitarsus) and the recorded images: (d) focusing on housefly labellum, (e) focusing on honeybee barsitarsus, and (f) focus-stacked image that brings object A and B simultaneously in focus. Case II: Schematic illustration of object A (housebee glossae) and object B (honeybee barsitarsus) and the recorded images: (g) focusing on housebee glossae, (h) focusing on honeybee barsitarsus, and (i) focus-stacked image that brings object A and B simultaneously in focus. Case III: Schematic illustration of object A (onion epidermis I) and object B (onion epidermis II) and the recorded images: (j) focusing on onion epidermis I, (k) focusing on onion epidermis II, and (k) focus-stacked image that brings object A and B simultaneously in focus. Scale bars: 200 µm.
Similar tests were performed on test Case II (labial palp/honeybee barsitarsus) and test Case III (two pieces of onion epidermis) and resulting recorded videos are shown in Supplementary Movies S3 and S4, respectively. The final processed images are respectively shown in Figures 4g-i and 4j-l. The To demonstrate system customizability, we repeated the same tests using the miniaturized microscope assembled with E30 (Figure S6 and Supplementary Movies S5-S7) and T30 (Figure S7 and Supplementary Movies S8-S10). Although low apparent image contrast led to reduced focus stacking reconstruction fidelity, we successfully integrated optical components from different fabrication methods, demonstrating the benefits of the unified AM fabrication and PCR strategies reported.
3. Conclusion
In this study, we have established a unified AM process implementing PCR strategy and passive alignment features, which led to improved ease of assembly and overall cost savings for miniaturized imaging systems. The PCR strategy we employed consolidates the lens mount, ring magnet mount, and compliant foundation into a monolithic part, greatly reducing component manufacturing and assembly costs. The 3D printed passive alignment features further simplify system assembly, as all components snap-fit together without requiring any precise machinery for active alignment. Collectively, this leads to the demonstration of a miniature optical microscope at a unit cost less than $4 without compromising performance or customizability. The 3D printed lens demonstrates a spatial resolution of 3.10 μm under 532 nm illumination, exhibiting a better contrast than its commercial counterparts. The assembled microscope employs an integrated VCM to focus the imaging lens on objects at different distances. Synergizing successive image acquisition and VCM actuation results in a greatly extended DOF through focus-stacking. The microscope can be readily customized and rapidly manufactured to respond to task-specific needs in imaging magnification and working distance. The capability to manufacture the system from a single resin provides an opportunity for this system to serve as an exemplar device, readily available to transform the novel materials developed by the materials research community into functional devices to demonstrate their advantages. This demonstrated flexibility associated with the digital manufacturing process enables this low-cost imaging platform to be readily customized and disseminated to broader user community as an open-source project and greatly expand the application scenario of AM.
Experimental Section
Magnetic Force Simulations.
To calculate the magnetic force between the coil and ring magnet, we adopted previously reported algorithms and code[16–17]. The thick coil, which has multiple radial turns Nr, is modeled as superposition of a group of coaxial thin coils which carry same current and have same number of axial turns Na. The ring magnet is modeled as a superposition of two cylindrical magnets carrying opposite magnetization, with their radii corresponding to the inner and outer radius of the ring magnet, respectively. The magnetic force exerted on a cylindrical magnet with radius by a thin coil with radius is given by[17]:
| (1) |
where the intermediate term is:
| (2) |
where K, E and Π are first, second and third elliptic integrals respectively. where is the current and is the coil length; is the magnet remanence; is the distance between the centers of mass of magnet and coil and other parameters are:
| (3) |
| (4) |
| (5) |
We calculated Eq. (1) for a cylindrical magnet of with magnetization and for a cylindrical magnet of with magnetization, where and are outer and inner diameter of the ring magnet, respectively. The total magnetic force is then obtained by adding those two results together. The ring magnet we used in our simulations and experiments was a N50 Neodymium ring magnet (R0545, SuperMagnetMan) with a 3 mm inner diameter (ID) and a 4 mm outer diameter (OD). The coil was manufactured upon customization from WireWinders and has an ID of 4 mm, an OD of 6 mm and a wire diameter of 0.0799 mm (40 AWG). The heights of the ring magnet and coil are 1 mm and 3 mm, respectively.
Lens Mount ANSYS Simulations.
Lens mount designs were input into ANSYS and given a mesh of 64,100 nodes and 35,132 linear elements, typically. As-Printed HDDA (no-UV flood exposure) was given a Young’s Modulus of 171.85 MPa, Yield Strength of 6.7 MPa, and UTS of 18.04 MPa, with Poisson’s ratio of 0.3. Loadings and constraints are shown in Figure 3a, which were applied to all models. Frictionless supports were applied to the base of the design and the largest diameter faces of the top portion of the lens mount. An applied loading meant to simulate magnetic actuation is applied on the top surface (Figure 3a). The Force loading was ramped up from 0 to 60 mN, which produced the desired axial displacements before the struts contact each other. Noted deformations are the radial deformation and the axial deformation and the ratio of radial and axial (R/A, Design Relation Poisson’s ratio). Shown in Figure 3b are the largest axial deformation and Poisson’s ratio with respect to applied force (ANSYS) for designs with different strut angles. Max R/A (design-related Poisson’s Ratio) of the system was determined either at the maximum applied force (F = 60 mN) or when the struts came into contact with one another (F < 60 mN).
Ellipsometry Measurement.
A thin film of photocurable resin was cured asfor use as an ellipsometry sample to obtain its wavelength-dependent refractive index. The thin film was made by casting the photocurable resin onto a piece of glass slide which was partly covered by a layer of palladium (100 nm). Then Aanother piece of glass slide is used tois covered on the firstormer one and peeled off after the photocurable resin is cured. The palladium layer here serves as a spacer to offer uscreate a thin, repeatable film of photocurable resin with a desired thickness. The wavelength-dependent refractive index was measured by using a spectroscopic ellipsometer (M2000U, J. A. Woollam Co.) using the reflection mode. The spectroscopic ellipsometry (SE) method measures the complex reflectivity comprising reflection ratio Ψ and phase difference Δ. The SE data analysis process begins by constructing parametrized layered optical model which corresponds to the sample structure. Each layer of the sample is parametrized by its thickness and optical constants. The retrieval process simultaneously determines the complex refractive index and the thickness of each of the constituting layers. The original data wasere obtained at incident angles from 55° to 75° with an interval of 5° and were further fitted with Cauchy-film model.
Optimization of Aspherical Surface.
The surface profile of the aspherical lens was designed and optimized for minimizing spherical aberration and image distortion under 632.8 nm (Design 1) and 532 nm (Design 2) illumination, respectively. Their surface profiles are defined by following equation:
| (6) |
where is the radius of curvature (in millimeter), is the conic constant, and are the aspherical coefficients, respectively. The optimized parameters for lens design 1 are , , and , respectively. The optimized parameters for lens design 2 are , , and .
Supplementary Material
Acknowledgments
This work made use of the EPIC, Keck-II, and/or SPID facility(ies) of Northwestern University’s NUANCE Center, which has received support from the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSFECCS-1542205); the MRSEC program (NSFDMR-1121262) at the Materials Research Center; the International Institute for Nanotechnology (IIN); the Keck Foundation; and the State of Illinois, through the IIN. This work has been funded by NIH R01GM140478, R01DE030480 and Nissan USA. CS would like to thank Dr. Yong Guo in helping for selecting the CMOS image sensors.
Footnotes
Competing interests
Cheng Sun has financial interests in Opticent Inc. All other authors declare no competing financial interests.
Supporting Information
Supporting Information is available for this paper.
Data Availability
All data needed to evaluate the conclusions in the paper are present in the paper or the Supporting Information. Source data are provided with this paper. The CAD models are available upon request.
References
- [1].a)August I, Oiknine Y, AbuLeil M, Abdulhalim I, Stern A, Scientific reports 2016, 6, 1; [DOI] [PMC free article] [PubMed] [Google Scholar]; b)Sigal I, Koletar MM, Ringuette D, Gad R, Jeffrey M, Carlen PL, Stefanovic B, Levi O, Biomedical Optics Express 2016, 7, 3596; [DOI] [PMC free article] [PubMed] [Google Scholar]; c)Cybulski JS, Clements J, Prakash M, PloS one 2014, 9, e98781; [DOI] [PMC free article] [PubMed] [Google Scholar]; d)Aharoni D, Hoogland TM, Frontiers in cellular neuroscience 2019, 13, 141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].a)Wang CY, Wang PJ, Applied optics 2014, 53, 2523; [DOI] [PubMed] [Google Scholar]; b)Tsai K-M, Applied Optics 2010, 49, 6149; [Google Scholar]; c)Zhang L, Liu W, Frontiers of Mechanical Engineering 2017, 12, 3. [Google Scholar]
- [3].a)Duda T, Raghavan LV, Ifac Papersonline 2016, 49, 103; [Google Scholar]; b)Kawata S, Sun HB, Tanaka T, Takada K, Nature 2001, 412, 697; [DOI] [PubMed] [Google Scholar]; c)Martin JH, Yahata BD, Hundley JM, Mayer JA, Schaedler TA, Pollock TM, Nature 2017, 549, 365; [DOI] [PubMed] [Google Scholar]; d)MacDonald E, Wicker R, Science 2016, 353, aaf2093. [DOI] [PubMed] [Google Scholar]
- [4].a)Savastano M, Amendola C, Massaroni E, in Digitally supported innovation, Springer, 2016; [Google Scholar]; b)Lecklider T, EE-Evaluation Engineering 2017, 56, 16; [Google Scholar]; c)Ichida Y, IFEAMA SPSCP 2016, 5, 69. [Google Scholar]
- [5].a)Shapiro AA, Borgonia J, Chen Q, Dillon R, McEnerney B, Polit-Casillas R, Soloway L, Journal of Spacecraft and Rockets 2016, 952;; b)Kobryn P, Ontko N, Perkins L, Tiley J, Air Force Research Lab Wright-Patterson AFB OH Materials and Manufacturing …, 2006;; c)Dehoff R, Duty C, Peter W, Yamamoto Y, Chen W, Blue C, Tallman C, Advanced Materials & Processes 2013, 171, 19. [Google Scholar]
- [6].a)Popov VV, Muller-Kamskii G, Kovalevsky A, Dzhenzhera G, Strokin E, Kolomiets A, Ramon J, Biomedical engineering letters 2018, 8, 337; [DOI] [PMC free article] [PubMed] [Google Scholar]; b)Tetsuka H, Shin SR, Journal of Materials Chemistry B 2020, 8, 2930; [DOI] [PMC free article] [PubMed] [Google Scholar]; c)Yu C, Schimelman J, Wang P, Miller KL, Ma X, You S, Guan J, Sun B, Zhu W, Chen S, Chemical reviews 2020, 120, 10695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].a)Cruz PJ, Knaack U, Figueiredo B, D. d. Witte, presented at Proceedings of IASS Annual Symposia, 2017; [Google Scholar]; b)Rael R, San Fratello V, Printing architecture: Innovative recipes for 3D printing, Chronicle Books, 2018. [Google Scholar]
- [8].Yang S, Zhao YF, Journal of mechanical design 2018, 140.
- [9].a)Gissibl T, Thiele S, Herkommer A, Giessen H, Nat Commun 2016, 7, 11763; [DOI] [PMC free article] [PubMed] [Google Scholar]; b)Gissibl T, Thiele S, Herkommer A, Giessen H, Nature Photonics 2016, 10, 554; [Google Scholar]; c)Toulouse A, Drozella J, Motzfeld P, Fahrbach N, Aslani V, Thiele S, Giessen H, Herkommer AM, Optics Express 2022, 30, 707; [DOI] [PubMed] [Google Scholar]; d)Li J, Thiele S, Kirk RW, Quirk BC, Hoogendoorn A, Chen YC, Peter K, Nicholls SJ, Verjans JW, Psaltis PJ, Small 2022, 2107032. [DOI] [PubMed]
- [10].a)Assefa BG, Pekkarinen M, Partanen H, Biskop J, Turunen J, Saarinen J, Optics express 2019, 27, 12630; [DOI] [PubMed] [Google Scholar]; b)Biehl S, Danzebrink R, Oliveira P, Aegerter MA, Journal of Sol-Gel Science and Technology 1998, 13, 177. [Google Scholar]
- [11].a)Groet G, presented at SPIE AVR21 Industry Talks II, 2021; [Google Scholar]; b)Gawedzinski J, Pawlowski ME, Tkaczyk TS, Optical engineering 2017, 56, 084110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].a)Shao G, Hai R, Sun C, Advanced Optical Materials 2019, 8;; b)van Lith R, Baker E, Ware H, Yang J, Farsheed AC, Sun C, Ameer G, Advanced Materials Technologies 2016, 1;; c)Chen X, Liu W, Dong B, Lee J, Ware HOT, Zhang HF, Sun C, Adv Mater 2018, 30, e1705683; [DOI] [PubMed] [Google Scholar]; d)Zhang Y, Wu L, Zou M, Zhang L, Song Y, Advanced Materials 2022, 34, 2107249. [DOI] [PubMed] [Google Scholar]
- [13].Tumbleston JR, Shirvanyants D, Ermoshkin N, Janusziewicz R, Johnson AR, Kelly D, Chen K, Pinschmidt R, Rolland JP, Ermoshkin A, Samulski ET, DeSimone JM, Science 2015, 347, 1349. [DOI] [PubMed] [Google Scholar]
- [14].a)Toombs JT, Luitz M, Cook CC, Jenne S, Li CC, Rapp BE, Kotz-Helmer F, Taylor HK, Science 2022, 376, 308; [DOI] [PubMed] [Google Scholar]; b)Dylla-Spears R, Yee TD, Sasan K, Nguyen DT, Dudukovic NA, Ortega JM, Johnson MA, Herrera OD, Ryerson FJ, Wong LL, Science advances 2020, 6, eabc7429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Collins JT, Knapper J, Stirling J, Mduda J, Mkindi C, Mayagaya V, Mwakajinga GA, Nyakyi PT, Sanga VL, Carbery D, Biomedical Optics Express 2020, 11, 2447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Robertson W, Cazzolato B, Zander A, IEEE Transactions on Magnetics 2012, 48, 2479. [Google Scholar]
- [17].Robertson W, Ravaud R, Cazzolato B, Zander A, IEEE Transactions on Magnetics 2011, 47, 2045. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data needed to evaluate the conclusions in the paper are present in the paper or the Supporting Information. Source data are provided with this paper. The CAD models are available upon request.


