Effect of surface plasmon on optical detection of picosecond ultrasonic pulses generated in aluminum nanofilms

Abstract

Photoacoustic and thermoacoustic detection methods, including picosecond ultrasonic laser sonar based on metallic thin films, are widely used in industrial applications for their noninvasiveness. Herein, we present our findings on the phase advance effect of laser-induced picosecond ultrasonic signals in surface plasmon detection in Al nanofilms. Al has been extensively studied as a promising surface plasmon material in the ultraviolet region. Reflection time-resolved spectroscopy was integrated with a Kretschmann configuration to study the optical detection mechanisms with and without meeting the surface plasmon phase-matching condition. Through a comparison of the phase changes in picosecond ultrasonic pulses at different optical detection angles, we attributed the observed phase delay modification to the displacement of the detection region under the surface plasmon phase-matching condition.

1. Introduction

Picosecond laser ultrasonics is a widely used technique taking advantage of the ability of sound waves to propagate through opaque objects [1]. Nondestructive metrology methods, including time-domain thermoreflectance and picosecond ultrasonic laser sonar, enable the study of the thermal and elastic properties of opaque materials [2], [3], [4], [5]. Echoes with different reflective properties are used to profile the under-surface structure of an opaque object by using a photoacoustic ultrasonic probe. Photoacoustic studies, in combination with different plasmonic systems, have attracted extensive interest from researchers. For example, studies have investigated how the detection sensitivity of the optical response can be enhanced by surface plasmon polaritons [6], [7], [8], the influence of the size and shape effects of plasmonic nanoparticles [9], [10], [11], and the use of plasmonic nanodisks and arrays [12], [13], [14], [15]. Studies have also demonstrated that through direct combination with picosecond laser ultrasonic sonar, surface plasmons based on noble metal nanofilms are a promising tool for detecting picosecond ultrasonic pulses [16], [17], [18], [19], [20], [21], [22].

Al plasmonic is widely used in various applications for its ability to generate surface plasmons from the ultraviolet to the visible spectrum [23]. Al plasmonic has been used in localized surface plasmon resonance sensors to improve sensitivity in processes involving nanostructures [24], [25], [26] and in biosensors that detect changes in the refractive index caused by analyte binding [27], [28], [29]. Prism coupling is a convenient method for detecting picosecond pulses under surface plasmon resonance conditions. At a specific incident angle, the electric field at the metal–air interface is enhanced by momentum matching between incident light and surface plasmons, whereby collective free electron oscillations create a nonradiative surface wave that propagates along the interface [30], [31]. Al, the most abundant metallic element on earth, is a relatively affordable and versatile material. Because of its affordable cost and low resistance, Al is used as a primary conductor between various components. Al film serves as a photoacoustic transducer that can generate ultrasonic waves in the subterahertz frequency range through femtosecond laser pulsing [32], [33]. Additionally, Al film can optically resolve picosecond ultrasonics within a femtosecond timeframe.

In this study, we demonstrate the photoacoustic phase change induced by surface plasmon detection in Al nanofilms achieved with a Kretschmann configuration. The surface plasmon effect was expected to have a substantial effect on the optical detection of picosecond ultrasonic waves in Al. Without the surface plasmon effect, the optical field amplitude decreases as an evanescent wave upon entering the Al film from the glass substrate, and the optical detection capability primarily lies on the glass prism side of the Al film, where the incident light is located. By contrast, when the surface plasmon is stimulated, the optical detection region is expected to shift toward the air–metal interface. As a result, here we report our observation of a corresponding phase change of the optically-detected picosecond ultrasonic signals. The observation was made on a 16 nm-thick Al nanofilm on a BK7 glass substrate while changing the probe light angle away from the minimum reflectivity plasmon angle toward the high reflectivity angle. We attribute the observed phase change to the surface plasmon effect to modify the photoacoustic detection region from the usual Al/glass interface to the air-metal interface. This study also illustrates a physical mechanism to optically control the photoacoustic detection region depth by changing the probe light angle.

2. Materials and methods

2.1. Time-resolved pump–probe system

The surface plasmon detection effect of transient photoacoustics in an Al nanofilm was studied using a colinear counter-propagating reflection pump–probe system. A light source with a pulse duration of 220 fs and a central wavelength of 404 nm was generated through frequency doubling of a Kerr lens mode-locked Ti/sapphire fs laser with a repetition rate of 76 MHz. The s-polarized pump beam stimulated the Al nanofilm and initiated longitudinal picosecond acoustic pulses that traveled back and forth in the sample. The longitudinal acoustic strain pulses were monitored by the p-polarized probe pulse through the change in reflectivity (Fig. 1). The pump pulses were designed with an optical fluence of 210 µJ/cm² to stimulate the Al film at the metal–air interface, and a probe with an optical fluence of 42 µJ/cm² was used to detect the photoacoustic signal. The optical path difference was controlled using a linear motorized stage for time-resolved measurements, and various incident angles were selected to perform the measurements either with or without the resonance conditions by controlling a rotary sample stage.

Fig. 1.

Surface plasmon resonance detection stage.

2.2. Surface plasmon resonance

Surface plasmon resonance is a phenomenon whereby free electrons collectively oscillate on a metal surface as a response to electromagnetic waves [34]. Nonradiative surface waves are highly sensitive to the material’s dielectric constant and can be stimulated through several configurations [35], [36], [37]. In our study, the Al nanofilm was arranged in the Kretschmann configuration with a right-angle prism, and the optical probe light was used to detect the surface plasmon resonance in the Al nanofilm through the prism at a specific angle. The probe light was p-polarized, allowing its wavevector to be aligned parallel to the dielectric–metal interface and adjusted to match the dispersion relation of surface plasmon conditions along the air–metal interface. Upon this surface plasmon phase matching angle, the coupling of incident energy to the surface plasmon field resulted in a significant decrease in reflectivity.

3. Results and discussion

3.1. Sample characteristics

Thermal evaporation was used to deposit the Al nanofilm onto a BK7 glass substrate, and a refractive index-matching optical adhesive was used to bond the substrate and the prism to achieve the Kretschmann configuration. The thickness of the Al nanofilm was determined using scanning transmission electron microscopy (STEM). The average thickness was 16.55 nm with a standard deviation of 0.15 nm (Fig. 2b). Energy dispersive X-ray microanalysis was performed to map the composition distribution (Fig. 2c). The results indicate that the Al film had oxide in both the metal–air interface and throughout the entire film.

Fig. 2.

Sample characterizations. (a) Sample structure with selected observation positions for STEM and X-ray microanalysis marked as 1–4. (b) STEM images of the Al nanofilm sample, (c) energy dispersive X-ray microanalysis result displaying oxygen distribution in the Al nanofilm.

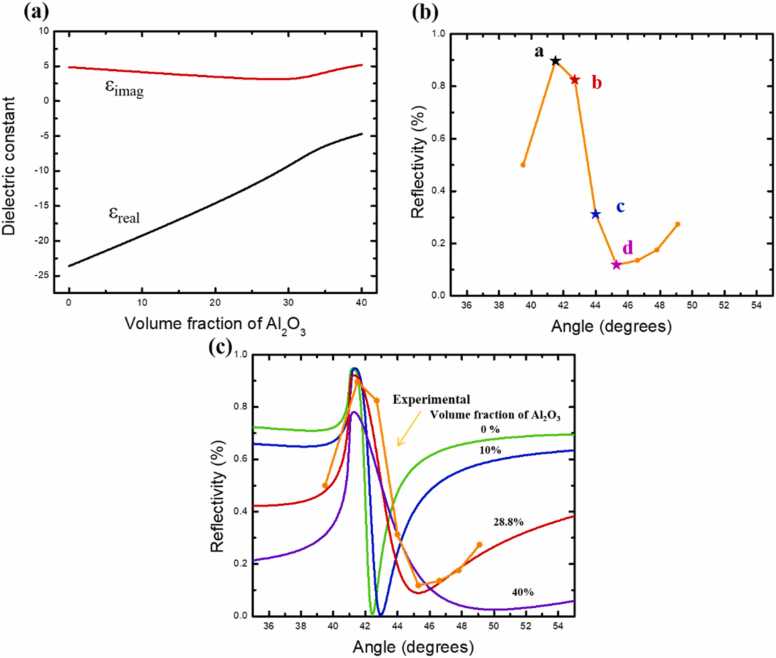
Al has a high chemical affinity to oxygen. To prevent oxidation from influencing the results, optical measurements were performed within 1 h of the Al nanofilm being deposited. The oxidation rate of the film is fastest within 5 min after the film is removed from the vacuum chamber. After a stable layer is established, the oxygen volume fractions remain relatively constant throughout the experiment [38]. The angle-resolved reflectivity of the probe beam was quickly measured using a power meter (Fig. 3b). The reflectivity indicated the presence of a significant surface plasmon resonance dip at the resonance angle around 45.3°. The measured reflectivity was (a) 0.89, (b) 0.82, (c) 0.31 and (d) 0.12 at incident angles of (a) 41.5°, (b) 42.7°, (c) 44.0°, and (d) 45.3°, respectively. By introducing Fresnel’s equations and Snell’s law, we can calculate the theoretical reflectivity dependence on the incident angle of p-polarized light through the glass–metal–air system [30], [31] with different volume fractions of Al₂O₃. The Bruggeman effective medium approximation [39] was used to determine the equivalent relative permittivity by combining the intrinsic dielectric constants of Al (${\epsilon }_{\mathit{Al}}$) and Al₂O₃ (${\epsilon }_{\mathit{ox}}$) on the basis of their respective volume fractions within the material. The results obtained through this method were more accurate than those obtained using the Maxwell–Harnett theory [23]. Both the real and imaginary parts were able to be derived using Eq. (1) as follows (Fig. 3a):

$$n_{\mathit{Al}}\left(\frac{{\epsilon }_{\mathit{Al}}-\epsilon }{{\epsilon }_{\mathit{Al}}+2\epsilon }\right)+n_{\mathit{ox}}\left(\frac{{\epsilon }_{\mathit{ox}}-\epsilon }{{\epsilon }_{\mathit{ox}}+2\epsilon }\right)=0.$$ (1)

Fig. 3.

(a) Dielectric constant calculated using Bruggeman effective medium theory for different Al oxide volume fractions at central wavelength of 404 nm. (b) Measured reflectivity as a function of incident angle. Minimum reflectivity occurs at angle d, which is the plasmon resonance angle of our studied sample. The time-resolved experiments were measured at points a–d. (c) Calculated reflectivity curves of various volume fractions of Al oxide are represented by solid curves.

The theoretical plasmon resonance curves were then calculated using different volume fractions of Al oxides, which strongly affected the surface plasmon profile (Fig. 3c). The calculated reflectivity curve for an Al oxide volume fraction of 28.8 % was in best agreement with the experimental results, and the real and imaginary parts of the corresponding dielectric constant were − 9.9729 and 3.1363, respectively.

3.2. Time-resolved pump–probe spectroscopy

Several studies have used pump–probe measurements of transient absorption and reflection to investigate the laser-induced photoacoustic process and the physics of carrier scattering [40], [41]. The photoacoustic effect occurring when pulse energy is absorbed by a metallic film has been elucidated through electron–electron and electron–phonon interactions [42]. Ultrafast electron scattering and thermalization had been previously examined using the two-temperature model [43], [44]. The process of achieving equilibrium in the free electron gas was initiated by femtosecond laser excitation and resulted in rapid internal thermalization with the surrounding electrons, followed by external thermalization with energy coupled to the lattice [43]. Heat transfer and lattice dynamics had been studied numerically and theoretically [44]. The energy coupling with the lattice caused a thermal expansion pulse after photoexcitation, and the thermal stress was mainly caused by pressure from hot electrons and lattice expansion [45], [46]. Macroscopic continuum elasticity can explain the longitudinal photoacoustic effect in homogeneous materials [47]. The propagation of phonons caused changes in the refractive index, which in turn disturbed the reflectivity of the probe light. This disturbance is used to monitor acoustic vibrations generated by impulsive excitation. Ultrafast lasers have been used to study the thermal and elastic effects of propagating strain pulses on the refractive index [48]. However, no studies have focused on the phase delay versus the plasmon resonance conditions.

Time-resolved pump–probe experiments were performed at incident probe angles of (a) 41.5°, (b) 42.7°, (c) 44.0°, and (d) 45.3° to study the phase advance effect (Fig. 4). Angle (d) corresponds to the plasmon resonance dip.

Fig. 4.

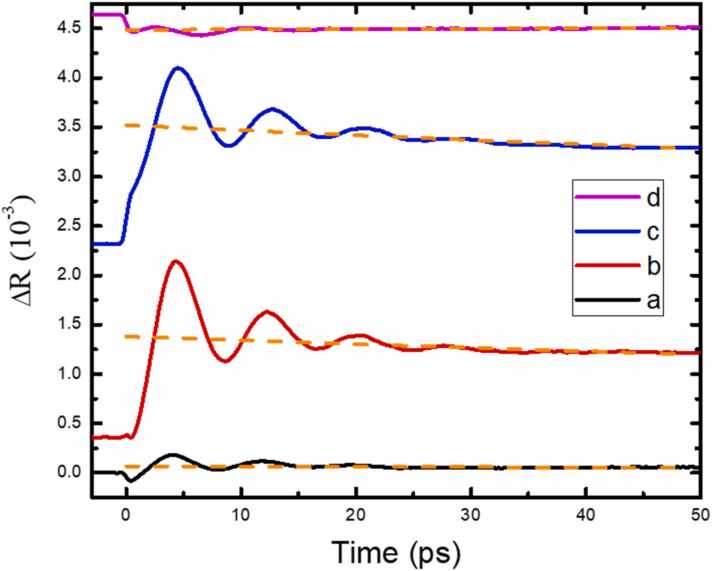
Phase advance effect measured using time-resolved reflectivity pump–probe system with probe incident angles of (a) 41.5°, (b) 42.7°, (c) 44.0°, and (d) 45.3°. Angle d corresponds to plasmon resonance dip angle. Appropriate offset was applied for better visualization. Carrier dynamic background fittings with single exponential decay are represented by orange dashed lines.

We observed that the amplitudes of the measured reflectivity change were greater at angles b and c compared with reflectivity peak angle a and reflectivity dip angle d. Fig. 3b indicates that angles b and c are within the quick transition region between reflectivity extremes a and d. Our experimental results indicate that these angles have the highest reflectivity sensitivity to the optical pump, as suggested by the orange dashed fitting lines in Fig. 4. In one study [49], the femtosecond pump pulse induced a step-like optical transmission change in Al nano-objects within 500 fs, after rapid electron–electron and electron–phonon thermalization. By considering the small decrease in the imaginary component of the dielectric constant during the calculation of the reflectivity curves (Fig. 3c), we numerically observed an increase in reflectivity that reached a peak at an angle of 43.3° between two extreme angles of reflectivity, a and d, agreeing well with our observation. We also observed a strong oscillation signal in conjunction with the step-like change in reflectivity. To further analyze the oscillatory signals, a single exponential decay was fitted to the step-like response induced by carrier dynamics [49], represented by the dashed lines in Fig. 4, and then removed by subtracting. After undergoing a simple background removal process, the oscillatory signals were extracted (Fig. 5a). Enlarged signals of angles a and d are presented in Fig. 5b.

Fig. 5.

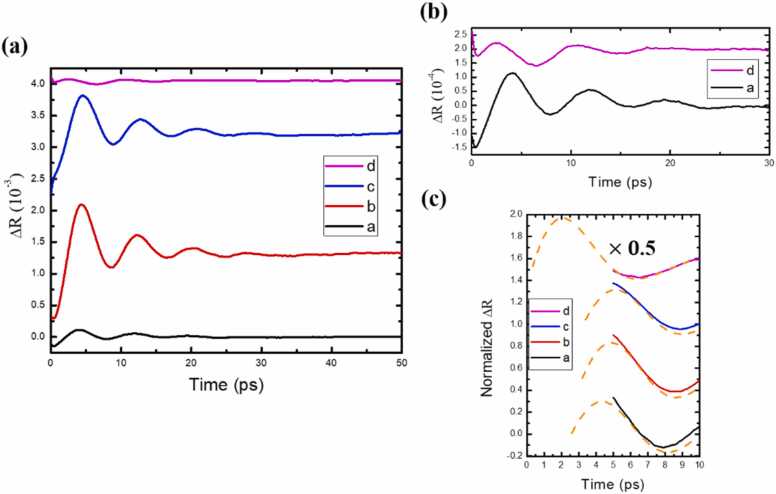
(a) Background-removed photoacoustic signals observed at angles a–d. Appropriate offset was applied for better visualization. (a) Enlarged background-removed signals observed at angles a and d. (c) Comparison of oscillation phases at different incident angles. Solid traces are background-removed experimental traces. Orange dashed lines are lines of best fit determined using a damped sinusoidal function.

To minimize fitting error, we performed time-domain fitting to the experimentally observed oscillatory signals after 5 ps by using a damped sinusoidal function (Fig. 5c). Upon examination of all traces, a consistent oscillation period of 8.1 ps was observed with a standard deviation of 0.5 ps. We attributed the observed oscillation to the pump-induced picosecond ultrasonic pulse traveling back and forth inside the Al nanofilm. In another study [17], simple relation $v_s=\frac{2d_{\mathit{AL}}}{T}$ was used to indicate the relation between speed of sound and oscillation period, where $v_s$ is the longitudinal speed of sound, $d_{\mathit{AL}}$ is the film thickness according to STEM, and T is the observed oscillation period [50]. The origin of the oscillatory signal was further supported by an independent thickness study [51], which demonstrated a linear trend in period as thickness increased. In the present study, this equation yielded a softening effect with a decreased Al longitudinal sound velocity of 4.1 nm/ps. Another study reported a reduction in the longitudinal sound velocity in an Al nanofilm when the thickness was less than 20 nm and explained the softening effect as being caused by surface strains producing a disordered transition layer [52].

By contrast with the frequency domain analysis [17] performed on Au nanofilms, our time-domain analysis revealed a significant phase difference in the detection of Al film vibration between angle d and other angles (Fig. 5c). By extrapolating the fitted damped sinusoidal function back to the initial zero phase, the starting time of the measured impulsive sinusoidal vibration, which can be defined as the delay from the time the signal started to oscillate, was 2.6, 3.2, 3.4, and 0.38 ps for angles a–d, respectively. We observed a significant reduction in the initial starting time at detection angle d, which was the plasmon resonance dip angle. This angle-dependent result indicates that the surface plasmon effect leads to distinct probing conditions compared with off-resonance conditions.

Given that the pump–probe pulses were directed toward opposite sides of the opaque Al film, two factors should be considered to determine detection delay. The first is the thermal expansion time after the pump, and the second is the traveling time of the ultrasonic pulse from the excitation region on the air side of the Al film to the probe region.

A study that used a femtosecond transmission pump–probe technique revealed a 0.5-ps delay in electron–electron and electron–phonon thermalization in Al nanostructures [49]. By using femtosecond electron diffraction, the lifetimes measured in bulk electron–electron and electron–phonon scattering were reported to be approximately 0.2 and 0.5 ps, respectively [53], [54]. We applied the two-temperature model to calculate the thermal expansion time [33]. Changes in electron and lattice temperatures over time were solved numerically in MATLAB (MathWorks, Natick, Massachusetts, USA), with times ranging from − 2 to 10 ps. The heat capacity of the lattice ($2.443J/{\mathit{cm}}^{3}K$) was approximately 100 times greater than that of the electrons ($C_e=\gamma T_e$ with $\gamma =9.2\times {10}^{-5}J/{\mathit{cm}}^3{K}^2$) [33]. Electron–phonon coupling factor $\mathit{G}$ was equal to $4.9\times {10}^{11}W/{\mathit{cm}}^{3}K$ [33]. The initial temperature was 300 K. Reflectivity R under central wavelength 404 nm was 0.93. The pulse energy was 0.66 nJ. Absorption length $\xi$ for Al was 6.6 nm, area diameter was approximately 20 µm, and the pulse duration was 220 fs. The simulation demonstrated that the electron and lattice reached an equilibrium within the pulse duration, and after the pulse excitation the heated temperatures of the electrons and lattice were similar. Al is considered to have strong electron–phonon coupling potential with coupling factor values approximately one order greater than those of gold and silver. Our simulation indicated a thermal expansion time of 0.28 ps with a 0.22-ps pulse excitation, consistent with other experimental reports and on the same order as the phase delay observed under the plasmon resonance dip condition.

To evaluate the traveling time of the photoacoustic pulse from the excitation region to the probe region, the probe field intensity distribution within the Al must be examined. According to another report, the optimal thickness of metal films that can be used in BK7-based Kretschmann geometry is approximately 50–70 nm for Au, 37–48 nm for Ag, 45–55 nm for Cu, and 10–21 nm for Al [55]. Our film thickness (16 nm) was within the optimal range for Al. In the present study, when the wavenumber of the electromagnetic field matched the surface plasmon condition, the electron gas oscillation was a result of efficient energy coupling. The plasmon resonance effect greatly enhanced the probe field at the air–Al interface [56]. As a result, for the trace at angle d, immediately after the generation of the thermal expansion pulse at the air–Al interface within the initial 0.5 ps, the probe pulse immediately detected the launched photoacoustic pulse with no traveling delay because at the plasmon resonance, the probe field distribution inside the Al nanofilm overlapped with the pump field, which was incident from the air side.

By contrast, when other angles were probed, no surface plasmon would occur and additional acoustic traveling time from the pump excitation air side to the probe located prism side of the Al is required. Considering the penetration depths of the pump and probe lights, the additional time delay was 2.2–3 ps, corresponding to a distance traveled by the sound waves of 9–12.3 nm. The cause of this delay was attributed to the shift in the probe detection region back toward the prism side of the Al nanofilm.

The probe field intensity within the Al film was simulated in Ansys Lumerical FDTD (Ansys Lumerical, Vancouver, BC, Canada) as shown in Fig. 6. The simulation was performed with a wavelength of 404 nm, with a sample composed of glass, metal, and air, and with refractive indices of 1.53, 0.4907 + 3.1959i, and 1, respectively. The metal thickness was 16 nm. The cross-section intensity distribution within the metal was selected for analysis in relation to the plasmon dip angle and its corresponding angles. At plasmon dip angle d, the probe field intensity peaked at the air–Al interface. When we moved the angle away from the resonance angle, the probe field intensity at the air–Al interface greatly decreased, due to the strong attenuation of the Al film for probe light to reach the Al interface. Without the plasmon resonance, the probe field will be confined in the prism-Al interface, including angles a–c. It is interesting to notice that for the field at the prism–Al interface, the simulation shows a stronger field intensity at angle c as compared to the field intensities at angles a and b. The angle-dependent field intensity at the prism–Al interface (c > b > a) correlated well with the increased phase delay time observed in our experiment (c > b > a), thus further supporting our suggestion that the observed long phase delay for the off-resonance condition should be attributed to the shift of the probe detection region back toward the prism-Al interface.

Fig. 6.

Simulated electric field intensity distribution inside 16-nm-thick Al film. Distance is from the dielectric–metal interface to the air–metal interface. Prism-Al interface is at 0 nm, and the air-Al interface is at 16 nm, and the calculation is performed for the incident light at 404 nm. Probe light was incident from prism size. Angle d is plasmon resonance angle with minimum reflectivity. Angles a–c are plasmon angles − 3.8°, − 2.6°, and − 1.3° respectively.

Even though one might expect that the phase shift should change with the change of the light fraction that is converted into surface plasmons, the surface plasmon field only peaks at the air/metal interface. As a result, no gradually changing phase delay was observed when we changed the probe light angle away from the plasmon dip angle toward the high reflectivity angle, further supporting our suggestion that the phase delay should be attributed to the probe detection position change, switching only between the air-metal interface and the glass-metal interface. It is further noted that the plasmon resonance condition did not yield the highest detection sensitivity for the vibration of the film induced by pumping. This is because the detected reflectivity signal was diminished for perfect resonances under the plasmon resonance condition.

4. Conclusion

This study examined the effect of surface plasmon resonance on picosecond ultrasonic detection in an Al nanofilm. By combining the Kretschmann configuration with time-resolved measurements, we observed a substantial oscillation phase delay. The delay can be explained by the detection region displacement inside the Al film when the plasmon resonance condition was modified. This finding may indicate a new mechanism for optical control of the detection region in metallic films for picosecond laser ultrasonics.

CRediT authorship contribution statement

Ting-Shan Lee: experiments—sample growth and ultrafast pump–probe measurements, Validation, Formal analysis, Writing – original draft, Writing – review & editing. Chi-Kuang Sun: Conceptualization, Methodology, Writing – original draft, Writing – review & editing, Supervision, Funding acquisition.

Declaration of Competing Interest

The authors have no conflicts of interest to disclose.

Biographies

Ting-Shan Lee received his B.S. degree in physic from National Chung Hsing University in 2020 and M.S. degree in Photonics and Optoelectronics from National Taiwan University in 2023. His research focuses on THz photoacoustics, ultrafast optics, and mesoscopy.

Chi-Kuang Sun received his Ph.D. in applied physics from Harvard University in 1995 and was an assistant researcher in the UCSB QUEST Center from 1995 to 1996. In 1996, he joined National Taiwan University, where he is now a distinguished professor of photonics and optoelectronics. He founded the NTU Molecular Imaging Center. His research focuses on nano-acoustics, femtosecond optics, THz optoelectronics, and biomedical imaging. He is a fellow of OSA, SPIE, and IEEE and is currently the president of Taiwan Photonics Society.

Data Availability

No data was used for the research described in the article.