Abstract
Haplotype networks are graphs used to represent evolutionary relationships between a set of taxa and are characterized by intuitiveness in analyzing genealogical relationships of closely related genomes. We here propose a novel algorithm termed McAN that considers mutation spectrum history (mutations in ancestry haplotype should be contained in descendant haplotype), node size (corresponding to sample count for a given node) and sampling time when constructing haplotype network. We show that McAN is two orders of magnitude faster than state-of-the-art algorithms without losing accuracy, making it suitable for analysis of a large number of sequences. Based on our algorithm, we developed an online web server and offline tool for haplotype network construction, community lineage determination, and interactive network visualization. We demonstrate that McAN is highly suitable for analyzing and visualizing massive genomic data and is helpful to enhance the understanding of genome evolution. Availability: Source code is written in C/C++ and available at https://github.com/Theory-Lun/McAN and https://ngdc.cncb.ac.cn/biocode/tools/BT007301 under the MIT license. Web server is available at https://ngdc.cncb.ac.cn/bit/hapnet/. SARS-CoV-2 dataset are available at https://ngdc.cncb.ac.cn/ncov/. Contact: songshh@big.ac.cn (Song S), zhaowm@big.ac.cn (Zhao W), baoym@big.ac.cn (Bao Y), zhangzhang@big.ac.cn (Zhang Z), ybxue@big.ac.cn (Xue Y).
Keywords: population genetics, haplotype network, minimum-cost arborescence, network visualization, SARS-CoV-2
INTRODUCTION
Understanding how species evolve over millions of years requires the processing of massive amounts of genomic data, which would be a challenge without powerful bioinformatic tools. One of these tools, haplotype networks, plays important roles in tracing the evolution and migration of diverse species and is fundamental to determine and visualize genealogical relationships of population genomes [1, 2]. Over the past decades, several algorithms have been proposed for haplotype network construction, including minimum spanning network (MSN) [3], median-joining network (MJN) [3], Templeton Crandall and Sing algorithm (TCS) [4] and randomized minimum spanning tree (RMST) [5]. These algorithms have been applied to analyze a variety of genome sequences, including virus genomes, human mitochondria [1], plant chloroplast [2] and mammalian Y chromosome [6]. Haplotype network is extensively used in viral studies, with the aim to identify possible transmission routes of viruses, including the virus responsible for the ongoing COVID-19 pandemic [7–11].
Typically, these algorithms use a haplotype distance matrix to construct network, which are crucial for inferring ancestry-descendant relationships between haplotypes; however, they are limited in many ways. First, they ignore several important features when constructing haplotype network, such as sampling time, number of sequences in haplotypes and mutation spectrum history, which can mislead the tracing of evolution/transmission routes. Second, they generate undirected networks and thus are unable to reflect the evolutionary directions of variants. Third, running these algorithms is time-consuming and memory-intensive. The time complexities of MSN, MJN and TCS are O(m2) (worst case), O(n2.2) (average case) and O(m5) (worst case), respectively, where m is the number of haplotypes and n is the number of sequences (Supplementary Table S1). Therefore, these algorithms are incapable of processing the massive datasets, such as the tens of millions of SARS-CoV-2 sequences currently available. In practice, MJN takes more than three days to build haplotype networks for 1000 SARS-CoV-2 sequences, mainly due to the calculation of distance between any two haplotypes.
The visualization of haplotype networks is also vital for tracing and analysis of the genealogical relationships. In recent decades, various frameworks for network visualization have emerged. For instance, igraph [12], Gephi [13], Pajek [14] and Tulip [15] provide network visualization services for desktop users, and WiGis [16] for large graphs online. Furthermore, visualization platforms specific for multi-dimensional biological data have also been developed, such as Cytoscape [17], VisANT [18], PopArt [19], CoV Genome Tracker [20] and TPD [21]. However, most of them are not capable of fully supporting large-scaled genome data or dynamically fine-tuning network layouts.
To address these issues, we proposed a new haplotype network construction algorithm called Minimum-cost Arborescence Network (McAN), which is designed to build a directed, rooted tree spanning all vertices with minimum cost by taking into account both genome-wide mutation spectrum features and epidemiological characteristics, and is capable to run two orders of magnitude faster than existing algorithms. Moreover, we developed a web-based haplotype network visualization platform, which integrates spatial–temporal information and supports determination of community lineage and interactive fine-tuning of network layouts. We evaluated the performance of our algorithm and platform on both simulated datasets and multiple real datasets, which illustrated the advantage of McAN in analyzing and visualizing massive genomic data.
MATERIALS AND METHODS
Overview of the method
McAN was built based on minimum-cost arborescence for haplotype network construction, a well-known graph theory widely used in multiple applications. In McAN, haplotype network is represented by a directed, rooted arborescence [22], in which each haplotype is a cluster of identical sequences (with same mutations after filtering), each edge reflects directed ancestor–descendant relationship between haplotypes, and optimal arborescence is determined by minimum distances of all summed edges.
McAN factors in three features when constructing a haplotype network, including mutation spectrum histories, sample sizes and sampling times for every haplotype. Specifically, McAN takes account of the mutation spectrum history of all samples and assumes that mutations of an ancestral haplotype should be inherited by its descendant haplotypes, and haplotypes with more sequences should be more likely to be intermediate ancestor nodes, due to a higher probability of propagating outwards of the haplotypes with more sequences. If sampling time is available, ancestral mutants are assumed to be earlier sampled than derived mutants.
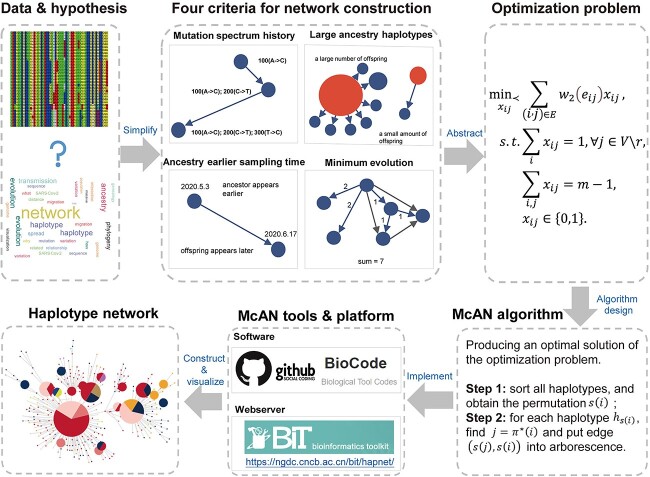
For convenience, these assumptions are summarized as the following four criteria (Figure 1): (1) mutation spectrum history, (2) large ancestry haplotype, (3) ancestry earlier sampling time and (4) minimum evolution (ME). The last criterion means the optimal haplotype network for a set of haplotypes is assumed to be an arborescence whose sum of distances of all directed edges is minimal [23]. We defined the distance between a pair of haplotypes as the number of different mutations between two haplotypes.
Figure 1.
Schematic illustration for haplotype network construction by McAN. To infer the genealogical relationship among multiple genomic sequences, four criteria were adopted for haplotype network construction. Then, optimization problem was abstracted and the McAN algorithm was designed. Furthermore, McAN tool and online webserver was developed to implement this algorithm. Finally, a haplotype network was constructed and visualized interactively by McAN platform.
When all data including mutation and metadata are read by McAN, pairs of accession ID and mutations for all sequences are stored in a hash map, and sequences with the same mutations are clustered into a group and regarded as a haplotype. The reference sequence (users need to select the earliest high-quality sequence as reference) is designated as the root node of the haplotype network. Next, all haplotypes are sorted by mutation count and sequence count in descending order and the earliest sampling time (if available) in ascending order (Supplementary Figure S1A). Based on this sorting, the closest ancestor is determined and minimized for each haplotype (Supplementary Figure S1B). To save memory and running time, McAN calculates distances between adjacent haplotypes instead of any two haplotypes (Supplementary Figure S1C). Then, the directed edges representing the candidate immediate ancestor–descendant relationships are established under the constraint of the ‘mutation spectrum history’ criterion. The immediate ancestor–descendant relationships are determined by the ‘minimum evolution (ME)’ criterion. In practice, the haplotype networks may not be unique, so we propose the ‘large ancestry haplotype’ and ‘ancestry earlier sampling time’ criterion to determine, which one is the best among all haplotype networks. In addition, we further paralleled the algorithm of McAN to satisfy huge amount sequences data.
Detailed algorithm of McAN
Suppose there are 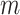 haplotypes, denoted by
haplotypes, denoted by 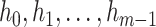 , respectively. Let
, respectively. Let
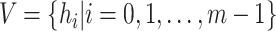 |
(1) |
be the set of all haplotypes and 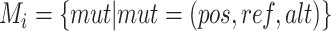 be the set of mutations in haplotype
be the set of mutations in haplotype 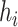 including all SNPs, insertions and deletions, where
including all SNPs, insertions and deletions, where 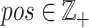 represents the genomic position of mutation
represents the genomic position of mutation 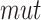 and
and 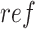 (
(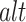 ) a reference (mutated) nucleotide base or a sub-sequence of the reference (mutated) sequence. Let
) a reference (mutated) nucleotide base or a sub-sequence of the reference (mutated) sequence. Let 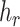 be the haplotype containing the reference sample. Obviously, the set of mutations
be the haplotype containing the reference sample. Obviously, the set of mutations 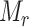 in haplotype
in haplotype 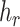 is equal to an empty set. According to the ‘mutation spectrum history’ criterion, the set of candidates of directed edges should then be
is equal to an empty set. According to the ‘mutation spectrum history’ criterion, the set of candidates of directed edges should then be
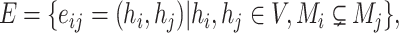 |
(2) |
where 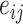 is a directed edge from haplotype
is a directed edge from haplotype 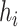 to
to 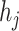 , which also be denoted as an ordered pair
, which also be denoted as an ordered pair 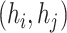 or
or 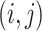 . Notice that, no self-cycle belongs to set E. The distance between two haplotypes
. Notice that, no self-cycle belongs to set E. The distance between two haplotypes 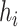 and
and 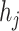 satisfying
satisfying 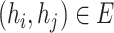 is
is
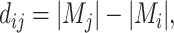 |
(3) |
where 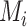 and
and 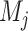 are sets of mutations of haplotypes
are sets of mutations of haplotypes 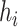 and
and 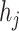 , respectively,
, respectively,  denotes the cardinality of a set. Let
denotes the cardinality of a set. Let 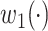 be a cost function (or weight function) on
be a cost function (or weight function) on 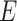 ,
,
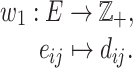 |
(4) |
By ‘minimum evolution (ME)’ criterion, the haplotype network must be the minimum-cost arborescence of the weighted directed graph 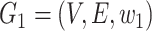 . Formally, the minimum-cost arborescence problem can be represented as an integer programming problem:
. Formally, the minimum-cost arborescence problem can be represented as an integer programming problem:
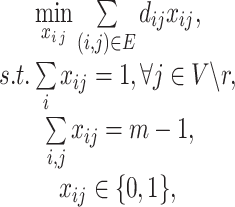 |
(5) |
where 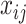 ,
, 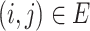 , are the decision variables,
, are the decision variables, 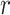 is the index of haplotype containing reference. If edge
is the index of haplotype containing reference. If edge 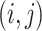 is in the minimum-cost arborescence,
is in the minimum-cost arborescence, 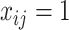 , otherwise
, otherwise 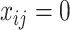 . The first constraint represents that the number of ancestors of haplotypes except for
. The first constraint represents that the number of ancestors of haplotypes except for 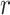 should be 1, and the second one represents that the total number of edges in haplotype network must be
should be 1, and the second one represents that the total number of edges in haplotype network must be 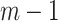 . Note that a decision variable
. Note that a decision variable 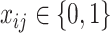 satisfies these two constraints if and only if
satisfies these two constraints if and only if 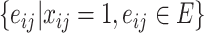 is a spanning arborescence of the unweighted directed graph
is a spanning arborescence of the unweighted directed graph 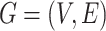 .
.
To deal with the minimum-cost arborescence problem (problem (5)), one should determine the root of arborescence, handle directed cycles in graph and examine the uniqueness of the solution. The root of minimum-cost arborescence is supposed to be provide by the use, which is the haplotype 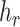 containing the reference sequence. The following Theorem 1 shows that there is no directed cycle in
containing the reference sequence. The following Theorem 1 shows that there is no directed cycle in 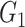 .
.
Theorem 1.
Let
be a directed graph, where
and
is defined by Equations (1) and (2), respectively. Then, there is no directed cycle in
.
Proof. Suppose for contradiction that there exists at least one directed cycle in 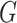 . Then, let
. Then, let 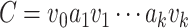 be a directed cycle in
be a directed cycle in 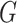 , where
, where 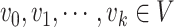 ,
, 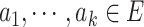 ,
, 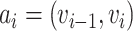 and
and 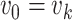 . And let
. And let 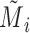 be the set of mutations in vertex (or haplotype)
be the set of mutations in vertex (or haplotype) 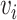 , for any
, for any 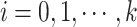 . By Equation (2), we have
. By Equation (2), we have 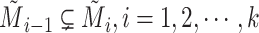 . Therefore, we obtain
. Therefore, we obtain 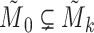 . However,
. However, 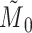 is equal to
is equal to 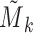 since
since 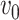 is equal to
is equal to 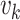 . This is a contradiction. Hence, our assumption that “there exists at least one directed cycle in
. This is a contradiction. Hence, our assumption that “there exists at least one directed cycle in 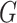 ” cannot be true. We thus have proved “there is no directed cycle in
” cannot be true. We thus have proved “there is no directed cycle in 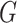 ”. Q.E.D.
”. Q.E.D.
However, the minimum-cost arborescence of 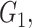 may not be unique. Therefore, two other criteria are involved in to further constrain possible solutions. If more than one haplotype exists that is both closest ancestry of a given haplotype, then the haplotype containing more sequences is chosen to be the ancestry of the given haplotype by ‘large ancestry haplotype’ criterion. If more than one haplotype exists that is both closest ancestry of a given haplotype and is both meeting ‘large ancestry haplotype’ criterion, then the one meeting the ‘ancestry earlier sampling time’ criterion is retained in the haplotype network. Formally, let
may not be unique. Therefore, two other criteria are involved in to further constrain possible solutions. If more than one haplotype exists that is both closest ancestry of a given haplotype, then the haplotype containing more sequences is chosen to be the ancestry of the given haplotype by ‘large ancestry haplotype’ criterion. If more than one haplotype exists that is both closest ancestry of a given haplotype and is both meeting ‘large ancestry haplotype’ criterion, then the one meeting the ‘ancestry earlier sampling time’ criterion is retained in the haplotype network. Formally, let 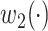 be a cost function on
be a cost function on 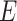
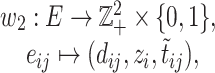 |
(6) |
where 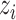 is the number of sequences in
is the number of sequences in 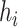 ,
, 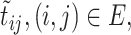 is defined as
is defined as
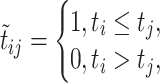 |
(7) |
representing whether edge 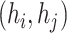 in E meet ‘ancestry earlier sampling time’ criterion,
in E meet ‘ancestry earlier sampling time’ criterion, 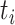 is the sampling time of the
is the sampling time of the 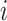 th haplotype
th haplotype 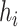 (which is defined as the earliest sampling time of sequences in
(which is defined as the earliest sampling time of sequences in 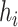 ). Considering all the four criteria, the haplotype network is a minimum spanning arborescence of
). Considering all the four criteria, the haplotype network is a minimum spanning arborescence of 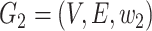 with order relation
with order relation 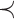 , where order relation
, where order relation 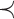 is defined on
is defined on 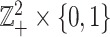 such that for any
such that for any 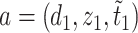 and
and 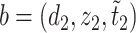 in
in 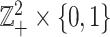 ,
, 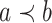 if and only if
if and only if 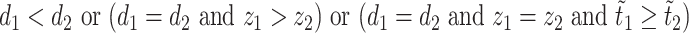 . The overall optimization problem becomes
. The overall optimization problem becomes
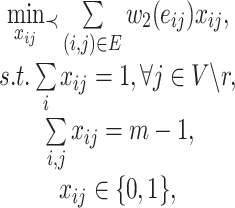 |
(8) |
where 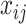 ,
, 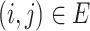 , are the decision variables.
, are the decision variables.
Optimization problem (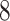 ) is not a standard minimum-cost arborescence problem with a numerical cost, but with a vectorial cost. However, we can follow the framework of Chu-Liu-Edmonds’ algorithm [24, 25] to solve problem (
) is not a standard minimum-cost arborescence problem with a numerical cost, but with a vectorial cost. However, we can follow the framework of Chu-Liu-Edmonds’ algorithm [24, 25] to solve problem (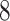 ), although we cannot use the algorithm directly. Specifically, we firstly find all the edges in E, and calculate the distance for all edges in E. Next, we find an edge
), although we cannot use the algorithm directly. Specifically, we firstly find all the edges in E, and calculate the distance for all edges in E. Next, we find an edge 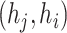 , incoming to
, incoming to 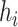 with the lowest cost (according to relation
with the lowest cost (according to relation 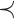 , and weight
, and weight 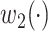 ) for each haplotype
) for each haplotype 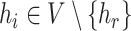 , where
, where 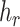 represent the haplotype containing the reference,
represent the haplotype containing the reference, 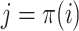 is defined as
is defined as
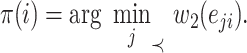 |
(9) |
The pseudo-code of constructing haplotype network by following the framework of Chu-Liu-Edmonds’ algorithm is represented as Algorithm S1. The output 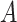 generated by Algorithm S1 must be an optimum arborescence of problem (
generated by Algorithm S1 must be an optimum arborescence of problem ( ). Chu-Liu-Edmonds’ algorithm takes the set of edges
). Chu-Liu-Edmonds’ algorithm takes the set of edges 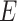 and the weight of each edge as input. However, the input of constructing haplotype network are the mutations set, the sampling time and the number of samples of each haplotype. If we directly use the framework of Chu-Liu-Edmonds’ algorithm to solve the problem of constructing haplotype network, the computation of determining if
and the weight of each edge as input. However, the input of constructing haplotype network are the mutations set, the sampling time and the number of samples of each haplotype. If we directly use the framework of Chu-Liu-Edmonds’ algorithm to solve the problem of constructing haplotype network, the computation of determining if 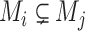 for each pair of
for each pair of 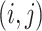 satisfying
satisfying 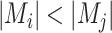 cannot be saved. Meanwhile the storage of the weight
cannot be saved. Meanwhile the storage of the weight 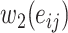 (that is
(that is 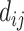 and
and 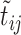 in Algorithm S1) of each edge in
in Algorithm S1) of each edge in 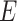 cannot be reduced. Therefore, both best-case and worst-case time complexity of Algorithm S1 are
cannot be reduced. Therefore, both best-case and worst-case time complexity of Algorithm S1 are 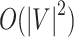 and space complexity of Algorithm S1 are
and space complexity of Algorithm S1 are 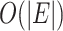
To reduce the time and space complexity of Algorithm S1, we proposed McAN (Algorithm 1). McAN firstly sort all haplotypes by the number of mutations and sequences in descending order, and the earliest sampling time in ascending order. Haplotypes and their mutation sets under the new order are denoted by 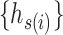 and
and 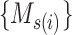 ,
, 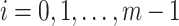 , respectively, where
, respectively, where 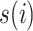 is a permutation of set
is a permutation of set 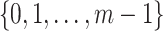 . For each haplotype
. For each haplotype 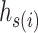 , its directed ancestor
, its directed ancestor 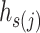 is determined by searching from
is determined by searching from 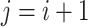 and finding the smallest
and finding the smallest 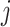 satisfying
satisfying 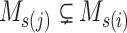 , that is
, that is
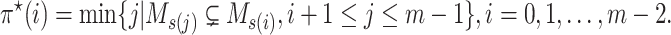 |
(10) |
The pseudo-code of the proposed McAN is represented as Algorithm 1, where sort is a sorting algorithms (sort generate the permutation 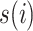 remaining
remaining 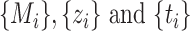 unchanged), and
unchanged), and 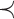 is an order relation defined on
is an order relation defined on 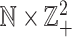 such that for any
such that for any 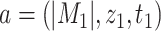 and
and 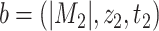 ,
, 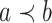 if and only if
if and only if 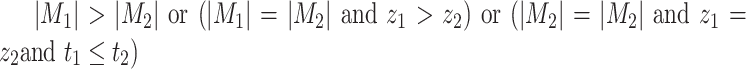 . So, we have
. So, we have
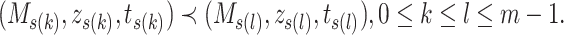 |
(11) |
The output 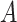 of Algorithm 1 is proved to be an optimal solution of problem (
of Algorithm 1 is proved to be an optimal solution of problem ( ) by Theorem 2 (Lemma 1–3 in the proof of Theorem 2 is provided in the supplementary materials).
) by Theorem 2 (Lemma 1–3 in the proof of Theorem 2 is provided in the supplementary materials).
Algorithm 1.
McAN
| Input: |
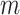 , the number of haplotypes, , the number of haplotypes, 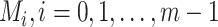 , the set of mutations in haplotype , the set of mutations in haplotype 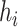 , , 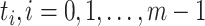 , the sampling time of haplotype , the sampling time of haplotype 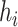 , , 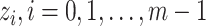 , the number of samples in haplotype , the number of samples in haplotype 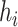 . . |
| Output: |
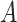 , the minimum-cost arborescence, which is a set of edges. , the minimum-cost arborescence, which is a set of edges. |
Step 1 (sort all haplotypes by generating a permutation 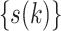 ) ) 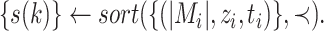
|
Step 2 (find minimum-cost arborescence 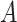 ) ) 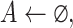 for each for each 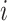 from 0 to from 0 to 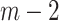 , for each , for each 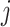 from from 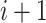 to to 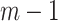 , if , if 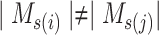 , then if , then if 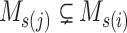 , then , then 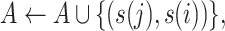
|
| break, |
end if, end if, end for, end for, return 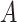 . . |
Theorem 2.
The output
of Algorithm 1 is an optimal solution of problem (
).
Proof. First, we will show that 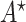 is a feasible solution of problem (
is a feasible solution of problem (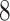 ). For each
). For each 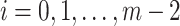 , by Lemma 1, we have
, by Lemma 1, we have 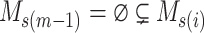 . Therefore, for any
. Therefore, for any 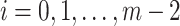 in step 2 of Algorithm 1, there exists at least one
in step 2 of Algorithm 1, there exists at least one 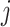 , satisfying
, satisfying 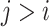 and
and 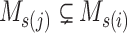 . Then the output of Algorithm 1 can be represented as
. Then the output of Algorithm 1 can be represented as
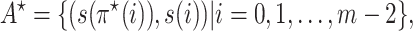 |
(12) |
where 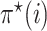 is defined by Equation (10). Then we have
is defined by Equation (10). Then we have
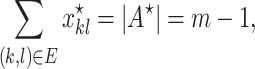 |
and
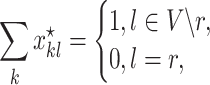 |
where 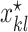 is the decision variable corresponding to
is the decision variable corresponding to 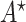 , defined as
, defined as
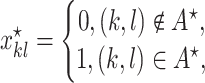 |
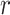 is the index of the haplotype containing reference. Thus,
is the index of the haplotype containing reference. Thus, 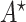 is a feasible solution of problem (
is a feasible solution of problem (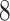 ).
).
Second, we will show that “the output 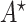 of Algorithm 1 is an optimal solution of problem (
of Algorithm 1 is an optimal solution of problem (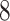 )”. Let
)”. Let 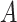 be any feasible solution of problem (
be any feasible solution of problem (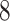 ). Then, by the constraints of problem (
). Then, by the constraints of problem (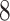 ),
), 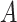 can be represented as
can be represented as
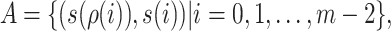 |
(13) |
where 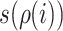 is the unique ancestor of
is the unique ancestor of 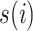 , for any
, for any 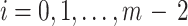 . Considering Equations (12) and (13), and Lemma 2, we have
. Considering Equations (12) and (13), and Lemma 2, we have
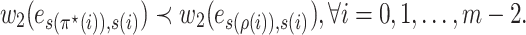 |
By Lemma 3, we have
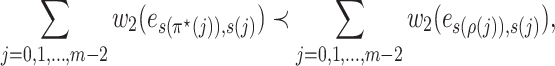 |
that is 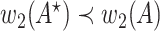 . Thus
. Thus 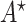 is an optimal solution of problem (
is an optimal solution of problem (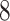 ). Q.E.D.
). Q.E.D.
By sorting the haplotypes in step 1 of Algorithm 1, McAN avoids the evaluation of the condition 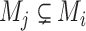 for any
for any 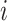 and
and 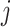 satisfying
satisfying 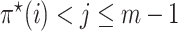 , and avoids storing the edges set E and the weight, including
, and avoids storing the edges set E and the weight, including 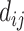 and
and 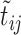 , of all edges in
, of all edges in 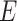 . The complexity of McAN depend on the selection of the sorting algorithms. If the quicksort is used in Algorithm 1, the best-case time complexity is reduced from
. The complexity of McAN depend on the selection of the sorting algorithms. If the quicksort is used in Algorithm 1, the best-case time complexity is reduced from 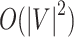 to
to 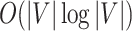 and the space complexity is reduced from
and the space complexity is reduced from 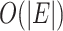 to
to 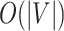 in Algorithm 1, compared with Algorithm S1.
in Algorithm 1, compared with Algorithm S1.
Compared with the other haplotype network construction algorithms, the worst-case time complexity of McAN is 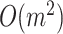 , which is equal to the worst-case time complexity of MSN and smaller than the time complexities of MJN (
, which is equal to the worst-case time complexity of MSN and smaller than the time complexities of MJN (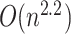 ) (average-case) [3] and TCS (
) (average-case) [3] and TCS (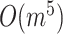 ) (worst-case) [26], where
) (worst-case) [26], where 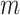 is the number of haplotypes and
is the number of haplotypes and 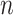 is the number of sequences.
is the number of sequences.
RESULTS
Performance testing on simulated datasets
We evaluated the accuracy of McAN by comparison with four existing popular algorithms MSN, MJN, TCS and RMST on a simulated dataset with 1001 sequences. We found that the AUC (area under the curve) of McAN, MSN, MJN, TCS, and RMST are 0.997, 0.998, 0.997, 0.997 and 0.998, respectively, showing that McAN is as good as MJN and TCS, and is slightly lower than MSN and RMST (Supplementary Figure S2A-E, Table 1). We also evaluated the memory cost, and found that McAN consumed less than a tenth of the memory of the other four algorithms. On a large-scaled dataset including 20 001 sequences, the AUC of McAN remains 0.997 (Supplementary Figure S2F).
Table 1.
Evaluation of accuracy and memory cost on a simulated dataset including 1001 sequences
| Algorithms | AUC | Memory cost (KB) |
|---|---|---|
| McAN | 0.997 | 5844 |
| MSN | 0.998 | 59 960 |
| MJN | 0.997 | 63 676 |
| TCS | 0.997 | 62 928 |
| RMST | 0.998 | 114 725 |
Performance testing on real SARS-CoV-2 datasets
The running performance of McAN was tested using 1 124 837 SARS-CoV-2 genome sequences retrieved from RCoV19 [7, 8] as of 26 July 2021 on a personal laptop (Intel Core i5-6200 U CPU and 8GB memory running with Ubuntu 20.04 operating system). We first established a small dataset by randomly sampling SARS-CoV-2 sequences. When the number of sequences ranges from 200 to 1000, McAN consistently obtained higher efficiency, running about 1000 times faster than, TCS and MJN and 100 times faster than RMST and MSN (Figure 2A). While on a larger dataset with different sequence counts ranging from 100 thousand to one million, even when sequence count reaches 1 million, McAN required less than 20 minutes, demonstrating that McAN is able to construct a haplotype network using large-scale dataset.
Figure 2.
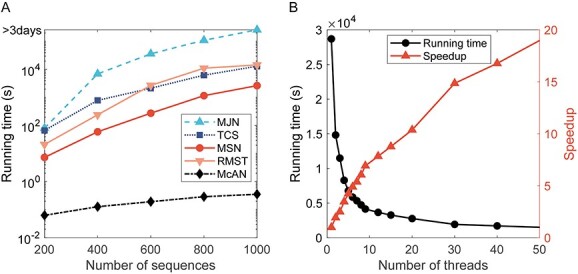
Running time for MJN, TCS, MSN, RMST and McAN. (A) Comparison of running time for MJN, TCS, MSN, RMST and McAN with the number of sequences ranging from 200 to 1000 (single thread). (B) Running time of McAN with number of threads ranging from 1 to 50 for 4 990 399 sequences.
Given that tens of millions of SARS-CoV-2 sequences are currently available, the performance of paralleled McAN was tested on a server (2 Hygon C86 7185 32-core Processor, 512GB memory with CentOS Linux release 7.4.1708 (Core) operating system) using 4 990 399 SARS-CoV-2 sequences from RCoV19 as of 20 April 2022. When the number of threads ranges from 1 to 50, the running time of paralleled McAN rapidly declined from 28 696.5 to 1511.9 s (Figure 2B).
Performance evaluation using independent datasets
Independent datasets are usually used to assess the performance of a newly developed algorithm. Thus, we established two independent datasets for SARS-CoV-2 [9, 27] and evaluated performance of McAN. First, we tested on a real dataset of 482 SARS-CoV-2 genome sequences including 72 isolated from the Diamond Princess cruise and 410 from multiple countries/regions globally as detailed in [9]. Unlike MSN, TCS and MJN algorithms, McAN produced a direct evolutionary route from the reference (MN908947.3) to the Diamond Princess cluster (Supplementary Figure S3). This result is in agreement with a finding that SARS-CoV-2 dissemination on the Diamond Princess cruise is originated from a single introduction event [9]. Moreover, the haplotype network constructed by McAN using 130 major haplotypes of sublineages of L and S lineages from 121 618 SARS-CoV-2 genomes [27] shows a distinct delineation among these sublineages (Supplementary Figure S4), suggesting that McAN is capable of accurately tracking the evolution of SARS-CoV-2 during the development of the global pandemic of COVID-19.
In addition to SARS-CoV-2, we further tested McAN on other kinds of viruses including Monkeypox virus (MPXV) [28] and human influenza A viruses [29]. The haplotype network of monkeypox shows that most monkeypox samples collected in 2022 form a separate outbreak cluster except for two monkeypox samples collected from the USA in 2022 (Supplementary Figure S5A), supporting a previous study that 2022_FL001 and 2022_VA001 are unrelated to other cases occurring in 2022 in the USA. While using human influenza A viruses in 1918, we found that the main haplotype of these viruses consists of three samples collected in Germany and five samples collected in the USA (Supplementary Figure S5B). This finding strongly suggests that no geographic segregation exists between Europe and North America.
Web server guide and tools for haplotype network construction
To enable scholars to use McAN regardless of their computational skills, we established a free and user-friendly web server, which is available at https://ngdc.cncb.ac.cn/bit/hapnet/. On the web-server page, after a short introduction of the functions incorporated in McAN (Supplementary Figure S6), users can upload the genomic variants data either in VCF or customized genovar format, together with the corresponding metadata (Figure 3A). If the genomic data are from SARS-CoV-2, users can easily combine their data with a particular subset of SARS-CoV-2 sequences and metadata in RCoV19 by setting sampling date or country, or by sampling randomly. Next, users can filter sites by setting a minimum mutation rate. Haplotype network of user provided sequences will be constructed and community lineages will be determined meanwhile by hierarchical agglomeration algorithm [30] via McAN. The haplotype network results can be downloaded directly or viewed interactively in a viral haplotype network viewer developed in-house (Figure 3B), or sent via email.
Figure 3.
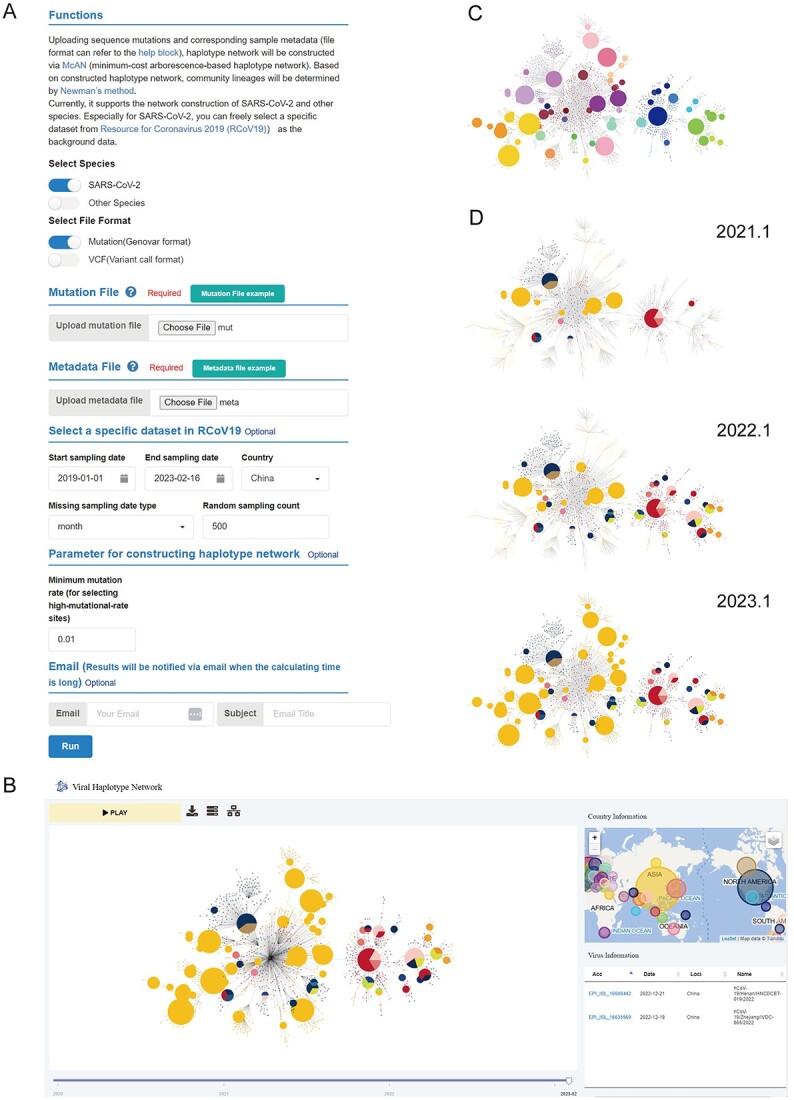
Web server for haplotype network construction. (A) Homepage of McAN’s web server, where users can upload their genome mutation data and metadata, and set parameters to construct haplotype network online. (B) In-house developed haplotype network viewer, allowing users to interactively view the haplotype network constructed by McAN. (C) In the haplotype network viewer, nodes of interested lineages can be highlighted. (D) Sequential screenshots showing interactive functions, where network nodes can be hidden or make visible by dragging the timeline bar below the viewer page.
Because of the bottleneck of network transmission, webservers cannot work when the number of inputted sequences is too large. To allow users to run McAN locally, we also developed an offline tool in C/C++ that can be freely downloaded from https://ngdc.cncb.ac.cn/biocode/tools/BT007301 and https://github.com/Theory-Lun/McAN. This tool supports input files in VCF format as well as customized genovar formats, and generate output files in TSV, JSON and GraphML formats, all of which are suitable for visualization and publication.
Interactive web-based visualization platform for haplotype network
We further developed an interactive web-based haplotype network visualization platform to facilitate tracing the genealogy, i.e. viral haplotype networks integrating spatial–temporal information. The platform features four major interconnected panels, each presenting spatial information, haplotype network, timeline and concise meta information of sequences. In spatial panel, it depicts colored circles that correspond to different locations, mirroring the colors in the haplotype network graph. The size of each circle reflects the number of samples in the current location, relative to the overall sample size. While on the network, it can be zoomed in and out and can be moved as a whole. Hovering over a node provides cluster information, while dragging a node makes it easier to observe and format. Clicking on a node highlights both the node and its branch for focused analysis, and the map and table dynamically update when nodes are clicked. For the timeline, the visibility of nodes can also be adjusted by dragging the timeline. With the ‘PLAY’ button, users can visualize how their sequences evolve over time in various locations. (Figure 3C). Additionally, lineages of evolving clusters are analyzed simultaneously and colored in different colors, which can be viewed by clicking on the 'View group' button (Figure 3D). All haplotype network figures can be saved in PNG format. This platform is capable of displaying networks with tens of thousands of nodes.
CONCLUSION AND DISCUSSION
This paper proposed McAN, a novel haplotype network construction algorithm and platform based on minimum-cost arborescence. McAN is capable for analyzing a large number of sequences and helpful for molecular tracing of pathogens for pandemics (e.g. COVID-19). McAN outperforms existing algorithms and achieves higher accuracy and efficiency in haplotype network construction by testing on multiple datasets. Its visualization platform enables the display of a haplotype network with tens of thousands of nodes across space and time, which offers multiple panels that present different facets of the network and remain synchronized while interacting. These results strongly suggest that McAN is a desirable platform for analyzing massive dynamic data, especially SARS-CoV-2 datasets, and will be beneficial to the study of genome evolution.
While McAN is clearly useful for constructing haplotype network of viruses, it is limited in a number of ways. First, the mutation spectrum history (mutations in ancestry haplotype should be contained in descendant haplotype) implies that McAN cannot detect any reverse mutations, which have been occurred in SARS-CoV-2 [31]. Second, we used arborescence to represent a haplotype network and therefore McAN cannot detect any recombination, which have been reported in the Omicron variant of Covid-19 virus [32, 33]. Third, the preprocessing of sequences and selection of root might affect the edges of the haplotype network constructed by McAN. User should use a high-quality sequence as the reference. If the quality of reference is low; i.e. the length of sequence is short or the number of ambiguous nucleotides is large, the accuracy of mutation detection may decrease. This will further affect the accuracy of haplotype network. In addition, we advise choosing the earliest sequence as reference. If a relatively late sequence is used as reference, the direction of edges in haplotype network may not reflect the direction of evolution correctly.
Key Points
Minimum cost arborescence network (McAN) algorithm constructs haplotype network by considering mutation spectrum history, node size and sampling time simultaneously.
McAN platform provides a user-friendly web server as well as an offline tool, allowing users to construct haplotype network, detect lineages and visualize the results interactively online.
McAN is capable to build haplotype network for millions of sequences data with high accuracy and efficiency (about 20 minutes for millions of sequences using one to fifty threads).
McAN is helpful for the molecular tracing of pathogens for pandemics and is beneficial to deepening the understanding of viruses including but not limited to SARS-CoV-2, Monkeypox virus and human influenza A viruses.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank the members of the China National Center for Bioinformation for providing SARS-CoV-2 mutation data and metadata.
Author Biographies
Lun Li received his Ph.D. degree in Operational Research and Cybernetics from University of Chinese Academy of Sciences. He is currently a postdoc at Beijing Institute of Genomics.
Bo Xu received his Ph.D. degree in bioinformatics from Beijing Institute of Genomics. His research interests include molecular evolution, phylogenetics and computational statistics.
Dongmei Tian received her Master of Science Degree in Probability Theory and Mathematical Statistics at People's University of China. Her current research interests include data mining, deep learning and bioinformatics.
Anke Wang received her M.Sc. degree in GeoSpatial Science from the University College London in 2019. She is now serving as an engineer at Beijing Institute of Genomics.
Junwei Zhu is an engineer at Beijing Institute of Genomics. His current research interests include big data integration and analytics, bioinformatics tools online analysis and database system design and development.
Cuiping Li is an engineer of Beijing Institute of Genomics. Her current research works mainly include genomic variation analysis and population genetic analysis.
Na Li received her Ph.D. degree in condensed matter physics from Fudan University, China. She is working as a Postdoc at Beijing Institute of Genomics. Her research interests include complex networks.
Wei Zhao received her B.Sc. degree in Bioinformatics from Huazhong Agricultural University, China. She is pursuing a doctorate in Bioinformatics at the National Genomics Data Center.
Leisheng Shi is a doctoral candidate at Bioinformatics from National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation.
Yongbiao Xue is the director and a professor at Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation.
Zhang Zhang is a professor at Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation.
Yiming Bao is the current director of the National Genomic Data Center, and a professor in ‘100-Talent’ Program of CAS, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation.
Wenming Zhao is a professor at Beijing Institute of Genomics. He focuses on bioinformatics database construction.
Shuhui Song is a professor at Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation.
Contributor Information
Lun Li, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China.
Bo Xu, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China.
Dongmei Tian, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China.
Anke Wang, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China.
Junwei Zhu, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China.
Cuiping Li, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China.
Na Li, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China.
Wei Zhao, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China; University of Chinese Academy of Sciences, Beijing 100049, China.
Leisheng Shi, University of Chinese Academy of Sciences, Beijing 100049, China; Key Laboratory of Genomic and Precision Medicine, Beijing Institute of Genomics, Chinese Academy of Sciences, and China National Center for Bioinformation, Beijing, China.
Yongbiao Xue, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China; University of Chinese Academy of Sciences, Beijing 100049, China.
Zhang Zhang, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China; CAS Key Laboratory of Genome Sciences and Information, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China; University of Chinese Academy of Sciences, Beijing 100049, China.
Yiming Bao, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China; CAS Key Laboratory of Genome Sciences and Information, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China; University of Chinese Academy of Sciences, Beijing 100049, China.
Wenming Zhao, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China; CAS Key Laboratory of Genome Sciences and Information, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China; University of Chinese Academy of Sciences, Beijing 100049, China.
Shuhui Song, National Genomics Data Center, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China; CAS Key Laboratory of Genome Sciences and Information, Beijing Institute of Genomics, Chinese Academy of Sciences and China National Center for Bioinformation, Beijing 100101, China; University of Chinese Academy of Sciences, Beijing 100049, China.
FUNDING
This research was funded by grants from the National Key Research & Development Program of China (2021YFF0703703, 2021YFC0863300 to S.H.S.), the Key Collaborative Research Program of the Alliance of International Science Organizations (ANSO-CR-KP-2022-09 to S.H.S.), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB38060100 to Y.M.B.), the National Natural Science Foundation of China (32270718 to S.H.S., 32170678 to W.M.Z.), Youth Innovation Promotion Association of CAS (2017141 to S.H.S.) and the Beijing Nova Program (Z211100002121006 to L.L.).
References
- 1. Bandelt H-J, Forster P, Sykes BC, et al. . Mitochondrial portraits of human populations using median networks. Genetics 1995;141:743–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Yue X, Zheng X, Zong Y, et al. . Combined analyses of chloroplast DNA haplotypes and microsatellite markers reveal new insights into the origin and dissemination route of cultivated pears native to East Asia, Frontiers. Plant Sci 2018;9:591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Bandelt H-J, Forster P, Röhl A. Median-joining networks for inferring intraspecific phylogenies. Mol Biol Evol 1999;16:37–48. [DOI] [PubMed] [Google Scholar]
- 4. Templeton AR, Crandall KA, Sing CF. A cladistic-analysis of phenotypic associations with haplotypes inferred from restriction endonuclease mapping and DNA-sequence data.3. Cladogram estimation. Genetics 1992;132:619–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Paradis E. Analysis of haplotype networks: the randomized minimum spanning tree method. Methods in Ecology and Evolution 2018;9:1308–17. [Google Scholar]
- 6. Felkel S, Wallner B, Chuluunbat B, et al. . A first Y-chromosomal haplotype network to investigate male-driven population dynamics in domestic and wild Bactrian camels. Front Genet 2019;10:423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Song S, Ma L, Zou D, et al. . The global landscape of SARS-CoV-2 genomes, variants, and haplotypes in 2019nCoVR. Genomics Proteomics Bioinformatics 2020;18:749–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Zhao W-M, Song S-H, Chen M-L, et al. . The 2019 novel coronavirus resource. Yi Chuan 2020;42:212–21. [DOI] [PubMed] [Google Scholar]
- 9. Sekizuka T, Itokawa K, Kageyama T, et al. . Haplotype networks of SARS-CoV-2 infections in the diamond princess cruise ship outbreak. Proc Natl Acad Sci U S A 2020;117:20198–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Kemenesi G, Kornya L, Tóth GE, et al. . Nursing homes and the elderly regarding the COVID-19 pandemic: situation report from Hungary. GeroScience 2020;42:1093–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Song S, Li C, Kang L, et al. . Genomic epidemiology of SARS-CoV-2 in Pakistan. Genomics Proteomics Bioinformatics 2021;19:727–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Csardi G, Nepusz T. The igraph software package for complex network research. InterJournal, Complex Systems 2006;1695:1–9. [Google Scholar]
- 13. Bastian M, Heymann S, Jacomy M. Gephi: an open source software for exploring and manipulating networks, proceedings of the international AAAI conference on web and social. Media 2009;3:361–2. [Google Scholar]
- 14. Mrvar A, Batagelj V. Analysis and visualization of large networks with program package Pajek. Complex Adaptive Systems Modeling 2016;4:6. [Google Scholar]
- 15. Auber D, Archambault D, Bourqui R, et al. . TULIP 5. In: Reda A, Jon R (eds). Encyclopedia of Social Network Analysis and Mining. Springer, 2017, 1–28. [Google Scholar]
- 16. Gretarsson B, Bostandjiev S, O’Donovan J, et al. . WiGis: A Framework for Scalable Web-Based Interactive Graph Visualizations. GD, 2009, 119–34. [Google Scholar]
- 17. Shannon P, Markiel A, Ozier O, et al. . Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res 2003;13:2498–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Hu Z, Mellor J, Wu J, et al. . VisANT: an online visualization and analysis tool for biological interaction data. BMC Bioinformatics 2004;5:17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Leigh JW, Bryant D. Popart: full-feature software for haplotype network construction. Methods in Ecology and Evolution 2015;6:1110–6. [Google Scholar]
- 20. Akther S, Bezrucenkovas E, Sulkow B, et al. . CoV genome tracker: tracing genomic footprints of Covid-19 pandemic bioRxiv. 2020: 2020.2004.2010.036343. [Google Scholar]
- 21. Chen P, Zhong J, Yang K, et al. . TPD: a web tool for tipping-point detection based on dynamic network biomarker. Brief Bioinform 2022;23:bbac399. [DOI] [PubMed] [Google Scholar]
- 22. Gordon G, McMahon E. A greedoid polynomial which distinguishes rooted arborescences. Proceedings of the American Mathematical Society 1989;107:287–98. [Google Scholar]
- 23. Catanzaro D. The minimum evolution problem: overview and classification, networks: an. International Journal 2009;53:112–25. [Google Scholar]
- 24. Edmonds J. Optimum branchings. Journal of Research of the national Bureau of Standards B 1967;71:233–40. [Google Scholar]
- 25. Chu Y-J, Liu T-H. On the shortest arborescence of a directed graph. Sci Sin 1965;14:1396–400. [Google Scholar]
- 26. Clement M, Snell Q, Walker P, et al. . TCS: estimating gene genealogies. In: Parallel and Distributed Processing Symposium, International. IEEE Computer Society, 2002, 0184–4. [Google Scholar]
- 27. Tang X, Ying R, Yao X, et al. . Evolutionary analysis and lineage designation of SARS-CoV-2 genomes. Science Bulletin 2021;66:2297–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Gigante CM, Korber B, Seabolt MH, et al. . Multiple lineages of Monkeypox virus detected in the United States, 2021-2022 bioRxiv. 2022. [DOI] [PMC free article] [PubMed]
- 29. Patrono LV, Vrancken B, Budt M, et al. . Archival influenza virus genomes from Europe reveal genomic variability during the 1918 pandemic. Nat Commun 2022;13:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Clauset A, Newman ME, Moore C. Finding community structure in very large networks. Physical Review E 2004;70:066111. [DOI] [PubMed] [Google Scholar]
- 31. Tuekprakhon A, Nutalai R, Dijokaite-Guraliuc A, et al. . Antibody escape of SARS-CoV-2 omicron BA.4 and BA.5 from vaccine and BA.1 serum. Cell 2022;185:2422–2433.e2413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Lacek KA, Rambo-Martin BL, Batra D, et al. . SARS-CoV-2 Delta-omicron recombinant viruses, United States. Emerg Infect Dis 2022;28:1442–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Turakhia Y, Thornlow B, Hinrichs A, et al. . Pandemic-scale phylogenomics reveals the SARS-CoV-2 recombination landscape. Nature 2022;609:994–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.