Abstract
The genetic etiologies of common diseases are highly complex and heterogeneous. Classic methods, such as linear regression, have successfully identified numerous variants associated with complex diseases. Nonetheless, for most diseases, the identified variants only account for a small proportion of heritability. Challenges remain to discover additional variants contributing to complex diseases. Expectile regression is a generalization of linear regression and provides complete information on the conditional distribution of a phenotype of interest. While expectile regression has many nice properties, it has rarely been used in genetic research. In this paper, we develop an expectile neural network (ENN) method for genetic data analyses of complex diseases. Similar to expectile regression, ENN provides a comprehensive view of relationships between genetic variants and disease phenotypes, which can be used to discover variants predisposing to sub-populations. We further integrate the idea of neural networks into ENN, making it capable of capturing non-linear and non-additive genetic effects (e.g., gene-gene interactions). Through simulations, we showed that the proposed method outperformed an existing expectile regression when there exist complex genotype-phenotype relationships. We also applied the proposed method to the data from the Study of Addiction: Genetics and Environment (SAGE), investigating the relationships of candidate genes with smoking quantity.
Keywords: non-linear, gene-gene interaction, expectile regression, neural networks
1. Introduction
Converging evidence suggests that the genetic etiologies of complex diseases are highly heterogeneous [1], [2] and various genetic factors and environmental determinants could play different roles in subgroups of the population. Linear regression has been commonly used in genetic studies to investigate the effects of genetic variants on the mean of a continuous phenotype. However, if we are interested in a complete view of genetic effects across the entire distribution of phenotypes or are interested in investigating genetic contribution to a sub-population(e.g., a high-risk population), quantile regression and expectile regression are great alternative choices [3], [4]. Quantile regression generalizes median regression and has been widely used in fields such as economics [5], medicine [6], [7] and environmental science [8]. While quantile regression has many good properties (e.g., being robust to distribution assumption and outliers), as pointed out by Newey and Powell [4], quantile regression has several limitations. First, quantile regression uses the check function with the absolute least error as loss function, which is not continuously differentiable and is computationally difficult for parameter estimation. Second, quantile regression is relatively inefficient for error distributions that are close to Gaussian or have low densities at the corresponding percentile. Third, it is challenging to estimate the density function values of quantile regression.
To address these issues, Newey and Powell [4] proposed expectile regression, which uses the sum of asymmetric residual squares as the loss function. Since the loss function is convex and differentiable, expectile regression has a computational advantage over quantile regression. Similar to quantile regression, expectile regression makes no assumption on error distribution (e.g., homoscedasticity) and can be used to study the entire distribution of the responses. Expectile regression can be viewed as a generalization of linear regression. A typical expectile regression assumes a linear relationship between the expectile and the covariates, which may not be suitable for genetic data analysis as genetic variants likely influence phenotypes in a complicated manner (e.g., through interactions) [23]. Simply considering linear and additive genetic effects can’t fully take this complexity into account.
In this paper, we integrate the idea of neural networks into expectile regression and develop an expectile neural network (ENN) method to model the complex relationship between genotypes and phenotypes. Neural networks based methods have been developed to solve biological problems [28], [29], [30], [31], [32], [33], [34]. While several methods have been developed to integrate neural networks into quantile regression [9], [10], [11], few studies have been focused on investigating non-linear expectile regressions, especially using neural networks. Compared to quantile regression neural networks (QRNN), ENN has several advantages. The empirical loss function in ENN is differentiable everywhere. Moreover, ENN can detect the heteroscedasticity in the data since ENN is more sensitive to extreme values than QRNN [12], [14], [15], [16], [17].
The rest of the paper is organized as follows: in Section 2, we review expectile regression and propose an ENN method. We then give an inequality that bounds the integrated squared error of an expectile function estimator in terms of risk functions. The proof of inequality is detailed in the Appendix. Simulations were conducted in Section 3 to evaluate the performance of the new method. In Section 4, we applied ENN to the SAGE data, studying genetic contribution to smoking quantity. We provide the summary and concluding remarks in Section 5.
2. Method
In this section, we briefly introduce expectile regression and then propose an expectile neural network. Suppose we have samples, , where and denote a –dimensional covariates and the response (e.g., smoking quantity) for the sample, respectively. In this paper, the covariates are primarily genetic variants, such as single nucleotide polymorphisms (SNPs), which are typically coded as the number of the minor frequent allele (e.g., AA=2, Aa=1, aa=0). The covariates can also include personal characteristics (e.g., gender) and environmental determinants.
2.1. Expectile regression
Given the data, linear regression is commonly used to model the relationship between the covariates and the mean response. However, if we want to explore a complete relationship between the covariates and the response (e.g., the genetic contribution to a high-risk population), an expectile regression can be used. To simplify the notation, we denote expectile regression as ER. The ER model for the −expectile can be expressed as,
| (1) |
where is the estimator of coefficients . The regression parameters can be obtained by minimizing an asymmetric loss function,
| (2) |
where is asymmetric squared loss with a convex form
| (3) |
For a model with a large , a penalty term can be added to the risk function to control the model complexity,
| (4) |
is a parameter between 0 and 1. By varying , we have different conditional distributions of the response, which can be used to study the relationship between genetic variants and the response in sub-populations (e.g., a high-risk population). When , the corresponding expectile regression degenerates to a standard linear regression. Therefore, expectile regression can also be viewed as a generalization of linear regression.
2.2. Expectile neural network
A typical expectile regression model focuses on linear relationships between covariates and responses. In reality, the underlying relationship could be non-linear and involve complicated interactions among covariates. In order to model complex relationships between covariates and responses, we integrate the idea of neural networks into expectile regression and propose an ENN method. A neural network is a universal approximator. A one-hidden-layer neural network with sufficient hidden units could approximate arbitrarily well any continuous functions [21]. In ENN, We don’t assume a particular functional form of covariates and use neural networks to approximate the underlying expectile regression function. ENN can be considered as a nonparametric expectile regression or a neural network with asymmetric loss function. We illustrate ENN with one hidden layer. The method can be easily extended to an expectile regression deep neural network with multiple layers.
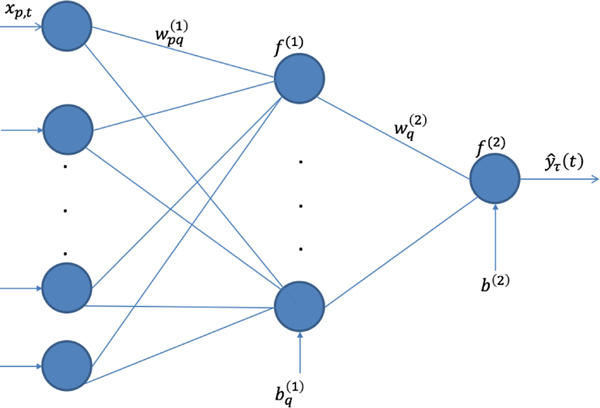
Given the covariates , we first build the hidden nodes ,
| (5) |
where is the number of nodes in the first hidden layer, denotes weights and denotes the bias; is the activation function for the hidden layer that can be a sigmoid function, a hyperbolic tangent function, or a rectified linear units(ReLU) function. Similar to hidden nodes in neural networks, the hidden nodes in ENN can learn complex features from covariates , which makes ENN capable of modeling non-linear and non-additive effects. Based on these hidden nodes, we can model the conditional -expectile, ,
| (6) |
where , , and are the link function (e.g., the identity function), weights, and bias in the output layer, respectively. To illustrate the structure of ENN, we provide a graphical representation of ENN in Figure 1.
Fig. 1.
A graphical representation of expectile neural network with one hidden layer
From equations (5) and (6), we can have the ENN model:
| (7) |
If we choose , and as identity function, ENN becomes linear regression. To estimate , , , , we minimize the empirical risk function
| (8) |
where
| (9) |
The model tends to be overfitted with the increasing number of covariates. To address the overfitting issue, a penalty is added to the risk function,
| (10) |
| (11) |
The loss function for ENN is differentiable everywhere, which provides the computation advantage. We can obtain the estimator of ENN by using gradient-based optimization algorithms, such as the quasi-Newton Broyden-Fletcher-Goldfarb-Shanno (BFGS) optimization algorithm. The BFGS algorithm is an iterative method commonly used to solve unconstrained non-linear optimization problems [22].
If we define the asymmetric absolute loss function (i.e., check function) as follows:
| (12) |
then the model becomes quantile regression neural networks (QRNN) [9]. QRNN has been implemented in the R package ‘qrnn’.
2.3. Theoretical result
Intuitively, if we fix , the upper and lower bound of −expectile is related to the risk function. We show that the upper bound and lower bound of error of −expectile are bounded by risk function . In ENN, −expectiles can be estimated by minimizing the asymmetric least squares (ALS) loss,
| (13) |
| (14) |
where is the distribution on and is some predictor. The following theorem describe the upper bound and lower bound of error of .
Theorem 1.
Let be the ALS loss function and be the distribution on We further assume that is the −expectile for fixed . Then, for an arbitrary neural network function , we have
| (15) |
| (16) |
where , .
Proof of this theorem can be found in the Appendix of the paper.
3. Simulation
Simulation studies were conducted to compare the performance of ENN, ER and QRNN under different settings. The genetic data used in the simulation is the real sequencing data from the 1000 Genomes Project, located on Chromosome 17 : 7344328 − 8344327 [18]. Totally 250 replicates were simulated for each simulation setting. In each replicate, we randomly selected a number of samples and SNPs from the 1000 Genomes Project. Given the genotypes, we further simulated the phenotype by using different linear/nonlinear functions or by assuming different types of interactions among SNPs or genes.
We divided the samples into training, validation, and testing sets with the ratio 3: 1: 1. ENN, ER and QRNN were applied to the training set to build models. While a variety of activation functions can be used in ENN, we choose ReLU due to its performance and computational advantage[ [13]]. Since the loss function of ENN is differentiable, we use the quasi-Newton BFGS optimization algorithm to estimate the parameters in ENN. We chose the starting points carefully to avoid the local minimum. To select a proper starting point, we generated a set of initial values from , ran the algorithm for a few steps, and chose the initial values achieving the smallest loss as the initial values. Based on the initial values, the quasi-Newton BFGS optimization algorithm was implemented to iteratively estimate the parameters until the convergence criterion was satisfied. The models built on the training set were then applied to the validation set to select the most parsimonious model with the optimal tuning parameter (i.e., ). To choose the best , we used the grid search with different values of 0,0.1,1,10, and 100. We used 1000 epochs to train the ENN model and chose 3–10 hidden units based on simulated scenarios. To reduce computation time, we did not use a large number of hidden units. The number of hidden units is chosen to ensure that the performance of the ENN model is reasonable well under different simulation scenarios. This final model was then evaluated on the testing set by using the mean squared error (MSE).
3.1. Simulation I - non-linear relationship
In the simulation I, we varied the relationships between genotypes and phenotypes. Specially, we considered the following four non-linear functions (i.e., a hyperbolic function, a mixed function, a quadratic function, and a cubic function) as true functions to simulate the relationship between genotypes and phenotypes. For the comparison purpose, we also included a linear function.
Linear function: ,
Hyperbolic function: ,
Mixed function: ,
Quadratic function: ,
Cubic function: ,
where is a vector of SNPs (coded as 0, 1 or 2), is the genetic effect generated from the uniform distribution of , and . Totally 250 replicates were simulated. For each replicate, we randomly chose 500 samples and 50 SNPs from the 1000 Genomes Project.
The results from the simulation I are summarized in Figure 2. ENN outperforms ER in terms of MSE under four different non-linear relationships, and has comparable performance with ER when the underlying relationship is linear. The pattern is consistent across different expectiles (i.e., 0.1, 0.25, 0.5, 0.75, and 0.9). While ENN outperforms ER for all four non-linear cases, ENN attains its best performance relative to ER when the underlying relationship is a high-order polynomial function (i.e., a cubic function).
Fig. 2.
Performance comparison between ENN and ER under various non-linear relationships between genotypes and phenotypes and different expectiles (i.e., 0.1, 0.25, 0.5, 0.75, and 0.9)
ENN: expectile neural network; ER: expectile regression; TR: training; TS: testing
3.2. Simulation II - interactions among SNPs
Increasing evidence from model organisms and human studies suggests that interactions among loci contribute to complex traits [24], [25], [26]. In simulation II, we considered three interaction models that mimic the underlying biological mechanisms. The three types of interactions include a two-way multiplicative interaction, a two-way threshold interaction, and a three-way interaction [2]. Similar to simulation I, we simulated 250 replicates for each type of interaction model. For each replicate, 500 samples and 50 SNPs were chosen from the 1000 Genomes Project. Among the 50 SNPs, we randomly selected a portion of SNPs and simulated different types of interactions among the selected SNPs. Specifically, to simulate two-way interactions, we randomly selected two sets of 10 SNPs and generated 100 cross-product terms. The two-way threshold interactions were simulated in a similar manner as the two-way multiplicative interactions but with threshold effects instead of multiplicative effects [2]. For three-way interactions, we randomly selected three sets of 5 SNPs and generated 125 three-way cross-product terms. Based on the simulated data, we compared MSEs of ENN and ER. For the comparison purpose, we also included a baseline model without any interaction.
The results of simulation II are summarized in Figure 3. Overall, ENN outperforms ER under all three interaction models due to its ability to take interactions into account. Among all interaction models, ENN attains its best performance as compared to ER when there are three-way interactions. ENN also has more advantage over ER at the upper and lower expectiles (e.g., 0.1 and 0.9). When there is no interaction, ENN has comparable performance with ER.
Fig. 3.
Performance comparison between ENN and ER for different types of interactions and different expectiles (i.e., 0.1, 0.25, 0.5, 0.75, and 0.9)
ENN: expectile neural network; ER: expectile regression; TR: training; TS: testing
3.3. Simulation III - interactions between genes
Gene-gene interactions could play an important role in the disease development process. Studying gene-gene interactions not only helps identify new genes but also elucidate the biological and biochemical pathways underpinning disease [23].
While a fully connected neural network can be built on all SNPs in the genes of interest, a neural network with a simpler architecture reflecting the underlying genetic data structure can be used to reduce the model’s complexity and improve the model’s performance. In this simulation, we illustrate the idea by modeling interactions between two genes with a non-fully connected architecture. In the non-fully connected architecture, the hidden units are only locally connected to SNPs in one gene (Figure 4). By using this simple architecture, we can reduce the number of parameters and build ”gene-specific” hidden units to capture abstract features of a specific gene. To evaluate the performance of such an architecture, we considered a two-way multiplicative interaction between two genes, and compared ENN with the non-fully connected architecture to ENN with the fully connected architecture.
Fig. 4.
An alternative architecture, a non-fully connected architecture, for gene-gene interaction analysis
Figure 5 summarizes the results from simulation III. The results show that ENN with the non-fully connected architecture attains lower MSE than ENN with the fully-connected architecture. As expected, the non-fully connected architecture requires fewer parameters and more reflects the underlying genetic data structure (i.e., genes are separate functional units), and therefore attains better performance than the fully-connected architecture.
Fig. 5.
Performance comparison between ENN with a fully connected architecture and ENN with a non-fully connected architecture for gene-gene interaction analysis
FUL: ENN with a fully connected architecture; NONFUL: ENN with a non-fully connected architecture;TR: training; TS: testing
3.4. Simulation IV - comparison between ENN and QRNN
QRNN is a method that integrates quantile regression with neural networks. In this simulation, we consider a similar asymmetric setting in the literature [36] and heteroscedastic setting [37]. Since both ENN and QRNN make no assumption on error distribution (e.g., homoscedasticity), they can be used to study the entire distribution of the responses (i.e., by varying ). In simulation IV, we compare both methods under the following settings:
Normal setting: ;
Asymmetric setting: ;
Heteroscedastic setting: .
The results of simulation IV are summarized in Figure 6. Overall, ENN achieves better performance than QRNN under the simulated settings. ENN has advantages over QRNN under the asymmetric and heteroscedastic settings [4] due to its efficiency. QRNN is also relatively inefficient for error distributions that are close to Gaussian or have low densities at the corresponding percentiles [4]. Therefore, ENN outperforms QRNN for error distributions such as the Gaussian distribution.
Fig. 6.
Performance comparison between ENN and QRNN under asymmetric, normal and heteroscedastic settings
ENN: expectile neural network; TR: training; TS: testing
4. Real data applications
Tobacco use is the leading cause of preventable disease and death in the United States. In 2019, nearly 34 million adults smoked cigarettes. More than 16 million Americans have a disease caused by smoking. Nearly 300 billion a year are spent in direct medical care for adults or in lost productivity due to premature death and exposure to secondhand smoke in the United States (https://www.cdc.gov/tobacco/data_statistics/index.htm). This burden is largely driven by the nicotine dependence process that is engaged with increasing occasions of smoking and other tobacco product use. The advances of genotyping technologies provide a comprehensive assessment of DNA variations, which enables us to systematically study the role of genetic variants and their interactions in nicotine dependence.
In this section, we applied both ENN and ER to a large-scale genetic dataset, studying genetic effects and gene-gene interaction effects on nicotine dependence in sub-populations. We varied values (i.e., 0.1, 0.25, 0.5, 0.75, 0.9) and compared ENN and ER based on MSE.
4.1. The relationship between candidate SNPs with smoking quantities
We applied both ENN and ER to the genetic data from the Study of Addiction: Genetics and Environment(SAGE). The participants of the SAGE are selected from three large and complementary studies: the Family Study of Cocaine Dependence(FSCD), the Collaborative Study on the Genetics of Alcoholism(COGA), and the Collaborative Genetic Study of Nicotine Dependence(COGEND). In this application, we selected 155 SNPs, which were previously shown to have a potential role in nicotine dependence. The detailed information regarding the 155 SNPs, including the imputation process, can be found in our previous paper [35]. After quality control, 149 SNPs remained for the analysis. There are a total of 3897 samples in the SAGE data from different ethnic groups. We only included 3888 Caucasian and African American samples due to the small sample size of other ethnic groups. By using ENN and ER, we built models on 149 SNPs and 3 covariates (i.e., sex, age, and race). The response of interest in the model is the smoking quantities, which is measured by the largest number of cigarettes smoked in 24 hours. We divided the whole sample into the training, validation and test samples in the ratio of 3:1:1 to build the models, select the turning parameter, and evaluate the models, respectively.
Table 1 summarizes MSE of the models built by ENN and ER for five expectile levels (i.e., , 0.25, 0.5, 0.75, and 0.9). Table 1 shows that ENN outperforms ER, indicating the possibility of non-linear or non-additive effects among candidate SNPs and covariates. To provide a comprehensive view of the conditional distribution of smoking quantity, we ordered the expectiles estimated based on ENN from lowest to highest and plotted their values for all five expectile levels. Figure 7 shows that the distributions of estimated expectiles are different across five expectile levels. When , ENN models the mean response, in which the estimated expectiles are similar for all individuals. Nonetheless, for high expectile levels (e.g., ), the estimated expectiles vary among individuals and high-ranked individuals have much higher expectiles than low-ranked individuals.
TABLE 1.
The accuracy performance of two models built by ENN and ER based on 149 candidate SNPs and 3 covariates
| ENN | ER | |||
|---|---|---|---|---|
|
|
|
|||
| Train | Test | Train | Test | |
| 0.1 | 409.612 | 678.331 | 504.215 | 694.809 |
| 0.25 | 346.118 | 579.164 | 394.836 | 588.759 |
| 0.5 | 358.783 | 502.752 | 342.144 | 535.925 |
| 0.75 | 344.399 | 604.969 | 421.955 | 613.676 |
| 0.9 | 570.994 | 809.733 | 699.654 | 882.781 |
Fig. 7.
The conditional distribution of smoking quantity for five expectile levels (i.e., 0.1, 0.25, 0.5, 0.75, and 0.9)
4.2. Gene-gene interactions between the CHRN A5-CHRN A3-CHRN B4 gene cluster
Previous evidence suggested potential interactions between the neuronal nicotinic acetylcholine receptors (nAChRs) subunit genes [19]. In the second real data application, we focused on the CHRNA5-CHRNA3-CHRNB4 gene cluster, and evaluated potential interactions by using ENN. We consider three pairwise interactions between CHRNA5 and CHRNA3, CHRNA5 and CHRNB4, CHRNA3 and CHRNB4. The phenotype of interest in this analysis is the number of cigarettes smoked per day (CPD), which has been popularly used in the genetic study of nicotine dependence.
Tables 2–4 summarize MSE values of the interaction models built by using a fully connected ENN and a non-fully connected ENN for five expectile levels. The hidden units in the non-fully connected ENN are only locally connected to SNPs in one gene. Such a neural network structure reflects the underlying genetic data structure and reduces the model complexity. Benefiting from its simple network structure, the non-fully connected ENN outperforms the fully connected ENN in terms of MSE for all three interaction analyses. To graphically view the conditional distribution of CPD, we ranked the expectiles estimated from ENN and plotted the values against the estimated expectiles (Figures 8–10). Overall, the estimated expectiles tend to be similar when (i.e., mean), while they are quite different for high expectile levels (e.g., ). This suggests that the gene-gene interactions may play a more important role in models with high expectiles than the mean model.
TABLE 2.
Evaluating a pairwise interaction between CHRNA5 and CHRNA3 by using a fully connected ENN and a non-fully connected ENN
| Non-fully connected | Fully connected | |||
|---|---|---|---|---|
|
|
|
|||
| Train | Test | Train | Test | |
| 0.1 | 1.111 | 2.034 | 1.003 | 2.044 |
| 0.25 | 0.924 | 1.754 | 0.919 | 1.767 |
| 0.5 | 0.894 | 1.270 | 0.874 | 1.289 |
| 0.75 | 1.037 | 1.126 | 1.019 | 1.176 |
| 0.9 | 1.786 | 1.915 | 1.769 | 2.012 |
TABLE 4.
Evaluating a pairwise interaction between CHRNA3 and CHRNB4 by using a fully connected ENN and a non-fully connected ENN
| Non-fully connected | Fully connected | |||
|---|---|---|---|---|
|
|
|
|||
| Train | Test | Train | Test | |
| 0.1 | 1.137 | 1.963 | 1.080 | 1.966 |
| 0.25 | 0.980 | 1.701 | 0.966 | 1.703 |
| 0.5 | 0.885 | 1.276 | 0.867 | 1.324 |
| 0.75 | 1.051 | 1.150 | 1.049 | 1.163 |
| 0.9 | 1.686 | 1.770 | 1.666 | 1.918 |
Fig. 8.
The conditional distribution of CPD considering the interaction between CHRNA5 and CHRNA3
Fig. 10.
The conditional distribution of CPD considering the interaction between CHRNB4 and CHRNA3
Our finding is consistent with previous literature, which found significant interactions among variants in CHRNA5, CHRNA3, and CHRNB4 [19]. These three genes are from the CHRNA5-CHRNA3-CHRNB4 cluster, which are well-known for their role in nicotine dependence. They are also important neuronal nicotinic acetylcholine receptors (nAChRs) subunit genes [38]. nAChRs activate the release of dopamine, playing an essential role in the dopaminergic reward system and the development of nicotine dependence.
5. Summary and discussion
In this paper, we develop an ENN method, which inherits advantages from both neural networks and expectile regression. Using the hierarchical structure from neural networks, ENN can learn complex and abstract features from genotypes, making it suitable for modeling the complex relationship between genotypes and phenotype. Similar to ER, ENN can also explore the conditional distribution and provide a comprehensive view of the genotype-phenotype relationship.
Through simulations and real data applications, we demonstrate that ENN outperforms ER when there are non-additive and non-linear effects. Evidence also suggests that ENN has more advantages than ER when the model involves high-order interaction effects or non-linear effects. This may suggest ENN has improved performance when the underlying genotype-phenotype relationship becomes more complicated. The real data analyses show that genetic effects can vary among different expertiles. Compared to the classical linear regression, ENN provides us more information about the genotype-phenotype relationship via the conditional distributions.
While regularization has been incorporated into ENN to avoid overfitting, ENN can still be subject to overfitting when the number of SNPs becomes extremely large (e.g., one million). To deal with such a large number of SNPs, we can model the overall genetic effect as a random effect in ENN, which is an interesting topic for future work. In this paper, we focus on introducing the ENN model and providing an inequality that bounds the integrated squared error of an expectile function estimator. Statistical properties of ENN (e.g., the rate of convergence) are also important topics worth further investigation in the future.
Supplementary Material
Fig. 9.
The conditional distribution of CPD considering the interaction between CHRNA5 and CHRNB4
TABLE 3.
Evaluating a pairwise interaction between CHRNA5 and CHRNB4 by using a fully connected ENN and a non-fully connected ENN
| Non-fully connected | Fully connected | |||
|---|---|---|---|---|
|
|
|
|||
| Train | Test | Train | Test | |
| 0.1 | 1.090 | 1.991 | 1.064 | 2.006 |
| 0.25 | 0.979 | 1.693 | 0.919 | 1.737 |
| 0.5 | 0.910 | 1.278 | 0.899 | 1.283 |
| 0.75 | 1.055 | 1.147 | 1.024 | 1.183 |
| 0.9 | 1.753 | 1.887 | 1.657 | 1.981 |
Acknowledgments
This work was supported by NIH 1R01DA043501-01 and NIH 1R01LM012848-01. Funding support for the Study of Addiction: Genetics and Environment was provided through the NIH Genes, Environment and Health Initiative [GEI] (U01 HG004422). The SAGE datasets used for the analyses were obtained from dbGaP at https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?studyid=phs000092.v1.p1 through dbGaP accession number phs000092.v1.p1.
Contributor Information
Jinghang Lin, Department of Statistics and Probability, Michigan State University, Michigan U.S.A..
Xiaoran Tong, Department of Epidemiology and Biostatistics, Michigan State University, Michigan U.S.A..
Chenxi Li, Department of Epidemiology and Biostatistics, Michigan State University, Michigan U.S.A..
Qing Lu, Department of Biostatistics, University of Florida, Florida, U.S.A..
References
- [1].McClellan J, & King MC (2010). Genetic heterogeneity in human disease. In Cell (Vol. 141, Issue 2). 10.1016/j.cell.2010.03.032. [DOI] [PubMed] [Google Scholar]
- [2].Marchini J, Donnelly P, & Cardon LR (2005). Genome-wide strategies for detecting multiple loci that influence complex diseases. Nature Genetics, 37(4). 10.1038/ng1537. [DOI] [PubMed] [Google Scholar]
- [3].Koenker R,& Bassett G. (1978). Regression Quantiles. Econometrica, 46(1). 10.2307/1913643. [DOI] [Google Scholar]
- [4].Newey WK, & Powell JL (1987). Asymmetric Least Squares Estimation and Testing. Econometrica, 55(4). 10.2307/1911031. [DOI] [Google Scholar]
- [5].Buchinsky M. (1995). Quantile regression, Box-Cox transformation model, and the U.S. wage structure, 1963–1987. Journal of Econometrics, 65(1). 10.1016/0304-4076(94)01599-U. [DOI] [Google Scholar]
- [6].Crowley J, & Hu M. (1977). Covariance analysis of heart transplant survival data. Journal of the American Statistical Association, 72(357). 10.1080/01621459.1977.10479903. [DOI] [Google Scholar]
- [7].Lipsitz SR, Fitzmaurice GM, Molenberghs G, & Zhao LP (1997). Quantile regression methods for longitudinal data with drop-outs: Application to CD4 cell counts of patients infected with the human immunodeficiency virus. Journal of the Royal Statistical Society. Series C: Applied Statistics, 46(4). 10.1111/1467-9876.00084. [DOI] [Google Scholar]
- [8].Pandey GR, & Nguyen VTV (1999). A comparative study of regression based methods in regional flood frequency analysis. Journal of Hydrology, 225(1–2). 10.1016/S00221694(99)00135-3. [DOI] [Google Scholar]
- [9].Cannon AJ (2018). Non-crossing nonlinear regression quantiles by monotone composite quantile regression neural network, with application to rainfall extremes. Stochastic Environmental Research and Risk Assessment, 32(11). 10.1007/s00477-018-1573-6. [DOI] [Google Scholar]
- [10].Cannon AJ (2011). Quantile regression neural networks: Implementation in R and application to precipitation downscaling. Computers and Geosciences, 37(9). 10.1016/j.cageo.2010.07.005. [DOI] [Google Scholar]
- [11].Kim M, & Lee S. (2016). Nonlinear expectile regression with application to Value-at-Risk and expected shortfall estimation. Computational Statistics and Data Analysis, 94. 10.1016/j.csda.2015.07.011. [DOI] [Google Scholar]
- [12].Jiang C, Jiang M, Xu Q, & Huang X. (2017). Expectile regression neural network model with applications. Neurocomputing, 247. 10.1016/j.neucom.2017.03.040. [DOI] [Google Scholar]
- [13].Goodfellow Ian, Bengio Yoshua, A. C. (2016). Deep Learning - Ian Goodfellow, Yoshua Bengio, Aaron Courville - Google Books. In MIT Press. [Google Scholar]
- [14].Liao L, Park C, & Choi H. (2019). Penalized expectile regression: an alternative to penalized quantile regression. Annals of the Institute of Statistical Mathematics, 71(2). 10.1007/s10463-018-0645-1. [DOI] [Google Scholar]
- [15].Waltrup LS, Sobotka F, Kneib T, & Kauermann G. (2015). Expectile and quantile regression—David and Goliath? Statistical Modelling, 15(5). 10.1177/1471082X14561155. [DOI] [Google Scholar]
- [16].Kim M, & Lee S. (2016). Nonlinear expectile regression with application to Value-at-Risk and expected shortfall estimation. Computational Statistics and Data Analysis, 94. 10.1016/j.csda.2015.07.011. [DOI] [Google Scholar]
- [17].Yao Q, & Tong H. (1996). Asymmetric least squares regression estimation: A nonparametric approach. Journal of Nonparametric Statistics, 6(2–3). 10.1080/10485259608832675. [DOI] [Google Scholar]
- [18].Altshuler DL, Durbin RM, Abecasis GR, Bentley DR, Chakravarti A, Clark AG, Collins FS, De La Vega FM, Donnelly P, Egholm M, Flicek P, Gabriel SB, Gibbs RA, Knoppers BM, Lander ES, Lehrach H, Mardis ER, McVean GA, Nickerson DA, . . . Peterson JL (2010). A map of human genome variation from population-scale sequencing. Nature, 467(7319). 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Li MD, Xu Q, Lou XY, Payne TJ, Niu T, & Ma JZ (2010). Association and interaction analysis of variants in CHRNA5/CHRNA3/CHRNB4 gene cluster with nicotine dependence in African and European Americans. American Journal of Medical Genetics, Part B: Neuropsychiatric Genetics, 153(3). 10.1002/ajmg.b.31043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Farooq M, & Steinwart I. (2019). Learning rates for kernel-based expectile regression. Machine Learning, 108(2). 10.1007/s10994-018-5762-9. [DOI] [Google Scholar]
- [21].Hornik K. (1991). Approximation capabilities of multilayer feedforward networks. Neural Networks, 4(2). 10.1016/0893-6080(91)90009-T. [DOI] [Google Scholar]
- [22].Chambers LG, & Fletcher R. (2001). Practical Methods of Optimization. The Mathematical Gazette, 85(504). 10.2307/3621816. [DOI] [Google Scholar]
- [23].Cordell HJ (2009). Detecting gene-gene interactions that underlie human diseases. In Nature Reviews Genetics (Vol. 10, Issue 6). 10.1038/nrg2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Mackay TFC (2001). Quantitative trait loci in Drosophila. In Nature Reviews Genetics (Vol. 2, Issue 1). 10.1038/35047544. [DOI] [PubMed] [Google Scholar]
- [25].Routman EJ, & Cheverud JM (1997). Gene effects on a quantitative trait: Two-locus epistatic effects measured at microsatellite markers and at estimated QTL. Evolution, 51(5). 10.1111/j.1558-5646.1997.tb01488.x. [DOI] [PubMed] [Google Scholar]
- [26].Zerba KE, Ferrell RE, & Sing CF (2000). Complex adaptive systems and human health: The influence of common genotypes of the apolipoprotein E (ApoE) gene polymorphism and age on the relational order within a field of lipid metabolism traits. Human Genetics, 107(5). 10.1007/s004390000394. [DOI] [PubMed] [Google Scholar]
- [27].Thorgeirsson TE, Gudbjartsson DF, Surakka I, Vink JM, Amin N, Geller F, ... & Stefansson K. (2010). Sequence variants at CHRNB3–CHRNA6 and CYP2A6 affect smoking behavior. Nature genetics, 42(5), 448–453 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Wang L, You Z-H, Li J-Q, & Huang Y-A (2020). IMS-CDA: Prediction of CircRNA-Disease Associations From the Integration of Multisource Similarity Information With Deep Stacked Autoencoder Model. IEEE Transactions on Cybernetics. 10.1109/tcyb.2020.3022852. [DOI] [PubMed]
- [29].Li HY, You ZH, Wang L, Yan X, & Li ZW (2021). DF-MDA: An effective diffusion-based computational model for predicting miRNA-disease association. Molecular Therapy, 29(4). 10.1016/j.ymthe.2021.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Su X, You Z, Wang L, Hu L, Wong L, Ji B, & Zhao B. (2021). SANE: A sequence combined attentive network embedding model for COVID-19 drug repositioning. Applied Soft Computing, 111. 10.1016/j.asoc.2021.107831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Zhang Q, Wang S, Chen Z, He Y, Liu Q, & Huang D-S (2021). Locating transcription factor binding sites by fully convolutional neural network. Briefings in Bioinformatics, 22(5). 10.1093/bib/bbaa435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].He Y, Shen Z, Zhang Q, Wang S, & Huang DS (2021). A survey on deep learning in DNA/RNA motif mining. Briefings in Bioinformatics, 22(4). 10.1093/bib/bbaa229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Wang L, You Z-H, Huang D-S, & Li J-Q (2021). MGRCDA: Metagraph Recommendation Method for Predicting CircRNA-Disease Association. IEEE Transactions on Cybernetics. 10.1109/tcyb.2021.3090756. [DOI] [PubMed]
- [34].Wang L, You ZH, Huang YA, Huang DS, & Chan KCC (2020). An efficient approach based on multisources information to predict circRNA-disease associations using deep convolutional neural network. Bioinformatics, 36(13). 10.1093/bioinformatics/btz825. [DOI] [PubMed] [Google Scholar]
- [35].Li M, Ye C, Fu W, Elston RC, & Lu Q. (2011). Detecting genetic interactions for quantitative traits with U-statistics. Genetic Epidemiology, 35(6), 457–468. 10.1002/gepi.20594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Yang Y,& Zou H. (2015). Nonparametric multiple expectile regression via ER-Boost. In Journal of Statistical Computation and Simulation (Vol. 85, Issue 7, pp. 1442–1458). 10.1080/00949655.2013.876024 [DOI] [Google Scholar]
- [37].Wang L, Wu Y, & Li R. (2012). Quantile regression for analyzing heterogeneity in ultra-high dimension. Journal of the American Statistical Association, 107(497), 214–222. 10.1080/01621459.2012.656014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Zhang X, Lan T, Wang T, Xue W, Tong X, Ma T, Liu G, Lu Q. (2019). Considering genetic heterogeneity in the association analysis finds genes associated with nicotine dependence. In Frontiers in Genetics (Vol. 10, Issue MAY). 10.3389/fgene.2019.00448. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.