Finding Excited-State Minimum Energy Crossing Points on a Budget: Non-Self-Consistent Tight-Binding Methods

Abstract

The automated exploration and identification of minimum energy conical intersections (MECIs) is a valuable computational strategy for the study of photochemical processes. Due to the immense computational effort involved in calculating non-adiabatic derivative coupling vectors, simplifications have been introduced focusing instead on minimum energy crossing points (MECPs), where promising attempts were made with semiempirical quantum mechanical methods. A simplified treatment for describing crossing points between almost arbitrary diabatic states based on a non-self-consistent extended tight-binding method, GFN0-xTB, is presented. Involving only a single diagonalization of the Hamiltonian, the method can provide energies and gradients for multiple electronic states, which can be used in a derivative coupling-vector-free scheme to calculate MECPs. By comparison with high-lying MECIs of benchmark systems, it is demonstrated that the identified geometries are good starting points for further MECI refinement with ab initio methods.

Photochemical processes have become an increasingly important way to steer molecular reactions and motions^1,2 and are routinely aided by computational studies. Describing the associated photoreactions through computational chemistry requires the treatment of non-adiabatic couplings to describe non-radiative transitions between the different electronic states.^3,4 Representative geometries for the corresponding non-adiabatic transitions are those structures of minimum energy that are located along the seam between energetically close potential energy surfaces (PES) of the electronic states, i.e., the minimum energy crossing point (MECP) and minimum energy conical intersection (MECI) geometries. These geometries play a crucial role in transitions between different electronic states and fulfill a similar purpose for photochemical processes as transition state geometries in a ground state reaction.^5,6

In spin-allowed photoreactions, many local MECIs are often accessible from the so-called Franck–Condon (FC) region. Identifying these MECI geometries, or at least plausible candidates, is essential for the computational modeling of excited-state photoreactions. The plausible candidates are MECPs between diabatic states, which are typically close to a true MECI between adiabatic states.⁷ Since no derivative coupling vectors are required for describing the MECP, the computational complexity is greatly reduced compared to MECI optimizations. Approaches to explore the associated MECI space by locating MECPs have been presented by the groups of Mitrić⁸ and Martínez.⁴ We recently presented a metadynamics-based MECP screening workflow leveraging the efficient semiempirical extended tight-binding methods (xTB).^9,10 A surprisingly good performance was observed for finding MECPs in combination with the GFN2-xTB method.^11,12 Using a gap-dependent potential, the MECPs between the lowest low-spin and high-spin potential energy surfaces were identified and shown to closely resemble S₁/S₀ MECIs obtained at a higher level of theory. However, a limitation is the use of a self-consistent field (SCF) treatment that can, in principle, only produce the ground state within a given spin multiplicity. Consequently, previous studies were limited to identifying MECPs resembling the S₁/S₀ MECIs or the T₁/S₀ MECPs. However, crossings between higher-lying electronic states are essential in many photochemical processes. Typical examples are T₂/T₁ and S₂/S₁ conical intersections^4,6,13,14 as well as T₁/S₁ MECPs, which play an important role in the so-called thermally activated delayed fluorescence.¹⁵ Identifying such points is impossible with the previously described approach,⁹ since the SCF solutions will collapse back to the respective ground state.

In this work, we therefore discuss an extension of the previous scheme that allows the quick calculation of higher-lying states and their associated MECPs, made possible by employing a non-self-consistent xTB treatment.^12,16 The proposed method is characterized by requiring only a single diagonalization of the Hamiltonian to determine the necessary orbitals. The desired states are then approximated by a single determinant generated by different occupation vectors that also provide access to non-Aufbau occupations. A modified version of Fermi smearing allows smearing of electrons and occupational holes, which provides robustness during optimization and dynamics simulations. Herein, the non-self-consistency provides a typical speed-up of 1–2 orders of magnitude compared to the already inexpensive GFN2-xTB method while providing nearly identical MECP geometries.

As in previous work, we are pursuing a “derivative coupling vector-free” treatment^9,17−21 that provides MECPs of two (or more) diabatic multidimensional PESs. These points can then serve as approximations to MECIs between adiabatic states that are obtained from multideterminant wave functions.⁷ The idea here is to locate the MECP on an artificial seam PES given by

1

combining two core components E_avg and a penalty function V_gap. For the considered n electronic states of the molecule, the seam PES is based on the arithmetic mean

2

This energy average is combined with a pairwise penalty

3

minimizing the energy gap |ΔE_ij| between two diabatic states i and j. The latter potential confines the overall energy to a lower dimensional hyperline where the states are degenerate. Inclusion of E_avg then helps to locate the minima on this hyperline that correspond to the MECPs.⁵ A key feature of this procedure, and the penalty functions in particular, is their ability to locate transition state analogues, i.e., the MECP, involving discontinuous first and second derivatives in the adiabatic framework.²² In eq 3, a total of three empirical parameters, σ, k, and α, are chosen to converge the energy gap to zero near the seam region while providing a linearly growing energy bias far away from it.^9,18 Detailed adjustment of the empirical parameters in the penalty potential may be required for some systems, but manually selected values of σ = 10.0, α = 0.005, and k = 0.25 often work well and were used throughout this study. While the σ and α parameters were chosen in accordance with earlier studies,^9,18k was selected to provide the linearly growing bias far away from the potential minimum. Selecting too small values for k will result in the formation of artificial maxima around the MECP. System dependent adjustment of V_gap should be done mainly through the interaction strength σ. The combination involving eq 1 is robust and may generally be extended, e.g., by metadynamics-based sampling techniques^10,23,24 or global optimization procedures,^25,26 to explore a larger portion of the crossing seam hyperplane.

One limiting factor for the MECP calculation is the ability of theoretical models to simultaneously describe the different electronic states near the intersection. While typically associated with costly high level ab initio calculations,^3,27 application of much less costly semiempirical approaches has proved to perform well.²⁸⁻³¹ Within the derivative coupling vector-free treatment, large reduction of the computational cost is achieved in combination with semiempirical methods of the GFNn-xTB level,^11,12,32 which provide reasonable estimates of S₀/S₁ MECIs via the S₀/T₁ MECP.^9,33 However, as discussed previously, only lowest-energy solutions for a priori specified differences in the net α and β occupation can be enforced in this framework. In consequence, states that involve higher energetic electronic states, or simply holes in the net occupations, are inaccessible within the GFNn-xTB framework. To remedy this problem, we make use of a less well-known non-self-consistent variant of GFNn-xTB methods, entitled GFN0-xTB.^12,16 The energy in GFN0-xTB is defined by

4

where E_rep, E_disp^D4, E_SRB, and E_EEQ are classical repulsion, dispersion, short-range, and charge equilibrium electrostatics terms, respectively.^12,16 The electronic energy within this method is given solely by the extended Hückel-type (EHT) energy

5

where P_μν is the valence electron density matrix in the non-orthogonal atomic orbital (AO) basis and H_νμ^EHT is the extended Hückel theory (EHT) type matrix. It is the single-particle treatment, reflected in eq 5, that enables an approximate treatment of higher-lying electronic states in the proposed procedure: For a given set of atomic coordinates, the Roothaan–Hall-type equations^34,35H^EHTC = SCϵ only need to be solved once, due to the purely one-electron “extended Hückel-type” Hamiltonian. Hence, the Hamiltonian matrix is independent of the electron distribution and, using other occupations differing from the Aufbau occupation, gives direct access to excited states in the one-electron approximation. Consequently, one only needs a single matrix diagonalization to calculate GFN0-xTB energies for multiple diabatic states from P_μν = ∑_i n_iC_μiC_iν by modifying the orbital occupation n_i^′ = n_iα + n_iβ^′ accordingly (see below) and employing it in eq 5. This treatment drastically differs from the SCF procedure in other xTB variants^11,32 and enables the computation of energies and gradients with arbitrary orbital occupation. Furthermore, since the diagonalization of the n × n Hamiltonian matrix, with formal scaling of , is the cost-determining step of the xTB calculation, significant savings of computation time are achieved by replacing the SCF with a non-self-consistent treatment. For the determination of MECPs, the use of GFN0-xTB will accelerate calculations by an additional factor since the multiple states can be obtained from the same diagonalization of the EHT matrix by simply changing the occupation.

As mentioned earlier, an important aspect is the treatment of spin multiplicities at our chosen level of theory. All GFNn-xTB variants have no spin-discriminating terms in the Hamiltonian and, furthermore, use a spin-restricted formalism.^12,32 Hence, the respective α and β orbitals have identical orbital energies and spatial parts and it is impossible to distinguish open-shell states with identical orbital occupation but different multiplicity. To mimic the simulation of multideterminant states via a single-determinant, orbitals may have non-integer, i.e., fractional occupation numbers (FON). We use Fermi smearing which allows us to handle near degeneracies.^11,36 For our current application, a modified FON n_iσ^′ for the ith spin-molecular orbital ψ_iσ (σ = {α, β}) is given by

6

7

where k_b is Boltzmann’s constant and ϵ_i is the orbital energy of ψ_i. The key novelty here is that the FON allows smearing of configurations that have holes in the net reference occupation σ_i^ref. These holes can be added separately to the occupation vector of α or β spins to provide non-Aufbau occupations. The modified Fermi smearing in eq 7 allows higher energetic MOs (placed above the predefined holes) to partially smear “back” into the lower-lying hole orbitals. This formulation enhances the numerical stability of the overall workflow during optimization and molecular dynamics runs. As usual, the Fermi level ϵ_F in the respective α or β orbital space is initially obtained as the average and then adjusted to match the total number of α and β electrons. The electronic temperature T_el serves as a simple adjustment parameter to steer the amount of smeared occupations and can often be set to a rather high value. Note that no electronic entropy term −T_elS_el is calculated from the FON for this specialized application of GFN0-xTB, which in contrast to regular xTB schemes ensures that eq 3 approaches zero close to the MECP.^9,12 In summary, the procedure employs GFN0-xTB (eq 4) to calculate energies and gradients for multiple diabatic states. The latter are obtained from a single diagonalization of the Hamiltonian matrix using different orbital occupations. If employed in molecular geometry optimization via eq 1, one obtains the corresponding MECPs. As indicated by the GFN abbreviation, which stands for geometries, frequencies, and non-covalent interactions, the goal here is not an exact description of the electronic structure but rather the qualitatively correct identification of low energy molecular geometries at the crossing seam. GFN0-xTB can therefore serve as a low level in multilevel schemes, enabling rapid testing of different net orbital occupations or for providing reference points for further refinement.

To illustrate the capabilities of the introduced scheme, azobenzene provides a helpful benchmarking example. From theoretical studies, mainly, the MECIs and MECPs of azobenzene are known to be dependent on the CNNC dihedral twist of the molecule, and the S₀/T₁ MECP and S₀/S₁ MECI, in particular, are located at around 90°.³⁷⁻³⁹ Performing a scan along the dihedral coordinate reveals the existence of such points at the semiempirical GFN0-xTB level, as shown in Figure 1.

Figure 1.

(a) Scan along the C—N=N—C torsional coordinate of azobenzene at the GFN0-xTB level (T_el = 3000 K). The scan was conducted in 1° steps, and each point was relaxed to the ground state (GS) S₀ geometry while keeping the dihedral angle constrained. Also shown are the two lowest open-shell (OS) energies and the doubly excited closed-shell (CS) energies. (b) Reference single-point energies at the hhTDA-BHLYP-D3(BJ)/def2-SV(P) level. The plotted energies (in eV) for different electronic states correspond to a calculation at the given GFN0-xTB S₀ structure. (c) The employed reference occupations for the GFN0-xTB calculation. Note that a clear state classification is not possible due to the spin-restricted treatment (see text). (d) Canonical HOMO–1, HOMO, and LUMO orbitals of azobenzene at C—N=N—C angles of 90° and 180°.

The four different electronic states shown in Figure 1a correspond to the closed-shell ground state (GS) configuration, the lowest open-shell OS1 configuration, and two different configurations that could represent a possible S₂ state: one corresponds to a HOMO to LUMO (n²π^*2) double excitation, while the other is a HOMO–1 to LUMO (ππ^*) open-shell configuration. The latter could either resemble a S₂ or T₂ state, since GFN0-xTB has no spin-discriminating terms in the Hamiltonian.¹² The OS1 and GS configurations are expected to closely resemble the S₁ and S₀ states near the GS minimum. Any MECP of interest between these configurations can nicely be identified from the scan, in particular a potential tristate S₀/S₁ (or T₁)/S₂ intersection at a CNNC torsion of about 90° (and, symmetrically, 270°). Apart from an overall underestimation of relative energies at the semiempirical level, the reference calculation at the hhTDA-BHLYP-D3(BJ)/def2-SV(P) level^38,40 in Figure 1b reveals a good correspondence of the adiabatic states to the configurations obtained via GFN0-xTB.

As the energies were obtained as single points at the GFN0-xTB geometries, there are no MECIs or proper state crossings observed for the adiabatic states from hhTDA. Potential MECI candidates at the hhTDA level are, however, clearly visible: the S₀/S₁ intersection at CNNC 90° as well as intersections of the ππ^* and n²π^*2 states at CNNC dihedral angles of approximately 40° and 140°. The modified GFN0-xTB scheme is clearly capable of qualitatively capturing the overall characteristics of the non-adiabatic potential energy surfaces for azobenzene, which strongly indicates its fitness for screening applications. The latter point is further strengthened by the overall computational cost: Each of the 360 single-point calculations at the hhTDA level in Figure 1b had an average wall-time of approximately 25 s utilizing the GPU-accelerated TeraChem program package^41,42 using 8 cores of an Intel Core i7-11700 (2.50 GHz) CPU together with a NVIDIA GeForce RTX 3070 GPU. In contrast, the entire relaxed scan at the GFN0-xTB level takes about 8 s on a laptop using 4 cores of a 2.3 GHz Intel Core i7-11800H CPU.

The data presented in Figure 1a is, to the best of our knowledge, the very first calculation of any extended tight-binding method for higher electronic states involving occupational holes. We test the applicability to describe different electronic states in the proposed one-electron approach using S₀/S₁ intersections from the literature. We refer here to two benchmarks: a set of benzene MECIs calculated at the FOMO-CASCI(6,5)/6-31G level^4,43−46 and a set of small organic molecule MECIs²⁸ calculated at the hhTDA-BHLYP-D3(BJ)/def2-SV(P) level.^9,38,40 While the latter was put forward as a general test set for typical conical intersection geometries, benzene offers an archetypal example of a small molecule with a multitude of MECIs. Comparisons between the GFN0-xTB optimized MECPs and the reference MECIs are shown in Figure 2 where, as a simple but insightful metric for comparison, the root-mean-square deviation (RMSD) of Cartesian coordinates⁴⁷ is given for each of the benchmark cases.

Figure 2.

Overlay of GS/OS1 crossing point geometries calculated at the semiempirical GFN0-xTB level (solid color) and (a) reference FOMO-CASCI(6,5)/6-31G S₀/S₁ MECI geometries for the benzene molecule (transparent blue) taken from ref (4) or (b) reference hhTDA-BHLYP-D3(BJ)/def2-SV(P) S₀/S₁ MECI geometries for a set of organic molecules (transparent blue) from refs (9) and (28). Structural Cartesian RMSD values are provided below each structure.

An in-depth discussion for these systems can be found in previous work⁹ and the citing literature.^4,28,48 To summarize the current findings, GFN0-xTB shows virtually identical characteristics as the related self-consistent GFN2-xTB method in the description of GS/OS1 MECPs, which clearly resemble the S₀/S₁ MECI between adiabatic states. RMSDs at the GFN0-xTB level compared to the reference structures are marginally worse than those with GFN2-xTB, as would be expected for this more approximate non-self-consistent method. As observed before, MECP structures at the GFNn-xTB level often lack pyramidalization features for non-polar systems compared to the reference MECIs, due to which some details cannot be distinguished, for example, the two styrene CIs.⁹ This finding can mostly be attributed to missing (Fock) exchange in the semiempirical potential.⁴⁸ The “worst case” molecule in the test set, stilbene, suffers from the same missing pyramidalization feature and additionally differs in the torsional conformation of the phenyl groups, which yields a high RMSD despite the qualitative similarity between the MECP and the reference. Nevertheless, the agreement between GFN0-xTB and the reference geometries is overall quite impressive, particularly considering the extremely low computational cost of the method.

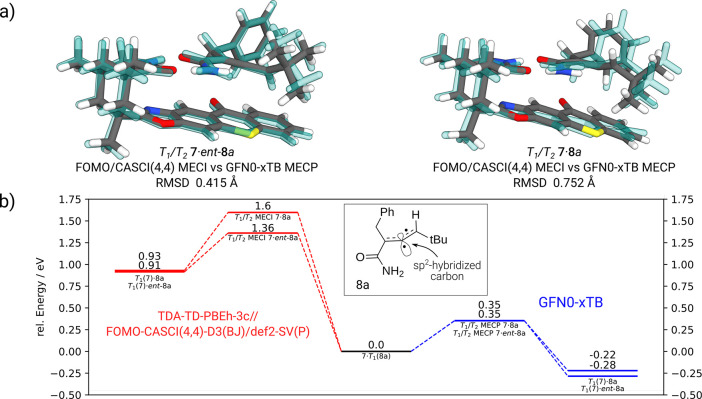
Moving on to higher-state MECPs, novel capabilities of the approach are demonstrated. As a first showcase, we refer to a representative “real life” example from a series of joint experimental and theoretical studies of the photochemical deracemization of primary allene amides.^6,33,49 In a recently studied deracemization photoreaction, two diastereomeric complexes of the chiral allene and chiral photocatalyst are formed, 7·8a and 7·ent-8a. It was shown that the distinguishing factor in this process is the T₁/T₂ MECI, where a triplet state is transferred from the catalyst to the allene. The theoretical description of this system is challenging due to its size and the triplet states being located on different sites. Here, we model the T₁ as HOMO–LUMO excitation (cf. OS1 in Figure 1) and the T₂ state as a HOMO–1 to LUMO+1 excitation at the GFN0-xTB level. The resulting geometries are depicted in Figure 3a in comparison with the FOMO-CASCI(4,4)-D3(BJ)/def2-SV(P) reference from ref (6).

Figure 3.

(a) T₁/T₂ MECIs of the 7·8a enantiomers from ref (6) (transparent blue) optimized as MECPs (see text) at the GFN0-xTB level (solid color). (b) Relative energies (in eV) for the Dexter-type energy transfer associated with (a). Energies at the TDA-TD-PBEh-3c//FOMO-CASCI(4,4)-D3(BJ)/def2-SV(P) level (red) are compared with GFN0-xTB energies (blue). At the reference point, the triplet state is located at the then achiral allene 8a.

Structurally, the triplet state located on the allene, 7·T₁(8a), is characterized by an sp²-hybridized central allylic carbon atom (cf. Figure 3b). This achiral form of the molecule is the crucial step during the deracemization, as it is formed primarily from one of the enantiomers. Employing GFN0-xTB, the structural characteristics of the triplet minima and, via eq 1, also the MECPs (as approximations to the MECIs) are reproduced. The relative energies between the structures with a triplet located at the catalyst T₁(7)·(ent-)8a and the respective MECPs are of similar magnitude (around 0.6 eV) with both the reference method TDA-TD-PBEh-3c//FOMO-CASCI(4,4)-D3(BJ)/def2-SV(P) (shown in red in Figure 3b), and GFN0-xTB (shown in blue). However, the energetic ordering of the substrate complex (triplet located on the catalyst) and of the product complex (triplet located on the then achiral allene) is inverted compared to the ab initio treatment. This effect is probably due to the purpose-specific parametrization and the lack of proper electrostatics in the GFN0-xTB method in particular.¹² While the quantitative calculation of photoreaction pathways is not the goal here, GFN0-xTB provides a sufficiently reasonable, fast, and robust level of theory for the efficient prescreening of plausible MECP structures between higher-lying states, which can then be refined at a higher level of theory.

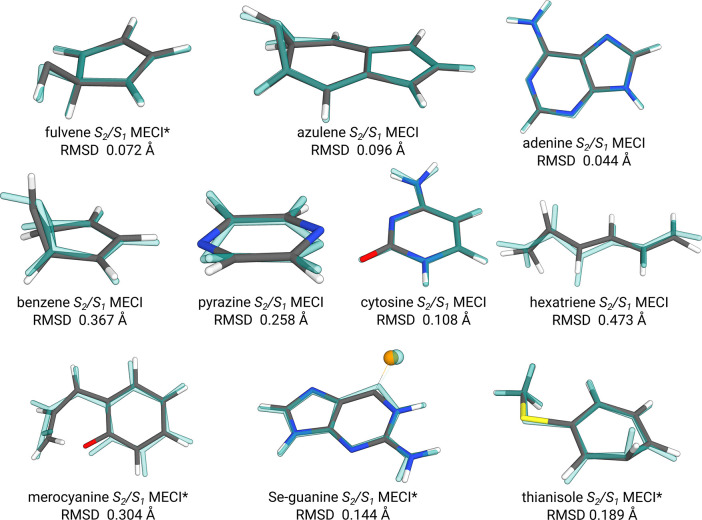
We further demonstrate the applicability of the GFN0-xTB-based approach to identifying high-lying MECPs for several other molecules in Figure 4. The depicted structures refer to molecules with S₂/S₁ conical intersections that are taken from the literature^4,50−57 to provide a set of appropriate benchmark examples. Comparison between the GFN0-xTB optimized MECPs and the reference MECIs reveals excellent agreement for the azulene, adenine, and cytosine molecules. Somewhat larger deviations are obtained for the cases of hexatriene, merocyanine, pyrazine, benzene, and fulvene, which differ with regard to one of their defining dihedral or pyramidalization angles, leading to a rather large RMSD, but overall still show the correct structural motif and correct bonding pattern. These differences are quite sensitive to the employed method and can also disagree between the two reference methods. For example, the fulvene MECI converges toward the benzene MECI structure at the hhTDA-BHLYP-D3(BJ)/def2-SV(P) level, apparently due to some preference for the doubly excited state. Likewise, the performance of FOMO-CASCI depends strongly on the chosen active space and the electronic temperature used in the orbital generation. For example, hexatriene optimizes to a flat structure at the FOMO(∞)-CASCI(4,3)-D3(BJ)/def2-SV(P) level. GFN0-xTB can describe both properly if the corresponding orbital occupation (OS1/OS2 vs OS1/CS1) is used. In Se-guanine, the selenium atom is removed from planarity of the guanine moiety at the reference level, while GFN0-xTB predicts it to be virtually identical to the ground state structure. However, both types of structures exist as S₂/S₁ CIs in the literature.⁵⁷ The largest differences occur for thioanisole, demonstrating the ambiguity in the theoretical description. Here, the CI is characterized by an out-of-plane bend of one of the phenyl carbon atoms. While at the hhTDA reference level the latter is at the position of the thiomethyl group, it is the β-carbon for the GFN0-xTB and FOMO-CASCI levels. Both results contradict findings in the literature, where the S₂/S₁ CI is identified as the pathway for a methyl radical dissociation with a corresponding S–C bond elongation and an overall planar geometry.⁵² On the GFN0-xTB side, the approximate monopole-based and non-self-consistent treatment of electrostatics may be responsible for observed deviations, particularly if orbitals other than π orbitals are involved in the respective states. Nonetheless, the examples shown in Figure 4 make a strong case for the proposed method and clearly show that a sensible screening of higher-lying MECPs is possible at a semiempirical xTB level. Computational wall times at the reference levels ranged from 6 min to 1 h 20 min, while at the GFN0-xTB level the optimizations, starting from the GS geometry, take 1 to 2 s, on the same machines mentioned above.

Figure 4.

Selection of molecules optimized as the S₂/S₁ MECP at the GFN0-xTB level (solid color) and either FOMO(∞)-CASCI(4,3)-D3(BJ)/def2-SV(P) (marked by *) or hhTDA-BHLYP-D3(BJ)/def2-SV(P) MECI (transparent blue). The Cartesian RMSD is indicated below each structure. Systems were calculated as OS2/OS1 MECPs at the GFN0-xTB level, with the exception of azulene, benzene, and merocyanine, which are obtained as CS1/OS1 MECPs.

Finally, eq 2 shows a summation of pairwise constraints between two states. The procedure can therefore be used to find MECPs that are close estimates to tristate conical intersections. In fact, tristate CIs are inherently difficult to obtain by conventional optimization procedures, so the derivative coupling vector-free treatment offers an excellent alternative, as recently demonstrated by Baek et al.²¹ Tristate CIs for a number of molecules have been described,⁵⁸⁻⁶⁰ but for brevity, we will focus only on the uracil nucleobase.^61,62 A comparison between the S₀/S₁/S₂ tristate CI calculated at the MRCI(12,9)/cc-pVDZ level and the corresponding GFN0-xTB calculation is shown in Figure 5.

Figure 5.

(a) Top- and side-view of the S₀/S₁/S₂ tristate MECP of the uracil nucleobase. Compared are the GFN0-xTB (solid color) and MRCI/cc-pVDZ (transparent blue) geometries. The Cartesian RMSD between the two is 0.263 Å. (b) S₀, S₁, and S₂ energy levels for the Franck–Condon point, the S₀/S₁ MECP, and the tristate MECP. The MRCI(12,9)/cc-pVDZ geometry and energies were reproduced from ref (62).

Despite much less theoretical sophistication compared to the MRCI level used in ref (62), GFN0-xTB is able to generate the tristate MECP closely resembling the given reference. Characteristic structural features that distinguish the tristate from the Franck–Condon point or the S₀/S₁ MECP, especially the non-planarity of the ∠OCCH dihedral angle, are qualitatively recovered at the tight-binding level. Looking at the corresponding energy levels (Figure 5b), one finds further similarities between the two levels of theory, in that the S₀/S₁ MECP is located at around 4 eV, and therefore lower than the tristate structure at around 6 eV, relative to the ground state. Again, we must stress that obtaining accurate energetics with GFN0-xTB is outside the intended scope and parametrization of the method.¹⁶ However, our observations reveal that the method is well-suited for preoptimization and sampling of MECP geometries, even multistate MECPs, for subsequent optimization at a higher level of theory. Evidently, the effective one-electron approach based on the presented single-determinant treatments may require some manual adjustments, particularly for the optimization of the tristate MECP. Here, different orbital occupations that could represent the higher-lying excited states need to be tested. Given the computational efficiency of the approach, however, multiple combinations of orbital occupations can quickly be investigated. Optimization (or single-point evaluations) at a higher level of theory like CASCI or hhTDA-BHLYP-D3(BJ)/def2-SV(P) will then quickly reveal if the sampled MECPs correspond to relevant MECIs.

In conclusion, we have introduced a novel application of the non-self-consistent SQM method GFN0-xTB. The main results from the presented work are the following: (1) Given a specific orbital occupation, one can qualitatively describe higher-lying electronic states using only a single determinant composed of a single set of orthogonal orbitals. These orbitals are obtained via a single diagonalization of the non-self-consistent “Hückel-type” Hamiltonian and are used to describe different electronic states simultaneously. (2) Combining this method with a “derivative coupling vector-free” treatment enables the optimization of MECPs as estimates for excited-state MECIs. The approach is easily extended to tristate intersections. The computational efficiency of the non-self-consistent treatment allows for rapid testing of different reference occupations. (3) Calculated MECP geometries at the GFN0-xTB level are of similar quality to those obtained with GFN2-xTB for MECPs between the ground state and first excited states. In addition, the new scheme extends the capabilities of the previous approach⁹ to higher-state intersections. Overall, the structural features of the MECI are retained at a qualitative level, while larger deviations are expected for corresponding energetics. This result qualifies the presented scheme as suitable for application in metadynamics-based screening of MECPs^4,8,9,63 and automated photoreaction analysis. Being parametrized for all elements up to radon (Z ≤ 86), GFN0-xTB is immediately applicable to a large variety of systems. Failures of GFN0-xTB are comparable to those previously observed for GFN2-xTB (e.g., missing pyramidalization features of the MECP in non-polar carbon-double bonds). Other known shortcomings, such as incorrect charge-transfer¹² are also expected. (4) To the best of our knowledge, we here presented the first approach to describe non-Aufbau occupations via a modified Fermi-smearing technique to generate holes in the reference orbital occupation vector while maintaining robustness in molecular simulations.

As outlined above, single-reference SQM methods are the most simplified levels of theory at which a qualitatively correct description of the electronic structure is possible. Within the family of SQM methods, non-self-consistent variants such as GFN0-xTB provide the greatest computational cost savings. In the context of optimizing MECPs, this approach offers a speed-up of roughly 1–2 orders of magnitude compared to semiemipirical SCF variants. Thus, the outlined procedures may pave the way for developments of photochemistry-specific xTB-type Hamiltonians, e.g., by including Fock exchange,⁴⁸ and automated workflows for photochemical applications.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.3c00494.

• The Supporting Information contains a zip archive with all optimized GFN0-xTB MECP geometries presented in the manuscript, including input files used to obtain these structures. Where appropriate, the respective hhTDA and FOMO-CASCI reference MECI geometries are also included. (ZIP)

The authors declare no competing financial interest.

Notes

Open-source implementations of this publication can be found on GitHub at https://github.com/crest-lab/crest and https://github.com/pprcht/gfn0.