Variance Measures for Symmetric Positive (Semi-) Definite Tensors in Two Dimensions

Abstract

Calculating the variance of a family of tensors, each represented by a symmetric positive semi-definite second order tensor/matrix, involves the formation of a fourth order tensor R_abcd. To form this tensor, the tensor product of each second order tensor with itself is formed, and these products are then summed, giving the tensor R_abcd the same symmetry properties as the elasticity tensor in continuum mechanics. This tensor has been studied with respect to many properties: representations, invariants, decomposition, the equivalence problem et cetera. In this paper we focus on the two-dimensional case where we give a set of invariants which ensures equivalence of two such fourth order tensors R_abcd and ${\tilde{R}}_{abcd}$. In terms of components, such an equivalence means that components R_ijkl of the first tensor will transform into the components ${\tilde{R}}_{ijkl}$ of the second tensor for some change of the coordinate system.

1. Introduction

Positive semi-definite second order tensors arise in several applications. For instance, in image processing, a structure tensor is computed from greyscale images that captures the local orientation of the image intensity variations [10, 17] and is employed to address a broad range of challenges. Diffusion tensor magnetic resonance imaging (DT-MRI) [1, 5] characterizes anisotropic water diffusion by enabling the measurement of the apparent diffusion tensor, which makes it possible to delineate the fibrous structure of the tissue. Recent work has shown that diffusion MR measurements of restricted diffusion obscures the fine details of the pore shape under certain experimental conditions [11], and all remaining features can be encoded accurately by a confinement tensor [19].

All such second order tensors share the same mathematical properties, namely, they are real-valued, symmetric, and positive semi-definite. Moreover, in these disciplines, one encounters a collection of such tensors, e.g., at different locations of the image. Populations of such tensors have also been key to some studies aiming to model the underlying structure of the medium under investigation [8, 12, 18].

Irrespective of the particular application, let R_ab denote such tensors,¹ and we shall refer to the set of n tensors as $\{R_{ab}^{(i)}{\}}_i$. Our desire is to find relevant descriptors or models of such a family. One relevant statistical measure of this family is the (population) variance

$$\frac{1}{n}\sum _{i=1}^n(R_{ab}^{(i)}-{\widehat{R}}_{ab})(R_{cd}^{(i)}-{\widehat{R}}_{cd})=\left(\frac{1}{n}\sum _{i=1}^n{R}_{ab}^{(i)}{R}_{cd}^{(i)}\right)-{\widehat{R}}_{ab}{\widehat{R}}_{cd},$$

where ${\widehat{R}}_{ab}=\frac{1}{n}{\sum }_{i=1}^n{R}_{ab}^{(i)}$ is the mean. (For another approach, see e.g., [8]). In this paper, we are interested in the first term, i.e., we study the fourth order tensor (skipping the normalization)

$$R_{abcd}=\sum _{i=1}^n{R}_{ab}^{(i)}{R}_{cd}^{(i)},R_{ab}^{(i)}\ge 0,$$ (1)

where $R_{ab}^{(i)}\ge 0$ stands for $R_{ab}^{(i)}$ being positive semi-definite. It is obvious that R_abcd has the symmetries R_abcd = R_bacd = R_abdc and R_abcd = R_cdab, i.e., R_abcd has the same symmetries as the elasticity tensor [14] from continuum mechanics. The elasticity tensor is well studied [13], e.g. with respect to classification, decompositions, and invariants. In most cases this is done in three dimensions. The same (w.r.t. symmetries) tensor has also been studied in the context of diffusion MR [2].

In this paper we will focus on the corresponding tensor R_abcd in two dimensions. First, there are direct applications in image processing, and secondly, the problems posed will be more accessible in two dimensions than in three. In particular we study the equivalence problem, namely, we ask the question: given the components R_ijkl and ${\tilde{R}}_{ijkl}$ of two such tensors do they represent the same tensor in different coordinate systems (see Sects. 2.1.2 and 4)?

1.1. Outline

Section 2 contains tensorial matters. We will assume some basic knowledge of tensors, although some definitions are given for completeness. The notation(s) used is commented on and in particular the three-dimensional Euclidean vector space V_(ab) is introduced.

In Sect. 2.1.2, we make some general remarks concerning the tensor R_abcd and specify the problem we focus on. Section 2.1 is concluded with some remarks on the Voigt/Kelvin notation and the corresponding visualisation in ${\mathbb{R}}^3$.

Section 2.2 gives examples of invariants, especially invariants which are easily accessible from R_abcd. Also, more general invariant/canonical decompositions of R_abcd are given.

In Sect. 3, we discuss how the tensor R_abcd can (given a careful choice of basis) be expressed in terms of a 3 × 3 matrix, and how this matrix is affected by a rotation of the coordinate system in the underlying two-dimensional space on which R_abcd is defined.

In Sect. 4 we return to the equivalence problem and give the main result of this work. In Sect. 4.1.1 we provide a geometric condition for equivalence, while in Sect. 4.1.2, we present the equivalence in terms of a 3 × 3 matrix. Both these characterisations rely on the choice of particular basis elements for the vector spaces employed. In Sect. 4.1.3 the same equivalence conditions are given in a form which does not assume a particular basis.

2. Preliminaries

In this section we clarify the notation and some concepts which we need. Section 2.1 deals with the (alternatives of) tensor notation and some representations. The equivalence (and related) problems are also briefly addressed. Section 2.2 accounts for some natural invariants, traces and decompositions of R_abcd.

We will assume some familiarity with tensors, but to clarify the view on tensors we recall some facts. We start with a (finite dimensional) vector space V with dual V*. A tensor of order (p,q) is then a multi-linear mapping $\underset{q}{\underbrace{V\times V\cdots \times V}}\times \underset{p}{\underbrace{V^{\ast }\times \cdots \times V^{\ast }}}\to \mathbb{R}$. Moreover, a (non-degenerate) metric/scalar product $g:V\times V\to \mathbb{R}$ gives an isomorphism from V to V* through v → g(v, ·), and it is this isomorphism which is used to ‘raise and lower indices’, see below. Indeed, for a fixed v ∈ V, g(v, ·) is a linear mapping $V\to \mathbb{R}$, i.e., an element of V*.

2.1. Tensor Notation and Representations

There is a plethora of notations for tensors. Here, we follow the well-adopted convention [16] that early lower case Latin letters (T^a_bc) refer to the tensor as a geometric object, its type being inferred from the indices and their positions (the abstract index notation). g_ab denotes the metric tensor. When the indices are lower case Latin letters from the middle of the alphabet, Tⁱ_jk, they refer to components of T^a_bc in a certain frame. The super-index i denotes a contravariant index while the sub-indices j, k are covariant. For instance, a typical vector (tensor of type (1, 0)) will be written v^a with components vⁱ, while the metric g_ab (tensor of type (0, 2)) has components g_ij. At a number of occasions, it will also be useful to express quantities in terms of components with respect to orthonormal frames, i.e., Cartesian coordinates. This is sometimes referred to as ‘Cartesian tensors’, and the distinction between contra- and covariant indices is obscured. In these situations, it is possible (but not necessary) to write all indices as sub-indices, and sometimes the symbol ≐ is used to indicate that an equation is only valid in Cartesian coordinates. For example T_i ≐ T_ijkδ_jk instead of Tⁱ = Tⁱ_jkg^jk = T^ik_k. Often this is clear form the context, but we will sometimes use ≐ to remind the reader that a Cartesian assumption is made. Here, the Einstein summation convention is implied, i.e., repeated indices are to be summed over, so that for instance $T^i=T_{jk}^i{g}^{jk}=T_k^{ik}=\sum _{j=1}^n\sum _{k=1}^n{T}_{jk}^i{g}^{jk}=\sum _{k=1}^n{T}_k^{ik}$ if each index ranges from 1 to n. We have also used the metric g_ij and its inverse g^ij to raise and lower indices. For instance, since g_ijvⁱ is an element of V*, we write g_ijvⁱ = v_j.

We also remind of the notation for symmetrisation. For a two-tensor $T_{(ab)}=\frac{1}{2}(T_{ab}+T_{ba})$, while more generally for a tensor T_a1a2⋯an of order (0, n) we have

$$T_{(a_1{a}_2\cdots a_n)}=\frac{1}{n!}\sum _{\pi }{T}_{a_{\pi (1)}{a}_{\pi (2)}\cdots a_{\pi (n)}}$$

where the sum is taken over all permutations π of 1, 2, …, n. Naturally, this convention can also be applied to subsets of indices. For instance, $H_{a(bc)}=\frac{1}{2}(H_{abc}+H_{acb})$.

2.1.1. The Vector Space of Symmetric Two-Tensors

In any coordinate frame a symmetric tensor R_ab (i.e., R_ab = R_ba) is represented by a symmetric matrix R_ij (2 × 2 or 3 × 3 depending on the dimension of the underlying space). In the two-dimensional case, with the underlying vector space $V^a\sim {\mathbb{R}}^2$, this means that R_ab lives in a three-dimensional vector space, which we denote by V_(ab). V_(ab) is equipped with a natural scalar product: < A_ab, B_ab >= A_abB^ab, making it into a three-dimensional Euclidean space. Here A_abB^ab = A_abB_cdg^acg^bd, i.e, the contraction of A_abB_cd over the indices a, c and b, d, and the tensor product A_abB_cd itself is the tensor of order (0, 4) given by (A_abB_cd)v^au^bw^cm^d = (A_abv^au^b)(B_cdw^cm^d) together with multi-linearity.

2.1.2. The Tensor R_abcd and the Equivalence Problem

As noted above, R_abcd given by (1) has the symmetries R_abcd = R_(ab)cd = R_ab(cd) and R_abcd = R_cdab, and it is not hard to see that this gives R_abcd six degrees of freedom in two dimensions. (See also Sect. 2.1.3.) It is also interesting to note that R_abcd provides a mapping V_(ab) → V_(ab) through

$$R_{ab}\mapsto R_{abcd}{R}^{cd},$$

and that this mapping is symmetric (due to the symmetry R_abcd = R_cdab). Given R_abcd there are a number of questions one can ask, e.g.,

• Feasibility—given a tensor R_abcd with the correct symmetries, can it be written in the form (1)?

• Canonical decomposition—given R_abcd of the form (1), can you write R_abcd as a canonical sum of the form (1), but with a fixed number of terms (cf. eigenvector decomposition of symmetric matrices)?

• Visualisation—since fourth order tensors are a bit involved, how can one visualise them in ordinary space?

• Characterisation/relevant sets of invariants—what invariants are relevant from an application point of view?

• The equivalence problem—in terms of components, how do we know if R_ijkl and ${\tilde{R}}_{ijkl}$ represent the same tensor when they are in different coordinate systems?

We will now focus on the equivalence problem in two dimensions. This problem can be formulated as above: given, in terms of components, two tensors (with the symmetries we consider) R_ijkl and ${\tilde{R}}_{ijkl}$, do they represent the same tensor in the sense that there is a coordinate transformation taking the components R_ijkl into the components ${\tilde{R}}_{ijkl}$? In other words, does there exist an (invertible) matrix P^m_i so that

$$R_{ijkl}={\tilde{R}}_{mnop}{P^m}_i{P^n}_j{P^o}_k{P^p}_l?$$

This problem can also be formulated when R_ijkl and ${\tilde{R}}_{ijkl}$ are expressed in Cartesian frames. Then the coordinate transformation must be a rotation, i.e., given by a rotation matrix Qⁱ j ∈ SO(2). Hence, the problem of (unitary) equivalence is: Given R_ijkl and ${\tilde{R}}_{ijkl}$, both expressed in Cartesian frames, is there a matrix (applying the ‘Cartesian convention’) Q_ij ∈ SO(2) so that

$$R_{ijkl}={\tilde{R}}_{mnop}{Q}_{mi}{Q}_{nj}{Q}_{ok}{Q}_{pl}?$$

2.1.3. The Voigt/Kelvin Notation

Since (in two dimensions) the space V_(ab) is three-dimensional, one can introduce coordinates, for example $R_{ij}=\left(\begin{array}{cc}\hfill x\hfill & \hfill y\hfill \\ \hfill y\hfill & \hfill z\hfill \end{array}\right)\sim \left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \end{array}\right)$ and use vector algebra on ${\mathbb{R}}^3$. This is used in the Voigt notation [15] and the related Kelvin notation [6]. As always, one must be careful to specify with respect to which basis in V_(ab) the coordinates $\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \end{array}\right)$ are taken. For instance, in the correspondence $R_{ij}=\left(\begin{array}{cc}\hfill x\hfill & \hfill y\hfill \\ \hfill y\hfill & \hfill z\hfill \end{array}\right)\sim \left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \end{array}\right)$, the understood basis for V_(ab) (in the understood/induced coordinate system) is $\left\{\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right),\left(\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right),\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\right\}$. These elements are orthogonal (viewed as vectors in V_(ab)) to each other, but not (all of them) of unit length.

Since the unit matrix plays a special role, we make the following choice. Starting with an orthonormal basis $\{\widehat{\xi },\widehat{\eta }\}$ for V, (i.e., $\{{\widehat{\xi }}^a,{\widehat{\eta }}^a\}$ for V^a) a suitable orthonormal basis for V_(ab) is $\{e_{ab}^{(1)},e_{ab}^{(2)},e_{ab}^{(3)}\}$ where $e_{ab}^{(1)}=\frac{1}{\sqrt{2}}({\xi }_a{\xi }_b-{\eta }_a{\eta }_b)$, $e_{ab}^{(2)}=\frac{1}{\sqrt{2}}({\xi }_a{\eta }_b+{\eta }_a{\xi }_b)$, $e_{ab}^{(3)}=\frac{1}{\sqrt{2}}({\xi }_a{\xi }_b+{\eta }_a{\eta }_b)$, i.e., in the induced basis we have

$$e_{ij}^{(1)}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill \end{array}\right)\sim \widehat{x},e_{ij}^{(2)}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right)\sim \widehat{y},e_{ij}^{(3)}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\sim \widehat{z}.$$ (2)

In this basis, we write an arbitrary element M_ab ∈ V_(ab) as $M_{ij}=\left(\begin{array}{cc}\hfill z+x\hfill & \hfill y\hfill \\ \hfill y\hfill & \hfill z-x\hfill \end{array}\right)$, which means that M_ab gets the coordinates ${\overline{M}}_i=\sqrt{2}\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \end{array}\right)$. Note that M_ij is positive definite if z² − x² − y² ≥ 0 and z ≥ 0. In terms of the coordinates of the Voigt notation, the tensor R_abcd corresponds to a symmetric mapping ${\mathbb{R}}^3\to {\mathbb{R}}^3$, given by a symmetric 3 × 3 matrix, which also shows that the degrees of freedom for R_abcd is six.

2.1.4. Visualization in ${\mathbb{R}}^3$

Through the Voigt notation, any symmetric two-tensor (in two dimensions) can be visualised as a vector in ${\mathbb{R}}^3$. Using the basis vector given by (2), we note that $e_{ij}^{(1)}$ and $e_{ij}^{(2)}$ correspond to indefinite quadratic forms, while $e_{ij}^{(3)}$ is positive definite. We also see that $e_{ij}^{(1)}+e_{ij}^{(3)}$ and $e_{ij}^{(2)}+e_{ij}^{(3)}$ are positive semi-definite.

In Fig. 1 (left) these matrices are illustrated as vectors in ${\mathbb{R}}^3$. The set of positive semi-definite matrices corresponds to a cone, cf. [4], indicated in blue. When the symmetric 2 × 2 matrices are viewed as vectors in ${\mathbb{R}}^3$, the outer product of such a vector with itself gives a symmetric 3 × 3 matrix. Hence we get a positive semi-definite quadratic form on ${\mathbb{R}}^3$, which can be illustrated by an (degenerate) ellipsoid in ${\mathbb{R}}^3$. In Fig. 1 (right) $(e_{ab}^{(1)}+e_{ab}^{(3)})(e_{cd}^{(1)}+e_{cd}^{(3)})$, $(e_{ab}^{(2)}+e_{ab}^{(3)})(e_{cd}^{(2)}+e_{cd}^{(3)})$ and $e_{ab}^{(3)}{e}_{cd}^{(3)}$ are visualised in this manner. Note that all these quadratic forms correspond to matrices which are rank one. (Cf. the ellipsoids in Fig. 2.)

Fig. 1.

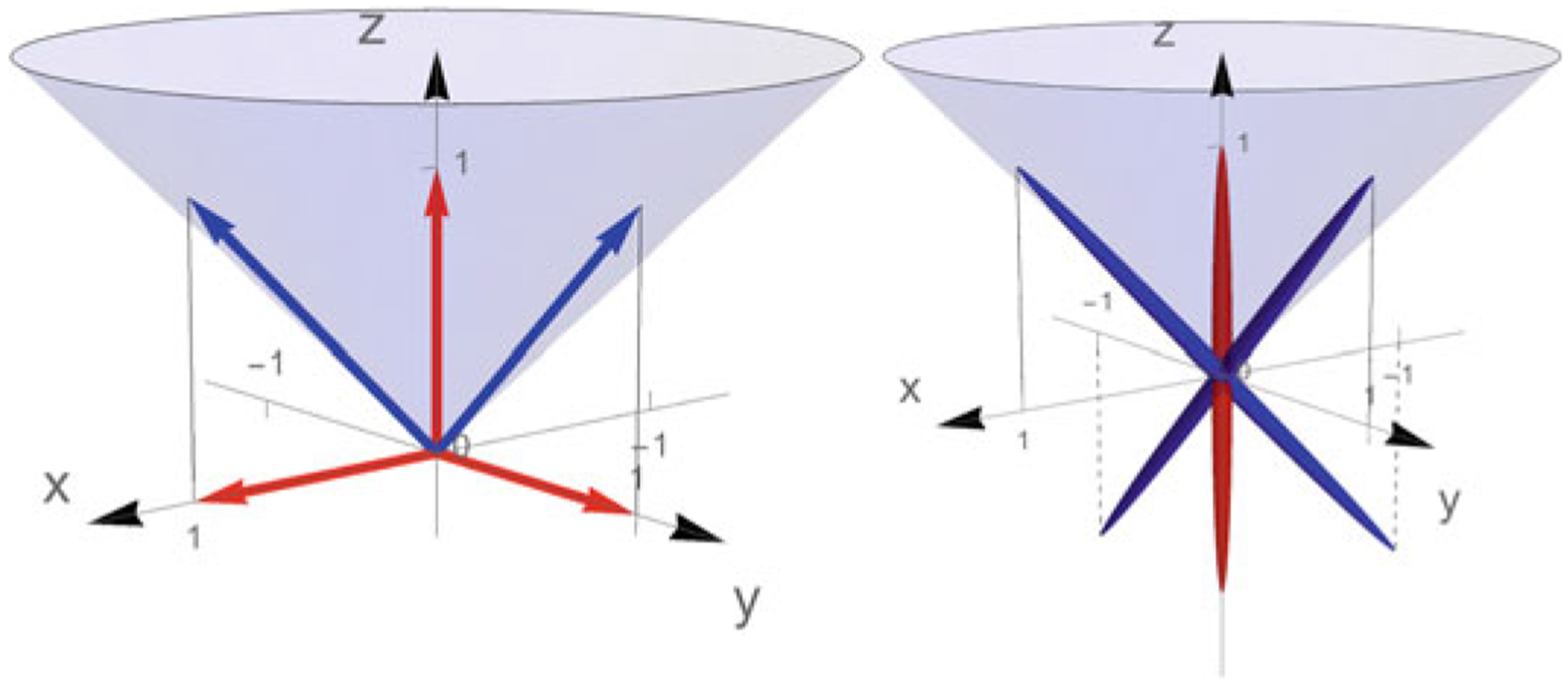
Left: the symmetric matrices $e_{ab}^{(1)}$, $e_{ab}^{(2)}$, $e_{ab}^{(3)}$ (red) and $e_{ab}^{(1)}+e_{ab}^{(3)}$, $e_{ab}^{(2)}+e_{ab}^{(3)}$ (blue) as vectors in ${\mathbb{R}}^3$. The positive semi-definite matrices correspond to vectors which are inside/above the indicated cone (including the boundary). Right: the fourth order tensors $(e_{ab}^{(1)}+e_{ab}^{(3)})(e_{cd}^{(1)}+e_{cd}^{(3)})$ and $(e_{ab}^{(2)}+e_{ab}^{(3)})(e_{cd}^{(2)}+e_{cd}^{(3)})$ depicted in blue, and $e_{ab}^{(3)}{e}_{cd}^{(3)}$ shown in red are viewed as quadratic forms and illustrated as ellipsoids (made a bit ‘fatter’ than they should be for the sake of clarity)

Fig. 2.

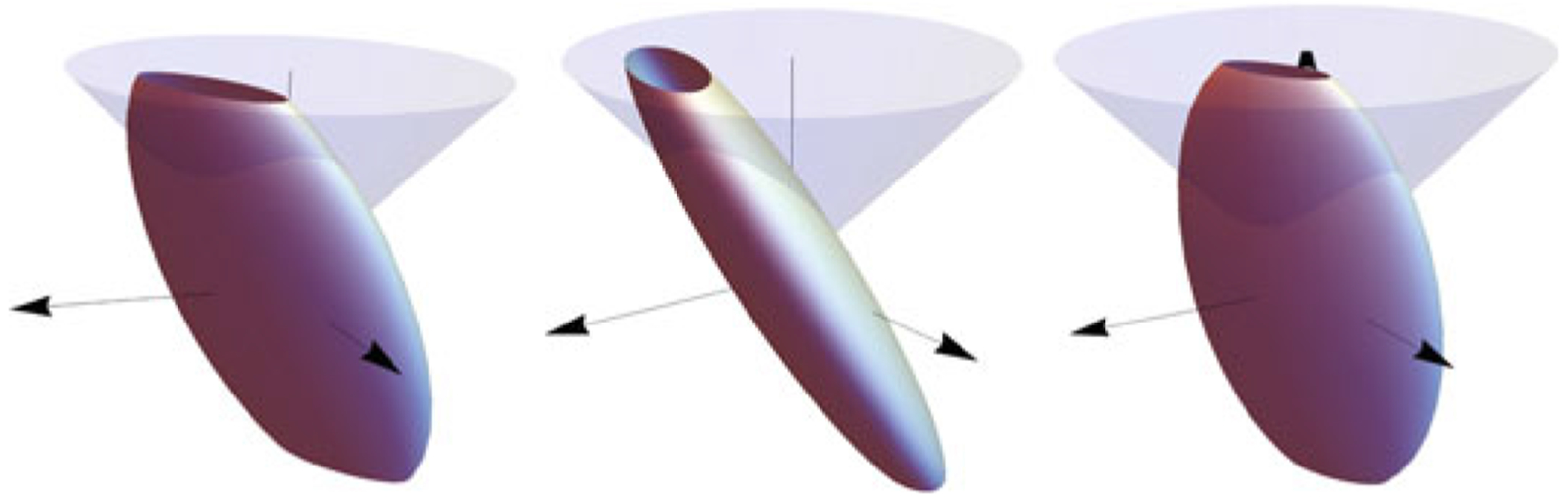
Three identical (truncated) ellipsoids in ${\mathbb{R}}^3$ with different orientations. The two leftmost ellipsoids can be carried over to each other through a rotation around the (vertical in the figure) z-axis, which implies that they represent the same tensor R_abcd (up to the meaning discussed). The right ellipsoid, despite identical eigenvalues with the two others, represent a different tensor since the rotation which carries this ellipsoid to any of the others is not around the z-axis

2.2. Invariants, Traces and Decompositions

By an invariant, we mean a quantity that can be calculated from measurements, and which is independent of the frame/coordinate system with respect to which the measurements are performed, despite the fact that components, e.g., Tⁱ_jk themselves depend on the coordinate system. It is this property that makes invariants important, and typically they are formed via tensor products and contractions, e.g., Tⁱ_jkT^k_ilg^jl. Sometimes, the invariants have a direct geometrical meaning. For instance, for a vector vⁱ, the most natural invariant is its squared length vⁱv_i. For a tensor Tⁱ_j of order (1,1) in three dimensions, viewed as a linear mapping ${\mathbb{R}}^3\to {\mathbb{R}}^3$, the most well known invariants are perhaps the trace Tⁱ_i and the determinant det(Tⁱ_j). The modulus of the determinant gives the volume scaling under the mapping given by Tⁱ_j, while the trace equals the sum of the eigenvalues. If Tⁱ_j represents a rotation matrix, then its trace is 1 + 2 cos ϕ, where ϕ is the rotation angle. In general, however, the interpretation of a given invariant may be obscure. (For an account relevant to image processing, see e.g., [9]. A different, but relevant, approach in the field of diffusion MRI is found in [20].)

2.2.1. Natural Traces and Invariants

From (1), and considering the symmetries of R_abcd, two (and only two) natural traces arise. For a tensor of order (1, 1), e.g., R_i ^j, it is natural to consider this as an ordinary matrix, and consequently use stem letters without any indices at all. To indicate this slight deviation from the standard tensor notation, we denote e.g., R_i ^j by $\overline{\overline{R}}$. Using [·] for the trace, so that $[\overline{\overline{R}}]=\text{Tr}(\overline{\overline{R}})=R_a^a$, we then have

$$T_{ab}=R_{abc}^c=\sum _{i=1}^n{R}_{ab}^{(i)}{R}_c^{(i{)}^c}=\sum _{i=1}^n{R}_{ab}^{(i)}[{\overline{\overline{R}}}^{(i)}],$$ (3)

and

$$S_{ab}=R_{acb}^c=\sum _{i=1}^n{R}_{ac}^{(i)}{R}_b^{(i{)}^c}.$$ (4)

Hence, in a Cartesian frame, where the index position is unimportant, we have for the matrices $\overline{\overline{T}}=T_{ij}$, $\overline{\overline{S}}=S_{ij}$

$$\overline{\overline{T}}=\sum _{i=1}^n{\overline{\overline{R}}}^{(i)}[{\overline{\overline{R}}}^{(i)}],\overline{\overline{S}}=\sum _{i=1}^n{\overline{\overline{R}}}^{(i)}{\overline{\overline{R}}}^{(i)}.$$

To proceed there are two double traces (i.e., contracting R_abcd twice):

$$T=T_a^a={R_a^a}_c^c=\sum _{i=1}^n{R}_a^{(i{)}^a}{R}_c^{(i{)}^c}=\sum _{i=1}^n[{\overline{\overline{R}}}^{(i)}{]}^2$$ (5)

and

$$S=S_a^a=R_{ac}^{ac}=\sum _{i=1}^n{R}_{ac}^{(i)}{R}^{(i{)}^{ac}}=\sum _{i=1}^n[({\overline{\overline{R}}}^{(i)}{)}^2].$$ (6)

In two dimensions, the difference T_ab−S_ab is proportional to the metric g_ab. Namely,

Lemma 1 With T_ab and S_ab given by (3) and (4), it holds that (in two dimensions)

$$T_{ab}-S_{ab}=\sum _{i=1}^n\text{det}({\overline{\overline{R}}}^{(i)})g_{ab}.$$

Proof By linearity, it is enough to prove the statement when n = 1, i.e., when the sum has just one term. Raising the second index, and using components, the statement then is $T_i^j-S_i^j=\text{det}({\overline{\overline{R}}}^{(1)}){\delta }_i^j$. Putting ${\overline{\overline{R}}}^{(1)}=A$, we see that T_i ^j − S_i ^j = A[A] − A² while $\text{det}({\overline{\overline{R}}}^{(1)}){\delta }_i^j=\text{det}(A)I$, and by the Cayley-Hamilton theorem in two dimensions, A[A] − A² is indeed det(A)I. □

From lemma 1, it follows that $T-S=2{\sum }_{i=1}^n\text{det}({\overline{\overline{R}}}^{(i)})\ge 0$. In fact the following inequalities hold.

Lemma 2 With T and S defined as above, it holds that S ≤ T ≤ 2S. If T = S, all tensors $R_{ab}^{(i)}$ have rank 1. If T = 2S, all tensors $R_{ab}^{(i)}$ are isotropic, i.e., proportional to the metric g_ab.

Proof Again, by linearity it is enough to consider one tensor ${\overline{\overline{R}}}^{(1)}=A$. In an orthonormal frame which diagonalises A, we have $A=\left(\begin{array}{cc}\hfill a\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill c\hfill \end{array}\right)$ (with a ≥ 0, c ≥ 0, a + c > 0). Hence

$$S=a^2+c^2\le a^2+c^2+2ac=(a+c{)}^2=T=2(a^2+c^2)-(a-c{)}^2\le 2S.$$

The first inequality becomes equality when ac = 0, i.e., when A has rank one. The second inequality becomes equality when a = c, i.e., when A is isotropic. □

Definition 1 We define the mean rank, r_m, by r_m = T/S, with T and S as above. Hence, in two dimensions, 1 ≤ r_m ≤ 2.

2.2.2. A Canonical Decomposition

It is customary [3, 7] to decompose a tensor with the symmetries of R_abcd into a sum where one term is the completely symmetric part:

$$R_{abcd}=H_{abcd}+W_{abcd},\text{where}{H}_{abcd}=R_{(abcd)},W_{abcd}=R_{abcd}-H_{abcd}.$$

It is also customary to split H_abcd into a trace-free part and ‘trace part’. We start by defining H_ab = H_abc^c, H = H_a^a and then the trace-free part of $H_{ab}:{\stackrel{{}_{{}_{\circ }}}{H}}_{ab}=H_{ab}-\frac{1}{2}H{g}_{ab}$ so that $H_{ab}={\stackrel{{}_{{}_{\circ }}}{H}}_{ab}+\frac{1}{2}H{g}_{ab}$. (These decompositions can be made in any dimension, but the actual coefficients, e.g., $\frac{1}{2}$ above and $\frac{1}{8}$ and $\frac{3}{8}$ et cetera below depend on the underlying dimension.) It is straightforward to check that

$${\stackrel{{}_{{}_{\circ }}}{H}}_{abcd}=H_{abcd}-g_{(ab}{H}_{cd)}+\frac{1}{8}H{g}_{(ab}{g}_{cd)}=H_{abcd}-g_{(ab}{\stackrel{{}_{{}_{\circ }}}{H}}_{cd)}-\frac{3}{8}H{g}_{(ab}{g}_{cd)}$$

is also trace-free. Hence we have the decomposition

$$H_{abcd}={\stackrel{{}_{{}_{\circ }}}{H}}_{abcd}+g_{(ab}{H}_{cd)}-\frac{1}{8}H{g}_{(ab}{g}_{cd)}={\stackrel{{}_{{}_{\circ }}}{H}}_{abcd}+g_{(ab}{\stackrel{{}_{{}_{\circ }}}{H}}_{cd)}+\frac{3}{8}H{g}_{(ab}{g}_{cd)}.$$

Moreover, due to the symmetry of R_abcd, we find that

$$H_{abcd}=\frac{1}{3}(R_{abcd}+R_{acbd}+R_{adbc})$$

and therefore that

$$W_{abcd}=\frac{1}{3}(2R_{abcd}-R_{acbd}-R_{adbc})$$ (7)

which implies that $H_{ab}=H_{abc}^c=\frac{1}{3}(T_{ab}+2S_{ab})$ and $W_{ab}=W_{abc}^c=\frac{2}{3}(T_{ab}-S_{ab})$.

The degres of freedom, which for R_abcd is six, is distributed, where $R_{abcd}\sim \{{\stackrel{{}_{{}_{\circ }}}{H}}_{abcd},H_{ab},W_{abcd}\}$, as

$$\underset{(6)}{R_{abcd}}\sim \{\underset{(2)}{{\stackrel{{}_{{}_{\circ }}}{H}}_{abcd}},\underset{(3)}{H_{ab}},\underset{(1)}{W_{abcd}}\}\sim \{\underset{(2)}{{\stackrel{{}_{{}_{\circ }}}{H}}_{abcd}},\underset{(2)}{{\stackrel{{}_{{}_{\circ }}}{H}}_{ab}},\underset{(1)}{H},\underset{(1)}{W_{abcd}}\}.$$

For H_ab (or the pair ${\stackrel{{}_{{}_{\circ }}}{H}}_{ab}$, H) this is clear. The total symmetry of ${\stackrel{{}_{{}_{\circ }}}{H}}_{abcd}$ leaves only five components (in a basis), ${\stackrel{{}_{{}_{\circ }}}{H}}_{1111}$, ${\stackrel{{}_{{}_{\circ }}}{H}}_{1112}$, ${\stackrel{{}_{{}_{\circ }}}{H}}_{1122}$, ${\stackrel{{}_{{}_{\circ }}}{H}}_{1222}$, ${\stackrel{{}_{{}_{\circ }}}{H}}_{2222}$. However, the trace-free condition ${\stackrel{{}_{{}_{\circ }}}{H}}_{abcd}{g}^{cd}=0$ imposes three conditions. (In an orthonormal frame, ${\stackrel{{}_{{}_{\circ }}}{H}}_{1122}=-{\stackrel{{}_{{}_{\circ }}}{H}}_{1111}$, ${\stackrel{{}_{{}_{\circ }}}{H}}_{2222}=-{\stackrel{{}_{{}_{\circ }}}{H}}_{1122}$ and ${\stackrel{{}_{{}_{\circ }}}{H}}_{1112}=-{\stackrel{{}_{{}_{\circ }}}{H}}_{1222}$.) That W_abcd has only one degree of freedom follows from the following lemma.

Lemma 3 Suppose that W_abcd is given by (7), and put W_ab = W_abcdg^cd, W = W_abg^ab. Then (in two dimensions)

$$W_{abcd}=\frac{W}{4}(2g_{ab}{g}_{cd}-g_{ac}{g}_{bd}-g_{ad}{g}_{bc})$$

Proof By linearity, it is enough to consider the case when R_abcd = A_abA_cd for some (symmetric) A_ab. In terms of eigenvectors (to A^a_b) we can write A_ab = αx_ax_b + βy_ay_b, where x_ax^a = y_ay^a = 1, x_ay^a = 0. In particular g_ab = x_ax_b + y_ay_b. From (7) we then get

$$\begin{gathered} W_{abcd}=\frac{1}{3}(2R_{abcd}-R_{acbd}-R_{adbc}) \\ =\frac{1}{3}(2A_{ab}{A}_{cd}-A_{ac}{A}_{bd}-A_{ad}{A}_{bc}) \\ =\frac{1}{3}(2(\alpha x_a{x}_b+\beta y_a{y}_b)(\alpha x_c{x}_d+\beta y_c{y}_d) \\ -(\alpha x_a{x}_c+\beta y_a{y}_c)(\alpha x_b{x}_d+\beta y_b{y}_d) \\ -(\alpha x_a{x}_d+\beta y_a{y}_d)(\alpha x_b{x}_c+\beta y_b{y}_c)). \end{gathered}$$ (8)

Expanding the parentheses, the components x_ax_bx_cx_d and y_ay_by_cy_d vanish, leaving

$$\begin{gathered} \frac{\alpha \beta }{3}(2x_a{x}_b{y}_c{y}_d+2y_a{y}_b{x}_c{x}_d-x_a{x}_c{y}_b{y}_d \\ -y_a{y}_c{x}_b{x}_d-x_a{x}_d{y}_b{y}_c-y_a{y}_d{x}_b{x}_c) \\ =\frac{\alpha \beta }{3}(2g_{ab}{g}_{cd}-g_{ac}{g}_{bd}-g_{ad}{g}_{bc}), \end{gathered}$$ (9)

where the last equality can be seen by inserting g_ab = x_ax_b + y_ay_b (for all indices) and expanding. Taking one trace, i.e., contracting with g^cd gives $W_{ab}=\frac{2\alpha \beta }{3}{g}_{ab}$, and another trace gives $W=\frac{4\alpha \beta }{3}$, which proves the lemma. □

3. R_abcd as a Quadratic Form on ${\mathbb{R}}^3$

Through the orthonormal basis for the space of symmetric two-tensors (in two dimensions) given by (2), the tensor R_abcd viewed as a quadratic form can be represented by a 3 × 3-matrix. Here, we will restrict ourselves to an orthonormal basis for V_(ab), namely the basis $\{e_{ab}^{(1)},e_{ab}^{(2)},e_{ab}^{(3)}\}$ from Sect. 2.1.3, defined in terms of the orthonormal basis [ξ^a, η^a} for V^a. Thus, given R_abcd, we associate the symmetric matrix M_ij, where (the choice of an orthonormal basis justifies the mismatch of the indices i, j)

$$M_{ij}\doteq R_{cd}^{ab}{e}_{ab}^{(i)}(e^{(j)}{)}^{cd},1\le i,j\le 3.$$

It is instructive to see how the various derived tensors show up in M_ij. In terms of the basis (2) it is natural to look at the various parts of M_ij as follows

$$M_{ij}\doteq \left(\begin{array}{ccc}\hfill \times \hfill & \hfill \times \hfill & \hfill \times \hfill \\ \hfill \times \hfill & \hfill \times \hfill & \hfill \times \hfill \\ \hfill \times \hfill & \hfill \times \hfill & \hfill ✕\hfill \end{array}\right)\doteq \left(\begin{array}{cc}A& \overline{v}\\ {\overline{v}}^t& a\end{array}\right).$$ (10)

This splitting is natural for reasons which will become apparent in the next sections. Note, however, that with this representation it is tempting to consider coordinate changes in ${\mathbb{R}}^3$, which is not natural in this case. Rather, of interest is the change of basis in V^a and the related induced change of coordinates in the representation (10). See Sect. 3.2.

3.1. Representation of the Canonically Derived Parts of R_abcd

It is helpful to see how the components of the various tensors T_ab, S_ab, T, S, ${\stackrel{{}_{{}_{\circ }}}{H}}_{abcd}$, ${\stackrel{{}_{{}_{\circ }}}{H}}_{ab}$, H and W show up as components of M_ij. As for ${\stackrel{{}_{{}_{\circ }}}{H}}_{ab}$, e.g., ${\stackrel{{}_{{}_{\circ }}}{T}}_{ab}$ denotes the trace-free part of T_ab. Immediate is M₃₃:

$$M_{33}\doteq R_{cd}^{ab}{e}_{ab}^{(3)}(e^{(3)}{)}^{cd}\doteq \frac{1}{2}{R}_{cd}^{ab}{g}_{ab}{g}^{cd}=\frac{1}{2}{T}_{cd}{g}^{cd}=\frac{1}{2}T.$$ (11)

Similarly, for i = 1, 2 we have

$$M_{i3}\doteq \frac{1}{\sqrt{2}}{R}_{cd}^{ab}{e}_{ab}^{(i)}{g}^{cd}\doteq \frac{1}{\sqrt{2}}{T}^{ab}{e}_{ab}^{(i)}\doteq \frac{1}{\sqrt{2}}{\stackrel{{}_{{}_{\circ }}}{T}}^{ab}{e}_{ab}^{(i)},$$ (12)

where the last equality follows form the trace-freeness of $e_{ab}^{(1)}$ and $e_{ab}^{(2)}$. This means that the components of ${\stackrel{{}_{{}_{\circ }}}{T}}_{ab}$ (properly rescaled) goes into M_ij as the components of $\overline{v}$ (and ${\overline{v}}^t$) in (10). The same holds for ${\stackrel{{}_{{}_{\circ }}}{S}}_{ab}$ and ${\stackrel{{}_{{}_{\circ }}}{H}}_{ab}$, as ${\stackrel{{}_{{}_{\circ }}}{S}}_{ab}={\stackrel{{}_{{}_{\circ }}}{T}}_{ab}$ by Lemma 1, which then implies that also ${\stackrel{{}_{{}_{\circ }}}{H}}_{ab}={\stackrel{{}_{{}_{\circ }}}{T}}_{ab}={\stackrel{{}_{{}_{\circ }}}{S}}_{ab}$. This latter relation follows from the trace-free part of the relation $H_{ab}=\frac{1}{3}(T_{ab}+2S_{ab})$. Hence

$$M_{ij}\doteq \left(\begin{array}{cc}A& \overrightarrow{\stackrel{{}_{{}_{\circ }}}{T}}\\ \overrightarrow{\stackrel{{}_{{}_{\circ }}}{T}}{}^{{}^{{}^t}}& \frac{1}{2}T\end{array}\right)\doteq \left(\begin{array}{cc}\frac{\sigma }{2}I+\mathrm{Å}& \overrightarrow{\stackrel{{}_{{}_{\circ }}}{T}}\\ \overrightarrow{\stackrel{{}_{{}_{\circ }}}{T}}{}^{{}^{{}^t}}& \frac{1}{2}T\end{array}\right),$$ (13)

where $\overrightarrow{\stackrel{{}_{{}_{\circ }}}{T}}=\overrightarrow{\stackrel{{}_{{}_{\circ }}}{S}}=\overrightarrow{\stackrel{{}_{{}_{\circ }}}{H}}$ encodes the two degrees of freedom in ${\stackrel{{}_{{}_{\circ }}}{T}}_{ab}={\stackrel{{}_{{}_{\circ }}}{S}}_{ab}={\stackrel{{}_{{}_{\circ }}}{H}}_{ab}$. The matrix A is decomposed as $A=\frac{\sigma }{2}I+\mathrm{Å}$ where I is the (2 × 2) identity matrix and Å is trace-free part of A. In particular, [A] = σ.

To investigate [M_ij] = M₁₁ + M₂₂ + M₃₃, i.e., the trace of M_ij we note that for a general symmetric matrix $R_{ij}\doteq \left(\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill b\hfill & \hfill c\hfill \end{array}\right)$ we have $R_{ij}{e}_{ij}^{(1)}\doteq \frac{a-c}{\sqrt{2}}$, $R_{ij}{e}_{ij}^{(2)}\doteq \frac{2b}{\sqrt{2}}$, $R_{ij}{e}_{ij}^{(3)}\doteq \frac{a+c}{\sqrt{2}}$. When M_ij is constructed from R_abcd which is an outer product R_abR_cd the trace is given by $M_{11}+M_{22}+M_{33}=(\frac{a-c}{\sqrt{2}}{)}^2+(\frac{2b}{\sqrt{2}}{)}^2+(\frac{a+c}{\sqrt{2}}{)}^2=a^2+2b^2+c^2$ and from (6) this is S. Together with linearity, this shows that [M] = M₁₁ + M₂₂ + M₃₃ = S also when R_abcd is formed as in (1). Taking trace in (13), this gives

$$S=\sigma +\frac{1}{2}T,\text{i.e.},\sigma =S-\frac{1}{2}T.$$

In addition, the relations below Eq. (7) show that

$$\{\begin{array}{c}H=\frac{1}{3}(T+2S)\hfill \\ W=\frac{2}{3}(T-S)\hfill \end{array}\phantom{\}}\text{i.e.},\{\begin{array}{c}T=H+W\hfill \\ S=H-\frac{1}{2}W\hfill \end{array}\phantom{\}}\text{so that}\sigma =\frac{1}{2}H-W.$$

The two degres of freedom in Å corresponds to the two degrees of freedom in ${\stackrel{{}_{{}_{\circ }}}{H}}_{abcd}$.

3.2. The Behaviour of M_ij Under a Rotation of the Coordinate System in V^a

The components of M_ij are expressed in terms of the orthonormal basis tensors given by (2), and these in turn are based on the ON basis $\{\widehat{\xi },\widehat{\eta }\}$ for V. Putting the basis vectors in a row matrix $\left(\widehat{\xi }\widehat{\eta }\right)$ and the coordinates in a column matrix $\left(\begin{array}{c}\hfill \xi \hfill \\ \hfill \eta \hfill \end{array}\right)$ so that a vector $\mathbf{u}=\xi \widehat{\xi }+\eta \widehat{\eta }=\left(\widehat{\xi }\widehat{\eta }\right)\left(\begin{array}{c}\hfill \xi \hfill \\ \hfill \eta \hfill \end{array}\right)$, and considering only orthonormal frames, the relevant change of basis is given by a rotation matrix $Q(v)=Q_v=\left(\begin{array}{cc}\hfill \cos v\hfill & \hfill -\sin v\hfill \\ \hfill \sin v\hfill & \hfill \cos v\hfill \end{array}\right)$, i.e., we consider the change of basis

$$(\widehat{\xi }\widehat{\eta })\to \left(\widehat{\tilde{\xi }}\widehat{\tilde{\eta }}\right)=(\widehat{\xi }\widehat{\eta })\left(\begin{array}{cc}\hfill \cos v\hfill & \hfill -\sin v\hfill \\ \hfill \sin v\hfill & \hfill \cos v\hfill \end{array}\right)=(\widehat{\xi }\widehat{\eta })Q(v).$$

This means that for a vector $\mathbf{u}=\left(\widehat{\tilde{\xi }}\widehat{\tilde{\eta }}\right)\left(\begin{array}{c}\hfill \tilde{\xi }\hfill \\ \hfill \tilde{\eta }\hfill \end{array}\right)=(\widehat{\xi }\widehat{\eta })\left(\begin{array}{c}\hfill \xi \hfill \\ \hfill \eta \hfill \end{array}\right)$, the coordinates transform as

$$\left(\begin{array}{c}\hfill \xi \hfill \\ \hfill \eta \hfill \end{array}\right)\to \left(\begin{array}{c}\hfill \tilde{\xi }\hfill \\ \hfill \tilde{\eta }\hfill \end{array}\right)=Q^{-1}(v)\left(\begin{array}{c}\hfill \xi \hfill \\ \hfill \eta \hfill \end{array}\right)=Q^t(v)\left(\begin{array}{c}\hfill \xi \hfill \\ \hfill \eta \hfill \end{array}\right)=Q(-v)\left(\begin{array}{c}\hfill \xi \hfill \\ \hfill \eta \hfill \end{array}\right).$$

For the components of the basis vectors $e_{ab}^{(1)}$, $e_{ab}^{(2)}$, $e_{ab}^{(3)}$ we find (omitting the factor $1∕\sqrt{2}$)

$$\begin{gathered} \left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill \end{array}\right)\to \left(\begin{array}{cc}\hfill \cos v\hfill & \hfill \sin v\hfill \\ \hfill -\sin v\hfill & \hfill \cos v\hfill \end{array}\right)\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill \end{array}\right)\left(\begin{array}{cc}\hfill \cos v\hfill & \hfill -\sin v\hfill \\ \hfill \sin v\hfill & \hfill \cos v\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill \cos 2v\hfill & \hfill -\sin 2v\hfill \\ \hfill -\sin 2v\hfill & \hfill -\cos 2v\hfill \end{array}\right) \\ \left(\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right)\to \left(\begin{array}{cc}\hfill \cos v\hfill & \hfill \sin v\hfill \\ \hfill -\sin v\hfill & \hfill \cos v\hfill \end{array}\right)\left(\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{cc}\hfill \cos v\hfill & \hfill -\sin v\hfill \\ \hfill \sin v\hfill & \hfill \cos v\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill \sin 2v\hfill & \hfill \cos 2v\hfill \\ \hfill \cos 2v\hfill & \hfill -\sin 2v\hfill \end{array}\right) \\ \left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\to \left(\begin{array}{cc}\hfill \cos v\hfill & \hfill \sin v\hfill \\ \hfill -\sin v\hfill & \hfill \cos v\hfill \end{array}\right)\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\left(\begin{array}{cc}\hfill \cos v\hfill & \hfill -\sin v\hfill \\ \hfill \sin v\hfill & \hfill \cos v\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right), \end{gathered}$$ (14)

and this means that the components M_ij transform as

$$M_{ij}\doteq \left(\begin{array}{cc}A& \overline{v}\\ {\overline{v}}^t& a\end{array}\right)\to {\tilde{M}}_{ij}\doteq \left(\begin{array}{cc}{Q}_{2v}^{t}A{Q}_{2v}& Q_{2v}^t\overline{v}\\ {\overline{v}}^t{Q}_{2v}& a\end{array}\right).$$ (15)

But this latter expression is just

$$\left(\begin{array}{cc}{Q}_{2v}^t& \overline{0}\\ {\overline{0}}^t& 1\end{array}\right)\left(\begin{array}{cc}A& \overline{v}\\ {\overline{v}}^t& a\end{array}\right)\left(\begin{array}{cc}{Q}_{2v}& \overline{0}\\ {\overline{0}}^t& 1\end{array}\right),$$

hence we have the following important remark/observation:

Remark 1 Viewing the matrix M_ij as an ellipsoid in ${\mathbb{R}}^3$, the effect of a rotation by an angle v in V^a corresponds to a rotation of the ellipsoid by an angle 2v around the z-axis in ${\mathbb{R}}^3$ (where the z-axis corresponds to the ‘isotropic direction’ given by g_ab).

4. The Equivalence Problem for R_abcd

The equivalence problem for R_abcd can be formulated in different ways (for an account in three dimensions, we refer to [3]). Given two tensors R_abcd and ${\tilde{R}}_{abcd}$, both with the symmetries implied by (1), the question whether they are the same or not is straightforward as one can compare the components in any basis. However, R_abcd and ${\tilde{R}}_{abcd}$ could live in different (but isomorphic) vector spaces, e.g. two tangent spaces at different points, and the concept of equality becomes less clear. On the other hand, in terms of components R_ijkl and ${\tilde{R}}_{ijkl}$, one could ask whether there is a change of coordinates which takes one set of components into the other. If so, one can find a (invertible) matrix Pⁱ_j so that

$$R_{ijkl}={\tilde{R}}_{mnop}{P^m}_i{P^n}_j{P^o}_k{P^p}_l,$$

and the tensors are then said to be equivalent. As already mentioned, it is convenient to restrict the coordinate systems to orthonormal coordinates. This means that two different coordinate systems differ only by their orientation, i.e., the change of coordinates are given by a rotation matrix Q ∈ SO(2). Under the ‘Cartesian convention’ that all indices are written as subscripts, R_abcd and ${\tilde{R}}_{abcd}$ are equivalent if there is a matrix Q ∈ SO(2) so that (their Cartesian components satisfy)

$$R_{ijkl}={\tilde{R}}_{mnop}{Q}_{mi}{Q}_{nj}{Q}_{ok}{Q}_{pl}.$$

4.1. Different Ways to Characterize the Equivalence of R_abcd and ${\tilde{R}}_{abcd}$

In this section, we will discuss three ways to determine whether two tensors R_abcd and ${\tilde{R}}_{abcd}$ are equivalent or not. In Sects. 4.1.1 and 4.1.2 we present two such methods briefly, while Sect. 4.1.3, which is more complete, contains the main result of this work.

As mentioned in Sect. 1.1, the results of Sects. 4.1.1 and 4.1.2, which may be used in their own rights, rely on particular choices of basis matrices for V_(ab). The formulation in Sect. 4.1.3 on the other hand, is expressed in the components of R_abcd (in any coordinate system) directly.

4.1.1. Orientation of the Ellipsoid in ${\mathbb{R}}^3$

A necessary condition for R_abcd and ${\tilde{R}}_{abcd}$ to be equivalent is that their corresponding 3 × 3-matrices M_ij and ${\tilde{M}}_{ij}$ have the same eigenvalues. On the other hand, this is not sufficient since the representation in ${\mathbb{R}}^3$ should reflect the freedom in rotating the coordinate system in $V^a\sim {\mathbb{R}}^2$. With the coordinates adopted, this corresponds to a rotation of the associated ellipsoid around the z-axis in ${\mathbb{R}}^3$ (see Remark 1 in Sect. 3.2). This is illustrated in Fig. 2 where three ellipsoids, all representing positive definite symmetric mappings having identical eigenvalues, are shown. The two first ellipsoids can be rotated into each other by a rotation around the z-axis. This implies that the corresponding tensors R_abcd and ${\tilde{R}}_{abcd}$ are equivalent. The third ellipsoid can also be rotated into the two others, but these rotations are around directions other than the z-axis, which means that this ellipsoid represents a different tensor.

In the generic case, with all eigenvalues different, it is easy to test whether two different ellipsoids can be transfered into each other through a rotation around the z-axis. This will be the case if the corresponding eigenvectors (of M_ij and ${\tilde{M}}_{ij}$) have the same angle with the z-axis. Hence it is just a matter of checking the z-components of the three normalized eigenvectors and see if they are equal up to sign.

4.1.2. Components in a Canonical Coordinate System

In a sense, this is the most straightforward method. In a coordinate system which respects $e_{ab}^{(3)}$ as the z-axis in $V_{(ab)}\sim {\mathbb{R}}^3$, two tensors R_abcd and ${\tilde{R}}_{abcd}$ are equivalent if there is a rotation matrix (in two dimensions) Q such that

$$\left(\begin{array}{cc}A& \overrightarrow{\stackrel{{}_{{}_{\circ }}}{T}}\\ \overrightarrow{\stackrel{{}_{{}_{\circ }}}{T}}{}^{{}^{{}^t}}& \frac{1}{2}T\end{array}\right)=\left(\begin{array}{cc}{Q}^t\tilde{A}Q& Q^t\overrightarrow{\stackrel{{}_{{}_{\circ }}}{\tilde{T}}}\\ \overrightarrow{\stackrel{{}_{{}_{\circ }}}{\tilde{T}}}{}^{{}^{{}^t}}Q& \frac{1}{2}\tilde{T}\end{array}\right).$$ (16)

Hence, equivalence can be easily tested by first checking that $T=\tilde{T}$ and that $\Vert \overrightarrow{\stackrel{{}_{{}_{\circ }}}{T}}\Vert =\Vert \overrightarrow{\stackrel{{}_{{}_{\circ }}}{\tilde{T}}}\Vert$. If this is the case, (and if $\Vert \overrightarrow{\stackrel{{}_{{}_{\circ }}}{T}}\Vert >0$) one determines the rotation matrix Q which gives $\overrightarrow{\stackrel{{}_{{}_{\circ }}}{T}}=Q^t\overrightarrow{\stackrel{{}_{{}_{\circ }}}{\tilde{T}}}$, and equivalence is then determined by if $A=Q^t\tilde{A}Q$ or not. If $\Vert \overrightarrow{\stackrel{{}_{{}_{\circ }}}{T}}\Vert =\Vert \overrightarrow{\stackrel{{}_{{}_{\circ }}}{\tilde{T}}}\Vert =0$, the equivalence of A and $\tilde{A}$ can be determined directly, i.e., by checking whether $[A]=[\tilde{A}]$ and $[A^2]=[{\tilde{A}}^2]$ or not.

4.1.3. Equivalence Through (algebraic) Invariants of R_abcd

If a solution is found, this is perhaps the most satisfactory way to establish equivalence, in particular if the invariants are constructed by simple algebraic operations only. (For instance, to a symmetric 3 × 3-matrix A one can take the three eigenvalues as invariants or else for instance the traces of A, A² and A³. The former set requires some calculations, but the latter is immediate.)

Examples of invariants are T = R_abcdg^abg^cd, S = R_abcdg^acg^bd and the invariants H = H_abg^ab, W = W_abg^ab. To produce the invariants, we use the tensor R_abcd and the metric g_ab. However, if we regard $V^a\sim {\mathbb{R}}^2$ as oriented, so that the orthonormal basis $\{\widehat{\xi },\widehat{\eta }\}$ for V^a also is oriented, then invariants can also be formed in another way. Namely, since the space of symmetric 2 × 2 matrices is 3-dimensional, and since the metric g_ab singles out a 1-dimensional subspace, it also determines a 2-dimensional subspace L; all elements orthogonal to g_ab. This subspace is the set of all symmetric 2 × 2 matrices which are also trace-free. L can be given an orientation through an area form, which in turn inherits the orientation from V^a.

In general, with right-handed Cartesian coordinates x¹, x², the area form ϵ is given by ϵ = dx¹ ∧ dx² where (ω ∧ μ)_ab = ω_aμ_b − ω_bμ_a. With the orthonormal basis $\{\widehat{\xi },\widehat{\eta }\}$ (for V^a ) also right handed, we define, cf. (2),

$$e_{ab}^{(1)}=\frac{1}{\sqrt{2}}({\widehat{\xi }}_a{\widehat{\xi }}_b-{\widehat{\eta }}_a{\widehat{\eta }}_b),e_{ab}^{(2)}=\frac{1}{\sqrt{2}}({\widehat{\xi }}_a{\widehat{\eta }}_b+{\widehat{\eta }}_a{\widehat{\xi }}_b).$$ (17)

The area form on L is then ϵ ~ e⁽¹⁾ ∧ e⁽²⁾, or

$$ϵ\sim E_{abcd}=e_{ab}^{(1)}{e}_{cd}^{(2)}-e_{ab}^{(2)}{e}_{cd}^{(1)}.$$ (18)

It is not hard to see that this definition is independent of the orientation of $\{\widehat{\xi },\widehat{\eta }\}$. We observe that $2E_{abcd}=({\widehat{\xi }}_a{\widehat{\xi }}_b-{\widehat{\eta }}_a{\widehat{\eta }}_b)({\widehat{\xi }}_c{\widehat{\eta }}_d+{\widehat{\eta }}_c{\widehat{\xi }}_d)-({\widehat{\xi }}_a{\widehat{\eta }}_b+{\widehat{\eta }}_a{\widehat{\xi }}_b)({\widehat{\xi }}_c{\widehat{\xi }}_d-{\widehat{\eta }}_c{\widehat{\eta }}_d)$. By replacing $\widehat{\xi }$ by $\widehat{\omega }=\cos v\widehat{\xi }+\sin v\widehat{\eta }$ and $\widehat{\eta }$ by $\widehat{\mu }=-\sin v\widehat{\xi }+\cos v\widehat{\eta }$, i.e., a rotated orthonormal basis, it is straightforward to check that

$$\begin{gathered} ({\widehat{\omega }}_a{\widehat{\omega }}_b-{\widehat{\mu }}_a{\widehat{\mu }}_b)({\widehat{\omega }}_c{\widehat{\mu }}_d+{\widehat{\mu }}_c{\widehat{\omega }}_d)-({\widehat{\omega }}_a{\widehat{\mu }}_b+{\widehat{\mu }}_a{\widehat{\omega }}_b)({\widehat{\omega }}_c{\widehat{\omega }}_d-{\widehat{\mu }}_c{\widehat{\mu }}_d) \\ =({\widehat{\xi }}_a{\widehat{\xi }}_b-{\widehat{\eta }}_a{\widehat{\eta }}_b)({\widehat{\xi }}_c{\widehat{\eta }}_d+{\widehat{\eta }}_c{\widehat{\xi }}_d)-({\widehat{\xi }}_a{\widehat{\eta }}_b+{\widehat{\eta }}_a{\widehat{\xi }}_b)({\widehat{\xi }}_c{\widehat{\xi }}_d-{\widehat{\eta }}_c{\widehat{\eta }}_d) \end{gathered}$$ (19)

so that E_abcd is well defined. We recollect that area form E_abcd is defined, through the induced metric, on the plane L (which in turn is also defined through the metric g_ab) and the orientation on V^a. Hence E_abcd can be used when forming invariants.

We will now state the result of this work, namely the existence of six invariants which can be used to investigate equivalence of two tensors R_abcd and ${\tilde{R}}_{abcd}$. We start by defining

$$\begin{gathered} S=R_{abcd}{g}^{ac}{g}^{bd} \\ T=R_{abcd}{g}^{ab}{g}^{cd} \\ {J}_0=R_{abcd}{R}^{abcd} \\ {J}_1=T^{ab}{T}_{ab} \\ {J}_2=R_{abcd}{T}^{ab}{T}^{cd} \\ {J}_3=T^{ab}{R}_{abcd}{E}^{cdef}{T}_{ef}. \end{gathered}$$ (20)

where E_abcd is defined by (17) and (18). Similarly, we define $\tilde{S}$, $\tilde{T}$, ${\tilde{J}}_0$, ${\tilde{J}}_1$, ${\tilde{J}}_2$ and ${\tilde{J}}_3$ as the corresponding invariants formed from ${\tilde{R}}_{abcd}$. We make the remark that for most of these invariants, their immediate interpretations still remain to be found. Rather, their value lie in the fact that they form a set which can be used to establish the equivalence in Theorem 1 below. On the other hand, some interpretations are possible. In particular, the quotient T/S (see Definition 1) lies in the interval [1, 2] and has the meaning given by Lemma 2.

Theorem 1 Suppose that $R_{abcd}={\sum }_{i=1}^n{R}_{ab}^{(i)}{R}_{cd}^{(i)}$, with $R_{ab}^{(i)}\ge 0$ and that R_ijkl are the components of R_abcd in some basis. Suppose also that ${\tilde{R}}_{abcd}={\sum }_{i=1}^{\tilde{n}}{\tilde{R}}_{ab}^{(i)}{\tilde{R}}_{cd}^{(i)}$, with ${\tilde{R}}_{ab}^{(i)}\ge 0$ and that ${\tilde{R}}_{ijkl}$ are the components of ${\tilde{R}}_{abcd}$ in some, possibly unrelated, basis. If (and only if) $S=\tilde{S}$, $T=\tilde{T}$, $J_0={\tilde{J}}_0$, $J_1={\tilde{J}}_1$, $J_2={\tilde{J}}_2$, $J_3={\tilde{J}}_3$, then there is a transformation matrix Pⁱ_j such that

$$R_{ijkl}={\tilde{R}}_{mnop}{P^m}_i{P^n}_j{P^o}_k{P^p}_l.$$

Proof Since the invariants are defined without reference to any basis, it is sufficient to consider the components expressed in an orthonormal frame, and in that case we must prove the existence of a rotation matrix Q ∈ SO(2) so that

$$R_{ijkl}={\tilde{R}}_{mnop}{Q}_{mi}{Q}_{nj}{Q}_{ok}{Q}_{pl}.$$

Since

$$R_{abcd}=M_{ij}{e}_{ab}^{(i)}{e}_{cd}^{(j)},$$ (21)

we can consider the invariants formed from the components of

$$M_{ij}=\left(\begin{array}{cc}A& \overline{u}\\ {\overline{u}}^t& c\end{array}\right)\text{and}{\tilde{M}}_{ij}=\left(\begin{array}{cc}\tilde{A}& \tilde{\overline{u}}\\ {\tilde{\overline{u}}}^t& \tilde{c}\end{array}\right)$$ (22)

and we must demonstrate the existence of a rotation matrix Q = Q_2v such that

$$\tilde{A}=Q_{2v}^{t}A{Q}_{2v},\tilde{\overline{u}}=Q_{2v}^t\overline{u},\tilde{c}=c.$$ (23)

We make the ansatz

$$M_{ij}=\left(\begin{array}{cc}\begin{array}{c}\hfill \frac{\sigma }{2}+a\hfill \\ \hfill b\hfill \end{array}\begin{array}{c}\hfill b\hfill \\ \hfill \frac{\sigma }{2}-a\hfill \end{array}& \begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\\ xy& c\end{array}\right),{\tilde{M}}_{ij}=\left(\begin{array}{cc}\begin{array}{c}\hfill \frac{\tilde{\sigma }}{2}+\tilde{a}\hfill \\ \hfill \tilde{b}\hfill \end{array}\begin{array}{c}\hfill \tilde{b}\hfill \\ \hfill \frac{\tilde{\sigma }}{2}-\tilde{a}\hfill \end{array}& \begin{array}{c}\hfill \tilde{x}\hfill \\ \hfill \tilde{y}\hfill \end{array}\\ \tilde{x}\tilde{y}& \tilde{c}\end{array}\right).$$ (24)

Through (21) it is straightforward to see that

$$\begin{gathered} S=\sigma +c,T=2c,J_0=2(a^2+b^2)+c^2+{\sigma }^2∕2+2(x^2+y^2), \\ {J}_1=2(c^2+x^2+y^2) \end{gathered}$$

so if $S=\tilde{S}$, $T=\tilde{T}$, $J_0={\tilde{J}}_0$, $J_1={\tilde{J}}_1$, it follows that $\sigma =\tilde{\sigma }$, $c=\tilde{c}$, $a^2+b^2={\tilde{a}}^2+{\tilde{b}}^2$ and $x^2+y^2={\tilde{x}}^2+{\tilde{y}}^2$. Since the isotropic part of A, i.e., $\frac{\sigma }{2}I$ is unaffected by a rotation of the coordinate system, we consider the traceless parts $\mathrm{Å}=\left(\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill b\hfill & \hfill -a\hfill \end{array}\right)$, $\stackrel{{}_{\circ }}{\tilde{A}}=\left(\begin{array}{cc}\hfill \tilde{a}\hfill & \hfill \tilde{b}\hfill \\ \hfill \tilde{b}\hfill & \hfill -\tilde{a}\hfill \end{array}\right)$, and the task is to assert a rotation matrix Q such that

$$\left(\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill b\hfill & \hfill -a\hfill \end{array}\right)=Q^t\left(\begin{array}{cc}\hfill \tilde{a}\hfill & \hfill \tilde{b}\hfill \\ \hfill \tilde{b}\hfill & \hfill -\tilde{a}\hfill \end{array}\right)Q,\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)=Q^t\left(\begin{array}{c}\hfill \tilde{x}\hfill \\ \hfill \tilde{y}\hfill \end{array}\right),$$

if also $J_2={\tilde{J}}_2$, $J_3={\tilde{J}}_3$. Again it is straightforward to calculate the remaining invariants, and we find

$$\begin{gathered} J_2=4bxy+2a(x^2-y^2)+2c^3+(4c+\sigma )(x^2+y^2) \\ {J}_3=4axy-2b(x^2-y^2). \end{gathered}$$

and similarly for ${\tilde{J}}_2$, ${\tilde{J}}_3$. Hence, (since $\sigma =\tilde{\sigma }$, $c=\tilde{c}$)

$$\begin{gathered} a^2+b^2={\tilde{a}}^2+{\tilde{b}}^2 \\ {x}^2+y^2={\tilde{x}}^2+{\tilde{y}}^2 \\ 2bxy+a(x^2-y^2)=2\tilde{b}\tilde{x}\tilde{y}+\tilde{a}({\tilde{x}}^2-{\tilde{y}}^2) \\ 2axy-b(x^2-y^2)=2\tilde{a}\tilde{x}\tilde{y}-\tilde{b}({\tilde{x}}^2-{\tilde{y}}^2). \end{gathered}$$ (25)

Suppose first that x² + y² > 0. The equality $x^2+y^2={\tilde{x}}^2+{\tilde{y}}^2$ then guarantees the existence of the rotation matrix Q which is determined via the relation $\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)=Q^t\left(\begin{array}{c}\hfill \tilde{x}\hfill \\ \hfill \tilde{y}\hfill \end{array}\right)$. This can also be expressed as $Q_1^t\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)=Q_2^t\left(\begin{array}{c}\hfill \tilde{x}\hfill \\ \hfill \tilde{y}\hfill \end{array}\right)$ for some rotation matrices Q₁, Q₂, where $Q=Q_2{Q}_1^t$. We now choose the rotation matrix Q₁ so that in the untilded coordinates, y = 0. Similarly we choose Q₂ so that for the tilded coordinates, we get a frame where $\tilde{y}=0$. The equalities between the invariants in (25) then become

$$\begin{gathered} a^2+b^2={\tilde{a}}^2+{\tilde{b}}^2 \\ {x}^2={\tilde{x}}^2 \\ a{x}^2=\tilde{a}{\tilde{x}}^2 \\ -b{x}^2=-\tilde{b}{\tilde{x}}^2, \end{gathered}$$

so that $a=\tilde{a}$, $b=\tilde{b}$. This proves the theorem when x² + y² > 0. When $x^2+y^2={\tilde{x}}^2+{\tilde{y}}^2=0$, i.e., $x=y=\tilde{x}=\tilde{y}=0$, the remaining equality $a^2+b^2={\tilde{a}}^2+{\tilde{b}}^2$ is sufficient since we can again choose frames in which $b=\tilde{b}=0$ and $a>0,\tilde{a}>0$. It then follows that $a=\tilde{a}$. □

5. Discussion

In this work, we started with a family of symmetric positive (semi-)definite tensors in two dimensions and considered its variance. This lead us to a fourth order tensor R_abcd with the same symmetries as the elasticity tensor in continuum mechanics. After listing a number of possible issues to address, we focused on the equivalence problem. Namely, given the components of two such tensors R_abcd and ${\tilde{R}}_{abcd}$, how can one determine if they represent the same tensor (but in different coordinate systems) or not? In Sect. 4, we saw that this could be investigated in different ways. The result of Theorem 1 is most satisfactory in the sense that it is expressible in terms of the components of the fourth order tensors directly.

There are two natural extensions and/or ways to continue this work. The first is to apply the result to realistic families of e.g., diffusion tensors in two dimensions. The objective is then, apart from establishing possible equivalences, to investigate the geometric meaning of the invariants. The other natural continuation is to investigate the corresponding problem in three dimensions. The degrees of freedom of R_abcd will then increase from 6 to 21, leaving us with a substantially harder, but also perhaps more interesting, problem.