Abstract
Additional treatment options for temporal lobe epilepsy are needed, and potential interventions targeting the cerebellum are of interest. Previous animal work has shown strong inhibition of hippocampal seizures through on-demand optogenetic manipulation of the cerebellum. However, decades of work examining electrical stimulation—a more immediately translatable approach—targeting the cerebellum has produced very mixed results. We were therefore interested in exploring the impact that stimulation parameters may have on seizure outcomes. Using a mouse model of temporal lobe epilepsy, we conducted on-demand electrical stimulation of the cerebellar cortex, and varied stimulation charge, frequency and pulse width, resulting in over 1000 different potential combinations of settings. To explore this parameter space in an efficient, data-driven, manner, we utilized Bayesian optimization with Gaussian process regression, implemented in MATLAB with an Expected Improvement Plus acquisition function. We examined three different fitting conditions and two different electrode orientations. Following the optimization process, we conducted additional on-demand experiments to test the effectiveness of selected settings. Regardless of experimental setup, we found that Bayesian optimization allowed identification of effective intervention settings. Additionally, generally similar optimal settings were identified across animals, suggesting that personalized optimization may not always be necessary. While optimal settings were effective, stimulation with settings predicted from the Gaussian process regression to be ineffective failed to provide seizure control. Taken together, our results provide a blueprint for exploration of a large parameter space for seizure control and illustrate that robust inhibition of seizures can be achieved with electrical stimulation of the cerebellum, but only if the correct stimulation parameters are used.
Keywords: personalized medicine, responsive neurostimulation, search algorithm, DBS, neuromodulation
Electrical stimulation of the cerebellum has variously been shown to increase, decrease, or have no effect on epileptic seizures. Stieve et al. show that successful cerebellar-targeted intervention is dependent on using specific stimulation parameters, which can be identified using a data-driven search algorithm.
Introduction
Temporal lobe epilepsy, the most common form of epilepsy in adults,1 is notoriously pharmacoresistent, leading the majority of patients to have a severe decline in their quality of life.2,3 Approximately 30–40% of epilepsy patients do not experience sufficient seizure control with antiseizure medications,4–7 leading many to seek neurostimulation adjunct therapies, including deep brain stimulation (DBS), responsive neurostimulation (RNS) and vagal nerve stimulation (VNS). However, even with these additional therapeutic options, many patients continue to have uncontrolled seizures. Illustrating patient need, in the initial RNS cohort, the average seizure frequency prior to initiating RNS treatment was over 50 seizures a month, despite on-going pharmacological approaches, one-third of patients having been treated with VNS and one-third of patients already having had neurosurgery.8 Unfortunately, while RNS was beneficial to many of those patients, less than 20% experienced even one year of seizure freedom over a 9-year period.8 Clearly, additional therapy options are needed.
The cerebellum is classically considered a motor structure,9 but is increasingly appreciated for its role in a range of functions.10–14 The cerebellum has been a potential intervention target of interest for epilepsy for decades.15–19 Recently, on-demand optogenetic work has suggested robust inhibition of both hippocampal20–22 and absence seizures23,24 in rodent models with cerebellar directed intervention. However, electrical stimulation of the cerebellum has produced very mixed results, both in human clinical studies25–36 and in various animal models.37–57 On-demand optogenetic approaches have a number of experimental benefits over open-loop electrical stimulation, including cell-type and temporal specificity, as well as direct control over the direction of modulation of neurons (excitation versus inhibition). However, optogenetic methods are not currently a clinical option for epilepsy patients (although exciting progress is being made on making this a potential future reality58). Therefore, we were interested in determining if electrical stimulation of the cerebellum could be done in a manner which provided robust inhibition of seizures.
When conducting electrical stimulation interventions, a range of parameters must be decided, often with insufficient a priori knowledge to guide the selection. For example, electrical stimulation can vary the frequency of stimulation, the strength of the stimulation, and the duration of each pulse of stimulation (among other variables). Previous studies examining cerebellar stimulation have used a wide range of parameters, often without a strong rationale for the chosen settings. We hypothesized that stimulation settings may be critical in determining outcomes of electrical stimulation of the cerebellum for seizure control. Notably, this includes the potential for interactions between variables (e.g. frequency and pulse width). Especially considering the combinatorial nature, the number of potential settings to test quickly becomes overwhelming. Given such challenges, it is not surprising that a proper optimization of cerebellar stimulation settings, even in animal models, has never occurred.
We therefore turned to Bayesian optimization59–61 to complete such an optimization and test if robust inhibition of hippocampal seizures is possible via cerebellar stimulation. Bayesian optimization allows for a thorough, data driven exploration of large parameter spaces and is being increasingly applied to neuroscience related areas, including epilepsy62,63 and DBS.64–67 We used a mouse model of temporal lobe epilepsy, detected spontaneous seizures online via hippocampal local field potential (LFP) recordings, and delivered on-demand electrical stimulation to the cerebellar vermis. We varied the frequency, charge and pulse width and computed effectiveness (measured as seizure duration) online. In parallel, we completed Gaussian process regression of the incoming data, allowing automated selection of the next set of parameters to try based on the modelling of the effectiveness across the parameter space. We designed the experiments to balance deeper exploration of areas predicted to be effective with broader exploration of the full parameter space. This broader exploration prevented mistaking local minima for a global minimum, and more generally provided a fuller picture of the parameter space. After identifying parameters predicted to be effective (optimized settings), we completed additional testing to directly compare seizure outcomes with this optimized intervention to no intervention. We additionally tested a set of parameters predicted to be ineffective. We tested different initial fitting conditions and different electrode orientations. Across our experiments, we found that robust seizure inhibition could be achieved, but only with effective stimulation settings. Across animals, modelling conditions, and electrode orientations, interventions using high frequency stimulation and relatively strong charge were identified as optimal and were able to provide robust seizure inhibition. Our findings illustrate the benefits of taking a Bayesian optimization approach and help resolve controversies around electrical stimulation of the cerebellum for seizure control. We show that electrical stimulation of the cerebellum can be highly effective, but outcomes are critically dependent on the stimulation parameters.
Materials and methods
Animals
For all experiments, male and female C57BL/6J (Jackson Laboratories stock #000664) mice, bred in-house, were used. Mice were sexed at the time of weaning based on external genitalia. Prior to electrographic recordings, mice lived in standard housing conditions in the animal facility at the University of Minnesota. Following kainate (KA) injections, male mice were singly housed to avoid fighting. After electrode implantation, all mice were singly housed to avoid damage to implants. During electrographic recordings, mice lived in investigator-managed housing. At all times, mice had ad libitum access to food and water and were on a 12-h light:12-h dark (low red light) cycle. All experimental protocols were approved by the University of Minnesota’s Institutional Animal Care and Use Committee (IACUC protocol 2011-238662A).
Stereotactic surgeries
Epilepsy induction
The mouse unilateral intra-hippocampal KA model of chronic temporal lobe epilepsy68,69 was implemented.70 In brief, mice (postnatal Day 45 or later) were anaesthetized with isoflurane and received local bupivacaine. Stereotaxic injection of 90–100 nl of 18.5 mM KA in sterile saline into the hippocampus [from bregma, anterior-posterior (AP): −2.0 mm, medial-lateral (ML) 1.25 mm left, dorsal-ventral (DV): 1.6 mm] was delivered with a microlitre syringe (Hamilton 2 μl, Neuros). Mice were rapidly recovered from anaesthesia (within 5 min of injection)71 and treated with Neo-Predef. As expected, spontaneous recurrent electrographic seizures were observed within several weeks post-injection.68 Optimization experiments started on average 10.7 ± 2.5 weeks post-KA injection (range: 2.9–52.1 weeks).
Electrode implantation
After at least 12 days post KA-injection, mice were implanted with two electrodes: a bipolar twisted microwire electrode (50 µm diameter stainless steel with polyimide insulation, P1 Technologies) for depth electrographic recordings in the hippocampus and a low-impedance bipolar stimulation electrode (200 µm diameter tungsten with polyimide insulation, P1 Technologies) on the cerebellum. Prior to implantation, stimulating electrodes were fashioned by bending a pair of untwisted electrodes 90° and trimming the ends to 0.5 mm beyond the bend, creating electrode feet 1 mm apart. The polyimide insulation along the 0.5 mm end was exposed with a blade. Under isoflurane anaesthesia with carprofen (5 mg/kg subcutaneous) and local subcutaneous bupivacaine, mice were implanted with the recording electrode in the hippocampus (from bregma, AP: −2.6 mm, ML 1.75 mm left, DV: 1.4 mm) and the stimulating electrode epidurally along the midline over cerebellar lobules 4/5 and 6. For the stimulating electrode, a 2.5 mm craniotomy, 6.75 mm posterior to bregma, along the midline was drilled. The electrode was placed in the centre of the craniotomy, with the feet positioned either perpendicular or parallel to the midline (Fig. 5A), lightly pressed into the dura and then sealed over with UV curing dental acrylic (Pentron FlowIt), insulating the dorsal surface of the electrodes, but keeping the ventral surface exposed to the tissue. Both recording and stimulating electrodes were secured with Metabond acrylic. Mice were treated with Neo-Predef and analgesics (ibuprofen, 50–80 mg/kg/day dissolved in drinking water, for one pre-surgical and three post-surgical days) and allowed to recover for at least a week prior to electrophysiology recordings.
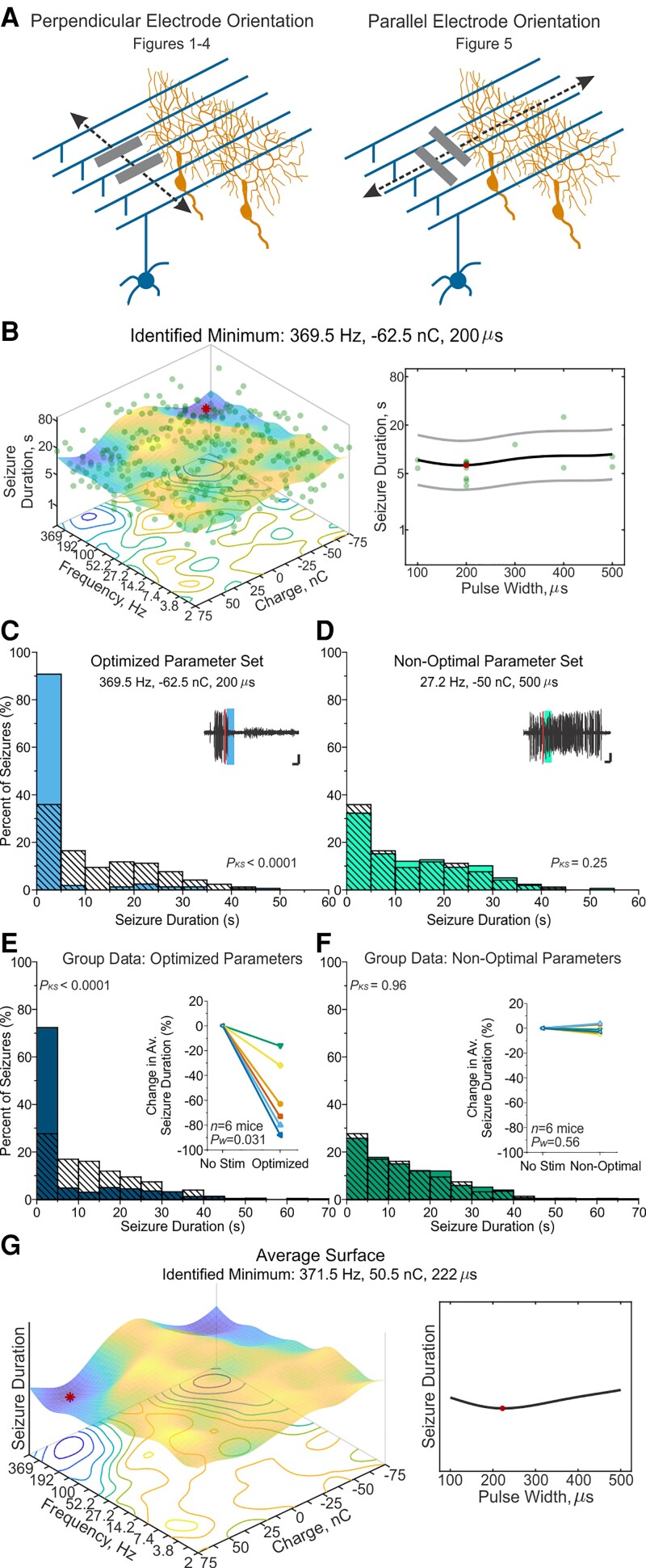
Figure 5.
Rotated electrode orientation still permits effective optimization and seizure-control. (A) Mice were initially implanted with electrode feet perpendicular to the midline (left). As varying the electrode orientation influences the direction of current flow relative to the stereotyped cytoarchitecture of the cerebellum—where parallel fibres of granule cells (blue) run perpendicular to the midline and perpendicular to the nearly-2D dendritic arbors of Purkinje cells (orange)—we also tested electrical stimulation of the cerebellar cortex with electrode feet positioned parallel to the midline (right). (B) Final response-surface from an example animal with a parallel electrode orientation. The minimum of 369.5 Hz, −62.5 nC, and 200 µs pulse width was identified from 1080 non-zero combinations. (C and D) Post-stimulation-onset seizure duration distributions for the example animal shown in B. Left filled light blue bars: Events receiving optimized stimulation; right filled light green bars: events receiving non-optimal stimulation; hashed bars: no-stimulation internal control. (C) When stimulation was applied with the optimized parameter set of 369.5 Hz, −62.5 nC charge and 200 µs pulse width, an 80% reduction in seizure duration was observed (P < 0.0001, Kolmogorov–Smirnov test). Inset: Example seizure event receiving the optimized stimulation (thick blue bar) following detection (thin red line). Scale = 3 s, 0.33 mV. (D) Seizure duration when stimulation was applied with the non-optimal parameter set of 4 Hz, −50 nC, and 400 µs pulse width produced a non-significant 4% increase in seizure duration in this animal (P = 0.25 two-sample Kolmogorov–Smirnov test). Inset: Example seizure event receiving non-optimal stimulation (thick green bar) following detection (thin red line). Scale = 3 s, 0.33 mV. (E and F) Post-stimulation-onset seizure duration distributions across animals (100 random seizure events per condition per animal). Left filled dark blue bars: Events receiving optimized stimulation; hashed bars: no-stimulation control; right filled dark green bars: events receiving non-optimal intervention. Inset: Individual animal data. Note that each colour/symbol represents a different animal, with colour coding consistent for E and F. Open symbols: Insignificant change at the individual animal level (P > 0.05). Closed symbols: Significant change for Kolmogorov–Smirnov and Mann–Whitney tests (P < 0.01) at the individual animal level. (E) Seizure duration when stimulation was applied with each animal’s individualized optimized parameter set on average reduced seizure duration by 58.7 ± 11.6% (P = 0.031 Wilcoxon test, significant in 6/6 mice). (F) Seizure duration with non-optimal parameter sets did not significantly change seizure duration (average 1 ± 1.5% reduction in seizure duration, P = 0.56 Wilcoxon test, not significant in 6/6 mice). (G) Average response-surface, based on the final response-surfaces of six mice. Red dot marks the minimum of the surface at 371.5 Hz, 50.5 nC, and 222 µs pulse width. Related data can be found in Supplementary Figs 4, 10 and 11 and Supplementary Tables 7 and 8. KS = two-sample Kolmogorov-Smirnov statistical test.
Real-time Bayesian optimization of on-demand seizure-intervention
Electrophysiological recordings and electrical stimulation
Epileptiform events were detected in real-time and used to trigger trains of current pulses applied to the cerebellar cortex (see online seizure detection below). Mice were tethered and freely behaving in a modified home cage during optimization and testing. Hippocampal LFPs were recorded using a BrownLee 440 amplifier (settings: 1–2000 Hz passband, 1 MΩ input impedance, 100–300-fold gain). These settings were selected to ensure stimulation artefacts never saturated input of the National Instruments data acquisition device (USB-6229 BNC). The analogue inputs and outputs were sampled and generated at 20 kHz with 16-bit resolution so that the artefacts could be recorded and removed, preserving the LFPs with no gaps (see below and Supplementary Fig. 1). Pulse trains were generated on-demand by a digital to analogue converter [DAQ, National Instruments, 6229 (BNC)] and converted into current-controlled pulses at 100 µA/V by an A-M Systems 2200 stimulator (A-M Systems). To avoid any non-zero voltage drift at the output, a first-order RC high pass filter [either R = 0.5 MΩ, C = 215 nF, corner frequency (fc) = 1.5 Hz; or R = 1 MΩ, C = 215 nF, fc = 0.75 Hz] was installed at the output of the stimulator. To ensure multi-day battery life, the stimulator’s batteries were replaced with large, sealed lead acid batteries (12 V, 7 AH).
Online seizure detection
LFPs were processed in real-time to detect and record seizure durations with custom MATLAB (Mathworks, Natick, MA) based software, using a series of digital filters, rectification, and thresholding to isolate epileptic spikes (Supplementary Fig. 1). Ictal spike detection was individualized for each mouse based on several features, including minimum and maximum inter-spike distance, spike width and spike amplitude (similar to Armstrong et al.70). Additionally, epileptic spikes were often associated with brief high frequency oscillations (HFOs)72; therefore, in some instances, an HFO detector (500–1500 Hz; using the same features as spike detection; spike width, amplitude, etc.) was used to improve spike discrimination. Spike and HFO coincidence detection was individualized, as well as the minimum number of spikes arriving in 2 s to constitute the beginning—or for online seizure duration analysis (see below) the end—of an event. In order to observe spikes during stimulation, the stimulus-locked artefacts were removed from the LFPs using a least mean squares adaptive filter73 with 20 ms of history at a 20 kHz sampling rate (MATLAB’s DSP toolbox, Supplementary Fig. 1). The adaptive filter fits a finite impulse response (FIR) filter by comparing the stimulus waveform to the recorded signal’s artefacts, similar to template removal, but generalized across waveforms. To enable the artefact-removal processing, and support optimization of up to four mice in parallel, data was processed in 1 s segments. Note that this caused a 1 s delay between seizure detection and delivery of stimulation. The performance and stability of the adaptive filter was improved by reapplying the adaptive filter three times to each second of data. The first two passes were used to adapt the filter and the artefact was removed in the third pass. In this manner, even artefacts near the beginning of the train were profoundly suppressed. Over fitting was not an issue; epileptiform spikes were not correlated in time to the stimulus onset and therefore did not appear to be affected by the adaptive filter (Supplementary Fig. 1). For the optimization process, the duration of epileptiform events were defined as the time between the first and last epileptic spike of the event and converted to a logarithmic scale using the natural log.
Subject-specific Gaussian process regression and Bayesian optimization
In real-time, we optimized cerebellar stimulation for suppression of hippocampal seizures. In brief, stimulation of the cerebellar cortex was delivered in response to seizure detection. The duration of the seizure was recorded and Gaussian process regression was used to form a response surface. The response surface predicts seizure duration as a function of stimulation parameters, across the entire parameter space, and can make estimates for even unsampled parameter combinations. Based on the response-surface, Bayesian optimization determines which parameters to test next, to efficiently explore the parameter space in a data-driven manner64,74 (Fig. 1A). This optimization process can be designed to balance exploration and exploitation. Given the exploratory nature of our study, we opted for greater exploration.
Figure 1.
On-demand Bayesian optimization of cerebellar-directed seizure-intervention. (A) Online hippocampal seizure detection triggers electrical stimulation of the cerebellar cortex (on-demand loop). Seizure duration is recorded in real-time and Gaussian process regression is used to build a response-surface (Bayesian optimization loop). The response-surface is updated with each event, and the next set of parameters to test is determined via Bayesian optimization. Note that only frequency and charge are illustrated here, but optimization occurred over frequency, charge, and pulse width. (B) An example final response-surface where cooler and warmer colours represent shorter and longer event durations, respectively. The larger (red) dot indicates the identified minimum, representing the optimal parameter. Due to the high dimensionality of the data, three planes are shown. In the top row, the interaction of frequency versus charge for combinations with 300 µs pulse width is shown on the left, while the impact of pulse width, at 369.5 Hz and 62.5 nC, is shown on the right. The next rows follow the same pattern, highlighting the interaction of frequency and pulse width, and the impact of charge (middle row), and the interaction of pulse width and charge, and the impact of frequency (bottom row). Note that in subsequent figures, only one plane for a given response-surface is illustrated, through the identified minimum. (C) A parameter walk from the same example animal as in B, demonstrating that the optimizer selects a range of parameters (green dots), and updates the estimate of the best set of parameters (blue line) with each event. In this example, the optimizer settles on 369.5 Hz, 62.5 nC and 300 µs, but continues to test several other combinations of settings. Note that tick marks on the y-axis indicate the discrete steps tested for each parameter. Related data can be found in Supplementary Figs 1 and 2 and Supplementary Table 1.
In further detail, we optimized across three stimulation parameters (frequency, charge per pulse, and pulse width) for seizure-suppression, using three different parameter spacing and fitting conditions. The maximum values of each parameter (i.e. the extrema of the parameter space) were selected to avoid adverse behavioural reactions and stimulation-induced tissue damage. Pulses were charge balanced (at a 3:1 ratio; Supplementary Fig. 1) to avoid adverse electrochemical reactions,75 allowing testing of pulse widths up to 500 µs and frequencies as high as 512 Hz. The charge range was chosen to remain within the safety guidelines reviewed by Cogan et al.75 with an estimated electrode area of 170 000 µm2 which is between that of a micro- and macroelectrode.
In the first two parameter spaces, optimized parameters included (i) frequency (2 to 512 Hz, 18 or nine steps spaced logarithmically); (ii) charge per pulse (−75 to 75 nC, 13 or seven steps spaced linearly); and (iii) pulse width (100–500 µs, five steps spaced linearly). Therefore, in addition to non-stimulation (zero charge) combinations, the discretized parameter space contained either 1080 or 270 stimulation (non-zero) parameter combinations. In a third, ‘restricted’ parameter space, all three parameters were divided into 10, linearly spaced, steps where frequency ranged from 62 to 512 Hz, charge ranged from 0 to +75 nC and pulse width ranged from 100 to 500 µs. In the restricted parameter space, there were therefore 900 non-zero parameter combinations. Stimulation parameters that were kept constant included the current waveform (biphasic; see Supplementary Fig. 1B) and stimulation train duration (3 s; used in previous optogenetic experiments20–22).
Bayesian optimization on a Gaussian process regression is a sequential method for exploring a space to efficiently find an optimum.59–61 Gaussian process regression, like the more familiar linear regression, fits a surface to data-points, but unlike a linear regression, Gaussian process regression is allowed to bend locally to better fit the data. The flexibility of the response-surface is determined by the kernel function. We used an ARD Matern 5/2 kernel76 (built into MATLAB’s Bayesian Optimization class77), where the surface flexibility is derived from the length-scale for each parameter axis. Smaller length-scales fit the observed data more tightly, reducing the influence of neighboring observations on expected outcomes of parameters, resulting in a more flexible response-surface. Larger length-scales allow for greater influence of previous observations, resulting in a more generalized, smoother surface. To start to determine whether effective optimization would depend on the length-scale, we changed the length-scale with the number of steps in each dimension. In the first two parameter spaces, pulse width (five steps) had a length-scale of 120 µs. In the parameter space with 1080 non-zero combinations (18 steps for frequency, 13 steps for charge), length-scales were 3.4 dB-Hz for the frequency and 15 nC for charge. In the parameter space with 270 non-zero combinations (nine steps for frequency, seven steps for charge), length-scales increased to 7.22 dB-Hz for the frequency and 30 nC for charge, resulting in a relatively less flexible parameter space (more generalized), compared to the parameter space with 1080 non-zero combinations. For the third, restricted parameter space with 900 non-zero combinations, frequency, charge, and pulse-width had length-scales of 60 Hz, 10 nC, and 53.3 µs, respectively.
At every point in space, the Gaussian process regression estimates the mean and confidence of the optimized variable. Bayesian optimization reads the response-surface created by the Gaussian process regression to decide what setting to test next. The optimizer must balance testing in areas that were previously found to be successful to improve confidence and find incremental improvement (reducing time spent in ineffective areas) and exploring more widely. This tradeoff is essential to the nature of optimization problems, and as noted above, we elected for a fairly large exploration component. We used the Expected-Improvement Plus acquisition function (EI-plus; MATLAB’s Bayesian Optimization class77). EI-plus chooses settings expected to most improve the optimum, with an additional comparison to avoid over-exploitation of a local minimum. Using a term called the exploration ratio (set at 0.5 for our study to favour exploration), the optimizer determines, based on the variance of the noise and the confidence of the estimate, whether the selected point in the parameter space is being over-exploited, and if so, modifies the kernel function and selects a new point to test.78 Progress of optimization was periodically monitored, and typically considered stable if the optimizer chose the same set of the three parameters as the predicted best for at least 100 consecutive events, after a minimum of 1000 events was collected. If over 1500 events were collected, and the optimizer had not stabilized at the time of observation, the last identified parameter combination was used as the optimized set. Optimization took on average 5.4 ± 0.35 days (range: 3–9 days).
Testing of settings with interleaved single-loop interventions
Following optimization, we first conducted a second round of testing using a single-loop on-demand approach (i.e. only the ‘on-demand loop’ in Fig. 1A). This allowed us to obtain a sufficient number of events for direct statistical comparisons. For each seizure detected, either (i) optimized stimulation; (ii) non-optimal stimulation; or (iii) no stimulation (as an internal control) was delivered in an interleaved, random fashion. The minimum of each animal’s individualized response-surface, associated with the shortest seizure durations, was used as the optimized parameter set. The maximum of the final response-surface, the point associated with the longest seizure durations, was used as the non-optimal parameter set. Note that for one animal (parallel electrode orientation, more flexible parameter space), the non-optimal setting was 0 nC, and therefore the same as the no-stimulation control (this animal is represented by a dark orange square in the inset in Fig. 5). In all other cases a non-zero charge was identified as the non-optimal setting.
Given that response-surfaces followed similar patterns across animals (i.e. that different animals seemed to respond in similar ways to the various stimulation settings), we conducted an additional round of single-loop on-demand testing to examine if group-derived settings (as opposed to individually optimized settings) could also provide sufficient seizure-suppression. First, average response-surfaces were calculated by taking the average of normalized final response-surfaces from all mice with the same electrode orientation, within the same parameter space, with each animal weighted equally. The minimum of this average response-surface (Fig. 2F) was deemed the ‘group average’ optimal settings. We also examined the ‘group mode’ optimal settings. The group mode setting was based on the most common setting (i.e. the mode) for each of the three parameters (Table 1). If two values were equally common, one was arbitrarily chosen to serve as the mode. Additionally, given that the polarity of charge did not appear to be a critical factor, to calculate the mode for optimal charges, we used the absolute value. Then, to determine the polarity of the charge to use when testing, the more common sign (i.e. negative charge) was selected. In total, four conditions were tested in this set of single-loop on-demand experiments: (i) the individualized optimized setting for each mouse (determined via the prior optimization process); (ii) the group average setting; (iii) the group mode setting; and (iv) no-stimulation.
Figure 2.
Electrical stimulation of the cerebellum with optimized parameters provides seizure-control. (A) Example seizure events from the same animal shown in Fig. 1. Events were detected online (thin red bar) and received, in a random, interleaved fashion, no stimulation (top), stimulation with optimal parameters (middle, blue bar) or stimulation with non-optimal parameters (bottom, green bar). Stimulation was delivered for 3 s, with frequency, charge, and pulse width determined by the final response-surface (Fig. 1B). Scale bar = 5 s, 0.5 mV. (B and C) Post-stimulation-onset seizure duration distributions for the example animal shown in A. (B) Seizure duration distributions when stimulation was applied with the optimized parameter set of 369.5 Hz frequency, 62.5 nC charge, and 300 µs pulse width (filled light blue bars) versus no-stimulation (hashed bars). In this example animal, an 87% reduction in seizure duration occurred (P < 0.0001, Kolmogorov–Smirnov test). (C) Seizure duration distributions for the non-optimal parameter set (filled light green bars; in this animal: 138.9 Hz, −25 nC, and 400 µs pulse width), or for comparison, no-stimulation (hashed bars). In this animal, a non-significant 4% increase in seizure duration was noted with non-optimal stimulation (P = 0.43, Kolmogorov–Smirnov test). Note that the same no-stimulation seizure duration distribution is overlaid in B and C. (D and E) Post-stimulation-onset seizure duration distributions across animals (n = 7 mice), using 100 randomly chosen seizure events per condition per animal, and with the same no-stimulation dataset illustrated for comparison (hashed bars) in both D and E. (D) Filled dark blue bars: Events receiving each animal’s optimized stimulation; hashed bars: no-stimulation control. Stimulation with optimized parameters provides significant and consistent seizure-reduction [inset: significant at the individual level in seven of seven animals tested; average 70.7 ± 8.2% reduction in seizure duration, P = 0.016, Wilcoxon test (W)]. (E) Filled dark green bars: Events with non-optimal parameters; hashed bars: no stimulation control. Inset: No significant change in seizure duration with non-optimal parameters (insignificant change in 7/7 animals; on average a 0.7 ± 2.7% reduction in seizure duration, P = 0.84, Wilcoxon test). (F) Average response-surface, based on the final response-surfaces of the seven mice. Red dot marks the minimum of the surface at 460.1 Hz, 59.7 nC, and 149 µs pulse width. (G) Group-level post-stimulation-onset seizure duration distributions; 100 random seizure events per condition per animal. Left: Filled dark blue bars: Seizure duration when stimulation was applied with each animal’s individualized optimized parameter set. Middle: Filled purple bars: Seizure duration with stimulation settings based on the most commonly identified optimal parameters (group mode parameters; 266.7 Hz, −62.5 nC, 400 µs pulse width; Table 1). Right: Filled red bars: Seizure duration with stimulation settings based on the minimum of the average surface (460.1 Hz, 59.7 nC, 149 μs pulse width, see F). Hashed bars = no stimulation control. (H) Stimulation with optimized parameters significantly reduces seizure duration whether parameters are derived from individualized optimization (left, average 52.1 ± 10.3% reduction, P = 0.016 Wilcoxon test), or group-derived settings based on the mode (middle, average 42.7 ± 10.0% reduction; P = 0.016 Wilcoxon test) or the minimum of the average surface (right, 47.4 ± 11.4% reduction, P = 0.016 Wilcoxon test). At the group level, there was no significant difference in seizure-reduction between any of the three optimized stimulation conditions (P > 0.375 for each comparison, Wilcoxon test). Note that each colour/symbol represents a different animal, with colour coding consistent throughout the panel. Open symbols: Insignificant change at the individual animal level (P > 0.05). Closed symbols: Significant change (P < 0.01) for Kolmogorov–Smirnov and Mann–Whitney tests at the individual animal level. Related data can be found in Supplementary Figs 3–6 and 11 and Supplementary Tables 1–3. KS = two-sample Kolmogorov-Smirnov statistical test.
Table 1.
Summary of data for individual animals presented in Fig. 2
| Optimized parameters | Non-optimal parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Animal ID, Sexa | Frequency (Hz) |
Charge (nC) |
Pulse width (µs) |
ΔSeizure duration (%)b |
P-values (KS; MW)c |
Frequency (Hz) |
Charge (nC) |
Pulse width (µs) |
ΔSeizure duration (%) |
P-values (KS; MW) |
| Yellow diamond, female | 266.7 | −75 | 400 | −82 | 7.9 × 10−47; 8.9 × 10−37 | 27.2 | −12.5 | 100 | 5 | 0.46; 0.97 |
| Dark orange filled square, male | 512 | −62.5 | 100 | −92 | 8.9 × 10−50; 1.3 × 10−43 | 3.8 | 12.5 | 400 | −5 | 0.84; 0.91 |
| Green filled inverted triangle, male | 369.5 | 62.5 | 300 | −87 | 3.0 × 10−73; 5.8 × 10−61 | 138.9 | −25 | 400 | 4 | 0.43; 0.89 |
| Light orange filled circle, male | 512 | 50 | 400 | −71 | 3.6 × 10−36; 1.8 × 10−37 | 2.8 | 50 | 500 | −12 | 0.13; 0.06 |
| Dark blue filled left arrowhead, male | 266.7 | −62.5 | 300 | −76 | 1.4 × 10−28; 4.6 × 10−22 | 14.2 | −12.5 | 100 | 8 | 0.67; 0.46 |
| Light blue filled triangle, female | 266.7 | 75 | 200 | −28 | 1.5 × 10−08; 3.1 × 10−06 | 10.2 | −62.5 | 200 | −6 | 0.62; 0.54 |
| Pink filled right arrowhead, male | 192.4 | −75 | 400 | −59 | 3.9 × 10−46; 1.1 × 10−33 | 7.4 | −25 | 300 | 1 | 0.40; 0.56 |
Colour and shape of each animal correspond to the symbols in Fig. 2.
ΔSeizure duration is calculated relative to the average post-stimulation-onset seizure duration of the no stimulation control.
Significant values (P-value < 0.05) are highlighted in bold.
Finally, results across animals showed that optimized, effective parameters tended to be relatively high frequency and high charge values. We therefore conducted optimization in a third restricted parameter space (as described above), where the frequency and charge ranges were restricted to 62 to 512 Hz and 0 to +75 nC, respectively. Then, to test whether maximizing the frequency and charge values would outperform optimized parameters, three conditions were examined with single-loop on-demand testing: (i) the individualized optimized setting for each mouse; (ii) maximum frequency (512 Hz), maximum charge (+75 nC) and the pulse width value corresponding to the individualized optimized setting (the ‘corner parameter set’); and (iii) no-stimulation.
Statistical analyses
During Bayesian optimization and single-loop data collection sessions, seizure duration was calculated online. Automated seizure-analysis was carefully monitored by manual inspection, and for single-loop datasets, results were confirmed through offline seizure duration analysis. Offline seizure duration analysis was completed using a combination of manual and automated methods, as described previously by Streng and Krook-Magnuson.21 The stimulation condition was hidden to the reviewer (blinded analysis). Seizure duration from the onset of stimulation (1 s following seizure detection) was used for all offline statistical analyses. Given typical interspike intervals for ictal spikes, seizures that stopped >500 ms prior to the onset of stimulation were excluded, and durations of seizures that stopped within 500 ms of stimulation were considered equal to 0 s. A minimum of 100 seizures per condition per animal were used for analysis. Previous power analyses indicate this provides a power of 0.82 for Mann–Whitney and 0.89 for two-sample Kolmogorov–Smirnov tests for a 20% decrease in seizure durations.20
Change in average seizure duration was calculated by subtracting the average no-stimulation duration from the stimulation duration and dividing by the no-stimulation duration. A Friedman ANOVA was used to determine, at the group level, if there were any differences in seizure durations between conditions for group sizes of six or more animals. Degrees of freedom were equal to two for Friedman ANOVAs, comparing optimal, non-optimal and no stimulation, and three for Friedman ANOVA, comparing personalized optimal, group mode settings, group average and no stimulation. Paired Wilcoxon rank sum tests were then used for direct comparisons between conditions (note that only Wilcoxon P-values are presented). For group comparisons between non-paired data (e.g. electrode orientation), a Mann–Whitney test was used. As an additional measure of group-level results, we sampled 100 events (randomly selected via MATLAB) per condition per animal and created summative histograms: post-stimulation-onset seizure durations were combined from each animal per stimulation condition and compared to the associated no-stimulation distribution. Note that at the group-level the percentage of seizures stopping within 5 s was calculated from this randomized subset of the data. Time from the end of a detected seizure until the start of the next seizure event was additionally calculated offline and underwent statistical analysis in a similar manner as seizure duration (Supplementary Fig. 4 and Supplementary Tables 2, 5 and 8).
Statistical analyses were conducted using MATLAB and Origin software. All statistical tests were conducted as two-tailed, and a P-value of <0.05 was considered statistically significant. Results are reported as mean ± SEM.
Data availability
Data presented in this manuscript is available upon any reasonable request. A version of the software for online seizure detection and Bayesian optimization, as well as the software used for offline seizure duration analysis, is available through GitHub (https://github.com/KM-Lab).
Results
Given the contrast between the success of on-demand optogenetic approaches targeting the cerebellum20–24 and the mixed literature on electrical stimulation of the cerebellum for seizure control,15,18 we hypothesized that on-demand electrical stimulation of the cerebellum could be consistently effective, but only with the correct combination of stimulation parameters. Spontaneous seizure events in chronically epileptic animals were detected online from LFP recordings from the hippocampus, and on-demand electrical stimulation was delivered to the midline cerebellum (vermis lobules 4/5 and 6) (Fig. 1A, ‘on-demand loop’). We first tested stimulation with the electrode feet perpendicular to the midline and examined three different stimulation parameters: (i) frequency; (ii) charge per pulse; and (iii) pulse width. The parameter space was bounded to maximize possible settings while remaining within safety limits of stimulation. Specifically, we examined 2 Hz to 512 Hz stimulation, charge from −75 nC to +75 nC, and pulse widths from 100 µs to 500 µs; this parameter space contained 1080 non-zero stimulation parameter combinations. Given this large number of possible combinations of stimulation settings, we utilized Gaussian process regression to fit response surfaces and Bayesian optimization (Fig. 1A, ‘Bayesian optimization loop’) to effectively search the parameter space in a data driven manner.
The subject-specific, personalized, search of the parameter space was implemented through an expected-improvement plus acquisition function77,78 designed to ensure an efficient, yet thorough, exploration of the parameter spaces (as outlined in the 'Materials and methods'section). Data collection was maximized near areas showing good seizure inhibition (i.e. currently identified minima in seizure durations; blue line in Fig. 1C and red dot on illustrated surfaces) and areas for which relatively less information about effectiveness was available. This allowed both good coverage of the space and increased confidence of effectiveness around identified minima. An example of a parameter walk is illustrated in Fig. 1C, showing both the sampled settings (green dots; note the range of tested settings), and the running estimate of the best set of parameters (blue line). Note that in this example the program settles on 369.5 Hz, 62.5 nC, and 300 µs, starting around 1500 events, but continues to sample other combinations of settings. Across animals, in five of seven optimization sessions all of the 1080 possible non-zero unique parameter combinations were tested at least once, but in all cases the majority of combinations were tested at most one time (Supplementary Fig. 2 and Supplementary Table 1), demonstrating that optimization tested across the space, but concentrated repeated testing to a few settings in effective areas.
Despite potential non-stationarity effects and the relatively high variability in seizure durations in this model of epilepsy, Bayesian optimization successfully identified stimulation parameters for effective seizure-control. The progression of the response-surface for an example animal is shown in Supplementary Video 1, and the same animal’s final surface is illustrated in Fig. 1B, with cooler colours illustrating shorter event durations and the red dots indicating the identified minimum (i.e. the predicted optimal combination of settings). Note that given the high dimensionality of the data, it is not possible to display all of the data in a single graph. Thus, three planes are shown, which each provide a partial representation of the entire multi-dimensional response-surface. The top left plot illustrates the interaction of frequency versus charge (for combinations with 300 µs pulse duration), and top right shows the impact of pulse width (at 369.5 Hz and 62.5 nC, i.e. the identified best combination for this animal). The middle plots show the same animal’s dataset, but instead plots the interaction of frequency with pulse width (at 62.5 nC), with the impact of charge shown to the right. Finally, the bottom row illustrates the interaction of charge and pulse width (at 369.5 Hz), with the impact of frequency shown to the right. From these graphs, it is apparent that stronger charges (of either polarity), and higher frequency stimulation tends to provide more robust seizure control, with pulse width tending to play a smaller role in modulating seizure duration.
Using this optimization protocol, we were able to identify, for each animal, a combination of frequency, charge and pulse width settings that were predicted to provide seizure inhibition (Table 1 and Supplementary Fig. 3). To validate the effectiveness of the individualized, optimized, parameter set we completed an additional set of experiments with each animal, utilizing a more traditional testing framework. Specifically, seizure detection resulted in either no stimulation (as a control), electrical stimulation to the cerebellum using that animal’s personalized optimal combination of settings (‘optimized’), or, as an additional control, intervention using a combination of parameters which, based on the previous Gaussian process regression, was predicted to be ineffective (‘non-optimal’) (Fig. 2). Specifically, non-optimal settings were associated with the longest seizure durations in the response-surface (e.g. the maxima). These were delivered in an interleaved, random, manner. This experimental setup provided a sufficient number of events with each of these three conditions to allow for direct comparison. The identified personalized best set of parameters provided strong seizure inhibition (70.7 ± 8.2% decrease in post-stimulation-onset seizure duration versus no intervention; n = 7 mice; P = 0.016 Wilcoxon test; 82% of seizures stopping within 5 s of the start of intervention; Fig. 2D and Table 1), confirming that our Bayesian optimization approach successfully identified a set of parameters capable of providing seizure inhibition. In contrast, non-optimal stimulation settings failed to provide seizure control (0.7 ± 2.7% decrease versus no intervention; n = 7 mice; P = 0.84; at the individual animal level, insignificant change in seizure duration in all seven of seven tested animals; Fig. 2E and Table 1). Accordingly, optimized settings produced significantly better seizure inhibition than non-optimized settings (percent seizure reduction optimized versus non-optimized: P = 0.016, Wilcoxon test). We additionally examined the time to the next seizure event.20 We found that optimized stimulation did not produce a consistent effect on the average time to next seizure but did change the overall distribution of time to next seizure (Supplementary Fig. 4 and Supplementary Table 2). Non-optimal stimulation typically had no effect on the time to next seizure (Supplementary Fig. 4). Analysis of seizure phenotypes over the course of optimization and single-loop on-demand testing suggested general stability, including regarding the effectiveness of intervention, during these experiments (Supplementary Fig. 5 and Supplementary Tables 1 and 3).
Together these results illustrate that electrical stimulation of the cerebellum can be an effective approach to seizure inhibition, and only if the correct combination of stimulation parameters is utilized.
Potential for non-individualized cerebellar stimulation settings
Across the animals tested, we noted similar final response surfaces (Table 1, Fig. 2F and Supplementary Fig. 3). This suggested that, at least for similar seizure aetiologies, once a set of effective settings is identified, it may be applicable in a broader setting. To test this, we completed an additional round of post hoc testing. In this set of experiments, upon seizure detection, animals received either (i) no stimulation; (ii) personalized optimized, where the parameters selected were the optimized parameters from the subject’s own data; (iii) group mode, where the parameters were the most common (mode) charge, frequency, and pulse width identified as being optimal (specifically, 266.7 Hz frequency, −62.5 nC charge, 400 µs pulse width; Table 1); or (iv) group average, where the parameters were selected as the minimum of the averaged response surface (specifically, 460.1 Hz frequency, 59.7 nC charge, 149 µs pulse width; red dot in Fig. 2F; note these specific frequency, charge, and pulse width settings were not directly tested during optimization, and were derived entirely from the Gaussian process regression). An expanded view with three planes of the average response-surface and clustering of individualized parameters near the group average are illustrated in Supplementary Fig. 6.
As before, these stimulations (or no-stimulation controls), occurred in an on-demand manner (selectively at the time of seizures), in a random, interleaved, order. While some animals showed greater seizure control with one parameter set versus another (Fig. 2H), across the animals, all three sets of stimulation parameters (personalized optimal, group mode, group average) produced strong inhibition of seizures (individualized versus no intervention: 52.1 ± 10.3% decrease, P = 0.016 Wilcoxon test, n = 7 animals, 70% of seizures stopping within 5 s of intervention; group mode versus no intervention: 42.7 ± 10.0% decrease, P = 0.016 Wilcoxon, n = 7 animals, 60% of seizures stopping within 5 s of intervention; group average versus no intervention: 47.4 ± 11.4% decrease, P = 0.016 Wilcoxon, n = 7 animals, 67% of seizures stopping within 5 s of intervention; Fig. 2G and H). At the group level, there was no significant difference in outcomes between personalized optimization, group mode optimal settings, and group average optimal settings (P > 0.375 for each comparison, Wilcoxon test). This further underscores that within a similar population, similar cerebellar stimulation settings can generally be effective, and therefore, once a good set of parameters is identified, personalized optimization may not always be critical.
Optimization process robust to different parameter spacing and fitting conditions
In initializing these experiments, a number of decisions were made, which could potentially impact the findings. These include how many gradations to try (i.e. step size) and how much each outcome for a given set of settings would impact neighbouring combinations (i.e. the length-scale). We were interested in determining if the optimization process was sufficiently robust to allow for some variation in these hyperparameters, or if it was particularly sensitive to the fitting conditions. We therefore completed an additional set of experiments, again using Gaussian process regression and Bayesian optimization, but now with larger step sizes and effective length-scales, essentially allowing for a less flexible (i.e. more generalized) surface.
We found that the process was robust to these changes, and while more smoothed surfaces were generated (as expected), effective minima were still identified (Fig. 3 and Supplementary Fig. 7). Identified optimal settings again provided robust inhibition of seizures (78.7 ± 4.4% decrease in seizure duration versus no intervention; n = 6 mice; P = 0.031 Wilcoxon test; 88% of seizures stopping within 5 s of the start of intervention; Fig. 3D and Supplementary Tables 4 and 5), while non-optimal settings failed to inhibit seizures (9.8 ± 3.5% decrease in seizure duration versus no intervention; n = 6 mice; P = 0.063 Wilcoxon; 33% of seizures stopping within 5 s of the start of intervention; Fig. 3E and Supplementary Tables 4 and 5). Surfaces between animals showed similar profiles (Supplementary Fig. 7). On average, as seen with a more flexible surface, a fairly high frequency (group average: 125.2 Hz), a fairly strong charge (71.9 nC), and fairly short pulse width (149 µs) was determined to be most effective (Fig. 3F).
Figure 3.
Bayesian optimization identifies effective parameters also under less flexible conditions. (A) Example animal’s final response-surface from optimization within the second parameter space, where the number of divisions was reduced from 18 to nine and 13 to seven across the frequency and charge dimensions, respectively. Total number of non-zero stimulation combinations was reduced from 1080 to 270. Additionally, the effective length-scales were increased, causing the surface to be less flexible, or more generalized. (This animal’s more flexible surface optimization can be seen in Supplementary Fig. 3). (B and C) Post-stimulation-onset seizure duration distributions for the example animal shown in A. Left filled light blue bars: Events receiving optimized stimulation; right light green bars: events receiving non-optimal stimulation; hashed bars: no-stimulation internal control for comparison. (B) A 96% reduction in seizure duration was observed in this animal when the optimized parameter set of 512 Hz, 75 nC, and 100 µs pulse width was applied (P < 0.0001 Kolmogorov–Smirnov test). Inset: Example seizure event receiving the optimized stimulation (thick blue bar) following detection (thin red line). Scale = 5 s, 0.5 mV. (C) This example animal showed a non-significant 6% increase in seizure duration (P = 0.98 Kolmogorov–Smirnov test) when stimulation was applied with the non-optimal parameter set of 4 Hz, −50 nC, and 400 µs pulse width. Inset: Example seizure event receiving non-optimal stimulation (thick green bar) following detection (thin red line). Scale = 5 s, 0.5 mV. (D and E) Post-stimulation-onset seizure duration distributions at the group level (100 random seizure events per condition per animal). Left filled dark blue bars: Events receiving optimized stimulation; right filled dark green bars: events with non-optimal parameters; hashed bars: no stimulation control. (D) Seizure duration when stimulation was applied with each animal’s individualized optimized parameter set (P < 0.0001 two-sample Kolmogorov–Smirnov test, n = 6 mice). Inset: Stimulation with individualized optimized parameters provides consistent, significant, seizure-reduction (78.7 ± 4.4% reduction in seizure duration, P = 0.031 Wilcoxon test (W), significant at the individual animal level in 6/6 mice). (E) Seizure duration with a non-optimal parameter set unique to each animal (P = 0.12 two-sample Kolmogorov–Smirnov test, n = 6 mice). Inset: Non-optimal parameters do not change seizure duration (9.8 ± 3.5% reduction in seizure duration, P = 0.063 Wilcoxon test, not-significant in 5/6 mice). Note that each colour/symbol represents a different animal, with colour coding consistent in D and E. Open symbols: Insignificant change at the individual animal level (P > 0.05). Closed symbols: Significant change for Kolmogorov–Smirnov and Mann–Whitney test (P < 0.01) at the individual animal level. (F) Average response-surface, based on the final response-surfaces of the six mice. Red dot marks the minimum of the surface at 125.2 Hz, 71.9 nC, and 149 µs pulse width. Related data can be found in Supplementary Figs 4, 7 and 11 and Supplementary Tables 4 and 5. KS = two-sample Kolmogorov-Smirnov statistical test.
These findings indicate that the Gaussian process regression and Bayesian optimization approach taken here was not strongly reliant on the hyperparameters chosen, but rather was sufficiently robust as to find effective stimulation settings with either a more or less flexible surface.
Optimization in a restricted parameter space
Across animals in both parameter spaces, optimized stimulation tended to contain higher frequency and charge values, with the surfaces generally mirrored for positive and negative charge values. We therefore conducted an additional optimization process, focused on one quadrant of the frequency × charge space, allowing a more thorough exploration of the higher frequency range (now with a linear, rather than logarithmic, spacing). Specifically, all parameters had 10 linearly spaced steps, between 62 to 512 Hz, 0 to +75 nC, and 100 to 500 µs for frequency, charge, and pulse width, respectively (represented in Fig. 4A).
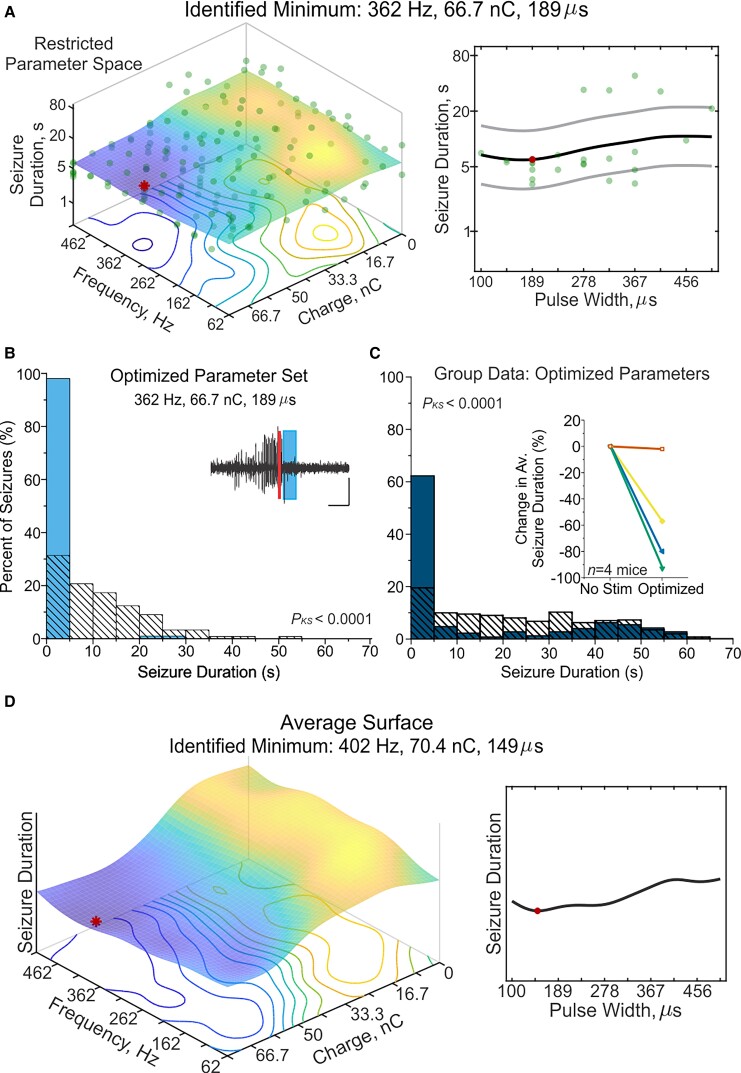
Figure 4.
Optimization in a restricted parameter space. Optimization was conducted using a third parameter space, where the range of the frequency and charge dimensions was restricted compared the two previous parameter spaces. Additionally, all parameters were explored with 10 linearly spaced step sizes; 62–512 Hz (frequency), 0–75 nC (charge), 0–500 μs (pulse width). (A) A final response-surface from the same example animal in Figs 1 and 2. (B) Post-stimulation-onset seizure duration distributions for the example animal shown in A. Filled light blue bars: Events receiving optimized stimulation; hashed bars: no-stimulation internal control for comparison. A 93% reduction in seizure duration was observed in this animal when the optimized parameter set of 362 Hz, 66.7 nC, and 189 µs pulse width was applied (P < 0.0001 Kolmogorov–Smirnov test). Note that optimized parameters were strikingly similar identified from the original and restricted parameter spaces in the same example animal (cf. Fig. 1B with Fig. 4A). Inset: Example seizure event receiving the optimized stimulation (thick blue bar) following detection (thin red line). Scale = 5 s, 0.5 mV. (C) Post-stimulation-onset seizure duration distributions at the group level (100 random seizure events per condition per animal). Filled dark blue bars: Events receiving optimized stimulation; hashed bars: no stimulation control. Seizure duration when stimulation was applied with each animal’s individualized optimized parameter set (P < 0.0001 two-sample Kolmogorov–Smirnov test, data from n = 4 mice). Inset: Stimulation with individualized optimized parameters provides significant seizure-reduction. Note that each colour/symbol represents a different animal, with the inverted green triangle corresponding to the same animal in Figs 1–3, but the other symbols representing new animals. (F) Average response-surface, based on the final response-surfaces of the four mice. Red dot marks the minimum of the surface at 402 Hz, 70.4 nC, and 149 µs pulse width. Related data can be found in Supplementary Figs 8 and 9 and Supplementary Table 6. KS = two-sample Kolmogorov-Smirnov statistical test.
An example animal’s response-surface shown in Fig. 4A demonstrates a consistent trend of shorter seizures clustered around higher frequency and charge values in the restricted parameter space, but notably, the highest possible values are not selected as optimal. Specifically, in this animal 362 Hz, 66.7 nC, and 189 µs pulse width were identified as the optimal settings, which is remarkably similar to its identified minimum in the original parameter space of 369.5 Hz, 62.5 nC, and 300 µs pulse width (cf. Fig. 1B and Fig. 4A; same example animal). This is especially relevant as it helps rule out possible edge effects—a similar frequency and charge was identified as optimal in this animal even when that location was a different number of steps from the edge of the space. Across animals, optimization tended to identify high—but not the highest—frequency and charge values (Supplementary Fig. 8). Additional testing revealed that in three of four animals optimized stimulation significantly reduced seizure duration compared to no stimulation (62% of seizures stopping within 5 s of the start of intervention across four animals; Fig. 4C and Supplementary Table 6). The group average response-surface further confirms that higher charge and frequency, and overall low pulse widths, are associated with shorter seizure durations. Additionally, the identified minimum was similar to that in the original parameter space (402 Hz, 70.4 nC, 149 µs pulse width versus 460.1 Hz, 59.7 nC, 149 µs pulse width; cf. Fig. 4D with Fig. 2F).
Following optimization, in addition to testing each animal’s individualized optimized setting, we also examined stimulation with a ‘corner parameter set’, using the highest frequency and charge possible (512 Hz, 75 nC). While stimulation with the corner parameter set significantly reduced seizure duration compared to no intervention, it did not improve seizure-suppression over optimized parameters, arguing against a the-more-the-better interpretation (Supplementary Fig. 9 and Supplementary Table 6).
Overall, these experiments point to the robustness of the optimization process, with successful parameters being identified regardless of specific step sizes or length constants.
Effective settings are robust to electrode orientation
Finally, given the striking cytoarchitecture of the cerebellum, in which Purkinje cells’ dendritic trees are oriented parallel to the midline and parallel fibres run orthogonal to the sagittal plane (Fig. 5A), we additionally tested how the relative orientation of stimulating electrodes could impact outcomes. Our initial testing scheme aligned the electrode feet perpendicular to the midline (Fig. 5A, left), such that the prominent path of current would run perpendicular to the parallel fibres (i.e. granule cell axons, which provide excitatory input to Purkinje cells, influencing simple spikes).
In a new set of animals, we oriented the stimulating electrodes such that the electrode feet were positioned parallel to the midline (Fig. 5A, right). In these animals, the main path of current flow would run perpendicular to the dendritic arbors of Purkinje cells (and parallel to parallel fibres). With this rotated orientation of the stimulating electrodes, we again completed Bayesian optimization and Gaussian process regression (using the initial, more flexible, full parameter space; Fig. 5B and Supplementary Fig. 10). Again, this approach allowed identification of predicted effective settings (red dot in example surface in Fig. 5B), which in subsequent experiments was confirmed to provide strong seizure inhibition (example animal illustrated in Fig. 5C). In contrast, the non-optimal parameter set failed to provide seizure control (illustrated for an example animal in Fig. 5D). Across animals, optimized stimulation settings reduced seizure duration by 58.7 ± 11.6% (P = 0.031, versus no-stimulation, Wilcoxon test; 72% stopping within 5 s of intervention, Fig. 5E and Supplementary Tables 7 and 8), while non-optimized stimulation settings produced no seizure inhibition (1 ± 1.5%, P = 0.56 versus no stimulation, Wilcoxon test; 26% stopping within 5 s of intervention; percent seizure reduction non-optimized versus optimized P = 0.031, Wilcoxon test, Fig. 5F). Therefore, as with the perpendicular electrode arrangement, stimulation with a rotated orientation was still able to provide strong seizure inhibition, if the correct combination of stimulation parameters was utilized. Indeed, in a head-to-head comparison between the seizure reduction achieved with optimal settings for the different orientations (Fig. 2 data versus Fig. 4 data), there was no significant difference (Mann–Whitney test = 0.29), suggesting that the orientation of the electrode is not a major determinant of effectiveness of these interventions.
Interestingly, we additionally noted similar surfaces with either electrode orientation scheme (cf. Fig. 5G and Fig. 2F), with fairly high frequencies, fairly strong charges, and somewhat short pulse durations being effective regardless of orientation (Table 1 and Supplementary Figs 3, 10 and Supplementary Table 7). Averaging across surfaces, the identified minimum (i.e. best combination of settings) for the parallel-to-midline electrode feet orientation had a frequency of 371.5 Hz (compared with 460.1 Hz for our original orientation, original search space), a charge of 50.5 nC (compared with 59.7 nC) and a pulse width of 222 µs (compared with 149 µs). The similarities of these optimal settings suggests that not only can seizure inhibition be achieved with either orientation, but also that effective stimulation parameters are similar regardless of the orientation. Therefore, the orientation of electrodes is unlikely to be a critical factor in the success of cerebellar cortex electrical stimulation for seizure inhibition, and therefore likely does not explain variability in past successes when investigating electrical stimulation of the cerebellum for seizure interventions. In contrast, for both orientations, the selection of stimulation settings was critical, with some combinations of stimulation settings providing strong seizure inhibition (‘optimized’) and other settings providing no seizure inhibition (‘non-optimal’). While generally higher frequencies and charges were favoured across parameter spaces and electrode orientation, there was not a significant correlation across optimizations between total charge output (based on frequency and charge) and the degree of seizure-suppression (Supplementary Fig. 11). Together with previous data (Fig. 4 and Supplementary Fig. 9 and Supplementary Table 6), this supports that while a relatively high output is required for effective stimulation, maximizing frequency and charge does not equate with greater seizure control.
Taken together our results indicate that electrical stimulation of the cerebellum can be an effective approach to seizure inhibition. They further illustrate that effective seizure inhibition is strongly reliant on stimulation settings, providing potential insight into previous mixed findings regarding the effectiveness of cerebellar stimulation for seizure control. Additionally, our work highlights a framework to investigate the importance of stimulation settings, allowing thorough investigation of a large number of possible combinations of settings, in a rationale, data driven, manner.
Discussion
Previous on-demand optogenetic work suggested strong seizure inhibition via cerebellar-targeted intervention,20–24 yet previous work targeting the cerebellum via electrical stimulation has suggested extremely mixed results, from no effect,34,36,43,45,52,56 to actually worsening the phenotype,28,32,37,38,42,44,48–50,53,54 to strong seizure inhibition.25–33,35,37–42,44,46–48,50,54,55,79 We hypothesized that electrical stimulation of the cerebellum could provide robust, consistent, seizure inhibition, and that the previous mixed results were likely due to experimental considerations. Specifically, we hypothesized that how the intervention was applied would be a critical determinant of successful intervention. We were therefore interested in how stimulation parameters, including stimulation frequency, charge, and pulse width, impacted results. Faced with a very large number of possible combinations of stimulation parameters, we turned to Bayesian optimization.59–61 Bounded to stay within safety limits, we varied frequency from 2 Hz to 512 Hz with 18 different steps, charge from −75 nC to +75 nC with 13 steps, and pulse width from 100 to 500 µs with five steps, resulting in over 1000 different combinations to explore. Such a large number of combinations would have been experimentally intractable to test serially; a rough power analysis suggests over 100 000 events per animal would have been required to test this number of combinations by simple iteration. However, Gaussian process regression and Bayesian optimization allowed a thorough, data-driven exploration of the space, and, importantly, allowed successful identification of parameter settings which were able to provide robust, consistent, seizure inhibition through cerebellar electrical stimulation. This success was not strictly dependent on the fitting conditions, and, surprisingly, was also not dependent on the orientation of the electrodes relative to the cytoarchitecture of the cerebellum. Together, our results highlight the utility of a Bayesian optimization approach to exploring a parameter space, illustrate that the cerebellum can be an effective target for electrical stimulation for seizure inhibition, and ultimately help resolve a decades long controversy, and point of uncertainty, in the field.
Extracting relevant, influential, experimental considerations from past work examining the cerebellum as a potential target for electrical stimulation for seizure inhibition has been remarkably difficult (recently reviewed by Streng and Krook-Magnuson18), given factors such as poor reporting of potentially important variables in some studies, and large variability from study to study, with multiple parameters differing. Therefore, a systematic, within-study, rigorous examination of stimulation parameters was critical. By completing our thorough review of a range of frequencies, a range of charge strengths, a range of pulse widths and, importantly, the various combinations of these, we were able to discern that seizure inhibition required relatively high frequency stimulation and relatively strong charge. Interestingly, the identified minimum (i.e. the ‘optimal’ settings) was often not the highest frequency and highest charge, suggesting that it is not simply a matter of the-more-the-better. This was further supported by optimization restricted to higher, linearly spaced, frequency steps, which identified similarly high, but not the highest possible, optimal parameters. Additionally, a head-to-head comparison of optimized parameters to stimulation with the highest frequency and charge possible confirmed that maximizing total charge output does not improve seizure-control. Furthermore, across experiments, total charge output of optimized stimulation and the degree of seizure-suppression was not correlated. Altogether, these results support that if we could expand the parameter space without risking adverse stimulation-induced effects, it would be unlikely to improve seizure-suppression over the observed effects.
While our specific stimulation parameters may not apply to other types of epilepsy, other electrode types or locations, or other species (e.g. humans have much larger brains than mice), it is still interesting to revisit past literature with this knowledge in hand. In doing so, we find that our surfaces and identified optimal settings may explain a large amount of the variability seen in previous studies. For example, high frequency stimulation was effective in inhibiting seizures in studies by Fanardjian41 (300 Hz), Hutton and colleagues46 (200 Hz) and Mutani79 (100 Hz), across a range of seizure models. In contrast, and fitting with the interaction noted in our data between parameters, Grimm and colleagues43 reported that high frequency (250–300 Hz) electrical stimulation of the cerebellum failed to inhibit epileptic activity, but, among other differences, they used a lower pulse strength as compared to some successful high frequency stimulation studies (i.e. 0.6–0.9 V versus e.g. 6–8 V in the report by Mutani79). Perhaps most tellingly, Godlevsky and colleagues42 directly compared low (10–12 Hz) and high frequency (100-300 Hz) stimulation and found that higher frequency stimulation inhibited seizures while low frequency stimulation actually evoked seizures.
In our dataset, fitted surfaces tended to predict that low frequency stimulation would result in even worse performance than no stimulation (Table 1 and Supplementary Tables 4 and 7). However, in direct, head-to-head comparisons, we never found a significant worsening of seizure durations with non-optimal stimulation. This suggests that something more may be at play in past studies where electrical stimulation actually made seizures worse,28,32,37,38,42,44,48–50,53,54 including the timing of stimulation (our work was entirely on-demand, with stimulation occurring only at the time of seizures, whereas previous studies were done in an open-loop fashion), experimental design (e.g. our work avoided a block design, where natural seizure clustering can make interpretability more challenging), and the potential for plasticity (discussed more below). It is also worth noting that our setup was designed to determine the optimal settings (with increased sampling around potential minima), rather than designed to determine the worst settings; it is possible that even worse settings existed. It should also be noted that it is not surprising that past studies did not do as thorough a review of different parameters and their various potential combinations. Without the regression and optimization approach taken here, examining even half as large of a parameter space would be far too labour-intensive. Additionally, optimization allowed us to avoid conducting direct statistical comparisons across the hundreds of stimulation combinations tested. Instead, by conducting a second round of testing with the identified optimal settings in a random interleaved approach, we were able to perform rigorous statistical analyses to determine if stimulation was effective, without the pitfalls of thousands of multiple comparisons.
A major advantage of electrical stimulation over optogenetic manipulation is the potential for more immediate translation. As noted before, it seems unlikely that the specific stimulation parameters identified in this study would transfer directly to the human population. However, it is of interest that two human studies report that >50% of patients showed either a reduction in seizures26 or full seizure-freedom29 when using high frequency stimulation of the cerebellum. It is also important to stress that while extreme caution should be taken when translating the specific settings identified in our study to another population, our results (i) highlight the potential for robust, consistent, seizure inhibition via cerebellar stimulation; and (ii) illustrate that Bayesian optimization can be a successful framework for determining effective stimulation parameters. Such a framework can be applied across settings,62,63,80,81 including potentially clinical settings, and improvement of interfaces collecting and relaying clinical seizure information is on-going.82 In our animals, a large number of seizures (over 1000) were required to adequately map the space and identify minima. While this may seem like far too many to make this a useful approach in a clinical setting, there are a number of important considerations. First, we examined the impact of intervention on non-convulsive, electrographic seizure events. The intrahippocampal KA model, like many human patients,83 has a high rate of these non-convulsive events.68 Beyond non-convulsive seizures, human patients will often have a high rate of other epileptiform activity,84 which can be (and is) targeted in on-demand interventions. Consider, for example, the rate of stimulations (sometimes over 1000 per day) often applied in epilepsy patients with the Neuropace device.8,85 Similarly, a different surrogate or biomarker for effective stimulation might be available.63,86 Moreover, there are several features of Bayesian optimization that can be altered, depending on goals. While we favored exploration, in a clinic setting the goal would obviously be to provide effective care, and therefore maximize instead exploitation of effective settings.
Additionally, future studies can identify methods to increase efficiency of optimization, while minimizing the loss of exploration. For instance, the less flexible surface in our study used smaller step sizes and therefore resulted in fewer potential combinations being directly tested. Similarly, our results showed similarity in surfaces and identified minima from animal to animal, suggesting that, at least for a similar population and seizure aetiology, optimization may not always be required. Indeed, we found no significant differences at the group level whether personalized optimized, group mode, or group average optimal settings were utilized (Fig. 2G and H). However, certain animals did appear to show greater sensitivity to the exact stimulation settings used (e.g. animal represented by the light blue triangle in Fig. 2H). In the clinical setting, one possibility is that a generic good setting could be used initially, and then, for poor responders, the surface could be explored to identify personalized optimal settings. Even in this circumstance, information from other patients may be able to inform the initial fitting. For example, a more restricted search could be conducted in the area around the traditional optimal settings. Additionally, our experiments did not make any a priori assumptions about the likely surface shape (beyond being multivariate normal); using previously collected data may allow faster convergence.
There are additional considerations that are important to note. First, we optimized only for seizure duration, but other aspects of stimulation, including potential unwanted side effects, can also be very important. For this, in addition to building such considerations directly into the optimization process,62,80 it may be possible to use unwanted side effects to bound the space examined (akin to e.g. empirically setting limits for DBS in Parkinson’s disease87). There are also additional potential variables to optimize across, including total duration of intervention, waveform structure, etc. We have also only examined acute, intermittent interventions. While providing intervention only in an on-demand manner minimizes stimulation, and therefore potentially plasticity, future work will be needed to examine the impact of chronic cerebellar intervention. Over the course of our experiments, non-stationarity did not seem to seem to be a major confound, and successful interventions were consistently effective across the time period examined (Supplementary Fig. 5 and Supplementary Tables 1 and 3). However, on a longer time scale, plasticity may play a larger role, as has been suggested for the Neuropace device.88 Indeed with two animals, data suggested an improvement over time (see dark orange square in Supplementary Table 3 and Supplementary Figs 8B and 9D).
The cerebellum has a striking cytoarchitecture: granule cell axons (i.e. parallel fibres, so called because they run parallel to one another) run orthogonal to and intersect Purkinje cells’ dendritic arbors, which fan parallel to the midline. We tested two different electrode orientations (one perpendicular to the midline and Purkinje cells’ dendrites, one parallel to the midline) and found both could be effective. Moreover, both orientations produced similar parameter surfaces, with similar average optimal parameters. Given the layout of the cerebellum and the impact therefore that direction of current flow can have,89 we were surprised that electrode orientation did not play a larger role in determining outcomes. Our electrode feet were relatively large (combined exposed surface area of ∼0.35 mm2) and were separated by a fairly large distance (∼1 mm), and, of course, the current would not have taken a direct linear path between the two feet. Stimulation with a different electrode setup may have produced a greater orientation-specific effect. Additionally, while we examined two different electrode orientations, we only examined interventions targeting the cerebellar vermis. Some of the heterogeneity in previous findings may be derived from differences in the location targeted.18 We found remarkably strong seizure inhibition targeting the midline of the cerebellar cortex (including a 96% decrease in seizure duration in one instance); other regions of the cerebellum may be less effective. Similarly, the parameter surface generated may be dependent on the location. For example, with optogenetic manipulation, excitation or inhibition of the cerebellar cortex (specifically Purkinje cells) is able to inhibit seizures,20 but at the level of the cerebellar nuclei, only excitation provides seizure control.21,23 Electrical stimulation of the cerebellar nuclei, instead of the cortex, may result in very different parameter surfaces and optimized settings, with potentially more restricted areas of the parameter surface showing seizure inhibition.
Our work clearly illustrates that electrical stimulation of the cerebellum can be effective, and that the stimulation parameters chosen for intervention are critical for success. Gaussian process regression and Bayesian optimization allowed us to complete a thorough, data-driven, exploration of a very large parameter space, have a visual readout of the process, and successfully identify effective settings. There is nothing that limits the optimization approach taken here to cerebellar-directed interventions, and the problem of many potential combinations of settings to choose from is an issue in a large number of contexts.62–67,90 Even for stimulation targets relatively well established for epilepsy treatment, an optimization approach may allow identification of better stimulation settings, including for non-responders. Beyond potentially missing the best combination of settings, current strategies rely heavily on clinicians modifying stimulation settings in a way that is labour-intensive and not as efficiently data driven. An automated data driven approach to determining optimal stimulation settings would reduce the burden on clinicians and likely improve patient outcomes. This is true for epilepsy patients, and for patients receiving or exploring electrical stimulation for a range of neurological and neuropsychiatric disorders and disabilities, including Parkinson’s disease,64,80 essential tremor,66,91 chronic pain,92,93 obsessive compulsive disorder94,95 and depression.96,97 Our work highlights the potential benefits of a Bayesian optimization approach.
Supplementary Material
Acknowledgements
The authors would like to thank Dr Andrew Lamperski for his insight and discussion of Bayesian optimization.
Contributor Information
Bethany J Stieve, Graduate Program in Neuroscience, University of Minnesota, Minneapolis 55455, USA.
Thomas J Richner, Department of Biomedical Engineering, University of Minnesota, Minneapolis 55455, USA; Department of Neuroscience, University of Minnesota, Minneapolis 55455, USA.
Chris Krook-Magnuson, Department of Neuroscience, University of Minnesota, Minneapolis 55455, USA.
Theoden I Netoff, Graduate Program in Neuroscience, University of Minnesota, Minneapolis 55455, USA; Department of Biomedical Engineering, University of Minnesota, Minneapolis 55455, USA.
Esther Krook-Magnuson, Graduate Program in Neuroscience, University of Minnesota, Minneapolis 55455, USA; Department of Neuroscience, University of Minnesota, Minneapolis 55455, USA.
Funding
This work was funded by NIH R01-NS112518 (to E.K.M. and T.N.), a Winston and Maxine Wallin Neuroscience Discovery Fund Award (to E.K.M. and T.N.), University of Minnesota McKnight Awards (E.K.M.), a Research Fellowship in Neuromodulation funded by the University of Minnesota’s MnDRIVE (Minnesota’s Discovery, Research and Innovation Economy) initiative (B.S.) and a University of Minnesota Informatics Institute-MnDRIVE Informatics Graduate Assistantship (B.S.).
Competing interests
T.N. holds equity in, and serves as Chief Scientific Officer of StimSherpa, which has licensed METHOD FOR ADAPTIVE CONTROL OF A MEDICAL DEVICE USING BAYESIAN OPTIMIZATION from the University of Minnesota. The University of Minnesota holds equity and is entitled to royalty and other payments under a license agreement with StimSherpa. These interests have been reviewed and managed by the University of Minnesota in accordance with its Conflict of Interest policies. The authors report no other competing interests.
Supplementary material
Supplementary material is available at Brain online.
References
- 1. England MJ, Liverman CT, Schultz AM, Strawbridge LM. Epilepsy across the spectrum: promoting health and understanding. A summary of the Institute of Medicine report. Epilepsy Behav. 2012;25(2):266–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Asadi-Pooya AA, Rostamihosseinkhani M, Farazdaghi M. Seizure and social outcomes in patients with non-surgically treated temporal lobe epilepsy. Epilepsy Behav. 2021;122:108227. [DOI] [PubMed] [Google Scholar]
- 3. Asadi-Pooya AA, Stewart GR, Abrams DJ, Sharan A. Prevalence and incidence of drug-resistant mesial temporal lobe epilepsy in the United States. World Neurosurg. 2017;99:662–666. [DOI] [PubMed] [Google Scholar]
- 4. Brodie MJ, Barry SJE, Bamagous GA, Norrie JD, Kwan P. Patterns of treatment response in newly diagnosed epilepsy. Neurology. 2012;78(20):1548–1554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Tian N, Boring M, Kobau R, Zack MM, Croft JB. Active epilepsy and seizure control in adults—United States, 2013 and 2015. MMWR Morb Mortal Wkly Rep. 2018;67(15):437–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Laxer KD, Trinka E, Hirsch LJ, et al. The consequences of refractory epilepsy and its treatment. Epilepsy Behav. 2014;37:59–70. [DOI] [PubMed] [Google Scholar]
- 7. Kwan P, Sander JW. The natural history of epilepsy: an epidemiological view. J Neurol Neurosurg Psychiatry. 2004;75(10):1376–1381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Nair DR, Laxer KD, Weber PB, et al. Nine-year prospective efficacy and safety of brain-responsive neurostimulation for focal epilepsy. Neurology. 2020;95(9):e1244–e1256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Ivry RB, Baldo JV. Is the cerebellum involved in learning and cognition? Curr Opin Neurobiol. 1992;2(2):212–216. [DOI] [PubMed] [Google Scholar]
- 10. Strick PL, Dum RP, Fiez JA. Cerebellum and nonmotor function. Annu Rev Neurosci. 2009;32:413–434. [DOI] [PubMed] [Google Scholar]
- 11. King M, Hernandez-Castillo CR, Poldrack RA, Ivry RB, Diedrichsen J. Functional boundaries in the human cerebellum revealed by a multi-domain task battery. Nat Neurosci. 2019;22(8):1371–1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Schmahmann JD. The cerebellum and cognition. Neurosci Lett. 2019;688:62–75. [DOI] [PubMed] [Google Scholar]
- 13. Argyropoulos GPD, van Dun K, Adamaszek M, et al. The cerebellar cognitive affective/Schmahmann syndrome: a task force paper. Cerebellum. 2020;19(1):102–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Zeidler Z, Hoffmann K, Krook-Magnuson E. HippoBellum: acute cerebellar modulation alters hippocampal dynamics and function. J Neurosci. 2020;40(36):6910-6926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Miterko LN, Baker KB, Beckinghausen J, et al. Consensus Paper: Experimental Neurostimulation of the Cerebellum. Cerebellum. 2019;18(6):1064–1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Miller JW. The role of mesencephalic and thalamic arousal systems in experimental seizures. Prog Neurobiol. 1992;39(2):155–178. [DOI] [PubMed] [Google Scholar]
- 17. Fountas KN, Kapsalaki E, Hadjigeorgiou G. Cerebellar stimulation in the management of medically intractable epilepsy: a systematic and critical review. Neurosurg Focus. 2010;29(2):E8. [DOI] [PubMed] [Google Scholar]
- 18. Streng ML, Krook-Magnuson E. The cerebellum and epilepsy. Epilepsy Behav. 2020;121(Pt B):106909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Kros L, Rooda OHJ, De Zeeuw CI, Hoebeek FE. Controlling cerebellar output to treat refractory epilepsy. Trends Neurosci. 2015;38(12):787–799. [DOI] [PubMed] [Google Scholar]
- 20. Krook-Magnuson E, Szabo GG, Armstrong C, Oijala M, Soltesz I. Cerebellar directed optogenetic intervention inhibits spontaneous hippocampal seizures in a mouse model of temporal lobe epilepsy. eNeuro. 2014;1(1):ENEURO.0005-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Streng ML, Krook-Magnuson E. Excitation, but not inhibition, of the fastigial nucleus provides powerful control over temporal lobe seizures. J Physiol. 2020;598(1):171–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Streng ML, Tetzlaff MR, Krook-Magnuson E. Distinct fastigial output channels and their impact on temporal lobe seizures. J Neurosci. 2021;41(49):10091–10107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Kros L, Eelkman Rooda OHJ, Spanke JK, et al. Cerebellar output controls generalized spike-and-wave discharge occurrence. Ann Neurol. 2015;77(6):1027–1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Eelkman Rooda OHJ, Kros L, Faneyte SJ, et al. Single-pulse stimulation of cerebellar nuclei stops epileptic thalamic activity. Brain Stimul. 2021;14(4):861–872. [DOI] [PubMed] [Google Scholar]
- 25. Bidzinski J, Bacia T. Chroniczna elektrostymulacja kory modzku w leczeniu padaczki. [Long-term electrostimulation of the cerebellar cortex in the treatment of epilepsy]. Neurol Neurochir Pol. 1982;16(1–3):111–114. [PubMed] [Google Scholar]
- 26. Chkhenkeli SA, Sramka M, Lortkipanidze GS, et al. Electrophysiological effects and clinical results of direct brain stimulation for intractable epilepsy. Clin Neurol Neurosurg. 2004;106(4):318–329. [DOI] [PubMed] [Google Scholar]
- 27. Cooper IS, Amin I, Gilman S. The effect of chronic cerebellar stimulation upon epilepsy in man. Trans Am Neurol Assoc. 1973;98:192–196. [PubMed] [Google Scholar]
- 28. Davis R, Gray E, Engle H, Dusnak A,. Reduction of intractable seizures using cerebellar stimulation. Appl Neuropysiol. 1983;46:57–61. [DOI] [PubMed] [Google Scholar]
- 29. Davis R, Emmonds SE. Cerebellar stimulation for seizure control: 17-year study. Stereotact Funct Neurosurg. 1992;58(1–4):200–208. [DOI] [PubMed] [Google Scholar]
- 30. Gilman S, Dauth GW, Tennyson VM. Clinical, morphological, biochemical, and physiological effects of cerebellar stimulation. Macel Dekker; 1977. [Google Scholar]
- 31. Klun B, Stojanović V, Strojnik P, Stanic U, Vodovnik L, Zirovnik S. Chronic cerebellar stimulation in the treatment of epilepsy. Springer; 1987. [Google Scholar]
- 32. Levy LF, Auchterlonie WC. Chronic cerebellar stimulation in the treatment of epilepsy. Epilepsia. 1979;20(3):235–245. [DOI] [PubMed] [Google Scholar]
- 33. Sramka M, Fritz G, Galanda M, Nádvornik P. Some observations in treatment stimulation of epilepsy. Acta Neurochir (Wien). 1976;(23 Suppl):257–262. [DOI] [PubMed] [Google Scholar]
- 34. Van Buren JM, Wood JH, Oakley J, Hambrecht F. Preliminary evaluation of cerebellar stimulation by double-blind stimulation and biological criteria in the treatment of epilepsy. J Neurosurg. 1978;48(3):407–416. [DOI] [PubMed] [Google Scholar]
- 35. Velasco F, Carrillo-Ruiz JD, Brito F, et al. Double-blind, randomized controlled pilot study of bilateral cerebellar stimulation for treatment of intractable motor seizures. Epilepsia. 2005;46(7):1071–1081. [DOI] [PubMed] [Google Scholar]
- 36. Wright GD, McLellan DL, Brice JG. A double-blind trial of chronic cerebellar stimulation in twelve patients with severe epilepsy. J Neurol Neurosurg Psychiatry. 1984;47(8):769–774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Babb TL, Mitchell AG, Jr, Crandall PH. Fastigiobulbar and dentatothalamic influences on hippocampal cobalt epilepsy in the cat. Electroencephalogr Clin Neurophysiol. 1974;36(2):141–154. [DOI] [PubMed] [Google Scholar]
- 38. Cooke PM, Snider RS. Some cerebellar influences on electrically-induced cerebral seizures. Epilepsia. 1955;4:19–28. [DOI] [PubMed] [Google Scholar]
- 39. Dauth G DS, Gilman S. Alteration of Purkinje cell activity from transfolial stimulation of the cerebellum in the car. Neurology. 1974;28:654–660. [DOI] [PubMed] [Google Scholar]
- 40. Dow RS, Fernandez-Guardiola A, Manni E. The influence of the cerebellum on experimental epilepsy. Electroencephalogr Clin Neurophysiol. 1962;14:383–398. [DOI] [PubMed] [Google Scholar]
- 41. Fanardjian VV, Donhoffer H. An electrophysiological study of cerebellohippocampal relationships in the unrestrained cat. Acta Physiol Acad Sci Hung. 1964;24:321–333. [PubMed] [Google Scholar]
- 42. Godlevskii LS, Stepanenko KI, Lobasyuk BA, Sarakhan EV, Bobkova LM. The effects of electrical stimulation of the paleocerebellar cortex on penicillin-induced convulsive activity in rats. Neurosci Behav Physiol. 2004;34(8):797–802. [DOI] [PubMed] [Google Scholar]
- 43. Grimm RJ, Frazee JG, Bell CC, Kawasaki T, Dow RS. Quantitative studies in cobalt model epilepsy: the effect of cerebellar stimulation. Int J Neurol. 1970;7(2):126–140. [PubMed] [Google Scholar]
- 44. Hablitz JJ, McSherry JW, Kellaway P. Cortical seizures following cerebellar stimulation in primates. Electroencephalogr Clin Neurophysiol. 1975;38(4):423–426. [DOI] [PubMed] [Google Scholar]
- 45. Hemmy DC, Larson SJ, Sances A, Jr, Millar EA. The effect of cerebellar stimulation on focal seizure activity and spasticity in monkeys. J Neurosurg. 1977;46(5):648–653. [DOI] [PubMed] [Google Scholar]
- 46. Hutton JT, Frost JD, Jr, Foster J. The influence of the cerebellum in cat penicillin epilepsy. Epilepsia. 1972;13(3):401–408. [DOI] [PubMed] [Google Scholar]
- 47. Iwata K, Snider RS. Cerebello-hippocampal influences on the electroencephalogram. Electroencephalogr Clin Neurophysiol. 1959;11(3):439–446. [DOI] [PubMed] [Google Scholar]
- 48. Kreindler A. Active arrest mechanisms of epileptic seizures. Epilepsia. 1962;3:329–337. [Google Scholar]
- 49. Lockard JS, Ojemann GA, Congdon WC, DuCharme LL. Cerebellar stimulation in alumina-gel monkey model: inverse relationship between clinical seizures and EEG interictal bursts. Epilepsia. 1979;20(3):223–234. [DOI] [PubMed] [Google Scholar]
- 50. Maiti A, Snider RS. Cerebellar control of basal forebrain seizures: amygdala and hippocampus. Epilepsia. 1975;16(3):521–533. [DOI] [PubMed] [Google Scholar]
- 51. Mutani R, Bergamini L, Doriguzzi T. Experimental evidence for the existence of an extrarhinencephalic control of the activity of the cobalt rhinencephalic epileptogenic focus. Part 2. Effects of the paleocerebellar stimulation. Epilepsia. 1969;10(3):351–362. [DOI] [PubMed] [Google Scholar]
- 52. Myers RR, Burchiel KJ, Stockard JJ, Bickford RG. Effects of acute and chronic paleocerebellar stimulation on experimental models of epilepsy in the cat: studies with enflurane, pentylenetetrazol, penicillin, and chloralose. Epilepsia. 1975;16(2):257–267. [DOI] [PubMed] [Google Scholar]
- 53. Reimer GR, Grimm RJ, Dow RS. Effects of cerebellar stimulation on cobalt-induced epilepsy in the cat. Electroencephalogr Clin Neurophysiol. 1967;23(5):456–462. [DOI] [PubMed] [Google Scholar]
- 54. Rucci FS, Giretti ML, La Rocca M. Cerebellum and hyperbaric oxygen. Electroencephalogr Clin Neurophysiol. 1968;25(4):359–371. [DOI] [PubMed] [Google Scholar]
- 55. Snider R. Cerebellar modifications of abnormal discharges in cerebral sensory and motor areas. Plenum Press; 1974. [Google Scholar]
- 56. Wada JA. Progressive seizure recruitment in subhuman primates and effect of cerebellar stimulation upon developed vs. developing amygdaloid seizures. Bol Estud Med Biol. 1974;28(8–10):285–301. [PubMed] [Google Scholar]
- 57. Ebner TJ, Bantli H, Bloedel JR. Effects of cerebellar stimulation on unitary activity within a chronic epileptic focus in a primate. Electroencephalogr Clin Neurophysiol. 1980;49(5–6):585–599. [DOI] [PubMed] [Google Scholar]
- 58. Sahel J-A, Boulanger-Scemama E, Pagot C, et al. Partial recovery of visual function in a blind patient after optogenetic therapy. Nat Med. 2021;27(7):1223–1229. [DOI] [PubMed] [Google Scholar]
- 59. Mockus J. On Bayesian methods for seeking the extremum. In: Marchuk, G.I. ed. Optimization Techniques IFIP Technical Conference Novosibirsk, July 1–7, 1974. Springer; 1975.
- 60. Mockus J. Bayesian approach to global optimization: theory and applications. Springer; 2012. [Google Scholar]
- 61. Matheron G. Principals of geostatistics. Econ Geol. 1963;58:1246–1266. [Google Scholar]
- 62. Ashmaig O, Connolly M, Gross RE, Mahmoudi B. Bayesian optimization of asynchronous Distributed microelectrode theta stimulation and spatial memory. Annu Int Conf IEEE Eng Med Biol Soc. 2018:2683–2686. [DOI] [PubMed] [Google Scholar]
- 63. Park S-E, Connolly MJ, Exarchos I, et al. Optimizing neuromodulation based on surrogate neural states for seizure suppression in a rat temporal lobe epilepsy model. J Neural Eng. 2020;17(4):046009. [DOI] [PubMed] [Google Scholar]
- 64. Grado LL, Johnson MD, Netoff TI. Bayesian adaptive dual control of deep brain stimulation in a computational model of Parkinson’s disease. PLoS Comput Biol. 2018;14(12):e1006606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Laferriere S, Bonizzato M, Cote SL, Dancause N, Lajoie G. Hierarchical Bayesian optimization of spatiotemporal neurostimulations for targeted motor outputs. IEEE Trans Neural Syst Rehabil Eng. 2020;28(6):1452–1460. [DOI] [PubMed] [Google Scholar]
- 66. Sarikhani P, Miocinovic S, Mahmoudi B. Towards automated patient-specific optimization of deep brain stimulation for movement disorders. Annu Int Conf IEEE Eng Med Biol Soc. 2019;2019:6159–6162. [DOI] [PubMed] [Google Scholar]
- 67. Smith AC, Shah SA, Hudson AE, et al. A Bayesian statistical analysis of behavioral facilitation associated with deep brain stimulation. J Neurosci Methods. 2009;183(2):267–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Bouilleret V, Ridoux V, Depaulis A, Marescaux C, Nehlig A, Le Gal La Salle G. Recurrent seizures and hippocampal sclerosis following intrahippocampal kainate injection in adult mice: electroencephalography, histopathology and synaptic reorganization similar to mesial temporal lobe epilepsy. Neuroscience. 1999;89(3):717–729. [DOI] [PubMed] [Google Scholar]
- 69. Bragin A, Engel J, Jr, Wilson CL, Vizentin E, Mathern GW. Electrophysiologic analysis of a chronic seizure model after unilateral hippocampal KA injection. Epilepsia. 1999;40(9):1210–1221. [DOI] [PubMed] [Google Scholar]
- 70. Armstrong C, Krook-Magnuson E, Oijala M, Soltesz I. Closed-loop optogenetic intervention in mice. Nat Protoc. 2013;8(8):1475–1493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Twele F, Tollner K, Brandt C, Loscher W. Significant effects of sex, strain, and anesthesia in the intrahippocampal kainate mouse model of mesial temporal lobe epilepsy. Epilepsy Behav. 2016;55:47–56. [DOI] [PubMed] [Google Scholar]
- 72. Lisgaras CP, Scharfman HE. Robust chronic convulsive seizures, high frequency oscillations, and human seizure onset patterns in an intrahippocampal kainic acid model in mice. Neurobiol Dis. 2022:105637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Hayes MH. Statistical digital signal processing and modeling. John Wiley & Sons; 1996. [Google Scholar]
- 74. Brochu E, Cora VM, de Freitas N. A tutorial on Bayesian optimization of expensive cots functions, with application to active user modeling and hierarchical reinforcemental learning. 2010. arXiv:1012.2599. 10.48550/arXiv.1012.2599 [DOI] [Google Scholar]
- 75. Cogan SF, Ludwig KA, Welle CG, Takmakov P. Tissue damage thresholds during therapeutic electrical stimulation. J Neural Eng. 2016;13(2):021001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Snoek J, Larochell H, Adams RP. Practical bayesian optimization of machine learning algorithms. In Advances in Neural Information Processing Systems. 2012;25. [Google Scholar]
- 77. Bayesian Optimization Algorithm. The MathWorks, Inc. https://www.mathworks.com/help/stats/bayesian-optimization-algorithm.html.
- 78. Bull A. Convergence rates of efficient global optimization algorithms. J Mach Learn Res. 2011;12:2879–2904. [Google Scholar]
- 79. Mutani R. Cobalt experimental hippocampal epilepsy in the cat. Epilepsia. 1967;8(4):223–240. [DOI] [PubMed] [Google Scholar]
- 80. Connolly MJ, Cole ER, Isbaine F, et al. Multi-objective data-driven optimization for improving deep brain stimulation in Parkinson’s disease. J Neural Eng. 2021;18(4):10.1088/1741-2552/abf8ca. doi:10.1088/1741-2552/abf8ca [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Connolly MJ, Park S-E, Laxpati NG, et al. A framework for designing data-driven optimization systems for neural modulation. J Neural Eng. 2020;18(1):10.1088/1741-2552/abd048. doi: 10.1088/1741-2552/abd048 [DOI] [PubMed] [Google Scholar]
- 82. Pal Attia T, Crepeau D, Kremen V, et al. Epilepsy personal assistant device-A mobile platform for brain state, dense behavioral and physiology tracking and controlling adaptive stimulation. Front Neurol. 2021;12:704170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Serrano-Castro PJ, Sanchez-Alvarez JC, Garcia-Gomez T. [Mesial temporal sclerosis (II): clinical features and complementary studies]. Rev Neurol. 1998;26(152):592–597. Esclerosis temporal mesial (II): manifestaciones clinicas y estudios complementarios. [PubMed] [Google Scholar]
- 84. Baud MO, Kleen JK, Mirro EA, et al. Multi-day rhythms modulate seizure risk in epilepsy. Nat Commun. 2018;9(1):88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Skarpaas TL, Jarosiewicz B, Morrell MJ. Brain-responsive neurostimulation for epilepsy (RNS((R)) System). Epilepsy Res. 2019;153:68–70. [DOI] [PubMed] [Google Scholar]
- 86. Gunnarsdottir KM, Li A, Smith RJ, et al. Source-sink connectivity: A novel interictal EEG marker for seizure localization. bioRxiv. [Preprint] 10.1101/2021.10.15.464594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Butson CR, Cooper SE, Henderson JM, Wolgamuth B, McIntyre CC. Probabilistic analysis of activation volumes generated during deep brain stimulation. Neuroimage. 2011;54(3):2096–2104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Khambhati AN, Shafi A, Rao VR, Chang EF. Long-term brain network reorganization predicts responsive neurostimulation outcomes for focal epilepsy. Sci Transl Med. 2021;13(608):eabf6588. [DOI] [PubMed] [Google Scholar]
- 89. Ito M. Cerebellar circuitry as a neuronal machine. Prog Neurobiol. 2006;78(3–5):272–303. [DOI] [PubMed] [Google Scholar]
- 90. Tervo AE, Metsomaa J, Nieminen JO, Sarvas J, Ilmoniemi RJ. Automated search of stimulation targets with closed-loop transcranial magnetic stimulation. Neuroimage. 2020;220:117082. [DOI] [PubMed] [Google Scholar]
- 91. Haddock A, Mitchell KT, Miller A, Ostrem JL, Chizeck HJ, Miocinovic S. Automated deep brain stimulation programming for tremor. IEEE Trans Neural Syst Rehabil Eng. 2018;26(8):1618–1625. [DOI] [PubMed] [Google Scholar]
- 92. Sheldon B, Staudt MD, Williams L, Harland TA, Pilitsis JG. Spinal cord stimulation programming: a crash course. Neurosurg Rev. 2021;44(2):709–720. [DOI] [PubMed] [Google Scholar]
- 93. Odonkor C, Kwak R, Ting K, Hao D, Collins B, Ahmed S. Fantastic four: Age, spinal cord stimulator waveform, pain localization and history of spine surgery influence the odds of successful spinal cord stimulator trial. Pain Physician. 2020;23(1):E19–E30. [PubMed] [Google Scholar]
- 94. van Westen M, Rietveld E, Bergfeld IO, et al. Optimizing deep brain stimulation parameters in obsessive-compulsive disorder. Neuromodulation. 2021;24(2):307–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. Morishita T, Fayad SM, Goodman WK, et al. Surgical neuroanatomy and programming in deep brain stimulation for obsessive compulsive disorder. Neuromodulation. 2014;17(4):312–319; discussion 319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Dandekar MP, Fenoy AJ, Carvalho AF, Soares JC, Quevedo J. Deep brain stimulation for treatment-resistant depression: an integrative review of preclinical and clinical findings and translational implications. Mol Psychiatry. 2018;23(5):1094–1112. [DOI] [PubMed] [Google Scholar]
- 97. Roet M, Boonstra J, Sahin E, Mulders AEP, Leentjens AFG, Jahanshahi A. Deep brain stimulation for treatment-resistant depression: Towards a more personalized treatment approach. J Clin Med. 2020;9(9):2729. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data presented in this manuscript is available upon any reasonable request. A version of the software for online seizure detection and Bayesian optimization, as well as the software used for offline seizure duration analysis, is available through GitHub (https://github.com/KM-Lab).