Characterization of an automated method to segment the human locus coeruleus

Abstract

Following the development of magnetic resonance imaging (MRI) methods to assay the integrity of catecholamine nuclei, including the locus coeruleus (LC), there has been an effort to develop automated methods that can accurately segment this small structure in an automated manner to promote its widespread use and overcome limitations of manual segmentation. Here we characterize an automated LC segmentation approach (referred to as the funnel‐tip [FT] method) in healthy individuals and individuals with LC degeneration in the context of Alzheimer's disease (AD, confirmed with tau‐PET imaging using [18F]MK6240). The first sample included n = 190 individuals across the AD spectrum from cognitively normal to moderate AD. LC signal assayed with FT segmentation showed excellent agreement with manual segmentation (intraclass correlation coefficient [ICC] = 0.91). Compared to other methods, the FT method showed numerically higher correlation to AD status (defined by presence of tau: Cohen's d = 0.64) and AD severity (Braak stage: Pearson R = −.35, cognitive function: R = .25). In a separate sample of n = 12 control participants, the FT method showed excellent scan–rescan reliability (ICC = 0.82). In another sample of n = 30 control participants, we found that the structure of the LC defined by FT segmentation approximated its expected shape as a contiguous line: <5% of LC voxels strayed >1 voxel (0.69 mm) from this line. The FT LC segmentation shows high agreement with manual segmentation and captures LC degeneration in AD. This practical method may facilitate larger research studies of the human LC‐norepinephrine system and has potential to support future use of neuromelanin‐sensitive MRI as a clinical biomarker.

The automated segmentation (funnel tip [FT]) method showed good agreement to manual segmentation in measuring LC signal and LC localization. FT method showed numerically higher correlation to Alzheimer's disease severity measures compared to other segmentation approaches. FT method demonstrated a high scan–rescan reliability and provided a practical method to segment the LC along its full rostrocaudal extent.

1. INTRODUCTION

Magnetic resonance imaging of catecholaminergic nuclei, sometimes referred to as neuromelanin‐sensitive MRI (NM‐MRI) has been applied in the context of neurodegenerative illness to assay the extent of signal loss in the locus coeruleus (LC) as a proxy of degeneration of noradrenergic neurons in this structure (Gannon et al., 2015; Theofilas et al., 2017; Weinshenker, 2018), a common feature of diseases such as Alzheimer's disease (AD) (Castellanos et al., 2015; Dahl et al., 2019; Dünnwald et al., 2020) and Parkinson's disease (Jacobs et al., 2020; Therriault et al., 2020). The LC is implicated in important pathophysiological and clinical features of these illnesses and the ability to measure its integrity in vivo may open doors to advances in knowledge and treatment of these illnesses. Beyond neurodegenerative illness, the method has also been applied to assay LC function in healthy individuals or those with psychiatric illness (Gannon et al., 2015; Weinshenker, 2018).

The LC is difficult to image due to its small size, extending approximately 12–17 mm along the rostrocaudal axis of the pons but having a cross‐sectional diameter of only around 1.5 mm (German et al., 1988; Keren et al., 2009). Thus, while some have attempted to measure LC signal via a conventional region‐of‐interest (ROI) approach segmenting the structure with an atlas mask (Fernandes et al., 2012) in standardized space, this may pose challenges for such a small structure. Consequently, many have opted for manual segmentation, or various semiautomated methods (Castellanos et al., 2015; Dahl et al., 2019; Dünnwald et al., 2020; Jacobs et al., 2020). Manual segmentation is labor‐intensive and introduces interrater variability, hindering research on large samples, multisite studies, or use as a clinical biomarker. On the other hand, automated segmentation (fully automated or semiautomated, the latter entailing visual inspection and manual corrections as needed) may provide a practical and accurate way to measure the integrity of the LC with minimal subjective bias (Castellanos et al., 2015), thereby greatly facilitating application of LC imaging to promote research of the norepinephrine system in the human brain.

The objective of this study was to characterize a semiautomated LC segmentation method developed by our group (Cassidy et al., 2022) (referred to as the funnel‐tip [FT] method). We determined its segmentation accuracy, reproducibility, and detection of signal loss in AD (confirmed with tau‐PET imaging using [18F]MK6240) compared to alternative LC segmentation approaches including manual segmentation (using a well‐established method), and segmentation in standardized space with an LC ROI mask (a simple automated method that we expected to perform suboptimally, justifying the need for the more complex FT method). We further tested variations of these approaches, for instance, examining LC signal from masks of different sizes and the merits of a semi‐ versus fully automated segmentation approach. Finally, we examined the 3D structure of the LC generated by FT segmentation. Tests examined FT segmentation performance for both commonly used LC imaging (NM‐MRI) sequences, turbo spin echo (TSE) and 2D gradient response echo with magnetization transfer pulse (2D‐GRE with MT). Note that for clarity and readability, we use the acronym NM‐MRI throughout the manuscript to refer to this imaging method although the extent of NM's contribution to the contrast has been questioned by some work (Betts et al., 2019; Priovoulos et al., 2020; Watanabe et al., 2019).

2. MATERIALS AND METHODS

2.1. Participants and clinical measures

The first study sample consisted of 190 participants from the community or outpatients at the McGill University Research Centre for Studies in Aging who were enrolled in the Translational Biomarkers of Aging and Dementia cohort (Therriault et al., 2020), McGill University, Canada. Clinical and demographic characteristics of the sample are shown in Table S1. The cohort participants had a detailed clinical assessment, including the Clinical Dementia Rating Scale (CDR) and Mini‐Mental State Examination. Cognitively unimpaired participants had no objective cognitive impairment and a CDR score of 0. Mild cognitive impairment (MCI) individuals had subjective and objective cognitive impairment, preserved activities of daily living, and a CDR score of 0.5. Patients with mild‐to‐moderate sporadic AD dementia had a CDR score between 0.5 and 2, and met the National Institute on Aging and the Alzheimer's Association criteria for probable AD determined by a physician (McKhann et al., 2011). Participants were excluded if they had other inadequately treated conditions, active substance abuse, recent head trauma, or major surgery, or if they had MRI/PET safety contraindication.

The second and third study samples consisted of healthy individuals enrolled from the community (Sample 2: n = 12, age = 27.1 ± 2.8 years, n = 4 males, 8 females; Sample 3: n = 30, age = 42.1 ± 16.2 years, n = 16 male, 14 females). Study procedures were approved by the Douglas Institute Research Ethics Board (Sample 1) and the University of Ottawa Research Ethics Board (Samples 2 and 3). All participants provided written informed consent.

2.2. Image acquisition

Neuroimaging data for Sample 1 were acquired at the Montreal Neurological Institute (MNI). Magnetic resonance (MR) images were acquired on a 3 T Siemens PrismaFit scanner. NM‐MRI images were collected via a TSE sequence with the following parameters: repetition time (TR) = 600 ms; echo time (TE) = 10 ms; flip angle = 120°; turbo factor = 4; in‐plane resolution = 0.6875 × 0.6875 mm²; partial brain coverage overlaying the pons and midbrain with field of view (FoV) = 165 × 220; number of slices = 20; slice thickness = 1.8 mm; slice gap = 0 mm; number of averages = 7; acquisition time = 8.45 min. Whole‐brain, T1‐weighted MR images (resolution = 1 mm, isotropic) were acquired using an MPRAGE sequence for preprocessing of the NM‐MRI and PET data.

Neuroimaging data for Samples 2 and 3 were acquired at the Brain Imaging Centre of the Royal Ottawa Institute for Mental Health Research on a 3 T Siemens Biograph MR‐PET scanner. For Sample 2, NM‐MRI images were collected via a 2D gradient‐recalled echo sequence with magnetization transfer pulse (2D‐GRE with MT) sequence with the following parameters: TR = 685 ms; TE = 3.97 ms; flip angle = 50°; in‐plane resolution = 0.639 × 0.639 mm²; partial brain coverage with FoV = 166 × 224; matrix = 260 × 352; number of slices = 18; slice thickness = 2 mm; slice gap = 0 mm; magnetization transfer frequency offset = 1200 Hz; number of excitations (NEX) = 5. Whole‐brain, T1‐weighted MR images (resolution = 1 mm, isotropic) were acquired using an MEMPRAGE sequence. The 2D‐GRE MT sequence was acquired twice for all participants within the same hour and subjects were asked to get on and off the scanning table to reposition their head between the test and retest scans. Sample 3 protocol included a 2D‐GRE sequence (very similar to that used in Sample 2 but with 24 thinner [1.5 mm] slices), a TSE sequence (very similar to the sequence used in Sample 1), and the same MEMPRAGE sequence as Sample 2. Immediately after acquisition, quality of MRI images was visually inspected for smearing of banding artifacts affecting the midbrain or pons and scans were repeated when necessary, time permitting.

2.3. Manual LC segmentation

We followed a commonly used protocol for manual LC segmentation (Clewett et al., 2016; Mather & Harley, 2016). This is a 2D segmentation method that localizes the LC on a single axial slice. Using MRIcron software for visualization, the LC was found by two trained raters (A.S., R.G.) on an axial slice 9 mm under the inferior colliculus (Sample 1; for Sample 2, the distance was slightly different, 8 mm, due to a change in slice thickness). On this slice, the LC was defined on the left and right sides as a five‐voxel cross covering hyperintense voxels near the fourth ventricle. In cases of discordance between raters, consensus was obtained between the raters and C.M.C. for a final mask. Contrast‐to‐noise ratio (CNR) was calculated using the same method as for the FT segmentation (Section 2.4; for all LC segmentation methods the reference region was segmented in the same automated manner in order to isolate the impact of variability of LC segmentation on LC metrics by avoiding variability in measurement of the reference region signal). The LC signal values were calculated by averaging CNR values for all voxels under the mask. LC signal from the manual masks from the two raters prior to consensus showed excellent agreement, intraclass correlation coefficient (ICC) = 0.86 (within the range of interrater agreement reported previously for manual segmentation, ICC ranging from 0.84 to 0.98 (Dahl et al., 2019; Gallant et al., 2022)). Three versions of the manual mask were generated, one retaining all five voxels per side, one with four voxels per side (dropping the voxel of lowest intensity in order to match the size of the LC mask generated by the automated method) and one with only a single, peak‐intensity voxel per side (Figure 2). These smaller masks were generated in part because the in‐plane resolution of our images was lower than that of some prior NM‐MRI studies (Clewett et al., 2016; Dahl et al., 2019), and therefore some voxels under a four‐voxel mask would be expected to show partial volume effects. We assumed partial volume effects would be minimal in the case of the peak‐intensity voxel.

FIGURE 2.

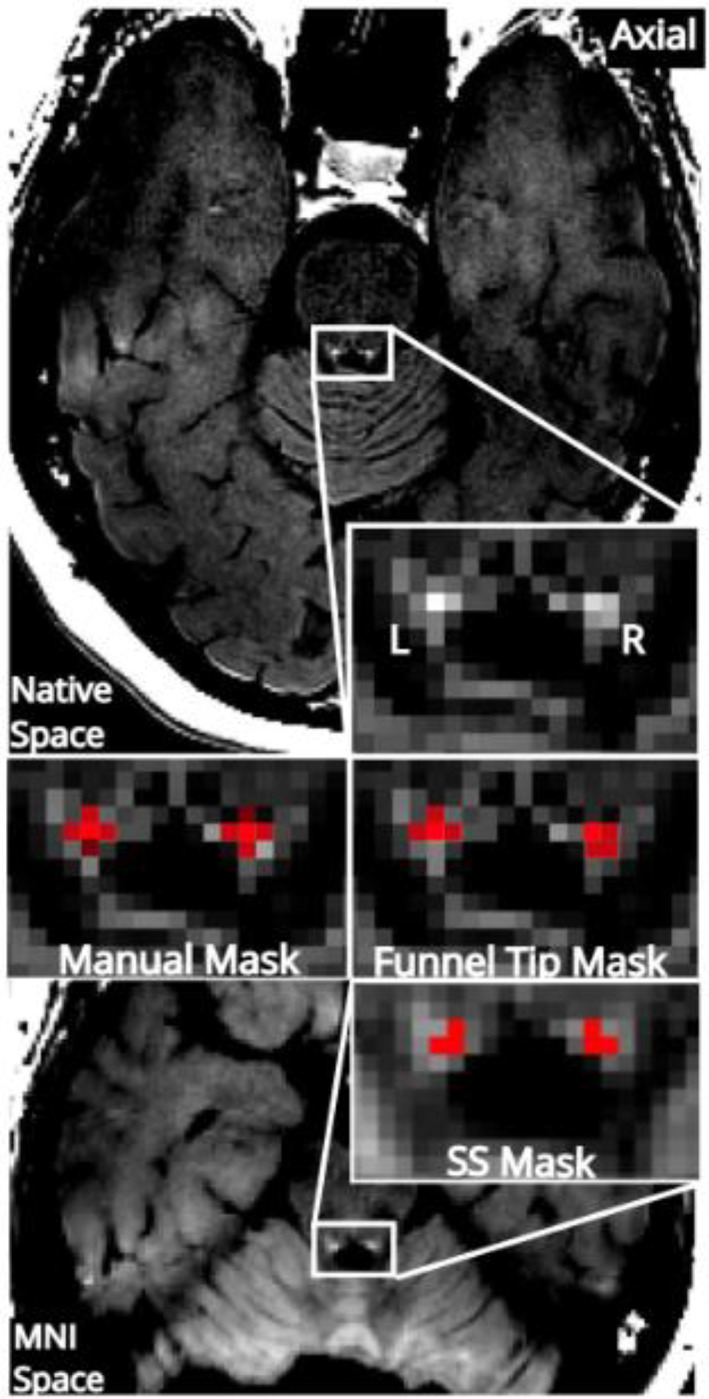
Three different locus coeruleus (LC) segmentation approaches. Neuromelanin‐sensitive‐magnetic resonance imaging (NM‐MRI) image from a representative participant is shown in native space (top) and standardized Montreal Neurological Institute (MNI) space (bottom). Magnification around the fourth ventricle shows LC segmented using a manual approach, the funnel tip (FT) approach, and a mask in standardized space mask (SS 2, the version created from this dataset is shown). For all subjects, full LC coverage was fixed as four voxels per slice (1.8 mm² on the left and right). The peak‐intensity voxel is shown in bright red on the manual and FT masks. To concord with previous implementations, a five‐voxel version of the manual mask was created and the lowest‐intensity voxel, excluded from the four‐voxel version, is shown in darker red.

2.4. Automated LC segmentation

LC signal was measured using a semi‐automated algorithm incorporates steps similar to previous studies including applying an LC search mask on native space NM‐MRI images (García‐Lorenzo et al., 2013) and dividing the LC into sections along its full rostrocaudal extent (Jacobs et al., 2020). This method performs an intensity‐threshold‐free cluster search within an overinclusive mask of the LC in native space. For simplicity, we refer to it as a FT method, see Figure 1 for summary of the steps in the algorithm. Although LC signal is measured on native‐space NM‐MRI images, it is necessary to spatially normalize the NM‐MRI images in order to register an overinclusive LC mask (referred to as the LC search mask) from MNI space to native space for each participant. Initial preprocessing steps were performed using ANTs software. To bring the NM‐MRI image of each participant into standardized space, T1‐weighted images were normalized to MNI152 space (MNI152NLin2009cAsym; 1 mm isotropic resolution), then NM‐MRI images were coregistered to the T1‐weighted images, and finally these two transforms were applied to the NM‐MRI images. A visualization template (Figure 1) was created by averaging the spatially normalized NM‐MRI images from all participants.

FIGURE 1.

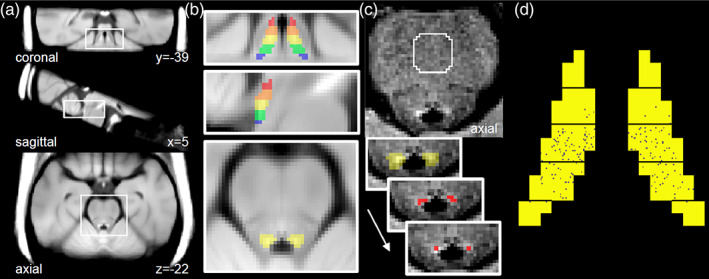
Locus coeruleus (LC) segmentation via funnel‐tip (FT) method. (a) Visualization template in Montreal Neurological Institute (MNI) space created by averaging the spatially normalized neuromelanin‐sensitive‐magnetic resonance imaging (NM‐MRI) images from participants in Sample 1. (b) Magnified views of the visualization template with the LC search mask overlaid. This mask was manually traced on the visualization template over the hyperintense region surrounding the LC and divided into five sections (displayed in different colors), each spanning 3 mm in the z‐axis. (c) Unprocessed NM‐MRI image showing the pons of a representative individual; the central pons reference region is encircled in white. Contrast‐to‐noise ratio for all voxels was calculated relative to signal extracted from this region. The LC search mask (yellow, signifying the middle section) was deformed from MNI space to native space to provide a search space wherein the LC was identified on left and right sides as the four adjacent voxels with highest signal contrast. The peak‐intensity voxel was then identified from these. (d) Variability in manual LC mask position within the sections of the FT mask. Each black speck represents the position of the manual LC mask from a single participant from Sample 1. The greatest proportion of manual LC masks was located in the middle LC section so this section was selected when comparing to the manual mask.

Subsequent steps used custom MATLAB scripts. An LC search mask was drawn over the MNI‐space visualization template to cover the LC, defined as the hyperintense voxels at the anterior‐lateral edge of the fourth ventricle spanning 15 mm in the rostrocaudal axis (from MNI space coordinates z = −16 to −30, see Figure 1). The rostrocaudal limits were set based on the position of the LC from a brainstem atlas (Naidich et al., 2009) and cell counting work (German et al., 1988), spanning from the inferior colliculus to the posterior recess of fourth ventricle, while excluding the extreme rostral and caudal ends to minimize edge effects. The mask was divided into five rostrocaudal sections of equal length (3 mm). The full LC search mask and the five mask sections were then warped to native space using the inverse transformation generated in the spatial normalization step and resampled to NM‐MRI image space. This warped LC search mask defined a search space wherein to find the LC for each participant. A cluster‐forming algorithm was used to segment the LC within this space, defined as the four adjacent voxels (total area = 1.96 mm²) on each side and axial slice with the highest mean signal. The automated segmentation was visually inspected and was found to perform some operations suboptimally, requiring manual correction (error rate Sample 1 = 1.2%, error rate Sample 2 = 4.6%, error rate Sample 3 MT = 4.6%, TSE = 4.6%). Manual corrections were performed if the automatically selected voxels appeared to be within a hyperintense artifact occasionally present within the bottom slices of the fourth ventricle or if they were far from the expected location of the LC based on anatomy (edge of fourth ventricle) and its position on adjacent slices (this issue most commonly occurs on the rostral and caudal ends where LC neurons are more scattered (German et al., 1988)). In most of these cases, the LC was redrawn in a probable position near the edge of the fourth ventricle and in rare cases, the LC mask was excluded from the slice if the hyperintense artifact appeared to obscuring the LC itself. CNR for each voxel v in a given axial slice was then calculated as the relative difference in NM‐MRI signal intensity I from a reference region RR in the same slice as:

$${\mathrm{CNR}}_{\mathrm{v}}=\frac{\left(I_v-\text{mode}\left(I_{\mathit{RR}}\right)\right)}{\text{mode}\left(I_{\mathit{RR}}\right)}$$

We selected a reference region used in our prior work (Cassidy et al., 2022; Chen et al., 2014), the central pons (Figure 1 (Priovoulos et al., 2018)), defined by a circle of radius 11.6 mm, centered on the midline, 32.6 mm anterior to the LC. Finally, every LC‐containing axial slice was linked to one of the five rostrocaudal LC sections based on which of the five sectioned LC masks was present on that slice (if two sectioned masks were present on the same slice, the LC section was defined for each side by the sectioned mask covering the most LC voxels). LC signal was calculated for each of the five sections by averaging CNR values from all LC voxels within the section (four‐voxel version) or only the peak‐intensity voxels from each side and slice within the section (peak‐intensity voxel version). Each section covered between one and two slices in native space. For instance, for the middle LC section, 53% of cases had two slices assigned, 47% of cases had one slice assigned, and no cases were missing the section entirely.

In order to compare the FT (3D) method to the manual (2D) method, it was necessary to determine in which of the rostrocaudal LC sections from the FT method that the manual mask tended to be located. For 66.5% of participants, the manual mask fell in the middle LC section, for 27.7% in the mid‐caudal section, for 5.0% in the mid‐rostral section, for 0.8% in the extreme‐caudal section, (see Figure 1d). Therefore, all analyses using the FT method (excepting those described in Section 2.5) retained only the LC signal from the middle section (MNI coordinates z = −22 to −24). Conveniently, the middle LC has shown the greatest signal loss seen in AD in some studies (Cassidy et al., 2022; German et al., 1992) (though some studies have found the rostro‐middle portion most affected (Theofilas et al., 2017)).

Finally, an alternative automated LC segmentation was applied using the conventional approach of applying a binary mask of the LC in NM‐MRI images warped to standardized space (no smoothing applied). To better match to the other segmentation methods, only the portion of the standardized space mask covering MNI coordinates z = −22 to −24 (the middle LC segment defined with the FT method) was retained. One binary mask was taken from a prior publication (Dahl et al., 2022) (standardized space mask 1 [SS 1]; rigid and affine transformations in ANTs with nearest‐neighbor interpolation brought the mask to MNI152NLin2009cAsym 1 mm space), and one was generated from our own dataset by thresholding the visualization template at CNR >11% (SS 2 mask; see Figure 2). The average of peak voxels from the left and right sides on all three slices was extracted for both masks and used in subsequent analyses.

2.5. 3D reconstruction of LC structure by FT method

The previous tests only assessed the middle portion of the LC; therefore, an additional test was needed to assess the accuracy of the FT segmentation of the LC along its entire rostrocaudal extent. We leveraged the known structure of the LC as a roughly contiguous, rod‐shaped structure and examined whether the position of FT‐segmented peak‐intensity voxels were consistent with a linear shape. Data were collected from 30 participants (Sample 3) scanned with both a 2D‐GRE with MT sequence and a TSE sequence and linear fit was assessed for both sequence types.

To assess linear fit along the x‐dimension, a linear regression was performed with the x‐coordinates for peak voxel locations as the dependent variable and the z‐coordinates as the independent variable. This was repeated for the y‐dimension (y‐coordinates as dependent variable and z‐coordinates as independent variable) and repeated for the left and right LC. Residuals from these regressions identified FT‐segmented LC voxels that were distant from the fit line (outliers). For comparison purposes, the FT mask's linear fit was compared to that of a highly linear set of coordinates (the center of the LC search mask) and an inconsistently linear set of coordinates (created by permuting LC voxel positions within the LC search mask, 1000 permutations in bootstrapped participants).

2.6. PET acquisition and analysis

All individuals in Sample 1 had [18F]MK6240 PET scans acquired to estimate tau levels with a brain‐dedicated Siemens high resolution research tomograph. See previous studies for more detailed PET methods (Lussier et al., 2020; Therriault et al., 2021). [18F]MK6240 standardized uptake value ratio (SUVR) was extracted from a temporal ROI used previously to define tau positivity (Jack et al., 2017). Tau positive cases were defined as those with SUVR >1.24 in the temporal ROI, as in our prior work using this threshold to define tau positivity (Cassidy, 2022). A continuous measure of SUVR from this ROI was also included as a measure of tau burden in the temporal cortex. Subjects were divided into Braak stage groups (Braak et al., 2006; Braak et al., 2011; Braak & Braak, 1991; Braak & Braak, 1997) according to [18F]MK6240 SUVR values in Braak stage ROIs using methods previously employed by our group (Pascoal et al., 2020). Discordant cases (where regional tau burden did not follow the anatomical progression proposed by Braak) were excluded from analyses of Braak stage.

2.7. Statistical analysis

Statistical tests were performed on MATLAB software. ICC(3,K) was used to test agreement between methods and between images. Dice similarity coefficient (DSC) was used to determine spatial overlap between LC masks. Linear regression and partial correlations were used to calculate effect‐size measures relating LC‐signal to clinical and biological measures of AD severity. Scan–rescan variability was calculated using the following equation:

$$\frac{2*\mid \text{scan}-\text{rescan}\mid }{\text{scan}+\text{rescan}}$$

3. RESULTS

3.1. Comparing LC segmentation methods

3.1.1. LC signal values

Three types of LC segmentation were performed (manual method, FT method, and standardized space method), and these were further subdivided based on the number of LC voxels retained in an axial slice (4/5 voxels or only 1 “peak‐intensity” voxel, see Figures 1 and 2). These were applied to NM‐MRI images from 190 older adults (Sample 1). We first examined the mean and variability of LC signal contrast (CNR) since this is our preferred metric for LC imaging. We found this was similar between the manual and FT methods (e.g., 22.2% ± 5.53 for manual peak‐voxel, 22.0% ± 5.22 for FT peak‐voxel, see Table 1). CNR values were significantly lower for the standardized space ROI approach. For instance, this was the case when comparing values from the peak‐voxel FT method (CNR = 22.0 ± 5.2) to those from the peak‐voxel in the standardized‐space method (SS mask 1, CNR = 15.0 ± 4.0, p < 10⁻⁸⁹, paired t test). This indicated that the FT method was segmenting hyperintense (high CNR) voxels with similar efficacy to the manual method, while the lower values in the standardized space method could be due to multiple factors (e.g., blunting of peak voxel values due to interpolation and changes in voxel size during transformation to standardized space or inaccurate targeting of peak‐voxels).

TABLE 1.

LC signal (CNR) as measured by different LC segmentation approaches and level of agreement between these metrics

	CNR mean ± SD	Agreement between methods (ICC(2,k)); constant bias reported in parentheses
		Manual five‐voxel	Manual four‐voxel	Manual peak‐voxel	FT four‐voxel	FT peak‐voxel	FT four‐voxel fully automated	FT peak‐voxel fully automated	SS mask 1 peak‐voxel
Manual five‐voxel	13.8 ± 3.7	‐	‐	‐	‐	‐	‐	‐	‐
Manual four‐voxel	15.9 ± 4.0	0.92 (2.1)	‐	‐	‐	‐	‐	‐	‐
Manual peak‐voxel	22.2 ± 5.5	0.49 (8.4)	0.65 (6.3)	‐	‐	‐	‐	‐	‐
FT four‐voxel	16.7 ± 3.9	0.78 (2.9)	0.90 (0.8)	0.62 (−5.5)	‐	‐	‐	‐	‐
FT peak‐voxel	22.0 ± 5.2	0.44 (8.2)	0.60 (6.1)	0.91 (−0.2)	0.70 (5.3)	‐	‐	‐	‐
FT four‐voxel fully automated	16.7 ± 3.8	0.77 (2.9)	0.89 (0.8)	0.61 (−5.5)	1.0 (0.0)	0.70 (−5.3)	‐	‐	‐
FT peak‐voxel fully automated	22.1 ± 5.2	0.42 (8.3)	0.57 (6.2)	0.90 (−0.1)	0.69 (5.4)	0.99 (0.1)	0.70 (5.4)	‐	‐
SS mask 1 peak voxel	15.0 ± 4.0	0.85 (1.2)	0.87 (−0.9)	0.52 (−7.2)	0.90 (−1.7)	0.57 (−7.0)	0.89 (−1.7)	0.55 (−7.1)	‐
SS mask 2 peak voxel	16.1 ± 4.0	0.81 (2.3)	0.90 (0.2)	0.60 (−6.1)	0.96 (−0.6)	0.66 (−5.9)	0.95 (−0.6)	0.64 (−6.0)	0.94 (1.1)

Note: FT = funnel‐tip segmentation method, SS mask 1 = standardized space from Dahl et al. (2019) (Gannon et al., 2015), SS mask 2 = standardized space created from this dataset.

Abbreviations: CNR, contrast‐to‐noise ratio; ICC, intraclass correlation coefficient; LC, locus coeruleus.

3.1.2. Agreement between LC metrics

There was excellent agreement between LC signal values measured using manual and FT methods for masks of the same size (ICCs ranged from 0.89 to 0.91) while the standardized‐space masks tended to show lower agreement to other peak‐voxel methods (ICCs ranged from 0.52 to 0.66; see Table 1). Agreement between FT and manual peak‐voxel methods was similar for the right and left LC (ICC(2,k) = 0.89 and 0.85, respectively). When comparing between masks of different sizes (e.g., peak voxel to four voxels), there was a bias with higher CNR in peak‐voxel masks, leading to lower ICC values (Table 1; however, consistency between all methods, as measured by ICC(3,k) was high, all ICC >0.83, see Table S2). Mean CNR was higher for peak‐voxel methods compared to four or five voxel methods (see Table 1 for mean CNR differences, constant bias, between all methods) and there was little indication of proportional bias when comparing manual peak‐voxel to FT peak voxel methods (see Figure S1 for Bland–Altman plot).

Spatial overlap of manual and FT LC masks was assessed on the axial slice containing the manual mask. DSC between the manual and FT masks was 0.54 ± 0.40 (four‐voxel mask) and 0.64 ± 0.47 (peak‐intensity voxel mask; see Figure S2 for heat maps of the overlap of LC masks). The main factor limiting overlap was the cruder anatomical targeting of the manual method along the rostrocaudal axis, which restricted the upper bound for the DSC to 0.67, the proportion of cases in which the manual method and FT method searched for the LC on the same axial slice (this was 121 cases for the left LC and 132 cases for the right LC; see Figure 1). Restricting analysis to these cases, the DSC for peak‐intensity‐voxel manual and FT masks was much higher, 0.98 ± 0.13 on the right and 0.95 ± 0.23 on the left. This indicates that, when searching on the same 2D image, the FT method and the manual method almost invariably identified the same peak‐intensity LC voxel.

Finally, we tested whether agreement between FT and manual methods was reduced in tau positive subjects (since reduced LC contrast due to degeneration may impair automated identification). We did not find evidence of this. For example, comparing FT peak‐voxel to manual peak‐voxel, the ICC was actually slightly higher in tau positive cases (0.94) than tau negative cases (0.90) and the DSC was 0.64 for both groups.

3.1.3. AD‐related LC signal loss

Given the well‐established loss of LC neurons in AD (German et al., 1992), as a test of convergent validity, the LC segmentation methods were compared on their ability to capture AD‐related LC signal loss (Table 2). When correlating LC signal values to clinical and pathophysiological measures of AD severity, the manual and FT methods showed similar correlation strengths, with effect sizes generally being in the medium range. The peak‐intensity voxel FT method showed numerically larger effects than any other method, for instance, in relation to Braak stage (r = −.35) or tau‐positivity (Cohen's d = 0.64). Notably, a fully automated version of the FT method (without any manual corrections) performed similarly to the standard (corrected) FT method (Table 2). Finally, the standardized space method showed somewhat weaker relationships to AD measures. Since this method showed lower performance on multiple tests, we did not proceed with further investigation of it.

TABLE 2.

Effect size estimates of the relationship between LC signal metrics and AD severity measures

	Control vs. AD (excluding MCI) (n = 139)	Tau positivity (n = 190)	Tau burden (n = 189)	Braak stage (n = 160)	Cognitive impairment (MMSE) (n = 187)	Dementia severity (CDR) (n = 187)
	Cohen's d	Cohen's d	Pearson R	Pearson R	Pearson R	Pearson R
Manual five‐voxel	0.39	0.45	−.24	−.25	.19	−.14
Manual four‐voxel	0.45	0.47	−.27	−.28	.21	−.18
Manual peak‐voxel	0.57	0.48	−.31	−.31	.25	−.23
FT four‐voxel	0.42	0.58	−.29	−.29	.21	−.21
FT peak‐voxel	0.56	0.64	−.33	−.35	.25	−.26
FT four‐voxel fully automated	0.37	0.59	−.26	−.28	.16	−.25
FT peak‐voxel fully automated	0.48	0.63	−.29	−.32	.18	−.25
SS mask 1 peak voxel	0.43	0.53	−.27	−.26	.21	−.17
SS mask 2 peak voxel	0.46	0.48	−.28	−.25	.22	−.19

Note: FT = funnel‐tip segmentation method, SS mask 1 = standardized space from Dahl et al. (2019) (Gannon et al., 2015), SS mask 2 = standardized space created from this dataset. Tau positivity and tau burden were measured in the temporal cortex. All analyses controlled for age and sex.

Abbreviations: AD, Alzheimer's disease; CDR, Clinical Dementia Rating Scale; LC, locus coeruleus; MCI, mild cognitive impairment; MMSE, Mini‐Mental State Examination.

3.2. Reproducibility of LC metrics within and across NM‐MRI sequence types

3.2.1. Scan–rescan reliability of LC signal values and LC locations

Scan–rescan data were available on a separate cohort of participants (Sample 2, n = 12) scanned twice on the same day using a 2D‐GRE with MT NM‐MRI sequence (first scan = scan, second scan = rescan). Reliability of LC CNR values measured with the manual and FT segmentation methods was at or near the “excellent” range (ICC values for all bilateral methods exceeded 0.7, see Table 3). Scan–rescan variability was low, ranging from 8.4 to 12.0% for these different methods (Table 3).

TABLE 3.

Reproducibility of LC signal

	CNR, bilateral LC (n = 12)	Reliability of CNR values				Scan–rescan variability (bilateral LC, %)
	Mean ± SD	ICC(3,k) bilateral LC	ICC(2,k) bilateral LC	ICC(2,k) left LC	ICC(2,k) right LC	Mean ± SD
Manual five‐voxel	16.9 ± 3.3	0.85	0.85	0.88	0.59	12.0 ± 7.4
Manual four‐voxel	19.0 ± 3.3	0.87	0.88	0.88	0.71	8.4 ± 7.2
Manual peak‐voxel	24.8 ± 3.6	0.78	0.79	0.51	0.71	10.2 ± 6.2
FT four‐voxel	19.5 ± 2.6	0.75	0.73	0.81	0.57	10.7 ± 8.6
FT peak‐voxel	24.5 ± 3.0	0.82	0.82	0.86	0.62	8.4 ± 5.7
FT four‐voxel fully automated	19.4 ± 2.7	0.73	0.73	0.80	0.58	11.3 ± 8.5
FT peak‐voxel fully automated	24.6 ± 2.9	0.79	0.79	0.67	0.61	9.3 ± 5.3

Abbreviations: CNR, contrast‐to‐noise ratio; FT, funnel‐tip; ICC, intraclass correlation coefficient; LC, locus coeruleus.

We also examined the consistency of LC localization from scan to rescan by examining overlap of LC masks between these pairs of images after rigid‐body registration of rescan images and LC masks to scan images. We considered only the four‐voxel versions of the FT and manual masks as interpolation during the registration procedure may not allow adequate precision to examine the peak‐intensity (single voxel) masks. First considering the FT segmentation, all participants (12/12) showed at least partial overlap between the scan and rescan FT masks (DSC = 0.48 ± 0.15). These overlapping mask voxels, present in both the scan and rescan FT masks, covered a portion of the LC with higher CNR (19.2% ± 3.2) relative to the nonoverlapping FT mask voxels (CNR = 15.3% ± 2.5; t ₁₁ = 4.92, p = .0005, paired t test), suggesting that the FT mask was most effective at targeting “core” LC voxels and nonoverlapping FT voxels from scan to rescan may have been the partial volume LC voxels.

Next, considering scan–rescan overlap of the manual (four‐voxel) masks, the extent of overlap was lower than the FT scan rescan masks (DSC = 0.24 ± 0.26) due in part to inconsistent selection of the axial slice on which to draw the mask.

3.2.2. Consistency of LC signal values between NM‐MRI sequence types

Because our study aimed to demonstrate the utility of the FT method for both of the commonly used families of NM‐MRI sequences (TSE and MT sequences; Sections 3.1 and 3.2.1, respectively), we estimated the consistency between data collected from these two sequence types. Scan–rescan data were available on a separate sample of participants (Sample 3, n = 30) scanned on the same day, once with a 2D‐GRE with MT and once with a TSE NM‐MRI sequence. LC signal was higher for the MT images (CNR = 28.8 ± 4.3) compared to the TSE images (CNR = 17.3 ± 5.0). Consistency between MT and TSE versions was at the upper end of the “good” range (ICC(3,k) = 0.71) according to the LC signal measured with the FT peak‐intensity voxel method.

3.3. Structure of LC as reconstructed using the FT method

Finally, as the previous tests only considered one rostrocaudal section of the LC (consistent with our objective of comparing to manual segmentation which is performed in 2D axial space), while the FT method is examining the LC along its full rostrocaudal extent (Figure 1), we sought a test to assess the performance of this method across all rostrocaudal LC sections. To do this, we compared the 3D reconstruction of the LC created by the FT method to the expected shape of the LC as a roughly linear and contiguous, rod‐shaped structure. Thus, to assess face validity of the structure of the LC, we performed linear regression on the coordinates of FT‐derived peak‐intensity voxels along the rostrocaudal extent of the LC for all Sample 3 participants. To further establish the utility of our method for both commonly used NM‐MRI sequences and to observe variability in performance across different implementations, we analyzed data from MT and TSE sequences.

The residuals from these regressions revealed LC voxels that were remote from the straight line estimating the LC structure (Figure 3 shows these fit lines, revealing an idealized LC for all participants and Table S3 reports the angles of these lines relative to the y‐axis). The vast majority of LC voxels were close to these fit lines, for instance, on the left side 96.1% of voxels were within 1 voxel diameter of the fit line in the x‐dimension in the TSE version and 91.7% in the MT version. The proportion of outlier voxels was even lower in the y‐dimension (Table 4). The amount of error tended to be larger for LC voxels on the rostral and caudal ends (Sections 1 and 5) compared to the middle LC section (Section 3; see Table S4).

FIGURE 3.

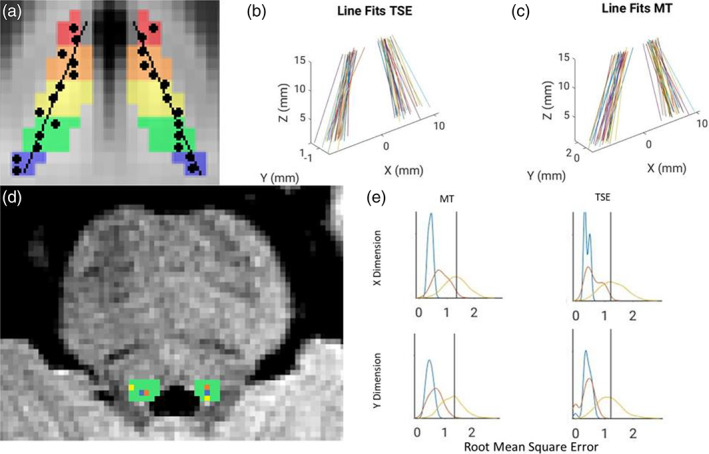
Linear structure of the funnel‐tip (FT) locus coeruleus (LC) mask. (a) Schematic of hypothetical data showing linear fit of peak‐intensity voxels (black circles) segmented using the FT method within the LC search mask (rainbow colors). (b, c) Idealized LC structure revealed by linear regression on LC peak voxel coordinates from the FT method. Lines for all participants are overlaid in native space after setting the origin as the midpoint between the left and right middle LC sections. (d) Axial view of the pons of a representative subject overlaid with the LC search mask (green). FT peak voxel coordinates are shown in orange, the center coordinate of the LC search mask is shown in blue (“LC core”), and a permuted coordinate is shown in yellow. (e) The distribution of linear fit error for all these types of coordinates for the right LC is shown with curves in matching colors. The LC core (blue) showed minimal error and the permuted coordinates (yellow) showed highly variable error. The FT peak‐intensity voxels (orange) often showed error of a similar magnitude to the LC core and never showed greater error than the mean of permuted voxels (black vertical line).

TABLE 4.

Fraction of FT peak‐intensity voxels deviating from linear structure

	>1 voxel diameter away				>2 voxels diameter away
	x‐Dimension (left)	x‐Dimension (right)	y‐Dimension (left)	y‐Dimension (right)	x‐Dimension (left)	x‐Dimension (right)	y‐Dimension (left)	y‐Dimension (right)
TSE	8 (3.9%)	7 (3.4%)	2 (1.0%)	3 (1.5%)	0 (0%)	0 (0%)	0 (0%)	0 (0%)
TSE fully automated	6 (3.0%)	9 (4.5%)	0 (0%)	4 (2.0%)	0 (0%)	0 (0%)	0 (0%)	0 (0%)
MT	21 (8.3%)	23 (9.1%)	10 (4.0%)	12 (4.8%)	0 (0%)	1 (0.4%)	1 (0.4%)	0 (0%)
MT fully automated	22 (8.8%)	26 (10.3%)	11 (4.4%)	11 (4.4%)	3 (1.2%)	3 (1.2%)	0 (0%)	1 (0.4%)

Abbreviations: FT, funnel‐tip; MT, magnetization transfer; TSE, turbo spin echo.

To help interpret the magnitude of error of these fit lines, the linear fit of FT LC coordinates was compared against the fit derived from the coordinates of the center of the LC search mask (the “LC core”, see Figure 3, a positive control that should always generate a good linear fit) and also to the fit from randomly permuted coordinates within the LC search mask (Figure 3, permuted 1000 times in bootstrapped participants, a condition that should lead to highly variable linear fits). For both MT and TSE sequences, all participants had lower error compared to the mean of the fits on permuted coordinates and many participants had error consistent with the “LC core” positive control, particularly in the y‐dimension (Figure 3, Table S5 shows error for all linear fits).

4. DISCUSSION

Our findings provide support for a semiautomated method to segment the LC (FT method). The FT method showed a high level of agreement with manual LC segmentation in terms of LC localization and LC signal values (ICC = 0.91), the latter being similar to other automated methods (ICCs ranging from 0.90 to 0.93) (Dahl et al., 2019; Gallant et al., 2022) Compared to manual segmentation, the FT method showed a similar degree of correlation to clinical and pathophysiological measures of AD severity, providing convergent validity given the well‐known impact of AD on the LC (Dahl et al., 2022) and indicating that it is effective at assaying the LC signal in both a healthy and degenerated state. The FT method had excellent scan–rescan reliability (ICC = 0.82 for the peak‐voxel method, near the higher end of previous reports of LC signal ICC ranging from 0.36 to 0.87 (Dahl et al., 2019; Langley et al., 2017; Tona et al., 2017)) and reasonably consistent spatial targeting of high contrast voxels from scan to rescan. Finally, the structure of the LC generated by the FT method was consistent with the known shape of the LC, a contiguous, rod‐shaped structure (Fernandes et al., 2012). The FT method showed good performance when handling data from both of the most commonly used NM‐MRI sequence types (MT and TSE), and demonstrated high consistency in extracting LC signal across these two sequences.

We found that a simpler automated LC segmentation using a fixed mask in standardized space showed lower CNR and somewhat reduced ability to capture AD‐linked degeneration compared to the other methods, including a fully automated FT method. Other groups have reported encouraging results using similar approaches (Betts et al., 2017; Castellanos et al., 2015; Dünnwald et al., 2020), and it is likely this method could be optimized compared to our implementation (e.g., optimizing the mask itself, methods for reference region signal extraction, LC voxel selection, and artifact exclusion, or warping the mask and extracting signal in native space). One difficulty with averaging all voxels (Dahl et al., 2019; Dahl et al., 2022) in a fixed LC mask is that such a mask must be small to avoid surrounding tissue/CSF but, at this size, may imperfectly target the LC. Methods similar to FT minimize this problem by starting with a larger, overinclusive mask (LC search mask) that covers surrounding tissue and CSF and thus has a low risk of missing the LC due to their larger size. On the other hand, the risk with such approaches is that, to segment the LC within this search mask, they rely not only on external information about anatomical location but also on the intensity of the image itself, introducing some circularity and positive bias. They may occasionally select voxels that are not the LC but are hyperintense due to noise, artifact, or other tissue properties. This risk could be exacerbated in the context of LC degeneration when the difference in signal intensity between the LC and surrounding tissue would be reduced. The risk of selecting an isolated single hyperintense voxel (less likely to be LC) is minimized by the algorithm's selection of a hyperintense cluster of adjacent voxels (“narrowing the funnel”) prior to finding the brightest single voxel in this cluster. The risk of inaccurate segmentation is further reduced by visual inspection and manual correction, although this step prevents the method from being fully automated and introduces subjectivity. Given these theoretical pros and cons of the FT approach, it would appear that the strengths may outweigh the limitations since the method was able to capture LC signal loss in AD better than a standardized space ROI approach and equally well as manual segmentation and furthermore, agreement with manual segmentation was not reduced in the context of loss of LC signal intensity in AD.

We tested variations in the types of methods, varying the size of the LC cross section and the application of manual corrections to the FT method. Smaller LC cross section (a single peak‐intensity voxel) tended to show numerically higher correlation to AD severity than larger cross sections while the differently sized masks performed similarly in terms of agreement to manual segmentation and scan–rescan reliability. However, our data may not have been best suited to determine the optimal size of the LC mask. Our images had lower in‐plane resolution compared to many studies (including those that developed the manual segmentation protocol (Clewett et al., 2016)), and, in a four‐voxel cross section, some voxels are likely impacted by partial voluming. At higher resolution, there could be benefits to including more than 1 voxel in the cross section to assay the structure more fully and reduce noise. On the other hand, assaying the peak‐intensity voxel may maximize the range of values, thereby facilitating detection of correlations. Whether the FT method is employed to assay a cluster of voxels or a single voxel, it is not designed to delineate the axial borders of the LC and, even at very high resolution, would not be able to extract signal from all LC voxels, but rather assay signal from a central portion of the LC on each axial slice. Regarding manual corrections, our data would suggest that they are beneficial when feasible but may not be essential as there was nearly perfect agreement between corrected and uncorrected versions of the FT segmentation (ICC = 0.99) and both captured AD‐related signal loss. The necessity of manual correction may depend on the particular dataset as we have noticed variability across NM‐MRI acquisition protocols in terms of the rate of errors (ranging from <1 to 6.5%), due to factors such as signal‐to‐noise ratio or the presence of hyperintense artifact in the fourth ventricle (more common in some acquisitions). The impact of segmentation errors in our dataset (Sample 1) may have been intermediate relative to others we have seen as the error rate was low (1.2%) but some were errors due to artifact (impactful errors causing extreme CNR values). The FT method allows a filtering option to automatically exclude extreme CNR values but we find that this needs to be applied carefully, likely using study‐specific thresholds. These results give confidence that it would be feasible to develop an acquisition protocol that would minimize the risk of errors and give good confidence to use the FT method in a fully automated manner, for instance, in a clinical context where manual correction would be challenging.

An important strength of the FT method is its ability to assess LC signal in up to five subsections along the full rostrocaudal extent of the LC. However, many of the tests performed here only assessed the middle LC section to better match the most commonly used manual approach (Clewett et al., 2016). Therefore, we developed a test to validate the ability of the FT method to reconstruct an LC with a structure matching its known shape as a roughly linear, rod‐shaped structure (Fernandes et al., 2012). The LC is a contiguous nucleus and it is expected that LC position on adjacent slices should be nearby and often overlapping. We found that the majority of LC voxels segmented by the FT method were nearby to a linear regression line. Those that were more distant from the line may have been due to errors in segmentation or at times due to the true structure of the LC deviating from linearity. This is likely to occur at times on the rostral and especially caudal ends of the LC where cell counting studies have shown higher scatter in LC cells (German et al., 1992). Indeed, we observed that the error in linear fit tended to be higher on the ends of the LC.

Our study had many strengths such as a large sample size that included both healthy participants and participants with neurodegenerative illness (Sample 1) that was available for most of the tests. An exceptional strength of our study was that AD diagnosis and severity (Braak stage (Pascoal et al., 2020)) was confirmed for all participants in the sample by tau PET imaging. Nonetheless, our study also had some limitations. While the FT method showed high scan–rescan reliability, consistent with other LC segmentation methods (Betts et al., 2017; Dahl et al., 2019; Dünnwald et al., 2020), our sample size for this test was relatively small, limiting precision of ICC estimates. Furthermore, while we demonstrated good performance of our method when applied to both commonly used NM‐MRI sequence types (TSE and MT) and showed good agreement between these sequences, both types were not available for all tests. While we developed a test to validate the FT segmentation along the rostrocaudal axis, ideally we would have also compared its performance to manual segmentation for all LC sections. Although prior work has devised manual methods to segment the full LC (Elman et al., 2021), doing so on a sample of this size would be extremely burdensome. Furthermore, the key validation step relating to AD severity would be less effective on these portions of the LC which show less pronounced signal loss in AD (Cassidy et al., 2022). Thus, the ICC, DSC, and effect size metrics presented in this article only reflect the performance of the FT method for the middle LC section and cannot be generalized to the rostral and caudal ends of the LC (although our tests of 3D structure provide some reassurance that the FT method achieves reasonable localization of rostral and caudal LC). As stated above, it would have been more consistent with prior studies using the manual method (Chen et al., 2014; Clewett et al., 2016) if we had collected NM‐MRI images at higher resolution since the fixed‐shape LC mask (a five‐voxel cross) covered a larger area at this resolution. This may have hampered the performance of the manual method to some degree, although we attempted to mitigate this risk by also considering four‐voxel and 1‐voxel manual LC masks. Also, regarding resolution, there was some variability across samples in the slice thickness (ranging from 1.5 to 2.0 mm). In general, we recommend a slice thickness closer to 1.5 mm for optimal performance of the FT method to maximize the number of measurements per LC section. Nevertheless, a 2.0 mm slice thickness may be adequate as all LC sections could be defined in all subjects at this thickness. Finally, while we had a large sample of healthy older adults and individuals on the AD spectrum, it would also be valuable to test the performance of our method in Parkinson's disease, another condition with pronounced degeneration of the LC (Castellanos et al., 2015; Ohtsuka et al., 2013; Reimão et al., 2015).

5. CONCLUSION

The FT method appears to offer a valid and reproducible method of LC segmentation that may perform similarly to manual segmentation but offers some advantages including minimizing burden and subjectivity and allowing segmentation of the LC along its full rostrocaudal extent. It may be a worthy option among other existing methods for automated LC segmentation and may have advantages over methods that may not allow subregional LC measurement (García‐Lorenzo et al., 2013) or may show reduced performance in the context of LC degeneration (Dünnwald et al., 2020). The proposed method has promise to advance study of the human LC‐norepinephrine system by facilitating measurement in larger research studies and providing a sufficiently practical option for clinical applications.

AUTHOR CONTRIBUTIONS

Ahmad Sibahi, Rushali Gandhi, Clifford M. Cassidy, and Pedro Rosa‐Neto made substantial contributions to the conception and design of the work, to the acquisition, analysis, or interpretation of data for the work and to drafting of the work and revising it critically for important intellectual content. Rami Al‐Haddad, Joseph Therriault, Tharick Pascoal, Krysta Boutin‐Miller, and Mira Chamoun contributed to collection of neuroimaging and/or clinical data. Ahmad Sibahi, Clifford M. Cassidy, Tharick Pascoal, Rushali Gandhi, and Christine Tardif contributed to implementation and analysis of neuroimaging measures. All authors contributed to writing and editing the manuscript.

CONFLICT OF INTEREST

The authors report no competing financial interest in relation to the study design, results, or discussion. CMC and PR‐N are inventors on a pending patent using the analysis method described here, licensed to Terran Biosciences, but have received no royalties.

Supporting information

DATA S1 Supplementary File

Sibahi, A. , Gandhi, R. , Al‐Haddad, R. , Therriault, J. , Pascoal, T. , Chamoun, M. , Boutin‐Miller, K. , Tardif, C. , Rosa‐Neto, P. , & Cassidy, C. M. (2023). Characterization of an automated method to segment the human locus coeruleus. Human Brain Mapping, 44(9), 3913–3925. 10.1002/hbm.26324

DATA AVAILABILITY STATEMENT

Data from Sample 1 are available on reasonable request through the Translational Neuroimaging Laboratory at McGill University: https://datashare.tnl-mcgill.com/ds/. Other study data are available from the corresponding author (CMC) upon reasonable request. CMC and PR‐N are inventors on a pending patent using the analysis method described here, licensed to Terran Biosciences. The analysis program is available to be shared for academic use upon request to CMC, following review and approval of a technology transfer agreement.