Studying the efficacy of isolation as a control strategy and elimination of tuberculosis in India: A mathematical model

Abstract

India has the highest burden of both tuberculosis (TB) and multidrug-resistant TB (MDR-TB) based on the WHO Global TB Report 2019. Although the available data suggest that the total TB incidence has declined, the absolute number of new cases is still increasing. The number of reported TB cases in India in 2018 was 2.2 million, which was 1.5 million in 2009. About 47% increment in TB case notification in India within a decade shows a persistent public health problem. India contributes about 22% of the World's TB burden. Indian National Strategic Plan 2017–2025, sets out the government plans to eliminate TB by 2025. However, the milestone seems unrealistic to achieve the TB eradication goal by 2025. We developed a five-dimensional mathematical model to understand the TB dynamics in India and investigate the possibility of the earliest TB eradication time frame. The model stratifies the entire TB class into three different classes as drug-sensitive (DS), MDR, and isolated classes. The effective reproduction number, equilibrium points, and stability analysis of the model were carried out. This model predicts the total estimated cases of DS-TB and MDR-TB from 2018 to 2035 through numerical simulation and suggests that TB may be eliminated by 2035 in India if the treatment success rate could be achieved to 95%, by contact tracing and isolating at least 50% of MDR-TB.

1. Introduction

TB is an airborne disease caused by the bacterium called Mycobacterium tuberculosis. It transmits from person to person via respiratory system during the close contact between people. TB is one of the top ten causes of deaths worldwide, with 1.5 million deaths in 2018 and 10 million people infected with its infection (Ai et al., 2016). TB is curable through vaccination and treatment therapies. The key challenges for the eradication of TB are the early diagnosis of the disease, follow-up, and clinical management of the patients. Fuelled by improper treatment of patients, poor management of supply and quality of drugs, and airborne transmission of bacteria in public places lead to MDR-TB. Drugresistance is the heritable ability of an organism to resist an antibiotic's effects to which its parent was susceptible (Koch et al., 2018). It usually occurs as a result of a mutation in the gene of the organism encoding either the target of the drug or the enzyme, which activates the prodrug. Drugresistance leads to a net decrease in the effectiveness of a drug, and a noticeable increase in the minimum concentration of drug required to kill the bacterial class (Koch et al., 2018). The emergence of MDR-TB is a major health issue. More than 30 percent of antimicrobial resistance (AMR) related deaths occur among MDR-TB patients (Drug-resistant tuberculosis, 2018). The major challenges currently facing the treatment of MDR-TB include: a regimen based on a combination of a large number of (4), (5), (6), (7) drugs; administration via injection being the only option for some drugs; poor tolerance to most drugs; a lengthy treatment period of 18–30 months. Moreover, some individuals have special TB risks because of their medical history and are especially vulnerable. Most commonly, the people at risk of developing drug-resistant TB are those who: do not take their TB medication regularly; do not take all of their TB medication as instructed by their doctor or nurse; develop TB disease again after having been previously treated for TB; come from areas of the world where drug-resistant TB is common; have spent time with someone known to have drug-resistant TB disease. Hence, MDR-TB can be controlled by preventing exposure of the healthy population class by isolation.

The objective of our research is to study the efficacy of isolation of MDR-TB cases on the control of TB and to predict its role in the eradication of TB by 2025 as per the goal set up by National Strategic Plan (NSP) 2017. Moreover, it aims at determining the total TB incidences and MDR-TB incidences from 2018 to 2035 through the mathematical modeling approach.

Mathematical models have been useful to predict the dynamics and impact of control strategies on the future outcomes of the disease. In epidemiology, modelling is based on past data that is used to give a prospective study of a disease. Several researchers have worked on TB and MDR-TB through mathematical modeling and analysed their models to study the dynamics and predict future outcomes of the disease. Mishra et al. (Mishra & Srivastava, 2014) proposed a compartment mathematical model to understand the dynamics of TB spread in the human class for the DR subjects. They considered vaccinated as well as isolated classes in the epidemic model and observed that both the control strategies play a central role in controlling the disease for the Jharkhand state of India. Agusto et al. (Agusto et al., 2015) presented a mathematical model with isolation and loss to follow-up for analyzing the dynamics of DS, MDR and XDR TB strains. They found that increase in isolation rate leads to a decrease in the total number of lost to follow-up individuals. Yu et al. (Yu et al., 2018) extended the standard SEIS mathematical model to take into account MDR-TB infection. They carried out numerical simulation and analysed the impact of significant model parameters on development of TB. Narula et al. (Narula et al., 2016) formulated a mathematical model and estimated its parameters using the Ensemble Kalman filter (EnKf) approach. They estimated the infection rate and a fraction of smear-positive cases of TB in India's context for the period 2006–2011. In this work, we have formulated a compartment mathematical model with separate DS-TB and MDR-TB compartments considering the effect of quarantining the MDR-TB patients and vaccination as a cover on susceptible classes. The model contains a separate isolated class for a fraction of those TB patients who are either highly contagious or acquired MDR-TB.

This paper is organized as follows: In section 2, the Mathematical Model is presented; the reproduction number for DS-TB and MDR-TB cases is computed in section 3 and an effective reproduction number is determined. In section 4, equilibrium points of the system are determined, followed by stability analysis of the equilibrium points in section 5. In section 6, the persistence conditions of endemic equilibrium point are determined. To perform numerical simulation, parameter estimation is conducted in section 7. Numerical simulation is performed in section 8 and results obtained are discussed therein. In section 9, Discussion about the implication of study is given. Section 10 contains the limitations of the mathematical model.

2. The model

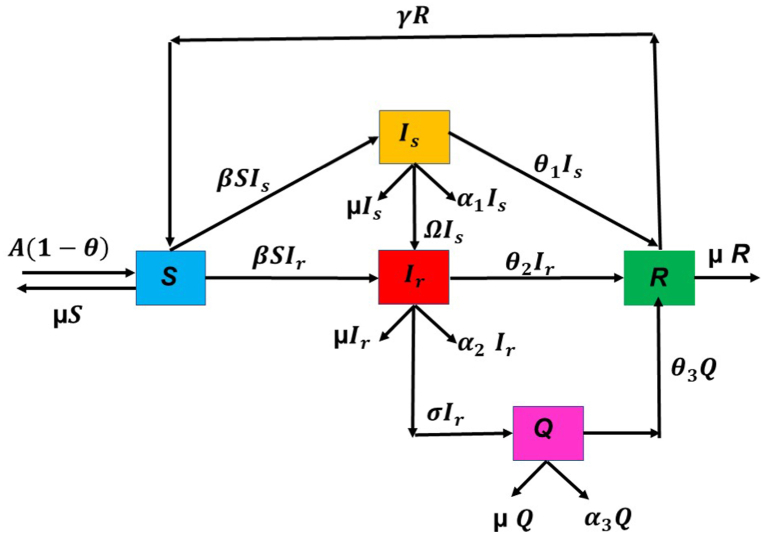
In this paper, a nonlinear mathematical model is formulated to study the efficacy of isolating MDR-TB cases in the control and elimination of TB in India. To formulate the model, we assume that total susceptible class, S(t) enters into the system at the rate A(1 − θ) where A is the recruitment rate and θ is the vaccination rate. We assume that the vaccination is perfect and TB is acquired only by unvaccinated individuals entering into the susceptible class. Transmission coefficient of infection or incidence rate of TB is denoted by β. In order to study the role of MDR cases in the incidence of TB we stratify the infected class into DS and MDR compartments denoted by I_s(t) and I_r(t) respectively. We assume that a fraction Ω of the DS-TB cases acquire drugresistance and enter into the I_r(t) class. Further, we introduce a new compartment of MDR-TB cases requiring special diagnosis and treatment termed as isolated class and denote it by Q(t). We assume that MDR-TB cases are isolated at the rate σ. Furthermore, θ₁, θ₂ & θ₃ are the rates at which DS-TB, MDR-TB and isolated class Q(t) respectively move to the recovered class R(t) after recovery. Since people might not develop full immunity after recovery, it is assumed that upon recovery from recovered class, a fraction γ of the recovered class R(t) again enters into the susceptible class S(t). Natural mortality of each class is assumed to be same denoted by μ. In addition, we consider disease induced death of I_s(t), I_r(t), and Q(t) compartments and denote it by α₁, α_2, and α₃ respectively.

The mechanism of the dynamical transfer of the TB through the total class is depicted in Fig. 1. Keeping these assumptions into consideration, the mathematical model can be written as a five dimensional system of non linear ordinary differential equations:

$$\frac{dS}{dt}=A(1-\theta )-\beta I_{s}S-\beta I_{r}S-\mu S+\gamma R$$ (1)

$$\frac{d{I}_s}{dt}=\beta I_{s}S-(\mu +{\theta }_1+\mathrm{\Omega }+{\alpha }_1)I_s$$ (2)

$$\frac{d{I}_r}{dt}=\beta I_{r}S-(\mu +\sigma +{\theta }_2+{\alpha }_2)I_r+\mathrm{\Omega }{I}_s$$ (3)

$$\frac{dQ}{dt}=\sigma I_r-(\mu +{\theta }_3+{\alpha }_3)Q$$ (4)

$$\frac{dR}{dt}={\theta }_1{I}_s+{\theta }_2{I}_r+{\theta }_{3}Q-(\mu +\gamma )R$$ (5)

where,

$$N=S+I_s+I_r+Q+R$$ (6)

and initial conditions are: S(0) > 0, I_s(0) ≥ 0, I_r(0) ≥ 0, I_s(0) ≥ 0, Q(0) ≥ 0, R(0) ≥ 0.

Fig. 1.

An S-Is-Ir-Q-R Model for Tuberculosis Dynamics.

If we denote Λ₁ = μ + θ₁ + Ω + α₁, Λ₂ = μ + σ + θ₂ + α₂, Λ₃ = μ + θ₃ + α₃,mathematical model can be given as:

$$\frac{dS}{dt}=A(1-\theta )-\beta I_{s}S-\beta I_{r}S-\mu S+\gamma R$$ (7)

$$\frac{d{I}_s}{dt}=\beta I_{s}S-{\mathrm{\Lambda }}_1{I}_s$$ (8)

$$\frac{d{I}_r}{dt}=\beta I_{r}S-{\mathrm{\Lambda }}_2{I}_r+\mathrm{\Omega }{I}_s$$ (9)

$$\frac{dQ}{dt}=\beta I_{r}S-{\mathrm{\Lambda }}_{3}Q+\sigma I_r$$ (10)

$$\frac{dR}{dt}={\theta }_1{I}_s+{\theta }_2{I}_r+{\theta }_{3}Q-(\mu +\gamma )R$$ (11)

Since the solutions of mathematical model remain feasible in the region

$$\kappa =\left\{(S,I_s,I_r,Q,R):0\le S+I_s+I_r+Q+R\le \frac{A(1-\theta )}{\mu }\right\}$$ (12)

for all t > 0, hence the problem is well posed and biologically meaningful.

3. Reproduction number

We find the reproduction number through next generation matrix approach given by P. Van Den Driessche and Watmough (van den Driessche & Watmough, 2002). Through this approach we find V and F where V is the rate of transfer of individuals into and outside the infectious compartment and F is the rate of new infection in the population. By the model equations (7), (8), (9), (10), (11) we obtain

$$F=\left[\begin{array}{ccc}\beta \frac{A(1-\theta )}{\mu }& 0& 0\\ 0& \beta \frac{A(1-\theta )}{\mu }& 0\\ 0& 0& 0\end{array}\right]$$

and,

$$V=\left[\begin{array}{ccc}{\mathrm{\Lambda }}_1& 0& 0\\ -\mathrm{\Omega }& {\mathrm{\Lambda }}_2& 0\\ 0& -\sigma & {\mathrm{\Lambda }}_3\end{array}\right].$$

The reproduction number, defined as the spectral eigen value of matrix FV⁻¹ can be obtained as:

$$R_e=Max\left(\frac{\beta A(1-\theta )}{\mu {\mathrm{\Lambda }}_1},\frac{\beta A(1-\theta )}{\mu {\mathrm{\Lambda }}_2},0\right)$$ (13)

where, Λ₁ is the average duration of infection of DS-TB and Λ₂ is the average duration of infection of MDR-TB cases. Obviously, Λ₂ > Λ₁ and in addition, it should be noted that $\frac{\beta A(1-\theta )}{\mu {\mathrm{\Lambda }}_1}$ represents the total number of secondary infections produced by DS-TB class and $\frac{\beta A(1-\theta )}{\mu {\mathrm{\Lambda }}_2}$ represents the total number of secondary infections produced by MDR-TB class. Hence, if we denote them as

$$R_e^{DS}=\frac{\beta A(1-\theta )}{\mu {\mathrm{\Lambda }}_1},$$

and

$$R_e^{\mathit{MDR}}=\frac{\beta A(1-\theta )}{\mu {\mathrm{\Lambda }}_2},$$

respectively, equation (13) can be expressed as

$$R_e=Max(R_e^{DS},R_e^{\mathit{MDR}},0).$$ (14)

Thus, effective reproduction number suggested by our model is contributed by DS-TB class and is given by

$$R_e=R_e^{DS}=\frac{\beta A(1-\theta )}{\mu {\mathrm{\Lambda }}_1}.$$ (15)

4. Equilibrium points

An equilibrium point in a dynamical system is a solution that does not change with time. Thus, if the system starts at an equilibrium point, the state will remain at the equilibrium forever. In epidemiology, we are interested in finding the conditions under which system will be free from disease that is, disease free equilibrium point and the conditions for persistence of disease by computing the endemic equilibrium point. In our model, Disease free equilibrium point is obtained as $E_1=\{A(\frac{1-\theta }{\mu }),0,0,0,0\}$ and Endemic equilibrium point is denoted by $E_2=\{S^{\ast },I_s^{\ast },I_r^{\ast },Q^{\ast },R^{\ast }\}$.

It is very easy to observe from equations (7), (8), (9), (10), (11) that $E_1=\{A(\frac{1-\theta }{\mu }),0,0,0,0\}$ is the disease free equilibrium point of the system. Now we use the theorems provided in Chavez et al. (Castillo-Chavez et al., 2002) to show the connection between existence and stability conditions of equilibrium points and reproduction number.

Theorem 1 states the conditions for the existence of endemic equilibrium point of the system as given below:

Theorem 1

Endemic equilibrium point$E_2=\{S^{\ast },I_s^{\ast },I_r^{\ast },Q^{\ast },R^{\ast }\}$exists if

• 1.R_e > 1,
• 2.${\theta }_3<\frac{({\theta }_1-{\theta }_2)(\mu +{\alpha }_3)}{(\sigma -{\theta }_1+{\theta }_2)}$

Solving the model equations (7), (8), (9), (10), (11) by equating their right hand side to zero, endemic equilibrium point $E_2=\{S^{\ast },I_s^{\ast },I_r^{\ast },Q^{\ast },R^{\ast }\}$ is obtained as:

$$S^{\ast }=\frac{{\mathrm{\Lambda }}_1}{\beta },$$ (16)

$$I_s^{\ast }=\frac{({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)}{\mathrm{\Omega }}{I}_r^{\ast },$$ (17)

$$Q^{\ast }=\frac{\sigma }{{\mathrm{\Lambda }}_3}{I}_r^{\ast },$$ (18)

and

$$R^{\ast }=\frac{1}{{\mu }_1+\gamma }\left\{\frac{{\theta }_1({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)}{\mathrm{\Omega }}+{\theta }_2+\frac{{\theta }_3\sigma }{{\mathrm{\Lambda }}_3}\right\}{I}_r^{\ast }$$ (19)

where,

$$I_r^{\ast }=\frac{A(1-\theta )-\frac{\mu {\mathrm{\Lambda }}_1}{\beta }}{\frac{{\mathrm{\Lambda }}_1}{\mathrm{\Omega }}({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)+{\mathrm{\Lambda }}_1-\frac{\gamma }{\mu +\gamma }\left\{\frac{{\theta }_1({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)}{\mathrm{\Omega }}+{\theta }_2+\frac{{\theta }_3\sigma }{{\mathrm{\Lambda }}_3}\right\}},$$ (20)

$$I_r^{\ast }=\frac{\frac{\beta }{\mu {\mathrm{\Lambda }}_1}(R_e-1)}{\frac{{\mathrm{\Lambda }}_1}{\mathrm{\Omega }}({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)+{\mathrm{\Lambda }}_1-\frac{\gamma }{\mu +\gamma }\left\{\frac{{\theta }_1({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)}{\mathrm{\Omega }}+{\theta }_2+\frac{{\theta }_3\sigma }{{\mathrm{\Lambda }}_3}\right\}}$$ (21)

On simplification, we observe that a positive equilibrium value of MDR-TB class $I_r^{\ast }$ exists if following two conditions hold:

• 1.R_e > 1,
• 2.${\theta }_3<\frac{({\theta }_1-{\theta }_2)(\mu +{\alpha }_3)}{(\sigma -{\theta }_1+{\theta }_2)}$.

Thus, it is inferred that a positive endemic equilibrium point $E_2=\{S^{\ast },I_s^{\ast },I_r^{\ast },Q^{\ast },R^{\ast }\}$ exists if the two conditions stated above are satisfied. This proves the theorem.

5. Stability analysis

Stability analysis (Shuai & van den Driessche, 2013; Bhadauria & Dhungana, 2022) of equilibrium point is significant in epidemiology for its capability to provide the nature of solution of system without actually solving them, as nonlinear differential equations are difficult to solve.

Theorem 2

Disease free equilibrium point is locally as well globally asymptotically stable ifR_e < 1.

It is important to discuss the local stability of equilibrium points as practically initial data is not known and we wish to find the impact of small perturbation in the equilibrium points on the system. To study the local stability of system, we find the variational matrix of system. Stability of an equilibrium point is determined by the signs of the real parts of the eigenvalues of the variational matrix. The general variational matrix of the system is as given below:

$$V(E)=\left[\begin{array}{ccccc}-\beta I_s-\beta I_r-{\mu }_1& -\beta S& -\beta S& 0& \gamma \\ \beta I_s& \beta S-{\mathrm{\Lambda }}_1& 0& 0& 0\\ \beta I_r& \mathrm{\Omega }& \beta S-{\mathrm{\Lambda }}_2& 0& 0\\ 0& 0& \sigma & -{\mathrm{\Lambda }}_3& 0\\ 0& {\theta }_1& {\theta }_2& {\theta }_3& -(\mu +\gamma )\end{array}\right].$$

Variational matrix of the system for the disease free equilibrium point is:

$$V(E_0)=\left[\begin{array}{ccccc}-\mu & -\beta \frac{A(1-\theta )}{\mu }& -\beta \frac{A(1-\theta )}{\mu }& 0& \gamma \\ 0& \beta \frac{A(1-\theta )}{\mu }-{\mathrm{\Lambda }}_1& 0& 0& 0\\ 0& \mathrm{\Omega }& \beta \frac{A(1-\theta )}{{\mu }_1}-{\mathrm{\Lambda }}_2& 0& 0\\ 0& 0& \sigma & -{\mathrm{\Lambda }}_3& 0\\ 0& {\theta }_1& {\theta }_2& {\theta }_3& -(\mu +\gamma )\end{array}\right].$$

Eigenvalues of the matrix are:

• 1.λ₁ = −μ
• 2.${\lambda }_2=\frac{\beta A(1-\theta )}{\mu }-{\mathrm{\Lambda }}_1$
• 3.${\lambda }_3=\frac{\beta A(1-\theta )}{\mu }-{\mathrm{\Lambda }}_2$
• 4.λ₄ = −Λ₃
• 5.λ₅ = −(μ + γ).

Thus, by Routh Hurwitz criterion [25], we conclude that disease free equilibrium point is locally asymptotically stable if.

$\frac{\beta A(1-\theta )}{\mu {\mathrm{\Lambda }}_1}=R_e<1$, since then the eigen value given by 3 becomes negative automatically.

To prove the global asymptotic stability of disease free equilibrium, we construct a Lyapunov function

$$\zeta =\frac{1}{{\mathrm{\Lambda }}_1}{I}_s+\frac{1}{{\mathrm{\Lambda }}_2}{I}_r+Q$$

On Differentiation, we have

$$\frac{d\zeta }{dt}=\frac{1}{{\mathrm{\Lambda }}_1}(\beta I_{s}S-{\mathrm{\Lambda }}_1{I}_s)+\frac{1}{{\mathrm{\Lambda }}_2}(\beta I_{r}S-{\mathrm{\Lambda }}_2{I}_r+\mathrm{\Omega }{I}_s)+(\sigma I_r-{\mathrm{\Lambda }}_{3}Q)\le \left\{\frac{\beta A(1-\theta )}{\mu {\mathrm{\Lambda }}_1}-1+\frac{\mathrm{\Omega }}{{\mathrm{\Lambda }}_2}\right\}{I}_s+\left\{\frac{\beta A(1-\theta )}{\mu {\mathrm{\Lambda }}_2}-1+\sigma \right\}{I}_r=-\left\{\left(1-\frac{\mathrm{\Omega }}{{\mathrm{\Lambda }}_2}\right)-R_e^{DS}\right\}{I}_s-\{(1-\sigma )-R_e^{\mathit{MDR}}\}{I}_r$$

Since all the parameters and variables of the model are non negative, it follows that $\frac{d\zeta }{dt}\le 0$ for $R_e^{DS}<1-\frac{\mathrm{\Omega }}{{\mathrm{\Lambda }}_2}$ and $R_e^{\mathit{MDR}}<1-\sigma$ or $R_e^{DS}<1$ and $R_e^{\mathit{MDR}}<1$ or R_e < 1 with $\frac{d\zeta }{dt}=0$ if and only if I_s = I_r = 0. Hence, ζ is a Lyapunov function on κ. Therefore, the largest compact invariant subset of the set where $\frac{d\zeta }{dt}=0$ is the singleton (I_s, I_r, Q) = (0, 0, 0). Thus, it follows, by the LaSalle's invariance principle (Mancilla-Aguilar & García, 2006), that (I_s, I_r, Q) → (0, 0, 0) as t → ∞.This proves the global stability of disease free equilibrium.

Theorem 3

Endemic equilibrium point of the system is locally asymptotically stable ifR_e > 1, $I_s^{\ast }>\frac{{\theta }_2}{\beta {\theta }_1}$ and conditions 1-4 hold.

Variational matrix of the system of equations (7), (8), (9), (10), (11) at endemic equilibrium point $E_2=\{S^{\ast },I_s^{\ast },I_r^{\ast },Q^{\ast },R^{\ast }\}$ is

$$V(E_2)=\left[\begin{array}{ccccc}-\beta I_s^{\ast }-\beta I_r^{\ast }-\mu & -\beta S^{\ast }& -\beta S^{\ast }& 0& \gamma \\ \beta I_s^{\ast }& \beta S^{\ast }{-\wedge }_1& 0& 0& 0\\ \beta I_r^{\ast }& \mathrm{\Omega }& \beta S^{\ast }{-\wedge }_2& 0& 0\\ 0& 0& \sigma & {-\wedge }_3& 0\\ 0& {\theta }_1& {\theta }_2& {\theta }_3& -(\mu +\gamma )\end{array}\right]$$

The characteristic equation of above variational matrix V(E₂) is

$${\lambda }^5+M_1{\lambda }^4+M_2{\lambda }^3+M_3{\lambda }^2+M_4\lambda +M_5=0.$$ (22)

where

$$M_1=\beta I_s^{\ast }+\beta I_r^{\ast }+\mu +{\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1+{\mathrm{\Lambda }}_3+\mu +\gamma ,$$

$$M_2={\mathrm{\Lambda }}_2(\beta I_s^{\ast }+\beta I_r^{\ast })+\mu ({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)+({\mathrm{\Lambda }}_3+\mu +\gamma )(\beta I_s^{\ast }+\beta I_r^{\ast }+\mu +{\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)+{\mathrm{\Lambda }}_3(\mu +\gamma ),$$

$$M_3=({\mathrm{\Lambda }}_3+\mu +\gamma )\{{\mathrm{\Lambda }}_2(\beta I_s^{\ast }+\beta I_r^{\ast })+\mu ({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)\}+{\mathrm{\Lambda }}_3(\mu +\gamma )(\beta I_s^{\ast }+\beta I_r^{\ast }+\mu +{\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)+{\mathrm{\Lambda }}_1\beta I_s^{\ast }({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)+\mathrm{\Omega }{\mathrm{\Lambda }}_1\beta I_s^{\ast }+\gamma (\beta I_s^{\ast }{\theta }_1-{\theta }_2)$$

$$M_4=({\mathrm{\Lambda }}_3+\mu +\gamma )\beta I_s^{\ast }{\mathrm{\Lambda }}_1({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1+\mathrm{\Omega })+{\mathrm{\Lambda }}_3(\mu +\gamma )\{{\mathrm{\Lambda }}_2(\beta I_s^{\ast }+\beta I_r^{\ast })+\mu ({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)\}+{\theta }_1\gamma \beta I_s^{\ast }({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)+{\theta }_2\gamma \mathrm{\Omega }\beta I_s^{\ast }+{\theta }_3\gamma I_r^{\ast }\sigma +{\mathrm{\Lambda }}_3\gamma (\beta I_s^{\ast }{\theta }_1-{\theta }_2)$$

$$M_5=2{\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_3(\mu +\gamma )\beta I_r^{\ast }({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)+\beta I_s^{\ast }\gamma \{{\theta }_1{\mathrm{\Lambda }}_3({\mathrm{\Lambda }}_2-{\mathrm{\Lambda }}_1)+{\theta }_2\mathrm{\Omega }{\mathrm{\Lambda }}_3+{\theta }_3\mathrm{\Omega }\sigma \}$$

Clearly, all $M_i^{\prime }s>0,i=1,2,3,4,5$ provided that R_e > 1 and $I_s^{\ast }>\frac{{\theta }_2}{\beta {\theta }_1}$. By Routh Hurwitz criteria (Morris, 1962), endemic equilibrium point is locally asymptotically stable if all the conditions stated below in 1–4 also hold.

• 1. $M_i^{\prime }s>0,i=1,2,3,4,5$
• 2.M₁M₂ − M₃ > 0
• 3.(M₁M₂ − M₃)M₃ − (M₁M₄ − M₅)M₁ > 0
• 4.$(M_1{M}_2-M_3)(M_3{M}_4-M_2{M}_5)-{(M_1{M}_4-M_5)}^2>0$.

Hence the theorem.

6. Persistence

The word ’Persistence’ stands for the survival of population in future time. We study persistence of the system to determine the conditions required for all time existence of each population in the system. From the mathematical point of view, persistence means that the strictly positive equilibrium does not have omega limit points on the boundary of the non-negative cone. However, from the epidemiological point of view, persistence or permanence stands for endemicity of disease. There are two approaches to obtain persistence result according to Waltman (Waltman, 1991); first one is by studying the behavior of the system near the boundary and the second approach uses a Liapunov like function. We will use the second approach given by Fonda (Fonda, 1988) in terms of repellers.

A semidynamical system π is said to be persistent if for all x ∈ intF,liminf_t→∞d(π(x, t), ∂F) > 0, where X is a locally compact metric space with metric d and F is a closed subset of a set X with boundary ∂F and interior intF. Moreover, π is said to be uniformly persistent if there is ξ > 0 such that for all x ∈ intF, liminf_t→∞d(π(x, t), ∂F) > ξ. The following theorem would help us to conclude that the semi dynamical system is uniformly persistent by proving that Z = {(S, I_s, I_r, Q, R) ∈ ξ: I_s = 0, I_r = 0, Q = 0} is a uniform repellor.

Theorem 4

The set Z is uniform repellor and henceπ is uniformly persistent in ξ if R_e > 1.

For the system of equations given by (7), (8), (9), (10), (11), there is a unique solution $\pi (x_0,t)={(S,I_s,I_r,Q,R)}_{(t,x_0)}$ defined in $R_0^{+5}$, lies in R₀ + 5 for any equilibrium point x₀ = (S₀, I_s0, I_r0, Q₀, R₀) that satisfies π(x₀, 0) = (S₀, I_s0, I_r0, Q₀, R₀). In order to show that π is uniformly persistent, we limit our study to the set

$$\xi =\left\{(S,I_s,I_r,Q,R):S+I_s+I_r+Q+R\le \frac{A(1-\theta )}{\mu }\right\}.$$

If x₀ ∈ ξ then π(x₀, t) ∈ ξ, for every $t\in R_0^{+5}$ and hence the restriction of π to ξ, that we will denote by π only, is a semi dynamical system in ξ. Let Z be a compact subset of ξ. It can be easily verified that ξ∖Z is positively invariant as I_s(0) > 0 ⇒ I_s(t) > 0, I_r(0) > 0 ⇒ I_r(t) > 0 and Q(0) > 0 ⇒ Q(t) > 0∀t > 0.

Define

$$P:\xi \to R_0^{+5}$$

such that P(S, I_s, I_r, Q, R) = lI_s + mI_r + nQ. Consider a set,

$${\xi }_1=\{(S,I_s,I_r,Q,R)\in \xi :P(S,I_s,I_r,Q,R)<\rho \}$$

with ρ sufficiently small such that

$$\frac{\mu R_e^{DS}}{2\beta \rho +\mu }>1,$$

$$\frac{\mu R_e^{\mathit{MDR}}}{2\beta \rho +\mu }>1.$$

Then by Margheri (Margheri, 1996) it will be sufficient to prove that all x ∈ ξ₁∖Z, there is a T_x such that P(π(x, T_x)) > P(x). On the contrary, we assume that there a x ∈ ξ₁ such that for each t > 0 we have P(π(x, t)) < p(x) < ρ, implying that I_s(t) < ρ and I_r(t) < ρ for each t > 0. Since the solutions are bounded we have

$$\frac{dS}{dt}\ge A(1-\theta )-(\beta \rho +\beta \rho +\mu )S\ge A(1-\theta )-(2\beta \rho +\mu )S$$

This implies that $limin{f}_{t\to \infty }S(t)\ge \frac{A(1-\theta )}{2\beta \rho +\mu }$. Hence,

$$S(t)\ge \frac{A(1-\theta )}{2\beta \rho +\mu }$$

for t ≥ T for a sufficiently large T > 0. Further, let us consider the auxiliary function,

$$\mathrm{\Gamma }=I_s(t)+I_r(t)$$

$$\frac{d\mathrm{\Gamma }}{dt}=\frac{d{I}_s}{dt}+\frac{d{I}_r}{dt}$$

$$\frac{d\mathrm{\Gamma }}{dt}\ge \beta I_s\frac{A(1-\theta )}{2\beta \rho +\mu }-{\mathrm{\Lambda }}_1{I}_s+\beta I_r\frac{A(1-\theta )}{2\beta \rho +\mu }-{\mathrm{\Lambda }}_2{I}_r+\mathrm{\Omega }{I}_s$$

$$={\mathrm{\Lambda }}_1\left\{\frac{\mu R_e^{DS}}{2\beta \rho +\mu }-1+\frac{\mathrm{\Omega }}{{\mathrm{\Lambda }}_1}\right\}{I}_s+{\mathrm{\Lambda }}_2\left\{\frac{\mu R_e^{\mathit{MDR}}}{2\beta \rho +\mu }-1\right\}{I}_r$$

$$\ge \delta \mathrm{\Gamma }.$$

Where,

$$\delta =min\left\{\frac{\mu R_e^{DS}}{2\beta \rho +\mu }-1+\frac{\mathrm{\Omega }}{{\mathrm{\Lambda }}_1},\frac{\mu R_e^{\mathit{MDR}}}{2\beta \rho +\mu }-1\right\}$$

then

$$\frac{d\mathrm{\Gamma }(t)}{dt}\ge \delta \mathrm{\Gamma }(t).$$

This inequality implies that Γ(t) → ∞ as t → ∞. But Γ(t) is bounded on the set ξ, so the assumption considered by us cannot be true. Thus, we have proved that there is some t = T_x such that P(π(x, T_x)) > P(x) for each x ∈ ξ∖Z with x belonging to a suitable small neighbourhood ξ₁ of Z. Thus, from Fonda's theorem we infer that the semidynamical system is uniformly persistent if $R_e^{DS}$ = R_e < 1.

7. Parameter estimation

To perform the numerical simulations, we estimate the parameters used in the model with the help of existing literature and NTEP. The values of the parameters are listed in Table 1.

Table 1.

Source of parameters used in model.

Parameters	Parameters description	Value and source
A	Births	24154133 person year−1 (Office of the registrar general, 2020)
μ	natural mortality rate	0.007 year−1 (World health organisation, 2018)
θ	immunization coverage	0.87 (The rntcp annual status report (2010–2019) tb india, 2019)
α1	disease induced death rate in DS-TB class	0.03 year−1 (Zhao et al., 2017)
α2	disease induced death rate in MDR-TB class	0.14 year−1 (Zhao et al., 2017)
α3	disease induced death rate in isolated class	0.14 year−1 (Zhao et al., 2017)
β	incidence rate of TB	5.11 × 10−10person−1year−1 (World health organisation, 2018)
Ω	transition rate from DS-TB to MDR-TB class	0.035 year−1 (Mirsaeidi, 2013)
σ	rate of isolating MDR-TB class	0.5 year−1 [Assumed]
θ1	recovery rate of DS-TB class	0.79 year−1, (Zhao et al., 2017)
θ2	recovery rate of MDR-TB class	0.48 year−1 (Zhao et al., 2017)
θ3	recovery rate of isolated class	0.48 year−1 (Zhao et al., 2017)
γ	TB relapse rate	0.42 year−1 (World health organisation, 2018)

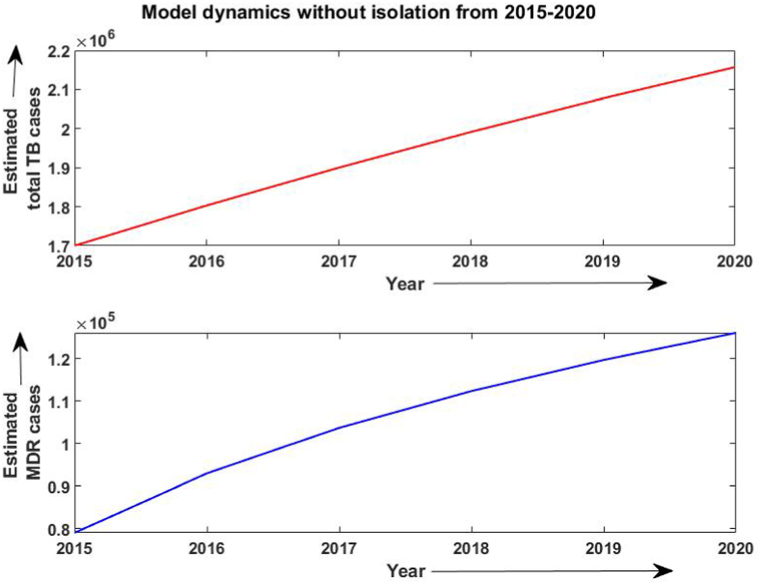
Moreover, since our objective is to find the efficacy of isolation as a control strategy and elimination of TB, we studied the dynamics of TB through our model from 2018 to 2035 to predict its role in plausible elimination of TB. To study the model within this range we calculated the initial values of the system variables as follows: in 2018, notified TB patients in India according to NTEP were 2155894 and notified drugresistant TB patients were 58347. We studied the model assuming isolation of 50% of MDR-TB cases. Therefore, initial value of isolated MDR-TB cases were Q(0) = 50% of 58347 = 29173.5 = 29174. Thus, initial population of people with MDR-TB is calculated as I_r(0) = 50% of 58347 = 29173.5 = 29174. With this population of I_r(0), initial value of DS-TB class is estimated as I_s(0) = 2155894-58347 = 2097547. Since 79% of total TB patients get recovered and in 2017 total notified TB patients were 1827959, therefore, initial value of recovered class is estimated as R(0) = 79% of 1827959 = 1444087. In addition, to validate our model we performed numerical simulation from 2015 to 2020 without isolated class. All the parameter values were same except the transmission coefficient of infection and recovery rate. We estimated transmission coefficient of infection, as β = 6.5 × 10⁻¹⁰ per person per year, and since recovery rate for the year 2015 was 72%, we took recovery rate for DS-TB class as θ = 0.72 per year. Initial values of the system variable for the year 2015, calculated in the same manner as described previously for 2018 are S(0) = 1304185403, I_s(0) = 1621000, I_r(0) = 79000 and R(0) = 1224000.

8. Numerical simulation from 2018 to 2035 and results obtained

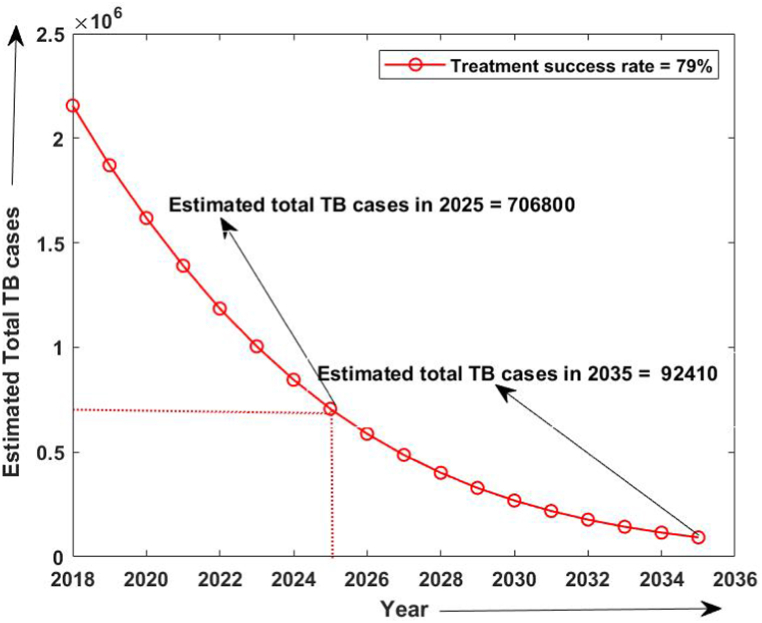
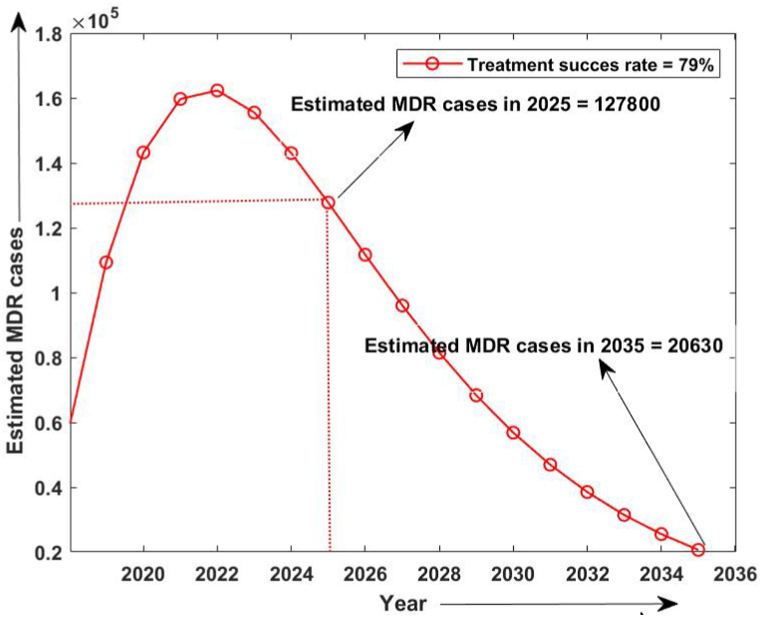
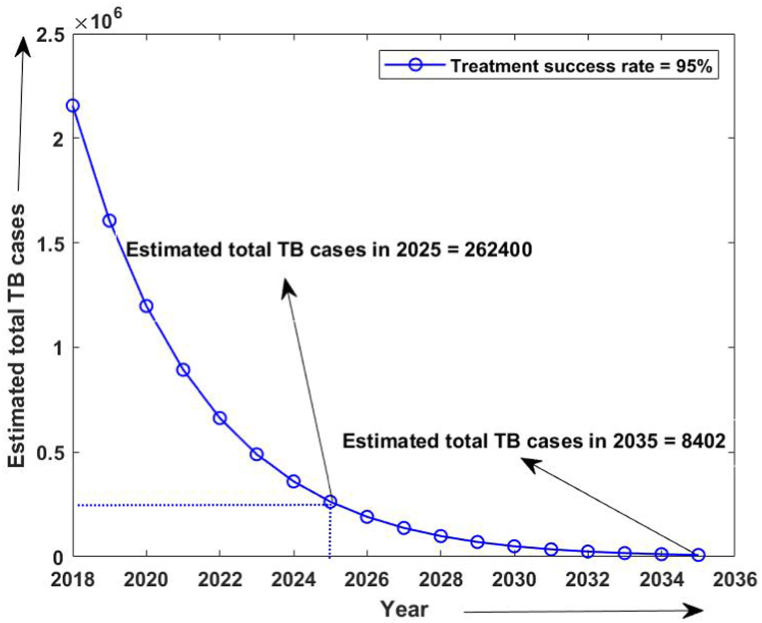
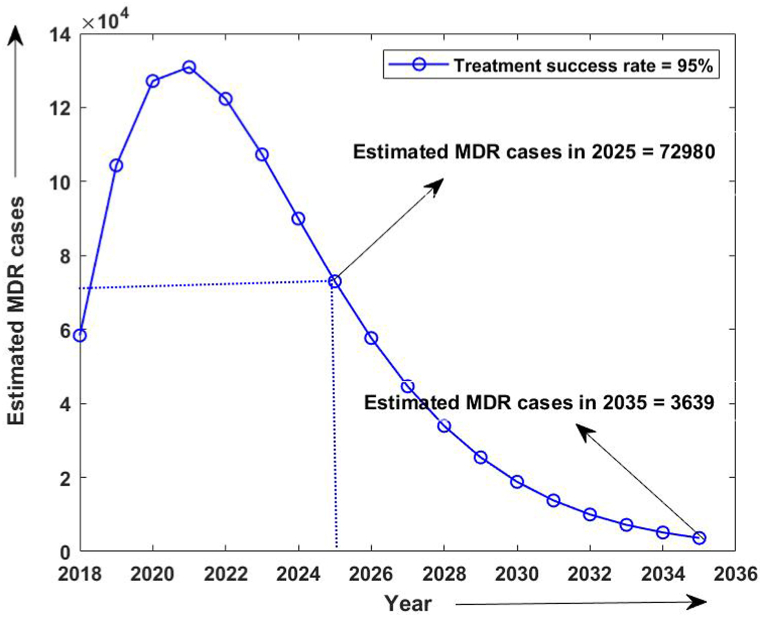
Firstly, the simulation of the model has been done from 2015 to 2020 without considering the isolated compartment to validate our model. The model simulates the estimated number of total TB and MDR-TB incidence from 2015 to 2025, which shows a good estimation for the total TB and MDR-TB incidence cases from 2015 to 2020 (data available) in Fig. 2. The simulation also validates our choice of model parameters and allows us for further simulation. Intending to predict TB incidence and the MDR-TB incidence with 50% isolation, we simulated our model for two different values of treatment success rates at ongoing 79% and intended 95% and determined its role in plausible elimination of TB by 2035. The model predicts that if the current TB control measures in India continue with no other immediate public health interventions, the TB burden in India remains persistent till 2035, which is beyond the prospect to eradicate TB in India by 2025 as outlined in NSP 2017. Further, if we isolate at least 50% MDR patients strictly and do not allow them for further contacts and transmission with ongoing TB treatment success rate (79%), we can make a difference. With these values, we observed from Fig. 3, Fig. 4 that the predicted TB cases in 2025 are 706800 (including 172800 MDR cases), and in 2035 are 92410 (including 20630 MDR cases) respectively. The isolation of at least 50% of MDR TB and other ongoing interventions may reduce TB transmission significantly in India by 2035. We further simulated the model to see the effect of a high TB treatment success rate (by assuming it 95%). Fig. 5, Fig. 6 demonstrate that the intended 95% TB treatment success rate with 50% MDR-TB isolation can lead to India's TB elimination by 2035. Achieving 95% TB treatment success rate is a highly ambitious goal, but approaching close to it will make India towards TB eradication.

Fig. 2.

Estimated number of TB cases (2015-2020) without isolation of MDR cases.

Fig. 3.

Estimated number of TB cases when 50% MDR isolation and with 79% treatment success rate.

Fig. 4.

Estimated number of MDR-TB cases when 50% MDR isolation and 79% treatment success rate.

Fig. 5.

Estimated number of TB cases with 50% MDR isolation and 95 % treatment success rate.

Fig. 6.

Estimated number of MDR- TB cases with 50% MDR isolation and 95 % treatment success rate

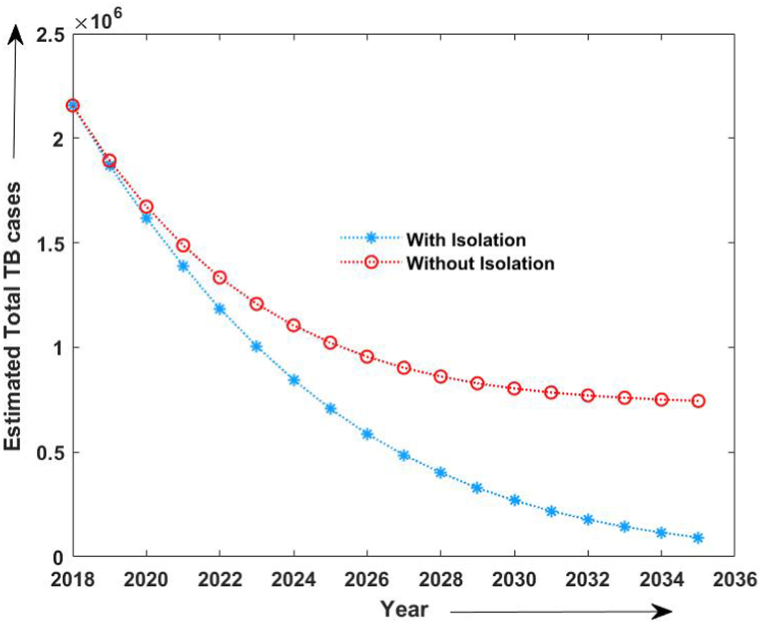
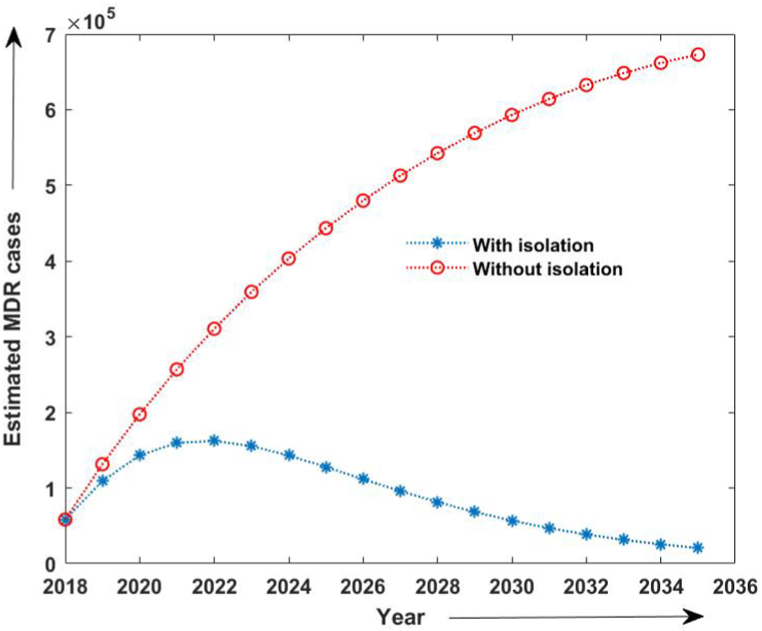
Moreover, to study the efficacy of isolation in TB control and its elimination, we compared the TB incidence and estimated MDR-TB incidence with and without isolation strategy, as shown in Fig. 7, Fig. 8. We observed that even 50% of isolation of MDR cases reduces the prospective incidence cases of TB. Also, we computed the effective reproduction number with the given set of parameters. With the assumption that the transmission coefficient of infection rises by 21 percent without strictly isolating MDR-TB patients, we estimated the reproduction number from 2015 to 2020 as 0.4 approximately, whereas with the estimated parameters and 50% isolation reproduction number was estimated to decrease up-to 0.3 during 2018–2035. Also, the reproduction number due to MDR-TB patients from 2015 to 2020 without isolation was estimated to be 0.26 and that with strict isolation strategy, it was estimated to be 0.20 from 2018 to 2035.

Fig. 7.

Estimated number of TB cases with 50% MDR isolation and without isolation

Fig. 8.

Estimated number of MDR- TB cases with 50% MDR isolation and without isolation

9. Discussion

Globally, India contributes 30% of the total TB incidence. The WHO ambitious Global TB Strategy of 2015 aims to end the global TB epidemic, with targets to reduce TB deaths by 95% and to cut new cases by 90% between 2015 and 2035, and to ensure that no family is burdened with catastrophic expenses due to TB (Ai et al., 2016). Achievement of this WHO goal depends significantly on the TB burdens by India. However, the current TB Statistics in India seem an obstacle to achieve the aim of TB eradication by 2025, as proposed by the National Strategic Plan (NSP ) 2017. The developed countries of the world isolate people suspected of having TB until they are proven to be not contagious.

In this paper, we develop a SIQR mathematical model on TB dynamics in India to study the efficacy of isolation in the eradication of TB cases in India from 2015 to 2035. This study's research question is whether the current TB interventions in India support the TB eradication aim by 2025 in India. Furthermore, the model also investigates how isolation can be a crucial intervention to reduce secondary transmission. Nevertheless, India does not have a quarantine policy for highly contagious MDR-TB patients as well. Although healthcare workers realize the necessity of isolating such patients, they fail to recommend as there is no directive in the national TB policy. The lack of such provision may be due to the reason that major MDR-TB cases come from underprivileged sections of the society. However, allowing these contagious patients to move around freely may ensure that India will probably never end to TB. Hence, it becomes imperative to isolate MDR-TB patients with minimal rights infringement to control pandemic. We, therefore, propose isolation of MDR-TB cases as an intervention strategy to combat DS-TB and MDRTB cases in India. Our model predicts that isolation of even half of the MDR-TB cases may produce a significant decline in TB incidence and estimated MDR-TB incidence by 2025 with an ongoing treatment success rate. However, if the treatment success rate increases to that of developed countries, India may be able to achieve the target of TB elimination by 2035. Literacy and income are significantly associated with the treatment success rate among MDR TB patients (Patel et al., 2016). Hence, a strong financial and political commitment is required to end the TB epidemic from the country, including an overall more considerable investment in RNTCP. The possible primary interventions may be an increased budget of Revised National Tuberculosis Control Program (RNTCP) to help the health system for early diagnosis, to reduce the secondary transmissions of infection, reduction in TB treatment defaulters, by increasing the TB treatment success rate, by reducing the MDR TB cases and by increasing the BCG vaccinations to decrease the pediatric TB incidence. Other broader long-term factors may be improved literacy rate, socio-economic condition, good dietary habits, early identification of other comorbidities such as HIV. The government's unprecedented lockdown to beat the novel COVID-19 epidemic has worked as a step of isolation of TB and MDR-TB patients as well. It may have reduced the transmission of infection from TB 16 patients to others as it may be assumed that plausible numbers of contacts have decreased. It may result in a decline in the number of new cases of TB. Recently, many researchers have reviewed and compared COVID-19 and TB. Wingfield et al. (Wingfield et al., 2020) deliberated about the adverse effects of COVID-19 on TB patients and control programs.

On the other hand, weekly detection of new tuberculosis cases in India has decreased by nearly 75% during the COVID-19 lockdown, a factor of significant concern since without appropriate medications, the condition could worsen owing to more MDR-TB cases and hence more deaths (Glaziou, 2020). Further, there may be grave consequences for existing and undiagnosed TB patients due to diversion of resources, and an inevitable loss of health system focus as some activities cannot or will not be prioritized. This is likely to lead to a reduction in TB care and worse outcome (Togun et al., 1186). Hence, the emergence of COVID-19 may impact the number of new cases of TB and MDR-TB, and hence, the variation in the Total TB incidence and MDR cases in our result is possible.

10. Limitations

The proposed mathematical model has some limitations, like considering the same transmission coefficient of infection from TB and MDR-TB cases, absence of latent class, and prevalence of TB and MDR-TB only among the unvaccinated population. The time-variant model parameters can be introduced for the long-term simulation of the model and the sensitivity analaysis for the model paramters can be performed in future work (Dhungana, 2020).

Declaration of competing interest

None.

Handling Editor: Dr. Jianhong Wu