Modeling breast cancer proliferation, drug synergies, and alternating therapies

Summary

Estrogen receptor positive (ER+) breast cancer is responsive to a number of targeted therapies used clinically. Unfortunately, the continuous application of targeted therapy often results in resistance, driving the consideration of combination and alternating therapies. Toward this end, we developed a mathematical model that can simulate various mono, combination, and alternating therapies for ER + breast cancer cells at different doses over long time scales. The model is used to look for optimal drug combinations and predicts a significant synergism between Cdk4/6 inhibitors in combination with the anti-estrogen fulvestrant, which may help explain the clinical success of adding Cdk4/6 inhibitors to anti-estrogen therapy. Furthermore, the model is used to optimize an alternating treatment protocol so it works as well as monotherapy while using less total drug dose.

Graphical abstract

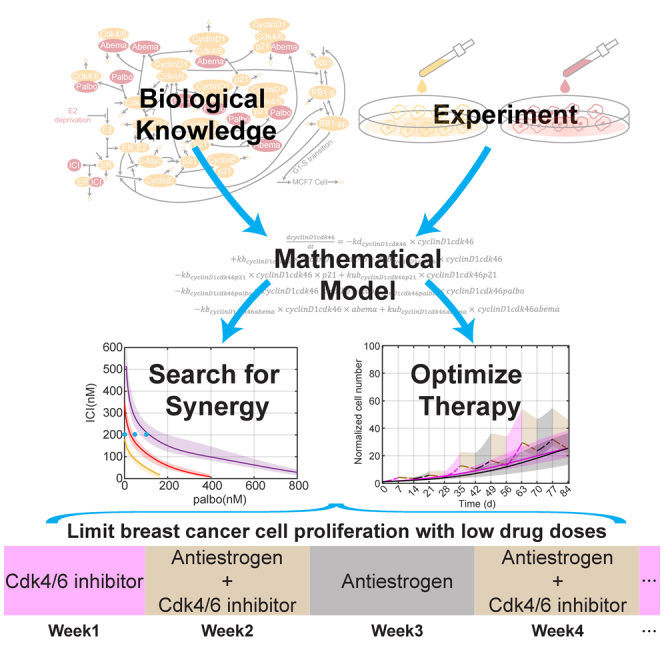
Highlights

• •Dynamic model of proliferation in response to anticancer therapies in breast cancer
• •Experimental verification of synergy between an anti-estrogen and CDK4/6 inhibitor
• •Optimizing alternating therapy protocols to limit proliferation and drug dosage

Mathematical biosciences; Computational bioinformatics; Pharmacoinformatics; Cancer systems biology; Cancer

Introduction

Metastatic breast cancer remains an incurable disease, and it is estimated that 43,250 women and men will die from breast cancer this year.¹ The most common type of breast cancer, estrogen receptor positive (ER+), which is present in approximately 70% of all breast cancers,² has targeted therapies that have dramatically improved long-term survival rates.^3,4,5 However, the continuous application of these drugs can ultimately lead to drug resistance and recurrence.^5,6,7,8,9 The resistance mechanisms are varied and include epigenetic changes, gene mutation, amplification, and deletion.^{10,11,12,13,14} Although targeted therapies are important methods for breast cancer treatment, eventually cancer cells become resistant and proliferate again, which makes the advantage of targeted therapies only temporary for many patients.

Constant application of one drug regimen over time may not be optimal, but to move beyond this approach requires addressing a number of critical questions such as (1) how long should a given therapy be applied, (2) what should the next therapy be, and (3) in any given therapy interval, what is the best combination of drugs to apply? These questions are difficult to answer experimentally, even in vitro, as long timescales are involved, and there are a huge number of possible solutions to explore. Systematic application of an experimentally calibrated mathematical model that integrates molecular cell biology and drug pharmacology can help us investigate better treatment regimens in terms of drug choice, combinations, dosing, and scheduling.^15,16,17,18 In this work, we take a step toward answering these questions in a common ER + breast cancer cell line, MCF7, by using a combination of mathematical modeling and experimental investigations.

Previously, we developed a mechanistic mathematical model based on key interactions between ER signaling and the cell cycle.¹⁹ This model was calibrated using protein and proliferation data from 7-day time courses of MCF7 cells growing under basal conditions or responding to standard clinical drugs in ER + breast cancer: (1) estrogen deprivation (–E2), a surrogate for an aromatase inhibitor that lowers the estradiol (E2) level by inhibiting aromatase;^13,20 (2) ICI 182 780 (ICI; Faslodex/fulvestrant), a proteasome-dependent ER degrader;²¹ or (3) palbociclib, a Cdk4/6 inhibitor.⁵ To address questions regarding synergies, longer timescales, and alternating treatments, more experimental data is required to either validate the initial model or show where extensions to the model are required.

In this study, we extend the model to handle a range of doses of ICI or palbociclib and to more accurately predict proliferation over longer timescales and in cases where drugs are changed periodically. Key extensions involve the accumulation of cyclinD1 and the long-term slowdown in growth rate in response to continuous palbociclib treatment. We use the resulting model to explore synergistic drug combinations and find a combination that allows a significant reduction in overall drug dose compared to monotreatment. The model is also used to optimize an alternating treatment intended to delay the development of resistance and finds a protocol that has the same proliferation as monotherapy while using a significantly lower total drug dose.

Results

Mathematical models with many parameters and limited experimental calibration data, as is the case here, have many possible parameter sets that do a reasonable job of fitting the data. Therefore, in addition to the best-fit parameter set, we created a cohort of 199 additional parameter sets that fit the data only slightly less well than the optimal one (increased squared deviation of experiment and simulation less than about 25% of the optimal, see STAR Methods). When plotting our results, we plot the best parameter set as a solid line and use shading to indicate the range of results from simulating the entire cohort. If the simulations of various parameter sets that reasonably fit the data yield results that do not have too great a spread, it provides confidence that we have not overfit the data. We also note that we only write that the model “predicts” something if the model simulation is being compared to experimental data on which it was not trained. In all other cases the plots show the simulations recapitulating the training data (see Table S1). While we explain numerous changes to the model in the following sections, all simulation results are for the final version of the model that was trained on all the calibration data (Table S1).

Simulating proliferation under constant therapy

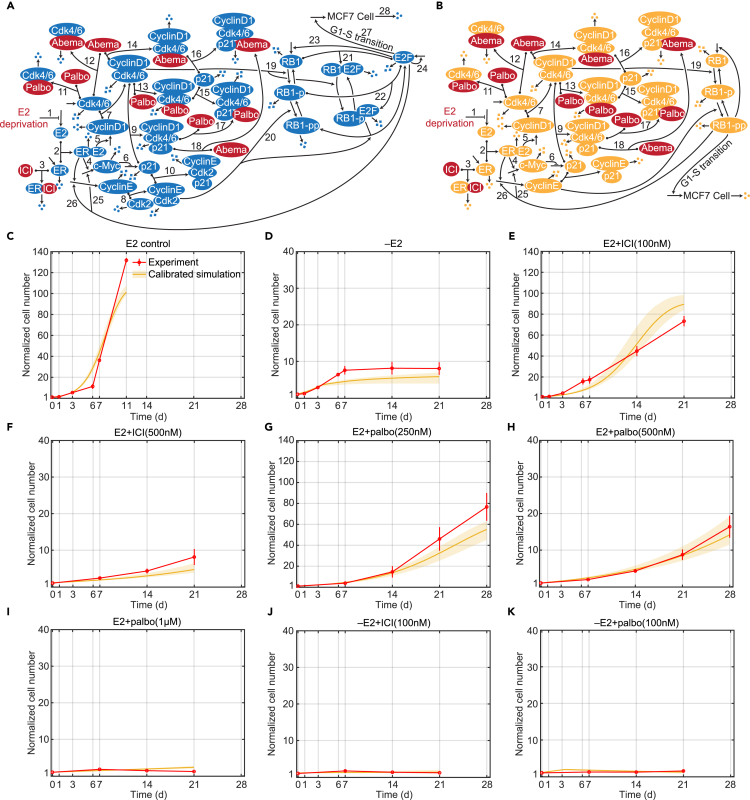
Based on the effect of estrogen signaling and Cdk4/6 inhibition on the G1-S transition of the cell cycle,^10,22,23 we built a mechanistic mathematical model using ordinary differential equations (ODEs). The biological interactions we considered are based on known mechanisms from the literature and are shown in Figure 1A. The details and references for each numbered interaction are provided in STAR Methods. To create the ODE model, we modified and simplified the interactions shown in Figure 1A. In particular, we used the RB1-pp (hyperphosphorylated form of retinoblastoma protein (RB1)) level to reflect the transcriptional activity of E2F and associated the RB1-pp level with proliferation. The model structure is shown in Figure 1B, and the explanations of the modifications and simplifications are provided in STAR Methods.

Figure 1.

Signaling diagram of the biological mechanism, model structure and model calibrations

(A) Detailed reactions of the biological mechanism related to estrogen signaling and Cdk4/6 inhibition. Reversible binding reactions are represented by dots on the components and an arrow to the complex. Three dots represent degradation of a protein or the death of a cell. Arrows pointing from blank space to a protein or MCF7 cell represent production of the protein or proliferation of the cell. Arrows pointing from one protein to another protein represent phosphorylation or dephosphorylation of the protein. Lines pointing to other lines represent enhancement (arrow) or inhibition (blunt head) of the reactions. Treatments are colored red. The numbered biological mechanism consisting of the following process: 1. –E2 decreases estrogen; 2. E2 binds to ER; 3. ICI binds to ER; 3. E2:ER increases transcription of c-Myc; 5. E2:ER increases transcription of cyclinD1; 6. c-Myc inhibits transcription of p21; 7. CyclinD1 binds to Cdk4/6; 8. CyclinE binds to Cdk2; 9. p21 binds to cyclinD1:Cdk4/6; 10. p21 binds to cyclinE:Cdk2; 11. Palbociclib binds to Cdk4/6; 12. Abemaciclib binds to Cdk4/6; 13. Palbociclib binds to cyclinD1:Cdk4/6; 14. Abemaciclib binds to cyclinD1:Cdk4/6; 15. p21 binds to cyclinD1:Cdk4/6:palbociclib; 16. p21 binds to cyclinD1:Cdk4/6:abemaciclib; 17. Palbociclib binds to cyclinD1:Cdk4/6:p21; 18. Abemaciclib binds to cyclinD1:Cdk4/6:p21; 19. CyclinD1:Cdk4/6 phosphorylates RB1; 20. CyclinE:Cdk2 phosphorylates RB1-p; 21. RB1 binds to E2F; 22. RB1-p binds to E2F; 23. E2F up-regulates RB1; 24. E2F up-regulates itself; 25. E2F up-regulates c-Myc; 26. E2F up-regulates cyclinE; 27. E2F drives the G1-S cell cycle transition and proliferation; 28. Cell death. (STAR Methods).

(B) Structure of the mathematical model, a simplified version of the biological mechanism in (A).

(C) Model calibration to experimental data (mean ± s.e., n = 3) in E2 control condition. The experimental data are shown in red and the calibration simulation results are shown in yellow (solid line represents the lowest cost value simulation and the shaded regions contains the central 98% of the cohort simulations).

(D) Model calibration to experimental data (mean ± s.e., n = 3) in –E2 condition.

(E) Model calibration to experimental data (mean ± s.e., n = 3) in E2+ICI(100 nM) condition.

(F) Model calibration to experimental data (mean ± s.e., n = 3) in E2+ICI(500 nM) condition.

(G) Model calibration to experimental data (mean ± s.e., n = 3) in E2+palbo(250 nM) condition.

(H) Model calibration to experimental data (mean ± s.e., n = 3) in E2+palbo(500 nM) condition.

(I) Model calibration to experimental data (mean ± s.e., n = 3) in E2+palbo(1 μM) condition.

(J) Model calibration to experimental data (mean ± s.e., n = 3) in –E2+ICI(100 nM) condition.

(K) Model calibration to experimental data (mean ± s.e., n = 3) in E2+palbo(100 nM) condition.

Figures 1C–1K compare the model simulation results of 21 or 28-day proliferation to experimental results for numerous treatments. Figure 1C shows the cell proliferation in the E2 control condition (E2 control), which is much faster than that in other mono and combination treatment conditions. The E2 control experiment was stopped early, at day 11, due to confluence. In the E2 deprivation (–E2) condition, shown in Figure 1D, cells proliferate during the first 7 days and then essentially stop proliferating due to the very low E2 concentration in the medium after several medium changes. This effect is captured by the model by adding the dynamics of E2 concentration to the model, where the E2 concentration decreases with each medium change, increasingly depriving the ER of its ligand (see STAR Methods and Figures S6A and S6B). The –E2 experiment illustrates how cell proliferation over longer timescales can be qualitatively different from that over short timescales, so a mathematical model calibrated on short timescale experiments may not be useful for simulations on a longer timescale, hence the necessity of long timescale experimental data. Figures 1E and 1F show the decrease in proliferation, due to increased ER degradation, as the dose of ICI treatment (E2+ICI) increases from 100 nM to 500 nM. Figures 1G–1I show the decreasing proliferation, due to increased Cdk4/6 inhibition, as the dose of palbociclib treatment (E2+palbo) increases from 250 nM, to 500 nM, to 1 μM. After showing that the model is capable of simulating –E2, ICI and palbociclib monotreatments, Figures 1J and 1K show the model simulation results for two combination treatments, –E2 plus 100 nM palbociclib (–E2+palbo), and –E2 plus 100 nM ICI (–E2+ICI). Not surprisingly, the combination treatments provide greater effect than either monotreatment by itself. The combination of –E2 and ICI treatments reduces supply of both E2 and ER, causing a larger decrease in the normalized cell number. The combination of –E2 and palbociclib inhibits Cdk4/6:cyclinD1 kinase activity by both reducing the cyclinD1 level and inactivating Cdk4/6, which also causes a larger reduction of proliferation. In addition to the cell number, the model can also capture the protein level changes under –E2 and E2+ICI (500 nM) treatments, which were measured in our previous work (see Figures S1 and S2).¹⁹

Adding a new drug to the model

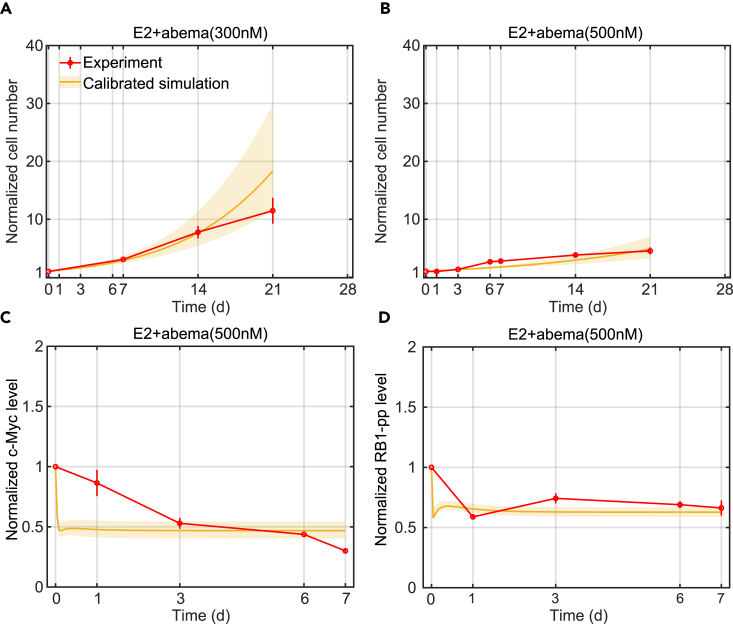
An advantage of a mechanistic mathematical model is that it is straightforward to incorporate a new drug into the model without requiring extensive experimentation, providing the drug acts on a signaling pathway already present in the model. As the original model already captured the mechanism driving changes due to the Cdk4/6 inhibitor palbociclib, adding new Cdk4/6 inhibitors should require only fitting a small number of new parameter values related to Cdk4/6 inhibition. We illustrate this by showing how we incorporated the Cdk4/6 inhibitor, abemaciclib (LY2835219), into the current model. Abemaciclib is a 2-anilino-2, 4-pyrimidine-[5-benzimidazole] derivative.²⁴ Unlike palbociclib, it has been reported to be effective as a single-agent.^25,26,27 It can inhibit cyclinD1:Cdk4 and cyclinD1:Cdk6 kinase activities at low nanomolar concentration.²⁸ While at higher micromolar concentrations abemaciclib has been shown to attack other targets,^29,30,31 we have focused on Cdk4/6 as the most relevant target at the concentrations we consider.

We modeled the new binding and unbinding reactions using mass-action kinetics with the unknown parameters determined by fitting measurements of cell number, c-Myc, and RB1-pp (two proteins in the model critical to proliferation) in response to abemaciclib treatment. Figures 2A and 2B show that the model can fit the experimental proliferation results for the 300 nM and 500 nM abemaciclib treatments (E2+abema), respectively. Figures 2C and 2D show the protein level changes for c-Myc and RB1-pp in response to 500 nM abemaciclib. As expected, abemaciclib inhibits Cdk4/6 activity and decreases the RB1-pp level, which in turn, leads to decreased transcription of c-Myc causing the c-Myc protein level to decrease. The simulated RB1-pp decrease is quite precipitous but does not conflict with the measured data at day 0 or day1. The simulated c-Myc decrease, however, does conflict with the data. This is because the decrease is governed by the decay rate of c-Myc, and we chose to use a value for this parameter from the literature, rather than choosing an unrealistic value to get a better fit. Ultimately, the poor fit is due to our simplified model. Because the mathematical model already captured the mechanism of Cdk4/6 inhibition, it was possible to add another inhibitor of cyclinD1:Cdk4/6 kinase activity without needing to perturb the other signaling pathways.

Figure 2.

Model calibration simulations compared to experimental data for abemaciclib treatments

(A) Model calibration of normalized cell number to experimental data (mean ± s.e., n = 3) in E2+abema(300 nM) condition. The experimental data are shown in red and the calibration simulation results are shown in yellow (solid line represents the lowest cost value simulation and the shaded regions contains the central 98% of the cohort simulations).

(B) Model calibration of normalized cell number to experimental data (mean ± s.e., n = 3) in E2+abema(500 nM) condition.

(C) Model calibration of normalized c-Myc level to experimental data (mean ± s.e., n = 3) in E2+abema(500 nM) condition.

(D) Model calibration of normalized RB1-pp level to experimental data (mean ± s.e., n = 3) in E2+abema(500 nM) condition.

Simulating alternating treatment involving estrogen deprivation

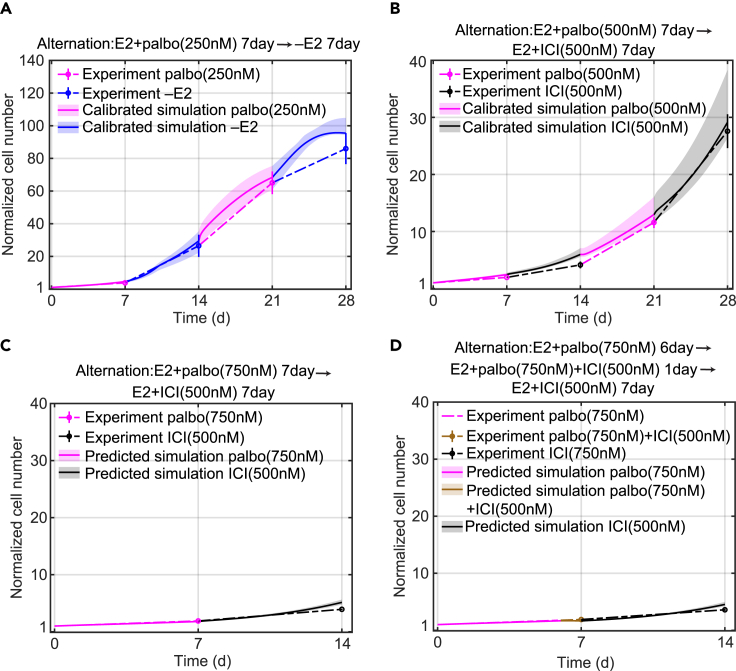
The resistance that develops to continuously applied mono or combination drug therapy represents a significant impediment to successful treatment, and we hypothesize that an alternating application of various treatments in a repeating cycle may provide a means of delaying or preventing resistance. Researchers have shown that cancer cell populations can display a transient, reversible, drug-tolerant state to protect the cell from eradication.^11,32 Therefore, alternating among various drugs may reverse a tolerant state to a given drug back to a sensitive state during the application of a different drug and thereby delay or prevent the development of resistance. Before testing whether alternating treatment can indeed delay the development of resistance, and with an eye toward using the model to design alternating therapies, we first show the model’s capability to simulate proliferation changes in response to alternating therapies.

Figures 3A and 3B show the model simulation results and experimental measurements of two alternating treatments, palbociclib alternating with –E2 and palbociclib alternating with ICI. The duration of each treatment is 7 days and the total treatment period is 28 days Figure 3A shows E2+palbo(250 nM) alternating with –E2. We can see that the model simulation is consistent with the experiment result and the cells proliferate about 90-fold in 4 weeks. This growth increase is larger than we initially expected based on the monotreatment data from Figures 1G and 1D, where cells proliferated about 80-fold under E2+palbo(250 nM) monotreatment and proliferation essentially stopped under –E2 after 1 week. The reason for the larger increase is the dynamics of the E2 concentration. The palbociclib treatment has E2 in the medium, which is absorbed by the cells, so when the medium is changed to the –E2 condition the cellular E2 diffuses back into the medium and the resulting concentration is sufficient to drive proliferation (Figure S6A). This palbociclib and –E2 alternating experiment confirms the necessity of incorporating E2 dynamics in alternating treatments involving deprivation. Figure 3B shows palbociclib (500 nM) alternating with ICI(500 nM). We can see that the model simulation is consistent with the experimental result and the cells proliferate about 27-fold in 4 weeks. We conclude that when alternating palbociclib with an endocrine treatment in cell culture, ICI is a better choice than –E2 in terms of controlling the proliferation.

Figure 3.

Model calibration and prediction simulations of normalized cell number compared to experimental data for alternating treatments

(A) Model calibration to experimental data (mean ± s.e., n = 3) of E2+palbo(250 nM) alternating with –E2 treatment. The experimental data is linked by dashed lines. The E2+palbo(250 nM) treatment is shown in purple and the –E2 condition in blue. The calibration simulation results are shown in the same colors as the experimental data with the solid line representing the lowest cost value simulation and the shaded regions containing the central 98% of the cohort simulations.

(B) Model calibration to experimental data (mean ± s.e., n = 3) of E2+palbo(500 nM) alternating with E2+ICI(500 nM) treatment. E2+palbo(500 nM) treatment is shown in purple and E2+ICI(500 nM) in black.

(C) Model prediction of experimental data (mean ± s.e., n = 3) for E2+palbo(750 nM) alternating with E2+ICI(500 nM). E2+palbo(750 nM) treatment is shown in purple and E2+ICI(500 nM) in black. The treatment started with E2+palbo(750 nM) with 7days then altered to E2+ICI(500 nM) with 7days.

(D) Model prediction of experimental data (mean ± s.e., n = 3) for E2+palbo(750 nM) alternating with E2+palbo(750 nM)+ICI(500 nM) and E2+ICI(500 nM) treatment. E2+palbo(750 nM) condition is shown in purple, E2+palbo(750 nM)+ICI(500 nM) in brown and E2+ICI(500 nM) in black. The treatment started with E2+palbo(750 nM) for 6days, then changed to E2+palbo(750 nM)+ICI(500 nM) for 1day and then changed to E2+ICI(500 nM) for 7 days.

After showing that the model can simulate these two alternating treatments, we check whether the model can predict the effects of other alternating treatments. Figures 3C and 3D show the model prediction and experimental measurements of the normalized cell numbers under two alternating treatments. The first alternating treatment shown in Figure 3C is palbociclib(750 nM) alternating with ICI(500 nM). The duration of each treatment is 7 days and the total treatment period is 14 days. The second alternating treatment shown in Figure 3D is palbociclib(750 nM) for 6 days, followed by palbociclib(750 nM) plus ICI(500 nM) for 1 day, followed by ICI(500 nM) for 7 days. The difference between the first and second alternating treatment is that the second treatment adds a 1 day overlap of palbociclib(750 nM) plus ICI(500 nM) treatments. Therefore, as shown in Figure 3D, the total experimental proliferation of the second alternating treatment is slightly smaller than the first alternating treatment due to this 1 day combination treatment that has a stronger inhibition effect compared with monotreatment (mean values are 3.9 and 3.5, respectively). The model prediction for the second alternating treatment is also smaller than the prediction for the first alternating treatment as well (mean values are 5.2 and 4.6, respectively).

Modeling palbociclib/ICI alternating therapy over longer time scales

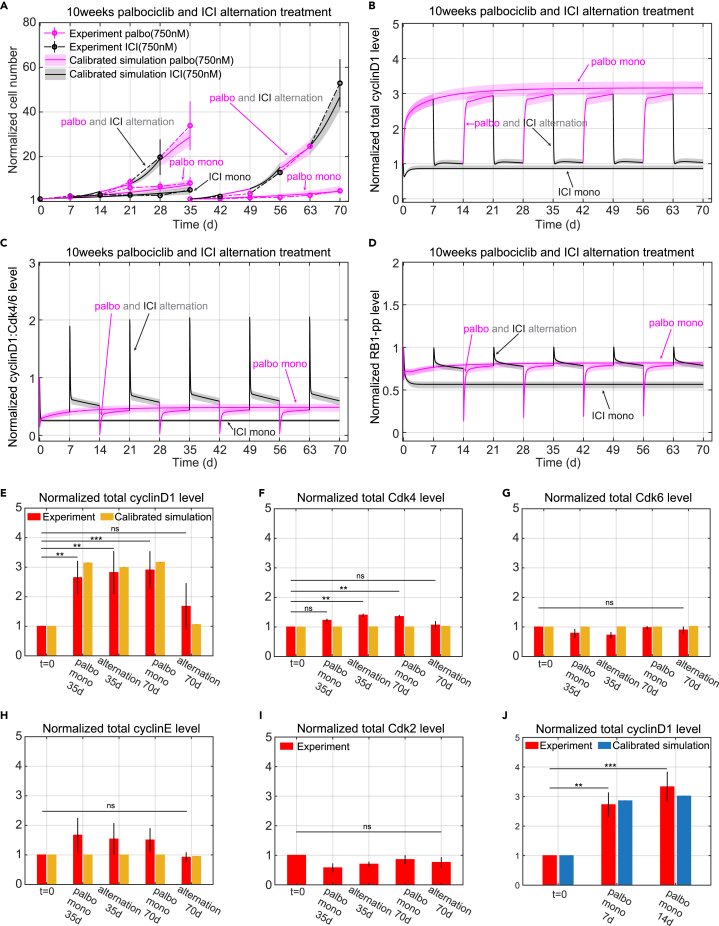
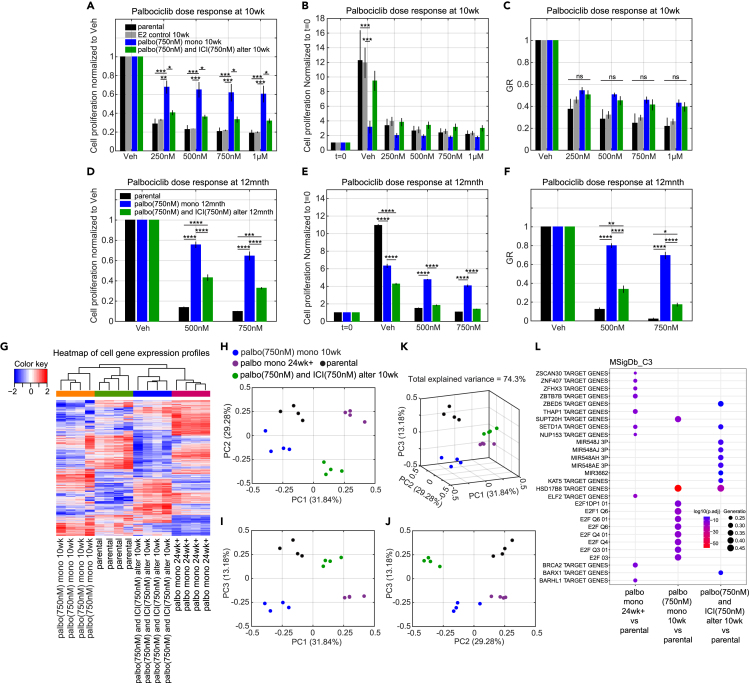
One goal of this study is to test whether an alternating treatment can indeed impact the development of resistance. In patients, resistance to Cdk4/6 inhibitors can occur within months,^33,34 compared with endocrine resistance that may take years to fully develop.^35,36,37 Based on this observation, we decided to test whether an alternating treatment of ICI and palbociclib can affect the development of resistance to palbociclib. A 10-week experiment was conducted where palbociclib was alternated with ICI at weekly intervals. Monotreatment with palbociclib or ICI were included as controls. Based on the results from Figures 1C–1K and 3, we chose the palbociclib and ICI drug doses to be 750 nM as our model at that time indicated this dose would cause relatively low proliferation for the controls as well as the alternating treatment and enable the experiment to run without replating. Figure 4A shows the experimental and simulated cell proliferation results for the 10-week protocol. Two major results from the experiment that required adjustments to the initial model were: (1) cells undergoing palbociclib monotreatment grew more slowly as time went on, and (2) cell proliferation was much greater than expected in cells that received the alternating drugs, forcing a replating at week 5 to avoid confluence.

Figure 4.

Model simulations of normalized cell number and protein level changes compared to experimental data for long time mono and alternating treatments

(A) Model calibration to experimental data (mean ± s.e., n = 3) for E2+palbo(750 nM), E2+ICI(750 nM), and E2+palbo(750 nM) alternating with E2+ICI(750 nM) treatments. The experimental data are linked by dashed lines. In both the mono and alternating treatments, the E2+palbo(750 nM) condition is shown in purple and the E2+ICI(750 nM) condition in black. In the alternating treatment, each treatment period is 7days, starting with E2+palbo(750 nM). MCF7 cells are re-plated at 35days in the E2+palbo(750 nM) mono and alternating treatments. The normalized cell number from 35 to 70 days is relative to the number plated at 35days. The calibration simulation results are shown in same color as the experimental data with the solid line representing the lowest cost value simulation and the shaded regions containing the central 98% of the cohort simulations.

(B) Model simulation of normalized total cyclinD1 level changes in the mono and alternating treatments shown in (A).

(C) Model simulation of normalized cyclinD1:Cdk4/6 level changes in the mono and alternating treatments shown in (A).

(D) Model simulation of normalized RB1-pp levels changes in the mono and alternating treatments shown in (A).

(E) Bar plot of model simulation for total cyclinD1 level compared to experimental data (mean ± s.e., n = 3) in E2+palbo(750 nM) and E2+palbo(750 nM) alternating with E2+ICI(750 nM) treatments shown in (A). Total cyclinD1 levels are measured at 35 days and 70 days. The simulation results shown in yellow are the average results from all cohort simulations. Statistical testing was performed by one-way ANOVA (ns: non-significant; ∗: p < 0.05; ∗∗: p ≤ 0.01; ∗∗∗: p ≤ 0.001; ∗∗∗∗: p ≤ 0.0001).

(F) Bar plot of model simulation and experimental results (mean ± s.e., n = 3) for total Cdk4 level changes in E2+palbo(750 nM) and E2+palbo(750 nM) alternating with E2+ICI(750 nM) treatments shown in (A).

(G) Bar plot of model simulation and experimental results (mean ± s.e., n = 3) for total Cdk6 level changes in E2+palbo(750 nM) and E2+palbo(750 nM) alternating with E2+ICI(750 nM) treatments shown in (A).

(H) Bar plot of model simulation and experimental results (mean ± s.e., n = 3) for total cyclinE level changes in E2+palbo(750 nM) and E2+palbo(750 nM) alternating with E2+ICI(750 nM) treatments shown in (A).

(I) Bar plot of experimental results (mean ± s.e., n = 3) for total Cdk2 level changes in E2+palbo(750 nM) and E2+palbo(750 nM) altering with E2+ICI(750 nM) treatments shown in (A).

(J) Bar plot of model calibration for total cyclinD1 level changes to experimental data (mean ± s.e., n = 3) in E2+palbo(750 nM) treatment. Total cyclinD1 levels are measured at 7days and 14days. The statistical testing is the same as (B). The simulation results are average results from all the cohort simulations.

The first 5 weeks of palbociclib monotreatment results in an 8.1-fold increase in cell number while the second 5 weeks results in a 4.6-fold increase (Figure S4). In order to account for this effect, a phenomenological equation (see Equations 10, 14, 15, and 16 in STAR Methods) was added to the model to gradually slow down growth in response to long-term palbociclib treatment. This inhibition effect increases gradually when palbociclib is being applied but decays in about a week when palbociclib is removed, so that the growth during a palbociclib interval of the alternating treatment is similar to its growth during the first week of palbociclib monotreatment (Figures S7A and S7B).

While the difference in proliferation between mono and alternating treatments was not dramatic during the first two weeks, it became significant thereafter, with the alternating treatment cells approximately doubling every week (average 33.8-fold increase at week 5, ⁵√33.8 ≈ 2, average 52.3-fold increase during the second 5 weeks, ⁵√52.9 ≈ 2.2). Part of the reason for this is that the palbociclib intervals of the alternating therapy do not experience the slowdown of the constant palbociclib cells to the same extent. But the other reason is that the growth during the ICI intervals is much greater than that of ICI monotherapy. To look for a mechanistic reason for the excessive proliferation, we measured the protein levels of cyclinD1, Cdk4, Cdk6, cyclinE1, and Cdk2 on days 35 and 70 for each arm of the experiment. Palbociclib treatment in both arms significantly increased the expression of cyclinD1 (Figure 4E). The increase of cyclinD1 during palbociclib treatment may be due to different degradation rates between the cyclinD1:Cdk4/6: palbociclib complex (number 14 in Table 1) and the cyclinD1:Cdk4/6 (number 12 in Table 1). When calibrating the model, we allowed the degradation rate of cyclinD1:Cdk4/6:palbociclib to be smaller than the degradation rate of cyclinD1:Cdk4/6 but greater than the degradation rate of cyclinD1:Cdk4/6:p21. This results in accumulation of cyclinD1 during palbociclib treatment that can partly explain the increase of cyclinD1 in the constant palbociclib cases at 35days and 70days, as well as the alternating case at 35days.

Table 1.

Model variables and initial values

Variable name	Description	Initial value	Half-life
(1) E2media	E2 concentration in the media	10 nM	–
(2) E2cell	E2 concentration in the cell	10 nM	–
(3) ER	Estrogen receptor α	1.97 nM	∼4-5h38
(4) E2ER	Estrogen bound estrogen receptor α	835.19 nM	∼3-4h38
(5) E2NSB	Estrogen bound non-specific binding	6697.83 nM	–
(6) ICIER	ICI 182,780 bound estrogen receptor	0 nM	<3-4h38
(7) rescyclinD1palbo	Variable induced by palbociclib increasing cyclinD1	0 nM	–
(8) cyclinD1	Protein cyclinD1	0.62 $\times$ 10−6nM	∼0.4h39
(9) cdk46	Protein Cdk4/6	3365.58	∼5h40
(10) cdk46palbo	Palbociclib bound Cdk4/6	0 nM	–
(11) cdk46abema	Abemaciclib bound Cdk4/6	0 nM	–
(12) cyclinD1cdk46	CyclinD1 bound Cdk4/6	33.83 nM	–
(13) cyclinD1cdk46p21	p21 bound cyclinD1:Cdk4/6	21.84 nM	–
(14) cyclinD1cdk46palbo	Palbociclib bound cyclinD1:Cdk4/6	0 nM	–
(15) cyclinD1cdk46abema	Abemaciclib bound cyclinD1:Cdk4/6	0 nM	–
(16) cyclinD1cdk46p21palbo	Palbociclib bound cyclinD1:Cdk46:p21	0 nM	–
(17) cyclinD1cdk46p21abema	Abemaciclib bound cyclinD1:Cdk46:p21	0 nM	–
(18) cMyc	Protein c-Myc	9.75 nM	∼0.3h41
(19) p21	Protein p21	0.0027 nM	∼0.3-1h42
(20) cyclinE	Protein cyclinE	0.16 nM	∼0.5h43
(21) cyclinEp21	p21 bound cyclinE	0.036 nM	–
(22) Rb	Retinoblastoma protein	53.01 nM	∼2-3h44
(23) pRb	Hypophosphorylated RB1 (RB1-p)	16.64 nM	∼2-3h44
(24) ppRb	Hyperphosphorylated RB1 (RB1-pp)	0.49 nM	>4h44
(25) respropalbo	Variable induced by palbociclib inhibiting proliferation	0 nM	–
(26) Nalive	Alive cell number	0.93a	–
(27) Ndead	Dead cell number	0.07a	–

Variable names are italicized.

^aThe values of Nalive and Ndead are assigned according to the alive and apoptotic percentage in Figure S5.

However, we also saw that cyclinD1 experimentally increases at 70 days in the alternating treatment, which is just finishing an ICI interval. This increase cannot be explained by the decreased degradation rate of cyclinD1:Cdk4/6:palbociclib as this effect rapidly decays during the ICI interval (Figure S7E). In order to account for this effect, we added a phenomenological variable, rescyclinD1palbo (number 7 in Table 1), to the model that gradually increased cyclinD1 in response to long-term palbociclib treatment. The effect decreases slowly once palbociclib is removed (Figures S7C and S7D), so that the cyclinD1 levels during the ICI intervals of the alternating treatment are increased over the levels in the ICI monotreatment (Figures 4B and 4E).

The above changes to the model enabled it to capture the proliferation under alternating therapy as shown in Figure 4A. The cyclinD1 level is higher during the ICI intervals of the alternating treatment compared to ICI monotreatment (Figure 4B), which results in higher cyclinD1:Cdk4/6 and RB1-pp levels (Figures 4C and 4D). This effect causes the growth after the cells are transitioned from palbociclib to ICI to be greater than would otherwise be expected. The rapidly decaying peaks of cyclinD1:Cdk4/6 and RB1-pp seen at the palbociclib to ICI transition are due to the sudden release of palbociclib free Cdk4/6 and its complexes after palbociclib withdrawal.

Protein changes at 10 weeks

Increased levels of the five proteins we measured, Figures 4E–4I are all associated with palbociclib resistance in the literature.^{14,31,45,46,47} In our experiment, Cdk6, cyclinE, and Cdk2 levels show no statistically significant difference among the different treatment conditions. Although Cdk4 does show a statistically significant increase compared to untreated cells, the up-regulation is small (mean value of 1.4 at alternating treatment 35 days and 1.3 at palbociclib monotreatment at 70 days). Only cyclinD1 shows a large increase compared to untreated cells. There is no significant difference in cyclinD1 level between palbociclib monotreatment and the alternating treatment during palbociclib intervals in Figure 4E. Moreover, in order to test whether the cyclinD1 gradually increases in response to long-term palbociclib treatment, as would be expected of a long-term resistance mechanism, we measured cyclinD1 changes at 7 days and 14 days after 750 nM palbociclib treatment. Figure 4J shows that the cyclinD1 level is already upregulated at 7 days and there are no significant differences in cyclinD1 levels among palbociclib monotreatment at 7 days, 14 days, 35 days, or 70 days. The observed increases in cyclinD1 can be explained by a rapid response to palbociclib treatment and do not represent a long-term change leading to resistance. Therefore, the five quantified proteins do not indicate any difference in moving toward resistance to palbociclib between the mono and alternating treatments.

Palbociclib dose-response changes at 10 Weeks versus 12 months

At the end of 10 weeks, a 7-day palbociclib dose-response assay was used to compare the proliferation of MCF7 cells after undergoing no treatment, monotreatment, or alternating treatment. Figures 5A–5C show the results for three different normalizations: growth in vehicle, number of initial cells at t = 0, and the growth-rate inhibition metric, GR.⁴⁸ Figure 5A normalizes the proliferation of each case to its proliferation in vehicle, which is the usual method of normalization in biological experiments. As expected, the treatment-naïve (parental and E2 control) cells are the most sensitive to palbociclib. This plot also shows that the alternating treatment cells are much more sensitive to palbociclib, compared with the monotreatment cells, at all doses of palbociclib. This would lead one to think that the alternating treatment is producing less resistant cells compared to monotreatment. However, when the dose-response results are normalized to t = 0, as shown in Figure 5B, we see that the proliferation of the palbociclib monotreatment cells is much less than that of the vehicle treated (E2 control). Because the proliferation is already low and palbociclib does not significantly upregulate apoptosis,²⁴ the proliferation cannot decrease much further. Thus, relatively speaking, the decrease in proliferation from the drug is smaller than in the other cases, making the cells appear less sensitive to palbociclib when normalized to vehicle as in Figure 5A. In contrast, the cells from alternating treatment have a relatively higher proliferation in vehicle and palbociclib can inhibit the proliferation more, which makes the cells appear sensitive to palbociclib. It should be noted, however, that for all doses, the alternating treatment cells proliferate faster than the monotreatment cells, which makes it impossible to claim an advantage for alternating treatment at 10 weeks, even if by standard measures the alternation results in cells that are more sensitive to palbociclib.

Figure 5.

Palbociclib dose response and gene expression profiles for cells after long time mono and alternating treatments

(A) Palbociclib dose response normalized to vehicle on cells after 10 weeks palbociclib (750 nM) monotreatment and alternating treatment compared to parental MCF7 cells and MCF7 cells in 10 weeks E2 control condition. The alternating treatment is the same as Figure 4A, which is E2+palbo(750 nM) alternating with E2+ICI(750 nM). Each treatment period is 7days and starts with E2+palbo(750 nM). The cells in all conditions are re-plated at 35days and the dose responses are tested at 70 days.

(B) Palbociclib dose response normalized to t = 0, otherwise same as (A).

(C) The GR value of palbociclib dose response, otherwise same as (A).

(D) Palbociclib dose response normalized to vehicle for cells after 12 months palbociclib (750 nM) monotreatment and alternating treatment compared to parental MCF7 cells. Treatments are the same as (A) except the alternation period is 1 month, the duration is extended to 12 months, and the dose responses are tested at 12 months.

(E) Palbociclib dose response normalized to t = 0, otherwise same as (D).

(F) The GR value of palbociclib dose response, otherwise same as (D).

(G) Heatmap of gene expression profiles for cells after 10 weeks palbociclib monotreatment, cells after 10 weeks alternating treatment, parental MCF7 cells and cells cultured over 24 weeks in palbociclib (500 nM). The cells from palbociclib monotreatment and alternating treatment are the same as (A).

(H) Principal component analysis of gene expression profiles on the same cells as (G). (PC1 vs. PC2).

(I) Principal component analysis of gene expression profile on the same cells as (G). (PC1 vs. PC3).

(J) Principal component analysis of gene expression profile on the same cells as (G). (PC2 vs. PC3).

(K) Principal component analysis of gene expression profile on the same cells as (G). (PC1 vs. PC2 vs. PC3).

(L) Gene Set Enrichment Analysis (GSEA) was performed on the same cells as (G). The C3 regulatory target gene sets in the Molecular Signatures Database (MSigDB) were used.

This problem of interpretation has been noticed previously and drove the development of a new metric, growth-rate inhibition (GR, see STAR Methods). GR is robust to variations in cell growth rate and quantifies the efficacy of a drug on a per-division basis, which can ensure that fast- and slow-dividing cells responding equally to a drug are scored equivalently.⁴⁸ Figure 5C shows the GR values for the palbociclib dose response and there is no significant difference between the mono and alternating treatments at 10 weeks. Therefore, although the dose response normalized to vehicle, Figure 5A, shows a difference between mono and alternating treatment, this effect comes from the different basal cell division rates of the mono and alternating treatment and obscures the true nature of the palbociclib dose response.

To explore what happens when resistance to monotherapy has more fully developed, a 12 months alternating experiment using the same drugs and doses was performed. The alternation took place at the end of each month when the cells were also re-plated. At the end of 12 months a dose response was performed and the results are shown in Figures 5D–5F. At this time, the palbociclib monotreatment cells were outgrowing the alternating cells in vehicle (Figure 5E), but the growth of each arm was more similar than at 10 weeks. The result is that all three normalizations show similar behavior: the alternating cells are significantly more sensitive to palbociclib than the palbociclib monotreatment cells, indicating a delay in acquiring resistance. The alternating cells are beginning to acquire resistance, however, as can be seen by comparison to the parental cells in Figure 5F. So, alternating therapies do show promise for delaying resistance, but better protocols are needed to hold down the excessive growth seen in the 10-week experiment. Also, accurate predictions at very long time scales will require adding resistance mechanisms to the model.

It can be argued that the reason the alternating cells were more sensitive to palbociclib was not due to the alternation, but rather that they experienced less total drug than the monotreatment cells and that cells exposed to a constant dose of 375 nM of palbociclib would show the same increased sensitivity. Even if true, the proliferation for the 375 nM case would be too excessive to be a viable therapy (see Figures 1G and 1H), as was also true for the alternating therapy in Figure 4A. Hence, the necessity of finding an alternating therapy that better holds down proliferation.

Gene expression changes at 10 weeks

Lastly, we analyzed gene expression profiles to look for differences between the palbociclib mono and alternating treatment cells at 10 weeks. Figure 5G shows the heatmap of differentially expressed genes for four cases of MCF7 cells: parental cells (control), 10 weeks of palbociclib monotreatment, 10 weeks of alternating treatment, and cells cultured for >6 months (palbo mono 24weeks+) in palbociclib (500 nM). Although the alternating treatment cells clustered with the palbo mono 24weeks+ cells, the heatmap revealed distinct expression patterns for the four different treatments. The reason that alternating cells are in the same cluster with the palbo mono 24weeks+ cells is likely because they both have positive values of the first principal component (PC1), as shown by principal component analysis (PCA) in Figures 5H–5K. The 2D and 3D PCA plots clearly show that cells under the four different treatments are separated into different groups. Gene Set Enrichment Analysis (GSEA) of the C3 regulatory target gene sets in the molecular signatures database (MSigDB) is shown in Figure 5L. The first 10 most significantly different regulatory target gene sets are plotted. Under the alternating treatment, the most changed gene sets are microRNA regulated, which might be caused by prolonged ICI treatment.^49,50,51 Under the palbociclib monotreatment, the E2F regulated gene sets are the most changed. The E2F transcription factor is the central player in regulating the expression of genes involved in the G1 to S phase transition and the target genes in the listed sets include cyclinD1, cyclinE, Cdk2, Cdc25A, cyclinA, etc.^52,53 In the palbo mono 24weeks+ cells, different gene sets are altered compared to the 10 weeks mono and alternating treatment cells, which might be related to the ongoing development of resistance such as BARHL1 target genes.⁵⁴

Using model-generated isobolograms to determine synergies

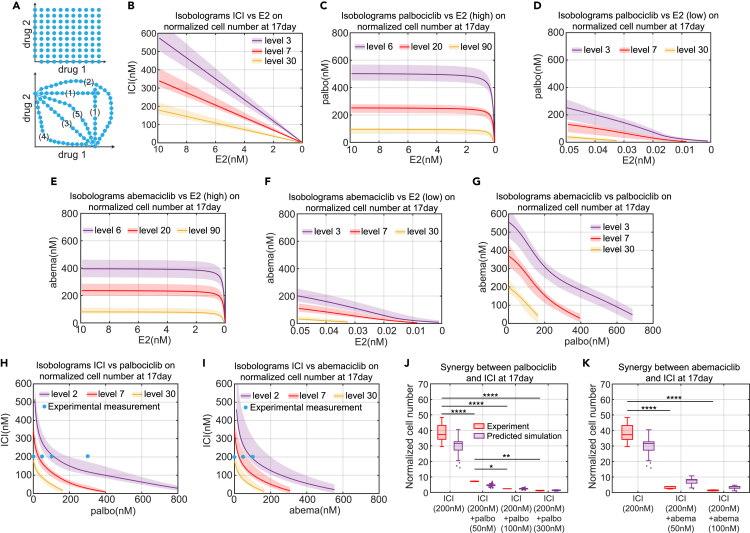
Cancer cells depend on a variety of molecular mechanisms for proliferation or survival, and therefore, drug combinations are often used to simultaneously target key molecular mechanisms to more effectively reduce proliferation, or help delay or overcome resistance.⁵⁵ A key question for drug combinations is whether there is a synergism between the drugs. A synergistic interaction between drugs may allow significantly lower doses of the individual drugs when used in combination as opposed to individually. It may benefit patients by reducing toxicity and adverse effects. There are numerous ways to define drug synergy, but we make use of the isobologram as we think it gives the clearest picture of the interaction of two drugs. An isobologram is a graph of lines of constant effect, called isoboles, proposed by Loewe in 1953.⁵⁶

The upper plot of Figure 6A illustrates an ideal sampling scheme, where each axis represents the dose for a specified drug. Each blue hexagon is a measurement of the effect either solely from drug 1, or solely from drug 2, or of the combination effect from the doses of drug 1 and drug 2 that make up its coordinates. The drug effect of interest in this paper is proliferation. After measuring the effect at each dosage point of the isobologram, we draw the isoboles, which are lines joining the points of equal measured effect. The lower plot of Figure 6A shows example isoboles, where the different drug doses at each point on the isoboles give the same effect. The various isoboles illustrate the various possibilities of independence of effect (1), antagonism (2), additivity (3), super-additivity (4), and sub-additivity (5).⁵⁷

Figure 6.

Model simulation of isobolograms among various treatment methods and experimental verifications

(A) Illustration of the isobologram. Each blue hexagon represents a measurement point for mono or combination drug treatment effects. The lines joining the (interpolated) points of equal measured effect are isoboles, such as lines in the lower plot, which represent different interaction types: (1) Independence of effect; (2) Antagonism; (3) Additive; (4) Super-additive; (5) Sub-additive.

(B) Model simulation of isobologram between ICI and E2 for the normalized cell number at 17days. Different colors of the isobole represents the different levels of normalized cell number. The solid line represents the lowest cost value simulation and the shaded regions contain the central 98% of the cohort simulations.

(C) Model simulation of isobologram between palbociclib and E2 (high concentration) for the normalized cell number at 17days.

(D) Model simulation of isobologram between palbociclib and E2 (low concentration) for the normalized cell number at 17days.

(E) Model simulation of isobologram between abemaciclib and E2 (high concentration) for the normalized cell number at 17days.

(F) Model simulation of isobologram between abemaciclib and E2 (low concentration) for the normalized cell number at 17days.

(G) Model simulation of isobologram between palbociclib and abemaciclib for the normalized cell number at 17days.

(H) Model simulation of isobologram between palbociclib and ICI for the normalized cell number at 17days.

(I) Model simulation of isobologram between abemaciclib and ICI for the normalized cell number at 17days.

(J) Boxplot of the model predictions and experimental verifications of normalized cell number showing the synergism between palbociclib and ICI. The doses of drug combinations used in the experiment are marked by the blue hexagons in (H). The prediction results shown in purple are from all cohort simulation results. Statistical testing was performed by two-way ANOVA (ns: non-significant; ∗: p < 0.05; ∗∗: p ≤ 0.01; ∗∗∗: p ≤ 0.001; ∗∗∗∗: p ≤ 0.0001). Center line on each box is the median. The bottom and top lines on each box are the 25^th and 75^th percentiles, respectively. The whiskers are maximum and minimum values without considering outliers. Data points are considered outliers if they are more than 1.5× IQR (interquartile range) below the 25^th percentile or above the 75^th percentile.

(K) Boxplot of the model predictions and experimental verifications of normalized cell number showing the synergism between abemaciclib and ICI. The doses of drug combinations used in the experiment are marked by the blue hexagons in (I). The prediction results shown in purple are from all cohort simulation results. The statistical testing used and explanation of the boxplot are the same as (J).

In this paper, we define a drug combination to be synergistic if it is super-additive. To obtain accurate isoboles, a large number of measurements are needed, as shown in Figure 6A. This makes the experimental determination of isoboles a challenging project. With a mathematical model, however, the generation of isoboles is essentially trivial, as a large number of simulations can easily be run and the results provided to a contour plotting program to get the isoboles. Figures 6B–6I show the isoboles computed by our model for cases ICI v. E2, palbociclib v. E2 (high), palbociclib v. E2 (low), abemaciclib v. E2 (high), abemaciclib v. E2 (low), abemaciclib v. palbociclib, ICI v. palbociclib, and ICI v. abemaciclib, respectively. The drug effect considered in these isoboles is the fold-change in cell number over 17 days of treatment and the results illustrate a range of different interaction types.

Figure 6B shows that the interaction between ICI and –E2 is additive. This is reasonable because both ICI and –E2 target the estrogen signaling pathway and decrease the E2:ER transcription factor level without directly influencing any other targets in the model. ICI and –E2 influence ER only through binding and unbinding reactions, so the level of E2:ER will linearly decrease after increasing ICI or decreasing E2. Therefore, the effects of ICI and –E2 as mono and combination treatments are the same, to linearly decrease E2:ER level.

Figures 6C and 6D show the interaction between palbociclib and –E2 and indicates that the effect of palbociclib is largely independent of the concentration of E2 until the E2 concentration gets into the picomolar range. Figure 6D provides a zoomed in plot of the isoboles for low concentrations of E2 and shows that the interaction between palbociclib and deprivation is additive or slightly super-additive in this region.

Figures 6E and 6F show the interaction between abemaciclib and –E2. As expected, the interaction between abemaciclib and –E2 is same as palbociclib with –E2, which is independent of the concentration of E2 until the E2 concentration gets into the picomolar range, where the interaction becomes additive or slightly super-additive. Figure 6G shows the interaction between abemaciclib and palbociclib is primarily additive. This is reasonable because abemaciclib and palbociclib both target the Cdk4/6 activity with a binding-unbinding reaction.

Figure 6H shows the interaction between ICI and palbociclib and indicates a significant synergism between ICI and palbociclib. To test the dramatic reduction in proliferation predicted by the model when adding small amounts of a second drug, an experiment was performed where the ICI dose was held constant at 200 nM and various doses of palbociclib were added (0 nM, 50 nM, 100 nM, and 300 nM, blue hexagon in Figure 6H). The dramatic decrease in population growth is borne out in the experimental results shown in Figure 6J. It should be emphasized that the model parameters were calibrated using only data from ICI and palbociclib monotreatments, not data from combination treatments. We believe the reason the model gives an experimentally consistent prediction of this significant synergism is because the structure of the model is based on the dominant signaling pathways of the system. In our mechanistic model, we include ICI’s effects on E2:ER, E2:ER’s effects on cyclinD1, and palbociclib’s effects on Cdk4/6. Therefore, the activity of the cyclinD1:Cdk4/6 kinase is attacked from both the cyclinD1 and Cdk4/6 directions to create the synergism. This may be the reason that palbociclib in combination with endocrine therapies achieved substantial improvement in survival outcomes in clinical trials and quickly became the first-line choice of treatment for ER + breast cancer.⁵ This synergy is in contrast to the combination of ICI and –E2, whose mechanisms both target E2:ER, and produce an additive but not synergistic response.

Figure 6I shows the interaction between ICI and abemaciclib, which also indicates a significant synergism. Likewise, experiments were performed to test the major reduction in proliferation predicted by the model, where the ICI dose was held constant at 200 nM and various doses of abemaciclib were added (0 nM, 50 nM, 100 nM, blue hexagons in Figure 6I). As expected, the dramatic decrease predicted in Figure 6I is borne out in the experimental results shown in Figure 6K. The explanation for the synergism between abemaciclib and ICI is same as for palbociclib and ICI.

The ability to easily produce isoboles for various metrics, such as proliferation over a specified time frame, allows us to propose optimal combination therapies. For example, considering a combination treatment of ICI and palbociclib, we can minimize the total dose of drugs, [ICI]+[palbociclib], that achieves our specified objective. Other possibilities include minimizing the total normalized dose of the drugs or some other weighted dose, [ICI]+λ[palbociclib], that reflects preferences based on toxicity or other concerns. Since palbociclib is typically used in the clinic in an intermittent fashion, three weeks on and one week off, due to neutropenia concerns, we could limit the above optimizations to lower doses of palbociclib that allow constant application so that excessive proliferation during the week off is avoided.

Alternating treatment predictions

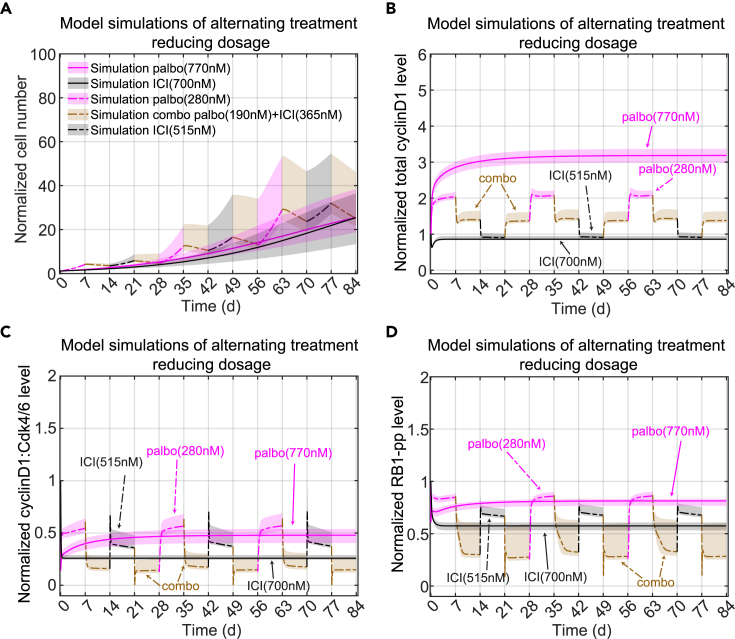
Ultimately, as mentioned above, we would like to show that the mathematical model allows us to propose optimal combination therapies. The experimental proliferation results in Figure 4A show that alternating palbociclib with ICI produces dramatically greater proliferation than the monotreatment. So, even if this alternation results in cells that are less resistant, it would not be a viable therapeutic approach. On the other hand, continuously applied monotreatment almost always leads to resistance and recurrence. So we used the model to look for better options to the simplistic alternating treatment we used above.

Simply trying to minimize proliferation will lead to the unhelpful answer of massive drug doses that would never be tolerable in any real application. Therefore, we decided to minimize the total drug dose over a 12-week time period, subject to the constraint that the overall fold-change be no greater than that of palbociclib monotreatment. Since this would likely lead to simply applying the best combination of palbociclib and ICI continuously, leading ultimately to resistance, we specified the repeating cycle to consist of 1 week of palbociclib, 1 week of a combination, 1 week of ICI, and 1 week of the same combination again. An optimization routine choses the drug doses in each week so as to minimize the total drug concentration applied over the 12-week period. The results are shown in Figure 7A. By design, the alternating treatment has the same fold-change as the monotreatment, but the optimized alternating treatment uses about 1200 nM less total drug dose per cycle compared to the palbociclib monotreatment, 1905 nM compared to 3080 nM, and about 900 nM less total drug dose per cycle than the ICI monotreatment, 1905 nM compared to 2800 nM. The combination treatment intervals not only find the synergistic sweet spot, noted above, to virtually stop growth and allow basal apoptosis to reduce the population, but they reduce the proliferation during the monotreatment intervals compared to switching directly from one monotreatment to another (Figures 7B–7D). This result shows that more sophisticated alternating treatments may provide benefits in terms of reduced drug dose while not continuously applying the same regimen, possibly delaying the onset of resistance.

Figure 7.

Optimal treatment design using the model

(A) Proposed Alternating treatment to reduce total drug dosage. E2+palbo(770 nM) monotreatment is shown in purple with a solid line. E2+ICI(700 nM) monotreatment is shown in black with a solid line. For the alternating treatment, each treatment period is 7days. In a 28 days cycle, the alternation starts with E2+palbo(280 nM) shown in purple with a dashed line, then changes to a combination treatment of E2+palbo(190 nM)+ICI(365 nM) shown in a brown dashed line, then changes to E2+ICI(515 nM) shown in a black dashed line, then changes to the combination treatment again. The cycle is repeated 3 times for a total of 84 days. The solid and dashed lines represent the lowest cost value simulation and the shaded regions contain the central 98% of the cohort simulations.

(B) Model simulation of normalized total cyclinD1 level changes in the proposed alternating treatments shown in (A). The lines and shaded regions have the same meaning as (A).

(C) Model simulation of normalized cyclinD1:Cdk4/6 level changes in the proposed alternating treatment shown in (A).

(D) Model simulation of normalized RB1-pp level changes in the proposed alternating treatment shown in (A).

Discussion

In this work, we built a mechanistic ODE model to capture the response of MCF7 cells to clinically used anticancer therapies for ER + breast cancer. We used the model to recapitulate and predict drug treatment effects on these cells and optimize drug combinations. As the model has a mechanistic basis and the relevant targets were already included when creating the model for palbociclib, we showed that the model can be easily extended to test the effect of one of the other Cdk4/6 inhibitors, abemaciclib. We also illustrated the usefulness of the model to efficiently investigate synergism among the different treatments included in the model.

While much of the work in cell lines to explore the impact of therapies takes place over short time frames of less than a week, most clinical therapy occurs over much longer time frames of months and years.^58,59 The work reported here looks for insights from cell lines over these longer time periods. Because of the limited number of such experiments that can be run, trial and error approaches are not viable. We used a mathematical model of the system, calibrated on limited data, to guide our explorations and search for better therapy options. Predicting drug responses over long time periods is not simply a matter of taking a model calibrated on data from a week long experiment and running it for a longer period, as there are significant factors affecting the model that are only clearly seen over longer time periods. This necessitates long-term experiments to calibrate the model. One example of this is that cell proliferation under –E2 treatment over a long timescale behaved qualitatively different than proliferation over a short timescale. Another example of this is the excessive growth observed when ICI treatment was applied after initially treating with palbociclib. This observation and additional experiments led us to the fact that treatment with palbociclib increases cyclinD1, something we had missed earlier. The revised mathematical model allowed us to propose a protocol to counter this effect.

Since our ultimate goal is to delay or prevent the onset of drug resistance, adding resistance mechanisms to the model is a critical requirement for future work.^{60,61,62,63,64} The cyclinD1 change mentioned above is a minor step in that direction, but the development of resistance is a complex, multi-faceted process and there are many different pathways that lead to a drug resistant state.^65,66 To see whether a therapeutic protocol delays the emergence of resistance compared to monotreatment will require experiments over time periods of many months, necessitating the use of mathematical models to propose the most promising protocols to explore.^58,67,68

The use of alternating therapies to delay resistance is predicated on the assumption that the initial stages of acquiring resistance are reversible, which appears likely in many cases.^{11,69,70,71,72,73,74,75} A critical mutation, however, can render most targeted therapies useless and thus upend any alternating protocol.^{76,77,78,79,80,81,82} To limit the probability of mutation, a much greater reduction in proliferation than is achieved in our current experiments is necessary. Periodically adding a more cytotoxic drug into the protocol is probably required.^83,84 In addition, although alternating treatment does not continuously apply a single drug to attack the cancer cells, our current approach using standard of care treatments for ER + breast cancer is to continuously arrest cells in the G1/S phase of the cell cycle with anti-estrogens and Cdk4/6 inhibitors.⁸⁵ Resistant cells can bypass the G1/S blockade and alter G2/M cell cycle proteins to survive.^76,81,86,87 Therefore, targeting of multiple cell cycle phases may be needed to avoid development of resistance to current therapies in ER + breast cancer.^63,88,89,90

The current model includes some phenomenological equations to deal with the long-term effects of drugs, the mechanisms of which are not clear. To determine whether this limits the predictive power of the model will need to be assessed with future long-term experiments. Finally, we recognize that work in cell lines may not directly translate to animals and humans, but hope that it may provide insights that can benefit work closer to the clinic.

Limitations of the study

Our model structure not only relies heavily on prior biological knowledge but also ignores many known and likely unknown processes in order to create a reasonably sized model. The large number of parameters in the model makes overfitting our noisy data a concern. We attempted to alleviate this concern by producing a large cohort of parameter sets that approximately fit the data and using this cohort to make predictions with the model.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
anti-β-Actin	Santa Cruz Biotechnology	Cat#sc-47778; RRID:AB_626632
anti-β-Tubulin I	Sigma-Aldrich	Cat#T7816; RRID:AB_261770
anti-Cdk2	Cell Signaling Technology	Cat#2546; RRID:AB_2276129
anti-Cdk4	Cell Signaling Technology	Cat#12790; RRID:AB_2631166
anti-Cdk6	Cell Signaling Technology	Cat#3136; RRID:AB_2229289
anti-CyclinD1	Cell Signaling Technology	Cat#2978; RRID:AB_2259616
anti-CyclinE (HE12)	Santa Cruz Biotechnology	Cat#sc-247; RRID:AB_627357
anti-c-Myc	Cell Signaling Technology	Cat#5605; RRID:AB_1903938
anti-ERα	ThermoFisher Scientific	Cat#MA5-14104; RRID:AB_10975403
anti-RB1	Cell Signaling Technology	Cat#9309; RRID:AB_823629
anti-RB1-pp(S612)	Aviva Systems Biology	Cat#OAAB16108
Chemicals, peptides, and recombinant proteins
phenol red-free improved minimal essential medium	ThermoFisher Scientific	Cat#A10488-01
Faslodex/Fulvestrant; ICI182,780	Selleck Chemicals, Houston, TX	Cat#S1191; CAS#129453-61-8
palbociclib	Selleck Chemicals, Houston, TX	Cat#S1116; CAS#827022-32-2
abemaciclib	Cayman Chemical	Cat#17740; CAS#1231930-82-7
Bovine Calf Serum Charcoal Stripped (CCS)	GeminiBio	Cat#100-213
17β-estradiol (E2)	Sigma-Aldrich, St. Louis, MO	Cat#E8875; CAS#50-28-2
cOmplete Mini Protease Inhibitor Cocktail Tablets	Roche Applied Science	Cat#11836153001
Apotracker	BioLegend, San Diego, CA	Cat#427402
propidium iodide	Thermofisher Scientific Waltham, MA	Cat#P1304MP
Critical commercial assays
Bicinchoninic Acid (BCA) Protein Assay Kit	ThermoFisher Scientific	Cat#23227
SurePrint G3 Human Gene Expression v3 8x60K Microarray Kit	Agilent, Santa Clara, CA	Cat# G4851C; Design ID #072363
Direct-zol RNA Miniprep Kit	Zymo Research, Irvine, CA	Cat#R2052
Deposited data
Microarray data shown in Figure 5	This paper	GEO accession numbers: GSE229002
Experimental models: Cell lines
MCF7	https://doi.org/10.3389/fonc.2021.681530	N/A
Software and algorithms
Code for modeling	This paper	https://doi.org/10.5281/zenodo.7792216
MATLAB 2021	MathWorks, Inc	RRID:SCR_001622; https://www.mathworks.com/products/matlab.html
R	R Core Team, 2013	https://www.r-project.org/
limma (R package)	Ritchie et al., 201591	RRID:SCR_010943; https://bioconductor.org/packages/release/bioc/html/limma.html
clusterProfiler (R package)	Yu et al., 201292 and Wu et al., 202193	RRID:SCR_016884; https://bioconductor.org/packages/release/bioc/html/clusterProfiler.html
msigdbr (R package)	Dolgalev, I. 202194	RRID:SCR_022870; https://cran.r-project.org/package=msigdbr
stats (R package)	R Core Team, 2013	https://www.r-project.org/
tidyverse (R package)	Wickham et al., 201995	RRID:SCR_019186; https://cran.r-project.org/web/packages/tidyverse/index.html
gplots (R package)	Warnes, 201196	https://cran.r-project.org/package=gplots
ggplot2 (R package)	Wickham, 201697	RRID:SCR_014601; https://cran.r-project.org/web/packages/ggplot2/index.html
plotly (R package)	Sievert, 202098	RRID:SCR_013991; https://cran.r-project.org/web/packages/plotly/index.html

Resource availability

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, William T. Baumann (baumann@vt.edu).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

Cell culture and reagents

MCF7 cells were obtained from Tissue Culture Shared Resources at Lombardi Comprehensive Cancer Center, Georgetown University, Washington, DC. MCF7 cells were grown in phenol red-free improved minimal essential medium (Life Technologies, Grand Island, NY; A10488-01) with 10% charcoal-stripped calf serum (CCS) and supplemented with 10nM 17β-estradiol (E2). ICI (Faslodex/Fulvestrant; ICI182,780) and palbociclib were obtained from Tocris Bioscience (Ellisville, MO). MCF7 cells were authenticated by DNA fingerprinting and tested regularly for Mycoplasma infection. All other chemicals were purchased from Sigma-Aldrich (St. Louis, MO).

Method details

Cell proliferation assay

Cells were seeded at a density of 4–5 × 10⁴ cells/well in 60 mm plates and treated with indicated drugs at 24 h post plating. E2 deprivation was obtained by washing cells 24 h post-plating (t = 0) with phosphate-buffered saline (PBS) and adding complete medium without E2 for the indicated times. To measure cell number at specific time-points, cells were trypsinized, resuspended in PBS and counted using a Z1 Single Coulter Counter (Beckman Coulter, Miami, FL).

Western blot analysis

For Western blot analysis, cells were lysed for 30 min on ice with lysis buffer (50 mM Tris-HCl, pH 7.5, containing 150 mM NaCl, 1 mM EDTA, 0.5% sodium deoxycholate, 1% IGEPAL CA-630, 0.1% sodium dodecyl sulfate (SDS), 1 mM Na3VO4, 44 μg ml−1 phenylmethylsulfonyl fluoride) supplemented with Complete Mini protease inhibitor mixture tablets (Roche Applied Science). Total protein was quantified using the bicinchoninic acid assay (Pierce). Whole-cell lysate (20 μg) was resolved by SDS–polyacrylaminde gel electrophoresis.

Apoptosis assay

2-5 x 10⁵ cells were plated in 6-well plates, were treated for 72 h, and stained with Apotracker green and propidium iodide, respectively (Thermofisher Scientific Waltham, MA) according to the manufacturer’s protocol and fluorescence was measures by the Flow Cytometry Shared Resources at Georgetown University Medical Center. Each experiment was repeated at least three times.

Microarray

Microarray analysis was performed using four biological replicates using Agilent Human Gene Expression V3 8x60k Microarray Kit, G4858A-Amadid:072363 G3 GEx Human V3 (Agilent, Santa Clara, CA, USA), at our Genomics and Epigenomics Shared Resources. Briefly, total RNA was extracted using the RNeasy kit (Qiagen, Valencia, CA, USA). RNA labeling and hybridization were performed according to the Agilent protocol for one-color target labeling. For each experiment, fragmented cDNA was hybridized in triplicates to the human gene expression arrays.

Dynamics of E2 deprivation

Removing E2 completely from cultured cells that have been growing in medium containing E2 cannot be accomplished by simply changing to a medium containing no E2. The E2 deprivation procedure is conducted by exchanging the E2 medium with 5% charcoal stripped calf serum (CCS) and phenol-red free media.⁹⁹ The E2 level in CCS is routinely measured to be less than 4 pM,⁹⁹ equating to 0.2 pM in 5% CCS media. But the E2 in the cell is at a significantly higher concentration than that in the medium and it can diffuse back into the medium and cause an increase in the E2 concentration. While the concentration of E2 might be low, its effect might not be negligible because a direct mitogenic effect of exogenous E2 on MCF7 can be initiated as low as 3 pM and maximized at 0.2 to 10nM.¹⁰⁰ Furthermore, other than estrogen receptors, there exist nonspecific bindings between estrogen and other elements inside the cell.¹⁰¹ Therefore, MCF7 cells growing in an E2 condition have a much higher internal concentration of E2 than that of medium due to non-specific binding of E2 in the cytoplasm as well as specific binding of E2 to various estrogen receptors in the cell. When we deprive the medium of estrogen, E2 from the cells leaches into the new medium and a new balance between the estrogen levels inside and outside the cell is achieved. The newly established E2 level that can be significant for maintaining proliferation. From the –E2 proliferation result shown in Figure 1D, the initial growth period is short and the cells nearly stop growing later on. As the medium is replaced as the experiment proceeds, the E2 level continues to drop and the cells stop proliferation.

In a one-week proliferation experiment (Figure S3), we changed the medium at time zero and at day 3 to –E2 medium and counted the cells on day 7. In a parallel experiment, an extra medium change was inserted at 3 hours. The experiment was conducted with two different plating densities. We can see that the extra media change, which further decreases the residual E2 level, significantly reduces the overall MCF7 proliferation at 1 week. Not only do the changes in E2 concentration with each successive medium change impact proliferation for long time continuous –E2 treatment, but these changes are also critically important when we consider alternating treatments. For example, if we alternate E2+palbo with –E2 treatment, after the transition from E2 to –E2 medium excess E2 will leach into the medium causing undesired growth. This issue drove us to model the E2 concentration dynamically. Thus, modeling the E2 dynamics is needed to capture the effect of alternating treatment.

Dynamic modeling of E2 deprivation

After a medium change, the total number ($\#$) of E2 molecules should be constant, so the amount of E2 leaving the cell should be equal to the amount of E2 entering the medium and vice versa. The rate of change in the number of E2 molecules in the cell caused by diffusion is:

$$\begin{array}{c}\frac{d{E2}_{\#cell}}{dt}=-k_{diff}\times \left({\left[E2\right]}_{cell}-{\left[E2\right]}_{media}\right)\times N\times S_{1cell}\end{array}$$ (Equation 1)

Where ${E2}_{\#cell}$ is the total number ($\#$) of E2 molecules in the cells, $k_{diff}$ is the diffusion rate across the cell membrane and ${-k}_{diff}\times \left({\left[E2\right]}_{cell}-{\left[E2\right]}_{media}\right)$ has units of $\#/\left(m^2\times t\right)$, ${\left[E2\right]}_{cell}$ is the E2 concentration in the cell, ${\left[E2\right]}_{media}$ is the E2 concentration in the medium, $N$ is the total cell number and $S_{1cell}$ is the surface area of a single cell.

Because ${E2}_{\#cell}={\left[E2\right]}_{cell}\times {Vol}_{cells}$, where ${Vol}_{cells}$ is the total volume of cells, which changes with time, Equation 1 becomes:

$$\begin{array}{c}\frac{d\left({\left[E2\right]}_{cell}\times {Vol}_{cells}\right)}{dt}=-k_{diff}\times \left({\left[E2\right]}_{cell}-{\left[E2\right]}_{media}\right)\times N\times S_{1cell}\end{array}$$ (Equation 2)

$$\begin{array}{c}\frac{d{\left[E2\right]}_{cell}}{dt}\times {Vol}_{cells}+\frac{dV{ol}_{cells}}{dt}\times {\left[E2\right]}_{cell}=-k_{diff}\times \left({\left[E2\right]}_{cell}-{\left[E2\right]}_{media}\right)\times N\times S_{1cell}\end{array}$$ (Equation 3)

$$\begin{array}{c}\frac{d{\left[E2\right]}_{cell}}{dt}=\frac{-k_{diff}\times S_{1cell}\times \left({\left[E2\right]}_{cell}-{\left[E2\right]}_{media}\right)}{{Vol}_{1cell}}-\frac{dV{ol}_{cells}}{dt}\times {\left[E2\right]}_{cell}\times \frac{1}{{Vol}_{cells}}\end{array}$$ (Equation 4)

setting $k_{diff}^{\prime }=\frac{k_{diff}\times S_{1cell}}{{Vol}_{1cell}}$, Equation 4 becomes

$$\begin{array}{c}\frac{d{\left[E2\right]}_{cell}}{dt}=-k_{diff}^{\prime }\times \left({\left[E2\right]}_{cell}-{\left[E2\right]}_{media}\right)-\frac{dV{ol}_{cells}}{dt}\times {\left[E2\right]}_{cell}\times \frac{1}{{Vol}_{cells}}\end{array}$$ (Equation 5)

Where the first term on the right is the rate of change related to diffusion and the second term is the rate of change related to variations in total cell volume. To simplify the second term, note that:

$$\begin{array}{c}\frac{d{Vol}_{cells}}{dt}\times \frac{1}{{Vol}_{cells}}=\left(\frac{dN}{dt}\right)\times {Vol}_{1cell}\times \frac{1}{{Vol}_{cells}}\end{array}$$ (Equation 6)

So Equation 5 becomes

$$\begin{array}{c}\frac{d{\left[E2\right]}_{cell}}{dt}=-k_{diff}^{\prime }\times \left({\left[E2\right]}_{cell}-{\left[E2\right]}_{media}\right)-\frac{\left(\frac{dN}{dt}\right)}{N}\times {\left[E2\right]}_{cell}\end{array}$$ (Equation 7)

If we suppose the volume of the culture media doesn’t change, since it is massive compared to the total cell volume, then the rate of E2 concentration changes in the media becomes

$$\begin{array}{c}\frac{d{\left[E2\right]}_{media}}{dt}=\frac{d{E2}_{\#media}}{dt}\frac{1}{{Vol}_{media}}=\frac{k_{diff}^{\prime }\times {Vol}_{1cell}\times N}{{Vol}_{media}}\times \left({\left[E2\right]}_{cell}-{\left[E2\right]}_{media}\right)\end{array}$$ (Equation 8)

since the total number of molecules diffusing into the medium is equal to the total number of molecules diffusing out of the cells.

Then Equations 7 and 8 are used to model the E2 dynamics during and after the deprivation. In Table 1, ${\left[E2\right]}_{cell}$ is denoted as ${E2}_{cell}$ and ${\left[E2\right]}_{media}$ as ${E2}_{media}$. Each time the medium is changed to –E2, the value ${\left[E2\right]}_{media}$ is set to the value of ${E2}_{dep}$ in table. Each time the medium is changed to control condition, the value ${\left[E2\right]}_{media}$ is set to the value of $E2$ in table.

Model parameter descriptions, values and declaration of fixed or calibrated

Parameter name	Description	Value	Fixed/Calibrated
(1) kdiff	Diffusion rate of E2	440.58/h	Calibrated
(2) kbNSB	Binding rate between non-specific binding and E2	670.08/(h $\times$ nM)	Calibrated
(3) kubNSB	Unbinding rate between non-specific binding and E2	1.0/h	Fixed
(4) Vol1cell	Volume of MCF7 cell	8 $\times$ 10−5mL	Fixed
(5) Volmedia	Volume of media	10 mL	Fixed
(6) kER	Translation rate of ER	250.75 nM/h	Calibrated
(7) kdER	Degradation rate of ER	0.10/h	Fixed
(8) kdE2ER	Degradation rate of E2ER	0.30/h	Fixed
(9) kbE2ER	Binding rate between E2cell and ER	55.13/(h $\times$ nM)	Calibrated
(10) kubE2ER	Unbinding rate between E2cell and ER	1.0/h	Fixed
(11) kbICIER	Binding rate between ICI and ER	0.29/(h $\times$ nM)	Calibrated
(12) kubICIER	Unbinding rate between ICI and ER	1.0/h	Fixed
(13) kdICIER	Degradation rate of ICIER	1.65/h	Calibrated
(14) kcyclinD1	Translation rate of cyclinD1	7.89 nM/h	Calibrated
(15) kdcyclinD1	Degradation rate of cyclinD1	1.39/h	Fixed
(16) kcyclinD1E2ER	Increased cyclinD1 translation by E2ER	11.54	Calibrated
(17) pcyclinD1E2ER1	Parameter 1 of cyclinD1 increased translation by E2ER	1122.99 nM	Calibrated
(18) pcyclinD1E2ER2	Parameter 2 of cyclinD1 increased translation by E2ER	4.85	Calibrated
(19) kbcyclinD1cdk46	Binding rate between cyclinD1 and cdk46	28546.18	Calibrated
(20) kubcyclinD1cdk46	Unbinding rate between cyclinD1 and cdk46	1.0/h	Fixed
(21) krescyclinD1palbo	Generation rate of rescyclinD1palbo	0.033 nM/h	Calibrated
(22) prescyclinD1palbo1	Parameter 1 of rescyclinD1palbo increased by palbo	505.73 nM	Calibrated
(23) prescyclinD1palbo2	Parameter 2 of rescyclinD1palbo increased by palbo	3	Calibrated
(24) kdrescyclinD1palbo	Degradation rate of rescyclinD1palbo	0.0032/h	Calibrated
(25) kcyclinD1palbo	Increase rate of cyclinD1 by rescyclinD1palbo	26.62 nM/h	Calibrated
(26) pcyclinD1palbo1	Parameter 1 of cyclinD1 increased by rescyclinD1palbo	7.09 nM	Calibrated
(27) pcyclinD1palbo2	Parameter 2 of cyclinD1 increased by rescyclinD1palbo	0.91	Calibrated
(28) kcdk46	Translation rate of cdk46	414.10 nM/h	Calibrated
(29) kdcdk46	Degradation rate of cdk46	0.1155/h	Fixed
(30) kbcdk46palbo	Binding rate between cdk46 and palbo	69.07/(h $\times$ nM)	Calibrated
(31) kubcdk46palbo	Unbinding rate between cdk46 and palbo	1.0/h	Fixed
(32) kbcdk46abema	Binding rate between cdk46 and abema	0.13/(h $\times$ nM)	Calibrated
(33) kubcdk46abema	Unbinding rate between cdk46 and abema	1.0/h	Fixed
(34) kdcyclinD1cdk46	Degradation rate of cyclinD1cdk46	0.71/h	Calibrated
(35) kbcyclinD1cdk46palbo	Binding rate between cyclinD1cdk46 and palbo	0.01/(h $\times$ nM)	Calibrated
(36) kubcyclinD1cdk46palbo	Unbinding rate between cyclinD1cdk46 and palbo	1.0/h	Fixed
(37) kbcyclinD1cdk46abema	Binding rate between cyclinD1cdk46 and abema	0.018/(h $\times$ nM)	Calibrated
(38) kubcyclinD1cdk46abema	Unbinding rate between cyclinD1cdk46 and abema	1.0/h	Fixed
(39) kbcyclinD1cdk46p21	Binding rate between cyclinD1cdk46 and p21	256.7/(h $\times$ nM)	Calibrated
(40) kubcyclinD1cdk46p21	Unbinding rate between cyclinD1cdk46 and p21	1.0/h	Fixed
(41) kdcyclinD1cdk46p21	Degradation rate of cyclinD1cdk46p21	0.063/h	Calibrated
(42) kbcyclinD1cdk46p21palbo	Binding rate between cyclinD1cdk46p21 and palbo	0.063/(h $\times$ nM)	Calibrated
(43) kubcyclinD1cdk46p21palbo	Unbinding rate between cyclinD1cdk46p21 and palbo	1.0/h	Fixed
(44) kbcyclinD1cdk46p21abema	Binding rate between cyclinD1cdk46p21 and abema	0.06/(h $\times$ nM)	Calibrated
(45) kubcyclinD1cdk46p21abema	Unbinding rate between cyclinD1cdk46p21 and abema	1.0/h	Fixed
(46) kbcyclinD1cdk46palbop21	Binding rate between cyclinD1cdk46palbo and p21	0.0028/(h $\times$ nM)	Calibrated
(47) kubcyclinD1cdk46palbop21	Unbinding rate between cyclinD1cdk46palbo and p21	1.0/h	Fixed
(48) kbcyclinD1cdk46abemap21	Binding rate between cyclinD1cdk46abema and p21	0.0081/(h $\times$ nM)	Calibrated
(49) kubcyclinD1cdk46abemap21	Unbinding rate between cyclinD1cdk46abema and p21	1.0/h	Fixed
(50) kdcyclinD1cdk46palboabema	Degradation rate of cyclinD1cdk46palbo and cyclinD1cdk46abema	0.2/h	Calibrated
(51) kcMyc	Translation rate of cMyc	3.1 nM/h	Calibrated
(52) kdcMyc	Degradation rate of cMyc	2.31/h	Fixed
(53) kcMycE2ER	Increased translation of cMyc by E2ER	5.88	Calibrated
(54) pcMycE2ER1	Parameter 1 of cMyc increased translation by E2ER	1066.31 nM	Calibrated
(55) pcMycE2ER2	Parameter 2 of cMyc increased translation by E2ER	2.13	Calibrated
(56) kcMycppRb	Increased translation of cMyc by ppRb	4224.72	Calibrated
(57) pcMycppRb1	Parameter 1 of cMyc increased translation by ppRb	1.46 nM	Calibrated
(58) pcMycppRb2	Parameter 2 of cMyc increased translation by ppRb	6.39	Calibrated
(59) kp21	Translation rate of p21	0.25 nM/h	Calibrated
(60) kdp21	Degradation rate of p21	1.39/h	Fixed
(61) kp21cMyc	Rate of p21 translation inhibited by cMyc	2.64	Calibrated
(62) pp21cMyc1	Parameter 1 of p21 inhibited translation by cMyc	8.6 nM	Calibrated
(63) pp21cMyc2	Parameter 2 of p21 inhibited translation by cMyc	1.78	Calibrated
(64) kcyclinE	Translation rate of cyclinE	0.25 nM/h	Calibrated
(65) kdcyclinE	Degradation rate of cyclinE	1.39/h	Fixed
(66) kcyclinEE2ER	Increased translation of cyclinE by E2ER	5.31	Calibrated
(67) pcyclinEE2ER1	Parameter 1 of cyclinE increased translation by E2ER	1206.68 nM	Calibrated
(68) pcyclinEE2ER2	Parameter 2 of cyclinE increased translation by E2ER	12.3	Calibrated
(69) kbcyclinEp21	Binding rate between cyclinE and p21	205.85/(h $\times$ nM)	Calibrated
(70) kubcyclinEp21	Unbinding rate between cyclinE and p21	1.0/h	Fixed
(71) kRb	Translation rate of Rb	2.46 nM/h	Calibrated
(72) kdRb	Degradation rate of Rb	0.35/h	Fixed
(73) kRbppRb	Increased Rb translation by ppRb	6184.66 nM/h	Calibrated
(74) pRbppRb1	Parameter 1 of Rb increased translation by ppRb	1.85 nM	Calibrated
(75) pRbppRb2	Parameter 2 of Rb increased translation by ppRb	4.27	Calibrated
(76) kRbcyclinD1cdk46	Phosphorylation rate of Rb by cyclinD1cdk46	25.25/h	Calibrated
(77) kpRbdepho	Dephosphorylation rate of pRb	38.38 nM/h	Calibrated
(78) kdpRb	Degradation rate of pRb	0.35/h	Fixed
(79) kpRbcyclinE	Phosphorylation rate of pRb by cyclinE	16.69/h	Calibrated
(80) kppRbdepho	Dephosphorylation rate of ppRb	251.99 nM/h	Calibrated
(81) kdppRb	Degradation rate of ppRb	0.05/h	Fixed
(82) pcyclinD1cdk461	Parameter 1 of cyclinD1cdk46 kinase activity	1.24 nM	Calibrated
(83) pcyclinD1cdk462	Parameter 2 of cyclinD1cdk46 kinase activity	0.079	Calibrated
(84) pcyclinD1cdk46Rb1	Parameter 1 of Rb phosphorylation by cyclinD1cdk46	0.41 nM	Calibrated
(85) pcyclinD1cdk46Rb2	Parameter 2 of Rb phosphorylation by cyclinD1cdk46	0.091	Calibrated
(86) ppRb1	Parameter 1 of pRb dephosphorylation	44.22 nM	Calibrated
(87) ppRb2	Parameter 2 of pRb dephosphorylation	2.59	Calibrated
(88) pcyclinEpRb1	Parameter 1 of pRb phosphorylation by cyclinE	7.44 nM	Calibrated
(89) pcyclinEpRb2	Parameter 2 of pRb phosphorylation by cyclinE	6.15	Calibrated
(90) pppRb1	Parameter 1 of ppRb dephosphorylation	10.28 nM	Calibrated
(91) pppRb2	Parameter 2 of ppRb dephosphorylation	1.51	Calibrated
(92) kpro	Basal proliferation rate	0.0011	Calibrated
(93) kproppRb	Proliferation rate increased by ppRb	2682.18	Calibrated
(94) pproppRb1	Parameter 1 of proliferation rate increased by ppRb	1.64 nM	Calibrated
(95) pproppRb2	Parameter 2 of proliferation rate increased by ppRb	3.95	Calibrated
(96) krespropalbo	Generation rate of respropalbo	0.0029 nM/h	Calibrated
(97) prespropalbo1	Parameter 1 of respropalbo increased by palbo	292.22 nM	Calibrated
(98) prespropalbo2	Parameter 2 of respropalbo increased by palbo	2.02	Calibrated
(99) prespropalbokd	Parameter of degradation rate of respropalbo	6.83	Calibrated
(100) kdrespropalbo	Degradation rate of respropalbo	0.015/h	Calibrated
(101) kpropalbo	Rate of proliferation inhibited by respropalbo	6.45	Calibrated
(102) ppropalbo1	Parameter 1 of proliferation inhibited by respropalbo	2.37 nM	Calibrated
(103) ppropalbo2	Parameter 2 of proliferation inhibited by respropalbo	0.87	Calibrated
(104) kcarrying	Carrying capacity	133.89	Calibrated
(105) kdeath	Basal death rate	0.0021/h	Calibrated
(106) klysis	Lysis rate of dead cell	0.0026	Calibrated
(107) E2dep	E2media in –E2 condition	1 $\times$ 10−6nM	Fixed
(108) percentagedeadt0	Percentage of dead cell at t = 0	0.07	Fixed
(109) E2	E2media in control condition	10 nM	Fixed
(110) ICI	Concentration of ICI 182,780	Varies depending on treatment condition	Fixed
(111) palbo	Concentration of palbociclib	Varies depending on treatment condition	Fixed
(112) abema	Concentration of abemaciclib	Varies depending on treatment condition	Fixed

h: hour.

Parameter names and model variable names are italicized.

Mathematical model

The model depends heavily on the principal interactions of the G1-S transition. This is a necessity, since fitting experimental observations with a relatively small model requires that the basic model structure captures the essential reality. But ignoring the potentially thousands of other interactions that affect this transition means that exactly fitting the data will not be possible. The cohort of parameter sets, discussed in the paper, are used to avoid potential overfitting by showing that different parameter sets that provide reasonable fits to the data also provide similar model predictions.

Biological signaling diagram

The structure of our ODE model is based on the signaling pathways of the G1-S transition since the drugs of interest, anti-estrogens and Cdk4/6 inhibitors, primarily affect progression through the G1 phase of the cell cycle.¹⁰ The justification of the numbered interactions of the signaling pathway and drugs, shown in Figure 1A is as follows:

1. –E2 decreases the level of estrogen⁹⁹; 2. E2 binds to ER and forms the transcription factor E2:ER¹⁰²; 3. ICI binds to ER and forms ICI:ER, which increases the degradation of ER and blocks its transcriptional activity⁵; 4. E2:ER increases transcription of c-Myc¹⁰³; 5. E2:ER increases transcription of cyclinD1¹⁰³; 6. E2:ER increases transcription of cyclinE¹⁰; 7. c-Myc inhibits transcription of p21¹⁰⁴; 8. CyclinD1 binds to Cdk4/6 and forms the cyclinD1:Cdk4/6 kinase¹⁰⁵; 9. CyclinE binds to Cdk2 and forms the cyclinE:Cdk2 kinase¹⁰³; 10. p21 binds to cyclinD1:Cdk4/6 and forms the cyclinD1:Cdk4/6:p21 complex, which inhibits its kinase activity¹⁰⁶; 11. p21 binds to cyclinE:Cdk2 and forms the cyclinE:Cdk2:p21 complex which inhibits its kinase activity¹⁰⁷; 12. Palbociclib binds to Cdk4/6 and inactivates its activity¹⁰⁸; 13. Abemaciclib binds to Cdk4/6 and inactivates its activity¹⁰⁸; 14. Palbociclib binds to cyclinD1:Cdk4/6 and forms the cyclinD1:Cdk4/6:palbociclib complex, which inactivates its kinase activity¹⁰⁸; 15. Abemaciclib binds to cyclinD1:Cdk4/6 and forms the cyclinD1:Cdk4/6:abemaciclib complex, which inactivates its kinase activity¹⁰⁸; 16. p21 binds to cyclinD1:Cdk4/6:palbociclib and forms the cyclinD1:Cdk4/6:p21:palbociclib complex¹⁰⁹; 17. p21 binds to cyclinD1:Cdk4/6:abemaciclib and forms the cyclinD1:Cdk4/6:p21:abemaciclib complex¹⁰⁹; 18. Palbociclib binds to cyclinD1:Cdk4/6:p21 and forms the cyclinD1:Cdk4/6:p21:palbociclib complex¹⁰⁹; 19. Abemaciclib binds to cyclinD1:Cdk4/6:p21 and forms the cyclinD1:Cdk4/6:p21:abemaciclib complex¹⁰⁹; 20. CyclinD1:Cdk4/6 phosphorylates RB1 to RB1-p (hypophosphorylated RB1)¹⁰³; 21. CyclinE:Cdk2 phosphorylates RB1-p to RB1-pp (hyperphosphorylated RB1)¹⁰³; 22. RB1 binds to E2F and inhibits its transcriptional activity¹⁰⁴; 23. RB1-p binds to E2F and inhibits it transcriptional activity¹⁰⁴; 24. E2F up-regulates RB1 expression¹¹⁰; 25. E2F up-regulates c-Myc expression¹¹¹; 26. E2F up-regulates cyclinE expression¹¹²; 27. E2F drives the G1-S cell cycle transition and proliferation⁵³; 28. Cell death.

Treatment with Cdk4/6 inhibitors will affect the stability of Cdk4/6 complexes bound to Cdk Interacting Protein/Kinase Inhibitory Protein (CIP/KIP) protein inhibitors (p21). The Cdk4/6 inhibitors can dissociate p21 selectively from Cdk4 but not Cdk6.¹⁰⁹ Because we didn’t differentiate between Cdk4 and Cdk6, we didn’t exclude the possibility of forming the tetramers cyclinD1:Cdk4/6:p21:palbociclib and cyclinD1:Cdk4/6:p21:abemaciclib. And the degradation rate of cyclinD1:Cdk4/6:p21:palbociclib and cyclinD1:Cdk4/6:p21:abemaciclib are assumed to be the same as the degradation rate of cyclinD1:Cdk4/6:p21 trimer. The binding interactions between cyclinD1, Cdk4/6, p21, palbociclib and abemaciclib can form different dimers, trimers and tetramers, depending on the subtypes of the Cdks and CIPs/KIPs.^109,113 Because both Cdk4/6:palbociclib (Cdk4/6:abemaciclib) and cyclinD1:Cdk4/6:palbociclib (cyclinD1:Cdk4/6:abemaciclib) lose their kinase activity, we didn’t include the binding reaction between Cdk4/6:palbociclib (Cdk4/6:abemaciclib) and cyclinD1. We only use the binding reactions between palbociclib (abemaciclib) and cyclinD1:Cdk4/6 to form the cyclinD1:Cdk4/6:palbociclib (cyclinD1:Cdk4/6:abemaciclib) complex. And we didn’t include the inhibition potency of abemaciclib on Cdk2 and cyclinE:Cdk2 since they are not needed to capture the abemaciclib treatment effects.¹⁰⁸ For conciseness, lines with arrowheads representing the unbinding reactions corresponding to each binding reaction included in the model are not shown in Figures 1A and 1B.

Model structure

Protein level changes in response to estrogen signaling and drug treatments are affected by thousands of interactions among proteins. Even though the interactions in Figure 1A are limited to the G1 phase of the cell cycle, the reactions shown are incomplete and many interactions at the G1-S phase transition are excluded. For example, in addition to RB1 and RB1-p, other pocket protein members p107 and p130 also bind to E2F and inhibit its transcriptional activity.¹¹⁰ And CyclinD1:Cdk4/6 can phosphorylate p107 and p130 and increase their degradation.^114,115 Also, E2F up-regulates the expression of itself¹¹⁰ and Cdc25A,⁵³ which is a protein phosphatase that removes the inhibitory phosphorylation on Cdk4/6 and Cdk2, positively regulating their kinase activities.¹¹⁶ It is impractical to include all possible reactions related to treatments in the biological mechanism. Because our goal is to build a model that can predict treatment responses over long time scales, we simplified the interactions shown in Figure 1A to those necessary to capture the effects of different treatments. The model structure we used is shown in Figure 1B and is modified from Figure 1A. First, we ignored interaction 26, E2F up-regulates cyclinE expression, in Figure 1A as this simplification doesn’t affect the model simulation results. Second, we didn’t include Cdk2 explicitly in the model but assumed that cyclinE not bound to p21 is bound to Cdk2 and active. This is because of the long-held presumption that Cdks are in excess of the cyclins in the cell and Cdk2 has been shown to be in excess of its cyclin partners.¹¹⁷Last, we didn’t include E2F in the model but assume that the level of RB1-pp reflects the transcriptional activity of E2F. While E2F, as the last driver of G1-S transition, may be the best protein to govern the proliferation rate,⁵³ the situation is complicated. Considering there are six E2F family members, having divergent roles as transcriptional activators or inhibitors, and the complexity of all possible combinations of E2Fs with their partners,¹¹⁸ it is difficult to use one measured protein level to denote E2F transcriptional activity. In order to govern the proliferation rate by one protein level and measure its level to calibrate the model, we decide to use hyperphosphorylated RB1 (RB1-pp) to represent E2F transcriptional activity and govern the proliferation rate. The is because E2Fs as transcriptional activators are regulated principally through binding to RB1¹¹⁹ and are only released to transactivate the genes required for the G1-S transition when RB1 is fully inactivated after phosphorylation by cyclinD1:Cdk4/6 and cyclinE:Cdk2.¹⁰⁴ These facts make it possible to drive the proliferation rate by one protein with a single specific phosphorylation site representing RB1-pp. It has been demonstrated that RB1 exists mainly in unphosphorylated, monophosphorylated and hyperphosphorylated form and measuring a specific phosphorylation site on RB1 can be used to infer the hyperphosphorylated state of RB1.¹²⁰ Over fifteen phosphorylation sites are found on RB1 and we found that RB1 phosphorylated on S612 reflects the decreased RB1-pp level changes after treatments based on our experiment results and the literature.¹¹⁹ Therefore, the binding reactions 22 and 23 in Figure 1A are ignored and the arrows of interactions 24, 25 and 27 start from RB1-pp in Figure 1B instead of E2F in Figure 1A. The other numbered interactions shown in Figure 1B are the same as in Figure 1A.

Long term palbociclib treatment effect on proliferation and cyclinD1

Figure S4 re-plots the 10-week palbociclib monotreatment data from Figure 4. MCF7 cells are treated with 750nM palbociclib for 10 weeks and the cells are re-plated at 5 weeks. The blue line is the cell number from 0 to 5 weeks normalized to the initial cell number at t=0. The red line is the re-plated cell number from 5 to 10 weeks normalized to the initial re-plated cell number at 5 weeks. The plot shows that the MCF7 proliferation rate significantly decreased from 5 weeks to 10 weeks compared to 0 to 5 weeks. In order to make the model match these proliferation changes, we introduced another variable in the model to control proliferation under palbociclib treatment (respropalbo in Table 1), which will increase under palbociclib treatment and decrease after removal of palbociclib. The proliferation rate is divided by a Hill function of this variable and will decrease as palbociclib treatment time increases. Without this variable, the model’s simulation of proliferation rate over the entire 10 week period will be nearly constant, which would be a poor fit to the experiment results. So, adding the variable is necessary to make the model match the proliferation difference shown in the experiment.

Figure 4E shows that the cyclinD1 level increased after mono or alternating palbociclib treatment, which is consistent with the literature.^69,86 In order to allow the model to simulate the increase of cyclinD1, we introduce another variable in the model (rescyclinD1palbo in Table 1) which will increase under the palbociclib treatment and decrease after removal of palbociclib. The generation rate of cyclinD1 is added to a hill function of this variable and will increase with palbociclib treatment time. Adding the variable is necessary to make the model match the cyclinD1 increase shown in the experiment. Although the cyclinD1 level increased after mono or alternating palbociclib treatment, the proliferation rate of the MCF7 cells remained suppressed under treatment. In our model, the increase of cyclinD1 can not counterbalance the palbociclib treatment effect of decreasing the cyclinD1:Cdk4/6 level. Although the increase of cyclinD1 causes the cyclinD1:Cdk4/6 level to rebound after the initial sharp decrease following the start palbociclib treatment, its level is still lower than the level before palbociclib treatment and the phosphorylation of RB1 by cyclinD1:Cdk4/6 is decreased. We model the phosphorylation rate of RB1 by cyclinD1:Cdk4/6 as a hill function of cyclinD1:Cdk4/6 multiplying a hill function of RB1, instead of cyclinD1:Cdk4/6 multiplying a hill function of RB1. This modification allows us to better control the phosphorylation rate of RB1 by cyclinD1:Cdk4/6 in the model to match the decreased proliferation and increased cyclinD1 level under the palbociclib treatments.

Model equations

$$\begin{array}{c}{N=N_{\mathsf{a}\mathsf{l}\mathsf{i}\mathsf{v}\mathsf{e}}+N}_{dead}\end{array}$$ (Equation 9)

(9) Total number of cells equals number of alive cells plus number of dead cells.

$$\frac{d{N}_{alive}}{dt}=\frac{k_{\mathsf{p}\mathsf{r}\mathsf{o}}\times \left(1+k_{proppRb}\times \frac{{ppRb}^{p_{{proppRb}_2}}}{{p_{{proppRb}_1}}^{p_{{proppRb}_2}}+{ppRb}^{p_{{proppRb}_2}}}\right)\times N_{alive}\times \left(1-\frac{N}{k_{carrying}}\right)}{1+k_{propalbo}\times \frac{{respropalbo}^{p_{{propalbo}_2}}}{{p_{{propalbo}_1}}^{p_{{propalbo}_2}}+{respropalbo}^{p_{{propalbo}_2}}}}$$ (Equation 10)

$$-k_{death}\times N_{alive}$$ (Equation 11)

(10) Basal proliferation, increased proliferation by $ppRb$ and inhibited proliferation by $respropalbo$.

(11) Basal death.

$$\frac{d{N}_{dead}}{dt}=k_{death}\times N_{alive}$$ (Equation 12)

$$-k_{lysis}\times N_{dead}$$ (Equation 13)

(12) Basal death.

(13) Lysis of dead cells.

$${hillfun}_{respropalbo}=\frac{{palbo}^{p_{{respropalbo}_2}}}{{p_{{respropalbo}_1}}^{p_{{respropalbo}_2}}+{palbo}^{p_{{respropalbo}_2}}}$$ (Equation 14)

$$\frac{drespropalbo}{dt}=k_{respropalbo}\times {hillfun}_{respropalbo}$$ (Equation 15)

$$-\frac{k{d}_{respropalbo}\times respropalbo}{1+p_{respropalbokd}\times hillfu{n}_{respropalbo}}$$ (Equation 16)

(14) Hill function for $respropalbo$.

(15) Generation of $respropalbo$ by $palbo$.

(16) Degradation of $respropalbo$ (fast if no palbociclib, but slow if there is palbociclib to allow slow buildup of respropalbo).

$$\begin{array}{c}\frac{d{E2}_{media}}{dt}=\frac{k_{diff}\times {N\times Vol}_{1cell}}{{Vol}_{media}}\times \left({E2}_{cell}-{E2}_{media}\right)\end{array}$$ (Equation 17)

(17) E2 concentration changes in media.

$$\frac{d{E2}_{cell}}{dt}=-k_{diff}\times \left({E2}_{cell}-{E2}_{media}\right)-\frac{\left(\frac{{dN}_{alive}}{dt}+\frac{{dN}_{dead}}{dt}\right)}{N}\times {E2}_{cell}$$ (Equation 18)

$$-{kb}_{E2ER}\times {E2}_{cell}\times ER+{kub}_{E2ER}\times E2ER$$ (Equation 19)

$$-{kb}_{NSB}\times {E2}_{cell}+{kub}_{NSB}\times E2NSB$$ (Equation 20)

$$+{kd}_{\mathsf{E}2\mathsf{E}\mathsf{R}}\times E2ER$$ (Equation 21)

(18) E2 concentration changes in cell.

(19) Binding and unbinding between $ER$ and ${E2}_{cell}$.

(20) Binding and unbinding between non-specific binding and ${E2}_{cell}$ in the cell.

(21) Degradation of $E2ER$.

$${\frac{dER}{dt}=k_{\mathsf{E}\mathsf{R}}-kd}_{ER}\times ER$$ (Equation 22)

$$-{kb}_{E2ER}\times {E2}_{cell}\times ER+{kub}_{E2ER}\times E2ER$$ (Equation 23)

$$-{kb}_{ICIER}\times ICI\times ER+{kub}_{ICIER}\times ICIER$$ (Equation 24)

(22) Translation and degradation of $ER$.

(23) Binding and unbinding between $ER$ and ${E2}_{cell}$.

(24) Binding and unbinding between $ER$ and $ICI$.

$$\frac{dE2ER}{dt}={-kd}_{\mathsf{E}2\mathsf{E}\mathsf{R}}\times E2ER$$ (Equation 25)

$$+{kb}_{E2ER}\times {E2}_{cell}\times ER-{kub}_{E2ER}\times E2ER$$ (Equation 26)

(25) Degradation of $E2ER$.

(26) Binding and unbinding between $ER$ and ${E2}_{cell}$.

$$\begin{array}{c}\frac{dE2NSB}{dt}={kb}_{NSB}\times {E2}_{cell}-{kub}_{NSB}\times E2NSB\end{array}$$ (Equation 27)

(27) Binding and unbinding between non-specific binding and ${E2}_{cell}$.

$$\frac{dICIER}{dt}={kb}_{\mathsf{I}\mathsf{C}\mathsf{I}\mathsf{E}\mathsf{R}}\times ICI\times ER-{kub}_{ICIER}\times ICIER$$ (Equation 28)

$$-{kd}_{ICIER}\times ICIER$$ (Equation 29)

(28) Binding and unbinding between $ICI$ and $ER$.

(29) Degradation of $ICIER$.

$$\frac{drescyclinD1palbo}{dt}=k_{rescyclinD1palbo}\times \frac{{palbo}^{p_{r{escyclinD1palbo}_2}}}{{p_{r{escyclinD1palbo}_1}}^{p_{r{escyclinD1palbo}_2}}+{palbo}^{p_{r{escyclinD1palbo}_2}}}$$ (Equation 30)

$$-{kd}_{rescyclinD1palbo}\times rescyclinD1palbo$$ (Equation 31)

(30) Generation of $rescyclinD1palbo$ by $palbo$.

(31) Degradation of $rescyclinD1palbo$.

$$\frac{dcyclinD1}{dt}=-{kd}_{cyclinD1}\times cyclinD1$$ (Equation 32)

$$+k_{cyclinD1}\times \left(1+k_{cyclinD1E2ER}\times \frac{{E2ER}^{p_{{cyclinD1E2ER}_2}}}{{p_{{cyclinD1E2ER}_1}}^{p_{{cyclinD1E2ER}_2}}+{E2ER}^{p_{{cyclinD1E2ER}_2}}}\right)$$ (Equation 33)

$${-kb}_{cyclinD1cdk46}\times cyclinD1\times cdk46+{kub}_{cyclinD1cdk46}\times cyclinD1cdk46$$ (Equation 34)

$$+k_{cyclinD1palbo}\times \frac{{rescyclinD1palbo}^{p_{{cyclinD1palbo}_2}}}{{p_{{cyclinD1palbo}_1}}^{p_{{cyclinD1palbo}_2}}{+rescyclinD1palbo}^{p_{{cyclinD1palbo}_2}}}$$ (Equation 35)

(32) Degradation of $cyclinD1$.

(33) Basal translation of $cyclinD1$ and the increased translation by $E2ER$.

(34) Binding and unbinding between $cyclinD1$ and $cdk46$.

(35) Increased translation of $cyclinD1$ by $rescyclinD1palbo$.

$$\frac{dcdk46}{dt}=k_{cdk46}-{kd}_{cdk46}\times cdk46$$ (Equation 36)

$$-{kb}_{cyclinD1cdk46}\times cyclinD1\times cdk46+{kub}_{cyclinD1cdk46}\times cyclinD1cdk46$$ (Equation 37)

$$-{kb}_{cdk46palbo}\times cdk46\times palbo+{kub}_{cdk46palbo}\times cdk46palbo$$ (Equation 38)

$$-{kb}_{cdk46abema}\times cdk46\times abema+{kub}_{cdk46palbo}\times cdk46abema$$ (Equation 39)

(36) Translation and degradation of $cdk46$.

(37) Binding and unbinding between $cyclinD1$ and $cdk46$.

(38) Binding and unbinding between $palbo$ and $cdk46$.

(39) Binding and unbinding between $abema$ and $cdk46$.

$$\frac{dcdk46palbo}{dt}=-{kd}_{cdk46}\times cdk46palbo$$ (Equation 40)

$$+{kb}_{cdk46palbo}\times cdk46\times palbo-{kub}_{cdk46palbo}\times cdk46palbo$$ (Equation 41)

(40) Degradation of $cdk46palbo$.

(41) Binding and unbinding between $palbo$ and $cdk46$.

$$\frac{dcdk46abema}{dt}=-{kd}_{cdk46}\times cdk46abema$$ (Equation 42)

$$+{kb}_{cdk46abema}\times cdk46\times abema-{kub}_{cdk46palbo}\times cdk46abema$$ (Equation 43)

(42) Degradation of $cdk46abema$.

(43) Binding and unbinding between $abema$ and $cdk46$.

$$\frac{dcyclinD1cdk46}{dt}=-{kd}_{cyclinD1cdk46}\times cyclinD1cdk46$$ (Equation 44)

$$+{kb}_{cyclinD1cdk46}\times cyclinD1\times cdk46-{kub}_{cyclinD1cdk46}\times cyclinD1cdk46$$ (Equation 45)

$$-{kb}_{cyclinD1cdk46p21}\times cyclinD1cdk46\times p21+{kub}_{cyclinD1cdk46p21}\times cyclinD1cdk46p21$$ (Equation 46)

$$-{kb}_{cyclinD1cdk46palbo}\times cyclinD1cdk46\times palbo+{kub}_{cyclinD1cdk46palbo}\times cyclinD1cdk46palbo$$ (Equation 47)

$$-{kb}_{cyclinD1cdk46abema}\times cyclinD1cdk46\times abema+{kub}_{cyclinD1cdk46abema}cyclinD1cdk46abema$$ (Equation 48)

(44) Degradation of $cyclinD1cdk46$.

(45) Binding and unbinding between $cyclinD1$ and $cdk46$.

(46) Binding and unbinding between $p21$ and $cyclinD1cdk46$.

(47) Binding between $palbo$ and $cyclinD1cdk46$.

(48) Binding between $abema$ and $cyclinD1cdk46$.

$$\frac{dcyclinD1cdk46p21}{dt}=-{kd}_{cyclinD1cdk46p21}\times cyclinD1cdk46p21$$ (Equation 49)

$$+{kb}_{cyclinD1cdk46p21}\times cyclinD1cdk46\times p21-{kub}_{cyclinD1cdk46p21}\times cyclinD1cdk46p21$$ (Equation 50)

$$-{kb}_{cyclinD1cdk46p21palbo}\times cyclinD1cdk46p21\times palbo+{kub}_{cyclinD1cdk46p21palbo}\times cyclinD1cdk46p21palbo$$ (Equation 51)

$$-{kb}_{cyclinD1cdk46p21abema}\times cyclinD1cdk46p21\times abema+{kub}_{cyclinD1cdk46p21abema}\times cyclinD1cdk46p21abema$$ (Equation 52)

(49) Degradation of $cyclinD1cdk46p21$.

(50) Binding and unbinding between p21 and $cyclinD1cdk46$.

(51) Binding and unbinding between $palbo$ and $cyclinD1cdk46p21$.

(52) Binding and unbinding between $abema$ and $cyclinD1cdk46p21$.

$$\frac{dcyclinD1cdk46palbo}{dt}=-{kd}_{cyclinD1cdk46palboabema}\times cyclinD1cdk46palbo$$ (Equation 53)

$$+{kb}_{cyclinD1cdk46palbo}\times cyclinD1cdk46\times palbo-{kub}_{cyclinD1cdk46palbo}\times cyclinD1cdk46palbo$$ (Equation 54)

$$-{kb}_{cyclinD1cdk46palbop21}\times cyclinD1cdk46palbo\times p21+{kub}_{cyclinD1cdk46palbop21}\times cyclinD1cdk46p21palbo$$ (Equation 55)

(53) Degradation of $cyclinD1cdk46palbo$.

(54) Binding and unbinding between $palbo$ and $cyclinD1cdk46$.

(55) Binding and unbinding between $p21$ and $cyclinD1cdk46palbo$.

$$\frac{dcyclinD1cdk46abema}{dt}=-{kd}_{cyclinD1cdk46palboabema}\times cyclinD1cdk46abema$$ (Equation 56)

$$+{kb}_{cyclinD1cdk46abema}\times cyclinD1cdk46\times abema-{kub}_{cyclinD1cdk46abema}\times cyclinD1cdk46abema$$ (Equation 57)

$$-{kb}_{cyclinD1cdk46abemap21}\times cyclinD1cdk46abema\times p21+{kub}_{cyclinD1cdk46abemap21}\times cyclinD1cdk46p21abema$$ (Equation 58)

(56) Degradation of $cyclinD1cdk46abema$.

(57) Binding and unbinding between $abema$ and $cyclinD1cdk46$.

(58) Binding and unbinding between $p21$ and $cyclinD1cdk46abema$.

$$\frac{dcyclinD1cdk46p21palbo}{dt}=-{kd}_{cyclinD1cdk46p21}\times cyclinD1cdk46p21palbo$$ (Equation 59)

$$+{kb}_{cyclinD1cdk46p21palbo}\times cyclinD1cdk46p21\times palbo-{kub}_{cyclinD1cdk46p21palbo}\times cyclinD1cdk46p21palbo$$ (Equation 60)

$$+{kb}_{cyclinD1cdk46palbop21}\times cyclinD1cdk46palbo\times p21-{kub}_{cyclinD1cdk46palbop21}\times cyclinD1cdk46p21palbo$$ (Equation 61)

(59) Degradation of $cyclinD1cdk46p21palbo$.

(60) Binding and unbinding between $palbo$ and $cyclinD1cdk46p21$.

(61) Binding and unbinding between $p21$ and $cyclinD1cdk46palbo$.

$$\frac{dcyclinD1cdk46p21abema}{dt}=-{kd}_{cyclinD1cdk46p21}\times cyclinD1cdk46p21abema$$ (Equation 62)

$$+{kb}_{cyclinD1cdk46p21abema}\times cyclinD1cdk46p21\times abema-{kub}_{cyclinD1cdk46p21abema}\times cyclinD1cdk46p21abema$$ (Equation 63)

$$+{kb}_{cyclinD1cdk46abemap21}\times cyclinD1cdk46abema\times p21-{kub}_{cyclinD1cdk46abemap21}\times cyclinD1cdk46p21abema$$ (Equation 64)

(62) Degradation of $cyclinD1cdk46p21abema$.

(63) Binding and unbinding between $abema$ and $cyclinD1cdk46p21$.

(64) Binding and unbinding between $p21$ and $cyclinD1cdk46abema$.

$$\frac{dcMyc}{dt}=-{kd}_{cMyc}\times cMyc$$ (Equation 65)

$$+k_{cMyc}\times (1+k_{cMycE2ER}\times \frac{{E2ER}^{p_{{cMycE2ER}_2}}}{{p_{{cMycE2ER}_1}}^{p_{{cMycE2ER}_2}}+{E2ER}^{p_{{cMycE2ER}_2}}}$$ (Equation 66)

$$+k_{cMycppRb}\times \frac{{ppRb}^{p_{{cMycppRb}_2}}}{{p_{{cMycppRb}_1}}^{p_{{cMycppRb}_2}}+{ppRb}^{p_{{cMycppRb}_2}}})$$ (Equation 67)

(65) Degradation of $cMyc$.

(66) Basal translation of $cMyc$ and the increased translation by $E2ER$.

(67) Increased translation of $cMyc$ by $ppRb$.

$$\frac{dp21}{dt}=k_{p21}-{kd}_{p21}\times p21$$ (Equation 68)

$$+k_{p21cMyc}\times \frac{{p_{{p21cMyc}_1}}^{p_{{p21cMyc}_2}}}{{p_{{p21cMyc}_1}}^{p_{p21{cMyc}_2}}{+cMyc}^{p_{{p21cMyc}_2}}}$$ (Equation 69)

$$-{kb}_{cyclinD1cdk46p21}\times cyclinD1cdk46\times p21+{kub}_{cyclinD1cdk46p21}\times cyclinD1cdk46p21$$ (Equation 70)

$$-{kb}_{cyclinD1cdk46palbop21}\times cyclinD1cdk46palbo\times p21+{kub}_{cyclinD1cdk46palbop21}\times cyclinD1cdk46p21palbo$$ (Equation 71)

$$-{kb}_{cyclinD1cdk46abemap21}\times cyclinD1cdk46abema\times p21+{kub}_{cyclinD1cdk46abemap21}\times cyclinD1cdk46p21abema$$ (Equation 72)

$$-{kb}_{cyclinEp21}\times cyclinE\times p21+{kub}_{cyclinEp21}\times cyclinEp21$$ (Equation 73)

(68) Translation and degradation of $p21$.

(69) Inhibition of translation by $cMyc$.

(70) Binding and unbinding between $p21$ and $cyclinD1cdk46$.

(71) Binding and unbinding between $p21$ and $cyclinD1cdk46palbo$.

(72) Binding and unbinding between $p21$ and $cyclinD1cdk46abema$.

(73) Binding and unbinding between $p21$ and $cyclinE$.

$$\frac{dcyclinE}{dt}=-{kd}_{cyclinE}\times cyclinE$$ (Equation 74)

$$+k_{cyclinE}\times \left(1+k_{cyclinEE2ER}\frac{{E2ER}^{p_{cyclinE{E2ER}_2}}}{{p_{{cyclinEE2ER}_1}}^{p_{cyclinE{E2ER}_2}}+{E2ER}^{p_{cyclinE{E2ER}_2}}}\right)$$ (Equation 75)

$$-{kb}_{cyclinEp21}\times cyclinE\times p21+{kub}_{cyclinEp21}\times cyclinEp21$$ (Equation 76)

(74) Degradation of $cyclinE$.

(75) Basal translation of $cyclinE$ and the increased translation by $E2ER$.

(76) Binding and unbinding between $p21$ and $cyclinE$.

$$\frac{dcyclinEp21}{dt}=-{kd}_{cyclinE}\times cyclinEp21$$ (Equation 77)

$$+{kb}_{cyclinEp21}\times cyclinE\times p21-{kub}_{cyclinEp21}\times cyclinEp21$$ (Equation 78)

(77) Degradation of $cyclinEp21$.

(78) Binding and unbinding between $p21$ and $cyclinE$.

$$\frac{dRb}{dt}=k_{Rb}-{kd}_{Rb}\times Rb$$ (Equation 79)

$$+k_{RbppRb}\times \frac{{ppRb}^{p_{{RbppRb}_2}}}{{p_{{RbppRb}_1}}^{p_{{RbppRb}_2}}+{ppRb}^{p_{{RbppRb}_2}}}$$ (Equation 80)

$$-k_{RbcyclinD1cdk46}\times \frac{{cyclinD1cdk46}^{p_{{cyclinD1cdk46}_2}}}{{p_{{cyclinD1cdk46}_1}}^{p_{{cyclinD1cdk46}_2}}+{cyclinD1cdk46}^{p_{{cyclinD1cdk46}_2}}}\times \frac{{Rb}^{p_{{cyclinD1cdk46Rb}_2}}}{{p_{{cyclinD1cdk46Rb}_1}}^{p_{{cyclinD1cdk46Rb}_2}}+{Rb}^{p_{{cyclinD1cdk46Rb}_2}}}$$ (Equation 81)

$$+k_{pRbdepho}\times \frac{{pRb}^{p_{p{Rb}_2}}}{{p_{{pRb}_1}}^{p_{{pRb}_2}}+{pRb}^{p_{p{Rb}_2}}}$$ (Equation 82)

(79) Degradation and basal translation of $Rb$.

(80) Increased translation of $Rb$ by $ppRb$.

(81) Phosphorylation of $Rb$ by $cyclinD1cdk46$.

(82) Dephosphorylation of $pRb$.

$$\frac{dpRb}{dt}=-{kd}_{pRb}\times pRb$$ (Equation 83)

$$+k_{RbcyclinD1cdk46}\times \frac{{cyclinD1cdk46}^{p_{{cyclinD1cdk46}_2}}}{{p_{{cyclinD1cdk46}_1}}^{p_{{cyclinD1cdk46}_2}}+{cyclinD1cdk46}^{p_{{cyclinD1cdk46}_2}}}\times \frac{{Rb}^{p_{{cyclinD1cdk46Rb}_2}}}{{p_{{cyclinD1cdk46Rb}_1}}^{p_{{cyclinD1cdk46Rb}_2}}+{Rb}^{p_{{cyclinD1cdk46Rb}_2}}}$$ (Equation 84)

$$-k_{pRbdepho}\times \frac{{pRb}^{p_{p{Rb}_2}}}{{p_{{pRb}_1}}^{p_{p{Rb}_2}}+p{Rb}^{p_{p{Rb}_2}}}$$ (Equation 85)

$$-k_{pRbcyclinE}\times cyclinE\times \frac{{pRb}^{p_{{cyclinEpRb}_2}}}{{p_{{cyclinEpRb}_1}}^{p_{{cyclinEpRb}_2}}+p{Rb}^{p_{{cyclinEpRb}_2}}}$$ (Equation 86)

$$+k_{ppRbdepho}\times \frac{ppR{b}^{p_{ppR{b}_2}}}{{p_{ppR{b}_1}}^{p_{ppR{b}_2}}+ppR{b}^{p_{ppR{b}_2}}}$$ (Equation 87)

(83) Degradation of $pRb$.

(84) Phosphorylation of $Rb$ by $cyclinD1cdk46$.

(85) Dephosphorylation of $pRb$.

(86) Phosphorylation of $pRb$ by $cyclinE$.

(87) Dephosphorylation of $ppRb$.

$$\frac{dppRb}{dt}=-{kd}_{ppRb}\times ppRb$$ (Equation 88)

$$+k_{pRbcyclinE}\times cyclinE\times \frac{{pRb}^{p_{{cyclinEpRb}_2}}}{{p_{{cyclinEpRb}_1}}^{p_{{cyclinEpRb}_2}}+p{Rb}^{p_{{cyclinEpRb}_2}}}$$ (Equation 89)

$$-k_{ppRbdepho}\times \frac{ppR{b}^{p_{ppR{b}_2}}}{{p_{ppR{b}_1}}^{p_{ppR{b}_2}}+ppR{b}^{p_{ppR{b}_2}}}$$ (Equation 90)

(88) Degradation of $ppRb$.

(89) Phosphorylation of $pRb$ by $cyclinE$.

(90) Dephosphorylation of $ppRb$.

Model parameter calibration and model summary

Parameters of degradation rates (k_d) for proteins were assigned according to half-lives found in literature (denoted as Fixed in Table 2), where k_d = -log(1/2)/t_half-life. Considering that the limited data we collected does not warrant the increase of parameter number, which would be unidentifiable, we facilitated the optimization and decreased the number of parameters to be calibrated by fixing the unbinding parameters to 1 (denoted as Fixed in Table 2). The other parameters were calibrated using the patternsearch function in MATLAB (R2021b), to reduce the discrepancy between the model simulation and the experimental results. The least-squares cost function was calculated as:

$$cost\left(p\right)=\sum _{i=1}^n\sum _{j=1}^m\frac{{\left(y_{ij}^E\left(t_j\right)-y_{ij}\left(t_j,p\right)\right)}^2}{{\sigma }_{ij}^2}$$

where $i$ indexes the model variables of proteins or alive cell number under a specific treatment, $j$ indexes the experimental measured times. $y_{ij}^E\left(t_j\right)$ is the experimental measurement of the specie $i$ at time $j$. $y_{ij}\left(t_j,p\right)$ is the simulation result of the variable $i$ at time $j$ using parameter vector $p$. ${\sigma }_{ij}$ is the standard deviation of the experimentally measured specie $i$ at time $j$. The data, time points and the model variables used in fitting the experimental data are listed in Table S1. The parameters were tuned manually at the beginning to get the gross treatment response roughly consistent with the experimental results. Then the default patternsearch in MATLAB was used for calibration of the parameters.

The culture media, including any drugs in the different treatments, was changed at t = 0 and every 3 or 4 days during the treatment period, so the longest period without resupply of any drug is 4 days. There is no data we are aware of for the half-life of the three drugs we used (ICI 182,780, palbociclib and abemaciclib) in in-vitro conditions. Most data are for the plasma or terminal half-life in-vivo determined by processing in the liver or excretion through the kidneys, which are not applicable to our model. There is data for the in-vitro stability of these drugs in human plasma, which is akin to our case. ICI 182,780 shows no degradation in human plasma at room temperature over 7 hours.¹²¹ Palbociclib and abemaciclib show less than 5% degradation in human plasma at room temperature over 3 days¹²² Based on this data, we believe the drug half-life is sufficiently long so as to be ignored in our in-vitro experiments. The drug concentrations are assumed to be constant throughout the treatment as a reasonable approximation.

The mathematical model contains 27 ordinary differential equations (ODEs) and 112 parameters (80 calibrated and 32 fixed), which is implemented in MATLAB. The generation, degradation, phosphorylation, dephosphorylation, binding and unbinding reactions are modeled by mass action laws and hill functions. Drug treatment effects are modeled by competitive binding to their targets. The ODEs are solved numerically by the ode23tb function in MATLAB.

Parameter cohort

To address the fact that the parameters in model may not be practically identifiable by our limited measured data, another 199 parameter sets that fit the data reasonably well (cost < 500) were identified to form a parameter cohort. All 200 parameter sets in the cohort were used for simulation and prediction. The resulting spread in the predictions show the degree to which the data used to calibrate the model parameters constrains the prediction results. The parameter cohort was generated by the default genetic algorithm function, ga, in the MATLAB optimization toolbox. We saved parameter sets found during the running of the ga function whose cost function value was smaller than 500.

The coefficients of variation of the parameters and the cost function values for the parameter sets in the cohort are plotted in Figures S8A and S8B. The coefficient of variation plot reflects the spread of the parameter values in the cohort and the large values represent parameters to which the model has low sensitivity. A local sensitivity analysis for each parameter in the cohort with respect to proliferation is shown in Figure S8D. The most significant sensitivity for cell proliferation involves parameters #6 and #90, which are related to the basal translation of the estrogen receptor and the dephosphorylation of RB1-pp, respectively. These results are not surprising as the estrogen receptor level impacts the response to –E2 and ICI endocrine treatments and dephosphorylation of RB1-pp directly regulates the RB1-pp level. Figure S8C plots a histogram of the fitting costs that were generated by all the perturbed parameter sets used in the sensitivity analysis used to create Figure S8D. The figure shows that across all the perturbations of parameter sets in the cohort there was not a major increase in the fitting cost.

Local sensitivity analysis

We used local sensitivity analysis to check how sensitive the model output was to the parameter values. The sensitivity value for a model output and a specific parameter is the change in the model output relative to the change in parameter value. It can be expressed as^123,124:

$$s_{ijk}=\frac{\partial \log \left(X_{ij}\right)}{\partial \log \left(p_k\right)}=\frac{\partial X_{ij}}{\partial P_k}\frac{p_k}{X_{ij}}$$

where $s_{ijk}$ is the local sensitivity value, which is the derivative of model output $X_{ij}$ with respect to parameter $p_k$ multiplied by the ratio $p_k/X_{ij}$. It gives the percent change in the model output produced by a 1% change in a parameter. In the equation, $i$ indexes the alive cell number under a specific treatment, $j$ indexes the timepoints and $k$ indexes the parameters. $s_{ijk}$ can be approximated by the second order central finite difference. Therefore, each parameter is individually varied by 1% of its value:

$$s_{ijk}\approx \frac{X_{ij}\left(p_k+1\%\times p_k\right)-X_{ij}\left(p_k-1\%\times p_k\right)}{2\%\times p_k}\frac{p_k}{X_{ij}\left(p_k\right)}=\frac{X_{ij}\left(p_k+1\%\times p_k\right)-X_{ij}\left(p_k-1\%\times p_k\right)}{2\%\times X_{ij}\left(p_k\right)}$$

The sensitivity analysis was performed on all 64 data-calibrated parameters in a parameter set, except the hill function powers, and all parameter sets in the cohort. The fixed parameters were excluded. Because we want to check whether the model output is very sensitive to certain parameters, the maximum values of $s_{ijk}$ across all $i$ and $j$, which is $s_k=\underset{i,j}{\max }\left|s_{ijk}\right|$, is used to represent the sensitivity value.

Growth rate inhibition (GR) metric

The GR metric is different from traditional drug response metrics, which are highly sensitive to the number of cell divisions during the experiment. It compares the growth rates in the presence and absence of drug and is largely independent of cell division rate and assay duration.⁴⁸ The GR metric is calculated according to the formula:

$$\begin{array}{c}GR\left(c\right)=2^{\frac{{\mathit{log}}_2\left(x\left(c\right)/x0\right)}{{\mathit{log}}_2\left(x_{ctrl}/x0\right)}}-1\end{array}$$

The cell count under the drug treatment is normalized to the vehicle control cell count. $x\left(c\right)$ is the cell count in the presence of drug at concentration $c$. $x_{ctrl}$ is the cell count for the vehicle control. $x_0$ is the cell count at t = 0 prior to drug treatment. The maximum value of GR is 1 (unless the drug increases proliferation) and the lowest value of GR is -1. GR = 0 means the drug treatment has a cytostatic response and a negative value means the drug treatment has a cytotoxic effect.⁴⁸

Microarray data analysis

The microarray data analysis was performed by the limma R package, which provides data normalization and differential gene expression analysis for gene expression experiments.⁹¹ The agilent microarray data files were read by the read.maimages function. The backgrounds were corrected using the backgroundCorrect function and the data were normalized using the normalizedBetweenArrays function. Differential expression analysis was performed by lmfit and eBayes functions. Heatmaps of the significantly differentially expressed genes (adjusted p-value <= 0.05) were plotted using the heatmap.2 function in the gplots R package. Hierarchical clustering of columns in the heatmap is based on the default setting in the heatmap.2 function, which used the dist and hclust functions in the stats R package. Principal component analysis was performed using the prcomp function in the stats R package. The Gene Set Enrichment Analysis (GSEA) was performed using the clusterProfiler R package^92,93 and the C3 regulatory target gene sets in the Molecular Signatures Database (MSigDB) provided by the msigdbr R package was used.¹²⁵ Data preparation and visualizations were performed in R using the tidyverse (v1.3.1), gplots (v3.1.1), ggplot2(3.3.5), and plotly(4.10.0) packages.

Quantification and statistical analysis

Statistical testing was carried out in MATLAB. Group comparisons were performed by the two-sided paired t test (ttest function). For comparison of multiple groups, one-way ANOVA or two-way ANOVA (anovan function) and Tukey’s HSD test for multiple comparisons (multcompare function) was used. Lower case n refers to the number of biological replicates noted in the figure legends. Statistical significance was considered with p values smaller than 0.05 and ns represents non-significant. The precise p values are noted in the figure legends with asterisks: p <0.05 (∗), p ≤ 0.01 (∗∗), p ≤ 0.001 (∗∗∗), p ≤ 0.0001 (∗∗∗∗).

Published: April 23, 2023

Data and code availability

• •All data reported in this study has been deposited at Zenodo with the original code. Microarray data has been deposited and is publicly available as of the date of publication. Accession number is listed in the key resources table in the Deposited Data section.
• •Original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this work paper is available from the lead contact upon request.