Deep learning architecture for 3D image super-resolution of late gadolinium enhanced cardiac MRI

Abstract.

Purpose

High-resolution late gadolinium enhanced (LGE) cardiac magnetic resonance imaging (MRI) volumes are difficult to acquire due to the limitations of the maximal breath-hold time achievable by the patient. This results in anisotropic 3D volumes of the heart with high in-plane resolution, but low-through-plane resolution. Thus, we propose a 3D convolutional neural network (CNN) approach to improve the through-plane resolution of the cardiac LGE-MRI volumes.

Approach

We present a 3D CNN-based framework with two branches: a super-resolution branch to learn the mapping between low-resolution and high-resolution LGE-MRI volumes, and a gradient branch that learns the mapping between the gradient map of low-resolution LGE-MRI volumes and the gradient map of high-resolution LGE-MRI volumes. The gradient branch provides structural guidance to the CNN-based super-resolution framework. To assess the performance of the proposed CNN-based framework, we train two CNN models with and without gradient guidance, namely, dense deep back-projection network (DBPN) and enhanced deep super-resolution network. We train and evaluate our method on the 2018 atrial segmentation challenge dataset. Additionally, we also evaluate these trained models on the left atrial and scar quantification and segmentation challenge 2022 dataset to assess their generalization ability. Finally, we investigate the effect of the proposed CNN-based super-resolution framework on the 3D segmentation of the left atrium (LA) from these cardiac LGE-MRI image volumes.

Results

Experimental results demonstrate that our proposed CNN method with gradient guidance consistently outperforms bicubic interpolation and the CNN models without gradient guidance. Furthermore, the segmentation results, evaluated using Dice score, obtained using the super-resolved images generated by our proposed method are superior to the segmentation results obtained using the images generated by bicubic interpolation ($p<0.01$) and the CNN models without gradient guidance ($p<0.05$).

Conclusion

The presented CNN-based super-resolution method with gradient guidance improves the through-plane resolution of the LGE-MRI volumes and the structure guidance provided by the gradient branch can be useful to aid the 3D segmentation of cardiac chambers, such as LA, from the 3D LGE-MRI images.

1. Introduction

Atrial fibrillation (AF) is the most common cardiac arrhythmia encountered in clinical practice.¹ It is estimated to affect 6 to 12 million people in the United States alone by the year 2050² and is associated with a high risk of comorbidity and mortality. In AF, the electrical activity within the atria is impaired, causing irregular and rapid heart rhythm. To restore regular heart rhythm for AF patients, minimally invasive radiofrequency ablation therapies are viable treatment options.³ AF is associated with left atrial (LA) fibrosis/scars and inherent reduction of the measured endocardial potentials.⁴ Hence, it is crucial to determine the extent and location of the LA fibrosis/scar and to identify the region of the LA that will benefit from ablation therapy, while avoiding scars.

Late gadolinium enhanced (LGE) cardiac magnetic resonance imaging (MRI) is an established method to identify and quantify compromised myocardial tissue. In a typical LGE-MRI image acquisition protocol, the MRI images are acquired 15 to 20 min post-injection of a gadolinium-based contrast agent. In LGE-MRI, the trapping and delayed wash-out of the gadolinium-based contrast agent from the intra-cellular space of the compromised tissue enables differentiation between healthy and diseased/scar/fibrotic tissues, rendering the compromised tissues brighter than the healthy tissues.⁵

In recent years, LGE-MRI has been increasingly adopted to assess the extent of the fibrosis/scars in the LA for patients with AF.^4,6 To localize and quantify LA fibrosis with high precision, high-resolution 3D LGE-MRI images are necessary. However, due to the limitations of the maximal breath-hold time achievable by the patient, high-resolution 2D stacks of LGE-MRI images are typically acquired, resulting in anisotropic 3D volumes of the heart. These images have high in-plane resolution (1 to 1.5 mm), but low through-plane resolution (5 to 10 mm). Therefore, the anisotropic 3D LGE-MRI images with poor through-plane resolution impose challenges on downstream tasks, such as the 3D segmentation of LA cavity and fibrosis quantification.

Conventional interpolation methods, such as bilinear, spline, and Lancoz resampling methods, can be used to upsample the low-resolution volumes to high-resolution volumes, however, these methods often cause artifacts, like blurring, and cannot recover the missing high-frequency semantic and structural information. To address this limitation, several researchers proposed learning-based super-resolution methods that learn the structural information between slices using low- and high-resolution image pairs.^7–9 In recent years, increasing research efforts proposed deep learning-based super-resolution algorithms for medical images,¹⁰ especially to enhance the through-plane resolution of anisotropic brain MRI images.^11–15

Subsequently, these deep learning-based super-resolution techniques have been applied to alleviate the through-plane resolution degradation in 3D cardiac MRI volumes. In response to the challenge of acquiring high resolution isotropic images, Steeden et al.¹⁶ demonstrated the potential of a convolutional neural network (CNN)-based approach for super-resolution reconstruction of balanced steady state free precession (bSSFP) cardiac MRI images using synthetic training data. Masutani et al.¹⁷ explored the feasibility of both single frame and multi-frame CNN models to generate super-resolution bSSFP cine cardiac MRI images. Basty et al.¹⁸ showed that recurrent neural networks can be used to reconstruct super-resolution cardiac cine MRI long-axis slices from low-resolution acquisitions by using the temporal recurrence, thereby, using the temporal context to improve the resolution of cardiac cine MRI volumes. Sander et al.¹⁹ proposed an unsupervised deep learning-based approach to enhance the through-plane resolution of cine cardiac MRI volumes by leveraging the latent space interpolation ability of the autoencoders; however, large variations in anatomy between adjacent slices affect the performance of the method. Zhao et al.²⁰ proposed a 2D CNN-based super-resolution method that takes advantage of the high-resolution information from the in-plane data to improve the through plane resolution. They applied this technique on cine cardiac, neural and tongue MRI images. These methods successfully improve the through-plane resolution of cine cardiac MRI images; however, limited efforts have been made to improve the resolution of LGE cardiac MRI images using the CNN-based methods due to the limited availability of the high-resolution LGE MRI images for training and validation.

To improve the through-plane resolution of LGE cardiac MRI images to aide LA segmentation for AF patients, in our previous work,²¹ we proposed a 2D CNN-based method to enhance the through-plane resolution of LGE cardiac MRI images by leveraging the information learnt by training short-axis 2D patches to learn the mapping from simulated low-resolution in-plane data and their corresponding high-resolution in-plane data and using this learnt information to enhance the poor through-plane resolution. While the proposed 2D patch-based method improves the through-plane resolution, it ignores the global context information, as well as the 3D information provided by the LGE-MRI images that is crucial for accurate segmentation; finally, it also requires the use of 2D patches during the inference stage, which can lead to inconsistencies during the fusion process.

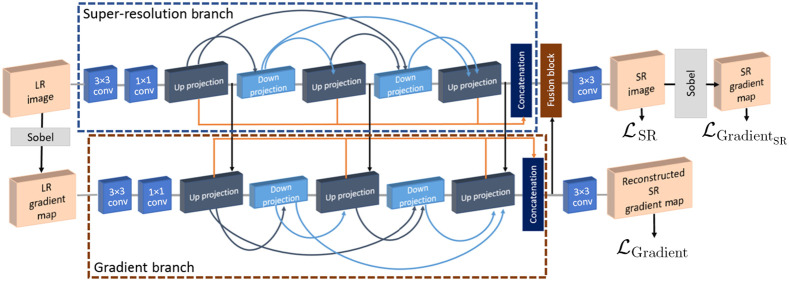
Therefore, in our earlier work,²² we developed and presented a 3D CNN-based architecture with gradient guidance to generate super-resolution cardiac LGE-MRI images. Here, inspired by the improved performance of our proposed method in our earlier work,²² we extended the 3D gradient branch that guides our 3D CNN model to “pay more attention” to the 3D structure of the tissues in the LGE-MRI images, as illustrated in Fig. 1. Our main contributions in this work can be summarized as follows.

Fig. 1.

Framework of the proposed dense DBPN-based super-resolution (SR) method with gradient guidance.²²

• 1.Firstly, to enhance the resolution of 3D cardiac LGE-MRI images, we present a 3D deep learning-based framework with two branches: a super-resolution branch with 3D dense deep back-projection network (DBPN)²³ as the backbone of our CNN architecture and an auxiliary gradient branch. As illustrated in Fig. 1, the super-resolution branch learns the mapping between the low-resolution input image and its corresponding high-resolution image, the gradient branch learns the mapping between the gradient map of the low-resolution input image and the gradient map of its corresponding high-resolution image. Here, in contrast to incorporating feature map representations from super-resolution branch to the gradient branch only at up-projection levels, as shown in our earlier work,²² we extend the CNN architecture by incorporating the feature map representations from the super-resolution branch to the gradient branch at every level. We evaluate the performance of the proposed super-resolution method by training and testing them on the 2018 atrial segmentation challenge dataset.⁶
• 2.Secondly, we further assess the performance of the proposed gradient guidance method by replacing the dense DBPN model with the enhanced deep super-resolution (EDSR)²⁴ network as the backbone of our deep learning framework.
• 3.Thirdly, in addition to evaluating our methods by training and testing them on the 2018 atrial segmentation challenge dataset,⁶ we also evaluate the generalization ability of our trained models by testing them on the left atrial and scar quantification and segmentation challenge (LAScarQS) 2022 dataset.^25–27
• 4.Finally, we investigate the effect of the proposed super-resolution framework on the downstream segmentation task, i.e., the segmentation of the LA from these LGE-MRI volumes.

2. Materials and Methods

2.1. Data

A set of 154 3D LGR-MRI volumes obtained from 60 patients with AF was available through the 2018 atrial segmentation challenge.⁶ These clinical images were acquired with either a Siemens 1.5 Tesla Avanto or a 3.0 Tesla Verio scanner. We split the available 154 LGE-MRI volumes to 80 for training, 20 for validation and 54 for testing.

The spatial dimensions of these LGE-MRI volumes are either $576\times 576\times 88$ or $640\times 640\times 88$, and feature an isotropic voxel spacing of $0.625\times 0.625\times 0.625{\mathrm{mm}}^3$. To train our CNN models, we need to simulate low-resolution LGE-MRI volumes from the available high-resolution LGE-MRI volumes. Therefore, we first center-crop the high-resolution images to $224\times 224\times 88$ and downsample them randomly on-the-fly during training using either Fourier or Gaussian downsampling,¹⁵ with uniform distribution. In Fourier downsampling,^12,28 we block the high frequency information in the $w$-axis of the Fourier domain by truncating the k-space to simulate the low-resolution data acquisition process in the Fourier domain. In Gaussian downsampling,²⁹ we simulate low-resolution images using Gaussian blur with a standard deviation uniformly distributed in the range of $[0.5,1.5]$ and downsample them using linear interpolation in the $z$-axis direction, i.e., slice-encoding direction. The Gaussian blur is applied isotopically, as it enables the CNN to learn the mapping between low-resolution and high-resolution images by deblurring in all spatial directions (i.e., $x$, $y$, and $z$). We downsample the LGE-MRI volumes using a scale factor of 2, 4, and 8. Subsequently, to train our 3D CNN models, we generate 3D LGE-MRI patches of size $96\times 96\times 44$, $96\times 96\times 22$, and $96\times 96\times 11$, respectively, with an overlap of 33.33%.

Additionally, to evaluate the generalization ability of our trained models, we use a subset (only the high-resolution isotropic LGE-MRI data) of the training dataset from the LAScarQS 2022 segmentation challenge dataset^25–27 as our external test set. These clinical images feature a spatial resolution of $1.4\times 1.4\times 1.4{\mathrm{mm}}^3$ and were acquired using a Philips Achieva 1.5 Tesla scanner from patients with AF. We test the models trained on the 2018 atrial segmentation challenge⁶ dataset on these 30 LGE-MRI volumes from the LAScarQS 2022 segmentation challenge dataset^25–27

2.2. Proposed CNN Framework

As illustrated in Fig. 1, our proposed CNN framework to generate super-resolution cardiac LGE-MRI volumes consists of two branches: a super-resolution branch and a gradient branch.

2.2.1. Super-resolution branch

The super-resolution branch takes in low-resolution images $I^{\mathrm{LR}}$ as input and aims to generate super-resolution images $I^{\mathrm{SR}}$ as output, given the high-resolution images $I^{\mathrm{HR}}$ as ground-truth. In our work, we use the dense DBPN²³ model to super-resolve the low-resolution LGE-MRI volumes. The dense DBPN model illustrated in Fig. 1 can be split into three parts: initial feature extraction, back-projection and reconstruction. In the initial feature extraction stage, we construct the initial low-resolution feature maps from $I^{\mathrm{LR}}$ using 32 filters, which is then further reduced to 16 filters before entering the back-projection stage. Following the initial feature extraction step, in the back-projection stage, we have a sequence of three up-projection and two down-projection blocks, wherein, we adapted the block architectures from one of the earlier 3D dense DBPN work,¹⁵ i.e., we used convolutional and transposed convolutional layers with parametric rectified linear units as activation functions, and without the batch normalization layers. We used a kernel size of $7\times 7\times 6$, $7\times 7\times 8$ and $7\times 7\times 12$, with anisotropic stride of $1\times 1\times 2$, $1\times 1\times 4$, and $1\times 1\times 8$, and padding of $3\times 3\times 2$, for the downsampling scale factor of 2, 4, and 8, respectively. Here, each block has access to outputs of all the previous blocks (Fig. 1). This enables the generation of effective feature maps.²³ Here, the up- and down-projection blocks are alternating between the construction of low-resolution and high-resolution feature maps and the number of filters used in each projection block is set to 16. As explained by Haris et al.,²³ the iterative up- and down-sampling focuses on increasing the sampling rate of the super-resolution features at different depths, thereby, distributing the computation of the reconstruction error to each stage. Therefore, the multiple alternating up- and down-sampling operators enable the network to preserve the high-resolution components while generating deeper features. The multiple back-projection stages between the mutually connected up- and down-sampling operators guide the super-resolution task by learning the non-linear relation of low-resolution and high-resolution images. Finally, in the reconstruction stage, all the high-resolution feature maps from the up-projection blocks are concatenated, along with the output of the gradient branch, to generate $I^{\mathrm{SR}}$ as output.

2.2.2. Gradient branch

The target of the gradient branch is to learn the mapping between the gradient map of the low-resolution images $G(I^{\mathrm{LR}})$ and the gradient map of their corresponding high-resolution images $G(I^{\mathrm{HR}})$, thereby, reconstructing a super-resolution gradient map $I_{\text{gradient}}^{\mathrm{SR}}$. Here, $G(·)$ stands for the operation that extracts the gradient map of the images, which in our case is a Sobel filter applied in voxel space. Similar to the super-resolution branch, we use a dense DBPN model to learn the mapping in the gradient branch. As illustrated in Fig. 1, the gradient branch incorporates feature map representations from the super-resolution branch by concatenation at every level, as opposed to incorporating features by concatenation only at the up-projection level, as shown in our earlier work.²² The advantage of this step is that it enables the reconstruction of the higher-resolution gradient map using the rich structural information from the super-resolution branch (strong prior) and reduces the number of parameters needed for the gradient branch. Next, the high-resolution feature maps from the up-projection blocks of the gradient branch are concatenated and integrated with the super-resolution branch by concatenation to guide reconstruction of the super-resolution 3D LGE-MRI images. The motivation behind the integration of high-resolution feature maps from the gradient branch to the super-resolution branch is that it can implicitly echo if the recovered region should be sharp or smooth, thus preserving the structure of the tissue as the CNN concentrates more on the spatial relationships of the outlines in the gradient branch. Meanwhile, the concatenated high-resolution feature maps from the up-projection blocks of the gradient branch are used to reconstruct super-resolution gradient map $I_{\text{gradient}}^{\mathrm{SR}}$.

2.2.3. Objective function

Our proposed CNN model is trained using the following objective function:

$$\mathcal{L}=\alpha .{\mathcal{L}}_{\mathrm{SR}}+\beta .{\mathcal{L}}_{\text{Gradient}}+\gamma .{\mathcal{L}}_{{\text{Gradient}}_{\mathrm{SR}}},$$ (1)

where ${\mathcal{L}}_{\mathrm{SR}}$ is the $L_1$ loss computed between $I^{\mathrm{SR}}$ and $I^{\mathrm{HR}}$, ${\mathcal{L}}_{\text{Gradient}}$ is the $L_1$ loss computed between $I_{\text{gradient}}^{\mathrm{SR}}$ and $G(I^{\mathrm{HR}})$, and ${\mathcal{L}}_{{\text{Gradient}}_{\mathrm{SR}}}$ denotes $L_1$ loss between $G(I^{\mathrm{SR}})$ and $G(I^{\mathrm{HR}})$. In Eq. (1), the $\alpha$, $\beta$, and $\gamma$ represent the scalar weights associated with the ${\mathcal{L}}_{\mathrm{SR}}$, ${\mathcal{L}}_{\text{Gradient}}$, and ${\mathcal{L}}_{{\text{Gradient}}_{\mathrm{SR}}}$ loss functions, respectively. In all our experimental results reported in this paper, the scalar value of $\alpha$, $\beta$, and $\gamma$ is 1; thus, imposing more importance to the edge information.

2.3. Experiments

To evaluate the effectiveness of our proposed method, three experiments were designed.

In the first experiment, we compare the results of our proposed framework with bicubic interpolation and dense DBPN model without gradient guidance. Additionally, to assess the effectiveness of the gradient branch, we use the EDSR model²⁴ as the back-bone network in our proposed framework and compare the EDSR network with and without gradient guidance, as well as the DBPN network with and without guidance. Here, we split the 154 LGE-MRI dataset made available through the 2018 atrial segmentation challenge⁶ into 80 datasets for training, 20 datasets for validation and 54 datasets for testing. Here, the training and the test sets belong to the same challenge dataset. As discussed in Sec. 2.1, we train the models on low-resolution LGE-MRI volumes obtained by downsampling high-resolution volumes using a scale factor of 2, 4, and 8, respectively. We train these models on a NVIDIA RTX 2080 Ti GPU with 11 GB memory using the Adam optimizer with a learning rate of ${10}^{-4}$ and a gamma decay of 0.5 every 15 epochs, for 50 epochs.

In the second experiment, we apply the models trained on the 2018 atrial segmentation challenge⁶ to test them on a subset of the LAScarQS 2022 segmentation challenge dataset.^25–27 This is done to assess the generalization ability of the proposed framework. We test the trained models on 30 LGE-MRI volumes from the LAScarQS dataset, which is the total number of high-resolution isotropic LGE-MRI data available in the training set of the LAScarQS dataset.

In our third experiment, we use the super-resolved LGE-MRI volumes generated by each of the above-mention algorithms to train the U-Net³⁰ models to segment the LA chamber, and compare the segmentation results, to investigate the effect of the proposed super-resolution framework on the downstream segmentation tasks. Here, all the 3D images were first resized to $96\times 96\times 64$ and then, used to train a 3D U-Net model³¹ to segment the LA chambers. We use the similar split, i.e., 80 for training, 20 for validation and 54 for testing from the 2018 atrial segmentation challenge⁶ dataset to train the U-Net models. The ground-truth LA segmentation masks provided by the 2018 atrial segmentation challenge dataset⁶ were manually annotated by experts in the field and were used to train the U-Net models. While training, we augment the LGE-MRI images randomly on-the-fly using translation operation uniformly distributed in the range of $[\mathrm{1,10}]$ pixels in any spatial direction, rotation operation with the angle uniformly distributed in the range of $[-180\mathrm{deg},180\mathrm{deg}]$ and gamma correction operation with the gamma value uniformly distributed in the range of $[0.75,1.25]$. These U-Nets models are trained on the NVIDIA RTX 2080 Ti GPU with 11 GB memory using the Adam optimizer with a learning rate of ${10}^{-5}$ and a gamma decay of 0.99 every alternate epoch, for 100 epochs.

3. Results

3.1. Validation on 2018 Atrial Segmentation Challenge Dataset

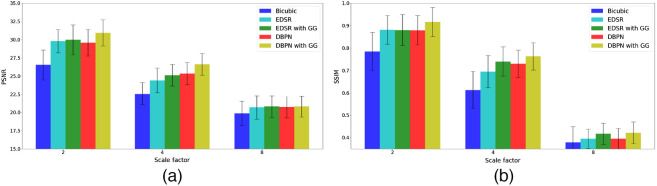
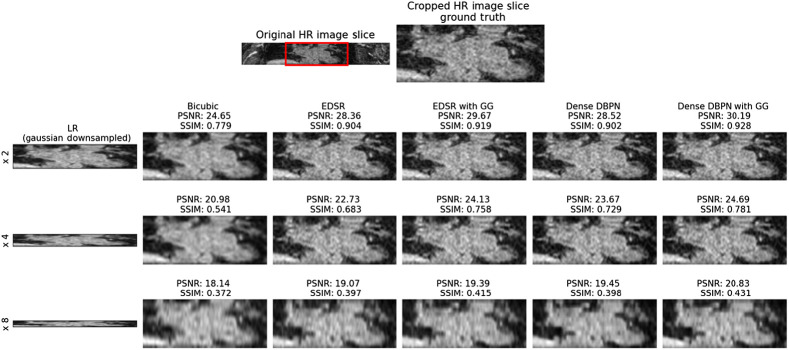
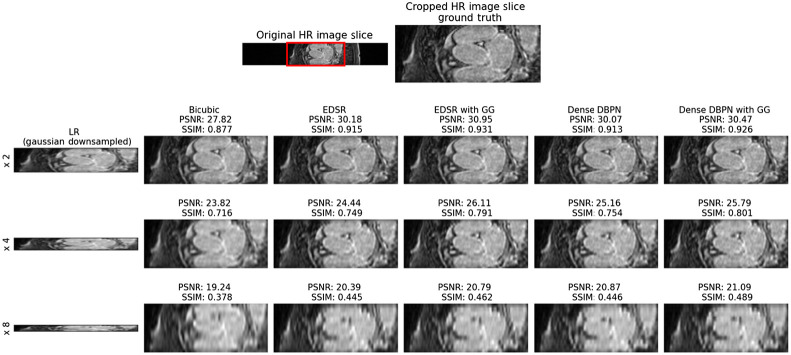
The performance of the proposed CNN framework is evaluated by computing the mean peak signal-to-noise ratio (PSNR) and mean structural similarity index (SSIM) between the super-resolution 3D LGE-MRI volumes and ground-truth high-resolution 3D LGE-MRI volumes. In Table 1 and Fig. 2, we show the super-resolution results of different methods, namely, bicubic interpolation, EDSR model with and without gradient guidance, and dense DBPN model with and without gradient guidance, respectively, on the 2018 atrial segmentation challenge⁶ test set. The super-resolution models are trained and tested on simulated low-resolution images downsampled by a scale factor of 2, 4 and 8, respectively. To compare the performance of the experimented models, we conducted a statistical significance (paired Student’s $t$-test) test. While the CNN models outperform the bicubic interpolation ($p<0.01$) for all the three downsampling scale factors, our experiments show higher PSNR and SSIM for the EDSR and dense DBPN models with gradient guidance compared to their stand-alone counterparts. In our experiments, the dense DBPN models with gradient guidance obtained the best PSNR and SSIM values, and are significantly ($p<0.01$) better than the stand-alone EDSR model, which obtained the least PSNR and SSIM values among the CNN models. To show the improvement in through-plane resolution using the proposed CNN framework, in Fig. 3, we show an example of a Gaussian downsampled low-resolution LGE cardiac MRI slice along the $z$-axis with its corresponding high-resolution image slice, and the super-resolution images obtained using the above-mentioned methods for all three downsampling scale factors.

Table 1.

Test set evaluation on the 2018 atrial segmentation challenge dataset: mean (std-dev) PSNR and SSIM achieved using bicubic interpolation; EDSR model with and without gradient guidance; and dense DBPN model with and without gradient guidance for a downsampling scale factor of 2, 4, and 8, respectively. The best evaluation metrics achieved are labeled in bold. Statistically significant differences were evaluated between the CNN models with and without gradient guidance using the Student’s $t$-test and are reported using * $p<0.05$ and ** for $p<0.01$.

Methods	Scale factor: 2		Scale factor: 4		Scale factor: 8
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
Bicubicinterpolation	26.55	0.785	22.56	0.613	19.86	0.378
	(2.04)	(0.085)	(1.54)	(0.083)	(1.68)	(0.070)
EDSR24	29.80	0.881	24.41	0.695	20.69	0.395
	(1.60)	(0.064)	(1.70)	(0.071)	(1.62)	(0.043)
EDSR withgradient guidance	29.97	0.880	25.13	0.740	20.80	0.417
	(2.04)	(0.069)	(1.48)	(0.065)**	(1.51)	(0.047)*
Dense DBPN23	29.59	0.879	25.36	0.730	20.74	0.395
	(1.80)	(0.065)	(1.55)	(0.061)	(1.48)	(0.046)
Dense DBPN with gradient guidance	30.93	0.916	26.63	0.763	20.81	0.421
	(1.79)*	(0.065)**	(1.48)*	(0.061)**	(1.45)	(0.048)

Fig. 2.

Comparison of (a) mean PSNR and (b) mean SSIM values achieved on the 2018 atrial segmentation challenge dataset by bicubic interpolation, EDSR model with and without gradient guidance, and dense DBPN model with and without gradient guidance for a downsampling scale factor of 2, 4, and 8, respectively.

Fig. 3.

Visual assessment of reconstructed super-resolution images from 2018 atrial segmentation challenge⁶ dataset. Row 1: high-resolution (HR) LGE cardiac MRI slice along $z$-axis and its cropped version (ground truth). Row 2: Low-resolution (LR) Gaussian downsampled image with downsampling scale factor 2 upsampled by bicubic interpolation, the super-resolution image from EDSR model, super-resolution image from EDSR model with gradient guidane (GG), the super-resolution image from dense DBPN model, and the super-resolution image from dense DBPN model with GG, respectively. Row 3: LR with downsampling scale factor 4 upsampled by the above-mentioned methods. Row 4: LR with downsampling scale factor 8 upsampled by the above-mentioned methods. The PSNR and SSIM evaluated between each super-resolved image and the original high-resolution grounds truth image is also labeled for interpretation vis-a-vis visual assessment.

3.2. Generalization Testing: Validation on LAScarQS Dataset

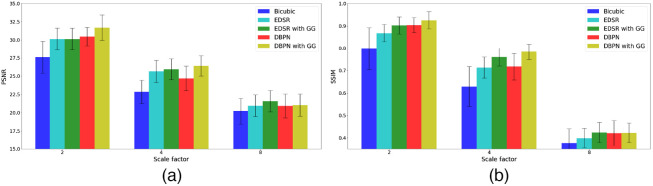
The generalization ability of our method is evaluated using the LAScarQS 2022 dataset^25–27 (Table 2). The CNN models trained on the 2018 atrial segmentation challenge⁶ were tested on this LAScarQS 2022 dataset.^25–27 Similar to the 2018 atrial segmentation challenge⁶ data, low-resolution images were simulated by a downsampling scale factor of 2, 4, and 8, respectively, in order to compute super-resolution LGE-MRI volumes. The super-resolution results on the LAScarQS 2022 dataset^25–27 (Fig. 4) dataset are analogous to the 2018 atrial segmentation challenge⁶ dataset, i.e., the CNN models outperform the bicubic interpolation results and the PSNR and SSIM achieved by the CNN models with gradient guidance are significantly higher than the the stand-alone CNN models. Also, similar to results obtained on 2018 atrial segmentation challenge⁶ dataset, the dense DBPN models with gradient guidance obtained significantly ($p<0.01$) better PSNR and SSIM values compared to the stand-alone EDSR model, which obtained the least PSNR and SSIM values. We also show an example of the improved through-plane resolution on the LAScarQS 2022 dataset^25–27 in Fig. 5.

Table 2.

Generalization evaluation on the LAScarQS 2022 dataset.

Methods	Scale factor: 2		Scale factor: 4		Scale factor: 8
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
Bicubicinterpolation	27.60	0.798	22.86	0.629	20.21	0.377
	(2.21)	(0.094)	(1.59)	(0.089)	(1.78)	(0.064)
EDSR24	30.13	0.868	25.65	0.713	20.94	0.399
	(1.51)	(0.039)	(1.50)	(0.047)	(1.49)	(0.044)
EDSR with gradient guidance	30.44	0.902	25.94	0.760	21.57	0.424
	(1.49)	(0.038)*	(1.42)	(0.040)**	(1.47)	(0.045)
Dense DBPN23	30.46	0.904	24.69	0.718	20.91	0.421
	(1.27)	(0.033)	(1.68)	(0.059)	(1.64)	(0.056)
Dense DBPN with gradient guidance	31.69	0.925	26.39	0.784	21.03	0.423
	(1.73)*	(0.038)*	(1.39)*	(0.034)**	(1.53)	(0.044)

Fig. 4.

Comparison of (a) mean PSNR and (b) mean SSIM values achieved on the generalization evaluation dataset for a downsampling scale factor of 2, 4, and 8, respectively.

Fig. 5.

Visual assessment of the reconstructed super-resolution images from the generalization dataset (LAScarQS 2022 dataset).

3.3. Effect of Super-Resolution on Downstream Segmentation Task

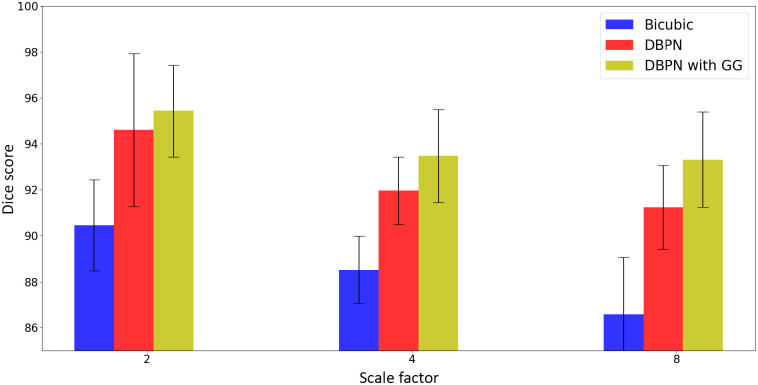
To show the effect of super-resolution on downstream segmentation task, we train 3D U-Net models to segment the LA from LGE-MRI images. Since the dense DBPN model has resulted in higher PSNR and SSIM values compared to the EDSR models, we train the U-Net models on the 2018 atrial segmentation challenge⁶ dataset by simulating low-resolution images and upsampling them by dense DBPN model with gradient guidance, and comparing them with the segmentation results obtained by training U-Net models on images generated using dense DBPN model without gradient guidance and bicubic interpolation. We summarize the segmentation performance on these upsampled images in Table 3 using Dice score. We can see that the segmentation results obtained by training the images upsampled using dense DBPN model with gradient guidance is significantly better than bicubic interpolation ($p<0.01$) and dense DBPN model without gradient guidance ($p<0.05$), for all the three downsampling scale factors (Fig. 6).

Table 3.

LA segmentation evaluation, mean (std-dev) Dice score (%) using the 2018 atrial segmentation challenge dataset. U-Net models are trained on LGE-MRI volumes downsampled by a scale factor of 2, 4, and 8, respectively, and upsampled using bicubic interpolation and dense DBPN model with and without gradient guidance. Statistically significant differences were evaluated between the dense DBPN model with and without gradient guidance using the Student’s $t$-test and are reported using by * $p<0.05$

Methods	Scale factor: 2	Scale factor: 4	Scale factor: 8
	Dice score	Dice score	Dice score
Bicubic interpolation	90.46 (1.98)	88.52 (1.47)	86.58 (2.49)
Dense DBPN23	94.60 (3.33)	91.96 (1.47)	91.24 (1.83)
Dense DBPN with gradient guidance	95.43(2.01)*	93.47(2.02)*	93.31(2.07)*

Fig. 6.

Dice score comparison of U-Net models are trained on LGE-MRI volumes downsampled by a scale factor of 2, 4, and 8, respectively, and upsampled using bicubic interpolation and dense DBPN model with and without gradient guidance.

3.4. Ablation Studies

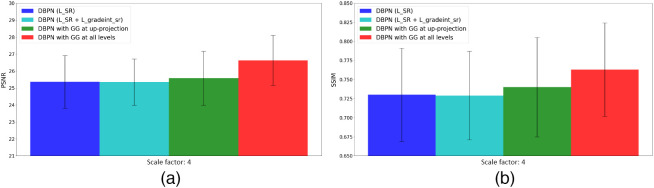
In Table 4, we show the results and the number of trainable parameters of the models we trained as part of the ablation studies we performed to understand the contributions of the various components of the loss functions and the network. These studies were performed using the dataset from 2018 atrial segmentation challenge⁶ and downsampling them by a factor of 4. We show the super-resolution results on the dense DBPN model with only ${\mathcal{L}}_{\mathrm{SR}}$ as a loss function and without gradient guidance, followed by the dense DBPN model with $\alpha .{\mathcal{L}}_{\mathrm{SR}}+\gamma .{\mathcal{L}}_{{\text{Gradient}}_{\mathrm{SR}}}$ as loss function and without gradient guidance, where ${\mathcal{L}}_{\mathrm{SR}}$ is the $L_1$ loss computed between the generated super-resolution images, $I^{\mathrm{SR}}$ and ground-truth high-resolution images, $I^{\mathrm{HR}}$, and ${\mathcal{L}}_{{\text{Gradient}}_{\mathrm{SR}}}$ denotes $L_1$ loss between $G(I^{\mathrm{SR}})$ and $G(I^{\mathrm{HR}})$, where $G(·)$ stands for the gradient map of the images. Next, we show the super-resolution results of the dense DBPN model with gradient guidance at only up-projection levels,²² followed by the dense DBPN model with gradient guidance at all the levels (ours). As evident in Fig. 7, the dense DBPN model with gradient guidance at all the levels (ours) yields the highest PSNR and SSIM values across all tested models.

Table 4.

Ablation study results: mean (std-dev) PSNR, SSIM, and number of trainable parameters (in millions) achieved on the 2018 atrial segmentation challenge⁶ test set for downsampling scale factor of 4. The best evaluation metrics achieved are labeled in bold. Statistically significant differences were evaluated between the dense DBPN model with only ${\mathcal{L}}_{\mathrm{SR}}$ loss and rest of the models using the Student’s $t$-test and are reported using * $p<0.05$.

Methods	Scale factor: 4
	PSNR	SSIM	Number of parameters
Dense DBPN ${\mathcal{L}}_{\mathrm{SR}}$	25.36	0.730	1.13
	(1.55)	(0.061)
Dense DBPN $\alpha .{\mathcal{L}}_{\mathrm{SR}}$ + $\gamma .{\mathcal{L}}_{{\text{Gradient}}_{\mathrm{SR}}}$	25.35	0.729	1.13
	(1.36)	(0.058)
Dense DBPN gradient guidance at up-projection	25.58	0.740	3.48
	(1.59)	(0.065)
Dense DBPN with gradient guidance at all levels (ours)	26.63	0.763	5.41
	(1.48)*	(0.061)*

Fig. 7.

Comparison of (a) mean PSNR and (b) mean SSIM values of the ablation study.

4. Discussion

In this paper, we presented a 3D CNN-based framework with gradient guidance for super-resolution of cardiac LGE-MRI data. There are four major contributions in this work. First, a 3D deep learning-based architecture with two branches, a super-resolution branch and a gradient branch, is presented, wherein the dense DBPN model is the backbone of the CNN architecture. Inspired by the effects of the gradient branch on 2D natural images’ super-resolution,³² we exploited the structural information learnt by the gradient branch to provide structural guidance to the super-resolution branch of our CNN, thus preserving the 3D cardiac structures in the LGE-MRI images. To the best of our knowledge, this is the first work that presents a 3D CNN-based method to improve the through-plane resolution of cardiac LGE-MRI data. Second, we established that the presented gradient guidance method could improve the through-plane resolution of LGE-MRI data using other CNN models, such as the EDSR model, as the backbone of the proposed deep learning framework. Third, we demonstrated the generalization ability of the proposed method by testing it on the LAScarQS 2022 dataset^25–27 that was not used while training our models. Fourth, we investigated and showed the effect of the proposed super-resolution framework on the downstream segmentation task by training a vanilla U-Net model to segment the LA from the super-resolved LGE-MRI volumes.

In our first experiment (Table 1), we compared the results of bicubic interpolation method and the CNN models, with and without gradient guidance on the 2018 atrial segmentation challenge⁶ dataset. We can observe that the results of the CNN models with gradient guidance are significantly better than their stand-alone counterparts for all the three downsampling scale factors, wherein the dense DBPN model with gradient guidance provides the best super-resolution results. This is more obvious in the SSIM comparison, as it is a combination of three comparison measures: luminance, contrast and structure,³³ and as mentioned earlier, the gradient branch provides structural guidance to the proposed CNN framework.

In our second experiment (Table 2), we evaluated the above-mentioned models on the LAScarQS 2022 dataset^25–27 to assess their generalization ability. We can observe that the results are similar to the results achieved on the 2018 atrial segmentation challenge⁶ datasets, where CNN models with gradient guidance outperform their stand-alone counterparts, thus, generalizing well. It can be observed that the PSNR and SSIM values of the models when evaluated on the LAScarQS 2022 dataset^25–27 are higher than those achieved when the models were evaluated on the 2018 atrial segmentation challenge⁶ dataset. This could be attributed to the fact that the 2018 atrial segmentation challenge⁶ dataset features a high isotropic spatial resolution of $0.625\times 0.625\times 0.625{\mathrm{mm}}^3$, whereas the LAScarQS 2022 dataset^25–27 feature a relatively low high isotropic spatial resolution of $1.4\times 1.4\times 1.4{\mathrm{mm}}^3$. In Figs. 3 and 5, we show an example of an image slice along the z-axis from both 2018 atrial segmentation challenge⁶ and LAScarQS 2022 dataset,^25–27 respectively. The super-resolution images generated using the CNN models with gradient guidance show improved through-plane resolution; the reconstructed images feature less blurring and look sharper than the images upsampled using bicubic interpolation and CNN models without gradient guidance. In both figures, this observation is most obvious for the super-resolution images generated from the low-resolution images downsampled by a scale factor of 4.

In our final experiment (Table 3), we investigated the effect of the super-resolution models on the downstream segmentation task by training 3D U-Net models to segment LA from the super-resolved LGE-MRI volumes. Since the dense DBPN models performed better than the EDSR models in improving the through-plane resolution of LGE-MRI volumes, we used the super-resolved images obtained using dense DBPN models with and without gradient guidance to train the U-Net models and compared them. To serve as baseline comparison, we also train the U-Net models using the images obtained using bicubic interpolation. We can observe that the Dice score of the LA segmentation computed by training super-resolved images obtained from the dense DBPN models with gradient guidance is significantly higher than the Dice score computed by training super-resolved images obtained from the stand-alone dense DBPN models and bicubic interpolation methods, for all the three downsampling scale factors, thus, corroborating our hypothesis that providing structural guidance using the gradient branch to improve the through-plane resolution of LGE-MRI volumes could improve the segmentation of cardiac structures.

One of the limitations of our work, as shown in Tables 1 and 2, is that the PSNR and SSIM values of the super-resolved LGE-MRI volumes decrease as the downsampling scale factor increases. This is due to the loss of information due to downsampling; however, there is a considerable improvement in the Dice score associated with the segmentation of the LA from the super-resolved images, therefore speaking for the benefit and significance of the super-resolved images as far as improving feature segmentation and biomarker quantification. Another major limitation of this work is the use of simulated low through-plane resolution images due to the lack of real-world high-resolution and low-resolution image pair datasets. Therefore, we could not comprehensively assess our method on real-world low-resolution images. However, we employed two downsampling methods: Gaussian and Fourier downsampling methods, and demonstrated the effectiveness of our method to reliably super-resolve the simulated low-resolution images.

5. Conclusion

In this work, we presented a 3D CNN architecture for image super-resolution and demonstrated that the proposed method can be used to improve the through-plane resolution of LGE-MRI volumes, which in turn, enables accurate segmentation of the cardiac chambers. We also demonstrated the generalization ability of our proposed approach. Our approach takes advantage of the information learnt from the gradient branch to provide structural guidance to the super-resolution branch; thereby, generating super-resolution 3D LGE-MRI images while preserving the cardiac structure information.

Our results clearly show the improved PSNR and SSIM achieved via the dense DBPN with gradient guidance (Table 1 and Fig. 2), the improved PSNR and SSIM upon generalization (Table 2 and Fig. 4), as well as improved performance of the LA segmentation from the super-resolved images (Table 3 and Fig. 6).

In addition, the ablation study conducted clearly showed the effect of the various losses (${\mathcal{L}}_{\mathrm{SR}}$, ${\mathcal{L}}_{\text{Gradient}}$, and ${\mathcal{L}}_{{\text{Gradient}}_{\mathrm{SR}}}$) as additions to the dense DBPN model, as well as the effect of the gradient guidance not only at the up-projection level, but at all levels, on the quality of the super-resolved images and the performance of the downstream segmentation task. As shown, each of these components provide an improvement in both the PSNR and SSIM values, with the most significant improvement being contributed by the dense DBPN with gradient guidance at all levels (Table 4 and Fig. 7).

Biographies

Roshan Reddy Upendra received his BS and MS degrees in biomedical engineering from Ramaiah Institute of Technology, India and Drexel University, United States, respectively. Currently, he is a PhD candidate at Chester F. Carlson Center for Imaging Science, Rochester Institute of Technology. His research interests include machine learning and deep learning for medical applications.

Biographies of the other authors are not available.

Disclosures

No conflicts of interest, financial or otherwise, are declared by the authors.