Interrelated effects of chromosome size, mechanics, number, location-orientation and polar ejection force on the spindle accuracy: a 3D computational study

Abstract

The search-and-capture model of spindle assembly has been a guiding principle for understanding prometaphase for decades. The computational model presented allows one to address two questions: how rapidly the microtubule–kinetochore connections are made, and how accurate these connections are. In most previous numerical simulations, the model geometry was drastically simplified. Using the CellDynaMo computational platform, we previously introduced a geometrically and mechanically realistic 3D model of the prometaphase mitotic spindle, and used it to evaluate thermal noise and microtubule kinetics effects on the capture of a single chromosome. Here, we systematically investigate how geometry and mechanics affect a spindle assembly’s speed and accuracy, including nuanced distinctions between merotelic, mero-amphitelic, and mero-syntelic chromosomes. We find that softening of the centromere spring improves accuracy for short chromosome arms, but accuracy disappears for long chromosome arms. Initial proximity of chromosomes to one spindle pole makes assembly accuracy worse, while initial chromosome orientation matters less. Chromokinesins, added onto flexible chromosome arms, allow modeling of the polar ejection force, improving a spindle assembly’s accuracy for a single chromosome. However, spindle space crowding by multiple chromosomes worsens assembly accuracy. Our simulations suggest that the complex microtubule network of the early spindle is key to rapid and accurate assembly.

INTRODUCTION

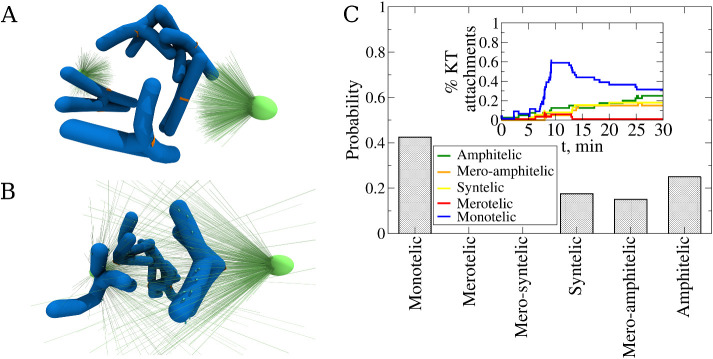
Before the most dramatic mitotic event—segregation of chromosomes (CHs) in anaphase, the CHs must be integrated into a mitotic spindle during prometaphase (Heald and Khodjakov, 2015). In a proper segregation event, sister kinetochores (KTs) on sister chromatids are attached to microtubules (MTs) amphitelically (O’Connell and Khodjakov, 2007), so that a set of MTs extending from one centrosome (spindle pole) connects with their plus ends to one KT, while another set of MTs from the opposite pole connects to the sister KT (Figure 1E). Several other types of erroneous attachments, most notably monotelic, syntelic, and merotelic (Figure 1E), present problems of various degrees of severity (Cimini and Degrassi, 2005) causing missegregation of the CHs, developmental defects, and diseases (Cimini, 2008; Silk et al., 2013). For example, monotelic attachment, in which one KT is connected to one pole, while its sister KT is unconnected (Figure 1E), would not lead the unconnected chromatid to the second pole. In a syntelic attachment, both sister KTs are connected to the same pole and are unconnected to the other pole (Figure 1E); as a result, in anaphase both sister chromatids could move to one pole (Figure 1E). Merotelic attachment, in which at least one KT is bound to MTs from both poles, could leave the respective chromatid in the middle of the spindle.

FIGURE 1:

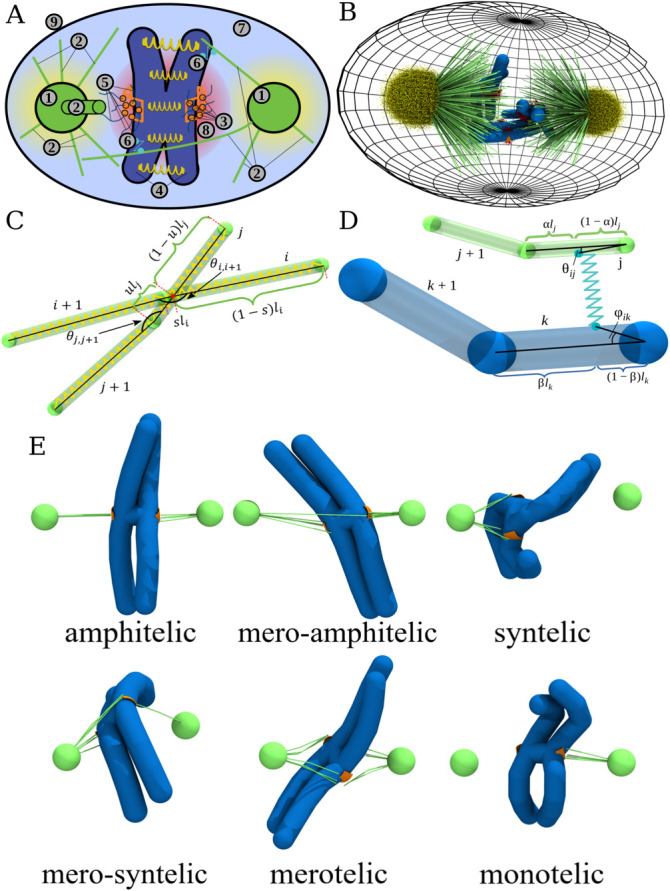
Components of the stochastic reaction-diffusion-dynamics model implemented in the CellDynaMo package: (A) Schematic of the model. 1) Centrosomes (green); 2) MTs (green); 3) KTs (orange) on which the Ndc80 complexes are bound to MTs with their KT-associated domains are labeled (orange beads); 4) chromosomes (CHs); 5) Ndc80 KT–MT links; 6) chromokinesin (CK) modeled as two harmonically coupled beads with one bead connected to a CH arm and the other bead connected to a MT; 7) blue space is phosphatase (enzyme dephosphorylating Ndc80), which is uniformly distributed in the cell interior; 8) Aurora B kinase (enzyme phosphorylating Ndc80) described by the spherical gradient of its concentration with the central maximum in the space between the KTs (red cloud); and 9) cell boundary (black) is modeled as a repulsive potential for all cell components. Components 1–6 and 9 are described using the Langevin dynamics in the overdamped (Brownian diffusion) limit (see Supplemental Eqs. S14–S17; see also Table 1 and Supplemental Table S2); components 5–8 are modeled using the reaction-diffusion master equation (see Supplemental Eq. S1; see also Supplemental Tables S1 and S2). (B) Snapshot in 3D from the CellDynaMo-based simulation that shows all the components. (C) More detailed representation of cylindrical potential (for cylindrical segments of MTs or CH arms) including stretching, bending, and excluded volume interactions between cylinders. Each beginning and end of the cylinder are connected by harmonic springs (shown in yellow). Transparent areas show the excluded volume of each structure. At the intersection point of these volumes, each cylinder is divided into two parts, parametrized by u ∈ [0, 1] and s ∈ [0, 1] (see Supplemental Eq. S2). (D) More detailed MT–CH interaction interface. A cylinder-based scheme is used in the CellDynaMo force field to model MTs and CH arms. Transparent areas show the excluded volume of each structure. CK is represented as a harmonic potential between two beads on the surfaces of bound cylinders (see Supplemental Eq. S8). Positions of the beads are determined by stochastic chemical reactions and force-velocity relationship (see SM). (E) Types of KT–MT attachments are illustrated by examples coming from snapshots taken from the simulations.

In healthy cells, a missegregating CH is extremely rare—approximately one CH in hundreds of dividing cells, or about 1 out of 10,000 CHs, is missegregated (Santaguida and Amon, 2015). In cancer cell lines and perturbed cells, where the frequency of erroneous connections is much higher than in cells from healthy tissue, tens of percent of attachments are syntelic and merotelic, transiently (Cimini et al., 2003; Silkworth et al., 2012). However, most of the misattachments are successfully corrected in the cells before anaphase (Cimini et al., 2003, 2006). The attachment error-correction mechanisms are not completely understood, and in this study, we discuss three of them (Gregan et al., 2011; Lampson and Grishchuk, 2017).

The first such mechanism, geometric in nature, prevents the errors rather than corrects those already made: when a monotelic connection is made, a pull toward the pole from which the connection is made rotates the CH so that the unconnected sister KT is fully or partially shielded from this pole by the body of the centromere, making a syntelic connection less likely (Ostergren, 1951; Gregan et al., 2011; Lampson and Grishchuk, 2017). Similarly, the connected KT is now partially obscured from another pole, making a merotelic connection less probable. Note that monotelic connections are not errors per se; they just indicate that the spindle assembly is incomplete, and the quantitative question is how much additional time is needed to connect the unattached sister KTs to their proper poles.

The second mechanism is related to correction of syntelic errors. Classical experiments by Bruce Nicklas provided direct experimental evidence that KT–MT attachments are stabilized through tension developed across the centromere (Nicklas and Koch, 1969; Nicklas and Ward, 1994; Nicklas, 1997). This suggests the following mechanism of error control (Maresca and Salmon, 2009; Lampson and Cheeseman, 2011; Cane et al., 2013; Krenn and Musacchio, 2015): in amphitelic CH attachments, sister KTs are pulled apart, toward the opposite poles, by molecular motors on the MT plus ends. In contrast, with a syntelic CH attachment, both sister KTs are pulled in the same direction, toward the same spindle pole, and so there is no stretching between the sister KTs. If there is a way to make MT stability sensitive to the inter-KT stretch, so that the greater the inter-KT stretch, the longer the KT–MT connection’s lifetime, then in syntelic attachment, MTs will keep detaching from the KTs, until the correct amphitelic attachment emerges (Liu et al., 2009). Indeed, multiple experimental studies demonstrated that at early stages of assembly, the number of syntelic attachments is large, and then later diminishes to a smaller number close to zero (Cimini et al., 2003; Silkworth et al., 2012). The hypothesized pathway that is likely behind such mechanism is as follows: if Aurora B kinase molecules are tethered to KTs by flexible linkers, their diffusion is limited to a “cloud” around the centromere, like in our model (Figure 1, A and B). Then, stretching between the sister KTs places the KTs outside the Aurora B “cloud.” Aurora B phosphorylates long elastic Ndc80 molecular linker regions between the KT and MTs, and as a result of the pull, the Ndc80’s phosphorylation level decreases, and the KT–MT attachments become more stable. If, on the other hand, both KTs are kept closer to the center of the Aurora B cloud, as in syntelic attachment, then increasing the phosphorylation level of Ndc80 complexes decreases the attachment stability. This mechanism, which we will call syntelic correction mechanism for brevity, implies that a soft centromeric spring allowing significant centromere deformation and fast MT turnover would benefit the repair of syntelic errors. One of our goals is to test whether this is, indeed, true. Cells typically delay anaphase in the presence of syntelic attachments, likely allowing sufficient time for the syntelic correction mechanism to work. However, prometaphase in animal cells is relatively fast, from minutes to tens of minutes (Wollman et al., 2005; Magidson et al., 2011), and so the question is whether this time is sufficient to repair all syntelic connections.

Merotelic attachments are more dangerous because anaphase can start before correcting them (Cimini, 2008), and the syntelic correction mechanism probably does not work to fix them because merotelic MTs do not necessarily negate the centromere stretch. Indeed, existing data suggest that the number of merotelic attachments is small, but increases with time during prometaphase (Cimini et al., 2003; Silkworth et al., 2012). One of the hypothesized merotelic error-correction pathways is the “brute-force” mechanism: if the number of merotelic MTs is much smaller than that of amphitelic MTs, then the “wrong” connections could simply be stretched across the spindle (Cimini et al., 2003, 2004) or broken mechanically (Gregan et al., 2011; Gay et al., 2012) in anaphase. Then, the important quantitative question is: what is the expected relative number of merotelic MTs?

The search-and-capture model has been a guiding principle for understanding the speed and accuracy of the spindle assembly for decades (Heald and Khodjakov, 2015). According to this model, dynamically unstable MTs grow from the spindle poles, shorten and regrow in random directions, connecting to the KTs by chance (Hill, 1985; Kirschner and Mitchison, 1986; Rieder and Alexander, 1990). In early computational versions of the search-and-capture model, MT attachments to KTs were considered permanent, allowing crude estimates of the speed of the assembly process (Holy and Leibler, 1994; Wollman et al., 2005; Paul et al., 2009; Gopalakrishnan and Govindan, 2011). One of the results of these models was that rapid KT captures are not easily achieved, largely because multiple CHs arms block MT access to many KTs geometrically. Another result was a large number of predicted merotelic connections (Paul et al., 2009). Indeed, if all attachments are permanent, then if one waits long enough, many KTs will capture MTs from both poles.

Several years ago, Zaytsev and Grishchuk simulated a single CH and two dynamic MT asters emanating from two spindle poles in 2D, and demonstrated that without geometric error prevention, MT turnover improves the spindle assembly accuracy very little (Zaytsev and Grishchuk, 2015). With geometric error prevention and rapid MT turnover (independent of the centromere stretch in their model), the number of errors can be decreased to a few tens of percent, but the assembly takes a long time. Another notable model in a simplified 3D geometry predicted that a combination of stabilization of KT–MT attachment by centromere stretching, destabilization of misaligned attachments, and hypothetical restriction of a new attachment to an already attached KT to perpendicular MTs only, leads to a very accurate spindle (Edelmaier et al., 2020). Several other recent models addressed these and other aspects of the spindle assembly accuracy (Saka et al., 2015; Tubman et al., 2017; Baudoin et al., 2020; Li et al., 2022).

In our previous study (Kliuchnikov et al., 2022), we revisited the search-and-capture paradigm using the stochastic reaction-diffusion-dynamics model (SRDDM) in conjunction with the CellDynaMo computational platform. The SRDDM accounts for 1) molecularly explicit KT–MT connections; 2) kinetics of KT–MT interactions mediated by multiple phosphorylation states of the Ndc80 linkers; 3) diffusing and reacting Aurora B kinase and phosphatase enzymes; and 4) elastic CH arms, MTs, and centromeres. For a single CH, we confirmed earlier results, namely, that there is an optimal rate of MT turnover. We also established that large CH arms slow down CH movements, which has a positive effect on the accuracy, and we found that thermal noise has a complex effect on the accuracy.

In the present study, we made further progress in the SRDDM development and we extended the CellDynaMo computational platform, described briefly in Materials and Methods and in more detail in the Supplemental Material (SM). These efforts enabled us 1) to systematically explore geometric and mechanical factors affecting accuracy, 2) to consider integration of multiple CHs into the spindle, and 3) to include actions of chromokinesins and polar ejection force (Brouhard and Hunt, 2005; Ye et al., 2016; Almeida and Maiato, 2018). We found that the polar ejection force improves the accuracy by moving the CHs toward the spindle equator, that CH arms limit the effectiveness of the syntelic correction mechanism, and that crowding of cellular space is the greatest impediment to the spindle assembly. We also found that truly merotelic attachments are predicted to be very rare, which is good news, meaning the reduced CH missegregation rate.

RESULTS

Classification of the KT–MT connections and geometry of CH positioning

It is useful to make the classification of the KT–MT connections more nuanced, differentiating merotelic connections into 1) mero-amphitelic, 2) mero-syntelic, and 3) simply merotelic (Figure 1E; Gregan et al., 2011). This classification is based upon the fact that multiple MTs connect a spindle pole with a KT. First, let us define quantities L1 and L2 to be the numbers of MTs connecting the left pole (pole 1) and one of the KTs, that is, KT 1 and KT 2, respectively. Similarly, R1 and R2 are the numbers of MTs growing from the right pole connected to KT 1 and KT 2, respectively. Then, if the total number of MTs connected to KTs is A1 = L1 + R2 and the total number of MTs connected to KTs is A2 = L2 + R1, then these are two possible types of amphitelic attachments. If there are several MTs connecting a KT to pole 1, and only one MT connecting this KT to pole 2, while the sister KT is only connected to pole 2, then this connection is “almost” amphitelic (we call it mero-amphitelic, if A1/A2 < 0.25 or A1/A2 > 4). In this case, the majority of MTs stretch the respective centromere, stabilizing the connections, while the single erroneous MT could be broken by overwhelming force from the majority of MTs in later stages of mitosis (Cimini et al., 2003, 2004; Gregan et al., 2011; Gay et al., 2012). Similarly, if several MTs connect one KT to pole 1, several MTs connect the other KT also to pole 1, and very few MTs connect one of the KTs to pole 2, then this connection is “almost” syntelic (we call it mero-syntelic, if (L1 + L2)/(R1 + R2) < 0.25 or (L1 + L2)/(R1 + R2) > 4); in this case, the stretch between the sister KTs would be minimal, leading to repair by respective mechanisms. The only truly dangerous connections are purely merotelic if at least one of the sister KTs is connected to both poles, and none of the four inequalities above are satisfied.

In all computational case studies reported in this work, we simulate the assembly dynamics for 30 min of biological time, which is one of the longest times measured for prometaphase in animal cells (Wollman et al., 2005). We start with a single CH and investigate how the speed and accuracy of spindle assembly depends on the initial CH position between the poles and orientation. To this end, we test a total of five initial conditions (CH positions and orientations) depicted in Figure 2, A–E. The first three of these initial configurations share the same position at the equatorial plate, shifted by 1.5 µm away from the spindle (pole–pole) axis. The difference between these initial conditions is the initial orientation of the centromere: configuration 1 (Figure 2A) is beneficial for the formation of amphitelic attachments, with the centromere (KT–KT) axis parallel to the spindle axis, and sister KTs facing the opposite poles. Configurations 2 and 3 are more “difficult” for proper connections, with the centromere axis being initially perpendicular to the axis of the spindle. In initial configuration 2, one KT is proximal to the spindle axis and is “visible” equally from both poles, while another KT is shielded from both poles by the centromere body (Figure 2B), which suggests the possibility of formation of more merotelic connections. In initial configuration 3, both KTs are equidistant from the spindle axis and are “visible” equally from both poles (Figure 2C), which suggests the possibility of both merotelic and syntelic connections. In the other two initial configurations 4 and 5, we test how initial asymmetry of chromosome positioning affects the accuracy and the effect of shifting the CH closer to one of the poles (Figure 2, D and E). Here, we try two different initial orientations; in both orientations, however, the centromere axis is perpendicular to the vector connecting the proximal pole to the centromere center. In configuration 4 (Figure 2D), KT 1 is more accessible from the proximal pole, but KT 2 has maximum access to MTs from the distal pole, while KT 1 is almost hidden from the distal pole. In configuration 5 (Figure 2E), both KTs are equally accessible from the proximal pole, and both KTs have equal access to MTs from the distal pole.

FIGURE 2:

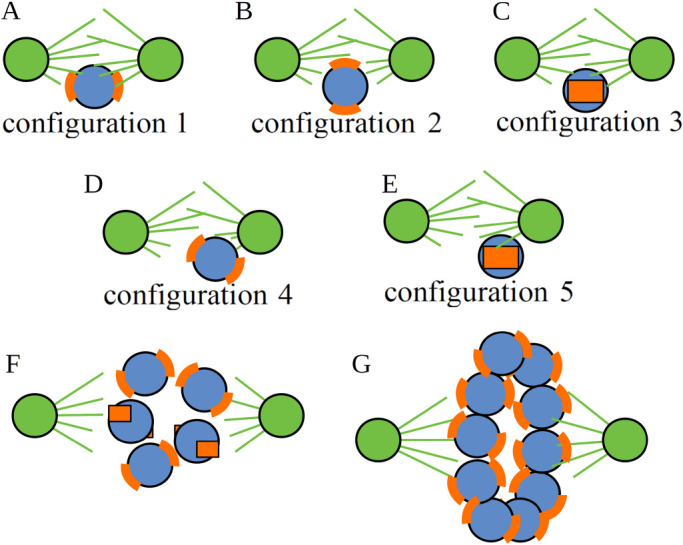
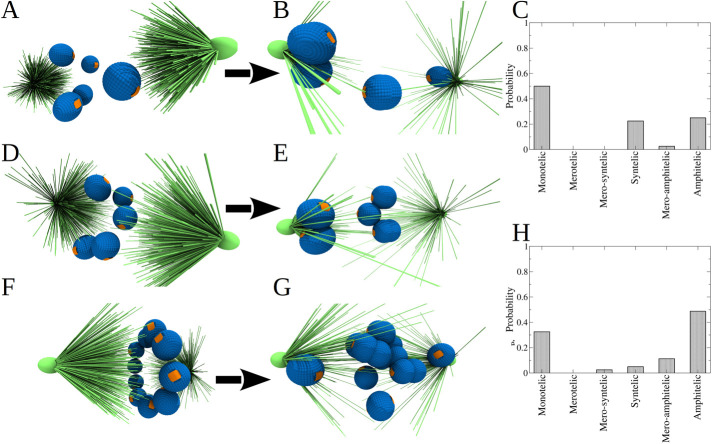
Initial cellular positions and orientations of chromosomes used in model simulations. Initial CH position/orientation configurations used in simulations: configuration 1 (A), configuration 2 (B), configuration 3 (C), configuration 4 (D), configuration 5 (E), configuration with multiple CHs placed and oriented randomly (F), and configuration with multiple CHs on a ring in the equatorial plate oriented randomly (G). Orange curved segments show the KT locations. Centrosomes and radiating MTs are indicated in green.

Next, we test simultaneous incorporation into the spindle of multiple CHs (Figure 2, F and G). We limit ourselves to simulating a cell with a small number of CHs, say five CHs, like cells of the Indian muntjac, which has just six CHs (Drpic et al., 2018). In one of these tests, the initial positioning and orientations of the CHs are random, but CHs are confined to an imaginary sphere with the poles at two opposite ends of the sphere’s diameter (Figure 2F). In another test, following recent findings (Magidson et al., 2011) that in early prometaphase the CHs are located along the equator of the spindle space (imagining that roughly spherical spindle space has “North” and “South” poles where the two centrosomes reside), the CHs are positioned with centromere axes of the CHs oriented in random directions (Figure 2G). These different scenarios of single and multiple CHs to be in different positions and orientations are used in subsequent sections to address the importance of specific factors in spindle assembly accuracy.

Softening of the centromere spring improves spindle assembly’s accuracy when CH arms are short, but the effect disappears for long CH arms

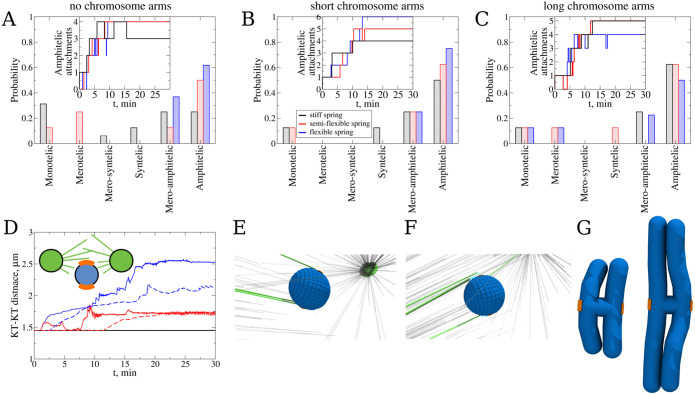
To test how centromere deformability affects the connection accuracy, we tested initial configuration 2 (Figure 2B), which is the most susceptible to forming merotelic KT–MT attachments, making it hard for the CH to achieve the correct amphitelic attachment state. We started with a “naked” CH without CH arms, which is basically a roughly spherical centromere volume with two KTs located on the opposite sides of the volume. Figure 3 (panels E and F) shows examples of erroneous syntelic and mero-syntelic connections, respectively. We carried out eight independent simulation runs for each of three values of the centromere spring constant, K_KT,r = 0.83 pN/nm (soft deformable spring), K_KT,r = 83 pN/nm (semiflexible spring), and K_KT,r = 333 pN/nm (stiff spring; see Table 2 and Supplemental Eq. S5). The statistics of attachment types shown in Figure 3A indeed illustrates that the softer the spring, the more accurate are the statistics of the attachments: for the soft spring (K_KT,r = 0.83 pN/nm), 62.5% attachments are amphitelic, with the rest being mero-amphitelic, possibly amenable to subsequent correction by brute-force pulling. The stiffer the spring, the lower the number of amphitelic attachments, and for stiffer springs, merotelic, syntelic, and monotelic attachments remain after 30 min of biological time (see Table 2). This indicates that the syntelic correction mechanism works. For the statistics of attachments, here and below, we counted an attachment as monotelic even when the CHs do not have any attachments.

FIGURE 3:

Probing the effect of the syntelic correction mechanism: (A) Probability to find each type of KT–MT attachments for the system with flexible centromere spring (data shown in blue color) between the sister KTs without chromosome arms, with stiff spring (in black color), and with semiflexible spring (in red color). Probabilities of attachments were determined from attachments collected from eight independent CellDynaMo simulations for all three case studies. The total number of amphitelic attachments over time collected from all eight simulations for all three case studies are shown in the inset. (B) The same as panel A, but for CHs with short CH arms. (C) The same as panel A, but for CHs with long CH arms. (D) Separation distance between the sister KTs as a function of time for the most representative simulation run for the systems with flexible (blue), semiflexible (red), and stiff centromere spring (black). Solid lines show the time series for the case with KTs without CH arms, and dashed lines show the time series for the case with CH arms. (E) Example of syntelic attachment. (F) Example of mero-syntelic attachment. Centrosomes are shown as green beads, the blue corrugated ball is the centromere, KTs are shown in orange, unconnected MTs are displayed in gray, connected MTs are shown in green, and cyan links are Ndc80 complexes. (G) Comparison of CHs with short and long CH arms.

TABLE 2:

Parameters varied in stochastic reaction-diffusion-dynamics model: numerical values of SRDDM parameters, which were varied and the simulation output.

Figure	Case study	Varied model parameters
		Parameter	Value	Findings
3	No chromosome arms	K KT,r	0.83 pN/nm	62.5% amphitelic, 0% merotelic
			83.0 pN/nm	50% amphitelic, 25% merotelic
			333.0 pN/nm	25% amphitelic, 0% merotelic
	Short chromosome arms (5 μm)	K KT,r	0.83 pN/nm	75% amphitelic, 0% merotelic
			83.0 pN/nm	62.5% amphitelic, 0% merotelic
			333.0 pN/nm	50% amphitelic, 0% merotelic
	Long chromosome arms (8 μm)	K KT,r	0.83 pN/nm	50% amphitelic, 12.5% merotelic
			83.0 pN/nm	62.5% amphitelic,12.5% merotelic
			333.0 pN/nm	62.5% amphitelic, 0% merotelic
4	Kinetochore surface area	A KT	0.03 μm2	0% amphitelic, 25% merotelic
			0.15 µm2	62.5% amphitelic, 0% merotelic
			0.36 μm2	25% amphitelic, 12.5% merotelic

Next, we repeated the simulations for CHs with short (5 μm in length) CH arms (Figure 3G), and found that the difference in the attachment accuracy between the cases with different centromere stiffness remains, with K_KT,r = 0.83 pN/nm being best, but then diminishes due to the increased number of amphitelic attachments for the cases of semiflexible and stiff springs (Figure 3B and Table 2). The explanation for the improved accuracy is based on consideration of the increased viscous drag of the CH arms: the source of many errors is that the very first attachment pulls (when the attached MT starts shortening, it maintains the connection to the KT and pulls the CH) the CH toward one of the poles, which makes connections from the other pole harder to establish. Analysis of the simulations confirms that bulkier CHs with arms move away from the spindle equator slower, allowing for a longer, more symmetric access of CHs to MTs from both poles (unpublished data).

Interestingly, when we repeated the simulations for CHs with long (8 μm in length) CH arms (Figure 3G), we found that the difference in the attachment accuracy between the cases with different centromere stiffness has disappeared entirely (Figure 3C and Table 2). The reason is that the CH arms’ drag is now so great that it damps the centromeric region movements enough to minimize its deformations. Figure 3D indeed illustrates that the KT–KT stretch of the soft centromere is sufficiently diminished when the CH arms are large. In fact, the softest centromere spring makes the number of amphitelic attachments slightly lower than for stiffer springs, probably because the softest spring allows for greatest displacements of the KTs from the equator without the benefit of the error correction, which requires greater centromere stretching. To conclude, the syntelic correction mechanism works for shorter CH arms, but not for long CH arms, because the arms’ bulk prevents sufficient centromere stretching. However, longer CH arms keep the CHs near the equator, thereby improving the attachment accuracy.

There is an optimal KT size

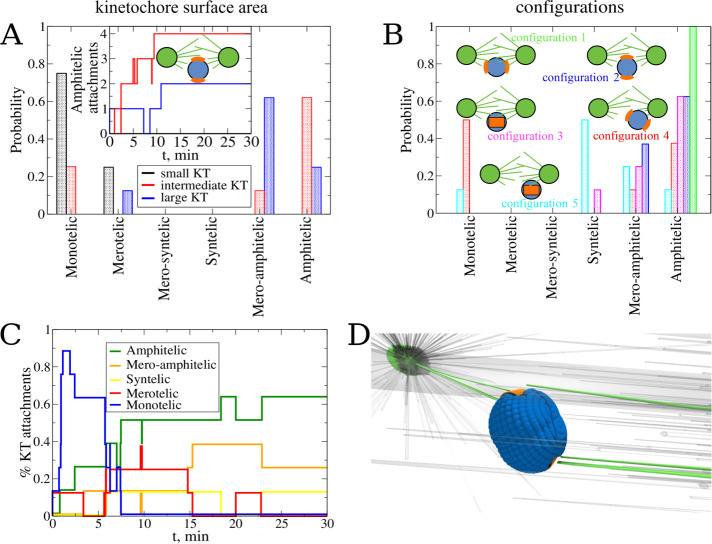
Several computational studies that used simpler geometries and less detailed models suggested that the assembly speed and accuracy impose conflicting requirements on the KT size: a small KT presents a small target for the searching MTs and requires a longer time to capture, but a large KT can be more easily captured from the opposite poles, thereby creating errors. To confirm that there is an optimal KT size for the spindle assembly, we simulated a “naked” CH in initial configuration 2 (Figure 2B), with the soft centromere spring constant (K_KT,r = 0.83 pN/nm). We varied the surface area of the curved KT from A_KT = 0.03 μm² (small KT) to A_KT = 0.15 μm² (intermediate KT), and to A_KT = 0.36 μm² (large KT). The statistics of KT–MT attachments shown in Figure 4A confirms the intuition: in the large KT case, just 25% of all attachments are amphitelic, while the majority of the attachments are mero-amphitelic. An example of merotelic connections made in this case is shown in Figure 4D (see Table 2).

FIGURE 4:

Exploring the effect of the kinetochore size and initial configuration of the chromosome. Panels A and B show the effect of the KT surface area on the attachment accuracy. (A) Probability to find each type of attachment for the system with large (blue), intermediate (red), and small (black) KT surface area. Statistics of attachments were collected from eight independent CellDynaMo simulations for all three case studies. The number of amphitelic attachments as a function of time collected from all eight simulation runs for all three case studies are shown in the inset. (B) Probability to find each type of attachment for the system with a single KT pair without CH arms. Different colors represent different initial positions and orientations (see Figure 2, A–E): configuration 1 is green, 2 is blue, 3 is magenta, 4 is red, and 5 is cyan. Statistics were collected from eight independent simulations for all initial configurations 1–5. (C) The normalized number of attachments of different types as a function of time collected from all eight simulation runs for initial configuration 3. (D) Snapshot of a final position and orientation for the largest KT surface (merotelic attachment).

KTs with the smallest surface area A_KT = 0.03 μm² did not result in a single amphitelic attachment; most attachments were monotelic. Inspection of the simulations shows that it is so difficult to capture such a small KT, so that a rare single attachment would lead to eventual pulling of the CH toward the pole from which the capture is made. During the time of the pull, the probability to capture the sister KT is too small, and after the CH is pulled to one of the poles, this probability is even smaller, due to the increased distance to the other pole with the decreased solid angle subtended by the KT array for MT searching and capture. The intermediate KT area (A_KT = 0.15 μm²) resulted in 62.5% amphitelic attachments, suggesting that this value is close to the optimal KT size, resulting in a compromise between the speed and accuracy of attachment. In all simulations described below (including the simulations described in the previous section), we used this optimal intermediate KT surface area of A_KT = 0.15 μm² (see Table 2).

Initial proximity to one spindle pole makes the accuracy of the spindle assembly worse

Another geometric factor affecting attachment accuracy is the initial position and orientation of the CH with respect to the spindle poles. To evaluate this factor, we carried out eight independent simulation runs for each initial configuration 1–5 (Figure 2, A–E). The statistics of resulting attachments summarized in Figure 4B confirm intuitive expectations. First, there are 100% amphitelic attachments for initial configuration 1 (Figure 2A), in which sister KTs face the opposite poles, are equally close to them, and are shielded by the centromere body from the other pole they are not facing. In the same initial position, changing the initial orientation of the centromere worsens the attachment accuracy, but not dramatically so. Starting from initial configurations 2 and 3 (Figure 2, B and C), about 60% of amphitelic connections emerge, with almost all the rest being mero-amphitelic attachments that could be corrected later by the brute-force mechanism. The only exception is the very small percentage of syntelic attachments emerging from the initial configuration 3 (Figure 2C), which is not unexpected because such an initial orientation has both sister KTs equally accessible from the same pole. As expected, many monotelic connections are made rapidly, within the first few minutes, and then as rapidly the number of such connections decreases (Figure 4C). We see that the numbers of syntelic, amphitelic, and mero-amphitelic attachments roughly increase in the first 10 min and then stabilize (Figure 4C).

Initially placing the CH close to one of the poles makes the attachment accuracy significantly worse, as initial configurations 4 and 5 (Figure 2, D and E) demonstrate. Many syntelic connections arise from initial configuration 5, as expected, because both KTs are equally accessible from the proximal pole, while being too far from the distal pole. No syntelic and many monotelic connections emerge from initial configuration 4. Inspection of the simulations indicates the reason, which is that one of the KTs now has large access from the proximal pole, while its sister KT is too far from the distal pole. This secures many attachments to the former KT locking the CH in the monotelic orientation. The overall conclusion from this study is that initial asymmetry of the CH positioning poses a great challenge for the accuracy of attachment, while the initial CH orientation matters less.

Crowding of the spindle space by multiple CHs makes the spindle assembly accuracy worse

Now that we have understood how a single CH is incorporated into the spindle, we next turned to describing multiple CHs undergoing interactions with MTs simultaneously, but still for the case of naked CHs without arms. To this end, we performed 10 independent simulations for the system with five CHs, initially randomly placed and randomly oriented within the sphere of 2.5-μm radius (Figure 5, A and D). Final spindle configurations are shown in Figure 5, B and E, and the statistics of attachments are shown in Figure 5C. We see that after 30 min of biological time, only 25% of attachments are amphitelic, with an almost equal percentage of syntelic attachments and 50% monotelic attachments. Inspection of the simulations shows that some of the CHs that are initially close to one of the poles become monotelic, as our previous case study showed; then, these CHs block many MTs from accessing the equatorial region of the spindle, thereby hindering the formation of amphitelic attachments. Some of the CHs that are very close to one of the poles, expectedly, form syntelic attachments.

FIGURE 5:

Assembly accuracy for the case of multiple “naked” CHs. (A, D) Initial frames of two examples of the system with 5 KT pairs randomly distributed and oriented. (B, E) Final frames (30 min of cell dynamics) of the systems shown in panels A and D, respectively. (C) Probability to find each type of KT–MT attachments for the system with 5 KT pairs randomly distributed. Statistics of attachments were collected from 10 independent CellDynaMo simulation runs. Snapshot for the initial configuration, where four out of five KT pairs have access to MTs from both CSs. (F) Snapshot of the initial configuration of the system, in which 10 KT pairs are placed in the equatorial plate forming a ring; the initial orientation of each KT pair is random. (G) Snapshot of the system with 10 KT pairs after 30 min of cell dynamics. (H) Probability to find each type of KT–MT attachments for the system with 10 KT pairs. Statistics of attachments were collected from 10 independent simulation runs.

Next, we carried out similar numerical experiments, but now for 10 naked CHs. Based on previous experimental observations suggesting that in early prometaphase the CHs are crowded to the ring-like region around the spindle equator (Magidson et al., 2011), we placed the CHs into such a ring and randomized the initial orientations of the centromere axes (Figure 5F). A total of 10 simulation runs for each of the random initial orientation set resulted in the statistics of attachments shown in Figure 5H; one of the final configurations is shown in Figure 5G. We see that, compared with the random initial positioning of multiple CHs, there is a significant accuracy improvement for CHs positioned in the ring-like region: the number of amphitelic attachments increases, and the numbers of syntelic and monotelic attachments decreases, confirming the previous result that initial equatorial positioning is the most important accuracy booster. However, the accuracy for the multiple CHs initially placed at the equator is worse than that for a single CH placed at the equator, and is comparable to that for a single CH initially placed near one of the poles. Inspection of the simulations shows that the reason is like that for the initial random CH positioning: just a few CHs pulled to the poles shield many remaining CHs from the MTs, thereby hindering new connections and also blocking each other’s access to MTs from the distal poles, which could subsequently improve the attachment accuracy.

Polar ejection force improves spindle assembly accuracy for a single CH

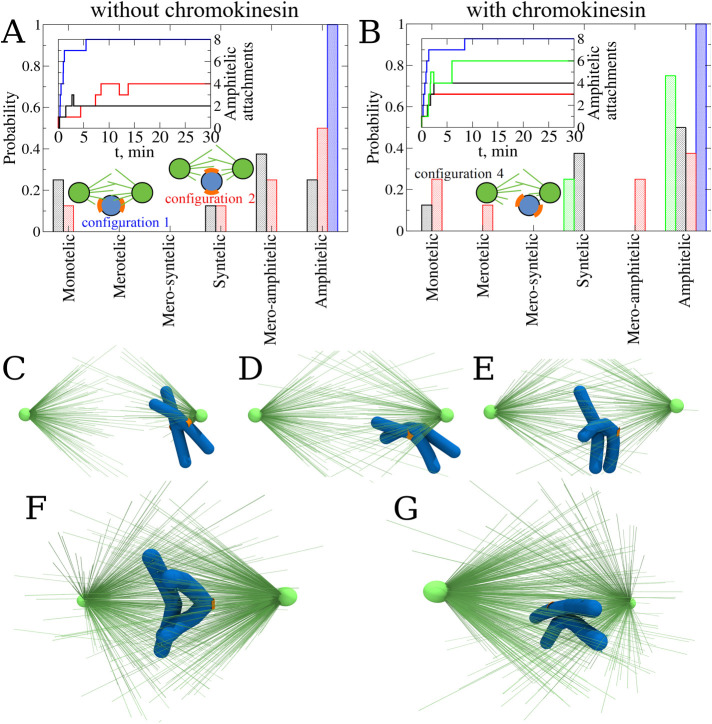
After having addressed the question of which geometric and mechanical factors affect the accuracy of the spindle assembly, we turned to the case of CHs with CH arms present (8 μm in length), starting with a single CH with deformable cylindrical arms placed in initial configurations 1, 2, and 4 (Figure 2, A, B, and D respectively). The statistics of attachments are shown in Figure 6A. Similar to the behavior of the naked CH, initial configuration 1 resulted in 100% amphitelic attachments. Initial configuration 2 resulted in slightly worse statistics than the same initial configuration for the naked CH in the sense that the number of amphitelic attachments decreased while the number of mero-amphitelic attachments increased. Inspection of the simulations shows that the reason is that the CH arms slow down CH turning after the very first attachment is made, allowing time for multiple attachments to the same KT from the opposite poles to form. Initial configuration 4 led to roughly similar attachment accuracy to that of the naked CH case.

FIGURE 6:

Probing the role of chromokinesin and polar wind. (A) Probability to find each type of KT–MT attachments for CHs without chromokinesins (CKs) in different initial configurations: 1 (blue), 2 (red), and 4 (black). Statistics of attachments were collected from eight independent CellDynaMo simulations for all three case studies. The number of amphitelic attachments as a function of time collected from all eight CellDynaMo simulation runs for all three case studies are shown in the inset. (B) Probability to find each type of KT–MT attachments for CHs in the presence of CK in different initial configurations: 1 (blue), 2 (red), and 4 (black). Green bars correspond to the case of CH in initial configuration 4, but with a limited number of MTs allowed to attach to the KTs. Statistics were collected from eight independent CellDynaMo simulation runs for all four case studies. The number of amphitelic attachments as a function of time collected from all eight trajectories for all four case studies are shown in the inset. (C) The most representative snapshot of the final position of CH (after 30 min of simulation) for the case without CK. (D) The most representative snapshot of the final position of CH (after 30 min of simulation) for the case with CKs and an unlimited number of MTs allowed to attach to the KTs (see Supplemental Movie S1). (E) The most representative snapshot of the final position of CH (after 30 min of simulation) for the case with CKs and a limited number of MTs allowed to attach to the KTs (see Supplemental Movie S2). (F) Snapshot of the final position and orientation for amphitelic attachment. (G) Snapshot of the final position and final orientation for merotelic attachment.

These results show that the mere presence of the CH arms does not improve the attachment accuracy, despite the expectation that growing MTs push on the CH arms and, therefore, generate the so-called polar ejection force pushing the CHs away from the poles into the equatorial region of the spindle, where the average MT numbers from both poles equalize and the net push from the poles balances. In fact, we found in our previous computational study that this expectation fails because the growing MTs slip off the CH arms’ surface, bend slightly and keep growing, therefore not generating the polar ejection force (Kliuchnikov et al., 2022). Thus, as simulations illustrate, a CH that is located near one of the poles by KT–MT connections to this pole, has its CH arms more or less straight indicating the negligible polar ejection force in this case (Figure 6C).

To further investigate the effect of polar ejection force, we added chromokinesin (CK) motors to the CH arms (Almeida and Maiato, 2018), so that the MTs that have lateral contacts with the CH arms provide tracks for the CK motors that move to the MT plus ends and generate the pushing forces (see Supplemental Eq. S8). Evidence that there is such a net polar ejection force is seen in Figure 6D, where the CH arms are bent away from the proximal pole. We found, though, that such forces are not sufficient to move the whole CH to the spindle equator (Figure 6D), because even when a CH is close to one of the poles, many MTs are captured by the KT proximal to the pole. Taken together, all such MTs generate pulling forces that overwhelm the polar ejection force. In this case, when the CH starts moving from initial configuration 2, there is little change in the attachment statistics (Figure 6B), which is not surprising because the CH starts off near the equator, where the ejection forces from both poles balance. When the CH starts off from initial configuration 4, CKs help improve the percentage of the amphitelic attachments, but they also increase the percentage of the syntelic attachments (Figure 6D), indicating that many CHs remain near the initially proximal pole. This is shown in Supplemental Movie S1. Examples of final CH states predicted by these simulations are shown in Figure 6, F and G. Note the CH arms are being pushed away from the cloud of the spindle MTs by the polar ejection forces. These V shapes of the CH arms resemble the experimentally observed CH arms’ shapes (see Supplemental Movie S1).

Movie S1.

Download video file ^{(11.7MB, mp4)}

Effect of chromokinesin on final CH position and orientation: This movie shows the first 5 min of cell dynamics and is related to Figure 6, B and D in the main text. The cell includes one CH with arms (blue); each centrosome has 1,500 MTs (green). The KT surface area is 0.5 μm² (orange). The pushing/pulling force per MT is 10 pN/10 pN, and the KT-MT dissociation rate depends on the phosphorylation degree of the Ndc80 linkers (see Table S2). A CH is shifted to one of the poles and the centromere axis is perpendicular to the vector connecting this pole to the centromere center (Figure 2D in the main text). The duration of the movie is 9 s (the movie is played ∼30 times faster than the process).

When, in addition to the existence of CKs on the CH arms, we limited the number of MTs that can connect to a KT (see Dynamics of microtubules—interactions with chromosomes in the SM), the attachment accuracy for the “worst” initial configuration 4 improved dramatically, as displayed in Figure 6B, with more than 70% amphitelic attachments formed. Note the characteristic position of the CH in Figure 6E that now is being pushed away from the pole significantly by the action of CKs. This positioning of the CH to the equatorial region significantly improves the probability of achieving amphitelic attachments. The still relatively high percentage of syntelic attachments likely can be repaired by error-correction mechanisms. Note also that before these simulations, the best we could achieve with monotelic attachments was to bring their numbers down to 10%. Now, the polar ejection force helps to keep the number of monotelic attachments around zero, even for the “worst” initial configuration 4. This is shown in Supplemental Movie S2.

Movie S2.

Download video file ^{(9.4MB, mp4)}

Effect of limited number of MTs that can connect to a KT on final CH position and orientation: This movie shows the first 5 min of cell dynamics and is related to Figure 6, B and E in the main text. The cell includes one CH with arms (blue); each centrosome has 1,500 MTs (green). The KT surface area is 0.5 μm² (orange). The pushing/pulling force per MT is 10 pN/10 pN, and the KT-MT dissociation rate depends on the phosphorylation degree of the Ndc80 linkers (see Table S2). The maximum of three MTs can be attached to a KT at the same time. A CH is shifted to one of the poles and the centromere axis is perpendicular to the vector connecting this pole to the centromere center (Figure 2D in the main text). The duration of the movie is 9 s (the movie is played ~30 times faster than the process).

Crowding effect largely cancels the effect of the polar ejection force

Finally, we carried out eight independent simulations for a system with five CHs with CH arms, CK action, and a limited number of allowable KT–MT attachments. In these simulations, the CHs were initially placed in random initial positions and orientations (see Figure 7A). The characteristic final configuration of the CHs is shown in Figure 7B. Note that now there are no CHs falling onto the poles because of the polar ejection force. Nevertheless, the attachment statistics shown in Figure 7C demonstrate that the accuracy remains low: just 25% of all CHs achieve amphitelic attachments by the end of the 30-min simulations, while more than 40% of all CHs end up forming monotelic attachments. Thus, the crowding and resulting shielding of many KTs from the poles reduce the likelihood of formation of proper attachments, even in the presence of the polar ejection force and better biasing of the CHs to the equator. This is illustrated in Supplemental Movie S3. The good news, though, is that there are no merotelic connections as predicted for the multiple CH system (Figures 5 and 7), probably because the crowding also protects KTs from the access to MTs from both poles. Note that the attachment statistics of this final case study is slightly better than that for multiple naked, initially randomly placed CHs (Figure 5C). The CH arms make the crowding worse, so without CKs and polar ejection force, the statistics are expected to be worse. Lastly, the time series for the attachment numbers (Figure 7C) show that the majority of monotelic connections are made between the first 5 and 10 min of simulations, that is, much later than in the case of a single CH (Figure 4C). After 10 min of the search, the monotelic connections are converted slowly but steadily into the syntelic, mero-amphitelic, and amphitelic connections; yet, the conversion is not complete. Note also a small transient number of merotelic connections. To conclude, the polar ejection force improves the accuracy of the spindle assembly, but crowding largely counteracts and cancels this improvement.

FIGURE 7:

Exploring cell dynamics with multiple chromosomes in the presence of chromokinesin. (A) Snapshot of a random initial configuration of the spindle. (B) Snapshot of the final spindle configuration after 30 min of CellDynaMo simulation (see Supplemental Movie S3). (C) Probability to find each type of attachment from eight independent CellDynaMo simulation runs. The normalized number of attachments of different types as a function of time collected for all 40 chromosomes (5 chromosomes times 8 simulation runs) is shown in the inset. Color denotation is shown in the graph.

Movie S3.

Download video file ^{(13.2MB, mp4)}

Crowding effect: The movie shows 15 min of cell dynamics and is related to Figure 7 in the main text. The cell includes five CH with arms (blue) and centrosomes each having 1,500 MTs (green). The KT surface area is 0.5 μm² (orange). The pushing/pulling force per MT is 10 pN/10 pN, and the KT-MT dissociation rate depends on the phosphorylation degree of the Ndc80 linkers (see Table S2). The maximum of three MTs can be attached to a KT at the same time. All five CHs are randomly placed and oriented within the area between the two poles. The duration of the movie is 30 s (the movie is played ∼30 times faster than the process).

DISCUSSION

Extension of 3D search-and-capture model

We developed the extension of the mechanochemical 3D SRDDM of the search-and-capture pathway of mitotic spindle assembly (Kliuchnikov et al., 2022) implemented in the CellDynaMo package. To make the dynamics of interactions between the cell components more realistic, that is, to model accurately excluded volume interactions, we implemented the cylindrical potential to the model (Figure 1C and Supplemental Eqs. S2 and S9). This made it possible to model molecular motors, such as CK motors, walking on MTs (Figure 1D and Supplemental Eqs. S8 and S13). The advantage of this approach, over the previous work (Kliuchnikov et al., 2022), is that one can now computationally describe more complex processes, such as the polar ejection force. This extension will enable us to explore in future studies the formation of the spindle interpolar bundles (via adding kinesin-5 to the model; Peterman and Scholey, 2009), and to describe the KT–MT interface by adding dynein to the model (Vaisberg et al., 1993).

Model’s implications for the accuracy of CH integration into the spindle

The CellDynaMo-based simulations we have performed, satisfyingly, confirm that the more deformable the centromere, the more accurate the assembly. The intuitive explanation is the following: the amphitelic attachments, associated with greater centromere stretch, move CHs away from the Aurora B cloud, and resulting biochemical pathways solidify this attachment type. Syntelic attachments lack the centromere stretching, keeping the sister KTs close to each other and inside the Aurora B cloud, which leads to destabilizing the KT–MT connections in these attachments. The nontrivial prediction from our study is that this effect is largely canceled by bulky CH arms; the same accuracy is achieved with stiff and soft centromeres if the arms are large. The reason is that a great viscous drag on the CH arms makes fast KT displacements and KT turns less likely, thereby negating the elastic deformations of the centromere, and preventing disastrous events of CHs collapsing onto the poles.

The SRDDM also demonstrates that the key for high attachment accuracy is keeping CHs near the equator: when a CH gets too close to one of the poles, the very likely outcome is a monotelic connection. The sister KT, while facing away from the proximal pole, is then too far from the distal pole to capture any of its growing MTs. The CellDynaMo simulations show that one possible strategy to improve the attachment accuracy is to initially position the CHs along the equator (Magidson et al., 2011), while another is to harness the polar ejection force generated by CKs to repel the CHs from the poles. For the latter, it is crucial to limit the number of MTs allowed to connect to a KT, so that the pulling force on the KT does not overwhelm the pushing force on the KT arms. Interestingly, the initial orientation of the CH matters less, likely because multiple pulls and pushes randomize the orientation before a significant number of attachments has been established.

The results of CellDynaMo simulations show that space crowding by CHs with large CH arms has the greatest deleterious effect on achieving proper and fast CH attachments, mainly because CHs block access of many KTs to MTs from the spindle poles. The signature of the crowded space for the spindle is a very high percentage of monotelic attachments, in which many KTs do not capture any MTs. In this study, we only simulated the spindles with a small number of CHs, and so, clearly, the simulations with a greater CH count would show even more dismal accuracy statistics.

Nevertheless, the good news is that monotelic attachments are not erroneous per se; they are the sign that the assembly goes slowly, and that there needs to be a way to accelerate the KT–MT access (as discussed below). Our simulations with multiple CHs often showed no merotelic attachments, which are the most dangerous of all incorrect attachments. Curiously, there were no mero-syntelic attachments formed in our computational experiments. The moderate numbers of syntelic attachments predicted in our simulations likely mean that more effective error-correction mechanism(s), capable of discriminating between the low- and high-tension states of the centromere, are missing from the model. Moderate numbers of predicted mero-amphitelic attachments could be corrected with the “brute-force” mechanism.

Additional comments on model parameters

In this article and in our earlier study (Kliuchnikov et al., 2022), we investigated how the speed and accuracy of the spindle assembly depend on key parameters, including (but not limited to) MT turnover time, KT size, centromere stiffness and CH initial position and orientation. Inevitably, current computational and presentational limitations precluded us from varying some important parameters. Here we make brief qualitative comments on several such model parameters. We have not varied the shape or volume of the cellular space or scaled them with the CH arms’ shape or volume. Intuitively, a larger cellular space relieves crowding, but also leads to fewer searching MTs per CH (Wollman et al., 2005), so it may be expected that there is an optimal complex scaling between the CH count and volume, cell volume, and number of MTs. Investigating such an optimum in the presence of a realistic MT network is an important problem for future studies. One of the important effects of the CH size is the slowing down of shifts and turns of the CHs. This effect seems to become noticeable from a few microns’ length of a CH. CH arms’ flexibility is another interesting parameter. Arms that are too stiff will likely hinder necessary CH movements in the crowded space, while arms that are too flexible will stop slowing centromeres down and diminish the effect of the polar ejection force. Lastly, motor forces have to be balanced in the spindle; in our case, this means that we chose the CK force, the number of these motors per CH, and the upper limit on the KT–MT connections so that the net effective poleward force is roughly equal to the net polar ejection force per CH. Significant (order of magnitude) shifts of this balance in either direction worsens the assembly accuracy.

What is missing in the current model

Crowding of the spindle space by the CHs is inevitable, and the likeliest mechanism to avoid the exceedingly slow formation of connections in the crowded space is for the spindle to deploy an MT network more complex and dynamic than that emanating solely from two centrosomal asters. Indeed, a recent study suggests that initially indiscriminate connections between short MTs, preconnected to or growing from KTs, and long centrosomal MTs improve the accuracy of the spindle assembly drastically, due to an action of dynein motors sorting out transient incorrect connections (Renda et al., 2022). It remains to be seen what the predictions of a 3D model with multiple CHs for such KT–MT-dynein motor arrays will be, but clearly future models will have to include more motor types than just CKs. MT branching can also potentially fill the space much more efficiently with MT plus ends (Thawani et al., 2019). Rapid MT pivoting is yet another mechanism that can accelerate the KT capture (Kalinina et al., 2013; Blackwell et al., 2017). Keeping CHs in the equatorial plane of the spindle is another important factor predicted (Magidson et al., 2011). One of the elegant ways that this can be achieved is for the spindle poles to segregate from each other rapidly and symmetrically, simply leaving the crowd of CHs at what will become the spindle equator (Magidson et al., 2011). Inclusion of the interpolar MT bundles (Nédélec, 2002) and interactions of the astral MTs with the cell cortex (Farhadifar et al., 2020), responsible for the pole–pole segregation, will also have to be included in the next-generation computational models. Other molecular mechanisms, potentially improving the accuracy of mitosis, include the dynamic “lock” that selectively and rapidly stabilizes proper end-on attachments (Conti et al., 2019), dynamic KT shapes (Magidson et al., 2015), KT behaving as a tension-sensitive catch bond (Akiyoshi et al., 2010), and regulation of MT dynamics by Ran protein (Pavin and Tolic’, 2016).

Why model the search and capture at all?

In the last few years, it became clear that the original search-and-capture model was not describing well enough the spindle assembly process (O’Connell and Khodjakov, 2007; Meunier and Vernos, 2016; Letort et al., 2019; Renda et al., 2022). Most notably, the majority of the initial contacts between the long centrosomal MTs and KTs are lateral (Magidson et al., 2011), not end-on attachments, and short MTs (Sikirzhytski et al., 2018) actively mediate connections formed between the KTs and long centrosomal MTs. Why then, explore the search-and-capture model further? There are three main reasons. First, design principles of the spindle assembly become clearer as a result. Second, like in machine engineering, it is likely that the cell uses redundant mechanisms (of which the search-and-capture is one) to achieve higher accuracy (Bentovim et al., 2017). Lastly, other unrelated cell biological phenomena also harness elements of the search-and-capture process (Lee et al., 2000; Gundersen, 2002; Drake and Vavylonis, 2010; Vinogradova et al., 2012; Sarkar et al., 2019).

MATERIALS AND METHODS

Request a protocol through Bio-protocol.

Model components

The SRDDM, implemented in the CellDynaMo package (Kliuchnikov et al., 2022) is described in detail in the SM and is graphically summarized in Figure 1. Briefly, the SRDDM model includes the mechanically active components, which participate in the mechanical processes (e.g., chromosome pulling and pushing, stretching and bending of chromosome arms, mechanical coupling between microtubules and kinetochores; see Supplemental Eqs. S2–S10), and the chemically active components, which interact in the chemical reactions (e.g., phosphorylation by Aurora B and dephosphorylation by phosphatase, microtubule polymerization and depolymerization, formation and dissociation of linkages between microtubules and kinetochores, attachment and detachment of chromokinesins). In addition, several components are active both mechanically and chemically, which builds the mechanochemistry into the model. For example, microtubule polymerization and depolymerization (chemistry) results in pushing and pulling forces exerted on chromosomes (mechanics; see Table 1, and Supplemental Tables S1 and S2). In SRDDM, the volume of the cell is constant in all simulations, and it does not scale with the CH number.

TABLE 1:

Components of stochastic reaction-diffusion-dynamics model: list of components of the SRDDM along with their component type and functional role, including chromosomes (CHs), their sister kinetochores (KTs), centrosomes (spindle poles), microtubules (MTs), Ndc80 protein linkers anchored at the KTs, chromokinesin (CK) motors, Aurora B kinase, phosphatase kinase, cohesin rings, and cell membrane (see Figure 1 for graphical illustration; see also Supplemental Tables S1 and S2 for more detailed information for each component).

Model component	Component type	Functional role
Chromosome (CH)	Mechanical	Flexible genomic DNA-nucleoprotein packages segregating during mitosis
Kinetochore (KT) corona	Mechanical	Interactions with growing and shortening MTs through the plus ends attachment
Centrosome (CS)	Mechanical	Microtubule organizing center
Microtubule (MT)	Mechanical/Chemical	Pushing and pulling forces acting on CHs through MT plus end growth and shortening
Ndc80 linker	Mechanical/Chemical	Formation and disruption of noncovalent linkages between MT plus end and KT corona
Chromokinesin (CK) motor	Mechanical/Chemical	Formation of the reversible linkages between a MT and a CH arm
Aurora B kinase	Chemical	Phosphorylation of Ndc80 linkers
Phosphatase	Chemical	Dephosphorylation of Ndc80 linkers
Cohesin rings	Mechanical	CH arms constraining
Cell membrane	Mechanical	Delineation of the interior space of the cell

Mechanical components

The SRDDM model involves the following mechanically active components: centrosomes (spindle poles), MTs, sister KT pairs on the centromeric regions of CHs, Ndc80 protein linkers anchored at the KTs, and CK motors (Table 1 and Figure 1; see also Supplemental Tables S1 and S2). The time evolution of all the mechanical components is described using the Langevin dynamics (LD) in the Brownian diffusion limit (see SM). The MTs are elastic filaments. The model also includes centromeres (“naked CHs”) described as spherical beads (the sister KT pair is described by a pair of beads connected by a harmonic spring); these centromeres can be modeled with or without the CH arms. Sister chromatids, CH arms, are described as elastic cylinders. The model also mimics the constraints on CH arms due to cohesin rings; the CH ends can swing away from each other, within limits. The KTs are described as a dense grid of small spherical particles connected by elastic springs that lie on the spherical bead surface of centromeres (see Supplemental Eq. S5). The Ndc80 proteins are represented by elastic springs attached to the KT surface that can form the reversible linkages with MTs (Supplemental Eq. S5). The rate of Ndc80 detachment from an MT, and thus the KT–MT connection’s stability, depends on the Ndc80 phosphorylation state, as explained in the SM. When an MT bumps into a KT, Ndc80 can form a linkage between the plus end of a growing MT (last bead of MT) and the closest bead on the KT surface. Each MT plus end is undergoing a stochastic dynamic instability process determined by four parameters: growth and shortening rates, and catastrophe and rescue frequencies.

Chemical components

The SRDDM has the following chemically active components: phosphatase and Aurora B kinase, Ndc80 linkers, and chromokinesin motors (Table 1 and Figure 1; see also Supplemental Tables S1 and S2). The chemical reactions, MT dynamic processes, and all of their rate constants, are listed in Supplemental Table S1, which also shows the transport properties (diffusion) of Aurora B. A bead-spring representation was also implemented to model CK, existing on the surface of a CH arm, such that when an MT is at a sufficiently close distance to the CH, a linkage is formed where one of the harmonically coupled beads is on the surface of the CH arm, and the other bead is on the surface of the MT (see Supplemental Eq. S8). The cell boundary of an ellipsoidal shape (Figure 1) delineates the interior space of the cell (Supplemental Eq. S10), which contains the uniformly distributed components, such as the phosphatase, as well as components localized to specific locations inside the cell, including Aurora B kinase.

Mechanochemistry

The SRDDM describes the following mechanochemical aspects: formation of the reversible noncovalent bonds between the MT plus ends and KT corona surface, and between the MT and CH arms, which facilitates the application of pulling and pushing forces by the MT (Table 1 and Figure 1; see also Supplemental Tables S1 and S2). For example, in addition to the polymerization and depolymerization dynamics, MTs are capable of forming noncovalent bonds with the KTs’ surface via Ndc80 linkers and with CH arms via CK motors. The Ndc80 linkers are modeled implicitly as harmonic springs between the plus end of an MT and the KT corona surface (see Supplemental Eq. S7). CKs are defined explicitly as harmonic springs: when a CK attachment reaction occurs (Supplemental Table S1), one of the harmonically coupled beads is placed on the surface of the MT cylinder, and the other bead is placed on the surface of the CH arm cylinder. The kinetics of MTs, Ndc80 linkers, and CK motors are described using the reaction–diffusion master equation (RDME; Supplemental Eq. S1); the mechanics of MTs, Ndc80s, and CKs are described using the LD (Supplemental Eqs. S7, S8, and S14–S17). After their detachment (see Supplemental Table S1), the Ndc80 linker and CK motor do not have any mechanical impact.

Force field and equations of motion for mechanical components

To describe the force-generating and force-dependent processes, we introduce the mechanical energies and forces for the mechanically active components, for the noncovalent bonds they form, and for their interactions with the cell boundary. The mechanically active components are listed in Table 1 and are graphically illustrated in Figure 1. All the potential energy functions (force field) and the force-field parameters for all these components are described in detail in the SM (see Supplemental Eqs. S2–S10 and Supplemental Table S2). We describe MTs and CH arms using cylinder representation. The effect of excluded volume interaction between any two particles is also considered. Mathematical formulas for the mechanical energies and excluded volume interactions are given in the SM (Supplemental Eq. S2). We used LD formalism to describe the mechanical coupling and force generation and transduction, for example, to compute deformations and movements of all the mechanical components (see Supplemental Eqs. S14–S17). The cell dynamic mechanical evolution is simulated by propagating the Langevin equations of motion forward in time in the overdamped (Brownian diffusion) limit for each mechanical component. Further information and mathematical details are described in the SM.

Chemical reactions and molecular transport

We used a numerical implementation of the RDME approach (Gardiner et al., 1976; Isaacson, 2009; Isaacson and Isaacson, 2009) to model the biochemical reactions that involve chemically active components and molecular transport (diffusion; see the SM for more details; Supplemental Eq. S1). In the RDME approach, all the chemical interactions are described based upon the propensities of chemical reactions (Gillespie, 1976, 1977). In our implementation, the cell volume is divided into a large number of small subcells (see Supplemental Table S2). The molecules within the cell are distributed among subcells. Chemical reactions are allowed between molecules within a subcell, and the molecules can diffuse randomly between the next-neighbor subcells (see Supplemental Table S1).

Model implementation

The SRDDM was mapped into the CellDynaMo package implemented on graphics processing units. We used the next-subvolume method extension (Elf and Ehrenberg, 2004) of the original Gillespie algorithm (Gillespie, 1976, 1977) in conjunction with the multiparticle diffusion approach (Roberts et al., 2013). Numerical routines for the generation of (pseudo)random numbers (Hybrid Taus), and for RDME and LD are described elsewhere (Zhmurov et al., 2010, 2011).

Abbreviations used:

CH

chromosome

CK

chromokinesin

CS

centrosome

KT

kinetochore

LD

langevin dynamics

MT

microtubule

RDME

reaction-diffusion master equation

SRDDM

stochastic reaction-diffusion-dynamics model.