Can artificial intelligence simplify the screening of muscle mass loss?

Abstract

Background

Sarcopenia is a risk factor for morbidity and preventable mortality in old age, with consequent high costs for the national health system. Its diagnosis requires costly radiological examinations, such as the DEXA, which complicate screening in medical centers with a high prevalence of sarcopenia.

Objectives

Developing a nearly zero-cost screening tool to emulate the performance of DEXA in identifying patients with muscle mass loss. This can crucially help the early diagnosis of sarcopenia at large-scale, contributing to reduce its prevalence and related complications with timely treatments.

Methods

We exploit cross-sectional data for about 14,500 patients and 38 non-laboratory variables from successive NHANES over 7 years (1999–2006). Data are analyzed through a state-of-the-art artificial intelligence approach based on decision trees.

Results

A reduced number of anthropometric parameters allows to predict the outcome of DEXA with AUC between 0.92 and 0.94. The most complex model derived in this paper exploits 6 variables, related to the circumference of key corporal segments and to the evaluation of body fat. It achieves an optimal trade-off sensitivity of 0.89 and a specificity of 0.82. Restricting exclusively to variables related to lower limb, we obtain an even simpler tool with only slightly lower accuracy (AUC 0.88–0.90).

Conclusions

Anthropometric data seem to contain the entire informative content of a more complex set of non-laboratory variables, including anamnestic and/or morbidity factors. Compared to previously published screening tools for muscle mass loss, the newly developed models are less complex and achieve a better accuracy. The new results might suggest a possible inversion of the standard diagnostic algorithm of sarcopenia. We conjecture a new diagnostic scheme, which requires a dedicated clinical validation that goes beyond the scope of the present study.

1. Introduction

The decline in muscle mass is a common condition with aging. It is typically associated with various diseases such as cachexia, malnutrition and sarcopenia [1]. Sarcopenia, in particular, represents a frequent pathology characterized by the contemporary presence of the loss of muscle mass, called pre-sarcopenia [2], and loss of muscle strength with a possible reduction of motor performance [1,3]. The epidemiology of sarcopenia varies greatly in consideration of the reference pathological cut-offs of muscle mass loss, with a prevalence between 12.9% and 40.4% [4] and with an incidence, which grows with age, varying between 1.6% and 3.6% depending on the ethnic community considered [[5], [6], [7]]. In addition, sarcopenia is a risk factor for morbidity (falls, frailty, functional deterioration and of the activities of daily living) and preventable mortality in old age [8], with enormous costs for the national health system [9].

Sarcopenia, according to the definition most commonly used in the literature of EWGSOP2, is suspected when there is a lower value at the reference cut-offs for the grip test (<27 kg for man and <16 kg for women) to evaluate muscle strength, while it is definitely confirmed if a decrease in muscle mass, usually assessed with the Dual Energy X-ray Absorptiometer (DEXA) radiological technique, is present at the same time (<7 kg/m² for male and <5.5 kg/m² for female individuals) [1,3]. However, DEXA is relatively costly, and it is not always easily and routinely used. Nonetheless, understanding whether the decline in muscle strength is linked to the decline in muscle mass is important to confirm the diagnosis and to exclude alternative diagnosis in which only the decline in muscle strength is present [1,3].

In this framework, an early and highly accurate identification of individuals affected by sarcopenia is clearly a key point to effectively reduce the incidence of sarcopenia and related complications in the general population. This is crucial for the clinical practice in rehabilitation centers, to predict the success of rehabilitation treatment, or in internal medicine centers, for the prognostic evaluation of the patient, considering that sarcopenia is an important morbidity and mortality factor [4,10]. In addition, an early identification of individuals at risk of sarcopenia allows a timely treatment of the patient with greater chances of recovery even with non-pharmacological treatments and with a consequent significant reduction of the costs for the national health system. To this end, a key goal is that of identifying nearly zero-cost variables, which do not require dedicated laboratory tests, that can suitably unveil a decline in muscle mass of the patient with an accuracy similar to that of the DEXA radiological technique.

The aim of this paper is to derive a simple and nearly zero-cost screening tool, capable to emulate the outcome of the DEXA technique in identifying patients with muscle mass loss, exploiting only variables that do not require dedicated laboratory tests. This way, one could perform the screening of muscle mass loss in an easy and timely manner, even before carrying out the muscle strength test. To this end, we exploit a state-of-the-art artificial intelligence technique and a broad collection of health data gathered by the National Health and Nutrition Examination Survey, representative of the U.S. general population.

2. Materials e methods

2.1. Study population (NHANES 1999–2006)

The population used to derive and test the model was built from the data obtained in successive National Health and Nutrition Examination Survey (NHANES) over 7 years (1999–2006). NHANES is a continuous collection of cross-sectional data conducted by the US National Center for Health Statistics in the Center for Disease Control and Prevention (CDC). NHANES is a representation of US population through surveys with the typical and various ethnics US characteristics. NHANES reports the health and nutritional status of adults and children in the US, thus giving the opportunity to investigate key medical variables and risk factors of diseases. From 1999, the NHANES survey is collected every 2 years. The data of such cross-sectional studies are divided in demographic, laboratory, examination, health questionnaire and dietary. More Details and NHANES data are free available at CDC website [11].

NHANES is an openly available dataset that can be used for research purposes only. NHANES allows to access a broad body of anthropometric, physical, and anamnestic data of a relatively large statistics of patients gathered in the reference period (1999–2006). The period considered in this study was chosen due to the availability of the key parameters for the DEXA muscle mass evaluation, thus making it possible to define whether an individual is pre-sarcopenic, and to make it easier the comparison of the derived tools with former studies published in the literature. NHANES is therefore an excellent dataset for assessing the state of muscle mass in the U.S. population.

2.2. Definition of muscle mass loss

We used the definition of the EWGSOP2 for the diagnosis of muscle mass loss in sarcopenic patients which considers ALM (Appendicular Lean Mass)/height² < 7 kg/m² in men and <5.5 kg/m² in women [3]. The ALM is the sum of the lean mass of the arms and legs which is approximated to the total muscle mass and the DEXA is the gold standard for its evaluation [1].

2.3. Inclusion and exclusion criteria

Inclusion criteria consisted in patients of any sex, aged more than 18 years, and having the complete information for the calculation of DEXA. We excluded patients with missing data in one of the 38 variables listed in Table 1, as previously done, for example, in Ref. [12].

Table 1.

Feature value distributions in the extended dataset used for the present analysis. For continuous variables, the average values for patients with muscle mass loss and individuals not having muscle mass loss are indicated. For categorical variables, we indicate the fraction of patients (in per cent of the total) in each sub-group, for both categories of individuals. For each variable, we have indicated also the correlation coefficient with the DEXA assessed muscle mass loss. This statistical indicator is closer to 0 if no correlation is present, and closer to +(−)1 if a positive (negative) correlation is present.

Variable description	Variable name	Muscle mass loss	Normal muscle mass	Corr. coefficient
Age	RIDAGEYR	54.515	48.070	0.144
Gender	RIAGENDR	-Male 32.6% -Female 67.4%	-Male 49.2% -Female 50.8%	0.133
Ethnic Group	RIDRETH1	-Mexican American 14.3% -Other Hispanic 2% -Non-Hispanic White 64% -Non-Hispanic Black 3.5% -Other Race - Including Multi-Racial 16.3%	-Mexican American 14.9% -Other Hispanic 2.9% -Non-Hispanic White 61.3% -Non-Hispanic Black 13.3% -Other Race - Including Multi-Racial 7.6%	−0.006
Citizenship Status	DMDCITZN	-US Citizen by Birth or Naturalization 88.8% -Not a Citizen of the US 11.2%	-US Citizen by Birth or Naturalization 89.9% -Not a Citizen of the US 10.1%	−0.015
Marital Status	DMDMARTL	-Married 59.7% -Widowed 23.6% -Divorced 16.8%	-Married 63.5% -Widowed 17.9% -Divorced 18.6%	0.006
Person Education Level	DMDHREDU	- Less Than 9th Grade 12.8% - 9-11th Grade 12.5% - High School Grad/GED or equivalent 24.2% - Some College or AA degree 25.4% - College Graduate or above 25%	- Less Than 9th Grade 9.6% - 9-11th Grade 12.4% - High School Grad/GED or equivalent 23.8% - Some College or AA degree 27.9% - College Graduate or above 26.2%	−0.026
Height (cm)	BMXHT	163.904	168.400	−0.148
Weight (kg)	BMXWT	58.369	77.292	−0.416
Maximal Calf Circumference (cm)	BMXCALF	33.596	38.277	−0.457
Arm Circumference (cm)	BMXARMC	27.167	32.255	−0.451
Upper Leg Length (cm)	BMXLEG	38.824	40.371	−0.151
Upper Arm Length (cm)	BMXARML	35.565	37.375	−0.222
Maximal Thigh Circumference (cm)	BMXTHICR	45.126	52.471	−0.458
Triceps Skinfold (mm)	BMXTRI	16.263	18.985	−0.098
Subscapular Skinfold (mm)	BMXSUB	15.188	20.847	−0.259
Systolic Blood Pressure (mmHg)	BPXSY	126.525	124.219	0.030
Differential Blood Pressure (mmHg)	BPXSY - BPXDI	56.642	52.225	0.079
Self-Reported Greatest Weight (pounds)	WHD140	133.679	259.792	−0.015
Ever being told had cancer or malignancy (1-yes, 2-no)	MCQ220	1–12.9% 2–87.1%	1–7.1% 2–92.9%	−0.093
Ever being told had osteoporosis/brittle bones (1-yes, 2-no)	OSQ060	1–9.4% 2–90.3%	1–3.8% 2–96.1%	−0.044
Ever being told had high blood pressure (1-yes, 2-no)	BPQ020	1–25.2% 2–74.8%	1–25.9% 2–74.1%	0.003
Smoked at least 100 cigarettes in life (1-yes, 2-no)	SMQ020	1–51.2% 2–48.8%	1–47.7% 2–52.3%	−0.040
Ever being told had asthma (1-yes, 2-no)	MCQ010	1–9.1% 2–90.9%	1–9.7% 2–90.3%	0.001
Ever being told had arthritis (1-yes, 2-no)	MCQ160a	1–23.1% 2–76.9%	1–20.7% 2–79.3%	−0.036
Ever being told had coronary heart disease (1-yes, 2-no)	MCQ160c	1–4.5% 2–95.5%	1–2.8% 2–97.2%	−0.044
Ever being told had angina/angina pectoris (1-yes, 2-no)	MCQ160d	1–3.7% 2–96.3%	1–2.2% 2–97.8%	−0.047
Ever being told had heart attack (1-yes, 2-no)	MCQ160e	1–3.9% 2–96.1%	1–2.5% 2–97.5%	−0.039
Ever being told had a stroke (1-yes, 2-no)	MCQ160f	1–2.9% 2–97.1%	1–1.5% 2–98.5%	−0.053
Ever being told had emphysema (1-yes, 2-no)	MCQ160g	1–3.0% 2–97.0%	1–0.9% 2–99.1%	−0.082
Ever being told had chronic bronchitis (1-yes, 2-no)	MCQ160k	1–6.3% 2–93.7%	1–4.5% 2–95.5%	−0.036
Ever being told had any liver condition (1-yes, 2-no)	MCQ160l	1–2.4% 2–97.6%	1–2.6% 2–97.4%	<0.001
General health condition	HUQ010	-Excellent 22.2% -Very good 31.7% -Good 31.3% -Fair 13.3% -Poor 1.5%	-Excellent 24.2% -Very good 33.8% -Good 30.3% -Fair 10.8% -Poor 1.0%	0.032
Physical, mental, emotional limitations (1-yes, 2-no)	PFQ059	1–7.1% 2–92.9%	1–5.8% 2–94.2%	−0.030
level of physical activity each day	PAQ180	-sitting 22.7% -walking 57.6% -lifting light load 15.8% -heavy work 4.0%	-sitting 20.2% -walking 52.5% -lifting light load 18.6% -heavy work 8.7%	−0.063
Vigorous activity over past 30 days (1-yes, 2-no, 3-unable to do activity)	PAD200	1–23.5% 2–75.1% 3–1.4%	1–38.1% 2–60.8% 3–1.1%	0.110
Moderate activity over past 30 days (1-yes, 2-no, 3-unable to do activity)	PAD320	1–52.4% 2–46.7% 3–1.0%	1–53.5% 2–45.9% 3–0.6%	0.012
Muscle strengthening activities over the past 30 days (1-yes, 2-no, 3-unable to do activity)	PAD440	1–22.1% 2–77.1% 3–0.9%	1–30.7% 2–68.5% 3–0.8%	0.072
Daily hours of TV, video or computer use (0-less than 1 h, 1-one hour, 2- 2 h, 3-three hours, 4-four hours, 5-five or more hours, 6-none)	PAQ480	0–10.4% 1–18.3% 2–26.8% 3–19.5% 4–11.1% 5–11.8% 6–1.3%	0–13.1% 1–16.3% 2–27.4% 3–18.9% 4–11.0% 5–10.7% 6–1.2%	0.017

2.4. Characteristics of the population under consideration

We considered 38 variables previously discussed and analyzed in the literature as good sarcopenia predictors [[13], [14], [15]]. Variables were selected based on their importance in the genesis of sarcopenia and omitting poorly important variables when a too large number of missing values were reported in the database. Laboratory variables were discarded, aiming to focus on a first-level screening tool that does not require laboratory tests. Diet variables were also excluded due to the large number of missing data. The variable set accounts for the principal risk factors of sarcopenia; it includes specific questionnaire about the individuals’ physical activity, anthropometric measurements that may be affected if sarcopenia is present, and the comorbidities that may frequently be associated with sarcopenia (i.e. diabetes, osteoporosis, cardiovascular diseases).

According to the definition of muscle mass loss in female or male subjects elucidated above, patients were categorized either has having muscle mass loss or not having muscle mass loss. Table 1 reports a list of the variables used in the present study alongside with the population statistics for both categories of individuals, i.e., individuals with muscle mass loss and individuals not having muscle mass loss. An inspection of their values in both classes of individuals shows that, in almost all cases, the variable average differs, in a statistically significant way, for patients with loss in muscle mass and for individuals not having muscle mass loss. This indicates the presence of a meaningful correlation with the occurrence of muscle mass loss.

Large care was devoted in producing a dataset representative of the US American population. This is a crucial step, as detailed in our previous works [12,16], in order to reduce biases in the derivation of a screening model for a given reference population and to meaningfully probe its accuracy. In addition, dealing with a population as close as possible to the one that is expected in clinic applications is key to improve the reproducibility of the results when the screening model is adopted in a real use case. In a similar way with what was done in Ref. [12], we adopted the prescriptions on the age and sex distributions of patients with muscle mass loss in the US population, previously published in the literature [17], as the reference for our study. When building the dataset from the NHANES data over the selected years, these distributions are usually not maintained, both due to the specific selection of the time period and because of the exclusion of patients with missing data. In order to restore the reference populations, each individual in our dataset is suitably weighted. In this way, the age and sex distributions of patients with muscle mass loss and normal muscle mass calculated in our study population matches with those of the reference population. This means upscaling classes underrepresented compared to the US national population. This procedure of patients weighting is usually adopted in many statistical approaches to reduce the biases arising from the choice of patterns to represent the reference population [18].

2.5. Data analysis and modeling

In the present analysis, we use a state-of-the-art artificial intelligence technique, based on boost decision trees, to inspect correlations between a set 38 variables, which include anthropometric and demographic data, as well as the results of questionnaires submitted to the patients by the general practitioner, and the outcome of the more costly DEXA radiological technique for the identification of individuals with muscle mass loss. The general aim of our analysis is that of deriving a classification model that can serve as a practical tool to perform large-scale screening of muscle mass loss at nearly zero-cost in the US adult population. This is crucial for the early identification of individuals with sarcopenia. To this end, we use the Extreme Gradient Boosting (XGBoost) algorithm [19], which has been recently proven to be extremely powerful to solve classification and regression tasks in supervised learning approaches in several areas of science including engineering and physics.

The technique used in the present paper exploits decision trees, which is a practical tool to efficiently represent a decision process starting from an initial information (root) up to the final outcome (leaf). A decision tree is a flowchart-like structure which suitably connects root to leaf through a series of internal nodes which represent a set of classification rules. Each node involves a test on a given attribute, e.g. takes a different decision whether that variable has a value lower or greater than a given reference value. More information about decision tree algorithms can be found for example in Ref. [20]. In the present case, attributes are represented by the medical variables used to describe a given patients, the decision nodes are done by comparing the variables to some threshold values, and the leaves are log-odd values that represent the probability of having a high or low DEXA muscle mass. In the XGBoost approach, decision trees are derived exploiting an ensemble machine learning technique that involve the combination of weak learners to construct the final prediction model. In XGBoost, advanced gradient descending algorithms are used to improve the performance of the model at each iteration [19]. Decision tree models are particularly interesting in medical applications because they can be easily represented with flowchart-like structures, which are of practical use in the diagnostic process. Furthermore, even in the case of particularly numerous variables, they have a low computational cost. This allows also the development of apps, of simple and fast use, even for low-cost mobile devices.

To derive and test the models proposed in this paper, we followed a process similar to what previously done in Ref. [12]. A preliminary learning dataset was initially built exploiting all the features (variables) of Table 1. This was used to derive a series of preliminary models exploited for feature selection, i.e. the exclusion of variables, among the initial set of variables used for model derivation, which do not lead to a significant improvement in the prediction capabilities of the resulting model. The definitive learning dataset was then built, restricting to uniquely the previously selected variables and thus significantly enhancing the statistics of patients. This dataset was finally used to derive the definitive models.

The preliminary learning dataset, after the exclusion of patients with missing data, contained 6717 patients with the complete information for the calculation of DEXA. Of these patients, 955 had muscle mass loss according to the DEXA screening test. A sub-set containing 70% randomly selected patients was used to train the XGBoost model, while the rest 30% of the patients were in the preliminary validation set. The latter was used for feature selection. This is a crucial step in the analysis of health data, as it allows to simplify the models making them suitable for clinical applications [12], avoiding the use of redundant information and reducing the cost for the national health system.

The preliminary model had 60 estimators (trees), each with a maximum depth of 4, i.e. 4 nodes are sufficient to reach the leaf outcome of each tree. After the preliminary learning phase, the preliminary model was used to infer the feature importance in the preliminary validation dataset and, consequently, to perform the feature selection.

The definitive modeling phase was carried out exploiting an extended dataset, obtained restricting the variables to only those suggested by the preliminary model feature selection. The extended dataset thus comprised 14,535 patients, with 2045 patients with positive outcome of the DEXA test. To derive the final screening models, patients in the definitive dataset were randomly subdivided into the definitive learning dataset (55% of the patients), the definitive cross-validation dataset (15% of the patients), and the definitive testing dataset (the remaining 30% of the patients). The definitive cross-validation dataset was used to perform the decision on the optimal hyperparameters of the model, while the definitive learning dataset was used for model training.

2.6. Analysis of model accuracy

All models were tested using the AUC, positive and negative predictive values, and sensitivity and specificity at various cut-offs, including all the patients in the definitive testing dataset.

3. Results

3.1. Preliminary model results and feature selection

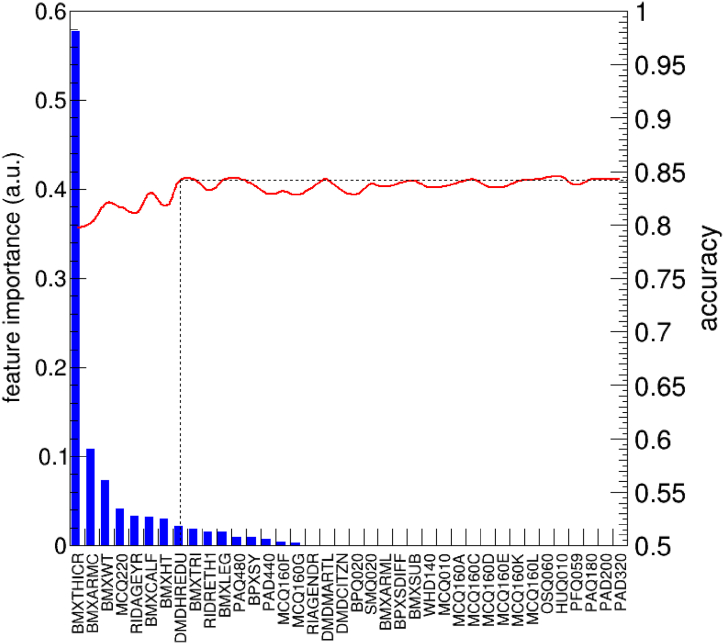
In Fig. 1 we show the feature importance score for each of the feature listed in Table 1. In the framework of the gradient boosting algorithms, feature importance is a parameter proportional to the number of patients (weighted, in the present case) discriminated by that particular attribute. In other words, the larger is the number of patients affected by a classification rule involving a given variable, the larger is the importance of that variable. We find that only 16 of the 38 features initially selected has a sizeable importance according to the preliminary model. Among them, BMXTHICR, which corresponds to the thigh circumference, has a much larger importance compared to all other features.

Fig. 1.

Feature importance for all variables in the preliminary validation dataset. The red line represents the accuracy of the model, in the preliminary validation set, when the model is derived (using all patients of the preliminary training dataset) excluding all the features with a smaller importance parameter than a given feature. No statistically significant degradation of the accuracy is observed until the first 8 most important features are used, as schematically indicated by the dashed line. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

Accuracy values, i.e. the fraction of patients correctly classified by the model, are found to fluctuate around a mean value of about 84% until the first 8 features are included. Between 8 and 3 features, a value of accuracy around 82% is obtained, while including less than 3 features lead to a lower accuracy. Area Under the Curve (AUC) values range from 0.90 to 0.93 depending on the number of features selected. With this feature selection method, we identify two relevant trade-offs between complexity and accuracy of the resulting model respectively at 8 and 3 features.1

Driven by the analysis of the preliminary dataset, we produced the extended dataset including all patients with the complete information for the calculation of DEXA and the following 8 features: BMXTHICR (thigh circumference), BMXCALF (calf circumference), BMXARMC (arm circumference), BMXWT (weight), MCQ220 (cancer), BMXHT (height), BMXTRI (triceps skinfold), RIDAGEYR (age), which resulted to carry basically the whole informative content of the totality of the features for the prediction of the DEXA. From a detailed analysis of the cross-validation dataset, the accuracy of the model turned out to be fairly similar if the first 6 most important features are used, instead of using the entire set of 8 features. Therefore, we finally decided to derive three models: a complex model exploiting the first 6 most important features, a simple model exploiting 3 features and an additional model exploiting only 2 features. The most complex model foresees 80 estimators with a maximum depth of 4. For the simpler models, a single estimator, with a depth between 4 and 5, was found to be sufficient to achieve an optimal accuracy value, thus enabling their representation with a single flowchart-like structure.

3.2. Definitive model results

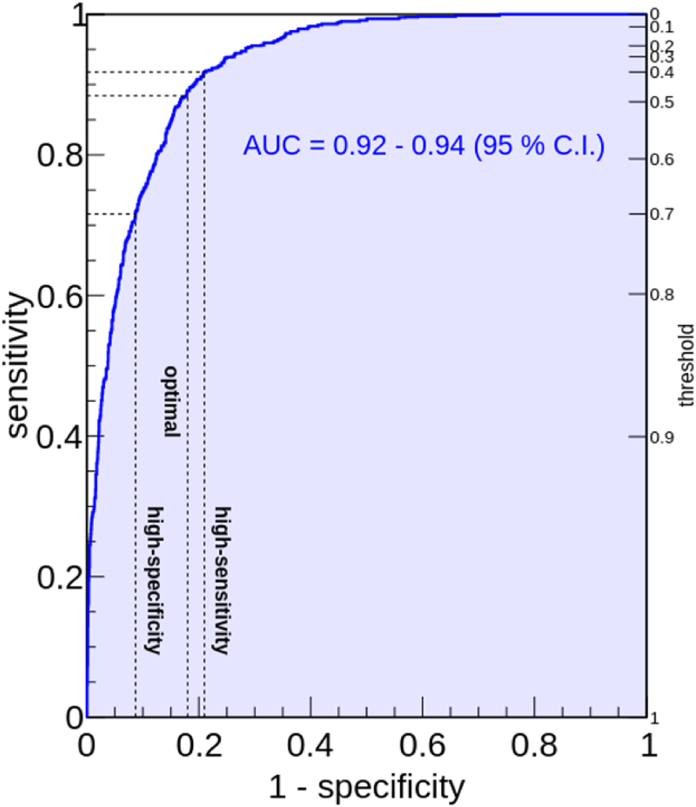
In all models derived in the present study, the thigh circumference is the most relevant, i.e. that associated with the maximum feature importance parameter. For the complex model, which is based on 80 estimators, we obtained an AUC value of 0.93, with a statistical variation from 0.92 to 0.94 (95% C.I.). Surprisingly, despite its particularly good performance, the complex model proposed here requires exclusively 6 features, which are all anthropometric variables: namely the thigh circumference in cm (BMXTHICR), the calf circumference in cm (BMXCALF), the arm circumference in cm (BMXARMC), the weight in kg (BMXWT), the standing height in cm (BMXHT), and the triceps skinfold in mm (BMXTRI). Fig. 2 shows the Receiving Operating Characteristic (ROC) curve for the complex model derived in this work. The optimal threshold value, which was obtained by inspecting sensitivity and specificity values at various threshold with a procedure similar to that of Ref. [24], turned out to be 0.47. With this value, the complex model has a sensitivity of 0.89 (0.87–0.90, 95% C.I.) and a specificity of 0.82 (0.81–0.83, 95% C.I.). In other words, it is able to correctly predict 89% of patients which are tested positive to the DEXA technique, while identifying as not having muscle mass loss 82% of the patients whose result of the DEXA technique is negative. For the same threshold value, we obtain also a positive predictive value of 0.83 (0.81–0.85, 95% C.I.) and a negative predictive value of 0.88 (0.87–0.89, 95% C.I.). In a similar manner with what was done in Refs. [12,16], we also propose two additional trade-offs, one to optimize the specificity and one to optimize the sensitivity. They are obtained by requiring that the sensitivity (specificity) is at least 0.90. The first, which is our most conservative cut-off, can be implemented with a correspondingly low threshold value of 0.40. With this threshold, the model has sensitivity 0.92 (0.90–0.93, 95% C.I.) and specificity 0.79 (0.78–0.80, 95% C.I.). This means that, when used with the most conservative cut-off proposed in this paper, the model can identify 92% of the patients that are tested positive to the DEXA technique, while misclassifying as having muscle mass loss only 21% of the patients who are tested negative to DEXA. The high-specificity cut-off requires a threshold of 0.67 and has sensitivity 0.74 (0.72–0.77, 95%) and specificity 0.90 (0.90–0.91, 95% C.I.). With the latter, our complex model identifies 74% of patients that have muscle mass loss according to the DEXA but misclassifies only 1% of the patients who are not tested positive to DEXA as having muscle mass loss.

Fig. 2.

Receiving Operator Characteristic (ROC) curve for the most complex decision tree model proposed in this work. The range of AUC values (95% C.I.) is indicated. The model achieves an AUC of 0.93. For each trade-off between sensitivity and specificity, the corresponding threshold on the model output is shown (right vertical axis). Dashed lines indicate the position of the optimal trade-off, alongside with the high-sensitivity and high-specificity trade-offs (see text for additional details).

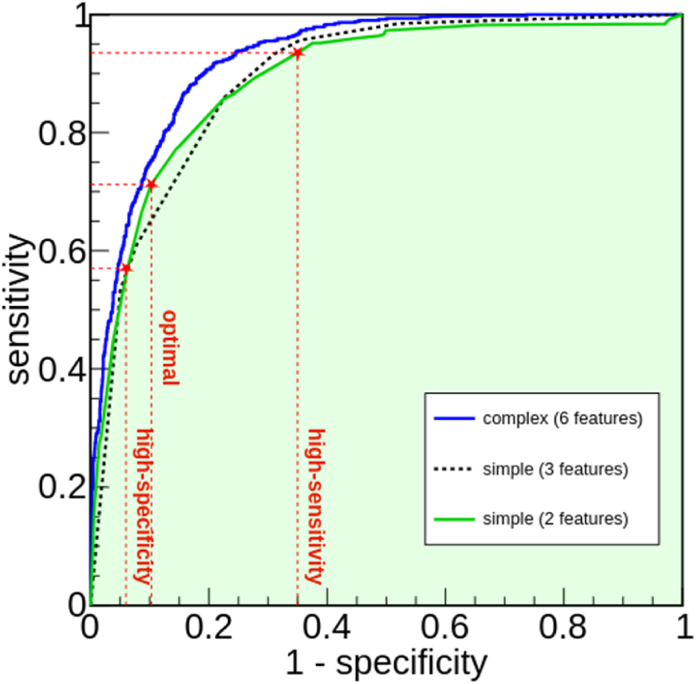
The simplest models proposed in this paper foresee only, respectively, 3 and 2 features. Interestingly, with such a reduced number of features, one single estimator (tree) is found sufficient to reach an optimal accuracy. Fig. 3 shows the ROC curves of the two simple models compared to that of the complex model, obtained using the data of the definitive testing dataset. In the figure, the blue line is the ROC of the complex model, previously shown in Fig. 2, while the dashed black line is the ROC of the simple 3-features model and the green line is that of the simple 2-features model. The features exploited by the simple 3-features model are thigh circumference (BMXTHICR), calf circumference (BMXCALF), and arm circumference (BMXARMC), while the 2-features model uses only thigh circumference and calf circumference. The latter performs very similarly to the 3-features model. Both have 0.89 AUC, with a confidence interval 0.88–0.90 (95%), as also evident from an inspection of Fig. 3. The 2-features model has a slight better accuracy than the 3-features model at mid-values of sensitivity, while the 3-features model overperforms the 2-features model at very large sensitivity values, where the corresponding specificity values are typically not particularly suitable for clinical applications. In the following, we will focus our attention on the 2-features model, as adding an additional feature does not lead to a significant increase in performance.

Fig. 3.

Receiving Operator Characteristic (ROC) curves for the simple models proposed in the paper, exploiting 2 features (green line) and 3 features (dashed black line), compared to that of the complex model (blue line). The 2 features model performs similarly compared to the model exploiting 3 features. Dashed lines indicate the position of the optimal trade-off, alongside with the high-sensitivity and high-specificity trade-offs, for the simplest model (see text for additional details). (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

For the simplest, 2-features, model proposed in this paper, we recommend three key trade-offs, as in the case of the complex model. The optimal trade-off can be obtained with a threshold value of 0.50. When used with the optimal threshold value, the simplest model has sensitivity 0.87 (0.85–0.88, 95% C.I.) and specificity 0.75 (0.75–0.77, 95% C.I.). A high-sensitivity trade-off can be implemented using a threshold of 0.48, achieving 0.94 (0.92–0.95, 95% C.I.) sensitivity and 0.65 (0.64–0.66, 95% C.I.) specificity, thus being capable to identifying 94% of patients with loss in muscle mass (according to DEXA), with a misidentification of 55% patients without loss in muscle mass as having muscle mass loss. The high-specificity cut-off threshold value is 0.52, which allows to identify 67% of patients with muscle mass loss by misidentifying only 9% of patients with normal muscle mass as having muscle mass loss.

The performance of both complex and simple (2-features) models are summarized in Table 2, which reports sensitivity, specificity, positive and negative predictive values, alongside with the corresponding confidence intervals.

Table 2.

Summary of the performance of the simplest model (2-features) and the complex model (6 features) derived in this paper in the definitive testing dataset. We used sensitivity, specificity, positive predictive value, and negative predictive value. Values in parenthesis indicate the 95% confidence interval. Corresponding threshold values are also indicated. It is worth mentioning that the simplest model can be used, for all the trade-offs between sensitivity and specificity proposed here, by simply inspecting Fig. 4.

Threshold type	Threshold value	Sensitivity (95% C.I.)	Specificity (95% C.I.)	Positive Predictive Value (95% C.I.)	Negative Predictive Value (95% C.I.)
Simple model (2 features)
Optimal	0.50	0.87 (0.85–0.88)	0.76 (0.75–0.77)	0.78 (0.76–0.80)	0.85 (0.84–0.86)
High-Sensitivity	0.48	0.94 (0.92–0.95)	0.65 (0.64–0.66)	0.73 (0.71–0.75)	0.91 (0.90–0.92)
High-Specificity	0.52	0.67 (0.64–0.69)	0.91 (0.91–0.92)	0.89 (0.86–0.91)	0.73 (0.72–0.74)
Complex model (6 features)
Optimal	0.47	0.89 (0.87–0.90)	0.82 (0.81–0.83)	0.83 (0.81–0.85)	0.88 (0.87–0.89)
High-Sensitivity	0.40	0.92 (0.90–0.93)	0.79 (0.78–0.80)	0.82 (0.80–0.84)	0.90 (0.89–0.91)
High-Specificity	0.67	0.74 (0.72–0.77)	0.90 (0.90–0.91)	0.89 (0.86–0.91)	0.78 (0.76–0.79)

The accuracy of the complex and simplified models is equivalent (or slightly better) to those reported in the literature. For example, Katano et al. [14], which generates a model from a relatively small NHANES cohort of individuals with cardiovascular disorders, has a sensitivity of 0.96 and a specificity of 0.65 using calf circumference, weight, and arm circumference; Santos et al. [25] has a Linn's concordance coefficient with DEXA of about 0.90 using calf circumference, sex, race, and age. In the study by Goodman et al. [13], which uses a different and less usual definition of pre-sarcopenia, age and BMI are used to derive the model with an AUC of 0.89 for males and females.

4. Discussion

With the most complex model derived here, which foresees 6 anthropometric variables: namely thigh circumference, calf circumference, arm circumference, triceps plicometry, height, and weight of an individual, we achieve an AUC of 0.93. The combination of these 6 variables thus allows a very precise assessment of the condition of muscle mass loss of a patient. Among those selected features, we identify variables that give an indication of muscle mass in the upper limbs (arm circumference) and three features linked instead to the evaluation of body fat: the plicometry, which evaluates the subcutaneous fat, and height and weight of the patient, which, in turn, are used in the calculation of body mass index (BMI) and are therefore linked to the evaluation of overall body fat and in particular visceral fat. Previous works published in the literature clearly stress the importance of some of these variables in the screening of muscle mass loss. For example, in the studies by Katano S et al. [14] and by Santos LP et al. [25], the calf circumference and arm circumference are some of the features of the muscle mass prediction equation at DEXA, while in the studies of Chien KY et al. [15] and Ishii S et al. [26] among the features considered there is in addition to the calf circumference and arm circumference also the thigh circumference. Weight, height and the derived BMI are also usually considered as important variables in the prediction of the status of muscle mass of an individual, as reported for example in Refs. [25,26] or in the study of Goodman MJ et al., where BMI and age of the patient are considered the only two variables to derive the muscular status at DEXA [13].

Surprisingly, in our simplified model, which achieves only a slightly lower performance if compared to the complex model (see Table 2), only two simple anthropometric parameters are exploited: namely calf circumference and thigh circumference. This seems to suggest that anthropometric parameters of the lower limb are more effective than upper limb quantities and body fat for the identification of muscle mass loss. On the other hand, different studies show how muscle mass is intimately linked to the thigh circumference, which is more easily and quickly affected by hypo or inactivity conditions [27,28]. Similarly, a muscle loss of the lower limbs area (thigh and calf) is usually an index of a poor overall muscular performance [29,30].

Even if muscle mass loss in adult individuals is linked to various well-known risk factors, including anamnestic relevant information (e.g. the level of physical activity of the patient) and/or morbidity (the presence of tumors, poor nutritional status), our study evidences that using only simple anthropometric parameters, such as the circumference of some key corporeal segments, can serve to predict the loss of muscle mass in a more objective way. We point out that, according to our analysis using NHANES cross-sectional data, anthropometric variables, which do not require laboratory tests, suitably contain the entire informative content of a larger set of variables (which includes the answer to questionnaires usually adopted to address muscle mass loss) for the purpose of predicting muscle mass loss. In other words, we can state that deriving a more complex model that exploits, besides the aforementioned anthropometric data, also variables linked to the overall health condition and the presence of several important activities for the prevention of muscle mass loss does not lead to a statistically significant improvement in the prediction of the pathology. These findings can be interpreted with some semi-quantitative deductions: intuitively, it is clear that the lack of physical activity or a general poor health condition that result in a loss of muscle mass might cause a decrease of the circumference of some corporal segments, and, in particular, the most prominent ones (i.e. the lower limb). This fact, which is largely supported by the state-of-the-art literature [[27], [28], [29], [30]], is in full agreement with the suggestions of our data-driven approach.

Based on the above points, it is clear that sarcopenia is a largely preventable and treatable condition through physical or rehabilitative activity that improves muscle mass and strength, therefore physical activity is considered as the primary treatment of sarcopenia in the main guidelines [31]. Physiotherapy characterized by muscular endurance exercises has a hypertrophic effect on the muscles, with a consequent increase of muscle mass and an improvement in muscle tone and strength and the motor performance of the subjects [32,33]. At the same time, the combination of physical activity and improved nutritional status seems to represent an excellent possibility of intervention [33]. It is therefore legitimate to assume, within the limits of our study, that the considerations elucidated above are in good qualitative agreement with the suggestions of our models: in fact, an improvement in muscle tone following diet and exercise, which leads to an increase in the circumference of the thigh, often leads to a resolution the state of pre-sarcopenia.

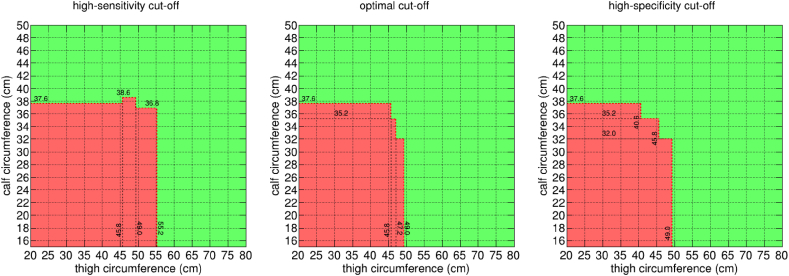
Differently from previous screening tools already published in the literature, the newly developed models exploit the most widely accepted definition of muscle mass loss [1,3]. In addition, for the first time in this field, we adopt an artificial intelligence approach based on decision trees, which allows, in turn, to derive a flowchart-like structure that is particularly easy to adopt in clinical practice. For example, the simplest model proposed in this paper can be used by producing exclusively 2 anthropometric measures (the calf circumference and the thigh circumference of the patient) and can be represented via a simple and readily applicable bi-dimensional graph. Fig. 4 shows a visual representation of the outcome of the model for the optimal, high-sensitivity, and high-specificity trade-offs proposed in this paper. In the figure, the horizontal axis of each panel reports thigh circumference values and the vertical axis is the calf circumference. Red regions are positive outcomes of the model, i.e. thigh circumference and calf circumference, which lead to a predicted muscle mass loss according to the DEXA technique. As it is very intuitive, patients possibly affected by muscle mass loss cover the bottom left region of the panels, i.e. they have reduced thigh circumference and calf circumference. Increasing the threshold, the red region in figure becomes smaller, representing a more stringent criterion to predict patients affected by muscle mass loss.

Fig. 4.

A graphical representation of the simplest model proposed in the paper, exploiting 2 features, when used with the high-sensitivity (left panel), optimal (central panel) and high-specificity (right panel) cut-offs proposed in the paper. This can be used to easily calculate the outcome of the model for an individual, given their thigh circumference and maximum calf circumference, expressed in cm. Green regions indicate patients classified as not having sarcopenia, while red regions indicate individuals classified as sarcopenic. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

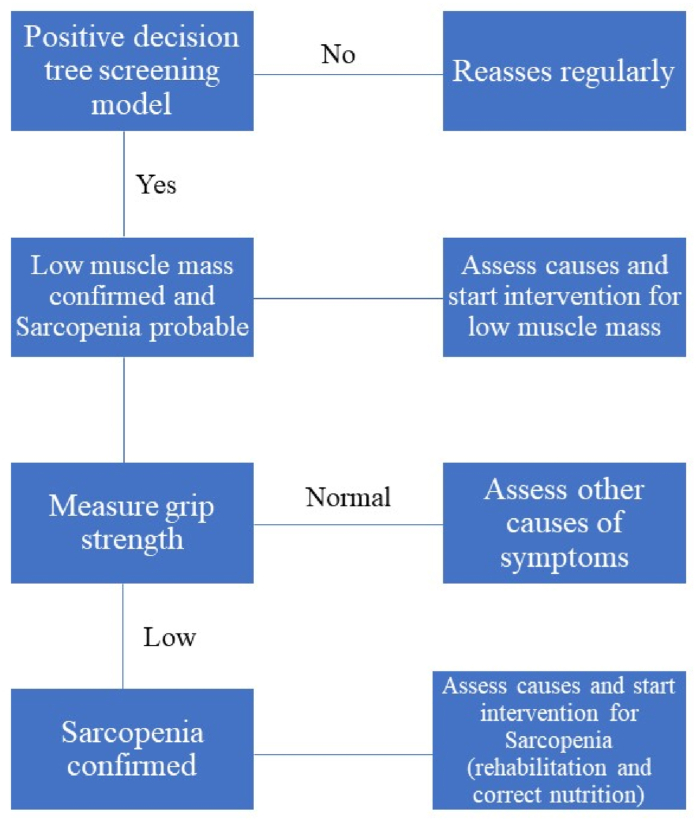
In a possible clinical application, in particular in rehabilitation centers or in internal medicine units where the prevalence of sarcopenia is very high, the models proposed in this paper could allow to rapidly assess the state of muscle mass, at nearly zero-cost, even before performing the muscle strength test (grip test). In this way, one could significantly reduce the number of patients that undergo the grip test, which would be performed only on patients addressed as having muscle mass loss via their anthropometric data. This proposed scheme would represent effectively an inversion of the standard diagnostic algorithm usually adopted in the literature [1,3], as schematically represented in Fig. 5. In turn, our models could be used like a case-finding tool and diagnostic tool avoiding the execution of DEXA, with consequent time and cost savings. However, this hypothesis, which is only conjectured in this paper, would require a dedicated clinical validation in order to be applied in real use cases (but this goes beyond the scope of the present study).

Fig. 5.

Newly suggested sarcopenia diagnostic algorithm.

4.1. Study limitations

Our study presents criticalities, which we try to elucidate in this section. The major criticalities are mainly related to the dataset used in the analysis. The NHANES dataset is a cross-sectional dataset, therefore there is no count of the possible changes of the individual data over time. In addition, the anthropometric features considered here, despite being measured with a rigorous and detailed protocol [11], might present an intrinsic measurement error linked to the operator and the reproducibility of the measurement method (single measurement, dominant limb, average between the 2 limbs, etc..). Another critical aspect of the present analysis is that the features used in the initial dataset are affected by a number of missing data, which have a negative impact when advanced feature selection analyses are performed [12]. We restrict here to a trade-off between the importance of the features in the genesis of sarcopenia and the number of missing data, which needs to be suitably reduced. Moreover, the time frame drawn from the dataset (1999–2006), although not too dated, is not very recent, as there have been changes in lifestyle in recent years. Nonetheless, this is a relative limitation since our results suggest the dominance of anthropometric data in the evaluation of the DEXA measured muscle mass loss. Finally, the new models only evaluate the state of loss of muscle mass or pre-sarcopenia and should be further tested in a dataset that fully evaluates the condition of sarcopenia.

5. Conclusions

In this paper, we discuss a novel comprehensive analysis of NHANES cross-sectional data with the aim to derive, in a completely data-driven way, a highly accurate model to predict muscle mass loss in adult individuals. To this end, we adopted state-of-the-art artificial intelligence techniques based on decision trees, which allows to describe the screening process using simple flowchart-like structures, thus being ideal for clinical applications. To our knowledge, this is the first time a similar problem is addressed with decision trees.

We considered 38 variables, which are identified in the literature as good sarcopenia predictors. Despite the large number of initial variables, we show that using 6 anthropometric parameters, related to the circumference of key corporal segments of both upper and lower limb and to the body fat composition, leads to a model capable to identify subjects with muscle mass loss with a statistically analogous accuracy than more complex models exploiting a series of variables related to the overall health condition of physical activity of the patient. Interestingly, an additional model based exclusively on 2 variables (thigh circumference and calf circumference) proposed in this paper, is found to have only slightly lower performance compared to the most complex model derived here. This allows to perform the screening of muscle mass loss even in a simpler way, through the inspection of simple graphs provided in this paper.

In clinical practice, our results introduce some key novelties: 1) the screening model of muscle mass loss using only anthropometric and constitutional variables is likely to be a more objective case-finding method than using a questionnaire, whose effectiveness depends of the individual perception of the patient; 2) the possibility to predict the DEXA in the evaluation of muscle mass loss with a nearly zero-cost and easy method enables to easily screen the patients with muscle mass loss, in a highly accurate way, and to confirm the presence of sarcopenia only in a successive time with a dedicated grip test; 3) the novel scheme for the diagnosis of sarcopenia proposed in this paper suggests to early treat patients with muscle mass loss, considering it as being a risk factor for sarcopenia, for other morbidity and a risk of mortality, regardless the grip test result and without the use of more costly and complicated methods for the diagnosis of sarcopenia; 4) our model highlights how the lower limb musculature plays a predominant role in the loss of overall muscle mass. The latter point might indicate that physical activity that stimulates the increase in the muscle circumference of the lower limbs, such as walking or running, may be the most effective way to prevent muscle mass loss and related complications.

Finally, our model seems to suggest the importance of evaluating anthropometric parameters, especially related to the lower limb, not only for the diagnosis of sarcopenia, but also for the assessment of the treatment effectiveness in the sarcopenic patients.

The present paper, in turn, focuses on the possibility to emulate the DEXA outcome using non-laboratory variables. A possible future perspective of this work would be to validate a specific protocol to identify patients with sarcopenia using the models derived in this work. These validations would require dedicated analyses exploiting a more extended population that also includes the grip test data, to fully diagnose the state of sarcopenia.

Production notes

Author contribution statement

Enrico Buccheri: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Daniele Dell'Aquila: Conceived and designed the experiments; Performed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Marco Russo: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data.

Rita Chiaramonte; Giuseppe Musumeci; Michele Vecchio: Conceived and designed the experiments.

Data availability statement

Data included in article/supplementary material/referenced in article.

Additional information

No additional information is available for this paper.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.