Thermodynamic Compensation in Peptides Following Liquid–Liquid Phase Separation

Abstract

Liquid–liquid phase separation of proteins often incorporates intrinsically disordered proteins or those with disordered regions. Examining these processes via the entropy change is desirable for establishing a quantitative foundation with which to probe and understand these phase transitions. Of interest is the effect of residue sequence on the entropy of the peptide backbone. In this work we model these systems via all atom simulations of liquid–liquid phase separation of peptides. Systems of supersaturated pentapeptides separate into a peptide-dense liquid droplet phase as well as a dilute (saturated) aqueous phase. An analysis of the change in backbone conformational entropy associated with the phase transition was performed. We examined systems of four different pentapeptides (GGGGG, GGQGG, GGNGG, and GGVGG) in order to explore the effect of sequence variation on the conformational entropy, as well as the effect of side chain variation on the physical characteristics of the droplet phases. We find that the loss of conformational entropy that accompanies aqueous → droplet transitions is more than compensated by a decrease in interaction enthalpy as contributions to the free energy change for the process.

Graphical Abstract

INTRODUCTION

Biomolecular liquid−liquid phase separation (LLPS) plays an important role in the field of cellular biophysics due to phenomena such as the formation of membraneless organelles, disease-associated protein aggregation, and the incorporation of intrinsically disordered protein domains in signaling.^1–5 Membraneless organelles are supramolecular structures located in the cytoplasm that are formed by heterogeneous liquid–liquid phase separation of proteins and nucleic acid, forming concentrated assemblies of macromolecules.^1–3 Examples include nucleoli,⁶ Cajal bodies,⁷ and stress granules⁸ to name just a few. These organelles perform a variety roles, such as ribosomal biogenesis,⁹ cellular signaling,¹⁰ and managing stress response.¹¹ The proteins involved in initiating LLPS into such organelles have been shown to favor those that are intrincally disordered (IDPs) or that contain disordered regions (IDRs); that is, structurally flexible proteins or domains with little to no secondary structure.^12,13 Along with their importance in cellular function, misfunction of membraneless organelles can be associated with disease. Increases in the number and size of nucleoli are observed in cancer cells,^14,15 and mutations in stress granule proteins are linked to neurodegenerative diseases including amyotrophic lateral sclerosis (ALS) and frontotemporal dementia.^15,16 LLPS has also been reported in protein aggregation diseases such as Alzheimer’s.¹⁷ Studies have shown that a variety of amyloidogenic protein solutions undergo LLPS at disease-associated concentrations although the exact role this plays in the cellular pathology is unclear.^17,18 Another area where LLPS is of interest is in protein signaling.^19,20 Many signaling proteins contain intrinsically disordered regions or domains that are conformationally dynamic and participate in signaling regulation processes. These disordered domains utilize LLPS to modulate binding partners and the chemical environment.

During LLPS, IDPs often remodel the disorder.^21–23 Such conformational remodeling can take many forms. Some IDPs transition from a disordered extended state to a disordered collapsed state as they begin to encounter and form interactions with other IDPs.^21,22 Many IDRs of signaling proteins are glycine rich. Systems rich in glycines can be used to model the protein backbone of an IDP effectively due to their flexibility and aversion to stable secondary structure.^24–28 Simulations of oligoglycine peptides in dilute solution show that they collapse conformationally,^24–27 a result that has been corroborated by experiment.²⁸ Glycine rich systems also are prone to phase separation.^29,30 Previous computational work by our group has shown that systems of GGXGG (X = G, N, Q, V) spontaneously undergo LLPS to form liquid peptide droplets at supersaturated concentrations in aqueous solution.^31,32 These studies^31,32 analyzed the intermolecular interactions present in the liquid droplets at the atomic level and found that a variety of peptide dipole–dipole interactions stabilize the phase separation. Unexpectedly, those studies found that hydrogen bonds (H-bonds) are not always the dominant attractive interaction present, but other backbone dipole–dipole interactions such as so-called CO–CO intermolecular interactions can be quite numerous as well. Other computational works have studied LLPS in systems of peptides, but most have utilized coarse-grained peptide ^22,33–35 models. While these simulations are useful for modeling spatial and temporal aspects of LLPS events, they do not allow the atomic level analysis of the interactions and energetics that atomistic oligoglycine systems provide. Several studies of small protein systems have investigated LLPS with all atom simulation techniques,^36–40 but due to computational time constraints imposed by atomistic simulations of LLPS, fewer studies have utilized this approach.

Murthy et al. complemented NMR work with atomistic molecular dynamics (MD) simulations of the FUS protein that supported their findings that glutamine and tyrosine residues contribute heavily to LLPS intermolecular interactions.³⁷ Rauscher and co-workers used atomistic MD simulations of elastin to observe a disordered liquid state that supports the fact that elastin does not adopt an ordered structure.³⁹ They also observe that nonpolar groups in elastin are preferentially buried inside the liquid droplet state. Recent work by Paloni et al. utilized atomistic MD simulations of the N-terminal disordered region of the DDX4 protein and NDDX4 fragments to model sequence specific interactions important for LLPS.³⁸

In this work, we simulate LLPS in glycine-rich peptide systems and probe the thermodynamic mechanisms at play when IDPs transition from a concentrated aqueous state to a compact droplet state. We specifically consider the entropic and enthalpic balance on undergoing LLPS. Previous studies⁴¹ by our group have utilized the mutual information expansion (MIE) method⁴² to calculate conformational entropies of protein model systems. Here we used this method to calculate the conformational entropy of peptides in both the aqueous and peptide-rich droplet states to observe the conformational entropic difference. This is one of the first studies to probe the entropy change a model peptide solution experiences upon LLPS. Our choices for pentapeptide sequence allow us to observe the effect that sequence has on the backbone entropy of peptides in aqueous and liquid droplet states. We also consider changes in peptides’ interaction enthalpy upon LLPS, both with other peptides as well as solvent. While globular proteins are often stabilized by a strong salt bridge or H-bond interactions, our previous work^31,32 indicates this is not the case for liquid protein droplets and instead implicates a variety of more numerous interactions. Studies by Auton et al.⁴³ further suggest that solute–solute interactions are the driving force in determining hydration of the backbone. Understanding the molecular interactions that stabilize liquid peptide droplets may allow future work to manipulate the LLPS properties of mixtures. We quantify the contributions of van der Waals and electrostatic intermolecular interactions to the enthalpy and its balance with entropy in this work.

METHODS

We performed MD simulations of four systems, each consisting of 625 identical pentapeptides solvated in water. The four systems were each composed of peptides with a different amino acid sequence: GGGGG, GGQGG, GGNGG, and GGVGG. To start, 625 peptides with acetylated N-termini and N-methylamidated C-termini were randomly placed in a cubic box using Packmol⁴⁴ with the specification that no peptide atom should be within 6 Å of an atom from another peptide to ensure that the starting state for each peptide is roughly aqueous. The systems were then solvated with ~90 000 explicit TIP3P water molecules using the xleap interface of Amber18,⁴⁵ yielding solvated systems of ~300 000 total atoms. These systems possess a total peptide concentration of around 0.3 M, which previous work^31,32 has shown is well above the solubility limit for these sequences using the current molecular model force fields stated below. As none of these sequences are charged, we did not use any neutralizing ions or excess salt in these systems.

A key component of the system preparation for this work was initializing the solvated systems with a layer of solute-free pure water at the edge of the cubic box; for these systems we used a 15 Å buffer. Prior to implementing this, our systems occasionally had a tendency to form liquid droplets that extended infinitely via the periodic boundary conditions in one or more directions rather than single globular droplets. The addition of a layer of pure water between the periodic images of the peptide solution impedes the system from immediately forming periodic peptide–peptide phases.

We used the conjugate gradient method to energy minimize the initial configurations of the systems. This was followed by 10 ns of equilibration with a temperature of 300 K and pressure of 1 atm using the isothermal–isobaric (NPT) ensemble. Following equilibration, 300 ns of production was performed using the same ensemble, temperature, and pressure. The NAMD package⁴⁶ was utilized to perform the MD simulations, and forces and potentials were described by the Amber14SB force field.⁴⁷ We used the Amber model in this work because prior LLPS studies in our group have also used this force field. A time step of 2 fs was used with the standard Verlet velocity integration scheme in NAMD. Nonbonded interactions were cut off at 12 Å and a switching function was implemented to truncate the nonbonded potential beginning at 10 Å. Long-range electrostatic interactions were calculated using the particle mesh Ewald method.⁴⁸ Covalent bonds involving hydrogen were constrained with the SHAKE algorithm. Images of the peptide systems were created with VMD, and all plotting was performed with Python’s matplotlib library.⁴⁹

Conformational entropies were calculated with the ACCENT-MM program,⁴² which makes use of the MIE method. In these calculations, backbone dihedral angle trajectories for peptides in aqueous and droplet states were extracted from the production simulation data and a corresponding conformational entropy curve for each peptide in each state was obtained. We concentrate on the backbone entropy to make comparisons between the systems for an equal number of degrees of freedom. Only entropy resulting from dihedral variations was considered in these calculations, as bonded and angular entropy are inconsequential in comparison. The third-order MIE approximation to the total entropy was used, as Drake et al.⁴¹ have shown that it is reasonably accurate while still being computationally tractable. Due to the well-known $t^{-1}$ behavior of conformational entropy convergence at long time scales, entropy curves were fit to a hyperbolic function to obtain an extrapolated entropy value. Rotational and translational entropy changes were calculated using the PDB2TRENT program.⁵⁰ Interaction enthalpies were obtained using the linear interaction energy (lie) function in Amber 18’s cpptraj suite,^45,51 which can calculate the van der Waals (vdW), electrostatic, and total potential energy. Each peptide’s interaction enthalpy is defined as the sum of the interaction of the peptide with all the other molecules, both water and peptide.

RESULTS

We consider the thermodynamics of protein liquid–liquid phase separation by exploring the interplay between entropy and enthalpy components in phase separations of short glycine-rich sequences. The sequences were chosen to give us an idea of the variation in how polar and nonpolar side chains modulate the LLPS properties and thermodynamics of predominately polyglycine sequences. Shortly into the MD simulations (few nanoseconds), the peptide solutions phase separated into distinct aqueous and peptide-concentrated liquid droplet (referred to as “droplet” here) phases. We categorized peptides as in either the aqueous or droplet phases during the simulation trajectories. For each of these states, we calculated the average conformational entropy of peptides in each system utilizing the MIE third-order approach,⁴² the accuracy of which has been demonstrated by previous work in the group.⁴¹ For these calculations, only the dihedral contribution to the absolute entropy is considered, which will be referred to as the conformational entropy ($S_{\text{conf}}^{\text{MIE}}$). We then quantify the average interaction enthalpy ($H_{\text{int}}$) of peptides in the aqueous and droplet phases to observe the enthalpic cost of the phase transitions. $H_{\text{int }}$is defined as the energy resulting from the interaction of a peptide with its environment, be it peptide or water, ignoring the small pressure–volume work. Since entropy would usually favor solubility, we consider thermodynamic compensation from other terms to drive the free energy needed for an aqueous → droplet transition.

We find that $S_{\text{conf }}^{\text{MIE}}$ is sacrificed but balanced by a decrease in $H_{\text{int}}$ resulting from favorable peptide interactions inside the droplet. To understand the origin of this phenomenon, $H_{\text{int}}$ values were broken down into their electrostatic ($H_{\text{int}}^{\text{elec}}$) and van der Waals ($H_{\text{int}}^{\text{vdW}}$) components to probe the types of interactions at play during these transitions. In these calculations, entropies are presented in cal mol⁻¹ K⁻¹ and enthalpies in kcal mol⁻¹.

Phase Separation.

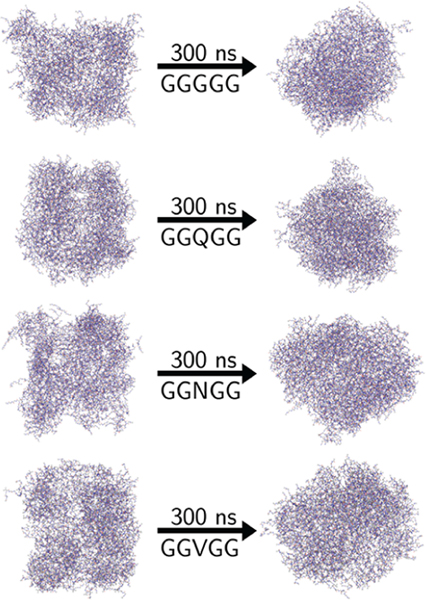
All four systems formed a single large peptide droplet phase within the first 5 ns of production, with a small number of peptides left in the saturated solution. For our purposes, peptides are categorized as being in the droplet phase if any atoms of the peptide are within 4 Å of any atoms of a different peptide at a given time point, while peptides with no atoms within this contact distance are considered to be in the aqueous phase. Figure 1 shows images of the peptide droplets formed in the simulated systems. The initial shapes of the droplets reflect the cubic box in which they were constructed early in the simulation, but they become more spherical as the simulations progress. We have shown previously³¹ and confirm here that water is able to penetrate the peptide-rich droplet, and peptides on the interior of the droplet still interact nontrivially with buried water molecules. This is further discussed below.

Figure 1.

Snapshots from MD simulations showing peptide liquid droplet phase in the GGGGG, GGQGG, GGNGG, and GGVGG systems initially following equilibration as well as at the end of the 300 ns simulation.

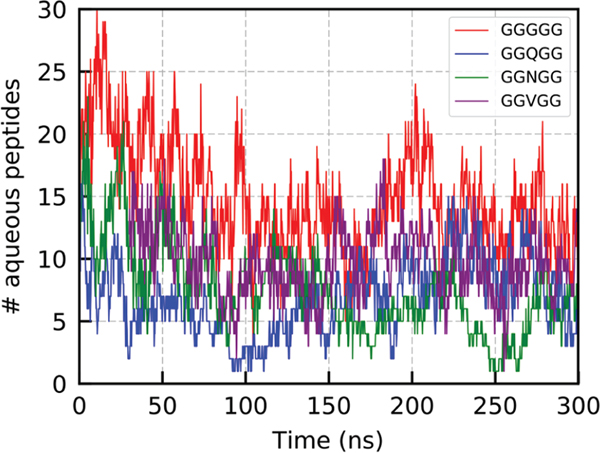
In order to monitor the equilibrium between the emergent phases in our MD simulations, the number of aqueous peptides for each frame of the trajectory was obtained. A plot of these data for the four systems of interest is provided in Figure 2. Inspection of these trends indicates that phase equilibrium is reached, by a conservative estimate, ~100 ns into the simulation. Data were only collected for entropy and enthalpy calculations following this point to ensure nonequilibrium artifacts did not affect these values.

Figure 2.

Plot of the number of aqueous peptides vs time for each simulated system.

Previous work has yielded solubility limits and cluster stability metrics for similar systems of these pentapeptide sequences.³² In our systems we find an average of 13.2, 7.33, 6.08, and 9.41 aqueous peptides per frame for the GGGGG, GGQGG, GGNGG, and GGVGG systems, respectively. These data match the trend of cluster stability and peptide solubility found previously of GGGGG < GGVGG < GGQGG <GGNGG. We performed a simple backbone radius of gyration ($R_{\text{g}}$) analysis of peptides in the aqueous and droplet states to observe any structural changes that might occur upon LLPS. This analysis (shown in Table 1) reveals that peptides in all four systems have similar values for $R_{\text{g}}$ regardless of their state, with peptides in the droplet state actually preferring slightly less collapsed conformations than those that are aqueous. This increase in $R_{\text{g}}$ shown in droplet peptides has also been observed in studies of LLPS of elastin systems by Rauscher and co-workers.³⁹ These data also indicate that GGGGG is marginally less collapsed than the other sequences in both the aqueous and droplet states.

Table 1.

Average Radius of Gyrations ($R_{\text{g}}$) and Standard Errors for Peptides in Aqueous and Droplet Phases (Å)

	GGGGG	GGQGG	GGNGG	GGVGG
avg $R_{\text{g}}$(aqueous)	4.19 ± 0.02	4.01 ± 0.02	4.01 ± 0.02	3.99 ± 0.02
avg $R_{\text{g}}$(droplet)	4.41 ± 0.02	4.27 ± 0.02	4.17 ± 0.02	4.24 ± 0.02

Entropy of Aqueous and Droplet Phase Peptides.

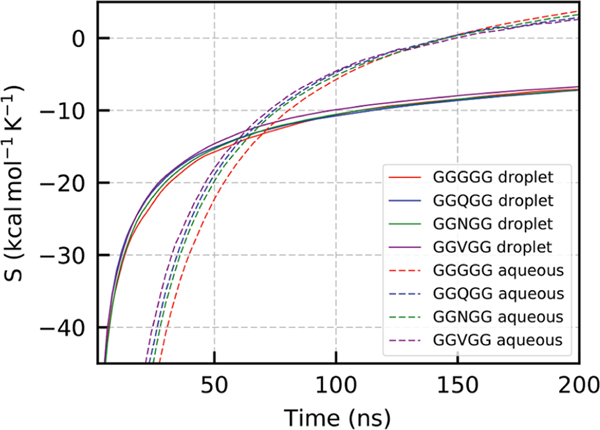
To obtain average conformational entropies for peptides in the various systems simulated here, we first identified which peptides are in either the aqueous or droplet phases for each time point. Average $S_{\text{conf}}^{\text{MIE}}$ vs time curves for all states and systems, as well as bar plots showing final $S_{\text{conf}}^{\text{MIE,fit}}$ values, are shown in Figures 3 and 4. Only the final 200 ns of the simulation trajectories were used for these calculations because equilibrium between the droplet and aqueous phase became evident ~100 ns into the ~300 ns total simulations.

Figure 3.

Conformational entropy vs time for aqueous and liquid states for the GGGGG, GGQGG, GGNGG, and GGVGG peptide sequences from MD simulation trajectories. Entropy data were calculated for the final 200 ns of the simulations.

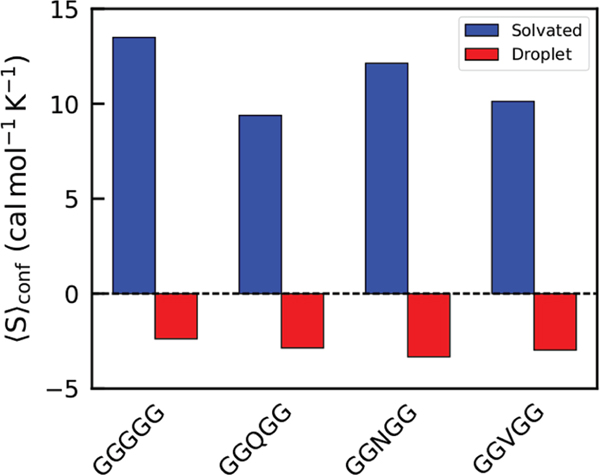
Figure 4.

Fitted conformational entropy values for aqueous (blue) and liquid droplet (red) phase peptides for the four systems. Form of fitting function is a-b/t.

Figure 3 shows $S_{\text{conf}}^{\text{MIE}}$ as a function of simulation time. Direct counting entropy calculation methods such as MIE tend to converge like $t^{-1}$ in the asymptotic regime while the initial stages have more noisy logarithmic behavior. Consequently, the tail (final 40%) of the curves in Figure 3 were fit to a hyperbolic function to determine the asymptote, and thus final $S_{\text{conf}}^{\text{MIE,fit}}$. Figure 4 contains $S_{\text{conf}}^{\text{MIE,fit}}$ values for the aqueous and droplet phases for the GGGGG, GGQGG, GGNGG, and GGVGG systems (also presented in Table 2). It is clear that aqueous peptides in all systems possess greater conformational entropy than peptides in the droplet phase. The entropy differences between peptides in the aqueous and droplet phases are 15.87, 12.24, 13.46, and 13.09 cal mol⁻¹ K⁻¹ for the GGGGG, GGQGG, GGNGG, and GGVGG peptides, respectively. The sequence appears to modulate the amount of conformational entropy available. Due to its conformational flexibility, GGGGG has the highest $S_{\text{conf}}^{\text{MIE,fit}}$ in both the aqueous and droplet phases. Identifying all the sources for the effects that individual side chains have on the conformational entropy, however, is not simple; GGQGG peptides have the lowest $S_{\text{conf}}^{\text{MIE,fit}}$ in the aqueous state followed by GGVGG and GGNGG in close succession. The entropies are grouped differently for the droplet phase data with GGNGG registering the lowest conformational entropy in that phase.

Table 2.

$S_{\text{conf}}^{\text{MIE,fit}}$Data for Aqueous and Droplet Phases and Transition $\text{Δ}{S}_{\text{tr}}^{\text{aq}\to \text{drop}}$ Data (cal mol⁻¹ K⁻¹)

	GGGGG	GGQGG	GGNGG	GGVGG
$S_{\text{conf}}^{\text{MIE,fit}}$(aqueous)	−2.38	−2.86	−3.33	−2.97
$S_{\text{conf}}^{\text{MIE,fit}}$(droplet)	13.49	9.38	12.13	10.12
$\text{Δ}{S}_{\text{tr}}^{\text{aq}\to \text{drop}}$	−18.02	−17.32	−17.54	−17.59

It is clear that the trend for $S_{\text{conf}}^{\text{MIE,fit}}$ does not dominate the solubility limits previously discussed. While GGGGG has the highest $S_{\text{conf}}^{\text{MIE,fit}}$ in the aqueous state and also the highest solubility limit, the trend with the other peptides does not reflect the solubility limits. The magnitude of the effect that sequence has on the conformational entropy is dampened by transition into the peptide droplet phase. While aqueous $S_{\text{conf}}^{\text{MIE,fit}}$ values vary by up to 4 cal mol⁻¹ K⁻¹ between sequences, the greatest variation between cal mol⁻¹ K⁻¹ in the droplet state is <1 cal mol⁻¹ K⁻¹.

We also sought to estimate the loss of translational and rotational entropy that occurs upon aqueous → droplet transition ($\text{Δ}{S}_{\text{tr}}^{\text{aq}\to \text{drop}}$) using Fogolari et al.’s PDBTRENT,⁵⁰ which employs a k-nearest neighbor approach described by Huggins.⁵² Using this method, we were able to obtain estimates for the average $\text{Δ}{S}_{\text{tr}}^{\text{aq}\to \text{drop}}$ of −18.02, −17.32, −17.54, and −17.59 cal mol⁻¹ K⁻¹ for the GGGGG, GGQGG, GGNGG, and GGVGG , respectively (shown in Table 2). The small change in $\text{Δ}{S}_{\text{tr}}^{\text{aq}\to \text{drop}}$ between sequences indicates that the addition of a side chain does not vary $\text{Δ}{S}_{\text{tr}}$ greatly for short sequences. It is evident that, for these pentapeptides, $\text{Δ}{S}_{\text{tr}}$is on the same order of magnitude as $\text{Δ}{S}_{\text{conf}}$ during LLPS. The longer side chain of the glutamine-containing peptide system causes the least negative backbone entropy change from aqueous to droplet, and the entropy changes of the other sequences get more negative with decreasing side chain length.

Interaction Enthalpy of Aqueous and Droplet Phase Peptides.

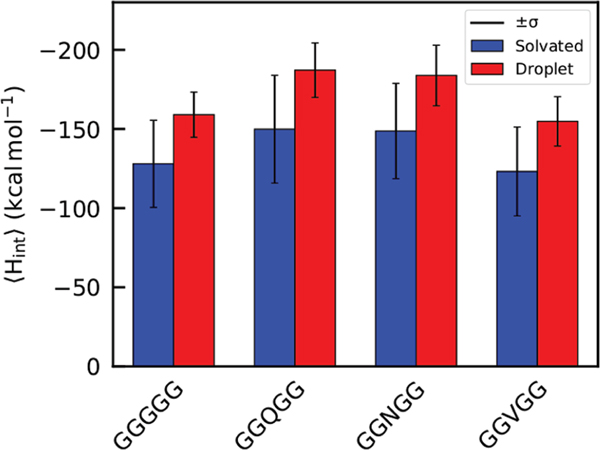
We have established that short pentapeptides forfeit backbone conformational entropy during aqueous → droplet phase separation. Next, we probed the nonbonding interactions of the peptides with their environment to consider enthalpy changes accompanying phase transition. Interaction enthalpies were calculated by obtaining the total nonbonded interaction energy of each peptide with its environment using the Amber14SB force field.⁴⁷ The energetic data are presented in bar graph format in Figure 5, with the droplet state data shown in the red bars and aqueous state data shown in blue. As evidenced in Figure 5, peptides in the droplet state possess higher interaction energies than those in the aqueous state. Tabulated $H_{\text{int}}$ values are presented in Table 3. From these data we observe that the addition of a polar side chain to aqueous pentaglycine grants GGQGG and GGNGG approximately 22 and 21 kcal mol⁻¹ greater $H_{\text{int}}$, respectively. In the droplet state this effect is enhanced, with GGQGG and GGNGG possessing $H_{\text{int}}$ values ~28 and 26 kcal mol⁻¹ greater than that of GGGGG. This is not unexpected. The peptide backbone is more polar than water. Also, glutamine and asparagine side chains can interact favorably with both water and peptides via electrostatic interactions. All of the peptide systems show a favorable decrease in $H_{\text{int}}$ when transitioned into the droplet phase. The amount of decrease varies between the four systems, with the GGQGG and GGNGG decreasing by 37.3 and 35.1 kcal mol⁻¹ while GGGGG and GGVGG decrease by 31.02 and 31.69 kcal mol⁻¹ respectively. This enhanced change in favorable $H_{\text{int}}$ when undergoing phase transition into liquid droplets also supports our previous findings that GGNGG and GGQGG form more stable droplets than GGGGG and GGVGG. We find, more generally, that the loss of conformational entropy that accompanies aqueous → droplet transitions is more than compensated by a decrease in interaction enthalpy as contributions to the free energy change for the process.

Figure 5.

Interaction enthalpy values for aqueous (blue) and liquid droplet (red) phase peptides. Error bars represent standard error of $H_{\text{int}}$ distribution.

Table 3.

Total $H_{\text{int}}$ Data for Aqueous and Droplet Phases (kcal mol⁻¹)

	GGGGG	GGQGG	GGNGG	GGVGG
$H_{\text{int}}$ (aqueous)	−128.0	−149.88	−148.71	−123.15
$H_{\text{int}}$ (droplet)	−159.03	−187.16	−183.83	−154.84

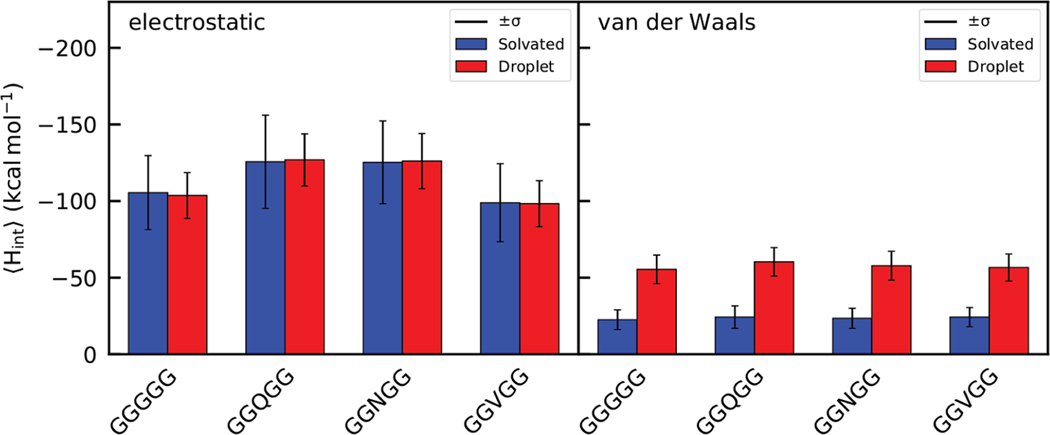
We decomposed the total interaction enthalpies into their electrostatic and van der Waals components for additional perspective into which interactions dominate during the phase transition. These data are presented in Figure 6. Average $H_{\text{int}}$ values from electrostatic interactions are shown on the left and those from van der Waals interactions are shown on the right. The vertical scale is the same for both graphs to emphasize differences in the size of the interactions. As expected, electrostatic interactions are significantly stronger in magnitude than van der Waals interactions for all phases and systems. However, the electrostatic $H_{\text{int}}$ does not change significantly upon phase transition, whereas the van der Waals $H_{\text{int}}$ shows a marked favorable decrease in the droplet phase compared to the aqueous phase. This result indicates that both water and peptide droplet environments are able to provide a similar amount of electrostatic interactions for the peptides, but the droplet environment enables more favorable van der Waals close contact interactions. This leaves the electrostatic enthalpy as mainly being a large background quantity, contributing a large proportion to the overall interaction enthalpy but not varying upon phase transition. Our simulations show that the observed difference between the $H_{\text{int}}$ in the aqueous and droplet phases originates with enhanced van der Waals interactions.

Figure 6.

Electrostatic and van der Waals interaction enthalpy values for aqueous (blue) and liquid droplet (red) phase peptides. Error bars represent standard error of $H_{\text{int}}$ distribution.

This is not unlike what has been observed for mixed solvent systems with peptides.^26,53 In aqueous peptide systems transferring to 1 M TMAO and/or urea, the electrostatics, while dominating in terms of absolute size in any one solution, contributed little discrimination to the solvation free energy differences of transfer with respect to chain length. The van der Waals interactions on the other hand, while smaller in magnitude in a given solution, were the main factor distinguishing the systems and revealing the experimental trends.⁵⁴

We also performed an analysis of the solvent interaction enthalpy of peptides on the interior of the peptide droplet. As stated earlier, we were able to observe many water molecules inside the droplet as seen previously,³¹ and we quantified this by calculating peptide–solvent interaction enthalpies for all systems. This analysis shows that interior droplet peptides, for the GGGGG, GGQGG, GGNGG, and GGVGG systems, have average peptide–solvent interaction enthalpies ($H_{\text{int}}$) of −57.7, −70.8, −69.0, and −60.7 kcal mol⁻¹ respectively. These energies represent over approximately one-third of the total $H_{\text{int}}$ (shown in Figure 5). This indicates that there is significant peptide–solvent interactions occurring inside the droplet, with interior droplet peptides possessing $H_{\text{int}}$ (peptide–water) over one-third that of solvated peptides. Histograms of the data can be found in Figure S2 in the Supporting Information.

DISCUSSION

Previous work at the atomic simulation level has explored the solubility of the glycine-rich pentapeptide systems studied here.³² In GGGGG, GGQGG, GGNGG, and GGVGG aqueous systems, the addition of a polar side chain (here Q and N) can cause larger, more stable aggregates to form, followed by a nonpolar sequence (V). This supports our previous study and also supports other studies in the field that implicate polar or charged amino acids in promoting disorder and aggregation.^55–57 More work needs to be done in the area of sequence-related relationships in the field of IDPs before accurate prediction of behavior based on sequence will become possible. For example, the optimal spacing of polar or charged residues for favoring disorder or phase separation is not generally understood but is an area of active study.⁵⁸

Investigation into the role of conformational entropy in liquid–liquid phase separation has been limited. Several studies have explored the role of the entropy of mixing^59,60 or solvation entropy⁶¹ in driving phase separation, but few have probed the exchange of entropy that takes place on the molecular level. Our study quantifies this effect for a set of peptides. The large difference between the $S_{\text{conf}}^{\text{MIE,fit}}$ values for the aqueous and droplet phases shown in Figure 4 illustrates the loss of backbone conformational entropy that occurs upon aqueous → droplet phase transition. Moreover, we have found that there is a loss of ~17–18 cal mol⁻¹ K⁻¹ in rotational and translational entropy that accompanies LLPS in these systems as well. Other studies and reviews have touched on the loss of conformational entropy stemming from more compact, conformationally restricted states during phase transitions,^62,63 but our results quantify this for disordered peptide LLPS. The $R_{\text{g}}$ analysis we performed indicates that peptides in the liquid droplet are less collapsed that those in solution but have lower conformational entropy. Caro et al.⁶⁴ have discussed how the latent conformational entropy of proteins can act as an entropic reservoir that can be coupled to molecular events such as ligand binding. Our results here suggest that disordered domains in proteins may be able to modulate the free energy of a process via liquid–liquid phase separation-associated entropy changes.

Our entropy findings here help explain the thermodynamics of liquid–liquid phase separation in systems of disordered peptides. Clearly, if there is an unfavorable loss of conformational entropy upon droplet transition, then other components must dominate the free energy surface. We find that favorable peptide–peptide interactions facilitated by the liquid droplet environment stabilize the droplets and compensate for the loss of free energy in the form of conformational entropy. Figure 5 contains the average total interaction enthalpies for peptides in the two phases and clearly shows that the enthalpies are uniformly lower, hence more favorable, in the droplet phase. Furthermore, Figure 6 shows that the intermolecular interactions responsible for this enthalpic disparity are van der Waals contacts arising from close contacts between peptides in the liquid droplet. Interestingly, in these pentapeptide systems, electrostatic $H_{\text{int}}$ does not appreciably vary between the aqueous and droplet phases. This indicates that, for glycine-rich peptides, the liquid droplet environment provides a similar level of electrostatic interaction as a water-solvated environment.

It has been observed that hydrophobic effects appear to play a role in some LLPS-linked proteins. Studies by Weiss et al.⁶⁵ and Rauscher et al.³⁹ as well as others indicate that the hydrophobic regions of elastin modulate its LLPS behavior. Solutions of elastin possess a lower critical solution temperature (LCST).⁶⁶ This is taken as an indicator of the dominance of hydrophic interactions. This is hypothesized to be a result of hydrophobic interactions being driven mainly by water entropy. The peptide sequences we have simulated here are primarily composed of glycine, which is not categorized as hydrophobic. We find here and previously³² that GGQGG is less soluble and thus forms more stable droplets than GGVGG, which is the sequence most similar to the repeating GVPGV motif in elastin. The nonpolar GGVGG shows the same decrease in conformational entropy and boost in vdW interaction enthalpy observed in the more polar peptide systems. Our systems do not suggest a naive hydrophobic effect dominating although we did not directly investigate the small differences in solvent thermodynamics.

The relationship between the van der Waals and electrostatic interaction enthalpy we observe echoes peptide osmolyte studies.^26,43,53 In that work, the majority of discrimination between urea and TMAO cosolvents on the solvation free energy originated in the van der Waals interactions whereas the electrostatic contribution was larger but did not change between structures. Our work here shows that peptides are able to achieve many more van der Waals contacts in a dense peptide phase than in water. The electrostatic interactions are larger in magnitude and dominate the total interaction enthalpy but are similar in size in both phases and do not change significantly during transition. Neither here nor in previous studies do we find H-bonding playing the dominant role in the droplet phase peptides’ electrostatic interactions.

CONCLUSIONS

In this study, we develop a thermodynamic framework for understanding the liquid–liquid phase separation of proteins. The polypeptide test compounds used here are not meant to represent the details of longer protein sequences where the entropy–enthalpy balance is more complex. We studied these simpler model systems to better understand some of the individual thermodynamic contributions in phase separation common to amino acid systems. Our backbone conformational entropy calculations from aqueous GGGGG, GGQGG, GGNGG, and GGVGG liquid–liquid phase separation show that ~28 cal mol⁻¹ K⁻¹ of absolute entropy is lost upon the aqueous → droplet transition. This fits a framework of viewing disordered protein backbones as containing latent rotational, translational, and conformational entropy, which may be accessed or expended by conformational rearrangement. Upon analysis of the average interaction enthalpy of peptides in both the aqueous and liquid droplet phases, we observe a significant increase in favorable interactions in droplet phase peptides. A component breakdown reveals this to be a consequence of many electrostatic interactions providing a large enthalpic background and more discriminating van der Waals interactions that are facilitated by the peptide droplet environment. These observations suggest that disordered peptides can utilize phase separation to modulate their free energy via balancing of backbone conformational entropy and van der Waals contact enthalpy.