Abstract
Percutaneous nephrolithotomy (PCNL) is considered a first-choice minimally invasive procedure for treating kidney stones larger than 2 cm. It yields higher stone-free rates than other minimally invasive techniques and is employed when extracorporeal shock wave lithotripsy or uteroscopy are, for instance, infeasible. Using this technique, surgeons create a tract through which a scope is inserted for gaining access to the stones. Traditional PCNL tools, however, present limited maneuverability, may require multiple punctures and often lead to excessive torquing of the instruments which can damage the kidney parenchyma and thus increase the risk of hemorrhage. We approach this problem by proposing a nested optimization-driven scheme for determining a single tract surgical plan along which a patient-specific concentric-tube robot (CTR) is deployed so as to enhance manipulability along the most dominant directions of the stone presentations. The approach is illustrated with seven sets of clinical data from patients who underwent PCNL. The simulated results may set the stage for achieving higher stone-free rates through single tract PCNL interventions while decreasing blood loss.
Keywords: Percutaneous Nephrolithotomy, Surgical Planning, Continuum Robotics, Nonlinear Optimization
1. Introduction
Percutaneous nephrolithotomy (PCNL) is a preferred treatment method for removing renal calculi (kidney stones) larger than 2 cm [7]. In PCNL, a urologist or radiologist determines the skin position and the primary calyx to puncture based on diagnostic CT scans for removing the stone, while considering smaller stones situated in harder to reach calyces [7]. In fact, the placement of percutaneous access is the most critical aspect of PCNL inasmuch as the clinical outcome is highly dependent on the accuracy of the preoperative image-based planning [17,19]. Largely due to difficulties in obtaining a percutaneuous access, a 2007 survey [11], found that only 27% of urologists who were trained in percutaneous access during residency continued to gain their own PCNL renal access with this percentage reducing to 11% amongst those who were untrained. In this setting, the best plan is one which allows the removal of the entire stone via a single tract while safeguarding surrounding tissues, organs, and blood vessels.
Owing to the structure of rigid nephroscopes and lithotripsy tools, accessing all stones from a single incision can be challenging. Once the tool is inserted into the renal collecting ducts, gentle torques must be applied to maintain skin and tissue integrity and decrease potential damage to the surrounding tissue. For many stone presentations, multiple punctures may be required to successfully break and clear all stone fragments. However, this can lead to increased hemorrhagic complications [10]. Additionally, multiple punctures may lead to increased radiation exposure due to the need for including fluoroscopic guidance [23], increased operating time, increased anesthesia use, and increased risk of damage to surrounding tissue, kidney, and skin. Kyriazis et al [10] compared multiple punctures to upper or lower kidney pole access, and showed that multiple-puncture patient groups required significantly more blood transfusion than their single puncture counterparts. In [8], single-tract patient groups had shorter hospital stay with no patient requiring blood transfusion. Lastly, the PCNL procedure for stones larger than 2 cm is reported to be 89.4% successful with an associated 13% complication rate due to the challenges of navigating the entire stone [15].
Against this background, the use of flexible robotic tools in PCNL may reduce the number of punctures and improve the stone-free rate while reducing the risk of tissue damage and hemorrhagic complications.
1.1. Concentric-Tube Robots (CTRs)
Our approach hinges on the use of CTRs as a means of gaining access to the renal collecting system. These special manipulators consist of a set of precurved and superelastic tubes that are concentrically inserted one inside another. Under independent and relative translational and rotational actuation of its component tubes, elastic interactions between overlapping sections of the tubes take place to yield the final equilibrium shape of the backbone [20]. Given their slender size and kinematic capability of achieving complex curved shapes, CTRs are particularly attractive for applications such as PCNL where the robot must navigate tortuous paths from the port of entry to the clinical targets while avoiding structures such as the lung, liver, spleen, colon and renal vessels.
For the purposes of this work, we consider a three-tube CTR whereby the innermost and intermediate tubes are composed of an initial straight transmission section followed by a curved section with constant curvature. The outermost tube, however, is restricted to be straight.
1.2. Related Work
The number of tubes in the concentric arrangement and their corresponding kinematic parameters govern the kinematic behavior of CTRs and, thus, provides this class of robotic manipulators considerable freedom with respect to the number of possible designs that can be considered. As such, the selection of suitable designs for minimally invasive medical interventions must be guided by both the application and the patient-specific anatomy.
Several approaches have been reported in the literature in which methods are devised to design task-oriented, patient-tailored CTRs. Burgner et al. [4,5] proposed a grid search, voxel-based algorithm for maximizing the volume coverage of the clinical target while accounting for anatomical constraints. Bergeles et al. [3] proposed a framework for CTR design that optimizes the reachability of a set of targets while minimizing the lengths and curvatures of the tubes for kinematic stability while satisfying anatomical constraints. Morimoto et al. [13,14] introduced a surgeon-in-the-loop approach in which the tube parameters are calculated based on via points created manually by a medical expert in a virtual reality environment. Torres et al. [22] goes further and proposes a method for designing CTRs accounting for collision-free deployment from the port of entry to the targets by integrating a sampling-based motion planner. On a similar note, [1] attains asymptotic global optimality in the design of a variety of robots, CTR included, by integrating a sampling-based motion planner and stochastic optimization.
1.3. Contribution of the Paper
In this paper, we report a set of results on the issues of surgical planning and the design of patient-specific CTRs for PCNL. In contrast to [13,14], we account for the constraint at the renal pyramids and calyces for all posible configurations in which the CTR is deployed in the kidney. As opposed to [2], our method returns one single CTR design, thus not requiring change of tools and consequent redeployment of the robot into the anatomy during the PCNL procedure. The main contributions of this paper consist of a comprehensive framework, independent of any user’s inputs, for devising surgical plans for percutaneous and renal access by virtue of patient-specific CTR designs. The algorithms developed can be applied seamlessly to different clinical cases. Once an optimized design is obtained, the proposed constrained inverse kinematics guides the navigation of the anatomically constrained manipulator within the kidney. In what follows, we briefly describe our method and demonstrate its usefulness by applying our algorithms to real clinical data of seven patients who underwent PCNL.
2. Surgical Planning
An appropriate percutaneous access is paramount to an effective PCNL as critical anatomical structures such as the bowel, spleen, liver, pleura and lungs must be avoided while allowing direct access to the kidney calculi, see Fig. 1. In addition, a suitable renal pyramid must be identified for renal access. To minimize damage to renal vassels, the CTR backbone must be contained within the caliceal ducts throughout the duration of the procedure.
Fig. 1:
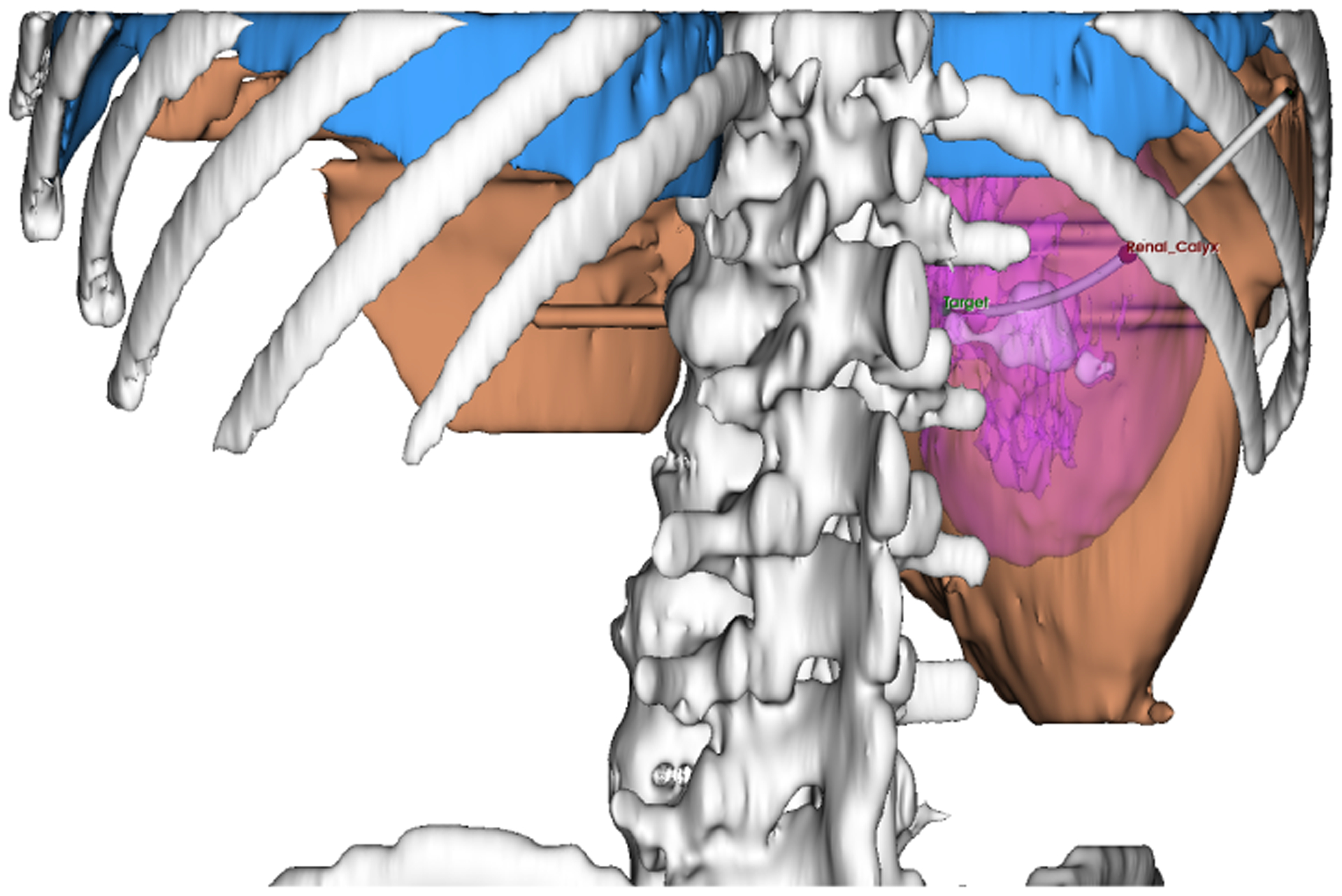
Skeleton (gray), liver (amber), pleura (blue), kidney (magenta), kidney stones (white), renal pyramid (red marker), distal target (green marker)
In our approach, the surgical planning phase starts from an initial arbitrary CTR design and its corresponding constrained inverse kinematics (C-IK). Computer tomography (CT) scans segmented in 3D Slicer [6] provide information on the geometry and location of the stones, kidney, renal pyramids, and a patch of skin in the patient’s supracostal region. Given the initial CTR design, the percutaneous access is selected by means of a grid search across skin points and renal pyramids such that the distal end of the CTR is delivered to the centroid of the stone with the smallest possible deviation at the pyramid. A surgical plan is described by a bijective transformation H ∈ SE(3) which defines a supracostal puncture location as well as an insertion angle for the CTR and surgical tools. Any remaining position deviations, either at the end-effector or renal calyx, will be dealt with subsequently during the CTR design optimization.
Constrained Inverse Kinematics (C-IK) for CTRs
Classically, the inverse kinematics (IK) problem for redundant manipulators has been addressed with by means of a composition of a minimum norm solution with local gradient projection techniques on the kernel of the corresponding Jacobians [18]. Here, we cast the IK for CTRs as a sequential quadratic programming (SQP) problem where the constraints and secondary goals are addressed in a more explicit manner.
Let and denote the augmented vector and augmented Jacobian of spatial velocities at the end-effector and renal calyx, respectively. Then the C-IK is cast as
| (1) |
where is the vector of joint velocities of the CTR, is a slack variable used to relax the kinematic constraints on spatial velocities at both the end-efector and the renal calices, Ω,Λ are positive definite matrices of appropriate dimensions, and q+,−,δ+,− impose upper and lower bounds on the joint positions (resolved-rate collision avoidance) and spatial velocities relaxation.
3. Patient-Specific Design of CTRs
A key aspect of our approach is an ellipsoidal approximation to a point cloud describing the geometry of the kidney stone. Simply put, the stone presentation is modeled as the minimum-volume covering ellipsoid (MVCE) which envelops all stone fragments. The computation of the MVCE is formulated as the following optimization problem [24]:
| (2) |
where is the center of the ellipsoid whose shape is defined by the positive definite matrix Q. By virtue of this ellipsoidal approximation, we lay the ground-work for the objective patient-specific design of CTRs across multiple patients with a single framework. More importantly, this approach allows us to claim that the semi-axes of the MVCE identify what we term as the dominant directions of the stone presentation, i.e., the most frequent directions that surgeons will find themselves navigating along during the stone ablation procedure.
3.1. Problem Formulation
Let us denote the MVCE in (2) by EQ,c and the extreme points of each of its semi-axes by pi, where each pi lies on the surface of EQ,c. We seek a set of tube kinematic parameters that allows the CTR to reach the points pi for i = 1,…, 6. As alluded to in Subsection 1.1, the structure of the CTR we consider for this problem is that of a three-tube CTR in which the outermost tube is straight whereas the remaining two consist of a straight section followed by a curved one. In view of this, we characterize the design space for the CTR as comprising the lengths of the straight and curved sections as well as the radii of curvature for tubes one and two (innermost and intermediate tubes). As a result, the design space is represented by a 6-dimensional vector of parameters, namely p = [ls1 lc1 ls2 lc2 r1 r2]⊺, where lsj, lcj, and rj represent the lengths of the straight and curved sections, and the radius of curvature of the jth tube respectively. For the sake of tractability, we limit the design space to the six aforementioned parameters by fixing the remaining kinematic parameters such as the inner/outer diameters of the tubes and their Young’s/shear modulus.
The shape and pose of the CTR backbone in the the patient’s coordinate frame is defined by means of an access port which dictates the skin puncture location as the position from which the CTR is deployed as well as the insertion angle (orientation) hport ∈ SO(3). For computing the CTR kinematics (see [20]), βi < βi+1 ≤ 0 defines the length of linear insertion/retraction of the ith CTR component tube and αi ∈ [0, 2π), its rotation. As such, any CTR configuration can be expressed as q = {βi, αi}i=1,2,3. Given any such configuration q, the CTR shape is defined by a parametric curved, via the arc-length variable s ∈ [0, L], such that Γ(q, L) yields the end-effector position xee while Γ(q, 0), the skin puncture position x0.
Define a vector valued distance function mapping the design space into a corresponding vector of accumulated minimum deviations at the distal end and renal calyx with respect to their desired positions. Namely, for any CTR design, the distance function f(·,·) yields the minimum accumulated deviation with respect to the end-effector and the renal calices after running the constrained inversed kinematics (1):
| (3) |
where is the point on the CTR backbone which is closest to the renal pyramid, computed via orthogonal projection, when the CTR’s end-effector is steered to the point pi of EQ,c.
From this background, the problem of determining a viable CTR design becomes a root-finding problem for the distance-like function (3), i.e., we seek a set of kinematic parameters which evaluate the ℒ2 norm of f(q, 𝒟) to zero within a specified numerical tolerance ε > 0. In this pursuit, we employ the iterative Nelder-Mead simplex algorithm, which is a direct search method for nonlinear multidimensional unconstrained minimization [16].
So that a box-constrained optimization problem can be considered with accepteable bounds on the tubes’ lengths and pre-curvatures, the Nelder-Mead algorithm is instantiated as a subsidiary optimization algorithm to an augmented Lagrangian method implemented in C++ using the NLopt library [9]. In other words, the design optimization of the CTR tubes’ is cast as the following nonlinear constrained optimization problem
| (4) |
where lower and upper bounds are imposed on the lengths of the straight ℓsi and curved ℓci sections of the tubes as well as on the pre-curvature vectors ui. Additionally, for any tube pair, the overall length of the innermost Li tube must exceed that of the outer tube Li+1 with a minimum prescribed tolerance γi > 0.
4. Study Cases
We apply the optimization algorithm (4) on the clinical data of seven patients who underwent PCNL at the Massachusetts General Hospital under an institutional review board (IRB) approved protocol. In this context, the clinical data consists of preoperative CT scans from which a digital segmentation on 3D Slicer [6] yields a point cloud representing the shape and pose of the stones in the patient coordinate frame. The seven cases considered in this paper, see Fig. 2, were drawn from a larger database of clinical patient data. Across all cases considered, a CTR design is deemed apropriate if it can deliver the distal end to the points pi, i = 1,…, 6 along the kidney stones’ main directions while maintaining a radial position deviation of ε = 5 mm at the chosen renal calyx.
Fig. 2:
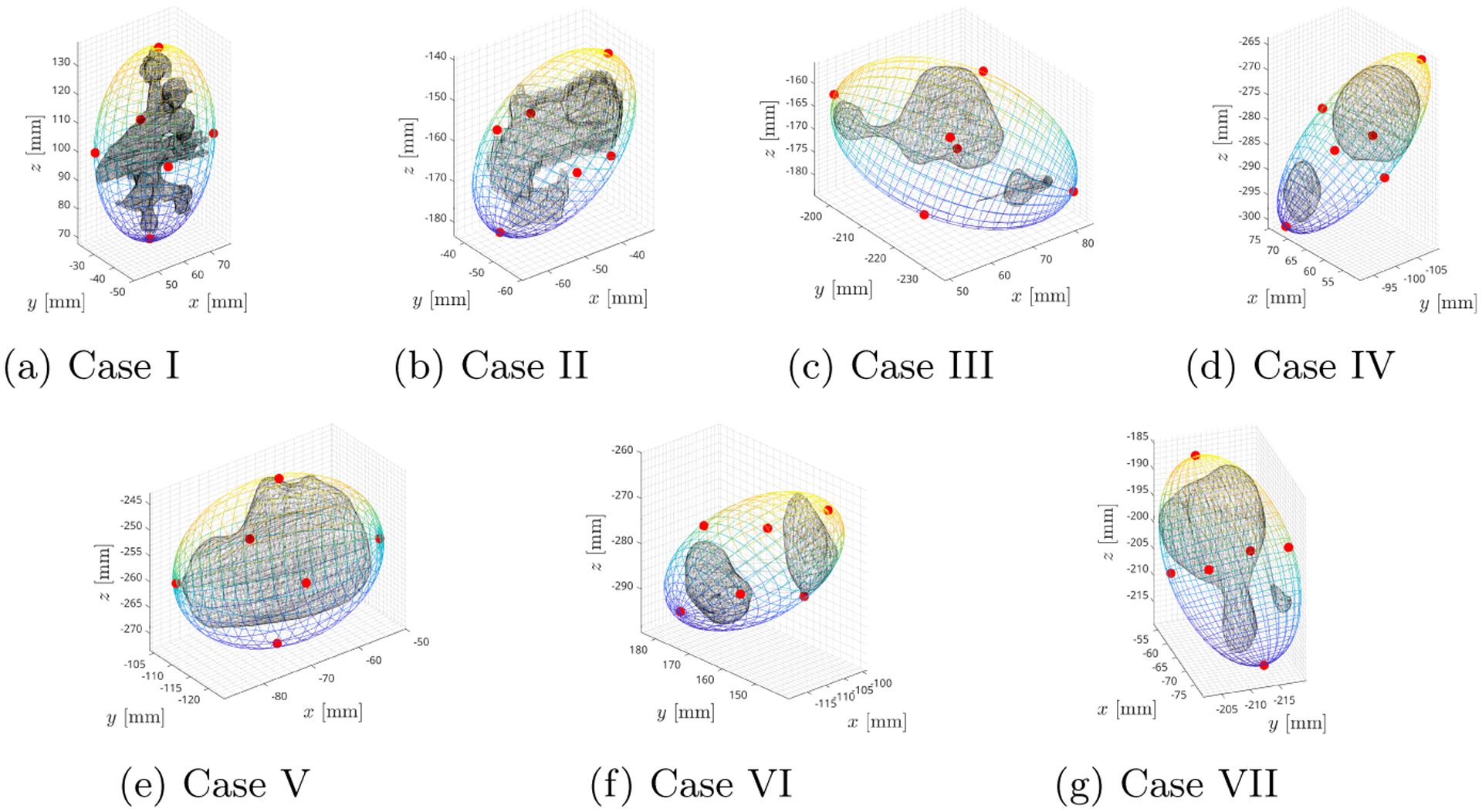
MVCE is shown with kidney stones (black) and the critical points pi which define the dominant directions of the kidney stone presentation (red markers).
5. Results
We applied the optimization algorithms to the seven clinical cases, as depicted in Fig. 2. The simulation results were obtained by running all seven cases in parallel on a Intel i5-7500, 3.40GHz Linux-based machine and took 5 hours. For all cases, the algorithm (4) was run three successive times for the purpose of refining the solutions obtained. With the aim of investigating the kinematic capabilities of the optimized CTR in each case, the corresponding CTRs were steered along the direction defined by the points pi ∈ EQ,c by means of the C-IK in (1). The error distributions at the calyx and distal ends are shown by the boxplots in Fig. 3.
Fig. 3:
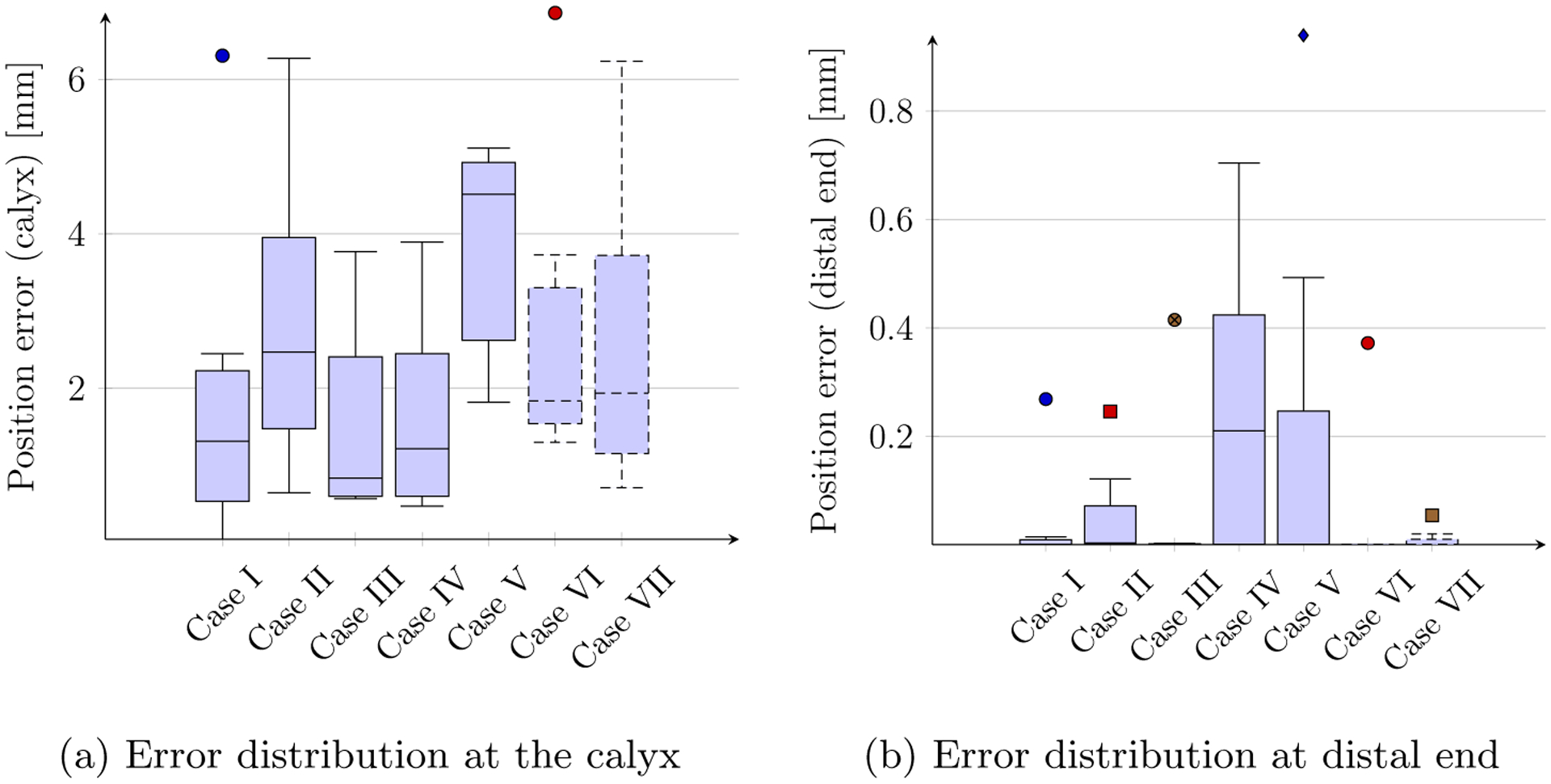
Position error distributions of the anatomically constrained CTR
It is worthwhile mentioning that, anatomically, in order to minimize vascular injury while obtaining the largest endoscopy angle, the ideal route for renal access passes through the axis of the target renal calyx [12,21]. However, given the diameter of the calyceal tracts, a 5 mm radial deviation with respect to the longitudinal axis of the targeted calyx during stone ablation is commonly deemed acceptable urologists. On the other hand, the distal end is also amenable to small position errors (usually < 3 mm) as the emitted shockpulse lithotripsy waves affect neighboring regions of each point in the stone.
6. Conclusion
In this paper, we described an ellipsoidal approximation to kidney stones which underpins our approach to surgical planning and patient-specific design of CTRs for PCNL. By optimizing a set of kinematic tube parameters and the reachability of 6 critical points of the MVCE enclosing the stone presentation, our approach strives to enhance the manipulability of the robot along the dominant directions of the stone presentation. The approach is illustrated by seven clinical cases which demonstrates the usefulness of the algorithms presented.
While other existing approaches (see Subsection 1.2) can be used, a priori, for the purpose of designing patient-specific CTRs, our approach can be applied seamlessly, as illustrated by the clinical cases of Section 4, to a myriad of cases of distinct clinical complexities while addressing the important constraint at the renal pyramid/calyces explicitly. Moreover, once an optimized CTR design is obtained, the proposed constrained inverse kinematics (C-IK) in (1) can be employed for guiding the navigation of the anatomically constrained CTR within the collecting system with clinically accepted tolerances as shown in Fig. 3.
In our future work, we plan to address the limitations in the current approach whereby intraoperative CT scans and ultrasound imaging modalites will allow us to depart from the static anatomy assumption in this paper and consider tissue deformation, fragmentation and shift of the stone burden in the kidney. We also plan to consider distinct optimization metrics and conduct a sensitivity analysis of the surgical plan and optimized CTR design in the face of dynamic effects in the anatomy.
Acknowledgements
This work was supported by the National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health through Grant Number R01DK119269 and by the Natural Sciences and Engineering Research Council (NSERC) of Canada grant RGPIN1345 (Discovery Grant), and the Canada Research Chairs Program.
References
- 1.Baykal C, Bowen C, Alterovitz R: Asymptotically optimal kinematic design of robots using motion planning. Autonomous Robots 43(2), 345–357 (Feb 2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Baykal C, Torres LG, Alterovitz R: Optimizing design parameters for sets of concentric tube robots using sampling-based motion planning. In: 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). pp. 4381–4387 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bergeles C, Gosline AH, Vasilyev NV, Codd PJ, del Nido PJ, Dupont PE: Concentric tube robot design and optimization based on task and anatomical constraints. IEEE Transactions on Robotics 31(1), 67–84 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Burgner J, Gilbert HB, Webster RJ: On the computational design of concentric tube robots: Incorporating volume-based objectives. In: 2013 IEEE International Conference on Robotics and Automation. pp. 1193–1198 (2013) [Google Scholar]
- 5.Burgner J, Rucker DC, Gilbert HB, Swaney PJ, Russell PT, Weaver KD,Webster RJ: A telerobotic system for transnasal surgery. IEEE/ASME Transactions on Mechatronics 19(3), 996–1006 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fedorov A, Beichel R, Kalpathy-Cramer J, Finet J, Fillion-Robin JC, Pujol S, Bauer C, Jennings D, Fennessy F, Sonka M, Buatti J, Aylward S, Miller JV, Pieper S, Kikinis R: 3D Slicer as an image computing platform for the quantitative imaging network. Magnetic Resonance Imaging 30(9), 1323 – 1341 (2012), quantitative Imaging in Cancer [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ganpule AP, Vijayakumar M, Malpani A, Desai MR: Percutaneous nephrolithotomy (PCNL) a critical review. International Journal of Surgery 36, 660–664 (2016) [DOI] [PubMed] [Google Scholar]
- 8.Hegarty NJ, Desai MM: Percutaneous nephrolithotomy requiring multiple tracts: Comparison of morbidity with single-tract procedures. Journal of Endourology 20(10), 753–760 (2006), [DOI] [PubMed] [Google Scholar]
- 9.Johnson SG, Schueller J: Nlopt: Nonlinear optimization library. Astrophysics Source Code Library pp. ascl–2111 (2021) [Google Scholar]
- 10.Kyriazis I, Panagopoulos V, Kallidonis P, Özsoy M, Vasilas M, Liatsikos E: Complications in percutaneous nephrolithotomy. World Journal of Urology 33(8), 1069–1077 (2015) [DOI] [PubMed] [Google Scholar]
- 11.Lee CL, Anderson JK, Monga M: Residency training in percutaneous renal access: does it affect urological practice? The Journal of urology 171(2), 592–595 (2004) [DOI] [PubMed] [Google Scholar]
- 12.Miller NL, Matlaga BR, Lingeman JE: Techniques for fluoroscopic percutaneous renal access. The Journal of urology 178(1), 15–23 (2007) [DOI] [PubMed] [Google Scholar]
- 13.Morimoto TK, Cerrolaza JJ, Hsieh MH, Cleary K, Okamura AM, Linguraru MG: Design of patient-specific concentric tube robots using path planning from 3-d ultrasound. In: 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). pp. 165–168 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Morimoto TK, Greer JD, Hawkes EW, Hsieh MH, Okamura AM: Toward the Design of Personalized Continuum Surgical Robots. Ann. Biomed. Eng 46(10), 1522–1533 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mousavi-Bahar SH, Mehrabi S, Moslemi MK: The safety and efficacy of PCNL with supracostal approach in the treatment of renal stones. International Urology and Nephrology 43(4), 983–987 (2011) [DOI] [PubMed] [Google Scholar]
- 16.Nelder JA, Mead R: A simplex method for function minimization. The computer journal 7(4), 308–313 (1965) [Google Scholar]
- 17.Netto NR Jr, Ikonomidis J, Ikari O, Claro JA: Comparative study of percutaneous access for staghorn calculi. Urology 65(4), 659–662 (2005) [DOI] [PubMed] [Google Scholar]
- 18.Ott C, Dietrich A, Albu-Schäffer A: Prioritized multi-task compliance control of redundant manipulators. Automatica 53, 416–423 (2015) [Google Scholar]
- 19.Rais-Bahrami S, Friedlander JI, Duty BD, Okeke Z, Smith AD: Difficulties with access in percutaneous renal surgery. Therapeutic Advances in Urology 3(2), 59–68 (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rucker DC, Jones BA, Webster RJ III: A geometrically exact model for externally loaded concentric-tube continuum robots. IEEE Transactions on Robotics 26(5), 769–780 (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Seitz C, Desai M, Häcker A, Hakenberg OW, Liatsikos E, Nagele U, Tolley D: Incidence, prevention, and management of complications following percutaneous nephrolitholapaxy. European urology 61(1), 146–158 (2012) [DOI] [PubMed] [Google Scholar]
- 22.Torres LG, Webster RJ, Alterovitz R: Task-oriented design of concentric tube robots using mechanics-based models. In: 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. pp. 4449–4455 (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yang YH, Wen YC, Chen KC, Chen C: Ultrasound-guided versus fluoroscopy-guided percutaneous nephrolithotomy: a systematic review and meta-analysis. World Journal of Urology 37(5), 777–788 (2019) [DOI] [PubMed] [Google Scholar]
- 24.Yildirim EA: On the minimum volume covering ellipsoid of ellipsoids. SIAM Journal on Optimization 17(3), 621–641 (2006) [Google Scholar]


