Abstract
Cryopreservation by vitrification to achieve an “ice free” glassy state is an effective technique for preserving biomaterials including cells, tissues, and potentially even whole organs. The major challenges in cooling to and rewarming from a vitrified state remain ice crystallization and cracking/fracture. Ice crystallization can be inhibited by the use of cryoprotective agents (CPAs), though the inhibition further depends upon the rates achieved during cooling and rewarming. The minimal rate required to prevent any ice crystallization or recrystallization/devitrification in a given CPA is called the critical cooling rate (CCR) or critical warming rate (CWR), respectively. On the other hand, physical cracking is mainly related to thermomechanical stresses, which can be avoided by maintaining temperature differences below a critical threshold. In this simplified analysis, we calculate ΔT as the largest temperature difference occurring in a system during cooling or rewarming in the brittle/glassy phase. This ΔT is then used in a simple “thermal shock equation” to estimate thermal stress within the material to decide if the material is above the yield strength and to evaluate the potential for fracture failure. In this review we aimed to understand the limits of success and failure at different length scales for cryopreservation by vitrification, due to both ice crystallization and cracking. Here we use thermal modeling to help us understand the magnitude and trajectory of these challenges as we scale the biomaterial volume for a given CPA from the milliliter to liter scale. First, we solved the governing heat transfer equations in a cylindrical geometry for three common vitrification cocktails (i.e., VS55, DP6, and M22) to estimate the cooling and warming rates during convective cooling and warming and nanowarming (volumetric heating). Second, we estimated the temperature difference (ΔT) and compared it to a tolerable threshold (ΔTmax) based on a simplified “thermal shock” equation for the same cooling and rewarming conditions. We found, not surprisingly, that M22 achieves vitrification more easily during convective cooling and rewarming for all volumes compared to VS55 or DP6 due to its considerably lower CCR and CWR. Further, convective rewarming (boundary rewarming) leads to larger temperature differences and smaller rates compared to nanowarming (volumetric rewarming) for all CPAs with increasing failure at larger volumes. We conclude that as more and larger systems are vitrified and rewarmed with standard CPA cocktails, this work can serve as a practical guide to successful implementation based on the characteristic length (volume/surface area) of the system and the specific conditions of cooling and warming.
Keywords: critical cooling rate, critical warming rate, temperature difference, vitrification
INTRODUCTION
Cryopreservation by vitrification has been increasingly studied in various biomaterials, including cells (1, 2), tissues (3, 4), organs (5, 6, 7), and organisms (8, 9), since the first practical demonstrations in the 1980s. Vitrification involves rapidly cooling of a sample to below its glass transition temperature (Tg) to surpass significant ice crystallization (ice nucleation and growth) and form a glassy (amorphous) state (4, 10). The cooling rate required to achieve the vitrified state should be at least higher than the critical cooling rate (CCR), which is defined as the minimum rate needed to avoid any significant ice crystallization (such as ice formation restricted to 0.2% of solution mass) (11). Similarly, the rewarming rate should be greater than the critical warming rate (CWR) to prevent devitrification and/or ice recrystallization. Here, practical vitrification success is usually assumed if the ice can be confined to less than 0.2–0.5% of solution mass (7, 12). Perhaps most importantly, once vitrified, a biomaterial can in theory be stored in this state indefinitely as metabolism effectively ceases at cryogenic temperatures.
Vitrification has been demonstrated and applied successfully since 1984 in a variety of systems ranging from embryos (13) to rabbit kidneys (4), but rewarming from a vitrified state remains the major hurdle in successful cryopreservation, especially in larger volume systems (14). For instance, convectively vitrified rabbit kidneys have only been rewarmed successfully once in the past (14), suggesting scale up for larger volumes such as human organs by convection alone will be difficult or impossible. Nanowarming is an emerging volumetric rewarming technology that may address this limitation through the use of radiofrequency-activated magnetic nanoparticles (e.g., iron-oxide nanoparticles IONPs). These IONPs can be perfused throughout the organ vasculature prior to vitrification and heated by magnetic hysteresis losses in the presence of an alternating magnetic field generated by a radiofrequency coil (15, 16). Recent studies in organs such as rat kidneys and hearts have shown promising results in terms of achieving rapid heating rates (~60°C/min and ~70°C/min) uniformly throughout the organ (17, 18, 19). This effectively changes the paradigm from failures most commonly occurring during warming to failures now during cooling when working at human organ scales (20). This failure can occur due to slow rates (i.e., cooling rate < CCR) and excessive thermomechanical stresses induced by cooling restricted to the edges of the container. Both of these issues are being actively investigated by careful analysis of human-scale kidney cooling and assessing the benefits of different containers to avoid stress accumulation, i.e., cryobags with expandable boundaries (21, 22, 23).
While many previous studies have focused on assessing vitrification success and failure in systems of various sizes, we have not found a clear, practical guide for vitrification in bulk systems that can help guide convection or nanowarming choices to achieve the necessary CCR and CWR and avoid thermal stress–generated cracks. Here we provide practical guidance on how to avoid ice formation as well as thermal stress–induced fractures, using several convective cooling and rewarming boundary conditions. In the case of nanowarming, iron oxide nanoparticles (IONPs) are assumed to be distributed throughout the modeled geometry with a constant heat generation per mg Fe (24). Correlations for cooling and warming rates and temperature differences (ΔT) as a function of the experimental conditions (i.e., characteristic length, convective condition, and CPA choice—VS55, M22, or DP6) have been derived. In summary, this work provides simple guidance on how to achieve vitrification success for given experimental conditions.
MATERIALS AND METHODS
A 2-D axisymmetric, finite cylindrical geometry is assumed for the bulk biomaterial undergoing cryopreservation. Heat transfer inside the geometry is assumed to occur primarily through conduction due to the very high viscosity of CPAs at cryogenic temperatures (i.e., the domain is assumed to be a solid in modeling) (25). We analyzed five different volumes of finite cylinders, ranging from 1 mL to >1 L, relevant to different biomaterial sizes, with varying diameters and heights, as listed in Figure 1. Characteristic length (Lc) was computed for each volume as the ratio of volume to total surface area of the cylinder. Equation [1] is the general form of the governing equation for the model, and additional details about boundary conditions, initial conditions, and non-homogenous terms are further provided in Table 1 and Figure 2. The geometry (containing the biological material such as organs, tissues, etc.) was assumed to be fully equilibrated with the CPA, so properties were also assumed to be uniform. The thermal and mechanical properties of each CPA were assigned to the geometry as listed in Table 2. A finite element analysis (FEA) was performed in the commercial package COMSOL 5.4 using the heat transfer module to solve the governing heat equation for the defined geometry. Domain point probes were attached at the center (r, z = 0) and edge (defined as 10% of the distance from the boundary in order to avoid immediate edge effects at the convective boundary).
Figure 1.
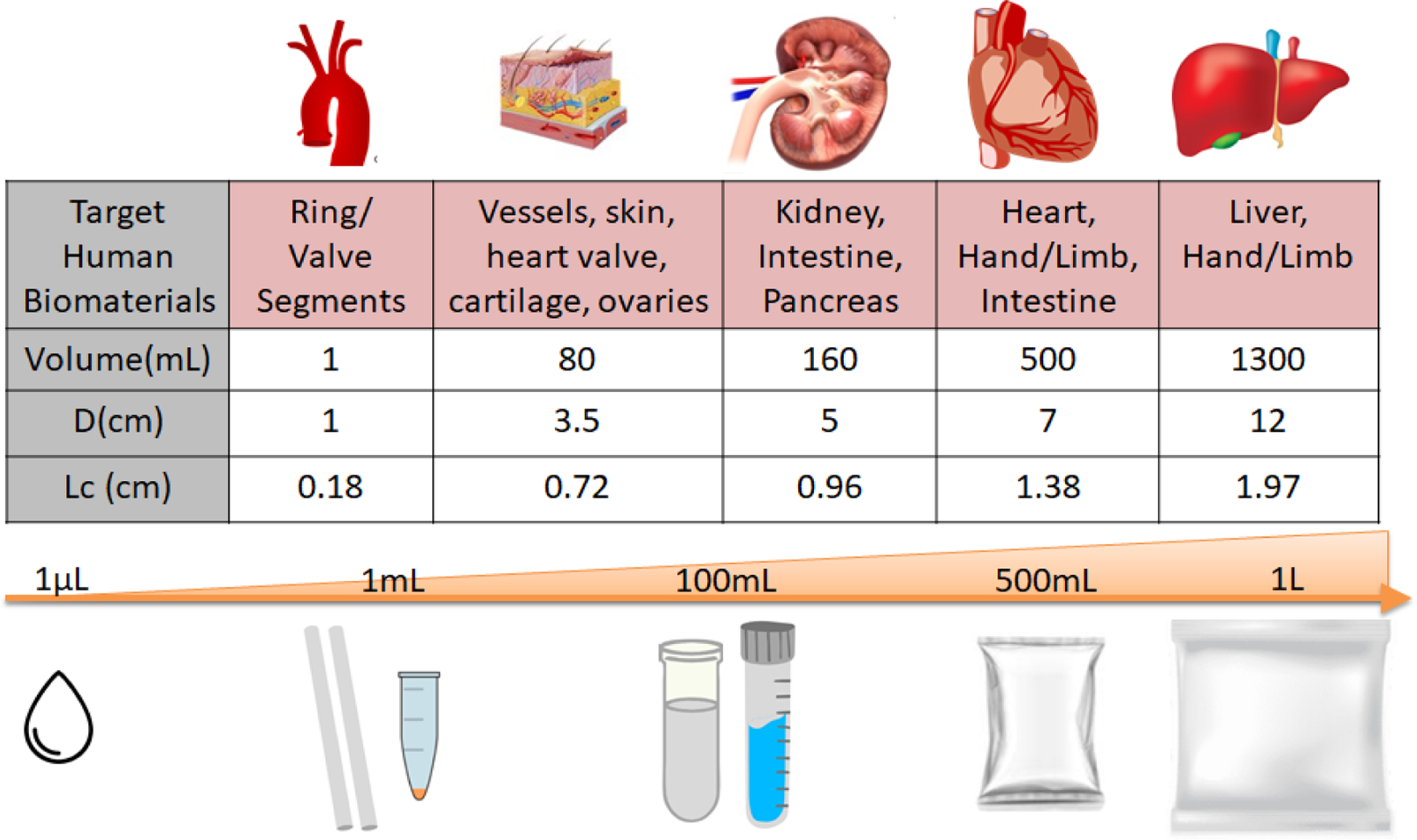
Representative dimensions and the corresponding characteristic length scales for common bulk systems that undergo vitrification.
Table 1.
Governing equations, boundary conditions, and initial conditions simulated for all three different cases analyzed in this study and relevant to cryopreservation by vitrification.
| Case | Convective Cooling | Convective Warming | Nanowarming |
|---|---|---|---|
| Governing Equation | |||
| Initial Condition | |||
| Boundary Condition |
Adiabatic |
Figure 2.
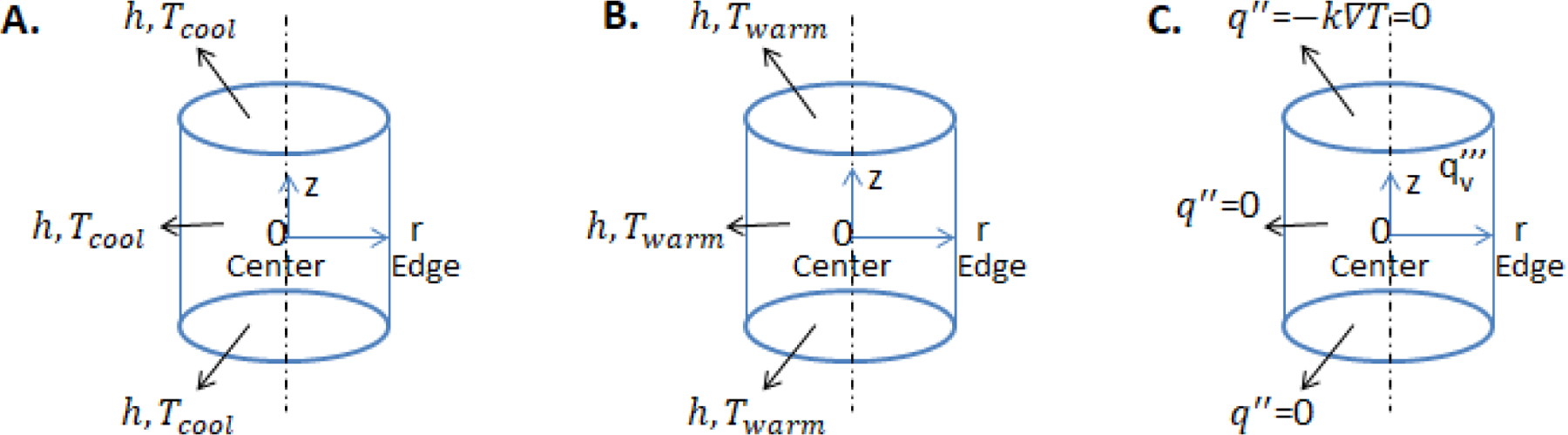
Schematic of modeled cylindrical geometry in FEA for (A.) convective cooling, (B.) convective warming, and (C.) nanowarming, depicting corresponding boundary conditions.
Table 2.
Thermo-physical properties and critical rates of VS55, DP6, and M22.
| CPA | Thermal conductivity, k [W/m.K] | Specific heat, Cp [KJ/kg.K] | Density, ρ [kg/m3] | Coefficient of linear thermal expansion, β [1/°C] | CCR [°C/min] |
CWR [°C/min] |
|---|---|---|---|---|---|---|
| VS55 | 0.3 (ref 29) |
3.011 [−1.5°C] 2.925 [−21°C] 2.819 [−44.5°C] 2.715 [−78.8°C] 2.968 [−118°C] 1.134 [−128°C] 0.985 [−150°C] (ref 47) |
1100 (ref 16) |
1.785*10−4 (ref 27) |
<~1 (ref 33) |
~50 (ref 33) |
| DP6 | 0.3 (29) |
2.984 [0°C] 2.824 [−21°C] 2.675 [−44°C] 2.460 [−88°C] 2.653 [−110°C] 1.224 [−121°C] 0.888 [−149°C] (47) |
1100 (16) |
1.893*10−4 (27) |
~40 (46) |
~200 (46) |
| M22 | 0.3 (29) |
3.43 [0°C] 3.378 [−18°C] 3.318 [−40°C] 3.180 [−76°C] 3.324 [−119°C] 1.461 [−130°C] 1.318 [−149°C] (47) |
1100 (16) |
2.52*10−4 (30, 31) |
0.1 (13, 28, 49, 50) |
0.4 (13, 28, 49, 50) |
Three different cases were analyzed for each given volume, namely convective cooling, convective warming, and nanowarming, as shown in Figure 2. Further, each case was simulated for three common CPAs, VS55, DP6, and M22 (13, 26, 28), resulting in nine numerical temperature solutions for a given volume. This provided a total of 9×5 = 45 numerical simulations for five different volumes ranging from mL to L range in this study.
| [1] |
An IONP concentration (CFe) of 10 mgFe/mL was assumed to be distributed uniformly throughout the modeled biomaterial geometry, based upon organ perfusion work in recent studies (17, 18). The IONP specific absorption rate (SARFe) was defined as the volumetric power deposited through hysteresis losses of the IONP within the biomaterial while placed within a radiofrequency coil (i.e., an alternating magnetic field). For the purpose of simplification, we assumed SARFe was constant at 651 W/gFe (temperature average) for a field of 64 KA/m and 185 KHz, as reported previously (15, 17, 18), since SAR temperature dependence doesn’t affect the results across size scale. This value was applied for IONPs in all CPAs modeled, VS55, M22, and DP6. Multiplying by the IONP concentration yields the volumetric heat generation term (qV’’’) for nanowarming. Center cooling rates and warming rates were estimated as the temperature averages (ΔT/time) in the range of 0°C to −100°C, as ice growth rates in the studied CPAs are practically negligible outside this range (32, 33, 34, 35, 36, 37). In practical scenarios, the temperature range for the rates should be limited till Tmelt of a CPA. However, for this study 0°C was chosen for convenience since melt temperatures for all three CPAs (DP6, VS55, M22) are quite different. Therefore, our range of estimated cooling and warming rates provides a worst-case analysis. These calculated cooling and warming rates were then compared to the CCRs and CWRs of the CPAs analyzed for evaluating failure due to ice crystallization during cooling and/or recrystallization (and/or devitrification) during rewarming. These critical rates have been listed in Table 2 for VS55, DP6, and M22.
For evaluating fracture failure resulting from thermal stresses, temperature difference, ΔT, was used to compute thermal stresses using the simplified form of the thermal shock equation, and these stresses were then compared to the tensile yield strength of the CPA from the literature (38). Further, for ease, the calculated ΔT can also be compared to a tolerable value ΔTmax derived for each CPA (VS55, DP6, and M22) from the simplified form of the thermal shock equation as shown below:
| [2] |
| [3] |
where g is the geometric coefficient (0.5 for cylindrical geometry), ν is Poisson’s ratio (adapted as 0.2 for typical brittle materials), E is the modulus of elasticity (adapted as 1 GPa for organic materials) and σ is the tensile yield strength of CPA (adapted as 3.2 MPa), based upon prior literature (38).
For simplification and lack of adequate availabile data for all three CPAs, we used the tensile strength (~3.2 MPa) of a closely related CPA (7 M DMSO) for all three CPAs analyzed here (38). Previous studies have measured thermal expansion and strain within CPAs such as DMSO, VS55, DP6, and recently M22 (26, 27, 30). For our simple analysis, we assumed a constant value of the coefficient of linear thermal expansion, as shown in Table 2, which if anything, would reduce at lower temperatures (27, 40) and hence decrease the estimated thermal stresses. Hence, our assumption results in a worst-case scenario analysis.
Further, it is to be noted that in such a high-viscosity regime, linear thermal expansion coefficients (thermal strain cycles) of CPAs (VS55 and DP6) don’t differ greatly during cooling vs. rewarming. Now, to consider the fracture failure mode, the largest occurring temperature difference ΔT |Tcenter˗Tedge|, was estimated in the region between −115 °C (~set temperature of DP6; Tset is 5 to −10°C higher than Tg, glass transition temperature) down to −150 °C (storage temperature). This is due to the fact that regions well below the set temperature (10–15°C below) are most vulnerable to cracking due to the regime’s very high-viscosity, elastic, solid-like behavior, where significant stresses start to arise and are proportional to the temperature difference in geometry (38, 39). During rewarming, the temperature difference, ΔT, was estimated when the center was still at −150°C whereas the edge was either in the glassy region or above it.
It is to be noted that ΔT in the region when the geometric center is still in the cryogenic temperature range and the edge is heated to around melt temperature is also critical to evaluate if any part of the geometry (more likely near the boundary) experiences suprazero temperatures, which could potentially enhance CPA toxicity and hence induce another mode of failure, though this was not the focus of this study (28, 41, 42, 43).
The details about initial and boundary conditions utilized in numerical FEA simulations for convective cooling, convective warming, and nanowarming are laid out in Table 1. Convective cooling was modeled as cooling inside a controlled-rate freezer (CRF) (for instance, Planar Kryo 560 II), wherein the flow of liquid nitrogen (LN2) vapors cool samples from their boundaries inward. For a best case of maximum cooling, we assumed the chamber temperature was maintained at a temperature similar to the storage temperature, i.e., Tcool (−150°C). Further, for simplicity, we assumed a value for the heat transfer coefficient inside the CRF based on the literature (17), which is in the range of heat transfer coefficients for forced convection in gases. For the convective rewarming case, the sample geometry was assumed to be submerged in a heated water bath maintained at Twarm (37°C) to achieve a convective heat flux at the boundary with a free convection heat transfer coefficient, as mentioned in Table 2 (44, 48). The effect of the change in the heat transfer coefficient (h) on cooling and warming rates diminishes as the size of the system increases. Similarly, to analyze the ideal and best case of nanowarming, we assumed an adiabatic boundary condition.
RESULTS
For all the cases, the temperature solution was numerically computed using FEA in COMSOL 5.4, where the model geometry was designed and simulated. During convective cooling, the geometry is subjected to convective heat flux, wherein the temperature starts at 0°C and the whole geometry reaches the ambient cold temperature of −150°C, the storage temperature of a vitrified biomaterial. Figure 3 shows the numerical results for the cooling rates (Fig. 3C) and temperature differences (Fig. 3D) for the convective cooling cases. As expected, the center of the geometry cools more slowly than the edge due to convective heat transfer (loss) occurring from the surroundings, i.e., the boundary of geometry, which can be seen in Figures 3A and 3B.
Figure 3.
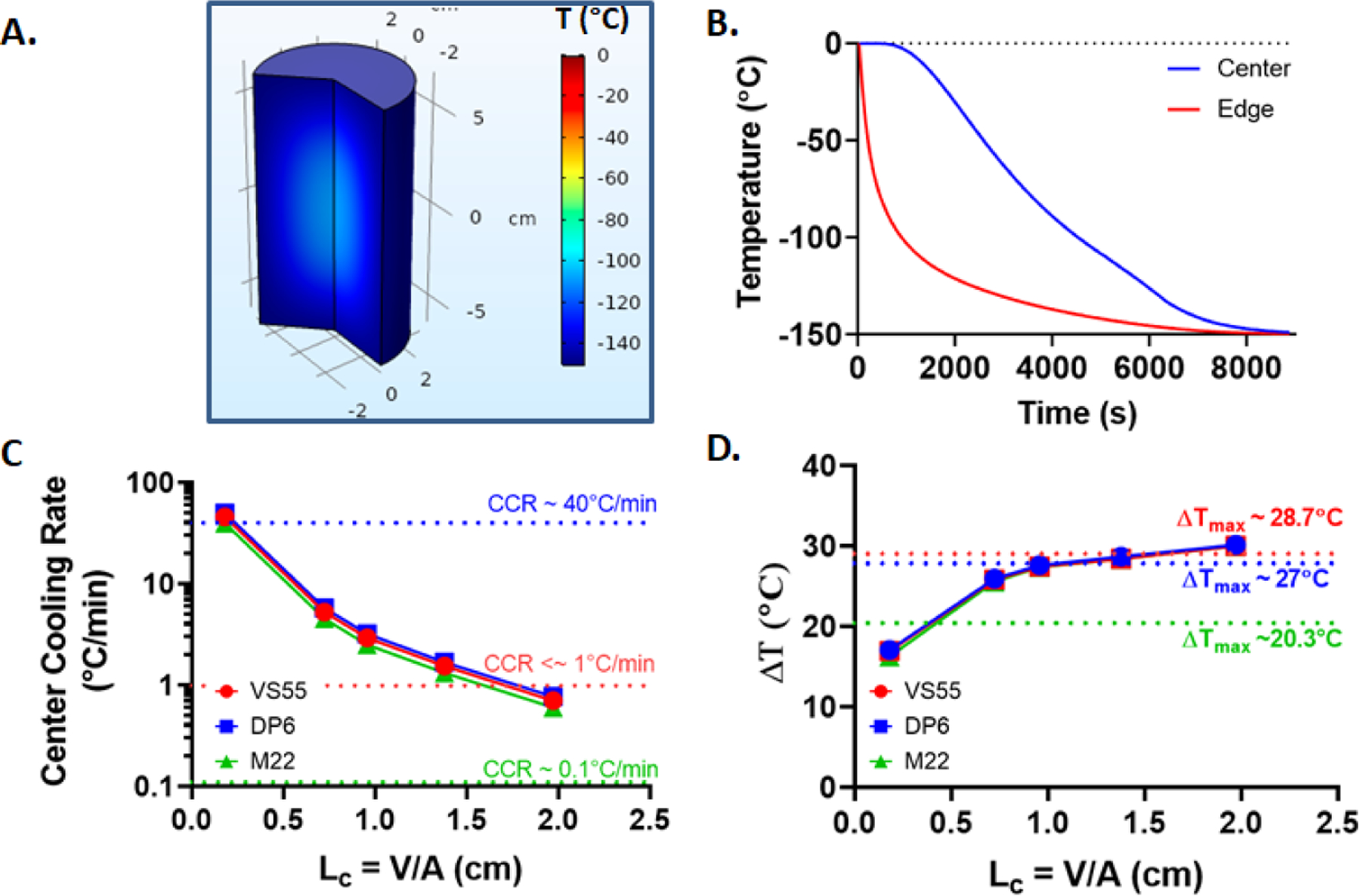
Convective cooling: For a representative case of LC = 1.38 cm (or 500mL) M22 system (A.) Temperature distribution inside the geometry around Tg (~120°C). (B.) Convective cooling temperature curve. (C.) Center cooling rate variation with characteristic length of geometry for all the three CPAs. (D.) Plot of temperature difference (ΔT) with characteristic length (LC) of geometry.
This means that the center of the geometry would be the limiting factor for achieving sufficient cooling rates (i.e., higher than CCR) to avoid any ice formation during the vitrification process. As the center of geometry is at the highest risk of ice crystallization, ensuring success at the center (center cooling rate > CCR) would naturally imply all the other regions of geometry having achieved successful vitrification. It is observed that significantly faster cooling rates (~50°C/min) can be achieved for a smaller characteristic length (LC < ~0.18 cm). As can be seen in Figure 3C, cooling rate decreases rapidly with increasing Lc (or volume) of the cylinder; therefore, for larger LC (or volumes), a CPA with a significantly low CCR is the ideal candidate for successful vitrification, e.g., M22 in our analysis (Figure 3). The temperature differences are greater for a larger characteristic length, as could be expected due to the convective heat flux boundary. However, the gradients seem to flatten with further increase in LC (> ~1cm) (or volume), as in Figure 3D. Table 3 contains the computed center cooling and warming rates and the maximum temperature differences (ΔT) based on the numerical solution for all characteristic lengths (or volumes) and boundary conditions.
Table 3.
Numerical simulation results for convective cooling, convective warming, and nanowarming for all cases.
| Convective Cooling | VS55 | DP6 | M22 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CRcenter (°C/min) |
ΔT (°C) |
σ (MPa) |
CRcenter (°C/min) |
ΔT (°C) |
σ (MPa) |
CRcenter (°C/min) |
ΔT (°C)) |
σ (MPa) |
|||||||
| Volume (mL) |
D (cm) |
Lc (cm) |
CCR<~1 | ΔTmax ~28.7 |
σmax~ 3.2 |
CCR~40 | ΔTmax ~27 |
σmax~ 3.2 |
CCR~0.1 | ΔTmax −20.3 |
σmax~ 3.2 |
||||
| 1 | 1 | 0.18 | 45.95 | 17.08 | 1 91 | 50.06 | 16.95 | 2.0 | 39.76 | 16.28 | 2.56 | ||||
| 80 | 3.5 | 0.72 | 5.27 | 25.96 | 2.89 | 5.76 | 25 83 | 3.05 | 4.54 | 25.58 | 4.03 | ||||
| 160 | 5 | 0.96 | 2.92 | 27.60 | 3.08 | 3.2 | 27.45 | 3.25 | 2.5 | 27.38 | 4.31 | ||||
| 500 | 7 | 1.38 | 1.54 | 28.67 | 3.19 | 1.68 | 28.42 | 3.36 | 1.32 | 28.41 | 4.47 | ||||
| 1300 | 12 | 1.97 | 0.70 | 30.15 | 3.36 | 0.77 | 30.0 | 3.54 | 0.60 | 30.0 | 4.72 | ||||
| Convective Cooling | VS55 | DP6 | M22 | ||||||||||||
| CRcenter (°C/min) |
ΔT (°C) |
σ (MPa) |
CRcenter (°C/min) |
ΔT (°C) |
σ (MPa) |
CRcenter (°C/min) |
CRcenter (°C/min) |
ΔT (°C) |
|||||||
| Volume (mL) |
D (cm) |
Lc (cm) |
CRW~50 | ΔTmax ~28.7 |
σmax~ 3.2 |
CRW~200 | ΔTmax ~27 |
σmax~ 3.2 |
CRW~0.4 | ΔTmax −20.3 |
σmax~ 3.2 |
||||
| 1 | 1 | 0.18 | 50.12 | 18.06 | 2.01 | 50.76 | 17.91 | 2.12 | 43.6 | 18.33 | 2.89 | ||||
| 80 | 3.5 | 0.72 | 5.7 | 31.54 | 3.52 | 5.8 | 30.81 | 3.64 | 5.05 | 31.8 | 5.00 | ||||
| 160 | 5 | 0.96 | 3.36 | 35.97 | 4.01 | 3.4 | 35.19 | 4.16 | 2.91 | 37.79 | 5.95 | ||||
| 500 | 7 | 1.38 | 1.75 | 43.61 | 4.86 | 1.78 | 42.97 | 5.08 | 1.52 | 47.26 | 7.44 | ||||
| 1300 | 12 | 1.97 | 0.85 | 56.34 | 6.28 | 0.86 | 55.68 | 6.59 | 0.74 | 59.02 | 9.29 | ||||
| Nanowarming | VS55 | DP6 | M22 | ||||||||||||
| CRcenter (°C/min) |
ΔT (°C) |
σ (MPa) |
CRcenter (°C/min) |
ΔT (°C) |
σ (MPa) |
CRcenter (°C/min) |
ΔT (°C) |
σ (MPa) |
CRcenter (°C/min) |
||||||
| Volume (mL) |
D (cm) |
Lc (cm) |
CRW~50 | ΔTmax ~28.7 |
σmax~ 3.2 |
CRW~200 | ΔTmax ~27 |
σmax~ 3.2 |
CRW~0.4 | ΔTmax −20.3 |
σmax~ 3.2 |
||||
| 1 | 1 | 0.18 | 126 | NA | 133 | NA | 108 | NA | |||||||
| 80 | 3.5 | 0.72 | 126 | 133 | 108 | ||||||||||
| 160 | 5 | 0.96 | 126 | 133 | 108 | ||||||||||
| 500 | 7 | 1.38 | 126 | 133 | 108 | ||||||||||
| 1300 | 12 | 1.97 | 126 | 133 | 108 | ||||||||||
For the case of convective warming (Fig. 4), faster warming occurs on the edges compared to the center of geometry. Thus, the center is the limiting region for achieving sufficient warming rates to avoid devitrification (and/or ice recrystallization). We have plotted these rates in Figure 4C and temperature distribution in Figure 4A. Indeed, rates actually fall below 1 °C/min for volumes greater than 1 L (LC > 1.9 cm) for all three CPAs. For all five volumes, the center warming rates and maximum temperature differences along with thermal stresses are tabulated in Table 3. Successful rewarming for DP6 and VS55 becomes more challenging even for smaller LC (or volumes) due to the high CWR required (since CWRs are order of magnitude or more larger than CCRs) (46, 51, 54). Further, in Figure 4B, the edge of the geometry heats up quickly, reaching a suprazero temperature while the rest of the geometry is still at cryogenic temperatures, leading to large temperature gradients (Fig. 4D), which could be detrimental due to excessive thermal stresses and other factors. While this study focuses on ice formation and fractures as the only modes of failure, other modes such as CPA toxicity could become important at high suprazero temperatures especially if held for longer times (41, 54).
Figure 4.
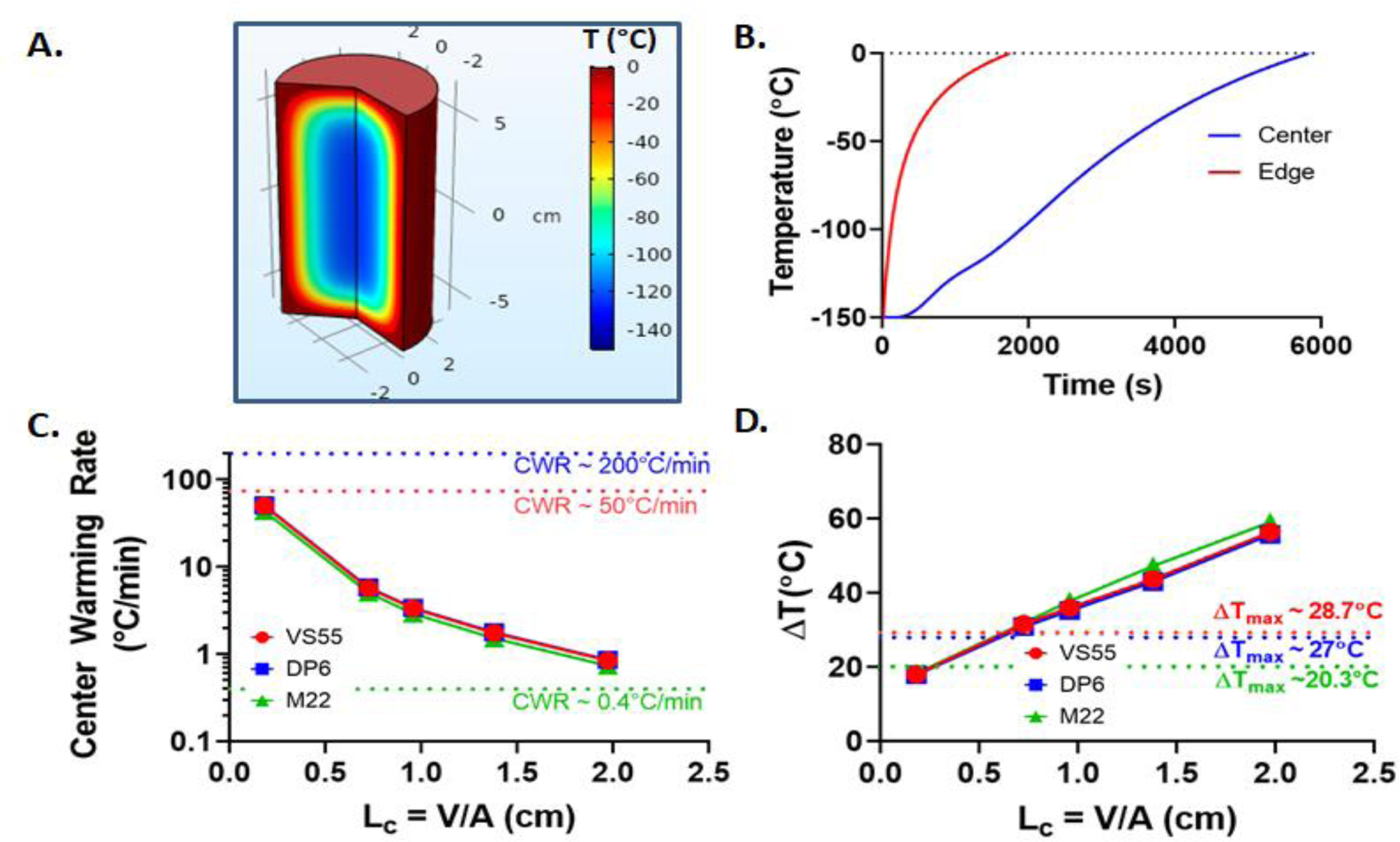
Convective warming: For a representative case of LC = 1.38 cm (or 500mL) M22 system (A.) Temperature distribution inside the geometry around Tg (~120°C). (B.) Convective warming temperature curve. (C.) Center warming rate variation with characteristic length of geometry for all the three CPAs. (D.) Plot of temperature difference (ΔT) with characteristic length (LC) of geometry.
Nanowarming is performed from the storage temperature of −150°C and terminated when the geometry reaches 0°C. Due to the internal heat generation and an ideal, i.e., adiabatic, boundary condition, the whole geometry heats up at the same rate. For DP6, the rate is around 133 °C/min, for VS55 it is 126 °C/min, and for M22 it is 108 °C/min (Figure 5). Further, the heat generation during nanowarming relies only on the IONPs and an external alternating magnetic field. Thus, heating can be both rapid and independent of sample size (volume), unlike convective or other boundary rewarming methods. The warming rates of the center during nanowarming can be seen in Figure 5C and are notably higher than those for convective warming for all the CPAs. Since the IONPs are assumed to be uniformly distributed, the heat generation during nanowarming is quite uniform and does not lead to temperature gradients, as shown in Figure 5D. Among the three CPAs studied, DP6 achieved the fastest cooling and warming rates. VS55 demonstrated slightly slower rates than DP6, and M22 had the slowest rate among all three CPAs. This is likely due to M22 having the highest specific heat, followed by VS55, and then DP6 (Table 2). It should be noted that in practice nanowarming might be performed in the absence of perfect insulation at the boundary. Under these conditions, some natural convective heat flux from the surroundings would be expected to increase the warming rates and might introduce non-uniformity (i.e., temperature gradients).
Figure 5.
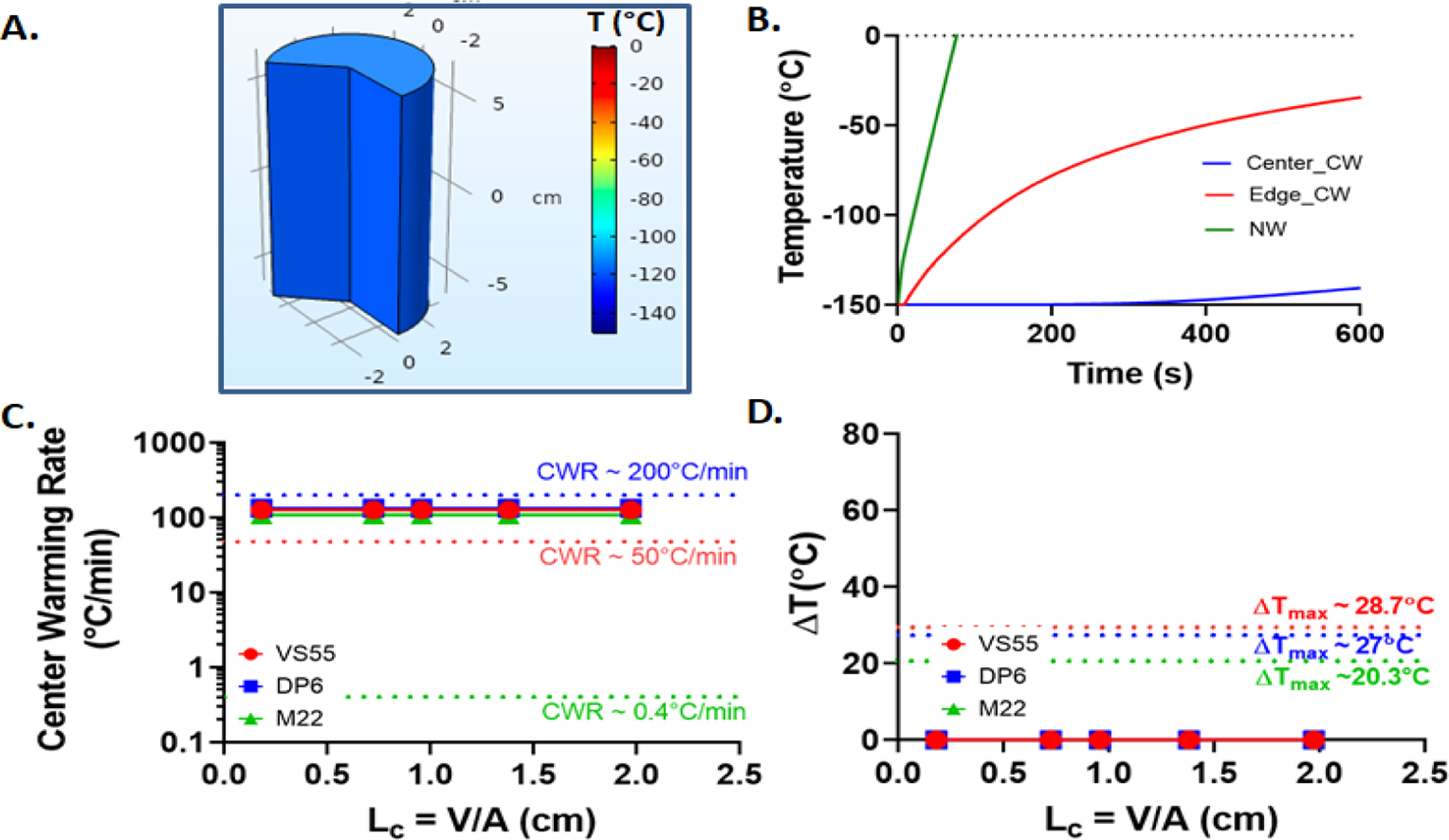
Nanowarming. For a representative case of LC = 1.38 cm (or 500mL) M22 system (A.) Temperature distribution inside the geometry around Tg (~120°C). (B.) Nanowarming temperature curve compared to convective warming. (C.) Center warming rate variation with characteristic length of geometry for all the three CPAs. (D.) Plot of temperature difference (ΔT) with characteristic length (LC) of geometry.
To further generalize the findings, we normalized the computed cooling and warming rates to the CCR and CWR of each CPA. Temperature difference is also normalized as deltaT_max to deltaT. All of these are plotted in Figure 6 and summarized in Table 4. These normalized figures help to clearly map success and failure during vitrification and rewarming (e.g., normalized values at >1 imply success and <1 failure). A parametric non-linear fit has been performed on these normalized values and these are given in Equations [4] and [5], thus:
| [4] |
| [5] |
Figure 6.
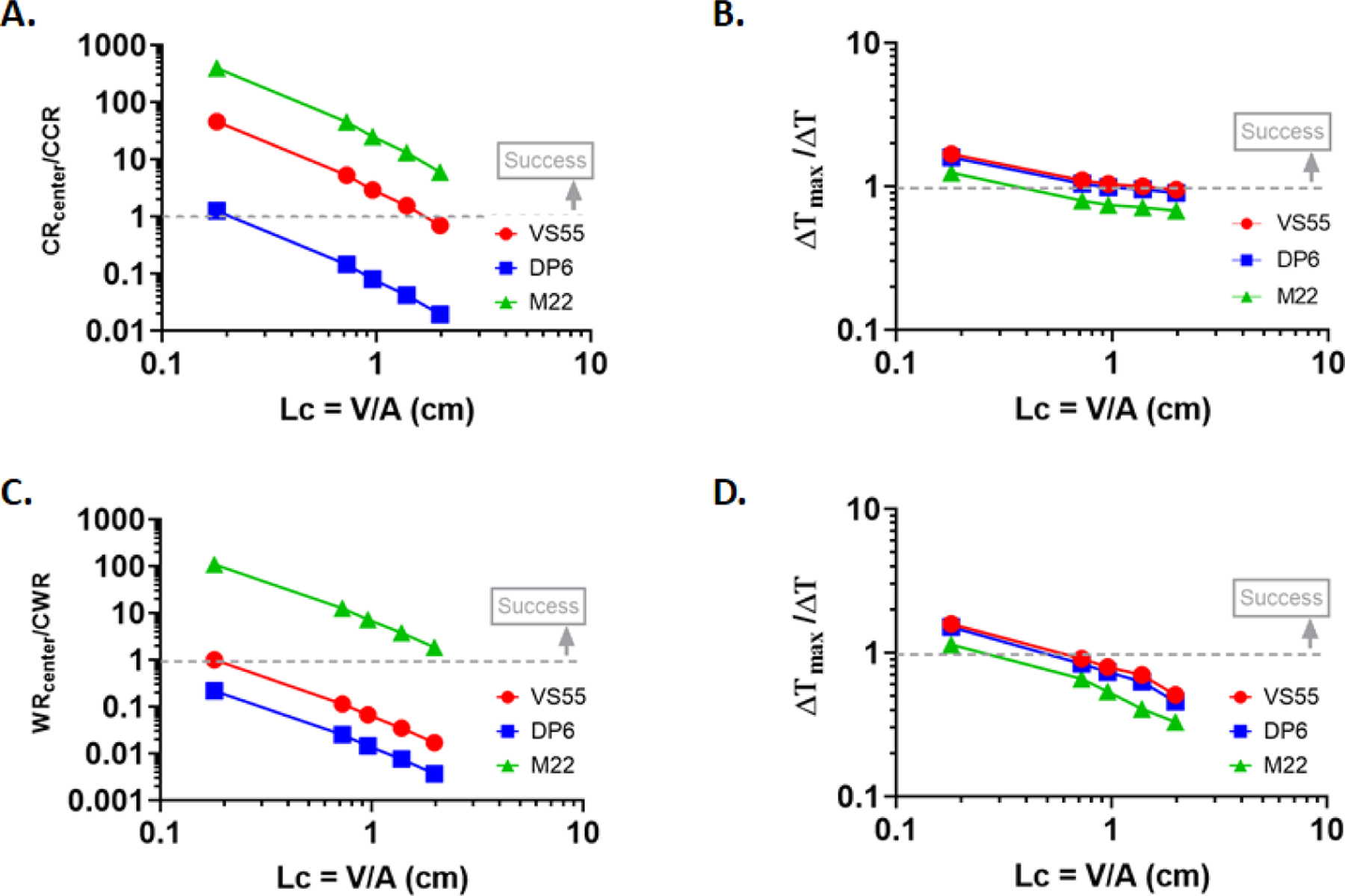
(A. & C.) Plots of non-linear fits for the normalized center cooling and warming rates to critical cooling (CCR) and critical warming rate (CWR) of the chosen CPAs during convective cooling and convective warming respectively. (B. & D.) Plots of non-linear fits for the normalized temperature difference (ΔT) to the maximum temperature difference (ΔTmax) calculated from “simplified thermal shock equation” of the chosen CPAs during convective cooling and convective warming respectively.
Table 4.
Coefficient of Fits for the normalized CR, WR & ΔT Equations (4) & (5).
| CPA | Fit Coefficient | |||
|---|---|---|---|---|
|
| ||||
| a1 | a2 | b1 | b2 | |
| Convective Cooling | ||||
|
| ||||
| VS55 | −1.605 | 0.465 | −0.257 | 0.028 |
| DP6 | −1.603 | −1.098 | −0.258 | 0.005 |
| M22 | −1.609 | 1.399 | −0.278 | −0.117 |
|
| ||||
| Convective Warming | ||||
|
| ||||
| VS55 | −1.595 | −1.189 | −0.426 | −0.114 |
| DP6 | −1.589 | −1.847 | −0.449 | −0.153 |
| M22 | −1.589 | 0.852 | −0.474 | −0.291 |
As seen in Figure 6A and 6C these normalized values clearly separate out for the three CPAs analyzed, thereby highlighting the importance of failure thresholds (i.e., CCR, CWR, and ΔTmax) and better fit of a CPA in potential success during vitrification and rewarming. For convective cooling, normalized CR of M22 seems to be above 1 (success) irrespective of LC (or volume) of geometry as opposed to VS55 where normalized CR falls below 1 (failure) for Lc approximately >1.8 cm, as is evident in Figure 6A. Similarly, for convective warming, M22 seems to be the only CPA that displays normalized WR >1 (success) for all the characteristic lengths of the geometry analyzed (Lc < 3.2 cm), as shown in Figure 6C. DP6 seems to be the most unlikely candidate to achieve success during convective cooling or rewarming, based on Figures 6A and 6C. Table 5 provides a summary of the critical Lc beyond which failure is likely to occur for any of the CPAs studied, i.e., Lc for normalized value (CR/CCR, WR/CWR or ΔTmax/ ΔT) = 1.
Table 5.
Characteristic length corresponding to potential failure either due to ice formation or thermal cracking for VS55, DP6 and M22.
| CPA | LC (cm) |
||
|---|---|---|---|
| Ice formation | Cracking/ fracture | ||
| VS55 | Convective Cooling | 1.95 | 1.28 |
| DP6 | 0.21 | 1.04 | |
| M22 | 7.4 | 0.38 | |
|
|
|||
| VS55 | Convective Warming | 0.18 | 0.54 |
| DP6 | 0.07 | 0.46 | |
| M22 | 3.43 | 0.24 | |
M22 seems to be the most ideal candidate for convective cooling and rewarming as its normalized CR and WR are greater than 1 for all characteristic lengths analyzed, which can be attributed to the fact it has an incredibly low CCR (0.1 °C/min) and CWR (0.4 °C/min) (49, 50). For fracture, VS55 and DP6 seem to be better as their critical LC seems to be >1 for convective cooling and ~0.5 during convective rewarming, as opposed to values of 0.38 and 0.24, respectively, for M22 which is listed in Table 5 and evident in Figures 6B and 6D. This result can be explained by the higher value of the linear thermal expansion coefficient of M22 assumed in this study. VS55 seems to work well during convective cooling for Lc up to 1.28 cm, where both the normalized CR and ΔT are > 1, but is not as viable an option during convective rewarming for LC < 0.18 cm. For DP6, success during convective cooling is more difficult to achieve (critical LC ~ 0.21 cm) and almost impossible for convective rewarming (critical LC ~ 0.07 cm), as evident in Figure 6B and Table 5. Therefore, the best performing CPA is M22 even though it has the potential of higher thermal stress, which needs to be evaluated further. Additionally, steps such as annealing and slow cooling below the glass transition temperature are known to be helpful in mitigating large temperature differences or thermal stresses (and hence fractures) when transitioning into the glassy phase, but they were not considered in this study. It is to be noted that ΔTmax would be higher, therefore, when using a cryobag (more similar to an ideal plate shape) as the geometric coefficient (g) in the thermal shock equation is smaller, i.e., g = 1/3 for a plate shape as opposed to g = 1/2 for a cylindrical shape (39). Further, the threshold ΔTmax here is quite conservative and will vary depending upon the above assumed parameters. For instance, the coefficient of linear thermal expansion (ß) depends on temperature range as opposed to constant assumption here. For the cryogenic range, it decreases, thereby increasing this threshold value and decreasing the estimated thermal stresses. Hence, the estimate here would be the worst-case scenario for evaluating fracture failure. Finally, it should be noted that the applicability of the simplified thermal shock equation for thermal stresses predictions at larger scale volumes (or LC) would need to be further evaluated experimentally so that the role of thermal gradients in fracture failure can be understood better.
To apply the results of this study in practical lab scenarios, it is important to understand and calculate the characteristic length (Lc) of the sample for any desired cooling or rewarming condition. To correlate a lab experiment scenario prediction based upon these numerical model results, here we compare with our modeling predictions the literature data for a rat kidney (17), consisting of a total cryopreserved volume of 30 mL (kidney + surrounding CPA solution) in a 5.5×4.4×1.5 cm cryobag. The characteristic length (Lc) for the above cryobag scenario can be calculated as ~0.75 cm, and using this value we can then estimate a cooling rate of 7 °C/min from Figure 3. This is close to the experimentally calculated value of 6.5 °C/min. Similarly, during nanowarming, the predicted warming rate is around 51 °C/min, which broadly agrees with the reported value of 55 °C/min measured during experiments. We note that for the nanowarming case, the warming rates are independent of the size of the system (or Lc). Therefore, the same heating rate should exist for different geometries for a fixed IONP concentration and other assumptions such as the adiabatic ambient medium. In this study, the IONP concentration of 10 mg Fe/mL was assumed to be uniformly distributed throughout the geometry; for other scenarios, one can still roughly estimate the nanowarming rates based upon linear normalization with the chosen IONP concentration in their experiments. Therefore, for the scenario of the rat kidney, discussed above, WR was predicted using this model as 126×(4 mg Fe/mL/10 mgFe/mL), which comes out to be 50.6 °C/min.
Lastly, it should be noted that these results are applicable for a convective heat transfer coefficient of ~100 W/m2K during convective cooling and convective rewarming. Therefore, for conditions with a significantly different h, the results would be expected to vary. For instance, for straws with microliter volumes, where h ~10,000 W/m2K as the boiling convection coefficient in LN2, the predicted CR using this model would be smaller than that expected based solely on experiments, i.e., an underprediction (52, 53).
DISCUSSION
This study demonstrates the conditions for the success and failure of vitrification and rewarming for various characteristic length systems and cooling or rewarming scenarios. Empirical fit Equations [4] and [5] have been derived for the variation of cooling rates, warming rates, and maximum temperature gradients, with the characteristic length of geometry applicable to the corresponding volume of biomaterial (i.e., VS55, DP6, or M22). These equations, i.e., [4] and [5], can be utilized for estimating cooling or warming rates along with temperature gradients for a given volume (or characteristic length) system, which can help predict success or failure during vitrification and/or rewarming. More specifically, we show that CPAs with low critical cooling and warming rates along with smaller linear thermal expansion coefficients have higher probabilities of success at larger volumes (~1 L) or larger characteristic lengths. Convective rewarming can be used for volumes with smaller characteristic lengths (Lc < ~0.2 cm) for most CPAs tested. However, it becomes inadequate to accomplish sufficient warming rates and uniformity to avoid any ice formation or cracking for larger volumes (44, 55, 56, 57). Volumetric rewarming through nanowarming is one alternative to extend the range of successful rewarming for some CPAs. Studies in the past have shown that modification of common CPAs such as DP6 by the addition of sugars (e.g., sucrose) or polymers (e.g., PEG400) can enhance the vitrification tendency leading to superior glass formation (57, 58, 59). Hence, further investigation of other CPAs, or modified CPAs, will continue to be an important area of research for cryopreserving larger volumes and characteristic length systems. Future studies should continue to experimentally examine the rates and gradients to validate success at larger volumes (L systems with >1.5 cm characteristic lengths). Unfortunately, a reduction in cooling rates during convection will always occur with an increase in characteristic length unless a volumetric cooling technique can be discovered or invented.
In summary, this work expands upon existing techniques to provide practical guidelines to avoid ice crystallization and cracking during cooling and warming from a vitrified state for several well-known CPAs across mL to L size scales.
Acknowledgements:
This work was supported by the National Institutes of Health (NIH) Grant 5R01DK117425–03, National Institute of Health (NIH) Grant 5R01HL135046–04, and National Science Foundation (NSF) Grant EEC 1941543.
Nomenclature
- Lc
Characteristic length (cm)
- D
Diameter of the geometry (cm)
- h
Effective heat transfer coefficient (W/m2˗°C)
- Tcool
Ambient temperature for convective cooling (°C)
- Twarm
Ambient temperature for convective warming (°C)
- CP
Specific heat at constant pressure (J/kg˗°C)
- ΔT
Temperature difference between center & edge (°C)
- qv ’’’
Volumetric heat generation (source) term (W/m3)
- CPA
Cryoprotective agent
- CCR
Critical cooling rate (°C/min)
- CWR
Critical warming rate (°C/min)
- SARFe
Specific absorption rate (W/gFe)
Greek Symbols
- ß
Coefficient of linear thermal expansion (1/°C)
- ρ
Density (kg/m3)
- σ
Thermal stress (MPa)
Subscripts
- Center
center of geometry
- Edge
edge of geometry
REFERENCES
- 1.Pegg DE (2007) in Cryopreservation and Freeze-drying Protocols, Methods in Molecular Biology 368, (eds) Day JG & Stacey GN, Springer, pp. 39–57. doi: 10.1007/978-1-59745-362-2_3 [DOI] [PubMed] [Google Scholar]
- 2.Finger EB & Bischof JC (2018) Current Opinion In Organ Transplantation 23(3), Opinion In Organ Transplantation 23(3), 353–360. doi: 10.1097/mot.0000000000000534. [DOI] [PubMed] [Google Scholar]
- 3.Giwa S, Lewis JK, Alvarez L, et al. (2017) Nature Biotechnology 35(6), 530–542. doi: 10.1038/nbt.3889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fahy GM, MacFarlane DR, Angell CA & Meryman HT (1984) Cryobiology 21(4), 407–426. doi: 10.1016/0011-2240(84)90079–8. [DOI] [PubMed] [Google Scholar]
- 5.Arav A & Patrizio P (2019) Clinical Medicine Insights: Reproductive Health 13, 1179558119884945. doi: 10.1177/1179558119884945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lujić J, Marinović Z, Sušnik Bajec S, Djurdjevič I, Kása E, Urbányi B & Horváth Á (2017) Cryobiology 76, 154–157. doi: 10.1016/j.cryobiol.2017.04.005. [DOI] [PubMed] [Google Scholar]
- 7.Fahy GM, Wowk B, Wu J, Phan J, Rasch C, Chang A & Zendejas E (2004) Cryobiology 48(2), 157–178. doi: 10.1016/j.cryobiol.2004.02.002. [DOI] [PubMed] [Google Scholar]
- 8.Daly J, Zuchowicz N, Nuñez Lendo CI, Khosla K, Lager C, Henley EM, Bischof J, Kleinhans FW, Lin C, Peters EC & Hagedorn M (2018) Scientific Reports 8(1), 1–10. doi: 10.1038/s41598-018-34035-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Khosla K, Kangas J, Liu Y, Zhan L, Daly J, Hagedorn M & Bischof J (2020) Advanced Biosystems 4(11), 2000138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mullen SF & Fahy GM (2011) in Principles and Practice of Fertility Preservation, (eds) Donnez J & Kim SS, Cambridge University Press, Cambridge, pp. 145–163. [Google Scholar]
- 11.Boutron P (1993) Cryobiology 30(1), 86–97 [Google Scholar]
- 12.Boutron P & Mehl P, (1990) Cryobiology 27(4), 359–377. doi: 10.1016/0011-2240(90)90015-v. [DOI] [PubMed] [Google Scholar]
- 13.Rall WF & Fahy GM (1985) Nature 313(6003), 573–575. [DOI] [PubMed] [Google Scholar]
- 14.Fahy GM, Wowk B, Pagotan R, Chang A, Phan J, Thomson B & Phan L (2009) Organogenesis 5(3), 167–175. doi: 10.4161/org.5.3.9974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Manuchehrabadi N, Gao Z, Zhang J, Ring HL, Shao Q, Liu F, McDermott M, Fok A, Rabin Y, Brockbank KG, Garwood M, Haynes CL & Bischof JC (2017) Science Translational Medicine 9(379), eaah4586. doi: 10.1126/scitranslmed.aah4586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Etheridge ML, Xu Y, Rott L, Choi J, Glasmacher B & Bischof JC (2014) Technology 2(03), 229–242. [Google Scholar]
- 17.Sharma A, Rao JS, Han Z, Gangwar L, Namsrai B, Gao Z, Ring HL, Magnuson E, Etheridge M & Wowk B (2021) Advanced Science 8(19), 2101691. doi: 10.1002/advs.202101691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gao Z, Namsrai B, Han Z, Joshi P, Rao JS, Ravikumar V, Sharma A, Ring HL, Idiyatullin D & Magnuson EC (2022) Advanced Materials Technologies 7(3), 2100873. doi: 10.1002/admt.202100873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chiu-Lam A, Staples E, Pepine CJ & Rinaldi C (2021) Science Advances 7(2), eabe3005. doi: 10.1126/sciadv.abe3005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fahy GM, Saur J & Williams RJ (1990) Cryobiology 27(5), 492–510. [DOI] [PubMed] [Google Scholar]
- 21.Solanki PK, Bischof JC & Rabin Y (2017) Cryobiology 76, 129–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Solanki PK & Rabin Y (2021) Cryobiology 100, 180–192. doi: 10.1016/j.cryobiol.2021.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ehrlich LE, Fahy GM, Wowk BG, Malen JA & Rabin Y (2018) Journal of Biomechanical Engineering 140(1), 0110051–0110058. doi: 10.1115/1.4037406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gao Z, Ring HL, Sharma A, Namsrai B, Tran N, Finger EB, Garwood M, Haynes CL & Bischof JC (2020) Advanced Science 7(4), 1901624. doi: 10.1002/advs.201901624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Eisenberg DP, Steif PS & Rabin Y (2014) Cryogenics 64, 86–94. doi: 10.1016/j.cryogenics.2014.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Plitz J, Rabin Y & Walsh JR (2004) Cell Preservation Technol 2, 215–226. [Google Scholar]
- 27.Rios JLJ & Rabin Y (2006) Cryobiology 52(2), 284–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fahy GM, Wowk B, Wu J & Paynter S (2004) Cryobiology 48(1), 22–35. [DOI] [PubMed] [Google Scholar]
- 29.Ehrlich LE, Gao Z, Bischof JC & Rabin Y (2020) PLoS ONE 15(9), e0238941. doi: 10.1371/journal.pone.0238941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Solanki P & Rabin Y (2022) CryoLetters 43(1), 1–9. [PMC free article] [PubMed] [Google Scholar]
- 31.Solanki PK (2020) Thermomechanical Stress in Cryopreservation with Applications to Large-Size Vitrification, Doctoral dissertation, Carnegie Mellon University. doi: 10.1184/R1/19148930.v1. [DOI] [Google Scholar]
- 32.Wowk B (2010) Cryobiology 60(1), 11–22. doi: 10.1016/j.cryobiol.2009.05.007 [DOI] [PubMed] [Google Scholar]
- 33.Mehl PM (1993) Cryobiology 30(5), 509–518. doi: 10.1006/cryo.1993.1051. [DOI] [PubMed] [Google Scholar]
- 34.Baicu S, Taylor MJ, Chen Z & Rabin Y (2007) Cell Preservation Technology 4(4), 236–244. doi: 10.1089/cpt.2006.9994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Taylor M, Song Y & Brockbank K (2004) in Life in the Frozen State, (eds) Fuller BJ, Lane N & Benson EE, CRC Press, Boca Raton, pp. 603–641. [Google Scholar]
- 36.Hey JM & Macfarlane DR (1998) Cryobiology 37(2), 119–130. doi: 10.1006/cryo.1998.2108 [DOI] [PubMed] [Google Scholar]
- 37.Hey JM & Macfarlane DR (1996) Cryobiology 33(2), 205–216. doi: 10.1006/cryo.1996.0021 [DOI] [PubMed] [Google Scholar]
- 38.Rabin Y, Steif PS, Hess KC, Jimenez-Rios JL & Palastro MC (2006) Cryobiology 53(1), 75–95. doi: 10.1016/j.cryobiol.2006.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Steif PS, Palastro MC & Rabin Y (2007) Cell Preservation Technology 5(2), 104–115. doi: 10.1089/cpt.2007.9994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rabin Y & Plitz J (2005) Annals of Biomedical Engineering 33(9), 1213–1228. doi: 10.1007/s10439-005-5364-0. [DOI] [PubMed] [Google Scholar]
- 41.Clark P, Fahy GM & Karow AM Jr (1984) Cryobiology 21(3), 274–284. doi: 10.1016/0011-2240(84)90323-7. [DOI] [PubMed] [Google Scholar]
- 42.Best BP (2015) Rejuvenation Research 18, 422–436. doi 10.1089/rej.2014.1656 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Joshi P, Ehrlich LE, Gao Z, Bischof JC & Rabin Y (2022) Journal of Heat Transfer 144, 031202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Manuchehrabadi N, Shi M, Roy P, Han Z, Qiu J, Xu F, Lu TJ & Bischof J (2018) Annals of Biomedical Engineering 46(11), 1857–1869. doi: 10.1007/s10439-018-2063-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Rabin Y, Taylor MJ, Walsh JR, Baicu S & Steif PS (2005) Cell Preservation Technology 3(3), 169–183. doi: 10.1089/cpt.2005.3.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Phatak S, Natesan H, Choi J, Brockbank KG & Bischof JC (2018) Biopreservation and Biobanking 16(4), 270–277. doi: 10.1089/bio.2018.0006. [DOI] [PubMed] [Google Scholar]
- 48.Incropera FP, DeWitt DP, Bergman TL & Lavine AS (1996) Fundamentals of Heat and Mass Transfer, Vol. 6, Wiley, New York, p. 116. [Google Scholar]
- 49.Fahy GM, Wowk B & Wu J (2006) Rejuvenation Research 9(2), 279–291. doi: 10.1089/rej.2006.9.279 [DOI] [PubMed] [Google Scholar]
- 50.Wowk B & Fahy GM (2005) Cryobiology 51, 362. [Google Scholar]
- 51.Han Z & Bischof JC (2020) CryoLetters 41(4), 185–193.33988646 [Google Scholar]
- 52.Kuleshova LL & Lopata A (2002) Fertility And Sterility 78(3), 449–454. doi: 10.1016/s0015-0282(02)03305-8. [DOI] [PubMed] [Google Scholar]
- 53.Vutyavanich T, Sreshthaputra O, Piromlertamorn W & Nunta S (2009) Journal Of Assisted Reproduction And Genetics 26(5), 285–290. doi: 10.1007/s10815-009-9324-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Brockbank KG, Wright GJ, Yao H, Greene ED, Chen ZZ & Schenke-Layland K (2011) The Annals Of Thoracic Surgery 91(6), 1829–1835. [DOI] [PubMed] [Google Scholar]
- 55.Brockbank KG, Chen ZZ, & Song YC (2010) Cryobiology 60(2), 217–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Brockbank KG, Chen ZZ, Greene ED & Campbell LH (2015) in Cryopreservation And Freeze-Drying Protocols, (eds) Wolkers WF & Oldenhof H, Springer, New York, NY, pp. 399–421. [Google Scholar]
- 57.Wowk B, Fahy GM, Ahmedyar S, Taylor MJ & Rabin Y (2018) Cryobiology 82, 70–77. doi: 10.1016/j.cryobiol.2018.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sutton RL (1992) Cryobiology 29(5), 585–598. doi: 10.1016/0011-2240(92)90063-8. [DOI] [PubMed] [Google Scholar]
- 59.Kuleshova LL, Macfarlane DR, Trounson AO & Shaw JM (1999) Cryobiology 38(2), 119–130. doi: 10.1006/cryo.1999.2153. [DOI] [PubMed] [Google Scholar]


