Summary
Prognostic models are useful tools for assessing a patient’s risk of experiencing adverse health events. In practice, these models must be validated before implementation to ensure that they are clinically useful. The concordance index (C-Index) is a popular statistic that is used for model validation, and it is often applied to models with binary or survival outcome variables. In this paper, we summarize existing criticism of the C-Index and show that many limitations are accentuated when applied to survival outcomes, and to continuous outcomes more generally. We present several examples that show the challenges in achieving high concordance with survival outcomes, and we argue that the C-Index is often not clinically meaningful in this setting. We derive a relationship between the concordance probability and the coefficient of determination under an ordinary least squares model with normally-distributed predictors, which highlights the limitations of the C-Index for continuous outcomes. Finally, we recommend existing alternatives that more closely align with common uses of survival models.
Keywords: Concordance Index, Prognostic Modeling, Risk Discrimination, Survival Analysis
1 |. INTRODUCTION
In medical practice and health research, it is often of interest to identify patients who have a high risk for adverse health outcomes and to distinguish these patients from lower-risk individuals. Predictive models can be applied to assess a patient’s risk of experiencing the outcome of interest. When patients are followed over time, prognostic survival models are especially useful for quantifying the risk of adverse events, and a high-performing model is expected to reliably discriminate patients with imminent events from patients who will avoid these events for longer periods of time.
The Concordance Index (C-Index) has become a popular statistic for evaluating a model’s ability to discriminate risk within a population 12. Originally developed for the assessment of binary classifiers such as binary logistic regression models, the C-Index has been extended to the survival analysis setting, with Harrell or Uno’s C-Index definitions being common choices for the validation of survival models1,2,3. In the binary outcome setting, the C-Index is equivalent to the Area Under the Receiver Operating Characteristic Curve (AUC). C-Index values range from zero to one, with a value of 0.5 corresponding to the performance of a random classifier. Several textbooks for physicians and applied statisticians arbitrarily suggest that only models with a C-Index above 0.7 adequately discriminate between risk profiles 4,5,6. These guidelines for interpreting the C-Index have become highly influential, as many reviewers rely heavily on the C-Index to scrutinize proposed models7.
While the C-Index continues to be used in practice, many limitations of the statistic have been noted. For example, several authors have questioned the utility of the C-Index in building and validating prognostic models of disease status 7,8,9. Most of this criticism has been presented in the context of binary classification, and few authors have discussed these and other limitations of the C-Index in the context of models with non-binary outcomes.
2 |. C-INDEX BACKGROUND AND PREVIOUS CRITICISM
As described by Harrell et al. (1996)1, the C-Index is based on a scenario in which the orderings of the predicted risk scores are compared to the orderings of the observed outcomes within pairs of subjects from a sample. For binary outcomes, concordance occurs when a subject who experiences the event of interest is assigned a higher predicted risk probability than a subject who does not experience the event. For survival outcomes, concordance occurs when a subject who experiences the event earlier in the study period is assigned a higher predicted risk score than a subject who experiences the event later or who never experiences the event in the study period. For a given model and corresponding method of risk prediction, the C-Index is an estimate of the concordance probability, which is defined as the probability that two randomly selected subjects will have correctly ordered risk predictions1,2:
It is often claimed that a high concordance probability is indicative of a model that performs well at discriminating between risk profiles1,2. In Section 3, we discuss the selection of comparable pairs in more depth and uncover certain implications of the various C-Index definitions.
The C-Index has been criticized from a statistical and clinical perspective7,8,9,10. Many authors have shown that the C-Index is insensitive to the addition of new predictors in a model, even if the new predictors are statistically and clinically significant7. Thus, the C-Index is generally not useful in evaluating new risk factors or in model building. Also, because the C-Index depends only on the ranks of the predicted values, models with inaccurate predictions can have C-Indices that are much larger than those from a competing model with more accurate predictions9. Cook (2007) notes that in populations with mostly low-risk subjects, the C-Index computation involves many comparisons of two low-risk patients with similar risk probabilities, and physicians may not be interested in these comparisons7. Multiple authors have also suggested that there are limitations in the C-Index interpretation. For example, Halligan et al. (2011) argue that the concepts of sensitivity and specificity can be very meaningful to physicians, but the C-Index, which combines sensitivity and specificity across all models, has an interpretation that is much less useful 10.
3 |. CONSEQUENCES OF COMPARABLE PAIRS
3.1 |. Comparable Pairs Overview
In all definitions of the C-Index (for models with either binary or survival outcomes), only certain pairs of subjects are selected to assess concordance between the outcome variable and the model predictions1,2. The differences in how these pairs are selected between the binary and survival versions of the C-Index have important consequences. We show that the definition of comparable pairs for a continuous or nearly-continuous response, such as in the survival setting, sets up a much more difficult discrimination problem that is often not clinically meaningful in assessing model performance. Therefore, we argue that certain limitations of the C-Index are accentuated for survival outcomes.
3.2 |. Comparable Pairs for Binary Outcomes
For binary outcome data, the C-Index only assesses concordance between patients in the sample who have different outcomes. For example, if disease status is the outcome of interest, the predicted probabilities for patients with the disease are only compared to those for patients without the disease. Comparisons are not made within the diseased or non-diseased groups. Let be the size of the study sample and define indices and . Then, the C-index for binary outcomes is1
| (1) |
where is the binary outcome variable, is the predicted probability of the outcome, and is the indicator function. One feature of the C-Index with binary outcomes is that pairs with very different underlying risk probabilities are more likely to be comparable. As an example, consider a pair of patients (Patient A and Patient B) that have nearly the same underlying risk probability for disease ( ). The probability that these patients have the same observed outcome in a sample is
Thus, the probability that patients A and B form a comparable pair in the sample is . Now, consider a different pair of patients (C,D) in the random sample, where and . In this setting,
so that the probability that patients C and D form a comparable pair is 0.68. Thus, patients C and D are included among the comparable pairs with a probability more than twice that for patients A and B. More generally, if is fixed, then the probability that the pair is comparable increases with . As we shall see, the selection against pairs with similar risks does not carry over to the continuous case.
3.3 |. Comparable Pairs for Time-to-Event Outcomes
For time-to-event outcomes that are potentially right-censored, two patients are said to be comparable if they have different failure times and the earlier failure time is actually observed (uncensored)1,2,11. Without loss of generality, we consider the Cox proportional hazards model, or any model where the risk scores are generated from a linear combination of the predictor vector, . The C-Index for time-to-event outcomes is
| (2) |
where is the predicted risk score, is the observed survival time, is the underlying survival time, and is the event status (1=event, 0=censored). Defining as the underlying censoring variable, and .
In the continuous case, the probability that two patients will have exactly the same underlying survival time is zero, regardless of how similar the true risk profiles are. In practice, the data are always subject to grouping, but unless the grouping is very coarse, the chance of equal observations is much smaller than in the binary case. As a result, it is very likely for subjects with similar or identical underlying risk profiles to form comparable pairs when evaluating a survival model.
4 |. CHALLENGES WITH TIES, CENSORING, AND TIME DEPENDENCE
4.1 |. Ties in the Predicted Risk Scores
As discussed above, Harrell’s definition of the C-Index for time-to-event outcomes frequently involves comparisons of patients with very similar risk profiles. For survival models with categorical or discrete predictors, the predicted risk scores can be identical within pairs of subjects. Therefore, it is important to define an appropriate method for handling tied risk scores. Yan & Greene (2008) show that scoring 0.5 for ties, as suggested in Equation (2), can decrease the C-Index, especially when there are many ties in the risk score distribution12. Thus, comparable pairs with either similar or identical risk scores can have deflating effects on the C-Index value.
For binary outcomes, a comparable pair that has a tie in the predicted risk probabilities must include one subject with the event and one subject without the event. However, in the continuous outcome setting, a comparable pair that has a tie in the risk scores could have small to very large differences in the outcome variable. A model that assigns the same risk score to patients with extremely different survival experiences is not performing well, but the C-Index does not detect this inadequacy. On the other hand, a model that assigns the same risk score to patients with very similar survival experiences may be appropriately capturing the similarities in underlying risk. While these two scenarios have very different interpretations, they are treated as the same in the C-Index calculation, since each of these pairs contributes a score of 0.5 in Equation (2).
4.2 |. Censoring
Survival data also bring the unique challenge of handling right-censoring in the time-to-event outcome variable. The limiting value of Harrell’s C-Index depends on the censoring distribution, which arguably results in misleading estimates of the concordance probability3,11. Using inverse probability weighting, Uno et al. (2011) developed a modified version of the C-Index, the limiting value of which does not depend on the censoring distribution3. Uno’s C-Index provides an alternative for handling right-censored data, but it still suffers from many of the same limitations presented in this paper. This is mainly because, like Harrell’s C-Index, it is based on pairwise comparisons of patients with potentially similar risks, and the definition of comparable pairs for Uno’s C-Index is nearly identical to that in Equation (2)3.
Gönen and Heller (2005) proposed an alternative concordance measure for proportional hazards models that is not influenced by the right-censoring distribution13. This measure is estimated by
In the above expression, if two patients have very similar risks such that is very close to zero, then the corresponding summand for these patients is approximately , which is the minimum value. Thus, by similar arguments as in Section 4.1. pairs of patients with very similar predicted risks can substantially decrease this concordance measure, even if these pairs are not of clinical interest, or are accurately reflecting true similarities in underlying risk. As a result, Gönen and Heller’s concordance measure shares the same pitfalls as the C-Index, and it can be low for models that are still very useful for discriminating clinically-meaningful risk differences, or for other purposes as described in Section 6.2. This is especially true in samples with little heterogeneity in the underlying risk levels. Furthermore, this measure heavily depends on the proportional hazards model assumption and cannot be applied to survival models outside of this class.
4.3 |. Time Dependence
Most C-Index estimators are based on the assumption that the risk scores do not change over time, and for models with timevarying covariates or coefficients, Harrell’s C-Index and its close variants (e.g. Uno’s C-Index) cannot be directly applied. To overcome this limitation, Heagerty and Zheng (2005) proposed a time-dependent C-Index estimator that treats the time-to-event outcome as a sequence of binary observations. For the “incident-dynamic” version of this estimator, and at event time , a binary outcome variable is defined for all subjects at risk (i.e. with ) such that . Then, using the risk score values at time (for all subjects at risk), a time-specific C-Index estimator is calculated based on Equation (1). An overall C-Index estimator for a given time interval is then derived by taking a weighted average of the time-specific C-Index estimators14.
While Heagerty and Zheng’s time-dependent C-Index estimator is flexible enough to evaluate a broader class of survival models, it has the same fundamental limitations as the conventional C-Index estimators. This is because the time-to-event outcome is dichotomized at each time point, which potentially generates many comparable pairs that are difficult to discriminate and are not clinically meaningful. For example, if a patient experiences the event of interest on day of the study, and another patient, with similar underlying risk, experiences the event shortly afterwards on day , then these two patients would be deemed comparable according to the time-dependent C-Index definition. In addition, it has been shown that the time-dependent C-Index is a consistent estimator for the population concordance probability14, as defined in Section 2. Thus, it has the same target parameter as the conventional C-Index estimators and shares many of the properties described in this paper.
5 |. CONCORDANCE UNDER THE NORMAL LINEAR REGRESSION MODEL
5.1 |. and Concordance Probability
We derive a relationship between the population concordance probability and the population parameter for Ordinary Least Squares (OLS), assuming the predictors are normally distributed. Suppose that the continuous outcome variable is generated from a multiple linear regression model with the predictor vector and its corresponding coefficient vector :
| (3) |
where is assumed to follow a multivariate normal distribution. Define as the population concordance probability under the model in Equation (3):
and define the following consistent estimator for :
Furthermore, let denote the sample coefficient of determination for the OLS model in Equation (3), such that . Under these assumptions, we show that
| (4) |
First, denote as Kendall’s tau correlation parameter for the association between and . Then, by Pencina and D’Agostino (2004)11
| (5) |
Assuming a bivariate normal distribution, Rupinski and Dunlap (1996) reference the following relationship between and Pearson’s correlation parameter, 15:
| (6) |
Since the predictors are normally distributed, and jointly follow a bivariate normal distribution. Also, assuming and are positively correlated
| (7) |
The relationship in Equation (4) follows from Equations (5), (6), (7) under the OLS model with normally-distributed predictors.
We demonstrate the above relationship through simulation. On each iteration of the simulation, we generate a single predictor from a standard normal distribution. Then, we condition on and generate from Equation (3) with and . We compute and for each simulated dataset, and obtain the average values across 1000 iterations. is a biased estimator of , but with the sample size of in our simulations, this bias is negligible and the empirical average is very close to the true parameter value16. We repeat the process for values of ranging from 1 to 400. As expected, the empirical relationship between the average and values matches the theoretical relationship between the and parameters in Equation (4) (Figure 1).
FIGURE 1.
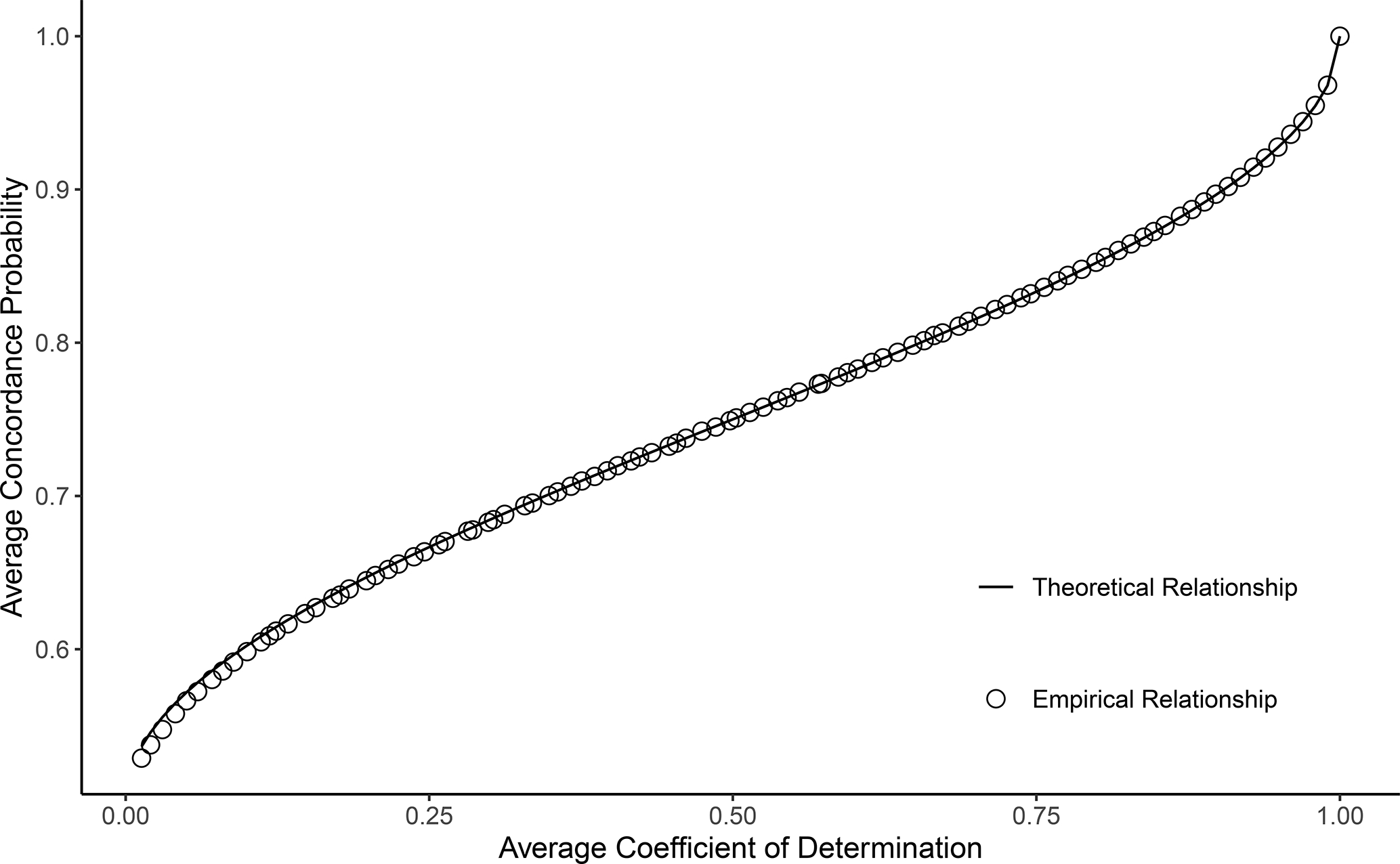
Theoretical and empirical relationship between the average estimated concordance probability and the average , from an Ordinary Least Squares model with normally-distributed predictors. The empirical relationship is based on a simulation with 1000 iterations and a sample size of . The derived theoretical relationship between the concordance probability and population parameters closely matches the observed empirical relationship, as expected.
As shown in Figure 1, the population concordance probability is a monotonic function of the parameter for the OLS model with normally-distributed predictors, and it achieves its maximum and minimum values at the maximum and minimum values of the parameter. Thus, in large samples, the estimated concordance probability shares certain properties with under the setting with normally-distributed predictors. For example, depends on the variances of the error term and the predictors, just like . In addition, a perfectly-specified OLS model (with normally-distributed predictors) that is practically useful can have an arbitrarily low value or estimated concordance probability17,18. High concordance probability values such as 0.8 or 0.9 correspond to extremely high values such as 0.75 or 0.85, which can be difficult to attain in many applications in the social and health sciences.
One limitation of , which several authors have noted, is that the value of strongly depends on how the predictors are sampled17,18. A higher value may be obtained by designing the study such that the are more dispersed, even if the assumed model remains unchanged. Thus, the is not only a function of the model specification, but also the amount of variability in the sample predictor values. This limitation also applies to the C-Index. Even for well-developed models that are perfectly specified and include many clinically-important predictors, the estimated C-Index will be low if there is little heterogeneity in the patient characteristics of the sample.
6 |. C-INDEX MISINTERPRETATION
6.1 |. Example: Survival Within Two Age Groups
The C-Index is based on a discrimination scenario that may not align with the true purpose of the model, especially in the time-to-event context. In this section, we show a simple example of a very useful model that can only achieve a modest C-Index value. Consider a population that consists of individuals in their 10th-year and 90th-year of age. It is valid to assume that the 90-year-olds are at a much greater risk for death, and the distribution of the underlying time-to-death variable within this population may look highly clustered (Figure 2). If one were to take a sample from the population described in Figure 2 and develop a survival model with age as the only predictor, the model would be able to discriminate nearly perfectly the mortality risk between the 10-year-olds and 90-year-olds. However, the model would include no relevant information for discriminating risk within each age group, so it would predict the same risk score for subjects of the same age. If the sample (with size ) has an equal number of 10-year-olds and 90-year-olds and there is no censoring, the C-Index for this model is approximately
FIGURE 2.
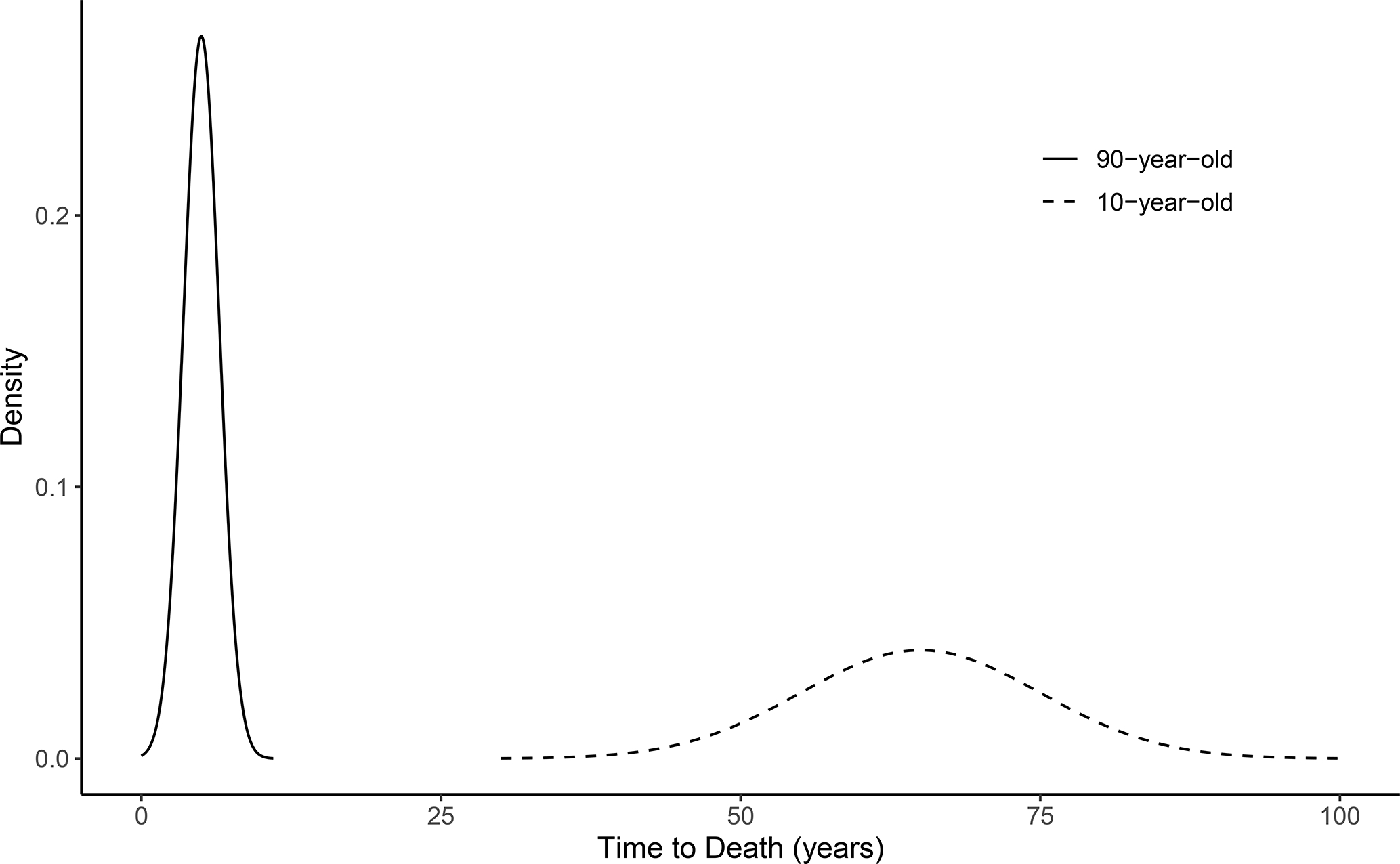
A hypothetical distribution of time-to-death outcomes within a population of 10-year-olds and 90-year-olds. The distribution is highly-clustered, and the differences in underlying mortality risks are large across the age groups and small within each age group. The C-Index calculation for a survival model with age as a predictor would involve many comparisons of patients with the same age and very similar underlying risks.
A naive interpretation of this result is that the model is only moderately useful for predicting risk because the C-Index is only moderately high. However, the model is able to perfectly discriminate between subjects who have an immediate risk for death and those who will live for many more years, making it very useful in practice. While this is an extreme example, it highlights what the C-Index actually measures and the consequences of misinterpreting the C-Index as a measure of overall model usefulness. Furthermore, as the age distribution becomes more imbalanced, the C-Index defined by Equation (2) decreases to 0.5 because fewer comparisons can be made between the groups (Table 1). This result demonstrates that the C-Index heavily depends on the underlying risk differences of the comparable pairs that are available in the sample.
TABLE 1.
C-Index values for different age group distributions, among a hypothetical population of patients in their 10th and 90th years of age (i.e. the proportion of patients that belong to the 90-year-old group). It is assumed that age is the only predictor, which nearly-perfectly discriminates mortality risk, and the sample size is set to . As the 90-year-old proportion increases, fewer comparisons are made across the two age groups in the C-Index calculation, and the C-Index decreases. The maximum possible C-Index value is one, and a C-Index of 0.5 corresponds to a model with random orderings of risk scores.
| 90-Year-Old Proportion | C-Index |
|---|---|
|
| |
| 0.50 | 0.75 |
| 0.60 | 0.74 |
| 0.70 | 0.71 |
| 0.80 | 0.66 |
| 0.90 | 0.59 |
| 1.00 | 0.50 |
Consider now the same example as in the previous section, but assume that only a binary response variable is recorded, indicating whether the patient is still alive 20 years after the start of the study, and that age is only recorded as 10 or 90. A binary-outcome regression model is almost-perfectly fit to the data with age as the only predictor. Based on Figure 2, the C-Index for the binary-outcome model is close to one, which is the highest possible value and much higher than the C-Index for the survival model in the previous section. Even as the age distribution becomes more imbalanced, the C-Index for the binary-outcome regression model remains equal to one. While the survival model is equally capable of discriminating between patients who will live 20 years from those who will not, it is penalized for not being able to discriminate between the risk levels of two patients having essentially the same age. In the binary version of the C-Index, there is never a comparison that involves two patients with the same age.
6.2 |. Some Uses of Survival Models
As discussed in previous sections, the C-Index describes a model’s ability to correctly distinguish the risk between any two subjects from the population of interest. It has been argued by previous authors that this is an unrealistic clinical scenario, meaning that physicians rarely use a predictive model to distinguish between pairs of patients8. In fact, there are many other uses of a survival model that are valid and potentially more clinically relevant such as
Evaluation of the strength, significance, and predictive ability of risk factors for adverse outcomes.
Accurate estimation of survival probabilities (i.e. calibration).
Risk grouping based on clinically-meaningful differences in underlying risk.
The C-Index, however, does not measure a model’s ability to perform any of these tasks. Therefore, evaluations that rely heavily on the C-Index often fail to describe the model’s performance with respect to the intended use in practice. If (1) is the main use of interest, the sizes of the hazard ratios and p-values are more meaningful than the C-Index for assessing the clinical and statistical significance of risk factors. To assess the prognostic value and clinical usefulness of a predictive model, cross-validated goodness-of-fit, net benefit measures, and decision curve analyses are more informative19,20,21. For (2), calibration statistics such as the calibration slope provide more informative model assessments than the C-Index4. For (3), discriminant analyses and the corresponding assessments are most appropriate22. In general, we recommend against the use of arbitrary hard thresholds or rules of thumb to decide whether a model’s performance is adequate, as this practice oversimplifies the model assessment process and can lead to the disposal of many useful models. Instead, we suggest that analysts carefully identify the intended use of the survival model, select an evaluation metric that matches this use, and interpret the value of the appropriate evaluation metric while considering the limitations of the available sample data.
In the field of reproductive medicine, for example, it has been argued that most patients with very high or low probabilities of becoming pregnant are often unobservable in samples drawn from fertility programs23. Therefore, evaluations of survival models for time-to-pregnancy, based on the C-Index, often involve many comparisons of patients with near-average underlying risks. Consistent with the arguments in this paper, it has been reported that the C-Index is generally very low for fertility survival models, but if these models are well-calibrated and can adequately aid in the treatment decisions of subfertile patients (related to items (1) and (2) above), they are still considered very clinically useful23.
The C-Index is most useful when the predicted risk levels are intended to be compared across patients. For example, when assigning livers to transplant candidates, the risk scores of patients (the MELD scores) on the waiting list are compared to determine who has the highest priority for receiving the transplant24. In this context, it is relevant to consider how well the survival model can correctly order patients in terms of risk. Therefore, the C-Index matches the clinical use of the model in this case, although here again, the value is heavily influenced by comparisons of patients with nearly identical underlying risk. Researchers and reviewers should recognize that this is just one specific context, and the C-Index cannot be interpreted as an overall metric for model adequacy in every application.
7 |. A REAL DATA EXAMPLE: GERMAN BREAST CANCER STUDY GROUP
We now demonstrate the pitfalls of the C-Index through an analysis of breast cancer survival data. In a 1984–1989 study conducted by the German Breast Cancer Study Group (GBSG), patients were followed to assess recurrence-free survival, and several clinical risk factors were measured at the start of the study25. We fit two different Cox proportional hazards models for recurrence-free survival, using data from 686 node-positive patients26,27. The first model (Model A) includes the number of positive lymph nodes and the progesterone receptor concentration as predictors; the second model (Model B) includes both of the predictors from Model A, plus an additional categorical predictor for the tumor grade (I, II, or III).
It is well-established that tumor grade is a very strong predictor of recurrence-free survival in cancer patients28,29. Figure 3 shows the estimated survival curves (from Model B) for a patient with an average number of positive lymph nodes and progesterone receptor concentration, stratified by tumor grade. We observe clinically-meaningful differences in the estimated survival probabilities across tumor grades, and the estimated median survival time for a patient with a grade III tumor is at least three years earlier than one with a grade I tumor. In addition, the estimated hazard ratios are very large and there is strong evidence of a statistically significant association between tumor grade and the hazard of cancer recurrence or death (Table 2).
FIGURE 3.
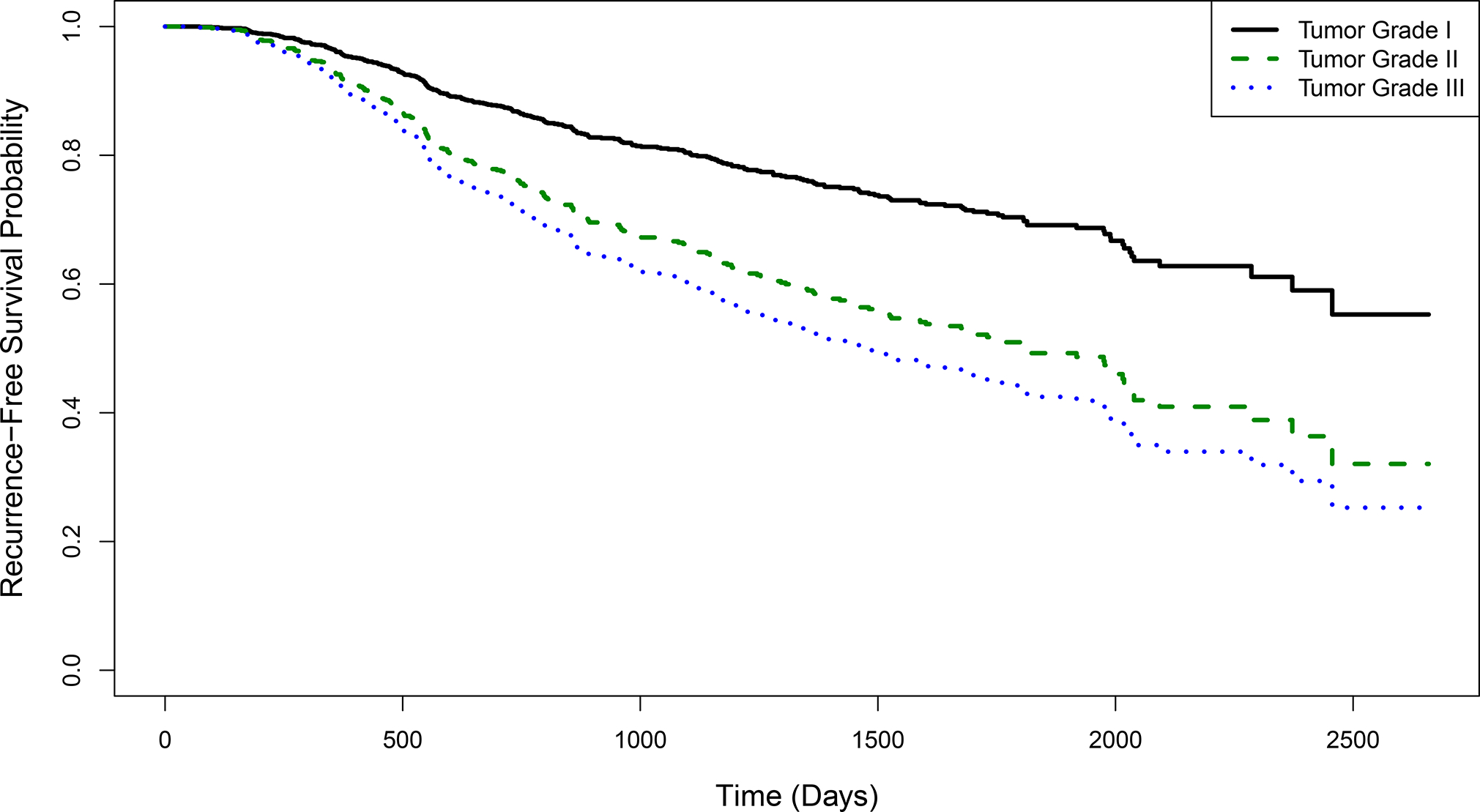
Recurrence-free survival curves by tumor grade, estimated by a Cox proportional hazards model with number of positive lymph nodes, progesterone receptor concentration, and tumor grade as predictors. Results are shown for a patient with an average number of positive lymph nodes and progesterone receptor concentration. The model is fit using data from 686 breast cancer patients from the German Breast Cancer Study Group.
TABLE 2.
Hazard ratios, p-values, counts of comparable pairs, and concordance rates for comparisons of different tumor grades, using data from the German Breast Cancer Study Group. The comparable pairs and concordance rates for the tumor grade comparisons are computed by restricting the traditional definition of comparable pairs to only include patients with a specific combination of tumor grades (Equation 8). The risk scores used to calculate the concordance rate are calculated from either of the following Cox proportional hazards models: Model A (which includes the number of positive lymph nodes and progesterone receptor concentration as predictors) and Model B (which includes the predictors from Model A plus a categorical tumor grade variable). The overall C-Indices for the models are weighted averages of the concordance rates in the fifth and sixth columns, where the weights are the number of comparable pairs in the fourth column. The values of these overall C-Indices for Models A and B are 0.679 and 0.682, respectively.
| Tumor Grade Comparison | Hazard Ratio (HR) | P-Value | Number of Comparable Pairs | Concordance Rate | |
|---|---|---|---|---|---|
| Model A | Model B | ||||
|
| |||||
| III vs. I | 2.32 | 0.002 | 6,499 | 0.77 | 0.82 |
| II vs. I | 1.92 | 0.009 | 16,122 | 0.69 | 0.74 |
| III vs. II | 1.21 | 0.159 | 44,011 | 0.69 | 0.67 |
| Same Grade | - | - | 66,451 | 0.66 | 0.66 |
Despite the strong impact of the tumor grade variable on the survival estimates and clinical interpretations of patients’ risks, the C-Indices for Models A and B are 0.679 and 0.682, respectively, giving the appearance that this variable has almost no prognostic value in terms of risk discrimination. In Table 2, we decompose the total number of comparable pairs based on whether the patients have different tumor grades, and we calculate the concordance rates within these subgroups of pairs as follows (written assuming no ties in the risk scores for simplicity):
| (8) |
where is the estimated concordance rate among comparable pairs with tumor grades and and ), and is the tumor grade variable. The overall C-Index is a weighted average of , and , where the weights are the denominators from Equation (8). We find that for certain comparable pairs of patients with different tumor grades (III vs. I and II vs. I), the concordance rate is much higher than the overall C-Index, and this is accentuated when Model B is used over Model A. This provides further evidence that patients with tumor grades II or III have elevated risks of recurrence or death, compared to patients with tumor grade I, and the inclusion of the tumor grade variable in the model is useful for identifying these higher-risk patients. However, as in the age group example from Section 6.1, the vast majority of the comparable pairs in the C-Index calculation involve patients with the same tumor grade, or two high-risk grades (i.e. grades III vs. II), so the C-Index is dominated by comparisons of patients with similar underlying risks and it fails to recognize the prognostic value of the model. As argued in Sections 3.2 and 6.1, many of these patients with the same tumor grade and similar underlying risks would not be considered comparable if the outcome were measured as a binary indicator. For the survival model, which has very few ties in the time-to-event outcome variable, these types of pairs are frequently considered comparable, which deflates the overall C-Index.
8 |. DISCUSSION
Through a direct comparison of the binary and survival versions of the C-Index, we have demonstrated the unique challenges in attaining high C-Index values for survival models. The differences in the concordance definitions for binary and survival outcomes have important implications in practice. In the survival case, the C-Index is negatively impacted by the existence of patients deemed comparable but with similar risks. Statisticians, physicians, and peer reviewers should consider the difficult comparisons involved in C-Index calculation for survival models when evaluating discrimination ability. It is also important to clearly identify the target population and determine whether it is actually of interest to discriminate risk levels across all patients within this population, regardless of how similar they are. Careful interpretation of the C-Index and its relationship with the actual use of the model is crucial for appropriate evaluation.
One potential modification of the C-Index, which could provide more meaningful information to clinicians, is to weight the comparable pairs by some measure of difference in underlying risk. Thus, the comparisons that are more clinically relevant are given more weight in the model evaluation. However, we note that it is challenging to nonparametrically estimate differences in underlying risk with censored time-to-event data. We also emphasize that many limitations of the C-Index would not be resolved by this modification. For example, weighted C-Indices still measure model performance with respect to pairwise comparisons of patients’ risks, which often does not match the intended uses of survival models for clinical applications.
The analytic relationship between the concordance probability and under the OLS setting provides a mapping from concordance probability values to a more familiar scale. The limitations of the measure are well-documented, and researchers across many scientific fields expect to observe low values even for useful models17,18. The relationship suggests that modest C-Index values correspond to values which are difficult to achieve in some applications. As with , understanding the limitations of the C-Index may help researchers adjust expectations and more accurately assess a model’s usefulness.
In this paper, we have described example models that are very useful in practice but have low C-Index values. Researchers may benefit from clearly defining the desired properties of a model, and examining statistics that reflect the model’s performance with respect to these goals7. We have described several common uses of survival models that are not captured by the C-Index, and we have suggested existing alternatives for assessing model performance in each application. Further work is needed to develop evaluation statistics that closely align with the varied clinical uses of survival models.
Financial disclosure
Research reported in this publication was supported by the National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health under award numbers R01DK070869 and R01DK129539. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Conflict of interest
The authors declare no potential conflict of interests.
Abbreviations: C-Index, Concordance Index; OLS, Ordinary Least Squares
Data availability statement
The German Breast Cancer Study Group data that support this paper are publicly available through the survival package in R (https://cran.r-project.org/web/packages/survival/index.html)26. The R codes are available with this paper at the Statistics in Medicine website on Wiley Online Library.
References
- 1.Harrell F, Lee K, Mark D. Multivariate prognostic models: Issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med 1996; 15: 361–387. doi: [DOI] [PubMed] [Google Scholar]
- 2.Harrell F, Califf R, Pryor D, Lee K, Rosati R. Evaluating the yield of medical tests. JAMA 1982; 247: 2543–2546. doi: 10.1001/jama.1982.03320430047030 [DOI] [PubMed] [Google Scholar]
- 3.Uno H, Cai T, Pencina M, D’Agostino R, Wei L. On the C-statistics for evaluating overall adequacy of risk prediction procedures with censored survival data. Stat Med 2011; 30: 1105–1117. doi: 10.1002/sim.4154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Steyerberg E Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. New York, NY: Springer. 2009 [Google Scholar]
- 5.DeMaris A, Selman S. Converting Data into Evidence: A Statistics Primer for the Medical Practitioner. New York, NY: Springer. 2013. [Google Scholar]
- 6.Jin V, Wang J, Tang B, eds. Integration of Multisource Heterogeneous Omics Information in Cancer. Lausanne: Frontiers Media SA. 2020. [Google Scholar]
- 7.Use Cook N. and misuse of the receiver operator curve in risk prediction. Circulation 2007; 115: 928–935. doi: 10.1161/CIRCULATIONAHA.106.672402 [DOI] [PubMed] [Google Scholar]
- 8.Vickers A Prediction models: Revolutionary in principle, but do they do more good than harm? J Clin Oncol 2011; 29: 2951–2952. doi: 10.1200/JCO.2011.36.1329 [DOI] [PubMed] [Google Scholar]
- 9.Vickers A, Cronin A. Traditional statistical methods for evaluating prediction models are uninformative as to clinical value: Towards a decision analytic framework. Semin Oncol 2010; 37: 31–38. doi: 10.1053/j.seminoncol.2009.12.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Halligan S, Altman D, Mallett S. Disadvantages of using the area under the receiver operating characteristic curve to assess imaging tests: A discussion and proposal for an alternative approach. Eur Radiol 2015; 25: 932–939. doi: 10.1007/s00330-014-3487-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pencina M, D’Agostino R. Overall C as a measure of discrimination in survival analysis: Model specific population value and confidence interval estimation. Stat Med 2004; 23: 2109–2123. doi: 10.1002/sim.1802 [DOI] [PubMed] [Google Scholar]
- 12.Yan G, Greene T. Investigating the effects of ties on measures of concordance. Stat Med 2008; 27: 4190–4206. doi: 10.1002/sim.3257 [DOI] [PubMed] [Google Scholar]
- 13.Gönen M, Heller G. Concordance probability and discriminatory power in proportional hazards regression. Biometrika 2005; 92: 965–970. doi: 10.1093/biomet/92.4.965 [DOI] [Google Scholar]
- 14.Heagerty P, Zheng Y. Survival model predictive accuracy and ROC curves. Biometrics 2005; 61: 92–105. doi: 10.1111/j.0006-341X.2005.030814.x [DOI] [PubMed] [Google Scholar]
- 15.Rupinski M, Dunlap W. Approximating Pearson product-moment correlations from Kendall’s tau and Spearman’s rho. Educ Psychol Meas 1996; 56: 419–429. doi: 10.1177/0013164496056003004 [DOI] [Google Scholar]
- 16.Mean Cramer J. and variance of R2 in small and moderate samples. J Econom 1987; 35: 253–266. doi: 10.1016/0304-4076(87)90027-3 [DOI] [Google Scholar]
- 17.Sapra R Using R2 with caution. Curr Med Res Pract 2014; 4: 130–134. doi: 10.1016/j.cmrp.2014.06.002 [DOI] [Google Scholar]
- 18.McGuirk A, Driscoll P. The hot air in R2 and consistent measures of explained variation. Am J Agric Econ 1995; 77: 319–328. doi: 10.2307/1243542 [DOI] [Google Scholar]
- 19.van Houwelingen H, Bruinsma T, Hart A, Van’t Veer L, Wessels L. Cross-validated Cox regression on microarray gene expression data. Stat Med 2006; 25: 3201–3216. doi: 10.1002/sim.2353 [DOI] [PubMed] [Google Scholar]
- 20.Simon N, Friedman J, Hastie T, Tibshirani R. Regularization paths for Cox’s proportional hazards model via coordinate descent. J Stat Softw 2011; 39: 1–13. doi: 10.18637/jss.v039.i05 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vickers A, Cronin A, Elkin E, Gönen M. Extensions to decision curve analysis, a novel method for evaluating diagnostic tests, prediction models and molecular markers. BMC Med Inform Decis Mak 2008; 8. doi: 10.1186/1472-6947-8-53 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ke W, Ye Y, Huang S. Discriminant function for prognostic indexes and probability of death in chronic severe hepatitis B. J Gastroenterol 2003; 38: 861–864. doi: 10.1007/s00535-003-1162-3 [DOI] [PubMed] [Google Scholar]
- 23.Coppus S, van der Veen F, Opmeer B, Mol B, Bossuyt P. Evaluating prediction models in reproductive medicine. Hum Reprod 2009; 24: 1774–1778. doi: 10.1093/humrep/dep109 [DOI] [PubMed] [Google Scholar]
- 24.Organ Procurement and Transplantation Network. Policies and Bylaws https://optn.transplant.hrsa.gov/policies-bylaws/policies/. Accessed December 12, 2022.
- 25.Schumacher M, Bastert G, Bojar H, et al. Randomized 2×2 trial evaluating hormonal treatment and the duration of chemotherapy in node-positive breast cancer patients. J Clin Oncol 1994; 12: 2086–2093. doi: 10.1200/JCO.1994.12.10.2086 [DOI] [PubMed] [Google Scholar]
- 26.Therneau T A Package for Survival Analysis in R. 2022. R package version 3.3–1. [Google Scholar]
- 27.Royston P, Altman D. External validation of a Cox prognostic model: Principles and methods. BMC Med Res Methodol 2013; 13. doi: 10.1186/1471-2288-13-33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rosenberg J, Chia Y, Plevritis S. The effect of age, race, tumor size, tumor grade, and disease stage on invasive ductal breast cancer survival in the U.S. SEER database. Breast Cancer Res Treat 2005: 47–54. doi: 10.1007/s10549-004-1470-1 [DOI] [PubMed] [Google Scholar]
- 29.Bloom H, Field J. Impact of tumor grade and host resistance on survival of women with breast cancer. Cancer 1971; 28: 1580–1589. doi: [DOI] [PubMed] [Google Scholar]
- 30.Kendall M Rank Correlation Methods. Liverpool: Charles Birchall and Sons, Ltd. 3rd ed. 1962. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The German Breast Cancer Study Group data that support this paper are publicly available through the survival package in R (https://cran.r-project.org/web/packages/survival/index.html)26. The R codes are available with this paper at the Statistics in Medicine website on Wiley Online Library.


