Abstract
The relationship between the volumetric thermodynamic coefficients of liquid metals at the melting point and interatomic bond energy was studied. Using dimensional analysis, we obtained equations that connect cohesive energy with thermodynamic coefficients. The relationships were confirmed by experimental data for alkali, alkaline earth, rare earth, and transition metals. Cohesive energy is proportional to the square root of the ratio of melting point Tm divided by thermal expansivity αp. Thermal expansivity does not depend on the atomic size and atomic vibration amplitude. Bulk compressibility βT and internal pressure pi are related to the atomic vibration amplitude by an exponential dependence. Thermal pressure pth decreases with an increasing atomic size. Fcc and hcp metals with high packing density, as well as alkali metals, have the relationships with the highest coefficient of determination. The contribution of electrons and atomic vibrations to the Grüneisen parameter can be calculated for liquid metals at their melting point.
Keywords: isobaric thermal expansivity, isothermal compressibility, thermal pressure, internal pressure, Grüneisen parameter, liquid metals, melting point
1. Introduction
Metal melting is the initial stage of most technological processes. Therefore, research on metallic liquids is of great practical importance. The simplest objects are monoatomic liquids. In the model of a simple liquid, atoms do not have dipole moments, are not chemically bound, and have a spherically symmetric interaction potential [1,2]. In the physical lattice model, it is assumed that the liquid has a lattice structure, at least in the first coordination sphere [3], and the atomic oscillation occurs inside the free volume, i.e., the space available for the movement of the atom [4].
The molecular kinetic theory also provides relationships that are adequately related to the experimental data. Lindemann [5] calculated the vibration frequency of atoms at the melting point. Using the frequency of atomic vibrations, Andrade [6] derived a formula that relates dynamic viscosity to molar mass, volume and melting point.
In the Einstein model, the substance contains a large number of independent quantum harmonic oscillators of the same natural atomic frequency, and above the Einstein temperature, the heat capacity increases slightly [7]. In the Debye model, quantum harmonic oscillators have different frequencies, and above the Debye temperature ΘD, all modes of atomic vibrations are excited. In the high temperature approximation, the Einstein and Debye temperatures differ slightly [8]. Grimvall and Sjödin [9] investigated the relationship between the different physical properties of materials and the Debye temperature. In [10], the analysis of the properties of metallic liquid is considered in detail.
In this work, we will investigate the thermodynamic coefficients that characterize the change in the volume of monatomic liquid metals. The isobaric thermal expansivity αp determines the temperature change of volume V at constant pressure p. Thermal expansion is associated with the asymmetry of interatomic interaction [11,12], and as a result, the repulsive force grows faster than the attractive force. Upon transition to the liquid state, bulk thermal expansion sharply increases [13]. The isothermal compressibility βT determines the change in volume under pressure at a constant temperature T. Isobaric thermal expansivity and isothermal compressibility are directly related to the thermal pressure pth, the internal pressure pi, and the Grüneisen parameter [14].
Molar mass and volume, as well as the interatomic bond energy, represent the most general atomic characteristic of a substance. Interatomic interaction characterizes the cohesion energy, which is equal to the energy required for the decomposition of a solid into independent atoms at 0 K. Thermal energy is used to compare the strength of an interatomic interaction with the destructive effect of thermal motion. It was demonstrated that isobaric thermal expansivity [15,16,17], bulk modulus [9,18], and internal pressure [19,20] are related to interatomic bond energy. In particular, the isobaric thermal expansivity is inversely proportional to cohesion energy [16] and melting point [21].
This article describes new data on the relationship between volumetric thermodynamic coefficients with atomic characteristics and the interatomic interaction in liquid metals at their melting point.
2. Method
We used dimensional analysis to identify the relationship between physical and chemical quantities [22,23]. Each object is characterized by a set of significant physical quantities. At the first stage, we identified these quantities. Then, we found relations between significant quantities that provided the same dimension on the left and right side of the equation. The dimensional analysis provided good results in the study on the viscosity, surface tension, and self-diffusion of metallic liquids [24,25,26]. The adjusted coefficient of determination R2adj was used to assess how well a relationship predicts outcomes. The better the linear regression fits the data in comparison to the simple average, the closer the value of R2adj is to 1.
The melting point at which the metal passes from the solid to the liquid state was chosen as the characteristic temperature. At this temperature, the short range order of liquid metals can be close to crystalline [27,28]. The quantities at the melting point are marked with subindex m. Data on the cohesion energy Ec (J·mol−1), melting point Tm (K) molar volume Vm (m3·mol−1), heat capacity at constant pressure Cp (J·mol−1·K−1) and atomic mass m (kg) were taken from [10]. Reference [29] contains the Debye temperature ΘD (K), and references [30,31] contain the Fermi energy EF (J·mol−1). Reference [32] contains the Wigner–Sietz radius rs (m) and the valency of chemical element z. The isothermal compressibility at melting point βTm (J−1·m3) was taken from [30,33], and the isobaric thermal expansivity at melting point αpm (K−1) was from [10,33]. In this work, we analyzed data for alkali, alkaline earth, rare earth, and transition metals.
3. Results and Discussion
The dimension analysis of significant thermophysical quantities allowed us to obtain the simple relations for the thermal expansivity αp and the isothermal compressibility βT:
| (1) |
| (2) |
where E is the molar energy of the interatomic bond (J·mol−1), V is the molar volume (m3·mol−1), and R is the universal gas constant (J·K−1·mol−1).
Figure 1 and Figure 2 show relations (1) and (2) at the melting point Tm in the form:
| (3) |
| (4) |
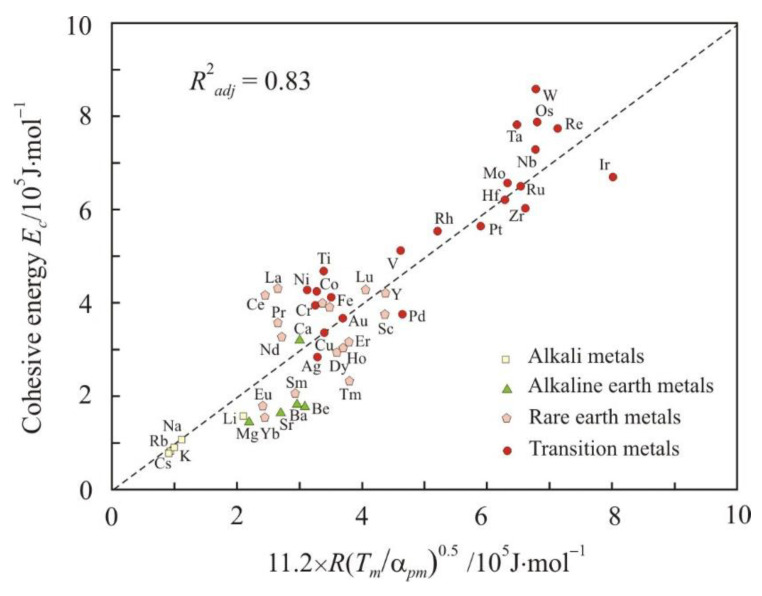
Figure 1.
Relationship between the cohesive energy Ec and 11.2 × R(Tm/αpm)0.5 parameter. The dashed line corresponds to the equality Ec = 11.2R(Tm/αpm)0.5.
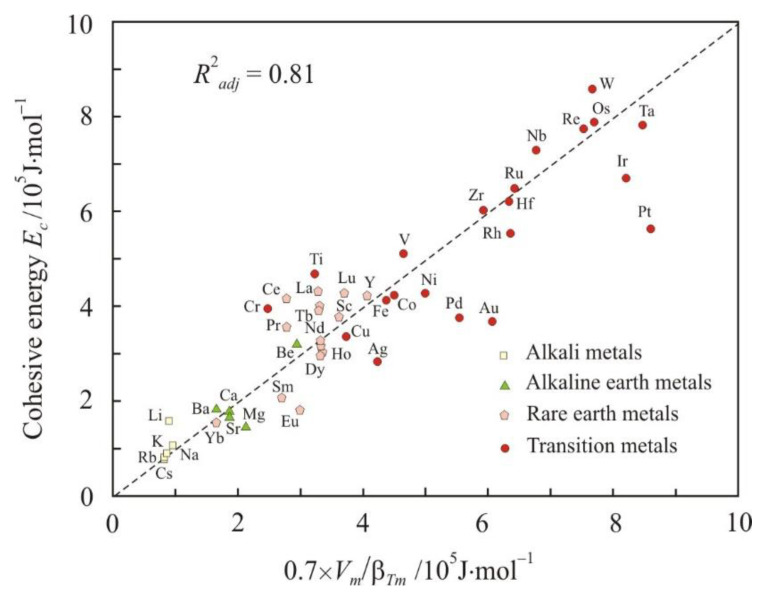
Figure 2.
Relationship between the cohesive energy Ec and 0.7 × Vm/βTm parameter. The dashed line corresponds to the equality Ec = 0.7 × Vm/βTm.
Here, the cohesive energy Ec was used as the energy of the interatomic bond. Dimensionless factor 11.2 in formula (3) is equal to the average ratio of Ec to R(Tm/αpm)0.5 for all metals, and dimensionless factor 0.7 in formula (4) is equal to the average ratio of Ec to Vm/βTm. For Equations (3) and (4), the coefficient of determination R2adj exceeds 0.80, and these equations can be assessed as good. Relation (3) between the cohesive energy and the thermal expansivity was obtained for the first time. Relation (4) is more obvious and has already been used in different versions [30,34].
The analysis shows that Equations (3) and (4) for alkali metals, with the exception of lithium, have a coefficient of determination greater than 0.95. In addition, a high coefficient of determination is observed in metals with face-centered cubic (fcc) and hexagonal closed-packed (hcp) lattices, which have the highest packing density, 74%. For example, the relationship between the cohesive energy and the R(Tm/αpm)0.5 parameter has R2adj = 0.96 for fcc metals. Body-centered cubic (bcc) metals, with a lower packing density of 68%, show more scattering around Equations (3) and (4). The influence of the lattices type on the properties of metals in the liquid state can be associated with the preservation of the local atomic structure near the melting point [35].
The isochoric thermal pressure coefficient pth characterizes the change in the pressure with a change in temperature at a constant volume, and from relations (1) and (2), we reduce it to this form:
| (5) |
The internal pressure characterizes the change in the internal energy U (J) with a change in volume at a constant temperature, and at normal pressure, one can use this approximation [20]:
| (6) |
If we take E = RTm, then relations (5) and (6) at the melting point can be reduced to this simple form:
| (7) |
| (8) |
Figure 3 and Figure 4 show relations (7) and (8) in the form of a linear regression. For clarity, relation (7) is presented on a logarithmic scale. The high coefficients of determination, especially for internal pressure pim, confirms the significance of initial relations (1) and (2) obtained using the dimensional analysis.
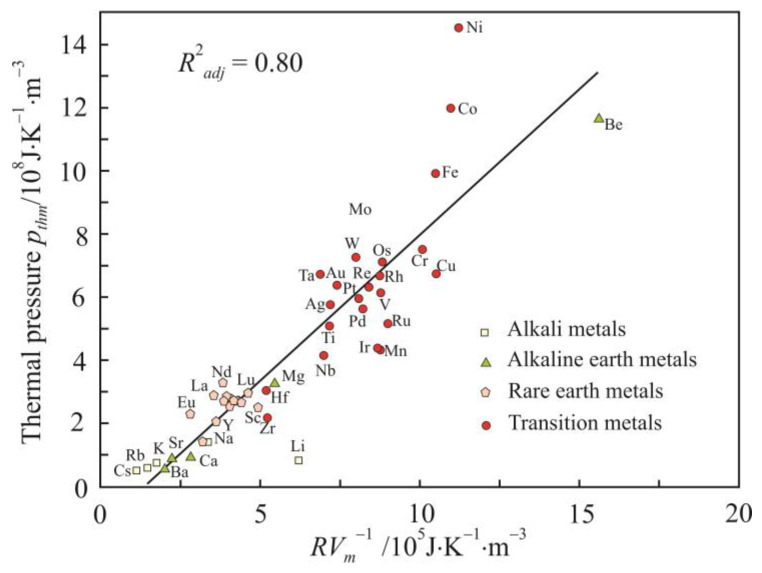
Figure 3.
Relationship between the thermal pressure pthm and RVm−1 parameter.
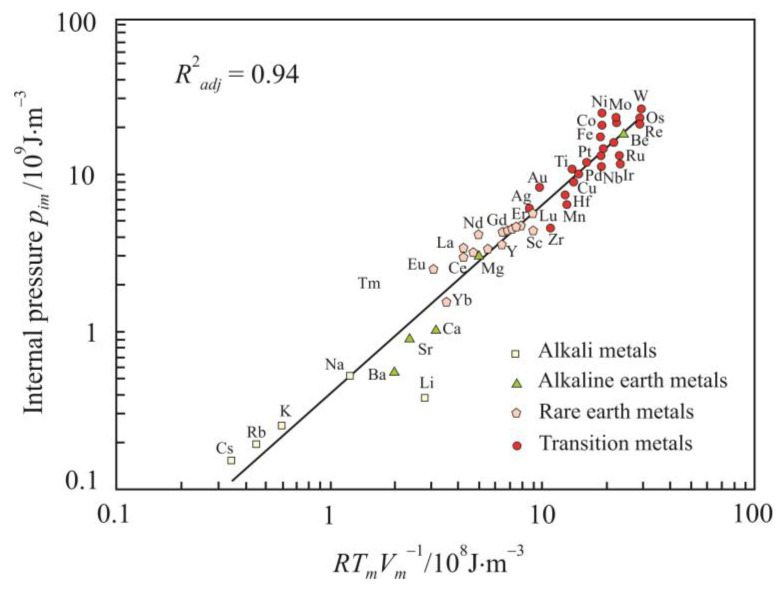
Figure 4.
Relationship between the internal pressure pim and thermal energy density RTmVm−1.
The thermal pressure pth is inversely proportional to the molar volume Vm (Figure 3). The ferromagnetic metals Ni, Co, and Fe noticeably deviate from the linear regression. The molar volume is related to the atomic size a by the relation
| (9) |
where NA is the Avogadro constant (mol−1). So, the thermal pressure decreases with increasing atomic size. Thermal expansivity analysis showed that αpm does not depend on the atomic size and does not affect dependency (5). The independence is confirmed by the random distribution of points on the experimental dependence of αpm on the atomic size a.
Figure 4 demonstrates the strong relationship between internal pressure pim and thermal energy density RTmVm−1. This suggests that the internal pressure at the melting point is mainly due to the thermal vibration of atoms.
Relations (7) and (8) also show a higher coefficient of determination for fcc and hcp metals. For alkaline earth metals, the coefficient of determination exceeds 0.995, and for alkali metals, with the exception of lithium, it is above 0.999.
The amplitude of atomic vibrations Am (m) was determined from the kinetic theory [24]:
| (10) |
where ΘD is the Debye temperature (K), h is the Plank constant (J·s), and m is the atomic mass (kg). It follows from (10) that the amplitude increases with an increase in the melting point Tm and a decrease in the atomic mass m and Debye temperature ΘD.
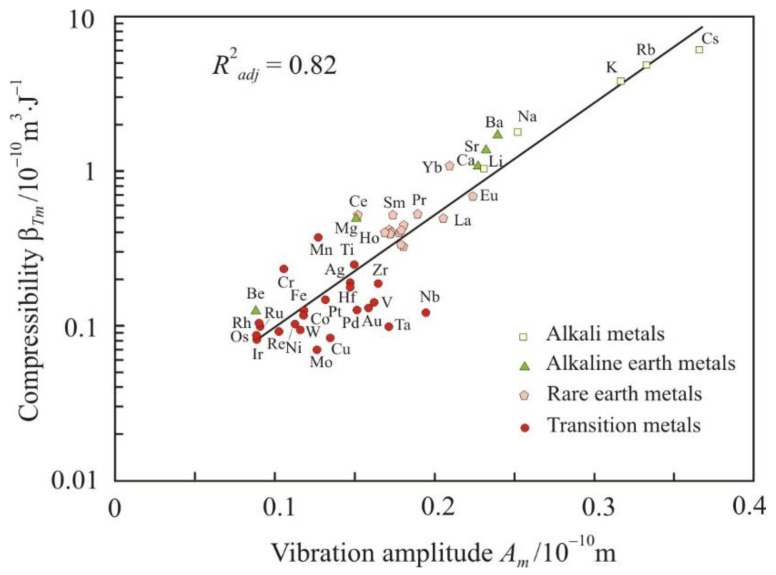
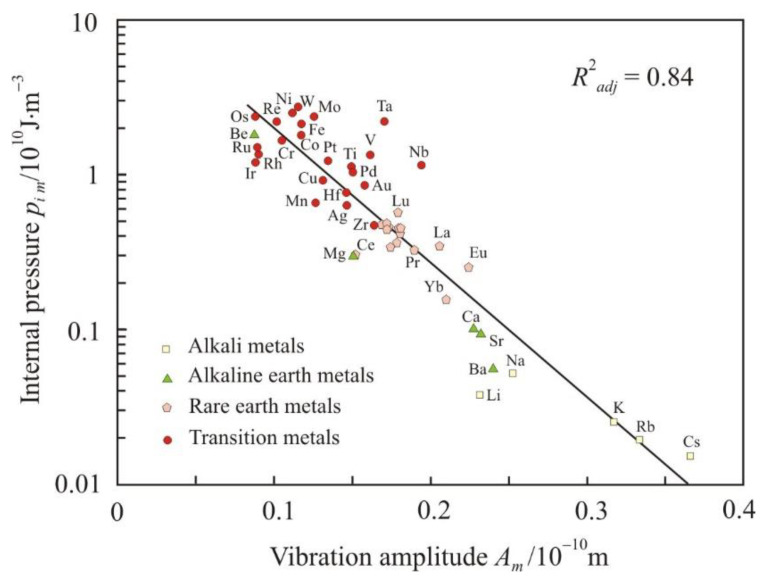
For strong interatomic bonds, the amplitude of atomic vibrations is smaller. Essentially, the amplitude also characterizes the interatomic interaction. Figure 5 and Figure 6 show the dependences of isothermal compressibility βTm and internal pressure pim on the amplitude of atomic vibrations at the melting point. The compressibility increases and the internal pressure decreases when the amplitude increase. Dependencies are linear if βTm and pim are presented on a logarithmic scale. Therefore, dependency can be written as an exponential:
| (11) |
| (12) |
where the vibration amplitude is given in picometers (pm) and the isothermal compressibility βTm and internal pressure pim are given in SI base units. The thermal expansivity αpm does not depend on the amplitude of atomic vibrations, and the thermal pressure pthm has a noticeably lower coefficient of determination of 0.67.
Figure 5.
Dependence of the isothermal compressibility βTm on the amplitude of atomic vibrations at the melting point Am.
Figure 6.
Dependence of the internal pressure pim on the amplitude of atomic vibrations at the melting point Am.
The relationship between the thermal expansivity αpm and the vibration amplitude Am is characterized by a coefficient of determination close to zero. This confirms the concept of anharmonicity [11,12], according to which the thermal expansion is related to the nonlinearity of the interatomic interaction force.
The thermal expansivity and isothermal compressibility are also included in the expression for the Grüneisen parameter [36]:
| (13) |
where CV (J·mol−1·K−1) is the heat capacity at constant volume. The Grüneisen parameter characterizes the isochoric change in the internal energy density U/V with a change in pressure.
In the Debye model, the parameter γ is related to the atomic vibration and is calculated using the formula
| (14) |
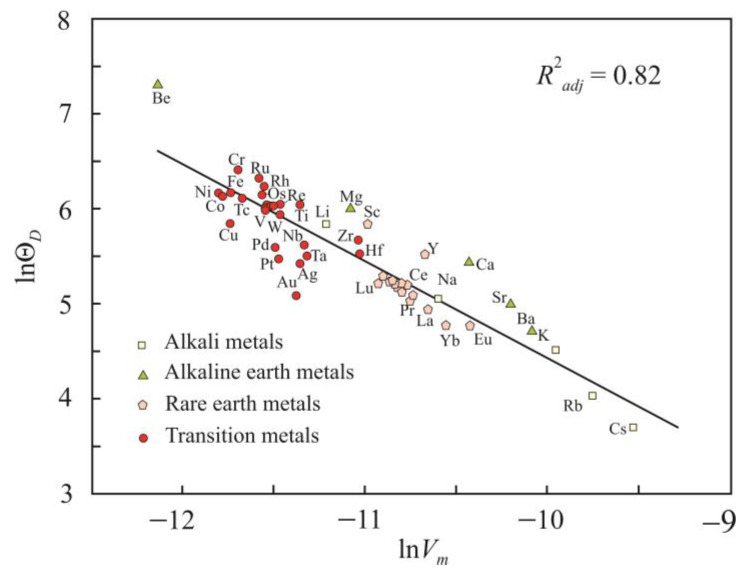
We choose melting point Tm as a fixed temperature. Figure 7 shows the dependence of lnΘD on lnVm, from which γvib = 1.02 can be found. Thus, the average vibrational component of the Grüneisen parameter of liquid metals at the melting point is 1.02.
Figure 7.
Dependence of the Debye temperature lnΘD on the molar volume lnVm for liquid metals at the melting point.
The electronic contribution to the Grüneisen parameter [37,38] is
| (15) |
where D (J−1) is the electronic density of states at the Fermi energy level, and ρ (m–3) is the concentration of free electrons. According to [7], the electron density of the state is
| (16) |
The free electron density ρ can be calculated from the Wigner–Seitz radius rs [39]:
| (17) |
The Wigner–Seitz radius is the radius of a sphere whose volume is equal to the volume per a free electron. The concentration of free electrons can also be obtained from the formula
| (18) |
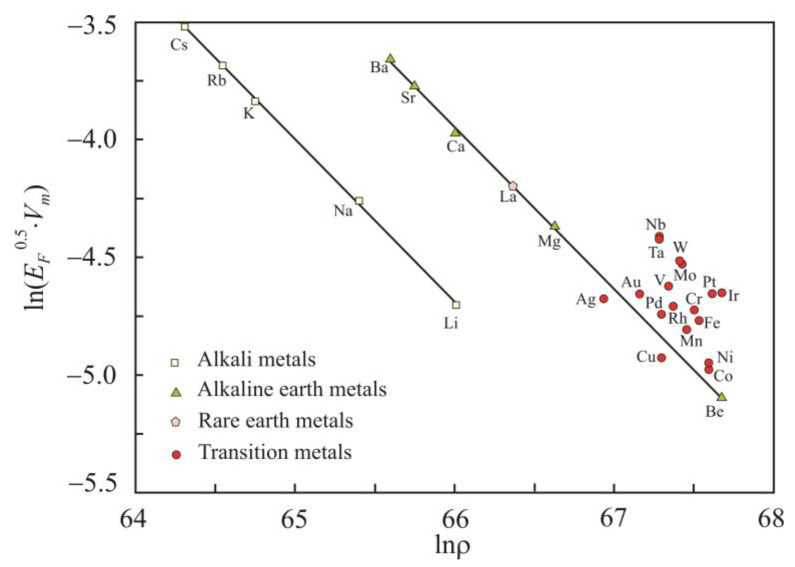
where z is the valency of chemical elements. Figure 8 shows the dependence of ln(EF0.5Vm) on lnρ. It follows that for alkali and alkaline earth metals, there is a strong relationship, with a determination coefficient of 0.999, and the electronic contribution to the Grüneisen parameter is 0.60.
Figure 8.
Dependence of ln(EF0.5Vm) on the electron concentration lnρ for liquid metals at the melting point.
Dimensionless Grüneisen parameter γ is a useful quantity for characterizing the vibrational anharmonicity that causes thermal expansion. The expression for the difference in heat capacities (Cp − Cv) contains the square of the thermal expansivity [40]:
| (19) |
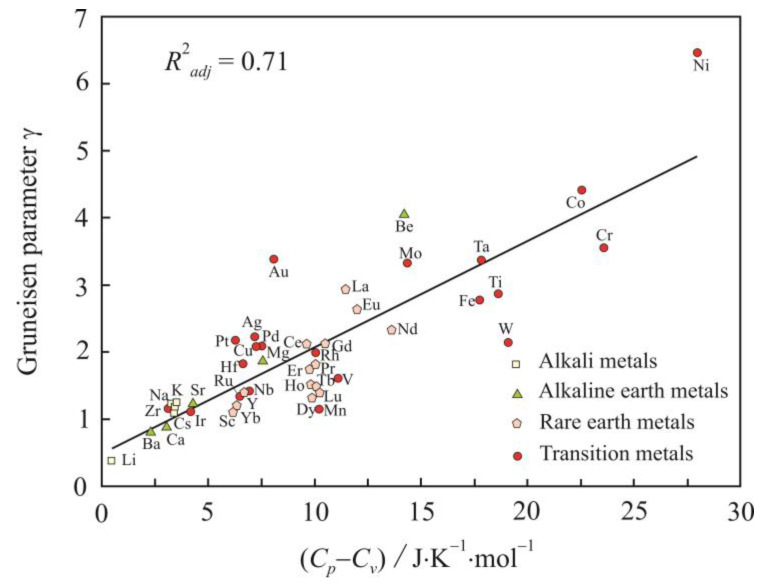
Figure 9 shows a fairly close relationship between the Grüneisen parameter γ and the difference in heat capacities (Cp − Cv) for metals at the melting point, and it confirms the relationship between γ and vibrational anharmonicity.
Figure 9.
Relation of Grüneisen parameter γ to the difference in heat capacities (Cp − Cv) for liquid metals at the melting point.
4. Conclusions
The relationships between the volumetric thermodynamic coefficients of liquid metals at the melting point and the energy of interatomic interaction were investigated. The isobaric thermal expansivity αp, isothermal compressibility βT, isochoric thermal pressure pth, internal pressure pi, and the Grüneisen parameter were used as thermodynamic coefficients. The energy quantities were molar cohesive energy Ec and thermal energy RTm. Using the dimensional analysis, we obtained equations that relate the cohesive energy to the thermodynamic coefficients. The relationships were confirmed with experimental data from alkali, alkaline earth, rare earth, transition metals.
The following results were obtained in this work: Thermodynamic coefficients at the melting point depend on the type of crystal lattice. Ratios for liquid metals with face-centered cubic and hexagonal closed-packed lattices as well as for alkali and alkaline earth metals have the highest coefficient of determination. Cohesive energy is proportional to the square root of the ratio of the melting point Tm divided by thermal expansivity αp. Thermal expansivity αp does not depend on atomic size and atomic vibration amplitude. This confirms the concept of anharmonicity of thermal expansion. Bulk compressibility βT and internal pressure pi are related to atomic vibration amplitude by an exponential dependence. Internal pressure is closely related to thermal energy density, and at melting point, it is mainly due to the thermal vibration of the atoms. Thermal pressure pth decreases with an increasing atomic size. The contribution of electrons and atomic vibrations to the Grüneisen parameter γ can be calculated for liquid metals at the melting point.
Acknowledgments
The article was made within the framework of state work No. FEUZ-2023-0015.
Author Contributions
Conceptualization, Y.N.S.; methodology; software, Y.N.S. and V.S.T.; validation, Y.N.S. and V.S.T.; formal analysis, V.S.T. and Y.N.S.; investigation, Y.N.S.; resources, V.S.T.; data curation, V.S.T.; writing—original draft preparation, Y.N.S.; writing—review and editing, Y.N.S.; visualization, Y.N.S.; supervision, V.S.T.; project administration, V.S.T.; funding acquisition, V.S.T. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this article are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Funding Statement
This research received no external funding.
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Temperly H.N.V., Rowlinson J.S., Rushbrooke G.S., editors. Physics of Simple Liquids. North-Holland Publishing Company; Amsterdam, The Netherlands: 1968. 713p [Google Scholar]
- 2.Barrat J.-L., Hansen J.-P. Basic Concepts of Simple and Complex Liquids. The University Press; Cambridge, UK: 2003. pp. 7–35. [Google Scholar]
- 3.De With G. Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications. Wiley-VCH; Weinheim, Germany: 2013. pp. 155–220. [Google Scholar]
- 4.Glasstone S., Laidler K.J., Eyring H. The Theory of Rate Processes: The Kinetics of Chemical Reactions, Viscosity, Diffusion and Electrochemical Phenomena. McGraw–Hill Book Co.; New York, NY, USA: 1941. pp. 477–551. [Google Scholar]
- 5.Lindemann F.A. Über die Berechnung molekularer Eigenfrequenzen. Phys. Z. 1910;11:609–612. [Google Scholar]
- 6.Andrade E.D.C. A theory of the viscosity of liquids—Part 1. Phil. Mag. 1934;17:497–511. doi: 10.1080/14786443409462409. [DOI] [Google Scholar]
- 7.Kittel C. Introduction to Solid State Physics. John Wiley & Sons; Hoboken, NJ, USA: 2005. 680p [Google Scholar]
- 8.Gopal E.S.R. Specific Heats at Low Temperatures. Plenum Press; New York, NY, USA: 1966. pp. 25–27. [Google Scholar]
- 9.Grimvall G., Sjödin S. Correlation of properties of materials to Debye and melting temperature. Phys. Scr. 1974;10:340–352. doi: 10.1088/0031-8949/10/6/011. [DOI] [Google Scholar]
- 10.Iida T., Guthrie R.I.L. The Thermophysical Properties of Metallic Liquids. University Press; Oxford, UK: 2015. pp. 497–543. [Google Scholar]
- 11.Ziman J.M. Principles of the Theory of Solids. The University Press; Cambridge, UK: 1972. pp. 66–67. [Google Scholar]
- 12.Drebushchak V.A. Thermal expansion of solids: Review on theories. J. Therm. Anal. Calorim. 2020;142:1097–1113. doi: 10.1007/s10973-020-09370-y. [DOI] [Google Scholar]
- 13.Blumm J., Henderson J.B. Measurement of the volumetric expansion and bulk density at metals in solid and molten regions. High Temp.-High Press. 2000;32:109–113. doi: 10.1068/htwu520. [DOI] [Google Scholar]
- 14.Tsagareyshvili D.S. Methods for Calculating Thermal and Elastic Properties of Crystalline Inorganic Substances. Metsniereba; Tbilisi, Georgia: 1977. pp. 22–26. [Google Scholar]
- 15.Kaptay G. A unified model for the cohesive enthalpy, critical temperature, surface tension and volume thermal expansion coefficient of liquid metals of bcc, fcc and hcp crystals. Mater. Sci. Eng. A. 2008;495:19–26. doi: 10.1016/j.msea.2007.10.112. [DOI] [Google Scholar]
- 16.Tsuru Y., Shinzato Y., Saito Y., Shimazu M., Shiono M., Mirinaga M. Estimation of linear thermal expansion coefficient from cohesive energy obtained by ab-initio calculation of metals and ceramics. J. Ceram. Soc. Jpn. 2010;118:241–245. doi: 10.2109/jcersj2.118.241. [DOI] [Google Scholar]
- 17.Gangopadhyay A.K., Bendert J.C., Mauro N.A., Kelton K.F. Inverse correlation between cohesive energy and thermal expansion coefficient in liquid transition metal alloys. J. Phys. Condens. Matter. 2012;24:375102. doi: 10.1088/0953-8984/24/37/375102. [DOI] [PubMed] [Google Scholar]
- 18.Aqra F. The cohesive energy density and the isothermal compressibility: Their relationships with the surface tension. Phys. B. 2014;446:28–31. doi: 10.1016/j.physb.2014.04.015. [DOI] [Google Scholar]
- 19.Marcus Y. The internal pressure and cohesive energy density of liquid metallic elements. J. Chem. Thermodyn. 2016;109:11–15. doi: 10.1016/j.jct.2016.07.027. [DOI] [Google Scholar]
- 20.Markus Y. Relationship between the internal pressure, the cohesive energy, and the surface tension of liquidus. Phys. Chem. Liq. 2016;55:522–531. doi: 10.1080/00319104.2016.1230739. [DOI] [Google Scholar]
- 21.Granato A.V., Joncich D.M., Khonik V.A. Melting, thermal expansion, and the Lindemann rule for elemental substances. Appl. Phys. Lett. 2010;97:171911. doi: 10.1063/1.3507897. [DOI] [Google Scholar]
- 22.Longo S.G. Principles and Applications of Dimensional Analysis and Similarity. Springer Nature Switzerland; Cham, Switzerland: 2021. 428p [Google Scholar]
- 23.Sedov L.I. Similarity and Dimensional Methods in Mechanics. CRC Press; Boca Raton, FL, USA: 1993. 479p [Google Scholar]
- 24.Starodubtsev Y.N., Tsepelev V.S. Analysis of the kinematic viscosity and self-diffusion of liquid metals at the melting temperature. High Temp. 2021;59:192–197. doi: 10.1134/S0018151X21030135. [DOI] [Google Scholar]
- 25.Starodubtsev Y.N., Tsepelev V.S. Analysis of surface tension and viscosity of liquid metals. Metall. Mater. Trans. B. 2021;52:1886–1890. doi: 10.1007/s11663-021-02157-y. [DOI] [Google Scholar]
- 26.Starodubtsev Y.N., Tsepelev V.S. Effect of atomic size on the isothermal bulk modulus and surface tension of liquid metals. Metall. Mater. Trans. B. 2022;53:2547–2552. doi: 10.1007/s11663-022-02550-1. [DOI] [Google Scholar]
- 27.Schenk T., Holland-Moritz D., Somonet V., Bellissent R., Herlach D.M. Icosahedral short-range order in deeply undercooled metallic melts. Phys. Rev. Lett. 2002;89:075507. doi: 10.1103/PhysRevLett.89.075507. [DOI] [PubMed] [Google Scholar]
- 28.Zhai Q., Luo J., Zhao P. Effect of thermal cycle on liquid structure of pure iron at just above its melting point. ISIJ Int. 2004;44:1279–1282. doi: 10.2355/isijinternational.44.1279. [DOI] [Google Scholar]
- 29.Stewart G.R. Measurement of the low-temperature specific heat. Rev. Sci. Instrum. 1983;54:1–11. doi: 10.1063/1.1137207. [DOI] [Google Scholar]
- 30.Blairs S. Review of data for velocity of sound in pure liquid metals and metalloids. Int. Mater. Rev. 2007;52:321–344. doi: 10.1179/174328007X212490. [DOI] [Google Scholar]
- 31.Sigalas M., Papaconstantopoulos D.A., Bacalis N.C. Total energy and structure of the 3d, 4d, and 5d metals. Phys. Rev. B. 1992;45:5777–5783. doi: 10.1103/PhysRevB.45.5777. [DOI] [PubMed] [Google Scholar]
- 32.Halas S., Durakiewicz T. Work functions of elements expressed in terms of the Fermi energy and the density of free electrons. J. Phys. Condens. Mater. 1998;10:10815–10826. doi: 10.1088/0953-8984/10/48/005. [DOI] [Google Scholar]
- 33.Marcus Y. On the compressibility of liquid metals. J. Chem. Thermodyn. 2016;109:11–15. doi: 10.1016/j.jct.2016.07.027. [DOI] [Google Scholar]
- 34.Wacke S., Górecki T., Górecki C., Książek K. Relations between the cohesive energy, atomic volume, bulk modulus and sound velocity in metals. J. Phys. Conf. Ser. 2011;289:012020. doi: 10.1088/1742-6596/289/1/012020. [DOI] [Google Scholar]
- 35.Delogu F. Homogeneous melting of metals with different crystalline structure. J. Phys. Condens. Matter. 2006;18:5639–5653. doi: 10.1088/0953-8984/18/24/006. [DOI] [Google Scholar]
- 36.Anderson O.L. The Grüneisen parameter for the last 30 years. Geophys. J. Int. 2000;143:279–294. doi: 10.1046/j.1365-246X.2000.01266.x. [DOI] [Google Scholar]
- 37.Boness D.F., Brown J.M., McMahan A.K. The electronic thermodynamics of iron under Earth core conditions. Phys. Earth Planet. Inter. 1986;42:227–240. doi: 10.1016/0031-9201(86)90025-7. [DOI] [Google Scholar]
- 38.Anderson O.L. Equations of State of Solids for Geophysics and Ceramic Science. Oxford University Press; New York, NY, USA: 1995. pp. 29–30. [Google Scholar]
- 39.Ashcroft N.W., Mermin N.D. Solid State Physics. Harcout College; Fort Worth, TX, USA: 1976. p. 4. [Google Scholar]
- 40.Swalin R.A. Thermodynamics of Solids. John Wiley & Sons; New York, NY, USA: 1972. pp. 63–65. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data presented in this article are available upon request from the corresponding author.