Pressure-induced superconductivity at 32 K in MoB₂

ABSTRACT

Since the discovery of superconductivity in MgB₂ (T_c ∼ 39 K), the search for superconductivity in related materials with similar structures or ingredients has never stopped. Although about 100 binary borides have been explored, only a few of them show superconductivity with relatively low T_c. In this work, we report the discovery of superconductivity up to 32 K, which is the highest T_c in transition-metal borides, in MoB₂ under pressure. The T_c of MoB₂ in the α phase can be well explained by theoretical calculations in the framework of electron-phonon coupling. Furthermore, the coupling between the d electrons of Mo and the out-of-plane Mo-phonon modes are the main driving force of the 32 K superconductivity of MoB₂. Our study sheds light on the exploration of high-T_c superconductors in transition metal borides.

Discover the superconductivity up to 32 K in MoB₂ under pressure and highlight roles of transitional metals in the high-Tc superconductors.

INTRODUCTION

Superconductors with high transition temperature (high T_c) are long-sought targets in the condensed matter physics and materials science communities. Materials with light elements [1–5] are especially favorable as they can provide high Debye frequency, which is proportional to the superconducting T_c according to Bardeen-Cooper-Schrieffer (BCS) theory [6]. In various light-element materials, metal borides have attracted much attention due to their unique crystal structure and rich physical phenomena. The discovery of superconductivity in MgB₂ at 39 K in 2001 has reinforced the scientific importance of metal diborides (MB₂) [1]. Nevertheless, after nearly two decades of exploration of superconductivity in the rich family of metal diborides, only a few MB₂ show superconducting behavior. Furthermore, the T_c of these superconducting MB₂ compounds are much lower than that of MgB₂ (Table S1 within the online supplementary material).

Molybdenum diboride (MoB₂) is unique among the MB₂ family since it is the only material that has two structural forms: the α-MoB₂ phase (AlB₂ type, space group P6/mmm) [7–9] and β-MoB₂ phase (CaSi₂ type, space group 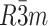) [10–12]. Although both phases of MoB₂ have similar triangular Mo layers, their B atom arrangements are quite different. The B atoms in α-MoB₂ constitute AA-staking two-dimensional (2D) graphitic boron layers. In contrast, there are two different kinds of B layers in β-MoB₂ (Fig. 1(a)): one forms a nearly planar quasi-2D honeycomb lattice similar to those in α-MoB₂ and MgB₂; the other builds a buckled honeycomb network. As a result, the Mo atoms in β-MoB₂ locate above the centers of hexatomic boron rings in the planar boron layers, but occupy the top sites right above B atoms in the buckled boron layers (Fig. 1(a)). MoB₂ may thus provide a good material platform to make a comparative study with MgB₂.

Figure 1.

Crystal structure of MoB₂ and its evolution with pressure. (a) Crystal structures of α-MoB₂ (space group P6/mmm) and β-MoB₂ (space group 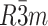). (b) XRD patterns of MoB₂ measured at room temperature with an increase of external pressure up to 90 GPa. The XRD wavelength λ is 0.6199 Å. Red and black curves are used to distinguish the structure transformation at 65.2 GPa.

Pressure, as a conventional thermodynamic parameter, is a clean and powerful tool to tune the electronic properties of materials. It is possible to trigger structural and electronic transitions, subsequently inducing novel quantum phenomena [13]. Here we report on the structure and transport properties of MoB₂ under various pressures. We find that MoB₂ exhibits superconductivity under high pressure, reaching a T_c of 32 K around 100 GPa, which is the second highest T_c among all known boride superconductors. Synchrotron X-ray diffraction (XRD) measurements indicate that β-MoB₂ transforms to α-MoB₂ around 65 GPa. Although the compressed MoB₂ has the same structure and comparable T_c with MgB₂, the superconducting mechanism of the former is completely different from that of the latter. Theoretical calculation suggests that the d electrons and phonon modes of transition metal Mo atoms play utterly different roles in the emergence of superconductivity in contrast to the dominance of p electrons and phonon modes of B atoms in the superconductivity of MgB₂.

RESULTS AND DISCUSSION

We performed in situ XRD measurements on the structural evolution of MoB₂ under various pressures. As shown in Fig. 1(b), all the diffraction peaks in the low-pressure range can be indexed well to a rhombohedral primitive cell of β-MoB₂ (space group 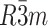), and both the a-axis and c-axis lattice constants decrease with increasing pressure (Figs. S2 and S3 and Table S2 within the online supplementary material). The structure of β-MoB₂ is robust until 65 GPa. Beyond ∼65 GPa, additional diffraction peaks emerge, indicating the occurrence of a structural phase transition. Meanwhile, we carried out a global minimization of the enthalpy of MoB₂ under high pressure by combining ab initio total energy calculations and the Calypso technique on structure predictions [14]. At 90 GPa, we theoretically predict two structural forms (space groups P6/mmm and I4₁/amd) of MoB₂ with lower enthalpies than the 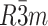structure (Fig. S4a within the online supplementary material). No imaginary frequency is found in the phonon dispersions of these two predicted structures, suggesting their dynamical stability (Fig. S4c and S4d within the online supplementary material). We find that the XRD pattern at 90 GPa can be well refined by using the hexagonal α-MoB₂ structure (space group P6/mmm; Figs S4b and S5 within the online supplementary material). These experimental and theoretical results suggest that, under high pressure, there is a structural phase transition from β-MoB₂ to α-MoB₂ with a critical pressure P_c ∼ 70 GPa. With the increasing pressure, the content of α-MoB₂ increases and almost reaches 100% at 90 GPa (Fig. S2a within the online supplementary material).

Since MoB₂ under high pressure possesses the same crystal structure as MgB₂, a question arises naturally: is it possible to achieve superconductivity in MoB₂ under high pressure? Hence, we measured the electrical resistivity ρ(T) of a β-MoB₂ single crystal at various pressures. Figure 2(a) shows the typical ρ(T) curves for pressure up to 109.7 GPa. The ρ(T) curves display a metallic-like behavior in the whole pressure range. When the pressure increases to 21.7 GPa, a small drop of ρ is observed at the lowest measuring temperature (T_min = 1.8 K), as shown in Fig. 2(b). With further increasing pressure, zero resistivity is achieved at low temperature for P > 38.5 GPa, indicating the emergence of superconductivity. The superconducting T_c increases dramatically with pressure. Beyond the critical pressure (P_c = 70 GPa), where the structural phase transition happens, the growth of T_c slows down and the maximum T_c of 32.4 K is attained at P = 109.7 GPa, which is the highest pressure we can exert on the sample. At this pressure, the superconducting transition width ΔT_c [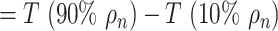] is about 4.2 K (Fig. 2(b)), which is rather sharp when compared with the large value of T_c. Figure 2(c) demonstrates that at 109.7 GPa the resistivity drop is continuously suppressed with increasing magnetic field and it shifts to about 5 K at 9 T. Such behavior further confirms that the sharp decrease of ρ(T) should originate from a superconducting transition. The derived upper critical field μ₀H_c2(T) as a function of temperature T can be fitted well using the empirical Ginzburg-Landau formula (Fig. 2(d)) μ₀H_c2(T) = μ₀H_c2(0)(1 − t²)/(1 + t²), where t = T/T_c is the reduced temperature with zero-field superconducting T_c. The fitted zero-temperature upper critical field μ₀H_c2(0) of MoB₂ from the 90% ρ_n criterion can reach 9.4(1) T with T_c = 31.7(2) K, which is consistent with the measured value of 32.4 K.

Figure 2.

Transport properties of MoB₂ as functions of pressure and magnetic fields in run IV. (a) Electrical resistivity ρ(T) of MoB₂ as a function of temperature at different pressures. (b) Enlarged ρ(T) curves in the vicinity of the superconducting transition. (c) Electrical resistivity ρ(T) under various magnetic fields at 109.7 GPa. (d) Temperature dependence of the upper critical field μ₀H_c2(T) at 109.7 GPa. Here the T_c are determined at 10%, 50% and 90% of the normal state resistivity just above the onset superconducting transition temperature. The solid lines represent the fits using the Ginzburg-Landau formula.

The measurements on different samples of MoB₂ for five independent runs provide consistent and reproducible results (Figs S6 and S7 within the online supplementary material), confirming this intrinsic superconductivity under pressure. The superconducting phase diagram of MoB₂ as a function of the pressure is summarized in Fig. 3. It can be seen that the superconducting state emerges around 20 GPa, and then the T_c increases further with applied pressure. The T_c raises dramatically at a rate of 0.7 K/GPa in the range of 40 to 70 GPa, and beyond the structure-transition pressure (P_c ∼ 70 GPa) the growth of T_c slows down (0.1 K/GPa). The T_c of MoB₂ rises to as high as ∼32 K at a pressure of 109.7 GPa and still does not exhibit the trend of saturation.

Figure 3.

Phase diagram of MoB₂. Pressure dependence of the superconducting transition temperature T_c for MoB₂ up to 109.7 GPa in different runs. The values of T_c are determined from the high-pressure resistivity (90% ρ_n criterion).

To explore the origin of the relatively high-T_c superconductivity in MoB₂ under pressure, we performed density functional theory (DFT) [15,16] and density functional perturbation theory (DFPT) [17,18] calculations on MoB₂ in the α phase at 90 GPa, for which the experimental T_c can reach ∼31.5 K at 91.4 GPa. The calculated band structure of α-MoB₂ at 90 GPa along the high-symmetry paths of the Brillouin zone is shown in Fig. 4(a). There are several bands crossing the Fermi level (E_F), indicating its metallic character. Based on the analysis of the total and partial density of states (Fig. 4(b)), Mo d orbitals (especially the d_z2 orbital) have larger contributions than B p orbitals around E_F. The phonon dispersion and the phonon density of states F(ω) for α-MoB₂ at 90 GPa are displayed in Figs. 4(c) and 4(d), respectively. Because of the large mismatch between the atomic masses of Mo and B, there is a gap between the low-frequency acoustic branch contributed by Mo atoms and the high-frequency optical branch contributed by B atoms. Obviously, the acoustic modes along the A-L path and around the L and H points make great contributions to the electron-phonon coupling (EPC, represented by the red dots in Fig. 4(c)), which is also manifested in the Eliashberg spectral function α²F(ω) (red line in Fig. 4(d)). Figure 4(e) demonstrates a representative phonon mode of α-MoB₂ at the H point at 90 GPa. For clarity, a 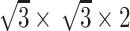supercell is employed and the arrows on the B atoms are magnified two times. It can be seen that this phonon mode consists of the relative vibrations of Mo atoms perpendicular to the B-B honeycomb plane and the related in-plane breath-like vibrations of B atoms. The calculated total EPC constant λ is 1.60. Based on the McMillan-Allen-Dynes formula [19,20], we can then calculate the superconducting T_c with an effective screened Coulomb repulsion constant μ*. By adopting several values of μ* in a commonly used empirical range of 0.08 to 0.15 [19,20], we obtained T_c between 27.2 and 33.3 K (see Fig. S8 within the online supplementary material), showing good order of magnitude with the measured one (∼32 K). These theoretical calculations confirm that the observed superconductivity in MoB₂ at high pressure should belong to the conventional BCS type.

Figure 4.

Calculated electronic structure and atomic displacements for the typical phonon modes of α-MoB₂ under 90 GPa. (a) Electronic band structure. (b) Density of states N(E). (c) Phonon dispersion. The sizes of the red dots schematically denote the electron-phonon coupling strength λ_qv. (d) Phonon density of states F(ω) (black line) and Eliashberg spectral function α²F(ω) (red line). (e) Atomic displacements of the lowest acoustic mode at the H point (Fig. 4(c)), which has a large EPC. A supercell is employed. The arrows on Mo/B atoms indicate vibrational directions and magnitudes, where the arrows on the B atoms are magnified two times for clarity. (f) The in-plane B-B stretching mode for MgB₂ at ambient pressure. The Mo, Mg and B atoms are represented by purple, red and yellow balls, respectively.

Although α-MoB₂ at high pressure shares the same crystal structure as MgB₂ and owns a comparable superconducting T_c with that of MgB₂ at ambient pressure [1], their electronic structures and superconducting ingredients are distinctly different. Firstly, for MgB₂, the p orbitals of B atoms in the B-B honeycomb lattice contribute most around the Fermi level [21,22], while for α-MoB₂ under high pressure, the states near E_F are dominated by the d electrons of Mo atoms (Fig. 4(b)) [23]. As a result, MoB₂ has very large band dispersion along the k_z direction (such as the Γ-A path; Fig. 4(a)) and its Fermi surface shows a three-dimensional characteristic, i.e. without two-dimensional Fermi surfaces as in MgB₂ [22,24] (Fig. S9 within the online supplementary material). Secondly, the main contribution to the EPC of α-MoB₂ under high pressure derives from the low-frequency phonon branch (Fig. 4(c) and 4(d)); instead, the high-frequency branch plays a major role in MgB₂ [25–28]. To be specific, for high-pressure α-MoB₂, the out-of-plane phonon mode of Mo atoms couples strongly with Mo d electrons near E_F (Fig. 4(b) and 4(e)). In comparison, it is the in-plane B-B stretching mode in MgB₂ that interacts intensively with the σ bond in the boron honeycomb lattice around E_F (Fig. 4(f)) [21]. Last but not least, previous theoretical studies suggest that the anisotropy in the EPC and the anharmonicity in the stretching phonon mode are very crucial for the high T_c of MgB₂ [27–29]. Here, for α-MoB₂ under high pressure, our calculations seem to coincide with the observed T_c without invoking the above two factors. These results reveal that the superconducting mechanism in high-pressure α-MoB₂ is distinct from that in MgB₂, suggesting the possibility of exploring new phonon-mediated high-T_c superconductors in transition metal borides.

In addition to the α phase of MoB₂, we have also calculated the superconducting T_c of β-MoB₂ using the same method. Nevertheless, the calculated T_c of β-MoB₂ is always lower than 5 K and shows a decreasing tendency with pressure (see Fig. S10 within the online supplementary material), which are inconsistent with our experimental observations (Fig. 3). The small calculated T_c of β-MoB₂ is related to its low electronic density of states N(E_F) at the Fermi level (Fig. S10), which originates from the strong bonding between the Mo atoms and the B atoms in buckled boron layers. In the real β-MoB₂ sample, the Mo atoms around the stacking fault or grain boundary can easily slide under pressure, which may drive some buckled boron layers to flat ones. As a result, the N(E_F) could increase along with more planar boron layers (Fig. S10), hence facilitating the enhanced superconductivity. On the other hand, the pressure evolution of the strength of EPC in the β-MoB₂ sample can be extracted from the fitting of the Raman spectrum by the Fano function [30–32], as shown in Fig. S11 within the online supplementary material. The Raman response to EPC manifests an asymmetric profile of the spectral line shape of Raman-active phonons. Explicitly, the inverse of the Fano asymmetric parameter |1/q| is proportional to the joint density of states, hence counting the strength of EPC. The representative fitting at 13.0 GPa is plotted in the inset of Fig. S11d. Combined with our first-principles calculations, we find that there are two Raman-active phonon modes that can provide strong EPC: one is the double-degenerated E_g mode around 200 cm⁻¹ and the other is a A_g mode around 300 cm⁻¹. Similar to the case in α-MoB₂, both these two strong EPC modes come from the relative vibrations of Mo atoms, as shown in Fig. S11c. From the pressure dependent |1/q|, we note that the one from the E_g mode is nearly independent of pressure. However, the other one extracted from the A_g mode increases dramatically with increasing pressure, which presents compelling evidence of the enhanced EPC in MoB₂ induced by increasing pressure. In addition, the A_g mode involves the vertical vibrations of Mo atoms relative to the B-B plane, which is similar to the corresponding phonon mode in α-MoB₂ at high pressure (Fig. 4(e)), suggesting that more Mo atoms get rid of bonding with the B atoms in buckled layers with increasing pressure. The increased frequency and the enhanced EPC of this A_g mode as well as the boosted N(E_F) mentioned above probably have a close connection with the increase of T_c in β-MoB₂ in the phonon-mediated superconductivity regime.

CONCLUSION

In summary, we found superconductivity up to 32 K in MoB₂ under pressure. Although compressed α-MoB₂ and MgB₂ both possess the AlB₂-type structures and comparable T_c, the features of their electron-phonon couplings that mediate the superconductivity are quite different. In both MgB₂ and α-MoB₂, the active phonon modes directly modulate the active electronic bands, causing the strong electron-phonon coupling [33]. However, it is the out-of-plane Mo phonon that directly modulates the d electrons of Mo in α-MoB₂, in comparison with the stretching B-phonon mode modulating the p orbitals of B in MgB₂. Thus, not only do the electrons in light-element atom networks need to be considered, but the relatively localized electrons of metal atoms may also be worthy of attention in the search for high-T_c superconductors.

MATERIALS AND METHODS

High-quality single crystals of MoB₂ were grown by Al flux (see the online supplementary material). In situ high-pressure XRD and resistivity measurements were performed in a diamond anvil cell. We employed the swarm-intelligence-based CALYPSO structure prediction method [14] to find the energetically stable structures of MoB₂ under high pressure. The electronic structure, phonon spectrum and EPC of AlB₂-type α-MoB₂ at 90 GPa were studied based on DFT [15,16] and DFPT [17,18] calculations. The details of the experiment are given in the online supplementary material.

Note added

After we submitted this paper, we learned that pressure-induced superconductivity was observed in WB₂ by another group [34]. Most of the data in that paper are consistent with our results [35]. We also observed superconductivity in itinerant antiferromagnet CrB₂ via the application of external pressure [36].

ACKNOWLEDGEMENTS

Computational resources were provided by the Physical Laboratory of High Performance Computing at Renmin University of China. The authors acknowledge support from the Analytical Instrumentation Center (♯ SPST-AIC10112914), SPST, ShanghaiTech University. The authors thank BL15U1 staff at Shanghai Synchrotron Radiation Facility for assistance during the data collection.

FUNDING

This work was supported by the National Key R&D Program of China (2018YFA0704300, 2018YFE0202600 and 2017YFA0302903), the National Natural Science Foundation of China (52272265, U1932217, 11774424, 11974246, 12004252, 12174443, 12274459 and 11804011), the Beijing Natural Science Foundation (Z200005), the CAS Interdisciplinary Innovation Team, the Fundamental Research Funds for the Central Universities, and the Research Funds of Renmin University of China (18XNLG14, 19XNLG13 and 19XNLG17).

AUTHOR CONTRIBUTIONS

Y.-P.Q., H.-C.L. and K.L. proposed and supervised the project. Q.W., C.-S.G., S.-J.T., R.-T.L. and H.-C.L. carried out the synthesis. C.-Y.P., Y.Z., L.-L.G., M.-T.L., W.-G.Y. and Y.-P.Q. performed the high-pressure experiments. J.-F.Z., Z.-Y.L. and K.L. carried out calculations. All authors discussed the results and participated in analyzing the experimental results.

Conflict of interest statement. None declared.