Assessing Enhanced Acoustic Absorption From Sonosensitive Perfluorocarbon Emulsion With Magnetic Resonance–Guided High-Intensity Focused Ultrasound and a Percolated Tissue-Mimicking Flow Phantom

Abstract

Objective

Sonosensitive high-boiling point perfluorocarbon F₈TAC₁₈-PFOB emulsions previously exhibited thermal enhancement during focused ultrasound heating in ex vivo pig livers, kidneys and a laminar flow phantom. The main objectives of this study were to evaluate heating under turbulent conditions, observe perfusion effects, quantify heating in terms of acoustic absorption and model the experimental data.

Methods

In this study, similar perfluorocarbon emulsions were circulated at incremental concentrations of 0.07, 0.13, 0.19 and 0.25% v:v through a percolated turbulent flow phantom, more representative of the biological tissue than a laminar flow phantom. The concentrations represent the droplet content in only the perfused fluid, rather than the droplet concentration throughout the entire cross-section. The temperature was measured with magnetic resonance thermometry, during focused ultrasound sonications of 67 W, 95% duty cycle and 33 s duration. These were used in Bioheat equation simulations to investigate in silico the thermal phenomena. The temperature change was compared with the control condition by circulating de-gassed and de-ionized water through the flow phantom without droplets.

Results

With these 1.24 µm diameter droplets at 0.25% v:v, the acoustic absorption coefficient increased from 0.93 ± 0.05 at 0.0% v:v to 1.82 ± 0.22 m^–1 at 0.25% v:v using a 0.1 mL s^–1 flow rate. Without perfusion at 0.25% v:v, an increase was observed from 1.23 ± 0.07 m^–1 at 0.0% v:v to 1.65 ± 0.17 m^–1.

Conclusion

The results further support previously reported thermal enhancement with F₈TAC₁₈-PFOB emulsion, quantified the increased absorption at small concentration intervals, illustrated that the effects can be observed in a variety of visceral tissue models and provided a method to simulate untested scenarios.

Introduction

Magnetic resonance-guided high-intensity focused ultrasound (MRgHIFU) is an extracorporeal and non-ionizing modality that can potentially provide improved ablative treatment for tumor sites in visceral intra-abdominal organs [1]. Colorectal liver metastases are stage 4 cancers with grim 5 y survival rates, low eligibility for curative surgery, unfavorable chemotherapy response, unfavorable improvement after transplantation and limitations for radiotherapy because of radiation-induced liver disease [2]. Radiofrequency ablation, microwave ablation and ultrasound-guided focused ultrasound (USgFUS) offer clinical benefits, particularly for hepatocellular carcinoma and oligometastatic colorectal liver metastases [2], [3], [4], [5]. However, ultrasound-guided procedures are not capable of temperature mapping, magnetic resonance imaging MRI offers superior tissue contrast to identify tumor margins, MRI is less prone to interference artifacts and MRI allows post-treatment assessment [6,7]. MRgHIFU liver tumor pilot studies proved possible but were limited to sites below the rib line [8], [9], [10], [11].

Limitations of focused ultrasound ablation include the potential need for anesthesia, the potential for rib resection, higher power requirements, pre-focal interactions, bone and skin burning, beam reflection at tissue–air interfaces, respiratory motion inaccuracies and reduced heating caused by fluid perfusion effects from large vessels [9,[12], [13], [14], [15], [16], [17], [18], [19], [20]]. Administration of microbubbles as sonosensitive thermal enhancers can improve USgFUS tumor ablation by reducing power requirements and treatment times [21], [22], [23], [24], [25], [26]. Droplet-enhanced heating might provide the capability to improve this technique. Rather than using sonosensitizers for therapeutic drug activation during sonodynamic therapy, these sonosensitizers were designed to increase local acoustic absorption and temperatures during HIFU ablation. The droplets have been reported in previous pre-clinical studies to exhibit favorable thermal enhancement, the capability to incorporate chemotherapeutics, long circulation times and robustness to repeated sonications, at concentrations below the expected toxicity limits determined from blood substitute studies [13,[27], [28], [29], [30]].

This formula was designed to remain in continuous systemic endovascular circulation and target the tumor microvasculature. The technology also allows potential adjustment of the emulsion to a smaller size by altering the surfactant, to improve the in vivo size-dependent pharmacokinetics [13]. The current size has anticipated benefits of transpulmonary circulation without pulmonary embolization while large enough to prevent liver filtration [27,28,[31], [32], [33]]. This allows the droplets to remain in the blood circulation for a prolonged duration, being readily available for repeated sonications and reducing the necessary administered dose. These features might benefit current microbubble-enhanced heating that can be limited by clearance rate and pre-focal microbubble interactions.

The tissue models offer a cost-effective testing platform for assessing the thermal characteristics of the emulsion formulas, previously exhibiting similar results when administered in ex vivo pig organs [27]. Unlike a previously reported perfused model, consisting of parallel strands with laminar perfusate flow [27,28], in this study a random 3D lattice mimicked biological tissue perfusion. In particular, to emulate the perfusion volume and rate reported from human liver studies. The model allowed extraction of sonosensitizer and other system properties to perform Bioheat simulations that matched the experimental data. The Pennes Bioheat equation is a continuum energy balance differential equation that can relate the HIFU applied energy to the temperature increase in the tissue [34], [35], [36]. This model was based on simplified assumptions of a homogeneous tissue medium, using an averaged thermal diffusivity and perfusion rate through a tissue volume. These assumptions applied to MR thermometry measurements as the voxel size limited spatial temperature resolution.

The objectives of this study were to observe the change in HIFU heating with incremental droplet concentrations, to match the heating to a biophysical model, to quantify the acoustic absorption with MRgHIFU and to determine critical concentration dependency on perfusion effects.

Methods

Percolated phantom model

Figure 1 is an overview of the flow phantom, with the tissue-mimicking material (TMM) pieces resembling small rice grains. The emulsion was pumped through the interstitial space while heated with focused ultrasound. The tissue-mimicking gel composition was similar to the approach previously reported [28]. The matrix gel was composed of 1.5% w:w agar (Alfa Aesar, ThermoFisher Gmbh, Kandel, Rhineland-Palatinate, Germany) in de-gassed and de-ionized water. The solution was boiled momentarily to mix homogeneously, cooled at room temperature to 50ºC, poured into a 3D-printed holder and then placed in an ice bath. The phantom was designed to encompass a 20 mL syringe that was removed after the gel solidified to leave a cylindrical void in the middle of the matrix gel. In this void, percolated gel pieces were placed to create the visceral tissue-mimicking region that was heated and perfused. The percolated bits used a slightly different formula from the bulk matrix, incorporating milk proteins to enhance acoustic absorption and increase the temperature elevation, and therefore the contrast to noise ratio for the control case. The solution was 400 mL and composed of 3% w:w agar powder, 11% w:w glycerol (87%, PanReac, AppliChem, ITW Reagents, Darmstadt, Hesse, Germany) and 30% w:w powdered milk (18% proteins, 1% fats). The solution was brought to a boil and mixed homogeneously, then drawn into a syringe and continuously dispensed through a 1 mm biopsy sheath into ice water. The gel solidified instantaneously, creating long strands that resembled food noodles. The pieces were collected and cut finely before being inserted into the phantom void. A 50 mL syringe dispensed the solution while submerged in de-gassed and de-ionized water. The pieces were inserted gently because applying force previously caused blockage and resulted in gel matrix fracture. Syringe tips with small foam filters were placed on each end of the gel holder to allow Luer connections to the pumping system and to prevent contaminants from entering the de-gassing system. The phantom was submerged in de-gassed and de-ionized water for 2 d before the experiment. The de-gassed water helped to remove small air bubbles and reduce the complications associated with de-gassing the fluid before thermometry measurements.

Figure 1.

(A) Magnetic resonance image of the phantom and perfusion system. (B) Coronal view of the percolated rice-like tissue-mimicking substance within the agarose matrix. (C) Actual sagittal view of the percolated gel pieces. (D) Transverse view of the tissue-mimicking phantom system. (E) Sagittal view of the perfused phantom system. (F) Actual transverse view of the percolated gel pieces.

The phantom was placed inside a perfusion chamber and connected to a perfusion pumping system to circulate fluid and emulate visceral tissue. Before performing focused ultrasound sonications, a continuous de-gassing system removed air bubbles in the flow phantom to prevent beam scattering and MRI artifacts. The flow rate was measured manually at 0.1 mL s⁻¹ by recording the time to fill a 1.0 mL volume.

MR-guided HIFU sonications

Magnetic resonance imaging (3 T, Prisma Fit, Siemens, Erlangen, Bavaria, Germany) scans used an 11 cm loop coil for the receiver. The MRI sequence parameters are listed in Table 1. The phantom structure and presence of air in the system were assessed with a T₁-VIBE sequence. The system was de-gassed for air removal to prevent MRI artifacts and HIFU beam scattering. Real-time control was monitored with a separate PC operating Thermoguide software (Image Guided Therapy, Pessac, Nouvelle-Aquitaine, France). The HIFU unit was a phased-array transducer (131 mm focal length, 140 mm aperture, Imasonic, Besançon, Bourgogne-Franche-Comté, France) connected to an impedance matching unit and beamformer (Image Guided Therapy, Pessac, Nouvelle-Aquitaine, France). The sonication conditions were 67 acoustic W power, 95% duty cycle, 1031 kHz frequency, 33 s duration and an emitted energy of 2.1 kJ. At the end of each sonication, a delay occurred to allow the specimen to cool. The post-sonication delay was 112 s (50 dynamics) for the perfused case and 157 s (70 dynamics) for the non-perfused case. Repeated sonications (n = 5.60 ± 0.55) were performed at each concentration increment.

Table 1.

Sequence parameters for the magnetic resonance imaging scans used in this experiment

Sequence	TE	TR	TA	FA	BW	EPI	PF	SL	NA	FOV	AM
T1-VIBE	1.81	05.44	4:09	10	390	1	1	1	1	256 × 256	320 × 320
A_EP_SEG_THERM	10.00	41.47	2.12	15	815	1	1	5	1	128 × 128	128 × 128
CSF_FLOW_FL2D	12.79	34.02	1:51	10	200	1	1	4	10	160 × 160	256 × 256

AM, acquisition matrix; BW, bandwidth (Hz); EPI, echo planar imaging factor; FOV, field of view (mm × mm); NA, number of acquisitions; PF, partial Fourier factor; SL, slice thickness (mm); TA, acquisition time (min:s); TE, echo time (ms); TR, repetition time (ms).

Perfluorocarbon emulsions

The sonosensitizer (MR053, concentrated 2.3% v:v F₈TAC₁₈–PFOB, 1.24 µm diameter, University of Avignon, Avignon, Provence-Alpes-Côte d'Azur, France) synthesis was detailed previously [13,27,28,37,38]. The PFOB was emulsified with amphiphilic F₈TAC₁₈ fluorinated surfactant in amounts above the critical micelle concentration. Original surfactant applications included improving membrane protein solubility and developing emulsions for oxygen and drug delivery [38], [39], [40], [41], [42]. As PFOB has a boiling point of 143ºC, the emulsions offer stability and the benefit of undergoing sterilization by autoclave. For instance, a duration of 20 min at 100 kPa and 120ºC might be sufficient for in vivo administration [43,44].

Temperature metrics

The spatial integral temperature increase in the focal region, also referred to as integral temperature, was assessed from the beginning to the end of sonication. The measurements were compared while circulating varying amounts of perfluorocarbon emulsions, with and without fluid flow. The temperature metrics were evaluated with a custom MATLAB (The MathWorks, Inc., Natick, MA, USA) script to perform baseline subtraction and generate thermal metrics.

The primary metrics assessed were maximum temperature increase at the focal point, integral temperature increase and acoustic absorption coefficient. The perfusion rate, the thermal diffusivity, the incident intensity field and the incident pressure field were also extracted from the MR thermometry temperature recordings. The values were input into an algorithm using the k-Wave toolbox to simulate the heating and compared with the experimental temperature measurements [45].

The baseline temperature measurements were performed with and without perfusion, with no emulsion in the perfusate and 200 mL of de-gassed and de-ionized water in the circulation system. The emulsion was added at 6 mL aliquot intervals to compare the effects of varying concentrations. The concentrations tested were 0.07% v:v, 0.13% v:v, 0.19% v:v and 0.25% v:v. These concentrations were tested without perfusion and with perfusion at the rate of 0.1 mL s^–1. Each aliquot was added with a sterile syringe to prevent cross-contamination. The aliquot was mixed with the dispensing syringe and then with the perfusion pump for 10 min at a flow rate of 2.0 mL s^–1. The region of interest (ROI) encompassing the heated area was meticulously chosen to account for the flow-dependent drift of the thermal buildup. The integral temperature values were determined with the equation

$$T_{\text{int}}=\sum _1^N{T}_{\mathrm{i}},T_{\mathrm{i}}>0.5^{\circ }\mathrm{C}$$ (1)

Here, T_int is the spatial integral temperature (ºC mm^–2), T_i is the temperature change in a single voxel (ºC) using a threshold of 0.5ºC and N is the number of voxels in the MRI ROI.

Comparison of the acoustic absorption coefficients allows better comparison than absolute temperature fields, for alternative sonication conditions. The acoustic absorption coefficient values were determined with the equation

$$\alpha =\frac{T_{\text{int}}}{E\Delta Z}{c}_{\mathrm{m}}\rho V_{\mathrm{p}}$$ (2)

α is the acoustic absorption coefficient (m^–1), ΔZ is the voxel and slice thickness (µm), E is the FUS transducer energy emitted during sonication (J), c_m is the specific heat capacity (J kg^–1 K^–1), ρ is the average voxel density of tissue or phantom (kg m^–3) and V_p is the pixel volume (m³).

The integral temperature and acoustic absorption coefficient were fit to a decreasing mono-exponential function in the equations

$$T_{\text{int}}=T_{\text{int},0}+\Delta T_{\text{int}}\left(1-e^{-\frac{\left[C\right]}{C_0}}\right)$$ (3)

$$\alpha ={\alpha }_0+\Delta \alpha \left(1-e^{-\frac{\left[C\right]}{C_0}}\right)$$ (4)

using a trust-region algorithm and a lower limit on the fit constants of zero. Then, the fit lines were overlaid on the data. Here T_int is the integral temperature (ºC mm^–2), T_int,0 is the fit constant for the initial integral temperature (ºC mm^–2), ΔT_int is the fit constant for the overall change in integral temperature (ºC mm^–2), α is the acoustic absorption coefficient (m^–1), α₀ is the fit constant for the initial acoustic absorption coefficient (m^–1), Δα is the fit constant for the overall change in acoustic absorption coefficient (m^–1), [C] is the concentration (v:v), and C₀ is the fit constant for the critical concentration (v:v). The critical concentration represents the dose required to reach 63% of the maximum response.

The fit lines estimated the critical concentration and maximum effective value. The interaction radius was evaluated in this percolated phantom model and compared with that of a phantom composed of perfused parallel gel fiber strands. The interaction radius was equated for the current sonosensitizers, based on the results of a previous study, using the equation [28]

$$\frac{R_{\text{int}}}{R_0}\sqrt[3]{C_0}=\frac{R_{int}^{\prime }}{R_0^{\prime }}\sqrt[3]{C_0^{\prime }}$$ (5)

R_int is the interaction radius (µm), R₀ is the physical droplet radius (µm) and C₀ is the critical concentration (v:v). The prime value distinguishes measurements between different experiments, with R'_int at 12.5 µm, R'₀ at 1.15 µm and C'₀ at 0.18% (v:v) obtained in previous studies [28].

Then, the increase in acoustic absorption was compared with the thermoviscous attenuation to estimate the thermoviscous contribution to thermal enhancement. The attenuation caused by thermoviscous attenuation is described by ECAH (Epstein–Carhart–Allegra–Hawley) theory [46,47] and given in the equation [48,49]

$$\frac{{\alpha }_{\text{tv}}}{\left[C\right]}=\frac{\frac{18\omega }{v_{\text{m}}}{\left(1-\frac{{\rho }_{\text{m}}}{{\rho }_e}\right)}^2\left(Y+1\right)Y^2}{4Y^4{\left(\frac{{\rho }_{\text{m}}}{{\rho }_e}+2\right)}^2+36Y^3{\left(\frac{{\rho }_{\text{m}}}{{\rho }_e}+2\right)}^{}+162Y\left(Y+1\right){\left(\frac{{\rho }_{\text{m}}}{{\rho }_e}\right)}^2+81{\left(\frac{{\rho }_{\text{m}}}{{\rho }_{\text{e}}}\right)}^2}$$ (6)

where α_tv is the thermoviscous attenuation (m^–1), R is the droplet radius (µm), v_m is the kinematic viscosity of the medium (1.0035E–6 m² s^–1 for water), [C] is droplet concentration (v:v), ω is the angular frequency (2πf, rad s^–1), f is the HIFU frequency (Hz), ρ_m is the medium density (kg m^–3) and ρ_e is the emulsion density (kg m^–3). The value for Y is related to the particle radius and skin depth of the shear wave, given as $R\sqrt{\omega /2v_{\mathrm{m}}}$.

Phase contrast velocity mapping

Phase-contrast imaging allows flow angiography images of the vasculature and quantitative velocimetry measurements [50,51]. For phase contrast velocity mapping, the pixel intensity is proportional to the velocity [52,53], and was performed on the phantom to visualize the flow field. The average flow rate was timed at 0.1 mL s^–1 before the experiment. After imaging, an ROI was chosen within the perfused region, and pixels were rescaled to the mean flow rate, giving pixelwise velocity measurements. Table 1 outlines the sequence parameters.

Extracting properties for thermal simulation

Numerous techniques for performing numerical simulations of focused ultrasound, based on the Bioheat equation, have been described [48,54,55]. MRgHIFU can estimate sample physical properties non-invasively [56], [57], [58], [59], [60]. Here, we extracted the medium properties during acoustic absorption measurements. The technique allowed non-invasive estimation of additional system properties, including perfusion rate, thermal diffusivity, incident pressure field and incident intensity field.

The following Bioheat equation provides an energy balance that relates the temperature change to the conductive heat dissipation, convective heat dissipation and heat generated from focused ultrasound:

$$\frac{\partial T\left(x,y,t\right)}{\partial t}=X{\nabla }^{2}T\left(x,y,t\right)-w_{\text{b}}\left[T\left(x,y,t\right)-T_{\text{o}}\right]+\frac{2\alpha I\left(x,y,t\right)}{c_{\text{b}}\rho }.$$ (7)

Here, I is the intensity (W m^–2), w_b is the perfusion rate (s^–1), α is the acoustic absorption coefficient (m^–1), c_b is the specific heat of fluid (J kg^–1 K^–1), T₀ is the ambient temperature (ºC), X is the thermal diffusivity (m² s^–1), ρ is the average voxel density of tissue or phantom (kg m^–3) and t is time (s).

The perfusion rate was determined from the integral temperature curve during the cooling period after HIFU heating, as [59]

$$T_{\text{int}}=T_{\text{int}}^{\mathrm{h}}{e}^{-w_{\text{b}}\left(t-t_{\mathrm{c}}\right)}$$ (8)

where T_int is the spatial integral temperature (ºC mm^–2), $T_{\text{int}}^{\mathrm{h}}$ is the spatial integral temperature at the end of heating (ºC mm^–2), t is time (s) and t_c is the time at the end of cooling (s).

During cooling without perfusion, the thermal diffusivity calculation was ascertained from the following equation and averaged over a set of temperature maps [60]:

$$X=\frac{\frac{\partial T\left(x,y,t\right)}{\partial t}}{{\nabla }^{2}T\left(x,y,t\right)}$$ (9)

During cooling with perfusion, the thermal diffusivity was determined using the equation

$$X=\frac{\frac{\partial T\left(x,y,t\right)}{\partial t}+w_{\mathrm{b}}\left[T\left(x,y,t\right)-T_{\mathrm{o}}\right]}{{\nabla }^{2}T\left(x,y,t\right)}$$ (10)

After these parameters were extracted, the pressure and intensity fields were estimated from the temperature maps. A 5 × 5 median filter was applied to smooth the temperature maps before processing. Then, the intensity and pressure fields were evaluated for each temperature map using eqns (11) and (12) [61]. Because the temperature profiles were observed as Gaussian and radially symmetric, a simulated Gaussian intensity and pressure field were also used. The maximum values of these intensity and pressure profiles were extracted in each frame using the equations

$$I\left(x,y,z\right)=\frac{1}{2\alpha }\left[c_b\rho \frac{\partial T\left(x,y,t\right)}{\partial t}-X{\nabla }^{2}T\left(x,y,t\right)+w_{\mathrm{b}}\left[T\left(x,y,t\right)-T_{\mathrm{o}}\right]\right]$$ (11)

$$I\left(x,y,t\right)=\frac{{\left|p\left(x,y,t\right)\right|}^2}{2\rho c_{\mathrm{o}}}$$ (12)

where p is the pressure (Pa), and c_o is the speed of sound in the fluid (m s^–1).

A custom MATLAB program allowed the simulation of a single-element focused ultrasound transducer with a 130 mm radius and 1 MHz frequency. The acoustic field was normalized and then scaled to the calculated intensity maximums. The intensity field was input as the heat source with the k-Wave BioheatExact function to solve for the simulated temperature fields [36,45].

Results

Magnetic resonance thermometry temperature mapping

The magnetic resonance thermometry measurements exhibited a characteristic mono-exponential increase as a function of droplet concentration. Fit constants are given in Table 2. Fit constants determined the critical concentration and maximum expected effect at high concentrations. The means and standard deviations are illustrated in Figure 2.

Table 2.

Fit constants, interaction radius and thermoviscous attenuation

V̇	Tint,0	ΔTint	α0	Δα	C0	Rint	αtv	Δα(C0)
0.0	648.9 (584.1, 713.6)a	303.6 (–306, 913.2)	1.32 (1.19, 1.45)	0.62 (–0.61, 1.85)	0.25 (–0.57, 1.08)	6.00	0.42	0.39
0.1	454.6 (390.8, 518.5)	543.7 (374.5, 712.9)	0.93 (0.80, 1.06)	1.11 (0.76, 1.45)	0.12 (0.03, 0.21)	7.64	0.20	0.70

V̇, volumetric flow rate (mL s^–1); C₀, critical concentration (% v:v); R_int, interaction radius (µm); α_tv, thermoviscous attenuation (m^–1); Δα(C₀), change in acoustic absorption coefficient at the critical concentration (m^–1); T_int, integral temperature (°C mm^–2); α, acoustic absorption coefficient (m^–1); T_int,0, initial integral temperature (C mm^–2); ΔT_int, overall change in integral temperature (C mm^–2); α₀, initial acoustic absorption coefficient (m^–1); Δα, overall change in acoustic absorption coefficient (m^–1).

^a95% confidence interval in parentheses.

Figure 2.

Magnetic resonance thermometry data for temperature measurements with varying concentrations of emulsions circulated through the percolated perfused phantom model. Data were obtained in a non-perfused case in which the circulating pump was depowered before sonications. Data were also obtained in the perfused case in which the fluid was circulated at 0.1 mL s^–1. Temperature maps were generated from thermometry measurements performed in the coronal plane. (A) Integral temperature measured with magnetic resonance thermometry. (B) Calculated acoustic absorption coefficient. (C) Extracted perfusion rate. (D) Calculated thermal diffusivity. Error bars represent standard deviations of the mean.

Phase contrast velocity mapping

The velocity mapping, illustrated in Figure 3, indicated similar overall behavior of the flow distribution throughout the perfused phantom, with some randomly distributed interstices with higher flow. No residual gas bubbles were identified in the percolated phantom, while some air bubbles were visible in the coupling layer of ultrasonic gel, provided the phase contrast sequence is also sensitive to susceptibility artifacts.

Figure 3.

Phase contrast velocimetry mapping of the percolated tissue-mimicking phantom. Cross section of the phantom apparatus. Susceptibility artifacts appear from the air bubbles in the ultrasound gel, used for coupling the phantom to the high-intensity focused ultrasound transducer.

Quantitative MRI for thermophysical properties and simulations

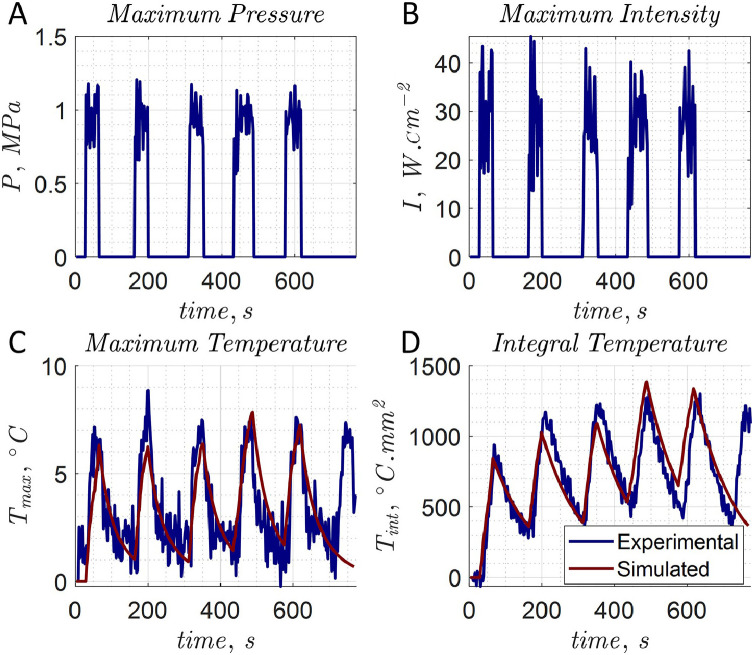
An example of the extracted pressure and intensity fields is provided in Figure 4. This spatial peak temporal average intensity (I_spta) was 28.1 ± 8.3 W cm^–2. Example simulations overlaid on experimental data for the focal temperature and integral temperature are illustrated in Figure 4. The flow rate was 0.1 mL s^–1, and the droplet concentration was 0.25% v:v. The last sonication was not simulated. An example temperature map simulation using the data from Figure 4 is given in Figure 5.

Figure 4.

Experimental data were compared with a simulated scan. (A) The calculated maximum pressure. (B) The calculated maximum intensity values. (C) Simulation of maximum focal spot temperature. (D) Spatial integral temperature with 0.1 mL s^–1 flow rate and 0.25% v:v.

Figure 5.

Simulations using extracted intensity field and thermophysical properties. The data are from the fifth shot in Figure 4. The temperature simulations exhibited good agreement with magnetic resonance thermometry experimental data. (A) Simulated intensity field. (B) Simulated pressure field. (C) Actual temperature map. (D) Simulated temperature map.

The extracted perfusion rate and thermal diffusivity are illustrated in Figure 2. The average flow rate was measured before the experiment to be 0.1 mL s^–1, with the extracted perfusion rate being 0.012 ± 0.011 s^–1. Without pumping, acoustic streaming resulted in a measurable perfusion rate of 0.0017 ± 0.0012 s^–1. Thermal diffusivity values were determined to be 0.25 ± 0.21 mm² s^–1. A value of 0.115 mm² s^–1 minimized the error on the experimental temperature and was used in simulations. The value was similar to that of human tissues measured at 0.11–0.16 mm² s^–1 [62].

Then, to simulate the effects on the maximum focal point temperature and the integral temperature, the values of the acoustic absorption coefficient, the perfusion rate and the thermal diffusivity were varied. The means and standard deviations of these simulations are given in Figure 6. The simulated temperature curves are provided in the Supplementary Figure S1 (online only). Increased perfusion rate and acoustic absorption coefficient affected both focal and integral temperature. Adjusting the thermal diffusivity affected the maximum temperature considerably but had a negligible impact on the integral temperature.

Figure 6.

(A) Using a constant acoustic absorption coefficient of 1.91 m^–1 and constant thermal diffusivity of 0.115 mm² s^–1, the simulations were performed by varying the perfusion rate with values of 0.005, 0.01, 0.02 and 0.04 s^–1. (B) At a constant perfusion rate of 0.0086 s^–1 and acoustic absorption coefficient of 1.91 m^–1, the thermal diffusivity was varied with values of 0.1, 0.4, 0.7, and 1.0 mm² s^–1. (C) At a constant perfusion rate of 0.0086 s^–1 and thermal diffusivity of 0.115 mm² s^–1, the acoustic absorption coefficient was varied between 1.0, 1.5, 2.0 and 2.5 m^–1. T_fp is the focal temperature. T_int is the spatial integral temperature. w_b is the perfusion rate. X is the thermal diffusivity. α is the acoustic absorption coefficient.

Discussion

The application of sonosensitive ablation effectors has been reported in a small number of pilot studies and randomized control trials. Studies included the treatment of uterine fibroids [22], [23], [24], [25], [26] adenomyosis [63,64] and hepatocellular carcinoma [21].

Comparing droplet heating with microbubble studies is not straightforward. Microbubbles are usually studied with USgFUS systems. These studies generally have not implemented temperature mapping. The procedures are clinically assessed by changes in gray scale and non-perfused volume. Microbubble-enhanced heating results from cavitational bubble clouds, increasing attenuation and heat generation. Diagnostic microbubbles undergo cavitation and disintegrate at pressures lower than those used in our measurements. The stable cavitation threshold of Sonovue microbubbles (Bracco Imaging S.p.A., Milan, Lombardy, Italy) has been measured at 0.25 MPa peak refractive pressure at 1 MHz and greater than 20 s pulse duration. The inertial cavitation threshold was measured at 0.4 MPa peak refractive pressure under the same conditions [65]. Microbubble acoustic absorption is usually provided as attenuation rather than a temperature-based acoustic absorption coefficient.

Nevertheless, some advantages of our micron-size droplets can be identified versus the gas-filled microbubbles. First, the circulatory half-life of microbubbles is short. Microbubbles are almost entirely cleared from circulation within 2 min, and the maximum dose limits the treatment [66]. Microbubbles are more prone to near-field interactions with the incident HIFU beam. These effects have been found to cause unwanted near-field heating, pre-focal burning and beam scattering that reduces focal temperatures. Our droplets are stable after repeated HIFU sonications and did not demonstrate near-field heating, nor did they yield the distortion of the apparent heating pattern [13]. In ex vivo studies, they exhibited a very long lifetime as circulating emulsion, at least several hours [27].

Table 3 compares the acoustic absorption for this non-evaporable emulsion formula between a series of studies. This droplet formula is thought to enhance heating through thermoviscous heating and stable cavitation [28,29]. A unique cavitation mechanism at the atomically smooth interface hydrophobic/hydrophilic has been observed and possibly influenced heat generation [67]. Previous studies illustrated the capability of repeated sonications from these emulsions and sixfold more effective enhancement of acoustic absorption in perfused fluid compared with semirigid gel samples [13,[27], [28], [29]]. In this study, the perfused measurements exhibited a factor of 2 increase in integral temperature and a 7ºC increase in focal temperature at 0.25% v:v, compared with baseline. Note that an increase of only a few degrees can significantly affect treatment times as the rate of cell death increases exponentially with temperature [68,69]. Equivalence between repeated measurements suggested sonications did not destroy the droplets.

Table 3.

Increase in acoustic absorption coefficient relative to the control condition

Study	Δα ± σ (m–1)
Lorton et al. 2020 [27]
Ex vivo pig liver
0.10% v:v	0.20 ± 0.17
0.19% v:v	0.79 ± 0.21
Ex vivo pig kidney
0.13% v:v	0.70 ± 0.20
0.24% v:v	1.20 ± 0.76
Laminar flow phantom
0.10% v:v, 0.1 mL s–1	0.56 ± 0.08
0.10% v:v, 0.15 mL s–1	0.73 ± 0.16
0.20% v:v, 0.15 mL s–1	1.05 ± 0.17
Ex vivo pig hepatic vein
0.19% v:v	0.37 ± 0.27
This study
Percolated phantom without fluid flow
0.10% v:v, 0.0 mL s–1	0.20 ± 0.35
0.20% v:v, 0.0 mL s–1	0.34 ± 0.51
0.30% v:v, 0.0 mL s–1	0.43 ± 0.57
Percolated phantom with turbulent flow
0.10% v:v, 0.1 mL s–1	0.63 ± 0.19
0.20% v:v, 0.1 mL s–1	0.90 ± 0.20
0.30% v:v, 0.1 mL s–1	1.02 ± 0.18

Δα, change in acoustic absorption coefficient relative to the control condition (m^–1); σ, standard deviation (m^–1).

Table 2 provides insight into the absorption mechanism. For the non-perfused case, ECAH theory [46,47] predicted that thermoviscous attenuation was the dominating mechanism for acoustic absorption. For the perfused case, an estimated 29% of the absorption was owing to thermoviscous attenuation and therefore suggested that stable cavitation became the dominant effect. A shortcoming was that ECAH thermoviscous attenuation is proportional to droplet concentration. However, the saturation of the acoustic absorption by the emulsion was observed at higher concentrations. The approximation was expected to hold in the linear regime at concentrations less than the critical concentration. The interaction radius was observed to be a factor of 12 higher than the physical droplet radius, giving an interaction volume three orders of magnitude larger than the physical droplet volume.

Random percolated effects in the flow phantom were similar to those of a porous liver tissue model described in many previous studies [70], [71], [72]. The model appeared to adequately represent the perfusion effects for the venous system of a capillary bed. The turbulent flow model benefited from simpler construction means and allowed grain size alterations to adjust perfusion volume as compared with a previously developed laminar flow phantom of parallel oriented gel fibers [27,28]. This percolated flow phantom featured a more turbulent flow model, thought to offer more similarity to the hemodynamics of diseased liver tissue [73]. The perfusion rate of 0.012 ± 0.011 s^–1 and the thermal diffusivity of 0.25 ± 0.21 mm² s^–1 were similar to those of in vivo human liver, at 0.019–0.021 s^–1 [74] and 0.11–0.16 mm² s^–1 [62], respectively. The acoustic absorption coefficient of the agar–milk phantom had a baseline near 1.23 ± 0.07 m^–1 . Measurements of acoustic attenuation at this frequency for pig and calf liver have been reported at 3–4 m^–1 [75,76]. Studies have reported that the human liver is composed of 25%–30% blood [77]. Large vessels and tributaries of the hepatic arteries, hepatic veins and portal veins contain approximately 40% of the hepatic blood volume. In comparison, the sinusoids encompass about 60% of the hepatic blood volume [78]. Hence, 15%–18% of the liver comprises blood perfused through the sinusoids. The phantom flow rate was 0.1 mL s^–1, the perfusion rate was 0.0121 s^–1 and the perfused volume was 29.4 mL. The fluid volume was calculated at 8.27 mL, indicating 28.1% of the perfusion volume was free fluid.

Conclusion

The TMM MRI phantom, using 3D percolation of the sonosensitizers, allowed valuable thermal metrics assessment. One main benefit was the capability to obtain measurements with standard MRgHIFU equipment. The thermal enhancement in this phantom was similar to values obtained using a previously described laminar flow phantom model. The acoustic absorption coefficient increased by 0.42 ± 0.19 m^–1 at 0.25% v:v with no perfusion relative to baseline. With a 0.1 mL s^–1 flow rate, the acoustic absorption coefficient rose 0.93 ± 0.22 m^–1 at 0.25% v:v, compared with the control case. This study further validated emulsion thermal enhancement and TMM flow phantom design. The apparatus would help test sonosensitizer performance before in vivo experiments. The Bioheat equation allowed the incident intensity and pressure fields to be extracted, along with the specimen's acoustic absorption coefficient, perfusion rate and thermal diffusivity. The experimental measurements matched simulations using these extracted properties. The simulations allowed insight into untested droplet concentrations, perfusion rates and thermal diffusivities.

Declaration of competing interest

The authors declare no competing interests.

Appendix. Supplementary materials

Supplementary material