Computational study on the reactivity of imidazolium-functionalized manganese bipyridyl tricarbonyl electrocatalysts [Mn[bpyMe (Im-R)](CO)₃Br]⁺ (R = Me, Me₂ and Me₄) for CO₂-to-CO conversion over H₂ formation

Abstract

We have recently reported a series of imidazolium-functionalized manganese bipyridyl tricarbonyl electrocatalysts, [Mn[bpyMe(Im-R)](CO)₃Br]⁺ (R = Me, Me₂, and Me₄), for CO₂-to-CO conversion in the presence of H₂O as the proton source [J. Am. Chem. Soc., 2019, 141, 6569]. These catalysts feature slightly acidic imidazolium moieties in the secondary coordination sphere and reduce CO₂ at mild electrochemical potentials. Here, we employ density functional theory (DFT) calculations to understand the electronic structure and reactivity for the CO₂ reduction reaction (CO₂RR) over the competing hydrogen evolution reaction (HER) using [Mn[bpyMe(ImMe)](CO)₃Br]⁺ (1⁺). Our work indicates that, in the absence of water, the imidazolium ligand stabilizes the Mn–CO₂ adduct through hydrogen bonding-like interactions, similar to the activated CO₂ molecule in the C-cluster of the Ni,Fe-carbon monoxide dehydrogenase II, and assists the protonation steps during CO₂RR and HER. More significantly, based on the energy span model, we demonstrate that the selectivity for CO₂ fixation over proton reduction results from a higher activation energy for yielding the manganese dihydrogen intermediate before H₂ release, which is the TOF determining transition state (TDTS) under an applied potential of Φ = −1.82 V versus Fc^0/+. The calculated TOF also reflects the selectivity for CO₂RR, which is four orders of magnitude larger than for HER, consistent with the CPE experiments that show no hydrogen was obtained. In the case of CO₂ reduction, the TOF determining intermediate (TDI) corresponds to the doubly reduced active catalyst, 1_C2(red2), which features a manganese(0) center that couples ferromagnetically with one unpaired electron in the π* orbital of bipyridine. On the other hand, for HER, the metal-hydride intermediate, 1_C2(I11-R), is the TDI. Finally, second-order perturbation analyses imply that the strongest hydrogen bonding-like interaction at the C2 position in 1⁺ contributes to the higher catalytic activity with respect to [Mn[bpyMe(ImMe₂)](CO)₃Br]⁺ (2⁺) and [Mn[bpyMe(ImMe₄)](CO)₃Br]⁺ (3⁺) for CO₂ fixation, consistent with the experimental data.

Introduction

CO₂ emissions have increased drastically due to the persistent burning of fossil fuels, which currently supply up to 85% of our energy.¹ The rising level of greenhouse gases, such as carbon dioxide (CO₂), contributes to global warming with dire consequences for the environment and human health.^2–10 Based on these imminent and growing threats, there is a critical need to transition our current energy infrastructure from fossil fuels to renewable energies.^11,12 Solar and wind are attractive renewable energy resources, but intermittent, which requires energy storage before being used to power society. One strategy is to use sunlight to convert CO₂ and H₂O (like biological systems) into value-added chemicals, whereby energy is stored in chemical bonds. However, despite the number of synthetic catalysts, current CO₂ reduction catalysts often exhibit high overpotentials and low selectivity for the CO₂ reduction reaction (CO₂RR) over the hydrogen evolution reaction (HER) in the presence of water as the proton source.^13–27 More importantly, they suffer from a lack of mechanistic understanding that hinders systematic improvement.

In contrast, biological organisms such as carbon monoxide dehydrogenase (CODH) enzymes can selectively and efficiently fix CO₂ under mild conditions. One CODH of interest is the Ni,Fe-carbon monoxide dehydrogenase II from Carboxydothermus hydrogenoformans (Ni,Fe-CODH), in which the active site is called the C-cluster (Fig. 1).^28,29 One structural feature of the C-cluster is the presence of a [3Fe–4S] cluster (highlighted in black, Fig. 1) that rigidly links the Ni (highlighted in maroon) and Fe_u atoms (known as the unique iron). X-Ray crystallographic structures of the metallocarboxylate state revealed a CO₂ ligand bridged between Ni and Fe_u.^28,29 This cooperative Lewis acid–base pair, which involves a nucleophilic Ni center and an electrophilic Fe center, is considered an essential feature for the high activity and selectivity of Ni,Fe-CODH.^29,31 Spectroscopic evidence also indicates that the one-electron reduced form of the C-cluster is composed of three ferrous and one ferric iron, implying that the [3Fe–4S] cluster serves as an electron reservoir.^28,32,33 Finally, the metallocarboxylate state shows the presence of interactions between the activated substrate and the protein matrix due to hydrogen bonds to His93 (highlighted in red, Fig. 1) and Lys563,^28,29 implying that these residues are critical for efficient catalysis.

Fig. 1.

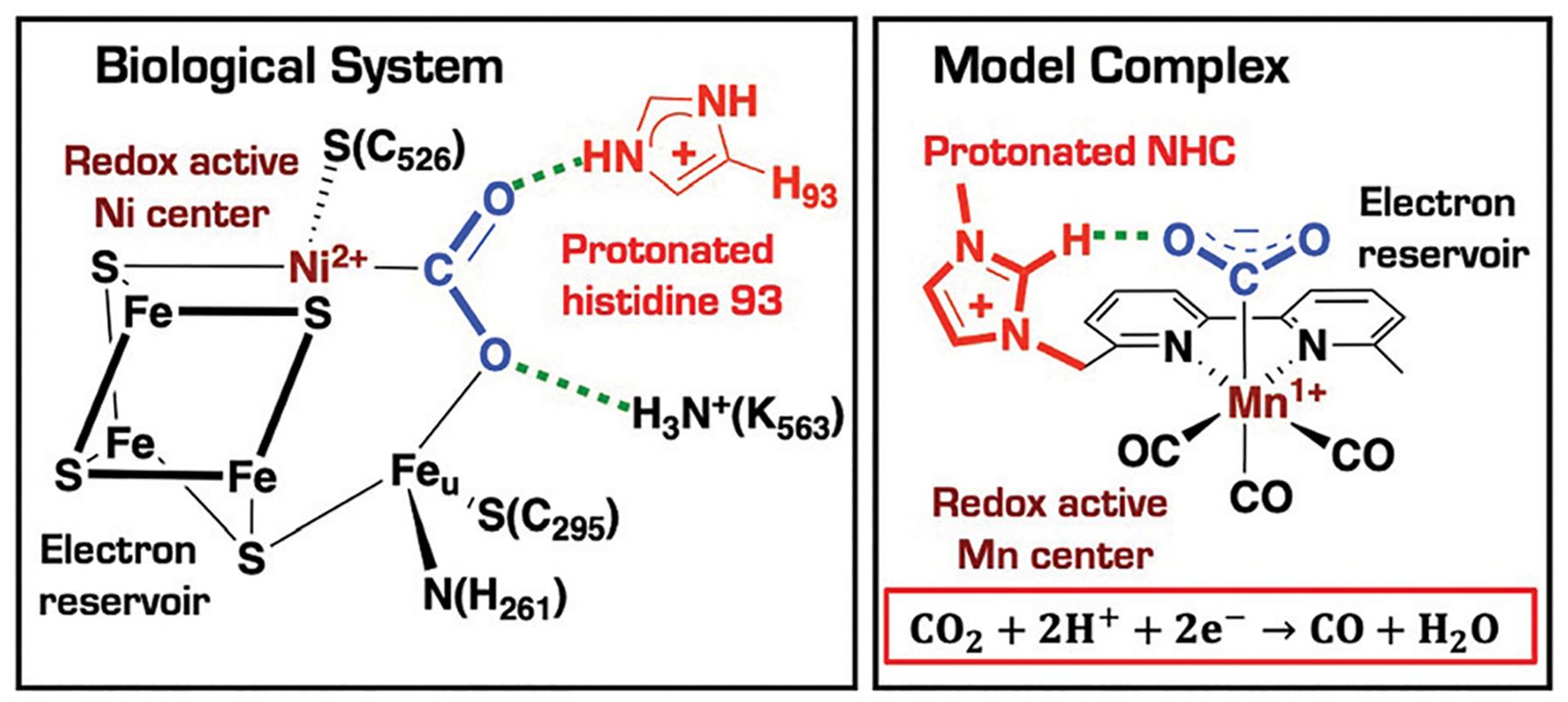
Schematic representation of the CO₂ adduct in the Ni,Fe carbon monoxide dehydrogenase adapted from Dobbeck et al.,^28,29 and diagram of the imidazolium-functionalized manganese bipyridine complex reported by Nippe and co-workers for CO₂-to-CO conversion in the presence of H₂O as the proton source.³⁰

As a result, tremendous efforts have focused on designing molecular catalysts as model systems that mimic this energy-relevant metalloenzyme’s critical structural features and functions. One approach is to use functional groups in the secondary coordination sphere to imitate the protein matrix of second-sphere ligands in Ni,Fe-CODH.^{13–24,26,27,34} One example is [Ni(cyclam)]²⁺ where the presence of amine ligands stabilizes the Ni–CO₂ adduct through hydrogen bond donor–acceptor interactions.^35–47 Another study demonstrates that the addition of Brønsted acids in iron tetraphenylporphyrin [Fe(TPP)] complexes drastically increases selectivity and reactivity for CO₂ fixation.^48–50 Consequently, [Fe(TPP)] species featuring functional groups in the secondary coordination sphere were experimentally extensively studied.^{23,26,51–67} The effects of second-sphere functional groups, as well as pendant proton relays, have also been employed in rhenium,^68–74 and manganese^30,75–77 bipyridyl species, and other molecular electrocatalysts.^78–82 These examples suggest that the first- (e.g., redox potential, nucleophilicity) and secondary-coordination sphere (e.g., hydrogen bonding, ion-pairing) control CO₂ binding and assist the C–O bond cleavage.

We have recently reported a series of imidazolium-functionalized manganese bipyridyl tricarbonyl electrocatalysts [Mn[bpyMe(ImMe)](CO)₃Br]⁺ (1⁺), [Mn[bpyMe(ImMe₂)](CO)₃Br]⁺ (2⁺), and [Mn[bpyMe(ImMe₄)](CO)₃Br]⁺ (3⁺) for CO₂-to-CO conversion at mild electrochemical potentials in the presence of H₂O without the need for a strong acid (Fig. 2).³⁰

Fig. 2.

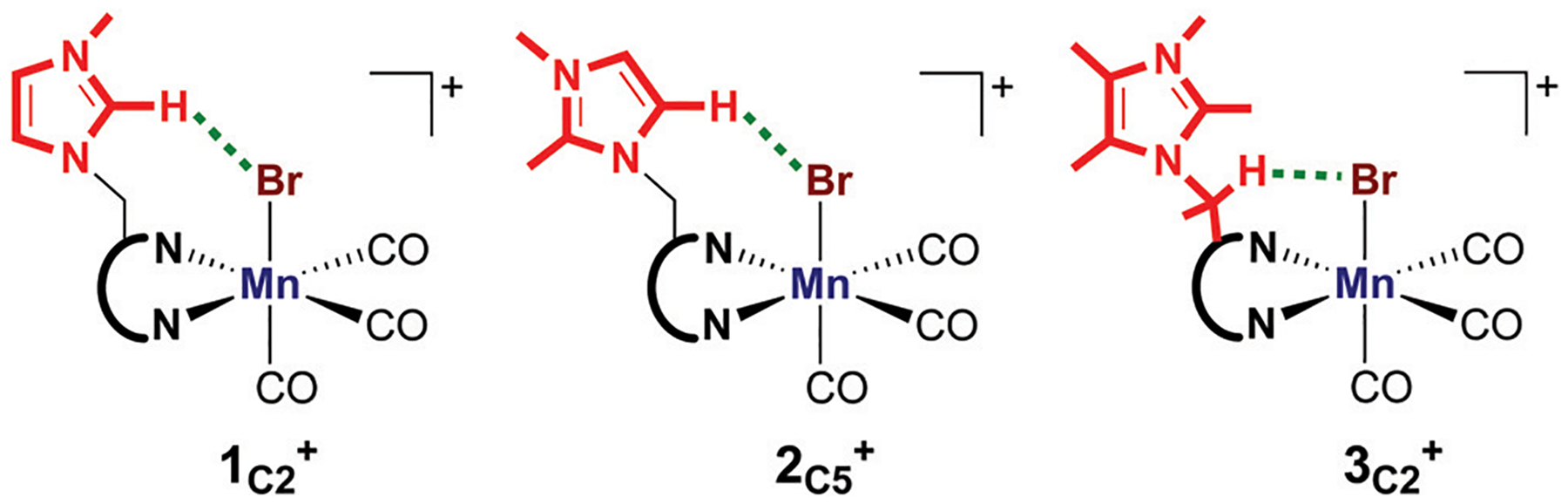
Schematic representation of the imidazolium-functionalized manganese bipyridyl tricarbonyl electrocatalysts that were investigated in this work. The lowest energy structure for ${\mathbf{3}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$ features a hydrogen-bonding interaction between the methylene bridge and bromide.³⁰

The main difference between these complexes exists in the functional groups on the imidazolium moiety at the C2 and C4/C5 positions. For instance, complex 1⁺ features a hydrogen atom at the C2 position of the imidazolium ligand, while a methyl substituent is located at the C2 position in 2⁺ and 3⁺. In addition, species 2⁺ and 3⁺ differ by the presence of methyl groups at the C4/C5 positions in the third catalyst.

Controlled potential electrolysis (CPE) experiments with a CH₃CN solution of 1.0 mM catalyst, 0.1 M NBu₄PF₆, and ca. 0.05 mM ferrocene at −1.82 V versus Fc^0/+ for one hour in the presence of 9.25 M H₂O as a proton source indicate that catalysts 1⁺–3⁺ consumed significantly more charge with higher faradaic efficiencies (~70%) than the mesityl substituted complex [Mn(mes₂bpy)(CO)₃(NCCH₃)]⁺,^30,83 and no hydrogen was detected. Here, we employ density functional theory (DFT) calculations to understand the selectivity of the most active catalyst 1⁺ for the CO₂ reduction reaction (CO₂RR) over the competing hydrogen evolution reaction (HER), as well as the effect of the substituents on the imidazolium moiety for CO₂RR using 1⁺–3⁺ (Fig. 2). Furthermore, our systematic approach allows us to understand the importance of forming hydrogen-bonding interactions between the imidazolium groups and the substrate in going from 1⁺ to 3⁺.

Computational details

Density functional theory (DFT) calculations were run using the Gaussian 09 (Revision E.01).⁸⁴ Geometry optimizations were carried out at the unrestricted ωB97X-D level of theory in acetonitrile (ε = 35.688) using the SMD approach.⁸⁵ All species were optimized using the Def2-TZVP basis set on Mn and Fe while the Def2-SVP basis set was employed for all other atoms except Br, in which the Def2-SVPD basis set was used (denoted BS1).⁸⁶ Additional single-point energy calculations were performed with the Def2-TZVPP basis set on all atoms except Br, in which the Def2-TZVPPD basis set was employed (denoted BS2). Exchange correlation integrals were evaluated with a quadrature grid of 99 radial shells and 590 angular points per shell. Stability analyses were performed in addition to analytical frequency calculations on all stationary points to ensure that geometries correspond to local minima (all positive eigenvalues) or transition state (one negative eigenvalue). IRC calculations and subsequent geometry optimizations were used to confirm the minima linked by each transition state.^87,88

All reported redox potentials were calculated using the direct approach in which free energies of the reactants and products are calculated directly in acetonitrile using the SMD approach rather than by a thermodynamic cycle involving gas-phase energies.⁸⁵ All redox potentials reported herein (in V) are versus the Fc^+/0 redox couple. Additional information regarding the electronic structure calculations can be found in the ESI.†

All energies were corrected for zero-point vibrational energy, while free energies were corrected using the modified harmonic oscillator approximation proposed by Grimme, where low-lying vibrational modes were treated by a free-rotor approximation.⁸⁹ An applied potential of Φ = −1.82 V versus the Fc^0/+ couple was employed to model each electrochemical step, which corresponds to the applied potential of the controlled potential electrolysis (CPE) experiments.³⁰ Finally, natural bond orbital (NBO) analyses were performed with NBO version 3.1,⁹⁰ as implemented in Gaussian 09.⁸⁴

Results and discussion

Formation of the metallocarboxylic intermediate ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}\left(\mathbf{\text{I}}\mathbf{5}\right)$

As previously reported, the initial reduction of ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$ gives the neutral species 1_C2(red1-Br), from which the bromine ligand dissociates to produce ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}\left(\mathbf{\text{red}}\mathbf{1}\right)$ (Fig. 3).³⁰ This last species can be further reduced at −1.53 V versus Fc^0/+ to form 1_C2(red2), which features an open-shell singlet ground-state with one unpaired electron on Mn (ρ_Mn = 0.75 at the ωB97X-D(SMD)/BS1 level of theory) that couples ferromagnetically with one unpaired electron in the π* orbital of bipyridine. It should be noted that the triplet state for 1_C2(red2) was found to be 3.0 kcal mol⁻¹ higher in energy. Moreover, the spin contaminated singlet was corrected using the broken spin symmetry procedure reported by Yamaguchi and co-workers.^91,92 In this case, the spin-purified singlet state becomes 7.4 kcal mol⁻¹ lower in energy than the triplet state, consistent with our characterization that 1_C2(red2) has an open-shell singlet ground-state.

Fig. 3.

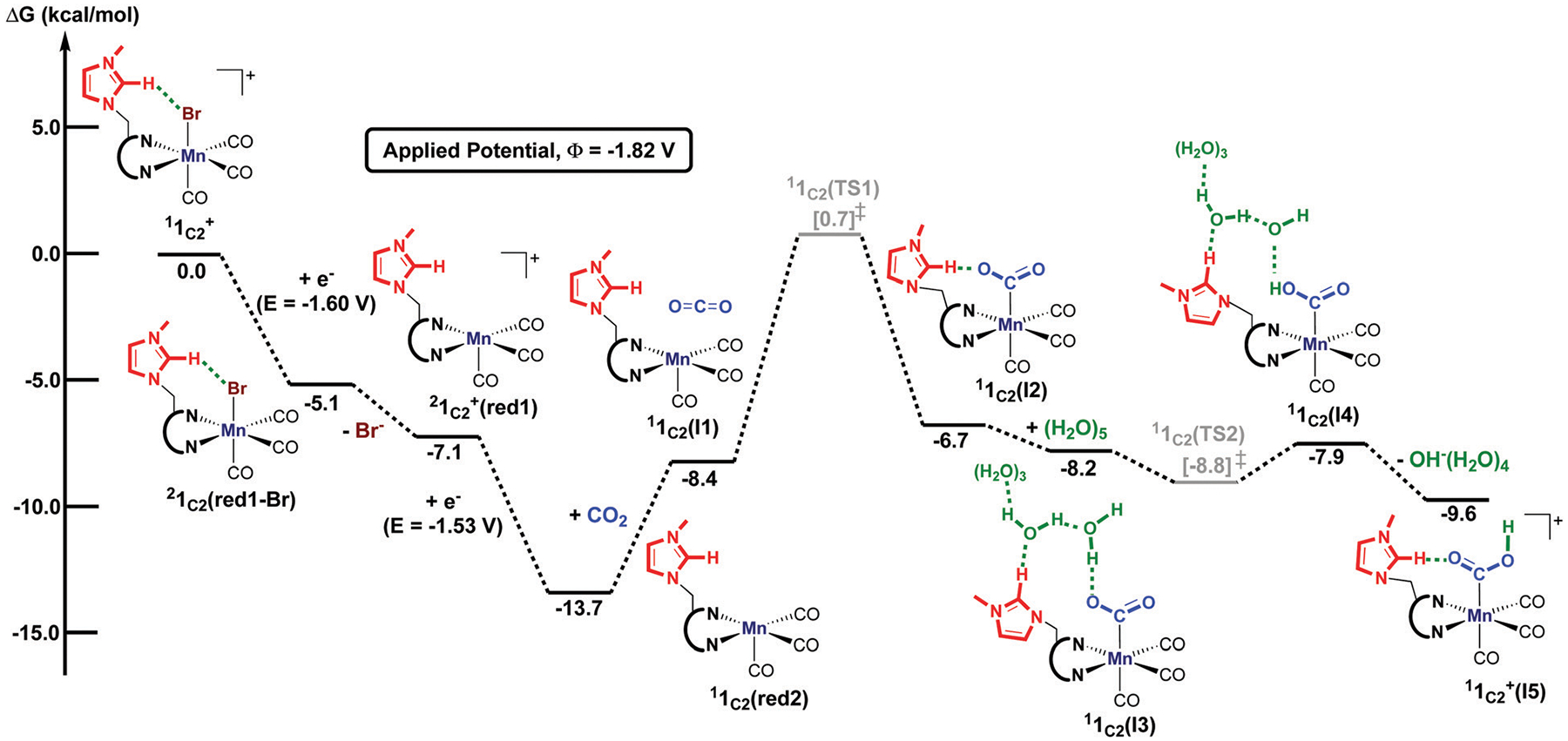
Computed free energy (kcal mol⁻¹) profile for yielding the metallocarboxylic acid species, ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\text{I}5)$. All free energies are calculated with respect to the separated reactants and the superscript corresponds to the spin multiplicity of a given species.

The formation of the Mn–CO₂ adduct is calculated to be slightly endergonic by 7.0 kcal mol⁻¹ and requires an activation energy of 14.4 kcal mol⁻¹ with respect to the separated reactants. The computed transition state 1_C2(TS1) shows that CO₂ is pre-activated with an O=C=O bond angle of 145.8° and 1.20 Å C–O bond length (Fig. 4). We note that 1_C2(TS1) has an open-shell singlet ground-state in which the Mulliken spin on manganese is ρ_Mn = 0.23. Moreover, the computed geometry for 1_C2(TS1) indicates that the imidazolium ligand weakly interacts with the axial carbonyl ligand, in which the distance between the carbon atom and the centroid of the imidazolium ligand is 3.30 Å (Fig. 4). This transition state is 1.1 kcal mol⁻¹ lower in energy than our previously reported transition state in which the imidazolium ligand cooperates with CO₂ (Fig. S2, ESI†) More notably, the computed metallocarboxylate intermediate 1_C2(I2) has a closed-shell singlet ground-state, and its electronic configuration is similar to the CO₂ moiety in the C-cluster in which CO₂ is reduced by two-electrons and is best described as a carboxyl group rather than an anionic CO₂^•− radical.²⁹ In addition, the computed angle for CO₂ of 124.6° in 1_C2(I2) displays similarity to the reported O–C–O angle in the atomic resolution structure (O–C–O = 117°) of the C-cluster.²⁹ Another comparable aspect to the C-cluster is observed with the imidazolium ligand stabilizing, in the absence of water, the activated CO₂ molecule through a hydrogen-bonding interaction (C2–H⋯O = 1.68 Å, Fig. 4). To further quantify the intermolecular interaction between the imidazolium group and CO₂,⁹³ second-order perturbation analyses were performed using the NBO program as implemented in Gaussian 09.^84,90 Intriguingly, the magnitude of the ${\text{n}}_{\text{O}}\to {\sigma }_{\text{CH}}^{*}$ in 1_C2(I2) is calculated to be 11.1 kcal mol⁻¹ and 7.7 kcal mol⁻¹, supporting the presence of intermolecular interactions between CO₂ and the C2–H group on the imidazolium ligand that acts as a hydrogen-bond acceptor (Fig. S18 and Table S16, ESI†).

Fig. 4.

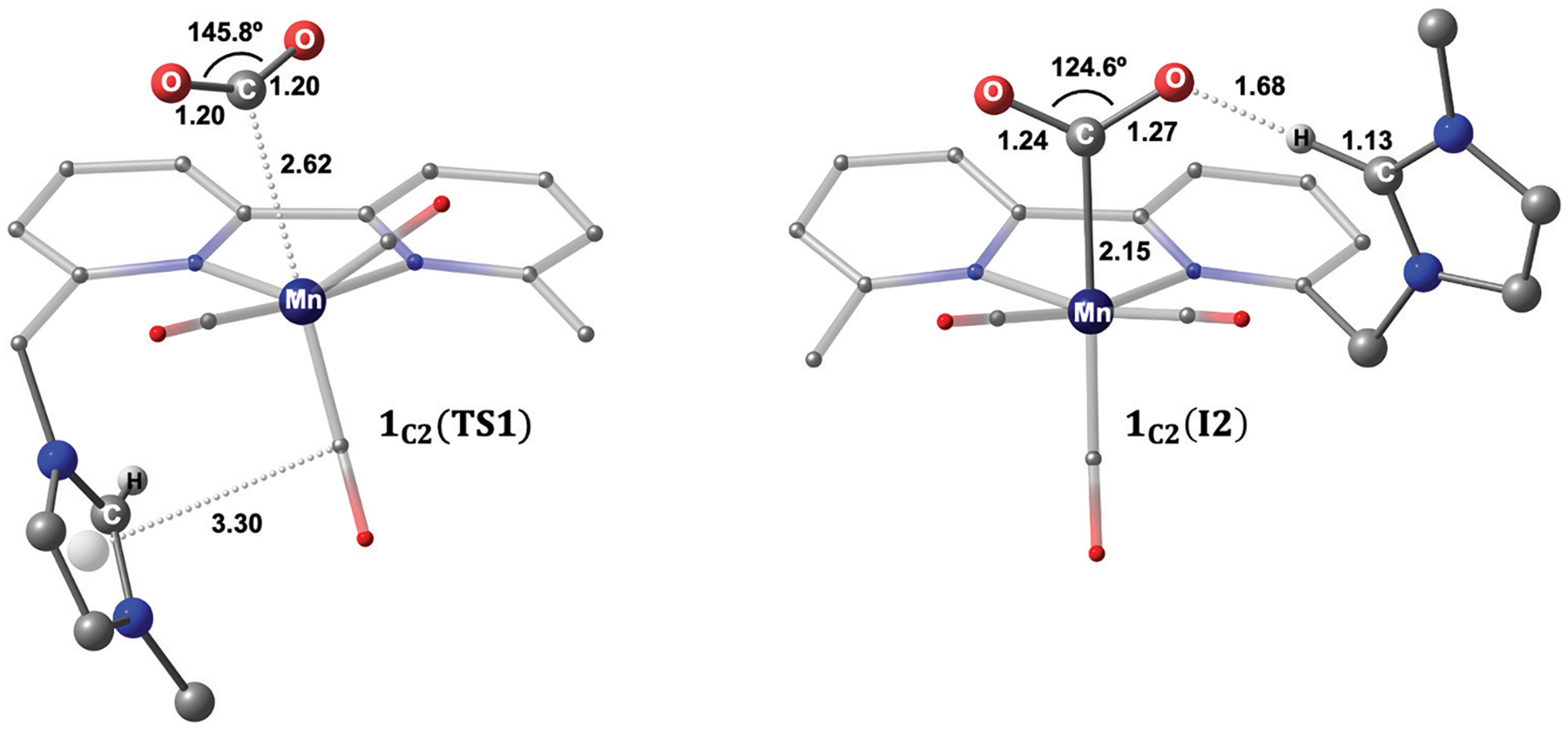
Optimized geometries of the transition state 1_C2(TS1) for CO₂ addition (left) and computed metallocarboxylate intermediate 1_C2(I2) (right). Distances are given in angstroms, and bond angles are in degrees. Non-participating hydrogen atoms are omitted for clarity.

We note that the IRC calculations from 1_C2(TS1) show that the imidazolium ligand interacts with the axial carbonyl ligand rather than with CO₂. However, the lowest energy structure for the metallocarboxylate intermediate, 1_C2(I2), indicates that the imidazolium moiety cooperates with carbon dioxide (Fig. 4), meaning that an isomerization process is required to rotate the imidazolium group. Several transition states were located, and a proposed reaction pathway is shown in Fig. S3 (ESI†). As expected, the exchange process is facile, demonstrating that the imidazolium moiety is highly fluxional during catalysis.Therefore, for clarity, only the lowest computed Gibbs free energies are reported in Fig. 3.

After forming the metallocarboxylate intermediate 1_C2(I2), the Mn–CO₂ adduct can be protonated in the presence of a Brønsted acid. The protonation of 1_C2(I2) was modeled by adding an explicit (H₂O)₅ cluster, as previously described in our published study,³⁰ to yield 1_C2(I3) (ΔG = −8.2 kcal mol⁻¹, Fig. 3). We note that here the water cluster in a chair configuration was used as a reference instead of the previously reported cyclic configuration, which is 5.6 kcal mol⁻¹ lower in energy.³⁰ This new approach was employed as our calculations show that the explicit (H₂O)₅ cluster adopts a chair configuration instead of the cyclic configuration. Furthermore, our methodology allows us to employ the energy span model (ESM) to identify the TDTS (TOF determining transition state) and TDI (TOF determining intermediate), which otherwise will be significantly underestimated due to the configuration of the water cluster.

The computed structure of 1_C2(I3) indicates that the imidazolium ligand stabilizes the proton source near CO₂ and facilitates the metallocarboxylic acid intermediate (Fig. 5). Second-order perturbation analyses also demonstrate that the imidazolium ligand acts as a hydrogen-bond acceptor for the water cluster (e.g., the magnitude of the ${\text{n}}_{\text{O}}\to {\sigma }_{\text{CH}}^{*}$ is 3.6 kcal mol⁻¹ and 2.2 kcal mol⁻¹, Fig. S19, ESI†), and the proton source also stabilizes CO₂ in 1_C2(I3) (Fig. S20, ESI†).

Fig. 5.

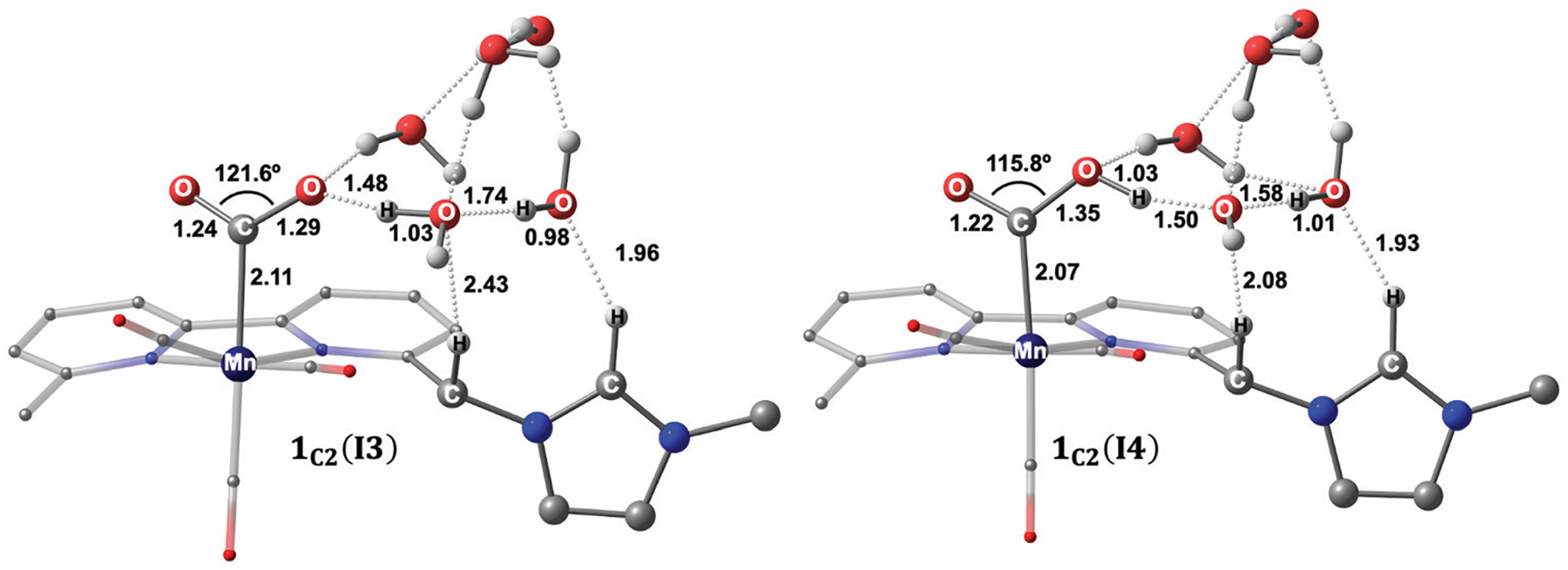
Optimized geometries of 1_C2(I3) (left) and 1_C2(I4) (right). Distances are given in angstroms, and bond angles are in degrees. Non-participating hydrogen atoms are omitted for clarity.

Overall, our calculations suggest that the formation of ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{5})$ is downhill by 2.9 kcal mol⁻¹ with respect to 1_C2(I2). Furthermore, based on previous studies in which a single H₂O molecule was employed to model the first protonation step,^43,94 the formation of the metallocarboxylate intermediate is here spontaneous (ΔG = −9.6 kcal mol⁻¹ with respect to the separated reactants, Fig. 3). This is due to the stabilization of the hydroxide anion via hydrogen-bonding interactions from the water cluster and imidazolium ligand, as indicated by the isosurface plots of the second-order perturbation interactions (Fig. S20–S22, ESI†). Finally, we note that the computed transition state for the first protonation step is lower in energy than 1_C2(I3) and 1_C2(I4). Indeed, the computed electronic energy for 1_C2(TS2) is higher than that of both intermediates. However, 1_C2(TS2) has a lower zero-point energy than 1_C2(I3) and 1_C2(I4), offsetting its higher Gibbs free energy.

Reduction-first pathway versus protonation-first pathway from ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{5})$.

After the formation of the metallocarboxylic acid species ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{5})$, the reaction mechanism can either go through the protonation-first pathway or the reduction-first pathway (Fig. 6 and 7).³⁰

Fig. 6.

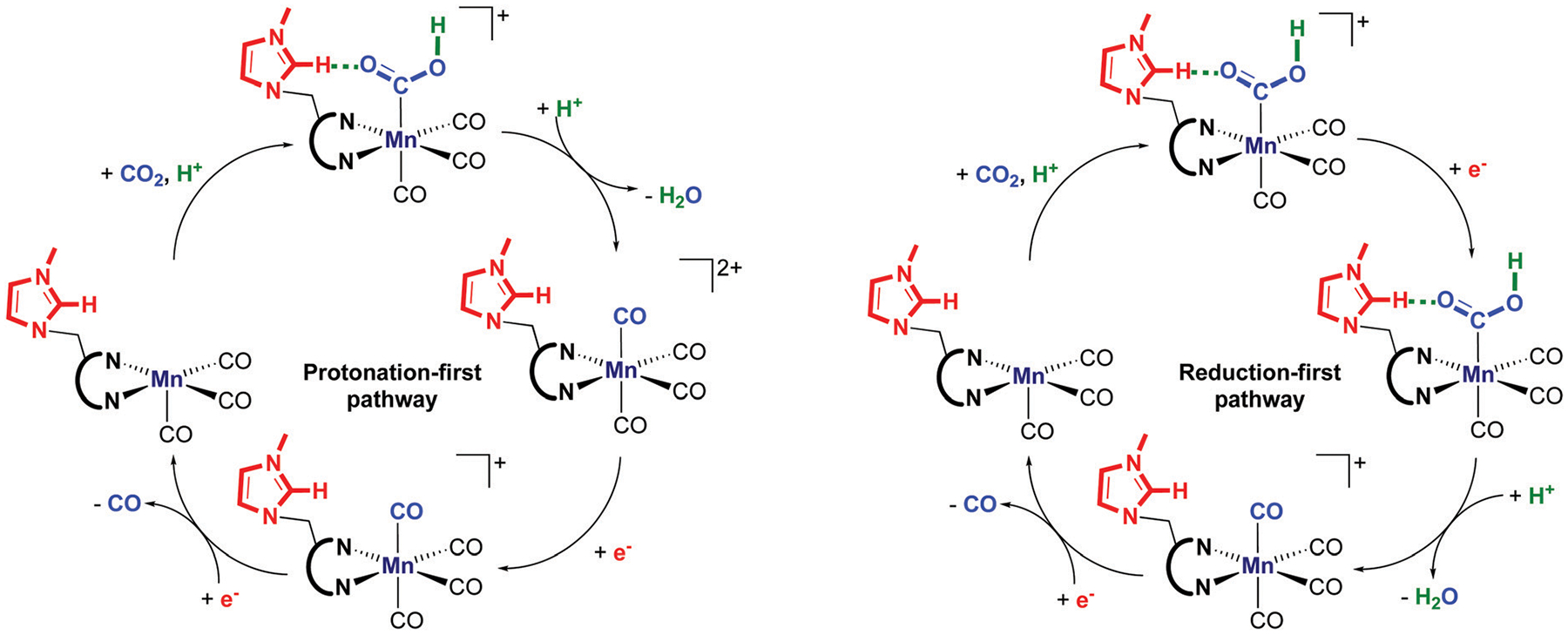
Comparison of the protonation-first pathway (left-side) and reduction-first pathway (right side) after the formation of the metallocarboxylic acid intermediate ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{5})$.

Fig. 7.

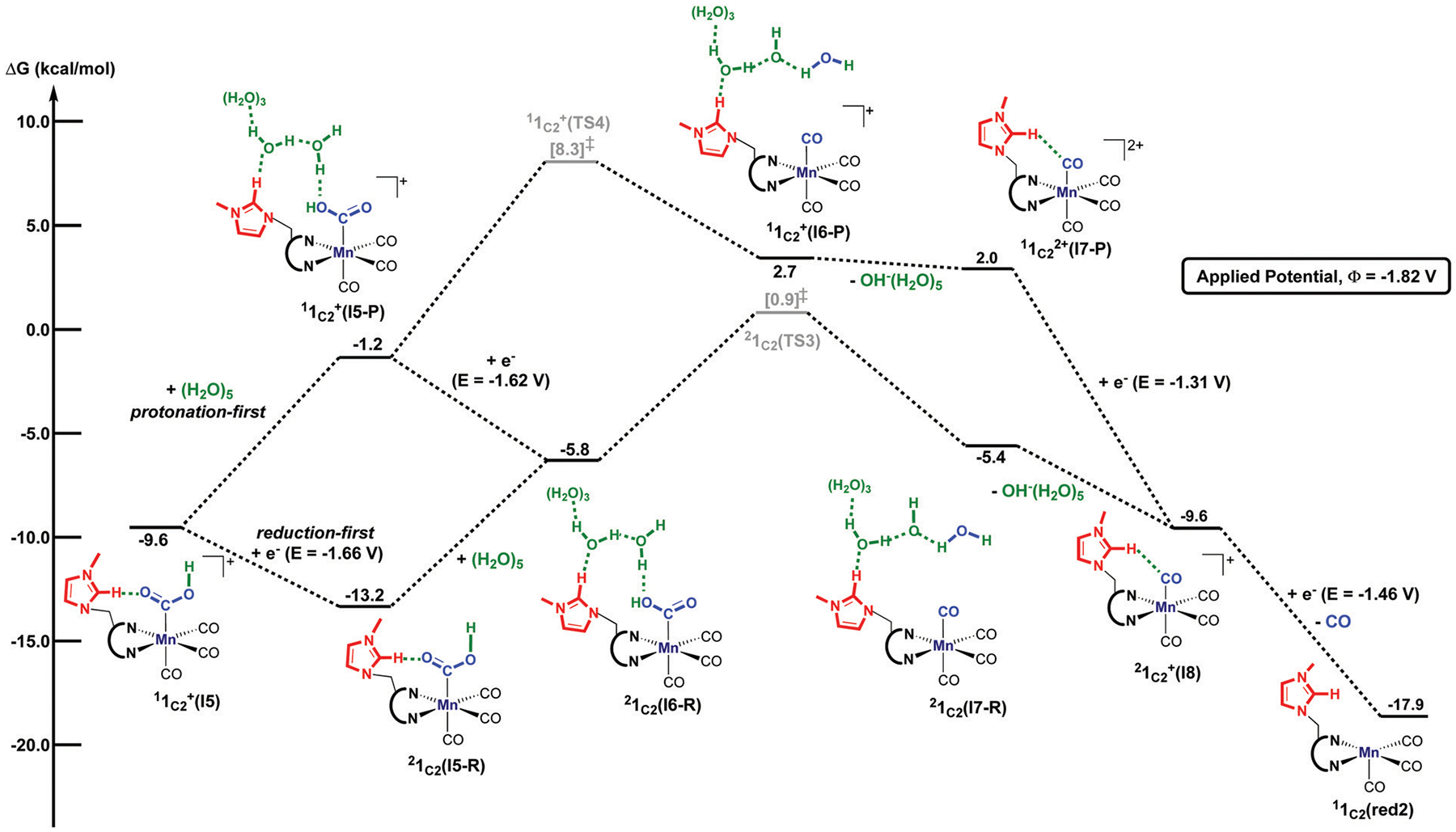
Computed free energy (kcal mol⁻¹) profile for the protonation-first and reduction-first pathway from the metallocarboxylic acid intermediate ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{5})$ in the presence of water. All free energies are calculated with respect to the separated reactants and the superscript represents the spin multiplicity of a given species.

In the case of the reduction-first mechanism, the metallocarboxylic acid species ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{5})$ is reduced at −1.66 V versus Fc^0/+, which is in the potential range where the catalytic current is experimentally observed to form 1_C2(I5-R). From this last intermediate, the addition of an explicit (H₂O)₅ cluster yields 1_C2(I6-R).³⁰ We note here that the water cluster’s addition is significantly uphill compared to adding (H₂O)₅ to the metallocarboxylate intermediate (Fig. 3). As shown with the second-order perturbation analysis calculations, this difference in energy can be explained by the weaker stabilization between the water cluster and the metallocarboxylic acid intermediate (Fig. S24, ESI†) compared to the stabilization between (H₂O)₅ and the metallocarboxylate species (Fig. S20, ESI†). Moreover, the transferred proton in 1_C2(I3) is slightly more acidic (computed natural charge, q_H = 0.53) than in 1_C2(I6-R) (q_H = 0.51), consistent with the elongated O⋯H bond interaction of 1.03 Å of the water molecule in 1_C2(I3) (cf. O⋯H = 0.98 Å in 1_C2(I6-R)) that facilitates the protonation step to yield the metallocarboxylic acid species. The transition state for C–O bond cleavage, 1_C2(TS3), features a hydrogen-bonding network between the imidazolium ligand and the water cluster (C2–H⋯(H₂O)₅ = 1.89 Å), as well as a secondary hydrogen-bonding stabilization of 2.45 Å between the bridging methylene ligand and H₂O (Fig. 8). This step occurs via an activation barrier of 14.1 kcal mol⁻¹ with respect to the infinitely separated metallocarboxylic acid species and the explicit (H₂O)₅ cluster to generate neutral tetracarbonyl intermediate 1_C2(I7-R). The subsequent hydroxyl removal generates species ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{8})$, which can be reduced at −1.46 V to give back the active species 1_C2(red2) after CO dissociation (Fig. 7).

Fig. 8.

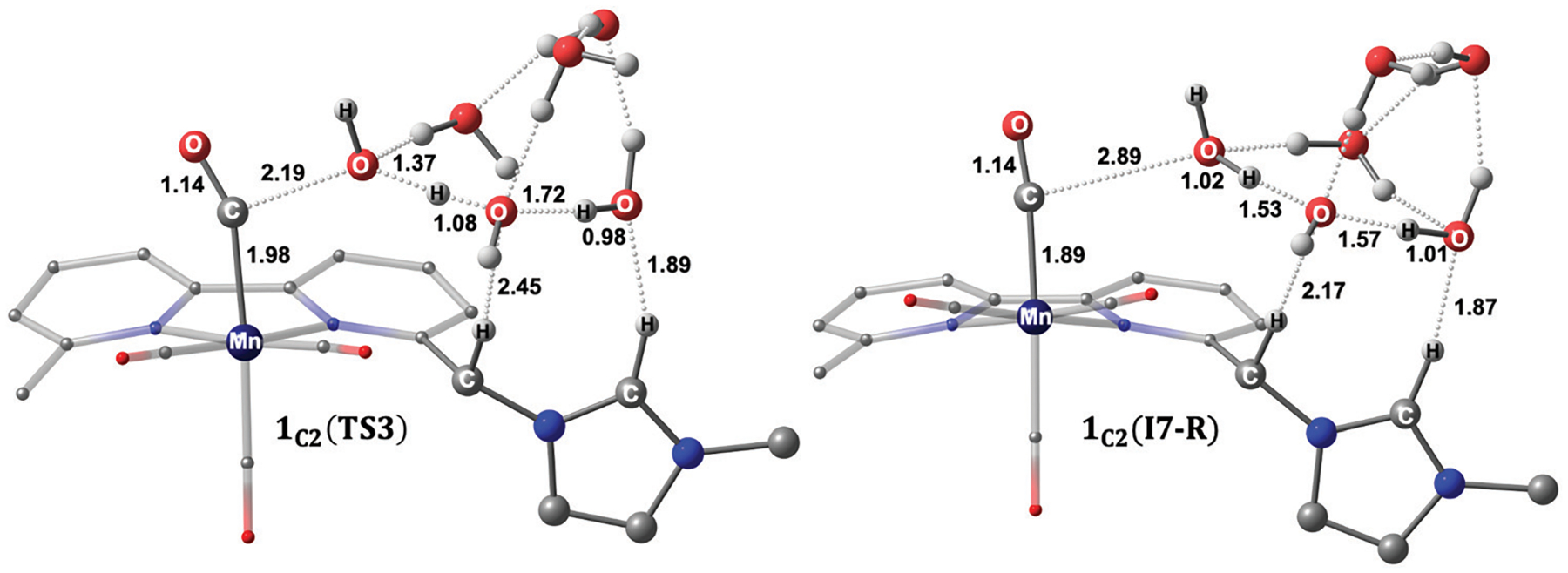
Optimized geometries of the transition state 1_C2(TS3) (left) and neutral tetracarbonyl intermediate 1_C2(I7-R) (right). Distances are given in angstroms, and non-participating hydrogen atoms are omitted for clarity.

Alternatively, the metallocarboxylic acid species can proceed through the protonation-first mechanism. In this instance, an explicit (H₂O)₅ cluster was added into the calculations to yield ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}\left(\mathbf{\text{I}}\mathbf{5}\mathbf{\text{-P}}\right)$, which is uphill by 8.4 kcal mol⁻¹ with respect to ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{5})$. Interestingly, the activation barrier for yielding the tetracarbonyl intermediate is 3.8 kcal mol⁻¹ higher in energy than in the reduction-first pathway but remains accessible. This suggests that ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$ may access both of the reduction-first and protonation-first pathways, similar to what reported Rochford and co-workers when using [Mn([MeO]₂Ph)₂bpy(CO)₃(CH₃CN)] (OTf).⁷⁷ However, based on our calculated potential energy surfaces, we hypothesized that the higher catalytic activity, which ranges from −1.50 V to −1.80 V, is attributed to the reduction-first pathway.³⁰ With the subsequent hydroxyl removal, the ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{\mathbf{2}+}\left(\mathbf{\text{I}}\mathbf{7}\mathbf{\text{-P}}\right)$ is generated and can be reduced at −1.31 V versus Fc^0/+ to give ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}\left(\mathbf{\text{I}}\mathbf{8}\right)$. As previously mentioned, the latter intermediate can generate the active species 1_C2(red2), after CO dissociation under a calculated redox potential of −1.46 V.

Formation of the Mn–H intermediate in 1⁺.

Previous studies have shown that manganese bipyridyl tricarbonyl electrocatalysts require the presence of external proton sources to drive catalysis for the CO₂ reduction reaction (CO₂RR).^{30,76,77,83,95–98} Therefore, the competitive hydrogen evolution reaction (HER) should be considered to ensure that [Mn[bpyMe(ImMe)](CO)₃Br]⁺ (1⁺) is selective for CO₂ fixation.Indeed, experimental data showed that 1⁺ could convert CO₂ to CO for one hour in the presence of 9.25 M H₂O with a faradaic efficiency of 70.3 ± 1.2%, and no hydrogen was detected.³⁰ To understand the selectivity for CO₂RR over HER, the reaction mechanism for proton reduction was computed using ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$ (Fig. 9 and 10).

Fig. 9.

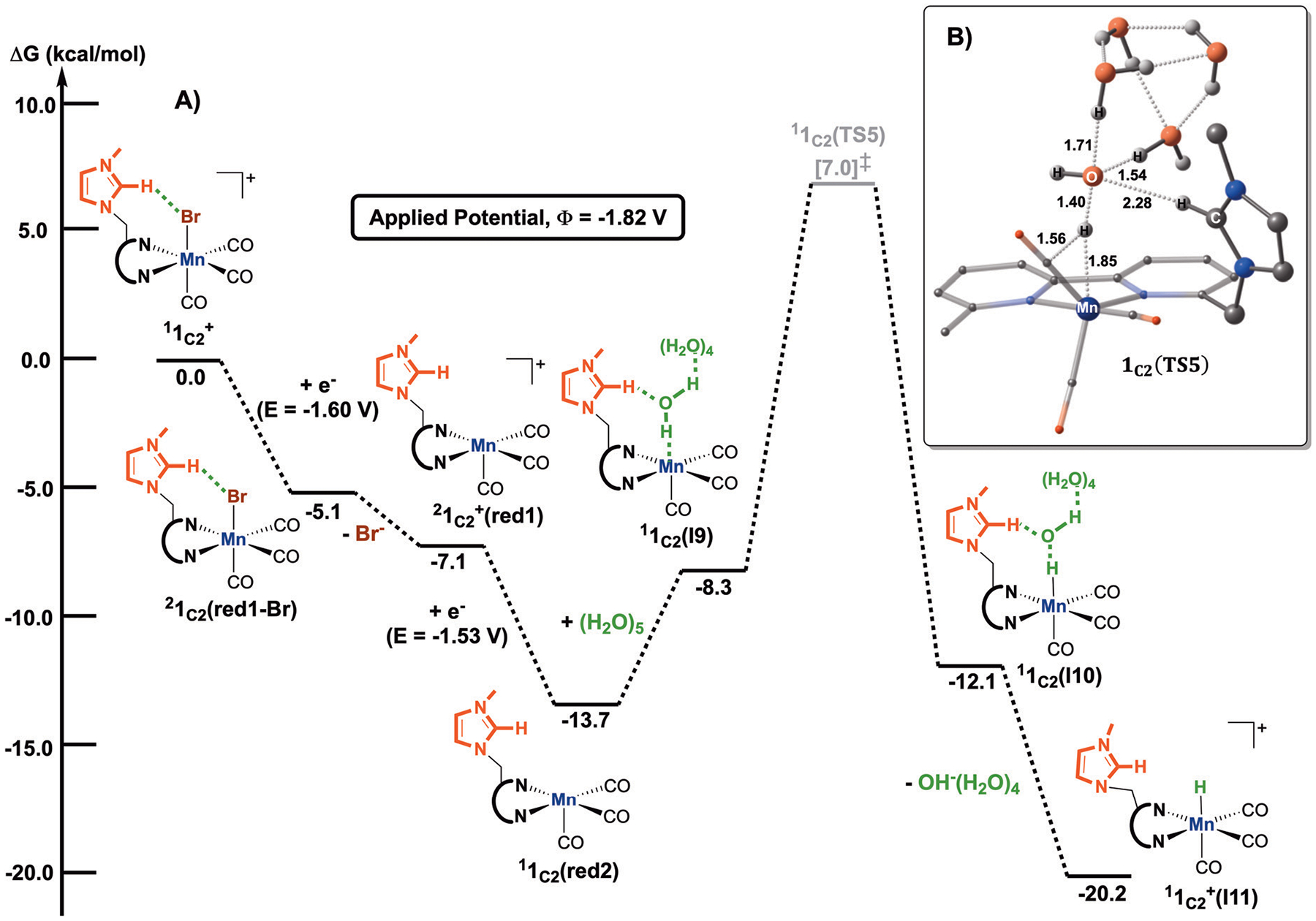
(A) Computed free energy (kcal mol⁻¹) profile for forming the metal-hydride complex, ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}\left(\mathbf{\text{I}}\mathbf{11}\right)$. All free energies are calculated with respect to the separated reactants and the superscript corresponds to the spin multiplicity of a given species. (B) Optimized geometry of the transition state 1_C2(TS5), leading to the formation of the metal-hydride complex, ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}\left(\mathbf{\text{I}}\mathbf{11}\right)$. Distances are given in angstroms, and non-participating hydrogen atoms are omitted for clarity.

Fig. 10.

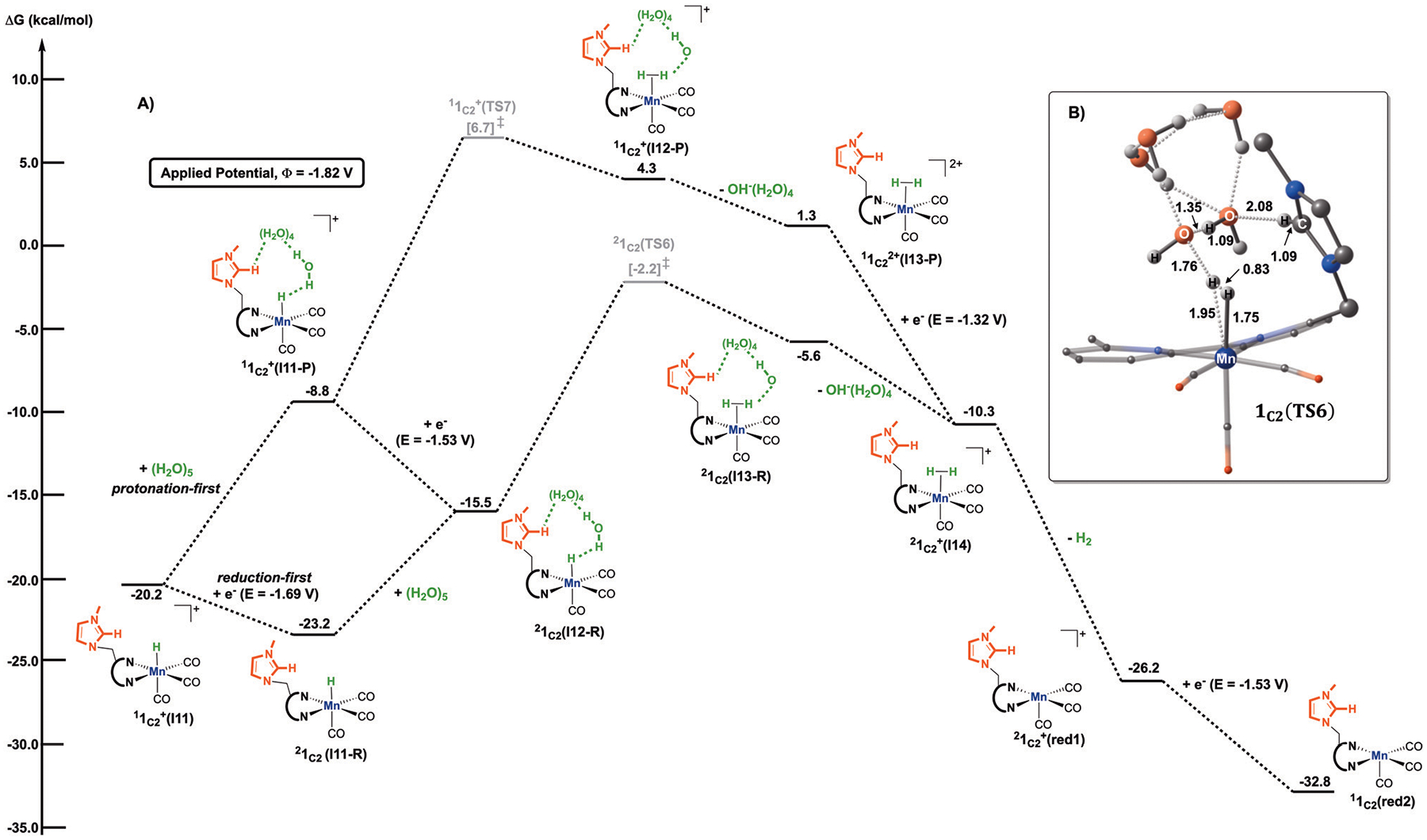
(A) Computed free energy (kcal mol⁻¹) profile for H₂ formation from the metal-hydride species ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{11})$ in the presence of water as the proton source. All free energies are calculated with respect to the separated reactants. The superscript corresponds to the spin multiplicity of a given species. (B) Optimized geometry of the transition state 1_C2(TS6) leading to the formation of the manganese dihydrogen complex, ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{14})$. Distances are given in angstroms. Non-participating hydrogen atoms are omitted for clarity.

Like CO₂-to-CO conversion, the initial formation of the active complex 1_C2(red2) is necessary for catalysis. From this compound, the association of the explicit water cluster gives 1_C2(I9), allowing one proton to be transferred from H₂O to the manganese center to give 1_C2(I10) (Fig. 9A and B). The activation energy for yielding the Mn–H intermediate is 20.7 kcal mol⁻¹,which is 6.3 kcal mol⁻¹ higher in energy than forming the Mn–CO₂ adduct (Fig. 3), signifying that HER is kinetically slower than CO₂RR (vide infra). As expected, the computed transition state entails that the imidazolium group stabilizes the proton transfer step by forming a hydrogen-bonding network (C2–H⋯(H₂O)₅ = 2.28 Å, Fig. 9B). After forming 1_C2(I10) and through the subsequent hydroxyl removal, the Mn–H intermediate, ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}\left(\mathbf{\text{I}}\mathbf{11}\right)$, is obtained. Overall, the process is spontaneous (ΔG = −20.2 kcal mol⁻¹ with respect to the starting materials, Fig. 9A cf. ΔG = −9.6 kcal mol⁻¹ for the metallocarboxylic acid intermediate, Fig. 3).

Following the formation of ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}\left(\mathbf{\text{I}}\mathbf{11}\right)$, H₂ formation can occur in the presence of one additional proton and electron. As done for CO₂RR, both the protonation-first and reduction-first pathways were considered (Fig. 10).

In the case of the reduction-first mechanism, the metal-hydride complex, ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}\left(\mathbf{\text{I}}\mathbf{11}\right)$, is reduced at −1.69 V to yield 1_C2(I11-R), from which the addition of an explicit (H₂O)₅ cluster gives 1_C2(I12-R). A transition state for H₂ formation was located, featuring a hydrogen-bonding network between the imidazolium ligand and the water cluster (C2–H⋯(H₂O)₅ = 2.08 Å, Fig. 10B). In this case, the calculated activation energy is 21.0 kcal mol⁻¹ with respect to the infinitely separated reactants. Again, this step is kinetically higher in energy than for the C–O bond cleavage step (Fig. 7). With the subsequent hydroxyl removal, the manganese dihydrogen compound, ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}\left(\mathbf{\text{I}}\mathbf{14}\right)$, is generated, which can release H₂ spontaneously and be reduced at −1.53 V to give back 1_C2(red2). Alternatively, the metal-hydride complex can proceed through the protonation-first mechanism. However, like the previous discussion for CO₂RR, this pathway remains competitive. Still, it requires higher activation energies, suggesting that the reduction-first mechanism is preferred for HER under an applied potential of Φ = −1.82 V versus Fc^0/+.

Energy span model and turnover frequency for CO₂RR and HER using ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$.

Based on the computed Gibbs free energy reaction profiles for the CO₂ reduction reaction (CO₂RR) and hydrogen evolution reaction (HER) using ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$, the energy span model proposed by Kozuch and co-workers was employed: (i) to identify the TOF determining transition state (TDTS) and TOF determining intermediate (TDI), as well as (ii) to calculate the turnover frequencies (TOFs) by employing the AUTOF program.^99,100 All key intermediates and transition states under an applied potential of −1.82 V versus Fc^0/+, corresponding to the controlled potential electrolysis (CPE) experiments,³⁰ are depicted in Fig. 11.

Fig. 11.

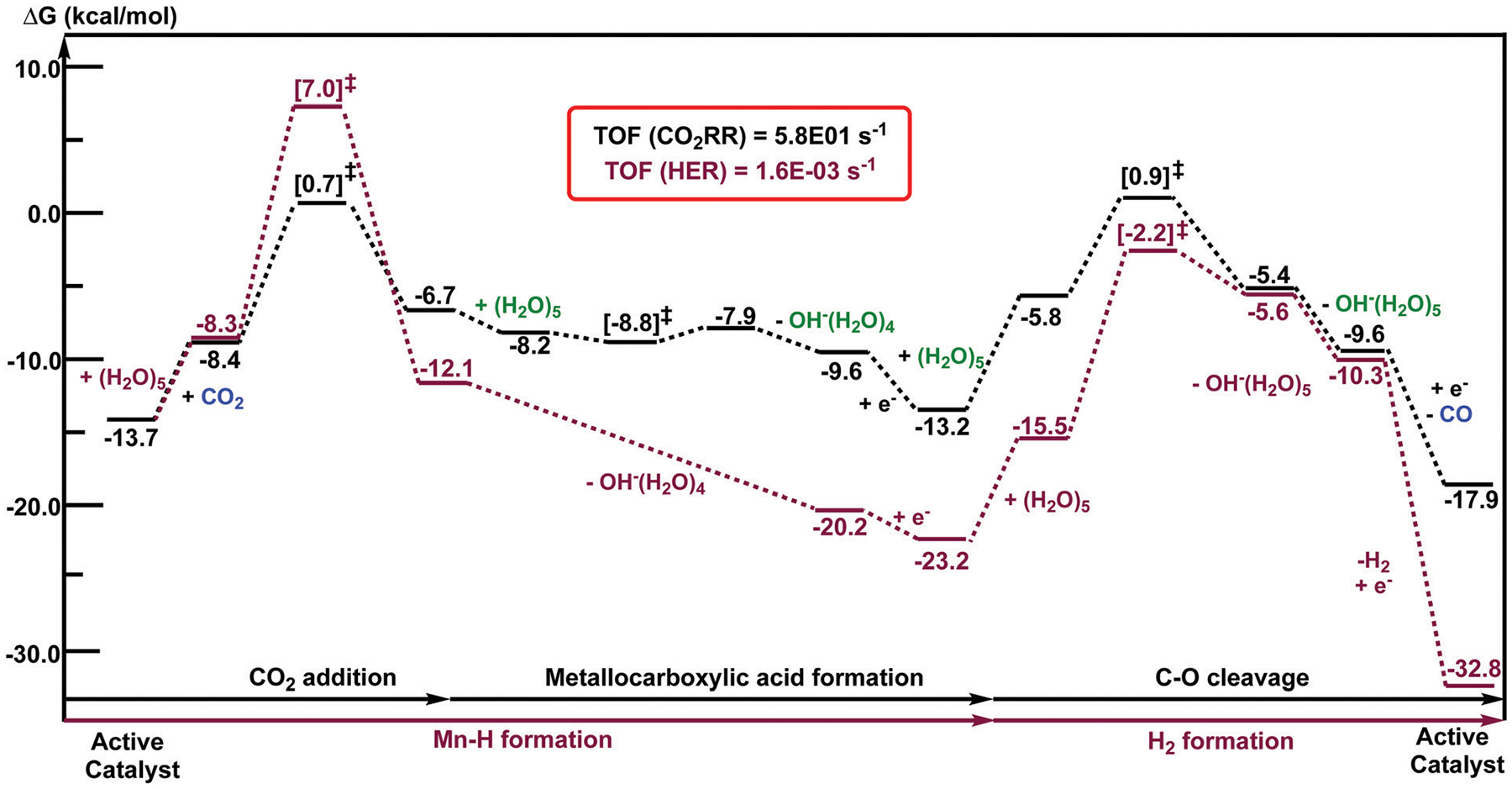
Computed free energy (kcal mol⁻¹) profiles of one catalytic cycle for the CO₂ reduction reaction (CO₂RR in black) and the hydrogen evolution (HER in maroon) using ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$ in the presence of H₂O as the proton source. All computed Gibbs free energies are reported with respect to the separated reactants at an applied potential of Φ = −1.82 V versus the Fc^0/+ couple.

Our DFT calculations reveal that the change in the Gibbs free energy of reaction for CO₂ fixation is negative (ΔG = −4.2 kcal mol⁻¹ with respect to the doubly reduced species), indicating that the reaction is spontaneous (Fig. 11). Furthermore, our computational data suggest that H₂ formation features higher activation energies than for CO₂ fixation, indicating that CO₂RR is favored over HER kinetically. This last observation is reflected by the calculated TOFs where the TOF for CO₂RR is 5.8 × 10¹ s⁻¹ and 1.6 × 10⁻³ s⁻¹ for HER. Our results are consistent with the CPE experiments that show no hydrogen was obtained. In this case, the TDTS for CO₂RR corresponds to the C–O bond cleavage step (X_TOF = 0.67, Tables S2 and S3, ESI†), while for HER, the formation of the manganese dihydrogen intermediate is the TDTS (X_TOF = 0.62, Tables S4 and S5, ESI†). On the other hand, the TOF determining intermediate (TDI) corresponds to the doubly reduced active catalyst, 1_C2(red2) for CO₂RR and the metal-hydride species, 1_C2(I11-R), for HER. We note that our proposed mechanism for CO₂ reduction matches with previously reported studies based on manganese catalysts.^76,77,95,101

Substituents effect on the imidazolium moiety for CO₂ reduction.

Until now, we have proposed a reaction mechanism for CO₂RR and HER using 1⁺ and discussed the involvement of the imidazolium ligand during catalysis. To further understand the effect of the substituents on the imidazolium group, the Gibbs free energy reaction profiles for [Mn[bpyMe(ImMe₂)](CO)₃Br]⁺ (2⁺) and [Mn[bpyMe(ImMe₄)](CO)₃Br]⁺ (3⁺) were computed and compared with [Mn[bpyMe(ImMe)](CO)₃Br]⁺ (1⁺). Specifically, catalysts ${\mathbf{2}}_{\mathbf{\text{C}}\mathbf{5}}^{+}$ and ${\mathbf{3}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$ were considered for CO₂RR in contrast with ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$. As discussed in detail in the ESI,† similar reaction mechanisms were obtained for CO₂RR using ${\mathbf{2}}_{\mathbf{\text{C}}\mathbf{5}}^{+}$ and ${\mathbf{3}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$ (Fig. S4–S11, ESI†). For instance, our calculations indicate that the initial formation of the doubly reduced complexes 2_C5(red2) and 3_C2(red2) is required to bind CO₂. From these intermediates, the addition of CO₂ is slightly uphill for all compounds and the calculated Gibbs free energies of the Mn–CO₂ adducts follow the expected trend: 1_C2(I2) (ΔG = −6.7 kcal mol⁻¹) < 2_C5(I2) (ΔG = −4.1 kcal mol⁻¹) = 3_C2(I2) (ΔG = −4.1 kcal mol⁻¹). We hypothesize that the energy difference comes from the weaker hydrogen-bonding interactions induced by the imidazolium ligand in the secondary coordination sphere, going from 1⁺ to 3⁺ (Fig. 4 and Fig. S6 and S7, ESI†). This proposed explanation was quantified by comparing the second-order perturbation interaction energies between CO₂ and the substituent on the imidazolium group for the metallocarboxylate intermediates, which indicates a larger ${\text{n}}_{\text{O}}\to {\sigma }_{\text{CH}}^{*}$ magnitude in 1_C2(I2) than in 2_C5(I2) and 3_C2(I2) (Table S16, ESI†), consistent with our hypothesis.

In the presence of H₂O, the formation of the metallocarboxylic acid species ${\mathbf{2}}_{\mathbf{\text{C}}\mathbf{5}}^{+}(\mathbf{\text{I}}\mathbf{5})$ and ${\mathbf{3}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{5})$ is downhill for all catalysts (Fig. S4 and S5, ESI†). The optimized geometries imply that the C5–H or C2–CH₃ groups on the imidazolium ligand in ${\mathbf{2}}_{\mathbf{\text{C}}\mathbf{5}}^{+}(\mathbf{\text{I}}\mathbf{5})$ and ${\mathbf{3}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{5})$, respectively, interact with the water cluster and assist the proton transfer from H₂O to the carboxyl group. Such enablement directly depends on the substituents at the C2 and C4/C5 positions of the imidazolium moiety (Fig. S8, ESI†). For instance, the magnitudes of the ${\text{n}}_{\text{O}}\to {\sigma }_{\text{CH}}^{*}$ in 2_C5(TS2) are 2.9 kcal mol⁻¹ and 0.9 kcal mol⁻¹ compared to 1.4 kcal mol⁻¹ in 3_C2(TS2) (Table S17, ESI†). These interactions are weaker than those in the first catalyst, reflecting the stronger hydrogen bonding-like interaction at the C2 position in 1⁺.

Finally, the subsequent protonation step of ${\mathbf{2}}_{\mathbf{\text{C}}\mathbf{5}}^{+}(\mathbf{\text{I}}\mathbf{5})$ and ${\mathbf{3}}_{\mathbf{\text{C}}\mathbf{2}}^{+}(\mathbf{\text{I}}\mathbf{5})$ to cleave the C–O bond and release water is, as seen for catalyst 1⁺, more favorable for the reduction-first pathway under an applied potential of Φ = −1.82 V versus the Fc^0/+ couple (Fig. S9 and S10, ESI†). More importantly, as seen in ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$, the imidazolium moieties in ${\mathbf{2}}_{\mathbf{\text{C}}\mathbf{5}}^{+}$ and ${\mathbf{3}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$ interact with the proton source to assist the C–O bond cleavage step. Again, these interactions are weaker in going from 1⁺ to 3⁺ due to the substituents on the imidazolium ligands (Fig. S11, ESI†), as mirrored by the second-order perturbation interaction analyses of the C–O bond cleavage transition states (Table S18, ESI†). We note that the selectivity for CO₂RR over HER using ${\mathbf{2}}_{\mathbf{\text{C}}\mathbf{5}}^{+}$ and ${\mathbf{3}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$ was also considered, and our study implies that the formation of the metal-hydride species required an activation energy of at least 19.6 kcal mol⁻¹, meaning that these catalysts are also selective for CO₂ fixation, as observed experimentally.³⁰

Based on the computed free energy profiles, the predicted TOFs for ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$, ${\mathbf{2}}_{\mathbf{\text{C}}\mathbf{5}}^{+}$, and ${\mathbf{3}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$ for CO₂RR using the energy span model were considered under an applied potential of Φ = −1.82 V versus the Fc^0/+ couple (Fig. 12). In this case, the calculated TOFs for all three catalysts are, respectively, 5.8 × 10¹ s⁻¹, 2.4 × 10¹ s⁻¹ and 1.6 × 10¹ s⁻¹. These values agree with the experimental data in terms of catalytic activity: ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}>{\mathbf{2}}_{\mathbf{\text{C}}\mathbf{5}}^{+}>{\mathbf{3}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$. Our study proposes that the functional groups at the C2 and C4/5 positions of the imidazolium moiety directly result in the catalytic performance 1⁺ > 2⁺ > 3⁺ observed experimentally for CO₂-to-CO conversion using H₂O as the proton source.

Fig. 12.

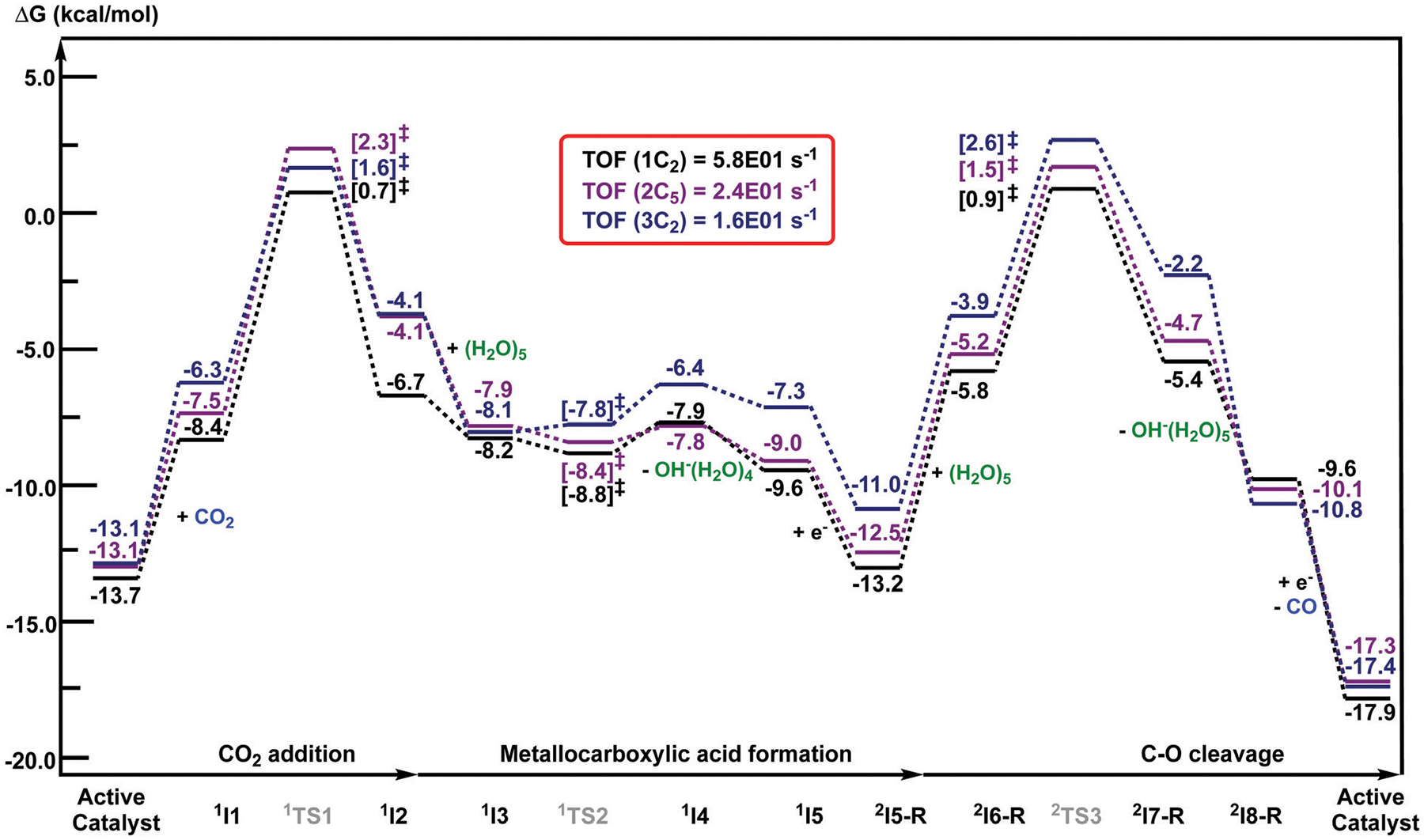
Computed free energy (kcal mol⁻¹) profiles of one catalytic cycle for CO₂-to-CO conversion using ${\mathbf{1}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$, ${\mathbf{2}}_{\mathbf{\text{C}}\mathbf{5}}^{+}$, ${\mathbf{3}}_{\mathbf{\text{C}}\mathbf{2}}^{+}$ in the presence of H₂O as the proton source. All computed Gibbs free energies are reported with respect to the separated reactants at an applied potential of Φ = −1.82 V versus the Fc^0/+ couple.

Conclusion

Density functional theory (DFT) calculations were employed to probe the electronic structure and reactivity of imidazolium-functionalized manganese bipyridyl tricarbonyl electrocatalyst [Mn[bpyMe(ImMe)](CO)₃Br]⁺ (1⁺) for the CO₂ reduction reaction (CO₂RR) over the hydrogen evolution reaction (HER) in the presence of H₂O as the proton source. The selectivity for CO₂RR over HER results from a higher activation energy for forming the manganese dihydrogen intermediate before H₂ release. The calculated TOF for CO₂RR is four orders of magnitude larger than for HER under an applied potential of Φ = −1.82 V versus the Fc^0/+ couple, consistent with the CPE experiments that indicate no hydrogen was obtained. For CO₂ fixation, the TOF determining intermediate (TDI) corresponds to the doubly reduced active catalyst, which is best described as a manganese(0) center that couples ferromagnetically with one unpaired electron in the π* orbital of the bipyridine ligand. On the other hand, the metal-hydride species, 1_C2(I11-R), is the TDI for HER. Furthermore, different configurations and substituents at the C2 and C4/C5 positions of the imidazolium moiety were considered to tune catalysis for CO₂RR by computing the reaction profiles for [Mn[bpyMe(ImMe₂)](CO)₃Br]⁺ (2⁺) and [Mn[bpyMe(ImMe₄)](CO)₃Br]⁺ (3⁺). Our second-order perturbation analyses indicate that the stronger hydrogen bonding-like interaction at the C2 position in 1⁺ contributes to the higher catalytic activity with respect to 2⁺ and 3⁺, in agreement with the experimental results. We believe that our approach shows great potential for the future design of novel molecular systems for selective CO₂ fixation in the presence of Brønsted acids.