Abstract
Lanthanides in the trivalent oxidation state are typically described using an ionic picture that leads to localized magnetic moments. The hierarchical energy scales associated with trivalent lanthanides produce desirable properties for e.g., molecular magnetism, quantum materials, and quantum transduction. Here, we show that this traditional ionic paradigm breaks down for praseodymium in the tetravalent oxidation state. Synthetic, spectroscopic, and theoretical tools deployed on several solid-state Pr4+-oxides uncover the unusual participation of 4f orbitals in bonding and the anomalous hybridization of the 4f1 configuration with ligand valence electrons, analogous to transition metals. The competition between crystal-field and spin-orbit-coupling interactions fundamentally transforms the spin-orbital magnetism of Pr4+, which departs from the Jeff = 1/2 limit and resembles that of high-valent actinides. Our results show that Pr4+ ions are in a class on their own, where the hierarchy of single-ion energy scales can be tailored to explore new correlated phenomena in quantum materials.
Subject terms: Magnetic properties and materials, Crystal field theory, Electronic properties and materials
Trivalent lanthanides are typically described using an ionic picture that leads to localized magnetic moments. Here authors show that the “textbook” description of lanthanides fails for Pr4+ ions where the hierarchy of single-ion energy scales can be tailored to explore correlated phenomena in quantum materials.
Introduction
The electronic structure of lanthanide and actinide materials inherits on-site correlations and unquenched orbital degrees of freedom from atomic f-electron states. In the most stable trivalent oxidation state (Ln3+), the core-like 4f orbitals are usually only weakly perturbed by the crystalline environment1. Yet, the energetic splitting of the otherwise 2J + 1 fold-degenerate (free-ion) ground-state yields rich physics and applications. For example, Ln3+ insulators can host anisotropic magnetic moments with effective spin-1/2 character (Jeff = 1/2) that are promising to stabilize entangled states in quantum magnets2,3. Metallic 4f and 5f systems also display a wealth of quantum phenomena rooted in the hybridization between localized f-electrons and conduction d-electrons such as the Kondo effect, valence fluctuations, correlated insulators, and unconventional superconductivity4,5.
In rare instances, Ce, Pr, Tb, (and less definitively Nd, and Dy) ions exist in a high, formally tetravalent, oxidation state, i.e., Ce4+ (4f0), Pr4+ (4f1), and Tb4+ (4f7)6,7. Although covalent metal-ligand interactions involving the 4f shell are generally weak in Ln3+ systems8,9, this paradigm breaks down for Ln4+ as 4f orbitals directly participate in bonding and hybridize with the valence orbitals of the ligands (e.g., the 2p states for oxygen) analogous to transition metals. A high oxidation state and strong 4f covalency are expected to significantly impact the redox, electronic, and magnetic properties of these systems, but, surprisingly, only a few Ln4+ insulators have been studied in detail to date10,11. As Ce4+ is nominally non-magnetic and Tb4+ has a half-filled 4f shell, the one-electron 4f1 configuration of Pr4+ makes it unique to search for new quantum phenomena at the nexus of strong electronic correlations, quantum magnetism, and spin-orbital entanglement.
The emergence of an insulating state in PrBa2Cu3O6+δ (PBCO)—a compound obtained by substituting Y by Pr in the high-Tc superconductor YBa2Cu3O6+δ (YBCO), and valence fluctuations driven metal-insulator transitions in Pr-containing complex oxides—epitomizes such anomalous behavior. In PBCO, the significant Pr-4f/O-2p covalency (Fehrenbacher-Rice hybridization) drives a mixed-valent state for Pr ions that competes with Cu-3d/O-2p hybridization (Zhang-Rice) and dramatically suppresses superconductivity in favor of local magnetism12. In Pr containing complex oxides like (Pr1−yYy)1−xCaxCoO3−δ and Pr1−xSrxCoO3, valence transition from Pr4+ to Pr3+ drives a spin state/metal-insulator transition, making them attractive for oxide-based electronics13–15. This observation stimulated early experimental and theoretical work to understand the magnetism of cubic Pr4+ oxides such as PrO2 and BaPrO310,11. More recently, the edge-sharing PrO6 octahedral in Na2PrO3 have attracted attention to stabilize antiferromagnetic Kitaev interactions between Jeff = 1/2 moments16. But much like in PrO211, the hallmark of Na2PrO3 magnetism is the unusually large crystal field (CF) splitting ΔCF ≥ 230 meV that competes with spin-orbit coupling (SOC) ζSOC ≈ 100 meV17. The competition between CF and SOC yields drastically different single-ion and exchange properties than expected in the ΔCF ≪ ζSOC limit where Jeff = 1/2 moments usually form, as illustrated in Fig. 1a. The most noticeable consequences for Na2PrO3 are the low effective magnetic moment with g ≈ 1 and the surprisingly large Jex ≈ 1 meV exchange interactions17. The precise mechanisms that endow Pr4+ ions with these unusual properties are poorly understood.
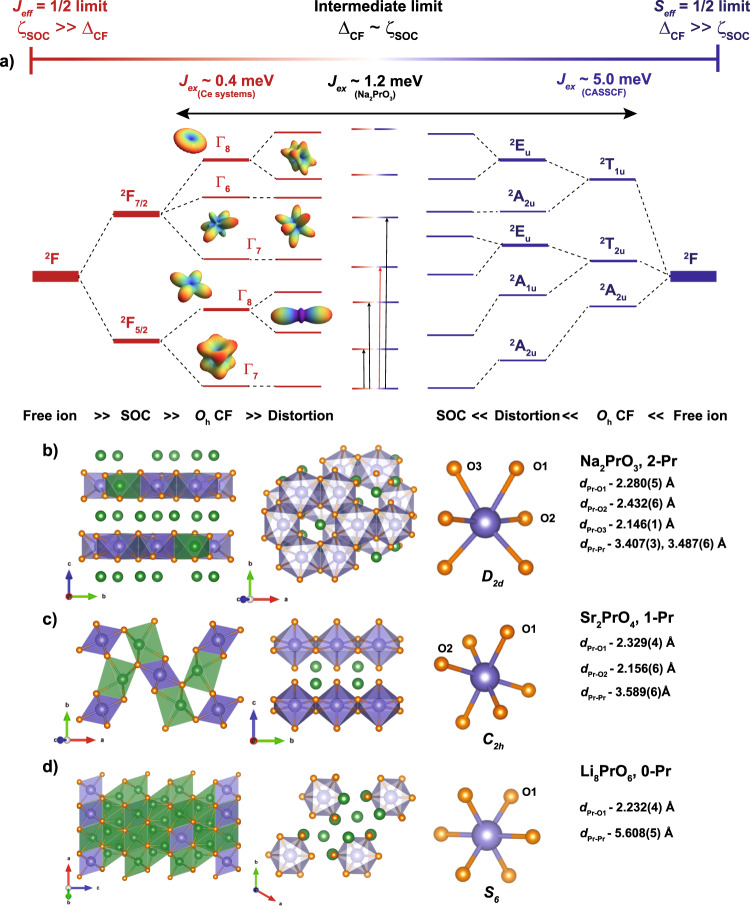
Fig. 1. Competing interactions in Pr4+ oxides.
a Hierarchy of single-ion energy scales for Pr4+ ions in octahedral oxygen environments starting from a 2F, (S = 1/2, L = 3) free-ion state. For spin-orbit coupling (SOC) as the dominant energy scale (Jeff = 1/2 limit, left, brown), the low-symmetry crystal field (CF) lifts the degeneracy of the ground-state 2F5/2 and excited 2F7/2 multiplets into seven Kramers doublets (KDs, with selected radial squared wave-functions represented). For approximate Oh symmetry, the Γ7 doublet, in the basis, is given by , where (See SI). For CF as the dominant energy scale (Seff = 1/2 limit, right, blue), SOC and distortion from Oh symmetry lift the 2A2u ground state and the triply degenerate 2T2u and 2T1u excited states into seven KDs. The ground-state doublet is given in the basis by , where and for the doublet62 (See SI). In the intermediate limit, the competition between ΔCF and ζSOC scales in Pr4+ yields seven KD (indicated by the mix of brown/blue lines) with magnetic properties that are distinct from the Jeff = 1/2 and Seff = 1/2 limits, such as large magnetic super-exchange achievable by tuning the ligand field. b–d Crystal structure, magnetic lattice dimensionality, and Pr4+ coordination environment for the oxides studied in this work: Na2PrO3 (2-Pr), Sr2PrO4 (1-Pr), and Li8PrO6 (0-Pr), respectively.
In this work, we focus on the microscopic mechanisms that underpin the electronic and magnetic behavior of Pr4+ materials comprising octahedral [PrO6]8− units. We examine a series of insulating oxides with decreasing order of lattice dimensionality: quasi-2D layers in Na2PrO3 (2-Pr, Fig. 1b, ref. 18) and quasi-1D chains in Sr2PrO4 (1-Pr, Fig. 1c, ref. 19) to understand magnetic exchange and the role of Pr-4f/O-2p hybridization, and quasi-isolated “0D” PrO6 octahedra in Li8PrO6 (0-Pr, Fig. 1d, ref. 20) to understand the intrinsic behavior of the [PrO6]8− moiety without the complication of magnetic exchange interactions. Using inelastic neutron scattering (INS) and infrared magnetospectroscopy (IRMS), we demonstrate that the magnetic ground-state of Pr4+ ions systematically deviates from the Jeff = 1/2 limit and can be understood from an intermediate coupling regime where significant admixture of nominally excited J-states enter the ground-state wavefunction. X-ray magnetic circular dichroism (XMCD) at the Pr-M4,5 edge strengthens this picture and elucidates the mechanism behind the low effective magnetic moments of Pr4+ ions. Oxygen K-edge and Pr M4,5-edge x-ray absorption spectroscopy (XAS) evidences Pr-4f/O-2p hybridization with a degree of Pr-O covalency influenced by the symmetry of the [PrO6]8− moiety. These results are supported and explained by first-principles calculations. Taken together, this study establishes Pr4+ ions as an important building block to design quantum magnetic behavior distinct from trivalent lanthanides. Furthermore, the study demonstrates that the competition between energy scales in the [PrO6]8− unit is reminiscent of 4d and 5d transition metals21, and can serve as a simplification of 5f1 actinide systems for which ΔCF, ζSOC and on-site Hubbard interaction U strongly compete22,23.
Results
Crystalline powder samples of 0-Pr, 1-Pr, and 2-Pr were synthesized using solid-state reactions and phase purity was confirmed using powder X-ray diffraction (See Methods and Supplementary Methods 1,2). These materials incorporate low symmetry, but close-to-octahedral [PrO6]8− units with D2d symmetry in 2-Pr (C2/c space group, Fig. 1b), C2h in 1-Pr (Pbam space group, Fig. 1c), and S6 in 0-Pr ( space group, Fig. 1d). 0-Pr contains spatially isolated PrO6 octahedral with the nearest-neighbor Pr-Pr distance of d ≈ 5.6 Å, which is significantly longer than d ≈ 3.5 Å in 1-Pr and 2-Pr, and sufficient to effectively magnetically isolate the [PrO6]8− units.
Broadband INS measurements were used to probe the CF states accessible to the dipole selection rule. Given that Pr4+ is a 4f1 Kramers ion (isoelectronic to Ce3+), the standard approach starts from a 2F free-ion manifold split by SOC into J = 5/2 and J = 7/2 multiplets. For a six-oxygen environment with Oh symmetry, the CF further splits the 2F5/2 multiplet into a doublet ground-state (Γ7) and an excited quartet (Γ8), and the 2F7/2 multiplet into two doublets ( and Γ6) and a quartet (). Any deviation from Oh symmetry, as is the case for our materials (see Fig. 1), splits the quartets and yields seven Kramers doublets (KDs). Thus, the magnetic properties of Pr4+ ions in the hypothetical ΔCF ≪ ζSOC limit are dominated by the Γ7 doublet ground-state, which is spanned by pseudospin variable associated with an effective angular momentum Jeff = 1/2. The wave function of the Γ7 doublet is well-known16 and can be written in either or basis (see Fig. 1a and SI).
However, as ζSOC ≈ ΔCF for Pr4+, the simple Jeff = 1/2 picture breaks down. Indeed, INS on 0-Pr readily reveals an intense magnetic signal at meV which we assign to the first CF excitation, see Fig. 2a. This energy is 2.5 times larger than reported for isoelectronic Ce3+ in KCeO224,25, and to the best of our knowledge, this is the largest first CF excited state observed for a lanthanide ion. Given the uncommonly large ΔCF, modeling the single-ion properties of 0-Pr requires an intermediate coupling approach11 that uses the complete set of 14 basis states and diagonalizes the single-ion CF Hamiltonian for a fixed value of the spin-orbit interaction ζSOC (see Methods and Supplementary Note 1 for definitions). The above single-ion CF Hamiltonian is written in a truncated symmetry basis to avoid over-parametrization and treat all materials on equal footing (see Methods). Irrespective, it is impossible to constrain the parameters of solely using the one observed excitation. Thus 1-Pr is examined first because the PrO6 octahedra further depart from ideal symmetry and is likely to present a richer spectrum in INS.
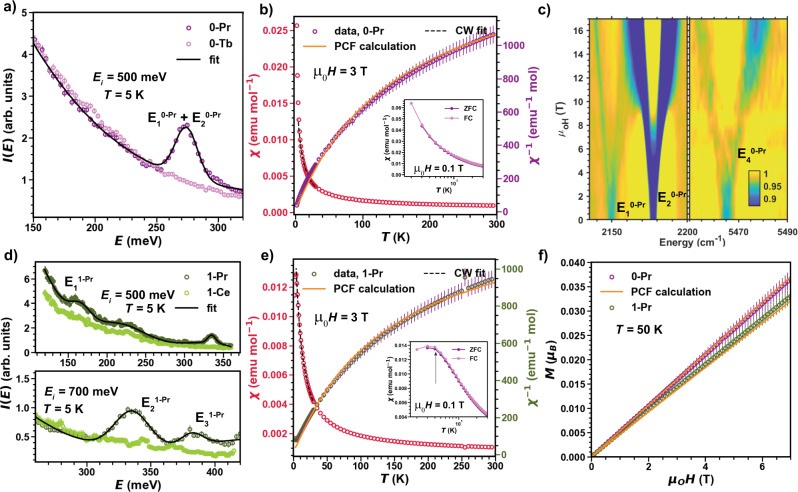
Fig. 2. Crystal field excitations and magnetic properties in Pr4+ oxides.
a, d Energy-dependent neutron-scattering intensity at low temperature integrated into the range 6 < Q < 7 Å−1 for several neutron energies and for 1-Pr (Sr2PrO4) and 0-Pr (Li8PrO6), respectively. b, e Magnetic susceptibility (χ(T)) and inverse susceptibility (χ(T)−1) data measured under μ0H = 3 T. Also plotted is a CF model and a Curie–Weiss analysis in the temperature range 4 < T < 40 K that yields K. The CF model calculations were carried out in Stevens operator formalism using the PYCRYSTALFIELD package58 with 14 basis states to account for intermediate coupling. The inset shows macroscopic magnetic behavior under an applied field of μ0H = 0.1 T. 1-Pr exhibits an AFM order with a pronounced peak in χ(T) with no splitting between ZFC and FC. c Normalized IR transmission spectra as a function of applied magnetic field for 0-Pr. The blue color indicates the area with intense CF transitions, while yellow corresponds to the flat line. The experimental data were taken at 5 K and normalized to the average spectra as described in Methods. f Isothermal magnetization M(H) at T = 50 K for 0-Pr and 1-Pr plotted together with the CF model. T = 50 K was chosen so that 1-Pr is well above the ordering temperature and free from short-range correlations.
Unlike 0-Pr, INS results on 1-Pr reveal three magnetic excitations at meV, meV, and meV (Fig. 2d); more states than available in the sole J = 5/2 manifold. Although 1-Pr exhibits an antiferromagnetic transition at TN = 3.0 K with a pronounced peak in χ(T) (Fig. 2e), the magnetic susceptibility at μ0H = 3 T above T > 40 K can be used to further constrain the parameters of the single-ion CF Hamiltonian. To proceed, is diagonalized with fixed ζSOC = 112 meV (free-ion value) and the CF parameters fit to the observed INS energies and magnetic susceptibility data (see Methods and Supplementary Note 1). This yields a model Hamiltonian that reproduces the isothermal magnetization at T = 50 K (Fig. 2f) and predicts an unusually small powder-averaged g factor and an effective moment /Pr comparable to the value extracted from a Curie–Weiss fit /Pr (Fig. 2e).
Having established an approach to model the single-ion Hamiltonian for Pr4+, 0-Pr is examined and employ IRMS measurements conducted up to 17.5 T. The normalized IR spectra reveal three field-dependent features around meV, meV, and meV (Fig. 2c) that can be associated with magnetic dipole allowed CF transitions from the ground-state doublet. The distinct features at and —resolved due to the excellent energy resolution of IRMS—correspond to the sole transition observed in INS. The first excited level in 0-Pr is thus a quasi-degenerate quartet (Γ8-like) split by the weak distortion of the PrO6 octahedra from an ideal Oh symmetry. This model is fully supported by ab-initio calculations (multireference CASPT2 + SOC, Methods and Supplementary Note 2), which predicts the quasi-degeneracy of and at 241 and 246 meV, respectively. The 670 meV transition is likely weak in INS and masked by the strong background (recoil intensity observed from hydroxide impurities, <5% in starting materials, see Supplementary Methods 1). The ab-initio calculations assign it as the fourth ground to excited state transition, and further predict a third (IR inactive)26 transition at 396 meV with 2T2u + 2A2u origin. The parameters of are fitted using the same procedure as for 0-Pr (Fig. 2b). The resulting model yields = 0.94, in good agreement with the isothermal magnetization (Fig. 2f), and /Pr consistent with /Pr (Fig. 2b) and first-principles calculations (See Discussion). Analysis of the INS spectrum of 2-Pr leads to similar conclusions17.
Analysis of the single-ion physics of these three materials therefore suggests that the ground-state wavefunction of Pr4+ systematically deviates from the Γ7 doublet expected in the Jeff = 1/2 limit. For example, the ratio of to basis states (parametrized by (A2/B2), see Fig. 1 caption and Methods for Definition and Supplementary Tables 5–7 for full wavefunction) changes from 2.6 for the doublet to 0.53, 2.13, and 1.51 for the ground-state doublet of 0-Pr, 1-Pr, and 2-Pr, respectively. When recast in the basis, our analysis suggests that intermediate coupling mixes and states into the ground doublet, leading to an increased character for the ground-state wavefunction (see Supplementary Note 1).
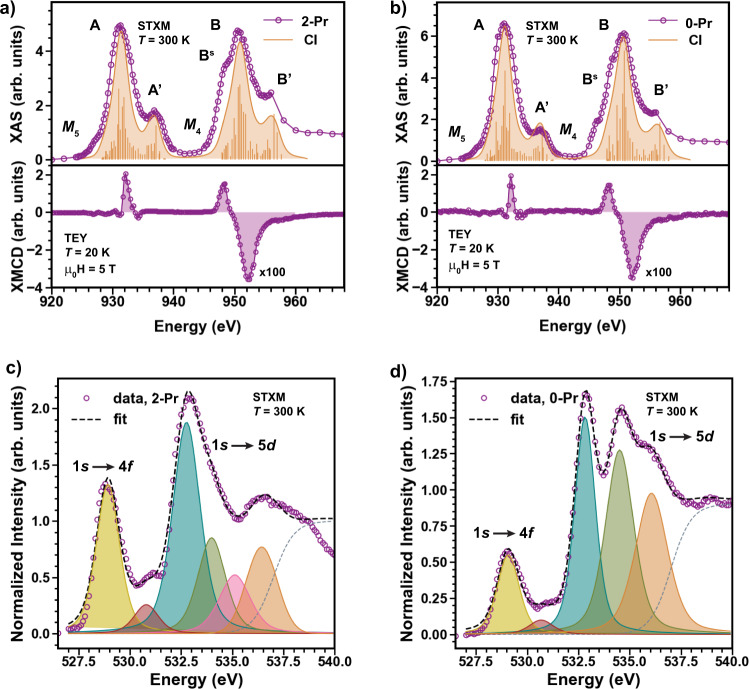
Probing the density of electronic states around the 4f level, XAS (see Methods) provides definitive spectroscopic evidence of this hypothesis and further elucidates the origin of the large ΔCF. The M5 (3d5/2 → 4f7/2 and 4f5/2) and M4 (3d3/2 → 4f5/2) edges for 2-Pr and 0-Pr are shown in Fig. 3a, b. The splitting between the Pr M5 edge at 931 eV and M4 edge at 951 eV originates from SOC within the 3d core-holes. The M5,4 edges for both 0-Pr and 2-Pr show intense main peaks (labeled A and B) followed by higher-energy satellites ( and ) raised by ≈5 eV, and a smeared shoulder (labeled BS) starting ≈3 eV below the main peaks. For a 4f1 ion with a ground-state wavefunction described by a pure J-multiplet, isotropic M5,4 edges are expected27 as predicted by the Wigner–Eckart theorem (Fig. S4). Thus, the complex spectral lineshapes observed in 0-Pr and 2-Pr, which resemble previous observations for PrO228 (see Supplementary Figs. 4,5), are direct evidence for the mixing of 2F7/2 and 2F5/2 multiplets in the ground and excited states of our compounds. This analysis is corroborated by the branching ratio (BR) , evaluated from the total spectral weight under all M5 or M4 peaks, with values of 0.445(17) (2-Pr), 0.443(10) (0-Pr), and 0.453(6) (PrO2). These values are less than ≈0.50 reported for ionic Ce3+ systems27,28 (a BR of ≈0.5 also applies for an ionic Pr4+ system with no hybridization, as shown in Fig. S4).
Fig. 3. Fingerprints of Pr-4f/O-2p hybridization from X-ray scattering spectra.
a, b Isotropic XAS (top) and XMCD (bottom) spectra at the Pr M5 and M4 edges for 2-Pr (left) and 0-Pr (right), respectively measured using the Scanning Transmission X-Ray Microscope (STXM) mode (XAS, μ0H = 0 T and T = 300 K) and the total electron tield (TEY) mode (XMCD, μ0H = 5 T and T = 20 K). For the XAS spectra, first-principle calculations (CI under AIM framework) are shown as orange sticks with Gaussian and Lorentzian broadening. For the XMCD spectra, the integration range for the sum-rule analysis is shown as a purple shaded region. c, d Isotropic XAS spectra at the oxygen K edge for 2-Pr (left) and 0-Pr (right), both measured in STXM mode (T = 300 K). The peak corresponding to Pr-4f/O-2p hybridization is shown in yellow. For comparison, reference data on PrO228 is shown in Table. S2 and Fig. S4 and S8.
The complex M5,4 lineshapes and multiplet mixing in 4f1 systems have previously been ascribed to electronic hybridization, i.e., covalent bonding, between 4f and O-2p states27,29. In the charge-transfer limit (Zaanen–Sawatzky–Allen (ZSA) scheme30), the electronic ground-state of Pr4+ is a superposition where is a hole in the O 2p band. Configuration-interaction (CI) calculations using the Anderson-impurity model (AIM)31,32 were carried out to understand the impact of 4f covalency on the M5,4 XAS spectra of the subject compounds. Within this framework, the initial and final states include the combination of & , and & , respectively (see Methods). In the limit of vanishing hybridization (V → 0), the energy difference between initial configurations is ΔEg = 2.0 eV (2-Pr) and 3.0 eV (0-Pr), and between final states is ΔEf = 0.5 eV (2-Pr) and 1.5 eV (0-Pr). Calculations for a realistic hybridization agree well with the experimental data (Fig. 3a, b) and allows to estimate the fraction of 4f1 and 4f2 configurations in to be 69–31% for 2-Pr, and 75–25% in 0-Pr; i.e., 0-Pr is the least hybridized system. The estimated contributions to in 2-Pr are similar to the values extracted for PrO2 (see Fig. S5)28. The smaller hybridization in 0-Pr relative to both 2-Pr and PrO2 is evident theoretically from the increased ΔEg and experimentally from the more dominant main peak at both edges. Due to the comparable energy scales of ΔEg ≈ Vg, Pr4+ oxide systems are thus strongly correlated insulators in the charge-transfer limit (Uff ≫ ΔEg) and require a quantum many-body description for the ground state. Indeed, these systems behave similar to CeO2 and the spectral features are describing ground and excited state charge transfer33.
The weak magnetic moment observed for the Pr4+ ion can also be understood directly from XAS. The XMCD spectra at the Pr M5,4 edge (See Methods) reveal sizeable dichroism (Fig. 3a (2-Pr) and 3b (0-Pr)). Quantitative analysis using sum rules (see Supplementary Note 1) allows for the extraction of the orbital μo = −〈Lz〉μB, spin (μs = −2〈Sz〉μB, and magnetic dipole 〈Tz〉 contributions to the total moment μt)34 (see Methods, note that 〈Tz〉 ≠ 0 reflects the departure from spherical symmetry for μs)). Applying the orbital sum-rule yields μo = 0.34(5)μB (2-Pr) and 0.33(7)μB (0-Pr). The measured absolute macroscopic magnetization yields μt = 0.028(4)μB (2-Pr) and 0.044(3)μB (0-Pr) at μ0H = 5 T and T = 20 K, and in turn yields μs = − 0.31(9)μB (2-Pr) and − 0.29(10)μB (0-Pr) based on μtotal = μspin + μorbital. These values correspond to ∣〈Tz〉/〈Sz〉∣ = 0.40(8) (2-Pr) and 0.38(1) (0-Pr) and ∣〈Lz〉/〈Sz〉∣ = 2.17(6) (2-Pr) and 2.29(9) (0-Pr); the latter is significantly lower than expected for a free 4f1 ion35 but resembles 5f–c hybridized uranium systems36,37 and is usually attributed to 4f electron delocalization in lanthanides. Despite a low bulk magnetic moment, XMCD data reveals the existence of sizable spin and orbital moments with a reduced ∣〈Lz〉/〈Sz〉∣ ratio that provides a fingerprint for Pr-4f/O-2p hybridization in Pr4+ systems.
Finally, to gain ligand-based information about Pr-4f/O-2p hybridization, O K-edge XAS38 were acquired. The spectra for 2-Pr and 0-Pr, Fig. 3c,d, reveal strong features in the 532.8 to 536 eV range attributed to excitations from the 1s shells of the ligand to states with Pr-5d and O-2p character. These features are a measure of the 5d-covalency of the Pr–O bond and show that nominally unoccupied 5d orbitals take part in covalent bonding39. The splitting of the 5d states is estimated to be 3.67(11) eV in 2-Pr and 3.61(4) eV in 0-Pr and compares well with the value calculated for PrO2 (≈3.6 eV, see Fig. S3)28. Contributions from Pr-6sp states cannot be entirely neglected in the 5d-driven region40. More subtle features common to both 2-Pr and 0-Pr include pre-5d-edge peaks at near ≈529 and ≈530.7 eV (labeled as 1s → 4f). These pre-edge peaks are a signature of strong Pr-4f/O-2p hybridization in the ground state () because they reflect transitions from the O 1s-core states to 2p-hole states of the oxygen in the narrow 4f-dominated bands. These low-energy pre-edge features are characteristic of Ln4+ ions; if at all present in spectra of Ln3+ systems39, they are quite weak. The integrated intensities of the 1s → 4f peaks is 3.4(1) and 2.5(1) larger for PrO2 and 2-Pr, respectively, than for 0-Pr. This result indicates that 0-Pr has the least Pr-4f/O-2p hybridization in good accord with the Pr M5,4 edge spectra. Overall, the presence of pre-edge features in the O K-edge XAS spectra confirms 4f covalency in the Pr-O bond and strongly indicates ligand holes induced by Pr-4f/O-2p hybridization40.
X-ray absorption provides unambiguous evidence for the presence of 4f − 2p hybridization. If the character is localized (as in a truly multiconfigurational ground state), it would be reflected as CF excitations corresponding to Pr3+ (usually ≤50 meV)2. It is evident that such CF transitions from localized Pr3+ are not observed in both neutron and IR spectra. The alternative and the most reasonable explanation is that the character is delocalized in the Pr-O bond as is the case for charge-transfer insulator like nickelates41 and cuprates42. This framework is inconsistent with described earlier, where the basis states are pure 4f functions. The hybridized orbitals are analogous to molecular orbitals with significant ligand contribution. Therefore, we use a modified by including an orbital reduction factor43,44 (κ = 0.9) which accounts for metal-ligand hybridization and yields similar results to the original model (see Supplementary Note 1).
Discussion
Taken together, the present experiments point at Pr-4f/O-2p hybridization as the essential microscopic mechanism behind the unusual electronic and magnetic properties of Pr4+ systems. A qualitative understanding of Pr-O bonding is enabled by ab-initio calculations (CASPT2/CASSCF+SOC, see Methods and Supplementary Note 2). Considering an isolated [PrO6]8− fragment with perfect Oh symmetry, the 4f atomic orbitals (AOs) can be easily described in the basis. Here, the CF splitting leads to three spin states: a 2A2u ground-state, and two excited 2T1u and 2T2u triply-degenerate states (Fig. 1a). The 2A2u state has a δ-symmetry with respect to surrounding oxygens and thus remains strictly non-bonding. In contrast, the 4f AOs underlying the 2T2u and 2T1u states overlap with oxygen’s 2p atomic orbitals leading to bonding and anti-bonding molecular orbitals (MOs) with π and σ + π character, respectively, about the Pr–O axes (See Fig. S14). When SOC is turned on, Table S10, the ground state corresponds to the admixture 58%2A2u + 42%2T2u (what identifies with the E5/2u term in the Oh double-group symmetry). Departing from Oh symmetry – as relevant for the PrO6 distorted-octahedra of 0-Pr and 2-Pr—lifts the degeneracies of the 2T1u and 2T2u excited states (Tables S11, S12). However, regardless of distortion, the ground state in both 2-Pr and 0-Pr remains solely an admixture of 2A2u and 2T2u states.
The spectroscopy and thermomagnetic measurements are well explained by this model and calculations. For instance, the calculated ∣〈Lz〉/〈Sz〉∣ ≈ 1.8 (See Table S12) is consistent with the XMCD data, and the small Pr4+ magnetic moment can be attributed to self-compensating spin and orbital moments combined with an unusually small ∣〈Lz〉/〈Sz〉∣ that signals a strong reduction of the orbital character in the original Γ7 ground-state doublet. This framework naturally explains the O K edge spectra of 2-Pr and 0-Pr through ligand holes induced by the formation of hybridized T1u2pσ + T2u2pσ+π states. The model also explains why the largest hybridization is observed for PrO2: the eight-, rather than six-, oxygen coordination environment allows the Pr 4f a2u orbital to covalently interact with the O 2p orbitals with σ symmetry, thereby exhibiting enhanced 4f-2p hybridization28. The difference in 4f-2p hybridization between 2-Pr and 0-Pr likely comes from different point-group symmetries for the PrO6 unit and the overall symmetry of the material. It is clear that 4f-2p hybridization can strongly influence single-ion energy scales such as the CF - this phenomenon is directly analogous to the behavior of d-block metals.
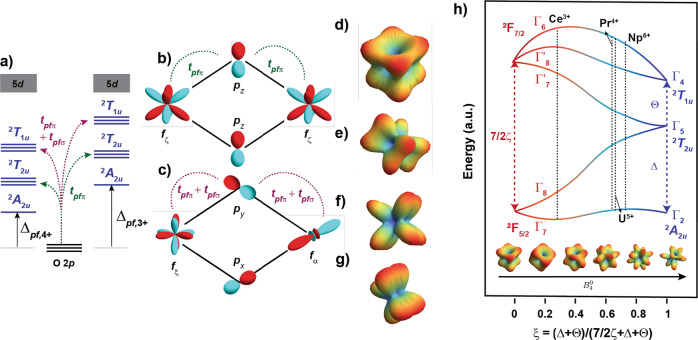
Beyond single-ion properties, Pr-4f/O-2p hybridization leads to unusually large two-ion magnetic exchange interactions. For example, J = 1.2 meV has been reported by some of us on 2-Pr17; a value 2.5 times larger than the typical scale of J ≈ 0.4 meV observed for 4f1 or 4f13 systems such as KCeO2 and NaYbO224,45. The Weiss constant of 1-Pr of around ∣ΘCW∣ = 7 K is also large, especially considering the quasi-1D nature of this system. MO theory can be used to understand these exchange interactions, as shown in Fig. 4a. In the charge transfer limit (Uff ≫ ΔEg), the nearest-neighbor exchange interaction scales as , where tpf is the hopping integral between 4f and 2p orbitals, and ΔEpf is their energy difference (i.e., the ligand to metal charge transfer (LMCT)). The enhancement of magnetic exchange in Ln4+ compounds is likely primarily driven by the reduction of the charge transfer energy ΔEpf, as evidenced by e.g., calculations of [CeCl6]3− (>5 eV) and [CeCl6]2− (~3.3 eV)46. Large tpf hopping and small Δpf implies a large ligand-hole character, consistent with our O K-edge spectra. First-principles calculations on a binuclear [Pr2O10]12− embedded cluster model for 2-Pr (see Supplementary Note 2) quantitatively confirm this picture. In the Seff = 1/2 limit, the spin-singlet minus spin-triplet energy, which identifies with the Heisenberg exchange interaction, yields J = 4.2 meV (See Table S13, Fig. S16). Upon including SOC, the energy splitting among the four lowest levels is ≈1.5 meV. To the extent that this energy separation approximates J, it is in good agreement with the measured value for 2-Pr (1.2 meV). Therefore exchange interactions in Pr4+ materials may change by an order of magnitude (0.3 to 4.2 meV) under changes of the ligand field (Fig. 1a). Similar effects have been observed in high-valent actinides, including U5+ and Np6+47. Inspecting hopping pathways is also informative to comment on the Kitaev (AFM/FM) interactions proposed for 2-Pr through the T2u − p − T1u pathway (Fig. 4b) analogous to the t2g − p − eg process in d5 systems16. While this contribution is small in d5 systems due to the large t2g to eg separation, it is proposed to be larger in 4f1-systems owing to the small CF energy scale16. However, as we have demonstrated, Pr4+ systems exhibit a very large CF splitting (or in other words, the Jeff = 1/2 limit is not adequate), making the T2u − p − T1u pathway energetically less favorable48 than the T2u − p − T2u pathway (Fig. 4c) responsible for the large Heisenberg AFM interaction.
Fig. 4. Microscopic origin of anomalous properties of Pr4+ and a universal model for f1 single-ions.
a Schematic of p and 4f energy levels for Pr4+ and Ce3+. tpfπ (tpf(π+σ)) is the hopping integral between p and 2T2u (2T1u) orbitals. The corresponding pf charge transfer gap is indicated with Δpf,4+ < Δpf,3+. b Sketch of the hopping processes between occupied fζ orbitals mediated by the π interacting 2p orbitals analogous to t2g − p − t2g hopping in d5 systems. c Sketch of the hopping processes between occupied fζ and unoccupied fα orbitals mediated by the π + σ interacting 2p orbitals analogous to t2g − p − eg hopping in d5 systems. d–g Probability density of the ground state KD in ideal Γ7, 2-Pr, 1-Pr, and 0-Pr, respectively and shows the impact of mixing excited states in to the original Γ7 doublet. h Schematic of the splitting of f orbitals as a function of CF (Δ and θ) relative to SOC (ζ). The value of ξ for Pr4+ was calculated from 0-Pr, and the values for Ce3+, U5+, and Np6+ were obtained from ref. 49. Using this as a universal model for f1 ions, Pr4+ is categorized together with the actinides, where the traditional Ln3+ picture breaks down. The figure also shows the evolution of the shape of the Γ7 KD as a function of in the , where . Increasing from ~0 (ζSOC > > ΔCF) yielding an almost perfect Γ7 KD (leftmost figure) to ~2000 (ζSOC < < ΔCF, rightmost figure) and the resultant drastic changes of the nature of the KD. The original nature of the Γ7 KD is retained until the eigenvalue of the Γ8 ≈ 75 meV where Jeff = 1/2 limit still applies.
Finally, and very importantly, the competition between CF and SOC energy scale in Pr4+ systems resembles that in high-valent actinide systems such as U5+ and Np6+ for which a CF energy scale as large as ≈800 meV is possible49,50. The chemistry and physics of high-valent actinides is further complicated by an extra competition between Coulomb repulsion, CF, and SOC51,52 leading to the dual nature of 5f electrons53. In order to develop a universal description for f1 single-ions, we argue that Pr4+ systems can facilitate the study of the delicate balance of various competing interactions in the absence of competing Coulomb repulsion. To showcase that idea, we use the model established by ref. 50 where, the CF transitions for a f1 ion in an ideal Oh symmetry can be written as a function of two CF parameters Δ and θ, and ζSOC, as shown in Fig. 4f. Using this framework and our experimentally determined values for 0-Pr, we calculate the parameter for Pr4+. When compared with other f1 ions, including Ce3+, U5+, and Np6+ (see Fig. 4h and refs. 49,54), it is evident that Pr4+ lies closer to U5+ than Ce3+. Qualitatively, the observed trend can be generalized by a simple f-orbital bonding picture that puts hybridization with the ligands np-orbitals as the key microscopic phenomenon leading to an enhanced CF energy scale.
In summary, our work elucidated the mechanisms behind the anomalously large CF energy scale in Pr4+ systems and discussed how exotic magnetic and electronic properties emerge as a result. The covalent character of the Pr–O bond plays a key role in determining the single-ion and macroscopic physics in Pr4+ compounds, similar to familiar systems such as cuprates and nickelates. It is in sharp contrast to Ln3+ systems for which, conventionally, the metal-ligand bond is described using an ionic picture. While the focus of this study has been oxides, Pr4+ materials do exist as fluorides which require rigorous synthetic conditions using pure F2 gas. The ability to stabilize Pr in the unusually high 4+ oxidation state demonstrates that there is a rich chemical space still to be explored beyond fluorides and oxides for designing new quantum materials, including mixed-anion materials. Our results define a strategy to design and control quantum materials by tuning the Pr–O covalency through site symmetry and ligand identity by moving to softer donors like S or Se. The inadequacy of the Jeff = 1/2 limit shows us how to change the fabric of spin-orbit entangled single-ion states to stabilize exotic exchange Hamiltonians or to develop universal models to understand the physics of high-valent actinides. Pr4+-based systems offer the rare possibility to tune the hierarchy of single-ion energy scales, as well as the p and f hole density, which may be harnessed to design new correlated phenomena in quantum materials.
Methods
Material synthesis
Na2LnO3 (1-Ln, Ln = Ce, Pr) were synthesized using established procedures18. Polycrystalline powder samples of Sr2LnO4 (2-Ln, Ln = Ce, Pr) and Li8LnO6 (3-Ln, Ln = Pr, Tb) were synthesized using traditional solid-state methods. The samples were fired under a flow of O2 in a tube furnace. The firing was performed at 1100 °C for 24 h. The samples were taken out of the quartz tubes in air and placed into the antechamber of the glovebox as quickly as possible in order to minimize contact with the ambient atmosphere (See SI for details).
Experimental characterizations
PXRD
Laboratory powder X-ray diffraction (PXRD) was collected on a PANalytical X’Pert PRO Alpha-1 diffractometer with Cu Kα source in reflection geometry equipped with a fixed divergence slit of 1/8”, a convergence slit of 1/4” and a working radius of 240 mm. The samples were homogenized by finely grinding them inside the glovebox using an agate mortar for about ~15 min. To avoid the exposure of the sample to atmospheric air, the PANalytical domed sample holder is equipped with stainless steel base and a polycarbonate dome with a 70% X-ray transmission. A 2θ range of 5−85∘ was used with a scan speed of 5 s and a step size of 0.1.
Physical property measurements
The d.c. magnetic susceptibility measurements and isothermal magnetization measurements were made using a Quantum Design MPMS3. The sample was sealed in a plastic capsule on a low-background brass holder.
Neutron-scattering measurements
Inelastic neutron-scattering measurements were carried out on ~8 g of polycrystalline samples of 1-Pr, 1-Ce, 0-Pr, and 0-Tb on the time-of-flight fine-resolution Fermi chopper spectrometer SEQUOIA, at the Spallation Neutron Source, ORNL55,56. The powder samples were enclosed in standard 15-mm diameter cylindrical annular aluminum cans (with 2 mm sample gap) under one atmosphere of 4He at room temperature. All four samples were cooled using a closed-cycle refrigerator reaching a base temperature of T = 5 K. Measurements were carried out using incident neutron energies Ei = 300, 500, 700 meV at T = 5 K. Background and sample holder contributions were measured using empty can measurements. The lattice phonon contributions for 0-Pr and 1-Pr were subtracted by measuring the analogous 0-Tb and 1-Ce, respectively.
STXM O K edge XAS
STXM methodology was similar to that discussed previously28. In an argon-filled glovebox, samples for STXM measurement were prepared by pulverizing the powder compounds and transferring particles to Si3N4 windows. Second windows were placed over the samples to sandwich the particles, and the windows were sealed together with Hardman Double/Bubble epoxy. Single-energy images and O K-edge XAS spectra were acquired using the STXM instrument at the Canadian light source (CLS) spectromicroscopy beamline 10ID-1, operating in decay mode (250 to 150 mA, in a ~0.5 atm He-filled chamber) at a base temperature of T = 300 K. The beamline uses photons from an elliptically polarizing undulator that delivers photons in the 130 to 2700 eV energy range to an entrance slit-less plane-grating monochromator. The maximum energy resolution E/ΔE was previously determined to be better than 7500, which is consistent with the observed standard deviation for spectral transitions of ±0.1 eV determined from the comparison of spectral features over multiple particles and beam runs. For these measurements, the X-ray beam was focused with a zone plate onto the sample, and the transmitted light was detected. The spot size and spectral resolution were determined from the characteristics of the 35 nm zone plate. Images at single energy were obtained by raster-scanning the sample and collecting transmitted monochromatic light as a function of the sample position. Spectra at particular regions of interest on the sample image were extracted from the “stack”, which is a collection of images recorded at multiple, closely spaced photon energies across the absorption edge. Dwell times used to acquire an image at a single photon energy were 2 ms per pixel and spectra were obtained using circularly polarized radiation. The incident beam intensity was measured through the sample-free region of the Si3N4 windows. In order to ensure that the spectra were in the linear regime of Beer–Lambert’s law, particles with an absorption of less than 1.5 OD were used. High-quality spectra were obtained by averaging measurements from multiple independent particles, samples, and beam runs.
STXM Pr M5,4 edge XAS
Measurements at the Pr M5,4-edges were conducted using the STXM instrument at the Canadian Light Source (CLS) spectromicroscopy beamline 10ID-1, operating in top-off mode (250 mA, in a ~0.5 atm He-filled chamber) at a base temperature of T = 300 K. The sample preparation and data acquisition methodology is the same as described above for the O K-edge measurements.
Pr M5,4 edge XMCD
The XAS and XMCD measurements at Pr M5,4-edges were conducted at beamline 4-ID-C of the Advanced Photon Source located at Argonne National Laboratory. XAS and XMCD spectra were collected simultaneously using total electron yield (TEY) and total fluorescence yield (TFY), respectively, with circularly polarized X-rays in a near normal (80∘) configuration using a cryostat reaching a base temperature of T = 20 K. The applied field was along the beam direction and it defines the positive Z direction. The data was obtained at both a zero field and an applied field of μOH = ±5 T. The XMCD spectra were obtained point by point by subtracting right from left circular polarized XAS data. Measurements were taken for both positive and negative applied field directions, and then a difference of these two spectra XMCD = [XMCD(Hz > 0) - XMCD(Hz < 0)] was taken to eliminate polarization-dependent systematic errors. The TFY XAS data is identical to the STXM data described above. However, the TFY XMCD signal is weak and distorted by self-absorption effects. The TEY XAS data is similar to STXM data as well, except the high energy satellite peaks at both M5,4 edges are weak and not as pronounced. Furthermore, the low-energy shoulder at the M4 edge is more pronounced in TEY XAS than in both TFY and STXM. For discussions in the main text regarding M5,4 edge isotropic XAS spectra, only the STXM data is discussed as it minimizes error due to self-absorption, saturation, and surface contamination. However, for our discussions with XMCD, we use the data collected in TEY mode. As noted in Fig. 3, the isotropic XAS was in the top panel and is measured in STXM mode, while the XMCD was at the bottom panel and is measured in TEY.
Infrared magnetospectroscopy
Broadband IR measurements were performed in the Voigt transmission configuration using a Bruker 80v Fourier-transform IR spectrometer. The incident IR light from a global source was guided to the top of the probe inside an evacuated beamline and then delivered to the bottom of the probe through brass light pipes. The sample was located in the middle of two confocal 90o off-axis parabolic mirrors mounted at the bottom of the probe. While the first mirror focuses the IR radiation on the sample, the second mirror collimates the radiation to the short light pipe with a 4K composite Si bolometer at the end. About 25 mg of the powder sample was mixed with KBr inside a glovebox in a 1:1 ratio. The resulting mixture was pressed into 3 mm pellets and was secured by a thin polypropylene adhesive film, and mounted on the brass plate with a clear aperture of 3 mm. The sample was placed at the center of a μ0H = 17.5 T vertical bore superconducting magnet in a helium exchange gas environment, providing the sample temperature of about 5.5 K. IR transmission spectra were collected for 3 min at a fixed magnetic field, changing with 1 T step. All spectra obtained at different magnetic fields were normalized to the same reference spectrum, which is their mean, computed after removing the outlier points at each frequency. Such normalization flattens those spectral features independent of magnetic fields and highlights those absorption peaks that shift as the magnetic field rises.
Crystal field modeling of inelastic neutron scattering (INS)
CF modeling was carried out using the truncated CF Hamiltonian where are the second, fourth, and sixth-order terms and are the corresponding Stevens operator equivalents57 for all three materials studied here. The Stevens operators are expressed in terms of L and Lz. Although the true symmetries of Pr4+ in each system require more parameters based on point-group symmetry, any mixing induced by these parameters would not induce any further loss of degeneracy and hence we choose to parameterize their effects and parameters. This approach was taken in order to minimize over-parametrization while fitting to experimental data. All Hamiltonian diagonalizations were performed using the PYCRYSTALFIELD package58. Fitting was carried out to a combination of eigen-energies extracted experimentally from INS and IRMS and to the temperature-dependent susceptibility data over T > 40 K in order to avoid short-range correlations present at lower temperatures. The final fit results are provided in Supplementary Table 3. The CF models were validated by calculating the isothermal magnetization at T = 50 K. The model calculation of g values for the ground state wavefunction was compared to experimentally determined values from Curie–Weiss fits and first-principles calculations. See Supplementary Note 1 for a detailed description of the fitting procedure. The f electron density plots were obtained using QUANTY59 and plotted using Wolfram-Mathematica60.
The Γ7 KD in the ΔCF < < ζSOC limit is written in the basis as , where . The same Γ7 KD can be written in the basis as , where A = 0.352, B = 0.215, C = 0.454, D = 0.79, yielding . The first two components of the Γ7 KD in (ml = ∓3, ∓2) map onto a linear combination of the , states in basis, while the last components (ml = ±1, ±2) map onto states. For the Γ7 KD, given that ΔCF < < ζSOC, the contributions from the SOC manifold are negligible. As ΔCF ~ ζSOC, non-negligible contributions from the SOC manifold enter the ground-state wavefunction making it impossible to deconvolute the individual contributions from each SOC manifold. Therefore, a better description of mixing can be obtained by looking at the ratios and . Within this framework, irrespective of the symmetry at the metal center, for a six-coordinate system, the ground state wavefunction is always a linear combination of ml = ±1, ±2, ∓3 states. This derives from the 2A2u + 2T2u symmetry (in Oh notation) as described in the main text and predicted by first-principles calculations. The introduction of intermediate coupling, changes only the relative mixtures of ml = ±1, ±2, ∓3 states and does not introduce any new admixture into the ground state wavefunction. The relative change in a mixture can be viewed as introducing and states and increasing the amount of character in the ground state. This is clearly evident in the toy model established in Supplementary Note 1.
Multiplet modeling of X-ray absorption spectroscopy (XAS)
Multiplet calculations were implemented using the original code written by Cowan (ref. 32) and further developed by de Groot based on AIM. The multi-electron configuration in the ground and the final states was implemented using a charge-transfer methodology analogous to nickelates and cuprates. For all calculations, a Gaussian broadening of 0.45 eV was applied to account for instrumental broadening and Lorentzian broadening of 0.3 and 0.6 eV were applied to the M5 and M4 edges, respectively. The model parameters had the following values for both 1-Pr and 3-Pr: Uff ~14.1 eV, Ufc ~8.5 eV, eV, and eV where Uff and Ufc are the 4f − 4f Coulomb interaction and the core-hole potential acting on the 4f electron, respectively. In the limit of vanishing V → 0, the difference between the two configurations in the ground state was ΔEg = ϵf − ϵn = 2.0 eV (1-Pr) and 3.0 eV (3-Pr), and ΔEf = ϵf − ϵn + Uff − Ufc = 0.5 eV (1-Pr) and 1.5 eV (3-Pr), where ϵf and ϵn are one-electron energies of Pr 4f and O 2p levels and V is the hybridization energy between atomic like localized 4f states and delocalized O 2p states which determines the mixing between the multi-electron configurations. Hybridization energy in the ground state (Vg) was set to 1.4 eV (1-Pr and 3-Pr), and final state (Vf) was set to 1.4 eV (1-Pr) and 1.8 eV (3-Pr).
Ab-initio calculations
Without symmetry restrictions, wavefunction theory (WFT) calculations were performed within a commonly applied two-step spin-orbit coupled configuration-interaction formalism using OpenMolcas61. WFT calculations (See SI for more details) were performed on an isolated PrO cluster and on embedded cluster models for Li8PrO6 and Na2PrO3. Additional calculations were performed with a binuclear Pr2O embedded cluster model of Na2PrO3. All geometries were extracted from the crystal structures and used without further optimization. A 40 Å sphere of atoms was generated from the crystal structure. An outer 32 Å sphere contained Pr4+, O2−, Na+/Li+ embedding point charges; the inner 8 Å sphere contained the PrO ion treated quantum-mechanically surrounded by Pr4+, O2−, Na+/Li+ pseudocharges represented by ab-initio model potentials (AIMPs). All atoms treated quantum-mechanically were modeled with all-electron atomic natural orbital relativistically contracted basis sets of valence triple-ζ quality (ANO-RCC-VTZP).
Supplementary information
Acknowledgements
We are thankful to Dr. Harry Lane for his insightful discussions. The work of A.R. and H.S.L.P. at Georgia Tech was supported by the Beckman Foundation as part of a Beckman Young Investigator Award to H.S.L.P. The work of J.K. and M.M. at Georgia Tech was supported by the National Science Foundation through Grant No. NSF-DMR-1750186 awarded to M.M. The work of Z.J. at Georgia Tech was supported by the US Department of Energy through Grant No. DE-FG02-07ER46451 awarded to Z.J. Some of this work was performed in part at the Materials Characterization Facility at Georgia Tech, which is jointly supported by the GT Institute for Materials and the Institute for Electronics and Nanotechnology, and is a member of the National Nanotechnology Coordinated Infrastructure supported by the National Science Foundation under Grant No. ECCS-2025462. This research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. Use of the Advanced Photon Source at Argonne National Laboratory was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract DE-AC02-06CH11357. The infrared measurements were performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement No. DMR-1644779 and the State of Florida. The work of D.-C.S. and J.A. at the University at Buffalo was supported by the US Department of Energy, Office of Basic Energy Sciences, Heavy Element Chemistry program, under grant DESC0001136 awarded to J.A. D.-C.S. and J.A. thank the Center for Computational Research (CCR) at the University at Buffalo for providing computational resources. D.-C.S. received research funding from the European Union’s Horizon 2020 Research and Innovation Program under Marie Sklodowska-Curie Grant Agreement No. 899546. D.-C.S. acknowledges infrastructure support provided through the RECENT AIR grant agreement MySMIS no. 127324. Work of J.A.B. and S.G.M at LBNL was supported by the Director, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences of the US Department of Energy (DOE) at LBNL under Contract No. DE-AC02-05CH11231. STXM research described in this paper was performed at the Canadian Light Source, which is supported by the Canada Foundation for Innovation, Natural Sciences and Engineering Research Council of Canada, the University of Saskatchewan, the Government of Saskatchewan, Western Economic Diversification Canada, the National Research Council Canada, and the Canadian Institutes of Health Research.
Author contributions
A.R., M.M., and H.S.L.P. conceived the project, which was led by A.R. and H.S.L.P. A.R. synthesized the samples at Georgia Tech. A.R., J.K., A.I.K., and M.M. performed the neutron-scattering measurements. A.R. and J.K. analyzed the neutron-scattering data. A.R., M.M., and J.K. carried out thermomagnetic measurements. M.O. and Z.J. performed the IR measurements and analyzed the data. J.A.B. and S.G.M. performed STXM XAS measurements and normalized the data. A.R., J.W.F., and H.S.L.P. measured XMCD data. A.R. analyzed the X-ray scattering data. D.-C.S. and J.A. carried out the theoretical calculations and accompanying analyses. A.R., M.M., and H.S.L.P. wrote the manuscript with input from all authors.
Peer review
Peer review information
Nature Communications thanks Andrew Boothroyd and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
The datasets generated and/or analyzed during the current study have been deposited in the Figshare database under the accession code 10.6084/m9.figshare.22626946 and in the Zenodo repository under the accession code 10.5281/zenodo.7932208.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-023-38431-7.
References
- 1.Newman DJ. Theory of lanthanide crystal fields. Adv. Phys. 1971;20:197–256. doi: 10.1080/00018737100101241. [DOI] [Google Scholar]
- 2.Kimura K, et al. Quantum fluctuations in spin-ice-like Pr2Zr2O7. Nat. Commun. 2013;4:1–6. doi: 10.1038/ncomms2914. [DOI] [PubMed] [Google Scholar]
- 3.Gao B, et al. Experimental signatures of a three-dimensional quantum spin liquid in effective spin-1/2 Ce2Zr2O7 pyrochlore. Nat. Phys. 2019;15:1052–1057. doi: 10.1038/s41567-019-0577-6. [DOI] [Google Scholar]
- 4.Coleman P. New approach to the mixed-valence problem. Phys. Rev. B. 1984;29:3035. doi: 10.1103/PhysRevB.29.3035. [DOI] [Google Scholar]
- 5.Lawrence J, Riseborough P, Parks R. Valence fluctuation phenomena. Rep. Prog. Phys. 1981;44:1. doi: 10.1088/0034-4885/44/1/001. [DOI] [Google Scholar]
- 6.Gompa TP, Ramanathan A, Rice NT, La Pierre HS. The chemical and physical properties of tetravalent lanthanides: Pr, Nd, Tb, and Dy. Dalton Trans. 2020;49:15945–15987. doi: 10.1039/D0DT01400A. [DOI] [PubMed] [Google Scholar]
- 7.Meyer, G. & Morss, L. R. Synthesis of Lanthanide and Actinide Compounds Vol. 2 (Springer Science & Business Media, 1990).
- 8.Crosswhite H, Crosswhite H, Carnall W, Paszek A. Spectrum analysis of U3+: LaCl3. J. Chem. Phys. 1980;72:5103–5117. doi: 10.1063/1.439742. [DOI] [Google Scholar]
- 9.Cotton, S. Lanthanide and Actinide Chemistry (John Wiley & Sons, 2013).
- 10.Kern S, Loong C-K, Lander G. Crystal-field transitions in f-electron oxides. Phys. Rev. B. 1985;32:3051. doi: 10.1103/PhysRevB.32.3051. [DOI] [PubMed] [Google Scholar]
- 11.Boothroyd AT, et al. Localized 4f states and dynamic jahn-teller effect in PrO2. Phys. Rev. Lett. 2001;86:2082–2085. doi: 10.1103/PhysRevLett.86.2082. [DOI] [PubMed] [Google Scholar]
- 12.Fehrenbacher R, Rice T. Unusual electronic structure of PrBa2Cu3O7. Phys. Rev. Lett. 1993;70:3471. doi: 10.1103/PhysRevLett.70.3471. [DOI] [PubMed] [Google Scholar]
- 13.Sannigrahi J, et al. First-order valence transition: neutron diffraction, inelastic neutron scattering, and x-ray absorption investigations on the double perovskite Ba2PrRu0.9Ir0.1O6. Phys. Rev. B. 2019;99:184440. doi: 10.1103/PhysRevB.99.184440. [DOI] [Google Scholar]
- 14.Chaturvedi V, et al. Room-temperature valence transition in a strain-tuned perovskite oxide. Nat. Commun. 2022;13:7774. doi: 10.1038/s41467-022-35024-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Leighton C, et al. Coupled structural/magnetocrystalline anisotropy transitions in the doped perovskite cobaltite Pr1−xSrxCoO3. Phys. Rev. B. 2009;79:214420. doi: 10.1103/PhysRevB.79.214420. [DOI] [Google Scholar]
- 16.Jang S-H, Sano R, Kato Y, Motome Y. Antiferromagnetic kitaev interaction in f-electron based honeycomb magnets. Phys. Rev. B. 2019;99:241106. doi: 10.1103/PhysRevB.99.241106. [DOI] [Google Scholar]
- 17.Daum MJ, et al. Collective excitations in the tetravalent lanthanide honeycomb antiferromagnet Na2PrO3. Phys. Rev. B. 2021;103:L121109. doi: 10.1103/PhysRevB.103.L121109. [DOI] [Google Scholar]
- 18.Ramanathan A, Leisen JE, La Pierre HS. In-plane cation ordering and sodium displacements in layered honeycomb oxides with tetravalent lanthanides: Na2LnO3 (Ln= Ce, Pr, and Tb) Inorg. Chem. 2021;60:1398–1410. doi: 10.1021/acs.inorgchem.0c02628. [DOI] [PubMed] [Google Scholar]
- 19.Fiscus JE, zur Loye H-C. Synthesis of Sr2PrO4: a Pr4+ -containing oxide in the Sr2PbO4 structure type. J. Alloys Compd. 2000;306:141–145. doi: 10.1016/S0925-8388(00)00785-4. [DOI] [Google Scholar]
- 20.Wolf R, Hoppe R. Über Li8PrO6 und Li8TbO6 (mit einer bemerkung über Li8CeO6) Z. Anorg. Allg. Chem. 1985;522:39–47. doi: 10.1002/zaac.19855220306. [DOI] [Google Scholar]
- 21.Bahrami F, et al. First demonstration of tuning between the kitaev and ising limits in a honeycomb lattice. Sci. Adv. 2022;8:eabl5671. doi: 10.1126/sciadv.abl5671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhou F, Ozoliņš V, et al. Self-consistent density functional calculations of the crystal field levels in lanthanide and actinide dioxides. Phys. Rev. B. 2012;85:075124. doi: 10.1103/PhysRevB.85.075124. [DOI] [Google Scholar]
- 23.Santini P, et al. Multipolar interactions in f-electron systems: the paradigm of actinide dioxides. Rev. Mod. Phys. 2009;81:807. doi: 10.1103/RevModPhys.81.807. [DOI] [Google Scholar]
- 24.Bordelon MM, et al. Magnetic properties and signatures of moment ordering in the triangular lattice antiferromagnet KCeO2. Phys. Rev. B. 2021;104:094421. doi: 10.1103/PhysRevB.104.094421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Eldeeb M, Petersen T, Hozoi L, Yushankhai V, Rößler U. Energy scales in 4f1 delafossite magnets: Crystal-field splittings larger than the strength of spin-orbit coupling in KCeO2. Phys. Rev. Mater. 2020;4:124001. doi: 10.1103/PhysRevMaterials.4.124001. [DOI] [Google Scholar]
- 26.Gelessus A, Thiel W, Weber W. Multipoles and symmetry. J. Chem. Edu. 1995;72:505. doi: 10.1021/ed072p505. [DOI] [Google Scholar]
- 27.Finazzi M, et al. Direct evidence of the role of hybridization in the x-ray magnetic circular dichroism of α-Ce. Phys. Rev. Lett. 1995;75:4654. doi: 10.1103/PhysRevLett.75.4654. [DOI] [PubMed] [Google Scholar]
- 28.Minasian SG, et al. Quantitative evidence for lanthanide-oxygen orbital mixing in CeO2, PrO2, and TbO2. J. Am. Chem. Soc. 2017;139:18052–18064. doi: 10.1021/jacs.7b10361. [DOI] [PubMed] [Google Scholar]
- 29.Okane T, et al. Magnetic behavior near the boundary of 4f delocalization in ferromagnetic CeRu2Ge2 and paramagnetic CeRu2Si2 observed by Ce M4,5 xas and xmcd. Phys. Rev. B. 2012;86:125138. doi: 10.1103/PhysRevB.86.125138. [DOI] [Google Scholar]
- 30.Zaanen J, Sawatzky G, Allen J. Band gaps and electronic structure of transition-metal compounds. Phys. Rev. Lett. 1985;55:418. doi: 10.1103/PhysRevLett.55.418. [DOI] [PubMed] [Google Scholar]
- 31.Anderson PW. Localized magnetic states in metals. Phys. Rev. 1961;124:41. doi: 10.1103/PhysRev.124.41. [DOI] [Google Scholar]
- 32.Cowan, R. D. The Theory of Atomic Structure and Spectra. (Univ. California Press, 1981).
- 33.Sergentu D-C, Booth CH, Autschbach J. Probing multiconfigurational states by spectroscopy: the cerium XAS L3-edge puzzle. Chemistry. 2021;27:7239–7251. doi: 10.1002/chem.202100145. [DOI] [PubMed] [Google Scholar]
- 34.Thole B, Carra P, Sette F, van der Laan G. X-ray circular dichroism as a probe of orbital magnetization. Phys. Rev. Lett. 1992;68:1943. doi: 10.1103/PhysRevLett.68.1943. [DOI] [PubMed] [Google Scholar]
- 35.Tripathi, S. XMCD Investigation at M4,5Edges of the Rare Earth Elements in High-Performance Permanent Magnet. PhD thesis (Universitat Stuttgart, 2018).
- 36.Finazzi M, et al. X-ray magnetic circular dichroism at the U M4,5 absorption edges of UFe2. Phys. Rev. B. 1997;55:3010. doi: 10.1103/PhysRevB.55.3010. [DOI] [Google Scholar]
- 37.Pedersen KS, et al. : a molecular hexafluorido actinide(IV) complex with compensating spin and orbital magnetic moments. Angew. Chem. Int. Ed. 2019;58:15650–15654. doi: 10.1002/anie.201905056. [DOI] [PubMed] [Google Scholar]
- 38.Frati F, Hunault MO, De Groot FM. Oxygen k-edge x-ray absorption spectra. Chem. Rev. 2020;120:4056–4110. doi: 10.1021/acs.chemrev.9b00439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Altman AB, Pacold JI, Wang J, Lukens WW, Minasian SG. Evidence for 5d − σ and 5d − π covalency in lanthanide sesquioxides from oxygen K-edge x-ray absorption spectroscopy. Dalton Trans. 2016;45:9948–9961. doi: 10.1039/C6DT00358C. [DOI] [PubMed] [Google Scholar]
- 40.Hu Z, et al. O − 2p holes in tetravalent oxides of Ce and Pr and the Fehrenbacher - Rice hybrid in PrBa2Cu3O7−δ. Phys. Rev. B. 1999;60:1460. doi: 10.1103/PhysRevB.60.1460. [DOI] [Google Scholar]
- 41.Medarde ML. Structural, magnetic and electronic properties of perovskites (r= rare earth) J. Phys. Condens. Matter. 1997;9:1679. doi: 10.1088/0953-8984/9/8/003. [DOI] [Google Scholar]
- 42.Walters AC, et al. Effect of covalent bonding on magnetism and the missing neutron intensity in copper oxide compounds. Nat. Phys. 2009;5:867–872. doi: 10.1038/nphys1405. [DOI] [Google Scholar]
- 43.King DM, et al. Molecular and electronic structure of terminal and alkali metal-capped uranium (v) nitride complexes. Nat. Commun. 2016;7:13773. doi: 10.1038/ncomms13773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gerloch, M. & Miller, J. Covalence and the orbital reduction factor, k, in magnetochemistry. Prog. Inorg. Chem.10, 1-47 (1968).
- 45.Bordelon MM, et al. Field-tunable quantum disordered ground state in the triangular-lattice antiferromagnet NaYbO2. Nat. Phys. 2019;15:1058–1064. doi: 10.1038/s41567-019-0594-5. [DOI] [Google Scholar]
- 46.Loble MW, et al. Covalency in lanthanides. an x-ray absorption spectroscopy and density functional theory study of J. Am. Chem. Soc. 2015;137:2506–2523. doi: 10.1021/ja510067v. [DOI] [PubMed] [Google Scholar]
- 47.Magnani N, et al. Superexchange coupling and slow magnetic relaxation in a transuranium polymetallic complex. Phys. Rev. Lett. 2010;104:197202. doi: 10.1103/PhysRevLett.104.197202. [DOI] [PubMed] [Google Scholar]
- 48.Liu H, Chaloupka J, Khaliullin G. Exchange interactions in d5Kitaev materials: from Na2IrO3 to α-RuCl3. Phys. Rev. B. 2022;105:214411. doi: 10.1103/PhysRevB.105.214411. [DOI] [Google Scholar]
- 49.Lukens WW, et al. Quantifying the σ and π interactions between U(V) f orbitals and halide, alkyl, alkoxide, amide and ketimide ligands. J. Am. Chem. Soc. 2013;135:10742–10754. doi: 10.1021/ja403815h. [DOI] [PubMed] [Google Scholar]
- 50.Eisenstein J, Pryce MHL. Theory of the magnetic and spectroscopic properties of neptunium hexafluoride. Proc. R. Soc. A. Math. Phys. Sci. 1960;255:181–198. [Google Scholar]
- 51.Moore K, et al. Failure of Russell - Saunders coupling in the 5f states of plutonium. Phys. Rev. Lett. 2003;90:196404. doi: 10.1103/PhysRevLett.90.196404. [DOI] [PubMed] [Google Scholar]
- 52.Shim J, Haule K, Kotliar G. Fluctuating valence in a correlated solid and the anomalous properties of δ-plutonium. Nature. 2007;446:513–516. doi: 10.1038/nature05647. [DOI] [PubMed] [Google Scholar]
- 53.Booth C, et al. Multiconfigurational nature of 5f orbitals in uranium and plutonium intermetallics. Proc. Natl Acad. Sci. USA. 2012;109:10205–10209. doi: 10.1073/pnas.1200725109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Edelstein, N. M. & Lander, G. H. In The Chemistry of the Actinide and Transactinide Elements. (eds Morss, L. R., Edelstein, N. M. & Fuger, J.) Ch. 21. 2225–2306 (Springer, 2008).
- 55.Granroth, G. et al. Sequoia: a newly operating chopper spectrometer at the SNS. J. Phys. Conf. Ser.251, 012058 (2010).
- 56.Stone MB, et al. A comparison of four direct geometry time-of-flight spectrometers at the spallation neutron source. Rev. Sci. Instrum. 2014;85:045113. doi: 10.1063/1.4870050. [DOI] [PubMed] [Google Scholar]
- 57.Stevens K. Matrix elements and operator equivalents connected with the magnetic properties of rare earth ions. Proc. Phys. Soc. A. 1952;65:209. doi: 10.1088/0370-1298/65/3/308. [DOI] [Google Scholar]
- 58.Scheie A. Pycrystalfield: software for calculation, analysis and fitting of crystal electric field hamiltonians. J. Appl. Crystallogr. 2021;54:356–362. doi: 10.1107/S160057672001554X. [DOI] [Google Scholar]
- 59.Haverkort M, Zwierzycki M, Andersen O. Multiplet ligand-field theory using wannier orbitals. Phys. Rev. B. 2012;85:165113. doi: 10.1103/PhysRevB.85.165113. [DOI] [Google Scholar]
- 60.Wolfram Research, Inc. Mathematica, version 13.2. https://www.wolfram.com/mathematica (2022).
- 61.Aquilante F, et al. Modern quantum chemistry with [Open]molcas. J. Chem. Phys. 2020;152:214117. doi: 10.1063/5.0004835. [DOI] [PubMed] [Google Scholar]
- 62.Willers T, et al. Correlation between ground state and orbital anisotropy in heavy fermion materials. Proc. Natl Acad. Sci. USA. 2015;112:2384–2388. doi: 10.1073/pnas.1415657112. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated and/or analyzed during the current study have been deposited in the Figshare database under the accession code 10.6084/m9.figshare.22626946 and in the Zenodo repository under the accession code 10.5281/zenodo.7932208.